Abstract
Purpose:
To implement a novel, accelerated, 2D radial echo-planar spectroscopic imaging (REPSI) sequence using undersampled radial k-space trajectories and compressed-sensing reconstruction, and to compare results with those from an undersampled Cartesian spectroscopic sequence.
Methods:
The REPSI sequence was implemented using golden-angle view-ordering on a 3T MRI scanner. Radial and Cartesian echo-planar spectroscopic imaging (EPSI) data were acquired at six acceleration factors, each with time-equivalent scan durations, and reconstructed using compressed sensing with total variation regularization. Results from prospectively and retrospectively undersampled phantom and in vivo brain data were compared over estimated concentrations and Cramer-Rao lower-bound values, normalized RMS errors of reconstructed metabolite maps, and percent absolute differences between fully sampled and reconstructed spectroscopic images.
Results:
The REPSI method with compressed sensing is able to tolerate greater reductions in scan time compared with EPSI. The reconstruction and quantitation metrics (i.e., spectral normalized RMS error maps, metabolite map normalized RMS error values [e.g., for total N-acetyl asparate, REPSI = 9.4% vs EPSI = 16.3%; acceleration factor = 2.5], percent absolute difference maps, and concentration and Cramer-Rao lower-bound estimates) showed that accelerated REPSI can reduce the scan time by a factor of 2.5 while retaining image and quantitation quality.
Conclusion:
Accelerated MRSI using undersampled radial echo-planar acquisitions provides greater reconstruction accuracy and more reliable quantitation for a range of acceleration factors compared with time-equivalent compressed-sensing reconstructions of undersampled Cartesian EPSI. Compared to the Cartesian approach, radial undersampling with compressed sensing could help reduce 2D spectroscopic imaging acquisition time, and offers a better trade-off between imaging speed and quality.
Keywords: compressed sensing, nonuniform Fourier transform, projection acquisition, total variation
1 |. INTRODUCTION
Magnetic resonance spectroscopic imaging is capable of providing metabolic information from multiple locations in biological tissues, allowing biochemical characterization of pathologies, and facilitating the diagnosing and monitoring of disease.1,2 One of the main challenges in MRSI is to shorten the data acquisition to clinically feasible scan times without compromising spectroscopic image quality. Conventional MRSI methods require long scan durations due to the sequential phase-encoding of each spatial dimension before spectral encoding.3 More advanced MRSI techniques based on echo-planar k-space trajectories significantly reduce the scan time by interleaving the collection of the spatial-spectral data.4 Apart from rectilinear or Cartesian trajectories, non-Cartesian echo-planar acquisitions using spirals, rosettes, and concentric circles have also been applied for efficient and fast MRSI,5–9 and these offer advantages relative to Cartesian approaches including lower gradient-slew rate demands, greater sampling efficiency, and increased robustness to phase errors caused by motion.
Radial k-space sampling techniques have gained widespread use in MRI due to their relatively decreased sensitivity to motion-related artifacts, inherent SNR advantage, and great potential for high acceleration.10,11 Recently in MRSI, radial trajectories were applied for hyperpolarized 13C imaging due to their repeated traversal of the central k-space, which enhances the capture of the short-lived image contrast.12 Three-dimensional radial acquisitions were used for high-field 31P in vivo spectroscopic imaging to benefit from the higher SNR per unit time that radial sampling offers.13 Most recently, radial sampling was implemented for 1H diffusion-weighted MRSI.14 However, to date, the application of radial sampling for 1H MRSI remains relatively unexplored.15 Furthermore, the potential of accelerated acquisitions through radial undersampling and compressed-sensing (CS) reconstruction is proven in the MRI field, but has yet to be demonstrated in 1H MRSI.
Compared to Cartesian undersampling, radial k-space undersampling is better suited for CS reconstruction, as it produces aliasing artifacts that are much less pronounced and more noise-like. This property of radial undersampling more closely meets the condition that the k-space undersampling pattern produce incoherent noise-like artifacts in the image domain, which is a prerequisite for effective CS.16 Additionally, the high central k-space density of radial acquisitions can improve CS reconstructions of the low spatial frequency components of the image, which is particularly advantageous due to the relatively low spatial resolutions that are usually acquired in MRSI. For radial undersampling, the golden-angle view-ordering scheme is ideal, as it continuously increments the angle of the radial views, or spokes, by 111.25° throughout the acquisition period, such that the k-space is covered as uniformly as possible for any given number of spokes.16,17 The combination of radial golden-angle undersampling and CS reconstruction has produced diagnostic-quality images from highly undersampled data in various accelerated MRI applications, especially dynamic imaging.18,19 One of the most widely used sparsity-promoting transforms in CS reconstructions from undersampled radial data is the total variation.20,21 This transform has led to good results in various Cartesian-based accelerated MRSI methods as well.22,23
Previous studies in accelerated non-Cartesian MRSI have used undersampled spiral trajectories in combination with CS and parallel imaging, applying other types of regularization based on variants of L1/total variation (TV) or low-rank minimization. In Chatnuntawech et al,24 random spiral-based trajectories were acquired and undersampled spiral k-space was reconstructed within a TV-SENSE framework to allow for acceleration factors of up to 4–4.5 for single-slice and 3D MRSI. In Kasten et al25 and Klauser et al,26 the total generalized variation, a second-order variant of TV, was used in conjunction with model-based low-rank subspace constraints to reconstruct high-resolution MRSI. Another subspace-based approach was reported in Lam et al,27 in which high-resolution spectra were obtained with the aid of a separate low-resolution scan to model the spatial component of the spatial-temporal signal. Both of the methods in Kasten et al25 and Lam et al,27 however, were based on Cartesian trajectories, yet similar studies involving non-Cartesian trajectories have also been the subject of recent research.28
Radial sampling has some unique advantages compared with other non-Cartesian trajectories. Similar to radial trajectories, spirals and rosettes also repeatedly sample the central portion of k-space, and can therefore be considered a relatively motion-robust technique. However, fast 1H MRSI using spiral and rosette trajectories at 3 T often require spatial and/or spectral interleaves, whereas radial trajectories only require spatial interleaves at 3 T.5,7,29 The additional requirement of spatial and spectral interleaves for spirals and rosettes can limit the achievable spectral bandwidth and makes these trajectories more susceptible to spectral artifacts due to potential inconsistencies between the spectral interleaves. Concentric circular trajectories can sample the k-space twice as fast as Cartesian trajectories, and require fewer spatial interleaves than radial sampling6,8,9,30; however, the main disadvantage of this approach is the loss of motion robustness, because the central k-space is not sampled in each spectral interleaf. However, generally all non-C artesian trajectories are more susceptible to errors due to off-resonance effects, leading to blurring and other imaging artifacts.
In this study, we evaluated accelerated 2D MRSI using radial echo-planar k-space trajectories and TV-regularized CS reconstruction, in both retrospectively and prospectively undersampled acquisitions of phantom and in vivo brain data. We evaluated the performance of radial relative to Cartesian echo-planar spectroscopic imaging (EPSI) by comparing the spectroscopic image quality and quantitation results obtained from both types of sampling techniques under various rates of undersampling. In the Supporting Information Section 1, we assess radial sampling of free-breathing, in vivo liver spectroscopic image data in terms of robustness to motion-related spectral and spatial artifacts.
2 |. METHODS
2.1 |. Pulse sequence
The REPSI and EPSI pulse sequences were implemented on a Siemens 3T Prisma MR system (Siemens, Munich, Germany) operating in the VE11C platform. For the spatial-spectral readout, a symmetric, bipolar trapezoidal gradient echo train was used, with a spectral bandwidth of 1136 Hz, an ADC bandwidth of 100 kHz, ramp durations of 60 μs, and 32 k-space points sampled during the gradient plateaus. Volumetric excitation31 was achieved using semi-LASER32 localization, with an initial 90° RF excitation pulse along the slice (z) direction followed by two pairs of adiabatic full-passage 180° RF pulses along the x and y directions (Figure 1A), to acquire an axial in-plane orientation. Outer-volume suppression bands were placed to suppress signal from lipid-dominant regions, and water suppression was done using a three-pulse water excitation–technique sequence.33 For all experiments, the slab thickness of the volume of interest (VOI) was set to 15 mm, and the matrix size was 32 × 32 with a FOV of 320 × 320 mm2, resulting in a voxel volume of 1.5 mL.
FIGURE 1.
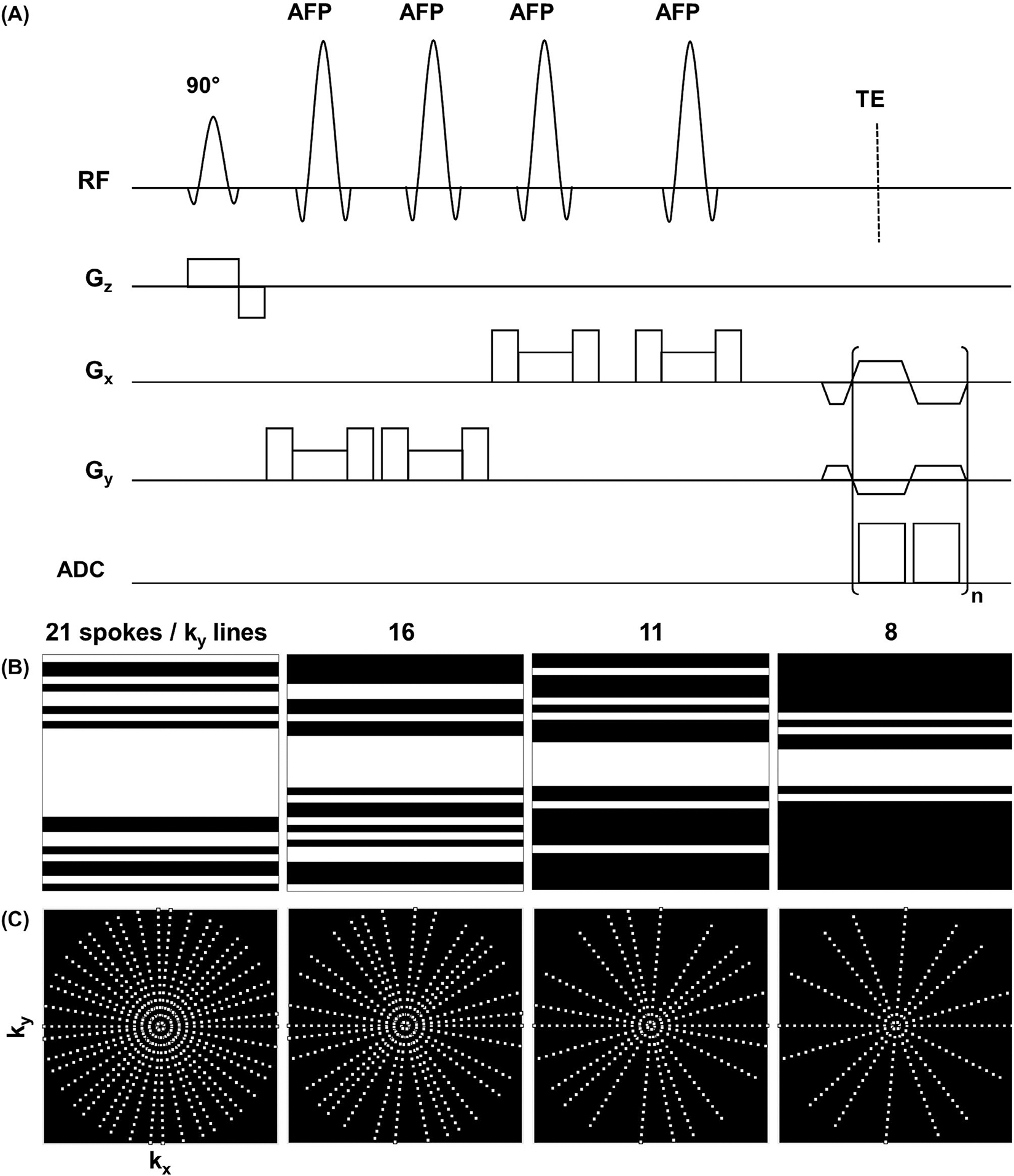
A, Pulse sequence diagram for radial echo-planar spectroscopic imaging (REPSI) in which n t points are acquired during the readout train. A pair of adiabatic full passage (AFP) pulses are played after the first 90° excitation pulse to achieve volumetric localization of an axial slab. B, Nonuniform undersampling masks for a 2D Cartesian 32 × 32 k-space matrix with 21, 16, 11, and 8 -lines, corresponding to acceleration factors (AFs) of 1.5, 2.0, 3.0, and 4. C, Golden-angle radial undersampling distributions with 21, 16, 11, and 8 spokes, corresponding to AFs of 1.5, 2.0, 3.0, and 4.0
2.2 |. Data acquisition
Accelerated REPSI and EPSI data were obtained on a time-equivalent basis: For each acceleration factor (AF), the same number of radial spokes and lines (phase-encoding steps) were acquired, resulting in identical scan times for both sequences. Based on the Nyquist sampling criterion for 2D spatial encoding of an N × N image, the radial AF is a factor of larger than the Cartesian AF, which is . Accordingly, a fully sampled 32 × 32 k-space grid requires 50 spokes and 32 -lines for REPSI and EPSI, respectively. However, for the sake of comparing accelerated REPSI and EPSI data, the AF is defined in terms of the reduced number of spokes or lines acquired relative to 32, which is the number of phase-encoding lines in a fully sampled 32 × 32 Cartesian k-space. This definition of the AF more accurately reflects a comparison between EPSI and REPSI in terms of the scan time instead of the number of sampled k-space points.
For undersampled REPSI acquisitions, six different numbers of spokes were acquired using the golden-angle view-ordering scheme: 21, 16, 13, 11, 8, and 6. For EPSI, nonuniform sampling patterns for the single phase-encoding dimension (Figure 1B) were generated from a Gaussian probability distribution function centered at , with at least four fully sampled central phase-encoding lines. Six Cartesian undersampling masks with 21, 16, 13, 11, 8, and 6 lines were implemented. The AFs for 21, 16, 13, 11, 8, and 6 spokes or -lines are defined as 1.5, 2.0, 2.5, 3.0, 4.0, and 5.0, respectively.
A phantom containing 17 representative brain metabolites at physiological concentrations was used to acquire fully sampled data for retrospective undersampling experiments. The phantom data were acquired with a 16-channel brain coil, and the VOI was prescribed at isocenter with in-plane dimensions of 80 × 80 mm2, encompassing a total of 64 voxels. For both REPSI and EPSI, six retrospectively undersampled data sets were generated at all AFs. In addition, 10 fully sampled and 10 prospectively undersampled REPSI and EPSI brain phantom data sets were acquired for each AF, giving a total of 70 data sets each for EPSI and REPSI. For each of these data sets, 25 voxels within the homogenous phantom were extracted, resulting in a total of 250 quantified voxels per AF or fully sampled set. For all phantom experiments, TR = 2 seconds, TE = 40 ms, and eight averages were acquired, resulting in fully sampled scan times of 8:32 minutes and 13:20 minutes for EPSI and REPSI, respectively. Accelerated phantom scan times were 5:36 minutes, 4:16 minutes, 3:28 minutes, 2:56 minutes, 2:08 minutes, and 1:36 minutes for AFs of 1.5, 2.0, 2.5, 3.0, 4.0, and 5.0, respectively. Separately, fully sampled water reference data were collected with one average, taking 1:04 minutes for EPSI and 1:40 minutes for REPSI.
Six healthy male volunteers and 1 female volunteer (ages 24–42 years) were scanned with approval of the University of California, Los Angeles institutional review broad and written, informed consent from each volunteer. Fully sampled REPSI and EPSI data sets were obtained for all volunteers. In addition, prospectively undersampled data with 11, 8, and 6 encodes or radial spokes were acquired for 3 volunteers; prospectively undersampled data sets with 11 and 8 spokes or encodes were acquired for 2 volunteers; a prospectively undersampled data set with 16, 11, and 8 spokes or encodes was acquired in 1 volunteer; and one prospectively undersampled data set with 16, 13, and 11 spokes was acquired for 1 volunteer. All in vivo data were obtained using a 16-channel brain coil and TR of 1.5 seconds, leading to fully sampled scan times of 6:24 minutes and 10 minutes for EPSI and REPSI, respectively, and accelerated scan times of 4:12 minutes, 3:32 minutes, 2:36 minutes, 2:12 minutes, 1:36 minutes, and 1:12 minutes for AFs of 1.5, 2.0, 2.5, 3.0, 4.0, and 5.0, respectively. Single-average, fully sampled water reference scans were acquired in 48 seconds for EPSI and 1:15 minutes for REPSI.
2.3 |. Reconstruction
2.3.1 |. Optimization algorithm
Due to the piecewise-smooth nature of spectroscopic images, especially for low resolutions common in MRSI, the TV acts as a natural sparsifying transform for the 2D spatial planes () of the acquired data (). The TV transform was not applied along the spectral dimension, because this dimension was already fully sampled and is typically not piecewise-smooth, as one-dimensional spectra may consist of several broad, crowded peaks with many nontrivial frequency components. We posed the CS reconstruction as the following unconstrained minimization problem:
| (1) |
where is the fast Fourier transform or the nonuniform fast Fourier transform34 for Cartesian and non-Cartesian data, respectively; is the data in space; is the acquired undersampled data in polar -space or space; is the isotropic total variation transformation; and is a regularization parameter that balances the minimization between the data fidelity term and the sparsity-based functional.
The monotone fast iterative soft-thresholding algorithm35 was used to solve this CS reconstruction problem, and the dual formulation of the isotropic TV minimization was implemented as described in Chambolle20 and Beck and Teboulle.35 The TV transform was applied to each spatial plane in the space—separately for each frequency point along the spectral dimension. For all experiments, the CS reconstruction was performed coil-by-coil, and all input data were normalized by , where is the acquired data in space and is the SD. The CS iterations continued until the normalized iterative update (defined as , where is the iteration index) was less than 10−3 or until the number of iterations reached a maximum of 100.
For radial-based CS, the data were reconstructed using the nonuniform fast Fourier transform algorithm from a MATLAB-based (The Math Works, Natick, MA) image-reconstruction toolbox made available by Fessler et al.36 At each iteration, the algorithm transformed the data from image to polar k-space using the nonuniform fast Fourier transform, and from the temporal to frequency domain using the standard fast Fourier transform. For density compensation, a ramp filter inversely proportional to the magnitude of the k-space radius, , was applied to each spoke.
2.3.2 |. Regularization parameters
The regularization parameter for each coil was defined as , where is the coil noise SD and is a proportionality factor. The parameter essentially defines the value by which the image is denoised in each iterative soft-thresholding step of monotone fast iterative soft-thresholding algorithm, so was adjusted in proportion to the level of the noise in each coil. Accordingly, the proportionality factor α was determined based on estimates of σ for each coil, which were obtained from an in-built prescan noise measurement.
Using the fully sampled phantom and in vivo brain data and estimates of , the factor was found by minimizing the l2-norm of the difference between the fully sampled spectra and the reconstructed spectra from retrospectively undersampled data:
| (2) |
where and are the fully sampled and reconstructed spectra between 0.5 and 4.3 ppm at the th voxel within the VOI, respectively. The minimization was performed by iterating over a range of values linearly spaced between 0.01 and 1. For both REPSI and EPSI and for all acceleration factors, the value of that minimized this metric was approximately 0.10. Thus, the regularization parameter was defined as for all REPSI and EPSI reconstructions.
2.4 |. Spectral preprocessing and postprocessing
Before CS reconstruction, the odd and even echoes from the bipolar readout were separated into two data sets, and the odd echo data were time-reversed. After Fourier-transforming the temporal dimension, a linear phase ramp was applied along the readout, to correct for chemical-shift displacement caused by the phase accrual of each resonance during sampling.37 Afterward, the data were Fourier-transformed back to the time domain, and both the water and non-water-suppressed data were averaged. The undersampled, water-suppressed even and odd echo data sets were reconstructed separately. Eddy current and zero-order phase corrections computed from the fully sampled non-water-suppressed data were applied to the CS-reconstructed data.38 Coil combination was performed using the singular valued decomposition method.39 After applying a first-order phase correction to the even echoes to account for the difference in TE relative to the odd echo, and then performing frequency and phase alignment using the FID-A toolbox,40,41 the coil-combined reconstructions from the even and odd echoes were averaged. Finally, the residual water peak was removed using the Hankel-Lanczos singular value decomposition method.42
All reconstructed spectral metabolite maps and quantitation were obtained using LCmodel (version 6.2–0T).43 The basis set for the phantom data was simulated using the VESPA software package44 and included the following metabolites: N-acetyl-aspartate (NAA), N-acetylaspartylglutamate, γ-aminobutyric acid, aspartate, Cho, Cr, glucose, glutamate, glutamine, glutathione, myo-inositol (mI), lactate, phosphocholine, phosphorylethanolamine, alanine, taurine, and threonine. The basis set for in vivo data sets included the previously listed metabolites in addition to glycerophosphorylcholine and scyllo-inositol.
2.5 |. Comparison across acceleration factors
To evaluate the performance of REPSI and EPSI for each AF, five metrics were considered. For retrospectively undersampled data, the reconstruction accuracy was compared using normalized RMS errors (nRMSEs) of the reconstructed spectra and metabolite maps derived from LCModel quantitation. Maps showing the Cramer-Rao lower bounds (CRLBs) of the metabolite concentrations for voxels within the VOI were compared, as well as the percent absolute difference (PAD) maps between the fully sampled and reconstructed metabolite maps. For prospectively undersampled data, the metabolite maps were compared qualitatively with those from the separately acquired fully sampled maps, and the CRLB maps for each AF were compared to determine the reliability of the quantified spectra from REPSI versus EPSI reconstructions.
Spectral nRMSE maps were obtained by computing the following metric for each voxel:
| (3) |
where and are the (complex-valued) reconstructed and fully sampled spectra, respectively, at the th voxel within the VOI. Only the range between 0.5 and 4.3 ppm was considered for this computation, and is the number of spectral points within this range. The metabolite map nRMSE value was defined as follows:
| (4) |
where and are the concentration estimates of metabolite from the reconstructed and fully sampled data, respectively. Percent difference maps were also computed as a way to visualize the reconstruction error across the VOI, and the PAD value was computed for each voxel as follows:
| (5) |
Finally, the average SNR values of spectra for voxels within the VOI, as measured by LCModel quantitation, were compared.
2.6 |. Comparison between time-equivalent fully sampled and accelerated acquisitions
To determine the benefit of CS, we compared fully sampled data acquired with fewer averages to CS reconstructions of time-equivalent, accelerated data obtained with eight or fewer numbers of averages. One in vivo data set was retrospectively undersampled with different numbers of averages to match the scan times of fully sampled data (AF = 1.0) with four, three, two, and one average(s). The following time-equivalent combinations were tested: (1) AF = 1.0 with four averages versus AF = 1.5 with six averages and AF = 2.0 with eight averages; (2) AF = 1.0 with three averages versus AF = 2.0 with six averages; (3) AF = 1.0 with two averages versus AF = 1.5 with three averages, AF = 2.0 with four averages, AF = 2.5 with five averages, AF = 3.0 and 6 averages, and AF = 4.0 with eight averages. Finally, single-average fully sampled data are time-equivalent to data acquired at AF = 2.0 with two averages, AF = 3.0 with three averages, and at AF = 4.0 with four averages. For REPSI, fully sampled data were reduced from 50 to 32 spokes to match the scan time of a fully sampled EPSI. For each combination, the nRMSEs of the metabolite maps of total NAA (tNAA: NAA + N-acetylaspartylglutamate), Cr, total choline (tCho: Cho + phosphocholine), Glx (glutamate + glutamine), and mI were computed. We applied only TV-denoising to the low-averaged fully sampled data to compensate for lower SNR, and fine-tuned the denoising parameter to λ = 0.05 · σ for best results. The ground-truth reconstruction used for computing nRMSEs was taken from the fully sampled data with eight averages (see Supporting Information Section 2).
3 |. RESULTS
Table 1 lists the means and SDs of the estimated concentrations of tNAA, tCho, Glx, Cr, and mI from reconstructions of prospectively undersampled brain phantom data, as well as the means and SDs of the corresponding CRLBs. Generally, the concentrations were more underestimated as the AF increased, but for REPSI, the estimates remained closer to those from the fully sampled data. For example, the difference between the fully sampled and reconstructed Cr concentration were 0.4 mM and 0.7 mM for REPSI and EPSI undersampled with 13 spokes or -lines, respectively. The REPSI method also had lower SDs of the concentration values, indicating a greater consistency in the quantitation compared with EPSI. It can be inferred that the coefficients of variation of the concentration estimates from REPSI were lower for all metabolites and AFs. The lower CRLB values confirmed that the concentration estimates from REPSI were more reliable than those from EPSI. Increased SNR from radial acquisitions is given in Table 2. For all AFs, REPSI CS reconstructions data had greater SNR, although the estimates of the FWHM values of reconstructed REPSI spectra were slightly higher than those of the EPSI spectra.
TABLE 1.
Concentration estimates and corresponding CRLB percentage values of tCho, Cr, mI, tNAA, and Glx quantified from CS reconstructions of prospectively undersampled REPSI and EPSI brain phantom data, for all AFs
| AF | tCho |
Cr |
mI |
tNAA |
Glx |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EPSI | REPSI | EPSI | REPSI | EPSI | REPSI | EPSI | REPSI | EPSI | REPSI | ||
| Concentration (mM) | 1 | 1.2 ± 0.1 | 1.2 ± 0.1 | 4.3 ± 0.4 | 4.2 ± 0.3 | 4.8 ± 0.6 | 4.7 ± 0.5 | 7.2 ± 0.7 | 7.1 ± 0.6 | 13.6 ± 1.7 | 13.5 ± 1.5 |
| 1.5 | 1.2 ± 0.1 | 1.1 ± 0.1 | 4.1 ± 0.4 | 4.0 ± 0.3 | 4.5 ± 0.5 | 4.3 ± 0.4 | 7.0 ± 0.7 | 6.8 ± 0.6 | 12.9 ± 1.7 | 12.5 ± 1.4 | |
| 2 | 1.0 ± 0.1 | 1.1 ± 0.1 | 3.8 ± 0.4 | 3.9 ± 0.3 | 3.9 ± 0.5 | 4.1 ± 0.4 | 6.5 ± 0.7 | 6.7 ± 0.6 | 11.4 ± 1.7 | 12.1 ± 1.4 | |
| 2.5 | 1.0 ± 0.1 | 1.1 ± 0.1 | 3.6 ± 0.3 | 3.8 ± 0.3 | 3.8 ± 0.4 | 4.0 ± 0.4 | 6.2 ± 0.6 | 6.6 ± 0.5 | 10.7 ± 1.2 | 11.9 ± 1.5 | |
| 3 | 1.0 ± 0.1 | 1.0 ± 0.1 | 3.5 ± 0.5 | 3.7 ± 0.4 | 3.7 ± 0.5 | 3.9 ± 0.4 | 6.1 ± 0.7 | 6.4 ± 0.6 | 10.8 ± 1.4 | 11.4 ± 1.6 | |
| 4 | 0.9 ± 0.1 | 1.0 ± 0.1 | 3.4 ± 0.5 | 3.5 ± 0.5 | 3.7 ± 0.5 | 3.6 ± 0.5 | 5.9 ± 1.0 | 6.2 ± 0.7 | 10.5 ± 1.5 | 10.6 ± 1.6 | |
| 5 | 0.9 ± 0.1 | 0.9 ± 0.1 | 3.2 ± 0.6 | 3.3 ± 0.5 | 3.5 ± 0.5 | 3.3 ± 0.5 | 5.4 ± 0.9 | 5.8 ± 0.7 | 9.90 ± 1.4 | 9.50 ± 1.5 | |
| CRLBs (%) | 1 | 10.4 ± 2.4 | 8.7 ± 2.2 | 7.6 ± 1.6 | 6.6 ± 1.6 | 12.0 ± 2.7 | 10.2 ± 2.6 | 6.4 ± 1.4 | 5.6 ± 1.5 | 10.3 ± 2.4 | 8.9 ± 1.7 |
| 1.5 | 9.9 ± 2.1 | 9.1 ± 2.1 | 7.4 ± 1.5 | 6.8 ± 1.6 | 11.6 ± 2.4 | 10.8 ± 2.4 | 6.1 ± 1.3 | 5.7 ± 1.4 | 9.9 ± 1.8 | 9.2 ± 1.7 | |
| 2 | 10 ± 2.1 | 9.2 ± 2.1 | 7.3 ± 1.4 | 6.8 ± 1.6 | 11.8 ± 2.5 | 10.8 ± 2.5 | 5.9 ± 1.2 | 5.6 ± 1.4 | 10.1 ± 1.8 | 9.3 ± 1.7 | |
| 2.5 | 10 ± 1.8 | 9.2 ± 2.0 | 7.2 ± 1.3 | 6.7 ± 1.5 | 11.7 ± 2.3 | 10.8 ± 2.4 | 5.9 ± 1.2 | 5.5 ± 1.5 | 10.1 ± 1.5 | 9.2 ± 1.7 | |
| 3 | 9.8 ± 1.8 | 9.2 ± 2.0 | 7.1 ± 1.3 | 6.7 ± 1.5 | 11.5 ± 2.1 | 11.0 ± 2.3 | 5.7 ± 1.2 | 5.5 ± 1.4 | 9.8 ± 1.8 | 9.4 ± 1.7 | |
| 4 | 9.6 ± 1.9 | 9.4 ± 1.9 | 6.9 ± 1.3 | 6.7 ± 1.3 | 11.3 ± 2.1 | 11.3 ± 2.1 | 5.6 ± 1.2 | 5.4 ± 1.3 | 9.8 ± 1.7 | 9.7 ± 1.8 | |
| 5 | 9.0 ± 1.6 | 9.8 ± 1.8 | 6.6 ± 1.0 | 6.8 ± 1.2 | 10.6 ± 1.9 | 11.5 ± 2.2 | 5.4 ± 0.9 | 5.4 ± 1.2 | 9.3 ± 2.1 | 10.2 ± 2.4 | |
TABLE 2.
The SNR and FWHM values (computed from LCModel) of spectra from CS reconstructions of prospectively undersampled brain phantom data
| AF | SNR |
FWHM (Hz) |
||
|---|---|---|---|---|
| EPSI | REPSI | EPSI | REPSI | |
| 1 | 13.6 ± 1.7 | 14.5 ± 1.3 | 2.3 ± 1.0 | 2.8 ± 1.4 |
| 1.5 | 14.7 ± 1.9 | 15.5 ± 1.4 | 2.3 ± 0.9 | 2.4 ± 1.2 |
| 2 | 15.3 ± 1.9 | 15.9 ± 1.7 | 2.2 ± 1.2 | 2.4 ± 1.3 |
| 2.5 | 15.3 ± 2.2 | 15.9 ± 1.9 | 2.2 ± 1.2 | 2.5 ± 1.7 |
| 3 | 15.2 ± 2.0 | 16.0 ± 1.7 | 2.4 ± 1.2 | 2.5 ± 1.4 |
| 4 | 14.8 ± 2.3 | 15.9 ± 2.3 | 2.4 ± 1.2 | 2.6 ± 1.5 |
| 5 | 14.9 ± 2.4 | 15.5 ± 2.7 | 2.6 ± 1.4 | 2.9 ± 2.0 |
Note: The total number of voxels extracted per AF was 250.
Figure 2C displays the PAD maps of tNAA from CS reconstructions of retrospectively undersampled REPSI and EPSI data. Clearly, the REPSI tNAA maps contain lower values across most of the VOIs. Due to effects from chemical-shift displacement, the edges of the VOI are more susceptible to error in both radial and Cartesian acquisitions, but as the AF increases, EPSI has higher reconstruction errors as measured by the PAD, particularly in the central portion of the VOI. In contrast, REPSI reconstructions maintain relatively low PAD values within the center of the VOI, even for data acquired with as few as eight spokes. Figure 2B shows the CLRB maps for the tNAA concentrations. Similar to the PAD maps, the CRLB maps show overall lower values across large portions of the VOI in comparison to the EPSI tNAA CRLB maps, except for the highest AFs corresponding to eight spokes and in some peripheral voxels.
FIGURE 2.

A, Localization image for brain phantom acquisitions. B, Maps of the Cramer-Rao lower bounds (CRLBs) as percentages of the estimated total NAA concentrations (tNAA), from fully sampled and compressed sensing (CS)–reconstructed REPSI and echo-planar spectroscopic imaging (EPSI) brain phantom data. C, Percent absolute difference (PAD) maps of tNAA from CS reconstructions of retrospectively undersampled REPSI and EPSI brain phantom data, for all AFs corresponding to 21 (1.5×), 16 (2×), 13 (2.5×), 11 (3×), and 8 (4×) radial spokes or -lines. All maps are interpolated by a factor of two
Table 3 lists the mean nRMSEs of the metabolite maps of tNAA, tCho, Cr, Glx, and mI from CS reconstructions of in vivo data, averaged across 7 healthy volunteers. For almost all AFs considered, the nRMSE values from REPSI reconstructions were much lower, indicating higher reconstruction accuracy. Figure 3A,B shows the spectral nRMSE maps for CS reconstructions of retrospectively undersampled REPSI and EPSI in vivo data. As with the PAD, CRLB, and metabolite map nRMSEs, the spectral nRMSE maps show that the REPSI spectra have higher reconstruction accuracy for all acceleration factors. For both in vivo brain data sets, the spectral nRMSE values from REPSI do not increase as sharply as those from EPSI, which demonstrates that REPSI is much more robust to higher AFs. Similarly, Table 3 lists lower mean CRLB values for REPSI, indicating more reliable in vivo quantitation compared with EPSI for all AFs.
TABLE 3.
Mean nRMSE values of metabolite maps obtained from LCModel quantitations of CS-reconstructed, retrospectively undersampled, in vivo brain data (top) and mean CRLB values from both REPSI and EPSI CS reconstructed, averaged across 7 healthy volunteers (bottom)
| AF | tNAA |
tCho |
Glx |
mI |
Cr |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| REPSI | EPSI | REPSI | EPSI | REPSI | EPSI | REPSI | EPSI | REPSI | EPSI | ||
| Mean nRMSEs | 1.5 | 11.9 | 10.3 | 16.4 | 32.5 | 22.7 | 31.6 | 75.4 | 36.5 | 14.1 | 14.6 |
| 2 | 13.6 | 18.7 | 18.6 | 34.1 | 25.3 | 76.8 | 75.1 | 46.4 | 16 | 23.7 | |
| 2.5 | 15.3 | 24.2 | 19.7 | 31.1 | 26.7 | 37 | 72.1 | 49.1 | 18.4 | 29.7 | |
| 3 | 18.3 | 26.2 | 22.8 | 32.4 | 28.9 | 37.3 | 46.1 | 56.9 | 20.6 | 30.6 | |
| 4 | 21.9 | 22.5 | 26.4 | 28.8 | 34.5 | 38.1 | 69.7 | 48.2 | 24.4 | 30.5 | |
| 5 | 25.9 | 32.2 | 27.8 | 36.3 | 35.1 | 42.3 | 85.8 | 56.5 | 25.6 | 41 | |
| Mean CRLBs | 1 | 8.4 | 9 | 11.6 | 13.7 | 16.9 | 19.8 | 37.8 | 28.2 | 7.8 | 9.5 |
| 1.5 | 8 | 8.5 | 12.3 | 13.3 | 17.6 | 18.7 | 22.3 | 30.2 | 7.7 | 8.8 | |
| 2 | 8 | 11.1 | 12.3 | 15.7 | 18.6 | 20.6 | 19.5 | 41.9 | 7.7 | 9.9 | |
| 2.5 | 8.1 | 11.8 | 12.4 | 17 | 16.8 | 22.8 | 24.3 | 64.2 | 7.6 | 11.8 | |
| 3 | 8.3 | 11.6 | 13.8 | 17.3 | 17.1 | 24.6 | 29.5 | 40.8 | 7.9 | 10.5 | |
| 4 | 8.8 | 10 | 13.8 | 15 | 17.5 | 23.1 | 33.1 | 32.8 | 8.1 | 9.5 | |
| 5 | 9.5 | 11.1 | 15 | 17 | 18.9 | 23.8 | 34.9 | 36.4 | 8.8 | 9.6 | |
Note: The mean values across 7 healthy volunteers are shown for AFs of 1.5, 2, 2.5, 3, 4 and 5. The bold numbers in the top half indicate a lower mean nRMSE value for that particular AF and metabolite. The bold numbers in the bottom half indicate a lower mean CRLB for that particular AF and metabolite. The mean CRLB and nRMSE values are shown for five metabolites: tNAA, tCho, Glx, mI, and Cr.
FIGURE 3.
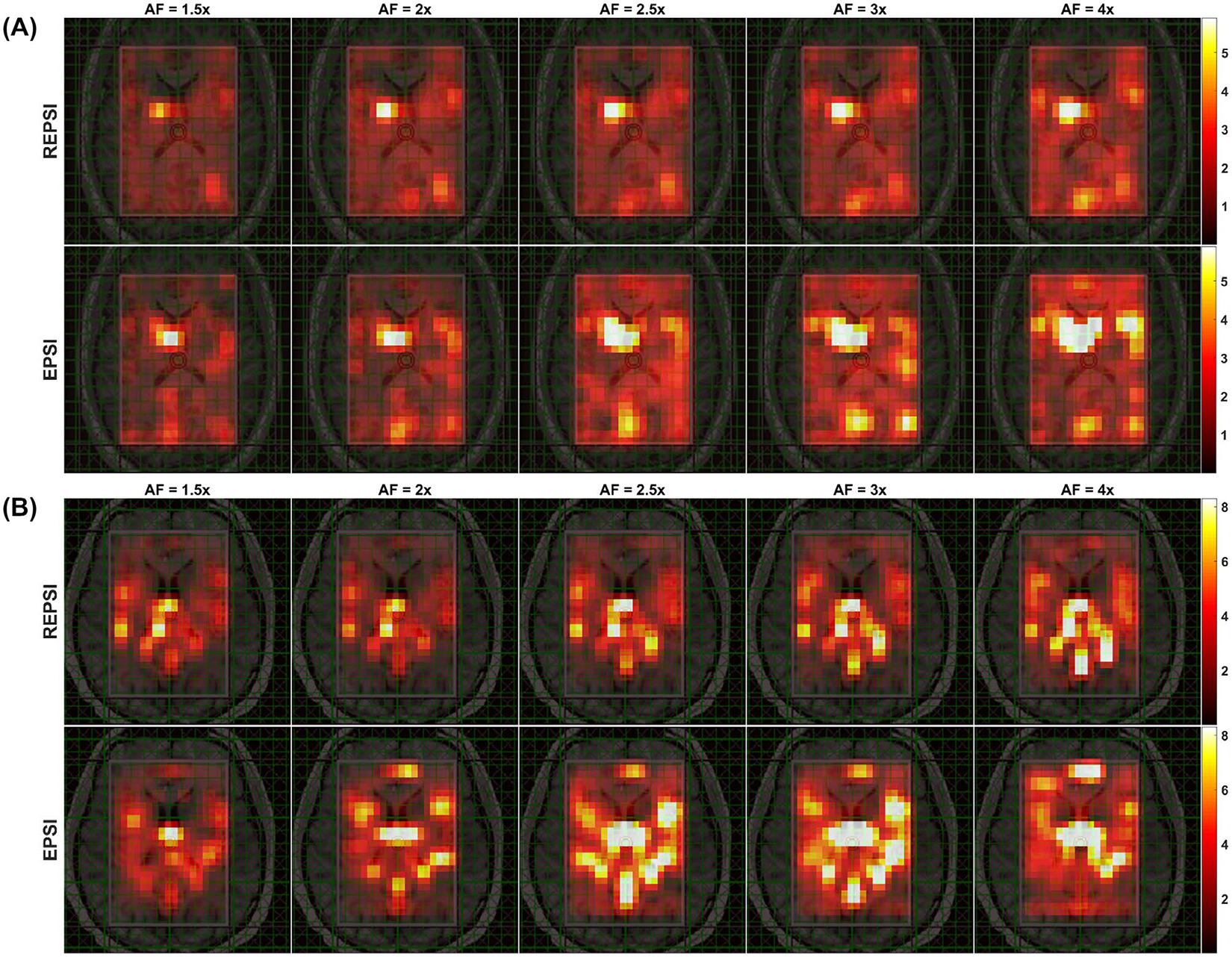
A, Maps of the spectral normalized RMS error (nRMSE) computed from CS reconstructions of retrospectively undersampled REPSI and EPSI in vivo data from a 26-year-old healthy volunteer, shown for AFs corresponding to 21 (1.5×), 16 (2×), 13 (2.5×), 11 (3×), and 8 (4×) radial spokes or -lines. B, Spectral nRMSE maps from CS reconstructions of retrospectively undersampled REPSI and EPSI in vivo brain data acquired from a healthy 33-year-old male volunteer, shown for AFs of 1.5, 2, 2.5, 3, and 4. All maps are interpolated by a factor of two
Metabolite and CRLB maps from reconstructions of prospectively undersampled in vivo REPSI and EPSI brain data are shown in Figure 4. The tNAA map from EPSI reconstructions degraded significantly, starting at the relatively low AF of 2 (16 -lines), whereas the maps from REPSI retained the underlying brain morphology, such as the outlines of the ventricles, even at the highest AFs. Overall, reconstruction artifacts were significantly less prominent in the REPSI tNAA maps. The corresponding CRLB maps in Figure 4B show that the concentration estimates from REPSI data have lower CRLBs across most of the VOI, except in voxels near the frontal cortex, where EPSI also has increased CRLBs. In both areas surrounding the ventricles and in the posterior regions of the brain, REPSI maintains more reliable estimates of the tNAA concentrations.
FIGURE 4.
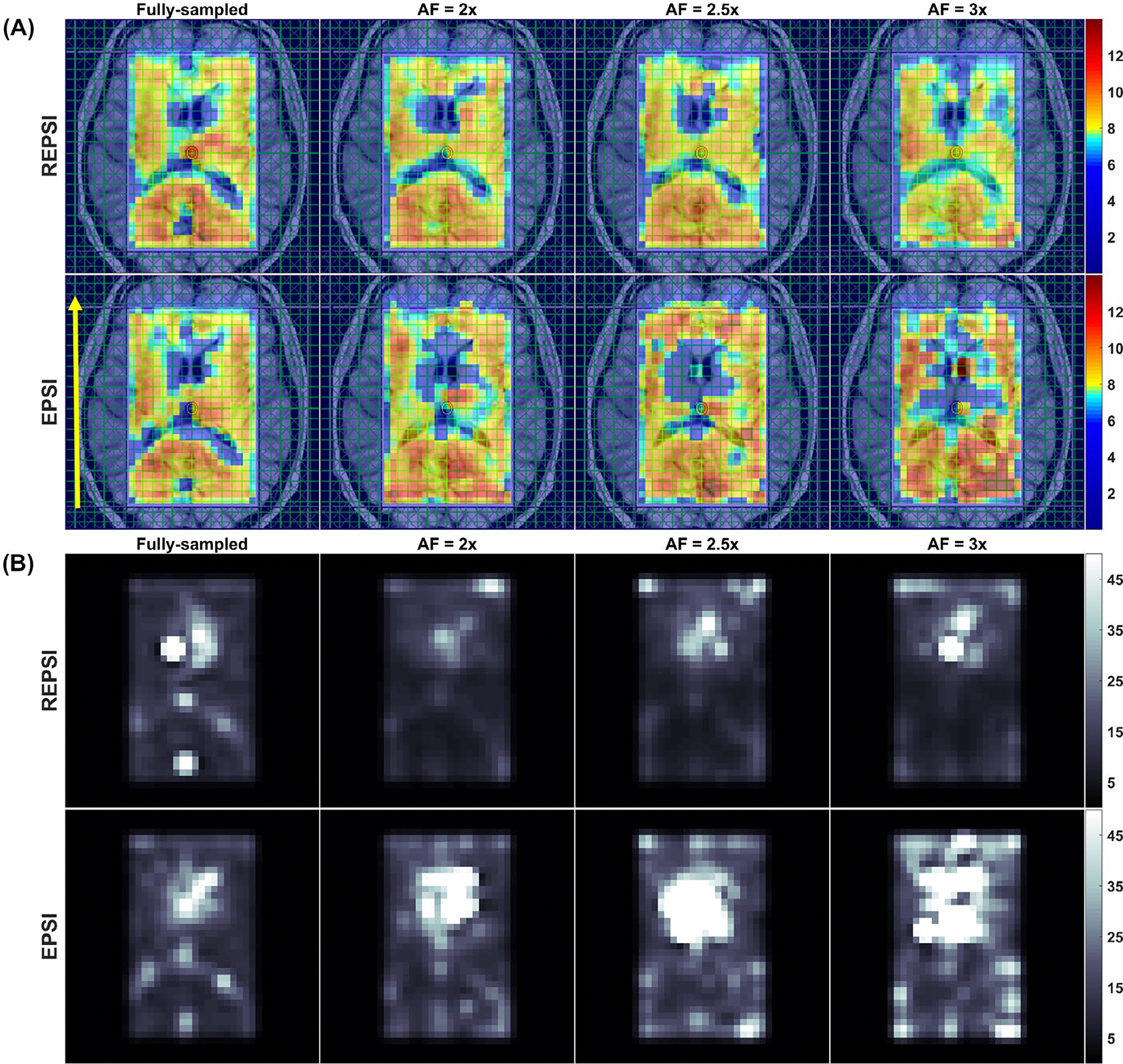
Brain MRSI scan of a 33-year-old healthy male volunteer. A, The tNAA maps from fully sampled (AF = 1.0) REPSI and EPSI brain data (leftmost column), and tNAA maps from CS reconstructions of prospectively undersampled brain data acquired with 16, 13, and 11 radial spokes or -lines. B, The CRLB maps for the tNAA maps shown in (A). The phase-encoding direction is indicated by the yellow arrow in the leftmost image of the EPSI row in (A). All maps are interpolated by a factor of two
Figure 5 shows extracted spectra from CS reconstructions of prospectively undersampled data in four brain areas, as indicated in the axial brain localization image: (1) right putamen to corona radiata, (2) occipital gray matter, (3) left posterior insular cortex, and (4) frontal white matter. As mentioned previously, REPSI has a greater SNR advantage over EPSI, which is evident from the higher peak amplitudes of REPSI spectra relative to those from EPSI. Due to the denoising effect from the CS reconstruction, both REPSI and EPSI spectra, however, were able to provide spectra with well-resolved NAA, Cr, mI, and tCho peaks up to the highest AF factors, although, expectedly, the peak intensity decreased as the AF increases. This slight reduction in intensity is caused by a decrease in SNR due to fewer k-space points sampled as the AF increases, although the central k-space remains densely sampled. However, the radial undersampling patterns at high AFs retain a greater concentration of the lower spatial frequency data compared with the undersampled Cartesian masks for high AFs, in which more samples are taken along the direction and fewer along . For the spectra shown in Figure 5, the tNAA peak height above the noise floor decreased by approximately 10% and 16% in REPSI and EPSI spectra at AF = 3.0, respectively, compared with the fully sampled spectra.
FIGURE 5.
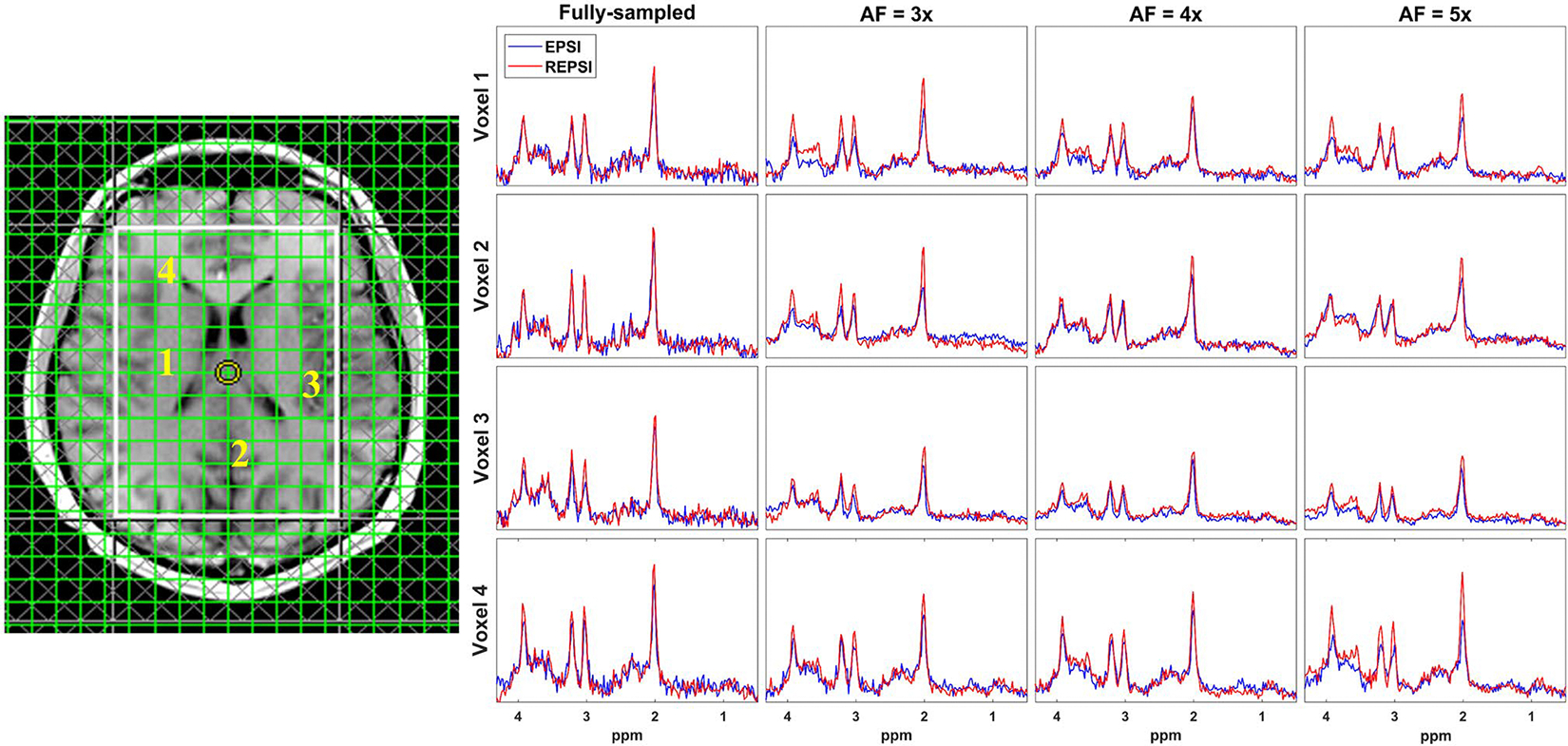
Representative spectra from fully sampled and CS reconstructions of prospectively undersampled in vivo brain data from a 32-year-old healthy male volunteer. Spectra extracted from four brain locations are shown: 1, right putamen to corona radiata; 2, occipital gray matter; 3, left posterior insular cortex; and 4, frontal white matter. Both the REPSI and EPSI data were prospectively undersampled with 11 (AF = 3), 8 (AF = 4), and 6 (AF = 5) acquired radial spokes or -lines, respectively. Baselines of the REPSI and EPSI spectra between 0.5 and 4.3 ppm were matched. The NAA peak (2.01 ppm) intensity from fully sampled REPSI spectra (red) had an approximately 16% increase in peak intensity compared with the EPSI spectra (blue) from the selected voxels. All spectra are shown in real mode (phase sensitive) and share the same scale
Figure 6 shows metabolite maps of tNAA, Cr, tCho, Glx, and mI from fully sampled (Figure 6A) and CS reconstructions (Figure 6B) of accelerated (AF = 2.5) REPSI and EPSI data. The morphological features in the accelerated REPSI maps more closely match those of the fully sampled data, whereas the EPSI maps show severe degradation. Figure 7 demonstrates the degree of reconstruction error, in which the PAD maps clearly indicate that CS reconstructions from undersampled REPSI data are more accurate. Supporting Information Figure S3 shows the fully sampled metabolite maps (Supporting Information Figure S3A) and the corresponding CRLB maps (Supporting Information Figure S3B), indicating that REPSI is better able to reliably estimate the concentrations of tNAA, Cr, tCho, Glx, and mI.
FIGURE 6.
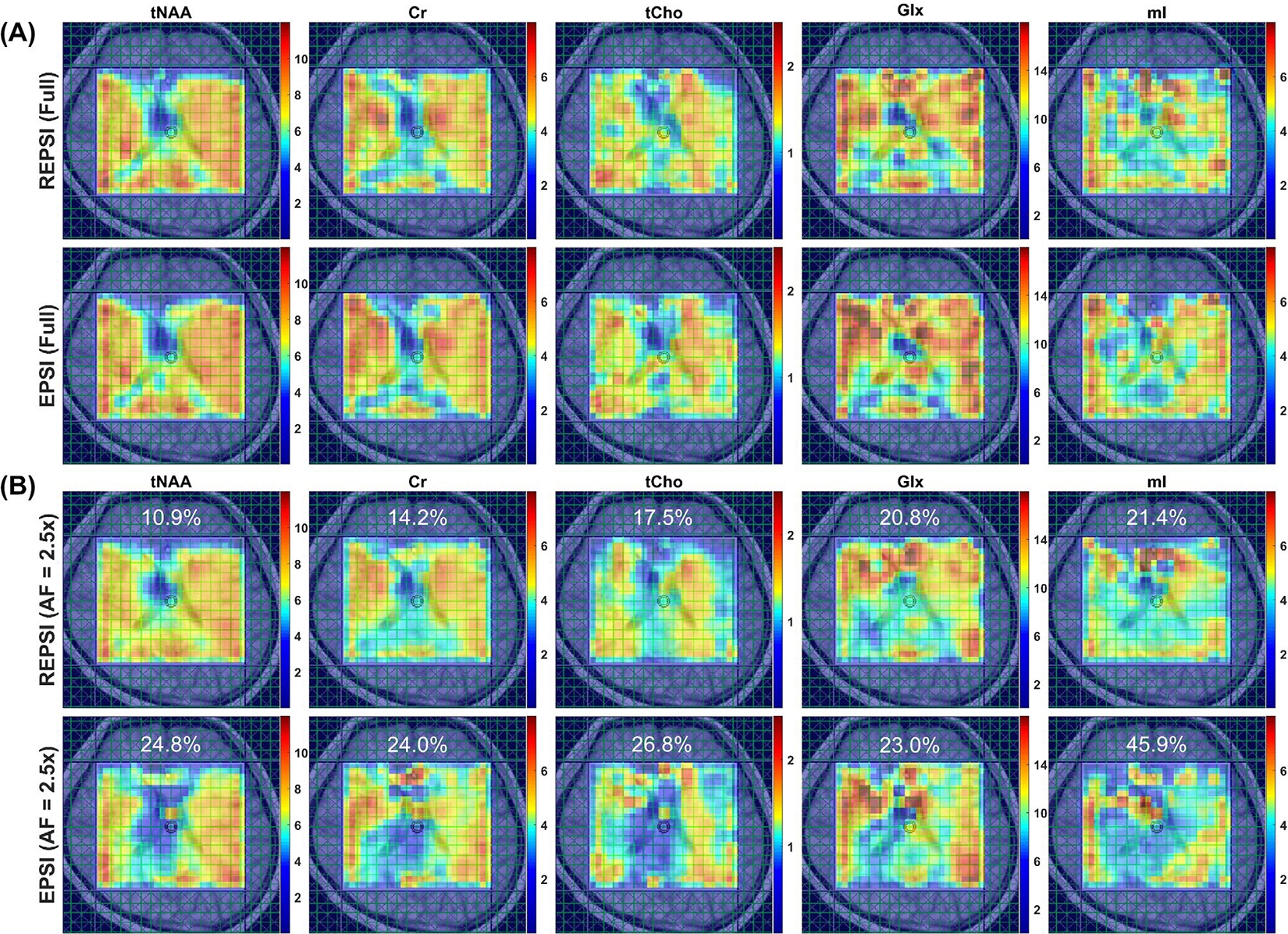
A, Metabolite maps of tNAA, Cr, total choline (tCho), Glx (glutamate + glutamine), and myo-inositol (mI) from fully sampled REPSI (top row) and EPSI (bottom row) reconstructions of in vivo brain data from a healthy 24-year-old healthy female volunteer. B, Metabolite maps of tNAA, Cr, tCho, Glx, and mI from CS reconstructions of retrospectively undersampled (AF = 2.5) REPSI (top row) and EPSI (bottom row) data. Note that the REPSI reconstructions at AF = 2.5 show greater similarity to the fully sampled metabolite maps, compared with the EPSI reconstructions. The nRMSEs of the metabolite maps are also shown. All maps are interpolated by a factor of two
FIGURE 7.
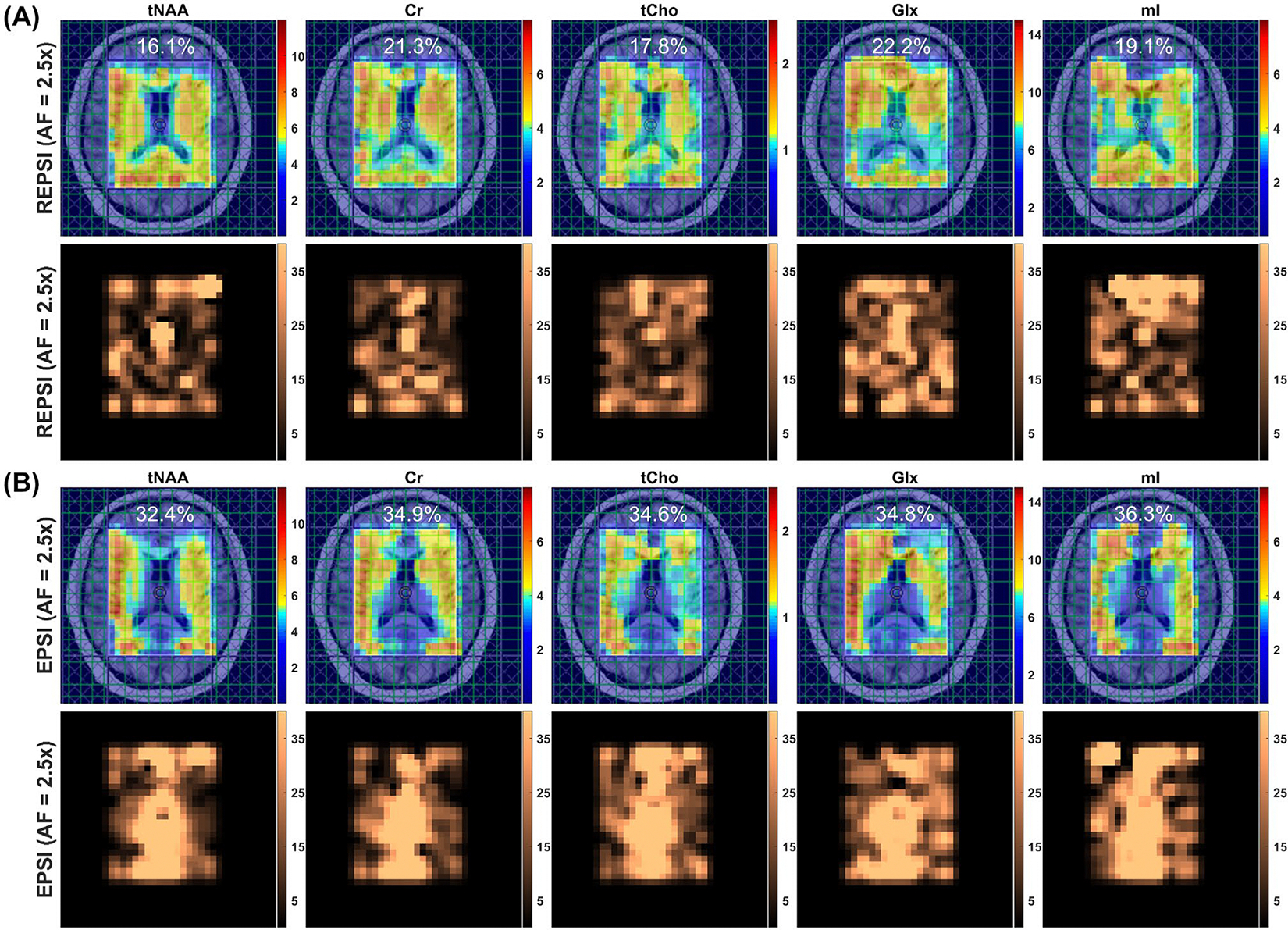
Metabolite maps of tNAA, Cr, tCho, Glx, and mI (top row) from CS reconstructions of retrospectively undersampled in vivo brain data (AF = 2.5) from a 34-year-old healthy male volunteer. The corresponding percent absolute difference (PAD) maps are shown in the bottom row. The maps in (A) correspond to an AF of 2.5 for REPSI reconstructions. B, Metabolite maps of tNAA, Cr, tCho, Glx, and mI (top row) and corresponding PAD maps (bottom row) from EPSI reconstructions of retrospectively undersampled data (AF = 2.5). The nRMSEs of the metabolite maps are also shown. All maps are interpolated by a factor of two
Supporting Information Table S1 provides the metabolite map nRMSEs from reconstructions of time-equivalent, fully sampled and accelerated REPSI and EPSI data with different numbers of averages. Generally, the CS-reconstructed data, particularly from REPSI, had lower metabolite-m ap nRMSEs than the time-equivalent, denoised fully sampled data. Additionally, the nRMSE values from REPSI were, in most cases, lower than those from the time-equivalent EPSI reconstructions. Therefore, it may be more beneficial to apply CS reconstruction to data with more averages than to acquire time-equivalent, fully sampled data with fewer averages, particularly for the REPSI data (Supporting Information Figure S6).
4 |. DISCUSSION
We have shown that, in combination with CS, REPSI is able to tolerate greater reductions in scan time compared with EPSI. The findings confirm the potential of using radial echo-planar k-space trajectories and CS for accelerated spectroscopic imaging. Quantitation of metabolites and spectroscopic imaging results from radial data were compared with those from CS reconstructions of undersampled Cartesian echo-planar spectroscopic data, on a time-equivalent basis. Thus, the degree of reconstruction and quantitation accuracy as well as spectroscopic image quality of CS reconstructions from undersampled EPSI and REPSI data were determined as a function of the scan-time duration. All reconstruction and quantitation metrics, including spectral nRMSE maps, metabolite map nRMSE values, PAD maps, and concentration and CLRB estimates, show that accelerated REPSI provides a better trade-off between imaging speed and spectroscopic imaging quality, compared with the EPSI approach.
The comparisons are in the context of 2D spatial MRSI. Highly undersampling the 2D k-space along the single phase-encoding dimension produces imaging artifacts that spread predominantly along that dimension. In contrast, the undersampled radial k-space results in streaking artifacts that are distributed uniformly outside of a reduced FOV.45 Thus, radially undersampled 2D k-space is better suited for CS reconstruction, as these streaking artifacts are more similar to incoherent noise.16 An additional advantage of radial sampling is that each spoke contains equal amounts of low and high spatial frequencies over , unlike in Cartesian sampling, which consistently samples the lowest spatial frequencies only along the readout direction. For these reasons, it is expected that the CS reconstructions of REPSI data would produce better results than those from EPSI data, particularly in the 2D case. However, radial imaging is relatively more susceptible to spatial blurring due to off-resonance effects.46 The slightly higher FWHM values of REPSI, particularly for fully sampled data, are probably the result of this limitation. Future studies need to be conducted to compare results from accelerated radial undersampling with those of Cartesian undersampling of two phase-encoding dimensions in 3D MRSI.
The in vivo brain REPSI results demonstrate the applicability of radial echo-planar trajectories for fast MRSI on a clinical scanner. Qualitatively, the tNAA metabolite map from the CS reconstruction of radial data undersampled with 13 spokes still appears very similar to the fully sampled tNAA map, whereas the EPSI result contains severe spatial artifacts. Further reductions in spokes or -lines worsens both the REPSI and EPSI reconstructions. This observation implies that spectroscopic 2D imaging time can be reduced by approximately a factor of 2.5 relative to a fully sampled Cartesian acquisition, but this can only be achieved with radial undersampling. Moreover, as shown in Supporting Information Figures S1 and S2, the motion-robustness of radial sampling allows for measuring spectra with minimal motion-related artifacts from a free-breathing liver scan. This property, along with the self-navigating ability of radial sampling, allows for the possibility of mitigating spectral artifacts in applications affected by motion-induced phase errors, such as diffusion-weighted spectroscopic imaging.14
One limitation of this work is that the reconstructions were done coil-by-coil, and separately for each odd and even echo. The reconstruction time was approximately 1.5–2 hours for a single 16-channel in vivo data set. Previous reports in accelerated MRSI, such as in Chatnuntawech et al24 and Nassirpour et al,23 used a combination of parallel imaging and CS to obtain good-quality, high-resolution MRSI at high acceleration factors in relatively short reconstruction times. Chatnuntawech et al24 used spiral undersampling schemes to measure 3D MRSI at AFs of 4–4.5 with high resolution (voxel size = 0.5 cc), and Nassirpour et al23 applied Cartesian undersampled FID-MRSI to reconstruct matrices of up to 64 × 64 in 3–3.75 minutes. In our case, it is possible to use parallel computing and coil compression47 to reduce the computation overhead, and to adopt flyback trajectories48,49 to avoid separate echo reconstructions. Future implementations will use a joint CS–parallel imaging approach,50 which requires a calibration scan. An advantage of radial sampling is that it is self-calibrating because it densely samples the central k-space, which is the most important data for estimating the coil sensitivities.51
Another limitation of this work is that errors due to field inhomogeneity were not corrected in the CS reconstruction. Correction for B0 inhomogeneity in non-Cartesian undersampled data has been shown in Refs 52–55, in which the B0 map can be incorporated into the undersampling operator to simultaneously correct for field inhomogeneity while performing the CS iterations. This approach requires a good low-resolution estimate of the field inhomogeneity map, which can be computed from the densely sampled central region of radial k-space. Future implementations will incorporate the B0 map into the CS reconstruction pipeline. Some effects of B0 inhomogeneity, such as frequency drift, can be corrected during postprocessing.56–58 In Supporting Information Section 4 and Figure S5, we show that a combination of Klose’s correction for eddy current– induced phase distortion, and frequency and phase alignment using the FID-A toolbox, can significantly improve the quality of the spectra and remove the frequency drifts among all spectra. Although lipid contamination is largely preventable with VOI-based excitation, it is possible to remove the lipid signal in postprocessing using the L2-based minimization technique by Bilgic et al.59 In Supporting Information Section 3, we demonstrate the robustness of our CS technique to lipid signals originating from large prescriptions of the VOI that include the intracranial lipid layer (Supporting Information Figure S4).
5 |. CONCLUSIONS
We demonstrated the potential benefits of accelerated 2D spectroscopic imaging using radial k-space undersampling and CS reconstruction with TV regularization. Compared with CS reconstructions of undersampled Cartesian EPSI data, REPSI provided greater reconstruction accuracy and more reliable quantitation for essentially all acceleration factors. Reconstruction results in the brain indicate that EPSI-based metabolite maps are much more degraded at the acceleration factor corresponding to 13 acquired -lines, whereas REPSI still maintains reasonable image quality from the same number of spokes. The consequence is that the minimum scan time can be reduced by using the REPSI sequence, in the present example from 6:24 minutes to 2:36 minutes. Compared with the standard Cartesian approach and in combination with CS, radial undersampling is a promising approach to reduce scan time for 2D spectroscopic imaging.
Supplementary Material
ACKNOWLEDGMENT
The authors thank Dr. Uzay E. Emir for the valuable discussions on L2 minimization– based lipid suppression, reconstruction strategies, field mapping, and spectroscopic imaging with concentric circular trajectories. They also thank Dr. Manoj K. Sarma and Dr. Mathews Jacob for insightful scientific discussions.
Funding information
National Institute of Health (R01 HL135562-02, R21 1R21MH125349-01, and R56 HL 131010-02) and a Breakthrough grant from the US Congressionally Directed Medical Research Program/Breast Cancer Research Program (W81XWH-16-1-0524)
Footnotes
SUPPORTING INFORMATION
Additional Supporting Information may be found online in the Supporting Information section.
FIGURE S1 (Left) Volume-of-interest (VOI) localization for a free-breathing radial echo-planar spectroscopic imaging (REPSI) and echo-planar spectroscopic imaging (ESPI) liver scan from a healthy 33-year-old male volunteer. (Right) The REPSI (red) and EPSI (blue) liver spectra extracted from four voxel locations, numbered in yellow on the left
FIGURE S2 (Left) The VOI localization for a free-breathing REPSI and ESPI liver scan from a healthy 42-year-old male volunteer. A, The REPSI and EPSI maps of the poly-methylene lipids at approximately 1.35 ppm, measured in the liver. B, Water maps of the liver from REPSI (left) and EPSI (right). Note the strong ghosting artifacts present along the phase-encoding dimension in the EPSI maps
FIGURE S3 A, Metabolite maps of total NAA (tNAA), Cr, total choline (tCho), Glx (glutamate + glutamine), and mI (upper row) from fully sampled reconstructions of REPSI brain data from a healthy 34 year-old male volunteer, and the respective CRLB maps (bottom row). (B) Fully sampled EPSI reconstructions of tNAA, Cr, tCho, Glx, and myo-inositol (mI) metabolite maps (upper row) with the corresponding CRLB maps (bottom row). Note the higher intensities in the EPSI CRLB maps, indicating that REPSI produces more reliable metabolite concentration estimates, in part due to relatively high SNRs. All maps are interpolated by a factor of two
FIGURE S4 A, left column: Fully sampled and accelerated (acceleration factor [AF] = 3×) non-lipid-suppressed EPSI tNAA metabolite map reconstructions from an in vivo brain data set acquired with a larger VOI that encompasses the intracranial lipids at the corners. Middle column: metabolite maps reconstructed after using an L2 minimization– based lipid suppression algorithm by Bilgic et al. Right column: reconstructed spectra for fully sampled and accelerated acquisitions (AF = 3×) before and after lipid suppression in postprocessing. B, Same as (A) except for REPSI. The metabolite maps are interpolated by a factor of two
FIGURE S5 Overlaid in vivo brain spectra from the voxels within the VOI (highlighted in red), shown on the localization image (left). A, Spectra with no eddy current or frequency drift corrections. B, Spectra shown with only eddy-current phase correction using Klose’s method. C, Spectra shown with eddy-current phase correction and with frequency and phase-drift corrections using FID-A
FIGURE S6 A, Left: The REPSI and EPSI metabolite maps of tNAA from the fully sampled reference (eight averages) compared with the maps from the fully sampled, denoised reconstructions (middle) with two averages (denoised), and the maps from compressed-sensing (CS) reconstructions (right) at AF = 2.5 with five averages. B, Left: Fully sampled reference metabolite maps of tNAA (eight averages), compared with the fully sampled, denoised map (middle) with two averages versus the map from CS reconstruction at AF = 4.0 with eight averages. The CS reconstructed maps in both cases showed improved SNR and greater similarity to the fully sampled reference (eight averages) compared with the denoised fully sampled data, especially for REPSI. All maps are interpolated by a factor of two
TABLE S1 Normalized RMS error values of reconstructions from time-equivalent, (denoised) fully sampled EPSI and REPSI acquisitions versus normalized RMS error values from CS reconstruction of time-equivalent accelerated data with different numbers of averages. Note: This data set is from a healthy 32-year-old male volunteer, and 99 voxels within the VOI were quantified with LCModel to produce the metabolite maps and the SNR estimates. The CS reconstructions were done with retrospective undersampling at different AFs and with varying numbers of averages, so that the accelerated acquisitions were time-equivalent to fully sampled acquisitions with one, two, three, and four averages (A-D, respectively). The percent difference in normalized RMS error (nRMSe) with respect to the fully sampled denoised data is shown in parentheses next to the nRMSE value. This percent difference is defined as 100*(nRMSEAF – nRMSEFull)/nRMSEFull (a negative percent difference indicates a reduction in the nRMSE value compared with the nRMSE of the fully sampled denoised data)
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.Nelson SJ Multivoxel magnetic resonance spectroscopy of brain tumors. Mol Cancer Ther. 2003;2:497–507. [PubMed] [Google Scholar]
- 2.Barker PB, Bizzi A, Stefano ND, Lin DDM, Gullapalli R Clinical MR Spectroscopy: Techniques and Applications. Cambridge, United Kingdom: Cambridge University Press; 2010. [Google Scholar]
- 3.Brown TR, Kincaid BM, Ugurbil K NMR chemical shift imaging in three dimensions. Proc Natl Acad Sci USA. 1982;79:3523–3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Posse S, Tedeschi G, Risinger R, Ogg R, Bihan DL High speed 1H spectroscopic imaging in human brain by echo planar spatial-spectral encoding. Magn Reson Med. 1995;33:34–40. [DOI] [PubMed] [Google Scholar]
- 5.Adalsteinsson E, Irarrazabal P, Topp S, Meyer C, Macovski A, Spielman DM Volumetric spectroscopic imaging with spiral-based k-space trajectories. Magn Reson Med. 1998;39:889–898. [DOI] [PubMed] [Google Scholar]
- 6.Furuyama JK, Wilson NE, Thomas MA Spectroscopic imaging using concentrically circular echo-planar trajectories in vivo. Magn Reson Med. 2012;67:1515–1522. [DOI] [PubMed] [Google Scholar]
- 7.Schirda CV, Tanase C, Boada FE Rosette spectroscopic imaging: optimal parameters for alias-free, high sensitivity spectroscopic imaging. J Magn Reson Imaging. 2009;29:1375–1385. [DOI] [PubMed] [Google Scholar]
- 8.Hingerl L, Bogner W, Moser P, et al. Density-weighted concentric circle trajectories for high resolution brain magnetic resonance spectroscopic imaging at 7T: DW-CONCEPT for high resolution brain MRSI at 7T. Magn Reson Med. 2018;79:2874–2885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Emir UE, Burns B, Chiew M, Jezzard P, Thomas MA Non-water-suppressed short-echo-time magnetic resonance spectroscopic imaging using a concentric ring k-space trajectory. NMR Biomed. 2017;30:e3714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Feng LI, Grimm R, Block KT, et al. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2014;72:707–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Glover GH, Pauly JM Projection reconstruction techniques for reduction of motion effects in MRI. Magn Reson Med. 1992;28:275–289. [DOI] [PubMed] [Google Scholar]
- 12.Ramirez MS, Lee J, Walker CM, et al. Radial spectroscopic MRI of hyperpolarized [1-13C] pyruvate at 7 Tesla: radial MRI of Hyperpolarized Pyruvate at 7T. Magn Reson Med. 2014;72:986–995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ludwig D, Korzowski A, Ruhm L, Ladd ME, Bachert P Three-dimensional 31P radial echo-planar spectrocopic imaging in vivo at 7T. In: Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, Hawaii, 2017. Abstract #1247. [Google Scholar]
- 14.Boer VO, Ronen I, Pedersen JO, Petersen ET, Lundell H Metabolite diffusion weighted imaging with golden angle radial echo planar spectroscopic imaging. In: Proceedings of the 27th Annual Meeting of ISMRM, Montréal, Canada, 2019. Abstract #3616. [Google Scholar]
- 15.Bogner W, Otazo R, Henning A Accelerated MR spectroscopic imaging—a review of current and emerging techniques. NMR Biomed. 2020:e4314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chan RW, Ramsay EA, Cheung EY, Plewes DB The influence of radial undersampling schemes on compressed sensing reconstruction in breast MRI. Magn Reson Med. 2012;67:363–377. [DOI] [PubMed] [Google Scholar]
- 17.Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE Trans Med Imaging. 2007;26:68–76. [DOI] [PubMed] [Google Scholar]
- 18.Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R XD-GRASP: golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn Reson Med. 2016;75:775–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chandarana H, Feng LI, Block TK, et al. Free-breathing contrast-enhanced multiphase MRI of the liver using a combination of compressed sensing, parallel imaging, and golden-angle radial sampling. Invest Radiol. 2013;4810–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chambolle A An algorithm for total variation minimization and applications. J Mathematical Imaging and Vision. 2004;20:89–97. [Google Scholar]
- 21.Block KT, Uecker M, Frahm J Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn Reson Med. 2007;57:1086–1098. [DOI] [PubMed] [Google Scholar]
- 22.Furuyama JK, Wilson NE, Burns BL, Nagarajan R, Margolis DJ, Thomas MA Application of compressed sensing to multidimensional spectroscopic imaging in human prostate. Magn Reson Med. 2012;67:1499–1505. [DOI] [PubMed] [Google Scholar]
- 23.Nassirpour S, Chang P, Avdievitch N, Henning A Compressed sensing for high-resolution nonlipid suppressed 1 H FID MRSI of the human brain at 9.4T. Magn Reson Med. 2018;80:2311–2325. [DOI] [PubMed] [Google Scholar]
- 24.Chatnuntawech I, Gagoski B, Bilgic B, Cauley SF, Setsompop K, Adalsteinsson E Accelerated 1H MRSI using randomly undersampled spiral-based k-space trajectories. Magn Reson Med. 2015;74:13–24. [DOI] [PubMed] [Google Scholar]
- 25.Kasten J, Lazeyras F, Ville DVD Data-driven MRSI spectral localization via low-rank component analysis. IEEE Trans Med Imaging. 2013;32:1853–1863. [DOI] [PubMed] [Google Scholar]
- 26.Klauser A, Courvoisier S, Kasten J, et al. Fast high-resolution brain metabolite mapping on a clinical 3T MRI by accelerated H-FID-MRSI and low-rank constrained reconstruction. Magn Reson Med. 2019;81:2841–2857. [DOI] [PubMed] [Google Scholar]
- 27.Lam F, Ma C, Clifford B, Johnson CL, Liang Z-P High-resolution 1H-MRSI of the brain using SPICE: data acquisition and image reconstruction. Magn Reson Med. 2016;76:1059–1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bhattacharya I, Jacob M Compartmentalized low-rank recovery for high-resolution lipid unsuppressed MRSI: high-resolution lipid unsuppressed MRSI. Magn Reson Med. 2017;78:1267–1280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Andronesi OC, Gagoski BA, Sorensen AG Neurologic 3D MR spectroscopic imaging with low-power adiabatic pulses and fast spiral acquisition. Radiology. 2012;262:647–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chiew M, Jiang W, Burns B, et al. Density-weighted concentric rings k-space trajectory for 1H magnetic resonance spectroscopic imaging at 7 T. NMR Biomed. 2018;31:e3838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bottomley PA Spatial localization in NMR spectroscopy in vivo. Ann N Y Acad Sci. 1987;508:333–348. [DOI] [PubMed] [Google Scholar]
- 32.Scheenen TWJ, Klomp DWJ, Wijnen JP, Heerschap A Short echo time 1H-MRSI of the human brain at 3T with minimal chemical shift displacement errors using adiabatic refocusing pulses. Magn Reson Med. 2008;59:1–6. [DOI] [PubMed] [Google Scholar]
- 33.Ogg RJ, Kingsley PB, Taylor JS WET, a T1-and B1-insensitive water-suppression method for in vivo localized 1H NMR spectroscopy. J Magn Reson B. 1994;104:1–10. [DOI] [PubMed] [Google Scholar]
- 34.Fessler JA, Sutton BP Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans Signal Processing. 2003;51:560–574. [Google Scholar]
- 35.Beck A, Teboulle M Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans Image Process. 2009;18:2419–2434. [DOI] [PubMed] [Google Scholar]
- 36.Fessler JA Michigan Image Reconstruction Toolbox. https://web.eecs.umich.edu/~fessler/code/index.html (Accessed June 25, 2018).
- 37.Hanson LG, Schaumburg K, Paulson OB Reconstruction strategy for echo planar spectroscopy and its application to partially undersampled imaging. Magn Reson Med. 2000;44:412–417. [DOI] [PubMed] [Google Scholar]
- 38.Klose U In vivo proton spectroscopy in presence of eddy currents. Magn Reson Med. 1990;14:26–30. [DOI] [PubMed] [Google Scholar]
- 39.Bydder M, Hamilton G, Yokoo T, Sirlin CB Optimal phased-array combination for spectroscopy. Magn Reson Imaging. 2008;26:847–850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Near J, Edden R, Evans CJ, Paquin R, Harris A, Jezzard P Frequency and phase drift correction of magnetic resonance spectroscopy data by spectral registration in the time domain: MRS drift correction using spectral registration. Magn Reson Med. 2015;73:44–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Simpson R, Devenyi GA, Jezzard P, Hennessy TJ, Near J Advanced processing and simulation of MRS data using the FID appliance (FID-A)—an open source, MATLAB-based toolkit. Magn Reson Med. 2017;77:23–33. [DOI] [PubMed] [Google Scholar]
- 42.Cabanes E, Confort-Gouny S, Le Fur Y, Simond G, Cozzone PJ Optimization of residual water signal removal by HLSVD on simulated short echo time proton MR spectra of the human brain. J Magn Reson. 2001;150:116–125. [DOI] [PubMed] [Google Scholar]
- 43.Provencher SW Estimation of metabolite concentrations from localized in vivo proton NMR spectra. Magn Reson Med. 1993;30:672–679. [DOI] [PubMed] [Google Scholar]
- 44.Soher BJ, Semanchuk P, Todd S, Steinberg J, Young K VeSPA: integrated applications for RF pulse design, spectral simulation and MRS data analysis. In: Proceedings of the 19th Annual Meeting of the ISMRM, Montréal, Canada, 2011. Abstract #1410. [Google Scholar]
- 45.Scheffler K, Hennig J Reduced circular field-of-view imaging. Magn Reson Med. 1998;40:474–480. [DOI] [PubMed] [Google Scholar]
- 46.Smith TB, Nayak KS MRI artifacts and correction strategies. Imaging Med. 2010;2:445–457. [Google Scholar]
- 47.Wang J, Chen Z, Wang Y, Yuan L, Xia L A feasibility study of geometric-decomposition coil compression in MRI radial acquisitions. Comput Math Methods Med. 2017;2017:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cunningham CH, Vigneron DB, Chen AP, et al. Design of flyback echo-planar readout gradients for magnetic resonance spectroscopic imaging. Magn Reson Med. 2005;54:1286–1289. [DOI] [PubMed] [Google Scholar]
- 49.Saucedo A, Sarma M, Thomas MA Radial flyback echo-planar spectroscopic imaging with golden angle sampling and total variation-based compressed sensing reconstruction. In: Proceedings of the ISMRM & SMRT Virtual Conference & Exhibition, 2020. Abstract #2865. [Google Scholar]
- 50.Ong F, Uecker M, Lustig M Accelerating non-C artesian MRI reconstruction convergence using k-space preconditioning. IEEE Trans Med Imaging. 2020;39:1646–1654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Uecker M, Lai P, Murphy MJ, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71:990–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sutton BP, Noll DC, Fessler JA Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Trans Med Imaging. 2003;22:178–188. [DOI] [PubMed] [Google Scholar]
- 53.Fessler JA, Lee S, Olafsson VT, Shi HR, Noll DC Toeplitz-based iterative image reconstruction for MRI with correction for magnetic field inhomogeneity. IEEE Trans Signal Processing. 2005;53:10. [Google Scholar]
- 54.Weller DS, Ramani S, Fessler JA Augmented Lagrangian with variable splitting for faster non-C artesian L1-SPIRiT MR image reconstruction. IEEE Trans Med Imaging. 2014;33:351–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bhave S, Eslami R, Jacob M Sparse spectral deconvolution algorithm for noncartesian MR spectroscopic imaging. Magn Reson Med. 2014;71:469–476. [DOI] [PubMed] [Google Scholar]
- 56.Rowland BC, Liao H, Adan F, Mariano L, Irvine J, Lin AP Correcting for frequency drift in clinical brain MR spectroscopy. J Neuroimaging. 2017;27:23–28. [DOI] [PubMed] [Google Scholar]
- 57.Johnson G, Jung KJ, Wu EX, Hilal SK Self-correction of proton spectroscopic images for gradient eddy current distortions and static field inhomogeneities. Magn Reson Med. 1993;30:255–261. [DOI] [PubMed] [Google Scholar]
- 58.Maudsley AA, Hilal SK Field inhomogeneity correction and data processing for spectroscopic imaging. Magn Reson Med. 1985;2:218–233. [DOI] [PubMed] [Google Scholar]
- 59.Bilgic B, Chatnuntawech I, Fan AP, et al. Fast image reconstruction with L2-regularization. J Magn Reson Imaging. 2014;40:181–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.


