Abstract
Credit card usage has surged, heightening concerns about fraud. To address this, advanced credit card fraud detection (CCFD) technology employs machine learning algorithms to analyze transaction behavior. Credit card data's complexity and imbalance can cause overfitting in conventional models. We propose a Bayesian-optimized Extremely Randomized Trees via Tree-structured Parzen Estimator (TP-ERT) to detect fraudulent transactions. TP-ERT uses higher randomness in split points and feature selection to capture diverse transaction patterns, improving model generalization. The performance of the model is assessed using real-world credit card transaction data. Experimental results demonstrate the superiority of TP-ERT over the other CCFD systems. Furthermore, our validation exhibits the effectiveness of TPE compared to other optimization techniques with higher F1 score.
-
•
The optimized Extremely Randomized Trees model is a viable artificial intelligence tool for detecting credit card fraud.
-
•
Model hyperparameter tuning is conducted using Tree-structured Parzen Estimator, a Bayesian optimization strategy, to efficiently explore the hyperparameter space and identify the best combination of hyperparameters. This facilitates the model to capture intricate patterns in the transactions, resulting in enhanced model performance.
-
•
The empirical findings exhibit that the proposed approach is superior to the other machine learning models on a real-world credit card transaction dataset.
Keywords: Credit card fraud detection, Machine learning, Optimization, Extremely Randomized Trees, Tree-structured Parzen Estimator
Method name: TP-ERT: TPE-optimized Extremely Randomized Trees
Graphical abstract
Specifications table
| Subject area: | Engineering |
| More specific subject area: | Finance with Artificial Intelligence |
| Name of your method: | TP-ERT: TPE-optimized Extremely Randomized Trees |
| Name and reference of original method: | Mihali, Sorin-Ionuț, and Ștefania-Loredana Niță. Credit Card Fraud Detection based on Random Forest Model. In 2024 International Conference on Development and Application Systems (DAS), pp. 111-114. IEEE, 2024. DOI: 10.1109/DAS61944.2024.10541240 |
| Resource availability: | Dataset available: https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud |
Background
The prevalence of credit card usage has surged due to its convenience as well as cashback and rewards programs. There were an estimated 724 billion global credit card transactions in 2023 with an average of 1.98 billion per day [1]. Nevertheless, the rise in credit card fraud intensifies the public's concerns. According to the Nilson Report which is the primary source of news and analysis of the card industry, payment-card fraud resulted in $32 billion in losses in 2021 [2]. This alarms the crucial need for advancements in credit card fraud detection (CCFD) technology to fight increasingly complicated fraud schemes. Numerous artificial technology tools leveraging machine learning algorithms have been employed to analyze transaction behavior and detect anomaly activity. For instance, Admel et al. explored the feasibility of naive Bayes, C4.5 decision tree and bagging ensemble machine learning algorithms for CCFD [3]. Experimental results demonstrate that C4.5 decision tree can correctly detect 92.7% of all predicted fraud transactions. Additionally, Sulabh and Asha proposed Adaptive XGBoost to identify credit card fraud [4]. Although the proposed model achieves the highest Area Under Curve (AUC) score, it shows a low F1 score of 0.267, owing to its low precision of 0.1574. This statistic highlights a limitation of the proposed model, which is the model tends to inaccurately classify a large proportion of transactions as fraudulent while they are non-fraudulent.
Sai and Khaing recognized the potential of boosting algorithms for CCFD and examined Adaboost, CatBoost, Gradient Boosting, XGBoost and LightGBM in identifying fraudulent transactions [5]. In the system, preprocessing with feature selection and data scaling is incorporated to ensure quality data before data learning. Experimental results demonstrate that XGBoost achieves the greatest accuracy among the tested boosting algorithms. On the other hand, Mihali and Nita employed Random Forest for CCFD [6]. The authors claimed the superiority of Random Forest with Synthetic Minority Oversampling Technique (SMOTE) in identifying credit card fraud. The approach has achieved a promising performance in minimizing the rate of undetected credit card fraud. Furthermore, Jena et al. [7], Aburbeian and Ashqar [8], Aghware et al. [9] and Jemima et al. [10] also incorporate Random Forest for CCFD. The randomness of the Random Forest from the random data sampling in the bootstrap aggregating process helps minimize the model variance, reducing the overfitting issue. This randomization characteristic enhances the interpretability and performance of Random Forest. However, the high data dimensionality, imbalanced data distribution and highly diverse patterns within both legitimate and fraudulent transactions make credit card transaction data highly complex. In the context of CCFD, fraudulent transactions are scarce, while legitimate transactions exhibit diverse patterns, such as increased spending during festivals or holidays and reduced spending during post-holiday periods. These spending behavior variations potentially trigger overfitting and complicate the data. To effectively handle this complexity, a machine learning model with higher randomness could be beneficial. Thus, in this work, we propose Extremely Randomized Trees (ERT) as a good alternative to Random Forest. Unlike Random Forest, ERT selects split points randomly without optimization and this facilitates more randomness in the decision-making process. The high randomness in split points and feature selection helps ERT minimize the overfitting to specific patterns in the training data [11]. With this, various patterns and behaviors in the dataset can be captured and this enhances the model generalization.
The performance of machine learning may be suboptimal without carefully tuning the model's hyperparameters. The model may fail to capture the intrinsic data patterns, leading to poor performance. Thus, model hyperparameter optimization is correspondingly vital for ERT. Specifically, the hyperparameters, such as the number of trees, the number of samples required to split a node, the number of features required for splitting, etc., can manipulate the model's performance. Appropriate tuning can optimize the configuration and help enhance the model's capability to generalize unknown data. To achieve this, we adopt a Tree-structured Parzen Estimator (TPE) for optimizing ERT. TPE selects the best hyperparameters according to the Bayesian Theorem. This technique accommodates diverse variables in parameter search space such as normally distributed values, log-uniform and uniform. The capability is significant to efficiently explore high-dimensional hyperparameter space, improving the optimization of ERT model. With the optimized hyperparameters, ERT can effectively apprehend intricate data structures and nonlinear relationships present in the transaction data. We name the proposed CCFD approach TP-ERT.
Method details
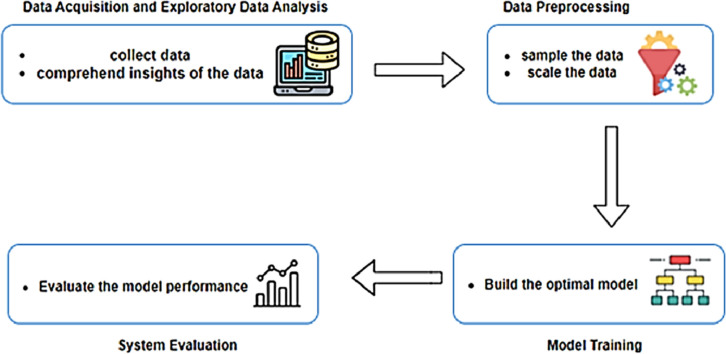
This work presents an enhanced ensemble learning approach for credit card fraud detection. The system design framework of the proposed TP-ERT is depicted in Fig. 1. In the proposed CCFD approach, there are four phases: data acquisition and exploratory data analysis, data preprocessing, model training and generation and model evaluation. After collecting the data samples as well as understanding the data distributions and trends, the collected data is further processed to prepare the data samples for model training. In this phrase, relevant features are determined for the next process. Additionally, some processes, such as addressing imbalanced data distribution, feature scaling or normalization, etc., are performed to ensure the data quality and suitability. Next, model training and generation are employed to develop a reliable classification model. Lastly, the constructed model is evaluated with unseen data for performance assessment.
Fig. 1.
The overview of the system design framework: TP-ERT.
Data acquisition and exploratory data analysis (EDA)
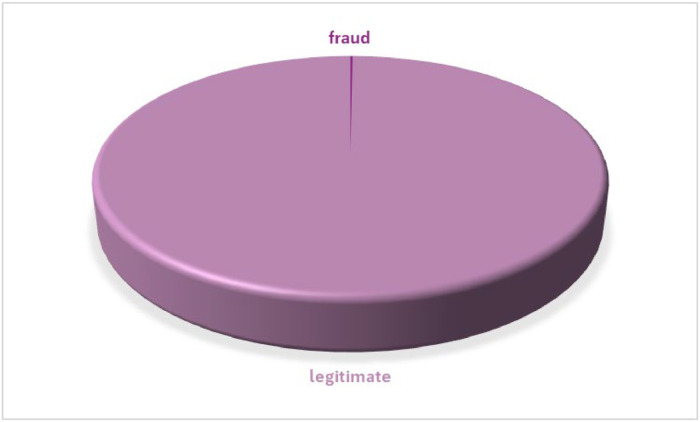
In this work, a real-world dataset containing two-day credit card transactions made by European cardholders in September 2013 is used to assess the performance of TP-ERT [12]. There are 284,807 transactions with 492 fraud instances in the dataset. This dataset is highly imbalanced with merely 0.172% positive class (frauds), as illustrated in Fig. 2. To preserve data confidentiality, the raw financial detail features and background information are processed. These features are transformed through Principal Component Analysis to produce 28 principal components, denoted as V1 to V28. The projection of Principal Component Analysis helps reduce the data dimensionality and preserve the data variance [13]. The transformation of the raw data into the orthogonal principal components could mitigate the noise of the data, enhancing the model's performance. In this work, there are three features kept original: “Time”, “Amount” and “Class”. “Time” feature is the time taken between the transaction and the first transaction, “Amount” feature is the transaction amount and “Class” feature is a class label with 1 for fraudulent transactions and 0 for legitimate transactions.
Fig. 2.
Imbalanced data distribution with only 0.172% fraud.
Data preprocessing
As observed in the EDA process, the dataset presents a severely imbalanced data distribution which is a common scenario in real-world binary classification tasks. In this work, we examine the efficiency of ERT with different data sampling techniques to rectify the imbalance:
-
•
Random Undersampling (RUS)- randomly deleting some majority class samples to achieve a class distribution balance of 0 (negative) and 1 (positive)
-
•
Random Oversampling (ROS)- randomly multiplying minority class samples for a balanced class distribution
-
•
Synthetic Minority Oversampling Technique (SMOTE)- producing synthetic samples for the minority class
-
•
Support Vector Machine Synthetic Minority Oversampling Technique (SVMSMOTE)- producing synthetic samples for the minority class based on support vectors supported by SVM decision.
Data scaling is important in machine learning to ensure useful data features contribute to the model. Credit card fraudulent transactions are usually high-amount transactions that fall in the tail of the distribution. Traditional scaling/ normalizing process which is based on the mean and standard deviation or the maximum and minimum values may compress the data range and distort data representation. Thus, Robust Scaling technique is employed in this work for its robustness to outliers [14]. Robust Scaling leverages robust statistics of median and interquartile range to scale numerical features. This technique ensures the scaled features accurately reflect the underlying data distribution which is useful in detecting frauds. Robust Scaling is formulated as below,
| (1) |
where is the data of feature i, is the median statistic of feature i and is the interquartile range of feature i.
Model training and generation
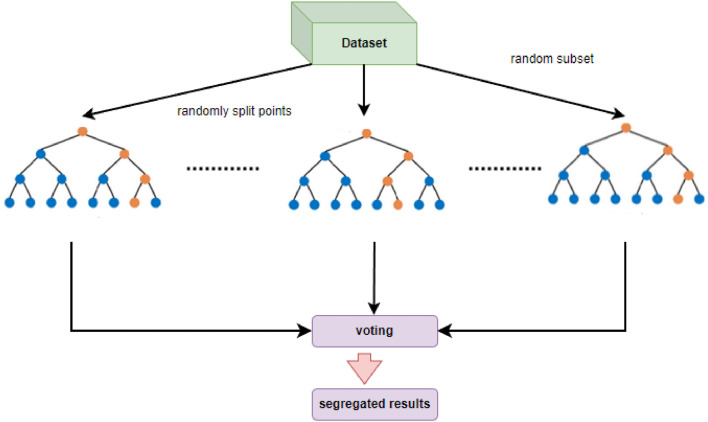
The high randomness inherent in Extremely Randomized Trees (ERT) facilitates enhanced model generalization with reduced overfitting [11]. Different noncorrelated assembled trees capture varied aspects of the transaction data, which is useful in the highly dynamic environment of card transactions where fraudulent behaviors are diverse. Similar to Random Forest, ERT is a kind of ensemble learner that constructs multiple decision trees and aggregates the prediction outputs to yield the results of segregation, as depicted in Fig. 3. However, ERT differentiates specifically in the way the trees are built and used. Unlike Random Forest which builds each tree using a bootstrap sample of the data, ERT utilizes the entire dataset to build each tree without bootstrapping. A random subset of features is chosen during the node splitting process. However, the split points are selected at random. This random selection introduces less correlation between the trees, commencing more randomness. The pseudocode algorithm of ERT's node splitting procedure is depicted in Fig. 4. In this work, there are two kinds of feature selection criteria (criterion* in Fig. 4) considered: Gini and Entropy. Entropy measures the impurity in a feature; whereas Gini is a measure of purity used while building a decision tree. The formulations of these criteria in the credit card fraud detection context are shown as follows,
| (2) |
| (3) |
where is the probability of positives and is the probability of negatives
Fig. 3.
The structure of ERT.
Fig. 4.
Pseudocode algorithm of node splitting procedure of ERT.
In machine learning, the classification performance of the selected classifier may be suboptimal if the model hyperparameters are not optimized. Thus, automating hyperparameter optimization is crucial for developing effective machine learners. Automatic hyperparameter optimization not only can minimize human labor in adopting machine learning, but also can enhance model performance with selected optimal values [15]. In this work, a Bayesian optimization variant, coined Tree-structured Parzen Estimator – TPE, is deployed for fine-tuning the proposed model's hyperparameters. The key factor of utilizing TPE is that the technique demands fewer function evaluations than other conventional optimization techniques such as random search or grid search. This is because the best hyperparameters are selected via probability guiding based on their distributions portraying the fitness scores in prior iterations [15]. Furthermore, by leveraging these prior evaluations for guiding the next hyperparameter choices, TPE can have better convergence on near-optimal or optimal hyperparameter configurations. The pseudocode algorithm of TPE is illustrated in Fig. 5. In the proposed TP-ERT, six hyperparameters in Table 1 are optimized by using the TPE with expected improvement from [16]. The optimized hyperparameter values are also recorded in the table.
Fig. 5.
Pseudocode algorithm of TPE.
Table 1.
Hyperparameters searching space and optimized values of TP-ERT.
| Hyperparameter | Searching Space | Optimized Value |
|---|---|---|
| The number of trees | 10-100 with step size 1 | 15 |
| The maximum depth of each tree | 5-50 with step size 1 | 38 |
| The maximum number of features for the best split | 1-13 with step size 1 | 11 |
| The minimum number of samples required to split an internal node | 2-11 with step size 1 | 9 |
| The minimum number of samples required to be at a leaf node | 1-11 with step size 1 | 1 |
| Splitting criterion | ‘gini’ or ‘entropy’ | gini |
Model evaluation
To assess the efficacy of TP-ERT, different performance metrics are adopted, including precision, recall, F1 score and confusion matrix. In the context of CCFD, precision measures the fraction of correctly detected frauds out of all fraud-flagged transactions. On the other hand, recall indicates the portion of actual frauds that are correctly detected. High precision and recall are desired for fewer false positives and false negatives. Anyhow, balancing recall and precision is significant because a high recall triggers more false positives and a high precision may result in missing fraud detection. F1 score offers a metric that balances these aspects. The confusion matrix details the model's predictions into true positives, true negatives, false positives and false negatives. This presentation allows a thorough insight into which aspect(s) the model excels and which aspect(s) the model needs further improvement. The formulations of the performance metrics are as follows,
| (2a) |
| (3a) |
| (4) |
Method validation
Five-fold cross-validation is performed during model hyperparameter tuning and training to ensure the performance metric, i.e. F1 score, is not biased by specific folds. In this work, the analysis of various data sampling techniques is performed to determine the most effective technique for addressing the imbalanced class distribution. Furthermore, we also examine the impact of hyperparameter optimization on the proposed TP-ERT model performance. Lastly, a performance comparison is conducted between TP-ERT and the other machine learning models.
Analysis of data sampling techniques
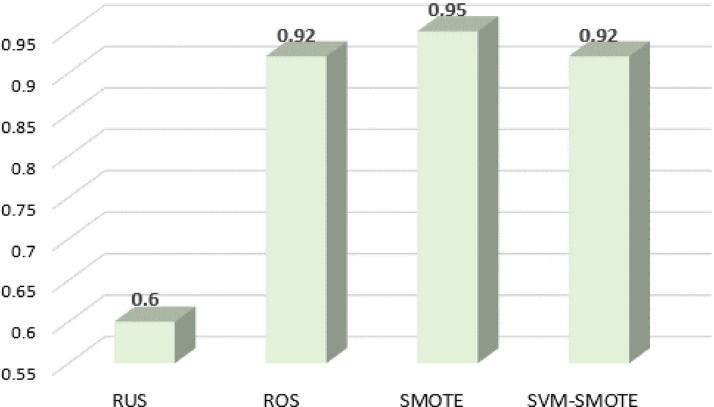
In this section, different data sampling techniques are adopted in the proposed TP-ERT and their performances are analyzed. Fig. 6 illustrate the F1 scores of these techniques. It is observed that RUS performs poorly with the lowest F1 score. This may be due to the information loss during the reduction of majority class data samples, which increases variance and leads to unstable predictions. On the other hand, SMOTE attains the best score. This indicates its ability to generate more diverse synthetic data samples, forming a representative distribution of legitimate and fraudulent transactions which is crucial to generalize the machine learning model.
Fig. 6.
F1 Scores of different data sampling techniques in TP-ERT.
Impact of hyperparameter optimization on TP-ERT performance
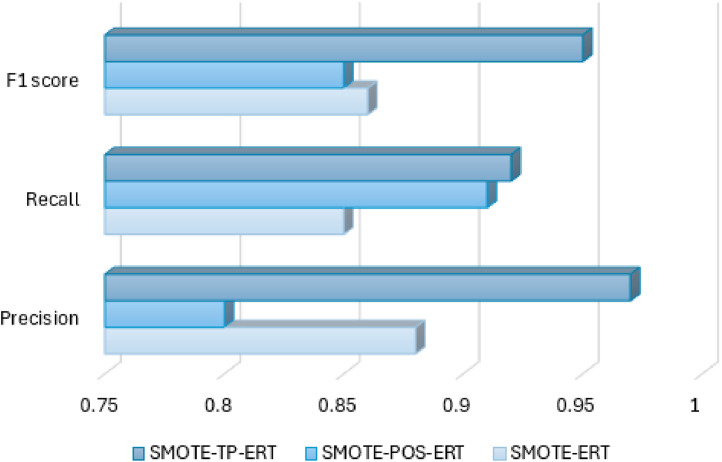
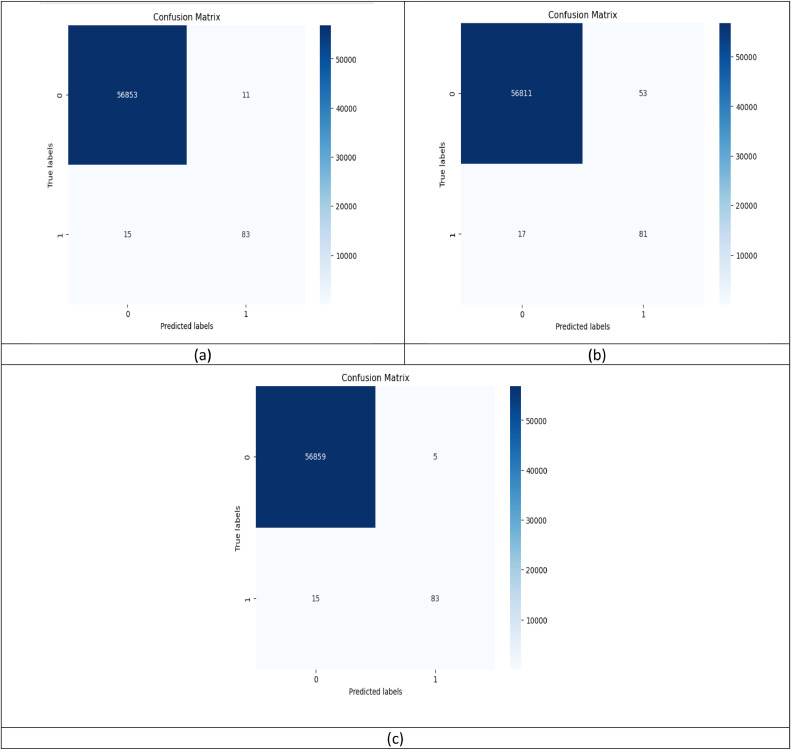
This section investigates how hyperparameter optimization influences the model performance of the proposed TP-ERT in the context of CCFD. Three optimization settings in the TP-ERT are explored: Tree-structured Parzen Estimator (TPE), Particle Swarm Optimization (PSO) and default settings as defined in the scikit-learn library. In this experiment, all the models undergo identical data preprocessing, i.e. SMOTE data sampling and Robust Scaling, to ensure consistency in feature processing since the focus is on assessing the impact of different optimizations. From Fig. 7, we can observe that TPE consistently outperforms the other optimization settings in terms of precision, recall and F1 score. From the confusion matrices in Fig. 8, it is noticed that the poor performance of PSO is mainly due to the higher rate of false positives compared to TPE. The high occurrence of false positives with PSO signifies that PSO-ERT more frequently incorrectly identifies legitimate transactions as fraudulent. This false alarm may cause extra operational costs or credit cardholder inconveniences. Additionally, we can observe that appropriate hyperparameter optimization, specifically employing TPE in this work, helps enhance model performance by reducing false positives. The occurrence of false positives declines from 11 to 5, demonstrating a substantial model improvement.
Fig. 7.
Precision, Recall and F1 score metrics with different hyperparameter optimizations.
Fig. 8.
Confusion matrices of (a) default setting in scikit-learn library, (b) PSO and (c) TPE.
Performance comparison with other models
The performance metrics of the proposed TP-ERT and the other existing CCFD models, including machine learning and deep learning models, are recorded in Table 2. From the table, it is observed that TP-ERT outperforms the deep learning models in terms of F1 score. While its precision is slightly lower than that of UAAD-FDNet [17], and its recall is marginally lower than that of CNN+SVM [18], TP-ERT's higher F1 score exhibits a more balanced performance between precision and recall. This balanced performance can alleviate the risks of false positives and false negatives, which may trigger customer dissatisfaction and result in financial losses, respectively. It is understood that high false positives can make customers experience interruptions during their purchases. When a legitimate transaction is flagged as fraudulent and the transaction is declined, this can result in customer frustration and dissatisfaction.
Table 2.
Performance comparison between the proposed TP-ERT and other models.
| Model | Precision | Recall | F1 score |
|---|---|---|---|
| Random Forest on imbalanced data (without SMOTE)* [6] | 0.95 | 0.79 | 0.86 |
| Random Forest on balanced data (with SMOTE)* [6] | 0.79 | 0.85 | 0.82 |
| Random Forest* [20] | 0.83 | 0.69 | 0.75 |
| UAAD-FDNet w/ FA* [17] | 0.9795 | 0.7553 | 0.8529 |
| CNN+SVM* [18] | 0.95 | 0.94 | 0.94 |
| AE-CNN_RNN* [21] | 0.8979 | 0.7525 | 0.8128 |
| Optimized XGB with Differential Evolution* [19] | 0.8721 | 0.8529 | 0.8624 |
| Optimized CatBoost with TPE | 0.91 | 0.93 | 0.92 |
| ERT | 0.88 | 0.85 | 0.86 |
| TP-ERT | 0.97 | 0.92 | 0.95 |
Results are extracted from the original papers
Furthermore, TP-ERT consistently outperforms the boosting algorithms, i.e. Optimized XGB [19] and Optimized CatBoost, in CCFD with higher precision, recall and F1 score. Although TP-ERT, XGB/ XGBoost and Catboost utilize ensembles of decision trees, the strategies for constructing the trees are different. XGBoost adopts gradient boosting to refine predictions based on a differentiable loss function, CatBoost integrates category embedding techniques to handle categorical data without numerical conversion, and TP-ERT employs random feature selection to diminish variance. From the empirical results, it is deduced that the adoption of random feature selection is advantageous for CCFD. The high level of randomness during tree creation ensures diverse trees in the ensemble which encompass various aspects of features related to transaction patterns in credit cards. Generally, TP-ERT shows superiority to the Random Forest-based models [6,20]. The higher scores of precision, recall and F1 score attained by TP-ERT demonstrate that this proposed model is more effective in identifying between legitimate and fraudulent transactions. The incorporation of Extremely Randomized Trees with TPE optimization further boosts the performance of Extremely Randomized Trees to better capture the intrinsic features of the transactions, yielding enhanced identification capability and reducing the occurrence of false positives and false negatives.
Limitations
None.
Ethics statements
Not applicable.
CRediT authorship contribution statement
Zheng You Lim: Conceptualization, Methodology, Validation, Formal analysis, Writing – original draft. Ying Han Pang: Conceptualization, Software, Resources, Writing – review & editing, Supervision, Project administration, Funding acquisition. Khairul Zaqwan Bin Kamarudin: Methodology, Software, Investigation, Data curation. Shih Yin Ooi: Methodology, Visualization. Fu San Hiew: Validation, Investigation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This research is supported by MMU Postdoctoral Research Fellow Grant, MMUI/240020.
Footnotes
Related research article: None
For a published article: None
Data availability
Data will be made available on request.
References
- 1.Capital One Shopping, Number of Credit Card Transactions per Second & Year: 2024 Data, Newsletter (2024). https://capitaloneshopping.com/research/number-of-credit-card-transactions/(accessed July 11, 2024).
- 2.N. Report, Newsletter Nilson Report 1232 December 2022, 2022. https://nilsonreport.com/newsletters/1232/.
- 3.Husejinović A. Credit card fraud detection using naive Bayesian and C4.5 decision tree classifiers. Period. Eng. Nat. Sci. 2020;8:1–5. [Google Scholar]
- 4.Jain S.K., Asha S. Proceedings of the IEEE 9th International Conference for Convergence in Technology. 2024. Credit Card fraud detection system using SMOTEENN and adaptive XGBoost and comparing the result with state-of-art-technique; pp. 1–7. [DOI] [Google Scholar]
- 5.Han S.S., Wai K.K. Proceedings of the 21st IEEE International Conference on Computer and Applications, ICCA 2024. 2024. A performance analysis of boosting algorithms for the identification of card fraud; pp. 260–265. [DOI] [Google Scholar]
- 6.Mihali S.I., Niță Ș.L. Proceedings of the International Conference on Development and Application Systems. 2024. Credit card fraud detection based on random forest model; pp. 111–114. [DOI] [Google Scholar]
- 7.Jena A.R., Sen S.K., Mishra M., Banerjee S., Dey N., Saha I. A comparative analysis of financial fraud detection in credit card by decision tree and random forest techniques. AIP Conf. Proc. 2023;2876 doi: 10.1063/5.0166542/2908828. [DOI] [Google Scholar]
- 8.Aburbeian A.H.M., Ashqar H.I. Proceedings of the Lecture Notes in Networks and Systems. 700 LNNS. 2023. Credit card fraud detection using enhanced random forest classifier for imbalanced data; pp. 605–616. [DOI] [Google Scholar]
- 9.Aghware F., Ojugo A.A., Odiakaose C.C., Aghware F.O., Adim Ojugo A., Adigwe W., Ojei E.O., Ashioba N.C., Okpor M.D., Geteloma V.O. Enhancing the random forest model via synthetic minority oversampling technique for credit-card fraud detection. J. Comput. Theor. Appl. 2024:3024–9104. doi: 10.62411/jcta.10323. [DOI] [Google Scholar]
- 10.Jebaseeli T.J., Venkatesan R., Ramalakshmi K. Fraud detection for credit card transactions using random forest algorithm. Adv. Intell. Syst. Comput. 2021;1167:189–197. doi: 10.1007/978-981-15-5285-4_18. [DOI] [Google Scholar]
- 11.Geurts P., Ernst D., Wehenkel L. Extremely randomized trees. Mach. Learn. 2006;63:3–42. doi: 10.1007/S10994-006-6226-1/METRICS. [DOI] [Google Scholar]
- 12.Credit Card Fraud Detection, (2017). https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud (accessed August 11, 2024).
- 13.Alfaiz S.M.F., Saleh N. Enhanced credit card fraud detection model using machine learning. Electronics. 2022;11:662. doi: 10.3390/ELECTRONICS11040662. [DOI] [Google Scholar]
- 14.Sezgin A., Boyacı A. Enhancing intrusion detection in industrial internet of things through automated preprocessing. Adv. Sci. Technol. Res. J. 2023;17:120–135. doi: 10.12913/22998624/162004. Vol. [DOI] [Google Scholar]
- 15.Nguyen H.P., Liu J., Zio E. A long-term prediction approach based on long short-term memory neural networks with automatic parameter optimization by Tree-structured Parzen Estimator and applied to time-series data of NPP steam generators. Appl. Soft Comput. 2020;89 doi: 10.1016/J.ASOC.2020.106116. [DOI] [Google Scholar]
- 16.Ozaki Y., Tanigaki Y., Watanabe S., Onishi M. Proceedings of the 2020 Genetic and Evolutionary Computation Conference, GECCO 2020. 2020. Multiobjective tree-structured parzen estimator for computationally expensive optimization problems; pp. 533–541. [DOI] [Google Scholar]
- 17.Jiang S., Dong R., Wang J., Xia M. Credit card fraud detection based on unsupervised attentional anomaly detection network. Systems. 2023;11:305. doi: 10.3390/SYSTEMS11060305. [DOI] [Google Scholar]
- 18.Yakshit, Kaur G., Kaur V., Sharma Y., Bansal V. Proceedings of the 2022 IEEE International Conference on Current Development in Engineering and Technology CCET 2022. 2022. Analyzing various machine learning algorithms with SMOTE and ADASYN for image classification having imbalanced data. [DOI] [Google Scholar]
- 19.Tayebi M., El Kafhali S. Credit card fraud detection based on hyperparameters optimization using the differential evolution. Int. J. Inf. Secur. Priv. 2022;16 doi: 10.4018/IJISP.314156. [DOI] [Google Scholar]
- 20.Prasad P.Y., Chowdarv A.S., Bavitha C., Mounisha E., Reethika C. Proceedings of the 7th International Conference on Trends in Electronics and Informatics, ICOEI 2023. 2023. A comparison study of fraud detection in usage of credit cards using machine learning; pp. 1204–1209. [DOI] [Google Scholar]
- 21.Fanai H., Abbasimehr H. A novel combined approach based on deep Autoencoder and deep classifiers for credit card fraud detection. Expert Syst. Appl. 2023;217 doi: 10.1016/J.ESWA.2023.119562. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.