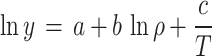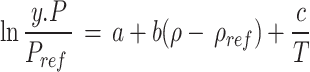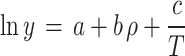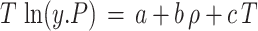Measuring and modeling the solubility of sulfasalazine in supercritical carbon dioxide to select methods for producing nanoparticles

Abstract

In the present study, the solubility of sulfasalazine in carbon dioxide was investigated at temperatures ranging from 313 K to 343 K and pressures ranging from 12 to 30 MPa. The experimentally determined molar solubilities of sulfasalazine in ScCO₂ were found to be in the range of 4.08 × 10^− 5 to 8.61 × 10^− 5 at 313 K, 3.54 × 10^− 5 to 11.41 × 10^− 5 at 323 K, 3.04 × 10^− 5 to 13.64 × 10^− 5 at 333 K, and 2.66 × 10^− 5 to 16.35 × 10^− 5 at 343 K. The solubility values were correlated via a number of different types of equations, such as semi-empirical correlations, the Peng-Robinson, the PC-SAFT equation, and the regular solution. Furthermore, the findings demonstrate that semi-empirical, equation of state models, and the regular solution model possess the capability of precisely determining the solubility. Moreover, the solubility magnitude suggests that the gas anti-solvent method may be a viable approach for nanoparticle production.

Introduction

Sulfasalazine, an anti-inflammatory drug utilized to treat rheumatoid arthritis and ulcerative colitis, was initially identified in the 1930s. The drug under consideration is classified as a class 4 compound in accordance with the Biopharmaceutical Classification System, primarily due to its restricted solubility (0.6 µg/ml) and permeation properties. Consequently, a recommended daily oral dose of 1–3 g/day has been established for patients with arthritis to compensate for the low level of exposure. Moreover, the low permeability and solubility of sulfasalazine would present considerable obstacles to achieving a considerable level of exposure following intravenous administration. This is due to the limited volume of doses that can be administered. It is therefore of great importance to enhance the APIs through the creation of diverse drug formulations. This objective can be met by undertaking a detailed examination of the physicochemical characteristics of sulfasalazine, with a particular focus on its solubility and distribution within the selected solvents¹.

Solubility represents a pivotal parameter that significantly impacts the absorption of oral drugs from the stomach and intestines. During the initial stages of drug discovery, solubility is a valuable parameter when considered alongside other properties, including ionization, lipophilicity, and permeability. In the later stages of drug development, it is also essential in classifying biopharmaceuticals, optimizing formulations, and designing a novel drug formulation².

Reducing the particle size of APIs is an effective method for improving solubility in poorly soluble APIs. Conventional techniques have limitations, including difficulty controlling particle size, the presence of solvent in the finished API, and potential degradation due to heating. Supercritical fluid technology is a promising approach for developing particle reduction technology for pharmaceuticals^3–7. A number of effective supercritical fluid techniques have been established for reducing particle size in drugs. The key factor in choosing the right supercritical fluid technique is understanding how the drug dissolves in supercritical carbon dioxide (ScCO₂). To industrialize and commercialize products derived from supercritical fluid (SCF) processes, it is essential to gain comprehensive knowledge of the quality, purity, extractability, and solubility of these materials.

Mathematical and experimental models have played a pivotal role in reducing the cost of solubility tests. By modeling solubility, we can accurately determine experimental measurements and investigate various aspects of thermodynamics and material properties. In the present era, we have advanced experimental models, equations of state, and intelligent models to achieve this objective. Accordingly, the solubility of sulfasalazine in ScCO₂ was determined under a range of temperature and pressure condition. The data were then subjected to modeling using a variety of techniques, including (1) density-based models, (2) PR with vdW2, (3) PC-SAFT, and (4) the regular solution model. Subsequently, the potential of semi-empirical models for the analysis of the data was explored. Furthermore, an assessment was conducted to evaluate the capacity of the models to be correlated. This involved a comparison between the calculated data and the experimental data, with the aim of identifying any potential discrepancies. Two statistical criteria were employed to assess the models’ capabilities: the average absolute relative deviation (AARD) and the adjusted correlation coefficient (R_adj). Following this analysis, the enthalpies of vaporization (ΔH_vap), solvation (ΔH_sol), and total enthalpy (ΔH_total) were determined.

Materials and methods

Materials

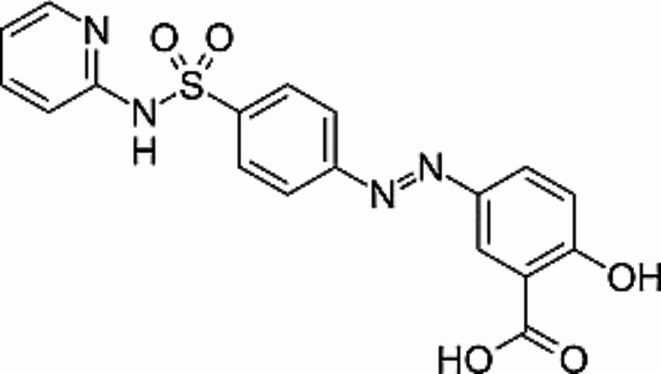
Sulfasalazine with below structure (Fig. 1) (CAS number 599-79-1) was procured from Sigma-Aldrich, while CO₂ of greater than 99.5% purity was obtained from a local supplier.

Fig. 1.

Structure of sulfasalazine.

Methods

Experimental procedure

The solubility of sulfasalazine in supercritical carbon dioxide was evaluated according to the procedure reported in previous articles^8,9. The initial stage of the experiment involved directing a CO₂ gas with a pressure of 5.5 MPa and a temperature of 298 K to a refrigerator with a temperature of 268 K, with the objective of observing the phase transition from gas to liquid. Subsequently, the liquid is subjected to pressure through a specialized pump in order to attain the targeted pressure range (12 to 30 MPa). A high-pressure stainless steel cell with a volume of 200 ml has been constructed for the purpose of conducting solubility experiments. The fixed value of API is recorded on the sheet and positioned at the base of the cell. Subsequently, the liquid is introduced into the cell, where the drug is mixed and dissolved in the carbon dioxide using a high-speed stirrer. The temperature of the process is set as the second impact parameter on solubility using an accurate temperature-control device with a precision of ± 1 K. Based on preliminary experiments; a static time of 4 h with a stirring rate of 200 rpm was identified as sufficient to achieve equilibrium. Finally, the drug mole fraction was determined by applying the following equation using the initial and final drug masses as variables:

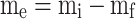1

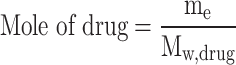2

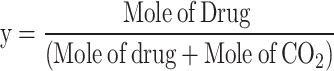3

Semi-empirical models

A plethora of semi-empirical models have been put forth with the aim of establishing a correlation between the solubility of a solute in scCO₂. The absence of a requirement for solute properties (in contrast to the EoSs), the ease of application, and the acceptable accuracy are the principal advantages of these models. The sole disadvantage of these models is the necessity for experimental solubility data. A number of equation have been formulated with varying adjustable parameters (ranging from three to eight) with the objective of enhancing the correlation with experimental data. As example, Bartle et al.¹⁰, MST^11,12, Chrastil¹³, Kumar and Johnston¹⁴, Garlapati et al.^15,16, Alwi and Garlapati¹⁷, del Valle and Aguilera¹⁸, Sung and Shim¹⁹, Adachi and Lu²⁰, Bian et al.^21,22, Sparks et al.²³, Si-Moussa et al.²⁴, Belghait et al.²⁵ and Amooey²⁶, Haghbakhsh et al.²⁷, Mitra and Wilson²⁸, Reddy et al.^29,30, Gordillo et al.³¹, sodeifian et al.^32–34 have been put forth as a means of correlating the solubility of solutes in supercritical carbon dioxide. In contrast to the EoSs, there is no necessity to consider the properties of the solute, the method of application is uncomplicated, and the accuracy is satisfactory. The only disadvantage associated with these models is that they necessitate the availability of experimental solubility data^35–38. The density-based models are founded upon the tenet of straightforward error minimization. The adjustable parameters of these models can be optimized by an algorithm, such as a genetic algorithm or simulated annealing, within the MATLAB software. As shown in Table 1, five of the most popular theory-based models were used in this work to estimate data consistency and values of solvation, evaporation, and total enthalpies.

Table 1.

Semi-empirical models.

Model	Function
Chrastil13
Bartle et al.39
Kumar- Johnston
Mendez-Santiago and Teja

Equation of state-based models

Although the use of thermodynamic models requires a lot of information about the solvent, many authors used these types of models^40–47. The solubility in scCO₂ can be modeled using a variety of techniques, including semi-empirical equations, statistical models, and theoretical frameworks. Nevertheless, the conventional methodology based on the equation of state, exemplified by the Peng-Robinson (PR) and Soave-Redlich-Kwong (SRK) models, frequently yields considerable discrepancies^48–50. In such cases, it is necessary to utilize the solid properties, which in some instances, particularly for complex solids, may not be readily accessible in a database. Mixing rules (e.g., van der Waals mixing rules) must be employed to ascertain the appropriate parameters by adjusting experimental solubility data in order to minimize this discrepancy. The precision of the EoS is contingent upon the specific mixing rule utilized and the number of parameters.

The use of these types of models necessitates the input of molar volume, acentric factor, melting temperature of solute, solvent vapor pressure, critical properties of the solvent, and thermodynamic properties of carbon dioxide. A plethora of experimental methodologies have been devised to identify these substances, each of which is susceptible to error. Among the most significant methods are the Joback et al.⁵¹, Marrero and Gani⁵², Lee Kessler⁵³, Fedors⁵⁴, and Stein et al.⁵⁵ methods. In recent years, models such as the Peng Robinson, and SRK models have been employed for drugs such as lsomeprazole⁵⁶, loratadine⁵⁷, sunitinib malate⁵⁸, and pregabalin⁸. The results and output of the articles indicate that, despite the numerous difficulties encountered in their use, these methods have yielded remarkable results on a consistent basis.

Moreover, the SAFT equations represent an additional class of models that have been utilized to establish correlations between the solubility of substances in supercritical carbon dioxide. These models encompass a range of variants, including SAFT, PC-SAFT, SAFT-VR, qCPA, and PCP-SAFT. In comparison to other equations of state, they are more complex in their structure. Consequently, the general or partial forms of these models have been employed in numerous published works^59–66. The most important point in using these types of models is the molecular relationship between carbon dioxide and the solutes, which many works consider these parameters as adjustable parameters.

To ascertain the solubility of a particular compound in a supercritical state, it is essential to establish a solid-CO₂ equilibrium. This procedure can be represented by means of the fundamental equilibrium relationship between a solid and ScCO₂ in a system.

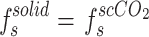4

On the basis of certain simplifying assumptions, the mole fraction is calculated using the following Eqs^67,68:

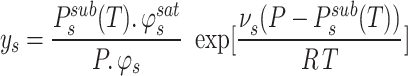5

In this context, the solute fugacity coefficient at 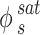and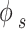 represents the sublimation pressure of the APIs, which is generally low. Therefore, it can be assumed that 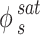is equal to one. In order to model an equilibrium process, the value of 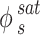is determined using an appropriate model. To assess the EoSs, the PR and PC-SAFT models were considered.

PC-SAFT model

The PC-SAFT model is formulated based on the residual molar Helmholtz energy (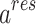) including the, which is the main basis of this model in the present work⁶⁹:

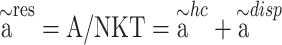6

In accordance with the tenets of first-order thermodynamic perturbation theory, the term “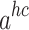” is defined as follows:⁶²:

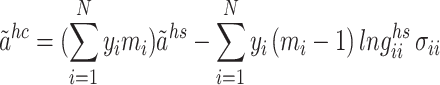7

In addition, the term 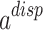is calculated by the below relationship⁶²:

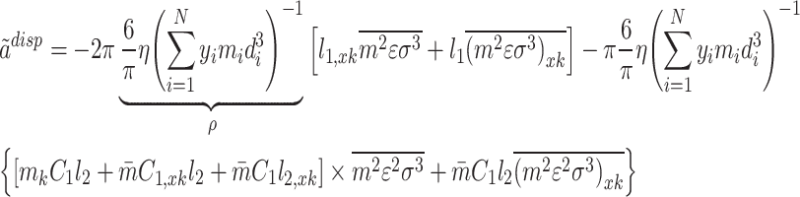8

In order to ascertain the two cross parameters (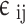 and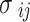) the conventional combination rules are employed⁶²:

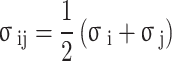9

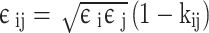10

In the aforementioned relationship, 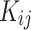represents an adjustable parameter that is dependent on temperature. The incorporation of this parameter into the relationship is intended to account for the interactions between the two disparate chains. The correlation between the compressibility factor (Z) and 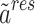can be defined as follows⁶²:

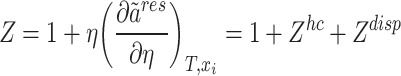11

In this context, the dimensionless volume parameter, denoted by the symbol ɳ, is defined as follows:

The fugacity coefficient of component k (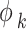 ) is ultimately established through the following methodology⁶²:

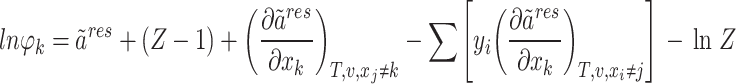12

Regular solution models

In recent years, other models have been employed to model solubility in supercritical carbon dioxide, including those related to regular solutions. Unlike equations of state, these models do not require much information about the solvent, but some thermodynamic properties such as the melting point and enthalpy of the APIs are still required. These types of models have been used in many articles^47,70–72. In the event that supercritical carbon dioxide is regarded as a solvent and the solubility is markedly low, the solubility in scCO₂ is derived from the solubility coefficient in the infinitesimal dilute state (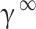), on the assumption that the fugacity of the API is identical in the two phases of solid and solvent^47,70:

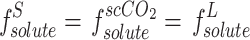13

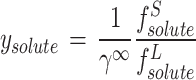14

where,

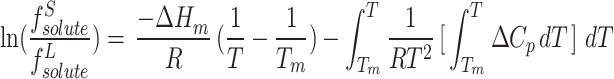15

With T_m being melting point and ΔH_m being enthalpy of fusion. If we disregard the discrepancy between the heat capacity ΔH_m of the solute in the solid and supercritical phases (which is nearly constant), then Eq. 15 can be rewritten as follows:⁷³:

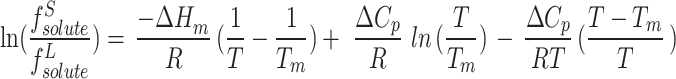16

Therefore,

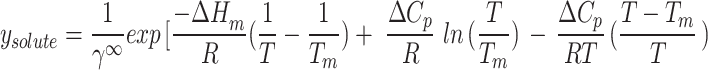17

In this study, the regular solution is employed in conjunction with the Flory-Huggins theory⁷⁴ for the purpose of determining :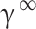

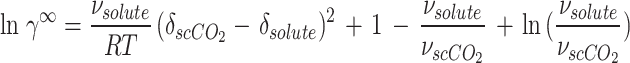18

In the absence of consideration of the parameter of ΔC_p in Eq. 17, the mole fraction in scCO₂ can be determined through the following equation:

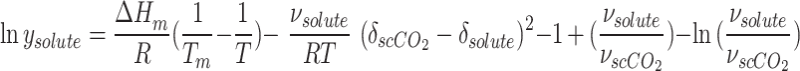19

Where:

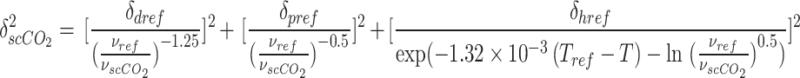20

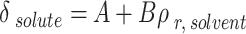21

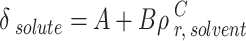22

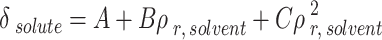23

The A, B, and C were obtained by helping the genetic algorithm. Also, the melting point and enthalpy of fusion were 513.1 K and 29.13 J.g^-1.

Results and discussions

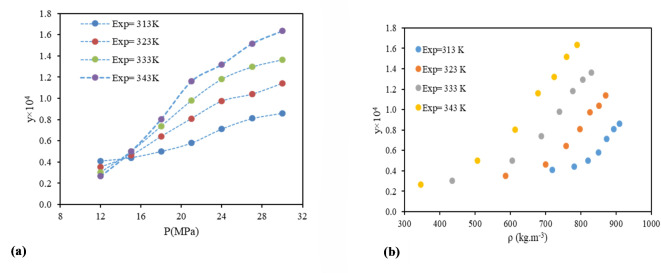
Table 2 shows the experimental pints for the solubility of sulfasalazine in scCO₂ at different pressures (12 to 30 MPa) and temperatures (313 K to 343 K). As previously stated, each data point was replicated three times to ensure the accuracy and precision of the measurements. Additionally, the standard deviation of mole fractions is presented in Table 2. The density of the CO₂ was determined in accordance with the Span-Wagner equation of state. The range of the mole fraction and the solubility of the drug were 2.660 × 10^− 5 to 1.635 × 10^− 4 and 0.083 to 1.168 kg/m³, respectively. The lowest and highest solubilities of sulfasalazine were observed under the highest temperature (343 K) and at the lowest pressure (12 MPa) and the highest pressure (30 MPa), respectively. As illustrated in Fig. 2, the solubility for each of the isotherms was found to increase with rising pressure, and the increase was more pronounced at higher temperatures. This effect is attributed to the increase in spacing of the CO₂ molecules at higher pressures due to the increase in density and performance of carbon dioxide.

Table 2.

Solubility values of sulfasalazine.

T (K)a	P (MPa)	ρ (kg.m− 3)	y × 104	SD (ȳ) × 104	S (kg.m− 3)	Expanded Uncertainty of mole fraction (U×105)
313	12	719.2	0.408	0.016	0.266	0.041
	15	781.2	0.44	0.020	0.311	0.042
	18	820.7	0.499	0.021	0.371	0.051
	21	850.4	0.579	0.024	0.446	0.051
	24	873.9	0.712	0.031	0.563	0.074
	27	893.5	0.811	0.036	0.656	0.081
	30	910.3	0.861	0.039	0.710	0.086
318	12	587.2	0.354	0.012	0.188	0.035
	15	701.1	0.464	0.021	0.295	0.046
	18	758.8	0.642	0.029	0.441	0.064
	21	797.4	0.810	0.033	0.585	0.083
	24	826.1	0.974	0.044	0.729	0.097
	27	851.7	1.04	0.047	0.801	0.104
	30	871.5	1.141	0.050	0.900	0.114
328	12	435.3	0.304	0.014	0.120	0.031
	15	606.8	0.499	0.021	0.274	0.050
	18	688.4	0.739	0.031	0.460	0.072
	21	740.3	0.98	0.044	0.657	0.098
	24	777.5	1.181	0.053	0.831	0.119
	27	806.7	1.296	0.054	0.946	0.130
	30	830.5	1.364	0.060	1.025	0.139
338	12	346.1	0.266	0.012	0.083	0.027
	15	507.5	0.499	0.021	0.229	0.050
	18	613.5	0.805	0.033	0.447	0.081
	21	678.9	1.161	0.050	0.714	0.115
	24	724.9	1.319	0.053	0.866	0.134
	27	760.3	1.515	0.064	1.043	0.150
	30	788.9	1.635	0.070	1.168	0.164

Fig. 2.

Solubility data based on pressure (a) and density (b) at different temperatures.

Figure 2 illustrates the experimental solubility profile for sulfasalazine at varying temperatures as a function of ScCO₂ density and pressure. At a fixed pressure, it becomes evident that two distinct opposing effects of temperature on solubility can be observed: firstly, the CO₂ density, and secondly, the sublimation pressure of the API. The most effective method for elucidating and contrasting these two parameters with regard to solubility is to introduce a parameter designated as the “crossover.” This point or range can serve as a valuable reference for comprehending the influence of these two parameters on solubility. A crossover point was identified at 15 MPa, which marked a notable shift in the solubility of the compound under investigation. Moreover, multiple researchers have identified consistent values for the SC-CO₂ crossover region across a range of compounds. These include decitabine (C₈H₁₂N₄O₄)⁷⁵, aripiprazole (C₂₃H₂₇Cl₂N₃O₂)⁷⁶, and oxzepam (C₂₃H₂₃NO₅S)⁷⁷. Additionally, the same findings were observed for other compounds including hydroxybenzaldehyde (C₇H₆O₂)⁷⁸, probenecid (C₁₃H₁₉NO₄S)⁷⁹, gemifloxacin (C₁₈H₂₀FN₅O₄)⁸⁰ and anthraquinone (C₁₄H₈O₂)⁸¹. At pressures below the crossover point, the value of the solubility exhibited a decline with increasing temperature. Conversely, at pressures above this point, the solubility of the drug demonstrated an increase with rising temperature. A comparable trend was observed for the solubility of other compounds in ScCO₂^{17,38,59,82,83}. As the temperature increases, the sublimation vapor pressure increases, leading to an increase in solubility. However, it is observed that below the crossover point, as the temperature increases, the density also decreases, resulting in a decrease in solubility. In the other words, at lower pressures, the effect of density becomes more pronounced than that of sublimation pressure, resulting in a decrease in solubility with increasing temperature. At higher pressures (above cross over point), the solubility increases with temperature, indicating that the sublimation pressure effect is the dominant factor. This is to be expected, given that the sublimation pressure increases exponentially with temperature.

Comparison of the correlation results

In this scientific work, an investigation was conducted into a number of different types of models. These models of solubility were created using a variety of approaches, such as, EoS, semi-empirical, and regular solution. As previously stated, each of these models requires a number of input parameters, which were discussed in detail in the preceding sections. In order to facilitate comparison between the models, two criteria were identified and considered: criteria AARD, R_adj^8,9.

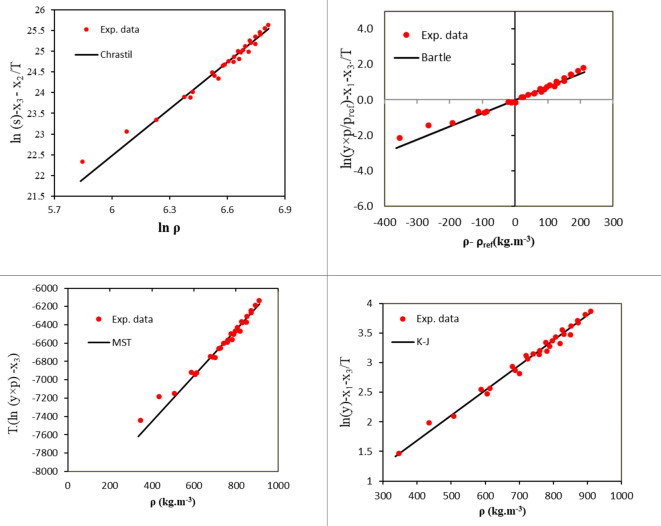
This work considers a number of density based models, namely Chrastil, Bartle et al., MST, and KJ. Each of the models is underpinned by a comprehensive theoretical framework. The findings from modelling these models are presented in Table 3, and it is evident from this that all of the models demonstrate satisfactory performance. The most precise results were produced by the KJ model with an error rate of 6.12% and a R_adj value of 0.994.

Table 3.

The outcome of the density based models.

Equation	Parameters				Criteria
	a	b	c	d	AARD (%)	R adj
Chrastil	3.71	-12.92	-4020.3	-	9.22	0.989
Bartle	6497.1	10.55	-6447.3	-	11.92	0.971
KJ	0.445	0.0042	-4203.4	-	6.12	0.994
MST	2.53	13.6	-8464.3	-	7.15	0.991

Furthermore, ensuring the precise portrayal of data represents a substantial obstacle in the domain of scientific investigation. Nevertheless, it is feasible to determine whether these data align with specific thermodynamic principles, thereby substantiating their thermodynamic coherence or incoherence. In order to assess the self-consistency of the data, the MST is a frequently employed instrument for the examination of experimental data, with the objective of determining its consistency. In addition to its capacity to correlate data, the ability to extrapolate is a crucial attribute of any model or correlation. Accordingly, the MST (self-consistency test) results were utilized to assess the extrapolation capabilities of the examined models (Fig. 3). As illustrated in Fig. 3, the examined samples exhibited linear trends under all pressures and temperatures, thereby enabling the estimation of data outcomes beyond the present range. Moreover, in accordance with the constants documented in Table 4 and the theoretical framework of the models, the enthalpy values of vaporization, solvation, and total were calculated and presented in Table 4.

Fig. 3.

Consistency solubility data of sulfasalazine.

Table 4.

The enthalpies for sulfasalazine.

Compound	ΔHtotal (kJ mol− 1) a	ΔHvap. (kJ mol− 1)b	ΔHsol. (kJ mol− 1)c
sulfasalazine	33.42	53.60	-20.18

^a Taken from Chrastil model. ^b Taken from Bartle et al., model. ^c The difference between Chrastil and Bartle et al., model.

In this study, Peng Robinson was employed alongside the Van der Waals mixing rule to analyze the data.

In addition, the sublimation vapor pressure associated with each temperature was determined to ensure that accurate comparisons could be made. Prior to using EoS to model solubility, it is of utmost importance to obtain the properties of the solute in question using an appropriate methodology. These properties include, but are not limited to, sublimation pressure, molar volume, critical temperature and pressure, acentric factor, and boiling point. Solubility is subject to several different influences that must be taken into account when modeling solubility. The value of the sublimation pressure depends on the acentric factor, which in turn is significantly influenced by the boiling temperature⁸⁴. Solubility is subject to considerable influence from a number of interdependent factors, the consideration of which is essential when attempting to ascertain the solubility of a given drug. In order to ascertain the critical temperature and pressure, the Marrero-Gani method is employed, which utilises group contributions. Subsequently, the Ambrose-Walton is employed for the calculation of the acentric factor by mentioned information (the critical temperature and pressure obtained). In conclusion, the aforementioned values are employed to ascertain the sublimation pressure via Grain-Watson method at four discrete temperatures (313, 323, 33, and 343 K). The boiling temperatures were determined using the Marrero-Gani while molar volume were calculated using the Immirzi–Perini method, as illustrated in Table 5.

Table 5.

Properties of Sulfasalazine.

Component	Boiling point (K)	Critical temperature (K)	Critical pressure (MPa)	Acentric factor	Molar volume (cm3/mol)
Sulfasalazine	844.58a	1177.3a	1.76a	0.495b	421.4c
Psub (Pa) d
	8.33 × 10− 5 (313 K)	3.52 × 10− 4 (323 K)	1.36 × 10− 3 (333 K)	4.81 × 10− 3 (343 K)

^a Calculated using Marrero and Gani Method⁵². ^bAmbrose–Walton corresponding states method⁸⁵. ^cImmirzi–Perini method⁸⁶. ^dGrain-Watson method⁸⁷.

As mentioned above, the Vander Waals mixing rule was used to evaluated the data by PR. The adjustable parameters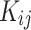 and 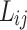as temperature dependent parameters were obtained by AARD. In addition, 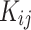was considered as a temperature dependent adjustable parameter for PC-SAFT. The intrinsic properties of the API were treated as variables in the PC-SAFT model. The segment diameter (σ), the segment number (m), and the segment energy parameter (ε/k) were estimated to be 4.13, 7.35, and 309 k, respectively, through a process of data fitting. The parameters show an opposite trend to temperature as shown in Table 6. 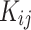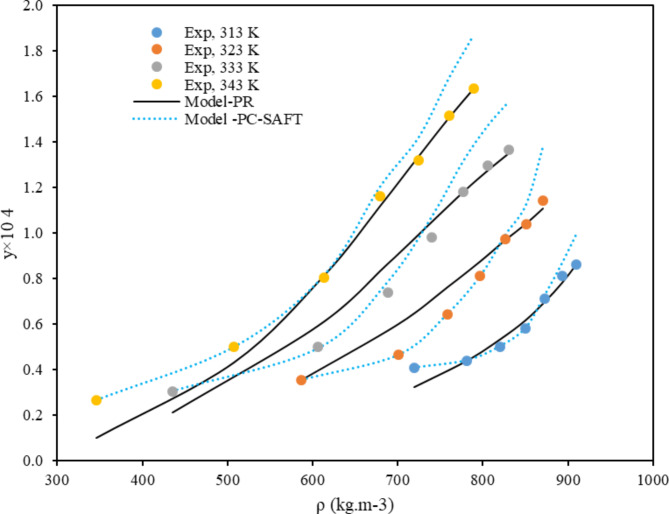The values of and 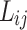were presented in Table 6 according to the minimum of AARD. The AARDs were 5.55, 8.50, 11.37 and 11.69 for temperatures of 313, 323, 333, and 343 K, respectively. The ARRD of 4.55, 6.95, 7.90, and 9.84 also reported for PC-SAFT at 313, 323, 333, and 343 K respectively. In addition, R_adj for each temperature was 0.9586, 0.9402, 0.9670, and 0.9805 for the PR model and 0.9625, 0.9477, 0.9761, and 0.9708 for the PC-SAFT model. The findings indicated that PC-SAFT and PR were effective in correlating the solubility with a high degree of accuracy, Fig. 4.

Table 6.

Correlation results for solubility of sulfasalazine in ScCO₂, by PR and PC-SAFT.

Model	Parameter	T = 313 K	T = 323 K	T = 333 K	T = 343 K	Overall
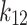
PR- vdW2		0.3961	0.3732	0.367	0.3597
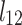
		0.2803	0.2241	0.2003	0.1842
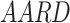
		5.55	8.50	11.37	11.69	9.27
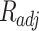
		0.9586	0.9402	0.9670	0.9805	0.9615
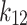
PC-SAFT		0.095	0.063	0.049	0.025
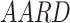
		4.55	6.95	7.90	9.84	7.31
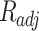
		0.9625	0.9477	0.9761	0.9708	0.9642

Fig. 4.

Modeling by PR and PC-SAFT models.

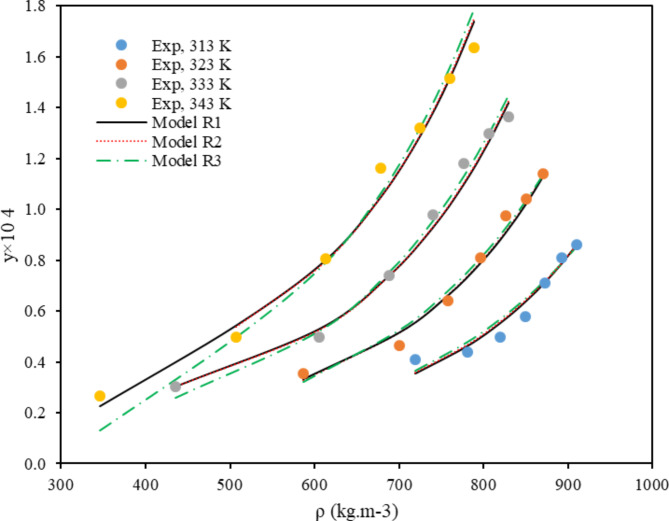
The outcomes of the regular solution with three-category solubility parameter calculation are presented in Table 7. The solute solubility parameter (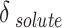 ) is a function of the reduced CO₂ density ( 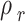), which can be expressed using the parameters of A, B, and C. Table 7 shows the values of adjustable parameters for different definitions of 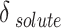with the statistical parameters of these models. Figure 5 also compares the experimental and the data obtained with these models for different descriptions of 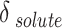. It is evident that the regular solution, using all given definitions of 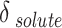, demonstrates an ability to align with the semi-empirical evidence. In consideration of the acquired AARDs, all temperature-independent models exhibit a satisfactory alignment with the data.

Table 7.

The outcomes of the regular solution method.

δsolute based on:	parameters			AARD%	R adj
	A	B	C
Equation (21)	-8.37	-0.589	-	9.80	0.979
Equation (22)	-6.87	-2.04	0.386	9.32	0.981
Equation (23)	-8.01	-1.044	8.19	9.24	0.982

Fig. 5.

Modeling by regular solution model.

Conclusion

The solubility of sulfasalazine (a compound with poor solubility in water) in scCO₂ was investigated at seven pressures (12, 15, 18, 21, 24, 27, and 30 MPa) and four temperatures (313, 223, 333, and 343 K). To the best of the authors’ knowledge, no previous experimental solubility data exist for this system. In light of the aforementioned considerations, the data presented herein constitute a notable addition to the existing body of literature on the subject. As previously demonstrated, the solubility outcomes exhibited a considerable range, spanning from 0.083 to 1.168 kg/m³. The minimum and maximum mole fractions were obtained at the highest of the four temperatures utilized in the experiments, namely, 343 K. The maximum measured mole fraction was 2.660 × 10^− 5 at 12 MPa, and the minimum was 1.635 × 10^− 4 at 30 MPa. The experimental data were modeled with five density-based models (Chrastil et al., Bartle et al., MST, Kumar-Johnston and, two EoS (PR, and PC-SAFT) and regular solution. The semi-empirical model that yielded the most precise results was that proposed by KJ model, with an absolute relative deviation (AARD) of 6.12% and R_adj, 0.994. In comparison, the model with the highest AARD (11.92%) was that proposed by Bartle et al. The results are of significant value in the context of an expanding pharmaceutical industry, particularly in light of the ongoing advancement of supercritical technology in this field. It is clear that this and similar research will contribute to the continued growth and development of this field.

List of symbols

The model adjustable parameters

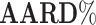
Average absolute relative deviation

Parameter of the EoS (Nm⁴ mol^− 2)

Helmholtz free energy

Parameter of the EoS (m³ mol^− 1)

k

Boltzman constant, J K^− 1

Binary interaction parameter in the mixing rules

Binary interaction parameter in the mixing rules

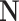
Number of data points, dimensionless

N_f

Number of fitted parameters

Pressure

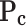
Critical pressure

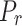
Reduced pressure

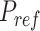
Reference pressure

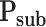
Sublimation pressure (Pa)

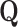
Number of independent variables

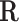
Gas constant, Jmol^− 1 K^− 1

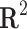
Correlation coefficient

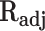
Adjusted correlation coefficient

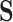
Equilibrium solubility

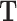
Temperature, K

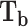
Boling point

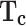
Critical temperature

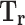
Reduced temperature

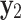
Mole fraction solubility

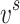
Solid molar volume

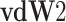
Van der Waals mixing rule with two adjustable parameters

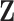
Compressibility factor

Greek symbols

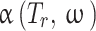
parameter of the EoS, Temperature-dependent

ε

Depth of pair potential, J

η

Packing fraction

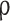
Density, kg m^− 3

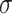
Segment diameter, Å

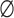
Fugacity coefficient

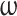
Acentric factor

Superscripts

cal

Calculated

disp

Contribution due to dispersive attraction

exp

Experimental

hc

Residual contribution of hard-chain system

hs

Residual contribution of hard-sphere system

i, j

Component

l

Liquid

s

Solid

scf

Supercritical fluid

Subscripts

i, j

Component

c

Critical property

2

Solute

Author contributions

Y.A. : Writing, drafting. editing, formal analysis, validation, conceptualization, supervisionM.G.: Writing, drafting. editing, modeling, resourcesS.T.: Writing, drafting. editing, investigation, analysisA.W.: Writing, drafting. editing, resources, analysis, modelingS.B.S.: Writing, drafting. editing, investigation, formal analysisF.F.: Writing, drafting. editing, resources, analysis, modelingU.H.: Writing, supervision, editing, validation, analysis, modeling.

Data availability

The datasets used and analysed during the current study are available from the corresponding author (Umme Hani) on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.