A Super‐Ionic Solid‐State Block Copolymer Electrolyte

Abstract

Polymer solid‐state electrolytes offer great promise for battery materials with high energy density, mechanical stability, and improved safety. However, their low ion conductivities have so far limited their potential applications. Here, it is shown for poly(ethylene oxide) block copolymers that the super‐stoichiometric addition of lithium bis(trifluoromethanesulfonyl) imide (LiTFSI) as lithium salt leads to the formation of a crystalline PEO block copolymer phase with exceptionally high ion conductivities and low activation energies. The addition of LiTFSI further induces block copolymer phase transitions into bi‐continuous Fddd and gyroid network morphologies, providing continuous 3D conduction pathways. Both effects lead to solid‐state block copolymer electrolyte membranes with ion conductivities of up to 1·10⁻¹ S cm⁻¹ at 90 °C, decreasing only moderately to 4·10⁻² S cm⁻¹ at room temperature, and to >1·10⁻³ S cm⁻¹ at −20 °C, corresponding to activation energies as low as 0.19 eV. The co‐crystallization of PEO and LiTFSI with ether and carbonate solvents is observed to play a key role to realize a super‐ionic conduction mechanism. The discovery of PEO super‐ionic conductivity at high lithium concentrations opens a new pathway for fabrication of solid polymer electrolyte membranes with sufficiently high ion conductivities over a broad temperature range with widespread applications in electrical devices.

The super‐stoichiometric addition of LiTFSI to poly(ethylene oxide) block copolymers leads to super‐ionic solid polymer electrolyte membranes reaching exceptionally high ion conductivities of up to 0.04 S cm⁻¹ at room temperature, with activation energies of only 0.19 eV. This opens a pathway for the fabrication of solid polymer electrolyte membranes with sufficiently high ion conductivities for widespread applications in lithium batteries.

1. Introduction

Lithium‐ion batteries (LIBs) are a key energy storage technology for electric vehicles and mobile portable devices. The currently used liquid electrolytes exhibit high ionic conductivities over a broad temperature range, but raise safety concerns due to the risk of leakage and flammability.^{[ 1} , ^{2 ]} For the future demand of LIBs with faster charging capability, enhanced energy density, and the required safety, solid‐state electrolyte batteries offer a promising alternative.^{[ 3 ]}

Solid inorganic electrolytes now achieve room temperature ionic conductivities (σ_rt) of 3·10⁻² S cm⁻¹,^{[ 4 ]} but are fragile and suffer from inferior contact with electrodes. Solid polymer electrolytes (SPEs) represent a promising alternative, because of their low mass density, ease of synthesis, compatibility with large‐scale manufacturing processes, mechanical stability, good electrode adhesion, and improved safety. SPEs have been already used in lithium metal batteries (LMB), but their low ionic conductivity, particularly at room temperature, and low transference numbers (t _Li+) have so far limited broad applications.^{[ 4 ]}

The most investigated polymer electrolytes are based on poly(ethylene oxide) (PEO), for which ionic conductivities of up to σ_100 °C = 3·10⁻³ S cm⁻¹ have been reported with lithium (Li) bis(trifluoromethanesulfonyl)imide (LiTFSI) as Li‐conducting salt.^{[ 5} , ⁶ , ^{7 ]} Their commercial relevance has been demonstrated for a Li‐metal‐polymer battery with a PEO‐based SPEs to power an electric car or bus^{.[ 8 ]} Still, the most important requirement for optimization is its low room temperature ionic conductivity σ_rt. Ion mobility in SPEs is coupled to the segmental motions of the polymer chains, which is particularly slow for crystalline polymers and polymers with high glass transition temperatures (ϑ_g). For polyethers, such as PEO, lithium‐ion (Li⁺)‐conduction primarily occurs through coordination with the oxygen atoms of the polyether chain via intersegmental hopping from one coordination site to another.^{[ 7 ]} Since PEO is crystalline below its melting temperature (ϑ_mp,PEO ≈60 °C), its segmental mobility at room temperature is particularly low.

An improvement of the room temperature ionic conductivity of an PEO‐based SPE is possible with the addition of plasticizers, e.g., alkyl dinitriles, which suppress crystallization. This increases the segmental mobility and thus the ionic conductivity σ, but softening reduces the mechanical stability of the SPE membranes. This could be overcome by the addition of fillers to increase the mechanical stability and the free volume, thereby creating ion conduction paths to reach values of σ_50 °C = 1·10⁻⁴ S cm⁻¹. The incorporation of “hard” components also contributes to inhibit Li‐dendrite growth.^{[⁠ 3 ]} According to the Monroe‐Newman model a modulus twice as large as for Li‐dendrites is needed to suppress dendrite formation and growth.^{[⁠ 9 ]} Therefore, PEO‐based block copolymers or PEO binary polymer systems have been proposed to independently adjust the mechanical and the electrochemical properties of the polymer membrane. For example, an interpenetrating network has been demonstrated that comprises a rigid support framework that inhibits dendrite growth and a soft network that provides high room temperature ionic conductivity to reach σ_rt = 2·10⁻⁴ S cm⁻¹.^{[ 10 ]} Polystyrene‐PEO (PS‐PEO) block copolymers (BCPs) with PS as a hard block with a high ϑ_g has demonstrated exceptional resistance to dendrite propagation.^{[ 11 ]} Still, PEO‐based SPEs with σ_rt‐values comparable to liquid electrolytes or solid inorganic electrolytes have not yet been achieved.^{[ 12} , ^{13 ]} New ion transport mechanisms need to be explored that decouple the ionic conductivity from polymer segmental dynamics. Routes to such super‐ionic polymers have been indicated, with examples of salt‐in‐polymer blends with σ_rt of up to 1·10⁻³ S cm⁻¹.^{[ 14 ]}

An obvious route to higher ionic conductivities is increasing the Li⁺‐salt concentration in the electrolyte, and thus the number of charge carriers. In SPEs such as PEO, raising the LiTFSI concentration increases the number of charge carriers, but at the same time, it promotes Li⁺‐association, thereby reducing the number of free charge carriers. Furthermore, Li⁺ ions through their coordination to the oxygen (O)‐donor atoms of the ethylene oxide (EO) units of the PEO chains effectively crosslink polymer chains, thereby reducing chain and thus ion mobility. The Li⁺ concentration is generally specified as the molar ratio of the lithium ions [Li⁺] from the LiTFSI salt to solvating oxygen (O)‐donor atoms [Li⁺:O], i.e., to the ethylene oxide units [O_EO] of the PEO chains [Li⁺:O_EO]. As a result of the competing effect of increased number of charge carrier and reduced segmental mobility, a maximum ionic conductivity is observed at a ratio [Li⁺:O_EO] = 1:12 = ≈0.1:1, where the Li⁺‐ions are solvated by 5–6 EO units of the PEO chains, and half of the PEO oxygen coordination sites are filled. At such optimal salt concentrations maximum ionic conductivities of σ = 3·10⁻³ S cm⁻¹ for LiTFSI/PEO and 1·10⁻³ S cm⁻¹ for LiTFSI/PS‐PEO have been reported at 100 °C.^{[⁠ 7 ]}

Therefore, a route to high ionic conductivities for PEO solid polymer electrolytes is highly desired. In two recent publications, the ionic conductivities of linear poly(isoprene)‐b‐poly(styrene)‐b‐poly(ethylene oxide) (PI‐PS‐PEO) BCP/LiTFSI mixtures for the rarely investigated concentration range of [Li⁺:O_EO] >1.0:1 were reported.^{[ 15} , ^{16 ]} Notably, with increasing LiTFSI concentration an again increasing ionic conductivity of up to 1·10⁻³ S cm⁻¹ together with a Li⁺‐transference number of t _Li+ = 0.7 and a low‐temperature dependence were observed, indicating that the Li⁺‐transport starts to become decoupled from the slow PEO segmental motion.^{[ 15} , ^{16 ]} Both studies used short PEO chains (M _n ≈ 2 kg mol⁻¹) such that the Li⁺ could be locally decoupled from the O‐donor atoms of the PEO by the addition of LiTFSI, i.e. [Li⁺:O_EO] >1.0:1.

In the two reports^{[ 15} , ^{16 ]} the LiTFSI/PI‐PS‐PEO membranes were fabricated by casting from tetrahydrofuran (THF), a solvent that dissolves LiTFSI as well as the PI‐, PS‐, and PEO‐polymer blocks. THF is known to play an active role in the Li⁺‐conduction mechanism. The effect of residual THF on the ionic conductivity of LiTFSI/PEO has been systematically investigated by Zhou et al.^{[ 17 ]} They reported σ_30 °C‐values of up to 1·10⁻⁴ S cm⁻¹ for a ternary mixture of LiTFSI/PEO/THF. Using Raman spectroscopy, they observed bound THF, with Li⁺‐THF‐ as well as Li⁺‐PEO‐oxygen coordination, and thus mixed PEO‐ and THF‐coordination sites. Similar ionic conductivities and ion conduction mechanisms for [Li⁺:O] >1.0:1 have also been observed for other solvents such as LiBF₄/sulfolane^{[ 18 ]} and lithium bis(fluorosulfonyl)imide (FSI)/dinitriles^{[ 19 ]} mixtures. Also, they proposed mixed bridged coordination sites involving Li‐FSI‐Li’‐ and Li‐solvent‐Li’‐ oxygen coordination, enabling a dynamic exchange of Li⁺ between coordination sites, faster than transport via PEO polymer segmental mobility.

Motivated by the observed increase of the ionic conductivity when increasing Li‐salt concentrations to [Li⁺:O_EO] >1.0:1, and the active role that THF plays in the conduction mechanism, we systematically investigated LiTFSI/PI‐PS‐PEO/THF mixtures to obtain a more detailed insight into the conduction mechanism and the achievable ionic conductivities. We therefore, investigated PI_x‐PS_y‐PEO_1.9‐based SPEs with different block molecular weights x and y (in kg mol⁻¹), in the range [Li⁺:O_EO] = 1.0–9.7:1 to systematically investigate the effect of salt amount and BCP morphology on the ionic conductivity. We find that at saturation salt concentrations of [Li⁺:O_EO] ≈2:1, a super‐ionic crystalline LiTFSI/PEO/THF phase is formed, which together with a bi‐continuous gyroid block copolymer morphology leads to SPE membranes with exceptionally high room temperature ionic conductivities σ_rt >1·10⁻² S cm⁻¹ and low activation energies E _a of 0.2 eV over a temperature range of −20 to 90 °C, comparable to the currently best solid inorganic electrolytes.

2. Results and Discussion

In the following Sections, we first derive the composition of the conducting PEO/LiTFSI/THF‐phase (Sect. 2.1–2.4; NMR, TGA, DSC) and subsequently its structure, first on an atomic scale (Sect. 2.5; XRD) and then on the length scale of the block copolymers (Sect. 2.6; TEM, SAXS). Finally, we address the ionic conduction mechanism (Sect. 2.7; EIS, NMR) and integrate the findings into a hierarchical scheme in Figure 6 that serves to explain the observed exceptionally high ionic conductivities.

Figure 6.

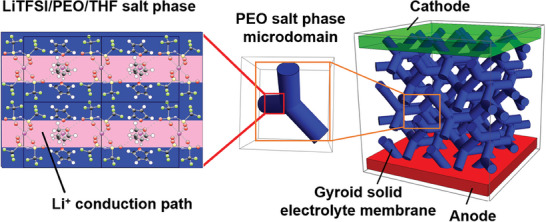
Proposed model for the super‐ionic block copolymer SPE membrane. Left, Li⁺‐conduction planes in the crystalline LiTFSI/PEO/THF phase, middle, PEO continuous domain in the gyroid structure, and right, bi‐continuous gyroid structured conduction paths connecting two electrodes.

2.1. Determination of the [Li⁺:O_EO] and [Li⁺:O_THF] Ratios

The synthesis of the PI_xPS_yPEO_1.9 block copolymers with narrow molecular weight distributions proceeds via sequential living anionic polymerization to obtain the PI_xPS_y blocks, which are subsequently coupled to a short PEO_1.9 block, ensuring a constant PEO chain length of M _n = 1.9 kg mol⁻¹, as described in a recently reported procedure.^{[ 20} , ²¹ , ^{22 ]} x and y indicate the number‐average molecular weights M _n of the corresponding blocks in kg mol⁻¹. The SPE membranes are prepared by slowly casting LiTFSI/PI_xPS_yPEO_1.9‐THF solutions in a dry argon stream.

When the PI_xPS_yPEO_1.9‐SPEs are cast from THF with an increasing amount of LiTFSI, i.e. [Li⁺:O_EO] ≥1.0:1, we observe that we reach a limiting LiTFSI amount, above which the mixture phase separates into a solid polymer‐based electrolyte SPE phase, and a dilute liquid phase. The liquid phase can be separated from the SPE phase after the membrane casting process (cf. Figure S1, Supporting Information). We observe that the separated solid block copolymer SPE phase contains bound THF in a certain ratio to its LiTFSI content. Therefore, we determined both the [Li⁺:O_EO] and the [Li⁺:O_THF] ratios in the SPE phase for an understanding of the relation between composition, structure, and ionic conductivity of the SPE phase. We note that neat PEO homopolymers and neat PI_xPS_yPEO_1.9 block copolymers do not retain bound THF after the membrane casting process. This indicates that THF is bound via its interaction with LiTFSI.

Because of the phase separation, we need to distinguish between the nominal amount of LiTFSI added to the mixture and the LiTFSI amount in the phase‐separated solid SPE phase. The Li⁺ amount in PEO electrolytes is given in terms of the molar ratio of Li⁺ to EO repeat units, i.e., as [Li⁺:O_EO]. We refer to the nominal (“n”) ratio of Li‐ions per PEO repeat unit oxygen atoms as [Li⁺:O_EO]_n when mixing the components before solvent casting. We further refer to the ratio [Li⁺:O_EO]_SPE in the phase‐separated solid polymer electrolyte (SPE) membrane obtained after solvent casting. This ratio can be smaller than the nominal ratio [Li⁺:O_EO]_n, because only a part of the LiTFSI‐salt is taken up by the SPE‐membrane. In addition, we refer to the saturation ratio [Li⁺:O_EO]_SPE,sat reached for ratios [Li⁺:O_EO]_n >3.0:1 as indicated in Figure 1a.

Figure 1.

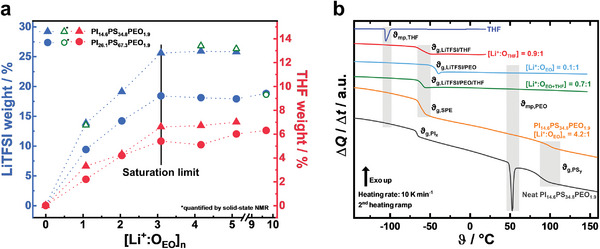
LiTFSI and THF uptake by the PEO phase were measured by 19F‐NMR and TGA, and characteristic DSC scans. a) LiTFSI (blue) and THF (red) uptake in the PEO block copolymer phase showing a saturation limit above [Li⁺:O_EO]_n ≥3.1:1, indicated by the black vertical line. In the saturation limit uptakes of 26 wt.% for LiTFSI and 7 wt.% for THF for the SPEs from PI_14.6PS_34.8PEO_1.9, and of 18 wt.% for LiTFSI and 6 wt.% for THF for the SPE from PI_26.1PS_67.3PEO_1.9 are reached. LiTFSI uptake was determined by ¹⁹F‐NMR spectroscopy, and THF uptake by TGA. b) DSC scans of the neat components and their binary and ternary mixtures. We observe that the glass transition temperature ϑ_g,SPE of the SPE from PI_14.6PS_34.8PEO_1.9 with [Li⁺:O_EO]_n = 4.2:1 (orange) is identical to the ternary mixture LiTFSI/PEO/THF (green), and differs from the binary mixtures LiTFSI/PEO (blue) and LiTFSI/THF (red). The DSC‐scan of the neat block copolymer (black) differs as well, exhibiting a strong PEO melting peak. The absence of the ϑ_mp,THF at −105 °C indicates that no uncoordinated THF exists in the SPE electrolyte.

2.2. Limiting [Li⁺:O_EO] Ratios

For the investigated PI_xPS_yPEO_1.9 block copolymers we observe a phase separation for [Li⁺:O_EO]_n ≥1.0:1. We find that the amount of phase‐separated liquid LiTFSI/THF phase increases with increasing [Li⁺:O_EO]_n, indicating a nearly constant stoichiometric composition of the solid block copolymer SPE phase. The amount of LiTFSI taken up by the solid SPE phase was determined by ¹⁹F‐solution nuclear magnetic resonance (NMR) spectroscopy. For this, the solid SPE phase membranes were dissolved together with a ¹⁹F‐standard. Measured values were confirmed by solid‐state ¹⁹F magic‐angle spinning (MAS) NMR. As shown in Figure 1a, we observe that the amount of taken‐up LiTFSI at [Li⁺:O_EO]_n ≥1.0:1 reaches a saturation limit [Li⁺:O_EO]_SPE,sat at [Li⁺:O_EO]_n ≥3.1:1 for both investigated PI_xPS_yPEO_1.9 block copolymers. As summarized in Table 1 , the saturation values are [Li⁺:O_EO]_SPE,sat = 1.5:1 for PI_14.6PS_34.8PEO_1.9 and [Li⁺:O_EO]_SPE,sat = 1.9:1 for PI_26.1PS_67.3PEO_1.9 (Figure S2, Supporting Information). Since the latter block copolymer has a lower PEO content, and since the saturation value is proportional to it, its saturation limit of 18 wt.% is lower compared to 26 wt.% observed for PI_14.6PS_34.8PEO_1.9 (see Figure 1a). We conclude that there is a maximum uptake of LiTFSI salt in the PEO phase, with a composition between [Li⁺:O_EO]_SPE,sat = 1.5:1–1.9:1.

Table 1.

Properties of neat block copolymers and their SPEs in dependence on the [Li⁺:O_EO]_n.

[Li+:OEO]n  a)	PI14.6PS34.8PEO1.9	0.0:1	1.1:1	2.0:1	3.1:1	4.2:1	5.0:1	–
	PI26.1PS67.3PEO1.9	0.0:1	1.0:1	2.1:1	3.1:1	4.1:1	5.2:1	9.7:1
LiTFSI / wt.%  b)		–	13.8 (13.5)  c)	19.1	25.6	25.9 (26.8)  c)	25.8 (26.3)  c)	–
		–	9.4	14.2	18.4	18.1	17.9	18.8 (18.6)  c)
THF / wt.%  d)		–	3.3	4.3	6.6	6.7	7.0	–
		–	2.2	4.2	5.4	5.1	6.0	6.3
[Li+:OEO]SPE  e)		–	0.7:1	1.0:1	1.5:1	1.5:1	1.5:1	–
		–	0.8:1	1.3:1	1.8:1	1.7:1	1.7:1	1.9:1
[Li+:OTHF]  f)		–	1.1:1	1.1:1	1.0:1	1.0:1	0.9:1	–
		–	1.1:1	0.8:1	0.9:1	0.9:1	0.7:1	0.7:1
[OTHF:OEO]  g)		–	0.6:1	0.9:1	1.5:1	1.6:1	1.6:1	–
		–	0.7:1	1.5:1	2.1:1	2.0:1	2.3:1	2.5:1
Morphology  h)		HEX (HEX)  i)	Fddd (Fddd)  i)	Fddd	Fddd	Gyr (Gyr/LAM)  i)	Gyr	–
		HEX	–	–	–	–	–	Fddd  i)
ϕPIx / vol.%  j)		32	28	27	25	25	25	–
		33	31	29	28	28	28	28
ϕPSy / vol.%  j)		65	59	56	52	52	51	–
		66	61	58	56	56	56	55
ϕPEO / vol.%  j)		3	13	17	23	23	24	–
		2	8	12	16	16	16	17
q* / nm−1  k)		0.20	0.13	0.11	0.09	0.09	0.09	–
		0.11	0.10	0.10	0.10	–	–	0.09
d* / nm  l)		31.0	49.1	56.1	67.8	67.8	67.8	–
		55.1	65.4	65.0	65.0	–	–	68.3
σ20 °C / S cm−1  m)		–	8·10−6	2·10−4	5·10−3	4·10−2	2·10−2	–
		–	5·10−7	2·10−4	2·10−3	5·10−3	–	1·10−2

^a,e) Nominal molar ratios between LiTFSI, THF, and EO units of the PI_xPS_yPEO_1.9 block copolymers calculated from their amounts in the block copolymer mixtures;

^b) Determined by liquid ¹⁹F‐NMR

^c) Determined by solid‐state ¹⁹F‐NMR;

^d) Determined by TGA;

^f) Molar ratio between embedded LiTFSI and THF;

^g) between embedded THF and EO unit of PI_xPS_yPEO_1.9;

^h) Determined by SAXS;

ⁱ⁾ Determined by TEM;

^j) Volume fraction on basis of published homopolymer densities (ρ_PIx = 0.83, ρ_PSy = 0.97, ρ_PEOz = 1.06 in g cm⁻³)^{[ 27 ]} and calculated with block wt.% (Table S1, Supporting Information). The volume fraction of the PEO phase, which additionally contains the embedded THF and LiTFSI amount; Calculated based on the respective wt.% and published densities (ρ_THF = 0.89,^{[ 28 ]} ρ_LiTFSI = 2.25^{[ 29 ]} in g cm⁻³);

^k) From the first scattering peak, determined by SAXS;

^l) Corresponds to the unit cell size or long‐period, calculated from: d* = 2π (q*)⁻¹.

^m) Ionic conductivity measured by EIS at 20 °C.

2.3. Limiting [Li⁺:O_THF] Ratios

The reports of Zhou et al. indicate that residual THF in the solid PEO phase plays an important role in the conduction mechanism.^{[ 17 ]} The amount of residual or bound THF for all samples was determined by thermogravimetric analysis (TGA) as shown in Figures S3–S5 (Supporting Information). Zhou et al. showed by TGA that the residual THF can be removed by heating up to 280 °C, with measured contents between 9.8 and 12.5 wt.%.^{[ 15} , ¹⁶ , ^{17 ]} Extended drying times had no influence on these values. In agreement, the TGA curves measured for the investigated LiTFSI/PI_xPS_yPEO_1.9/THF mixtures show a main weight loss due to evaporation of residual THF at temperatures up to 200 °C, reaching a plateau of nearly constant mass, until thermal decomposition of the BCP and LiTFSI starts above 280 °C (Figure S5, Supporting Information). We therefore took the total weight loss up to 280 °C as the amount of residual THF. The measured weight losses are summarized in Table 1. Figures 1a and S6 (Supporting Information) show that the weight losses are proportional to the amount of LiTFSI for all block copolymer SPEs, and are between 3.3 and 7.0 wt.% for PI_14.6PS_34.8PEO_1.9 and between 2.2 and 6.3 wt.% for PI_26.1PS_67.3PEO_1.9. As shown in Table 1, in the saturation region [Li⁺:O_EO]_n ≥3.1:1 this corresponds to [Li⁺:O_THF] = 1.0:1 or [O_THF:O_EO] = 1.6:1 for PI_14.6PS_34.8PEO_1.9 and [Li⁺:O_THF] = 0.7:1 or [O_THF:O_EO] = 2.5:1 for PI_26.1PS_67.3PEO_1.9. As a result, for all SPEs at the saturation point at [Li⁺:O_EO]_n ≥3.1:1, the THF content is proportional to the LiTFSI content, which in turn is proportional to PEO content in the BCPs.

2.4. LiTFSI/PEO/THF Ternary Micro‐Phase Formation

To determine whether the three components LiTFSI, PEO, and THF form separated or common phases, we performed differential scanning calorimetry (DSC) measurements on all different block copolymer SPEs of LiTFSI/PI_xPS_yPEO_1.9/THF, as well as on neat THF, the binary LiTFSI/THF and LiTFSI/PEO mixtures, the ternary LiTFSI/PEO/THF mixture and the neat PI_xPS_yPEO_1.9 BCPs for reference.^{[ 21 ]} For all samples, distinct signatures of the glass transition ϑ_g and melting transition ϑ_mp are observed. Figure 1b summarizes these characteristic signals, where the block copolymer SPE of LiTFSI/PI_14.6PS_34.8PEO_1.9/THF with [Li⁺:O_EO]_n = 4.2:1 is shown as an example. In Figure 1b ϑ_g,Pix. ϑ_g,PSy, and ϑ_g,SPE denote the glass transition temperatures of polyisoprene (PI), polystyrene (PS), and the solid polymer electrolyte (SPE) LiTFSI/PI_xPS_yPEO_1.9/THF, respectively. A detailed discussion of the DSC experiments can be found in the Supporting Information.

The neat BCP shows a melting transition ϑ_mp,PEO at 50 °C, which is not present in the SPEs (Figure S7, Supporting Information). The disappearance of ϑ_mp,PEO indicates that in the SPEs PEO does not form neat PEO‐crystals, but becomes incorporated into the LiTFSI/THF‐phase. The LiTFSI/PI_xPS_yPEO_1.9/THF block copolymer SPE shows a glass transition at ϑ_g,SPE = −70 to −60 °C, which is identical to the glass transition of the ternary LiTFSI/PEO/THF mixture (Figure S10 and Table S4, Supporting Information) and the binary mixture LiTFSI/THF (Figure S9 and Table S3, Supporting Information), but different compared to the LiTFSI/PEO ϑ_g,LiTFSI/PEO = −40 to −30 °C (Figure S8, Supporting Information). The glass transitions of the PI_x block at ϑ_g,PIx ≈−67 °C and the PS_y block at ϑ_g,PSy = 92–100 °C indicate their microphase separated state with no presence of THF, whose presence would lower the glass transition temperatures due to its plasticizing effect.^{[ 23} , ²⁴ , ²⁵ , ^{26 ]} THF is completely coordinated to LiTFSI, as indicated by the absence of ϑ_mp,THF at −105 °C (Figure S11, Supporting Information).

From the DSC‐scans, we can conclude that LiTFSI, PEO, and THF form a ternary LiTFSI/PI_xPS_yPEO_1.9/THF phase in the block copolymer SPEs, which is microphase‐separated from the PI_x and PS_y polymer blocks. The ¹⁹F‐NMR and TGA experiments show that the PEO microphase takes up both LiTFSI and THF to form the ternary mixture that in the saturation region [Li⁺:O_EO]_n ≥3.1:1 has an approximate stoichiometry of the molar ratios of [Li⁺:O_THF:O_EO] = 1.5:1.6:1 for PI_14.6PS_34.8PEO_1.9 and of [Li⁺:O_THF:O_EO] = 1.9:2.5:1 for PI_26.1PS_67.3PEO_1.9 as summarized in Table 1. The ¹H‐¹H‐FRDR NMR spectra (Figure S30) and the ¹H‐¹H‐NOESY‐spectra show that only a very small amount of THF, close to the NMR‐detection limit, is present in the PI‐domains, and no THF is present in the PS‐domains.

2.5. LiTFSI/PEO/THF‐co‐Crystallization

From wide‐angle X‐ray scattering (WAXS) we observe that the LiTFSI/PEO/THF phase in the block copolymer SPEs has a crystalline structure. We refer to this structure as a co‐crystal of LiTFSI, PEO, and THF as shown by the unit cell in Figure 2b, distinguishing it from the formation of pure PEO‐crystals. Figure 2a shows the measured X‐ray diffraction (XRD) curves for the SPEs from PI_14.6PS_34.8PEO_1.9 for LiTFSI concentrations increasing from [Li⁺:O_EO]_n = 1.1–5.0:1. For all LiTFSI concentrations we observe the same characteristic peak positions. In Figure 2a we also show for comparison the XRD curves reported by Zhou et al. for a binary LiTFSI/THF and a ternary LiTFSI/PEO/THF blend.^{[ 17 ]} We observe good agreement between the characteristic peak positions for the SPE of LiTFSI/PI_xPS_yPEO_1.9/THF phase and the reported ternary LiTFSI/PEO/THF blend, indicating that it is likely the same crystal structure. As shown in Figure S12 (Supporting Information), we observe the same XRD patterns also for the SPEs from PI_26.1PS_67.3PEO_1.9.

Figure 2.

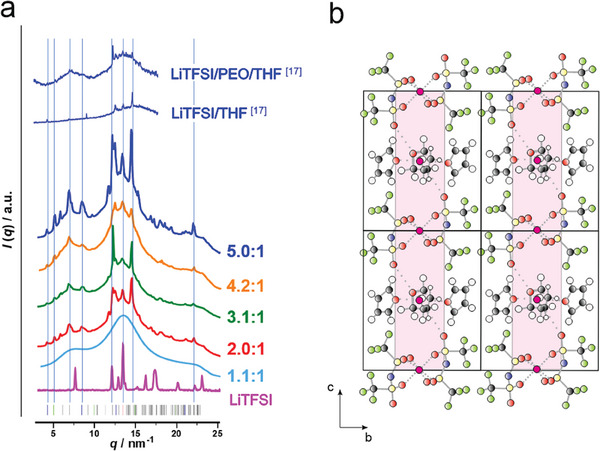
Crystal structure of the LiTFSI/PEO/THF phase. a) X‐ray diffraction (XRD) curves measured for the SPEs from PI_14.6PS_34.8PEO_1.9 at increasing LiTFSI concentrations of [Li⁺:O_EO]_n = 1.1–5.0:1. For comparison we also show the XRD curves (in blue) reported for the binary LiTFSI/THF and ternary LiTFSI/PEO/THF phase,^{[ 17 ]} for the neat LiTFSI (in pink), together with the peak positions expected for the trigonal unit cell. b) Structural model that is consistent with the unit cell dimensions and with structural information regarding the determined stoichiometry, from TGA and DSC, ¹⁹F‐NMR‐ and ¹⁹F‐¹H‐HOESY‐NMR spectroscopy. The color of the circles corresponds to the following atoms: yellow = sulfur, blue = nitrogen, gray = carbon, white = hydrogen, green = fluorine, and red = oxygen. Lithium is shown in dark pink, with dotted lines indicating oxygen coordinations. The PEO helix is viewed in axial direction. Pink rectangles indicate Li⁺‐mobility zones.

Similar as reported by Zhou et al.,^{[ 17 ]} it was not possible to derive a crystal structure from the measured XRD curves because of the large amorphous background of the non‐crystalline polymer blocks, the limited number of observed reflections, and the considerable peak widths due to small crystalline domains. Yet, from the main peak positions, we can suggest a triclinic unit cell (a = 0.47 nm, b = 1.29 nm, c = 1.53 nm, α = 82.5°, β = γ = 89°, Z(LiTFSI) = 2, V = 0.92 nm³) as indicated by the peak positions in Figure 2a. This unit cell is larger compared to the unit cell of neat LiTFSI (a = 0.96 nm, b = 0.54 nm, c = 1.63 nm, space group Pnaa, Z(LiTFSI) = 4, V = 0.85 nm³),^{[ 29 ]} and has similar dimensions as the triclinic unit cell reported for an alkyl‐imidazolium TFSI salt cell (a = 0.54 nm, b = 1.17 nm, c = 1.79 nm, α = 88.7°, β = 84.2° and γ = 82.7°, Z(LiTFSI) = 2, V = 1.11 nm³)^{[ 30 ]} and the orthorhombic unit cell reported for LiTFSI/EC (EC = ethylene carbonate, a = 0.58 nm, b = 1.27 nm, c = 1.69 nm, space group P2₁2₁2₁, Z(LiTFSI) = 4, V = 1.24 nm³).^{[ 31 ]} We suggest the simplest possible crystal structure model, as shown in Figure 2b, which is consistent with the triclinic unit cell and a stoichiometry of [LiTFSI:THF:EO] = 2:2:1 that would be close to the stoichiometries derived from the ¹⁹F‐NMR, TGA and DSC measurements. Furthermore, the suggested structure in Figure 2b is consistent with the 2D‐solid‐state ¹⁹F{¹H} heteronuclear Overhauser effect spectroscopy (HOESY)‐NMR measurements (Figure S13, Supporting Information) showing pronounced intermolecular cross‐peaks related to intermolecular correlations between THF CH₂‐protons and TFSI⁻‐anion CF₃‐fluorines. This suggests that all THF molecules are in close spatial proximity to the CF₃‐groups of the TFSI⁻‐anions.

In the suggested structure there are coordination sites I where the Li⁺‐ions are coordinated to six ‐S = O oxygen atoms from three different TFSI⁻‐anions, as is similarly observed for the alkyl‐imidazolium TFSI salts.^{[ 30 ]} Furthermore, there are Li⁺‐ions with mixed coordination sites II, i.e., to oxygen atoms from TFSI⁻, THF, and PEO, in agreement with Raman spectroscopy results reported in reference.^{[ 17 ]} The fact that the latter site bears a mixed coordination by TFSI−, THF, and PEO oxygens leads to an averaged ⁷Li chemical shift of this site, which differs from that of a pure TFSI‐ coordination. This observed mixed coordination site is supporting the fast Li⁺‐ion transport. The presence of two different Li‐coordination sites can also be observed in temperature‐dependent solid‐state MAS NMR measurements (Figure S14, Supporting Information), where the spectra show two different Li‐peaks. The two coordination sites can form a coordination network providing pathways for Li⁺‐conduction. In Figure 2b these pathways are possible within the (cb)‐plane as indicated by the magenta‐colored planes, and also normal to the (cb)‐plane, in a‐direction parallel to the chain backbone of the PEO chains.

2.6. Effect of LiTFSI/THF on Block Copolymer SPE Morphology

The block copolymer morphologies of the LiTFSI/PI_xPS_yPEO_1.9/THF SPEs were investigated by transmission electron microscopy (TEM). For this, the SPE membranes were cryo‐sectioned by ultramicrotomy to prepare ultrathin sections. Care was taken to handle all samples under exclusion of air and moisture.

The neat PI_14.6PS_34.8PEO_1.9 block copolymer forms large, well‐ordered domains of hexagonally packed PEO cylinders in a PI_14.6PS_34.8 matrix (HEX) as shown in Figure 3a.^{[ 21 ]} At a LiTFSI ratio of [Li⁺:O_EO]_n = 1.1:1, we observe the formation of an Fddd‐network phase. As shown in Figure 3b, we observe the characteristic alternating rectangular pattern of the [110]‐projection. Increasing the LiTFSI amount further leads to the formation of the gyroid phase. Figure 3c shows the gyroid phase for [Li⁺:O_EO]_n = 4.2:1 with its characteristic undulation pattern in the [211]‐direction.

Figure 3.

STEM images of SPEs from PI_xPS_yPEO_1.9 block copolymer morphologies with increasing LiTFSI concentrations. a) Hexagonally ordered cylindrical morphology (HEX) of the neat PI_14.6PS_34.8PEO_1.9 block copolymer. b) Ordered Fddd network structure observed for the SPEs from the same block copolymer at [Li⁺:O_EO]_n = 1.1:1, exhibiting alternating domains characteristic for the (110) projection. c) Gyroid structure observed for the SPE from the same block copolymer at [Li⁺:O_EO]_n = 4.2:1 with the undulating domain pattern characteristic for the (211) projection. d) Fddd network structure observed for the SPE from the PI_26.1PS_67.3PEO_1.9 block copolymer at a LiTFSI concentration of [Li⁺:O_EO]_n = 9.7:1 corresponding to the (001) projection. e–g) Schematically visualizations showing the HEX, Fddd, and Gyroid morphology.

The observation of a HEX‐Fddd‐Gyr transition is consistent with the PI_xPS_yPEO_z phase diagram reported by Bates et al.^{[ 32 ]} According to Table 1 for the neat PI_14.6PS_34.8PEO_1.9 BCP, we have a ternary volume fraction (ϕ_i) of (ϕ_PIx, ϕ_PSy, ϕ_PEO) = (0.32, 0.65, 0.03).^{[ 21 ]} This corresponds to the unexplored lower right region of the phase diagram in reference,^{[ 32 ]} which by assuming symmetry with respect to the vertical ϕ_PSy = 0.5‐line would correspond to the stability region of the HEX phase. Upon increasing the amount of LiTFSI, and taking into account the amount of bound THF, which both selectively swell the PEO phase, the volume fraction of the PEO phase according to Table 1 increases to ϕ_PEO = 0.13 for [Li⁺:O_EO]_n = 1.1:1, to ϕ_PEO = 0.17 for [Li⁺:O_EO]_n = 2:1, and further to ϕ_PEO = 0.23 for [Li⁺:O_EO]_n = 3.1:1 (Figure S15, Supporting Information). In the published phase diagram, the corresponding path ϕ_PEO = 0.03 → 0.13 → 0.17 → 0.23 at constant ϕ_PIx / ϕ_PSy‐ratio indeed transects the Fddd stability region, and is close to the adjacent gyroid phase region.^{[ 32 ]} With the tendency of crystalline phases to favor low‐curvature interfaces, the corresponding path would shift closer to the ϕ_PSy = 0.5‐line, thereby transecting the Fddd and subsequently the Gyr stability region, as observed in our experiments.

The Fddd network phase is not very commonly found. It was first reported by Bates et al. in a series of publications on PI_xPS_yPEO_z block copolymers for a range of volume fractions ϕ_PEO = 0.17–0.19.^{[ 33} , ³⁴ , ³⁵ , ^{36 ]} For higher volume fractions (ϕ_PEO = 0.18–0.20) the gyroid phase was observed,^{[ 34} , ^{36 ]} adjacent to the Fddd phase. Later, an Fddd/gyroid phase transition has been also reported for PI_xPS_y diblock copolymers,^{[ 37} , ^{38 ]} liquid crystalline azobenzene BCPs,^{[ 39 ]} sugar‐containing star‐BCPs^{[ 40} , ^{41 ]} and for rod‐coil BCPs.^{[ 42} , ^{43 ]} Both, the Fddd and Gyroid phase have close structural similarities, being bi‐continuous network phases with three‐arm connection points, as shown in Figure 3f,g. These bi‐continuous morphologies are ideal to provide continuous conduction paths. As shown in Figure 3d, we also observe the Fddd phase for the PI_26.1PS_67.3PEO_1.9 block copolymer SPE at high LiTFSI amount of [Li⁺:O_EO]_n = 9.7:1. According to Table 1 this corresponds to ϕ_PEO = 0.17, thus in the Fddd‐stability region due to the lower PEO content.

We used small‐angle X‐ray scattering (SAXS) to investigate a larger range of block copolymers and LiTFSI concentrations with their effect on the block copolymer morphology. Whereas with SAXS we could identify the morphologies of the neat PI_xPS_yPEO_1.9 block copolymers from the set of Bragg peaks,^{[ 21 ]} it was difficult to deduce the morphology for the corresponding block copolymer SPEs in which LiTFSI/THF was embedded. We found that LiTFSI/PEO/THF co‐crystallization, as evident from the emergence of the set of wide‐angle X‐ray reflections, clearly deteriorates long‐range order of the BCP domains. We attribute this effect to partial breakout crystallization of the LiTFSI/THF‐containing PEO microphase. This effect is frequently reported in crystalline BCPs,^{[ 43 ]} leading to loss of long‐range translational order as observed in the TEM images in Figures 3 and S16 (Supporting Information), and to broadening and near disappearance of higher order Bragg reflections in the SAXS curves as shown in Figure S17 (Supporting Information). Still, the position of the first‐order peaks q* can be well correlated to the LiTFSI‐content of the SPE.

As discussed, for the neat PI_14.6PS_34.8PEO_1.9 we observe higher‐order reflections that can be indexed on a 2D hexagonal lattice, with a cylinder‐cylinder distance of 36 nm in agreement with the TEM image in Figure 3a.^{[ 21 ]} Increasing the LiTFSI amounts from [Li⁺:O_EO]_n = 1.1:1 to 3.1:1 leads to a shift of the first‐order peak position (q*) to lower q‐values (Figure S17, Supporting Information). The q* values can be related to corresponding unit cell dimension or long periods.

$$\mathrm{d}\ast =\frac{2\pi }{\mathrm{q}\ast }$$ (1)

As expected, we observe an increase in d* with increasing LiTFSI concentrations (Table 1; Figure S18, Supporting Information). Compared to the clear higher‐order reflections of the neat BCP, we observe only very broad and low‐intensity higher‐order reflections. As shown in Figure S17a (Supporting Information), for the SPE from PI_14.6PS_34.8PEO_1.9, the positions of the weak shoulders in the q = 0.3–0.4 nm⁻¹ region, as observed for [Li⁺:O_EO]_n = 1.1:1 and 2.0:1, are consistent with a Fddd scattering curves and thus with the Fddd structure observed in the TEM image in Figure 3b. Regarding the SPEs from PI_14.6PS_34.8PEO_1.9 with LiTFSI concentrations of [Li⁺:O_EO]_n ≥3.1:1, we observe two broad maxima in the q = 0.3–0.4 nm⁻¹ range (Figure S17a, Supporting Information), which are consistent with sets of characteristic reflections for the gyroid scattering curve and thus with the corresponding TEM image in Figure 3c.

For the neat PI_26.1PS_67.3PEO_1.9, we also observe clear higher‐order peaks that can be indexed on a 2D hexagonal lattice, with a cylinder‐cylinder distance of 64 nm.^{[ 21 ]} Upon embedding with LiTFSI from [Li⁺:O_EO]_n = 1.0 – 9.7:1, we observe a shift of the q* to lower q, and reaching a constant value for [Li⁺:O_EO]_n = 2.1:1. Higher order peak features cannot be observed at all SPEs for this BCP (Figure S17b, Supporting Information).

Consequently, for the SPEs of both BCPs, we observe with increasing LiTFSI concentration a low‐q shift of the q*, reaching a lower plateau value for [Li⁺:O_EO]_n ≥3.1:1, consistent with the plateau value observed from the ¹⁹F‐NMR quantification experiments shown in Figure 1a. In agreement with the TEM images shown in Figure 3, the scattering curves and the determined ϕ_PEO, we assign the neat block copolymers a HEX phase, the SPEs with up to ϕ_PEO = 0.17 the Fddd network phase, and for the SPEs with ϕ_PEO ≥0.23 the gyroid phase. Since the neat PI_26.1PS_67.3PEO_1.9 has a lower ϕ_PEO volume fraction (ϕ_PEO = 0.02) compared to the neat PI_14.6PS_34.8PEO_1.9 (ϕ_PEO = 0.03) (Table 1), its PEO‐phase volume fraction swells only to ϕ_PEO = 0.17 in the saturation limit and thus only to the Fddd‐phase, whereas the first block copolymer swells up to ϕ_PEO = 0.24 in the saturation limit, and thus reaches the gyroid phase.

2.7. Ionic Conductivity and Transport Mechanism

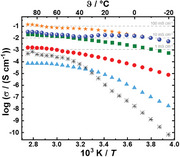
The ionic conductivities for the LiTFSI/PI_xPS_yPEO_1.9 block copolymer SPEs membranes were determined by electrochemical impedance spectroscopy (EIS) over a temperature range of −20 to 90 °C. Here, only the measurement cycle with the best, constant, and reproducible high ionic conductivity obtained after annealing (including storage at room temperature) is shown in Figure 4 and discussed. After the SPE membrane was installed into the coin cell, during the annealing process, the cell was heated and cooled in cycles between −20 and 90 °C, and between these cycles, the cell was stored at room temperature and not reopened. The annealing process improved the measured ionic conductivity due to improved SPE membrane‐electrode contact and likely also due to the formation of a percolating crystalline LiTFSI/PEO/THF phase in the bi‐continuous PEO domains of the Fddd and Gyr network phases (Figure S19, Supporting Information). Details of the annealing process are described in the Supporting Information (Figures S20–S23). Figure 4 shows the Arrhenius plots of the final ionic conductivities measured for the SPE membranes for both PI_xPS_yPEO_1.9 block copolymers depending on LiTFSI amounts increasing from [Li⁺:O_EO]_n = 1.0–10.2:1. For comparison, the standard LiTFSI/PEO electrolyte with a low ratio [Li⁺:O_EO] = 0.1:1 is also shown as a reference.

Figure 4.

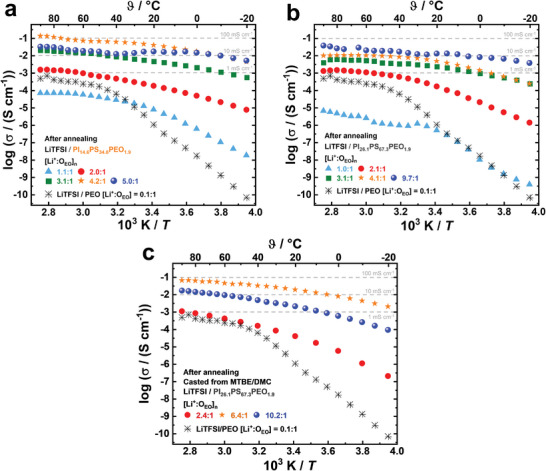
Arrhenius plots of ionic conductivities measured by electrochemical impedance spectroscopy (EIS) of the block copolymer SPE membranes for a) LiTFSI/PI_14.6PS_34.8PEO_1.9/THF, for b) LiTFSI/PI_26.1PS_67.3PEO_1.9/THF, and for c) LiTFSI/PI_26.1PS_67.3PEO_1.9/DMC for a series of LiTFSI concentrations increasing from [Li⁺:O_EO]_n = 1.0:1 to 10.2:1. In each case the standard LiTFSI/PEO electrolyte with [Li⁺:O_EO] = 0.1:1 is also shown as a reference, in a temperature range from −20 to 90 °C. Remarkably high ionic conductivities of σ_90 °C = 1·10⁻¹ S cm⁻¹ are observed in block copolymer SPEs from LiTFSI/PI_14.6PS_34.8PEO_1.9/THF at [Li⁺:O_EO]_n = 4.2:1, concomitantly with a small activation energy E _a of ≈0.2 eV.

For the standard LiTFSI/PEO electrolyte at the usually investigated low LiTFSI concentrations of [Li⁺:O_EO] = 0.1:1 we observe ionic conductivities of σ_20 °C = 1·10⁻⁶ S cm⁻¹ and σ_90 °C = 5·10⁻⁴ S cm⁻¹. The latter value is slightly lower in comparison to the best‐reported values for LiTFSI/PS_yPEO with [Li⁺:O_EO] = 0.1:1 and σ_100 °C = 1·10⁻³ S cm⁻¹.^{[ 7 ⁠]} Increasing the LiTFSI concentration for PI_14.6PS_34.8PEO_1.9 to [Li⁺:O_EO]_n = 1.1:1 results in a decrease to σ_90 °C = 7·10⁻⁵ S cm⁻¹ (Figure 4a). This is a similar trend as reported for the LiTFSI/PS_yPEO system, where a reduction of the ionic conductivity is observed for [Li⁺:O_EO] >0.2:1.^{[ 13 ]} This is commonly explained by an increased tendency of the Li⁺‐ions to coordinate to their TFSI⁻ counter‐ions, inducing a segregation into salt‐rich domains. The coordination reduces the number of free Li⁺ and therefore the related ionic conductivities σ.

Notably, increasing the LiTFSI concentration for PI_14.6PS_34.8PEO_1.9 further to [Li⁺:O_EO]_n = 2.0:1 leads to a considerable increase to σ_90 °C = 2·10⁻³ S cm⁻¹, which is among the best values observed for solid LiTFSI/PEO systems.^{⁠[ 6} , ⁷ , ^{13 ]} Concomitantly, σ_20 °C increases by several orders of magnitude to 2·10⁻⁴ S cm⁻¹. This indicates a decoupling of the Li⁺‐mobility from the PEO chain segmental mobility resulting in a notably increased ion conductivity with a lower temperature dependence. A further increase of the Li⁺ concentration to [Li⁺:O_EO]_n = 3.1:1 and 4.2:1 increases the ionic conductivity further to values of σ_90 °C = 2·10⁻² S cm⁻¹ and even to σ_90 °C = 1·10⁻¹ S cm⁻¹, respectively. For a concentration of [Li⁺:O_EO]_n = 4.2:1, a remarkably high room temperature ionic conductivity of σ_20 °C = 4·10⁻² S cm⁻¹ is measured, and due to the low activation energy E _a of ≈0.2 eV (Table S5, Supporting Information), i.e., low‐temperature dependence for the Li⁺‐transport, even at temperatures of −40 °C values of σ_‐40 °C = 2·10⁻³ S cm⁻¹ are obtained (Figure S24, Supporting Information). These values are by far higher than any ionic conductivity values previously reported for similar LiTFSI/PI_xPS_yPEO_z systems,^{[ 15} , ^{16 ]} and are sufficiently high for commercial applications. Moreover, all graphs in Figure 4 exhibit a small negative slope with increasing LiTFSI concentration, resulting in a low‐temperature dependence and thus also activation energy over the large temperature range from −20 to 90 °C. Although, as described above, achieving high ionic conductivities requires a set of annealing cycles, the measured final high ionic conductivities are reproducible and stable over years. The stability of the LiTFSI/PI_xPS_yPEO_z systems in stripping/plating experiments has already been demonstrated over 100 cycles in symmetrical pouchback Li|SPE|Li cells.^{[ 16 ]} We note that for PEO homopolymers at similarly high [Li⁺:O_EO]_n‐ratios we only find ionic conductivities in the common range of 10⁻⁴–10⁻³ S cm⁻¹ and therefore the block copolymer structure is essential.

The same behavior is observed for PI_26.1PS_67.3PEO_1.9‐SPEs, as shown in Figure 4b, where by increasing the LiTFSI concentration to [Li⁺:O_EO]_n = 1.0:1 the ionic conductivity decreases to σ_90 °C = 7·10⁻⁶ S cm⁻¹. Then, with higher LiTFSI concentration the ionic conductivity increases to σ_90 °C = 1·10⁻³ S cm⁻¹ for [Li⁺:O_EO]_n = 2.1:1, and further up to σ_90 °C = 1·10⁻² S cm⁻¹ for [Li⁺:O_EO]_n = 4.1:1, reaching a maximum value of σ_90 °C = 4·10⁻² S cm⁻¹ for [Li⁺:O_EO]_n = 9.7:1. At lower temperatures ionic conductivities of σ_20 °C = 1·10⁻² S cm⁻¹ and σ_0 °C = 8·10⁻³ S cm⁻¹ are measured, indicating a low activation energy (E _a ≈0.15 eV).

These encouraging results were obtained for block copolymer SPEs of LiTFSI/PI_xPS_yPEO_1.9/THF, which were systematically investigated in the present study. Motivated by these results, we exemplarily also investigated SPE membranes from PI_26.1PS_67.3PEO_1.9 casted from mixtures of methyl tert‐butyl ether (MTBE) and dimethyl carbonate (DMC). DMC is miscible with PEO_1.9, and a common solvent for liquid electrolyte used in lithium ion batteries LIBs. MTBE is volatile (boiling temperature (ϑ_B) = 55 °C),^{[ 44 ]} a non‐solvent for neat PEO, and serves to dissolve the PI_26.1PS_67.3PEO_1.9 BCP together with LiTFSI and DMC. Also, for block copolymer SPE membranes casted with this solvent mixture, we observe from DSC measurements (Figure S25, Supporting Information) the glass transitions of the neat polymer blocks ϑ_g,PIx and ϑ_g,PSy, as well as the glass transition of the LiTFSI/PEO/DMC phase at ϑ_g,SPE = ≈−68 °C (Table S6, Supporting Information). As shown in Figure 4c, we also observe high ionic conductivities for these block copolymer SPE membranes, with σ_90 °C = 1·10⁻³ S cm⁻¹ for [Li⁺:O_EO]_n = 2.4:1, further increasing with increasing LiTFSI concentration, and reaching a maximum value of σ_90 °C = 7·10⁻² S cm⁻¹ at [Li⁺:O_EO]_n = 6.4:1. We also find a remarkably high ionic conductivity at lower temperatures of σ_20 °C = 2·10⁻² S cm⁻¹ and σ_‐20 °C = 2·10⁻³ S cm⁻¹ indicating a low‐temperature dependence and a low activation energy (E _a ≈0.22 eV).

We note that the room temperature ionic conductivity σ_20 °C = 4·10⁻² S cm⁻¹ measured for LiTFSI/PI_14.6PS_34.8PEO_1.9/THF is comparable to the highest values reported for Li₁₀GeP₂S₁₂ (LGPS) (σ_20 °C = 3·10⁻² S cm⁻¹)^{[ 45 ]} or for Li_9.54Si_1.74P_1.44S_11.7Cl_0.3 (σ_rt = 3·10⁻² S cm⁻¹).^{[ 46 ]} Analogous to the best crystalline inorganic Li⁺ conductors, a low‐temperature dependence of the ionic conductivity can be observed over the entire temperature range (−20 to 90 °C). Also, the measured values for LiTFSI/PI_26.1PS_67.3PEO_1.9/THF (σ_20 °C = 1·10⁻² S cm⁻¹) and LiTFSI/PI_26.1PS_67.3PEO_1.9/DMC (σ_20 °C = 2·10⁻² S cm⁻¹) are favorably comparable.

The observed high ionic conductivity values and the low temperature‐dependent behavior over the wide temperature range suggest that at high LiTFSI concentrations, the Li⁺‐transport mechanism decouples from the polymer chain segment mobility. To obtain more insights into the conduction mechanism at the molecular level, we performed spin relaxation and pulsed‐field‐gradient (PFG)‐NMR measurements, focusing on two different compositions, i.e., LiTFSI/PI_26.1PS_67.3PEO_1.9/THF‐SPEs with a LiTFSI amount of [Li⁺:O_EO]_n = 9.7:1 and LiTFSI/PI_14.6PS_34.8PEO_1.9/THF‐SPEs with a LiTFSI amount of [Li⁺:O_EO]_n = 4.2:1. ⁷Li and ¹⁹F linewidths during a heating/cooling cycle within 0–90 °C are shown in Figure S26. Their decrease with increasing temperature documents the reduction of the inhomogeneous broadening, which is further promoted during annealing, after which the linewidth remains comparatively low even upon cooling. Thus, clear changes of the local structure are induced by annealing.

Diffusion coefficients of Li⁺ (D _Li+) and anions (D _TFSI−) are on the order of 10⁻¹¹ m² s⁻¹, increasing with temperature. A further increase is reached under annealing at 90 °C. Figure S27 (Supporting Information) shows D _Li+ and D _TFSI− during a full heating/cooling cycle for the SPE of LiTFSI/PI_14.6PS_34.8PEO_1.9/THF with a LiTFSI amount of [Li⁺:O_EO]_n = 4.2:1. Diffusion experiments performed at elevated temperature (>20 °C) showed a non‐exponential echo decay, which was fitted by two components, where a minor component (≈30% of the signal) exhibited a diffusion coefficient of roughly an order of magnitude lower. The underlying feature might be a distribution of diffusion coefficients, induced by structural heterogeneity. Given the observation time of Δ = 150 ms and the diffusion coefficient values observed at 0 °C and 90 °C (Figure S27, Supporting Information), the experiment probes the molecular displacement over a distance of 0.8 µm (at 0 °C) to 4 µm (at 90 °C). This implies that any heterogeneity at a smaller length scale would be averaged. Thus, the two components with fast and slow diffusion, respectively, must result from regions that extend over distances >4 µm. We additionally tested the dependence of diffusivity at 90 °C on the length/time scale by varying the observation time Δ from 25 to 300 ms. Figure S28 shows that there is only a very minor variation of D _fast and D _slow with increasing observation time. Thus, a convergence, implying averaging over regions with different diffusion coefficients does not occur on this time scale, and in conclusion, the regions with fast or slow diffusion, respectively, must expand over a size much larger than 4 µm. It is most likely that the fast component arises from ordered areas with defined channels, which form the major part of the material. These are coexisting with disordered areas with slower ion transport, which can also be structurally observed in the TEM images, e.g., Figure 3c. In the following discussion, we focus on the fast diffusing component as the one responsible for high ionic conductivity.

The temperature‐dependent D _Li+ and D _TFSI− values are shown in Figure S27 (Supporting Information). Table 2 , Table S8 and Figure S29 (Supporting Information) show the respective values obtained at 90 °C, which are D _Li+ = 5.6·10⁻¹¹ m² s⁻¹ and D _TFSI− = 5.3·10⁻¹¹ m² s⁻¹ for PI_14.6PS_34.8PEO_1.9‐SPEs with [Li⁺:O_EO]_n = 4.2:1, and D _Li+ = 3.0·10⁻¹¹ m² s⁻¹ and D _TFSI− = 2.6·10⁻¹¹ m² s⁻¹ for PI_26.1PS_67.3PEO_1.9‐SPEs with [Li⁺:O_EO]_n = 9.7:1. The values are larger compared to recently reported values for PEO ⁴⁷ and perfluoro‐PEO polymers,^{[ 12 ]} but similar to the values determined by recent MD‐simulations.^{[ 31 ]} It is particularly remarkable, that the Li⁺‐ and TFSI⁻‐diffusion coefficient are very similar (Table 2), while in PEO‐based electrolytes there is usually a large difference with a much slower transport of Li⁺‐ions due to their coordination to the chains.^{[ 12} , ^{47 ]} From the measured diffusion coefficients, we can estimate the transference numbers t _Li+ under neglect of ion correlation using:

$${\mathrm{t}}_{\mathrm{Li}+}=\frac{{\mathrm{D}}_{\mathrm{L}{\mathrm{i}}^{+}}}{{\mathrm{D}}_{\mathrm{L}{\mathrm{i}}^{+}}+{\mathrm{D}}_{\mathrm{TFS}{\mathrm{I}}^{-}}}$$ (2)

to obtain values of t _Li+ = 0.51 for the PI_14.6PS_34.8PEO_1.9‐SPEs and t _Li+ = 0.53 for the PI_26.1PS_67.3PEO_1.9‐SPEs. These results are comparable to those obtained for a similar PI_xPS_yPEO_z‐SPEs with t _Li+ of up to 0.70,^{[ 15} , ^{16 ]} and concentrated liquid electrolytes with t _Li+ = 0.6,^{[ 19 ]} but much higher if compared to standard LiTFSI/PEO electrolytes with t _Li+ = 0.2.^{⁠[ 6} , ¹² , ^{47 ]}

Table 2.

Ion diffusion coefficients determined by PFG‐NMR. Diffusion coefficients (D) of the fast component and their activation energies (E _a), Li⁺ transference numbers (t _Li+), and estimated limiting conductivity (σ_lim,90 °C) assuming full salt dissociation. All data at 90 °C after annealing.

Sample	D Li+ / m2 s−1	D TFSI− / m2 s−1	σlim,90 °C / S cm−1	t Li+	$E_{\mathrm{a},\mathrm{L}{\mathrm{i}}^{+}}$ / kJ mol−1	$E_{\mathrm{a},\mathrm{TFS}{\mathrm{I}}^{-}}$ / kJ mol−1
LiTFSI/PI14.6PS34.8PEO1.9/THF [Li+:OEO]n = 4.2:1	5.6·10−11	5.3·10−11	1·10−2	0.51	30.5	30.8
LiTFSI/PI26.1PS67.3PEO1.9/THF [Li+:OEO]n = 9.7:1	3.0·10−11	2.6·10−11	7·10−3	0.53	–	–

Using the Nernst‐Einstein equation and assuming full salt dissociation, an upper limit of the ionic conductivity σ_lim can be estimated on the basis of the diffusion coefficients. It is:

$${\sigma }_{\lim }=\frac{{\mathrm{F}}^2{\mathrm{c}}_{\mathrm{LiTFSI}}\left({\mathrm{D}}_{\mathrm{L}{\mathrm{i}}^{+}}+{\mathrm{D}}_{\mathrm{TFS}{\mathrm{I}}^{-}}\right)}{\mathrm{R}\mathrm{T}}$$ (3)

where F = 96485 C mol⁻¹ is the Faraday constant, c _LiTFSI is the molar concentration of LiTFSI, R = 8.314 J K⁻¹ mol⁻¹ is the gas constant, and T is the temperature. From the data of the crystal structure for the conductive LiTFSI/PEO/THF phase (Figure 2b), we calculate c _LiTFSI using:

$${\mathrm{c}}_{\mathrm{LiTFSI}}=\frac{\mathrm{Z}}{\mathrm{V}{\mathrm{N}}_{\mathrm{A}}}$$ (4)

where Z is the number of Li⁺ or TFSI⁻ per unit cell with Z = 2, V is the volume of the unit cells with V = 0.92 nm³, and N _A is the Avogadro constant with N _A = 6.022·10²³ mol⁻¹, resulting in c _LiTFSI = 3.6 mol L⁻¹. This value agrees well with the c _LiTFSI concentration calculated from ϕ_PEO and the embedded LiTFSI amount, which ranges from 3.7 to 4.2 mol L⁻¹ (Table S7, Supporting Information). For diffusion coefficients of D _Li+ = 5.6·10⁻¹¹ m²s⁻¹ and D _TFSI− = 5.3·10⁻¹¹ m²s⁻¹ (Table 2) at a temperature of 90 °C we thus obtain a value of σ_lim = 1·10⁻² S cm⁻¹ using Equations (3) and (4). Considering that the volume fraction of the ion‐conducting PEO‐phase in the PI_xPS_yPEO_1.9‐SPEs is <0.25, the measured ionic conductivity values shown in Figure 4 are an order of magnitude larger compared to σ_lim, indicating a cooperative conduction mechanism.

To gain further insights into the conduction mechanism we determined ⁷Li spin‐lattice relaxation rates R ₁ of the Li⁺‐ions. As shown in Figure 5 , the Li⁺ relaxation rates can be well‐fitted to a Bloembergen‐Purcell‐Pound (BPP) model.^{[ 48 ]} Details of the model fitting are provided in the Supporting Information, see Equations S4–S6 and accompanying text. The fit of the relaxation rates in Figure 5 shows that the local ⁷Li dynamics can indeed be described by a single characteristic relaxation time. Furthermore, the assumption of an Arrhenius behavior fits the relaxation rate data very well, thus the activation energy E _a, i.e., the activation threshold for local Li⁺ hopping, can be determined. We observe an activation energy E _a = 0.19 eV (19.6 kJ mol⁻¹), comparable to that of local Li⁺ motion in polyether‐based copolymers at low salt concentration.^{[ 49 ]} This value is also consistent with the order of magnitude of the E _a values determined from the EIS measurements for the fast‐conducting SPEs (Table S5, Supporting Information). The observed E _a is low, comparable to ion‐hopping mechanisms in super‐ionic solid‐state Li⁺‐conductors.

Figure 5.

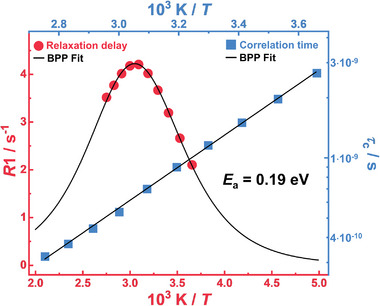
Temperature‐dependent ⁷Li relaxation times and relaxation rates. Spin relaxation NMR investigations in the temperature range from (0–90) °C for the SPE from LiTFSI/PI_14.6PS_34.8PEO_1.9/THF with [Li⁺:O_EO]_n = 4.2:1. In blue, correlation time (τ_c) as a function of the inverse temperature in an Arrhenius plot to determine the activation energy E _a = 0.19 eV, and in red the BPP fit with a single Lorentzian to determine the relaxation time.

High room temperature ionic conductivities σ_rt in the range of 1·10⁻³ S cm⁻¹–1·10⁻² S cm⁻¹, together with low activation energies E _a in the range of 0.2–0.3 eV is a known characteristic for super‐ionic Li⁺‐conductors such as LGPS or Li₇P₃S₁₁.^{[ 45 ]} Another common feature is that the ionic conductivity increases strongly with increasing ion content. For example, for SPEs from PI_xPS_yPEO_1.9, with LiTFSI concentrations increasing from [Li⁺:O_EO]_n = 1.0–4.2:1, we observe concomitant increase of σ_20 °C by a factor of 10⁴.

For solid‐state ion conductors, ion transport is described in terms of hopping of individual ions from one lattice site to an adjacent lattice site via inter‐connected diffusion channels in the crystal structural framework.^{[ 50 ]} The framework determines the energy landscape of the ion migration. The highest energy of the energy landscape along the diffusion channel determines the energy barrier E _a of ionic diffusion. To achieve high ionic conductivities thus requires low energy barriers E _a and high concentrations of mobile ions.

Li⁺ super‐ionic conduction is known to occur at high Li⁺ concentration, and in specific Li⁺ crystal structural frameworks achieved via materials doping. For example, a typical Li‐garnet material achieves the highest ionic conductivity in a certain range of 6.4–7.0 Li⁺ per formula unit. Particular insight in the super‐ionic conduction mechanism was recently provided by MD‐simulations.^{[ 51 ]} The simulations for a typical Li‐garnet structure show that at high Li⁺ concentrations high‐energy sites are populated since all low‐energy sites are already occupied. The MD‐simulations further show that during super‐ionic conduction ions migrate in a highly concerted fashion, i.e., multiple ions hop fast and simultaneously into their nearest neighbor sites along the diffusion channel. During this concerted migration, ions located at high‐energy sites energetically migrate downhill, which partially compensates the energy penalty for ions in low‐energy sites energetically climbing uphill. As a result, the concerted migration of multiple ions has a substantially low energy barrier.

For the structural model shown in Figure 2b, we indicated the possible Li⁺ diffusion channels along the TFSI⁻‐THF‐PEO‐TFSI⁻ paths. We note the presence of two different energy Li‐O‐TFSI⁻‐ and Li‐O‐THF/PEO coordination sites along the diffusion channel. Therefore, the experimentally observed exceptionally high ionic conductivities at high LiTFSI concentrations, the low activation energies E _a, and the strong increase of the σ‐values with increasing Li⁺ concentrations, which are characteristic for super‐ionic conduction, appears to be consistent with the mechanism reported in the MD‐simulations.

For the super‐ionic block copolymer SPE membranes, we therefore propose a hierarchical structure as shown in Figure 6 . The crystalline LiTFSI/PEO/THF phase shown in blue exhibits super‐ionic Li⁺‐conduction paths in horizontal direction, and also in the direction normal to the plane. The crystalline regions percolate within the PEO phase of the bi‐continuous gyroid structure to connect the two electrodes. The embedding of LiTFSI in the PI_xPS_yPEO_1.9 has a synergetic two‐fold effect at high [Li⁺:O_EO]_n ratios: i) it leads to the formation of the crystalline LiTFSI/PEO/THF phase providing mixed Li⁺‐coordination sites and Li⁺‐conduction pathways, and ii) induces a morphological transition from the HEX via Fddd to the gyroid phase. Both effects are important to achieve high ionic conductivities σ. The bi‐continuous LiTFSI/PEO/THF Fddd and gyroid phases provide 3D conduction paths that are very little affected by morphological defects. The high‐modulus bi‐continuous PS_y phase serves to suppress dendrite growth, in particular also because the Fddd and gyroid curved topologies define a tortuous path potentially retarding dendrite infiltration and growth. The soft PI_x phase serves to improve membrane toughness. The electrochemical stability of SPE membranes from LiTFSI/PI_xPS_yPEO_z has been previously demonstrated up to 4.5 V vs Li|Li⁺.^{[ 16} , ^{52 ]} The used high LiTFSI concentrations in our block copolymer SPEs accelerate mass transport and therefore potentially also reduce concentration gradients at the electrolyte/electrode interfaces.

We currently investigate i) how the annealing process to achieve high ionic conductivities can be simplified to be compatible with established cell fabrication methods, and ii) how THF may be substituted by less volatile and more oxidation‐stable compounds. With the use of DMC, we already present a first step into this direction. We note that THF, when co‐crystallized in the solid LiTFSI/PEO/THF phase, is tightly bound such that no flaming of such SPE membranes is observed even upon exposure to direct fire.^{[ 17 ]} THF itself is electrochemically stable and is already used in rechargeable Mg²⁺ batteries.^{[ 53} , ^{54 ]} We already demonstrated in Figure 4c, that THF can be substituted by DMC. Similarly, Li⁺ could be substituted to Na⁺ which binds less strongly to oxygen ligands. Therefore, the investigated PEO‐based super‐ionic SPE systems open a route to highly conductive battery electrolyte membranes over a large relevant temperature range, especially at room temperature, solving the problem of poor ionic conductivities of SPEs.

3. Conclusion

Before our study, it was generally accepted that the maximum ionic conductivity for LiTFSI/PEO electrolytes occurs for ratios [Li⁺:O_EO] = 0.1:1, while decreasing at higher LiTFSI concentrations.^{[ 7 ]} However, motivated by recent observations of again increasing ionic conductivities at [Li⁺:O_EO] >1.0:1,^{[ 15} , ^{16 ]} we here systematically investigated the ionic conductivities for SPEs based on PI_xPS_yPEO_1.9 triblock copolymers in the range [Li⁺:O_EO]_n = 1.0:1 up to 10.2:1. We find that increasing the LiTFSI concentration beyond [Li⁺:O_EO]_n >1.0:1 leads to macro‐phase separation, whereby a PI_xPS_yPEO_1.9 SPE with a LiTFSI/PEO/THF phase is formed. Increasing the LiTFSI amount to the saturation limit [Li⁺:O_EO]_SPE,sat = 1.9:1 has two synergistic effects for the LiTFSI/PI_xPS_yPEO_1.9/THF SPE systems: i) the formation of a super‐ionic LiTFSI/PEO/THF phase, and ii) a phase transition from the hexagonal to an Fddd phase, and finally a gyroid bi‐continuous network, providing 3D bi‐continuous conduction paths. Both effects concomitantly lead to exceptionally high ionic conductivities in the range of σ_‐20 °C >1·10⁻³ S cm⁻¹ up to σ_90 °C = 1·10⁻¹ S cm⁻¹, with low activation energies E _a = 0.19 eV in the temperature range of −20 to 90 °C, and ion diffusion coefficients with D _Li+ > D _TFSI− corresponding to transference numbers of t _Li+ >0.5. THF coordinating to Li⁺ as an O‐donor plays an important role in the conduction mechanism, and can be substituted by DMC to obtain similar high ionic conductivities. The observed ionic conductivities are in the range of the best crystalline inorganic Li⁺‐conductors.^{[ 45} , ^{46 ]} Combined these findings open a pathway to super‐ionic PEO SPE membranes designed with a set of materials with proven electrochemical performance to achieve strongly enhanced ionic conductivities, especially considering the room temperature ionic conductivities of σ_20 °C >1·10⁻² S cm⁻¹. This greatly enhanced ionic conductivity ultimately can enable the construction of ultrathin and ultralight solid‐state electrolytes for a broad range of battery applications.

4. Experimental Section

Materials

Methoxy poly(ethylene oxide) (PEO_1.9 equals to M _n = 1.9 kg mol⁻¹, VWR) was dried at 30 °C, 3 Å molecular sieve (VWR) was activated by drying at 300 °C, poly(isoprene)‐b‐poly(styrene)‐b‐poly(ethylene oxide) triblock copolymers (PI_xPS_yPEO_1.9 BCPs, synthesized as previously reported)^{[ 21 ]} were dried at 50 °C, and bis(trifluoromethanesulfonyl)imide lithium salt (LiTFSI, 99.95%, Sigma‐Aldrich) and bis(fluorosulfonyl)imide lithium salt (LiFSI, 99.9%, American Elements) were both dried at 100 °C, in all cases under vacuum to <1·10⁻⁶ mbar, and subsequently stored inside a glovebox (MBraun Unilab, ≤0.1 ppm of water and oxygen) under argon atmosphere. Methyl tert‐butyl ether (MTBE, 99.8%, Sigma‐Aldrich), tetrahydrofuran (THF, ≥99.8%, unstab., Alfa Aesar), and dimethyl carbonate (DMC, ≥99.0%, Sigma‐Aldrich) were dried using activated 3 Å molecular sieve until ≤5 ppm water, stored under argon atmosphere in a glovebox, and passed through a syringe filter (polytetrafluoroethylene (PTFE) membrane, pore size = 0.2 µm, VWR) directly before use.

PI_14.6PS_34.8PEO_1.9 and PI_26.1PS_67.3PEO_1.9 block copolymers were synthesized as previously described in,^{[ 21 ]} where experimental details of the synthesis and characterization of the BCPs can be found. Additionally, a description of the synthesis was provided in the Supporting Information.

Membrane Preparation

The entire SPE membrane casting process was carried out under argon atmosphere. An 8 wt.% solution of neat PI_xPS_yPEO_1.9 in THF was prepared. The calculated LiTFSI amount was added by using a 15 wt.% solution of LiTFSI in THF, both solutions were mixed and transferred into a 5 mL PTFE crucible. The filled PTFE crucible was placed in a Schlenk vessel, and under a very low and constant argon flow, slow and controlled solvent evaporation was performed in a THF saturated atmosphere to achieve distinct microphase separation over 6 days at room temperature. A mixture of MTBE and DMC in a 4:1 mass ratio was used as an alternative solvent to THF, with the casting procedure remaining the same. Detailed information on further sample preparation for each characterization method can be found in the Supporting Information.

Nuclear Magnetic Resonance (NMR)—¹⁹F‐Solution‐NMR

¹⁹F‐solution‐NMR spectra of all SPEs were recorded at 30 °C using a Benchtop Spinsolve 80 MHz. The LiTFSI content in the SPE membranes was quantified using ¹⁹F‐atomic quantity. For this purpose, LiFSI as a ¹⁹F‐containing internal standard was dissolved together with the SPE membrane in THF. NMR measurements with a number of scans = 4096 or 8192 were recorded, using an acquisition time of 0.41 s and a repetition time of 8 s.

Nuclear Magnetic Resonance (NMR)—Solid‐State‐NMR

All solid‐state NMR measurements performed were conducted using a Bruker Avance Neo console with a Bruker Ascend wide‐bore magnet operating at 11.76 T (ν_L(¹H) = 500.39 MHz; ν_L(¹⁹F) = 470.80 MHz, ν_L(⁷Li) = 194.47 MHz). A commercial Bruker 4 mm H/F/X MAS DVT probe equipped with magic‐angle gradient coils was used. All samples were packed in 4 mm o.d. ZrO₂ rotors with Vespel caps and spinning at 12.5 kHz using dry N₂ as driving gas at ambient temperature. The quantification was done via the ¹⁹F signal in a simple single pulse‐experiment using PTFE tape (DIN EN 751‐3) as an external reference sample for the replacement method.

2D ¹⁹F{¹H} heteronuclear Overhauser effect spectroscopy (HOESY)^{[ 55 ]} was conducted to probe the spatial proximity of ¹⁹F (the TFSI anion) and the protons present throughout the sample. Using the same experimental as described above, simultaneous irradiation of ¹H and ¹⁹F was possible using the 4 mm H/F/Y MAS DVT probe and a frequency diplexer. The sample was spinning 5 kHz in these experiments. A relaxation delay and a NOE mixing time of both 1 s were chosen. The chemical shifts of ¹H and ¹⁹F were externally referenced against solid adamantane (δ(¹H) = 1.85 ppm)^{[ 56 ]} and PTFE tape (δ(¹⁹F) = −122.0 ppm).^{[ 57 ]}

Nuclear Magnetic Resonance (NMR)—Spin Relaxation and Pulsed‐Field‐Gradient (PFG)‐NMR

NMR tubes were filled with the SPE membrane in a drying room followed by sealing. NMR spin relaxation and diffusion measurements were conducted on a 400 MHz spectrometer (Avance III HD, Bruker, Rheinstetten, Germany) with a static field of 9.39 T with a broadband probe head with gradient coils (“Diff BBFO”, Bruker). The temperature was calibrated with a PT100 thermocouple (Greisinger electronics).

Temperature‐dependent experiments (spectra, diffusion, and spin relaxation) were performed employing heating from 0 to 90 °C in 10 °C steps, annealing at 90 °C for 10 h with recording one measurement every hour, and then cooling down to 0 °C in 10 °C steps. An inversion recovery pulse sequence was applied to determine ⁷Li spin‐spin relaxation rates, and the Bloembergen‐Purcell‐Pound (BPP) model^{[ 48 ]} was employed to yield motional correlation times τ_c according to a procedure described earlier,^{[ 49 ]} see details in Supporting Information.

⁷Li‐ and ¹⁹F‐NMR pulsed‐field‐gradient (PFG)‐NMR measurements were performed using a stimulated echo pulse sequence with field gradient pulses. Diffusion coefficients D _i of a species i were obtained by a fit of the echo decay according to the Stejskal‐Tanner in Equation (5).

$$I={\mathrm{I}}_0\exp \left(-{\gamma }^2{\mathrm{g}}^2{\delta }^2\mathrm{D}\left(\mathrm{\Delta }-\frac{\delta }{3}\right)\right)$$ (5)

Here, γ was the gyromagnetic ratio, g was the gradient strength, which was varied up to 10 T m⁻¹ (⁷Li) or 4.5 T m⁻¹ (¹⁹F). δ was the gradient duration (1.2 ms for both nuclei) and Δ was the observation time between the two gradient pulses (Δ = 150 ms, if not stated otherwise). Echo decays were either exponential and fitted accordingly, or they could be well fitted with a biexponential function. A relative error of 5% of the diffusion coefficients was assumed.

Thermogravimetric Analysis (TGA)

For TGA, the sample was placed into a pan and hermetically sealed under argon atmosphere, subsequently loaded into the instrument with no contact with ambient air, and punctured inside the furnace under helium atmosphere. The measurement was performed under a helium flow through the TGA‐balance of 30 mL min⁻¹, a helium flow through the sample of 25 mL min⁻¹, and using a constant heating rate of 2 K min⁻¹ in a temperature range of 30–600 °C.

Differential Scanning Calorimetry (DSC)

DSC was carried out with a heat flux calorimeter with LNCS (Liquid Nitrogen Cooling System) and for precise baseline recording using Tzero^®‐technology. In an argon atmosphere, the sample was filled into a Tzero^®‐aluminum pan and hermetically sealed. Two heating ramps were determined in the temperature range from −140 to 190 °C with a heating rate of 10 K min⁻¹ under 25 mL min⁻¹ helium sample purge.

Electron Microscopy

To do scanning electron microscopy (SEM) or transmission electron microscopy (TEM), ultrathin sections of the sample were produced by cryo ultramicrotomy. Because of better contrast at low acceleration voltage, the neat and unstained BCP samples were examined at room temperature in a SEM with a STEM detector. Sections from SPE membranes were stored on a grid in liquid nitrogen to prevent contact to air/humidity. They were transferred into the TEM using a cryo transfer holder and imaged at cryogenic temperature in scanning transmission electron microscopy mode (STEM).

X‐Ray Scattering (SAXS, WAXS)

SAXS and WAXS measurements were performed using the laboratory‐based “Ganesha‐Air” system (SAXSLAB/XENOCS) equipped with a D2‐MetalJet (Excillum) anode operating at 70 kV and 3.57 mA with Ga‐Kα radiation (wavelength  λ = 0.134 nm). The beam was focused with a focal length of 55 cm to provide a 100 µm intense beam at the sample position. Two pairs of scatterless slits were used to adjust the beam size depending on the detector distance. SAXS data were acquired with a position‐sensitive PILATUS 300 K‐detector (Dectris), WAXS data with a position‐sensitive PILATUS 100k detector (Detris). The detector distances were calibrated with silver behenate for the SAXS measurements, and with silicon for the WAXS measurements. All samples were sealed in glass capillaries of 2 mm inner diameter under exclusion of moisture. Data reduction and background subtraction were done using the Python‐based project Jscatter.^{[ 58 ]}

Electrochemical Impedance Spectroscopy (EIS)

EIS was performed in a logarithmic frequency range from 1 Hz to 1 MHz and an alternating amplitude of 40 mV. EIS was carried out in a temperature range from −20 to 90 °C by varying the temperature in 5 or 10 °C steps. The ionic conductivity was determined by placing the prepared SPE membranes in contact with two ion‐blocking stainless steel electrodes assembled in coin cells.

Conflict of Interest

The authors declare no conflict of interest.

Supporting information

Supporting Information

Krause D. T., Förster B., Dulle M., Krämer S., Böckmann S., Mönich C., Hansen M. R., Schönhoff M., Siozios V., Grünebaum M., Winter M., Förster S., Wiemhöfer H.‐D., A Super‐Ionic Solid‐State Block Copolymer Electrolyte. Small 2024, 20, 2404297. 10.1002/smll.202404297

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.