CASTER-DTA: Equivariant Graph Neural Networks for Predicting Drug-Target Affinity

Abstract

Accurately determining the binding affinity of a ligand with a protein is important for drug design, development, and screening. With the advent of accessible protein structure prediction methods such as AlphaFold, several approaches have been developed that make use of information determined from the 3D structure for a variety of downstream tasks. However, methods for predicting binding affinity that do consider protein structure generally do not take full advantage of such 3D structural protein information, often using such information only to define nearest-neighbor graphs based on inter-residue or inter-atomic distances. Here, we present a joint architecture that we call CASTER-DTA (Cross-Attention with Structural Target Equivariant Representations for Drug-Target Affinity) that makes use of an SE(3)-equivariant graph neural network to learn more robust protein representations alongside a standard graph neural network to learn molecular representations, and we further augment these representations by incorporating an attention-based mechanism by which individual residues in a protein can attend to atoms in a ligand and vice-versa to improve interpretability. In this manner, we show that using equivariant graph neural networks in our architecture enables CASTER-DTA to approach and exceed state-of-the-art performance in predicting drug-target affinity without the inclusion of external information, such as protein language model embeddings. We do so on the Davis and KIBA datasets, common benchmarks for predicting drug-target affinity. We also discuss future steps to further improve performance.

1. Introduction

Determining drug-target affinity (DTA) is a critical component of the drug design and discovery process, serving as a metric of which drugs (ligands/molecules) may be high-priority for further testing in terms of binding to a target (protein) [1]. While experimental affinity determination is the gold standard, it is often not feasible or practical to perform experiments to determine affinity for what may be millions or billions of possible drug candidates for a given target. To address this, various computational methods have been developed for the purpose of predicting the binding affinity of an arbitrary protein and an arbitrary ligand to help prioritize or rank drugs for further exploration.

Some state-of-the-art methods, such as DeepDTA and AttentionDTA make use of deep learning used primarily sequence information, using the protein amino-acid sequence and the molecule Simplified Molecular Input Line Entry System (SMILES) string [2, 3]. Other methods make use of graph neural networks (GNNs), such as GraphDTA and DGraphDTA, which both used GNNs to process molecular graph information to learn molecular representations that were then used alongside trained sequence-based protein representations [4, 5].

More recently, there are methods that have made use of 3D protein information, such as DGraphDTA, which used predicted protein contact maps to construct a k-nearest-neighbors protein graph and then used graph neural networks to extract graph-based protein representations alongside graph-based molecular representations [5]. Additionally, several methods, including some of the above, have made use of external embeddings, such as protein language model embeddings, to augment their protein or molecule representations. For example, DGraphDTA made use of calculated position-specific-scoring-matrix (PSSM) embeddings [5].

However, to the present day, few methods have made use of the underlying geometric information contained within protein 3D structure beyond defining nearest-neighbor graphs for predicting binding affinity, despite work that has made use of this information in other paradigms. This includes information obtained from the protein backbone, such as bond angles to represent torsion, distance vectors between residues, and sidechain orientation directional vectors, among many others. Furthermore, to our knowledge, no methods have made use of SE(3)-equivariant graph neural networks to use these protein-level features in a rigorous way for the purposes of drug-target affinity prediction.

We present in this paper a method, Cross-Attention with Structural Target Equivariant Representations for Drug-Target Affinity (CASTER-DTA), inspired by work done in other paradigms [6, 7, 8], that makes use of SE(3)-equivariant graph neural networks in the form of Geometric Vector Perceptron (GVP)-GNNs to incorporate this 3D backbone information at the protein level alongside cross-attention to improve drug-target affinity prediction. We show that CASTER-DTA exceeds the performance of several existing state-of-the-art methods without the need for external pretrained embeddings on two different benchmark datasets. We additionally show that the use of equivariant graph neural networks provides a performance improvement for the prediction of drug-target affinity over non-equivariant GNNs.

2. Methods

2.1. Dataset Details and Preparation

We used two established datasets for the purposes of predicting drug-target affinity: the Davis dataset [9] and the KIBA dataset [10]. Davis contains binding affinity information for 30056 protein-molecule pairs, with 442 unique proteins and 68 unique molecules in the dataset. KIBA contains binding affinity information for 118254 protein-molecule pairs, with 229 unique proteins and 2111 unique molecules in the dataset. Amino-acid sequences for each protein and SMILES (Simplified Molecular Input Line Entry System; text strings that fully define the chemical structure of a compound) strings for each molecule are available in the Davis dataset. The same information is available for each protein and molecule in the KIBA dataset.

For Davis, the target is the K_d value representing the binding affinity between each protein-molecule pair. K_d values are converted to scaled pK_d values by performing the following transformation:

$$p{K}_d=-{\text{log}}_{10}\left(\frac{K_d}{{10}^9}\right)$$

For KIBA, the target is an integrated bioactivity score that integrates K_d, K_i, and IC50 values from each protein-ligand pair. For training, targets from each dataset are standardized to z-scores to improve training dynamics by subtracting the mean and dividing by the standard deviation to compute a distribution with a mean of 0 and a standard deviation of 1.

We acquired ligand-free (apo) structures for every protein in each dataset in the following manner, using the first method that yielded a result:

1. Search the Protein DataBank (PDBank) [11] for experimentally-determined structures with 100% sequence identity, filtering out any structures with any ligands bound (essentially, filtering down to only apo structures).

2. Search the AlphaFold2 database (co-hosted on PDBank) for pre-folded structures with 100% sequence identity [12].

3. Use a local version of AlphaFold2 [13] (ColabFold, using colabfold_batch [14]) to fold any remaining proteins using the sequences provided, with settings described in Appendix Table A1.

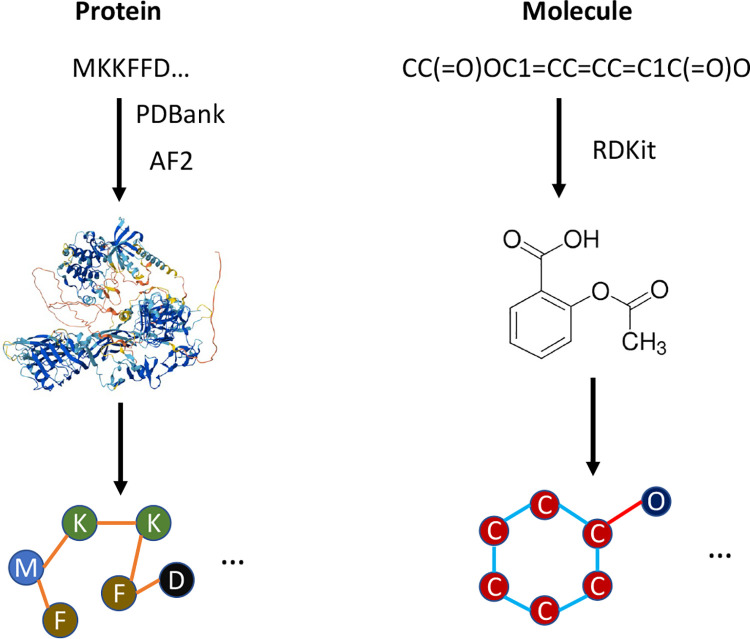
A visualization of the process of creating protein and molecule graphs can be seen in Figure 1.

Figure 1:

A visualization of the process of generating protein and molecular graphs, starting from protein sequence and molecular SMILES strings. Protein structures are acquired from PDBank or folded with AlphaFold2 and molecule SMILES are converted to graphs using RDKit.

2.2. Protein Graph Representations

We construct protein graphs from AlphaFold, inspired by previous work into using equivariant graph neural networks for other protein-related tasks; in particular, we took inspiration from the PocketMiner GNN for predicting cryptic pocket opening within proteins [8] and the original GVP-GNN papers and its extension [6, 7]. Similarly to PocketMiner and GVP-GNN, we define each residue as a node. Like PocketMiner and GVP-GNN, we also connect each residue with edges based on geometric distance; however, instead of connecting to the 30 nearest neighbors as in those two approaches, we instead connect each residue to every residue within a 4 Angstrom distance in 3D space, with the distance threshold determined through an ablation study.

For protein node (residue) and edge features, we include both scalar and vector-based features as inspired by PocketMiner and other work, as described in Appendix Section B. We additionally concatenate a one-hot-encoded representation of the amino acid identity (with 20 unique amino acids) to the node scalar features.

2.3. Molecular Graph Representations

We construct 2D molecular graphs from SMILES strings by using RDKit, where each node represents an atom and each edge represents a bond between atoms. For molecule node (atom) and edge (bond) features, we include a variety of features for atomic representations based on prior work, all of which were computed using RDKit, as described in Appendix Section C.

Additionally, a one-hot-encoded representation of the atomic identity is concatenated to the above features. We use 10 unique types representing hydrogen, carbon, nitrogen, oxygen, fluorine, phosphorus, sulfur, chlorine, bromine, iodine, and other, respectively, where “other” captures all other atomic identities. Additionally, a one-hot-encoded representation of whether the bond is a single, double, triple, or aromatic bond is concatenated to the bond features as a representation of the bond type.

2.4. Architecture

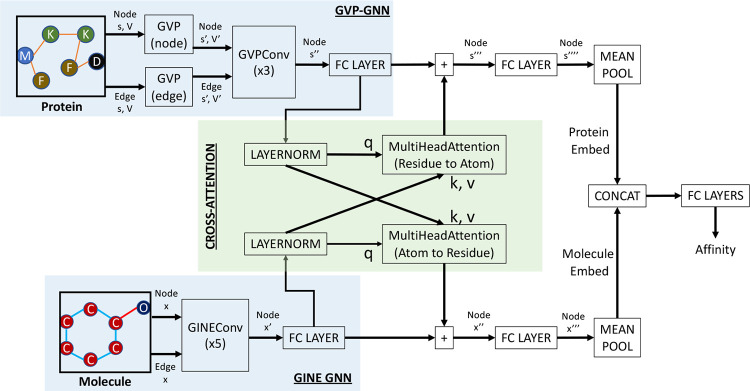
CASTER-DTA includes two graph neural networks that produce learned representations at the node level. Protein graphs are processed by Geometric Vector Perceptron (GVP) and GVPConv layers which are SE(3)-equivariant, as proposed by Jing et al. [6, 7]. Initial GVPs are used to create richer representations of the node and edge features before processing by GVPConv layers to update the node-level (residue) representations. Molecule graphs are processed by GINEConv layers, which represent an edge-enhanced version of the Graph Isomorphism Network (GIN) as described by Xu et al. and Hu et al. [15, 16]. Each GINEConv layer updates the node-level (atom) representations.

The node-level representations for proteins and molecules are subsequently processed by a linear layer and then used as queries, keys, and values in a cross-attention paradigm, where each cross-attention block updates either the protein or molecule embeddings based on the attention weights computed for residues attending to atoms or vice-versa. These updated node embeddings are processed by another linear layer and are each then pooled by taking the mean over all nodes to create a singular graph embedding for proteins and molecules; these embeddings are subsequently concatenated and passed into several fully-connected (FC) layers for the final regression prediction.

A visual summary of this architecture can be seen in Figure 2.

Figure 2:

A visualization of the architecture used to predict drug-target affinity from protein and molecule graphs. GVP = Geometric Vector Perceptron; GINE = Graph Isomorphism Network with Edge Enhancement.

2.5. Training and Evaluation

We split each dataset into 70% training, 15% validation, and 15% testing splits, doing so multiple times to evaluate the model’s performance and consistency. The output values for the dataset are standardized to have a mean of 0 and a standard deviation of 1. The model results are subsequently unscaled for the purposes of reporting and evaluation.

We trained CASTER-DTA on the training splits for 2000 epochs using an Adam optimizer with a base learning rate of 1e-4 on a Mean-Squared Error (MSE) loss function, using the validation split to tune hyperparameters. We reduced the learning rate after 50 epochs of no observed improvement in the validation loss by multiplying it by 0.8. We additionally implemented early stopping, ending training early if the validation loss did not improve for 200 epochs. In most cases, CASTER-DTA terminated early around 1000 epochs.

Due to variations in the size of protein and molecule graphs, the number of elements (including padding) in the batched attention matrix can vary substantially and so memory usage can fluctuate dramatically from batch to batch. To address this and stabilize training, we employ a dynamic mini-batching paradigm wherein we limit the total size of a batch to 16 million residue-atom pairs (as initialized in the attention matrix) with a maximum of 128 protein-molecule pairs in each batch for the Davis dataset. For the KIBA dataset, we limit the total size of a batch to 8 million residue-atom pairs and a maximum of 64 protein-molecule pairs. The difference in batch sizes is due to different memory requirements due to larger proteins being present in the KIBA dataset.

We used the model with the best validation loss during each of the above training cycles for downstream evaluation on the test set. To evaluate the model, we used the testing split and calculated the corresponding mean-squared error as well as the concordance index (CI) as a marker of performance, assessing performance across multiple iterations of training/validation/testing. To compare, we also trained and evaluated several preexisting state-of-the-art models on the same dataset splits, including DeepDTA, GraphDTA, DGraphDTA, and AttentionDTA. All hyperparameters for these models were replicated from their respective papers for both datasets, and these hyperparameters are described in Appendix Section D.

2.5.1. Ablation Studies

We also assessed how using edge definitions versus connecting to the 30 nearest neighbors to connect residues impacted performance of the model. We tested Angstrom distance thresholds of 4 Angstroms, 6 Angstroms, and 8 Angstroms, as well as defining edges as in PocketMiner by connecting to the 30 nearest neighbors on the Davis dataset.

We additionally assessed how much the GVP-GNN and 3D protein representation contributed to the model by performing an ablation study where we replaced the protein GNN with a graph attention network (GATv2) convolutional layer [17, 18] instead, as GAT has been used in prior work for protein graph processing [5]. We also assessed the use of a variety of molecular GNN architectures to assess the flexibility of GVP-GNN in working alongside various molecule representations and to determine the best architecture, including GIN [15], GINE [16], GATv2 [18], and AttentiveFP [19]. We performed these tests on a single seed/split of the Davis dataset.

3. Results

3.1. Performance on the Davis dataset

The performances of CASTER-DTA on Davis, as well as several other models that have been considered state-of-the-art in various ways, can be seen in Table 1.

Table 1:

Performance of Architectures on the Davis dataset

Architecture	MSE ↓	MAE ↓	PCC ↑	CI ↑
CASTER-DTA	0.209 ± 0.009	0.232 ± 0.004	0.861 ± 0.007	0.895 ± 0.004
DeepDTA	0.236 ± 0.016	0.252 ± 0.013	0.840 ± 0.013	0.889 ± 0.005
GraphDTA	0.241 ± 0.012	0.271 ± 0.008	0.836 ± 0.009	0.885 ± 0.003
DGraphDTA	0.220 ± 0.010	0.229 ± 0.008	0.852 ± 0.008	0.895 ± 0.004
AttentionDTA	0.225 ± 0.014	0.240 ± 0.008	0.848 ± 0.011	0.893 ± 0.005

± values are standard deviation.

As can be seen, CASTER-DTA improves on or closely matches the performances of other state-of-the-art models that make use of deep learning for drug-target affinity prediction, achieving an average MSE of 0.209 on the Davis dataset. For the MSE criterion, CASTER-DTA outperforms every architecture by a fairly substantial margin, and the next best architecture (DGraphDTA) achieves an average MSE of 0.225 on the same dataset splits. For the MAE criterion, CASTER-DTA has a performance of 0.232, second only to DGraphDTA which performed similarly with an MAE of 0.229. For the Pearson correlation (PCC) metric, CASTER-DTA exceeds every other method with an average PCC of 0.854 (which can be said to be comparable to DGraphDTA with a PCC of 0.852). For the concordance index (CI) metric, CASTER-DTA matches DGraphDTA with a CI of 0.895 and outperforms all other methods, with the next best being AttentionDTA with a CI of 0.893.

3.2. Performance on the KIBA dataset

Similarly, the performances of CASTER-DTA and the same comparison models on the KIBA dataset can be seen in Table 2.

Table 2:

Performance of Architectures on the KIBA dataset

Architecture	MSE ↓	MAE ↓	PCC ↑	CI ↑
CASTER-DTA	0.159 ± 0.002	0.215 ± 0.003	0.880 ± 0.003	0.886 ± 0.002
DeepDTA	0.189 ± 0.003	0.254 ± 0.003	0.856 ± 0.003	0.863 ± 0.004
GraphDTA	0.161 ± 0.002	0.233 ± 0.003	0.878 ± 0.002	0.877 ± 0.003
DGraphDTA	0.141 ± 0.004	0.199 ± 0.003	0.895 ± 0.002	0.897 ± 0.002
AttentionDTA	0.180 ± 0.003	0.259 ± 0.003	0.864 ± 0.003	0.861 ± 0.002

± values are standard deviation.

As the table shows, CASTER-DTA beats all other methods except for DGraphDTA on the KIBA dataset. For the MSE criterion, CASTER-DTA obtains an MSE of 0.159, second only to DGraphDTA which has an MSE of 0.141, and GraphDTA performs similarly to CASTER-DTA with an MSE of 0.161. For MAE, CASTER-DTA exhibits an MAE of 0.215 while DGraphDTA has an MAE of 0.199. For the Pearson correlation (PCC) metric, CASTER-DTA has an average PCC of 0.880, similar to GraphDTA which has a PCC of 0.878, and second only to DGraphDTA which has a PCC of 0.895. For the concordance index (CI) metric, CASTER-DTA with a CI of 0.886 is second in performance to DGraphDTA (0.897) and outperforms all other methods.

3.3. Edge Definition Ablation Performance

The results of the ablation study where we assessed the performance of the CASTER-DTA architecture as described above on different edge definitions on the Davis dataset can be seen in Table 3. We present the average and standard deviation of various metrics on 5 different seeds of the Davis dataset. The edge threshold of 4 Angstroms performed the best of all of the edge definitions, though all definitions including the 30 nearest neighbors definition performed well, with most still outperforming all of the methods on the Davis dataset as detailed in Table 1.

Table 3:

Performance of CASTER-DTA with Different Edge Definitions (on Davis)

Edge Definition	MSE ↓	MAE ↓	PCC ↑	CI ↑
4 Angstroms (Distance)	0.209 ± 0.009	0.232 ± 0.004	0.861 ± 0.007	0.895 ± 0.004
6 Angstroms (Distance)	0.220 ± 0.003	0.239 ± 0.003	0.853 ± 0.003	0.890 ± 0.001
8 Angstroms (Distance)	0.224 ± 0.011	0.240 ± 0.006	0.849 ± 0.009	0.891 ± 0.005
30 nearest (KNN)	0.217 ± 0.014	0.233 ± 0.007	0.854 ± 0.010	0.890 ± 0.004

± values are standard deviation.

3.4. Graph Convolution Ablation Performance

The results of the ablation study where we replaced the GVP-GNN layers in CASTER-DTA with GAT convolutional layers and tested various molecular GNN architectures can be seen in Table 4. For brevity and computational resource management (as some of the other architectures take a very long time to train), we simply report the performance on one seed of the Davis dataset.

Table 4:

Ablation Study of Various GNN Architectures

Protein GNN	Molecule GNN	MSE ↓	MAE ↓	PCC ↑	CI ↑
GVP-GNN *	GINE *	0.220	0.235	0.854	0.892
GATv2	GINE	0.320	0.306	0.783	0.846
GVP-GNN	GIN	0.240	0.247	0.841	0.886
GVP-GNN	GATv2	0.237	0.245	0.842	0.887
GVP-GNN	AttentiveFP	0.230	0.240	0.847	0.887

^*Represents combination used in CASTER-DTA.

The architecture using the GVP-GNN for proteins and GINE for molecules achieved the best performance of all of the architectures evaluated, with other architectures using the GVP-GNN for the protein having MSEs in the range of 0.230–0.240 and the architecture replacing the GVP-GNN with GAT having an MSE of 0.320. All other metrics (MAE, PCC, and CI) show similar trends, with the GVP-GNN + GINE combination as used in CASTER-DTA outperforming all other combinations.

4. Discussion

CASTER-DTA exhibits performance that exceeds or matches those of other models on the Davis drug-target affinity dataset. Specifically, CASTER-DTA exhibits the best performance on the MSE, Pearson correlation (PCC), and concordance index (CI) metrics, and it is the second-best on the MAE metric. On the KIBA dataset, CASTER-DTA performs very well; specifically, it has the second-best performance for all of the four metrics studied behind DGraphDTA, which is the best performing for all four metrics. Notably, DGraphDTA, makes use of external information obtained from multiple sequence alignment (MSA) in the form of position-specific-scoring-matrix (PSSM) embeddings, which are costly to compute. Determining these MSAs and computing their associated features is not necessary when a protein 3D structure is given in CASTER-DTA, which uses only features available within the protein 3D structure, and so while DGraphDTA performs better on KIBA, it requires much more preprocessing to run than CASTER-DTA, comparatively.

Ultimately, CASTER-DTA is able to perform well in predicting binding affinity with no external information beyond the structural information other than fundamental amino acid properties (such as molecular weight, hydrophobicity, and others), which are fixed values for each residue type across proteins. Furthermore, from preliminary performance benchmarking, this architecture is capable of evaluating tens of thousands of protein-drug pairs in under a minute on an NVIDIA 2080TI GPU, which greatly increases its ability to be used for arbitrary drug screening against specific targets.

Additionally, we find through our ablation studies evidence that the GVP-GNN is able to effectively make use of the 3D structural information and that it contributes to the prediction. Specifically, when we replace the protein GVP-GNN in CASTER-DTA with a GATv2 architecture, we find that performance is noticeably reduced, with the MSE going from 0.220 to 0.320, indicating that the equivariant expressiveness of the GVP-GNN was essential for the performance of the overall architecture. Furthermore, we find that other molecular GNNs such as GIN, GATv2, AttentiveFP are able to perform relatively well alongside the GVP-GNN with MSEs of 0.240, 0.237, and 0.230, respectively, with some of these subpar combinations still outperforming several existing state-of-the-art methods on the Davis dataset. This exhibits the flexibility of equivariant graph neural networks for processing protein representations in working with a variety of different molecular representation approaches and exhibiting a strong potential for improvement as molecular representation learning advances.

5. Future Directions

There are several promising avenues for improvement and continued evaluation that we plan to explore in future work with this architecture. Most notably, the work and performance described in this paper is the result of relatively simplistic fine-tuning of architecture and hyperparameters in part due to time and computational constraints. Furthermore, we have obtained preliminary results that seem to imply that the performance can be further improved by tweaking the architecture slightly (for example, embedding rather than one-hot-encoding the amino acid and atom identities), by changing the training hyperparameters (for example, using a lower learning rate of 5e-5), by increasing the batch size from 128 protein-molecule pairs to 256 if memory allows, and by setting the dropout rates in a heterogeneous manner (for example, having the protein GNN dropout being higher than the molecule GNN rather than being equivalent).

In this paper, we have also not fully explored the interpretability that using graph neural networks in this way allows - through introspecting the cross-attention module by extracting the attention matrices for each protein-molecule pair, we can identify which residues and atoms contribute most to the prediction. Furthermore, we have preliminarily implemented a form of GNNExplainer that allows us to identify important residues and atoms within the graphs for the prediction, which allows one to identify the substructures within each of the two modalities that may contribute to the affinity or binding prediction, further improving our ability to iterate on drug structures.

Additionally, there are other datasets that people have used in the paradigm of drug-target affinity, such as BindingDB [20] and PDBbind [21], which all have different distributions of noise and data completeness. Our hope is to further benchmark CASTER-DTA against other methods on these datasets, to better understand the properties of the protein-ligand pairs where CASTER-DTA performs well and where it performs poorly, and to better characterize the advantages and disadvantages of our approach across related paradigms. Notably, in this approach, we did not make use of 3D structural information for the molecules (drugs) due to the relative lack of availability of 3D molecular conformations for arbitrary molecules; however, there do exist some resources, such as GeoMol, that can produce 3D molecular conformers in the form of ensembles [22]. By making use of predicted 3D molecular conformers, we could implement another equivariant GNN to process the molecular graphs in a way that may provide even more useful information for the prediction of binding affinity or other related tasks. Alternatively, even using 2D coordinates of the drug graph may provide information on bond lengths and putative bond angles, serving to add additional feature information that further improves performance.

In addition to the aforementioned datasets, a new resource known as PLINDER has recently become available; this resource provides a much more robust means for splitting datasets to avoid leakage and purports to provide a wealth of binding affinity information as well as structural information on protein-ligand interactions [23]. We plan to evaluate our architecture as well as other state-of-the-art architectures on this dataset as an extension to this paper. Furthermore, with the wealth of data that PLINDER provides, it is possible to develop a modified version of CASTER-DTA that not only predicts binding affinity, but also predicts the 3D conformation of the protein-ligand complex as a whole; we are actively exploring this possibility in future work involving equivariant graph neural networks.

A. AlphaFold2/ColabFold Parameters

Parameters that were used to fold any proteins not already present in the Protein DataBank or the AlphaFold2 database can be found in A1.

Table A1:

ColabFold parameters (blank indicates a flag)

Argument	Parameter
-num-models	5
-num-recycle	3
-stop-at-score	85
-random-seed	9
-templates
-amber
-num-relax	1
-relax-max-iterations	2000

B. Protein Graph Features

B.1. Node Features

Each node (residue) has 17 scalar features and 3 vector features:

• The sin and cos of the three dihedral angles computed from the residue’s central carbon to its bonded atoms. (6 scalars)

• Various amino acid properties, including weights, pK and pI, hydrophobicity, and binary features of aliphaticity, aromaticity, whether the residue is acidic or basic, and whether the residue is polar neutral. (11 scalars)

• A unit vector pointing from the residue’s central carbon towards the sidechain, computed by normalizing from tetrahedral geometry. (1 vector)

• One unit vector each pointing from the residue’s central carbon to the next residue’s central carbon and the previous residue’s central carbon. The first and last residues have zero-vectors for their backward and forward vectors, respectively. (2 vectors)

B.2. Edge Features

Each edge (as constructed between the 30-nearest-neighbors of each residue) has 32 scalar features and 1 vector feature:

• Gaussian RBF encodings of the distance between the two residues. (16 scalars)

• Sinusoidal positional encodings of the difference in residue indices in sequence. (16 scalars)

• The unit vector pointing in the direction of the source residue’s central carbon to the destination residue’s central carbon. (1 vector)

C. Molecule Graph Features

C.1. Node Features

Each node (atom) has 41 total features:

• Multiple one-hot encodings of various properties, including: chirality, hybridization, number of bound hydrogens, degree, valence, formal charge, and number of electron radicals. (38 features)

• Binary features for whether the atom is in a ring and is aromatic. (2 features)

• Computed Gasteiger partial charges. (1 feature)

C.2. Edge Features

Each edge (bond) has 9 features:

• The stereoconfiguration of the bond. (7 features)

• Binary features for whether the bond is conjugated and in a ring. (2 features)

D. Benchmark Method Implementation Details

Information about the implementations of other benchmark drug-target affinity methods can be found in D2. All methods with the exception of DeepDTA were implemented using their original source code, while DeepDTA was reimplemented using PyTorch to facilitate easier comparison.

Table D2:

Parameters and Settings for Benchmark Methods

Method	Code source	LR	Epochs	Batch Size
DeepDTA	Reimplemented	0.001	100	256
GraphDTA	Original code	0.0005	1000	128
DGraphDTA	Original code	0.001	2000	512
AttentionDTA	Original code	0.0001	100	512