Force balance of opposing diffusive motors generates polarity-sorted microtubule patterns

Significance

Microtubule networks in cells can adopt different polarized architectures. Most of these architectures are thought to result from the localization of microtubule nucleators. However, microtubules can be transported by molecular motors. This process can generate radial asters. It is also thought to generate bipolar spindles, but the underlying process is less clear. These data and theory show that two types of motors of opposite directions and microtubules can self-organize into parallel alignment of polarity-sorted microtubules, acting as an active barrier that segregates the two motors on either side of the polar barrier. These results reveal a self-organization process that could be responsible for the emergence of polar or bipolar structures in cells.

Abstract

The internal organization of cells is largely determined by the architecture and orientation of the microtubule network. Microtubules serve as polar tracks for the selective transport of specific molecular motors toward either their plus or minus ends. How both motors reciprocally move microtubules and organize the network’s arrangement and polarity is unknown. Here, we combined experiments on reconstituted systems and theory to study the interaction of microtubules with both plus- and minus-end directed motors bound to a fluid membrane. Depending on motor concentrations, the system could lead either to the constant transport of microtubules or to their alignment, stacking, and immobilization in regular bands that separate motors into domains of opposite polarities. In bands, microtubules shared the same polarity and segregated the two opposing motors accordingly. These regular patterns resulted from the balance of forces produced by the two motors as they walked in opposite directions along microtubules. The system was maintained in a dynamic steady state in which the directional transport of microtubule-bound motors compensates for the random diffusion of lipid-bound motors. The size of motor domains depended on their respective concentrations. The constant flow of motors allowed the system to respond to variations in motor concentrations by moving microtubules to adapt to the new force balance. The polar sorting and linear arrangement of microtubules associated with the segregation of motors of opposite polarity are typical of cellular architectures, which these data may help to better understand.

Microtubules serve as tracks for intracellular transport by molecular motors. Comprising heterodimers of alpha and beta tubulin, microtubules are inherently polar filaments capable of guiding the transport of organelles in a specific direction—either toward their “plus” or “minus” ends—depending on the type of molecular motors transporting the cargo (1, 2). Hence, the architecture of the microtubule network determines the position of organelles, the spatial organization of cell compartments, and the global orientation of cell polarity (3–6).

It has long been held that microtubule orientation and network architecture are controlled by microtubule organizing centers, such as the centrosome and Golgi apparatus, given their ability to nucleate microtubules and anchor their minus ends (7). Nevertheless, it is now clear that a significant portion of the network architecture arises from the self-organization of microtubules and molecular motors (8, 9). They can mutually transport each other and generate large and highly ordered structures (10–12). These self-organizing properties of microtubules and motor collective are particularly striking in mitotic and meiotic spindles. In these structures, motors with opposite directions of motion, along with microtubules, can move freely and form large, polarized, regular, and ordered architectures (13, 14). Polarized radial arrays can also form without a template in interphasic egg extracts (15). As they form, these asters repel each other and define clear peripheral limits despite the absence of spatial boundaries (16). This process is suggestive of the emergence of self-organized cellular units (9). As such, cellular networks of cytoskeleton filaments can be seen as active matter, dissipating energy to self-organize into complex yet regular architectures (17). Determining whether common self-organizing principles underlie these different structures and could extend to govern a broader range of cellular architectures is an exciting possibility that has proven challenging to explore experimentally.

Reconstitution assays based on the bulk self-organization of microtubules with a single type of motor showed that radial asters can form through motor transport and accumulation at one end of microtubules (18, 19). In response to two motors with opposite directionalities, microtubules coalesce into an array of asters with alternating polarities (18, 20). Further efforts to associate two opposite motors in order to obtain spindle-like organizations, with both clustering of microtubule minus-end in radial asters and sorting of plus-end in parallel alignment of microtubules forming midzone-like structures, have remained a challenge (21, 22). When microtubules are aligned by external crowding forces, and when motors cannot accumulate at the ends, the microtubules slide along each other in a continuously flowing dense nematic-like phase (23–25). However, in these systems, microtubules are not polarity-sorted and continuously move and transform (26–30).

In reconstituted systems where motors are attached to surfaces, microtubules are transported and can move collectively when aligned by external crowding forces (31). In response to two motors with opposite directionalities, the motion of microtubules is generally dominated by one motor, but they can also become immobilized in a tug-of-war scenario within a narrow range of motor concentration combinations (20, 32, 33). However, in these conditions, immobilized microtubules could not self-organize into regular structures at large scale.

Noteworthy, in most reconstituted systems, motors are either immobilized or completely free. However, motors can also be anchored to diffusible lipid membranes. Lipid-bound motors can transmit forces and move microtubules (34) while diffusing and concentrating along microtubules (35, 36). We wondered whether these conditions could allow for both the self-organization of microtubules into regular macroscopic structures and the sorting of opposite motors into segregated domains.

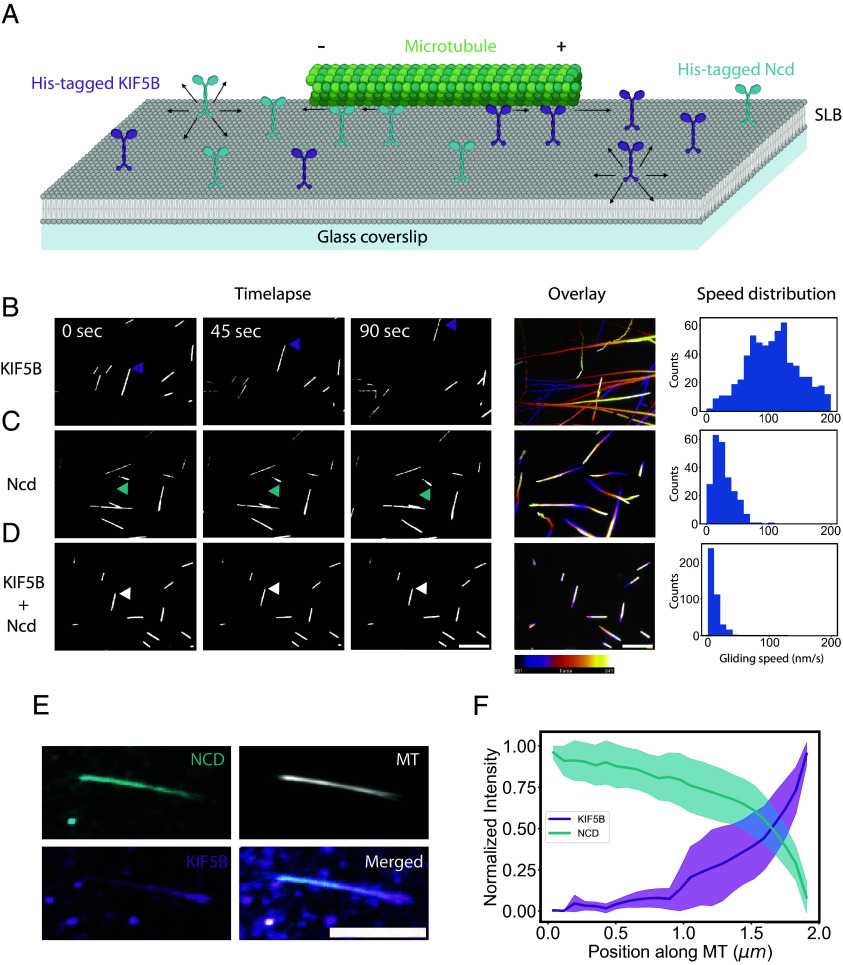
We hence first tested the ability of two types of molecular motors with opposite directionalities to balance their forces as they walk along microtubules and diffuse in a supported lipid bilayer (SLB). Motors were bound to NTA (Ni) lipids via their His tag. Stabilized microtubules were then laid down on the bilayer (Fig. 1A). In contact with KIF5B, a plus-end directed motor of the kinesin 1 family, microtubules were propelled at about 100 nm/s (Fig. 1B and Movie S1). As expected, microtubule gliding speed was lower on a lipid bilayer than on glass (600 nm/s) (34). In contact with Nonclaret disjunctional (Ncd), a minus-end directed motor of the kinesin-14 family (37), microtubules were propelled at about 30 nm/s (Fig. 1C and Movie S1). When both motors were present, their competition led to a tug-of-war and the immobilization of the microtubules (Fig. 1D and Movie S1). In contrast to the case of immobilized motors, in these conditions, the motors are still continuously walking on the microtubule. This results in an inhomogeneous accumulation of motors along the filament, with KIF5B accumulating toward the plus-end of the microtubule, and Ncd toward the minus-end (Fig. 1E). As a result, the two motors exhibited steady, reproducible, and opposite increasing concentration profiles along the microtubule (Fig. 1F).

Fig. 1.

The transport of motors with opposite polarities results in a tug-of-war and sorting of the motors. (A) Schematic of the experimental setup. Plus-end directed KIF5B and minus-end directed Ncd are attached to a SLB and microtubules are added. (B–D) Left, microscopy imaging of microtubules at low-density gliding on KIF5B 0.6 nM (B) Ncd 2 nM (C) or both motors (D) Arrows indicate the leading tip of a microtubule. Middle, maximum projections of the microtubules gliding over 10 min with a temporal color code. Right, histograms of the microtubules gliding speeds (N = 1 n = 632 for KIF5B, N = 1 n = 245 for Ncd, and N = 1 n = 445 for both motors). (E) Motors accumulated under the microtubules and were sorted toward their respective microtubule end. Images show the maximum projection of images acquired during 15 min of a single microtubule, in the presence of both KIF5B and Ncd. (F) Normalized intensities of KIF5B (magenta) and Ncd (cyan) along microtubules (N = 1, n = 32, error bar = SE). (In all panels, scale bars represent 10 µm).

We wondered whether the local increases of motor concentrations at microtubule ends could be sensed by neighboring microtubules. We tested such a potential collective effect by increasing the density of microtubules on the lipid bilayer. The conditions leading to a tug-of-war among motors allowed only for transient and limited microtubule displacements. However, at slightly higher densities, we found that when two microtubules of similar orientation were close enough, they slid along one another, bringing their ends close together (Fig. 2A and Movie S2). We attributed this effect to the local increase in motor densities generated by their transport along microtubules, which pushed or pulled nearby microtubules and thereby forced them to align with the reference microtubule. Step by step, this attraction led to the formation of bundles of multiple microtubules (Fig. 2A). Like individual microtubules, bundles were kept in a frustrated gliding by a tug-of-war between opposing motors. As we increased the density of microtubules, bundles were drawn closer together, forming larger “bouquets.” The mutual attraction of these bouquets resulted in the formation of linear stacks of microtubules (Fig. 2B). The width of these bands corresponded to the length of individual microtubules, which, in those conditions, were close to 10 mm. Strikingly, these bands of parallel microtubules could self-organize over several hundreds of micrometers and generate regular patterns over areas of several millimeters squared (Fig. 2C). Bands of microtubules enclosed alternating domains enriched in either KIF5B or Ncd (Fig. 2D). Depending on the density of microtubules and the respective concentrations of motors, enclosed domains could appear less linear and more compact (Fig. 2E and SI Appendix, Fig. S1). To further confirm that the alternation of motors of opposite polarities was associated with the polarized orientation of microtubules, we tested the self-organization of dynamic microtubules assembled from stabilized seeds, which marked the minus-end of microtubules. These minus-ends were localized above the domain containing Ncd, i.e., the minus-end directed motor (SI Appendix, Fig. S2), confirming that the self-organizing process sorted microtubules based on their polarity. These regular alignments of polarity-sorted microtubules were reminiscent of the “pineapple” patterns formed spontaneously by stabilized microtubules in Xenopus meiotic egg extracts (38).

Fig. 2.

Microtubules and plus and minus-end directed motors self-patterning. (A) Microtubules can align into bundles in the presence of motors of opposite polarities. Microscopy imaging of bundling microtubules in the presence of 4 nM of KIF5B, 4 nM of Ncd, and a density 0.04 Microtubule/µm². (Scale bar, 10 µm.) (B) Effect of increased microtubule density on the organization of microtubules by motors of opposite polarities. Images show microtubules organization after 30 min of gliding in the presence of 4 nM of KIF5B, 4 nM of Ncd, at various densities of microtubule. (Scale bar, 20 µm.) (C) Pattern formation at large scale. Images show the stitching of multiple pictures of microtubules taken over a 6 mm PDMS well at various magnifications. White squares show the area which is zoomed in the right image. (D) Self-sorting of KIF5B (magenta) and Ncd (cyan) in segregated domains during microtubule gliding and alignment in the presence of 4 nM of KIF5B, 4 nM of Ncd. The patterns are observed after 60 min of gliding. Microtubule density was about 1 microtubule per µm². (Scale bar, 20 µm.) (E) Merged images showing microtubules (yellow), KIF5B (magenta), and Ncd (cyan) at different concentrations of the two motors. From left to right images, concentrations of KIF5B diminished from 4 to 1 nM while concentrations of Ncd increased from 1 to 6 nM. Microtubule density was about 1 microtubule per µm². (Scale bar, 20 µm.)

The self-patterning of motors and microtubules was likely driven by the transient transport of microtubules and the concurrent translocation of motors along them. As motors push the microtubules and walk in the opposite direction, they can naturally create a feedback loop in which the propelling unit is pushed away from the propelled object (28). According to this view, the moving microtubules would stop when encountering an area enriched by the opposite motor, which in turn had been generated by another set of microtubules with opposite polarity (Fig. 3A and Movie S3). Consistently, patterns of motors appeared in about 10 min, which corresponds to the time for microtubules of opposite polarities to move at 30 nm/s over their average length of 10 to 20 µm (Fig. 3B). Once formed, the patterns of microtubules remained steady during the following hour. However, the motors could keep on walking along these stationary microtubules. These dynamics could be tested by analyzing individual components recovery after the photobleaching of an elementary unit of the pattern. The fluorescence of microtubules did not recover, showing that there was almost no transport and exchange of microtubules once the unit was assembled. By contrast, the fluorescence of the two types of motors reappeared under the microtubule and accumulated near the microtubule ends in a few minutes (Fig. 3C and Movie S4). Furthermore, the bleaching of motors along a section of microtubule showed a directional recovery from the unbleached toward the bleach section (SI Appendix, Fig. S3 and Movie S5). These data showed that the morphological steady-state of microtubules and motor patterns was associated to a permanent flux of motors along the active boundaries formed by aligned and polarity-sorted microtubules (Fig. 3D). The key role of this boundary in maintaining the patterns was further demonstrated by the local destruction of a few microtubules with a pulsed laser, which led to the rapid dissolution of the patterns and the transient reactivation of the gliding of the remaining microtubules (Movie S6). The gentler severing of microtubules resulted in the two severed pieces gliding toward each other (Fig. 3E and Movie S7). This showed that at steady-state microtubules are held in position by a force balance resulting from the constant transport of motors toward their respective domains.

Fig. 3.

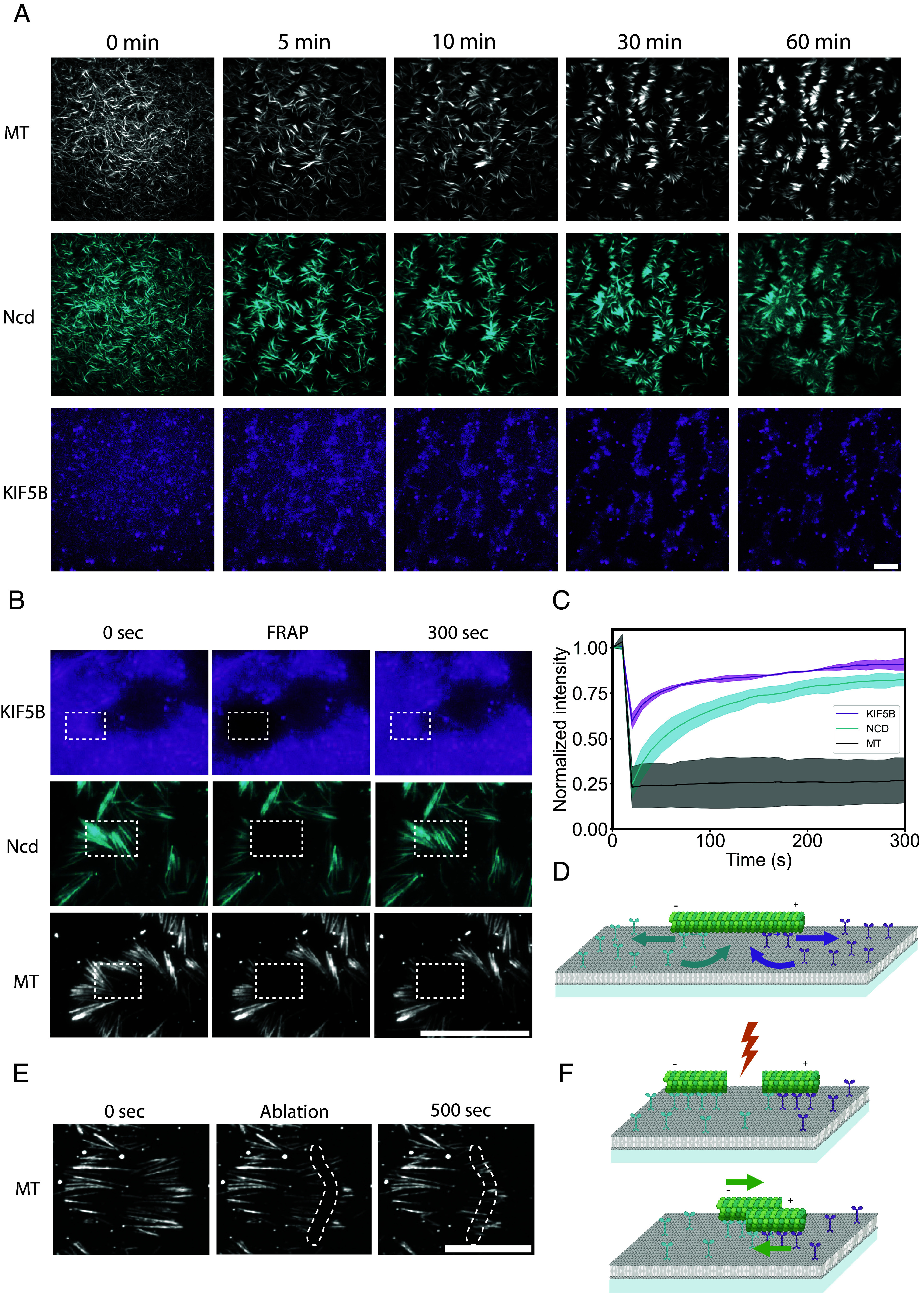
Microtubule and motors pattern dynamics. (A) Patterns emerge from an initial disordered state and remain steady over time. Images show time-lapse acquisition of microtubules, Ncd, and KIF5B in the presence of 4 nM of KIF5B, 4 nM of Ncd over 60 min. (B) While microtubules are immobilized, motors keep on diffusing in the lipid bilayer as well as attaching to, walking along, and detaching from microtubules (SI Appendix, Fig. S3). Images show time-lapse acquisition of microtubules, KIF5B, and Ncd after photobleaching in the rectangular area. (C) Graph shows the normalized fluorescence recovery of the three bleached signals (N = 1, n = 3, error bar = SE). (D) Schematic of the dynamic behavior of motors on each side of a patterned microtubule. (E) Time-lapse sequence showing the transport of microtubules sections after laser-based severing. (F) Schematic representation of the severing and transport of microtubules sections driven by segregated motors. In all these conditions, microtubule density was about 1 microtubule per µm². (Scale bars, 20 µm.)

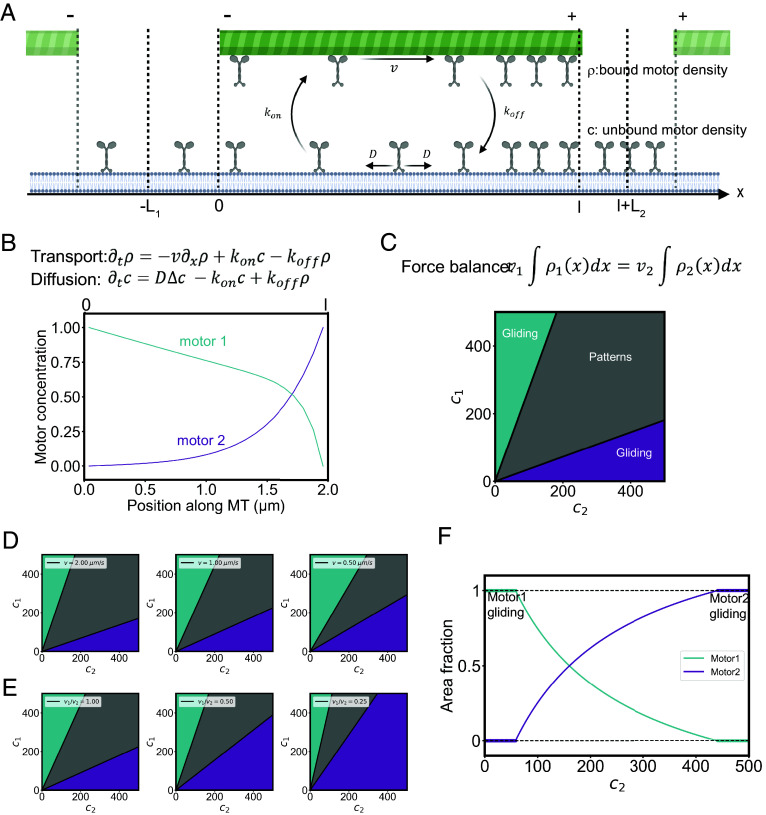
In order to understand the formation and maintenance of the regular patterns of motors and microtubules, we modeled the transport steady state and force balance leading to their self-organization in periodic arrays. We built a simplified one-dimensional model where the microtubules of length l make periodic bands all along the same direction, perpendicular to the microtubule orientation and separated by regions containing the two molecular motors and no microtubules. The distance between two neighboring bands L is imposed by the concentration of microtubules and the microtubules in two consecutive bands have opposite polarities. The pattern of microtubules and motors is invariant along the band direction and its properties depend only on the direction x of the microtubules. Because the system is periodic along x, it is sufficient to study one period as sketched in Fig. 4A. The two types of motors with different polarities are pumped along the microtubule and accumulate each on one of the regions outside the microtubule depending on its polarity. In these two regions of sizes L₁ and L₂, the motors diffuse freely with a diffusion constant D and because of the one-dimensional geometry, their concentrations are constant. In the region occupied by the microtubule, each type of motor can be in two states, either bound to the microtubule where it walks at constant velocity v or unbound and freely diffusing. In addition, the motors bind and unbind on the microtubules with rates k_on and k_off. The transport equations describing active transport, diffusion, and the binding unbinding kinetics are given Fig. 4B. We only discuss here the steady state for the concentration of free motors c and the concentration of bound motors ρ.

$$\frac{d^{2}c}{{\mathit{dz}}^2}+2\beta \frac{\mathit{dc}}{\mathit{dz}}-c=0,$$

$$\rho =\left(\frac{2\beta k_{\mathit{on}}}{k_{\mathit{off}}}\right)\frac{\mathit{dc}}{\mathit{dz}}.$$

Fig. 4.

Model and simulations of microtubules and motors self-organization. (A) Schematic representation of the model parameters. In a box of length L (equal to L1 + l + L2), motors beneath a microtubule of length l are separated in two populations: bound ρ and unbound c, motors have a diffusion coefficient D, a gliding speed on the microtubule v and transition rates between the two populations kon and koff. (B) Motors diffusion and sorting along the microtubule. Top: transport and diffusion equations. Bottom: plot of the theoretical prediction of the motor concentrations profiles along the microtubule with D = 1.5 µm²/s, l = 2 µm, kon = 1 s⁻¹ koff = 25 s⁻¹ v = 0.3 µm/s for motor 1 and kon = 12 s⁻¹ koff = 1 s⁻¹ v = 0.5 µm/s for motor 2. (C) Conditions for the emergence of self-patterning. Top: force balance equation between motor 1 and motor 2. Bottom: phase diagram showing the emergence of the different behaviors in response to combinations of motor concentrations. The model predicts that the boundaries between the “gliding” and “self-patterning” behaviors in this diagram are linear (SI Appendix). (D) Phase diagrams for different gliding speeds (here v1 = v2 = v). (E) Phase diagrams for different speed ratios between the motors. (F) Size of motor domains in self-patterning conditions. The graph shows the theoretical area fraction of each motor for a given concentration of motor 1 and increasing concentration of motor 2.

where we rescaled the length $z=x/\lambda$ by the diffusion screening length the diffusion screening length $\lambda ={\left(D/k_{\mathit{on}}\right)}^{1/2}$ and the relevant inverse Peclet number is ${\beta }^2={\left(\frac{k_{\mathit{off}}}{2v}\right)}^2\frac{D}{k_{\mathit{on}}}$. These two parameters take different values for the two types of motors. These equations are solved for the two types of motors in SI Appendix with boundary conditions ensuring the continuities of the concentrations of the two motors and of their fluxes. The average concentrations of the two motors c₁ and c₂ are also imposed in the experiment. The calculated concentration profiles of the motors are shown in Fig. 4C. The boundary conditions are not sufficient to fix all the parameters and one of them related to the position of the microtubule remains undetermined because we have fixed the microtubule at an arbitrary position.

The two types of motors walking along the microtubule exert a force on the microtubule each in one direction. The stable position of the microtubule is therefore the position, if it exists, where the total force exerted on the microtubule vanishes. In SI Appendix, we write explicitly the force balance on the microtubule and we find that the existence of a stable position and therefore the existence of the periodic band pattern only depends on the ratio c₁/c₂ and not on the individual concentrations of the two motors. Therefrom, we can construct a phase diagram where the stability of the patterned structure has two linear boundaries in a (c₁, c₂) plane (c₁/c₂ > f_min and c₁/c₂ < f_max, where f_min and f_max are dimensionless functions of the motor properties). In between these boundaries, patterns form while beyond them microtubules keep on gliding despite the opposite actions of the two motors (Fig. 4C).

This model also predicts that the range of concentrations leading to the emergence of patterns is centered at c₁ = c₂ for identical but opposing motors, it is narrower if motors are slower (Fig. 4D), larger if microtubules are shorter or if diffusion is slower (SI Appendix, Fig. S4) and shifted toward higher concentrations of the slowest motor if their velocities are different (Fig. 4E). Finally, the relationship between the motor concentrations and system dimensions gives a prediction of the size of the motor domains for a given combination of motor concentrations (Fig. 4F).

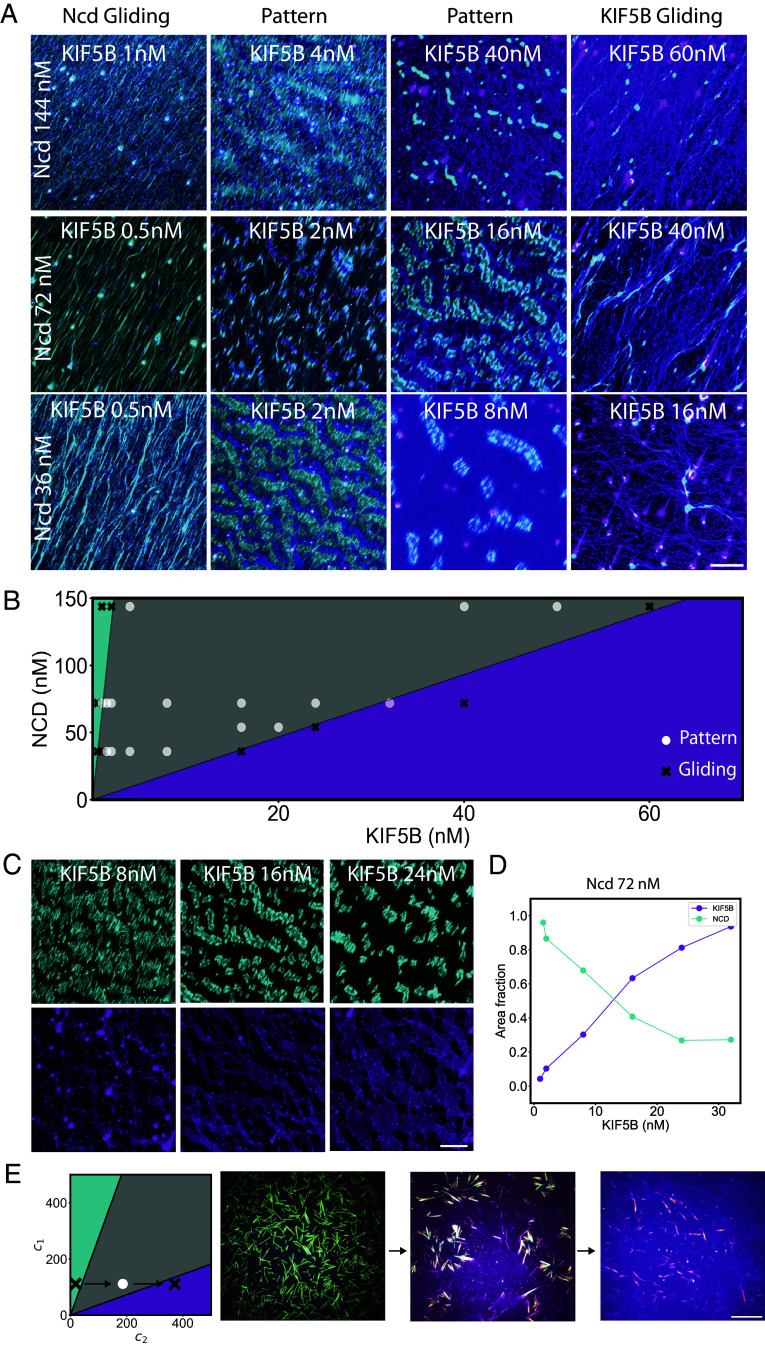
We then tested these predictions experimentally. We first performed model simulations to estimate the distribution of motors along microtubules serving as active boundary between motor domains. We used known parameters of KIF5B and Ncd affinities for microtubules (36, 37). The shape of these profiles fitted well with experimental measurements, suggesting that our model based on the balance between random diffusion and directed transport properly accounted for the process inducing motors segregation (SI Appendix, Fig. S5). To challenge the prediction of the model regarding the transition between gliding and self-patterning states, we tested multiple combinations of concentrations of KIF5B and Ncd. When one of the two motors was in large excess, microtubules glided and aligned as expected under such high concentration of microtubules gliding on lipids (31). At more balanced concentrations of motors, microtubules and motors self-patterned in active microtubule boundaries and segregated motor domains. The transition between the two states occurred at a higher concentration of KIF5B if the concentration of Ncd was increased (and vice versa) (Fig. 5A). More precisely, we found that in the phase diagram projected in the plane of the two motors concentrations, the boundaries between the self-patterning and gliding domain were indeed linear as predicted by the model (Fig. 5B).

Fig. 5.

Experimental investigation of the phase diagram of microtubule and motors self-organization. (A) Experimental observations of KIF5B-dominated, or Ncd-dominated, microtubule gliding or motors and microtubule self-patterning depending on motors concentrations. Images show KIF5B (magenta) and Ncd (cyan). Microtubule density was about 1.6 microtubule per µm². (Scale bar, 50 µm.) (B) Diagram of the experimental and theoretical behaviors as a function of motor concentration. Experimental conditions leading to gliding are shown with black cross, whereas those leading to self-patterning are shown with white dots. Theoretical predictions of the model are shown with the colored area as in Fig. 4. (C) Variations of domain sizes depending on motor relative concentrations. Images show domains of Ncd (Top, cyan) and KIF5B (Bottom, magenta) for a fixed concentration of Ncd (72 nM) and increasing concentrations of KIF5B. Microtubule density was about 1.6 microtubule per µm². (Scale bar, 50 µm.) (D) The graph shows the measurements of the area fraction of each motor in the conditions of panel C. (E) Transitions in real time within the phase diagram. Left: illustration of the conditions used in the experiment. Arrows represent steps of KIF5B increase over time. Images show KIF5B (magenta) and Ncd (cyan) upon sequential addition of KIF5B. At first, KIF5B concentration is low and Ncd forced microtubule to glide (Left image). The addition of more KIF5B counterbalanced the effect of Ncd and led to the self-patterning of microtubules and motors (Central image). The second addition of KIF5B destabilized the force balance and led to the dissolution of the patterns and the gliding of microtubules (Right image). Microtubule density was about 0.7 microtubule per µm². (Scale bar, 20 µm.)

Other key predictions could also be validated experimentally. The characteristic length of the motor domains relative to the unit size, which can be characterized by the area fraction occupied by these motors, showed a progressive increase with motor concentration (Fig. 5 C and D and SI Appendix, Fig. S1). The transition between self-patterning to the gliding state could be obtained by reducing the speed of motors (SI Appendix, Fig. S6). Altogether, these results show that the ability of microtubules to self-organize with two opposite motors into regular and steady patterns results from a balance of fluxes between motor diffusion and motor transport along microtubules coupled to a balance of the mechanical forces associated with this transport. Importantly, this also implied that pattern maintenance is based on the constant flux of motors and equilibration of the pools of the two motors along the microtubules. This dynamical balance appears as a possible mechanism of fast adaptation of the pattern size and shape to changes in the concentrations of motors. Indeed, starting from conditions in which microtubules were gliding in response to the dominating role of Ncd, a progressive addition of KIF5B led first to the self-patterning of the entire system, which could be later dismantled by further addition of more KIF5B (Fig. 5E and Movie S8). This suggests that the non-equilibrium nature of the self-assembly ensures the robustness of the patterns and allows for constant adaptation of their spatial structure to external perturbations such as changes in motor concentrations, velocities, affinities, or microtubule length.

These results demonstrate that free microtubules and motors of opposite directionalities can self-organize into regular patterns, which form by the sorting of motors into segregated domains and their constant transports along immobilized microtubules that act as a sorting barrier between motor domains. The self-organization process appears robust yet flexible, and the permanent underlying dynamics of transport confers additional adaptive properties to the system. Similar patterns of motor domains and aligned microtubules can also be obtained from microtubule–microtubule interactions and single motor transport (18, 19, 39), but it is the competition between the forces generated by the sorting of the two motors that imparts our system with the ability to reconfigure itself into different patterns or disassemble in response to variations in motor concentrations. Here, we only tested a few parameters, and a minimal model of the process in one dimension, but the underlying mechanisms of pattern assembly, maintenance, and disassembly that we uncovered may open possibilities to further understand the emergence of cellular units (9, 15, 38), bipolar spindles (14), and other microtubule-based architectures that can be found in differentiated cells (12). The spatial segregation of plus- and minus-end motors and the associated development of opposing forces that drive and then stabilize microtubule positioning, as described here, can be considered as common principles in the self-assembly of these architectures.

Materials and Methods

Lipids Preparation.

First, 96% L-α-phosphatidylcholine (EggPC) (Avanti, 840051C) (10 mg/mL in chloroform), 2% DGS-NTA(Ni) (Avanti, 790404C), and 1% DOPE-ATTO390 (ATTO-TEC, 390-161) were mixed into glass tubes, dried with argon gas, and incubated under vacuum overnight. The dried lipids were then resuspended in a buffer that we further refer to as the “small unilamellar vesicle (SUV) buffer” (150 mM NaCl, 10 mM Tris-HCl pH 7.4 and 2 mM CaCl₂) and sonicated on ice for 10 min. The mixture was centrifuged at 20,238 g for 10 min to remove contaminants and the supernatant was collected. The final lipid concentration was 1 mg/mL. For experiments using KIF5B-SNAP-430, unmarked lipids were used [98% EggPC and 2% DGS-NTA(Ni)]. Lipids were stored at 4 °C for up to a month.

Stabilized Microtubules Preparation.

Unlabeled tubulin (18 µM), Atto-565 tubulin (2 µM), and GMP-CPP (1 mM) were mixed in BRB80 and incubated at 37 °C for 2 h. The mixture was then centrifuged at 20,238×g for 30 min and the microtubules were resuspended in BRB80 supplemented with 10 µM of Taxol. Stabilized microtubules were kept at room temperature for 4 d.

Gliding Experiments.

Cover glasses and slides were first wiped with lint-free tissues and Ethanol 96%, rinsed in ultrapure water, put in Hellmanex III (2% in water, Hellmanex), and sonicated for 30 min at 60 °C. The glass was then rinsed in ultrapure water and kept in water for 4 d. We used either flow cell (Figs. 1, 2A, 3 B and E, and 5 A and C, and SI Appendix, Figs. S2 and S6) or open well (Figs. 2 B–E, 3A, and 5E and SI Appendix, Fig. S1) to perform the gliding assays. In both cases, the bottom glass coverslip was dried with compressed air, activated with air plasma for 3 min. In the case of open wells, a PDMS square with a punched out 6 mm hole in the center was placed on the glass creating a well. In the case of flow cells, two bands of double-side tape (70 μm height) were covered by a glass coverslip to contain an approximate volume of 15 μL. In both cases, 20 µL of lipids was added, incubated for 10 min then rinsed with SUV buffer. For additional passivation, 1% w/v BSA in HKEM (10 mM HEPES pH = 7.2, 50 mM KCl, 1 mM EGTA, 5 mM MgCl₂) was incubated for 5 min. BSA was washed out with TicTac buffer (10 mM HEPES buffer (pH 7.2), 16 mM PIPES buffer (pH 6.8), 50 mM KCl, 5 mM MgCl₂, 1 mM EGTA, 20 mM dithiothreitol (DTT), 3 mg.mL^–1 glucose, 20 μg.mL^–1 catalase, 100 μg.mL^–1 glucose oxidase, 0.3% BSA) supplemented with 1 mM ATP (Sigma Aldrich, A3377). Motors diluted in TicTac buffer were added and incubated for 5 min, then washed, and microtubules diluted in TicTac buffer were added and incubated for 3 min before being washed as well. Finally, TicTac buffer supplemented with 2.7 mM of ATP and 0.2% methyl cellulose was added prior to imaging. Experiments were performed at room temperature.

Due to space limitation, experimental protocols describing protein expression, purification, and labeling, microscopy, photobleaching, photoablation, as well as image analysis procedures for microtubule tracking, motor domains size measurement and motor density measurement are provided in SI Appendix.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

Microtubule gliding. Microscopy imaging of microtubules at low density gliding on KIF5B, NCD and both motors. Data is also shown in Figure 1B. Movie duration is 10 min and it is compressed in JPEG at 20 frames per second.

Movie S2.

Microtubule alignment and bundling. Microscopy imaging of microtubules gliding on opposite motors and bundling upon contact. Data is also shown in Figure 2A. Movie duration is 26 min and it is compressed in JPEG at 30 frames per second.

Movie S3.

Microtubules and motors self-patterning. Microscopy imaging of microtubules (yellow), NCD (cyan) and KIF5B (magenta), at high microtubule density, self-organizing into patterns. Data is also shown in Figure 3A. Movie duration is 60 min and it was compressed in JPEG at 30 frames per second.

Movie S4.

Microtubules and motors turnover in self-patterned domains. Microscopy imaging of microtubules on the left, and NCD (cyan) and KIF5B (magenta) on the right, during a photo-bleaching and FRAP experiment where the three proteins fluorescent signals are extinguished. Movie duration is min 20 sec and it is compressed in JPEG at 20 frames per second.

Movie S5.

Motors transport in self-patterned domains. Microscopy imaging of NCD (cyan) motors during a photo-bleaching and FRAP experiment. Movie duration is 1 min 20 sec and it is compressed in JPEG at 20 frames per second.

Movie S6.

Patterns dissolution by partial microtubule destruction. Microscopy imaging of microtubules (yellow), NCD (cyan) and KIF5B (magenta) during a laser ablation experiment where an entire microtubule band is destroyed on the side of the pattern. Movie duration is 22 min and it is compressed in JPEG at 20 frames per second.

Movie S7.

Microtubule severing Microscopy imaging of microtubules (yellow), NCD (cyan) and KIF5B (magenta) during a laser ablation experiment, where microtubules on the side of a pattern are cut in the middle. Data is shown in Figure 3E. Movie duration is 8 min 20 sec and it is compressed in JPEG at 20 frames per second.

Movie S8.

Transition between gliding and self-patterning states. Microscopy imaging of microtubules (yellow), NCD (cyan) and KIF5B (magenta) going from NCD gliding to patterns after KIF5B addition, and finally to KIF5B gliding after a second KIF5B addition. Data is also shown in Figure 5E. Movie duration is 83 min and it is compressed in JPEG at 30 frames per second.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.