Neural responses to social rejection reflect dissociable learning about relational value and reward

Significance

To build supportive social connections, individuals must identify partners likely to reciprocate their interest. People might do this by tracking whether others have provided rewarding opportunities for interaction in the past. Yet, the outcomes others provide do not always reflect their feelings toward us; a person can be ranked last for a team but get selected or ranked highly for a job but get rejected. We provide evidence that the human brain uses two distinct learning computations to affiliate with others, tracking how much partners value us and whether they provide rewarding acceptance outcomes. These findings reveal how the brain identifies promising social partners, using social feedback in two ways to build positive relationships that support physical and mental health.

Abstract

Social rejection hurts, but it can also be informative: Through experiences of acceptance and rejection, people identify partners interested in connecting with them and choose which ties to cement or to sever. What is it that people actually learn from rejection? In social interactions, people can learn from two kinds of information. First, people generally learn from rewarding outcomes, which may include concrete opportunities for interaction. Second, people track the “relational value” others ascribe to them—an internal model of how much others value them. Here, we used computational neuroimaging to dissociate these forms of learning. Participants repeatedly tried to match with others in a social game. Feedback revealed whether they successfully matched (a rewarding outcome) and how much the other person wanted to play with them (relational value). A Bayesian cognitive model revealed that participants chose partners who provided rewarding outcomes and partners who valued them. Whereas learning from outcomes was linked to brain regions involved in reward-based reinforcement, learning about relational value was linked to brain regions previously associated with social rejection. These findings identify precise computations underlying brain responses to rejection and support a neurocomputational model of social affiliation in which people build an internal model of relational value and learn from rewarding outcomes.

Rejection hurts: Social rejection breeds feelings of distress, physiological signals of stress, decreased self-esteem, and, in some cases, increased aggression, all of which can harm well-being (1–6). Yet, rejection can also be informative: Through experience, people learn which partners are likely to accept them in the future, allowing them to approach the same partner again or seek new ones instead. When people learn which ties to cement and which to let wither, they can invest in relationships likely to reciprocate care, forming thriving and healthy relationships. When people fail to learn adaptively, they may underestimate caring partners or overestimate disinterested ones, preventing them from building a supportive network. Learning thus provides a rate-limiting step on social connection: Just as organisms cannot eat if they fail to learn where to find food, people cannot connect if they fail to identify willing partners. How does the human brain learn from past rejection and acceptance to build future connection?

When people feel the sting of rejection in the moment, they display brain activity in regions including the dorsal and ventral anterior cingulate cortex (dACC and vACC), anterior insula (AI), and ventrolateral prefrontal cortex (vlPFC)—a putative “social rejection” network (7, 8). These responses have been interpreted as reflecting social pain, given that these regions also activate in response to physical pain and pain regulation (9) (though see ref. 10). In contrast, when people feel accepted, they display responses in the ventral striatum (VS)—a region strongly linked to reward and positive affect (11, 12). These responses may therefore reflect the pains and pleasures of social connection.

Yet, these brain regions also play key roles in learning. For instance, the dACC responds during Bayesian model updating (13)—when people update an internal model of their environment—and vlPFC responds when people revise their impressions of humans or objects (14, 15). At the same time, the VS processes reward prediction error—the difference between rewards expected and rewards accrued—letting people learn to repeat actions that led to better-than-expected rewards (16). Rather than reflecting social pain and pleasure, these regions might therefore reflect learning from social experience.

Consistent with this possibility, recent work demonstrates that the dACC and AI show larger responses to both rejection and acceptance—each of which can lead people to update their expectations—when compared to neutral feedback (12). However, it remains uncertain which learning signals might be represented by this activity or whether these findings reflect more general responses to expectancy violation (17). Computational neuroimaging can offer unique insights into the functional role of these regions in response to social rejection, shedding light on how they may contribute to adaptive or maladaptive behaviors.

Here, we test two computations that may explain patterns of brain activation as people learn from social acceptance and rejection. First, acceptance offers a rewarding outcome, providing people with concrete opportunities for connection such as an invitation to attend a wedding or join a baseball team. People generally track rewarding outcomes across social and nonsocial settings, and people tend to repeat actions that lead to reward (18, 19). After acceptance or rejection, people may update an estimate of the rewards of interacting with another person. In turn, people may choose partners who have offered rewarding outcomes in the past. This pathway offers an affective form of learning, as people repeat social interactions that lead to pleasing outcomes.

However, the outcomes other people provide do not always reflect their feelings toward us. When a person is excluded from a friend’s small wedding due to a tight budget or picked last for a large team, they may recognize that their friend still values them but the team does not. People care about the “relational value” others ascribe to them (20, 21), and they may build an internal model of how much others like them and want to interact with them. After new instances of acceptance or rejection, people may update this internal model. In turn, people can use this knowledge as a compass to approach partners who value them and avoid partners who do not. This pathway offers a conceptual form of learning, in which people update an internal model of their social value to another person.

These learning computations may rely on distinct neural substrates. Updating a model of relational value may be consistent with the functions of the social rejection network in conceptual forms of learning, including Bayesian model updating and impression updating (13, 15). In contrast, interacting with rewarding partners may fit with the reward learning functions of the VS (16). This framework therefore suggests that distinct computations may underlie patterns of brain activation observed across these regions in past work. However, these forms of learning have typically been confounded in studies of social rejection, as rejection outcomes are more common when relational value is low and acceptance outcomes are more common when relational value is high. As a result, it is challenging to determine whether people are responding to the reward value of an outcome or the relational value an outcome reveals. It thus remains unclear which computations are reflected in neural responses to rejection or how these computations lead people to choose or avoid social partners.

We used computational neuroimaging to dissociate these learning computations while participants learned to affiliate with others through experiences of acceptance and rejection. Participants repeatedly tried to match with other players for an economic game, much as individuals may try to match with others on dating apps. Feedback revealed how much others wanted to match with them, providing a cue to relational value, and revealed whether others succeeded in matching with them, providing a rewarding acceptance outcome. We tested whether the brain’s social rejection network would respond to negative feedback, consistent with a social pain response; any surprising events, consistent with expectancy violation; or specific computations for tracking relational value as distinct from reward value, consistent with the learning hypothesis. By linking different learning computations to the brain, this approach allowed us to compare different accounts of the brain’s social rejection network and advance our understanding of its impact on behavior and well-being.

Results

Forty participants played a social game involving other players who had supposedly participated in prior sessions; in reality, the responses of other players were computer generated. In an initial session, participants completed a profile about themselves with questions relevant to their trustworthiness (e.g., “Describe a time you were honest even though you didn’t have to be”). A week later, they were told that they were in a sequential study in which they would see prerecorded decisions made by other participants over the last week. Specifically, they were told that other participants in a “Decider” role had read their profile, along with the profiles of other players in a “Responder” role, and formed impressions of them. Based on these impressions, Deciders had made choices about which Responders they wanted as partners in a Trust Game (22). For every round of the game, Deciders could send points worth money to a varying number of Responders; points would be tripled, and Responders would then choose whether to return half of the points to that Decider or keep all of them. Deciders had ranked how much they wanted to play with several potential Responders on each round.

To play the game on a particular round, participants needed to find a Decider with whom they could match. Participants repeatedly tried to match with Deciders, choosing one Decider out of two available on screen on each round (Fig. 1A). Participants’ interaction choices were followed by feedback revealing i) how the chosen player had ranked the participant relative to seven other Responders, reflecting relational value, as well as ii) whether the participant actually got to match with the chosen partner, reflecting a positive or negative outcome. Deciders could sometimes play with many Responders (e.g., matching with their seven top-ranked Responders and sending points to all of them) and could sometimes only play with few others (e.g., matching with their two top-ranked Responders) (Fig. 1B). This procedure ensured that relational value and rewarding outcomes were orthogonal. In other words, participants could be ranked poorly but succeed in matching (negative relational value, positive outcome), or they could be ranked highly but fail to match (positive relational value, negative outcome). This situation is analogous to joining a large team as a last choice or failing to be admitted to a small team but knowing one would have been the next choice. In prior behavioral work, both kinds of feedback had independent effects on affect, such that participants felt better after good ranks and successful matches than after bad ranks and nonmatches, and both kinds of feedback guided learning, such that participants chose partners who ranked them highly and who tended to match with them (23). This task was therefore used to investigate learning computations in the brain.

Fig. 1.

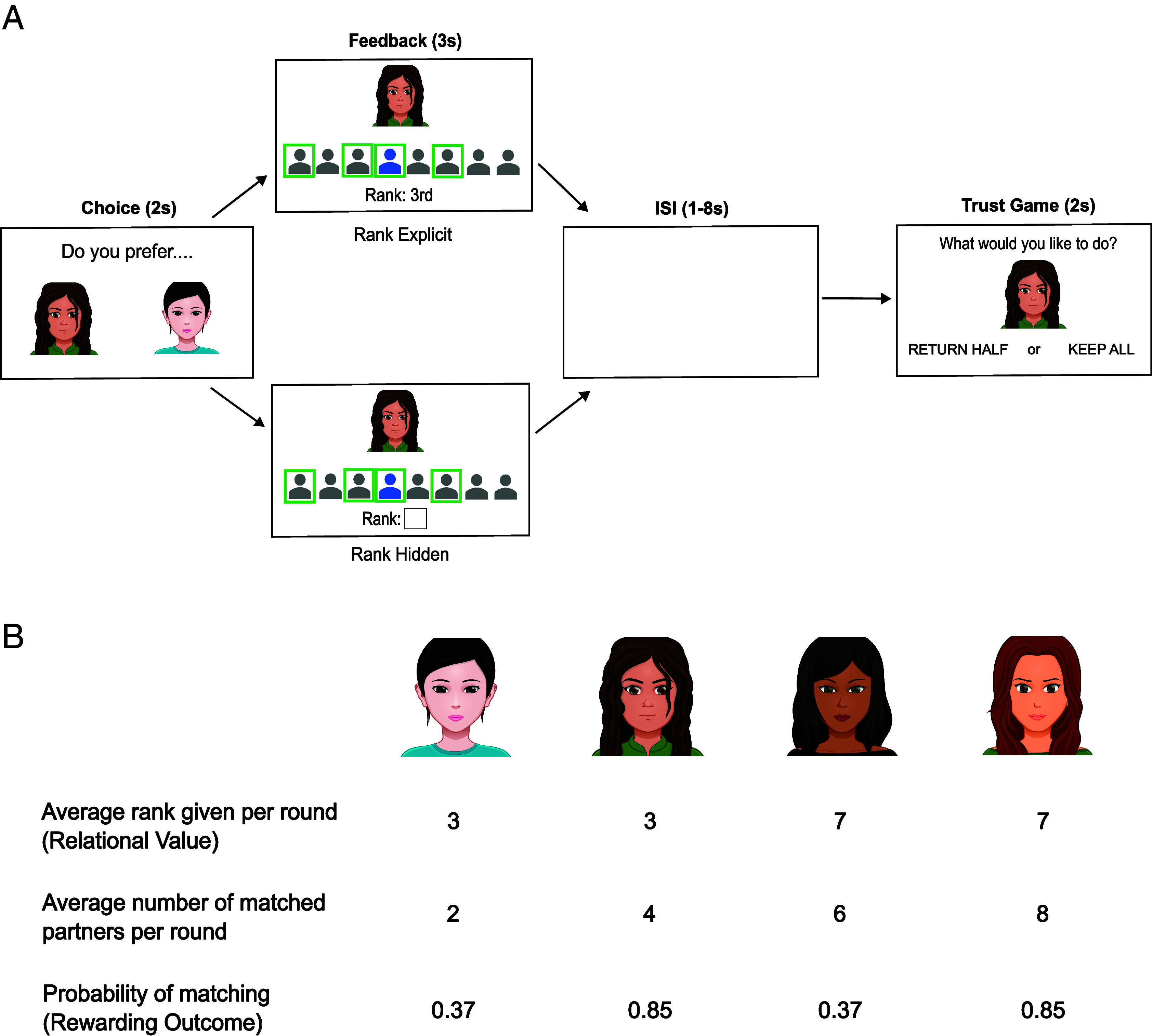
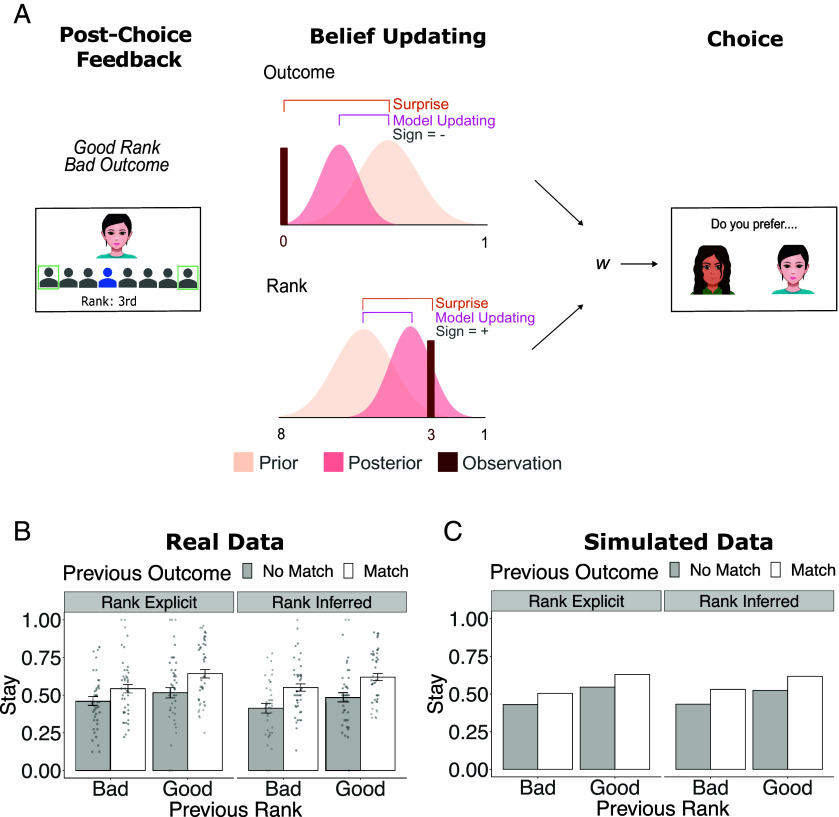
Diagram of the learning task and average feedback provided by Deciders. (A) In each round, participants saw two Decider avatars and selected who they wanted to try to match with. A feedback screen following the choice indicated how highly the Decider had ranked them (relational value) and whether they matched or not (reward outcome). The blue icon represents the participant and did not change its position on the screen, while the gray icons represent seven other Responders. If participants matched, a green box appeared around their icon. Green boxes also surrounded any other Responders who had successfully matched with that Decider. In half the trials, rank feedback was explicit; the participant’s rank was displayed under their avatar and it varied across rounds. In the other half, participants had to infer the rank they received, based on how many other Responders had matched; the participant’s rank was hidden by a white square. If participants matched with the Decider, they played a trust game, either returning half of the points that were given to them or keeping all the points to themselves. Decider avatars were matched to the participants’ gender. (B) Participants encountered four kinds of Deciders, who varied in the average rank they gave to participants (relational value) and the probability of matching with the participant (reward outcome). By varying the average number of Responders that Deciders could match with, the probability of matching with a Decider was manipulated independently of the rank provided by that Decider. The contingencies above were repeated across two sets of four Deciders—one set associated with explicit rank feedback and one with hidden rank feedback—for a total of eight Deciders.

On half of the trials, participants explicitly saw how they had been ranked by others, mirroring situations in which people explicitly discover relational value, such as a job applicant learning they were the second-ranked candidate. On the other half of trials, participants had to infer how they were ranked based on long-run patterns, mirroring situations in which people encounter more ambiguous cues, such as a worker noticing that a coworker consistently invites others to lunch. For instance, if a Decider in the task repeatedly accepted a participant only in a large group of seven, but never included the participant in a smaller group of six, then the participant could infer the Decider had ranked them seventh. Trials in which ranks were explicit or hidden were pseudorandomly interleaved. Four Deciders were always viewed with explicit feedback and four Deciders were always viewed with hidden feedback, and participants always chose between two Deciders of the same kind, ensuring that participants did not choose Deciders based on the amount of information they would receive in return. This feature of the task therefore tested neural responses that learn from explicit and inferred feedback.

Participant Choices Reflect Learning about Both Relational Value and Acceptance Outcomes.

To quantify learning over time, we fit behavior to a Bayesian cognitive model (Fig. 2A). This model updated two beliefs on each trial. First, the model assumed participants updated an internal model of relational value, instantiated as a belief distribution indicating how the other person tends to rank them. Second, the model assumed participants updated a reward prediction, instantiated as a belief distribution reflecting the probability the other person would match with them. On each trial, a prior distribution of beliefs was updated based on feedback to form a posterior distribution for each belief type. These two beliefs were combined as a weighted average to estimate the value of choosing a player, fit using a free parameter (w) that could allow any weighting from choices based entirely on past acceptance outcomes (w = 0) to choices based entirely on relational value (w = 1). (For further details, see Materials and Methods and SI Appendix).

Fig. 2.

Schematic of the Bayesian learning model, as well as choice patterns observed in participant behavior and simulated by the model. (A) A Bayesian cognitive model assumed learners update beliefs about how they are ranked and the outcomes others tend to provide, integrating evidence with a prior belief distribution to form a posterior belief distribution. This model defines signals related to model updating (how much beliefs shifted), surprise (how unexpected an observation was given a prior belief distribution), and a sign corresponding to feedback valence (whether beliefs are updated for better or for worse). After updating, beliefs about rank and outcome are combined as a weighted average, using a weighting parameter w, to choose a Decider on the next trial. For an example featuring a trial with rank hidden and for sample belief trajectories, see SI Appendix, Figs. S1 and S2. (B) The plot shows the proportion of trials on which participants stay with their previously chosen Decider as a function of the outcome on the last trial (no match or match) and the rank received on the last trial (above or below the median). Participant choices depended on both ranks and outcomes. (C) Simulated choices from the computational model replicated this qualitative pattern of results.

Supporting past behavioral work (23), a model including both relational value (ranks) and reward value (probability of matching) provided a better fit to the data than models including one strategy or the other alone (protected exceedance probability = 1; median w = 0.52). Furthermore, data simulated using the model reproduced key patterns of behavioral results, wherein participants were more likely to choose a Decider both if they had received a positive outcome (match vs. no match) and high rank (above vs. below the median) in the previous trial featuring that Decider (Fig. 2 B and C). This inference was supported by supplemental regression analyses, demonstrating that participants gravitated toward partners who ranked them highly (b = 0.21, SE = 0.06, z = 3.56, P < 0.001) and toward partners who provided matching outcomes (b = 0.22, SE = 0.05, z = 4.23, P < 0.001; see SI Appendix, Supplemental Methods, Fig. S3, and Table S1 for further details; for robustness analyses controlling for additional task variables, see SI Appendix, Supplemental Results and Tables S2 and S3). Thus, participants simultaneously tracked relational value and rewarding experiences, and they learned to choose partners based on both kinds of feedback.

Activity in the Social Rejection Network Reflects Social Learning.

We next asked whether neural activity during feedback reflected social pain, expectancy violation, or distinct learning computations related to relational value and reward. Using the computational model, learning signals were quantified as the Kullback–Leibler (KL) divergence between the prior and posterior distributions on each trial; this quantity reflects the degree of change from a prior distribution to a posterior distribution, thus indicating how much beliefs have been updated in light of feedback. This value is unsigned, indicating that feedback led to an update of one’s internal model in any direction (model updating). However, changes in belief can also be signed, indicating the model was updated for better or for worse. To account for the direction of learning, a second regressor was created by multiplying KL Divergence by the sign of the update, defined as whether the mean of a belief distribution increased (1) or decreased (−1). The resulting value indicates whether a belief distribution became more positive or more negative, consistent with reward learning or pain (signed model updating). Finally, in Bayesian models, surprise can be quantified as the Shannon Information of a given observation, reflecting how unexpected an observation was given a prior distribution (13). We regressed blood oxygenation dependent (BOLD) signal on the unsigned model updates, signed model updates, and surprise, for both ranks and outcomes (Fig. 2A).

According to the “social pain” hypothesis, the social rejection network should respond to negatively signed updates for rank and/or outcomes; when people learn they are less valued or accepted than previously believed, they should feel worse, and this might be true when they are ranked poorly or fail to match. According to an “expectancy violation” view, these regions should respond to surprise signals for rank and/or outcomes, either of which reveals an unexpected event. Finally, according to the learning hypothesis, distinct brain regions should correlate with unsigned model updates for ranks, which reflect updates of an internal model of relational value, and with signed updates for rewarding outcomes, which reflect reward learning.

Results supported the learning hypothesis. On a trial-by-trial basis, responses in the social rejection network—including the dACC, vACC, AI, and vlPFC—correlated with unsigned model updates for rank (Fig. 3A). These regions therefore responded more when people updated their beliefs about how others had ranked them, for better or for worse. Additional activations were observed in the dorsal striatum and superior temporal sulcus (SI Appendix, Fig. S4)—regions also previously observed in studies of social and nonsocial learning (13, 15).

Fig. 3.

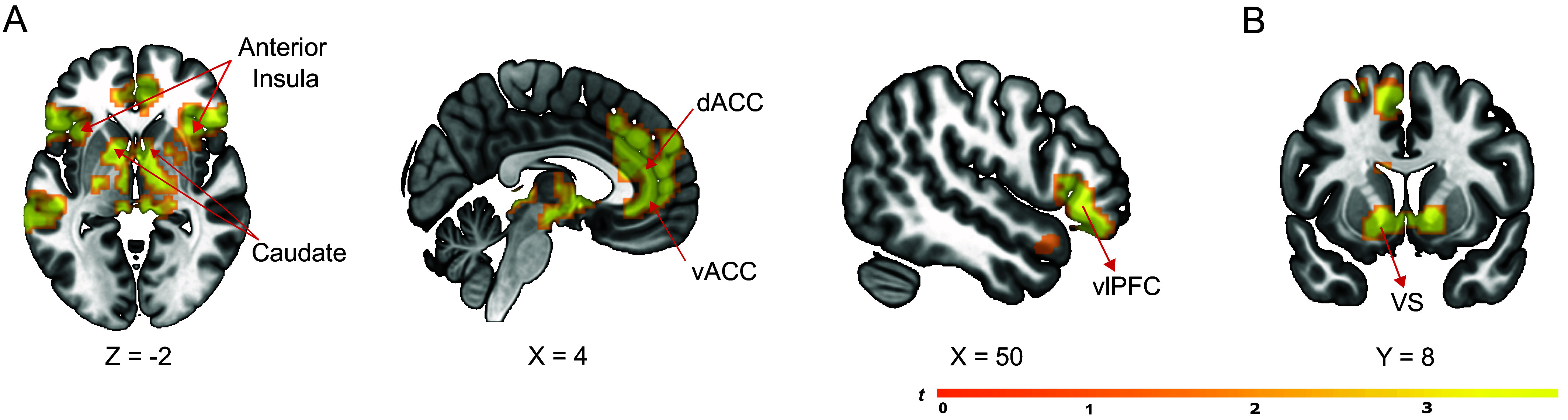
Statistical maps showing significant brain activation correlated with belief updates about relational value and reward. (A) Unsigned updates for rank correlated with responses in the social rejection network, including the AI, dACC/vACC, and vlPFC. (B) Rewarding outcomes (signed outcome updates) correlated with responses within the bilateral VS. A cluster-level significance threshold was set at P < 0.05 corrected for family-wise error rate for all analyses.

To test the “social pain” hypothesis, we tested for voxels that track negative updates in rank or outcome (i.e., when participants learned that they were less valued or less frequently accepted than expected). A whole-brain analysis did not identify significant negative responses for signed rank update, while activity in the bilateral temporoparietal junction (TPJ) was negatively associated with signed outcome update (SI Appendix, Fig. S5). When conducting region of interest analyses within the dACC and vACC based on a meta-analysis of social pain (24), neither region was associated with signed rank update (dACC: M = −0.03, SD = 0.28, t(39) = −0.59, P = 0.56; vACC: rank: M = −0.03, SD = 0.33, t(39) = −0.66, P = 0.51). dACC activity was not associated with outcome update (M = 0.08, SD = 0.32, t(39) = 1.66, P = 0.10), while the vACC was positively associated with outcome update, which is in the opposite direction predicted by the social pain hypothesis (M = 0.17, SD = 0.34, t(39) = 3.19, P = 0.003).

To test the expectancy violation hypothesis, we tested for voxels that track surprise in rank or outcome. A whole-brain analysis again yielded no significant responses. In ROI analyses, a response to outcome surprise was observed in the dACC (M = 0.20, SD = 0.56, t(39) = 2.20, P = 0.03) but not the vACC (M = 0.14, SD = 0.64, t(39) = 1.38, P = 0.17), suggesting that some surprise information may be encoded alongside model updating in the dACC. A significant response to rank surprise was not observed in the dACC or vACC (dACC: M = −0.01, SD = 0.26, t(39) = −0.31, P = 0.76; vACC: M = −0.06, SD = 0.37, t(39) = −1.11, P = 0.27).

Altogether, the present results did not detect evidence for social pain and detected limited evidence for expectancy violation, but they did provide evidence supporting a learning account. All analyses included trials in which participants explicitly saw how the Decider ranked them and trials in which participants had to infer rankings. Supplemental analyses further indicated that the effect of updating held across trials in which rank was visible and trials in which rank was hidden (and when adjusting for additional task variables; see SI Appendix, Table S4). These findings suggest these regions reflect an abstract model of relational value regardless of how this information is acquired.

Activity in the VS Is Associated with Learning about Reward Outcomes.

Demonstrating distinct learning computations, positive updates for outcomes correlated with BOLD signal in the bilateral VS (Fig. 3B), a region consistently associated with reward learning (16). Activation was also observed in the medial orbitofrontal cortex, a region also commonly observed to respond during reward-based learning and value-based choice (25) (for further activations, see SI Appendix, Fig. S4). This finding suggests that participants learned to affiliate with others in part through domain-general mechanisms of reward-based reinforcement. These findings dissociate two kinds of learning computations through which people learn to affiliate with others and specify a role for the “social rejection network” in updating an internal model of relational value.

Players with Similar Relational Value Are Encoded More Similarly in the Social Rejection Network.

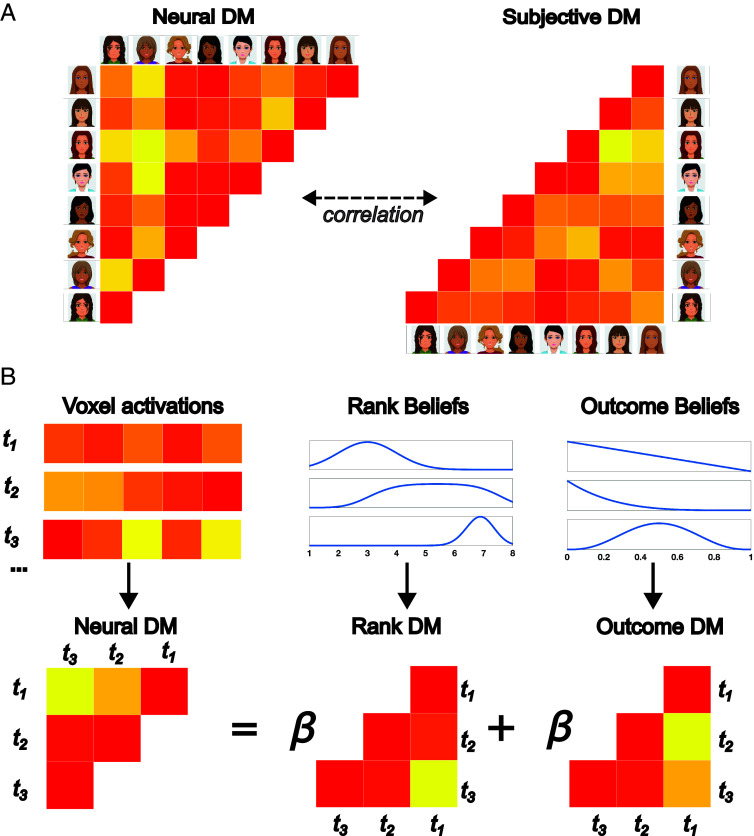
These findings indicate that brain regions in the social rejection network respond to changes in relational value. Do these areas also encode an internal model of relational value? To test this possibility, we examined voxel patterns in these regions using representational similarity analysis (RSA). If these regions encode participants’ internal model of relational value, then voxel patterns in these regions should be similar when participants view Deciders who valued them to a similar degree.

We first tested this hypothesis in a manner independent of the computational model by relying on participants’ subjective perceptions of the Deciders at the end of the experiment. After the task, participants rated how much they believed each Decider liked them, providing a final subjective perception of relational value. We asked whether Deciders who a participant rated similarly after the task also elicited more similar voxel patterns within regions sensitive to learning about ranks. For each participant, we extracted the average voxel pattern elicited by each Decider across these regions and correlated the average patterns evoked by each pair of Deciders, generating a measure of neural similarity between Deciders (converted to dissimilarity as 1 − r). Analogously, we computed the absolute difference in posttask ratings for each pair of Deciders, generating a measure of (dis)similarity in subjective perceptions of being liked (Fig. 4A). Across participants, Deciders who elicited more similar voxel patterns during the task were rated more similarly by participants after the task (M = 0.11, SD = 0.20, t(39) = 3.59, P < 0.001). Thus, brain regions that responded to updates about rank reflected participants’ final subjective ratings of being liked by each Decider.

Fig. 4.

Schematic of RSA. (A) Voxel activations toward each Decider were correlated with one another to create a neural representational dissimilarity matrix. Neural dissimilarity in responses toward Deciders was compared to dissimilarity in participants’ subjective ratings of being liked by each Decider, as reported after the task. (B) Trial-by-trial dissimilarity in voxel activations was regressed on trial-by-trial dissimilarity in rank beliefs and outcome beliefs, as derived from the computational model.

We next examined the trial-by-trial content of these voxel patterns, asking whether voxel patterns were more similar on trials featuring similar beliefs about ranks. To do so, we computed the voxel pattern similarity between each pair of trials during feedback. We then used the computational model to estimate whether participants perceived similar relational value and similar outcome probabilities across each pair of trials. Similarity was defined as the symmetrized KL divergence (26) between the posterior distributions of perceived rank or outcome on the two trials. Neural similarity was regressed on both rank similarity and outcome similarity, allowing us to test the effects of each variable above and beyond the other (Fig. 4B). As hypothesized, voxel patterns were more similar when participants had more similar beliefs about the ranks offered by a partner (M = 0.01, SD = 0.02, t(39) = 3.08, P = 0.004). Voxel patterns in regions linked to rank updating thus reflected trial-by-trial beliefs about rank, as estimated from the computational model, and predicted subjective perceptions of each Decider, as self-reported by participants.

Reward Outcomes “Corrupt” Perceptions of Relational Value.

Although participants learned about ranks and outcomes through distinct computations, these forms of learning need not remain independent in their subjective perceptions. In the game, Deciders could only control how they ranked Responders, meaning that only rank offered a valid signal of relational value; matches depended on the number of partners allowed by the experimenters, which Deciders could not control. Yet, reward responses in the VS can bias Bayesian inferences (27). Accordingly, past work suggests rewarding outcomes can bias social impressions: Rewards prompt positive affect, leading people to think positively of individuals who provide them with large rewards (28, 29). As a result, when two partners provide identical ranks but one provides more positive outcomes, people tend to develop an inflated impression of relational value for the latter (23). Consistent with this view, participant ratings of the Deciders in the present study not only depended on ranks but also were biased by outcomes. Specifically, in an analysis predicting ratings from both average ranks and outcomes, participants reported they were well liked by those who ranked them highly (F(1,41) = 20.39, P < 0.001, η_p² = 0.33); this effect was larger when ranks were explicit (F(1,41) = 13.02, P < 0.001, η_p² = 0.24). However, participants also believed they were better-liked by players who had provided more matching outcomes (F(1,41) = 13.76, P < 0.001, η_p² = 0.25; see Fig. 5A and SI Appendix, Table S5). Outcomes thus “corrupted” participants’ subjective perceptions of relational value.

Fig. 5.

Subjective perceptions of being liked. (A) Participants believed they were liked by those who had ranked them highly, which provided an accurate cue to relational value, but also believed they were liked by those who frequently matched with them due to factors outside their control, thus providing high reward value. (B) In brain regions sensitive to learning about relational value, participants for whom voxel patterns encoding Deciders were more similar to patterns encoding rank information, as opposed to outcome information, also based their postscan subjective perceptions more on ranks as opposed to outcomes.

If the social rejection network reflects subjective perceptions of relational value, then neural representations of Deciders might also reflect a combination of rank and outcome information. Indeed, RSA indicated that voxel patterns were also more similar during trials with similar beliefs about outcomes (M = 0.03, SD = 0.03, t(39) = 5.17, P < 0.001), above and beyond effects of how the player ranked the participant, suggesting a neural basis for conflation in subjective perception of Deciders.

To explore this possibility, for each participant, we assessed the extent to which neural representations of Deciders were biased by outcome. We then explored whether these neural patterns related to individual differences in subjective perception. We first assessed the extent to which voxels in the social rejection network encoded Decider identity, using RSA testing whether voxel patterns were more similar when participants saw the same (versus different) Deciders across trials (for additional details, see SI Appendix). We then used feature permutation analysis (30, 31) to assess the importance of each voxel in encoding Decider identity; this approach measures how much RSA is disrupted if a given voxel’s data are randomly shuffled. For example, if shuffling a voxel greatly reduces the RSA association between Decider identity and brain activity, that voxel has high importance in encoding Decider identity.

Next, we used the same approach to assess the importance of each voxel in encoding rank and outcome. We then assessed, for each participant, whether the encoding of Deciders was more similar to the encoding of rank or outcome. Individuals whose voxel scores for Deciders were more correlated to their voxel scores for Rank, as compared to Outcomes, were more likely to believe they were liked based on ranks than outcomes (r = 0.57, P < 0.001) (Fig. 5B). That is, participants for whom the voxels encoding Decider identity were similar to those encoding rank exhibited little to no outcome bias in their subjective ratings, perceiving that they were liked primarily based on ranks. In contrast, participants for whom the voxels encoding Decider identity were more similar to those encoding outcomes showed a stronger bias toward believing they were liked by those who provided frequent matches.

Altogether, these findings suggest an abstract representation of relational value—influenced by ranks but corrupted by outcomes— that corresponds to participants’ subjective perceptions revealed in self-reports. Voxel pattern results remained the same in robustness analyses adjusting for additional task variables (SI Appendix).

Discussion

Although social rejection hurts, people can learn from rejection and acceptance, using these experiences to navigate their future interactions. What lessons do people draw from these experiences? We found that the human brain implements two distinct learning computations to affiliate with others following acceptance and rejection. First, people learn whether partners tend to provide rewarding bottom-line instances of acceptance, such as being accepted to a team or offered a job. Second, people learn whether others value them, such as finding out whether one was the first or last choice when getting picked for the team or job. Participants gravitated toward partners who provided both kinds of acceptance, choosing to interact with individuals who provided concrete opportunities to match in a game and with individuals who ranked them highly. These computations were associated with distinct brain regions linked to reward learning and social rejection, respectively.

These findings inform how the human brain responds to social rejection. Responses to rejection in the dACC, vACC, and AI have been interpreted as signals of social pain or of expectancy violation (9, 17). Although people do feel worse after rejection than acceptance, we did not observe responses in these regions reflective of social pain in the present study (i.e., when people observed a worse rank or outcome than expected) (23). We advise caution when interpreting null results, and it remains possible that these regions may encode pain responses. In the present study, responses to negative outcomes (but not negative ranks) were instead observed in TPJ—a region previously observed during studies of social learning (32). Given that the activation included the supramarginal gyrus, which also activates during pain (33), it remains possible that this finding reflects an alternative neural basis for social pain. At the same time, given that this region has not been regularly observed in past studies of social exclusion (34, 35); that no responses were observed to negative ranks, which more directly reveal negative social evaluations; that no other such responses were observed in regions linked to pain; and the role of TPJ in mentalizing, this finding may also reflect social computations related to processing the cause of negative outcomes (36). The present results also cannot be accounted for by expectancy violation alone. Although ROI analyses did reveal dACC responses to surprising outcomes, whole-brain analyses revealed responses above and beyond surprise signals.

Alternatively, recent work has proposed that responses in the dACC, vACC, and AI may reflect a barometer of one’s social worth, given that these regions respond to both acceptance and rejection (12; see also ref. 37). Supporting this view, we found that responses in these regions correlated with participants’ learning about how they were ranked by others, as indexed by a Bayesian model that tracked trial-by-trial updates of relational value. Altogether, these findings suggest that these regions play a role in learning how one is valued by others, explaining why people often show similar neural and physiological responses after both rejection and acceptance (12, 17, 38).

Although these regions responded to any updates in relational value, the brain must further differentiate whether the update was favorable or unfavorable. While overall activity in these regions reflected the degree of update, distinct voxel patterns may encode whether one is liked or disliked. We found that activity patterns in these regions encoded whether a partner was perceived to like or dislike the participant, which can provide a neural substrate for encoding the direction of the feedback. Furthermore, the results were consistent across trials when participants explicitly saw how others ranked them and when they had to infer how others ranked them, suggesting shared neural mechanisms across implied and explicit feedback.

More broadly, the present findings support a hybrid neurocomputational model of social learning, in which people learn through both simple reward reinforcement and through more complex social inferences (19, 39). In contrast to learning about relational value, learning through rewarding outcomes tracked responses in the VS—a region strongly linked to reward-based reinforcement learning across social and nonsocial domains (16, 18, 40). Thus, although people use more complex inferences to track the minds of others, they also track simpler reward contingencies in social interactions. This finding informs how reinforcement learning supports choice in complex social environments. More generally, this finding coheres with the perspective that people form social and moral judgments based not only on the intentions others bear but also on the outcomes they generate (19, 36, 41). Altogether, the present work demonstrates that people learn to affiliate with others in part based on the acceptance outcomes others provide, mediated by domain-general reward learning systems.

Although distinct brain regions tracked rewards and relational value, these types of learning did not remain independent in participants’ subjective perceptions. Replicating prior behavioral work (23), participants came to believe they were better liked by individuals who gave them rewarding outcomes, compared to individuals who ranked the participant equally well but who provided fewer positive outcomes. This finding held true across trials in which participants inferred or explicitly saw how they were ranked by others. This finding is consistent with an affective bias in social perception, in which affective responses to reward may bias one’s representation of the world. Notably, this bias was evident in voxel patterns within regions tracking relational value, and similarity between voxel patterns encoding outcomes and Deciders predicted the extent to which individuals’ subjective perceptions of being liked were biased by outcomes. Affective learning from rewards may thus influence subjective perceptions of relational value, much as rewards can bias other kinds of Bayesian inference (27).

Relational value and acceptance outcomes were manipulated independently in the current experiment. Although relational value and outcomes are often coupled, many daily life examples dissociate them, as when a child is chosen last for a recess basketball team or a friend learns they would have been invited to a wedding if the budget allowed for one more guest. Yet, even in cases where relational value and outcomes are coupled, this coupling makes it difficult to know what signal people learn from. By experimentally dissociating these signals, the present work distinguishes their impact on social affiliation and neural activity, which may help pinpoint computations supporting well-being.

Both kinds of learning computations studied here could serve adaptive social choice. To form thriving friendships, people may need to recognize that a friend still values them even when that friend provides disappointing outcomes, like missing a birthday party due to caring for a sick parent. Without this recognition, people may suffer from volatile relationships—and indeed, some forms of psychopathology are marked by both volatile social relationships and extreme reactions to perceived kindnesses or slights (42–45). On the other hand, people who are sensitive to social rewards may be motivated to approach others and garner experiences of connection, allowing them to build positive relationships (46, 47). Indeed, other forms of psychopathology involve both social withdrawal and insensitivity to rewards (48). By dissociating neurocomputational bases of learning, the present work provides a basis for future work testing learning computations that support adaptive social behavior in healthy populations or maladaptive social behavior in psychopathology.

In sum, we identify two neural computations through which people learn which individuals to approach or avoid following acceptance and rejection, transforming past social feedback into future affiliation. This work illuminates neural responses to rejection, providing insight into the computations performed by distinct brain regions previously observed to respond to rejection or acceptance and characterizing what inferences people draw from social feedback. By identifying how people use social feedback to guide their choices, these findings can inform, in future work, how individuals learn to affiliate with others in everyday life, building positive relationships that support physical and mental health.

Materials and Methods

Participants.

Forty-two participants were recruited from the University of Southern California community in exchange for payment (22.36 ± 4.60 y, 22 females). All participants were right handed, spoke English fluently, had normal or corrected-to-normal vision, with no history of psychiatric and neurological disorders, and did not have any metal implants or parts in their body. An initial sample size of 40 subjects was planned. For two subjects, functional magnetic resonance imaging (fMRI) data could not be collected due to technical issues with scanner equipment. These two subjects were replaced for fMRI analysis purposes but included in behavioral analyses for the sake of completeness. For one additional subject, fMRI data could not be collected during one run of the task. Participants gave informed consent in accordance with approval from the University of Southern California Office for the Protection of Research Subjects, which approved the study procedures.

Experimental Paradigm.

In an initial survey completed online, participants filled out six open-ended getting-to-know-you questions that would supposedly be viewed by other players to form impressions of the participant (SI Appendix). Participants then completed the Adult Rejection Sensitivity Questionnaire (49).

Five to ten days later, participants completed their second session, in which they completed the social game while undergoing functional MRI. On each round, participants saw two Decider avatars out of the possible eight, which were matched to the participants’ gender, and chose whom they would try to match with. Feedback was generated such that Deciders varied independently in the rank they gave participants (high or low) and their probability of matching (high or low) (Fig. 1B). If participants matched with the Decider they selected, they played a trust game, in which they could return half the points sent by a Decider or keep all the points to themselves. If they did not get to match, they saw a screen that said “No Game” for an equivalent length of time. This period was preceded and followed by a jittered intertrial interval (1 to 8 s). Participants completed 96 rounds of the task across six functional runs. Rank-explicit and rank-hidden trials were pseudorandomly interleaved with the constraint that no more than eight of the same kind of trials could occur in a row. See SI Appendix for detailed task procedures and instructions.

Postscan Measures.

After the scan, participants rated their perceptions of how much each Decider had liked them using a sliding scale from 0 (Not at all) to 100 (Very much), along with their confidence in their estimates on a scale from 0 (Not at all) to 100 (Very much). For purposes of computational model validation, participants also indicated how they thought each Decider had ranked them on average from 1st (Highest) to 8th (Lowest) and rated their confidence in these estimates (SI Appendix). For exploratory purposes, participants rated how much they would like to partner with each Decider if they were to participate in a cooperative puzzle-solving task in the future, on a scale from 0 (Not at all) to 100 (Very much).

Computational Model.

Choices during the learning task were fit to a Bayesian reinforcement learning model, adapted from prior work (23). This model assumes subjects use Bayesian inference to update estimates of outcomes (i.e., the probability of matching with a Decider) and relational value (i.e., how a Decider tends to rank them) and then combine these estimates to choose a Decider on subsequent trials. This model maintained two belief distributions toward each Decider: an outcome distribution, describing the probability of matching with a Decider, and a rank distribution, describing the rank expected from each Decider. These distributions were initialized as uniform distributions ranging from zero to one, for the outcome distribution, and from one to eight, for the rank distribution. On each trial, when participants received feedback, these distributions were updated.

Outcomes on each trial were binary (acceptance or rejection), and beliefs about the probability of acceptance can therefore be modeled as a beta distribution Beta(α, β), where α and β track the number of past acceptances and rejections, respectively. Following each outcome, the distribution is updated according to Bayes’ rule, which can be implemented by adding to running counts of “acceptance” and “rejection” feedback (50):

$${\alpha }_{i,t+1}={\alpha }_{i,t}+pos,$$ [1]

$${\beta }_{i,t+1}={\beta }_{i,t}+neg,$$ [2]

where pos = 1 and neg = 0 for acceptance outcomes and pos = 0 and neg = 1 for rejection outcomes. This distribution describes a subject’s beliefs about their probability of acceptance for a given Decider i, given the past history of acceptance and rejection by this Decider.

Expected ranks were modeled as normal distributions centered on particular ranks, N(M, 1) with mean M and SD of 1, which corresponds to the SD in the generative model underlying feedback. (Modeling was robust to this distributional choice; see SI Appendix for alternate specification using a Dirichlet distribution). On the first trial, the uniform distribution described above served as a prior belief, corresponding to uncertainty about each Decider. Upon receiving feedback, the subject’s beliefs were updated by combining their prior beliefs with a likelihood function that maximizes the likelihood of the rank received. On “rank visible” trials, the likelihood function was a normal distribution centered on the rank received; for instance, a received rank of four is most likely to emerge from a distribution centered on four. On “rank hidden” trials, subjects did not know exactly how they were ranked; instead, subjects knew possible ranks they could have received. For instance, if a subject was accepted along with two others, they knew their rank could have been 1st, 2nd, or 3rd; conversely, if a subject was rejected along with two others, they knew their rank could have been 6th, 7th, or 8th. The model therefore averaged the likelihood functions for each possible rank given the feedback, and the resulting curve was combined with a subject’s prior belief to generate a posterior distribution (SI Appendix, Fig. S1). The new posterior was then used as the prior on the next trial in which the subject encounters the Decider, reflecting an updated belief about the Decider’s ranking of the subject.

To make a choice on the next trial, the model assumes that subjects compute the reward value of each Decider, RV, as the mean of the outcome distribution, indicating the expected probability of matching with the Decider in light of past matches. Second, the model assumes subjects compute the Decider’s mean rank of them, K, as the mean of the rank distribution. Next, subjects use this expected rank to compute an expected value based on rank (KV); this is the likelihood of being accepted given an expected ranking K, assuming a uniform distribution over each possible number of partners that could be allotted to a Decider (from 1 to 8). Estimates of outcome were thus agnostic about ranks and estimates of rank were agnostic about outcomes. Finally, the model assumes that subjects compute an overall expected value (EV) as a weighted average of RV and KV, thus combining beliefs about reward outcomes and beliefs about relational value. This weighted average uses a weighting parameter (denoted w) ranging between 0 and 1, indicating the extent to which individuals make choices based on outcomes (w = 0) and rankings from Deciders (w = 1):

$$\mathrm{EV}=w\left(\mathrm{KV}\right)+\left(1-w\right)\mathrm{RV}.$$ [3]

Participant choices were modeled as a function of this value using a softmax choice function, which allows for stochasticity in choice with an inverse temperature parameter β:

$$p_{i,t}=\frac{exp(\beta \times {\mathit{\text{EV}}}_{i,t})}{{\sum }_{j}exp(\beta \times {\mathit{\text{EV}}}_{j,t})}.$$ [4]

The model thus included two free parameters, w and β (see SI Appendix, Table S6 for parameter fits). This model was fit to each participant’s choices using maximum a posteriori estimation (19, 51, 52), identifying parameters that best predict each person’s choices. Weak priors were used for the inverse temperature parameter, β ~ Gamma(1.2, 5), and the weighting parameter, w ~ Beta(1.1, 1.1). The weighting parameter was bounded between 0 and 1, and the inverse temperature parameter was bounded between 0 and 20. To fit the model, the continuous belief distributions were discretized into 500 units. For further details of model comparison, model validation, and supplemental regression analyses, see Supplemental Information, including SI Appendix, Fig. S6 and Tables S1–S3 and S7.

The model was used to estimate updating on each trial, defined as KL Divergence from prior to posterior. Surprise was estimated as Shannon Information, computed as −log(p), where p refers to the prior probability of an observation given a belief distribution (13).

Analysis of Posttask Ratings.

Participant ratings of being liked, collected after the scan, were entered into a 2 (Rank: High, Low) × 2 (Outcome: High, Low) × 2 (Rank Visibility: Visible, Hidden) repeated measures ANOVA. To examine individual differences, we computed Rank Reliance as ratings for [Positive Rank] − [Negative Rank] Deciders, collapsing across Deciders who provide different outcomes, and Outcome Reliance as ratings for [Positive Outcome] − [Negative Outcome] Deciders, collapsing across Deciders who provide different ranks. The difference of [Rank Reliance] − [Outcome Reliance] indexed the relative extent to which a participant’s ratings were sensitive to each kind of feedback.

fMRI Data Acquisition.

All images were acquired using a Siemens Trio 3.0 Tesla MRI scanner. Functional images (TR = 2,000 ms; effective TE = 25 ms; flip angle = 90°, 41 3-mm slices with a 0-mm gap for whole-brain coverage, matrix = 64 × 64; FOV = 192 × 192 mm; acquisition voxel size = 3 × 3 × 3.00 mm) were acquired using a customized echo planar imaging sequence developed in conjunction with the University of Southern California Dana and Dornsife Cognitive Neuroimaging Center. Phase encoding direction was anterior to posterior.

fMRI Data Preprocessing.

Image volumes were preprocessed using the default processing pipeline of fmriPrep 20.2.1 (53), including slice timing correction, coregistration, motion correction, and resampling to a Montreal Neurological Institute template. For univariate analyses, data were additionally smoothed with an 8 mm kernel using SPM12 software. For representational similarity analyses, data were smoothed with a 4 mm kernel.

Parametric General Linear Model (GLM) Analyses of fMRI Data.

Analyses were conducted using SPM12. We ran a GLM analysis that included the onsets of choice, feedback, and trust game choice (or the delay period if participants did not match) on each trial. Each feedback event was parametrically modulated by time series representing signed updates, unsigned updates, and surprise for reward (based on match vs. nonmatch) and time series representing signed updates, unsigned updates, and surprise for relational value (based on ranks), as derived from the computational model. All parametric regressors were entered into one model, ensuring unique variance was assigned to each regressor.

Data were concatenated across runs. Choice epochs were modeled as lasting the duration of reaction time (54), and feedback onsets were modeled as an impulse, following prior work on social learning (19). Trials with missing responses were modeled as regressors of no interest, and six motion parameters resulting from realignment served as covariates. First-level contrasts for each parametric regressor were created and entered into a second-level random effects analysis. All whole-brain analyses were corrected for multiple comparisons using a voxel-wise threshold of P < 0.001 and a cluster extent to maintain pFWE < 0.05, using Gaussian field theory as implemented in SPM (55). For region of interest analyses, we generated 10 mm spheres around peak voxels identified in a past meta-analysis of social pain in the vACC [4, 36, −4] and dACC [8, 24, 24] (24).

RSA between Neural Similarity and Subjective Ratings.

Our interest was in how the brain learns from social feedback, and we therefore focused our analyses on the feedback stage of each trial. For RSA, a second GLM modeled the feedback stage of each trial as a separate event. Choice and trust game epochs served as regressors of no interest. The model was otherwise identical to GLM 1. A contrast was performed for the feedback stage of each trial, and beta-weights corresponding to each trial were extracted. These beta weights were used in RSA. To increase reliability (56) and reduce potential biases due to task structure (57), spatial whitening was applied using the variance–covariance matrix of residuals and only cross-run similarities were used, such that similarity was never computed from pairs of data points within the same scanner run (for further details, see SI Appendix).

For the first analysis linking neural patterns to subjective ratings of Deciders, trials featuring a given Decider were averaged together to generate an average voxel pattern toward that Decider, separately for odd and even runs. To derive neural similarity for each pair of Deciders, Pearson correlations were computed between odd runs of a given Decider and even runs of all other Deciders, and between even runs of a given Decider and odd runs of all other Deciders. The odd-to-even and even-to-odd correlations for each Decider pair were averaged and converted to dissimilarity (as 1 − r), generating an 8 × 8 representational dissimilarity matrix indicating average neural dissimilarity of each pair of Deciders (Fig. 4A). For posttask subjective ratings, the absolute difference between the ratings given to each pair of Deciders provided a measure of rating dissimilarity. Neural dissimilarity and rating dissimilarity were compared for each subject using Spearman correlations. The average (Fisher-transformed) correlation was computed across subjects and compared to zero in a one-sample t test (two tailed).

RSA between Neural Similarity and Trial-by-Trial Model Variables.

For the second analysis examining trial-by-trial relationships between task variables and brain activity, the neural similarity of each pair of trials was computed using Pearson correlation. Similar to the prior analysis, only cross-run similarities were computed, excluding any trial pairs within the same run, and similarity was converted to dissimilarity as 1 − r. Using multiple regression RSA (58), neural dissimilarity was regressed onto dissimilarity in rank beliefs and dissimilarity in outcome beliefs. Multiple regression RSA was used to ensure unique effects of each predictor. Dissimilarity in beliefs was computed by using the computational model to estimate the belief distribution on each trial and then calculating the symmetrized KL Divergence (26) between the distributions across each pair of trials. This was done separately for beliefs about rank and outcome. To ensure similarity between trials in this analysis was not due to seeing the same Decider across two trials, only pairs of trials featuring different Deciders were included in this analysis. The predictors and dependent variable were z-scored to produce standardized coefficients. The average coefficients for rank and outcome were compared against zero using one-sample t tests (two tailed). Results remained the same when adjusting for additional task variables, including whether trials featured the same kind of feedback (rank explicit or rank inferred; see SI Appendix).

Examining Overlap between Encoding of Deciders and Trial-by-Trial Variables.

To identify voxels important for encoding Decider identity, we first used RSA to compare trial-by-trial neural dissimilarity with an indicator for whether a pair of trials featured the same or different Deciders, using Spearman correlations. Next, to link neural responses to individual differences in social perception, we conducted permutation feature importance analyses (30, 31). This approach identifies how important a given voxel is by randomly permuting that voxel’s responses across trials and measuring how this changes the analysis. Each voxel's responses were permuted 50 times and the three trial-by-trial RSA effects—Decider identity, rank, and outcome—were recomputed. A voxel importance score was computed as the difference between the true coefficient and the coefficient when permuting the voxel. Importance scores were averaged across the 50 permutations for each voxel, with a larger score indicating a voxel was more important for the observed relationship. To test for similarity in encoding, the importance scores for Decider identity were correlated with importance scores for rank, and separately, with importance scores for outcome. These scores indicate whether voxels encoding Decider identity were similar to those encoding rank and to those encoding outcome. Finally, individual differences were examined by subtracting Decider-Outcome similarity from Decider-Rank similarity and comparing this difference score with the analogous rating difference score described above.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Anonymized statistical maps and behavioral response data have been deposited in Open Science Framework (https://osf.io/zc8er/?view_only=b591032b89724f2587b0c2540f2c84d0) (59).