Recognition of Conus species using a combined approach of supervised learning and deep learning-based feature extraction

Abstract

Cone snails are venomous marine gastropods comprising more than 950 species widely distributed across different habitats. Their conical shells are remarkably similar to those of other invertebrates in terms of color, pattern, and size. For these reasons, assigning taxonomic signatures to cone snail shells is a challenging task. In this report, we propose an ensemble learning strategy based on the combination of Random Forest (RF) and XGBoost (XGB) methods. We used 47,600 cone shell images of uniform size (224 x 224 pixels), which were split into an 80:20 train-test ratio. Prior to performing subsequent operations, these images were subjected to pre-processing and transformation. After applying a deep learning approach (Visual Geometry Group with a 16-layer deep model architecture) for feature extraction, model specificity was further assessed by including multiple related and unrelated seashell images. Both classifiers demonstrated comparable recognition ability on random test samples. The evaluation results suggested that RF outperformed XGB due to its high accuracy in recognizing Conus species, with an average precision of 95.78%. The area under the receiver operating characteristic curve was 0.99, indicating the model’s optimal performance. The learning and validation curves also demonstrated a robust fit, with the training score reaching 1 and the validation score gradually increasing to 95 as more data was provided. These values indicate a well-trained model that generalizes effectively to validation data without significant overfitting. The gradual improvement in the validation score curve is crucial for ensuring model reliability and minimizing the risk of overfitting. Our findings revealed an interactive visualization. The performance of our proposed model suggests its potential for use with datasets of other mollusks, and optimal results may be achieved for their categorization and taxonomical characterization.

Introduction

Conus Linnaeus is a large genus of gastropods that has been well-preserved in fossil records since its first appearance about 55 million years ago in the Lower Eocene. Cone snails are major predators in tropical reef communities [1, 2]. Their venom contains a diverse array of small peptides (conotoxins) that target neuromuscular receptors and are extensively utilized in drug development [3–5]. Taxonomic classification of the highly similar cone shell patterns is challenging due to variations in size, color, and geographical distribution. In particular, some Conus species exhibit nearly identical morphological characteristics, making identification difficult and requiring researchers to spend more time on differential analysis. To address these challenges, there is a pressing need to develop more sophisticated computational algorithms or models to automate Conus species recognition and streamline taxonomic classification.

In recent years, due to technological advancements, artificial intelligence (AI) and machine learning (ML) models have emerged as ideal solutions for image recognition [6]. ML algorithms are routinely used to perform various tasks, including pulmonary embolism segmentation via computed tomographic (CT) angiography [7], polyp detection through virtual colonoscopy or CT during colon cancer diagnosis [8], breast cancer detection through mammography [9], brain tumor segmentation using magnetic resonance (MR) imaging [10], and the detection of brain cognitive states through functional MR imaging for diagnosing neurological disorders [11, 12]. ML techniques, such as feature selection and classification, have become crucial for the accurate and automatic diagnosis and prognosis of various brain diseases [13, 14]. For instance, Ronneberger et al. utilized a Convolutional Neural Network (CNN) and data augmentation techniques, achieving promising results by training on an image dataset [15]. Ke et al. proposed a method to enhance the spatial distribution of hue, saturation, and brightness in X-ray images (as image descriptors) to identify unhealthy lung tissues using Artificial Neural Network-based heuristic algorithms [16]. Jaiswal et al. employed Mask-Region-based CNN, a deep neural network approach, which utilizes both global and local features for pulmonary image segmentation, combined with image augmentation, dropout, and L2 regularization for pneumonia identification [17]. Wozniak and Połap simulated the X-ray image inspection process to identify infected tissue locations [18].

Hu et al. used gene eigenvalues and MRI imaging, together with a genetic-weighted random forest (RF) model, to identify key genetic and imaging biomarkers for diagnosis and personalized treatment [19]. Jing et al. applied RF to optical sensors for foreign object debris detection, crucial for aerospace safety [20]. Chen et al. optimized chemical exchange saturation transfer MRI by analyzing frequency contributions using a permuted RF model [21]. Wang and Zhou improved soil organic matter estimates by combining multitemporal Sentinel-2A imaging with RF to benefit agricultural practices [22]. Matese et al. highlighted the role of unmanned aerial vehicle-based hyperspectral imaging in advancing crop health monitoring and management [23]. Barrett et al. emphasized the importance of predictive models in early Huntington’s disease intervention [24]. Waldo-Benitez et al. demonstrated ML’s impact on enhancing glioblastoma diagnosis and treatment planning through MRI analysis [25]. Huang et al. showed how stacked models improve wheat quality control using hyperspectral imaging [26]. Feng et al. emphasized the need for accurate plume injection height measurements to improve smoke exposure estimates during Australian wildfires [27]. Grandremy et al. provided insights into zooplankton monitoring through advanced imaging in a 16-year Bay of Biscay study [28]. Nobrega et al. applied deep transfer learning to classify lung nodule malignancy [29]. Philips and Abdulla proposed a method for detecting honey adulteration using hyperspectral imaging and ML, enhancing classification models with a feature-smoothing technique [30]. Tao et al. demonstrated the benefits of combining hyperspectral imaging and ML for municipal solid waste characterization, significantly improving material identification and sorting efficiency by capturing detailed spectral information [31].

ML strategies, together with advancements in AI, have been employed in the early detection of diseases through the accurate interpretation of chest X-rays [32]. Similarly, the use of these innovations is accelerating in other areas. A valuable addition of deep learning in image recognition facilitates aircraft target recognition, enabling air defense systems to quickly determine the target category of an acquired aircraft image and automatically estimate countermeasures, potentially saving significant reaction time and reducing combat risks [33]. In this study, we propose an automated method for identifying Conus species using a cohesive ML algorithm framework through feature-assisted training on imaging datasets. Additionally, by designing a local database, this study may serve as a basis for cataloging cone snail species, including their sequence information and family-wise distribution.

Materials and methods

Data collection

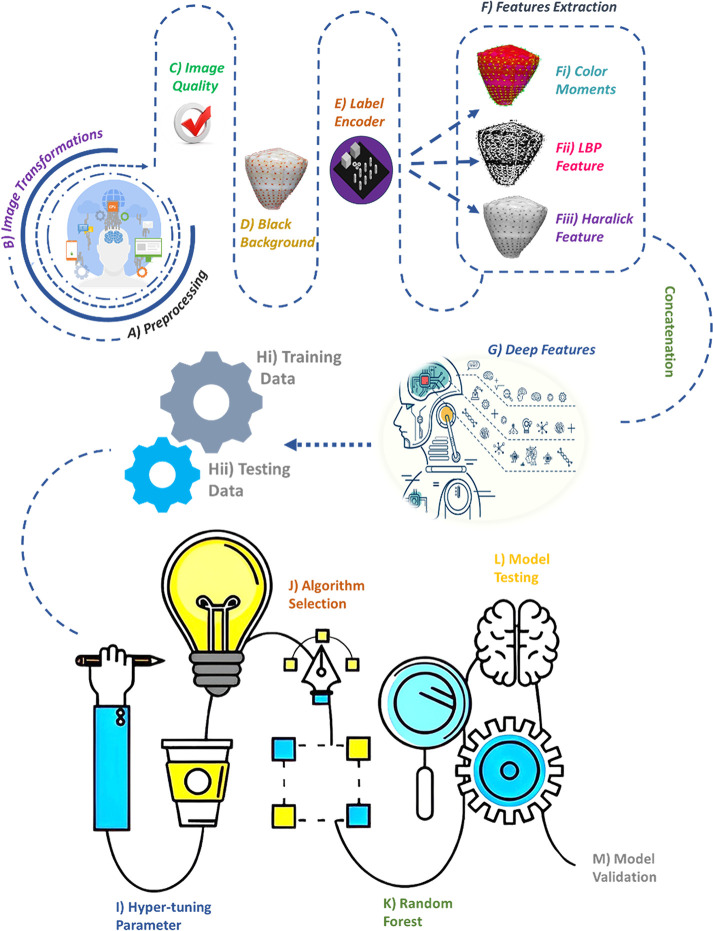
The image dataset of 119 Conus species was obtained from the ConoServer database [34]. Our proposed methodology is illustrated in the flowchart (Fig 1).

Fig 1. Flowchart scheme of the ML-based model.

A) Image preprocessing. B) Image transformation. C) Image quality analysis of preprocessed images. D) Background removal by obtaining the largest contour followed by masking. E) Conversion of species labels into numerical values using a label encoder. F) Feature extraction using three different steps: Fi) Color moments in different orders based on color distribution. Fii) Texture information using local binary patterns. Fiii) Additional texture information using Haralick texture features. G) Deep feature extraction using VGG16. H) Training data comprising 80% of the dataset. I) Testing data consisting of 20% of the entire dataset. J) Optimization of hyperparameter tuning. K) Algorithm selection from all models. L) Random forest selection. M) Model testing. N) Model validation using different methods.

Image preprocessing

Initially, each image file format (JPG, JPEG, or PNG) and size was checked for uniformity. The Pillow library was used to resize the images to a standard size of 224 x 224 pixels. Next, cvtColor was applied to find contours, and the images were converted to grayscale to remove background noise. A Canny filter was used to compute edge strength, utilizing linear filtering with a Gaussian kernel to smooth out noise [35]. The edges were then overlayed on the original RGB images. All images were processed through these steps and stored in a local folder.

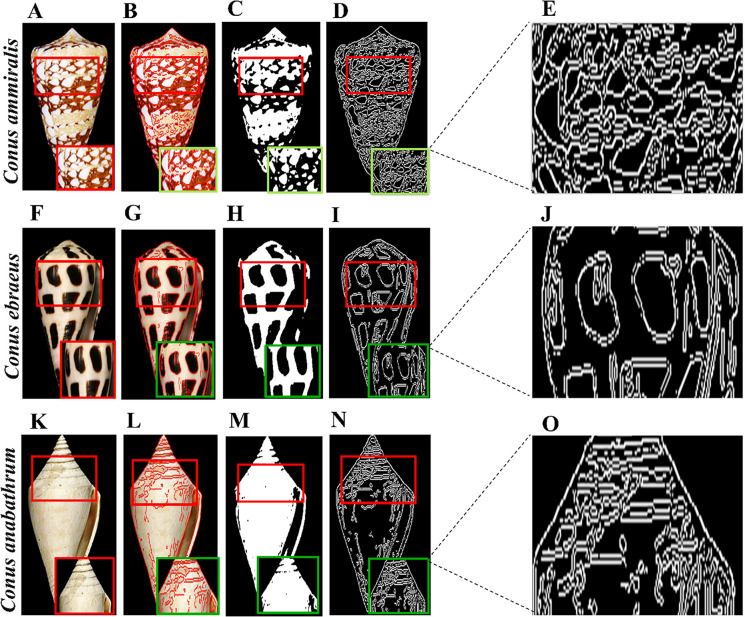
We also applied some pre-processing to each highlighted image. First, using cv2.COLOR_BGR2GRAY, we converted the image to grayscale. Gaussian blur was applied to remove noise from each image, and the images were normalized for enhancement. We used the Canny and Sobel functions [36] with a kernel size of 5 to detect edges in each image. The original images of Conus ammiralis, Conus ebraeus, and Conus anabathrum, along with the binary and Canny edge-detected images, are shown in Fig 2. These species exhibit specific patterns and shapes (pointed or round). In Conus ammiralis, few patterns are separated by filled brown areas with varying distances, while in the case of Conus ebraeus, the patterns are more pronounced, making it easily distinguishable from other species. In contrast, Conus anabathrum contains a line pattern at the pointed end.

Fig 2. Image preprocessing.

A) Original image of the Conus ammiralis shell, B) Highlighted enhanced image, C) Binary image, D) Canny edge-highlighted image, E) Enhanced edge-highlighted image. F-J) Conus ebraeus with enhanced, highlighted, binary, edge detected and respective enhanced images, respectively. K-O) Conus anabathrum with all respective images.

Image transformation

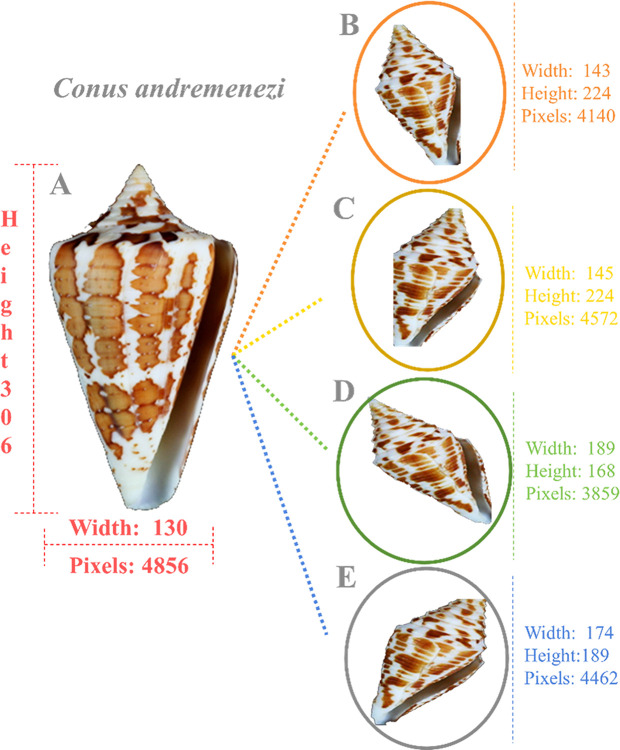
Image transformation was performed on each pre-processed image, with the total number set to 400. We initialized the ImageDataGenerator [37] using various parameters, such as width shift range, height shift range, zoom range, and shear range, all set to 0.2. Subsequently, we modified the rotation range to 30 degrees, set the horizontal flip to ’True,’ and used ’nearest’ for the fill mode. Each transformed image was stored in a unique folder. For each transformation, we applied a random transformation with a size of 224 x 224 pixels. Image transformation was cross-validated before further processing. In total, we obtained 47,600 transformed images. The original Conus andremenezi and its transformed images are shown in Fig 3, along with a detailed description of each image, highlighting distinct height, width, and pixel count.

Fig 3. Image transformation.

A) The original image of the Conus andremenezi shell and its dimension details are indicated in pink color. B-E) Its four transformed images, with pixel sizes ranging from 3,859 to 4,462, have different shell sizes (width × height). Each transformed image and its details are mentioned in their respective colors.

Proposed methodology

The next step was to check the image quality, and all images below the standard were removed. Noisy backgrounds were eliminated, and the cvtColor module was used to convert the images to grayscale, followed by the application of a threshold to segment the background and obtain the largest contour. A mask was applied to remove the background. Later, we combined all these images into a list and used a label encoder to encode each cone snail species label as a numerical value.

Color moments and local binary patterning

Subsequently, color moments of different orders were calculated for each channel, revealing color distribution and variation. The local binary pattern (LBP) texture feature was computed for each grayscale image to extract texture information. LBP works by measuring the intensity levels of neighboring and central pixels, forming a binary number [38]. The threshold is obtained by comparing the neighborhood pixel g_p with the center pixel g_c. This operator yields a binary value of 1 if g_p is larger than g_c and 0 otherwise. The final form of the LBP is represented in decimal value. The features extracted by the LBP operator are displayed in a histogram. This operation can be expressed as:

$${LBP}_{PR}={\sum }_{p=0}^{p-1}s\left(g_p-g_c\right)2^p,s(x)=\left\{\left(\frac{1,x\ge 0}{0,x<0}\right)\right\}$$ (1)

After the thresholding stage, a histogram was developed on the LBP values. With a neighborhood of P = 24P = 24P = 24 and R = 3R = 3R = 3, a 256-bin histogram represents the image features. The mathematical representation of the LBP histogram is denoted by [39]:

$$H\left(k\right)={\sum }_{i=1}^I{\sum }_{j=1}^{J}f\left({LBP}_{PR}\right(i,j)k),k\in [0,K],wheref(x)=\left\{\frac{1,x=y}{0,otherwise}\right\}$$ (2)

Haralick texture feature extraction

Next, we computed feature extraction through a method proposed by Haralick, named as spatial gray-level dependence method (SGLDM). These features are routinely used for diagnosis purposes and Alzheimer’s disease diagnosis by MR images [40]. For quantifying the texture through SGLDM, 13 features were calculated in each phase. These features were extracted from the co-occurrence matrix, which represents an estimate of the second-order probability function C (i; j| x; y). This matrix represented the occurrence rate of a pixel pair with gray levels i and j, given the distances between the pixels were x and y in the x and y directions, respectively [41]. The elements of the matrix were calculated by:

$$C\left(i,j\right|{\mathrm{\Delta }}_x{\mathrm{\Delta }}_y)=\frac{No.of\left(x,y\right)forwhichI\left(x,y\right)=i,I\left(x+{\mathrm{\Delta }}_x,y+{\mathrm{\Delta }}_x\right)=jandboth\left(x,y\right)and\left(x+{\mathrm{\Delta }}_x,y+{\mathrm{\Delta }}_y\right)arewithintheROI}{No.of\left(x,y\right)forwhichboth\left(x,y\right)and\left(x+{\mathrm{\Delta }}_x,y+{\mathrm{\Delta }}_y\right)arewithintheROI}$$ (3)

The Haralick texture features were computed using the Haralick function, which included texture information such as contrast, correlation, and entropy in the image. In the next step, we concatenated these three features as trained features.

Visual Geometry Group with 16-layer deep model architecture

The Visual Geometry Group with 16-layer deep model architecture (VGG16) [42] was used for extracting deep features that were utilized in a pre-trained deep learning model. It included 16 layers, comprising 13 convolutional layers and 3 fully connected layers. VGG16 employed a small 3x3 kernel (filter) on all convolutional layers with a single stride. Max pooling layers always followed the convolutional layers. The input for VGG16 was fixed at 224 x 224 three-channel images. In VGG16, the three fully connected layers exhibited different depths. The first two layers contained a similar channel size of 4096, while the last fully connected layer had a channel size of 1000, representing the number of class labels in the ImageNet dataset. The output layer was the softmax layer, which is responsible for providing the probability of the input image [43]. We added deep features to the feature vector by horizontally stacking the deep and trained features.

Random Forest

The RF classifier was used due to its ideal prediction capabilities, stability, and high accuracy rate compared to a single decision tree. RF is a powerful ensemble and supervised learning method, characterized by balanced bias, minimal hyperparameter input, reduced variance, and minimized risk of overfitting in both classification and regression tasks. These features make RF an invaluable tool for prediction, modeling, and data analysis across various domains. The RF algorithm performs better with larger datasets and accelerates the decision-making process through a higher number of trees [44]. RF is an extension of the Classification and Regression Tree (CART) method, employing bagging (bootstrap aggregation) and voting to determine classification results. It consists of k classification trees, and its basic idea is to convert multiple weak classifiers into one strong classifier. The number of generated bootstrap samples determines the number of trees in the model. After the bootstrap method, each tree (bootstrap sample) is formed using the following rules: If there are M input variables, the number of m predictor variables at each node satisfies m≤Mm. The variable m is chosen randomly from M. The selection of the best predictor variable from m is determined by calculating the measure of purity (Gini or entropy). The Gini index G_gini (D) is used to decide the optimal binary cut point for each feature. G_gini represents the uncertainty of the set D. In the classification problem, suppose there are N classes; for a given set of samples D, the G_gini index is:

$$G_{gini}\left(D\right)=1-{\sum }_{n=1}^N{\left(\frac{\left|C_n\right|}{D}\right)}^2$$ (4)

where Cn is the subset of samples in D that belong to the nth class [45]. If a sample set D is divided into two parts, D1 and D2, according to the value of feature A,

$$D_1=\left\{\left(x,y\right)\in D\left|A\right(x)=a\right\},D_2=D-D_1$$ (5)

The best split on m is used to separate the nodes. The amount of m is kept constant during the growth of forests. Each tree is formed to the maximum extent without pruning. The final result of RF is the optimal result chosen by voting on all classification trees [45]. The best predictor variable provides more decision-making information. More tree formation and their usage in the decision-making process yield more robust result [46].

Next, data was divided into training (80%) and testing or validation data (20%), about 38,080 and 9,520 images out of 47,600, respectively. As a result, we extracted X_Train, X_Valid, Y_Train, and Y_Valid for further optimization of hyperparameters [47]. Enhancing the RF algorithm’s ability is crucial for extracting high-quality features and optimizing parameter selection. This can significantly help reduce the model’s generalization error and improve the RF algorithm’s classification accuracy. We used 100 trees or estimators and a minimum sample split of 2 for splitting the internal nodes.

The model was then trained and evaluated by fitting X_Train and Y_Train and by predicting the model by X_Valid.

XGBoost

Tree-based gradient boosting integrated model XGBoost (XGB) [48], is composed of multiple classification regression trees (CART) that acquire the residual value through the sum of target and predicted values based on the prior decision trees. Upon training of all decision trees, they reach a consensus and finally compute the prediction result through the accumulation of samples from the previous findings. Every new tree in the XGB model training phase is trained using the previously trained tree as a model, and once a decision tree has been generated, it is stripped to avoid overfitting. The XGB model trains the obtained error to minimize the overall error. The input from each tree is utilized to train the subsequent tree again to progressively minimize the prediction error and gradually drive the model’s predicted value closer to reality. The prediction model for XGB can be represented as:

$$y_i={\sum }_{k=1}^K{f}_k\left(x_i\right),f_k\in F$$ (6)

Where x_i and y_i are training samples. x represents the eigenvector, y represents the sample label, and f_k(xi) represents the kth decision tree. The corresponding objective function is defined as follows [49]:

$$Obj\left(O\right)={\sum }_{i=1}^{n}L\left(y_i,{y_i}^{\prime }\right)+{\sum }_{k=1}^K\mathrm{\Omega }\left(f_k\right)$$ (7)

The objective function Obj(O) is divided into two parts: the regularization term, which reduces the chances of a model demonstrating overfitting, and the loss function, which indicates a specific objective to evaluate the accuracy of the model’s prediction. The function is as follows:

$$\mathrm{\Omega }\left(f\right)=\gamma T+\frac{1}{2}\lambda {\left|\left|\omega \right|\right|}^2$$ (8)

Where γ is the leaf node coefficient, its goal is to optimize and modify the objective function using XGBoost, similar to a pre-pruning operation (i.e., γT regulates the tree’s complexity; the higher the value, the higher the objective function value, which subsequently suppresses the model’s complexity). The leaf node weight percentage is regulated by the full L2 regularization term, and λ, the coefficient of the squared mode of L2, prevents overfitting. The objective function is gradient boosting decision tree (GBDT) if the regularization term has a value of 0 [50].

This model lessens the chance of overfitting by including regularization elements in the objective function. It utilizes both the first and second derivatives to enhance the accuracy of the loss function and customize the loss. We used the ‘Extreme Gradient Boosting’ classifier of the XGB library by specifying the evaluation metric to measure cross-entropy loss (which is a multi-class logarithmic loss) and avoid any deprecation issues in the disabled labels.

Confusion matrix

The performance of the chosen strategy was determined by a confusion matrix, which showed the number of correct and incorrect predictions made by the model as compared to the actual data [51, 52]. The confusion matrix comprises four components: True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN). The following metrics evaluate the performance of a classification model on a dataset:

Precision = TP / (TP + FP)

Recall (Sensitivity) = TP / (TP + FN)

F1-score = 2 * (Precision * Recall) / (Precision + Recall)

Other analyses, including bar plots and histogram generation, were performed to check the proportion and prediction results through the classification report of the desired RF model. The Area Under the Receiver Operating Characteristic Curve (AUC-ROC) [53] is a performance metric for binary classification problems. The AUC-ROC value ranges from 0 to 1, where a higher value indicates better performance. A curve closer to the top-left corner represents a better model. It was plotted to estimate the true positive rate (sensitivity) against the false positive rate (specificity) at various threshold settings.

Results

Cone snail shell image processing

Conus species exhibit diverse characteristics in terms of shell shape, size, color, and localization. The differentiation characteristics, including mean intensity, intensity standard deviation, edge pixel number, mean key point, vary significantly among Conus species (Table 1). In particular, images obtained from different sources need to be processed for color variation, background noise removal, pixel adjustment, and color intensity correction. To accurately process shell images, we scaled the RGB (red, green, and blue) intensity in the image. The average predicted RGB values were 70.23, 88.12, and 107.98 for R, G and B, respectively (S1 Fig). These values were distinct for each image, which largely facilitated enhancing model efficiency.

Table 1. Statistical analysis of raw images of Conus species before preprocessing.

Size (S), mean intensity (MI), intensity standard deviation (ISD), number of edge pixels (NEP), and mean key point size (MKS) are presented in different columns.

Specie name	Size	MI	ISD	NEP	MKS
Conus abbreviatus	126 x 196	114.900551	85.24146037	2070	3.855107131
Conus achatinus	234 x 469	90.1004501	72.62897095	17287	3.738486035
Conus adamsonii	166 x 309	81.5929543	64.52867715	10219	3.394759074
Conus amadis	137 x 283	89.7953625	81.18837988	7880	3.242136133
Conus ammiralis	147 x 266	101.342642	90.00906917	7293	3.558139329
Conus anabathrum	113 x 236	102.825859	91.64173238	2811	5.372164498
Conus andremenezi	130 x 306	77.2646053	78.52747464	4856	4.783157641
Conus anemone	140 x 333	102.90532	87.34408651	6528	5.295740278
Conus araneosus	190 x 344	95.4301561	89.64749384	10002	4.042105765
Conus archon	173 x 325	78.0636372	76.09148881	6231	3.903034503
Conus arenatus	150 x 258	127.868966	88.99116882	5384	3.248078797
Conus aristophanes	125 x 209	115.918813	84.83766222	3292	3.536915887
Conus asiaticus	160 x 303	91.0680693	93.87201536	5579	3.533550901
Conus ateralbus	147 x 251	65.5442177	66.74975933	7071	3.789925593
Conus aulicus	127 x 305	95.9198916	75.00209789	6079	3.877136884
Conus aurisiacus	172 x 309	99.8640777	80.66912726	5803	3.930534717
Conus austini	167 x 318	82.4746545	77.49197812	4362	3.392523493
Conus australis	115 x 306	94.9256323	82.35290923	5929	3.427619775
Conus bandanus	646 x 1202	83.4092946	78.0616978	44765	7.77255379
Conus bayani	114 x 227	67.7127676	71.5729914	2925	4.299335957
Conus betulinus	224 x 335	101.927159	81.59713297	7407	3.679199442
Conus brunneus	154 x 191	66.2547766	62.9423698	6141	3.567691536
Conus bullatus	114 x 219	107.642193	67.27182937	5300	3.453630916
Conus californicus	462 x 846	80.9327341	69.53473463	15680	5.947179261
Conus capitaneus	169 x 252	80.4169954	65.4770939	7079	3.501728312
Conus caracteristicus	163 x 225	102.626667	82.49999629	5106	3.704006016
Conus catus	135 x 240	90.7333025	71.40495938	6002	3.917673782
Conus cervus	136 x 274	100.219381	76.16191665	6241	3.530832996
Conus chiangi	153 x 264	85.9632601	76.05567255	5952	3.216992084
Conus circumcisus	116 x 279	109.326319	72.72633786	5200	4.345783836
Conus consors	141 x 299	86.4395266	67.08034587	2973	6.904867876
Conus coronatus	83 x 133	97.6019567	81.97972403	2303	3.625967436
Conus dalli	157 x 267	93.0402681	77.21764877	8964	3.322457316
Conus delessertii	161 x 307	83.4159063	81.82363518	5977	5.091297852
Conus diadema	194 x 307	89.0702173	73.76674884	7057	4.010664793
Conus distans	89 x 160	105.306812	85.94422289	2571	4.76245108
Conus ebraeus	209 x 311	73.9946615	79.35979636	5273	5.99292686
Conus eburneus	222 x 349	92.4428612	88.25812038	8119	5.578738826
Conus emaciatus	251 x 405	81.1571197	60.17887854	4533	5.640602514
Conus episcopatus	150 x 320	91.8544583	80.46877076	9376	3.610899895
Conus ermineus	185 x 329	88.6190421	76.6154946	6962	4.545134057
Conus ferrugineus	210 x 416	83.9429831	70.89388376	7075	5.904191236
Conus figulinus	282 x 407	80.4968547	71.85676559	16639	3.399929217
Conus flavidus	170 x 295	97.7092921	74.24410961	4067	3.978458209
Conus floridulus	667 x 1131	87.5026585	80.04923969	14478	7.446896809
Conus frigidus	156 x 265	103.462821	72.74093208	4527	3.876202816
Conus fulmen	196 x 357	83.4306723	72.73174627	2611	6.047156509
Conus gauguini	89 x 163	103.28214	76.99108538	2067	4.176049745
Conus generalis	135 x 287	98.3426249	85.07910231	2625	4.553597675
Conus geographus	76 x 178	69.1569338	59.76345165	3261	4.091072835
Conus gladiator	168 x 249	82.6303548	72.62570646	5498	4.632142848
Conus gloriamaris	119 x 343	80.1448661	70.72475205	10025	3.040092381
Conus imperialis	82 x 156	73.2795497	77.08575888	3229	3.322255486
Conus inscriptus	161 x 330	102.096951	88.50804845	6676	4.308585652
Conus judaeus	186 x 311	80.9460291	91.12290436	5677	5.282902826
Conus kinoshitai	133 x 306	109.052312	87.59792953	4673	4.002651231
Conus kintoki	171 x 362	110.7324	82.19116586	3015	3.805836274
Conus leopardus	120 x 211	100.795616	79.70195154	5007	3.217252134
Conus limpusi	166 x 335	80.9515015	66.41763157	2640	5.178752613
Conus litteratus	91 x 156	128.705128	101.7086228	2609	2.857512904
Conus lividus	137 x 249	88.3807639	77.07639339	2551	4.272186609
Conus longurionis	116 x 351	79.9143089	72.36931846	5730	4.66598781
Conus loroisii	172 x 273	54.6943948	46.1643957	9412	3.114201716
Conus lynceus	174 x 386	106.663123	82.14609781	8848	5.149299075
Conus magnificus	116 x 261	111.673438	84.23736161	7044	3.127516587
Conus magus	279 x 582	102.056319	77.61301005	21916	5.131758487
Conus marmoreus	464 x 987	71.0377253	75.10760805	35820	8.258521537
Conus memiae	210 x 350	78.1916871	85.53722763	9499	5.492338902
Conus miles	136 x 207	74.5656081	76.81322467	5401	3.088816641
Conus miliaris	180 x 296	90.4191254	74.03838125	8054	3.592617067
Conus milneedwardsi	69 x 223	87.232274	80.6165129	2860	3.355763269
Conus monachus	226 x 424	118.874885	87.78246128	11436	4.074395915
Conus moncuri	195 x 342	83.8184885	75.0833367	7482	4.94113918
Conus monile	161 x 337	87.6115709	82.27396067	5175	4.915662615
Conus mus	84 x 150	95.6694444	76.5681594	3144	3.750667921
Conus mustelinus	149 x 272	92.0070322	77.31240476	5208	4.039098181
Conus natalis	157 x 318	74.0708449	67.42437807	10205	4.775390739
Conus nigropunctatus	127 x 216	92.907699	73.07321996	4902	4.230405607
Conus nux	194 x 332	77.2799186	71.9322076	4320	7.542459114
Conus obscurus	70 x 160	74.8146429	52.24022396	2667	3.338338166
Conus omaria	86 x 194	107.138576	65.92997092	4084	3.085670003
Conus parius	182 x 303	100.761923	82.87203435	1756	4.551220399
Conus pennaceus	104 x 174	78.9077697	86.20071699	2587	4.316248887
Conus pergrandis	136 x 344	76.2034456	77.06110854	5116	3.972704224
Conus pictus	182 x 340	77.9745637	73.67581946	7533	4.965593014
Conus planorbis	113 x 207	75.9901672	69.28186747	4616	3.446087527
Conus princeps	155 x 273	110.268746	91.49685066	5370	4.075615161
Conus profundineocaledonicus	155 x 333	87.7985857	74.28470619	1865	6.221098957
Conus purpurascens	554 x 932	64.4792845	59.42204983	57556	4.533820502
Conus quercinus	160 x 272	106.95347	78.62236341	1603	10.07662979
Conus radiatus	114 x 244	81.7528401	61.54902861	2578	3.766189418
Conus rattus	185 x 298	85.1469617	71.41448917	7632	4.262023336
Conus regius	146 x 261	89.9245263	76.46770287	7479	3.76844333
Conus regularis	134 x 285	86.8535219	78.17037418	5597	4.388107317
Conus rolani	151 x 300	106.889382	82.66212069	4221	4.337546096
Conus sanguinolentus	153 x 262	91.726987	73.29265179	2704	5.807804724
Conus sponsalis	304 x 381	85.6163835	83.54710968	7368	5.747592142
Conus spulicarius	216 x 346	86.9485389	74.4378499	9807	5.313243719
Conus spurius	166 x 270	106.758188	82.90364202	3524	5.422410713
Conus stercusmuscarum	113 x 236	111.163154	77.06938388	4015	3.110592977
Conus striatus	135 x 306	109.730864	80.91233496	6460	4.263692126
Conus striolatus	149 x 268	90.6919764	74.36637035	7842	4.19279689
Conus sulcatus	150 x 266	87.610802	73.93412992	7816	3.80518956
Conus sulturatus	109 x 175	123.898768	81.81499109	735	10.90305368
Conus terebra	102 x 237	104.010176	80.97356016	1960	4.921096532
Conus tessulatus	163 x 252	86.5140715	76.07680221	4052	5.229228191
Conus textile	114 x 228	88.8001693	75.83345613	6716	2.816846265
Conus tinianus	99 x 192	104.217119	77.25270464	2544	4.685287444
Conus tulipa	115 x 228	105.702021	65.36394178	6445	3.410149088
Conus varius	136 x 266	104.889761	82.3494734	3056	6.092001697
Conus ventricosus	158 x 277	93.4467395	81.42046926	9519	3.198309433
Conus vexillum	152 x 249	96.2798563	81.22803912	6762	4.179350178
Conus victoriae	86 x 183	66.5662727	67.5775656	3900	3.02614837
Conus villepinii	76 x 183	94.9417601	87.01109306	2081	4.106920018
Conus virgo	164 x 316	109.196955	84.3636481	1928	4.158706044
Conus vitulinus	146 x 282	93.9529049	78.04338245	4788	4.153326996
Conus ximenes	80 x 140	93.75125	81.05532005	2199	2.958279716
Conus zeylanicus	146 x 251	125.553376	92.91948417	6446	3.69964845
Conus zonatus	66 x 129	94.6779422	74.00836486	2014	3.002186416

The dataset of 47,600 images were split into 80% training and 20% testing data, resulting in 38,080 and 9,520 images. X_Train, X_Valid, Y_Train, and Y_Valid were extracted for hyperparameter optimization [54]. Enhancing the RF algorithm is crucial for extracting high-quality features and optimizing parameter selection. This may significantly help reduce the model’s generalization error and improve the RF algorithm’s classification accuracy. The model was trained and evaluated by fitting X_Train and Y_Train and by predicting with X_Valid.

Model validation

Next, we added more data to check the predictions for each search image as validation data. Among the 119 species, five species were wrongly predicted: Conus monile was predicted as Conus kintoki, Conus monachus was predicted instead of Conus virgo, Conus tinianus as Conus catus, Conus vitulinaus was predicted as Conus regularis and Conus flavidus was predicted as Conus betulinus. All other species were accurately predicted by the trained RF model, achieving a high accuracy rate (S1 Table). For these species, structural similarity index ranged from 0.33 to 0.99, which measures similarity between test and reference images by calculating variations in contrast, brightness, and edge information [55].

We included images of some species other than cone snails, such as Miter shells, Olive shells, Cypraea argus, Aulica imperialis, and Eloise Beach, along with Conus species Conus literatus, Conus asiaticus, and Conus ebraeus for further validation of our model (Fig 4). Training results revealed no irrelevant species due to feature differentiation. These shell images were ranked in the range of 27,674, 27,413, 27,584, 26,522, and 26,549, while Conus shells exhibited 27,143 features. Overall, the proposed model in this report is 95% efficient in cone snail species recognition through shell images.

Fig 4. Prediction results of species other than Conus species.

A-C) Conus species that are accurately recognized by our model as Conus litteratus, Conus asiaticus, and Conus ebraeus, respectively. D-H) Feature differentiation led to no species recognition in cases of Aulica imperalis, Cypraea argus, Eloise beach, Miter shells, and Olive shells.

Model performance assessment

Precision and recall analysis

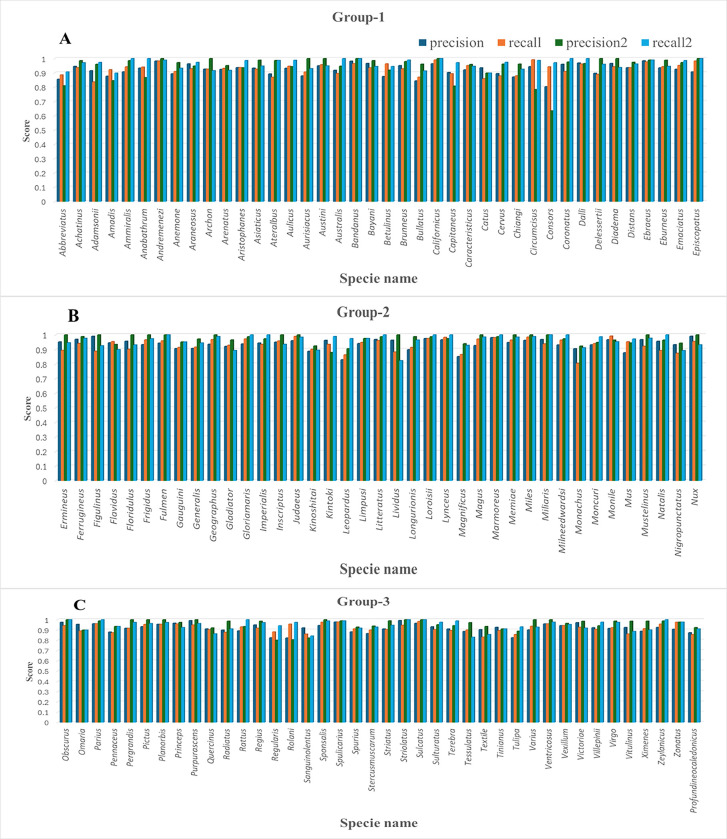
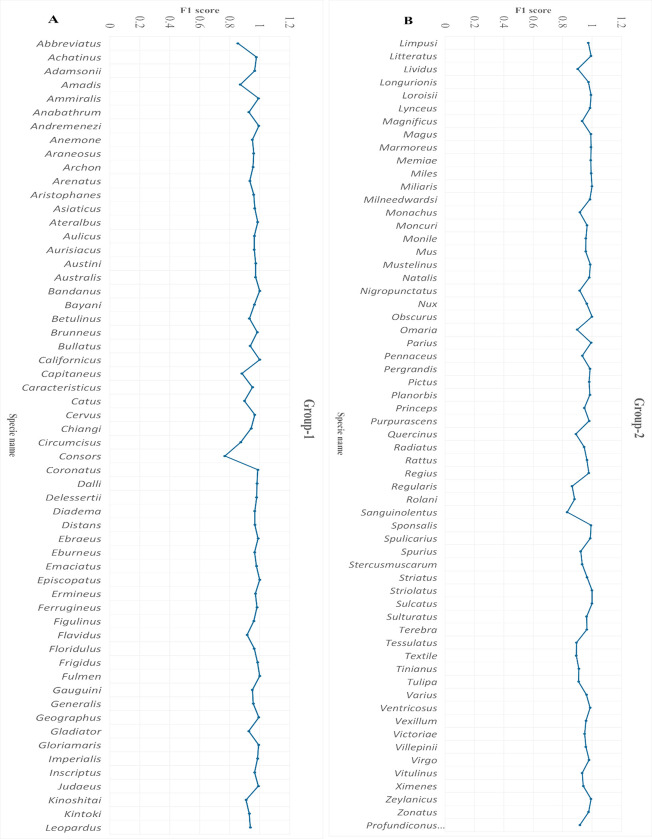
The RF classification report indicated a significant proportion of TP predictions as compared to XGB. Multiple species exhibiting precision score values close to 1 demonstrated accurate predictions through the RF model. These species were categorized into three groups for better representation in bar plots (Fig 5). Among the 119 Cone snail species, group 1 contained 40 species, group 2 exhibited 39 species, and group 3 included 40 members.

Fig 5. Bar plot for precision and recall values for 119 Cone snail species are categorized into three groups.

Bar plot illustrating precision and recall values for 119 Cone snail species categorized into three groups. A) Group 1 contains 40 species. B) Group 2 exhibits 39 species, while C) Group 3 comprises 40 members. In all plots, species names are presented on the X-axis, while the corresponding precision and recall rates obtained through RF and XGB models are indicated on the Y-axis. The dark blue and orange bars represent the respective values of precision and recall for each species by XGB, while the green and blue bars represent precision and recall values obtained by the RF model.

In group 1, nine members (Conus andremenezi, archon, aurisiacus, austini, bandanus, californicus, delessertii, diadema and episcopatus) exhibited RF precision scores of 0.98, 0.92, 0.87, 0.95, 0.98, 0.96, 0.89, 0.96, and 0.90, respectively. Group 2 comprised 15 members (ermineus, figulinus, floridulus, frigidus, fulmen, geographus, inscriptus, judaeus, lividus, magus, memiae, miles, miliaris, mustelinus and nux) demonstrating precision scores of 0.95, 0.99, 0.95, 0.93, 0.94, 0.93, 0.95, 0.96, 0.96, 0.92, 0.94, 0.96, 0.96, 0.96, 0.99 scores. In contrast, 10 species in group 3, including obscurus, pergrandis, pictus, planorbis, purpurascens, sponsalis, striolatus, sulcatus, varius, and ventricosus contained precision scores of 0.97, 0.91, 0.93, 0.95, 0.99, 0.94, 0.99, 0.96, 0.90, 0.95, respectively through the RF model. The minimum precision value (0.64) was observed for Conus consors.

Notably, Conus anabathrum, araneosus, kintoki, and sanguinolentus exhibited better precision scores using XGB. Nevertheless, the high proportions of TP predictions among actual positive instances underscored the effectiveness of the RF model. The presence of a high recall value (a measure of model quantity) further bolstered the model’s accuracy, with 24 species considered FN. Conus lividus exhibited a score of 0.8227. These 24 species were ammiralis, anabathrum, australis, bandanus, californicus, coronatus, dalli, episcopatus, fulmen, gloriamaris, imperialis, litteratus, loroisii, lynceus, marmoreus, miliaris, milneedwardsi, natalis, obscurus, parius, rattus, striolatus, sulcatus, zeylanicus. Out of these, 7 species were members of group 1, 11 were in group2, and 6 species were part of group 3. The recall scores for the XGB model ranged from 0.80–0.98 (Fig 5). The harmonic mean of precision and recall, known as the F1 score, ranged from 0.76 to 1 for the RF model. It balances precision and recall, serving as a single metric for evaluating model performance. The number of actual occurrences of each class in the dataset was captured by the support value. We focused on the RF model for further validation and evaluation results.

F1 score and support analysis

The F1 score (harmonic mean) ranged from 0.76 to 1 for the RF model, revealing a balanced performance between recall and precision. The class distribution was analyzed by examining the support, reflecting actual class occurrences. The F1 score and support plots demonstrated model performance across several classes. The model accurately predicted multiple classes with high F1 scores. Conus sanguinolentus was observed in the range of 0.82 to 0.83, while other species fell within the ranges of 0.85–0.88, 0.88–0.91, 0.91–0.94, 0.94–0.97, and 0.97–0.99, with counts of 6, 9, 17, 34, and 43 species, respectively. Eight species exhibited maximum scores, including Conus bandanus, californicus, episcopatus, and fulmen from group 1 (Fig 6A), while miliaris, obscurus, striolatus, and sulcatus belonged to group 2 (Fig 6B). Some classes with low F1 scores were also observed, such as Conus consors with a score of 0.76, indicating slightly poor prediction. Overall, these findings provided evidence that the model operated effectively with significant F1 score values.

Fig 6. F1 score analysis.

The line graphs indicate the performance scores for each class in the dataset. A) Group 1 contains 59 species (X-axis) against performance scores (Y-axis). B) Group 2 comprises 60 species (X-axis) with their respective F1 scores (Y-axis). The blue color indicates the F1-score values, showcasing the model’s accurate predictions for multiple classes with high F1 scores.

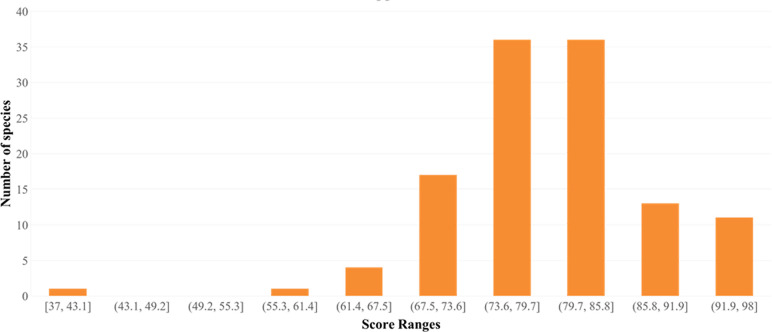
To comprehend class distribution, a support analysis was performed. The histogram indicated varying class numbers in terms of their distribution. Conus sulcatus exhibited a score in the range of 37 to 43. One, four, and seventeen species were noticed in the ranges of 55.3–61.4, 61.4–67.5, and 67.5–73.6, respectively. The number of species significantly increased to 72 for the range of 73.6–85.8. Finally, 13 and 11 species were observed with the highest range values of 85.8–91.9 and 91.9–98, respectively (Fig 7). Classes with high support values were well represented in the dataset, whereas those with low values were less common.

Fig 7. Support value histogram plot.

It indicates the variation in species distribution patterns against score ranges obtained through the model classification report.

Confusion matrix

A confusion matrix revealed the instances where the RF model accurately predicted a positive class. The FPR is represented by a negative value. Confusion matrix analysis revealed 24 species with TPR values of 1, indicating accurate predictions. These species included Conus ammiralis, anabathrum, australis, bandanus, californicus, coronatus, dalli, episcopatus, fulmen, gloriamaris, imperialis, litteratus, loroisii, lynceus, marmoreus, miliaris, milneedwardsi, natalis, obscurus, parius, rattus, striolatus, sulcatus, and zeylanicus. The lowest TPR values were 0.8227 and 0.8292 for Conus tessulatus and Conus lividus, respectively. For FNR, values should be close to zero, indicating instances where the model incorrectly predicts a negative class as positive, while TNR denotes the correct prediction of the negative class. FNR values for all 24 species were zero. In contrast, Conus lividus and Conus tessulatus exhibited the highest FNR values of 0.177 and 0.171, respectively.

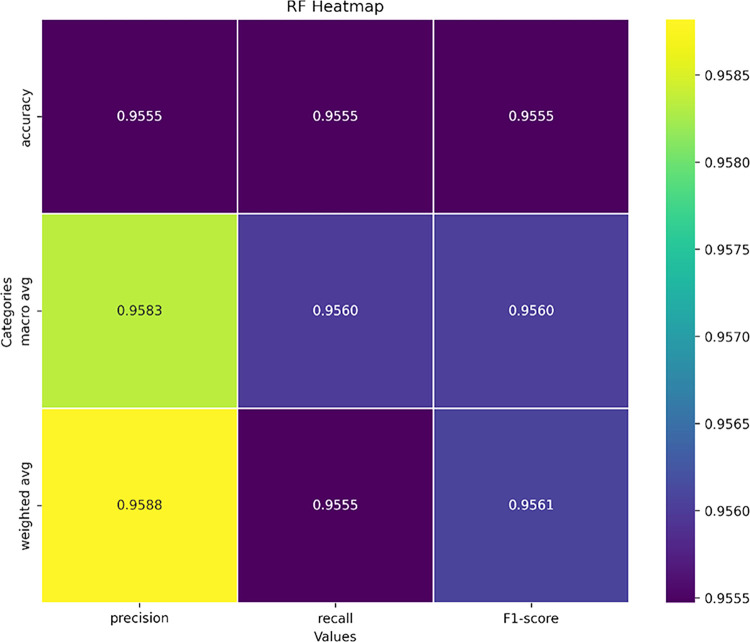
A deeper insight into the model’s performance was obtained using a heatmap. Fig 8 represents the macro average, average, and weighted average of recall, precision, and F1 scores based on the values obtained from the model. Due to the narrow range (0.955–0.958), color differences were minimal. Darker hues (purple) indicated somewhat lower values (0.955) for accuracy in F1 score, recall, precision, and weighted average of recall. In contrast, lighter hues indicated slightly higher values. These findings suggest that all metrics and classes contributed to consistent model performance. The highest weighted precision average was 0.958, indicating improved performance.

Fig 8. Heatmap of different categories against the precision, recall, and F1-score.

Categories include accuracy, macro-average, and weighted average. The color variations from darker to lighter indicate differences in their values.

Model performance evaluation

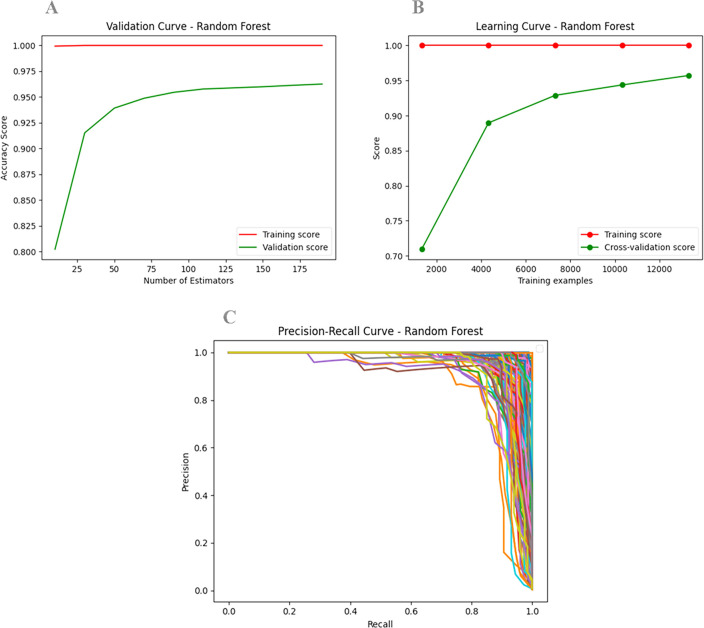
To evaluate model performance, both training and validation scores were plotted (Fig 9A and 9B). The validation curve showed a high training score across the range of hyperparameters, suggesting that the model fit the training data very well. The validation score curve indicated that the model generalized well to unseen data for these hyperparameter values. Both training and validation scores were high and closely aligned, reflecting a good balance between bias and variance. This indicates that the model is well-performing and appropriately tuned, with strong generalization capabilities (Fig 9A).

Fig 9. Model performance analysis.

A) The validation curve plots hyperparameter values (X-axis) against model performance metrics (accuracy score on the Y-axis). The training score (red) and validation score (green) curves represent performance on the training and validation datasets as a function of the hyperparameter values. B) The learning curve illustrates training examples versus accuracy, with the X-axis showing training examples and the Y-axis representing accuracy. A small gap between training and validation scores indicates that the model’s complexity is appropriate for the data, avoiding overfitting and ensuring good performance on both sets. C) The precision-recall curve plots precision (Y-axis) against recall (X-axis) for various thresholds. Curves that localize closer to the top-right corner indicate better model performance.

In the learning curve, a training score close to 1 (or 100%) revealed that the model learned and fitted the training data effectively. The validation score stabilized at approximately 95%, indicating good generalization performance for new data. The small gap between training and validation scores suggests that the model’s complexity is appropriate for the given data, achieving a favorable balance between variance and bias (Fig 9B). The model is neither significantly overfitted, as it performs well on both training and validation datasets, nor underfitted (as both training and validation scores are low), making it a “Good Fit” model.

Next, we plotted a Precision-Recall (PR) curve, which shows precision against recall for different thresholds. A curve closer to the top-right corner indicates better model performance. The area under the PR curve serves as a single metric to assess overall performance (Fig 9C). Thus, the current model demonstrates favorable precision and recall values, indicating its accurate prediction ability.

Discussion

Identifying Conus species presents significant challenges due to the similarities in shell patterns among various mollusks. The classification of cone snail taxonomic features requires considerable effort because of variations in size, distinct color patterns, and geographical distributions. Here, we propose an automated strategy to identify cone snail species using a cohesive machine learning (ML) algorithm framework based on feature-assisted training of the Conus shell imaging dataset. Our proposed ML model achieved an accuracy of 95% with an 80:20 train-test data ratio, utilizing 38,080 and 9,520 cone snail shell images, respectively.

To ensure clear feature delineation and consistency, we implemented a preprocessing scheme that included grayscale conversion [56], binary image generation [57], image quality enhancement, and Canny edge detection [35, 58]. Edge detection is a crucial preprocessing step that enhances the visibility of key features for accurate identification [59]. This process refines image comparison and improves feature visibility by employing methods used in image recognition. Here, edge detection supports object segmentation and RF-based recognition, thereby strengthening overall performance [60]. Further preprocessing steps included background removal [61], quality checks, image transformation [62, 63], and feature extraction using Haralick features [41], deep features [42], color moments, and local binary patterns [39], which collectively enhanced the training dataset’s quality.

In this study, we utilized a conventional Local Binary Pattern (LBP) approach combined with additional features, significantly improving the recognition rate compared to LBP variants such as LBP Variance (LBPV) and Center Symmetric LBP (CS-LBP). The integration of these additional features addressed the limitations of conventional LBP and its derivatives. Faudzi and Yahya evaluated four LBP derivatives—conventional LBP, LBP Variance (LBPV), Center Symmetric LBP (CS-LBP), and Completed-LBP (CLBP)—under varying environmental conditions [39]. Their findings suggested that LBPV had a higher recognition rate, while CS-LBP excelled under contrast changes, highlighting that applying conventional LBP with additional features can yield better results.

Next, we employed a genetic algorithm for feature selection. Soltanian-Zadeh et al. utilized a comprehensive methodology to extract features from mammographic images using four distinct methods: shape features, Haralick features, wavelet features, and multi-wavelet features [41]. Our approach mirrored this strategy by leveraging a deep learning model (VGG16) for feature extraction, enabling automated learning of complex shell patterns [64]. Deep learning, particularly through convolutional neural networks like VGG16, facilitates hierarchical feature extraction from image objects [65–67]. For cone snail shell images, which exhibit subtle morphological differences [68], deep learning effectively captures fine details such as shell patterns and color gradients. Jaderberg et al. reported that deep learning techniques significantly enhance recognition accuracy for complex image targets [69]. In this study, we integrated Haralick features with additional features derived from the deep learning model, resulting in a robust and informative feature set that improved accuracy.

The model’s efficiency was cross-validated by including data from unrelated species, ensuring that features from other species differed significantly from those of Conus. The species support histogram (to assess the distribution of different species number ranges) demonstrated multiple species with high support values, positively contributing to model efficiency. Additionally, we generated a heatmap to depict the macro average, accuracy, weighted average for recall, precision, and F1 score, revealing the highest weighted precision average of 0.958, indicating improved performance. We observed minimal fluctuations in F1-score values across different species, with a value of 0.76 for Conus consors. The Structural Similarity Index Metric (SSIM) results ranged from 0.33 to 0.99, indicating varying levels of structural similarity among individual images. As reported by Zhou et al., SSIM can effectively assess structural similarity and serves as a reliable evaluation tool for image quality assessment [70]. These findings suggest that our proposed model recognized multiple species as positive instances, making it more reliable and scalable than manual feature extraction, particularly for handling large datasets (Fig 10).

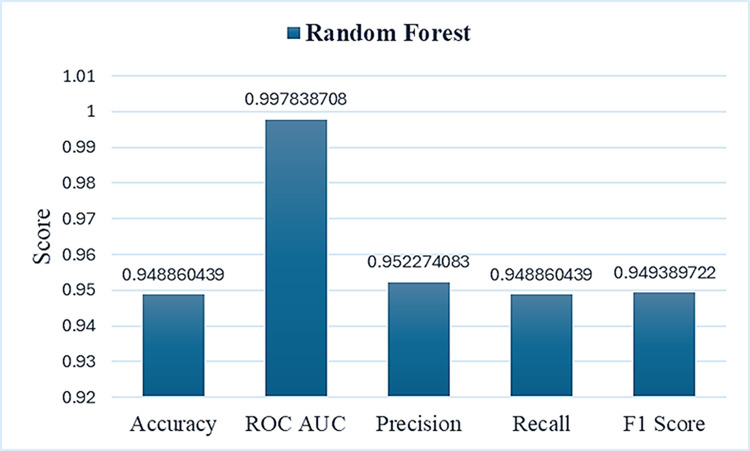
Fig 10. The overall model metric analysis.

The blue bars represent the average accuracy rates of the model, displaying metrics such as recall, precision, F1 score, and ROC AUC value.

Among various classification models, the RF model demonstrated reliable results [44, 71], validating Conus species recognition. The RF approach incorporates random feature selection and serves as an effective tool for high-dimensional complex datasets, ensuring robust classification results [72, 73]. The effectiveness of the RF approach has been proven in various applications, including pattern recognition and species identification [74]. The novelty of our approach lies in integrating deep learning-based feature extraction with a supervised learning RF model. Deep learning captures nuanced details through the image dataset [75], while supervised learning optimizes classification accuracy [76], creating a robust and automated system capable of efficiently handling species recognition tasks.

A thorough analysis of learning and validation curves can inform model selection and parameter tuning. Goriya et al. focused on applying fine-tuned ResNet and DenseNet models for classifying choroidal neovascularization (CNV) from optical coherence tomography (OCT) images, demonstrating promising results with high accuracy and validation scores [77]. In our study, the DenseNet model achieved a validation accuracy of approximately 0.95, with both training and validation curves exhibiting similar trends. Specifically, our training accuracy reached 99%, while the validation accuracy gradually increased to 95% (Table 2). These values indicate a well-trained model that generalizes effectively to validation data without significant overfitting. This observation suggests that our model, similar to DenseNet, effectively captures the underlying patterns of cone snail shell images through accurate classification. The gradual improvement of the validation score curve is crucial for ensuring model reliability and minimizing the risk of overfitting [77]. The training accuracy of our proposed model resembles the learning curve reported for the RF model by Afuwape et al., which exhibited similar performance metrics [78]. Such similarities in learning curves reinforce the robustness of the RF algorithm in handling classification tasks.

Table 2. The statistical report for RF model evaluation.

	Precision	Recall	F1-Score	Support	TPR	FPR	FNR	TNR
mean	0.9583	0.9560	0.9560	79.6386	0.9560	0.0439	0.00011	0.9998
std	0.0572	0.0411	0.0405	8.5645	0.0410	0.0411	0.00015	0.00015
min	0.6346	0.8228	0.7674	37	0.8227	0	0	0.9991
25%	0.9426	0.9289	0.9341	74	0.9289	0.0117	0	0.9998
50%	0.9762	0.9714	0.9664	80	0.9714	0.0285	0.00007	0.9999
75%	1	0.9882	0.9864	84.5	0.9882	0.0710	0.00017	1
max	1	1	1	98	1	0.1772	0.00088	1

Conclusion

Overall, machine learning approaches, particularly the Random Forest model, are instrumental in the categorization of cone snail species and in distinguishing them from other marine invertebrates. The proposed RF model, tested on diverse datasets encompassing both cone snail and other mollusk shells, demonstrates its capability in effective pattern matching and decision-based ranking. This model could also be adapted to detect and classify various other mollusk species, showcasing its versatility and potential for broader applications in marine biology.

Supporting information

S1 Fig. Species distribution on the basis of RGB intensities.

Average predicted values were 70.23 for R, 88.12 for average G, and 107.98 for B. A) First 59 species (X-axis) with their respective RGB values (Y-axis). B) Last 60 species (X-axis) with their respective RGB values (Y-axis).

(TIF)

S1 Table. Specie prediction results.

Highlighted five rows indicate wrong predictions.

(DOCX)

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

This work has been supported by Higher Education Commission, Pakistan via grant No. 20-15051/NRPU/R&D/HEC/2021. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.