Balancing efficacy and computational burden: weighted mean, multiple imputation, and inverse probability weighting methods for item non-response in reliable scales

Abstract

Importance

Scales often arise from multi-item questionnaires, yet commonly face item non-response. Traditional solutions use weighted mean (WMean) from available responses, but potentially overlook missing data intricacies. Advanced methods like multiple imputation (MI) address broader missing data, but demand increased computational resources. Researchers frequently use survey data in the All of Us Research Program (All of Us), and it is imperative to determine if the increased computational burden of employing MI to handle non-response is justifiable.

Objectives

Using the 5-item Physical Activity Neighborhood Environment Scale (PANES) in All of Us, this study assessed the tradeoff between efficacy and computational demands of WMean, MI, and inverse probability weighting (IPW) when dealing with item non-response.

Materials and Methods

Synthetic missingness, allowing 1 or more item non-response, was introduced into PANES across 3 missing mechanisms and various missing percentages (10%-50%). Each scenario compared WMean of complete questions, MI, and IPW on bias, variability, coverage probability, and computation time.

Results

All methods showed minimal biases (all <5.5%) for good internal consistency, with WMean suffered most with poor consistency. IPW showed considerable variability with increasing missing percentage. MI required significantly more computational resources, taking >8000 and >100 times longer than WMean and IPW in full data analysis, respectively.

Discussion and Conclusion

The marginal performance advantages of MI for item non-response in highly reliable scales do not warrant its escalated cloud computational burden in All of Us, particularly when coupled with computationally demanding post-imputation analyses. Researchers using survey scales with low missingness could utilize WMean to reduce computing burden.

Introduction

Within survey data, scales of related questions arise from multi-item questionnaires, but can be hindered by the presence of item non-response. This results in missing data, which must be handled by the researcher utilizing survey data. One traditional solution is the weighted mean (WMean), which is equivalent to single imputation with the missing value imputed by the average of available responses from the same subject. While this is a straightforward solution, the drawback is that it can overlook missing data intricacies, which can also yield biased results, especially when data are missing not at random (MNAR) or missing at random (MAR) depending on other covariates.¹ A more advanced technique, multiple imputation (MI), is often recommended as a less biased and more efficient method for missing data handling.² While this technique can address broader missingness with an enhanced performance, it demands much greater computational intensity.³ Inverse probability weighting (IPW) is another important advanced technique to address the missing data problem; however, it often exhibits larger variability.⁴

This issue of missing data handling arises during the evaluation of highly reliable scales which have been impacted by non-response. This can greatly impact research studies such that the generalizability of the results is reduced, the results can be biased, and statistical power is greatly diminished.^5–7 Not properly adjusting for missing data can bias studies involving groups historically underrepresented in biomedical research, as missingness patterns may be influenced by certain demographic and socioeconomic factors.⁸ Additionally, depending on the reason behind item missingness, and whether the cause is related to the outcome of interest, research using survey data can overestimate or underestimate the association between survey responses and outcomes of interest.⁶ As a result, failing to handle missing data can reduce the impact of research and create challenges for researchers using survey data with missingness.

MI is a proven technique which very often produces estimates with lower bias than more straightforward missing data handling, like the WMean approach.⁹ However, this method does not always yield estimates which are superior to WMean, and at times a more computationally efficient method can yield sufficient estimates, especially when missingness is completely at random.^10,11 Conversely, more advanced imputation techniques require a greater strain on computing resources. As such, the increased computation time may not be worth the tradeoff of decreased estimation bias, especially if there are other methods which may require fewer resources and are still able to produce estimates with minimal bias.

IPW, on the other hand, is computationally efficient and straightforward to further address survey non-response, another common issue in survey research where participants fail to provide any information. Despite its advantages, IPW can become unstable when the estimated probability of missingness approaches 1.⁴ This instability arises because extremely high weights can lead to increased variability in estimates, potentially affecting the reliability of statistical analyses.

The All of Us Research Program (All of Us) is a longitudinal cohort study which collects information such as health surveys, electronic health records, and biological data and makes those data available for research via a cloud-based analysis environment.^12,13 Health survey content is created through selection of existing items from other well-established and fielded instruments and include a mixture of item types including categorical and open-ended questions as well as Likert and dichotomous scales.¹⁴ The All of Us Social Determinants of Health (SDOH) survey, for example, is made up almost entirely of well-established scale measures including the measure discussed in this article.¹⁵ These survey scales naturally have missing data, but handling them requires computational power and resources within the All of Us cloud environment. In expansive biorepositories such as All of Us, increased computational demand may not be advisable, particularly for tasks involving intensive post-imputation analysis.¹²

Our research seeks to compare the performance and resource intensity of WMean, MI, and IPW methods. Using the 5-item Physical Activity Neighborhood Environment Scale (PANES) included within SDOH survey, the primary objective of this study is to compare the tradeoff between the increased efficacy with the corresponding increased computational demand to assess whether the advanced techniques should be recommended for item non-response within survey questionnaires in All of Us.¹⁶ We selected PANES in this study since it had by far the greatest amount of non-response out of all survey scales in which scores were assigned. PANES also has ties to public health, and increasing researchers’ ability to use these survey results through more complete data can better inform public health initiatives.¹⁷ This article is meant to inform researchers on considerations for handling incomplete data in participant surveys, utilize the data received as efficiently and accurately as possible, and better understand how to use surveys with missingness to conduct accurate research.

Methods

Data used

Data from version 7 (April 2023) of the All of Us Controlled Tier curated data repository (CDR) were used for the study and analysis was conducted on the All of Us Researcher Workbench platform.^12,18 Based on the participant responses to the questions, each Likert-type question response was assigned a score from 1 to 4, where higher scores corresponded with greater neighborhood accessibility. The questions, responses, and corresponding scores are in Table 1. The final score for each participant was the average of all 5 item scores. Our initial cohort size of 117 183 participants included everyone who participated in the SDOH survey. When constrained to only those who responded to all 5 PANES questions, the cohort yielded a total of 77 350 participants, a decrease of 34.3% (Figure S1).

Table 1.

A list of items comprising the physical activity neighborhood environment scale (PANES), and the way the responses to these questions are scored.

Question
Q1: My neighborhood has several free or low-cost recreation facilities
Q2: There are facilities to bicycle in or near my neighborhood
Q3: Many shops, stores, markets, or other places to buy things I need are within easy walking distance of my home
Q4: There are sidewalks on most of the streets in my neighborhood
Q5: It is within a 10-15 minute walk to a transit stop
Scoring system
Strongly disagree	1
Disagree	2
Agree	3
Strongly agree	4

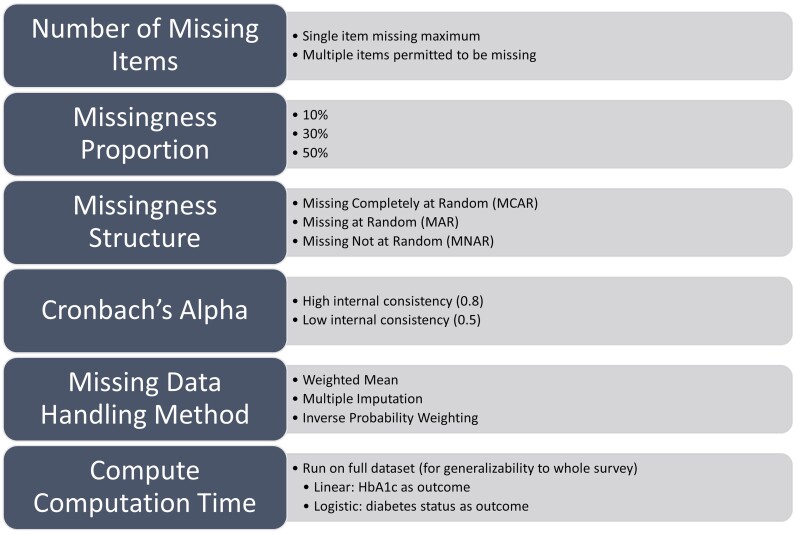
Missing data handling methods

Within our study, 3 separate methods of handling missing data were considered. These were: (1) WMean, where the average of the non-missing items were used as the final score; (2) MI, where chained equations using 10 imputations were used to fill in the missing items; and (3) IPW, which involves weighting each participant with a complete response to each item by the inverse of its estimated probability of being observed. The probability was estimated from a logistic regression model with outcome being the missing indicator and covariates including the demographic variables. Unlike WMean and MI, IPW does not inherently impute the missing values but rather adjusts the weights of the complete data. For MI, in addition to the remaining complete items and the outcome variable, we used the following demographic variables from the Basics survey to impute the missing scores: sex at birth, annual income, highest education level achieved, and age at survey completion. These demographic variables were also used in IPW. For each missing data handling type, we conducted 1000 simulations using a variety of missingness proportions, missingness mechanisms, and regression types to evaluate the performance of the 3 methods (Figure 1).

Figure 1.

An outline of the choices made during the simulation process. The steps included: selecting the missingness proportion, maximum number of missing items per person, the underlying missingness mechanism, the internal consistency, and the method to handle the missing data.

Number of missing items

For each imputation method, we considered 2 different question missingness scenarios. The first was single-question missingness, where each participant was only permitted to have one item response missing. In the second, multiple questions could be missing per participant. Under both circumstances, each question had approximately the same amount of incomplete responses overall.

Missingness proportions

Since the performance of missing data handling can depend on the overall proportion of missing responses, we used 3 separate missingness proportions to assess the performance and computation time for the methods: 10%, 30%, and 50% missingness. In the full PANES score, approximately 34% of the responses are missing, but we also considered higher and lower missingness to allow for our findings to apply to datasets outside the All of Us, which may have differing degrees of missingness. Additionally, missingness in the SDOH scales ranged from 5% to 34%, so these 3 missingness scenarios allow us to capture degrees of missingness which exist within the All of Us surveys. Table 2 displays the distribution of the number of missing questions for scenarios where individuals could have multiple items missing. Each distribution was chosen so that the overall missingness proportion was as close to the target as possible, and marginal probabilities of having an incomplete response were used to reach this target.

Table 2.

Question missingness breakdown for the scenarios with multiple synthetic question missingness.

Missingness proportion (%)	Questions missing	MCAR	MCAR	MAR	MAR	MNAR	MNAR
		Alpha 0.8 (%)	Alpha 0.5 (%)	Alpha 0.8 (%)	Alpha 0.5 (%)	Alpha 0.8 (%)	Alpha 0.5 (%)
10	0	90.4	90.4	89.1	89.0	89.1	91.8
	1	9.2	9.2	10.1	10.2	9.5	7.5
	2	0.4	0.4	0.7	0.8	1.2	0.6
	3	<0.1	<0.1	<0.1	<0.1	0.1	<0.1
	4	0	0	<0.1	<0.1	<0.1	<0.1
	5	0	0	0	0	0	0
	Tot. Miss. P.	9.6	9.6	10.9	11.0	10.9	8.2
30	0	65.9	65.9	66.4	66.1	70.8	74.8
	1	28.6	28.6	26.0	26.2	21.2	19.3
	2	5.0	5.0	6.3	6.6	6.5	4.7
	3	0.4	0.4	1.1	1.2	1.0	1.0
	4	<0.1	<0.1	<0.1	0.2	0.6	0.2
	5	0	0	<0.1	<0.1	0	<0.1
	Tot. Miss. P	34.1	34.1	33.6	33.9	29.2	25.2
50	0	48.7	48.7	52.3	50.9	50.3	53.7
	1	37.6	37.6	31.6	32.1	25.4	27.3
	2	11.7	11.7	11.9	12.6	13.8	12.4
	3	1.8	1.8	3.4	3.6	7.0	5.0
	4	0.1	0.1	0.7	0.7	2.9	1.6
	5	<0.1	<0.1	<0.1	0.1	0.6	0.3
	Tot. Miss. P	51.3	51.3	47.7	49.1	49.7	46.6

Abbreviations: MAR, missing at random; MCAR, missing completely at random; MNAR, missing not at random; Tot. Miss. P, total missing percentage. 

Missingness mechanism

To test the impact of the imputation techniques, we induced missingness using 3 underlying missingness mechanisms. The first, missing completely at random (MCAR) assigned missingness to a select group of participants at random. After selecting the proportion of participants to have missing items, each participant was randomly assigned a value from 1 to 5, corresponding to the question to be set to missing. The next scenario, MAR used a binary logistic regression to assign the probability of missingness for an item to depend on demographic information, but not the other questions. Finally, the MNAR scenario allowed item missingness probability to depend on both demographic information and the average score of all items before missingness was introduced. In both the MAR and MNAR settings, the coefficients for missingness probability were set so that the overall missingness probability matched the amount that was set for that scenario (10%, 30%, or 50%). We selected missingness to be at the item-level since MI techniques have improved performance at the individual question level for higher proportions of non-response.¹⁹ The MI and IPW methods were used here without tailoring for an MNAR assumption. If evidence of MNAR were present in the study, using MI or IPW methods tailored for MNAR would likely lead to better performance.

Internal consistency

The internal consistency of the scale, measured by Cronbach’s Alpha, is a measure of the agreement between the individual items of the scale, with higher values corresponding to greater agreement and lower values to less agreement. For this study, we considered 2 different internal consistency measures. First, we used the original PANES scale’s Cronbach’s Alpha, which was approximately 0.8. To test the impact of lower item agreement on the results of the missing data handling methods, we introduced noise to the PANES scale by randomly selecting 37% of the data to be rescored at random, which led to a noised-PANES scale with poor internal consistency of roughly 0.5.

Regressions to evaluate methods

To evaluate and compare the performance of the missing data handling methods, we used regressions to determine the bias and standard errors. We created synthetic outcomes based on the combination of the demographic variables and the average PANES score prior to missingness being introduced to establish a true regression coefficient. Two synthetic outcomes were created using (1) a linear regression with an error term generated from normal distribution with mean 0 and standard deviation 2.5 to simulate a continuous outcome, and (2) a logistic regression with a binary outcome. We used 2 regression types to see if missing data methods would perform differently when evaluated using a continuous or a binary outcome. To test the missing data techniques, missingness was induced into the data, and the 3 methods were applied. We evaluated the statistical performance of each method in estimating the regression coefficient for the average score. These outcomes were included as covariates in the imputation model for missing scale items. In addition, we compared the computation time for each method. To maintain reasonable computational burden while meeting the research goal, 500 participants were randomly selected from the study cohort in each simulation.

Computational time

Finally, a major objective was to determine the total computing time required to run WMean, MI, and IPW methods, since higher runtimes may not offset the improvement in statistical performance. To provide a comprehensive analysis, we recorded the computing time for each simulated scenario and reported the ratio of mean computing times.

Furthermore, we also reported the computing time required for the full All of Us data using commonly used regression models. We included all 117 183 participants who participated in the SDOH survey and may have missing responses in some items. We extracted hemoglobin A1C (HbA1c) as the continuous outcome to illustrate the linear regression model and diabetes status for the logistic regression model. This analysis was used to maintain the missingness structure and provided the scale of the computational time for WMean, MI, and IPW for full data analysis.

A total of 72 different scenarios were considered for combinations of missingness proportion, regression type, internal consistency, missingness mechanism, and number of missing questions a person could have (single versus multiple). For each scenario, we presented the bias for estimated regression coefficients, empirical standard error, average standard error, coverage probability for 95% confidence interval, and ratio of computing time of MI and IPW to WMean. To normalize the scale of bias, we also reported percent bias, which is bias/(true value)*100%. The acceptable level of bias depends on the research question and appropriate sample size. For our simulation studies, we considered an acceptable percent bias of 6%, which corresponded to absolute bias of 0.03 in the simulation studies, based on prior literature.²⁰

The internal consistency of the scale questions was determined by Cronbach’s Alpha. The coefficient of determinations, denoted as R², were reported for the full and reduced models for each item in PANES. The reduced model is a linear regression model with individual item score as the response variable and the scores of the remaining individual items as the independent variables. The full model adds demographic variables included in the independent variables. The difference in R² measured the additional variability of outcome explained by the demographic variables. All analysis was conducted in R version 4.3.1.

This study is considered non-human subjects research according to the All of Us Research Program’s IRB.

Results

The PANES scale exhibited acceptable internal consistency with a Cronbach’s Alpha of 0.788,²¹ which indicates acceptable agreement between the scale questions.²² Comparing the full and reduced models for each item in the PANES scale, the average R² gains to include additional covariates in the full model is minimum (∼0.5%).

Single-question missingness

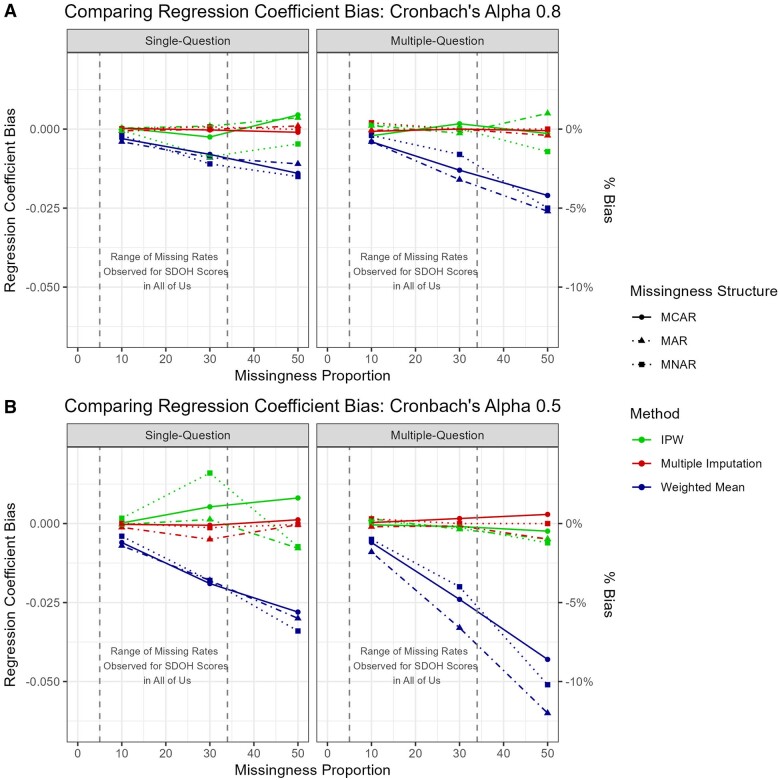
The simulation results for linear regression with at most one question subject to missingness are in Table 3 and Figure 2. For the original Cronbach’s alpha of 0.8, all methods yielded minimal bias for the regression coefficient of the total score. While the bias is always lower for the MI and IPW methods, the difference from WMean never exceeds 0.02 (true value is 0.5 in all scenarios) for any scenario, with the absolute biases among the MI typically around 0.001, and no more than 0.01 for IPW, while WMean could be 0.002-0.015. The bias increased with lower Cronbach’s alpha of ∼0.5 for all methods, however, WMean suffered most with nearly doubled bias ranging from 0.004 to 0.034. Similarly, the bias increased as the proportion of item non-response increased, but the bias increased fastest within the WMean and most gradually for MI.

Table 3.

Results from the simulation run with single-question synthetic missingness.

Missing percent (%)	Missing structure	Cronbach’s alpha: 0.8				Cronbach’s alpha: 0.5				Time ratio to WMean (Alpha 0.8)	Time ratio to WMean (Alpha 0.5)
		Bias	ESE	ASE	CP (%)	Bias	ESE	ASE	CP (%)
WMean
10	MCAR	−0.003	0.128	0.134	94.7	−0.006	0.166	0.165	95.1	1.00	1.00
	MAR	−0.004	0.130	0.132	95.7	−0.007	0.163	0.165	95.5	1.00	1.00
	MNAR	−0.002	0.139	0.132	94.5	−0.004	0.162	0.166	95.7	1.00	1.00
30	MCAR	−0.008	0.126	0.128	94.8	−0.019	0.164	0.164	95.3	1.00	1.00
	MAR	−0.009	0.131	0.136	96.1	−0.018	0.159	0.163	95.3	1.00	1.00
	MNAR	−0.011	0.130	0.131	95.4	−0.018	0.170	0.163	93.6	1.00	1.00
50	MCAR	−0.014	0.122	0.128	96.1	−0.028	0.162	0.162	93.6	1.00	1.00
	MAR	−0.011	0.124	0.128	96.0	−0.030	0.163	0.162	93.6	1.00	1.00
	MNAR	−0.015	0.131	0.128	94.0	−0.034	0.160	0.161	94.1	1.00	1.00
MI
10	MCAR	0.000	0.129	0.135	94.8	−0.000	0.168	0.167	94.9	696	902
	MAR	−0.001	0.131	0.133	95.8	−0.001	0.165	0.167	95.1	525	947
	MNAR	0.000	0.140	0.133	94.4	0.000	0.163	0.167	95.8	543	973
30	MCAR	0.000	0.128	0.130	95.7	−0.001	0.170	0.170	95.3	674	901
	MAR	−0.000	0.134	0.140	95.7	−0.005	0.162	0.171	96.5	839	1133
	MNAR	0.000	0.132	0.133	95.5	−0.001	0.172	0.168	93.6	884	1156
50	MCAR	−0.001	0.125	0.131	96.3	0.001	0.172	0.172	94.5	659	1183
	MAR	0.001	0.127	0.131	95.7	−0.000	0.172	0.172	94.6	708	1225
	MNAR	−0.000	0.133	0.130	94.3	−0.000	0.165	0.166	95.3	704	1261
IPW
10	MCAR	0.000	0.138	0.139	95.1	0.000	0.176	0.173	94.5	1.50	2.72
	MAR	0.000	0.141	0.140	94.8	−0.000	0.174	0.174	94.8	1.51	2.72
	MNAR	−0.000	0.152	0.153	94.5	0.002	0.190	0.184	93.9	1.50	3.08
30	MCAR	−0.003	0.160	0.158	94.8	0.005	0.202	0.196	94.4	1.27	2.18
	MAR	0.001	0.171	0.160	93.8	0.001	0.205	0.199	94.7	1.31	2.46
	MNAR	−0.009	0.213	0.208	94.7	0.016	0.249	0.242	93.8	1.29	2.51
50	MCAR	0.005	0.198	0.188	94.3	0.008	0.238	0.233	94.7	1.14	2.11
	MAR	0.004	0.199	0.194	93.6	−0.008	0.252	0.242	93.5	1.22	2.26
	MNAR	−0.005	0.319	0.297	92.8	−0.007	0.357	0.336	93.5	1.22	2.27

Abbreviations: ASE, average standard error; CP, coverage probability for 95% confidence interval; ESE, empirical standard error; and Time Ratio to WMean, ratio of computing time between the method used and WMean; MCAR, missing completely at random; MAR, missing at random; MNAR, missing not at random; WMean, weighted mean; MI, multiple imputations; IPW, inverse probability weighting.

Figure 2.

The bias in the regression coefficient for the total survey score for the linear regression model (A) high internal consistency (Cronbach’s Alpha of 0.8) and (B) low internal consistency (Cronbach’s Alpha of 0.5). MI, WMean, and IPW methods are compared across missingness mechanisms and number of questions missing as the proportion of item non-response increases.

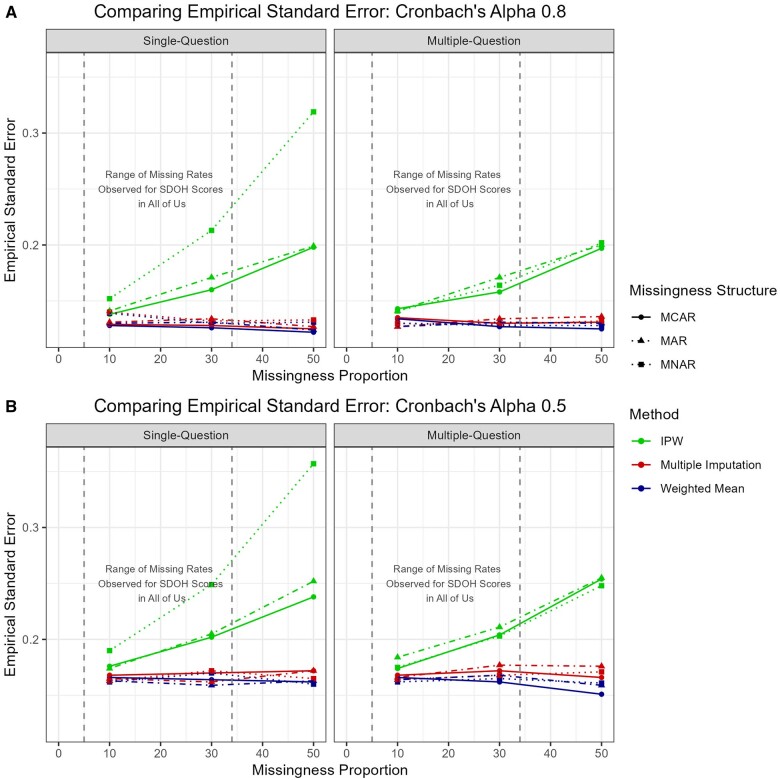
For MI and WMean, empirical and average standard errors were consistently low (0.10-0.15 for alpha 0.8, 0.15-0.18 for alpha 0.5) across all missingness mechanisms and proportions, remaining close to each other. Those associated with MI were slightly higher due to the incorporation of additional imputation variability into the estimates. The standard errors were considerably larger in the IPW method (0.14-0.32 for alpha 0.8 and 0.17-0.36 for alpha 0.5) with increasing variability for higher missing percentage and MNAR (see Table 3 and Figure 3).

Figure 3.

Empirical standard errors for the coefficient estimates for the linear regression model (A) high internal consistency and (B) low internal consistency.

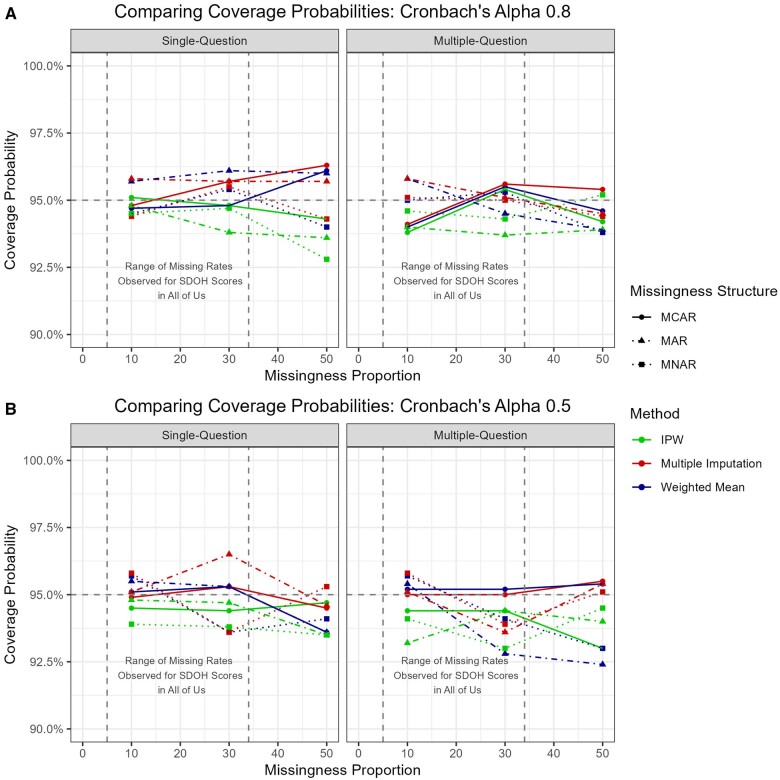
Coverage probabilities for the 95% confidence interval ranged from 92.8% to 96.5% and remained around the target level (ie, 95%) for all scenarios and methods (see Table 3 and Figure 4).

Figure 4.

Coverage probabilities for the linear regression model (A) high internal consistency and (B) low internal consistency. Based on the values seen, we can be confident in the validity of our imputed regression coefficients.

Multiple-question missingness

Table 4 and Figure 2 show the simulation results for linear regression model in the scenarios where participants were permitted to have multiple missing responses. In the original scale, the results are similar to those for single-question missingness, where bias is lowest for MI results, but all biases are negligible. However, the differences between the methods are more pronounced when multiple responses could be missing, especially for higher proportions of missing responses. For 50% missingness, the bias in the WMean could be as high as 5.5%. In contrast, the bias from MI yields at most 2% bias for any scenario. Bias for IPW was slightly higher with mostly within 0.01. In all situations, the biases were within the acceptable range.

Table 4.

Results from the simulation run with multiple-question synthetic missingness.

Missing percent (%)	Missing structure	Cronbach’s alpha: 0.8				Cronbach’s alpha: 0.5				Time ratio to WMean (Alpha 0.8)	Time ratio to WMean (Alpha 0.5)
		Bias	ESE	ASE	CP (%)	Bias	ESE	ASE	CP (%)
WMean
10	MCAR	−0.004	0.134	0.132	94.0	−0.006	0.166	0.165	95.2	1.00	1.00
	MAR	−0.004	0.127	0.132	95.8	−0.009	0.164	0.165	95.4	1.00	1.00
	MNAR	−0.002	0.130	0.128	95.0	−0.005	0.162	0.166	95.7	1.00	1.00
30	MCAR	−0.013	0.127	0.130	95.5	−0.024	0.162	0.162	95.2	1.00	1.00
	MAR	−0.016	0.131	0.130	94.5	−0.033	0.168	0.161	92.8	1.00	1.00
	MNAR	−0.008	0.128	0.133	95.3	−0.020	0.165	0.163	94.1	1.00	1.00
50	MCAR	−0.021	0.125	0.127	94.6	−0.043	0.151	0.159	95.4	1.00	1.00
	MAR	−0.026	0.130	0.127	93.9	−0.060	0.159	0.157	92.4	1.00	1.00
	MNAR	−0.025	0.128	0.127	93.8	−0.051	0.161	0.158	93.0	1.00	1.00
MI
10	MCAR	−0.001	0.135	0.133	94.1	0.000	0.168	0.167	95.0	513	900
	MAR	−0.000	0.127	0.133	95.8	−0.001	0.166	0.168	95.1	511	909
	MNAR	0.002	0.130	0.129	95.1	0.002	0.164	0.168	95.8	503	932
30	MCAR	0.000	0.130	0.133	95.6	0.002	0.172	0.171	95.0	622	903
	MAR	−0.000	0.134	0.134	95.1	−0.001	0.177	0.171	93.6	646	913
	MNAR	−0.000	0.129	0.134	95.0	0.000	0.168	0.166	93.9	676	938
50	MCAR	−0.000	0.131	0.132	95.4	0.003	0.166	0.174	95.5	664	1185
	MAR	−0.002	0.136	0.133	94.5	−0.005	0.176	0.174	95.4	677	1188
	MNAR	0.000	0.132	0.129	94.4	0.000	0.171	0.166	95.1	669	1212
IPW
10	MCAR	−0.002	0.143	0.139	93.8	−0.000	0.174	0.172	94.4	1.54	2.96
	MAR	0.001	0.141	0.139	94.0	0.002	0.184	0.173	93.2	1.64	2.95
	MNAR	0.001	0.141	0.139	94.6	0.000	0.175	0.172	94.1	1.56	2.98
30	MCAR	0.002	0.158	0.163	95.4	−0.000	0.204	0.202	94.4	1.07	2.37
	MAR	−0.001	0.171	0.166	93.7	−0.002	0.211	0.206	94.4	1.11	2.39
	MNAR	0.000	0.164	0.160	94.3	−0.001	0.203	0.196	93.0	1.15	2.28
50	MCAR	−0.001	0.197	0.190	94.2	−0.002	0.254	0.237	93.0	1.20	2.13
	MAR	0.005	0.200	0.195	93.9	−0.005	0.255	0.242	94.0	1.24	2.25
	MNAR	−0.007	0.202	0.200	95.2	−0.006	0.248	0.243	94.5	1.20	2.16

Abbreviations: ASE, average standard error; CP, coverage probability for 95% confidence interval; ESE, empirical standard error; Time ratio WMean, ratio of computing time between the method used and WMean; MCAR, missing completely at random; MAR, missing at random; MNAR,  missing not at random; WMean, weighted mean; MI, multiple imputations; IPW, inverse probability weighting.

The differences in bias among the methods is greater for lower-consistency scales. The bias within WMean is approximately double that of the original scale, exceeding 10% (0.05) for both MAR and MNAR patterns. In contrast, the bias for MI never exceeds 1% (0.005).

Empirical standard error had a similar range as single-question missingness and is slightly lower for WMean than MI, but the difference remains negligible. In contrast, the standard errors continued to be much higher in the IPW results. The coverage probabilities drop slightly for multi-question missingness, but all remain at 92.4% or above (Figure 4).

Binary outcome

The results for binary outcomes were similar to those of linear regression models, with IPW displaying larger bias at higher missing percentages or in MNAR scenarios due to its large variability. Detailed results can be found in the Supplementary materials (Tables S1 and S2, Figures S2-S4).

Computational time

For all scenarios, MI was consistently much more computationally expensive than the WMean or IPW. While the WMean took approximately 0.01 seconds to run 1 iteration on the full data, MI took 1.66 minutes using linear regression and 2.68 minutes using logistic regression, resulting in an over 8000-fold increase in the computational burden. IPW was modestly more expensive than WMean, taking 73 times as long to run, but was 118 times faster than MI. This magnitude of cloud computing resources was consistent across all scenarios.

Discussion

This study assessed the performance of 3 missing data handling techniques on simulations involving multiple different underlying missingness proportions, mechanisms, internal consistencies, and regressions to evaluate the performance. In all scenarios, while MI performed the best when the bias of the regression coefficient estimate was examined, which is consistent with prior research on the topic,² this performance difference was very small in most scenarios, especially those with the higher internal consistency. However, the major tradeoff is that there is a considerable increase in the computational time for the more advanced MI method, requiring over 8000 times the resources of WMean and over 100 times the resources of IPW. This overhead on computational burden will further escalate for larger datasets, additional questions, and/or analytically intensive models.

For databases like All of Us which require the use of cloud computing, running methods on virtual environments comes with associated costs, and while MI is clearly a method with better statistical properties for missing data, the increased computing requirements are significant. In the original scale, the difference in bias between the 2 methods was most pronounced when 50% of the data were missing, but this level of missingness was not observed in the All of Us survey data. In prior literature, differences between the 2 methods’ biases became noticeable at higher levels of missingness and were not pronounced at lower missingness.² The majority of survey scales fielded in the All of Us SDOH survey had 5% or less non-response for associated items. In such a situation, the increased accuracy of more advanced methods is outweighed by the increased demand on cloud computing resources, and results in much higher costs for minimal gains.

Additionally, a large increase in bias was observed when the Cronbach’s Alpha was reduced to 0.5, with bias reaching up to 10% when missingness reached 50%. However, a Cronbach’s Alpha of 0.5 is considered unacceptable for a scale, and no scale within All of Us drops below the 0.8 seen in SDOH. A scoring scale with such a low Cronbach’s Alpha would not be considered valid and would rarely be used in a survey scale for research databases. Thus, while MI’s clear superiority over WMean is highlighted for low internal consistency, it is uncommon in practice.

IPW demonstrated low bias and comparable computation time to WMean. However, this method produces unstable coefficient estimates, evidenced by the high empirical standard error. The estimates become unstable as missingness increased, particularly in MNAR scenarios. While IPW can effectively handle missingness for survey data, the instability of the estimates limits its impact in scenarios where methods are not tailored to mitigate extreme weighting.

For researchers working with survey data in All of Us, while MI methods can slightly improve statistical accuracy, the scales within the SDOH surveys have high internal consistency and do not have significant missingness to warrant the increased resource allocation demanded by MI, and WMean is a sufficient missing data handling technique when computing power must be considered. By utilizing WMean, researchers can efficiently manage missingness in large datasets, saving significant time and reducing computational burden associated with the Workbench platform. This is particularly useful for post-imputation follow-up analyses, such as those involving high-dimensional genetics and Fitbit data or using machine learning and artificial intelligence models. This is because for MI, every imputed dataset must undergo post-imputation analysis, which results in a linear increase in computing resources. Finally, it is recommended that WMean be used only for scales with low missingness and high internal consistency, in which the relative bias and efficiency loss are minimal and researchers can save computational resource handling missing data on large-scale datasets.

Limitations

This study has some limitations to note. We only ran our methods on 1 specific scale using 2 Cronbach’s alphas: the original scale with an acceptably high Cronbach’s alpha, and an altered version with a poor alpha value.²² Since the original alpha value was relatively high and the R² gains with additional covariates in the MI models were small, it meant that the observed items are good predictors for the item(s) with missing value, and thus a WMean could yield a reasonable estimate for the total score with the non-missing items comparing to MI. In a scale with a lower Cronbach’s alpha, the non-missing items would not be as strong of predictors of missing item(s), and larger bias would have been introduced using WMean. It is unclear what alpha threshold would result in an unacceptable WMean bias where MI would be preferred despite its higher computational demands.

In the simulation studies, we used 10 imputations in MI, which resulted in a relative efficiency loss of 1.0% for 10% missingness, 2.9% for 30% missingness, and 4.8% for 50% missingness.²³ Although these efficiency losses are acceptable, employing a greater number of imputations can potentially mitigate such losses, albeit at the expense of increased computational demands and longer imputation times.

Finally, the relative performance of these missing data handling methods depends on the additional predictability of other covariates included in the MI model. Incorporating influential predictors into the MI model has the potential to enhance the performance of MI, as these variables can contribute valuable information for imputation, thereby refining the accuracy and robustness of the imputed data. Consequently, the enhanced performance achieved through MI, despite the associated increase in computational burden, may outweigh concerns for certain research questions, especially those where accuracy and reliability are significant.

Conclusion

Item non-response can hinder research conducted using survey data. Several techniques to handle missing data exist but vary in their accuracy and computational requirements. Compared to the simpler WMean, the advanced MI method for missingness within PANES provided better estimates but with higher computational burden, while IPW provided accurate but unstable estimates. Considering the tradeoff among computing demand, stability, and performance, WMean is likely adequate for scales with low missingness and sufficiently high internal consistency. Therefore, researchers with limited resources can use the computationally efficient WMean method when survey scales have high internal consistency and low levels of missingness. This method allows researchers to conduct faster missingness handling without sacrificing significant prediction accuracy. However, researchers should first examine the internal consistency and missingness before pursuing this simpler approach. Further research is necessary to determine if more straightforward imputation methods are sufficient for scales containing greater missingness, and to what degree the tradeoff of computational intensity merits the usage of more intense missing data handling methods.

This article responds to the Call for Papers to “raise awareness and build researcher competencies in utilizing the All of Us Researcher Workbench.” The workspace for this article will be included in the Researcher Workbench’s featured library collection, which allows us to self-publish our workspaces as viewable and reproducible artifacts for other registered users.

Author contributions

Andrew Guide ran all simulations and drafted the manuscript. Andrew Guide and Shawn Garbett developed the code for the simulations. Qingxia Chen conceptualized the methodology. All the authors contributed to investigation, writing, and revising the manuscript.

Supplemental material

Supplementary material is available at Journal of the American Medical Informatics Association online.

Funding

This work was supported by the National Institutes of Health Office of the Director: Data and Research Center [grant number 3OT2OD035404 to A.G., L.S., S.G., X.F., B.M.M., J.C., L.S., R.M.C., and Q.C.] and the National Institute on Minority Health and Health Disparities [grant number R21MD019103 to A.G., L.S., R.M.C., and Q.C.].

Conflicts of interest

The other authors have no competing interests.

Data availability

Data are available to approved researchers through the All of Us Researcher Workbench. Researchers are granted access to the All of Us Researcher Workbench after their affiliated institution signs a Data Use and Registration Agreement, and they create an account. For additional information about the Workbench, including details regarding registration, please visit ResearchAllofUs.org.