Abstract
In recent years, advances in image processing and machine learning have fueled a paradigm shift in detecting genomic regions under natural selection. Early machine learning techniques employed population-genetic summary statistics as features, which focus on specific genomic patterns expected by adaptive and neutral processes. Though such engineered features are important when training data are limited, the ease at which simulated data can now be generated has led to the recent development of approaches that take in image representations of haplotype alignments and automatically extract important features using convolutional neural networks. Digital image processing methods termed α-molecules are a class of techniques for multiscale representation of objects that can extract a diverse set of features from images. One such α-molecule method, termed wavelet decomposition, lends greater control over high-frequency components of images. Another α-molecule method, termed curvelet decomposition, is an extension of the wavelet concept that considers events occurring along curves within images. We show that application of these α-molecule techniques to extract features from image representations of haplotype alignments yield high true positive rate and accuracy to detect hard and soft selective sweep signatures from genomic data with both linear and nonlinear machine learning classifiers. Moreover, we find that such models are easy to visualize and interpret, with performance rivaling those of contemporary deep learning approaches for detecting sweeps.
Keywords: feature extraction, machine learning, selective sweep, signal processing
Introduction
The rapid increase in computational power over the last decade has fueled the development of sophisticated models for making predictions about diverse evolutionary phenomena (Angermueller et al. 2016; Schrider and Kern 2018; Azodi et al. 2020; Korfmann et al. 2023; Rymbekova et al. 2024). In particular, artificial intelligence has been major a driver, with approaches employing linear and nonlinear modeling frameworks (Hastie et al. 2009). These novel methodologies have been applied for detecting selection, estimating evolutionary parameters, and inferring rates of genetic processes (Williamson et al. 2007; Chun and Fay 2009; Ronen et al. 2013; Schrider and Kern 2016; Sheehan and Song 2016; Flagel et al. 2019; Adrion et al. 2020; Wang et al. 2021; Burger et al. 2022; Hejase et al. 2022; Kyriazis et al. 2022; Gower et al. 2023; Hamid et al. 2023; Smith et al. 2023; Zhang et al. 2023; Ray et al. 2024).
Multiple strategies have been pursued to address evolutionary questions using machine learning. One such attempt has been to use summary statistics calculated in contiguous windows of the genome as input feature vectors to detect natural selection (Ronen et al. 2013; Pybus et al. 2015; Sheehan and Song 2016; Sugden et al. 2018; Mughal and DeGiorgio 2019; Mughal et al. 2020; Arnab et al. 2023; Korfmann et al. 2024), as natural selection is expected to leave a local footprint of altered diversity within the genome (Hudson and Kaplan 1988; Hermisson and Pennings 2017; Setter et al. 2020). To train such models, summary statistics are calculated from simulated genomic data, with frameworks ranging from linear models, such as regularized logistic regression (Mughal and DeGiorgio 2019; Mughal et al. 2020), to nonlinear models, such as ensemble methods that combine the effectiveness of different classifiers and deep neural networks (Lin et al. 2011; Pybus et al. 2015; Schrider and Kern 2016; Sheehan and Song 2016; Kern and Schrider 2018; Hejase et al. 2022; Arnab et al. 2023; Mo and Siepel 2023; ). However, when opting to use summary statistics to train these models, we are making an assumption that the chosen set of summary statistics is sufficient to discriminate among different evolutionary events, thereby providing satisfactory classification. Summary statistics can thus lead to subpar model performance if suitable measures are not chosen, with these statistics often selected based on theoretical knowledge and experience.
A complementary strategy is to use raw genomic data in the form of haplotype alignments as input to machine learning models, and for the model to perform automatic feature extraction. Attempts at this have mainly adopted convolutional neural networks (CNNs) (LeCun et al. 1998), which have been successfully applied to a number of problems in population genomics, including detection of diverse evolutionary phenomena, estimation of genetic parameters such as recombination rate, and inference of demographic history (Chan et al. 2018; Flagel et al. 2019; Torada et al. 2019; Gower et al. 2021; Isildak et al. 2021; Qin et al. 2022; Cecil and Sugden 2023; Lauterbur et al. 2023; Whitehouse and Schrider 2023; Riley et al. 2024). By construction, CNNs are not sensitive to small differences in details among different neighborhoods in a sample because of the smoothing that is accomplished through the one or more pooling layers in the CNN architecture (Goodfellow et al. 2016). Because such subtle details are often noise, it is typically beneficial to remove them as they might impact model predictions. However, other times those small differences in details could prove to be important enough to provide an improvement in predictive performance, as we will show in this article. In many of the population-genomic problems that machine learning methods have been applied to, the data are expected to have appreciable levels of autocorrelation (i.e. correlation of neighboring genomic locations due to linkage disequilibrium), which have been handled by using input features deriving from contiguous windows of the genome (e.g. Lin et al. 2011; Schrider and Kern 2016; Kern and Schrider 2018) and by explicitly modeling such autocorrelations (e.g. Flagel et al. 2019; Mughal and DeGiorgio 2019; Mughal et al. 2020; Isildak et al. 2021; Arnab et al. 2023).
A recent attempt to improve input data modeling was taken by Mughal et al. (2020), which used signal processing tools to extract features from input summary statistics calculated in contiguous windows of the genome, with those features automatically modeling the spatial autocorrelation of the data. Mughal et al. (2020) demonstrated that signal processing techniques can help improve true positive rate and accuracy for detecting positive natural selection, even within a linear model. Moreover, the trained models could be easily visualized, resulting in an interpretable framework for understanding what features are important for making predictions. Therefore, we believe such approaches, which have a long-standing foundation within engineering (e.g. Starck et al. 2002; Liu and Chen 2019), can further be used to make more accurate inferences from raw signals and haplotype data.
To apply such methods on raw haplotype data, we consider basis expansions (see supplementary methods, Supplementary Material online) in terms of wavelet (Daubechies 1992) and curvelet (Candes et al. 2006) bases. Wavelets and curvelets are part of a generalized framework termed α-molecules (Grohs et al. 2014), which have been extensively employed in image (two-dimensional signal) analysis (Starck et al. 2002). Here, the parameter α symbolizes the amount of anisotropy permitted in the scaling of basis functions. Isotropic scaling means that both coordinate axes are scaled by the same amount. In contrast, anisotropic scaling means that the x and y axes can have different scaling factors. As an example, isotropic scaling of a circle would lead to other circles of different sizes, whereas anisotropic scaling of a circle would lead to ellipses of different lengths and widths. For wavelets, the basis functions are scaled isotropically, whereas for curvelets, the basis functions can be rotated and are scaled anisotropically (parabolic scaling; see supplementary methods, Supplementary Material online). The resulting wavelet and curvelet coefficients used to decompose an image can be used as input features to machine learning models, and we expect wavelets and curvelets to embed key components in the data to aid machine learning models in achieving better performance.
As a proof of concept, we highlight the utility of α-molecules for extracting features from image representations of haplotype alignments when applied to the problem of uncovering genomic regions affected by past positive natural selection. Positive selection leads to the increase in frequency of beneficial traits within a population. Because genomic loci underlie traits, beneficial genetic variants at these loci that code for such traits will also elevate in frequency. This rapid rise of these beneficial mutations leads to alleles at nearby neutral loci to also increase in frequency by a phenomenon known as genetic hitchhiking (Smith and Haigh 1974). This hitchhiking causes a loss of diversity at neighboring neutral loci in addition to the lost diversity at the site of selection due to positive selection. The resulting ablation of haplotype diversity is known as a selective sweep (Przeworski 2002; Hermisson and Pennings 2005, 2017; Pennings and Hermisson 2006), and this is a key pattern that researchers exploit when developing statistics for detecting positive selection from genomic data.
Evidence of natural selection garnered by identifying selective sweeps aids in our understanding of the natural history of populations. For example, detection of sweeps can lend insight into the pervasiveness of positive selection in shaping genomic variation, whereas the prediction of the particular type of adaptive process (i.e. as hard sweep, soft sweep, or adaptive introgression) (Hermisson and Pennings 2005; Pennings and Hermisson 2006; Setter et al. 2020) can serve as a blueprint for pinpointing particular mechanisms that have driven adaptation (Hernandez et al. 2011; Granka et al. 2012; Huerta-Sánchez et al. 2014; Schrider and Kern 2016). However, sweep detectors can be confused by false signals due to other common evolutionary phenomena. For example, other forms of natural selection (e.g. background selection) (Charlesworth et al. 1993; Braverman et al. 1995; Charlesworth et al. 1995; Hudson and Kaplan 1995; Nordborg et al. 1996; McVean and Charlesworth 2000; Boyko et al. 2008; Akashi et al. 2012; Charlesworth 2012) as well as demographic history, such as population bottlenecks (Jensen et al. 2005; Stajich and Hahn 2005), can leave similar imprints on genetic data (though see Schrider 2020). Therefore, the problem of detecting sweep patterns from genomic variation has been extensively studied for decades, and represents a difficult yet suitable setting for evaluating novel modeling frameworks.
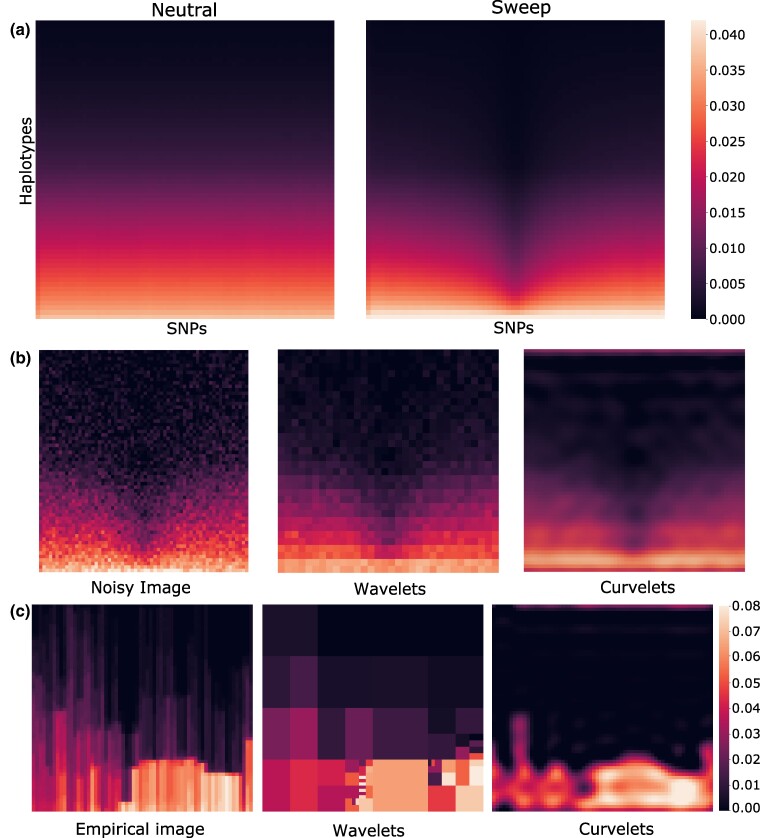
As an illustration of applying α-molecules to raw haplotype data, we depict the effect of decomposing and reconstructing image representations of haplotype alignments from wavelet and curvelet basis expansions (Fig. 1). Specifically, Fig. 1a shows heatmaps of haplotype images, averaged across many simulated replicates, for two evolutionary scenarios: neutrality (left) and a selective sweep (right). The sweep image displays a prominent vertical dark region in the image center, which symbolizes the loss of diversity due to positive selection. This pattern can be further illustrated an example of how such an image was created (supplementary fig. S1, Supplementary Material online), where we see that after processing a haplotype alignment, regions with greater numbers of major alleles will have a concentration of values close to zero toward the top of the image and values close to one toward the bottom of the image. The sharp contrast in the center of the sweep image (Fig. 1a) signifies the presence of major alleles (zeros) at high frequency in the center of the image, which presents a reduction in diversity. However, in more practical settings, this dark region will not be as easy to detect, as there will be some noise involved. Figure 1b shows a noisy image of the sweep setting, together with reconstructions from wavelet and curvelet decomposition that recover the purity of the original image. Noise in this scenario may have arisen due to both technical and biological factors, such as the particular set and number of sampled individuals, the accuracy of genotype calling and haplotype phasing in these individuals, and whether there have been mutation or recombination events recently in the history of some of those samples. The reconstructions are the result of wavelet and curvelet decomposition for which only the top one percent of coefficients with largest magnitude values are retained and the remaining coefficients have their values set to zero. This hard percentile-based thresholding results in a sparse set of coefficients such that only a few have nonzero values (). We depict a more realistic setting of haplotype variation expected from empirical data in Fig. 1c, which shows original and sparse wavelet and curvelet reconstructions of an image of diversity surrounding a gene on human autosome 7. Both wavelet and curvelet processes can capture the details of the original sweep image fairly well, with the curvelet reconstructed image smoother due to the greater freedom that is afforded to it by the curvelet decomposition of the functions (see supplementary methods, Supplementary Material online).
Fig. 1.
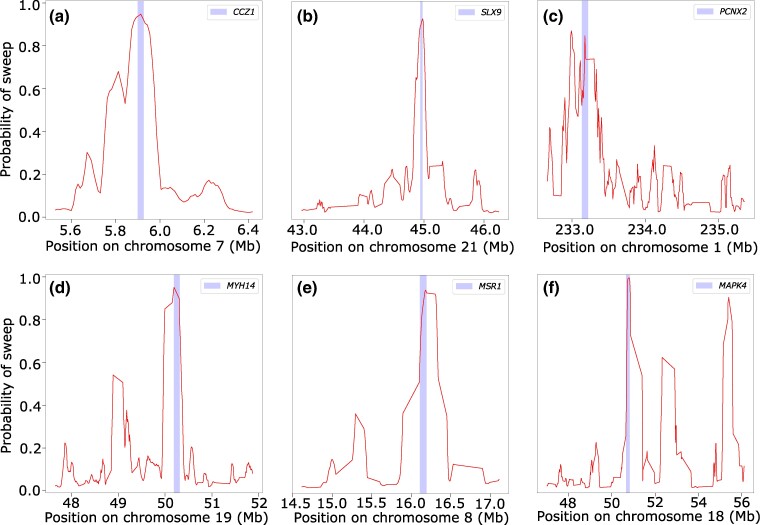
Image representations of haplotype alignments and their sparse reconstructions. Darker regions correspond to higher prevalence of major alleles. a) Heatmaps representing the -dimensional original haplotype alignments used as input to α-DAWG, averaged across 10,000 simulated replicates for either neutral (left) or sweep (right) settings. The mean sweep heatmap (right) shows the characteristic signature of positive selection, with a loss of genomic diversity (vertical darkened region) at the center of the haplotype alignments where a beneficial allele was introduced within sweep simulations. In contrast, this feature is absent in the mean neutral heatmap (left). b) Reconstructed images of a noisy signal with wavelet and curvelet decomposition. The noisy image was generated by adding Gaussian noise of mean zero and standard deviation one to the mean sweep image depicted in panel (a). For sparse reconstruction from wavelet and curvelet coefficients, we employed a hard percentile-based cutoff, where only the one percent of coefficients with largest magnitude values were retained for the image and the remaining coefficients were set to zero. While both sparse reconstruction approaches capture the overall signal in the noisy image, the curvelet reconstructed image is smoother than the wavelet reconstructed image. c) Sparse reconstruction of haplotype alignments for a genomic region encompassing the CCZ1 gene on human chromosome 7 from wavelet and curvelet coefficients in which hard percentile-based thresholding was employed as in panel (b).
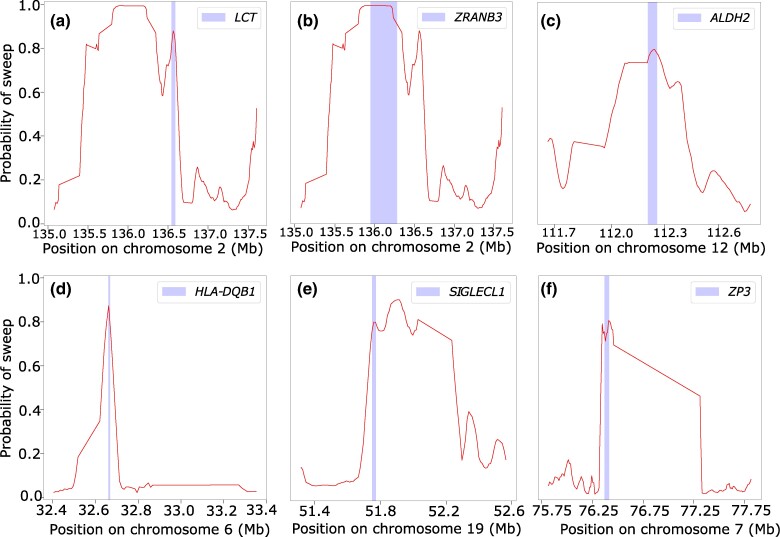
In the following sections, we introduce a set of linear and nonlinear methods that we term α-DAWG (α-molecules for Detecting Adaptive Windows in Genomes), where such methods first decompose an image representation of a haplotype alignment in terms of α-molecules, specifically with wavelets and curvelets, and then use extracted α-molecule basis coefficients as features to train and test models to discriminate sweeps from neutrality. We validate the true positive rate, accuracy, and robustness of our proposed α-DAWG framework, and show that models trained to detect sweeps from neutrality perform favorably on a number of demographic and selection scenarios, as well as the confounding factors of background selection, recombination rate variation, and missing genomic segments. We also demonstrate that α-DAWG attains superior true positive rate and accuracy relative to a CNN-based sweep classifier, and expand upon potential reasons for this in the section “Discussion”. As a product of employing wavelet and curvelet analysis on images, we are also able to visualize the parameters underlying the α-DAWG sweep classifiers, which provides a framework for understanding the learned characteristics of input images important for detecting sweeps. As a proof of effectiveness on realistic data, we apply α-DAWG to phased whole-genome data of central European (CEU) humans (The 1000 Genomes Project Consortium 2015) and recover a number of established candidate sweep regions (e.g. LCT, ZRANB3, ALDH2, and SIGLECL1), as well as predict some novel genes as sweep candidates (e.g. CCZ1, SLX9, PCNX2, and MSR1). Finally, we make available open-source software for implementing α-DAWG at https://github.com/RuhAm/AlphaDAWG.
Results
Sweep Detection with Linear α-DAWG Implementations
We decompose two-dimensional genetic signals (haplotype alignments) using wavelets or curvelets before using them to train models to differentiate between sweeps and neutrality. For the wavelet transform, we employed Daubechies least asymmetric wavelets as the basis functions (Daubechies 1988). Each sampled observation of the data are composed of a dimensional matrix (see section “Haplotype alignment processing”). Each sample is wavelet decomposed and the resulting coefficients are flattened into a single vector of length 4,096. Likewise, the curvelet transform gives a vector of coefficients with a length of 10,521 for each sample. We train individual linear models that use as input either wavelet or curvelet coefficients (α-DAWG[W] and α-DAWG[C]), and we also train a model that jointly uses as input wavelet and curvelet coefficients (α-DAWG[W-C]) with a flattened vector of length 14,617 per sample.
We first test α-DAWG on two datasets of differing difficulty that are inspired by a simplified population genetic model. Specifically, we initially explore application of α-DAWG on a constant population size demographic history with diploid individuals (Takahata 1993), as well as a mutation rate of per site per generation (Scally and Durbin 2012) and a recombination rate drawn from an exponential distribution with a mean of per site per generation (Payseur and Nachman 2000) and truncated at three times the mean (Schrider and Kern 2016) for 1.1 megabase (Mb) simulated sequences. Under these parameters, we generated simulated sequences using the coalescent simulator discoal (Kern and Schrider 2016) for 200 sampled haplotypes that we assigned as neutral observations. Additionally, to generate selective sweep observations from standing variation, we introduced a beneficial mutation at the center of simulated sequences with per-generation selection coefficient (Mughal et al. 2020) drawn uniformly at random on a scale, frequency of beneficial mutation when it becomes selected drawn uniformly at random on a scale, and generations in the past in which the beneficial mutation becomes fixed t. The first dataset (denoted by Constant_1), we set such that sampling occurs immediately after the selective sweep completes. For the second dataset (denoted by Constant_2), we draw uniformly at random, such that the distinction between sweeps and neutrality is less clear. We outline these parameters for generating the four datasets in section “Protocol for simulating population genetic variation”.
To evaluate the performance of α-DAWG on the two datasets, we generated training sets of 10,000 observations per class and test sets of 1,000 observations per class under each of the Constant_1 and Constant_2 datasets. We applied glmnet (Friedman et al. 2010) for training and testing under a logistic regression model with an elastic net regularization penalty. We used 5-fold cross validation to identify the optimum regularization hyperparameters (Hastie et al. 2009). Moreover, for α-DAWG[W] and α-DAWG[W-C], we treated the wavelet decomposition level as an additional hyperparameter, which we also determined using 5-fold cross validation across the set . Additional details describing the model and its fitting to training data can be found in the section “Methods” and supplementary methods, Supplementary Material online. Optimum values for the three hyperparameters estimated for the Constant_1 and Constant_2 datasets are displayed in Table 1.
Table 1.
Optimum hyperparameters chosen through 5-fold cross validation for the elastic net logistic regression classifier across the four datasets (Constant_1, Constant_2, CEU_1, and CEU_2) and three feature sets (wavelet, curvelet, and joint wavelet-curvelet [W-C])
| Hyperparameters | Constant_1 | Constant_2 | CEU_1 | CEU_2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wavelet | Curvelet | W-C | Wavelet | Curvelet | W-C | Wavelet | Curvelet | W-C | Wavelet | Curvelet | W-C | |
| Wavelet level | 1 | N/A | 1 | 1 | N/A | 1 | 1 | N/A | 1 | 1 | N/A | 1 |
| γ | 0.9 | 0.8 | 0.9 | 0.7 | 0.9 | 0.9 | 0.1 | 0.4 | 0.1 | 0.9 | 0.9 | 0.9 |
| λ | 0.00189 | 0.002 | 0.001 | 0.00168 | 0.001 | 0.021 | 0.0013 | 0.038 | 0.0012 | 0.0019 | 0.011 | 0.0017 |
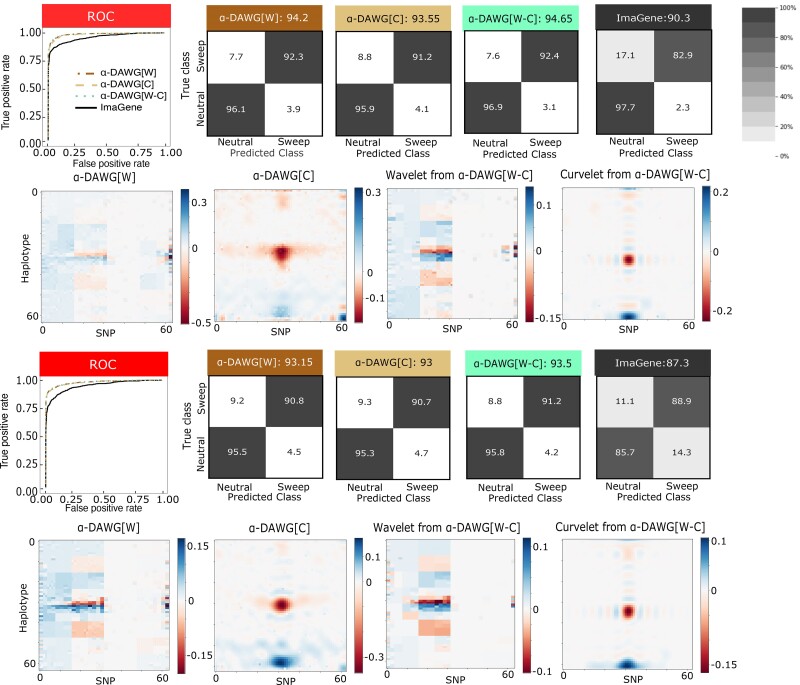
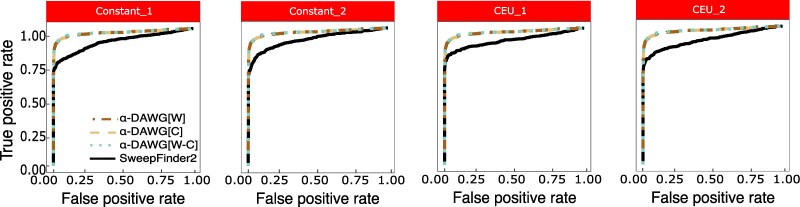
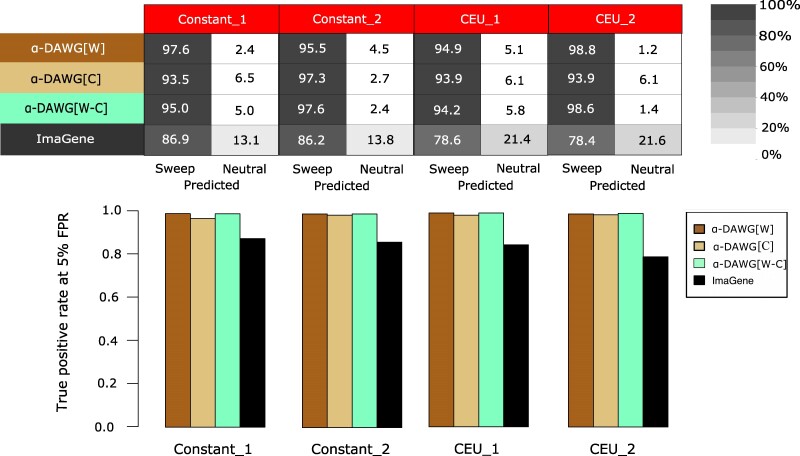
To assess classification ability, we evaluated model accuracy, relative classification rates through confusion matrices, and true positive rate with receiver-operating characteristic (ROC) curves. Using these evaluation metrics, all three linear α-DAWG models have similar classification abilities when applied on either the Constant_1 or Constant_2 dataset (Fig. 2). However, for both Constant_1 and Constant_2 datasets, linear α-DAWG[W-C] performs slightly better than linear α-DAWG[W] and α-DAWG[C]. As expected, method true positive rate and accuracy are higher for the Constant_1 dataset compared with Constant_2, as there is greater class overlap in the latter dataset. For both datasets, all three linear α-DAWG models outperform ImaGene, and the linear α-DAWG models classify neutral regions with higher accuracy than sweep regions (Fig. 2). However, though our three linear α-DAWG models exhibit relatively balanced classification rates between neutral and sweep settings, ImaGene is more unbalanced on the Constant_1 dataset. Specifically, for the Constant_1 dataset, ImaGene classifies only 2.3% of neutral regions incorrectly, which is slightly better than the linear α-DAWG models, but also misclassifies 17.1% of sweeps as neutral, which ultimately leads to its lower overall accuracy but is preferable to a high misclassification of neutral regions as sweeps. Interestingly, for the Constant_2 dataset, ImaGene displays more balanced classification rates, with 11.1% and 14.3% rates of misclassification for sweep and neutral regions, respectively. This finding could be the result of the Constant_2 dataset having more overlap between the two classes. For both of these datasets, the linear α-DAWG models exhibit superior classification accuracy relative to ImaGene, as well as higher true positive rate at low false positive rates based on the ROC curves (Fig. 2).
Fig. 2.
Performances of the three linear α-DAWG models and ImaGene applied to the Constant_1 (top two rows) and Constant_2 (bottom two rows) datasets that were simulated under a constant-size demographic history and 200 sampled haplotypes. The training and testing sets respectively consisted of 10,000 and 1,000 observations for each class (neutral and sweep). Sweeps were simulated by drawing per-generation selection coefficient and the frequency of beneficial mutation when it becomes selected , both uniformly at random on a scale. Moreover, the generations in the past in which the sweep fixed t was set as for the Constant_1 dataset and drawn uniformly at random as for the Constant_2 dataset. Model hyperparameters were optimized using 5-fold cross validation (Table 1) and ImaGene was trained for the number of epochs that obtained the smallest validation loss. The first and third rows from the top display the ROC curves for each classifier (first panel) as well as the confusion matrices and accuracies (in labels after colons) for the four classifiers (second to fifth panel). The second and fourth rows from the top display the two-dimensional representations of regression coefficient functions reconstructed from wavelets or curvelets for α-DAWG[W] (first panel), α-DAWG[C] (second panel), and α-DAWG[W-C] (third and fourth panels). Cells within confusion matrices with darker shades of gray indicate that classes in associated columns are predicted at higher percentages. The white color at the center of the color bar associated with a β function represents little to no emphasis placed by linear α-DAWG models, whereas the dark blue and dark red colors signify a positive and negative emphasis, respectively.
In addition to their accuracies and true positive rates, an important aspect of predictive models in population genetics is their interpretability in terms of the ability to understand what features of the input image representations of haplotype alignments are important for discriminating between sweeps and neutrality. To explore how well each classifier captures characteristic differences between sweep and neutral observations, we collected the fitted regression coefficients and applied inverse wavelet and curvelet transforms to reconstruct the function describing the importance of different regions of the haplotype alignment that we use as input to linear α-DAWG (see section “Linear α-DAWG models with elastic net penalization” of the supplementary methods, Supplementary Material online). For both datasets, the resulting β functions display elevated importance in places where we would expect differences between sweep and neutral variation to arise—i.e. increased importance for features at the center of simulated sequences near the site of selection, tapering off toward zero with distance from the center (Fig. 2). This pattern of importance is reflected in the mean two-dimensional images for the 10,000 training observations per class, with sweeps showing (on average) valleys of diversity toward the center of simulated sequences, whereas diversity of neutral simulations is (on average) flat across the simulated sequences (Fig. 1a). We also notice that the β function for the linear α-DAWG[W] models generally has a step-wise structure (ignoring local noise), whereas the β functions from linear α-DAWG[C] models are smoother. Similar characteristics are found in the corresponding β functions under linear α-DAWG[W-C] models (one function for wavelet coefficients and one for curvelet coefficients).
Robustness to Background Selection
Though we have shown that α-DAWG performs well at distinguishing the pattern of lost genomic diversity due to positive selection from neutral variation, it is important to consider other common forces that may lead to local reductions in diversity within the genome. In particular, the pervasive force of negative selection (McVicker et al. 2009; Comeron 2014) that constrains variation at functional genomic elements can lead to not only reductions in diversity at selected loci, but also at nearby linked neutral loci through a phenomenon termed background selection (Charlesworth et al. 1993; Hudson and Kaplan 1995; Charlesworth 2012), much like genetic hitchhiking that leads to a pattern of a selective sweep resulting from positive selection. Moreover, background selection can lead to distortions in the distribution of allele frequencies that can mislead sweep detectors (Charlesworth et al. 1993, 1995, 1997; Keinan and Reich 2010; Seger et al. 2010; Nicolaisen and Desai 2013; Huber et al. 2016). We expect that α-DAWG should be robust to background selection, as background selection is not expected to substantially alter the distribution of haplotype frequencies as it does not lead to the increase in frequencies of haplotypes (Charlesworth et al. 1993; Charlesworth 2012; Enard et al. 2014; Fagny et al. 2014; Schrider 2020). Nevertheless, it is important to explore whether novel sweep detectors are robust to false signals of selective sweeps due to background selection.
To assess whether α-DAWG is robust to background selection, we simulated 1,000 new test replicates of background selection under a constant-size demographic history using the forward-time simulator SLiM (Haller and Messer 2019), as the original simulator discoal that we used to train α-DAWG does not simulate negative selection. Specifically, we evolved a population of diploid individuals for generations, which includes a burn-in period of generations and a subsequent generations of evolution after the burn-in, under the same genetic and demographic parameters used to generate the Constant_2 dataset. At the end of each simulation, we sampled 200 haplotypes from the population for sequences of length 1.1 Mb. In addition to these parameters, we also introduced a functional element located at the center of the 1.1 Mb sequence for which deleterious mutations may arise continuously throughout the duration of the simulation and with a structure that mimics a protein-coding gene of length 55 kb where we might expect selective constraint. Using the protocol of Cheng et al. (2017), selection coefficients for recessive () deleterious mutations that arise within this coding gene were distributed as gamma with shape parameter 0.2 and mean 0.1 or 0.5 for moderately and highly deleterious alleles, respectively. Moreover, this gene consisted of 50 exons each of length 100 bases, 49 introns interleaved with the exons each of length 1,000 bases, and 5’ and 3’ untranslated regions (UTRs) flanking the first and last exons of the gene of lengths 200 and 800 bases, respectively. The lengths of these components of the coding gene structure were selected to roughly match the mean values from human genomes (Mignone et al. 2002; Sakharkar et al. 2004). Sampled haplotype alignments were processed according to the steps described in the section “Haplotype alignment processing”, and these 1,000 background selection test observations were then used as input to α-DAWG trained on the Constant_2 dataset.
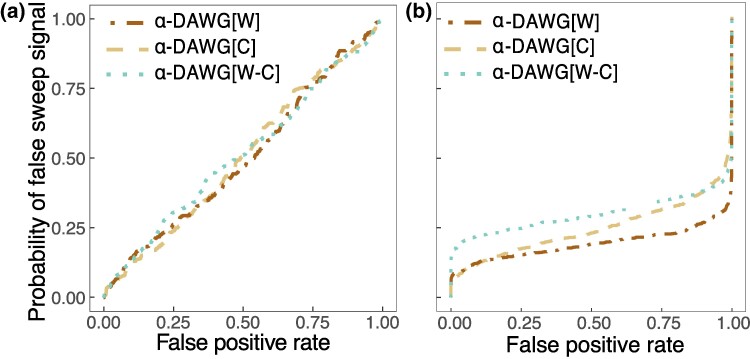
We find that the probability linear α-DAWG falsely detects moderate background selection as a sweep is roughly equal to the false positive rate based on neutral replicates (Fig. 3a), indicating that from the lens of linear α-DAWG, the distribution of sweep probabilities under background selection is approximately the same as under neutrality. When it comes to detecting moderately strong background selection, linear α-DAWG performs even better as the probability of falsely detecting background selection as a sweep is even lower than the false positive rate based on neutral replicates, emphasizing robustness under moderately strong background selection (Fig. 3b). Thus, as expected, because linear α-DAWG operates on features extracted from haplotype alignments, it is robust to patterns of lost diversity locally in the genome due to background selection in settings of moderately strong and weaker background selection under human-inspired demographic and genetic parameters.
Fig. 3.
Probability of falsely detecting moderate background selection a) and moderately strong background selection b) as a sweep as a function of false positive rate under neutrality for the three linear α-DAWG models trained using the Constant_2 dataset as in Fig. 2. The probability of a false sweep signal is the fraction of background selection test replicates with a sweep probability higher than the sweep probability under neutral test replicates that generated a given false positive rate. Details regarding the simulation of background selection can be found in the section “Robustness to background selection”.
Effect of Population Size Fluctuations
Our evaluation of the performance of α-DAWG classifiers in comparison to ImaGene focused on equilibrium demographic settings in which the population size is held constant. However, this is a highly unrealistic scenario, as true populations tend to fluctuate in their sizes over time for a number of reasons. We therefore sought to explore whether demographic models with population size changes would substantially hamper the accuracies and true positive rates of α-DAWG classifiers. Extreme population bottlenecks have been demonstrated to cause false signals of selective sweeps due to their increased variance in coalescent times, as well as to make sweep detection more difficult through their global loss of haplotype diversity across the genome. We therefore simulated a setting of a severe population bottleneck, using a demographic history inferred (Terhorst et al. 2017) from whole-genome sequencing of CEU individuals from the CEU population in the 1,000 Genomes Project dataset (The 1000 Genomes Project Consortium 2015).
Neutral simulations were run under this demographic history, and sweep simulations were performed with a beneficial mutation added on top of the demographic history, using the same selection parameters as in the constant-size demographic history that we previously explored—i.e. per-generation selection coefficient (Mughal et al. 2020) and frequency of beneficial mutation when it becomes selected , each drawn uniformly at random on a scale. Moreover, similarly to our previous experiments, we considered two datasets of varying difficulty, each with 10,000 simulations per class for the training set and 1,000 simulations per class for the testing set. The first dataset (denoted by CEU_1) with time of sweep completion set to generations in the past and the second, more difficult, dataset (denoted by CEU_2) with drawn uniformly at random. All classification models were trained and tested in an identical manner to the earlier Constant_1 and Constant_2 datasets, with optimum estimated values for the three hyperparameters displayed in Table 1.
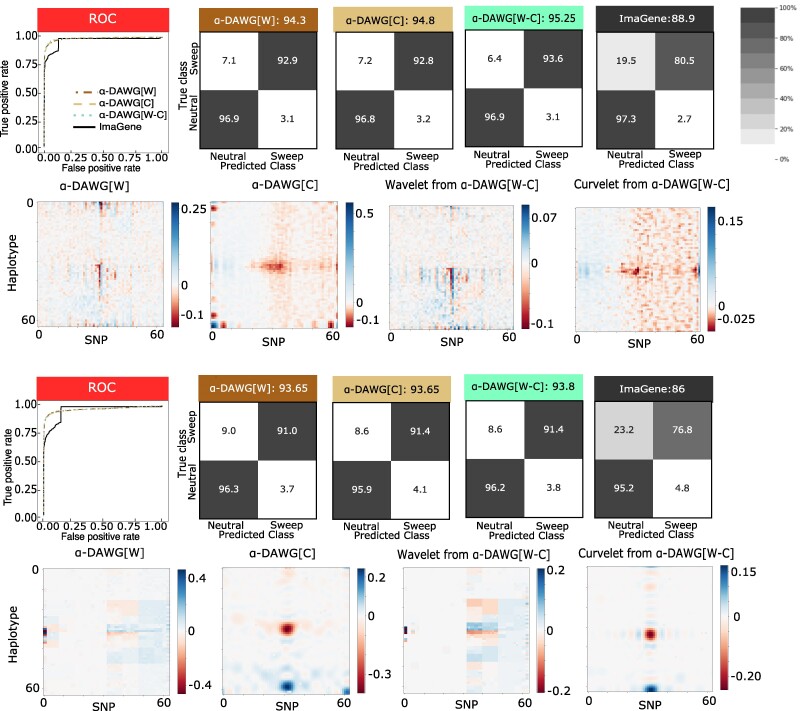
Comparing Figs. 4 to 2, we can see that demographic histories with extreme bottlenecks have actually lead to an improvement (though marginal) in the true positive rates and accuracies of the three linear α-DAWG models compared with the constant size demographic histories, with linear α-DAWG[W-C] displaying slighting elevated true positive rate and accuracy compared with linear α-DAWG[W] and α-DAWG[C]. In contrast, ImaGene has slightly decreased accuracy and true positive rate compared with the constant-size histories. Similarly, the three linear α-DAWG models have relatively balanced classification rates between neutral and sweep settings (with a slight skew toward neutrality), whereas ImaGene has highly unbalanced with a strong, yet conservative, skew toward neutrality for both the CEU_1 and CEU_2 datasets.
Fig. 4.
Performances of the three linear α-DAWG models and ImaGene applied to the CEU_1 (top two rows) and CEU_2 (bottom two rows) datasets that were simulated under a fluctuating population size demographic history estimated from CEU humans (Terhorst et al. 2017) and 200 sampled haplotypes. The training and testing sets, respectively, consisted of 10,000 and 1,000 observations for each class (neutral and sweep). Sweeps were simulated by drawing per-generation selection coefficient and the frequency of beneficial mutation when it becomes selected , both uniformly at random on a scale. Moreover, the generations in the past in which the sweep fixed t was set as for the CEU_1 dataset and drawn uniformly at random as for the CEU_2 dataset. Model hyperparameters were optimized using 5-fold cross validation (Table 1) and ImaGene was trained for the number of epochs that obtained the smallest validation loss. The first and third rows from the top display the ROC curves for each classifier (first pane) as well as the confusion matrices and accuracies (in labels after colons) for the four classifiers (second to fifth panel). The second and fourth rows from the top display the two-dimensional representations of regression coefficient functions reconstructed from wavelets or curvelets for α-DAWG[W] (first panel), α-DAWG[C] (second panel), and α-DAWG[W-C] (third and fourth panels). Cells within confusion matrices with darker shades of gray indicate that classes in associated columns are predicted at higher percentages. The white color at the center of the color bar associated with a β function represents little to no emphasis placed by linear α-DAWG models, whereas the dark blue and dark red colors signify a positive and negative emphasis, respectively.
To ascertain whether more training data may aid in boosting the performance of ImaGene, we simulated additional training data using the same protocols used to generate the CEU_2 dataset, resulting in a training set comprised of 30,000 observations per class. We trained ImaGene on this larger set, and evaluated it on the same test dataset consisting of 1,000 observations per class. Our experiments reveal that, using more training data results in a 5.5% increase in overall accuracy and a 9.4% increase in sweep detection accuracy for ImaGene (supplementary fig. S2, Supplementary Material online). Furthermore, the true positive rates at small false positive rates also improved with this additional training data, showing a quicker ascent to the upper left-hand corner of the ROC curve (supplementary fig. S2, Supplementary Material online). Despite the improvement in performance by ImaGene with additional training data, linear α-DAWG models still outperformed it by at maximum 1.95% (compare third row of Fig. 4 to supplementary fig. S2, Supplementary Material online) while the nonlinear models outperformed ImaGene with at maximum 3.1% (compare fourth row of supplementary figs. S8 to S2, Supplementary Material online) higher overall classification accuracy with the smaller training set.
Though this increase in classification performance by ImaGene is promising, it comes at a significant cost of additional computational and time requirements. Time requirements could potentially have been reduced by employing a population genetic simulator that is faster than the coalescent simulator that we used, such as some the forward time simulator SLiM (Haller and Messer 2023) that can employ advances parameter scaling and tree-sequence recording for speedup. However, even with such advances, replicate generation can remain slow for sweeps deriving from weak selection coefficients, which may require many simulation restarts, and the parameter scaling has recently been shown to potentially bias the integrity of the simulation (Dabi and Schrider 2024).
From these results, linear α-DAWG appears to be robust for this classical problematic setting for detecting sweeps. We also reconstructed the linear α-DAWG β functions for these bottleneck scenarios, showing increased importance for features near the center of image representations of haplotype alignments for which diversity from sweeps is expected to differ from neutrality in our simulations (Fig. 4), similar to the results from the constant-size history settings (Fig. 2). We also observe that the β functions are noisier when trained on the CEU_1 dataset than on the CEU_2 dataset. This increased noise is due to the optimal hyperparameter γ (see Table 1) estimated closer to zero for all three linear α-DAWG models trained on CEU_1, whereas γ is estimated closer to one on CEU_2. Because smaller γ values result in greater -norm penalization compared with -norm, the lack of sparsity in the estimated wavelet coefficients for reconstructing the β functions from CEU_1 likely led to more noise. Moreover, the significant peaks near the pixels toward the bottom rows and middle columns of the β functions (e.g. α-DAWG[C] in both Figs. 2 and 4) likely reflect emphasis in the model contributed by the most recent, strongest, and hardest sweeps.
Robustness to Recombination Rate Heterogeneity
Recombination rate varies across genomes, and therefore has an impact in shaping haplotypic diversity observed among populations within and among species (Smukowski and Noor 2011; Cutter and Payseur 2013; Singhal et al. 2015; Peñalba and Wolf 2020; Winbush and Singh 2020). In particular, low recombination rates may decrease local haplotypic diversity, which may resemble the pattern of a selective sweep, whereas high recombination rates may elevate local haplotypic diversity, which may eliminate sweep signatures. The genomes across a variety of organisms exhibit a complex recombination landscape in which we observe isolated genomic regions with extremely high (known as hotspots) and low (known as coldspots) recombination rates (Petes 2001; Hey 2004; Myers et al. 2005; Galetto et al. 2006; Grey et al. 2009; Baudat et al. 2010; Singhal et al. 2015; Booker et al. 2020; Lauterbur et al. 2023). Therefore, it is important to evaluate the degree with which α-DAWG is robust against scenarios of recombination rate heterogeneity, including at hotspots and coldspots.
To test the robustness of α-DAWG under recombination rate heterogeneity, we simulated 1,000 neutral test replicates under both constant (i.e. Constant_1 and Constant_2) and fluctuating population size (i.e. CEU_1 and CEU_2) models using the coalescent simulator discoal (Kern and Schrider 2016), fixing genetic parameters identical to their respective original datasets (Constant_1, Constant_2, CEU_1, and CEU_2) while only changing the recombination rate. Specifically, for a given replicate the recombination rate was drawn from an exponential distribution with mean of or per site per generation and truncated at three times the mean, resulting in a respective decrease in the mean recombination rate across the entire simulated 1.1 Mb region by one or two orders of magnitude relative to distribution used to train the α-DAWG classifiers. To simulate recombination hotspots and coldspots under constant and fluctuating population size models, we simulated 1,000 neutral test replicates using the coalescent simulator msHOT (Hellenthal and Stephens 2007), fixing genetic parameters identical to their respective original datasets (Constant_1, Constant_2, CEU_1, and CEU_2) with the exception of the recombination rate. In particular, for each test replicate, the recombination rate (r) was drawn from an exponential distribution with mean of per site per generation and truncated at three times the mean (as in the settings used to train α-DAWG), except that the central 100 kb region of the sequence evolved with a recombination rate of or for coldspots and or for hotspots, resulting in a localized decrease or increase in the recombination rate at the center of the simulated sequences, respectively.
Our results reveal that under a shift in the mean recombination rate by one or two orders of magnitude lower than what was used for training, linear α-DAWG models exhibit an increased neutral misclassification rate up to 14% for constant-size demographic histories when compared with results in which the recombination rate distribution in test data matched what the models were trained on (supplementary fig. S3, Supplementary Material online). For the more-realistic CEU demographic history, the neutral misclassification rate observed for linear α-DAWG models is somewhat lower, maxing out at about an 11% increase in neutral misclassification (supplementary fig. S3, Supplementary Material online). Of these models, linear α-DAWG[W] often had the smallest misclassification error, though the ranking of the linear α-DAWG models based on neutral misclassification errors were not consistent across tested settings. Therefore, in the face of significant reductions in mean recombination rates relative to what was employed during training, linear α-DAWG models show modest inflation of neutral misclassification rates when compared with results under the usual training settings for realistic demographic settings.
Furthermore, when faced with recombination hotspots and coldspots, linear α-DAWG models show a slight rise (as high as 10%) in misclassification rate, whereas some models show proportional deflation in misclassification rates (as much as 4%) of neutrally evolving regions (supplementary fig. S4, Supplementary Material online). In general, increasing the recombination rate from extreme coldspot to extreme hotspot tends to reduce the neutral misclassification rate under the realistic CEU demographic history (supplementary fig. S4, Supplementary Material online). When it comes to coldspots, linear α-DAWG models show decreases in neutral misclassification rates up to 2% as well as elevations in neutral misclassification rates as high as 10% (supplementary fig. S4, Supplementary Material online). In the case of hotspots, linear α-DAWG models exhibit diminishing neutral misclassification rates as low as 4% and inflations in neutral misclassification as high as 8% (supplementary fig. S4, Supplementary Material online). In summary, we observe that even under recombination hotspot or coldspots, linear α-DAWG models show a general resilience as evidenced by their minimal change in misclassification rate from original settings, with fewer errors made for hotspots compared with coldspots (supplementary fig. S4, Supplementary Material online).
In addition to testing the resilience of linear α-DAWG models on recombination rate heterogeneity, we went on to evaluate how a reduced sweep footprint affects sweep detection accuracy when applied to the CEU_2 dataset. In particular, the sweep footprint size F can be computed as , where s is the selection coefficient per generation, r is the recombination rate per site per generation, and is the effective population size (Gillespie 2004; Garud et al. 2015; Hermisson and Pennings 2017). Thus, the sweep footprint size is inversely proportional to the recombination rate. To this end, we simulated 1,000 sweep test replicates with recombination rates drawn from an exponential distribution with mean of (twice that used for training) per site per generation and truncated at three times the mean leading to a sweep footprint size that is on average half the width of the original replicates, with the mean footprint size across the original replicates approximately 329 kb. We find that the reduced footprint size indeed presents a challenge for the linear α-DAWG models, as we observe a drop in sweep detection accuracy from original results (supplementary fig. S5, Supplementary Material online). This drop in sweep detection accuracy due to reduced sweep footprint size falls in the range of 3.7% to 4.5% when compared with the sweep detection accuracy obtained from test replicates using the original recombination rate (supplementary fig. S5, Supplementary Material online). Overall, a 2-fold reduction in sweep footprint size has minimal to moderate effects on the ability of linear α-DAWG models to detect sweeps, adding to the potential robustness of our models.
Performance Under Mutation Rate Variation
Mutation rate varies within the genome and across species (Kumar and Subramanian 2002; Bromham 2011; Bromham et al. 2015; Harpak et al. 2016; Castellano et al. 2020) due to factors including transcription-translation conflicts and DNA replication errors (Bromham 2009; Dillon et al. 2018), and this mutation rate heterogeneity could affect the performance of predictive models that use genomic variation as input. Like with recombination rate, genomic regions with low mutation rates can be mistaken as evidence of a selective sweep, as they will harbor low haplotypic diversity, whereas genomic regions with high mutation rates can mask footprints of past selective sweeps, as they will exhibit elevated haplotypic diversity (Harris and Pritchard 2017). Thus it is paramount that α-DAWG perform well under such conditions of mutation rate variation.
To evaluate whether α-DAWG is resilient to, and performs well under, mutation rate heterogeneity, we simulated an additional 1,000 sweep and 1,000 neutral replicates using discoal (Kern and Schrider 2016), where we deviated from simulation protocol for generating training data for α-DAWG in which we fixed the mutation rate as per site per generation. Specifically, for each new test replicate, we sampled the mutation rate uniformly at random within the interval and evaluated how α-DAWG models fare under this setting of mutation rate variation. We outlined the performance in terms of accuracy and classification rates using confusion matrices and true positive rate using ROC curves (supplementary fig. S6, Supplementary Material online).
We found that linear α-DAWG models show excellent overall accuracy (from 89.55 to 96.9%) under mutation rate variation (supplementary fig. S6, Supplementary Material online). In terms of detecting neutrally evolving regions, linear α-DAWG[W] exhibits accuracy in the range of 90.5 to 96%, whereas linear α-DAWG[C] and α-DAWG[W-C] display a better neutral detection rate in the range of 95.2 to 98.7% and 93.5 to 98.2%, respectively (supplementary fig. S6, Supplementary Material online). Moreover, all linear α-DAWG models retain high true positive rates across scenarios tested, evidenced by quick rises to the upper left hand corner of the ROC curve, with linear α-DAWG[C] and α-DAWG[W-C] models demonstrating higher true positive rates than linear α-DAWG[W]—an exception being the applications of these models on the Constant_1 dataset for which linear α-DAWG[W] edges out the other two (supplementary fig. S6, Supplementary Material online). These results suggest that all linear α-DAWG models retain high true positive rates and are accurate when confronted with mutation rate variation.
Comparison with a Summary Statistic Based Deep Learning Classifier
Though we have benchmarked the linear α-DAWG models with the nonlinear classifier ImaGene that also uses images of haplotype alignments as input, it is important to consider classifiers that instead use statistics summarizing variation as input. We specifically investigate the performance of the nonlinear diploS/HIC classifier (Kern and Schrider 2018), which was originally developed for distinguishing among five classes, namely, soft sweeps, hard sweeps, linked soft sweeps, linked hard sweeps, and neutrality from unphased multilocus genotypes (MLGs) using a feature vector of 12 summary statistics calculated across 11 windows, where the central window is being classified. We have adjusted diploS/HIC from its native state as a multiclass classifier, to instead make decisions as a binary classifier to distinguish sweeps from neutrality for comparison purposes with α-DAWG. We trained and tested diploS/HIC on the Constant_1, Constant_2, CEU_1, and CEU_2 datasets.
We find that diploS/HIC displays excellent overall accuracy (supplementary fig. S7b, Supplementary Material online) and high true positive rates (supplementary fig. S7a, Supplementary Material online) across different false positive rate thresholds in both the constant and fluctuating population size settings. On all four test datasets, diploS/HIC outperforms the best performing linear α-DAWG[W-C] by between and (compare Figs. 2 and 4 with supplementary fig. S7b, Supplementary Material online) in terms of overall accuracy. The edge of diploS/HIC over the linear α-DAWG models in terms of performance is further evident in the ROC curves, where on all datasets we observe a rapid ascent to the upper left-hand corner of the curve (supplementary fig. S7a, Supplementary Material online). Though diploS/HIC outperforms linear α-DAWG across all datasets, a possible opportunity to close this performance gap would be to employ a nonlinear α-DAWG, which we explore further in the section “Performance boost with nonlinear models”.
Comparison with a Likelihood Ratio Based Classifier
Though we have elected to evaluate the performance of our α-DAWG methods in comparison to ImaGene, as it also uses images as input to a machine learning classifier, it is informative to explore classification ability relative to more traditional methods of sweep detection, such as the maximum likelihood approach SweepFinder (Nielsen et al. 2005; DeGiorgio et al. 2016). Comparing linear α-DAWG to SweepFinder2 (DeGiorgio et al. 2016) on all four test datasets, we see that linear α-DAWG models consistently demonstrate superior true positive rate across the range of false positive rates compared with SweepFinder2 (Fig. 5). Though SweepFinder is a powerful sweep classifier, this result is expected, because the test sweep datasets have varying degrees of sweep softness, strength, and age. The sweep model employed by SweepFinder2 is one of a recent, hard, and effectively immediate (i.e. strong) sweep, and thus the method has limited true positive rate in detecting soft sweeps. On the other hand, the sweep training data given to linear α-DAWG models were generated across a range of sweep softness, strength, and age, and so α-DAWG is more suited to detecting a broad set of sweep modes relative to traditional model-based approaches.
Fig. 5.
ROC curves of the three linear α-DAWG models and SweepFinder2 applied to the Constant_1, Constant_2, CEU_1, and CEU_2 test datasets, with the linear α-DAWG models trained and applied in Figs. 2 and 4.
Ability to Detect Hard Sweeps from de Novo Mutations
Our experiments have explored α-DAWG classification ability when trained and tested on settings for which the initial frequency of the beneficial mutation (f) was allowed to vary across a broad range of values from 0.001 to 0.1, with adaptation from beneficial mutations at these frequencies occurring through selection on standing variation. The lower frequency range would likely lead to harder sweeps, as only one or a few haplotypes would rise to high frequency, whereas the upper range would yield softer sweeps. However, a more classic example of a hard sweep would occur through selection on a de novo mutation for which the beneficial allele is present on a single haplotype (Przeworski 2002; Hermisson and Pennings 2005). We therefore elected to examine the accuracy of α-DAWG for detecting hard sweeps from de novo mutations.
To evaluate this scenario, we simulated an additional 1,000 test sweep replicates with discoal (Kern and Schrider 2016) for each of the Constant_1, Constant_2, CEU_1, and CEU_2 datasets, with protocol identical to those for simulating sweeps under these datasets with the exception that , where is the diploid effective population size rather than . We then deployed our three linear α-DAWG models and ImaGene that were trained on settings for which to evaluate relative classification accuracy and true positive rate of hard sweeps from de novo mutations. We find that linear α-DAWG and ImaGene showcase relative classification ability consistent with prior experiments, with all approaches having high accuracy and true positive rate and with linear α-DAWG edging out ImaGene for sweep detection (Fig. 6). Though the setting of hard sweeps from de novo mutations was not explicitly included within the domain of the linear α-DAWG training distribution, it is not surprising that linear α-DAWG models still retain high accuracy and true positive rate for such scenarios, as the footprints of hard sweeps are more prominent than those of soft sweeps (Hermisson and Pennings 2017).
Fig. 6.
Performances of the three linear α-DAWG models and ImaGene applied to the Constant_1, Constant_2, CEU_1, and CEU_2 test datasets of hard sweeps from de novo mutations (see Performance on hard sweeps from de novo mutations) using the linear α-DAWG models and ImaGene trained as in Figs. 2 and 4. The top panel depicts the percentage of 1,000 hard sweep from de novo mutation test replicates classified as a sweep or neutrality, whereas the bottom panel shows true positive rate at a 5% false positive rate (FPR) to detect such sweeps. Cells within confusion matrices at the top with darker shades of gray indicate that classes in associated columns are predicted at higher percentages.
Performance Boost with Nonlinear Models
So far we have only discussed linear classifiers. However, if the decision boundary separating sweeps from neutrality is nonlinear, then a nonlinear model may be expected to yield better performance than a linear model. We therefore considered extending our logistic regression classifier to a multilayer perceptron neural network. The number of hidden layers or the number of nodes within a hidden layer of the network is related to the models capacity, or its flexibility in the set of functions that it can model well (Goodfellow et al. 2016). Because a neural network with enough hidden layers or enough nodes within the hidden layers can approximate arbitrarily complicated functions, it is possible to overfit the model to the training data (Cybenko 1989; Hornik et al. 1989). Common solutions to this overfitting issue include limiting the network capacity (number of hidden layers and nodes) or constraining the model through regularization (Goodfellow et al. 2016).
With this in mind, we considered a neural network with one hidden layer containing eight hidden nodes within the layer so that we can still model nonlinear functions while also having limited capacity of the network. This limited capacity also heavily reduces the number of parameters that need to be estimated in the model, thereby reducing the computational cost of fitting he model. As with our previous linear models, we also included an elastic net regularization penalty to constrain the model, and employed 5-fold cross validation to identify the optimum regularization hyperparameters. This neural network was implemented using keras with a tensorflow backend, and we fit this model to all four datasets that we considered earlier: Constant_1, Constant_2, CEU_1, and CEU_2. Additional details describing the model and its fitting to training data can be found in the section “Methods” and supplementary methods, Supplementary Material online. Optimum values for the three hyperparameters estimated on the four datasets are displayed in Table 2.
Table 2.
Optimum hyperparameters chosen through 5-fold cross validation for the elastic net eight node and one hidden layer perceptron classifier across the four datasets (Constant_1, Constant_2, CEU_1, and CEU_2) and three feature sets (wavelet, curvelet, and joint wavelet-curvelet [W-C])
| Hyperparameters | Constant_1 | Constant_2 | CEU_1 | CEU_2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wavelet | Curvelet | W+C | Wavelet | Curvelet | W+C | Wavelet | Curvelet | W+C | Wavelet | Curvelet | W+C | |
| Wavelet level | 1 | N/A | 1 | 1 | N/A | 1 | 1 | N/A | 1 | 1 | N/A | 1 |
| γ | 0.3 | 1 | 0.9 | 1 | 0.1 | 0.9 | 1 | 0.9 | 0.1 | 1 | 0.9 | 0.1 |
| λ | ||||||||||||
Using nonlinear versions of the α-DAWG models instead of linear, we see once again that the three nonlinear α-DAWG classifiers perform similarly to each other on each dataset (supplementary fig. S8, Supplementary Material online). In contrast to the linear classifiers (Figs. 2 and 4), nonlinear α-DAWG[W-C] outperforms other nonlinear models in only Constant_2, and CEU_2 datasets while lagging slightly behind α-DAWG[C], and α-DAWG[W] in Constant_1 and CEU_1 datasets, respectively (supplementary fig. S8, Supplementary Material online). These scenarios in which the nonlinear α-DAWG[W-C] performs the best are settings in which there is greater overlap between the neural and sweep classes. Comparing Figs. 2, 4, and supplementary fig. S8, Supplementary Material online, we see that nonlinear α-DAWG[C] and α-DAWG[W-C] models showcase increased overall classification accuracy on the Constant_1 and CEU_2 datasets. Moreover, nonlinear α-DAWG[W] and α-DAWG[W-C] models exhibit increased overall classification accuracy on the CEU_1 dataset, with a neutral detection rate as high as 98.5%, which provides the nonlinear models with an edge over their linear counterparts with the same image decomposition method. We also observe a deviation from nonlinear models having superior performance over linear ones on the Constant_2 dataset, for which all nonlinear all α-DAWG models have overall decreased accuracy. That is, no single model among the six α-DAWG models (three linear and three nonlinear) consistently performs better than the others. However, when examining the performance boost of our nonlinear models, we need to consider the robustness scenarios where the test inputs may have been generated from genomic regions with missing data, which may give rise to false detection of sweep signals at neutrally evolving regions. We discuss more about how nonlinear α-DAWG models fare when faced with technical hurdles like missing data in section “Robustness to missing genomic segments”.
In addition to predictive ability, as with the linear model, we collected the regression coefficients from the eight hidden nodes and inverse transformed them to reconstruct the functions at each of the hidden nodes. We then averaged these maps according to their weights with which they contribute to the output node (see section “Nonlinear α-DAWG models with elastic net penalization” of the supplementary methods, Supplementary Material online). Supplementary fig. S9, Supplementary Material online shows that the functions for each of the nonlinear α-DAWG models display expected patterns, with increased importance for features at the center of the haplotype images, tapering off toward zero with distance from the center, as well as curvelet coefficient functions typically smoother than wavelet coefficient functions. Though the β functions observed differ from each other, they each emphasize the center of input images (supplementary fig. S9, Supplementary Material online). Importantly, the β functions are not an indicator of model performance, as they simply depict areas of an image that nonlinear α-DAWG models place emphasis. We also note that we observe markedly different β functions across nonlinear α-DAWG models in both smoothness and magnitude, which depends on the signal decomposition method applied as well as the optimal regularization hyperparameters associated with the model.
To further evaluate the performance of the nonlinear α-DAWG models, we compared it with diploS/HIC. We find that the gap in overall accuracy between nonlinear α-DAWG models and diploS/HIC closes in with diploS/HIC outperforming the best nonlinear α-DAWG models between and (compare fourth row of supplementary fig. S8, Supplementary Material online with supplementary fig. S7b, Supplementary Material online). The edge diploS/HIC has over nonlinear α-DAWG models is likely owed to the fact that diploS/HIC uses summary statistics, which have been chosen because they are adept at detecting sweep patterns and also for discriminating among evolutionary processes in general (Panigrahi et al. 2023). On the other hand, this is an ideal setting without some of the potential technical hurdles that might be encountered in empirical data. Thus, in the section “Robustness to missing genomic segments”, we explore how diploS/HIC and the linear and nonlinear α-DAWG models fare when challenged with artificial drops in haplotypic diversity due to missing data.
Robustness to Missing Genomic Segments
So far we have explored experiments that mimicked the biological process that would allow simulated haplotype variation to approximate real empirical haplotype variation as closely as possible. However, we assumed that this variation was known with certainty, and have not yet considered flawed data due to technical artifacts. One particular technical issue is that some regions of the genome are difficult to assay variation at, leading to chunks of missing genomic segments in downstream datasets due to the inability to access the portion of the genome or because that region was filtered as the data were found to be unreliable. The presence of such missing segments can reduce the number of SNPs and, thus, the number of distinct observed haplotypes, causing spurious drops in haplotype diversity locally in the genome that may masquerade as selective sweeps. Indeed, previous studies have found that such forms of missing data can mislead methods to erroneously detect sweeps at neutrally evolving regions (Mallick et al. 2009; Mughal and DeGiorgio 2019). It is therefore desirable that sweep classifiers are robust against this kind of confounding factor.
To evaluate the robustness of α-DAWG to missing data, we removed portions of SNPs in the test set using the identical protocol of Mughal and DeGiorgio (2019). Briefly, we removed 30% of the total number of SNPs in each simulated replicate by deleting 10 nonoverlapping chunks of contiguous SNPs, each of size equaling 3% of the total number of simulated SNPs. The starting position for each missing chunk was chosen uniformly at randomly from the set of SNPs, and this position was redrawn if the chunk overlapped with previously deleted chunks. Image representations of haplotype alignments were then created from these modified genomic segments by applying the same data processing steps as in our nonmissing experiments (see section “Haplotype alignment processing”). All models were trained assuming no missing genomic segments, with missing segments only in the test dataset.
Figure 7 shows the true positive rates, accuracies, and classification rates of the three linear α-DAWG models and ImaGene applied to the four datasets in which the test data have missing segments. Comparing the results to those of Figs. 2 and 4, in all cases the three linear α-DAWG models have unbalanced classification rates, with a skew toward predicting neutrality. Though missing data ultimately reduces accuracy of the three linear α-DAWG models, the misclassifications are conservative, as it is preferable to misclassify sweeps as neutral (i.e. fail to detect the sweep event) than to falsely classify neutral regions as sweeps (i.e. detect a nonexistent process). Moreover, as evident from comparing Fig. 7 to Figs. 2 and 4, the three linear α-DAWG models have sacrificed only a small margin of overall performance. These experiments therefore suggest that the three linear α-DAWG models are robust to missing data, in that they do not falsely detect sweeps, which is what we might expect from missing genomic segments due to the loss of haplotype diversity. In contrast, missing data have a more critical impact on the performance of ImaGene, with it now exhibiting a strong skew toward classifying sweeps. Unfortunately, such skew is detrimental as a high percentage of neutral simulations are now falsely predicted as sweeps, which diverges from conservative classification rates of the three linear α-DAWG models under missing genomic regions. The diminished performance of ImaGene under missing data suggests that the alignment processing method employed by α-DAWG may help it guard against false sweep footprints due to the reduced haplotypic variation caused by missing genomic regions.
Fig. 7.
Performances of the three linear α-DAWG models and ImaGene applied to the Constant_1, Constant_2, CEU_1, and CEU_2 (from top to bottom) test datasets with missing genomic segments (see Robustness to missing genomic segments) using the linear α-DAWG models and ImaGene trained and applied in Figs. 2 and 4. Each row displays the ROC curves (first panel) as well as the confusion matrices and accuracies (in labels after colons) for the four classifiers (second to fifth panels). Cells within confusion matrices with darker shades of gray indicate that classes in associated columns are predicted at higher percentages.
We also ran identical missing data analyses for our nonlinear α-DAWG models, with supplementary fig. S10, Supplementary Material online highlighting the considerable robustness of α-DAWG to the technical artifacts generated by missing genomic segments. We observe that among our nonlinear α-DAWG models, α-DAWG[W-C] shows higher overall classification accuracy compared with the other two nonlinear α-DAWG models (supplementary fig. S10, Supplementary Material online). This elevated accuracy comes at an increased computational cost due to the greater number of coefficients that are needed to optimize in the nonlinear α-DAWG[W-C] model (supplementary fig. S11, Supplementary Material online). Specifically, the nonlinear α-DAWG[W-C] model has the highest computational demand with a mean CPU usage of 18.75% and mean memory overhead of about 52.14 GB per epoch, whereas the nonlinear α-DAWG[W] and α-DAWG[C] models respectively have mean CPU usages of 9.45 and 14.95% and mean memory overheads of about 49.91 GB and 49.64 GB per epoch (supplementary fig. S11, Supplementary Material online).
We further went on to compare the performance of diploS/HIC against α-DAWG when the test data contains missing segments on all four datasets. We find that all linear α-DAWG models have better overall accuracy compared with results obtained utilizing diploS/HIC (compare Fig. 7 and supplementary fig. S7d, Supplementary Material online). Though diploS/HIC shows high sweep detection accuracy, it suffers in correctly detecting neutrally evolving regions as it misclassifies at minimum 30.6% of neutral replicates with missing segments as sweeps (supplementary fig. S7d, Supplementary Material online). This high misclassification rate of neutral regions as sweeps is likely due to the fact that diploS/HIC uses physical based windows to compute summary statistics (Mughal and DeGiorgio 2019). On the other hand, misclassification of neutral regions as sweeps does not exceed 7.7% across all linear α-DAWG models on all datasets in the presence of missing segments (Fig. 7). It is also possible diploS/HIC has suffered here on missing genomic segments because it is a nonlinear model, and maybe the model has learned too many of the fine details within the idealistic training data. Thus, we also evaluate how a nonlinear α-DAWG models would behave when encountering missing genomic segments in test input data. We find that nonlinear α-DAWG models misclassify at most 9.4% of neutral replicates with missing segments as sweeps across all datasets as opposed to a 30.6% misclassification rate of such neutral observations by diploS/HIC (compare supplementary fig. S10, Supplementary Material online with supplementary fig. S7d, Supplementary Material online). These results underscore the apparent disadvantage of using physical based windows when faced with missing genomic tracts. Overall, both linear and nonlinear α-DAWG models show better resilience when confronted with scenarios involving missing genomic segments compared with diploS/HIC.
These missing data experiments assumed a fixed percentage of missing SNPs (30%) distributed evenly across 10 genomic chunks of roughly 3% missing SNPs, which is likely to be less realistic than missing data distributions observed empirically. To consider such a scenario, we selected missing genomic segments inspired from an empirical distribution for which the missing segments are arranged in blocks with mean CRG (Centre for Genomic Regulation) mappability and alignability score (Talkowski et al. 2011) lower than 0.9 (Mughal et al. 2020). To generate test replicates with missing segments, we randomly selected one of the 22 human autosomes, where the probability of selecting a particular autosome is proportional to its length. Once an autosome is selected, we chose a 1.1 Mb region uniformly at random, and identified blocks within this region with low mean CRG scores. In the case where this region does not harbor blocks with low mean CRG score, we chose another starting position for a 1.1 Mb region until a region was found with blocks of low mean CRG score. We then scaled the genomic positions of this 1.1 Mb region to start at zero and stop at one to adhere to the discoal position format for simulated replicates, and subsequently removed SNPs from the test replicate that intersected positions of blocks with low mean CRG scores. As it is likely to find only a few (typically one) long block of missing segment in a 1.1 Mb region, this protocol for generating missing data in a contiguous stretch is different and more realistic than our prior protocol for removing SNPs within 10 short blocks. The mean percentage of missing SNPs using this empirical inspired protocol is about 10.87%, which is lower than and contrasts with the 30% missing SNPs observed in our original experiment.
Comparing the results of our empirically inspired experiments (supplementary fig. S12, Supplementary Material online) to those without missing data (Figs. 2 and 4), in all cases the three linear α-DAWG models with missing data performed on par with nonmissing scenarios in terms of overall accuracy (from 91.30 to 96.55%). In general, when compared with settings without missing data, all methods on all datasets display a relative increase in sweep detection accuracy, with the exception of linear α-DAWG[C] applied to the Constant_2 dataset for which sweep detection accuracy is slightly decreased by 0.4%. Moreover, our empirically inspired experiments show promising results using nonlinear α-DAWG models, in which the nonlinear α-DAWG[W-C] model shows an edge over the other two nonlinear α-DAWG models with overall accuracies ranging from 92.55 to 96.40% (supplementary fig. S13, Supplementary Material online). Furthermore, when compared with our previous missing data experiments, we find the empirically inspired missing data distribution has better overall accuracy as well as fewer sweep misclassifications on all datasets for both linear (compare Fig. 7 and supplementary fig. S12, Supplementary Material online) and nonlinear (compare supplementary figs. S10 and S13, Supplementary Material online) models. This improved accuracy is owed to the fact that in the empirically inspired experiments, the mean percentage of missing SNPs is lower than that of the original missing data experiments. Overall, α-DAWG models are robust to different degrees and distributions of missing loci, and are unlikely to falsely attribute lost haplotypic diversity due to missing segments as a sweep.
Robustness of α-DAWG Models Against Class Imbalance
Class imbalance during training can potentially cause the trained machine learning models to be biased toward more accurately predicting the major class at the expense of the minor class (Libbrecht and Noble 2015), making the exploration of classifier robustness to such settings important. Moreover, a minority of the genome is expected to be evolving under positive selection (Sabeti et al. 2006), and so we expect that in many empirical applications, the sweep class would be a minor class within the test (empirical) set. We therefore set out to explore whether α-DAWG models are able to surmount class imbalance in the training and test sets using precision-recall curves. Precision is defined as the proportion of true positives among all the predictions that are positives, whereas recall is the proportion of true positives among actual positives in a dataset. Precision-recall curves provide a more transparent view of classifier performance than ROC curves under class imbalance. To evaluate the effect of training imbalance, we considered training sets of 10,000 observations, each with different combinations of observations from each class that ranged from balanced (5,000 observations per class) to severely imbalanced (1,000 observations in one class and 9,000 in the remaining class). Furthermore, to assess the impact of testing imbalance, we considered training sets of 10,000 observations per class and test sets composed of varying combinations of observations from each class that ranged from balanced (500 observations per class) to severely imbalanced (100 observations in one class and 900 in the remaining class), totaling 1,000 observations per test set.
Our results show that despite infusing severe class imbalance during training, all linear α-DAWG models exhibit high precision for the majority of the recall range (supplementary fig. S14, Supplementary Material online). This excellent performance is further accentuated by the area under the precision-recall curve (AUPRC), which shows that all linear α-DAWG models have an AUPRC ranging from 96.23% to 99.15% (supplementary fig. S14, Supplementary Material online). Specifically, when linear α-DAWG models are trained with a balanced dataset (5,000 observations per class), the AUPRC is highest (ranging from 97.17% to 99.15%), whereas the lowest AUPRC (96.23%) is obtained when only 1,000 of the training observations were neutral (supplementary fig. S14, Supplementary Material online). These results suggest that class imbalance during training has only a minor affect on performance of linear α-DAWG. When it comes to resilience of linear α-DAWG models under imbalanced testing sets, all linear α-DAWG models have high AUPRC, ranging from 94.03 to 99.98% (supplementary fig. S15, Supplementary Material online). Moreover, in most cases, as the proportion of sweep observations increased, the AUPRC also increased (supplementary fig. S15, Supplementary Material online). Overall, the observed robustness to training imbalance is echoed by the results of testing imbalance.
Effect of Selection Strength on α-DAWG Models
Selection strength of a beneficial mutation influences the prominence of the valley of lost diversity left by a selective sweep, with stronger sweeps contributing to a wider sweep footprint on average (Willoughby et al. 2017; Roze 2021; Sultanov and Hochwagen 2022). Moreover, this adaptive parameter also impacts the sojourn time of the sweeping haplotypes, which may lead to the erosion of sweep footprints by recombination (Hamblin and Di Rienzo 2002; Pennings and Hermisson 2017; Garud 2023). Therefore, it is important to assess the ability of α-DAWG models to detect sweeps when the range of selection coefficients (s) is varied, to better understand the effectiveness of α-DAWG models under different selection regimes. To this end, we simulated sweep test replicates with selection strength that differs from the range used in the training set, which was drawn uniformly at random on a logarithmic scale. We instead simulated five test sets each with 1,000 sweep replicates, where the selection coefficient was drawn uniformly at random within the restricted ranges of , , , , or , and with all other genetic, demographic, and adaptive parameters identical to those of the CEU_2 dataset (see the section “Effect of population size fluctuations” for details).
Upon analyzing the sweep detection accuracy of three linear α-DAWG models, we find as expected that there is a pattern of increasing sweep detection accuracy as we move toward stronger sweeps (supplementary fig. S16, Supplementary Material online). Sweep detection accuracy is the lowest (in the range of 61% to 63%) when the replicates are drawn as that encompasses the weakest sweep strength and that is outside the range of selection coefficients used to train α-DAWG (supplementary fig. S16, Supplementary Material online). This low accuracy underscores the assumption that weaker adaptive alleles do not leave pronounced sweep footprints, thereby making it challenging for α-DAWG models to detect such sweeps, particularly as they are out of the training distribution. However, the sweep detection accuracy sharply increases to a minimum of 83.6% when s falls within the range used to train linear α-DAWG (supplementary fig. S16, Supplementary Material online), with detection rates reaching 92.7% for all three models for the strongest sweeps of (supplementary fig. S16, Supplementary Material online). Overall, linear α-DAWG models show greater ability to detect sweeps as adaptive strength increases, with detection rate significantly elevated when selection coefficients fall within in the range used to train the models.
We further went on to test the robustness of linear α-DAWG models when trained and tested on weaker sweeps. We simulated an additional 10,000 sweep replicates for training and 1,000 sweep replicates for testing with selection coefficients in the range drawn uniformly at random on a logarithmic scale, keeping other genetic, demographic, and selective parameters identical to the CEU_2 dataset. Under this setting, we find that linear α-DAWG models exhibit overall accuracies ranging from 89.05 to 89.55% (supplementary fig. S17, Supplementary Material online), which is roughly 4% lower than the accuracies from the original model trained with stronger sweeps with coefficients (Fig. 4). This reduction in overall accuracy is unsurprising, given that selection coefficients of the training and test sweep replicates () are smaller than those of roughly 50% of the sweep replicates in our original protocol (). Because sweep footprints under this weaker setting would lead to greater class overlap between neutral and sweep replicates, it is more difficult to distinguish positive selection from neutrality. The ROC curves also echo the diminished performance, with lower true positive rates at small false positive rates (first panel of supplementary fig. S17, Supplementary Material online). These results may partially explain the surprising finding that population bottlenecks did not significantly reduce classification accuracy of linear α-DAWG models (Fig. 4) compared with a constant size demographic history (Fig. 2), suggesting that maintenance of overall high classification accuracy may be explained in part by replicates with strong selection coefficients. Overall, linear α-DAWG models show an expected dip in terms of overall accuracy when trained and tested on weaker sweeps compared with original results.
Application to a European Human Genomic Dataset
So far we have shown that α-DAWG performs well on simulated datasets. To examine its efficacy on real world data, we applied it to whole-genome haplotype data from a CEU human population (CEU) in the 1,000 Genomes Project dataset (The 1000 Genomes Project Consortium 2015). We utilize this population as it is historically well-studied for signals of selection and, therefore, provides a setting to evaluate whether α-DAWG can uncover expected and well-established sweep candidate genes. To train α-DAWG, we employ 10,000 simulation replicates per class for neutral and sweep settings, simulated under the same protocol as the CEU_2 dataset, with the exception that we sample 198 haplotypes instead of 200 to match the CEU empirical dataset. We chose to employ the nonlinear α-DAWG[W-C] model for our empirical application, as we expect empirical data to contain missing genomic segments and in our missing data experiments involving two different settings, nonlinear α-DAWG[W-C] shows higher overall classification accuracy compared with the other two nonlinear α-DAWG models (supplementary figs. S10 and S13, Supplementary Material online). This promise of nonlinear α-DAWG[W-C] for empirical application is further substantiated by its superior performance over linear α-DAWG[W-C] on ideal settings for a realistic demographic history (i.e. CEU_2) (compare supplementary figs. S8 and S10, Supplementary Material online).
To initially explore the consistency in empirical predictions among α-DAWG models, we examine the overlap of sweep probability windows above a certain threshold among different α-DAWG models. We chose the threshold to be 0.9 averaged across seven consecutive windows (supplementary fig. S18a, Supplementary Material online) in one scenario and chose this cutoff to be greater than the 99th percentile of the probabilities for a given α-DAWG model (supplementary fig. S18b, Supplementary Material online) in another scenario. Our results suggest that the nonlinear α-DAWG[W-C] model, which we focus on in our empirical analysis, has 96.5% of its windows that are above a probability cutoff of 0.9 are also identified by the linear α-DAWG[W-C] model with the same probability threshold (supplementary fig. S18a, Supplementary Material online). Conversely, 98% of such windows in the linear α-DAWG[W-C] model reach the threshold in the nonlinear α-DAWG[W-C] model (supplementary fig. S18a, Supplementary Material online).
We also find similar concordance in the nonlinear α-DAWG[C] model, such that 94.1% and 86.3% of its windows passing the probability cutoff of 0.9 are also identified by the linear α-DAWG[C] and α-DAWG[W-C] models, respectively (supplementary fig. S18a, Supplementary Material online). While such windows exceeding the threshold in the linear α-DAWG[W-C] model are also uncovered by the linear α-DAWG[C] model (90.7% of windows), there is a lack of reproducibility of these windows in the nonlinear α-DAWG[C] scan (37.1% of windows). In contrast to these results, when it comes to the threshold that is above 99th percentile of the probabilities for each model, we find that any two models show symmetry in their overlapping windows (supplementary fig. S18b, Supplementary Material online). For both thresholds employed, the pair of models that yield the highest similarity in general utilize the same decomposition input (W, C, or W-C) (supplementary fig. S18, Supplementary Material online), though there exist some exceptions. Also, we find pairs of models where one is employing solely wavelets (e.g. α-DAWG[W]) and the other is either using curvelets (e.g. α-DAWG[C]) or a combination of wavelets and curvelets (e.g. α-DAWG[W-C]) are highly dissimilar (similarity score zero or close to zero), which alludes to less concordance between a wavelet-based model and a model that uses wavelet features only in part or not at all. Overall, α-DAWG models are able to recapitulate the sweep signals of other α-DAWG models with moderate to high degree of concordance when both models in question employ curvelets either in a standalone model (e.g. α-DAWG[C]) or in a combined model with wavelets (e.g. α-DAWG[W-C]).
Applying the nonlinear α-DAWG[W-C] model,the overall pattern in α-DAWG predictions across the genome suggests that, as expected, sweeps are generally rare in humans (supplementary fig. S19, Supplementary Material online), with 1.56% of classified windows with a sweep probability greater than 0.9. These results suggest that α-DAWG is robust to potential technical artifacts and forces that lead to patterns other than sweeps, which may mislead a classifier to predict sweeps with high confidence. We next sought to identify candidate genes that show characteristic sweep patterns by finding peaks with high mean predicted sweep probability. Specifically, to average out potential noise from a single window with high sweep probability and for smoothness, we computed mean predicted sweep probabilities through a seven-point moving average across sweep windows, spanning three windows before and after a given target window. We define these peaks as the genomic interval in which this seven-point moving average of predicted sweep probabilities increases from below to above followed by a decline to below . We find that of windows have sweep probability greater than 0.9 following this averaging process (supplementary table S1, Supplementary Material online), and list the associated autosomal regions in supplementary table S2, Supplementary Material online. We further present genes ranked in the order of their peak probabilities (supplementary table S3, Supplementary Material online), and highlight some candidates that either are supported by previous literature (Fig. 8) or are novel candidates (Fig. 9) with noteworthy associations to various immune functions or diseases.
Fig. 8.
Probabilities of sweep in select positions of interest of genome of CEU population. The plots are smoothed by seven-point moving average. The locations of the genes are marked by the shaded regions. The figure shows predictions of selective sweeps made by nonlinear α-DAWG[W-C] that agree with existing literature.
Fig. 9.
Probabilities of sweep in select positions of interest of genome of CEU population. The plots are smoothed by seven-point moving average. The locations of the genes are marked by the shaded regions. The figure shows the novel predictions of selective sweeps made by nonlinear α-DAWG[W-C].
As expected, α-DAWG identified high sweep support at LCT (Fig. 8a) on chromosome two, which is widely accepted as having undergone past positive selection (Bersaglieri et al. 2004). The LCT gene is responsible for lactase persistence, which has recently evolved due to increased consumption of animal milk and other dairy products (Sabeti et al. 2006). Based on the plotted probabilities around the LCT region on chromosome two (Fig. 8a), we observe a sharp spike in probability at the location of LCT. Upstream of LCT, α-DAWG predicts another gene, ZRANB3, to have high sweep support (Fig. 8b), which echos a prior finding of Liu et al. (2013). ZRANB3 helps repair DNA lesions, allowing the DNA replication process to continue on an undamaged DNA strand without introducing mutations (Weston et al. 2012; Sebesta et al. 2017).
Among the other candidates for sweep uncovered by α-DAWG is the ALDH2 gene on chromosome 12 (Fig. 8c), for which a selective sweep is also supported by Oota et al. (2004). ALDH2 is responsible for intolerance to large quantities of alcohol (Chang et al. 2017). We also have found evidence for a selective sweep at the HLA-DQB1 gene (Fig. 8d) within the major histocompatibility complex (MHC) on chromosome six. MHC is a family of closely related and highly polymorphic genes that code for cell surface proteins that are involved in adaptive immune system (Mignot et al. 1997). HLA-DQB1 is part of the subfamily of MHC molecules termed MHC class II, which are responsible for providing instructions for producing proteins that are responsible for initiating immune responses (Janeway Jr et al. 2001). Due to their high polymorphism, MHC genes are also widely thought to evolve under balancing selection (Bernatchez and Landry 2003), but recent studies have also found evidence for past positive selection acting on genes within the MHC (Meyer and Thomson 2001; Goeury et al. 2018; Harris and DeGiorgio 2020a). SIGLEC-L1 on chromosome 19 is another of α-DAWG sweep prediction (Fig. 8e). Gagneux and Varki (1999) argued that this gene might be under positive selection due to its potential involvement in host-pathogen interactions. The ZP3 gene on chromosome seven is also detected by α-DAWG (Fig. 8f), with evidence for positive selection at this gene supported by previous studies (e.g. Hart et al. 2018). ZP3 encodes zonal pellucida glycoproteins, which comprise the protective coating of the eggs and precipitates sperm-egg recognition during fertilization (Litscher et al. 2009). This finding is also compatible with the results of Schrider and Kern (2017), which found an enrichment of candidate sweep genes that were involved in sperm-egg recognition,
In addition to finding instances of selective sweeps that have already been identified in the literature, α-DAWG also uncovers several novel sweep candidates with high support and that exhibit haplotype patterns consistent with sweeps for which we observe extended regions with high frequencies of major alleles coincident with high α-DAWG sweep probabilities (supplementary fig. S20, Supplementary Material online). One of these candidates is CCZ1 on chromosome seven (Fig. 9a), which facilitates GDP/GTP exchange (Gerondopoulos et al. 2012). α-DAWG also classifies the gene SLX9 on chromosome 21 as undergoing positive selection (Fig. 9b), which is a protein-coding gene thought to be involved in the creation of ribosomes through ribosome biogenesis in the nucleolus (Fischer et al. 2015). Another identified candidate gene is PCNX2 on chromosome one (Fig. 9c), which is involved in tumorigenesis of colorectal carcinomas with high microsatellite instability (Kim et al. 2002). MYH14 on chromosome 19 shows high predicted sweep probability as well (Fig. 9d), and is part of the Myosin superfamily, which is responsible for cytokinesis, cell motility, and cell polarity (Donaudy et al. 2004). Moreover, MYH14 has also been implicated in tumor development (De Miranda et al. 2014; Landau et al. 2015). α-DAWG identified MSR1 on chromosome eight with high sweep probability (Fig. 9e), and this gene has been implicated in atherosclerosis, Alzheimer’s disease (Herber et al. 2010), and prostate cancer (Hsing et al. 2007). As a final example, MAPK4 on chromosome 19 is also identified as undergoing positive selection by α-DAWG (Fig. 9f). MAPK4 is a member of the mitogen-activated protein kinase family, which is involved in breast cancer (Wang et al. 2022). This pattern of detecting sweeps at cancer-related genes was also found by a number of prior studies (Lou et al. 2014; Schrider and Kern 2017, 2018; Mughal et al. 2020; Amin et al. 2023; Arnab et al. 2023). In particular, past sweeps may have caused deleterious alleles to hitchhike to high frequency due to linked selection (Schrider and Kern 2017), leading to combinations of alleles that may contribute to contemporary maladaptive phenotypes. These results hint at an interesting pattern that many past positively selected alleles reside in genes that are currently involved in cancer within humans.
Furthermore, we sought to examine the correlation of the nonlinear α-DAWG[W-C] scores at candidate genes with a more traditional method. For comparison, we chose to scan the CEU population data using (Ferrer-Admetlla et al. 2014), which evaluates how haplotype homozygosity decays with distance from a test SNP, and use the implementation within selscan (Szpiech and Hernandez 2014) while normalizing the scores within frequency bins across the genome. To assign a score to each gene, we used a score for α-DAWG as the peak seven-point moving averaged sweep probability predicted by the nonlinear α-DAWG[W-C] falling within each gene and for we chose the peak absolute score intersecting each gene. We retained only genes for which both and the nonlinear α-DAWG[W-C] model had a value. To assess correlation between these two methods, we employed both the Spearman rank correlation and the Pearson correlation, with the Pearson correlation computed on the scores that have been adjusted by Box-Cox transformations (Box and Cox 1964; Griffith et al. 1998) to satisfy normality assumptions as well as possible. For both approaches, we estimated a correlation coefficient to be roughly 0.15 with significant P-values for the Spearman and Pearson correlation tests of and , respectively. Furthermore, we found that 178 shared genes exceed the 90th percentile for both and nonlinear α-DAWG[W-C] score distributions. The extremely small P-values indicate statistically significant relationships and given the large sample size of genes considered, the correlation coefficients, though small, suggest a reliable association between the scores yielded by and nonlinear α-DAWG[W-C].
Discussion
In this article, we have implemented a framework termed α-DAWG for detecting genomic windows with footprints of past adaptation. In particular, α-DAWG uses α-molecules to extract features from image representations of haplotype alignments, which are then used as input to machine learning classifiers. We have tested the true positive rate and accuracy of both linear and nonlinear models combined with α-molecule feature extraction through wavelet and curvelet transformed data (Figs. 2, 4, and supplementary fig. S8, Supplementary Material online). We have also tested α-DAWG on data with missing genomic regions and demonstrated that it is robust against such common technical artifacts in modern sequencing data (Fig. 7, supplementary figs. S10, S12, and S13, Supplementary Material online). None of the variants of α-DAWG perform decisively and consistently better than the others, yet all display better true positive rate and accuracy than a leading CNN-based sweep classifier ImaGene in most cases. Moreover, we collected the regression coefficients from our trained linear and nonlinear α-DAWG models into dimensional coefficient matrices (the same size as the input data), which enable interpretability of the trained models by highlighting particular regions of haplotype alignments that the models place greatest emphasis (Figs. 2, 4, and supplementary fig. S9, Supplementary Material online).
In addition to classification tasks, the α-DAWG modeling framework can be retooled for regression tasks by changing the model response from a qualitative to a quantitative output. Such problems would include predicting adaptive and genetic parameters. For example, similar to Mughal et al. (2020), the model could be used to estimate the selection coefficient (s), frequency of the adaptive allele when it became beneficial (f), and the time at which the sweep completed (t) that we have drawn for creating the training and test datasets in this study. Estimation of such parameters would refine our understanding of the mechanisms specifically leading to sweep footprints. For instance, estimating s would provide information about how much adaptive pressure there was on the beneficial allele, f would help interpret whether selection occurred on a de novo mutation or on standing variation, and t would contribute to interpreting whether adaptive events coincide with other factors, such as past climate and pathogen pressures. Therefore, reframing α-DAWG as a regression model would allow us to glean additional insight about a population at identified adaptive regions.
To reliably train our α-DAWG models, substantially more training data are needed than when given hand-engineered features through summary statistics for a similar task (e.g. Lin et al. 2011; Schrider and Kern 2016; Sheehan and Song 2016; Kern and Schrider 2018; Mughal and DeGiorgio 2019; Mughal et al. 2020; Arnab et al. 2023). In exchange, the models have the property of universality, in the sense that we do not need to worry about choosing appropriate summary statistic features a priori, as the features are selected automatically with α-molecules. We therefore expect these methods to have a wider range of applications than those that employ hand-engineered features. These models are also interpretable, which is evident from the plots of the regression coefficients where we observe higher magnitude coefficients at the center of the matrix, corresponding to lower regions of diversity (Figs. 2, 4, and supplementary fig. S9, Supplementary Material online). These regression coefficient maps are similar to those used by Mughal et al. (2020) when employing hand-engineered summary statistics as input. Our regression coefficient maps represent an alternative to the class activation and saliency maps used by CNN models (Yu et al. 2015), which have been shown to also carry similar levels of interpretability for explaining models for detecting adaptation (Gower et al. 2021; Arnab et al. 2023).
The regression coefficient matrices in Figs. 2, 4, and supplementary fig. S9, Supplementary Material online indicate where to focus to uncover differences between neutral and sweep regions, which is along the center of the SNP axis. This finding agrees with what we have seen for the mean image representation of haplotype alignments in Fig. 1a. We also notice that coefficient matrices from wavelet models are coarser than those from curvelet models, which could be due to several reasons. First, wavelets do not provide directional specificity, meaning that wavelet basis functions cannot be aligned in different directions, and so the only way for wavelets to capture a particular feature in the signal is to move the wavelet basis to the position of the feature. Second, translation happens in discrete amounts, which leads to the coarse pattern in the wavelet model regression coefficients. Curvelets, on the other hand, can be aligned in different directions (in addition to translation), and so to capture any feature curvelets can rotate as well as translate (see supplementary fig. S21, Supplementary Material online for an illustration). This flexibility grants curvelets enhanced ability compared with wavelets to reproduce specific features, making the regression coefficient matrix smoother than the corresponding wavelet matrix (Fig. 1b and c). Third, the curvelet transform simply has a greater number of coefficients for each data sample than wavelets, even though curvelets are sparser than wavelets as most of the coefficients are estimated to be zero. This increased number of modeled features increases the α-DAWG penalization hyperparameter for curvelets more so than wavelets (Table 1), as more regularization is needed to reach an optimal effective number of features used in the model. This more aggressive regularization may contribute to the smoother regression coefficient matrices for curvelets compared with wavelets.
Despite curvelets reconstructing smoother appearing images than wavelets due to their anisotropic scaling properties (Fig. 1), the curvelet-based α-DAWG[C] models still do not significantly outperform the wavelet-based α-DAWG[W] models. A possible reason for this finding may lie in the nature of the data. In particular, the input images to α-DAWG models exhibit a block-like structure (first panel of Fig. 1c), which α-DAWG[W] may be capable of better exploiting as wavelets also produce a block-like structures (second panel of Fig. 1c), making for easier matching of patterns in such images. In contrast, curvelets are especially adept at detecting line-like edges or geometric shapes found in nature and are able to detect finer edges compared with wavelets (Gebäck and Koumoutsakos 2009; Ma and Plonka 2009; Mishra and Sharma 2022). Because the patterns found in our original input images are block-shaped and do not contain fine edges, the angular rotation capabilities of curvelets by themselves may not offer a significant advantage in our current α-DAWG framework. However, studies have found that images extracted from summary statistics, such as moments of pairwise linkage disequilibrium (Mughal et al. 2020) or the creation of two-dimensional images through spectral decomposition of summary statistic signals (Arnab et al. 2023) harbor structures that may deviate from block-like patterns, and curvelets may offer a more considerable edge on input images from such settings. Furthermore, curvelets may also aid in detection of selection in more complicated scenarios that may lead to peaks and valleys of diversity within a stretch of a chromosome, such as adaptive introgression (Setter et al. 2020) or balancing selection acting at multiple nearby loci (Barton and Navarro 2002; Navarro and Barton 2002; Tennessen 2018), due to their anisotropic scaling properties.
Considering the performances of α-DAWG models under different demographic histories, an interesting observation is that the models perform considerably well under bottleneck scenarios (i.e. the CEU demographic history), with performance metrics comparable to that under the equilibrium constant-size demographic history. This finding is somewhat surprising, as population bottlenecks can lead to significant variance in diversity along chromosomes that may give rise to sharp peaks and valleys that affect the local and global genetic diversity across the genome, resulting in challenges for detecting sweeps (Barton 1998; Thornton and Jensen 2007; Pavlidis et al. 2008). Yet, wavelet and curvelet transformations are able to capture features, including these sharp features, that contribute to components of the local and global structure of a signal (Hüpfel et al. 2008; Shan et al. 2009; Kobitski et al. 2021; Yulong et al. 2023). Because the -norm regularization penalty used in fitting the α-DAWG models encourages sparsity by performing feature selection, noise components due to sharp peaks and valleys that might be expected from population bottlenecks may be removed from the model. The removal of such noise components may be an important contributor to the comparable performance of α-DAWG models on the equilibrium and nonequilibrium demographic scenarios that we evaluated.
All three of our α-DAWG models were found to perform consistently better than ImaGene in all tested cases. However, there are several factors that may have led to this performance differential. First, for equal comparison among all test methods across experiments, we initially trained ImaGene using 10,000 observations per class, which is significantly fewer observations than the 50,000 per class used by Torada et al. (2019). Deep CNN architectures, like that of ImaGene, have enormous numbers of model parameters that need to be estimated and are notorious for requiring extensive amounts of training data to estimate such parameters (Chollet 2021). Keeping these data requirement in mind, we embarked on an experiment in which we supplied ImaGene with 30,000 training samples per class, while training α-DAWG on the same 10,000 training observations per class. We found that α-DAWG models having minimal numbers of parameters required fewer training observations to achieve a certain level of classification accuracy or true positive rate, whereas even after utilizing the additional training data, ImaGene lags behind α-DAWG. Other considerations are that, ImaGene resizes each observed input haplotype alignment to a dimensional matrix, whereas α-DAWG uses dimensional matrices as input. This smaller sized input matrix used by α-DAWG may help smooth away some noise within each input observation, making the signal within each haplotype alignment easier to extract.
The simulated datasets we have used in this article to train and test α-DAWG were from phased haplotypes. However, without high-enough quality genotypes and sufficiently large reference panels, phasing genotypes into haplotypes can be error prone. Importantly, such haplotype phasing may be currently impossible for certain study systems. As an alternative, α-DAWG could use as input unphased multilocus genotype alignments (Harris et al. 2018), which would each represent a string of the number (zero, one, or two) of minor alleles observed in the genotype of each individual at each SNP in the alignment, in contrast to the strings of zeros and ones that we employ for haplotype data. Such a conversion would reduce the effective sample size of the variation observed within a given genomic region, and would have less information than if phased haplotypes were available. Because of this, we would expect that using such data would reduce the true positive rate and accuracy of the α-DAWG models. However, a number of articles have demonstrated that the true positive rate and accuracy to detect sweeps and other evolutionary phenomena from unphased multilocus genotypes often remains high, just not as high as with phased haplotypes, and so conversion to such data remain a viable option (Harris et al. 2018; Kern and Schrider 2018; Mughal and DeGiorgio 2019; Adrion et al. 2020; Harris and DeGiorgio 2020a, 2020b; Mughal et al. 2020; DeGiorgio and Szpiech 2022).
We have used the proposed α-DAWG models to identify evidence of positive selection from genomic data. Wavelets and curvelets methods are well-suited for identifying characteristic features in signals and ignoring noise, and therefore the use of wavelet or curvelet coefficients instead of raw data to train the models ensures that identification of selective sweep is more heavily influenced by those characteristic features rather than other artifacts, like noise. As a result, the models are more accurate and more insensitive to imperfections in the data (e.g. noise or missing genomic segments), and are thus more robust to misclassification due to confounding factors. In addition, because of the flexibility that α-DAWG allows in terms of the type of data it can take as input (i.e. any two-dimensional image), this method can be used to solve a number of classification or prediction problems given appropriate training data, and thus represents a general framework for predictive modeling in evolutionary genomics.
Methods
Haplotype Alignment Processing
We found that processing haplotype alignments in a particular manner improves the performance of α-DAWG. Here, a haplotype alignment is a matrix in which rows are haplotypes, columns are biallelic SNPs, and the value in row i and column j is a zero if haplotype i has the major allele at SNP j and is a one if it has the minor allele. Because we use as input image representations of sorted haplotype alignments spanning a large physical distance of 1.1 Mb, true signals of reductions of haplotype diversity may be missed if selective sweeps were too soft, weak, or old, as their footprints may not span such a large window. Thus, the sorting of haplotype alignments within sweep regions may be too heavily affected by neutral loci unaffected by the sweeps. To tackle this issue, we constructed image representations of sorted haplotype alignments, where haplotypes are sorted locally in overlapping windows of a fixed number of SNPs (columns), and variation at SNPs in overlapping windows was subsequently averaged. Specifically, we create a new haplotype alignment by processing this haplotype alignment through several steps. Starting at the first column, we extract a submatrix of length 100 SNPs, and sort the rows in ascending order from top to bottom using the -norm, which will ensure that haplotypes with more major alleles are at the top of the submatrix and haplotypes with more minor alleles are at the bottom. Using a stride of 10 SNPs, we then extract subsequent submatrices of 100 SNPs (the final submatrix is discarded if it has fewer than 100 SNPs), and sort them in the same way. We then align the sorted submatrices such that each column of the submatrices occupies the same column index of the original matrix. We then average the number of minor alleles in a particular row and column across the corresponding elements of all sorted submatrices that aligned to the particular column. We then use the python library skimage (Pedregosa et al. 2011) with linear interpolation to resize this locally sorted haplotype alignment matrix to a dimensional matrix to facilitate wavelet and curvelet decomposition. A depiction of the haplotype alignment processing procedure employed by α-DAWG is presented in supplementary fig. S1, Supplementary Material online.
We have found that averaging in this way using the CEU_2 dataset yields at minimum about an 11.3% performance boost in terms of accuracy across all linear models (compare third row of Fig. 4 and first row of supplementary fig. S22, Supplementary Material online) and at minimum a 6.65% performance boost in terms of accuracy across all nonlinear models (compare fourth row of supplementary fig. S8, Supplementary Material online and second row of supplementary fig. S22, Supplementary Material online) relative to results obtained without using local sorting. A possible reason for this performance boost using local sorting is that local sorting ignores more distant drops in diversity and ignoring such drops is important, as the locally sorted windows in the central SNPs are unaffected by diversity at the periphery of the classified window.
Protocol for Simulating Population Genetic Variation
The four main datasets that we used to train and test α-DAWG models were of varying difficulty and cover both constant and fluctuating size demographic histories. For the constant size model, we chose diploid individuals (Takahata 1993), a mutation rate of per site per generation (Scally and Durbin 2012), and a recombination rate drawn from an exponential distribution with a mean of per site per generation (Payseur and Nachman 2000) and truncated at three times the mean (Schrider and Kern 2016). Each simulation modeled sequences drawn from a segment of the genome of length 1.1 Mb. In addition to these parameters, the selective sweep simulations had a beneficial mutation introduced at the center of the sequences (position 550 kb). This beneficial mutation evolved with per-generation selection coefficient s drawn uniformly at random on the interval (Mughal et al. 2020), permitting a consideration of moderate to strong selection positive selection. Furthermore, the frequency of the beneficial mutation when it becomes selected f was drawn uniformly at random on the interval , permitting a range of hard and soft sweep scenarios to be evaluated. Finally, we created two different datasets for each demographic history that depended on the number of generations in the past that the beneficial mutation becomes fixed t. For the Constant_1 dataset, which represented an ideal setting, we set to such that sampling happens immediately after the selective sweep completes, whereas for Constant_2 dataset, which represents a more complex scenario, we draw t uniformly at random on the interval . The second scenario permits more time for the signal of the completed sweep to erode due to neutral processes, thereby leading to potentially greater class overlap between the neutral and sweep settings. Similarly, for the fluctuating size demographic model, keeping the selection parameters the same as the constant size model, we generated two datasets of varying difficulty, such that the CEU_1 dataset was created when and the CEU_2 dataset was constructed by letting be drawn uniformly at random. We detail the demographic and simulation parameters on supplementary table S4, Supplementary Material online.
Training α-DAWG Classifiers to Detect Sweeps
We employ both linear and nonlinear classification algorithms to classify image representations of haplotype alignments as one of two classes: neutral or sweep. Specifically, we employ elastic net (- and -norms) penalized logistic regression and multilayer perceptrons for the linear and nonlinear algorithms. The linear models were trained using glmnet (Friedman et al. 2010), while the nonlinear models represented by a feed-forward neural network with an output layer consisting of one node with a sigmoid activation and one hidden layer consisting of eight hidden nodes each with a ReLU activation were trained with keras (Chollet 2015) using a TensorFlow backend (Abadi et al. 2015). To extract features from the image representations of haplotype alignments, we perform wavelet and curvelet analysis to estimate basis expansion coefficients, which are then subsequently fed into the classifiers for training. The wavelet transform was performed with the waveslim (Whitcher 2005), and selected Daubechies wavelets as they have been demonstrated to have an edge over other forms of wavelet and perform well in empirical applications involving signal processing (Lina 1998; Ding and Cao 2011). In particular, we chose Daubechies least asymmetric wavelets as they provide better smoothness and more vanishing moments than many other wavelet forms (Usevitch 2001), and this smoothness has translated into smooth β maps for when attempting to understand the features that other population genetic classifiers place greatest emphasis (Mughal et al. 2020). More vanishing moments result in smaller high-frequency coefficients after the signal decomposition, which leads to more concentrated signal that results in better signal compression suitable for machine learning applications (Guo et al. 2022). Curvelet transform was accomplished with the curvelab package (Candes et al. 2005). Wavelet and curvelet analyses have the potential to provide greater control of the high-frequency components of decomposed images than Fourier analysis. Moreover, wavelet and curvelet analyses lead to fewer nonzero coefficients compared with Fourier analysis, yielding sparser models.
We use 5-fold cross validation over five detail levels of wavelet decomposition, regularization hyperparameter parameter λ, and hyperparameter controlling the proportion of -norm penalty during model fitting, to identify the optimum hyperparameters , , and , respectively. Note that for the curvelet-based models, we only considered hyperparameters λ and γ, as is not a parameter of the curvelet decomposition. During cross validation, we partitioned the data with 80% reserved for training and 20% for validation on each of the 5-folds, such that on each fold the training set consisted of 8,000 observations per class and the validation set 2,000 observations per class. The software glmnet searches automatically across the regularization hyperparameter (λ), whereas for the nonlinear model we performed an explicit search over a predefined grid of . The best-fit values for these hyperparameters estimated by cross validation are presented in Table 1 for the linear models and Table 2 for the nonlinear models. For our linear models trained with glmnet, we set the parameters family to “binomial”, nfolds to five, and type.measure to “deviance” during model fitting. For our nonlinear models, we employed the Adam optimizer (Kingma and Ba 2017) to find the minimum of the penalized cross entropy cost function through minibatch gradient descent applied to a batch size of 100 observations. We set the number of epochs to be 100, as in our initial experiments the binary cross-entropy loss on the validation set stabilized within the first 100 epochs. Moreover, for all α-DAWG implementations, the training features (wavelet and curvelet coefficients) were standardized to have a mean zero and unit standard deviation across all training observations. Validation and test observations were placed on the same scale, such that their features were standardized with the same mean and standard deviation parameters as the training features.
Also, when it comes to runtime, it takes on average s to create an image representation of a haplotype alignment followed by wavelet and curvelet decomposition using MacOS with 16 GB memory. For a training set size of 10,000 observations per class, running the linear models with 5-fold cross validation takes around 7 h on average per model, whereas the nonlinear models with 5-fold cross validation take around 5 h on average per model while working with 64 GB memory.
Training and Testing the ImaGene Classifier
To provide a benchmark for the results of our α-DAWG models, we compared α-DAWG to a state-of-the-art sweep classifier ImaGene (Torada et al. 2019), which also attempts to classify genomic regions as sweeps using image representations of sorted haplotype alignments—similar to α-DAWG. A key distinction between ImaGene and α-DAWG is that ImaGene uses CNNs to extract features from input images, whereas α-DAWG employs α-molecules. Moreover, ImaGene uses a different approach to mitigate model overfitting termed simulation-on-the-fly, in which new datasets are generated (simulated) for each training epoch of ImaGene. To ensure that α-DAWG and ImaGene are using the same training data to build models, we instead train ImaGene for multiple epochs and track the training and validation loss curves, where we used 9,000 and 1,000 observations per class for training and validation, respectively. We used the epoch with the smallest validation error to ultimately train the final ImaGene model. We trained ImaGene on the full set of 10,000 training observations per class, and tested ImaGene on an independent set of 1,000 test observations (the same training and test sets employed by α-DAWG). In another experiment, we trained ImaGene on 30,000 training observations per class and tested on the same 1,000 observations to see if training with a significantly larger dataset would improve performance. In this scenario involving 30,000 training observations per class, we used 27,000 and 3,000 observations per class for training and validation, respectively, and then retrained the entire ImaGene model on the full set of 30,000 training observations per class based on the number of epochs that results in the smallest validation loss.
Processing of European Human Genomic Data
We applied α-DAWG to the CEU human population from the 1,000 Genomes Project dataset (The 1000 Genomes Project Consortium 2015), which consisted of 99 diploid individuals and thus a sample of 198 haplotypes. Before application of α-DAWG, we performed several filtering operations to the dataset. First, we only retained biallelic nucleotide sites that were polymorphic (SNPs). We further removed SNPs with a minor allele count less than three, as Mughal et al. (2020) demonstrated that frequencies of singletons and doubletons were poorly predicted from the inferred CEU demographic model (Terhorst et al. 2017) that we employ to train α-DAWG.
Each chromosome was divided into windows of 1.1 Mb, with a stride length 10 kb. While processing the empirical data, we should remember that α-DAWG is trained to detect samples of sweeps where the region showing lost diversity is in the middle of the sampled sequence (Fig. 1a). For this reason, we employ a stride length of 10 kb so that many neighboring windows overlap in an attempt to ensure that any probable region of reduced diversity or sweep resides close to the middle of some window. At each 1.1 Mb window, we process haplotype alignments (see the section “Haplotype alignment processing”) before applying wavelet and curvelet transforms. We then apply denoizing on the wavelet and curvelet coefficients of the sampled windows. Denoizing is performed by thresholding or shrinkage, with absolute values of coefficients larger than a certain cutoff are left untouched, while coefficients smaller than the cutoff are set to zero. We chose to apply a simple scheme of thresholding for our purposes, which differs somewhat from more common thresholding approaches used on image processing or other applications (Antoniadis 1997). In particular, we set a cutoff based on percentiles rather than some fixed value, with all wavelet or curvelet coefficients larger in magnitude than the 99th percentile left untouched, while other coefficients set to zero. This procedure helps remove noise in addition to the - and -norm penalties enforced by elastic net. To train the α-DAWG classifier for application to these data, we used the CEU_2 dataset, but sampled only 198 haplotypes to match the sample size from the empirical data, and we applied the same filtering denoizing steps used for the empirical dataset.
To evaluate the effect of this denoizing protocol, we applied the identical procedure on the CEU_2 training and testing dataset. Our results indicate that though both the linear and nonlinear α-DAWG models have excellent true positive rate and overall accuracy (as high as 92.75%; supplementary fig. S23, Supplementary Material online), and these performance metrics only slightly lag behind those under settings where denoizing was not performed (compare supplementary fig. S23, Supplementary Material online with Fig. 4 and supplementary fig. S8, Supplementary Material online).
Supplementary Material
Acknowledgments
This work was supported by National Institutes of Health grant R35GM128590 and by National Science Foundation grants DBI-2130666, DEB-1949268, and BCS-2001063. Computations for this research were performed using the services provided by Research Computing at the Florida Atlantic University.
Contributor Information
Md Ruhul Amin, Department of Electrical Engineering and Computer Science, Florida Atlantic University, Boca Raton, FL 33431, USA.
Mahmudul Hasan, Department of Electrical Engineering and Computer Science, Florida Atlantic University, Boca Raton, FL 33431, USA.
Michael DeGiorgio, Department of Electrical Engineering and Computer Science, Florida Atlantic University, Boca Raton, FL 33431, USA.
Supplementary Material
Supplementary material is available at Molecular Biology and Evolution online.
Data Availability
We release the source code for α-DAWG under the MIT open source license, and this code can be accessed on GitHub (https://github.com/RuhAm/AlphaDAWG). This repository also includes the three linear and three nonlinear pretrained α-DAWG models, together with scripts for simulating training data and plotting results. The CEU data from the 1,000 Genomes Project can be accessed from the project website (https://www.internationalgenome.org/category/phase-3/). The CurveLab software used in our analysis for the curvelet transformation can be accessed at https://www.curvelet.org/.
References
- Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, et al. TensorFlow: large-scale machine learning on heterogeneous systems. [Software] available from tensorflow.org. https://www.tensorflow.org/. 2015.
- Adrion JR, Galloway JG, Kern AD. Predicting the landscape of recombination using deep learning. Mol Biol Evol. 2020:37(6):1790–1808. 10.1093/molbev/msaa038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akashi H, Osada N, Ohta T. Weak selection and protein evolution. Genetics. 2012:192(1):15–31. 10.1534/genetics.112.140178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amin MR, Hasan M, Arnab SP, DeGiorgio M. Tensor decomposition based feature extraction and classification to detect natural selection from genomic data. Mol Biol Evol. 2023:40(10):msad216. 10.1093/molbev/msad216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angermueller C, Pärnamaa T, Parts L, Stegle O. Deep learning for computational biology. Mol Syst Biol. 2016:12(7):878. 10.15252/msb.20156651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antoniadis A. Wavelets in statistics: a review. J Ital Stat Soc. 1997:6(2):97–130. 10.1007/BF03178905. [DOI] [Google Scholar]
- Arnab SP, Amin MR, DeGiorgio M. Uncovering footprints of natural selection through time-frequency analysis of genomic summary statistics. Mol Biol Evol. 2023:40(7):msad157. 10.1093/molbev/msad157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azodi CB, Tang J, Shiu S. Opening the black box: interpretable machine learning for geneticists. Trends Genet. 2020:36(6):442–455. 10.1016/j.tig.2020.03.005. [DOI] [PubMed] [Google Scholar]
- Barton NH. The effect of hitch-hiking on neutral genealogies. Genet Res. 1998:72:123–133. 10.1017/S0016672398003462. [DOI] [Google Scholar]
- Barton NH, Navarro A. Extending the coalescent to multilocus systems: the case of balancing selection. Genet Res. 2002:79(2):129–140. 10.1017/S0016672301005493. [DOI] [PubMed] [Google Scholar]
- Baudat F, Buard J, Grey C, Fledel-Alon A, Ober C, Przeworski M, Coop G, de Massy B. PRDM9 is a major determinant of meiotic recombination hotspots in humans and mice. Science. 2010:327(5967):836–840. 10.1126/science.1183439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernatchez L, Landry C. MHC studies in nonmodel vertebrates: what have we learned about natural selection in 15 years? J Evol Biol. 2003:16(3):363–377. 10.1046/j.1420-9101.2003.00531.x. [DOI] [PubMed] [Google Scholar]
- Bersaglieri T, Sabeti PC, Patterson N, Vanderploeg T, Schaffner SF, Drake JA, Rhodes M, Reich DE, Hirschhorn JN. Genetic signatures of strong recent positive selection at the lactase gene. Am J Hum Genet. 2004:74(6):1111–1120. 10.1086/421051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Booker TR, Yeaman S, Whitlock MC. Variation in recombination rate affects detection of outliers in genome scans under neutrality. Mol Ecol. 2020:29(22):4274–4279. 10.1111/mec.v29.22. [DOI] [PubMed] [Google Scholar]
- Box GEP, Cox DR. An analysis of transformations. Roy Stat Soc. 1964:26:211–243. 10.1111/j.2517-6161.1964.tb00553.x. [DOI] [Google Scholar]
- Boyko AR, Williamson SH, Indap AR, Degenhardt J, Hernandez RD, Lohmueller KE, Adams MD, Schmidt S, Sninsky JJ, Sunyaev SR, et al. Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet. 2008:4(5):e1000083. 10.1371/journal.pgen.1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braverman JM, Hudson RR, Kaplan NL, Langley CH, Stephan W. The hitchhiking effect on the site frequency spectrum of DNA polymorphisms. Genetics. 1995:140(2):783–796. 10.1093/genetics/140.2.783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bromham L. Why do species vary in their rate of molecular evolution? Biol Lett. 2009:5:401–404. 10.1098/rsbl.2009.0136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bromham L. The genome as a life-history character: why rate of molecular evolution varies between mammal species. Philos Trans R Soc Lond B Biol Sci. 2011:366(1577):2503–2513. 10.1098/rstb.2011.0014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bromham L, Hua X, Lanfear R, Cowman PF. Exploring the relationships between mutation rates, life history, genome size, environment, and species richness in flowering plants. Am Nat. 2015:185(4):507–524. 10.1086/680052. [DOI] [PubMed] [Google Scholar]
- Burger KE, Pfaffelhuber P, Baumdicker F. Neural networks for self-adjusting mutation rate estimation when the recombination rate is unknown. PLoS Comput Biol. 2022:18(8):e1010407. 10.1371/journal.pcbi.1010407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Candes E, Demanet L, Donoho D, Ying L. Fast discrete curvelet transforms. Multiscale Model Simul. 2006:5(3):861–899. 10.1137/05064182X. [DOI] [Google Scholar]
- Candes EJ, Demanet L, Donoho DL, Ying L. Curvelab toolbox. Version 2.0. CIT. 2005.
- Castellano D, Eyre-Walker A, Munch K. Impact of mutation rate and selection at linked sites on DNA variation across the genomes of humans and other homininae. Genome Biol Evol. 2020:12(1):3550–3561. 10.1093/gbe/evz215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cecil RM, Sugden LA. On convolutional neural networks for selection inference: revealing the lurking role of preprocessing, and the surprising effectiveness of summary statistics. PLoS Comput Biol. 2023:19(11):e1010979. 10.1371/journal.pcbi.1010979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan J, Perrone V, Spence J, Jenkins P, Mathieson S, Song Y. A likelihood-free inference framework for population genetic data using exchangeable neural networks. Adv Neural Inf Process Syst. 2018:31:8594–8605. 10.1101/267211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang JS, Hsiao JR, Chen CH. ALDH2 polymorphism and alcohol-related cancers in asians: a public health perspective. J Biomed Sci. 2017:24(1):1–10. 10.1186/s12929-017-0327-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B. The effects of deleterious mutations on evolution at linked sites. Genetics. 2012:190(1):5–22. 10.1534/genetics.111.134288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B. The role of background selection in shaping patterns of molecular evolution and variation: evidence from variability on the Drosophila X chromosome. Genetics. 2012:191(1):233–246. 10.1534/genetics.111.138073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B, Morgan MT, Charlesworth D. The effect of deleterious mutations on neutral molecular variation. Genetics. 1993:134(4):1289–1303. 10.1093/genetics/134.4.1289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B, Nordborg M, Charlesworth D. The effects of local selection, balanced polymorphism and background selection on equilibrium patterns of genetic diversity in subdivided populations. Genetics. 1997:70:155–174. 10.1017/S0016672397002954. [DOI] [Google Scholar]
- Charlesworth D, Charlesworth B, Morgan MT. The pattern of neutral molecular variation under the background selection model. Genetics. 1995:141(4):1619–1632. 10.1093/genetics/141.4.1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng X, Xu C, DeGiorgio M. Fast and robust detection of ancestral selective sweeps. Mol Ecol. 2017:26(24):6871–6891. 10.1111/mec.2017.26.issue-24. [DOI] [PubMed] [Google Scholar]
- Chollet F. Keras; 2015. https://github.com/fchollet/keras.
- Chollet F. Deep learning with python. New York (NY): Simon and Schuster; 2021. [Google Scholar]
- Chun S, Fay JC. Identification of deleterious mutations within three human genomes. Genome Res. 2009:19(9):1553–1561. 10.1101/gr.092619.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeron JM. Background selection as baseline for nucleotide variation across the Drosophila genome. PLoS Genet. 2014:10(6):e1004434. 10.1371/journal.pgen.1004434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutter AD, Payseur BA. Genomic signatures of selection at linked sites: unifying the disparity among species. Nat Rev Genet. 2013:14(4):262–274. 10.1038/nrg3425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cybenko G. Approximation by superpositions of a sigmoidal function. Math Control. 1989:2(4):303–314. 10.1007/BF02551274. [DOI] [Google Scholar]
- Dabi A, Schrider DR. Population size rescaling significantly biases outcomes of forward-in-time population genetic simulations. Genetics. 2024. 10.1093/genetics/iyae180. Published online ahead of print. [DOI] [Google Scholar]
- Daubechies I. Orthonormal bases of compactly supported wavelets. Commun Pur Appl Math. 1988:11(7):909–996. 10.1002/cpa.3160410705. [DOI] [Google Scholar]
- Daubechies I. Ten lectures on wavelets. Philadelphia (PA): SIAM; 1992. [Google Scholar]
- DeGiorgio M, Huber CD, Hubisz MJ, Hellmann I, Nielsen R. Sweepfinder2: increased sensitivity, robustness and flexibility. Bioinformatics. 2016:32(12):1895–1897. 10.1093/bioinformatics/btw051. [DOI] [PubMed] [Google Scholar]
- DeGiorgio M, Szpiech ZA. A spatially aware likelihood test to detect sweeps from haplotype distributions. PLoS Genet. 2022:18(4):e1010134. 10.1371/journal.pgen.1010134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Miranda NF, Georgiou K, Chen L, Wu C, Gao Z, Zaravinos A, Lisboa S, Enblad G, Teixeira MR, Zeng Y, et al. Exome sequencing reveals novel mutation targets in diffuse large B-cell lymphomas derived from Chinese patients. Blood. 2014:124(16):2544–2553. 10.1182/blood-2013-12-546309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillon MM, Sung W, Lynch M, Cooper VS. Periodic variation of mutation rates in bacterial genomes associated with replication timing. MBio. 2018:9(4). 10.1128/mBio.01371-18. [DOI] [Google Scholar]
- Ding F, Cao T. Application of Daubechies wavelet transform in the estimation of standard deviation of white noise. Proc Second Int Conf Digit Manuf Autom. 2011:212–215. 10.1109/ICDMA.2011.59. [DOI] [Google Scholar]
- Donaudy F, Snoeckx R, Pfister M, Zenner HP, Blin M, Di Stazio M, Ferrara A, Lanzara C, Ficarella R, Declau F, et al. Nonmuscle myosin heavy-chain gene MYH14 is expressed in cochlea and mutated in patients affected by autosomal dominant hearing impairment (DFNA4). Am J Hum Genet. 2004:74(4):770–776. 10.1086/383285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enard D, Messer PW, Petrov DA. Genome-wide signals of positive selection in human evolution. Genome Res. 2014:24(6):885–895. 10.1101/gr.164822.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fagny M, Patin E, Enard D, Barreiro LB, Quintana-Murci L, Laval G. Exploring the occurrence of classic selective sweeps in humans using whole-genome sequencing data sets. Mol Biol Evol. 2014:31(7):1850–1868. 10.1093/molbev/msu118. [DOI] [PubMed] [Google Scholar]
- Ferrer-Admetlla A, Liang M, Korneliussen T, Nielsen R. On detecting incomplete soft or hard selective sweeps using haplotype structure. Mol Biol Evol. 2014:31(5):1275–1291. 10.1093/molbev/msu077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer U, Schäuble N, Schütz S, Altvater M, Chang Y, Faza MB, Panse VG. A non-canonical mechanism for Crm1-export cargo complex assembly. Elife. 2015:4:e05745. 10.7554/eLife.05745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flagel L, Brandvain Y, Schrider DR. The unreasonable effectiveness of convolutional neural networks in population genetic inference. Mol Biol Evol. 2019:36(2):220–238. 10.1093/molbev/msy224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J Stat Softw. 2010:33(1):1–22. 10.18637/jss.v033.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabaix X. A sparsity-based model of bounded rationality. Q J Econ. 2014:129:1661–1710. 10.1093/qje/qju024. [DOI] [Google Scholar]
- Gagneux P, Varki A. Evolutionary considerations in relating oligosaccharide diversity to biological function. Glycobiology. 1999:9(8):747–755. 10.1093/glycob/9.8.747. [DOI] [PubMed] [Google Scholar]
- Galetto R, Véron M, Negroni M, Giacomoni V. Dissection of a circumscribed recombination hot spot in HIV-1 after a single infectious cycle. J Biol Chem. 2006:281(5):2711–2720. 10.1074/jbc.M505457200. [DOI] [PubMed] [Google Scholar]
- Garud NR. Understanding soft sweeps: a signature of rapid adaptation. Nat Rev Genet. 2023:24(7):420–420. 10.1038/s41576-023-00585-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garud NR, Messer PW, Buzbas EO, Petrov DA. Recent selective sweeps in North American drosophila melanogaster show signatures of soft sweeps. PLoS Genet. 2015:11(2):e1005004. 10.1371/journal.pgen.1005004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebäck T, Koumoutsakos P. Edge detection in microscopy images using curvelets. BMC Bioinformatics. 2009:10. 10.1186/1471-2105-10-75. [DOI] [Google Scholar]
- Gerondopoulos A, Langemeyer L, Liang J, Linford A, Barr FA. BLOC-3 mutated in Hermansky-Pudlak syndrome is a Rab32/38 guanine nucleotide exchange factor. Curr Biol. 2012:22(22):2135–2139. 10.1016/j.cub.2012.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie JH. Population genetics: a concise guide. Baltimore (MD): JHU Press; 2004. [Google Scholar]
- Goeury T, Creary LE, Brunet L, Galan M, Pasquier M, Kervaire B, Langaney A, Tiercy J-M, Fernández-Viña MA, Nunes JM, et al. Deciphering the fine nucleotide diversity of full HLA class I and class II genes in a well-documented population from sub-saharan Africa. HLA. 2018:91(1):36–51. 10.1111/tan.2018.91.issue-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodfellow T, Bengio Y, Courville A. Deep learning. Cambridge (MA): MIT Press; 2016. [Google Scholar]
- Gower G, Picazo P, Lindgren F, Racimo F. Inference of population genetics parameters using discriminator neural networks: an adversarial Monte Carlo. bioRxiv 538386. 10.1101/2023.04.27.538386, 2023, preprint: not peer reviewed. [DOI] [Google Scholar]
- Gower G, Picazo PI, Fumagalli M, Racimo F. Detecting adaptive introgression in human evolution using convolutional neural networks. Elife. 2021:10:e64669. 10.7554/eLife.64669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granka JM, Henn BM, Gignoux CR, Kidd JM, Bustamante CD, Feldman MW. Limited evidence for classic selective sweeps in African populations. Genetics. 2012:192(3):1049–1064. 10.1534/genetics.112.144071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grey C, Baudat F, de Massy B. Genome-wide control of the distribution of meiotic recombination. PLoS Biol. 2009:7(2):e1000035. 10.1371/journal.pbio.1000035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffith DA, Paelinck JHP, van Gastel RA. Econometric advances in spatial modelling and methodology: essays in honour of jean paelinck. US: Springer; 1998. [Google Scholar]
- Grohs P, Keiper S, Kutyniok G, Schäfer M. α-molecules; 2014.
- Guo T, Zhang T, Lim E, Lopez-Benitez M, Ma F, Yu L. A review of wavelet analysis and its applications: challenges and opportunities. IEEE Access. 2022:10. 10.1109/ACCESS.2022.3179517. [DOI] [Google Scholar]
- Haller BC, Messer PW. SLiM 3: forward genetic simulations beyond the Wright–Fisher model. Mol Biol Evol. 2019:36:632–637. 10.1093/molbev/msy228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller BC, Messer PW. SLiM 4: multispecies eco-evolutionary modeling. Am Nat. 2023:201(5):E127–E139. 10.1086/723601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamblin MT, Di Rienzo A. Detection of the signature of natural selection in humans: evidence from the duffy blood group locus. Am J Hum Genet. 2002:70(2):369–383. 10.1086/338628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamid I, Korunes KL, Schrider DR, Goldberg A. Localizing post-admixture adaptive variants with object detection on ancestry-painted chromosomes. Mol Biol Evol. 2023:40(4). 10.1093/molbev/msad074. [DOI] [Google Scholar]
- Harpak A, Bhaskar A, Pritchard JK. Mutation rate variation is a primary determinant of the distribution of allele frequencies in humans. PLoS Genet. 2016:12(12):e1006489. 10.1371/journal.pgen.1006489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris AM, DeGiorgio M. A likelihood approach for uncovering selective sweep signatures from haplotype data. Mol Biol Evol. 2020a:37(10):3023–3046. 10.1093/molbev/msaa115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris AM, DeGiorgio M. Identifying and classifying shared selective sweeps from multilocus data. Genetics. 2020b:215(1):143–171. 10.1534/genetics.120.303137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris AM, Garud NR, DeGiorgio M. Detection and classification of hard and soft sweeps from unphased genotypes by multilocus genotype identity. Genetics. 2018:210(4):1429–1452. 10.1534/genetics.118.301502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris K, Pritchard JK. Rapid evolution of the human mutation spectrum. Elife. 2017:6. 10.7554/eLife.24284. [DOI] [Google Scholar]
- Hart MW, Stover DA, Guerra V, Mozaffari SV, Ober C, Carina FM, Kaj I. Positive selection on human gamete-recognition genes. PeerJ. 2018:6:e4259. 10.7717/peerj.4259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The elements of statistical learning: data mining, inference, and prediction. 2nd ed. New York (NY): Springer; 2009. [Google Scholar]
- Hejase HA, Mo Z, Campagna L, Siepel A. A deep-learning approach for inference of selective sweeps from the ancestral recombination graph. Mol Biol Evol. 2022:39(1). 10.1093/molbev/msab332. [DOI] [Google Scholar]
- Hellenthal G, Stephens M. msHOT: modifying Hudson’s ms simulator to incorporate crossover and gene conversion hotspots. Bioinformatics. 2007:23(4):520–521. 10.1093/bioinformatics/btl622. [DOI] [PubMed] [Google Scholar]
- Herber DL, Cao W, Nefedova Y, Novitskiy SV, Nagaraj S, Tyurin VA, Corzo A, Cho H, Celis E, Lennox B, et al. Lipid accumulation and dendritic cell dysfunction in cancer. Nat Med. 2010:16(8):880–886. 10.1038/nm.2172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermisson J, Pennings PS. Soft sweeps: molecular population genetics of adaptation from standing genetic variation. Genetics. 2005:169(4):2335–2352. 10.1534/genetics.104.036947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermisson J, Pennings PS. Soft sweeps and beyond: understanding the patterns and probabilities of selection footprints under rapid adaptation. Methods Ecol Evol. 2017:8(6):700–716. 10.1111/mee3.2017.8.issue-6. [DOI] [Google Scholar]
- Hernandez RD, Kelley JL, Elyashiv E, Melton SC, Auton A, McVean G, 1000 Genomes Project, Sella G, Przeworski M. Classic selective sweeps were rare in recent human evolution. Science. 2011:331(6019):920–924. 10.1126/science.1198878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J. What’s so hot about recombination hotspots? PLoS Biol. 2004:2(6):e190. 10.1371/journal.pbio.0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989:2(5):359–366. 10.1016/0893-6080(89)90020-8. [DOI] [Google Scholar]
- Hsing AW, Sakoda LC, Chen J, Chokkalingam AP, Sesterhenn I, Gao Y, Xu J, Zheng SL. MSR1 variants and the risks of prostate cancer and benign prostatic hyperplasia: a population-based study in China. Carcinogenesis. 2007:28(12):2530–2536. 10.1093/carcin/bgm196. [DOI] [PubMed] [Google Scholar]
- Huber CD, DeGiorgio M, Hellmann I, Nielsen R. Detecting recent selective sweeps while controlling for mutation rate and background selection. Mol Ecol. 2016:25(1):142–156. 10.1111/mec.2016.25.issue-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL. The coalescent process in models with selection and recombination. Genetics. 1988:120(3):831–840. 10.1093/genetics/120.3.831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL. Deleterious background selection with recombination. Genetics. 1995:141(4):1605–1617. 10.1093/genetics/141.4.1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huerta-Sánchez E, Jin X, Bianba Z, Peter BM, Vinckenbosch N, Liang Y, Yi X, He M, Somel M, Ni P, et al. Altitude adaptation in tibetans caused by introgression of denisovan-like DNA. Nature. 2014:512(7513):194–197. 10.1038/nature13408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hüpfel M, Kobitski AY, Zhang W, Nienhaus GU. Wavelets, ridgelets, and curvelets for poisson noise removal. IEEE Trans Image Process. 2008:17. 10.1109/TIP.2008.924386. [DOI] [Google Scholar]
- Isildak U, Stella A, Fumagalli M. Distinguishing between recent balancing selection and incomplete sweep using deep neural networks. Mol Ecol Resour. 2021:21(8):2706–2718. 10.1111/men.v21.8. [DOI] [PubMed] [Google Scholar]
- Janeway CAJr, Travers P, Walport M, Shlomchik MJ. The major histocompatibility complex and its functions. Immunobiology: the immune system in health and disease. 5th ed. Cambridge (MA): Current Biology Limited; 2001. [Google Scholar]
- Jensen JD, Kim Y, DuMont VB, Aquadro CF, Bustamante CD. Distinguishing between selective sweeps and demography using dna polymorphism data. Genetics. 2005:170(3):1401–1410. 10.1534/genetics.104.038224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keinan A, Reich D. Human population differentiation is strongly correlated with local recombination rate. PLoS Genet. 2010:6(3):e1000886. 10.1371/journal.pgen.1000886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kern AD, Schrider DR. Discoal: flexible coalescent simulations with seleciton. Bioinformatics. 2016:24:3839–3841. 10.1093/bioinformatics/btw556. [DOI] [Google Scholar]
- Kern AD, Schrider DR. diploS/HIC: an updated approach to classifying selective sweeps. G3: Genes Genomes Genet. 2018:8(6):1959–1970. 10.1534/g3.118.200262. [DOI] [Google Scholar]
- Kim N, Rhee H, Li LS, Kim H, Lee J, Kim J, Kim NK, Kim H. Identification of MARCKS, FLJ11383 and TAF1B as putative novel target genes in colorectal carcinomas with microsatellite instability. Oncogene. 2002:21(33):5081–5087.. 10.1038/sj.onc.1205703. [DOI] [PubMed] [Google Scholar]
- Kingma DP, Ba J. Adam: a method for stochastic optimization, arXiv, arXiv:1412.6980, 10.48550/arXiv.1412.6980, preprint: not peer reviewed. 2017. [DOI] [Google Scholar]
- Kobitski AY, Zhang W, Nienhaus GU, Hüpfel M. Wavelet-based background and noise subtraction for fluorescence microscopy images. Biomed Opt Expr. 2021:12:969–980. 10.1364/BOE.413181. [DOI] [Google Scholar]
- Korfmann K, Gaggiotti OE, Fumagalli M. Deep learning in population genetics. Genome Biol Evol. 2023:15(2). 10.1093/gbe/evad008. [DOI] [Google Scholar]
- Korfmann K, Sellinger TPP, Freund F, Fumagalli M, Tellier A. Simultaneous inference of past demography and selection from the ancestral recombination graph under the beta coalescent. Peer Community J. 2024:4. 10.24072/pcjournal.397. [DOI] [Google Scholar]
- Kumar S, Subramanian S. Mutation rates in mammalian genomes. Proc Natl Acad Sci U S A. 2002:99:803–808. 10.1073/pnas.022629899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kyriazis CC, Robinson JA, Lohmueller KE. Using computational simulations to quantify genetic load and predict extinction risk. bioRxiv 503792. 10.1101/2022.08.12.503792, July 2022, preprint: not peer reviewed. [DOI] [Google Scholar]
- Landau DA, Tausch E, Taylor-Weiner AN, Stewart C, Reiter JG, Bahlo J, Kluth S, Bozic I, Lawrence M, Böttcher S, et al. Mutations driving CLL and their evolution in progression and relapse. Nature. 2015:526(7574):525–530. 10.1038/nature15395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauterbur ME, Munch K, Enard D. Versatile detection of diverse selective sweeps with flex-sweep. Mol Biol Evol. 2023:40(6): 10.1093/molbev/msad139. [DOI] [Google Scholar]
- LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 1998:86(11):2278–2324. 10.1109/5.726791. [DOI] [Google Scholar]
- Libbrecht MW, Noble WS. Machine learning applications in genetics and genomics. Nat Rev. 2015:16(6):321–332. 10.1038/nrg3920. [DOI] [Google Scholar]
- Lin K, Li H, Schlotterer C, Futschik A. Distinguishing positive selection from neutral evolution: boosting the performance of summary statistics. Genetics. 2011:187(1):229–244. 10.1534/genetics.110.122614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lina JM. Inverse problems, tomography, and image processing. Boston (MA): Springer US; 1998. [Google Scholar]
- Litscher ES, Williams Z, Wassarman PM. Zona pellucida glycoprotein ZP3 and fertilization in mammals. Mol Reprod Dev. 2009:76(10):933–941. 10.1002/mrd.v76:10. [DOI] [PubMed] [Google Scholar]
- Liu W, Chen W. Recent advancements in empirical wavelet transform and its applications. IEEE Access. 2019:7:103770–103780. 10.1109/Access.6287639. [DOI] [Google Scholar]
- Liu X, Ong RT, Pillai EN, Elzein AM, Small KS, Clark TG, Kwiatkowski DP, Teo Y. Detecting and characterizing genomic signatures of positive selection in global populations. Am J Hum Genet. 2013:92(6):866–881. 10.1016/j.ajhg.2013.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lou DI, McBee RM, Le UQ, Stone AC, Wilkerson GK, Demogines AM, Sawyer SL. Rapid evolution of BRCA1 and BRCA2 in humans and other primates. BMC Evol Biol. 2014:14(1):1–13. 10.1186/1471-2148-14-155. [DOI] [Google Scholar]
- Ma J, Plonka G. Computing with curvelets: from image processing to turbulent flows. Comput Sci Eng. 2009:11(2):72–80. 10.1109/MCSE.2009.26. [DOI] [Google Scholar]
- Mallick S, Gnerre S, Muller P, Reich D. The difficulty of avoiding false positives in genome scans for natural selection. Genome Res. 2009:19(5):922–933. 10.1101/gr.086512.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean GAT, Charlesworth B. The effects of hill-robertson interference between weakly selected mutations on patterns of molecular evolution and variation. Genetics. 2000:155(2):929–944. 10.1093/genetics/155.2.929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVicker G, Gordon D, Davis C, Green P. Widespread genomic signatures of natural selection in hominid evolution. PLoS Genet. 2009:5(5):e1000471. 10.1371/journal.pgen.1000471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer D, Thomson G. How selection shapes variation of the human major histocompatibility complex: a review. Ann Hum Genet. 2001:65(1):1–26. 10.1046/j.1469-1809.2001.6510001.x. [DOI] [PubMed] [Google Scholar]
- Mignone F, Gissi C, Liuni S, Pesole G. Untranslated regions of mRNAs. Genome Biol. 2002:3(3):1–10. 10.1186/gb-2002-3-3-reviews0004. [DOI] [Google Scholar]
- Mignot E, Hayduk R, Black J, Grumet FC, Guilleminault C. HLA DQB1*0602 is associated with cataplexy in 509 narcoleptic patients. Sleep. 1997:20:1012–1020. [PubMed] [Google Scholar]
- Mishra S, Sharma D. A review on curvelets and its applications. SCRS Conf Proc Int Syst. 2022:10:213–220. 10.52458/978-93-91842-08-6-20. [DOI] [Google Scholar]
- Mo Z, Siepel A. Domain-adaptive neural networks improve supervised machine learning based on simulated population genetic data. PLoS Genet. 2023:19(11):e1011032. 10.1371/journal.pgen.1011032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mughal MR, DeGiorgio M. Localizing and classifying adaptive targets with trend filtered regression. Mol Biol Evol. 2019:36(2):252–270. 10.1093/molbev/msy205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mughal MR, Koch H, Huang J, Chiaromonte F, DeGiorgio M. Learning the properties of adaptive regions with functional data analysis. PLoS Genet. 2020:16(8):e1008896. 10.1371/journal.pgen.1008896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers S, Bottolo L, Freeman C, McVean G, Donnelly P. A fine-scale map of recombination rates and hotspots across the human genome. Science. 2005:310:321–324. 10.1126/science.1117196. [DOI] [PubMed] [Google Scholar]
- Navarro A, Barton NH. The effects of multilocus balancing selection on neutral variability. Genetics. 2002:161(2):849–863. 10.1093/genetics/161.2.849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolaisen LE, Desai MM. Distortions in genealogies due to purifying selection and recombination. Genetics. 2013:195(1):221–230. 10.1534/genetics.113.152983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R, Williamson S, Kim Y, Hubisz MJ, Clark AG, Bustamante C. Genomic scans for selective sweeps using SNP data. Genome Res. 2005:15(11):1566–1575. 10.1101/gr.4252305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg M, Charlesworth B, Charlesworth D. The effect of recombination on background selection. Genet Res. 1996:67(2):159–174. 10.1017/S0016672300033619. [DOI] [PubMed] [Google Scholar]
- Oota H, Pakstis AJ, Bonne-Tamir B, Goldman D, Grigorenko E, Kajuna SLB, Karoma NJ, Kungulilo S, Lu R, Odunsi K, et al. The evolution and population genetics of the ALDH2 locus: random genetic drift, selection, and low levels of recombination. Ann Hum Genet. 2004:68(2):93–109. 10.1046/j.1529-8817.2003.00060.x. [DOI] [PubMed] [Google Scholar]
- Panigrahi M, Rajawat D, Nayak SS, Ghildiyal K, Sharma A, Jain K, Lei C, Bhushan B, Mishra BP, Dutt T. Landmarks in the history of selective sweeps. Anim Genet. 2023:54(6):667–688. 10.1111/age.v54.6. [DOI] [PubMed] [Google Scholar]
- Pavlidis P, Hutter S, Stephan W. A population genomic approach to map recent positive selection in model species. Mol Ecol. 2008:17(16):3585–3598. 10.1111/mec.2008.17.issue-16. [DOI] [PubMed] [Google Scholar]
- Payseur BA, Nachman MW. Micorsatelllite variation and recombination rate in the human genome. Genetics. 2000:156(3):1285–1298. 10.1093/genetics/156.3.1285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. Scikit-learn: machine learning in python. J Mach Learn Res. 2011:12:2825–2830. 10.48550/arXiv.1201.0490. [DOI] [Google Scholar]
- Peñalba JV, Wolf JBW. From molecules to populations: appreciating and estimating recombination rate variation. Nat Rev. 2020:21:476–492. 10.1038/s41576-020-0240-1. [DOI] [Google Scholar]
- Pennings PS, Hermisson J. Soft sweeps II—molecular population genetics of adaptation from recurrent mutation or migration. Mol Biol Evol. 2006:23(5):1076–1084. 10.1093/molbev/msj117. [DOI] [PubMed] [Google Scholar]
- Pennings PS, Hermisson J. Soft sweeps and beyond: understanding the patterns and probabilities of selection footprints under rapid adaptation. Methods Ecol Evol. 2017:8:700–716. [Google Scholar]
- Petes TD. Meiotic recombination hot spots and cold spots. Nat Rev Genet. 2001:2(5):360–369. 10.1038/35072078. [DOI] [PubMed] [Google Scholar]
- Przeworski M. The signature of positive selection at randomly chosen loci. Genetics. 2002:160(3):1179–1189. 10.1093/genetics/160.3.1179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pybus M, Luisi P, Dall’Olio GM, Uzkudun M, Laayouni H, Bertranpetit J, Engelken J. Hierarchical boosting: a machine-learning framework to detect and classify hard selective sweeps in human populations. Bioinformatics. 2015:31(24):3946–3952. 10.1093/bioinformatics/btv493. [DOI] [PubMed] [Google Scholar]
- Qin X, Chiang CWK, Gaggiotti OE. Deciphering signatures of natural selection via deep learning. Brief Bioinform. 2022:23(5):bbac354. 10.1093/bib/bbac354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray DD, Flagel L, Schrider DR. Introunet: identifying introgressed alleles via semantic segmentation. PLoS Genet. 2024:20(2):e1010657. 10.1371/journal.pgen.1010657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley R, Mathieson I, Mathieson S. Interpreting generative adversarial networks to infer natural selection from genetic data. Genetics. 2024:226. 10.1093/genetics/iyae024. [DOI] [Google Scholar]
- Ronen R, Udpa N, Halperin E, Bafna V. Learning natural selection from the site frequency spectrum. Genetics. 2013:195(1):181–193. 10.1534/genetics.113.152587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roze D. A simple expression for the strength of selection on recombination generated by interference among mutations. Proc Natl Acad Sci U S A. 2021:118(19). 10.1073/pnas.2022805118. [DOI] [Google Scholar]
- Rymbekova A, Huang X, Dolgova O, Lao O, Kuhlwilm M. Harnessing deep learning for population genetic inference. Nat Rev Genet. 2024:25:61–78. 10.1038/s41576-023-00636-3. [DOI] [PubMed] [Google Scholar]
- Sabeti PC, Schaffner SF, Fry B, Varilly P, Lohmueller J, Shamovsky O, Palma A, Mikkelsen TS, Altshuler D, Lander ES. Positive natural selection in the human lineage. Science. 2006:312(5780):1614–1620. 10.1126/science.1124309. [DOI] [PubMed] [Google Scholar]
- Sakharkar MK, Chow VTK, Kangueane P. Distributions of exons and introns in the human genome. In Silico Biol. 2004:4:387–393. [PubMed] [Google Scholar]
- Scally A, Durbin R. Revising the human mutation rate: implications for understanding human evolution. Nat Rev Genet. 2012:13(10):745–753. 10.1038/nrg3295. [DOI] [PubMed] [Google Scholar]
- Schrider DR. Background selection does not mimic the patterns of genetic diversity produced by selective sweeps. Genetics. 2020:216(2):499–519. 10.1534/genetics.120.303469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrider DR, Kern AD. S/HIC: robust identification of soft and hard sweeps using machine learning. PLoS Genet. 2016:12(3):e1005928–31. 10.1371/journal.pgen.1005928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrider DR, Kern AD. Soft sweeps are the dominant mode of adaptation in the human genome. Mol Biol Evol. 2017:34(8):1863–1877. 10.1093/molbev/msx154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrider DR, Kern AD. Supervised machine learning for population genetics: a new paradigm. Trends Genet. 2018:34(4):301–312. 10.1016/j.tig.2017.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebesta M, Cooper CD, Ariza A, Carnie CJ, Ahel D. Structural insights into the function of ZRANB3 in replication stress response. Nat Commun. 2017:8(1):15847. 10.1038/ncomms15847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seger J, Smith WA, Perry JJ, Hunn J, Kaliszewska ZA, Sala LL, Pozzi L, Rowntree VJ, Adler FR. Gene genealogies strongly distorted by weakly interfering mutations in constant environments. Genetics. 2010:184(2):529–545. 10.1534/genetics.109.103556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setter D, Mousset S, Cheng X, Nielsen R, DeGiorgio M, Hermisson J. VolcanoFinder: genomic scans for adaptive introgression. PLoS Genet. 2020:16(6):e1008867. 10.1371/journal.pgen.1008867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shan H, Ma J, Yang H. Comparisons of wavelets, contourlets, and curvelets in seismic denoising. J Appl Geophy. 2009:69(2):103–115. 10.1016/j.jappgeo.2009.08.002. [DOI] [Google Scholar]
- Sheehan S, Song YS. Deep learning for population genetic inference. PLoS Comput Biol. 2016:12(3):e1004845. 10.1371/journal.pcbi.1004845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singhal S, Leffler EM, Sannareddy K, Turner I, Venn O, Hooper DM, Strand AI, Li Q, Raney B, Balakrishnan CN, et al. Stable recombination hotspots in birds. Science. 2015:350(6263):928–932. 10.1126/science.aad0843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith CCR, Tittes S, Ralph PL, Kern AD. Dispersal inference from population genetic variation using a convolutional neural network. Genetics. 2023:224(2). 10.1093/genetics/iyad068. [DOI] [Google Scholar]
- Smith JM, Haigh J. The hitch-hiking effect of a favourable gene. Genet Res. 1974:23(1):23–35. 10.1017/S0016672300014634. [DOI] [PubMed] [Google Scholar]
- Smukowski CS, Noor MA. Recombination rate variation in closely related species. Heredity (Edinb). 2011:107(6):496–508. 10.1038/hdy.2011.44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stajich JE, Hahn MW. Disentangling the effects of demography and selection in human history. Mol Biol Evol. 2005:22(1):63–73. 10.1093/molbev/msh252. [DOI] [PubMed] [Google Scholar]
- Starck J, Candès EJ, Donoho DL. The curvelet transform for image denoising. IEEE Trans Image Process. 2002:11(6):670–684. 10.1109/TIP.2002.1014998. [DOI] [PubMed] [Google Scholar]
- Sugden LA, Atkinson EG, Fischer AP, Rong S, Henn BM, Ramachandran S. Localization of adaptive variants in human genomes using averaged one-dependence estimation. Nat Commun. 2018:9(1):1–14. 10.1038/s41467-018-03100-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sultanov D, Hochwagen A. Varying strength of selection contributes to the intragenomic diversity of rRNA genes. Nat Commun. 2022:13(1). 10.1038/s41467-022-34989-w. [DOI] [Google Scholar]
- Szpiech ZA, Hernandez RD. selscan: an efficient multithreaded program to perform EHH-based scans for positive selection. Mol Biol Evol. 2014:31(10):2824–2827. 10.1093/molbev/msu211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahata N. Allelic genealogy and human evolution. Mol Biol Evol. 1993:10:2–22. 10.1093/oxfordjournals.molbev.a039995. [DOI] [PubMed] [Google Scholar]
- Talkowski ME, Ernst C, Heilbut A, Chiang C, Hanscom C, Lindgren A, Kirby A, Liu S, Muddukrishna B, Ohsumi TK, et al. Next-generation sequencing strategies enable routine detection of balanced chromosome rearrangements for clinical diagnostics and genetic research. Am J Hum Genet. 2011:88(4):469–481. 10.1016/j.ajhg.2011.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tennessen JA. Gene buddies: linked balanced polymorphisms reinforce each other even in the absence of epistasis. PeerJ. 2018:6:e5110. 10.7717/peerj.5110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terhorst J, Kamm JA, Song YS. Robust and scalable inference of population history from hundreds of unphased whole-genomes. Nat Genet. 2017:49(2):303–309. 10.1038/ng.3748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The 1000 Genomes Project Consortium . A global reference for human genetic variation. Nature. 2015:526:68–74. 10.1038/nature15393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton KR, Jensen JD. Controlling the false-positive rate in multilocus genome scans for selection. Genetics. 2007:175(2):737–750. 10.1534/genetics.106.064642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torada L, Lorenzon L, Beddis A, Isildak U, Pattini L, Mathieson S, Fumagalli M. ImaGene: a convolutional neural network to quantify natural selection from genomic data. BMC Bioinformatics. 2019:20(S9):337. 10.1186/s12859-019-2927-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usevitch B. A tutorial on modern lossy wavelet image compression: foundations of jpeg 2000. IEEE Signal Process Mag. 2001:18(5):22–35. 10.1109/79.952803. [DOI] [Google Scholar]
- Wang W, Han D, Cai Q, Shen T, Dong B, Lewis MT, Wang R, Meng Y, Zhou W, Yi P, et al. MAPK4 promotes triple negative breast cancer growth and reduces tumor sensitivity to PI3K blockade. Nat Commun. 2022:13(1):245. 10.1038/s41467-021-27921-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Wang J, Kourakos M, Hoang N, Lee HH, Mathieson I, Mathieson S. Automatic inference of demographic parameters using generative adversarial networks. Mol Ecol Resour. 2021:21. 10.1111/1755-0998.13386. [DOI] [Google Scholar]
- Weston R, Peeters H, Ahel D. ZRANB3 is a structure-specific ATP-dependent endonuclease involved in replication stress response. Genes Dev. 2012:26(14):1558–1572. 10.1101/gad.193516.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitcher B. Waveslim: basic wavelet routines for one-, two-and three-dimensional signal processing. R package, ver; Jan 2005.
- Whitehouse LS, Ray D, Schrider DR. Tree sequences as a general-purpose tool for population genetic inference. Mol Biol Evol. 2024. 10.1093/molbev/msae223. [DOI] [Google Scholar]
- Whitehouse LS, Schrider DR. Timesweeper: accurately identifying selective sweeps using population genomic time series. Genetics. 2023:224(3). 10.1093/genetics/iyad084. [DOI] [Google Scholar]
- Williamson SH, Hubisz MJ, Clark AG, Payseur BA, Bustamante CD, Nielsen R. Localizing recent adaptive evolution in the human genome. PLoS Genet. 2007:3(6):e90. 10.1371/journal.pgen.0030090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willoughby JR, Ivy JA, Lacy RC, Doyle JM, DeWoody JA. Inbreeding and selection shape genomic diversity in captive populations: implications for the conservation of endangered species. PLoS One. 2017:12(4):e0175996. 10.1371/journal.pone.0175996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winbush A, Singh ND. Genomics of recombination rate variation in temperature-evolved drosophila melanogaster populations. Genome Biol Evol. 2020:13. 10.1093/gbe/evaa252. [DOI] [Google Scholar]
- Yu C, Dang Y, Zhou Z, Wu C, Zhao F, Sachs MS, Liu Y. Codon usage influences the local rate of translation elongation to regulate co-translational protein folding. Mol Cell. 2015:59(5):744–754. 10.1016/j.molcel.2015.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yulong D, Ke D, Chunsheng O, Yingshe L, Yu T, Jianyi F, Wei W, Yaguang DD. Wavelets and curvelets transform for image denoising to damage identification of thin plate. Results Eng. 2023:17:100837. 10.1016/j.rineng.2022.100837. [DOI] [Google Scholar]
- Zhang X, Kim B, Singh A, Sankararaman S, Durvasula A, Lohmueller KE. Maladapt reveals novel targets of adaptive introgression from neanderthals and denisovans in worldwide human populations. Mol Biol Evol. 2023:40. 10.1093/molbev/msad001. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
We release the source code for α-DAWG under the MIT open source license, and this code can be accessed on GitHub (https://github.com/RuhAm/AlphaDAWG). This repository also includes the three linear and three nonlinear pretrained α-DAWG models, together with scripts for simulating training data and plotting results. The CEU data from the 1,000 Genomes Project can be accessed from the project website (https://www.internationalgenome.org/category/phase-3/). The CurveLab software used in our analysis for the curvelet transformation can be accessed at https://www.curvelet.org/.