Influences of Variability in Attenuation Compensation on the Estimation of Backscatter Coefficient of Median Nerves in Vivo

Abstract

Objective

Peripheral nerves remain a challenging target for medical imaging, given their size, anatomical complexity, and structural heterogeneity. Quantitative ultrasound (QUS) applies a set of techniques to estimate tissue acoustic parameters independent of the imaging platform. Many useful medical and laboratory applications for QUS have been reported, but challenges remain for deployment in vivo, especially for heterogeneous tissues. Several phenomena introduce variability in attenuation estimates, which may influence the estimation of other QUS parameters. For example, estimating the backscatter coefficient (BSC) requires compensation for the attenuation of overlying tissues between the transducer and the underlying tissue of interest. The purpose of this study is to extend prior studies by investigating the efficacy of several analytical methods of estimating attenuation compensation on QUS outcomes in the human median nerve.

Methods

Median nerves were imaged at the volar wrist in vivo and beam‐formed radiofrequency (RF) data were acquired. Six analytical approaches for attenuation compensation were compared: 1–2) attenuation estimated by applying spectral difference method (SDM) and spectral log difference method (SLDM) independently to regions of interest (ROIs) overlying the nerve and to the nerve ROI itself; 3–4) attenuation estimation by applying SDM and SLDM to ROIs overlying the nerve, and transferring these properties to the nerve ROI; and 5–6) methods that apply previously published values of tissue attenuation to the measured thickness of each overlying tissue. Mean between‐subject estimates of BSC‐related outcomes as well as within‐subject variability of these outcomes were compared among the 6 methods.

Results

Compensating for attenuation using SLDM and values from the literature reduced variability in BSC‐based outcomes, compared to SDM. Variability in attenuation coefficients contributes substantially to variability in backscatter measurements.

Conclusion

This work has implications for the application of QUS to in vivo diagnostic assessments in peripheral nerves and possibly other heterogeneous tissues.

Abbreviations

BSC

backscatter coefficient

iBSC

integrated backscattered coefficient

QUS

quantitative ultrasound

RF

radiofrequency

ROI

region of interest

SDM

spectral difference method

SLDM

spectral log difference method

Peripheral nerves are responsible for movement, sensation, and autonomic function. Nerve damage, therefore, whether via traumatic injury or neuropathy, has a devastating impact on sensorimotor function and quality of life. ¹ , ² , ³ , ⁴ Nerve damage is predominantly diagnosed using physical examinations and electrodiagnostic testing. ⁵ , ⁶ Medical imaging has the potential to provide additional insight into nerve adaptation after injury, including improved localization of the site of injury and changes to nerve geometry and morphology. High frequency ultrasound is a rapid, portable, and low‐cost imaging modality that is increasingly used to evaluate peripheral nerve health in the clinic. ⁷ , ⁸ , ⁹ Common clinical ultrasound assessments, including nerve cross‐sectional area and relative echogenicity, are based on conventional B‐mode images. Despite the diagnostic potential of such measures, B‐mode outcomes may be confounded by system‐specific differences in hardware and software as well as user bias. In contrast, quantitative ultrasound (QUS) applies a set of techniques that reduce system‐dependent effects by exploiting beam‐formed radiofrequency (RF) data referenced to calibrated phantoms with known acoustic properties. Commonly used QUS parameters include the attenuation and backscatter coefficients ($\alpha \left(f\right)$, BSC(f)), which are 2 fundamental quantitative descriptors of a tissue's acoustic properties. ¹⁰ , ¹¹ , ¹²

$\alpha$ and BSC, as well as other QUS parameters, have been successfully applied to diagnose and characterize disease and injuries in several tissues, including liver, breast, and blood. ¹¹ , ¹³ , ¹⁴ , ¹⁵ In vivo research is emerging but characterization to date has been mainly ex vivo, ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ with well‐controlled sizes of the samples selected ²¹ , ²² and typically at frequencies <15 MHz. ²¹ Several studies already addressed the issue of the repeatability and reproducibility of $\alpha$ and BSC measurements in well controlled phantoms. ²³ , ²⁴ A commonly used analytical approach to estimating $\alpha \left(f\right)$, the spectral difference method (SDM), requires an assumption of medium homogeneity and the use of a calibrated reference phantom. Another standard method based on spectral log difference method (SLDM), which treats a given ROI with a different algorithm, is theoretically less dependent on changes in scatterer density or reflections but has the same assumption of homogeneity. ²⁵ These prior studies expose 2 challenges associated with characterizing more diverse imaging targets: 1) complexity of structures between the tissue of interest and the transducer (ie, signal energy loss from overlying tissues attenuation), and 2) the structural complexity within the tissue of interest (ie, effects of tissue heterogeneity). ²⁶ , ²⁷ , ²⁸ Both of these challenges challenge in vivo application of QUS to peripheral nerves, which are well‐organized but architecturally complex composite tissues residing beneath and between several layers of skin, fat, muscle, and/or tendon. Although QUS has been successfully applied to nerve imaging both in situ ²⁹ , ³⁰ and in vivo despite these potential limitations, ³¹ , ³² understanding how tissue complexity and heterogeneity may confound QUS remains an important goal to increase confidence in QUS outcomes.

The purpose of this study was to assess the variability of BSC‐related QUS outcomes in the human median nerve in vivo, using different attenuation compensation methods. In particular, we assessed variability in attenuation compensation and calculation of BSC using methods based on SDM and SLDM. We also evaluated the utility of 2 literature‐value‐based analytical approaches, in which the influences of overlying tissues were compensated using published attenuation values of each layered tissue type. ³² , ³³ , ³⁴ , ³⁵ Our study examines advantages and disadvantages of each analytical method when applying in vivo QUS to peripheral nerves and other heterogeneous tissues and provide a basis for future analytical improvements.

Materials and Methods

Imaging

The protocol was approved by the VA San Diego institutional review board and data were collected under informed consent. Phantom and in vivo ultrasound acquisitions were made with a VevoMD system (Fujifilm, Toronto, Ontario, Canada) using a UHF22 array with center frequency of 11 MHz, for a −6 dB bandwidth ranging from 5 to 16 MHz. The scanner research mode allowed acquisition of beam‐formed RF signals. Maximal imaging depth was set to 25 mm, focal depth set to 10.5 mm, dynamic range was set to 65 dB, and time gain compensation was set to 50 dB (ie, neutral) at each of the 2 allowable depths, so as not to influence attenuation outcomes.

We performed 3 acquisitions in a tissue‐mimicking reference phantom custom‐designed for the range of frequencies appropriate for the UHF22 transducer (Mirion/CIRS, Norfolk, Virginia, USA, formula RDG 5435) (Figure 1A). The probe was removed from the surface of the phantom for 5 seconds between acquisitions. The phantom was cylindrical (~25‐mm thick, ~30‐mm radius) with saran windows on top and bottom. It was characterized by a through‐transmission technique ³³ , ³⁴ between 5 and 55 MHz following a frequency (f) dependence model for attenuation α of the form:

$$\alpha \left(f\right)=A·f^b+c$$ (1)

where $A$ is the attenuation coefficient in $\mathrm{dB}·\mathrm{c}{\mathrm{m}}^{-1}·\mathrm{MH}{\mathrm{z}}^{-\mathrm{b}}$, b is the nonlinearity coefficient, and c is an offset in $\mathrm{dB}·\mathrm{c}{\mathrm{m}}^{-1}$; our reference phantom has A = 0.2089 $\mathrm{dB}·\mathrm{c}{\mathrm{m}}^{-1}·\mathrm{MH}{\mathrm{z}}^{-\mathrm{b}}$, b = 1.4183, and c = 0.2712 $\mathrm{dB}·\mathrm{c}{\mathrm{m}}^{-1}$.

Figure 1.

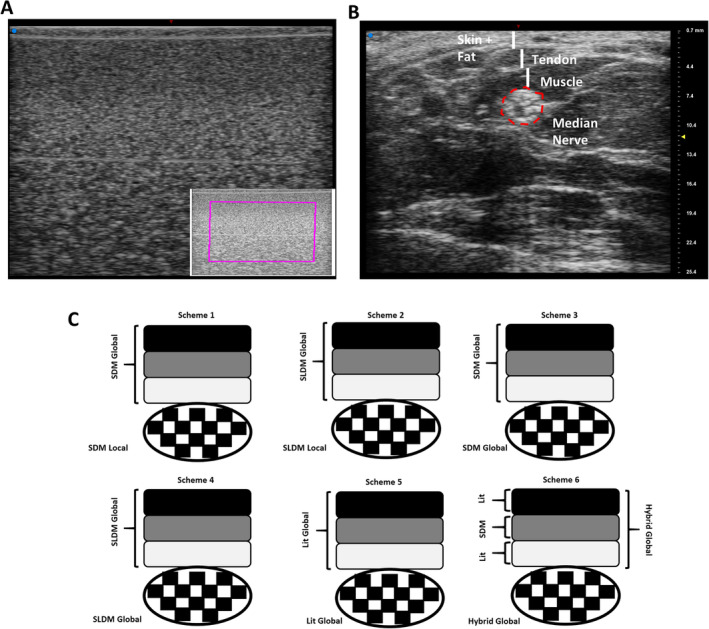
Example images of (A) phantom with region of interest in purple and (B) median nerve. Layers of skin, fat, tendon, and muscle are indicated with vertical white lines. Median nerve is outlined in red, inclusive of epineurium. C, Six analytical schemes for attenuation compensation were evaluated. Black, dark grey, and light grey boxes represent tissue layers overlying the nerve, represented by the checkered ellipse. (A and B are shown in the same scale displayed on the right in B in millimeters.)

A single skilled ultrasound operator then performed 9 transdermal in vivo acquisitions of the volar aspect of the median nerve in each of 5 volunteers with no reported symptoms of median neuropathy based on the Boston Carpal Tunnel Syndrome Questionnaire (Figure 1B, Table 1). Each nerve was assessed to be healthy (ie, asymptomatic). ³⁵ Axial images and their corresponding RF data were acquired at the distal wrist crease, as described in a prior repeatability and reproducibility study. ³²

Table 1.

Demographics Table of Participants

	Variables Categories	Frequency	Percentage
Gender	Females	1	20%
	Males	4	80%
Age	18–29	2	40%
	30–39	1	20%
	40–49	1	20%
	50–59	1	20%

Estimation of Attenuation and Backscatter Coefficient

Three different attenuation compensation methods were evaluated individually or in combination to assess attenuation, for a total of 6 analytical schemes (Figure 1C). First, attenuation within a region of interest (ROI) comprised of tissue layers overlying the nerve or an ROI outlining the nerve boundary, inclusive of the epineurium, as a function of frequency using SDM, as described in previous studies ³⁶ , ³⁷ using

$${\alpha }_{\mathrm{SDM}}=a_{\mathrm{SDM}}+f^{b_{\mathrm{SDM}}}$$ (2)

The ROI was subdivided into sub‐ROIs, which were assessed in accordance with recommendations from the literature, taking 12 A‐lines in the lateral direction and 12 wavelengths in the axial direction for each sub‐ROI, for at least 4 sub‐ROIs, overlapping each other for 50% of their areas. ²⁵ , ³⁸ In scheme 1, SDM was applied separately for overlying tissue and the nerve ROI (“SDM global–local”). In scheme 3, SDM was applied to overlying tissue and attenuation characteristics transferred to the nerve ROI (“SDM global–global”).

Second, the SLDM was used to compute frequency dependent attenuation, as published in previous study ³⁶ :

$${\alpha }_{\text{SLDM}}=a_{\text{SLDM}}+f^{b_{\text{SLDM}}}$$ (3)

SLDM is similar to SDM in principle. However, SDM provides a value for an averaged local attenuation within an ROI, whereas SLDM considers the global variation between signals from posterior (deep) and anterior (superficial) faces of the ROI. As such, SLDM is posited to be less sensitive to changes in scatterer density and reflections than SDM, as long as they appear between the 2 sub‐ROIs; additional details on this approach may be found in earlier studies. ³⁶ , ³⁷

Third, attenuation of tissues overlying the region of interest inscribing the nerve boundary, ${\alpha }_{\mathrm{lit}}$, was estimated using attenuation values from the literature for skin, ³⁹ fat, tendons, ⁴⁰ and muscles. ⁴¹ A composite literature‐based attenuation value was determined based on these values and the measured anterior–posterior thickness of each tissue layer, which was manually segmented in each B‐mode image. Scheme 5 applied these published values to all layers (“literature”), while scheme 6 used measured attenuation characteristics from the relatively homogeneous muscle layer and combined these values with published values for the other nonmuscle layers (“hybrid”). SDM and SLDM were also applied to phantom data acquired with the same scanner settings.

The BSCs presented in this study were assessed using Equation (4) ⁴² :

$$\mathrm{BS}{\mathrm{C}}_{\text{meas}}\left(f\right)=\mathrm{BS}{\mathrm{C}}_{\mathrm{ref}}\left(f\right)\frac{P_{\text{meas}}\left(f\right)}{P_{\mathrm{ref}}\left(f\right)}{e}^{-4z\left[A·f^b-{\alpha }_{\mathrm{ref}}\left(f\right)\right]}$$ (4)

where BSC is the backscatter coefficient in $\mathrm{s}{\mathrm{r}}^{-1}·\mathrm{c}{\mathrm{m}}^{-1}$, z the depth of the ROI in cm, and attenuation parameters from Equation (1), $\mathrm{BS}{\mathrm{C}}_{\mathrm{ref}}$ is the backscatter coefficient of the reference phantom in $\mathrm{s}{\mathrm{r}}^{-1}·\mathrm{c}{\mathrm{m}}^{-1}$. ${\alpha }_{\mathrm{ref}}$ is phantom attenuation in $\mathrm{dB}·\mathrm{c}{\mathrm{m}}^{-1}$, and ${\alpha }_{\text{meas}}\left(f\right)$ replaced with values for attenuation noted above (Equation 1). $P_{\text{meas}}$ and $P_{\mathrm{Ref}}$ are the signal from the tissue and from the reference, respectively. Based on these attenuation compensation techniques, corresponding BSCs and their integrated backscattered coefficients (iBSCs), assessed on the –6 dB bandwidth of the signal spectra, were calculated.

Signal treatment and analysis were performed offline using a custom graphical user interface (MATLAB, The Math Works, Natick, MA, USA). ⁴³

Statistics

Mean parameter values were compared using one‐way analysis of variance. Post hoc comparisons between individual experimental groups were performed by the Tukey's honestly significant difference test, which accounts for multiple comparisons. Sample size for each group was n = 5 participants. This sample size was determined based on a power calculation with α = 0.05, 1 – β (power) = 0.8, 6 experimental groups, and a moderate effect size of 0.75 (G*Power 3.1.9.7). ⁴⁴ , ⁴⁵ Data are represented as mean ± standard error. Significant differences are designated as *P < .05; **P < .01; ***P < .001.

Results

We first evaluated how SDM and SLDM analytical methods influenced the calculation of attenuation‐based parameters in idealized conditions ex vivo, using a homogeneous phantom. Both approaches provide low variability and a stable numerical solution, meaning that the fit of the attenuation curves as a function of frequency do not reach the limit boundaries set for the analysis (ie, the fitting algorithms converge ⁴⁶ , ⁴⁷ ). The SLDM approach results in slightly higher values for the attenuation coefficient A and slightly lower values for the nonlinearity b coefficient than the SDM method, and the SDM method more accurately reproduces coefficients measured from the transmission method (Figure 2).

Figure 2.

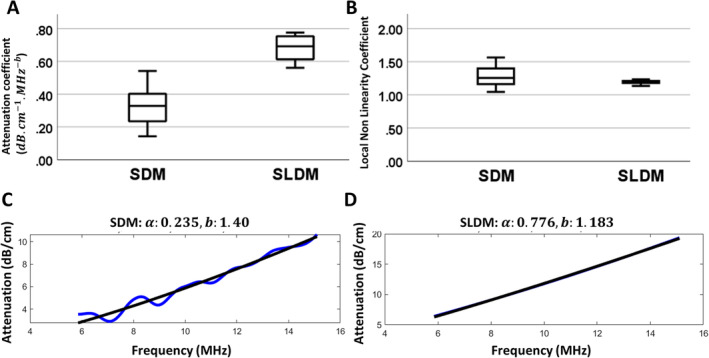
A and B, Boxplots of attenuation coefficient (α) and nonlinearity coefficient (b) estimated based on spectral difference method (SDM) and spectral log difference method (SLDM). C and D, One example of attenuation coefficient estimation in the homogeneous phantom for SDM (C) and SLDM (D). (The attenuation and nonlinearity coefficients measured from transmission method are $A=0.209,b=1.420$.)

We next calculated attenuation‐based parameters from acquisitions in vivo, for which heterogeneity of targeted peripheral nerves and overlying layers of tissue could confound analysis. Within‐participant variability as well as between‐participant parameter values were compared among several schemes (Figure 1C), allowing comparisons among SDM (schemes 1 and 3), SLDM (schemes 2 and 4), and literature‐based approaches (schemes 5–6). These schemes also allowed us to evaluate the utility of independently estimating attenuation parameters from the local nerve ROI (schemes 1 and 2 [“global–local”]) versus assigning global values from overlying tissue to underlying nerve ROIs (schemes 3 and 4 [“global–global”]).

Within‐participant variance in the global attenuation coefficient A was highest in the hybrid method (Figure 3A, scheme 6; Table 4), though this variability was over an order of magnitude lower than that of the local attenuation coefficient estimated using the SDM method (Figure 3B, scheme 1; Table 2). Correspondingly, between‐participant variability in the global attenuation coefficient for scheme 6 (Figure 3C) and local attenuation coefficient for scheme 1 (Figure 3D) were also higher. For nonlinearity coefficients, variance in both global and local nonlinearity coefficients were higher for SDM methods, irrespective of whether the nerve ROI was evaluated independently or assigned attenuation values from overlying tissues (Figure 3, E and F; schemes 1 and 3 versus 2, 4, 5, and 6). Correspondingly, between‐participant variability in global and local nonlinearity coefficients were also higher for SDM‐associated methods (schemes 1 and 3, Figure 3, G and H) compared to SLDM‐ and literature‐based methods (schemes 2, 4, 5, and 6; Figure 3, G and H), irrespective of whether nerve ROIs were treated independently (schemes 1 versus 3 and 2 versus 4).

Figure 3.

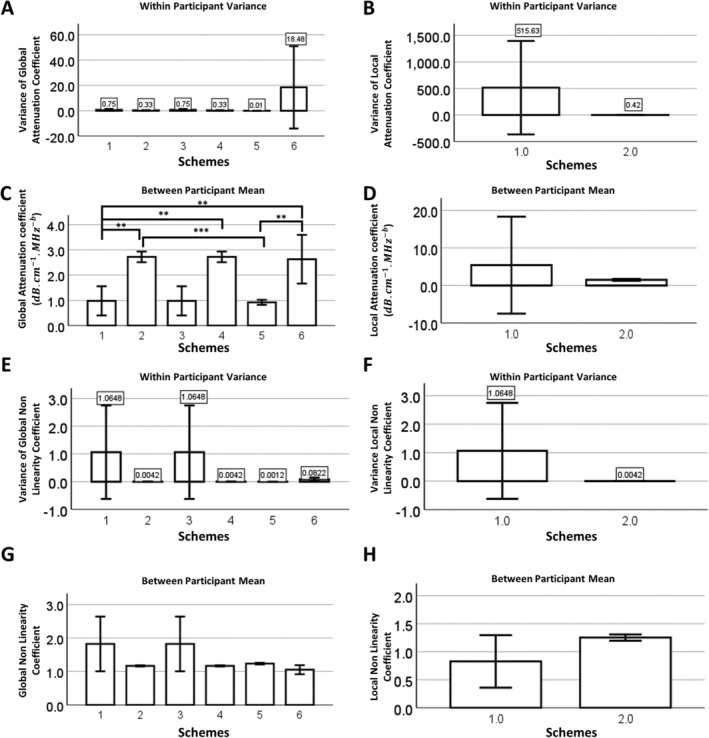
Attenuation coefficient assessments from different analytical schemes. Variance of the (A) global attenuation coefficient and (B) local attenuation coefficients for each analytical scheme. Local attenuation coefficients were only applied to schemes 1 and 2. Mean (C) global attenuation coefficients and (D) local attenuation coefficients for each analytical scheme. Variance of (E) global nonlinearity coefficient and (F) local nonlinearity coefficient for each analytical scheme. Mean (G) global nonlinearity coefficient and (H) local nonlinearity coefficients for each analytical scheme. Significance between individual groups based on Tukey's multiple comparison test (*, <.05; **, <.01; ***, <.001).

Table 4.

The Variance of Global Attenuation a ($\mathrm{dB}.\mathrm{c}{\mathrm{m}}^{-1}·\mathrm{MH}{\mathrm{z}}^{-\mathrm{b}}$) Between Repeated Images From 5 Participants for 6 Different Schemes

Variance of Global Attenuation Between Repeated Images
Schemes	1	2	3	4	5	6
Participant A	0.036	0.236	0.036	0.236	0.014	0.208
Participant B	0.863	0.340	0.863	0.340	0.026	6.897
Participant C	0.585	0.519	0.585	0.519	0.009	83.264
Participant D	0.369	0.420	0.369	0.420	0.002	1.495
Participant E	1.908	0.153	1.908	0.153	0.009	0.513

Table 2.

The Variance of Local Attenuation a ($\mathrm{dB}·\mathrm{c}{\mathrm{m}}^{-1}·\mathrm{MH}{\mathrm{z}}^{-\mathrm{b}}$) Between Repeated Images From 5 Participants for 6 Different Schemes

Variance of Local Attenuation Between Repeated Images
Schemes	1	2
Participant A	2265.777	0.443
Participant B	23.751	0.625
Participant C	15.892	0.116
Participant D	259.769	0.473
Participant E	12.958	0.420

As also found for the analyzed phantom, SLDM‐based attenuation coefficients were significantly higher and nonlinearity coefficients trended lower than SDM‐based coefficients (Figure 3, C, D, G, and H).

Given the differences in attenuation parameters depending on analytical strategy, we next tested the impact of variability in these parameters on BSC (Figure 4). As was the case for attenuation parameters, within‐participant variance in iBSC and slope were higher when SDM was separately applied to overlying tissues in combination with the local nerve ROI (scheme 1) compared to any other method (schemes 2–6; Figure 4, A and C). For the y‐intercept, all 3 analytical schemes with an SDM component (schemes 1, 3, and 6) also had higher within‐participant variance than SLDM‐ or pure literature‐based groups (schemes 2, 4, and 5). Mean values of iBSC and slope were higher for all SLDM groups (schemes 2 and 4) compared to all other groups (Figure 4, B and D). There were no differences in y‐intercept among all groups. These differences were also observed in the frequency dependence of BSC. When SDM‐based schemes were deployed, BSC values stayed generally constant across all frequencies and were substantially lower than for other schemes over the analyzed range of frequencies (schemes 1, 3, and 6; Figure 4G). On the other hand, when SLDM‐ or pure literature‐based approaches were applied to overlying tissues, BSC displayed a positive relationship with frequency (schemes 2, 4, and 5; Figure 4G).

Figure 4.

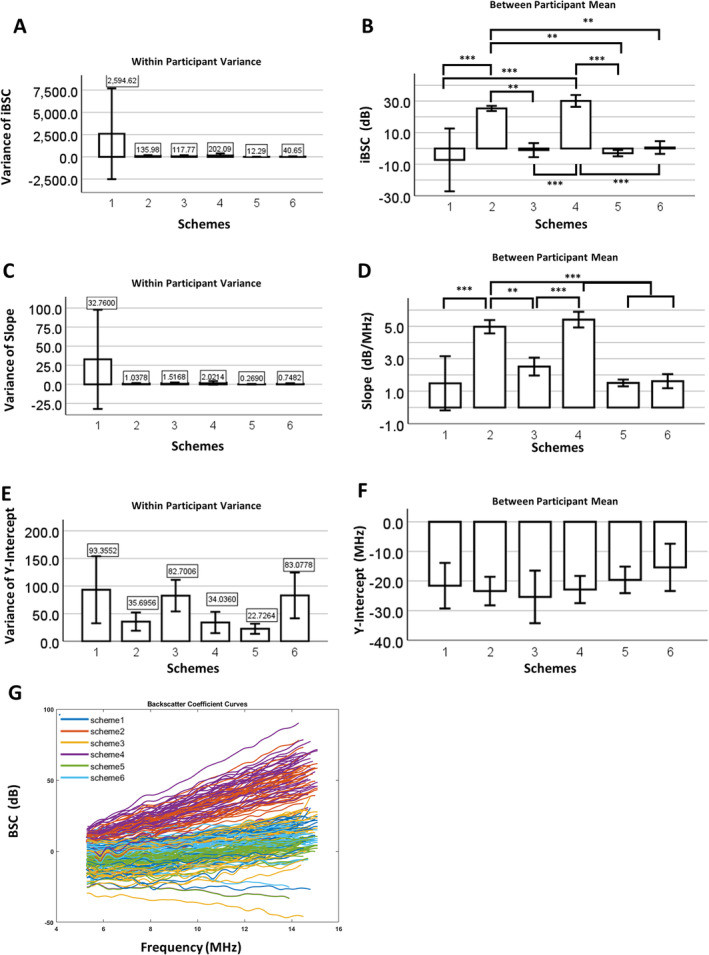
Backscatter coefficient results for different schemes. Within‐subject variance and between‐subject mean of (A and B) iBSC, (C and D) slope, and (E and F) y‐intercept for different analytical schemes. Significance between individual groups based on Tukey's multiple comparison test (*, <.05; **, <.01; ***, <.001). G, Raw BSC versus frequency curves from 5 participants of 6 different analytical schemes.

Discussion

QUS approaches are posited to have low sensitivity to platform‐specific effects, due to the use of known reference phantoms. However, they remain a challenge to deploy widely for soft tissues in vivo, such as for peripheral nerves, because of the complexity and heterogeneity of layered tissues, especially at high frequencies and possibly because of the small nerve size so ROIs are also smaller. These challenges are hypothesized to substantially influence attenuation compensation, which is a key step in BSC assessment. In this study, we investigated several analytical approaches to understand and account for the influence of variability in attenuation compensation on variability in BSC values.

SDM and SLDM Analytical Schemes

Baseline results calculated using SDM and SLDM approaches in a homogeneous phantom (Figure 1) allowed a number of useful comparisons to experimental configurations in vivo (Figure 2). In phantoms, both SDM and SLDM approaches were stable, with SDM‐based outcomes better matching parameters characterized using through‐transmission‐based methods. ²⁵ In vivo, ROIs were selected in accordance with recommendations from the literature. Application of SDM to ROIs of tissues overlying the nerve or the nerve ROI itself (schemes 1, 3, and 6) resulted in high variability in attenuation and BSC parameters. This is not surprising, given tissue heterogeneity within the ROI standing in contrast to the assumption of medium homogeneity for SDM; nevertheless, the substantial variability provided the “worst‐case scenario” against which other strategies could be compared.

Application of the SLDM (schemes 2 and 4) to in vivo imaging of nerves markedly reduced variability in attenuation parameters and BSC‐based outcomes. SLDM is conceptually analogous to SDM, with the exception that the attenuation is obtained between sub‐ROIs at anterior and posterior faces of the ROI, providing a global attenuation value between the 2 sub‐ROIs. ²⁵ While still sensitive to heterogeneity in the ROI, this method has the potential to reduce the impact of discontinuities across an interface between media. This may explain the lower variability of outcomes obtained with SLDM (Figures 3, 4, Tables 2, 3, 4). These patterns were consistent for multiple participants, where between‐participant variance scaled with within‐participant variance; indeed, for those schemes with low within‐participant variance (SLDM‐ and literature‐based schemes 2, 4, 5, and 6), mean values were consistent between participants (Figures 3, 4). With respect to the utility of estimating attenuation parameters independently in nerve ROI (ie, “global–local” vs. “global–global”), there appeared to be no advantage (schemes 1 and 2 versus 3 and 4), and in fact for SDM‐based approaches, independent measurement in the nerve ROI increased the variability of attenuation coefficients (Figure 3B, Tables 4 and 5) and ultimately, iBSC and slope (Figure 4, A and C, Table 6). It is not clear why SDM applied to a nerve ROI yielded such variability but may reflect impacts of substantial heterogeneity within a comparatively small ROI. In terms of mean parameter values, as for the phantom, SLDM resulted in increased attenuation coefficients and decreased nonlinearity coefficients and increased iBSC and slope compared to SDM. This is likely in part to reflect fitting of the analytical model, which varies in number of sub‐ROIs (fewer in SLDM) and also the details of the fitting function itself (Figure 2, C and D). ²⁵

Table 3.

The Variance of Local Nonlinearity Coefficient Between Repeated Images From 5 Participants for 6 Different Schemes

Variance of Local Nonlinearity Coefficient Between Repeated Images
Schemes	1	2
Participant A	1.693	0.021
Participant B	0.391	0.015
Participant C	0.425	0.009
Participant D	0.138	0.028
Participant E	0.111	0.016

Table 5.

The Variance of Nonlinearity Coefficient Between Repeated Images From 5 Participants for 6 Different Schemes

Variance of Global Nonlinearity Coefficient Between Repeated Images
Schemes	1	2	3	4	5	6
Participant A	4.431	0.003	4.431	0.003	0.002	0.012
Participant B	0.325	0.003	0.325	0.003	0.002	0.052
Participant C	0.168	0.009	0.168	0.009	0.001	0.164
Participant D	0.245	0.005	0.245	0.005	0.000	0.154
Participant E	0.155	0.001	0.155	0.001	0.001	0.029

Table 6.

The Variance of iBSC Between Repeated Images From 5 Participants for 6 Different Schemes

iBSC Variance Between Images
Schemes	1	2	3	4	5	6
Participant A	12,792.734	201.654	84.868	44.559	10.166	25.061
Participant B	63.603	32.686	256.288	52.439	4.852	59.265
Participant C	37.812	143.355	124.266	549.324	4.722	60.611
Participant D	36.706	184.020	36.452	231.667	36.968	45.072
Participant E	42.237	118.172	86.977	132.480	4.722	13.248

Literature‐Based Approaches

An alternative strategy for reducing the variability in vivo was to account for overlying tissues using literature‐based values for attenuation (schemes 5–6). There was no longer an impact of acoustic measurements in overlying layers on variability (ie, attenuation properties for each layer were constant, excepting any variability in manual segmentation), so this convenient technique efficiently decreased the variance of nerve QUS measurements in vivo, compared with SDM (Figures 3, 4). A hybrid approach in which literature values for overlying tissues were combined with measurements of more homogeneous tissue layers (scheme 6), also generally yielded lower variance for attenuation parameters and iBSC‐related outcomes compared to SDM‐based approaches, with the exception of global attenuation coefficient, where variability was high. This finding suggests that variability in slope and iBSC appears to be driven by high local nerve ROI attenuation variability. It also suggests that the variability exhibited by SDM outcomes may be due to the multi‐layered complexity of the composite medium, rather than generalized heterogeneity in and of itself. It may be interesting to compare the literature method with composite attenuations from permutations of different overlying tissue layers.

Coupling Between Variability in Attenuation Parameters and Variability in BSC

Multiple results suggested that reducing variability in attenuation parameters can reduce variability in BSC (Figures 3, 4, Tables 2, 3, 4). This is expected conceptually, based on the importance of attenuation correction for BSC estimates, irrespective of analytical scheme. On the other hand, the degree of such coupling was not always predictable. An examination of BSC theoretically sheds some light on this dependence. The differential expression of the analytic BSC in Equation (4) can be expressed as:

$$\begin{array}{l}\mathrm{dBS}{\mathrm{C}}_{\text{meas}}\left(A,\mathit{dA},b,\mathit{db},f\right)\\ =\frac{\mathrm{\partial BS}{\mathrm{C}}_{\text{meas}}\left(A,b,f\right)}{\partial A}\mathit{dA}+\frac{\mathrm{\partial BS}{\mathrm{C}}_{\text{meas}}\left(A,b,f\right)}{\partial b}\mathit{db}\end{array}$$ (5)

For $\frac{\mathrm{\partial BS}{\mathrm{C}}_{\text{meas}}\left(A,b,f\right)}{\partial A}\mathit{dA}=C\left(-4z{f}^b{e}^{-4\mathit{zA}{f}^b}\right)\mathit{dA}$, and $\frac{\mathrm{\partial BS}{\mathrm{C}}_{\text{meas}}\left(A,b,f\right)}{\partial b}\mathit{db}=C\left(-4\mathit{zA}{f}^b\ln \left(b\right)\times e^{-4A{f}^b}\right)$, where $C=\frac{\mathrm{BS}{\mathrm{C}}_{\mathrm{ref}}\left(f\right)P_{\text{meas}}\left(f\right)}{P_{\mathrm{ref}}\left(f\right)}{e}^{4z{\alpha }_{\mathrm{ref}}\left(f\right)}$, $d\mathrm{BS}{\mathrm{C}}_{\text{meas}}\left(A,\mathit{dA},b,\mathit{db},f\right)=C\left(-\frac{4z{f}^b}{e^{4\mathit{zA}{f}^b}}\right)\left(\mathit{dA}+A\ln \left(b\right)\mathit{db}\right)$, which upon simplification is as follows:

$$d\mathrm{BS}{\mathrm{C}}_{\text{meas}}\left(A,\mathit{dA},b,\mathit{db},f\right)=-4\mathrm{BS}{\mathrm{C}}_{\text{meas}}z{f}^b\left(\mathit{dA}+A\ln \left(b\right)\mathit{db}\right)$$ (6)

If dA and db reflect perturbations in attenuation coefficient and nonlinearity coefficient (ie, error or variability in these parameters), then their propagation to perturbation (“error”) in BSC is driven by the expression $\left[\mathit{dA}+A\ln \left(b\right)\mathit{db}\right]$. This reveals a direct scaling of dBSC with dA; however, given typical values for b ~ 1.0 (and thus ln(b) ~ 0), db is less likely to influence dBSC. This may explain why high within‐participant variability was observed in both local attenuation coefficient and iBSC (scheme 1, Figure 3A versus 4A), but a higher variability in nonlinearity coefficient in scheme 3 did not propagate to increased variance of iBSC (scheme 3, Figure 3A versus 4A).

Additional Sources of Variability and Limitations

Attenuation is assumed to be homogeneous for reference phantom‐based QUS analytical techniques, thus introducing a bias in attenuation and BSC measurements for both SDM‐ and SLDM‐based approaches ¹² , ⁴⁸ and also precluding evaluation of accuracy of these approaches when evaluating the heterogeneous nerve. This bias may be minimized in approaches such as literature‐based compensation. However, compensation based on values from the literature is dependent on the accuracy of published values, which were often captured ex vivo or at lower frequencies, and also neglects influences of reflections at interfaces between tissues. Such reflections lead to a loss in energy for the transmitted signal in vivo and potential artifacts in the assessment of attenuation, leading to contributions from both error in attenuation and an error on the speckle features themselves (in power and structure of the signal). ²⁶ , ²⁷ , ²⁸ , ⁴⁸ In addition, the SDM and SLDM approaches to calculate attenuation assume a linear relationship between the emitted and the received signal; nonlinearities from the medium were not considered. For high intensities in particular, a part of the energy might shift to higher frequencies. Appropriate models to those nonlinear components in backscattered signals have already been proposed for the general case. ⁴⁹ Finally, the heterogeneity of the tissue within the ROI as well as artifacts due to reverberation and shadows in the tissues located between the ROI and the transducer are sources of variability in BSC as well as in attenuation parameters, as described previously. The size and shape of the selected nerve ROI and the tissue components within it may also create some variability. A minimum of 12 A‐lines or 12 pulse lengths in each direction were employed for suitable organization of rectangular sub‐ROIs ²⁵ thus dictating a minimum size and orientation for the ROI. In a prior study of smaller rat nerves, these approaches showed stability, ⁵⁰ but some analytical error is nevertheless expected for SDM and SLDM schemes. Also, the epineurium was included in the nerve ROI due to its histopathologic importance diagnostically, ⁵¹ but increases heterogeneity. Finally, while outcomes were compared for multiple samples, participants do not represent a normative control cohort as limited sample size and age range were evaluated in this study; a larger and more diverse cohort will ultimately be required to test diagnostic efficacy. The relative strengths and weaknesses of each method presented in this study, with respect to potential sources of variability identified, are summarized in Table 7. These should be considered depending on study objectives, when developing imaging and analytical approaches for in vivo imaging.

Table 7.

A Nonexhaustive List of Potential Sources of Variability Are Listed, as Well as the Corresponding Sensitivity of Each Technique

	Scheme
Source of Variability	1	2	3	4	5	6
Interfaces/Reflections	++	+	++	+	−	−
Tissue heterogeneity	++	+	++	+	−	+
Heterogeneity and size of nerve ROI	++	+	NA	NA	NA	NA
Published values of attenuation	NA	NA	NA	NA	++	++
Performance in homogeneous phantom	−	+	−	+	NA	NA

“–” stands for little sensitivity; “+” stands for high sensitivity; and “++” stands for critical sensitivity.

Conclusion and Perspectives

Given higher variability in attenuation‐based outcomes, SDM may not be a suitable analytical approach to account for multilayered tissues overlying peripheral nerves. In contrast, SLDM and literature‐based methods exhibited more stability. Thus, despite their own limitations, these methods may provide more confidence for potential diagnostic application. Accuracy of the measurements was not studied and is difficult to perform in vivo. However, future studies with models and phantoms developed specifically for heterogeneous tissues as well as more accurate assessments of attenuation in nerves under more controlled experimental conditions (eg, in situ/in vivo without overlying tissue or ex vivo in idealized media) will allow more effective evaluation of the accuracy of attenuation‐based QUS outcomes. Collectively, our data provide suggestions for applying QUS approaches for in vivo nerve imaging, and raise potential considerations that must be considered for other applications.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.