Abstract
CH–π interactions between carbohydrates and aromatic amino acids play an essential role in biological systems that span all domains of life. Quantifying the strength and importance of these CH–π interactions is challenging because these interactions involve several atoms and can exist in many distinct orientations. To identify an orientational landscape of CH–π interactions, we constructed a dataset of close contacts formed between β-d-galactose residues and the aromatic amino acids, tryptophan, tyrosine, and phenylalanine, across crystallographic structures deposited in the Protein Data Bank. We carried out quantum mechanical calculations to quantify their interaction strengths. The data indicate that tryptophan-containing CH–π interactions have more favorable interaction energies than those formed by tyrosine or phenylalanine. The energetic differences between these amino acids are caused by the aromatic ring system electronics and size. We use individual distance and angle features to train random forest models to successfully predict the first-principles computed energetics of CH–π interactions. Using insights from our models, we define a tradeoff in CH–π interaction strength arising from the proximity of galactose carbons 1 and 2 versus carbons 4 and 6 to the aromatic amino acid. Our work demonstrates that a feature of CH–π stacking interactions is that numerous orientations allow for highly favorable interaction strengths.
Over hundreds of PDB structures of protein–sugar complexes, our work demonstrates the prevalence of CH–π stacking interactions, and energetic analysis shows that numerous orientations allow for highly favorable interaction strengths.
1. Introduction
Glycans coat the surface of all cells on Earth, serving as protection and identification to other cells and macromolecules.1–4 Glycan-binding proteins, including lectins, engage specific carbohydrate residues on these glycans to activate downstream functions.4–7 The proteins distinguish structurally similar monosaccharides within glycans through non-covalent binding interactions.8,9 However, saccharides, unlike other small-molecule ligands, are largely hydrophilic and, as a result, often form weak, micromolar interactions with proteins. Carbohydrate-binding proteins rely on binding motifs that involve three key intermolecular interaction types: hydrogen bonding, metal-ion bridges, and carbohydrate–aromatic interactions.9–22 While the first two are relatively well understood, there is no consensus on the energetic favorability of carbohydrate–aromatic interactions nor the relationship between their orientation and energetics.23,24 Thus, modeling carbohydrate–aromatic interactions is essential to understanding their role in enabling selective recognition. Doing so will increase our understanding of protein–glycan interactions in biology and assist in the development of glycomimetic therapeutics.
Many experimental techniques, such as isothermal titration calorimetry (ITC), bio-layer interferometry (BLI), and nuclear magnetic resonance (NMR) spectroscopy, have been used to provide key insights into protein–small molecule binding. NMR, in particular, has been useful in evaluating the energetics of carbohydrate–aromatic interactions.22,25–33 However, the use of these experimental techniques is limited by the time required to produce each candidate system, the low binding affinities of the candidate interactions, and the inability to probe and compare specific interaction orientations. Alternatively, computational first-principles methods, including density functional theory (DFT) and symmetry-adapted perturbation theory (SAPT), enable rapid energetic assessments of numerous instances of intermolecular interactions from many distinct biological systems.34–40 While limited by the approximations inherent to the electronic structure methods used, the difficulty of computing entropic differences, and the effects of the full, solvated protein environment, these methods are essential tools in the analysis of carbohydrate–aromatic interactions.
Carbohydrate–aromatic interactions can involve CH–π interactions, which are favorable contacts formed by electron donation from the π-system of an aromatic moiety into the antibonding orbital(s) of a carbon–hydrogen (C–H) bond.24 Individual CH–π interactions, like cation–π and π–π interactions, are considered weaker than hydrogen bonding interactions and typically thought to involve only dispersive forces.36,41–44 They are present in many systems and can facilitate protein folding and protein-ligand binding. Notably, they are especially prevalent in protein–carbohydrate interactions.25,45–50 Unlike other systems containing CH–π interactions, carbohydrate–aromatic interactions are made up of multiple CH–π interactions formed between distinct CH groups on the carbohydrate that are stacked upon the π system of an aromatic amino acid. The resulting CH–π stacking interactions are believed to be more favorable than some hydrogen bonds and play an essential role in protein–carbohydrate recognition.22,23 Nevertheless, the overall range of interaction strengths of CH–π interactions in comparison to more conventional non-covalent interactions, such as hydrogen bonds, remains poorly understood.
Toward the goal of characterizing CH–π interactions in known glycan-binding proteins, a bioinformatic analysis of the Protein Data Bank (PDB), determined that 39% of all protein entries with a carbohydrate contained at least one CH–π stacking interaction formed between the protein and carbohydrate.51 However, it is worth noting that this analysis included both covalently and non-covalently bound carbohydrates. Because carbohydrates that are covalently bound to the protein have a lower propensity for favorable non-covalent stabilization, this analysis may be a significant underestimate of the frequency of CH–π stacking interactions in non-covalent protein–carbohydrate interactions.23
Prior computational and experimental analyses have probed the energetic favorability of certain carbohydrate–aromatic interactions. Most NMR evaluations observed that the carbohydrate–aromatic CH–π stacking interaction free energies range from 1–2 kcal mol−1,52–55 while calorimetry and computational studies of these interactions observe electronic interaction energies ranging from 3–8 kcal mol−1.35,51,56–62 However, all CH–π stacking interactions are not equivalent. The stereochemistry of each carbohydrate informs the orientation of CH bonds and the polarization of these bonds by the neighboring hydroxyl groups. For example, electron-poor C–H bonds should result in more stabilizing CH–π interactions, and hydroxyl group stereochemistry influences the electronics of the glycan C–H bonds. NMR studies have demonstrated that β-d-galactose forms particularly favorable CH–π stacking interactions with indoles,23 yet detailed energetics of these interactions and those formed by other amino acid side chains have not been evaluated. Further study is required to determine the energetic favorability of these interactions and the orientational factors that influence their strength.
Because carbohydrates can have multiple interacting CH groups, a number of CH–π stacking orientations can form between a given carbohydrate–amino acid pair. Attempts to determine preferred orientations for certain carbohydrates interacting with aromatic systems have been explored.51,56–58 Analyses of protein–carbohydrate interactions in the PDB showed that there is a propensity for glycan CH groups to be positioned at consistent distances and angles relative to the center of the interacting aromatic ring.51 However, no complete orientational energetic landscape for CH–π stacking interactions has been determined. Thus, to effectively evaluate protein–carbohydrate interactions, it is essential to develop a comprehensive understanding of CH–π stacking interaction energetics and the orientational features that lead to their favorability.
We compiled a dataset of over 500 CH–π stacking interactions formed between β-galactose residues and tryptophan, tyrosine, or phenylalanine from the PDB. We conducted first-principles calculations using DFT and SAPT0 benchmarked against the domain-localized pair natural orbital coupled cluster singles doubles with perturbative triples (DLPNO-CCSD(T)) level of theory. We subsequently trained random forest machine learning models to predict interaction energies and identified an energetic landscape that defines these CH–π stacking interactions. We found that they are energetically favorable and therefore contribute significantly to the energy of protein–carbohydrate binding, thereby playing a key role in protein–carbohydrate complexation. The energetic landscape for these interactions demonstrates that they have high orientational flexibility and explains the difference in energetics of CH–π stacking interactions formed by tryptophan, tyrosine, and phenylalanine. This information is essential for understanding protein–carbohydrate binding interactions and the rational design of new therapeutics that target these binding sites.
2. Dataset curation
We built a dataset of CH–π interactions formed by β-d-galactose (galactose) residues and aromatic amino acids in protein–carbohydrate binding pockets to assess their orientational dependence and energetics. We used the advanced search tool in the Protein Data Bank (PDB)63 on 11.19.2021 to identify protein structures containing a galactose residue in a carbohydrate lacking any covalent bond to the protein. For inclusion in our analysis, we required that the protein structure determined by X-ray crystallography has an R factor of at most 20% and an overall resolution of no worse than 2 Å. We first identified close contacts between galactose and three aromatic amino acids: tryptophan, tyrosine, and phenylalanine by selecting all amino acid–galactose pairs in which the centroids of the two species were within 7 Å of one another. Histidine was excluded from this dataset because it is believed to primarily form hydrogen bonding interactions, not CH–π interactions.23 We obtained the electron density score for individual atoms64 (EDIA) and its combination for molecular fragments (EDIAm) for each relevant protein residue and carbohydrate monomer. We retained close contacts for those species that had EDIAm scores of at least 0.8, the previously suggested cutoff,64 to ensure that all heavy atoms are well resolved. Finally, because we included structures with monomeric galactose or with galactose as a component of a larger polysaccharide ligand, the anomeric oxygen substituent (O1) atoms often participated in glycosidic linkages and were assigned to another carbohydrate monomer. Thus, we omitted any attached O1 atoms when processing the PDB structures and reinserted them by adding an oxygen atom bound to C1 by a 1.43 Å sp3 bond along the PyMOL v. 2.5.2 (ref. 65)-inserted equatorial C–H bond vector (ESI Fig. S1†). In total, this screen identified 351 tryptophan, 154 tyrosine, and 45 phenylalanine side chains with close contacts to galactose (ESI Table S1†).
Due to the structural similarity between tyrosine and phenylalanine and the small size of those datasets, we augmented our data by transforming tyrosine into phenylalanine and vice versa to generate additional close contacts. We removed the phenol group moiety from the set of tyrosine–galactose pairs to generate new phenylalanine interactions and carried out the reverse operation on the phenylalanine interactions, creating a 1.38 Å C–O bond para to the β carbon (ESI Fig. S2†). For all close contacts, hydrogen atoms were added by PyMOL v. 2.5.2 and optimized using DFT (see Computational methods). Two structures that formed residue–carbohydrate interatomic clashes (i.e., defined as having a distance relative to the sum of van der Waals radii of <0.75 for any pair of atoms) after the addition of the tyrosine phenol group were removed from the dataset of newly generated tyrosine–galactose close contacts (ESI Fig. S2†). The resulting dataset contains 351 tryptophan, 197 tyrosine (i.e., 43 non-native), and 199 phenylalanine (i.e., 154 non-native) close contacts.
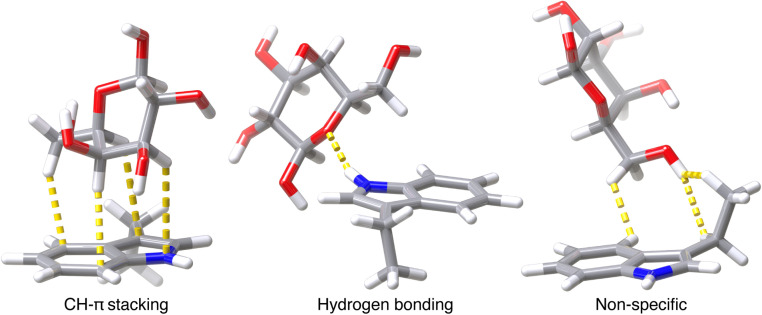
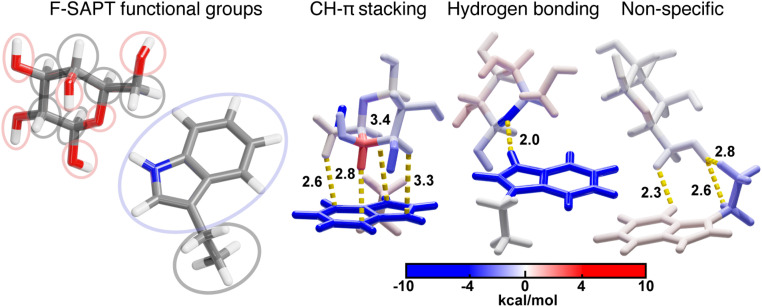
Because some close contacts in this dataset do not contain CH–π interactions, we grouped each contact into one of the following three categories: CH–π stacking interactions, hydrogen bonding interactions, or all other non-specific contacts (Fig. 1). CH–π stacking interactions are defined as instances in which the galactose stacks on top of the amino acid and three or more CH bonds are localized over the aromatic ring system (Fig. 1). CH bonds are considered localized over the aromatic ring when the carbon atom is positioned within 4.15 Å of a heavy atoms in the aromatic system of the protein residue (Fig. 1). The resulting dataset contained 272 tryptophan, 69 tyrosine, and 69 phenylalanine CH–π stacking interactions. Hydrogen bonding interactions formed between the galactose and the aromatic side chain were identified, after hydrogen positions were optimized with DFT, by using the polar contacts function in PyMOL, which annotates potential hydrogen bonding interactions that have a maximum acceptor–donor distance of 3.6 Å and a minimum acceptor–hydrogen–donor angle of 120° (Fig. 1 and ESI Fig. S3†). There were 29 tryptophan and 4 tyrosine sidechains that formed hydrogen bonds that met these criteria. In these cases, the N–H and O–H atoms on the sidechains primarily acted as hydrogen bond donors to oxygen atoms on the galactose. The remaining 50 tryptophan, 124 tyrosine, and 130 phenylalanine side chains formed non-specific interactions that did not meet either criterion. These sidechains had two or fewer C–H bonds localized over the aromatic ring system and no hydrogen bonds (Fig. 1). Thus, from 550 native close contacts, 62% of the close contacts form a CH–π stacking interaction, 6% form a hydrogen bond, and the other 32% are in proximity but form non-specific close contacts (ESI Fig. S4 and Table S2†).
Fig. 1. Visualization of one example for each of the three categories of contacts; CH–π stacking interactions, hydrogen bonding interactions, and other, non-specific close contacts. Atomic contacts are shown in yellow. Atoms are colored as follows: carbon in gray, oxygen in red, hydrogen in white, and nitrogen in blue.
The close contacts in this dataset are initially derived from 499 protein structures that have a non-covalently bound β-galactoside. Analysis of the types of protein structures contained in the set reveals that 42% were carbohydrate-binding proteins, 20% hydrolases, 16% viral proteins, 7% toxins, 7% transferases, and 8% other miscellaneous types. For 169 of these structures, we did not observe close contacts between galactose and an aromatic amino acid with good density support (i.e., from EDIA scores), whereas we identified 550 well-resolved close contacts for the other 330 structures (i.e., 1 or more per protein). All unique close contacts were retained, including those where multiple amino acids interact with the same carbohydrate (i.e., multiple close contacts), and cases where contacts were found on repeated protein subunits (ESI Fig. S5 and Table S3†).
3. Results and discussion
3.1. Energetic evaluation of β-galactoside–aromatic amino acid interactions
We evaluated the interaction strength of the close contacts between galactose and aromatic amino acids to assess the contribution of individual side chains to non-covalent protein–carbohydrate binding. We computed interaction energies using low-cost hybrid DFT (i.e., B3LYP-D3)66,67 and performed energetic decomposition analysis using symmetry-adapted perturbation theory (SAPT0),68,69 and functional group SAPT (F-SAPT)70 for the full dataset of close contacts (ESI Fig. S6†). These methods were selected for computational efficiency. Still, B3LYP-D3 has important limitations in evaluating long-range dispersion interactions from first-principles and SAPT0 has limitations in energetic accuracy given truncations in the perturbative expansion. Some prior analyses of computational method accuracy have been carried out for the study of CH–π interactions,71–77 yet these generally focused on alkane-containing interactions. Thus, further validation of B3LYP-D3 and SAPT0 method accuracy on these carbohydrate aromatic interactions was necessary.
We assessed the validity of B3LYP-D3 and SAPT0 by computing interaction energies using solvent-corrected DLPNO-CCSD(T) and SAPT2 on a benchmarking set of 50 CH–π stacking interactions (see Computational methods and ESI Fig. S6–S11†). Using this same set, we also confirmed that B3LYP-D3 and SAPT0 energies were not dependent on the number of intramolecular hydrogen bonds formed after hydrogen optimization (ESI Fig. S12†). Comparisons between B3LYP-D3 with implicit solvent and solvent-corrected DLPNO-CCSD(T) show a good agreement with an R2 of 0.91. We found more favorable B3LYP-D3 interaction energies by 1 kcal mol−1, on average (ESI Fig. S7†). Comparing gas-phase SAPT0 and SAPT2 gives an R2 of 0.96, while the analogous gas-phase DLPNO-CCSD(T) energetics give an R2 of 0.90 (ESI Fig. S8 and S9†). As expected, comparing SAPT0 interaction energies to solvated DLPNO-CCSD(T) energies yields a lower R2 of 0.75, and SAPT0 interaction energies are roughly 1.5 times more favorable than DLPNO-CCSD(T) counterparts (ESI Fig. S10†). These limitations of SAPT0 primarily derive from the lack of solvent treatment to mimic the screening effect of the protein environment. Nevertheless, we use SAPT0 and F-SAPT for energetic decomposition analysis rather than DFT-based energy decomposition analysis (EDA) schemes because the former methods recover dispersive interactions from first-principles and enable energetic decomposition to understand the contributions of protein functional groups (i.e., with F-SAPT, see Section 3.2). We report total interaction energy comparisons using values computed with B3LYP-D3. It was selected for its ability to incorporate solvent and its good reproduction of solvent-environment-corrected DLPNO-CCSD(T) interaction energies.
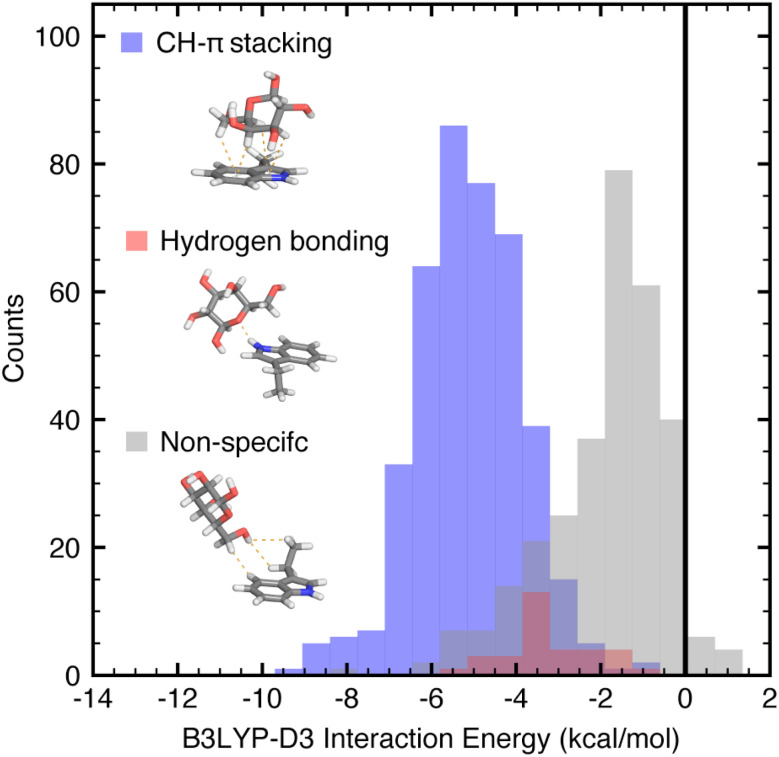
The B3LYP-D3 DFT interaction energies in the full data set of both native and non-native 774 close contacts range from −10.1 to −0.6 kcal mol−1. Comparing the three general categories, CH–π stacking interactions, hydrogen bonding interactions, and all other close contacts, we observe that the categories have distinct, albeit overlapping, DFT interaction energy distributions (ANOVA p-value = 9 × 10−145, Fig. 2). On average, the CH–π stacking interactions have B3LYP-D3 interaction energies of −6.1 kcal mol−1, whereas hydrogen bonding interactions have interaction energies of −4.4 kcal mol−1 and the other close contacts have an average of −3.2 kcal mol−1 (Fig. 2 and ESI Table S4†). Thus, CH–π stacking interactions are the strongest interactions formed between galactose and isolated tryptophan, tyrosine, or phenylalanine side chains.
Fig. 2. Unnormalized distributions of B3LYP-D3 DFT interaction energies for the three categories of galactose–aromatic amino acid close contacts shown as translucent histograms with bin width 0.65 kcal mol−1: CH–π stacking interactions (blue), hydrogen bonding interactions (red), and other, non-specific contacts (gray), of the full dataset. Interaction energies were evaluated using the aug-cc-pVDZ basis set and implicit solvent corrections were computed using the conductor-like polarizable continuum model (C-PCM) and reported in kcal mol−1. Atoms are colored as follows: carbon in gray, oxygen in red, hydrogen in white, and nitrogen in blue.
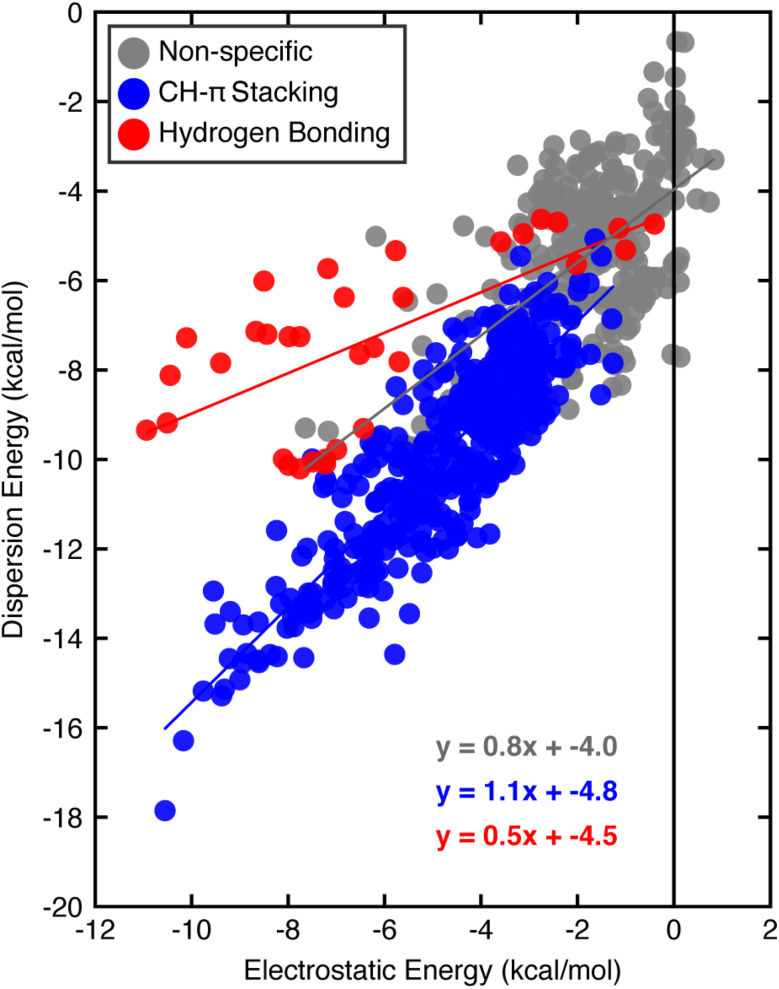
Turning to SAPT0 to quantify interaction energy components (i.e., electrostatic versus dispersion) further highlights differences between the categories of close contacts. The non-specific contacts behave most similarly to the weakest CH–π stacking or hydrogen bonding interactions, suggesting that they may include some favorable dispersive and electrostatic contacts without forming stacking interactions or hydrogen bonds. CH–π stacking interactions have a favorable one-to-one relationship between the electrostatic and dispersion energies (Fig. 3). Thus, although CH–π stacking interactions are predominantly thought to be dispersive, the electrostatic contribution is significant. In contrast, hydrogen bonding interactions are stabilized more by the electrostatic contribution, which outweighs the dispersion component by a factor of two on average (Fig. 3). While both interaction types have energetic contributions from dispersion and electrostatics, we previously noted that CH–π stacking interactions are more favorable overall than the hydrogen bonding interactions we examined. Although both interactions have a similar electrostatic contribution, the CH–π stacking interaction has a considerably larger favorable dispersion contribution. All other close contacts that form two or fewer C–H interactions (i.e., less than our criteria for CH–π stacking) or a non-specific contact have an intermediate contribution from dispersion and electrostatic energies.
Fig. 3. Comparison of SAPT0 dispersion and electrostatic energies for the three categories of interactions: CH–π stacking interactions (blue), hydrogen bonding interactions (red), and non-specific interactions (gray), of the full dataset. Best-fit lines for the CH–π stacking interactions (blue), hydrogen bonding interactions (red), and other close contacts (gray) are shown. All energies are reported in kcal mol−1. SAPT0 energies were evaluated using the aug-cc-pVDZ basis set.
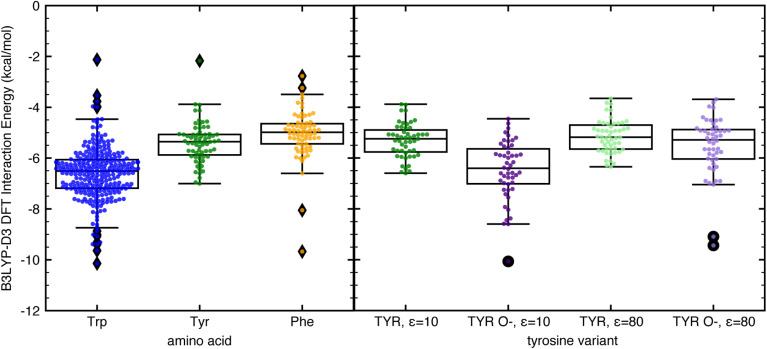
Next, we compared the interaction strengths of CH–π stacking interactions formed by tryptophan, tyrosine, and phenylalanine. While the 410 relevant interactions in our dataset have hybrid DFT interaction energies that range from −10.1 to −2.1 kcal mol−1, the strongest are those formed with tryptophan, the most highly enriched amino acid in protein–carbohydrate binding pockets23 (Fig. 4). These CH–π stacking interactions are more energetically favorable on average by 3 kcal mol−1 than those formed with tyrosine and phenylalanine (Fig. 4). Tryptophan has a larger and more electron-rich aromatic ring system enabling more favorable CH–π contacts and stronger dispersion and electrostatic energy contributions (ESI Fig. S13†). These highly favorable CH–π stacking interactions are essential along with other electrostatic interactions (e.g., hydrogen bonding and metal-mediated interactions) to stabilize protein–carbohydrate binding (see ESI Table S5, Fig. S14, and ESI data†).
Fig. 4. Box and whisker plot comparisons with all data points shown of B3LYP-D3 DFT interaction energies computed with C-PCM implicit solvent corrections of (left) CH–π stacking interactions formed with tryptophan (blue), tyrosine (green), and phenylalanine (light orange); and (right) CH–π stacking interactions formed with tyrosine with ε = 10 (green), deprotonated tyrosine in its phenoxide form with ε = 10 (purple), tyrosine with ε = 80 (light green), and phenoxide with ε = 80 (light purple). Each box is bounded by the upper and lower quartiles of the dataset and split by the median. The whiskers extend up to 1.5 times the interquartile range on either side of the box. All points that lie outside that range are defined as outliers and shown as filled diamonds on the left plot and filled circles on the right plot. The IEs were evaluated using the aug-cc-pVDZ basis set and are reported in kcal mol−1.
Both the native and non-native, constructed CH–π stacking interactions formed with tyrosine have comparable energetics to those involving phenylalanine, indicating that the effect of the neutral alcohol group on the overall interaction energy is minimal when evaluating CH–π stacking interactions (Fig. 4). However, when the phenol group of tyrosine is fully deprotonated (pKa 10.1) or hydrogen bonded to negatively charged amino acids, the increased electron density in the aromatic ring could lead to stronger CH–π interactions. To examine the potential impact of increased electron density on CH–π stacking interaction strength, we converted the 51 native tyrosine CH–π stacking interactions to phenoxide CH–π stacking interactions by deprotonating the acidic hydrogen and coordinating an explicit water molecule to the charged oxygen atom for charge stabilization (see Computational methods and ESI Fig. S15†). The resulting energetics indicate that phenoxide can form more stable CH–π stacking interactions than neutral tyrosine by 1.1 kcal mol−1. This value was calculated at the low dielectric conditions (ε = 10) representative of a buried binding pocket, and the enhancement is more limited in the high dielectric conditions (ε = 80) representative of exposure to aqueous solution (Fig. 4 and ESI Fig. S15†). Thus, increasing the electron density in aromatic ring systems can stabilize CH–π stacking interactions, demonstrating the importance of the electrostatic contribution. These observations provide some rationale for the increased propensity of tyrosine, but not phenylalanine, in glycan binding sites23 and may enable rational design of more favorable protein–carbohydrate binding interactions in therapeutic efforts.
3.2. Evaluating individual CH–π contributions
The identified CH–π stacking interactions involve multiple glycan C–H bonds positioned over the aromatic ring. Thus, we used functional group SAPT (i.e., F-SAPT) to decompose the interaction energies into the energetic contributions from different regions of galactose. This analysis provides a measure of interaction strength between distinct functional groups (i.e., portions of a molecule). For galactose residues, we defined each “functional group” as containing one galactose heavy atom (either carbon or oxygen) and any bonded hydrogen atom(s) (Fig. 5). For the amino acids, we distinguished only the aromatic and aliphatic regions (Fig. 5). We compared this analysis against second-order perturbative estimates of donor–acceptor interactions in the NBO basis and found that F-SAPT had better performance (see Computational details and ESI Fig. S16–S18†).
Fig. 5. (left) Delineation of selected F-SAPT functional groups. 14 functional groups are shown that are differentiated by ovals that each contain one functional group. Oxygen-containing functional groups are shown in red ovals, the aromatic ring functional group is shown in a blue oval, and all other carbon-containing functional groups are shown with gray ovals. Atoms are colored as follows: carbon in gray, oxygen in red, and nitrogen in blue. (right) F-SAPT visualizations of interaction energy contributions (in kcal mol−1) for representative structures from each of the three categories of tryptophan close contacts with functional groups colored by their interaction energy following the inset colorbar and defined corresponding to the groupings on the left.
Using F-SAPT, we demonstrated that CH–π stacking interactions involve favorable contributions from the aromatic ring(s) and multiple CH and OH groups on galactose (Fig. 5). They can also include one or more weakly repulsive interactions between the aromatic ring system and closely interacting CH groups from the galactose in which the repulsive exchange energy outweighs the favorable dispersion energy. As a result, optimizing the total energy of a CH–π stacking interaction can require a tradeoff where interacting atoms in too close proximity to the aromatic ring have energetics dominated by an unfavorable exchange repulsion energy that is offset by favorable dispersion and electrostatic energies of other, connected atoms (Fig. 5). Notably, the CH–π stacking interactions involve favorable contributions from more participating atoms on galactose than hydrogen bonding or other non-specific interactions, demonstrating the cohesive nature of the interactions (Fig. 5). Additionally, CH–π interactions are also favorable at longer distances than hydrogen bonding and other electrostatic interactions.
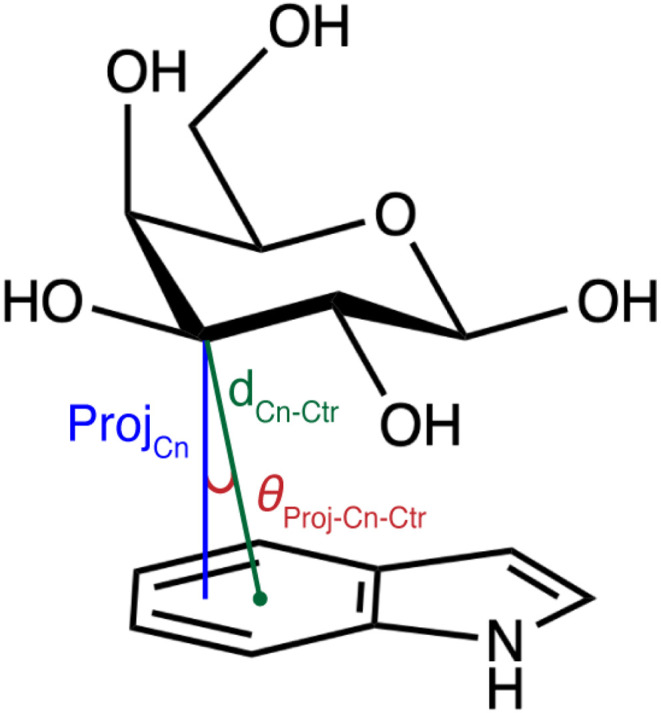
Given the range of contributions of individual CH and OH groups to the stabilization of carbohydrate–aromatic CH–π stacking interactions, we aimed to quantify the relationship between orientation and energetic contribution for all defined functional groups (Fig. 5). We evaluated the orientation of each galactose CH group by computing the distance of the galactose carbon atom (Cn) to the centroid (Ctr) of the nearest aromatic ring (dCn–Ctr), and the angle between the distance vector, dCn–Ctr, and the projection of Cn onto the aromatic ring plane (θProj–Cn–Ctr), as proposed by Houser and coworkers51 (Scheme 1). Using the previous maximum distance cutoff of 4.6 Å, we observe that the CH–π interactions in our data set preferentially occupy angles between 5° and 50° (ESI Fig. S19†). The angles and distances are linearly correlated, with shorter distances associated with more acute angles (ESI Fig. S19†).
Scheme 1. Visualization of carbon distance and angle features used to train random forest models. The feature dCn–Ctr (green) is the distance between a carbon atom (n) on galactose and the centroid of the nearest aromatic ring. The feature θProj–Cn–Ctr (red) is the angle between the distance vector and the vector ProjCn (blue) formed by the projection of Cn onto the plane of the aromatic ring system.
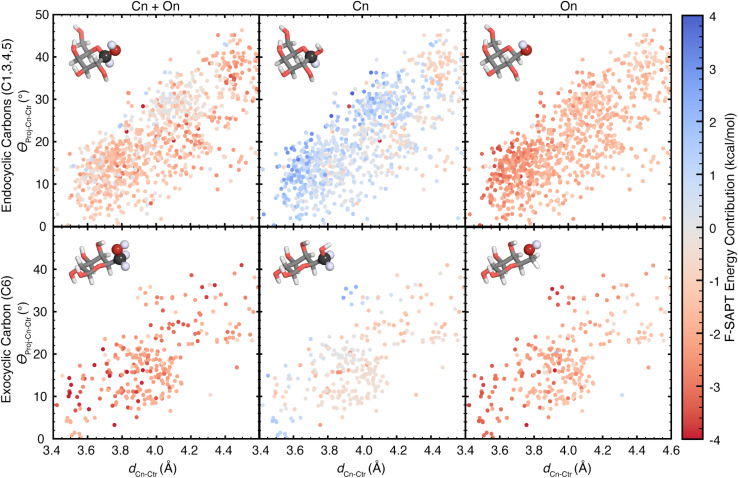
Using these orientational features, we analyzed the F-SAPT energetics of all 1706 carbon atoms capable of forming a CH–π interaction. These include carbon atoms within the distance cutoff of 4.6 Å for which the covalently-bound hydrogen atom is closer to the aromatic ring than the covalently-bound oxygen atom (i.e., carbon atoms C1, C3, C4, C5, and C6). However, all galactose CH–π donors are also polarized by a neighboring oxygen atom. Depending on glycan stereochemistry, some of these will engage in hyperconjugative interactions with neighboring hydroxyl groups. Thus, for each potential CH group (Cn), we evaluated the energetic contributions from three functional group sets: Cn, containing the carbon atom only; On, containing the bound oxygen atom only; and Cn + On, containing the two together (Fig. 6).
Fig. 6. Scatter plots showing the dependence of F-SAPT energy contributions on the orientations of the listed galactose atoms to the aromatic ring centroids in CH–π stacking interactions, reported in kcal mol−1. Rows are separated by the included carbon atoms: (top row) endocyclic galactose carbon atoms in the pyranose ring for which the attached hydrogen is closer to the aromatic ring than the attached hydroxyl and (bottom row) exocyclic galactose carbon atom 6, which is outside of the pyranose ring. Columns are separated by the F-SAPT “functional groups” included in the energy contribution reported: (left) the sum of the contributions from the carbon atom's group and its attached oxygen atom's group, (center) the carbon atom's group, and (right) the oxygen atom's group. The F-SAPT contribution is shown according to the color scale at the far right. Molecule insets show example functional groups included for each plot, with atoms included in the functional group shown in a sphere representation with saturated coloring. Atoms are colored as follows: carbon in gray, oxygen in red, and hydrogen in white.
Comparing the position–energy relationships for each carbon atom, we found notable differences in the energetic landscapes of endocyclic carbon atoms (C1, C3, C4, and C5) versus exocyclic carbon atoms (C6) (Fig. 6). Exocyclic carbon atoms have more favorable energetic contributions, with an average contribution of −0.5 kcal mol−1, whereas endocyclic carbons have less favorable energy contributions, with an average of +0.5 kcal mol−1 (Fig. 6 and ESI Table S6†). These energetic differences can be attributed to two factors. First, exocyclic carbon atoms have two alkyl hydrogen atoms capable of forming favorable contacts, and second, the exocyclic CH groups can rotate to form more optimal CH–π interactions, unlike the more conformationally restricted endocyclic CH groups (ESI Fig. S20 and S21†).
In analyzing all CH–π donors, some C–H groups (Cn) contribute favorable energetic contributions, while others (59%) have unfavorable interaction energies, (ESI Table S6†). In contrast, the oxygen groups (On) have nearly exclusively (99%) favorable energetic contributions, with an average value of −1.6 kcal mol−1, and therefore play a significant role in stabilizing CH–π interactions (ESI Table S6†). The trend is consistent: the most favorable On contributions and the least favorable Cn contributions occur at positions with the shortest observed distances for each angle (Scheme 1 and Fig. 6). This behavior is driven for the Cn groups by a repulsive exchange energy contribution and for the On groups by a stabilizing electrostatic energy contribution (ESI Fig. S22–S25†). Summing these to get the total Cn + On contribution, we observe a range of favorable local minima, which indicates that polarized CH–π interactions found in galactose–aromatic interactions contribute favorable energetics in a range of orientations.
3.3. Predicting CH–π interaction energies from orientations
Given the observed dependence of the component interaction energies on the orientation of a given CH–π interaction, we examined the relationship between orientation and energetics for the full set of carbohydrate–aromatic CH–π stacking interactions. We used random forest regression models to learn this relationship due to their strong performance on small datasets and good interpretability. We trained these models to predict total interaction energies from B3LYP-D3 and SAPT0 as well as the SAPT0 energetic components (i.e., dispersion, electrostatic, exchange, and induction). As inputs to our model, we used features that defined the CH–π stacking orientation without requiring any knowledge of hydrogen atom positions. These features include the distance (dCn–Ctr) and angle (θProj–Cn–Ctr) of each carbon (i.e., where n corresponds to 1–6 for C1–C6) in galactose to the centroid of the interacting aromatic ring (Scheme 1). While these features are correlated, they fully define the locations of the galactose atoms relative to the aromatic ring centroids, capturing the variability in the observed orientations (ESI Table S7†).
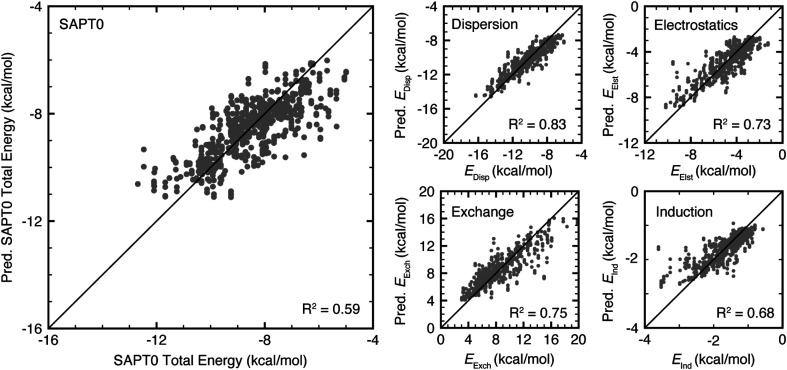
The trained random forest models predicted all target energies with a mean absolute error (MAE) of less than 1.2 kcal mol−1 and a mean absolute percentage error (MAPE) of less than 16% (ESI Table S8 and Fig. S26†). Using R2 as a figure of merit, the SAPT0 component dispersion, electrostatics, and exchange energies were predicted most accurately (R2 values of 0.83, 0.73, and 0.75, respectively), while B3LYP-D3 and SAPT0 interaction energies were predicted less accurately (R2 values of 0.47 and 0.59, respectively, Fig. 7). Nevertheless, the MAE of 0.51 kcal mol−1 for B3LYP-D3 and 0.69 kcal mol−1 for SAPT0 are still lower than the expected error of the underlying methods (ESI Table S8†). All models underestimate the strongest interactions, likely due to the small dataset size and limited number of structures with these interaction strengths (Fig. 7 and ESI Fig. S26†). Comparing these results to models trained on interactions containing only tryptophan or only tyrosine and phenylalanine, the models trained on all data perform as well as or better than models trained on specific data subsets (ESI Tables S9, S10 and Fig. S27, S28†).
Fig. 7. Parity plots of test set (left) SAPT0 total energy, (top center) dispersion, (upper right) electrostatics, (bottom center) exchange, and (bottom right) induction energy predicted by random forest models. All energies are reported in kcal mol−1. R2 values are reported in the bottom right of all plots.
In evaluating the feature importance for each model (see Computational methods), we identified the features most critical for predicting the energetic strength of a given CH–π stacking orientation. Despite differences in the most important features for each model, four features, dC2–Ctr, dC3–Ctr, dC5–Ctr, and dC6–Ctr, consistently rank among the most important (ESI Table S11†). These features involve carbon atoms that are distributed across the carbohydrate. These descriptors effectively capture the interaction proximity via dC3–Ctr and dC5–Ctr, because C3 and C5 participate in all galactose CH–π stacking interactions. These descriptors also capture the participating CH groups via dC2–Ctr and dC6–Ctr, which quantify which face of the carbohydrate is participating in the interaction (ESI Fig. S29†). Surprisingly, no angle features are critical across models, suggesting that the distance features effectively capture the interaction orientation.
3.4. Mapping the relationship between the CH–π interaction energy and orientation
Motivated by the limited number of features selected by random forest feature importance analysis, we aimed to further identify a minimal set of features that define an energy landscape for galactose–aromatic CH–π interactions. Because carbon atoms C3 and C5 consistently participate in component CH–π interactions, they do not distinguish between the different systems in our set. In contrast, carbon atoms C1, C4, and C6 are involved in some but not all CH–π stacking interactions (ESI Fig. S29†). For this reason, we used the distances dC1–Ctr, dC4–Ctr, and dC6–Ctr to define which portion of the ring participates in the CH–π stacking interaction. This analysis indicated only dC6–Ctr is universally essential in our feature set (see Section 3.3). Since the identity of the aromatic ring system influences the strength of the CH–π stacking interaction, we considered features that are sums of multiple distances to capture the number and proximity of CH groups interacting with the aromatic ring system and differentiate interactions formed by tryptophan from those formed by tyrosine and phenylalanine.
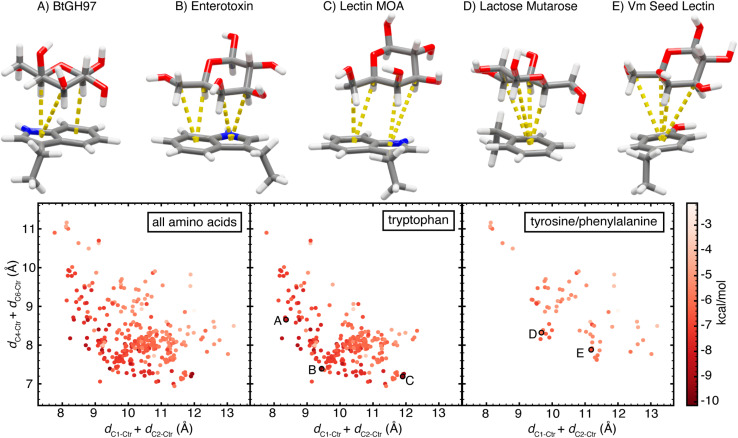
Finally, we selected two composite features to delineate the CH group proximity, dC1–Ctr+dC2–Ctr and dC4–Ctr+dC6–Ctr. These features capture an energetic landscape for CH–π stacking interactions, effectively differentiating interactions by their energetic favorability (Fig. 8). Importantly, these features contain no direct information regarding the face or orientation of the aromatic ring system. The relative facial positioning and rotation of the aromatic ring(s) has no intrinsic influence on the energetics of the interaction. Conversely, CH group proximity informs the interaction strength (Fig. 8). That is, the most favorable interactions have the smallest dC1–Ctr + dC2–Ctr and dC4–Ctr + dC6–Ctr values. However, the conformation of galactose, the size of the aromatic ring systems, and the exchange energy prevent the minimization of both features to very small values, giving rise to an energetic tradeoff (Fig. 8). Exploring this tradeoff, we find that it is possible to form CH–π stacking interactions with maximal interaction strength by minimizing either or both features, and thus, bringing any subset of 3 or more galactose C–H groups into close proximity of the aromatic ring. This demonstrates that CH–π stacking interactions do not have one energetic minimum, but rather, multiple relative orientations give rise to highly favorable CH-π interactions.
Fig. 8. Scatterplots of the orientations of CH–π stacking interactions formed by (left) all three aromatic amino acids, (center) only tryptophan, or (right) only tyrosine and phenylalanine. Each data point is plotted according to dC1–Ctr + dC2–Ctrversus dC4–Ctr + dC6–Ctr and colored by the B3LYP-D3 DFT interaction energy computed using the aug-cc-pVDZ basis set reported in kcal mol−1, according to the color scale shown at the far right. Five data points (A–E) are highlighted on the plots and the corresponding CH–π stacking interactions are shown. Atoms are colored as follows: carbon atoms in gray, oxygen atoms in red, nitrogen atoms in blue, and hydrogen atoms in white. Each component CH–π interaction with dCn–Ctr < 4.6 Å and θProj–Cn–Ctr < 50° is visualized by a dotted yellow line between the interacting carbon atom and the nearest aromatic ring centroid.
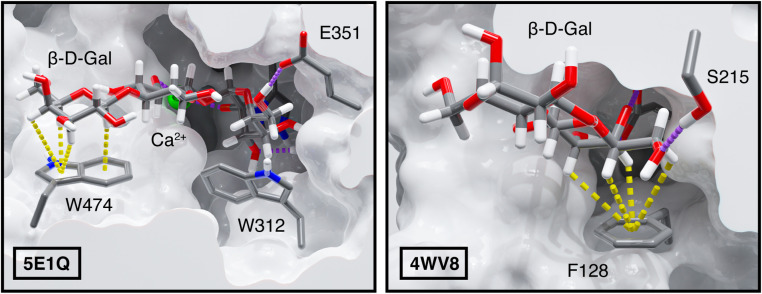
We explore optimal orientations by examining examples of galactose–tryptophan CH–π stacking interactions formed by three proteins, a Bacteroides thetaiotaomicron glycoside hydrolase (BtGH97, PDB ID 5E1Q78), an Escherichia coli heat-labile enterotoxin (PDB ID 2XRS79), and Marasmius oreades agglutinin (MOA) an M. oreades lectin (PDB ID 3EF2 (ref. 80)). All three CH–π stacking interactions determined from the carbohydrate–amino acid pair from these proteins have highly favorable interaction energies. The B3LYP-D3 interaction energy of the CH–π stacking interaction formed by BtGH97 is −8.3 kcal mol−1, that of the enterotoxin is −9.6 kcal mol−1, and that of the MOA lectin is −9.4 kcal mol−1. Each protein-carbohydrate interaction has a distinct orientation and value along the dC1–Ctr + dC2–Ctr and dC4–Ctr + dC6–Ctr landscape (Fig. 8). BtGH97 forms CH–π component interactions with carbon atoms C1, C3, and C5, while the enterotoxin and MOA lectin form component interactions with carbon atoms C3, C4, C5, and C6, each at a unique interaction angle (Fig. 8). These differences in the CH–π stacking orientation enable each carbohydrate ligand to form optimal hydrogen bonds to neighboring amino acid residues while maintaining a favorable carbohydrate–aromatic stabilization (Fig. 9 and ESI Fig. S30–S32†).
Fig. 9. Protein-carbohydrate interactions of (left) Bacteroides thetaiotaomicron glycoside hydrolase and (right) Vatairea macrocarpa seed lectin with their carbohydrate ligands. CH–π interactions are shown as yellow dashed lines, and calcium ion coordinating and hydrogen bonding interactions are shown as purple dashed lines. The surface of the protein structure is shown in light gray. Atoms are colored as follows: carbon in gray, oxygen in red, hydrogen in white, nitrogen in blue, and calcium in green. Component CH–π interactions with dCn–Ctr < 4.6 Å and θProj–Cn–Ctr < 50° are visualized as dotted yellow lines between the interacting hydrogen atom and nearest aromatic ring centroid.
Next, comparing the CH–π stacking interactions formed by each of the different amino acids, we observe that while the lowest-energy stacking interactions formed by tyrosine and phenylalanine occupy overlapping regions of the conformational space as those formed by tryptophan, the galactose–tryptophan interactions tend to have shorter values for dC1–Ctr + dC2–Ctr and dC4–Ctr + dC6–Ctr than tyrosine and phenylalanine interactions, with minima at 7.7 Å and 6.9 Å versus 8.1 Å and 7.6 Å, respectively (Fig. 8). This indicates that the same minimization of dC1–Ctr + dC2–Ctr and dC4–Ctr + dC6–Ctr possible for the bicyclic indole on tryptophan is not possible for smaller, unicyclic aromatic rings on tyrosine and phenylalanine and confirms that the size of the aromatic ring system is a driving factor that enables tryptophan to make stronger interactions.
Evaluating the distribution of tyrosine and phenylalanine CH–π stacking interactions, we note that, although distinct from tryptophan interactions, these do follow the same energetic tradeoff with multiple optimal orientations (Fig. 8). Two representative proteins, Lactococcus lactis galactose mutarotase (PDB ID 1NSM81) and Vatairea macrocarpa seed lectin (PDB ID 4WV8 (ref. 82)), form CH–π stacking interactions with similar energetic favorability. The CH–π interaction formed by a phenylalanine in galactose mutarotase has an interaction energy of −6.6 kcal mol−1, while the one formed by a non-native tyrosine in the seed lectin is −7.0 kcal mol−1 (Fig. 8). The galactose mutarotase forms component interactions with carbon atoms C1, C3, C4, and C5, while the seed lectin forms component interactions with carbon atoms C3, C4, C5, and C6 (Fig. 8 and 9). Examining the structures of these protein binding pockets reinforces that carbohydrate binding is stabilized by hydrogen bonds to nearby amino acids that further influence the galactose orientation. Thus, the orientational flexibility of the CH–π stacking interactions enables the optimization of all involved interactions, while still contributing to the selectivity of protein–carbohydrate recognition by requiring a proper orientation of C–H bonds (Fig. 9 and ESI Fig. S33, S34†). This analysis provides insight into the role of carbohydrate–aromatic interactions in enzyme processivity,83–85 demonstrating their ability to stabilize a bound substrate through the range of orientations that must occur during processive catalysis.
4. Computational methods
A total of 550 close contacts between β-d-galactose and aromatic amino acids, tryptophan, tyrosine, and phenylalanine, were identified from a search of the Protein Data Bank (PDB).63 To obtain coordinates for electronic structure calculations of each close contact, the heavy atom positions of β-d-galactose and the amino acid sidechain were obtained from each PDB structure. Protein backbone atoms (C, Cα, O, and N) were not included to reduce the computational complexity. From these structures, hydrogen atoms were added using PyMOL v. 2.5.2.65 Final geometries were obtained by freezing heavy atom coordinates and performing a DFT geometry optimization on all hydrogen atoms to preserve the close contact observed in the protein structure. These geometry optimizations were performed using the developer version 1.9–2018.11 of TeraChem86 with the global hybrid B3LYP66,67 DFT functional and the aug-cc-pVDZ basis set. The semiempirical DFT-D3 (ref. 87) dispersion correction with default Becke–Johnson damping88 was applied. To approximate the contribution of the protein environment, the implicit conductor-like polarizable continuum model (C-PCM),89,90 as implemented in TeraChem,91 was used with ε = 10. The L-BFGS algorithm, as implemented in DL-FIND92 was used to perform the optimizations. The default thresholds of 4.5 × 10−4 hartree bohr−1 for the maximum gradient and 1 × 10−6 hartree for self-consistent field (SCF) convergence were employed. All calculations were closed-shell singlet calculations.
Tyrosine phenoxide contacts were generated from initial structures by deprotonating the acidic phenol hydrogen and placing a water molecule beneath the oxygen atom of the resulting phenoxide. The water molecule was optimized in Avogadro to satisfy a constraint of an O–O distance of 2.8 Å between water and the phenoxide oxygen using the built in MMFF94 force field. Final geometries were again obtained by freezing all heavy atom coordinates and performing a B3LYP-D3/aug-cc-pVDZ geometry optimization on hydrogen atoms only using TeraChem. To explore the effect of solvent on these interactions, (C-PCM)89 was used with ε = 10 and 80.
Single-point calculations were carried out to compute DFT-level interaction energies. Specifically, B3LYP-D3/aug-cc-pVDZ DFT interaction energies (IE) were calculated as follows:
| IE = Ecomplex − Ecarbohydrate − Eamino acid | 1 |
where Ecomplex is the energy of the non-covalently interacting amino acid and carbohydrate monomer pair, and Ecarbohydrate and Eamino acid are the energies of each separate component. Energy decomposition analysis was also performed with SAPT0 (ref. 68 and 69) using Psi4 v. 1.4 (ref. 93) and the aug-cc-pVDZ basis set.94 Superposition of atomic densities (SAD) guess orbitals and density fitting for the SCF computation with the aug-cc-pVDZ-jkfit auxiliary basis set along with resolution of the identity (i.e., aug-cc-pVDZ-ri) were employed for the SAPT calculations.
We used higher-cost SAPT2 and DLPNO-CCSD(T)95,96 methods to benchmark B3LYP-D3 DFT and SAPT0 energetics. The SAPT2 (ref. 97) calculations were carried out in Psi4 with the aug-cc-pVDZ and aug-cc-pVTZ basis sets and extrapolated to the augmented complete basis set limit using the two-point formula.98,99 Single-point DLPNO-CCSD(T) calculations were carried out using ORCA v. 4.2.1 (ref. 100) with the TightSCF convergence keyword. Interaction energies were computed using eqn (1) and were extrapolated to the augmented complete basis set (CBS) limit using the two-point formula and the aug-cc-pVDZ and aug-cc-pVTZ basis sets.101 An extrapolation to the limit of the complete pair natural orbital space (CPS)102 was performed using a two-point formula and calculations with paired natural orbital (PNO) cutoffs of 10−6 and 10−7.
Because implicit solvent was not implemented for DLPNO-CCSD(T) calculations in ORCA v. 4.2.1, a solvent correction was obtained by evaluating the interaction energy of the complex via Møller–Plesset second-order perturbation theory (MP2) with and without implicit solvent as follows:
| IEDLPNO-CCSD(T) solvated = IEDLPNO-CCSD(T) + IEMP2 solvated − IEMP2 | 2 |
MP2 calculations were performed in ORCA100 using all DLPNO-CCSD(T) parameters except for the RI approximation, which was employed with auxiliary basis sets automatically selected with the AutoAux103 keyword. The MP2 implicit solvent calculations were carried out with the C-PCM model (ε = 10) with COSMO-type epsilon functions.
We used Gaussian 16.C.01 (ref. 104) to perform second-order perturbative estimates of donor–acceptor interactions in the NBO105 basis treated at the B3LYP/aug-cc-pVDZ level. We obtained the E(2) energy contribution from C–H groups by summing all E(2) energy contributions attributed to the given hydrogen Rydberg orbital and the carbon–hydrogen bond and antibond.
Random forest regression models were trained on 12 orientational features to learn the relationship between conformation and binding affinity (ESI Table S6†). These models were implemented using Scikit-learn106 v. 1.1.3 with 200 estimators. A grid search was performed to identify hyperparameters that minimize the R2 of the training set while maximizing the R2 of the test set to avoid overfitting. The selected hyperparameters are as follows: a maximum depth of 8, a minimum of 4 samples required to split an internal node, a maximum of 20 leaves, and a minimum of 6 samples per leaf. All models were evaluated using 5-fold cross-validation and an 80 : 20 train : test split. Feature importance for each model was calculated based on the mean decrease in impurity using the sklearn_feature_importances method.
5. Conclusion
Our analysis of non-covalent protein–carbohydrate binding interactions in the PDB reveals critical attributes of CH–π interactions between β-d-galactose and tryptophan, tyrosine, and phenylalanine residues. We found that the single amino acid–carbohydrate interaction energies are energetically favorable by 4 to 8 kcal mol−1 (i.e., more favorable than hydrogen bonding interactions formed by those same pairs), demonstrating the importance of CH–π stacking interactions in protein–carbohydrate binding. The strongest interactions were formed with tryptophan, while those with tyrosine and phenylalanine were generally weaker. This effect is predominantly driven by the size and electronics of the aromatic ring system, with larger rings and those with higher electron density enabling more favorable CH–π contacts.
We then trained random forest machine learning models to predict CH–π stacking interaction energies based on their orientations and found distances between the galactose carbon atoms and the aromatic ring centroids to be the most predictive features. Finally, we identified an energetic landscape for β-galactose–aromatic CH–π stacking interactions using only the distances between galactose carbon atoms and aromatic amino acid ring centroids. This landscape demonstrates that CH–π stacking interactions have high orientational flexibility with a continuous minimum energy well that corresponds to many distinct orientations. Optimal CH–π stacking interactions can be formed by maximizing favorable contacts between different subsets of hydrogen atoms and the aromatic ring(s).
Many diverse orientations of CH–π stacking interactions contribute significant stabilization to protein–carbohydrate interactions. This observation enables further evaluation of the role of CH–π stacking interactions in conferring selectivity for protein–carbohydrate binding and processivity in enzymatic reactions. In total, our studies reveal the molecular underpinnings of protein–carbohydrate binding interactions and the importance of improving molecular simulation force fields and docking energy functions to account fully for this contribution.
Data availability
Structures, computed energies, and random forest models are all included in the ESI† as follows: initial and optimized 3D structures of all native and synthetic close contacts; EDIAm scores, raw electronic energies and interaction energies from DFT, and SAPT0 total and component energies for the full dataset of close contacts; interaction energies of the interaction in the benchmarking dataset, as determined by DLPNO-CCSD(T), MP2, DFT, SAPT0 and SAPT2; PyMOL session files for select protein binding pockets; random forest models trained to predict the DFT interaction energy, SAPT0 interaction energy, dispersion, electrostatics, exchange, and induction energies (ZIP).
Author contributions
A. M. K., L. L. K., and H. J. K. conceived and designed the project. A. M. K. performed all computation and analyzed the data. A. M. K. and D. W. K. designed figures. A. M. K., L. L. K., and H. J. K. wrote the manuscript.
Conflicts of interest
The authors declare no competing financial interest.
Supplementary Material
Acknowledgments
The authors acknowledge primary support from the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing, Office of Basic Energy Sciences, via the Scientific Discovery through Advanced Computing (SciDAC) program (H. J. K.) and the National Institute of Allergy and Infectious Diseases under grant number R01 AI055258 (L. L. K.). The authors acknowledge the MIT SuperCloud and Lincoln Laboratory Supercomputing Center for providing HPC resources that have contributed to the research results reported within this paper. A. M. K. acknowledges partial support from the Hugh Hampton Young Memorial Fund Fellowship, MIT Office of Graduate Education and NIH Training grant T32 GM087237 from the National Institute of General Medical Sciences. H. J. K. acknowledges a Sloan Foundation Fellowship in Chemistry and a Simon Family Faculty Research Innovation Fund grant. The authors thank Adam Steeves, Vyshnavi Vennelakanti, Clorice Reinhardt, Ilia Kevlishvili, Amanda Peiffer, and Rajeev Chorghade for helpful discussions.
Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc06246a
References
- Shen H. Lee C. Y. Chen C. H. Protein Glycosylation as Biomarkers in Gynecologic Cancers. Diagnostics. 2022;12:3177. doi: 10.3390/diagnostics12123177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsubo K. Marth J. D. Glycosylation in cellular mechanisms of health and disease. Cell. 2006;126:855–867. doi: 10.1016/j.cell.2006.08.019. [DOI] [PubMed] [Google Scholar]
- Raman R. Tharakaraman K. Sasisekharan V. Sasisekharan R. Glycan-protein interactions in viral pathogenesis. Curr. Opin. Struct. Biol. 2016;40:153–162. doi: 10.1016/j.sbi.2016.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Kooyk Y. Rabinovich G. A. Protein-glycan interactions in the control of innate and adaptive immune responses. Nat. Immunol. 2008;9:593–601. doi: 10.1038/ni.f.203. [DOI] [PubMed] [Google Scholar]
- Pinho S. S. Alves I. Gaifem J. Rabinovich G. A. Immune regulatory networks coordinated by glycans and glycan-binding proteins in autoimmunity and infection. Cell. Mol. Immunol. 2023;20:1101–1113. doi: 10.1038/s41423-023-01074-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandes A. Azevedo C. M. Silva M. C. Faria G. Dantas C. S. Vicente M. M. Pinho S. S. Glycans as shapers of tumour microenvironment: a sweet driver of T-cell-mediated anti-tumour immune response. Immunology. 2023;168:217–232. doi: 10.1111/imm.13494. [DOI] [PubMed] [Google Scholar]
- Collins B. E. Paulson J. C. Cell surface biology mediated by low affinity multivalent protein-glycan interactions. Curr. Opin. Chem. Biol. 2004;8:617–625. doi: 10.1016/j.cbpa.2004.10.004. [DOI] [PubMed] [Google Scholar]
- Raposo C. D. Canelas A. B. Barros M. T. Human Lectins, Their Carbohydrate Affinities and Where to Find Them. Biomolecules. 2021;11:188. doi: 10.3390/biom11020188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bojar D. Meche L. Meng G. Eng W. Smith D. F. Cummings R. D. Mahal L. K. A Useful Guide to Lectin Binding: Machine-Learning Directed Annotation of 57 Unique Lectin Specificities. ACS Chem. Biol. 2022;17:2993–3012. doi: 10.1021/acschembio.1c00689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Modenutti C. P. Capurro J. I. B. Di Lella S. Marti M. A. The Structural Biology of Galectin-Ligand Recognition: Current Advances in Modeling Tools, Protein Engineering, and Inhibitor Design. Front. Chem. 2019;7:823. doi: 10.3389/fchem.2019.00823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klamer Z. Staal B. Prudden A. R. Liu L. Smith D. F. Boons G. J. Haab B. Mining High-Complexity Motifs in Glycans: A New Language To Uncover the Fine Specificities of Lectins and Glycosidases. Anal. Chem. 2017;89:12342–12350. doi: 10.1021/acs.analchem.7b04293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kletter D. Singh S. Bern M. Haab B. B. Global comparisons of lectin-glycan interactions using a database of analyzed glycan array data. Mol. Cell. Proteomics. 2013;12:1026–1035. doi: 10.1074/mcp.M112.026641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith D. F. Song X. Cummings R. D. Use of glycan microarrays to explore specificity of glycan-binding proteins. Methods Enzymol. 2010;480:417–444. doi: 10.1016/S0076-6879(10)80033-3. [DOI] [PubMed] [Google Scholar]
- Gout E. Garlatti V. Smith D. F. Lacroix M. Dumestre-Perard C. Lunardi T. Martin L. Cesbron J. Y. Arlaud G. J. Gaboriaud C. Thielens N. M. Carbohydrate recognition properties of human ficolins: glycan array screening reveals the sialic acid binding specificity of M-ficolin. J. Biol. Chem. 2010;285:6612–6622. doi: 10.1074/jbc.M109.065854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porter A. Yue T. Heeringa L. Day S. Suh E. Haab B. B. A motif-based analysis of glycan array data to determine the specificities of glycan-binding proteins. Glycobiology. 2010;20:369–380. doi: 10.1093/glycob/cwp187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jimenez-Barbero J. Canada F. J. Cuevas G. Asensio J. L. Aboitiz N. Canales A. Chavez M. I. Fernandez-Alonso M. C. Garcia-Herrero A. Mari S. Vidal P. Protein-carbohydrate interactions: a combined theoretical and NMR experimental approach on carbohydrate-aromatic interactions and on pyranose ring distortion. ACS Symp. Ser. 2006;930:60–80. doi: 10.1021/bk-2006-0930.ch004. [DOI] [Google Scholar]
- Vyas N. K. Atomic features of protein-carbohydrate interactions. Curr. Opin. Struct. Biol. 1991;1:732–740. doi: 10.1016/0959-440X(91)90172-P. [DOI] [Google Scholar]
- Quiocho F. A. Protein-Carbohydrate Interactions - Basic Molecular-Features. Pure Appl. Chem. 1989;61:1293–1306. [Google Scholar]
- Vennelakanti V. Qi H. W. Mehmood R. Kulik H. J. When are two hydrogen bonds better than one? Accurate first-principles models explain the balance of hydrogen bond donors and acceptors found in proteins. Chem. Sci. 2021;12:1147–1162. doi: 10.1039/d0sc05084a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi H. W. Kulik H. J. Evaluating Unexpectedly Short Non-covalent Distances in X-ray Crystal Structures of Proteins with Electronic Structure Analysis. J. Chem. Inf. Model. 2019;59:2199–2211. doi: 10.1021/acs.jcim.9b00144. [DOI] [PubMed] [Google Scholar]
- Rooney T. P. Filippakopoulos P. Fedorov O. Picaud S. Cortopassi W. A. Hay D. A. Martin S. Tumber A. Rogers C. M. Philpott M. Wang M. Thompson A. L. Heightman T. D. Pryde D. C. Cook A. Paton R. S. Muller S. Knapp S. Brennan P. E. Conway S. J. A series of potent CREBBP bromodomain ligands reveals an induced-fit pocket stabilized by a cation-pi interaction. Angew. Chem., Int. Ed. 2014;53:6126–6130. doi: 10.1002/anie.201402750. [DOI] [Google Scholar]
- Diehl R. C. Chorghade R. S. Keys A. M. Alam M. M. Early S. A. Dugan A. E. Krupkin M. Ribbeck K. Kulik H. J. Kiessling L. L. CH−π Interactions Are Required for Human Galectin-3 Function. JACS Au. 2024;4:3028–3037. doi: 10.1021/jacsau.4c00357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson K. L. Bartlett G. J. Diehl R. C. Agirre J. Gallagher T. Kiessling L. L. Woolfson D. N. Carbohydrate-Aromatic Interactions in Proteins. J. Am. Chem. Soc. 2015;137:15152–15160. doi: 10.1021/jacs.5b08424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiessling L. L. Diehl R. C. CH-Pi Interactions in Glycan Recognition. ACS Chem. Biol. 2021;16:1884–1893. doi: 10.1021/acschembio.1c00413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platzer G. Mayer M. Beier A. Bruschweiler S. Fuchs J. E. Engelhardt H. Geist L. Bader G. Schorghuber J. Lichtenecker R. Wolkerstorfer B. Kessler D. McConnell D. B. Konrat R. PI by NMR: Probing CH-pi Interactions in Protein-Ligand Complexes by NMR Spectroscopy. Angew. Chem., Int. Ed. 2020;59:14861–14868. doi: 10.1002/anie.202003732. [DOI] [Google Scholar]
- Gimeno A. Valverde P. Arda A. Jimenez-Barbero J. Glycan structures and their interactions with proteins. A NMR view. Curr. Opin. Struct. Biol. 2020;62:22–30. doi: 10.1016/j.sbi.2019.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roldos V. Canada F. J. Jimenez-Barbero J. Carbohydrate-protein interactions: a 3D view by NMR. ChemBioChem. 2011;12:990–1005. doi: 10.1002/cbic.201000705. [DOI] [PubMed] [Google Scholar]
- Laigre E. Goyard D. Tiertant C. Dejeu J. Renaudet O. The study of multivalent carbohydrate-protein interactions by bio-layer interferometry. Org. Biomol. Chem. 2018;16:8899–8903. doi: 10.1039/C8OB01664J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji Y. Woods R. J. Quantifying Weak Glycan-Protein Interactions Using a Biolayer Interferometry Competition Assay: Applications to ECL Lectin and X-31 Influenza Hemagglutinin. Adv. Exp. Med. Biol. 2018;1104:259–273. doi: 10.1007/978-981-13-2158-0_13. [DOI] [PubMed] [Google Scholar]
- Clarke C. Woods R. J. Gluska J. Cooper A. Nutley M. A. Boons G. J. Involvement of water in carbohydrate-protein binding. J. Am. Chem. Soc. 2001;123:12238–12247. doi: 10.1021/ja004315q. [DOI] [PubMed] [Google Scholar]
- Santana A. G. Jimenez-Moreno E. Gomez A. M. Corzana F. Gonzalez C. Jimenez-Oses G. Jimenez-Barbero J. Asensio J. L. A Dynamic Combinatorial Approach for the Analysis of Weak Carbohydrate/Aromatic Complexes: Dissecting Facial Selectivity in CH-Pi Stacking Interactions. J. Am. Chem. Soc. 2013;135:3347–3350. doi: 10.1021/ja3120218. [DOI] [PubMed] [Google Scholar]
- del Carmen Fernandez-Alonso M. Diaz D. Berbis M. A. Marcelo F. Canada J. Jimenez-Barbero J. Protein-carbohydrate interactions studied by NMR: from molecular recognition to drug design. Curr. Protein Pept. Sci. 2012;13:816–830. doi: 10.2174/138920312804871175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenbussche S. Diaz D. Fernandez-Alonso M. C. Pan W. D. Vincent S. P. Cuevas G. Canada F. J. Jimenez-Barbero J. Bartik K. Aromatic-carbohydrate interactions: An NMR and computational study of model systems. Chem.–Eur. J. 2008;14:7570–7578. doi: 10.1002/chem.200800247. [DOI] [PubMed] [Google Scholar]
- Parrish R. M. Parker T. M. Sherrill C. D. Chemical Assignment of Symmetry-Adapted Perturbation Theory Interaction Energy Components: The Functional-Group SAPT Partition. J. Chem. Theory Comput. 2014;10:4417–4431. doi: 10.1021/ct500724p. [DOI] [PubMed] [Google Scholar]
- Raju R. K. Ramraj A. Vincent M. A. Hillier I. H. Burton N. A. Carbohydrate-protein recognition probed by density functional theory and ab initio calculations including dispersive interactions. Phys. Chem. Chem. Phys. 2008;10:6500–6508. doi: 10.1039/B809164A. [DOI] [PubMed] [Google Scholar]
- Paton R. S. Goodman J. M. Hydrogen bonding and pi-stacking: how reliable are force fields? A critical evaluation of force field descriptions of nonbonded interactions. J. Chem. Inf. Model. 2009;49:944–955. doi: 10.1021/ci900009f. [DOI] [PubMed] [Google Scholar]
- Kumar K. Woo S. M. Siu T. Cortopassi W. A. Duarte F. Paton R. S. Cation-pi interactions in protein-ligand binding: theory and data-mining reveal different roles for lysine and arginine. Chem. Sci. 2018;9:2655–2665. doi: 10.1039/C7SC04905F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringer A. L. Sherrill C. D. Substituent effects in sandwich configurations of multiply substituted benzene dimers are not solely governed by electrostatic control. J. Am. Chem. Soc. 2009;131:4574–4575. doi: 10.1021/ja809720r. [DOI] [PubMed] [Google Scholar]
- Sherrill C. D. Energy component analysis of pi interactions. Acc. Chem. Res. 2013;46:1020–1028. doi: 10.1021/ar3001124. [DOI] [PubMed] [Google Scholar]
- Hohenstein E. G. Sherrill C. D. Effects of heteroatoms on aromatic pi-pi interactions: benzene-pyridine and pyridine dimer. J. Phys. Chem. A. 2009;113:878–886. doi: 10.1021/jp809062x. [DOI] [PubMed] [Google Scholar]
- Carter-Fenk K. Liu M. Pujal L. Loipersberger M. Tsanai M. Vernon R. M. Forman-Kay J. D. Head-Gordon M. Heidar-Zadeh F. Head-Gordon T. The Energetic Origins of Pi-Pi Contacts in Proteins. J. Am. Chem. Soc. 2023;145:24836–24851. doi: 10.1021/jacs.3c09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asensio J. L. Arda A. Canada F. J. Jimenez-Barbero J. Carbohydrate-Aromatic Interactions. Accounts Chem. Res. 2013;46:946–954. doi: 10.1021/ar300024d. [DOI] [Google Scholar]
- Tsuzuki S. Fujii A. Nature and physical origin of CH-Pi interaction: significant difference from conventional hydrogen bonds. Phys. Chem. Chem. Phys. 2008;10:2584–2594. doi: 10.1039/B718656H. [DOI] [PubMed] [Google Scholar]
- Spiwok V. CH-Pi Interactions in Carbohydrate Recognition. Molecules. 2017;22:1038. doi: 10.3390/molecules22071038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perras F. A. Marion D. Boisbouvier J. Bryce D. L. Plevin M. J. Observation of CH-Pi Interactions between Methyl and Carbonyl Groups in Proteins. Angew. Chem., Int. Ed. 2017;56:7564–7567. doi: 10.1002/anie.201702626. [DOI] [Google Scholar]
- Nishio M. Umezawa Y. Fantini J. Weiss M. S. Chakrabarti P. CH-Pi hydrogen bonds in biological macromolecules. Phys. Chem. Chem. Phys. 2014;16:12648–12683. doi: 10.1039/C4CP00099D. [DOI] [PubMed] [Google Scholar]
- Pace C. J. Kim D. Gao J. Experimental evaluation of CH-Pi interactions in a protein core. Chemistry. 2012;18:5832–5836. doi: 10.1002/chem.201200334. [DOI] [PubMed] [Google Scholar]
- Nishio M. The CH-Pi hydrogen bond: implication in chemistry. J. Mol. Struct. 2012;1018:2–7. doi: 10.1016/j.molstruc.2012.03.012. [DOI] [Google Scholar]
- Nishio M. The CH-Pi hydrogen bond in chemistry. Conformation, supramolecules, optical resolution and interactions involving carbohydrates. Phys. Chem. Chem. Phys. 2011;13:13873–13900. doi: 10.1039/C1CP20404A. [DOI] [PubMed] [Google Scholar]
- Brandl M. Weiss M. S. Jabs A. Suhnel J. Hilgenfeld R. C-H center dot center dot center dot pi-interactions in proteins. J. Mol. Biol. 2001;307:357–377. doi: 10.1006/jmbi.2000.4473. [DOI] [PubMed] [Google Scholar]
- Houser J. Kozmon S. Mishra D. Hammerova Z. Wimmerova M. Koca J. The CH-Pi Interaction in Protein-Carbohydrate Binding: Bioinformatics and In Vitro Quantification. Chem.–Eur. J. 2020;26:10769–10780. doi: 10.1002/chem.202000593. [DOI] [PubMed] [Google Scholar]
- Laughrey Z. R. Kiehna S. E. Riemen A. J. Waters M. L. Carbohydrate-pi interactions: What are they worth? J. Am. Chem. Soc. 2008;130:14625–14633. doi: 10.1021/ja803960x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jimenez-Moreno E. Jimenez-Oses G. Gomez A. M. Santana A. G. Corzana F. Bastida A. Jimenez-Barberodef J. Asensio J. L. A thorough experimental study of CH-Pi interactions in water: quantitative structure-stability relationships for carbohydrate/aromatic complexes. Chem. Sci. 2015;6:6076–6085. doi: 10.1039/C5SC02108A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramirez-Gualito K. Alonso-Rios R. Quiroz-Garcia B. Rojas-Aguilar A. Diaz D. Jimenez-Barbero J. Cuevas G. Enthalpic Nature of the CH-Pi Interaction Involved in the Recognition of Carbohydrates by Aromatic Compounds, Confirmed by a Novel Interplay of NMR, Calorimetry, and Theoretical Calculations. J. Am. Chem. Soc. 2009;131:18129–18138. doi: 10.1021/ja903950t. [DOI] [PubMed] [Google Scholar]
- Hsu C. H. Park S. Mortenson D. E. Foley B. L. Wang X. Woods R. J. Case D. A. Powers E. T. Wong C. H. Dyson H. J. Kelly J. W. The Dependence of Carbohydrate-Aromatic Interaction Strengths on the Structure of the Carbohydrate. J. Am. Chem. Soc. 2016;138:7636–7648. doi: 10.1021/jacs.6b02879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsuzuki S. Uchimaru T. Mikami M. Magnitude and Nature of Carbohydrate-Aromatic Interactions in Fucose-Phenol and Fucose-Indole Complexes: CCSD(T) Level Interaction Energy Calculations. J. Phys. Chem. A. 2011;115:11256–11262. doi: 10.1021/jp2045756. [DOI] [PubMed] [Google Scholar]
- Tsuzuki S. Uchimaru T. Mikami M. Magnitude and Nature of Carbohydrate-Aromatic Interactions: Ab Initio Calculations of Fucose-Benzene Complex. J. Phys. Chem. B. 2009;113:5617–5621. doi: 10.1021/jp8093726. [DOI] [PubMed] [Google Scholar]
- Wimmerova M. Kozmon S. Necasova I. Mishra S. K. Komarek J. Koca J. Stacking interactions between carbohydrate and protein quantified by combination of theoretical and experimental methods. PLoS One. 2012;7:e46032. doi: 10.1371/journal.pone.0046032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma R. McNamara J. P. Raju R. K. Vincent M. A. Hillier I. H. Morgado C. A. The interaction of carbohydrates and amino acids with aromatic systems studied by density functional and semi-empirical molecular orbital calculations with dispersion corrections. Phys. Chem. Chem. Phys. 2008;10:2767–2774. doi: 10.1039/B719764K. [DOI] [PubMed] [Google Scholar]
- Sujatha M. S. Sasidhar Y. U. Balaji P. V. Insights into the role of the aromatic residue in galactose-binding sites: MP2/6-311G++** study on galactose- and glucose-aromatic residue analogue complexes. Biochemistry. 2005;44:8554–8562. doi: 10.1021/bi050298b. [DOI] [PubMed] [Google Scholar]
- Sujatha M. S. Sasidhar Y. U. Balaji P. V. Energetics of galactose- and glucose-aromatic amino acid interactions: implications for binding in galactose-specific proteins. Protein Sci. 2004;13:2502–2514. doi: 10.1110/ps.04812804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- del Carmen Fernandez-Alonso M. Canada F. J. Jimenez-Barbero J. Cuevas G. Molecular recognition of saccharides by proteins. Insights on the origin of the carbohydrate-aromatic interactions. J. Am. Chem. Soc. 2005;127:7379–7386. doi: 10.1021/ja051020+. [DOI] [PubMed] [Google Scholar]
- Berman H. M. Westbrook J. Feng Z. Gilliland G. Bhat T. N. Weissig H. Shindyalov I. N. Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyder A. Nittinger E. Lange G. Klein R. Rarey M. Estimating Electron Density Support for Individual Atoms and Molecular Fragments in X-ray Structures. J. Chem. Inf. Model. 2017;57:2437–2447. doi: 10.1021/acs.jcim.7b00391. [DOI] [PubMed] [Google Scholar]
- The PyMOL Molecular Graphics System, Version 2.5.2, Schrödinger, LLC [Google Scholar]
- Lee C. Yang W. Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B:Condens. Matter Mater. Phys. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-Functional Thermochemistry. 3. The Role of Exact Exchange. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]
- Hohenstein E. G. Parrish R. M. Sherrill C. D. Turney J. M. Schaefer H. F. Large-scale symmetry-adapted perturbation theory computations via density fitting and Laplace transformation techniques: investigating the fundamental forces of DNA-intercalator interactions. J. Chem. Phys. 2011;135:174107. doi: 10.1063/1.3656681. [DOI] [PubMed] [Google Scholar]
- Hohenstein E. G. Sherrill C. D. Density fitting and Cholesky decomposition approximations in symmetry-adapted perturbation theory: implementation and application to probe the nature of pi-pi interactions in linear acenes. J. Chem. Phys. 2010;132:184111. doi: 10.1063/1.3426316. [DOI] [Google Scholar]
- Parrish R. M. Parker T. M. Sherrill C. D. Chemical Assignment of Symmetry-Adapted Perturbation Theory Interaction Energy Components: The Functional-Group SAPT Partition. J. Chem. Theory Comput. 2014;10:4417–4431. doi: 10.1021/ct500724p. [DOI] [PubMed] [Google Scholar]
- Paytakov G. Dinadayalane T. Leszczynski J. Toward Selection of Efficient Density Functionals for van der Waals Molecular Complexes: Comparative Study of C–H···π and N–H···π Interactions. J. Phys. Chem. A. 2015;119:1190–1200. doi: 10.1021/jp511450u. [DOI] [PubMed] [Google Scholar]
- Sherrill C. D. Energy Component Analysis of π Interactions. Accounts Chem. Res. 2013;46:1020–1028. doi: 10.1021/ar3001124. [DOI] [PubMed] [Google Scholar]
- Dey R. C. Seal P. Chakrabarti S. CH-Pi Interaction in Benzene and Substituted Derivatives with Halomethane: a Combined Density Functional and Dispersion-Corrected Density Functional Study. J. Phys. Chem. A. 2009;113:10113–10118. doi: 10.1021/jp905078p. [DOI] [PubMed] [Google Scholar]
- Sherrill C. D., in Reviews in Computational Chemistry, Wiley, 2008, vol. 26, pp. 1–38 [Google Scholar]
- Tekin A. Jansen G. How accurate is the density functional theory combined with symmetry-adapted perturbation theory approach for CH–π and π–π interactions? A comparison to supermolecular calculations for the acetylene–benzene dimer. Phys. Chem. Chem. Phys. 2007;9:1680–1687. doi: 10.1039/B618997K. [DOI] [PubMed] [Google Scholar]
- Shibasaki K. Fujii A. Mikami N. Tsuzuki S. Magnitude of the CH-Pi Interaction in the Gas Phase: Experimental and Theoretical Determination of the Accurate Interaction Energy in Benzene-methane. J. Phys. Chem. A. 2006;110:4397–4404. doi: 10.1021/jp0605909. [DOI] [PubMed] [Google Scholar]
- Tsuzuki S. Honda K. Uchimaru T. Mikami M. Tanabe K. The Magnitude of the CH-Pi Interaction between Benzene and Some Model Hydrocarbons. J. Am. Chem. Soc. 2000;122:3746–3753. doi: 10.1021/ja993972j. [DOI] [Google Scholar]
- Okuyama M. Matsunaga K. Watanabe K. I. Yamashita K. Tagami T. Kikuchi A. Ma M. Klahan P. Mori H. Yao M. Kimura A. Efficient synthesis of alpha-galactosyl oligosaccharides using a mutant Bacteroides thetaiotaomicron retaining alpha-galactosidase (BtGH97b) FEBS J. 2017;284:766–783. doi: 10.1111/febs.14018. [DOI] [PubMed] [Google Scholar]
- Holmner A. Mackenzie A. Okvist M. Jansson L. Lebens M. Teneberg S. Krengel U. Crystal structures exploring the origins of the broader specificity of escherichia coli heat-labile enterotoxin compared to cholera toxin. J. Mol. Biol. 2011;406:387–402. doi: 10.1016/j.jmb.2010.11.060. [DOI] [PubMed] [Google Scholar]
- Grahn E. M. Winter H. C. Tateno H. Goldstein I. J. Krengel U. Structural characterization of a lectin from the mushroom Marasmius oreades in complex with the blood group B trisaccharide and calcium. J. Mol. Biol. 2009;390:457–466. doi: 10.1016/j.jmb.2009.04.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoden J. B. Kim J. Raushel F. M. Holden H. M. The catalytic mechanism of galactose mutarotase. Protein Sci. 2003;12:1051–1059. doi: 10.1110/ps.0243203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sousa B. L. Silva J. C. Kumar P. Graewert M. A. Pereira R. I. Cunha R. M. S. Nascimento K. S. Bezerra G. A. Delatorre P. Djinovic-Carugo K. Nagano C. S. Gruber K. Cavada B. S. Structural characterization of a Vatairea macrocarpa lectin in complex with a tumor-associated antigen: a new tool for cancer research. Int. J. Biochem. Cell Biol. 2016;72:27–39. doi: 10.1016/j.biocel.2015.12.016. [DOI] [PubMed] [Google Scholar]
- Rojel N. Kari J. Sorensen T. H. Badino S. F. Morth J. P. Schaller K. Cavaleiro A. M. Borch K. Westh P. Substrate binding in the processive cellulase Cel7A: transition state of complexation and roles of conserved tryptophan residues. J. Biol. Chem. 2020;295:1454–1463. doi: 10.1074/jbc.RA119.011420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zakariassen H. Aam B. B. Horn S. J. Vårum K. M. Sorlie M. Eijsink V. G. H. Aromatic Residues in the Catalytic Center of Chitinase A from Serratia marcescens Affect Processivity, Enzyme Activity, and Biomass Converting Efficiency. J. Biol. Chem. 2009;284:10610–10617. doi: 10.1074/jbc.M900092200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor C. B. Payne C. M. Himmel M. E. Crowley M. F. McCabe C. Beckham G. T. Binding Site Dynamics and Aromatic-Carbohydrate Interactions in Processive and Non-Processive Family 7 Glycoside Hydrolases. J. Phys. Chem. B. 2013;117:4924–4933. doi: 10.1021/jp401410h. [DOI] [PubMed] [Google Scholar]
- Ufimtsev I. S. Martinez T. J. Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics. J. Chem. Theory Comput. 2009;5:2619–2628. doi: 10.1021/ct9003004. [DOI] [PubMed] [Google Scholar]
- Grimme S. Antony J. Ehrlich S. Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Grimme S. Ehrlich S. Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011;32:1456–1465. doi: 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- York D. M. Karplus M. A smooth solvation potential based on the conductor-like screening model. J. Phys. Chem. A. 1999;103:11060–11079. doi: 10.1021/jp992097l. [DOI] [Google Scholar]
- Lange A. W. Herbert J. M. A smooth, nonsingular, and faithful discretization scheme for polarizable continuum models: the switching/Gaussian approach. J. Chem. Phys. 2010;133:244111. doi: 10.1063/1.3511297. [DOI] [PubMed] [Google Scholar]
- Liu F. Luehr N. Kulik H. J. Martínez T. J. Quantum Chemistry for Solvated Molecules on Graphical Processing Units Using Polarizable Continuum Models. J. Chem. Theory Comput. 2015;11:3131–3144. doi: 10.1021/acs.jctc.5b00370. [DOI] [PubMed] [Google Scholar]
- Kastner J. Carr J. M. Keal T. W. Thiel W. Wander A. Sherwood P. DL-FIND: An Open-Source Geometry Optimizer for Atomistic Simulations. J. Phys. Chem. A. 2009;113:11856–11865. doi: 10.1021/jp9028968. [DOI] [PubMed] [Google Scholar]
- Smith D. G. A. Burns L. A. Simmonett A. C. Parrish R. M. Schieber M. C. Galvelis R. Kraus P. Kruse H. Di Remigio R. Alenaizan A. James A. M. Lehtola S. Misiewicz J. P. Scheurer M. Shaw R. A. Schriber J. B. Xie Y. Glick Z. L. Sirianni D. A. O'Brien J. S. Waldrop J. M. Kumar A. Hohenstein E. G. Pritchard B. P. Brooks B. R. Schaefer H. F. Sokolov A. Y. Patkowski K. DePrince A. E. Bozkaya U. King R. A. Evangelista F. A. Turney J. M. Crawford T. D. Sherrill C. D. PSI4 1.4: open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020;152:184108. doi: 10.1063/5.0006002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kendall R. A. Dunning T. H. Harrison R. J. Electron-Affinities of the 1st-Row Atoms Revisited - Systematic Basis-Sets and Wave-Functions. J. Chem. Phys. 1992;96:6796–6806. doi: 10.1063/1.462569. [DOI] [Google Scholar]
- Riplinger C. Neese F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013;138:034106. doi: 10.1063/1.4773581. [DOI] [PubMed] [Google Scholar]
- Riplinger C. Sandhoefer B. Hansen A. Neese F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013;139:134101. doi: 10.1063/1.4821834. [DOI] [PubMed] [Google Scholar]
- Hohenstein E. G. Sherrill C. D. Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory. J. Chem. Phys. 2010;133:014101. doi: 10.1063/1.3451077. [DOI] [PubMed] [Google Scholar]
- Zhong S. J. Barnes E. C. Petersson G. A. Uniformly convergent n-tuple-zeta augmented polarized (nZaP) basis sets for complete basis set extrapolations. I. Self-consistent field energies. J. Chem. Phys. 2008;129:184116. doi: 10.1063/1.3009651. [DOI] [PubMed] [Google Scholar]
- Helgaker T. Klopper W. Koch H. Noga J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 1997;106:9639–9646. doi: 10.1063/1.473863. [DOI] [Google Scholar]
- Neese F. Software update: the ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018;8:e1327. doi: 10.1002/wcms.1327. [DOI] [Google Scholar]
- Weigend F. Kohn A. Hattig C. Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J. Chem. Phys. 2002;116:3175–3183. doi: 10.1063/1.1445115. [DOI] [Google Scholar]
- Altun A. Neese F. Bistoni G. Extrapolation to the Limit of a Complete Pair Natural Orbital Space in Local Coupled-Cluster Calculations. J. Chem. Theory Comput. 2020;16:6142–6149. doi: 10.1021/acs.jctc.0c00344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoychev G. L. Auer A. A. Neese F. Automatic Generation of Auxiliary Basis Sets. J. Chem. Theory Comput. 2017;13:554–562. doi: 10.1021/acs.jctc.6b01041. [DOI] [PubMed] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Petersson G. A., Nakatsuji H., Li X., Caricato M., Marenich A. V., Bloino J., Janesko B. G., Gomperts R., Mennucci B., Hratchian H. P., Ortiz J. V., Izmaylov A. F., Sonnenberg J. L., Ding F., Lipparini F., Egidi F., Goings J., Peng B., Petrone A., Henderson T., Ranasinghe D., Zakrzewski V. G., Gao J., Rega N., Zheng G., Liang W., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Throssell K., Montgomery Jr J. A., Peralta J. E., Ogliaro F., Bearpark M. J., Heyd J. J., Brothers E. N., Kudin K. N., Staroverov V. N., Keith T. A., Kobayashi R., Normand J., Raghavachari K., Rendell A. P., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Millam J. M., Klene M., Adamo C., Cammi R., Ochterski J. W., Martin R. L., Morokuma K., Farkas O., Foresman J. B. and Fox D. J., Gaussian 16 Rev. C.01, 2016
- Glendening E. D. Landis C. R. Weinhold F. NBO 7.0: new vistas in localized and delocalized chemical bonding theory. J. Comput. Chem. 2019;40:2234–2241. doi: 10.1002/jcc.25873. [DOI] [PubMed] [Google Scholar]
- Pedregosa F. Varoquaux G. Gramfort A. Michel V. Thirion B. Grisel O. Blondel M. Prettenhofer P. Weiss R. Dubourg V. Vanderplas J. Passos A. Cournapeau D. Brucher M. Perrot M. Duchesnay E. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Structures, computed energies, and random forest models are all included in the ESI† as follows: initial and optimized 3D structures of all native and synthetic close contacts; EDIAm scores, raw electronic energies and interaction energies from DFT, and SAPT0 total and component energies for the full dataset of close contacts; interaction energies of the interaction in the benchmarking dataset, as determined by DLPNO-CCSD(T), MP2, DFT, SAPT0 and SAPT2; PyMOL session files for select protein binding pockets; random forest models trained to predict the DFT interaction energy, SAPT0 interaction energy, dispersion, electrostatics, exchange, and induction energies (ZIP).