Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2024 Nov 25;9(49):48748–48754. doi: 10.1021/acsomega.4c08297

Ferroelasticity and Canted Antiferromagnetism in Two-Dimensional Organic–Inorganic Layered Perovskite [C6H9(CH2)2NH3]2FeCl4

Naoto Tsuchiya †, Tatsuya Ishinuki †, Yuki Nakayama †, Xianda Deng £, Goulven Cosquer ‡,§, Takahiro Onimaru £, Sadafumi Nishihara †,‡,, Katsuya Inoue †,‡,§,*
PMCID: PMC11635508  PMID: 39676935

Abstract

graphic file with name ao4c08297_0006.jpg

Two-dimensional organic–inorganic perovskites have been attracted as candidates for multiferroic materials that exhibit two or more ferroic orders such as ferromagnetism, ferroelectricity, ferroelasticity, and ferrotoroidicity. Here, we introduce the structure, ferroelastic domains and magnetic properties of the two-dimensional organic–inorganic perovskite [C6H9(CH2)2NH3]2FeCl4 (CHEA-Fe) composed of 2-(1-cyclohexenyl)ethylammonium and FeCl42–. CHEA-Fe underwent two ferroelastic phase transitions from tetragonal to orthorhombic at 332 K and to monoclinic at 232 K with decreasing temperature and exhibited ferroelastic domains under polarized light as a consequence of these ferroelastic phase transitions. Magnetization measurements exhibited two magnetization jumps at the transition temperature, which agrees with ferroelastic phase transitions. Furthermore, CHEA-Fe acted as canted antiferromagnetism below TN = 85.7 K. The isothermal magnetization revealed a magnetic hysteresis when the magnetic field was applied along the stacking axis of the layers.

1. Introduction

Spin orbital coupling (SOC) has the ability to couple the orbital angular momentum to the spin angular momentum, which is a crucial key for designing magnetic materials including chiral magnets, that can be switched by external stimuli, such as temperature, pressure, and magnetic field.1,2 Spin crossover and its related phenomena are examples of switchable molecular materials where the magnetic properties are affected by the transition between different electronic states,3,4 metal–ligand electron transfers,5,6 and structural rearrangements of the complex.7−10 Such spin changes and structural rearrangements are related to changes in SOC. Coherent coupling between crystal symmetry and spin orders via SOC is called Dzyaloshinskii–Moriya interaction (DMI), which is key to chiral magnetism.11,12

In addition to such molecular multistable materials, materials with ferroic orders, such as ferromagnetism, ferroelectricity, ferroelasticity, and ferrotoroidicity, exhibit switching properties by external stimuli.13,14 Recently, multiferroic properties with the coexistence of two or more ferroic orders are of wide interest due to the strong cooperativity between different ferroic orders.15−17 Except for magnetoelectric coupling and ferrotoroidal orders, SOC plays a role in coupling different ferroic orders. Two-dimensional organic–inorganic perovskite compounds are known as candidates to be multiferroic materials due to their easily tunable SOC.18−25 In particular, the materials containing larger and complex organic cations are suitable for control to develop multiferroic materials.26,27 By incorporating flexible organic cations, two-dimensional organic–inorganic perovskite compounds can be used as magnetic switching materials, as well as multiferroic ones. In most previous reports on multiferroic materials, the ferroelastic and magnetic properties have been investigated separately. However, the relationship between ferroelasticity and magnetic order, which is a desirable feature in the multiferroic field, has rarely been investigated. Therefore, we design two-dimensional organic–inorganic perovskites with both the spin change and the coupling of ferroelasticity and magnetic order to study the relationship between ferroelasticity and magnetic order and develop magnetoelastic materials.

In this work, we synthesized a novel two-dimensional organic–inorganic perovskite compound, [C6H9(CH2)2NH3]2FeCl4 (CHEA-Fe), composed of 2-(1-cyclohexenyl)ethylammonium cation (CHEA) and FeCl42– anion (Figure S1). CHEA-Fe exhibited both ferroelasticity and canted antiferromagnetism. Moreover, CHEA-Fe shows magnetic bistability and an anisotropic spin system based on SOC. Our results demonstrate that CHEA-Fe is a candidate to test the quantitative model of the coupling between ferroelasticity and magnetization in two-dimensional organic–inorganic layered perovskites.

2. Results and Discussion

2.1. Thermal Study

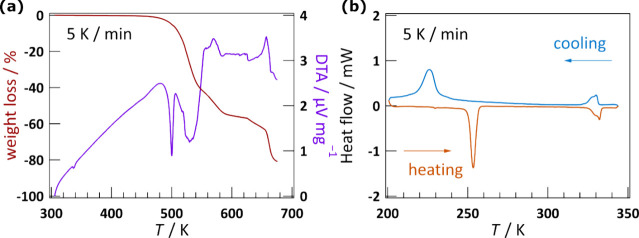
TG-DTA analysis of CHEA-Fe showed an endothermic anomaly at 333 K and a thermal stability up to 490 K (Figure 1a). DSC measurements showed anomalies at 250 (TC1↑) and 326 K (TC2↑), with enthalpy variations (ΔH) of 3.7 and 1.0 kJ mol–1 (Figure 1b) for the heating process, and at 232 (TC1↓) and 332 K (TC2↓) with ΔH of 3.8 and 0.9 kJ mol–1, respectively, for the cooling process. The entropy change, given by ΔS = ΔH/T, was 14.5 J K–1 mol–1 at TC1↑ and 3.0 J K–1 mol–1 at TC2↑, which gives calculated N values of 5.72 and 1.43, respectively, according to the Boltzmann equation, ΔS = RlnN, where R is the gas constant and N is the variation of the number of disorder positions during the transition.28 The thermal hysteresis of 18 K between TC1↑ and TC1↓ was larger than that of 6 K between TC2↑ and TC2↓. Both transitions are independent of the temperature scan rate (Figure S2). The thermal hysteresis of 18 K was comparable to other two-dimensional perovskites.29,30 TG-DTA and DSC measurements indicated that two structural phase transitions occurred in CHEA-Fe. The phase above TC2↑ and TC2↓ is mentioned as the paraelastic phase (PA), the phase between TC1↑ (TC1↓) and TC2↑ (TC2↓) as ferroelastic phase 1 (FA-1), and the phase below TC1↑ and TC1↓ as ferroelastic phase 2 (FA-2) (see Observation of Ferroelastic Domains for details). Two or more peaks can be observed in the TC2↑ and TC2↓ transitions, which means this ferroelastic transition contains several structural transitions, resulting in a lower TC2↑ thanTC2↓. However, the crystal structures of the mesophase were not determined due to the quite narrow temperature range.

Figure 1.

Figure 1

Open in a new tab

(a) TG-DTA and (b) DSC curves of CHEA-Fe at 5 K min–1.

2.2. Crystal Structures

According to thermal analysis, single crystal X-ray diffraction data were collected at 373, 273, and 173 K (Figure 2, Figure S3, Table S1). At all temperatures, the crystal structure has inorganic layers of corner-sharing FeCl6 octahedra separated by a double layer of CHEA. The distance between two adjacent inorganic layers is approximately 20 Å. This alternative stacking of inorganic and organic layers is a feature of the two-dimensional perovskite materials.26,27,31 At 373 K, in the PA phase, CHEA-Fe crystallized in the tetragonal I4/mmm space group, with the inorganic layers stacked along the c axis. The FeCl6 octahedron was distorted with the nonbridging axial Cl atoms closer (2.342(3) Å) than the intralayer bridged ones (2.62175(10) Å) to the Fe center (Table S2). CHEA was fully disordered by the 4-fold symmetry axis (Figure 2c and Figure S3c). Upon cooling to 273 K, in the FA-1 phase, CHEA-Fe crystal symmetry decreased to the orthorhombic Pnma space group, with the c axis in the PA phase parallel to the b axis in the FA-1 phase. At the FA-1 phase, the bond lengths between Fe atoms and bridged Cl atoms slightly contracted compared to that in the PA phase, while the ones between Fe atoms and nonbridged Cl atoms slightly extended (Table S2). The Fe–Cl–Fe bond angles decrease to average values of 179.39°. The dynamic disorder of the 1-cyclohexenyl group of CHEA also decreased (Figure 2b and Figure S3b). According to the DSC data, N was 1.43, indicating that the transition is close to a simple 2-fold order–disorder model.

Figure 2.

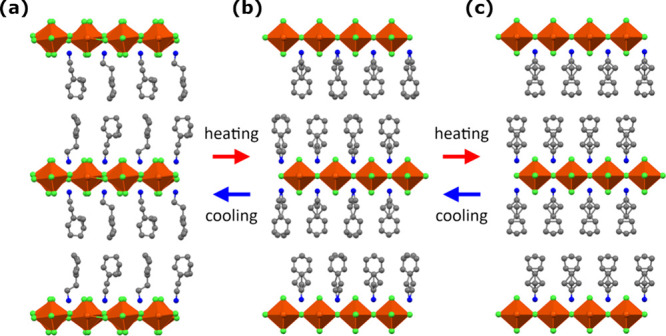
Figure 2

Open in a new tab

Crystal structures from the side view of the staking axis for CHEA-Fe in (a) FA-2, (b) FA-1 and (c) PA. FeCl6 units are shown as polyhedra, and H atoms are omitted for clarity. Color codes: Fe, orange; Cl, green; N, blue; C, gray.

At 173 K, in the FA-2 phase, CHEA-Fe changed in the monoclinic P21/c space group where the c axis in the PA phase became the a axis. The measured crystal is split into ferroelastic domains (twinning) arising from a decrease in temperature (Figure 3). As a result, the crystal structure is an average structure. The angle of the Fe–Cl–Fe bond along the b axis is 165.59(9)°, while the one along the c axis is 179.35(10)° (Table S2). In addition, the dynamic disorder of the ethyl group became orderly (Figure 2a and Figure S3a). The Fe–Cl–Fe bond angle of 165.59(9)° at the FA-2 phase suggested that ΔH at TC1 became larger than that at TC2 (Figure 1b). According to the DSC data, N was 5.72, indicating that the transition could not be attributed to a dynamic order–disorder type phase transition of organic cations. The transition has characteristics of both order–disorder- and displacement-type phase transitions due to the occurrence of the ordering of the ethyl group and the bending of the Fe–Cl–Fe.

Figure 3.

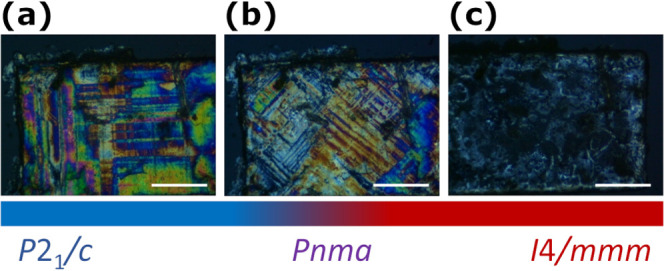
Figure 3

Open in a new tab

Polarized microscopy observations along the stacking axis of CHEA-Fe at (a) 100, (b) 293, and (c) 373 K. The corresponding phases are indicated. Scale bar: 0.1 mm.

Single crystal X-ray structure analysis at variable temperatures revealed a symmetry breaking of the crystal structure in both phase transitions involving concerted distortion and tilting of the FeCl6 octahedron accompanied by the ordering of the organic amines. By focusing on the FeCl6 octahedra, with lowering temperature, the distances between Fe and bridging Cl atoms are decreased while the distance between Fe and nonbridging Cl atoms is increased. This behavior can be derived from a combination of the lattice strain and Jahn–Teller distortion. The lattice strain induces the shortening of the bond length between Fe and bridging Cl atoms. It is well known that the Fe2+ (high spin) ion in octahedral symmetry has orbitally degenerate electronic configurations, leading the Jahn–Teller distortion active. The lattice strain combined with Jahn–Teller distortion leads to an elongation of the octahedron in a direction perpendicular to the direction of the shortened bond, i.e., elongation of bond length between Fe and nonbridging Cl atoms. Such behavior has been reported in another octahedral complex.32

2.3. Observation of Ferroelastic Domains

The two structural phase transitions of tetragonal to orthorhombic and orthorhombic to monoclinic, accompanied by a decrease of symmetry, correspond to the ferroelastic phase transition described by Aizu notation of 4/mmmFmmm and mmmF2/m, respectively.33 The numbers of symmetry elements of I4/mmm, Pnma, and P21/c are 16, 8, and 4. The symmetry element became half through the ferroelastic phase transition from I4/mmm to Pnma, indicating that the number of possible orientation states is two. For the ferroelastic phase transition from Pnma to P21/c, there are also two orientation states possible. The origin of ferroelasticity is attributed to the local distortions induced in the Fe/Cl sublattice due to the freezing of CHEA cations and the displacement of Fe2+ and Cl– ions.34,35 From a microscopic point of view, the formation of ferroelastic domains is one of the effective methods to confirm the ferroelastic behavior. Thus, observation of ferroelastic domains for CHEA-Fe single crystals was performed by a polarizing microscope along the stacking axis (Figure 3). At 373 K, transmitted light was not visible, which corresponded to a single crystal in the PA phase (Figure 3c). When the structural phase transition occurred from tetragonal to orthorhombic, ferroelastic domain structures (i.e., straight lines in Figures 3a,b) were observed along with the appearance of transmitted light. The ferroelastic domains were oriented along the [101] and [10–1] directions (Figure 3b). With further cooling, ferroelastic domains became unclear before clear new ferroelastic domains became visible, indicating that the structural phase transition from orthorhombic to monoclinic phase occurred (Figure 3a). These ferroelastic domains at low temperature are oriented along [011] and [01–1] directions. The variation of domain structures in CHEA-Fe is similar to that of other ferroelastic materials.36 As a result, polarized microscopy observation revealed that CHEA-Fe underwent two-step ferroelastic phase transitions.

To evaluate the ferroelastic domain structure of the single crystal of CHEA-Fe under mechanical stress, a compressive force was applied to the single crystal at room temperature (Figure S4a). The number of ferroelastic domain walls decreased when a compressive stress of 300 kPa was applied (Figure S4c,d). At 100 K, it was not possible to affect the domain structures by applying mechanical stress without breaking the crystal. The crystalline structure is more fragile than the domain structure is mobile.

2.4. Magnetism

The temperature dependence of χT, and its derivative, for powder and single crystal samples was measured during the cooling and heating processes (Figure 4). The χT values parallel and perpendicular to the stacking axis (χ∥T and χ⊥T, respectively) at 350 K for single crystal were 2.78 and 2.56 emu K mol–1. Upon cooling, a small transition of χ⊥T was observed at 248 K. On further cooling, χ⊥T value slowly decreased to a minimum value of 0.74 emu K mol–1 at 88 K, before increasing rapidly to a maximum value of 0.84 emu K mol–1 at 84 K. Below this temperature, χ⊥T value decreased again to reach a value of 0.02 emu K mol–1 at 2 K. This behavior is thermally reversible with only the small transition occurring at 260 K instead of 248 K. The temperature variations of χ∥T and χpT exhibited similar behavior to that of χ⊥T. This thermal hysteresis between 248 and 260 K was consistent with the DSC results, indicating that a small variation of magnetization was observed at the ferroelastic phase transition from FA-1 to FA-2. The transition from FA-1 to PA was also observed at 330 K in the magnetic measurements. The thermal hysteresis was independent of the magnetic field (Figure S5). Coupling of magnetization and ferroelasticity offers the possibility of either inducing a ferroelastic phase transition or rearrangement of ferroelastic domains in the ferroelastic state simply by an applied magnetic field via SOC, but it cannot be observed due to the small magnetization value of CHEA-Fe.

Figure 4.

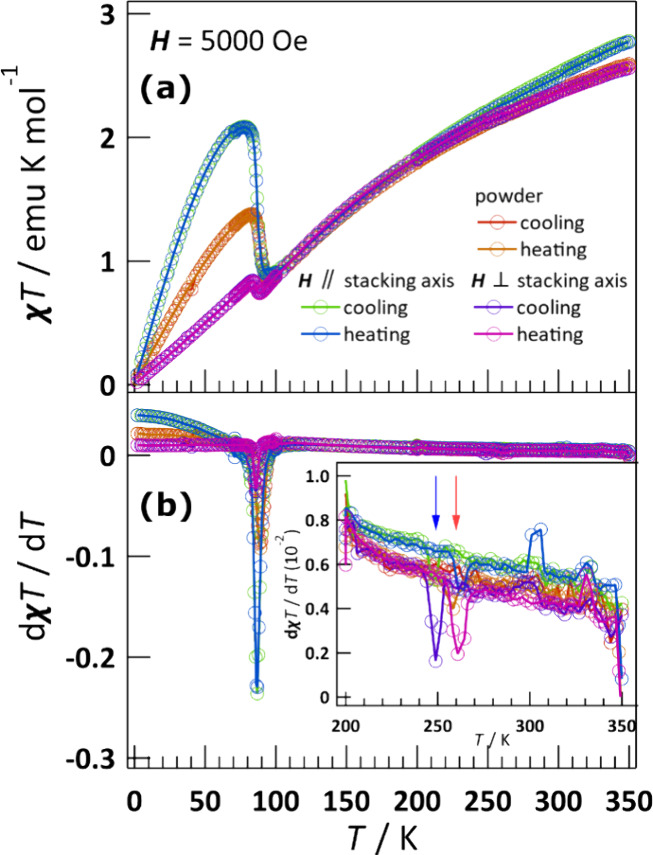
Figure 4

Open in a new tab

Temperature dependence of (a) χT and (b) its derivative under a magnetic field of 5000 Oe for powder and single crystal samples of CHEA-Fe. The red and blue arrows represent the thermal hysteresis (see the main text).

As described in the Crystal Structures section, the adjacent Fe2+ ions are connected by a Cl– ion, and the Fe2+···Fe2+ distance is 5.2435(3) Å, much shorter than the distances between two adjacent layers (approximately 20 Å) in the PA phase. Therefore, the high-temperature susceptibility data of the powder sample can be analyzed with the 2D Heisenberg antiferromagnet model37,38 (NAg2μB2)/(χJ) = 3z + ∑6n = 1(− 1)nαn/zn–1, where z = kBT/[JS(S + 1)], NA is the Avogadro’s number, J is the intralayer magnetic coupling between the adjacent Fe2+ ions bridged by Cl– ion (with negative value indicating antiferromagnetic interaction), kB is the Boltzmann constant, μB is the Bohr magneton, and for S = 2, the coefficients αn are given by α1 = 4, α2 = 1.500, α3 = 0.252, α4 = 0.258, α5 = 0.124, and α6 = 0.015. The best least-squares fitting parameters for the 1/χ data of powder from 350 to 260 K were obtained for antiferromagnetic coupling J = −28.8(1) K and g = 2.494(3), with the agreement factor R = Σ[(1/χobsd – 1/χcalcd)]2/Σ(1/χobsd)2 = 1.06 × 10–6 (Figure S6). The J value is analogous to the reported Fe2+-based material.39 The 2D Heisenberg model was used for phases PA and FA-1 only. In these two phases, the Fe–Cl–Fe angles are flat, but for FA-2, the Fe–Cl–Fe bonds are bent.

In the case of magnetic measurements for single crystals, the anisotropy of the system must be taken into consideration. The 2D Heisenberg model is suitable for an isotropic system or powder sample, but not suitable for an anisotropic system. Therefore, the analysis of the magnetic behavior of CHEA-Fe was performed using the following method which does not assume a specific temperature dependence of χ.40 We introduce the temperature-dependent term in the form χ∥,⊥(Τ) = (g∥,⊥)2f(Τ), which assumes that the anisotropy of the spin susceptibility χ derives from an anisotropic g-factor. Note that the g-factor of localized spins is related to SOC. In the paramagnetic region, f(T) values of χ∥(Τ) and χ⊥(Τ) are identical, leading to χ∥ = (g∥/g⊥)2 χ⊥. In the case of isotropic systems, the (g∥/g⊥)2 will be equal to one and in the case of anisotropic system the value will be greater (g∥ > g⊥) or smaller (g∥ < g⊥) than one; the more the anisotropy is large, the more (g∥/g⊥)2 will be far from one. For our system, a (g∥/g⊥)2 ratio of 0.68 was determined by the slope of the linear regression (Figure S7). This value is far from that of two-dimensional perovskite materials with an isotropic Mn2+ ions ((g∥/g⊥)2 ≈ 1),41,42 indicating that the magnetic moments of CHEA-Fe are treated with the anisotropic system based on SOC.

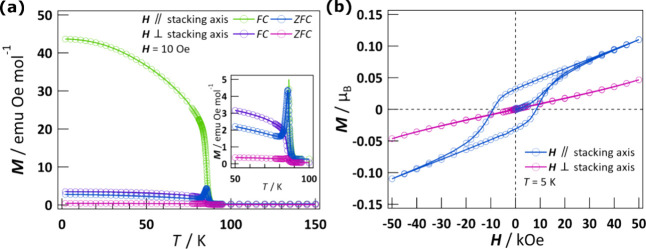
The magnetization versus temperature plots after zero-field cooling (ZFC) and field cooling (FC) for the single crystal were measured with a 10 Oe magnetic field applied parallel and perpendicular to the stacking axis (Figure 5a). The ZFC magnetizations parallel and perpendicular to the stacking axis at 2 K were 2.74 and 0.41 emu Oe mol–1, respectively. Upon heating, there were cusps in magnetization of 4.35 and 0.31 emu Oe mol–1, respectively, at 85 K. FC magnetization exhibited a rapid increase of magnetization at 88 K, and then the magnetization became saturation with decreasing temperature when the magnetic field was applied parallel and perpendicular to the stacking axis. At 2 K, the magnetization values parallel and perpendicular to the stacking axis were 43.6 and 3.5 emu Oe mol–1, respectively. The FC magnetization data measured at 10 Oe for H ∥ stacking axis can be described as M = M0(1 – T/TN)β where TN is Neel temperature and β is the critical exponent (Figure S8).43 The values of TN and β were given as 85.6(2) K and 0.21(1), respectively. The value of β is comparable to the magnetic property of a two-dimensional XY model.44 However, the magnetic behavior at high temperatures is described by the 2D Heisenberg model. The change in the fitted model is consistent with findings that the spin-dimensional crossover takes place from 2D Heisenberg model to Ising or XY models toward TN due to the finite contributions of interlayer coupling and magnetic anisotropy,45 reflecting the temperature limit of application of the 2D Heisenberg model for CHEA-Fe (Figure S6). We further evaluated the presence of long-range magnetic ordering by measuring the temperature dependence of the AC susceptibility and heat capacity (Figures S9 and S10). The temperature dependence of the in-phase (χ′) and out-of-phase (χ″) susceptibilities showed a sharp peak at 85.7 K when the AC field was applied parallel to the stacking axis (Figure S9). The position of the peak was independent of the AC frequencies, suggesting a phase transition. The temperature of this peak was comparable to the results of the magnetic measurement under a DC field. In the case of an AC field applied perpendicular to the stacking axis, a broad peak around 85 K was observed in the χ′ susceptibility while not observed in the χ″ susceptibility, implying that the easy axis for antiferromagnetism is perpendicular to the stacking axis. No frequency-dependent behavior was observed again. The specific heat of CHEA-Fe under zero magnetic field along the stacking axis exhibits a small shoulder around 85 K with increasing temperature, indicating the appearance of a long-range magnetic order below 85 K (Figure S10). The results of the AC susceptibility and specific heat measurements emphasize the existence of long-range magnetic order from 85.7 K for CHEA-Fe.

Figure 5.

Figure 5

Open in a new tab

Magnetic properties of CHEA-Fe when the magnetic field is parallel or perpendicular to the stacking axis. (a) ZFC and FC magnetization as a function of temperature under a magnetic field of 10 Oe. Inset: ZFC and FC magnetization as a function of temperature in the range of 50–100 K. (b) Field-dependence magnetization at 5 K.

The field dependence of magnetization at 5 K along the stacking axis exhibited hysteresis with a remanent magnetization (Mrem) of 0.03 μB and a coercive field (HC) of 8.5 kOe (Figure 5b). As the field increased, the magnetization curve was linear and reached 0.11 μB at 50 kOe, which was much smaller than the theoretical saturation value MS of Fe2+ ion (MS = gJJ = 6 μB, S = 2 and L = 2). The above behaviors are features of canted antiferromagnets, which exhibit the low-field spontaneous magnetization and linear high-field behavior due to the dominant antiferromagnetic interactions.46 The canting angle φ at 5 K was estimated to be 0.29° by sin φ = Mrem/MS.47 The Mrem and HC were decreased as the temperature increased and reached zero above TN where a linear increase of magnetization was observed (Figures S11 and S12). When the magnetic field was applied perpendicular to the stacking axis, only a linear increase in magnetization was observed at 5 K, reaching 0.05 μB at 50 kOe. The temperature and field dependence of the magnetization of CHEA-Fe suggested that canted antiferromagnetic behavior was observed below 85.7 K. Spin canting has been ascribed to DMI and/or single-ion anisotropy as described in previous reports on two-dimensional perovskite materials.19,31 In the case of CHEA-Fe, there is no inversion center between Fe2+ ions bridged by the Cl– ion, and each FeCl6 octahedron has a different orientation from its neighboring octahedra. Therefore, DMI results in spin canting for CHEA-Fe. DMI is affected by SOC, which may also lead to the coupling of ferroelasticity and magnetic long-range order as described above.

3. Conclusions

In summary, [C6H9(CH2)2NH3]2FeCl4 was composed of 2-(1-cyclohexenyl)ethylammonium cation and the FeCl42– anion, which exhibited ferroelasticity and antiferromagnetic long-range order with canted spin. DSC and X-ray structural analysis reveal two ferroelastic phase transitions. At TC2↑(TC2↓), CHEA-Fe undergoes a structural phase transition from tetragonal to orthorhombic where a distortion of the FeCl6 octahedron and the ordering of the cyclohexenyl group of CHEA is observed. At TC1↑ (TC1↓), the structural phase transition from orthorhombic to monoclinic occurs due to the tilted FeCl6 octahedron and the ordering of the ethyl ammonium groups of CHEA. Polarized light microscopy observations reveal that ferroelastic domains become visible at each ferroelastic phase transition. CHEA-Fe displays magnetic hysteresis below 85.7 K, with the coercive field increasing as the temperature decreases. Furthermore, a magnetic transition, with a temperature hysteresis, is observed at the TC1 ferroelastic phase transition. Thus, these results indicate that CHEA-Fe can be a candidate for multiferroic material with ferroelasticity and magnetic long-range order. As the ferroelastic domains and magnetic properties are identified for CHEA-Fe, future efforts will be directed toward the coupling of magnetic and ferroelastic domains, for example, pressure-induced magnetic domain rearrangement, and to elaborate a quantitative model of the coupling between ferroelasticity and magnetization.

4. Experimental Section

All reagents and solvents were used as purchased. 2-(1-cyclohexenyl)ethylamine hydrochloride (CHEA·Cl) was obtained quantitatively by slowly dropping 37% HCl solution into a diethyl ether solution containing 2-(1-cyclohexenyl)ethylamine, and evaporation.

4.1. Crystallization

CHEA-Fe crystals were grown by a slow cooling method. CHEA·Cl (114 mg, 0.7 mmol) and FeCl2·4H2O (78 mg, 0.4 mmol) were dissolved in 1.1 mL of hot ethanol (75 °C) under a N2 atmosphere. To prevent oxidation, the ethanol was passed through N2 gas before synthesis, and L-ascorbic acid (approximately 20 mg), as an antioxidant, was added to the reaction solution. The ethanol solution was left to cool naturally to room temperature and then kept at 277 K. After a few days, slightly brown plate-like transparent crystals were obtained in a yield of 20% (Figure S1). Elemental analysis was carried out in a PerkinElmer CHNS/O 2400 II elemental analyzer. Anal. calcd. for C16H32N2FeCl4: C, 42.70; H, 7.17; N, 6.22%; Found: C, 42.67; H, 7.41; N, 6.10%.

4.2. Crystallography

Data were collected at different temperatures using a Bruker D8-QUEST equipped with a Photon detector with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å). The structures were solved with SHELXT and refined with SHELXL programs operated in the Olex2 software.48−50 All non-H atoms were refined with anisotropic thermal parameters. H atoms were generated using a riding model. The crystallographic information on the crystal structures of CHEA-Fe determined at 373, 273 and 173 K have been deposited in the Cambridge Crystallographic Database Centre as Supporting Information (CCDC 2314193, 2314194, and 2314195, respectively).

4.3. Thermal Measurements

Thermogravimetry and differential thermal analysis (TG-DTA) were performed on a Seiko Instruments SII Exstar TG/DTA 6200 with a temperature range of 300–673 K and a heating rate of 5 K min–1. Differential scanning calorimetry (DSC) measurements were performed on a Mettler Toledo instruments DSC1 or a Seiko Instruments SII Exstar DSC6200 in the heating and cooling cycles with a temperature range of 203–343 K and temperature scanning rates of 0.2–5 K min–1. The sample was placed in a N2 atmosphere during both measurements. The temperature of the phase transitions was determined at the onset of the anomaly in the thermal analysis.

4.4. Microscope Observations

Optical polarized microscopy observations were carried out using a MEIJI TECHNO EMZ-5HPOL microscope with a HOZAN L-835 digital camera. The sample was heated on a hot plate and cooled with cold nitrogen gas generated from liquid nitrogen. The temperature of the sample was monitored with a thermocouple. Stress tests were carried out on a homemade setup (Figure S4a). A vial filled with metallic powder was applied pressure on a glass plate. To uniformize the stress, the crystal is glued to the glass plate with Araldite glue. An estimation of the pressure was obtained from the weight loaded on the crystal, and the cross-sectional area on the interface between the crystal and the plate (Figure S4b).

4.5. Heat Capacity Measurements

The specific heat measurements were performed by the thermal relaxation method using a physical properties measurement system (Quantum Design.) with a temperature range of 2–200 K under zero magnetic field for a single crystal.

4.6. Magnetic Measurements

The magnetic susceptibility (χ) and magnetization measurements were performed on an MPMS-5S, MPMS-7, or MPMS-XL7 superconducting quantum interference device magnetometer (Quantum Design) with a temperature and DC field range of 2–350 K and −50 to +50 kOe, respectively, for single crystal and powder samples. Especially, the magnetization measurements in the heating and cooling cycles with a temperature range of 200–350 K were carried out at the scan rate of 5 K min–1 for single crystal and powder. A single crystal was fixed by quartz cotton and put on a sample holder, while powder samples were fixed in gelatin capsules. The quartz cotton was used to avoid stress due to thermal expansion and contraction of the adhesive during the heating and cooling process. Diamagnetic contributions of the sample holder and sample were corrected by measurement of the sample holder and calculation of Pascal’s constants,51 respectively. The AC susceptibilities were measured with an AC field of 3 Oe and frequencies of 1, 10, and 100 Hz using a Quantum Design MPMS-5S.

Acknowledgments

This work was supported by JSPS Grants-in-Aid for Scientific Research (grant numbers 25220803, 15K13674, and 22H02053), the JSPS Core-to-Core Program “Advanced Research Networks”, SPRING (grant numbers JPMJSP2132) from Japan Science and Technology Agency (JST) and Advanced Research Infrastructure for Materials and Nanotechnology in Japan (ARIM) of the Ministry of Education, Culture, Sports, Science and Technology (MEXT). The work was conducted with the facilities in the Natural Science Center for Basic Research and Development (N-BARD) at Hiroshima University (NBARD-00105) and the Institute for Molecular Science (proposal number JPMXP1222MS1047b, S21MS1023, and S20MS1029). We thank Mr. Manabe for performing DSC measurements through the Cooperative Research Program of the Network Joint Research Center for Materials and Devices.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c08297.

  • Crystallographic data, photo of single crystal, TG-DTA, DSC, experimental setup for applying mechanical stress, heat capacity, and magnetic properties (PDF)

Accession Codes

CCDC 2314193–2314195 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: + 44 1223 336033.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ao4c08297_si_001.pdf (1.6MB, pdf)

References

  1. Sato O. Dynamic Molecular Crystals with Switchable Physical Properties. Nature Chem. 2016, 8 (7), 644–656. 10.1038/nchem.2547. [DOI] [PubMed] [Google Scholar]
  2. Togawa Y.; Koyama T.; Takayanagi K.; Mori S.; Kousaka Y.; Akimitsu J.; Nishihara S.; Inoue K.; Ovchinnikov A. S.; Kishine J. Chiral Magnetic Soliton Lattice on a Chiral Helimagnet. Phys. Rev. Lett. 2012, 108 (10), 107202 10.1103/PhysRevLett.108.107202. [DOI] [PubMed] [Google Scholar]
  3. Cambi L.; Szegö L. Über Die Magnetische Susceptibilität Der Komplexen Verbindungen (II. Mitteil.).. Ber. Dtsch. Chem. Ges. A/B 1933, 66 (5), 656–661. 10.1002/cber.19330660508. [DOI] [Google Scholar]
  4. Hayami S.; Gu Z.; Yoshiki H.; Fujishima A.; Sato O. Iron(III) Spin-Crossover Compounds with a Wide Apparent Thermal Hysteresis around Room Temperature. J. Am. Chem. Soc. 2001, 123 (47), 11644–11650. 10.1021/ja0017920. [DOI] [PubMed] [Google Scholar]
  5. Buchanan R. M.; Pierpont C. G. Tautomeric Catecholate-Semiquinone Interconversion via Metal-Ligand Electron Transfer. Structural, Spectral, and Magnetic Properties of (3,5-Di-Tert-Butylcatecholato)(3,5-Di-Tert-Butylsemiquinone)(Bipyridyl)Cobalt(III), a Complex Containing Mixed-Valence Organic Ligands. J. Am. Chem. Soc. 1980, 102 (15), 4951–4957. 10.1021/ja00535a021. [DOI] [Google Scholar]
  6. Gütlich P.; Dei A. Valence Tautomeric Interconversion in Transition Metal 1,2-Benzoquinone Complexes. Angew. Chem., Int. Ed. Engl. 1997, 36 (24), 2734–2736. 10.1002/anie.199727341. [DOI] [Google Scholar]
  7. Lanfranc de Panthou F.; Belorizky E.; Calemczuk R.; Luneau D.; Marcenat C.; Ressouche E.; Turek P.; Rey P. A New Type of Thermally Induced Spin Transition Associated with an Equatorial ↔ Axial Conversion in a Copper(II)-Nitroxide Cluster. J. Am. Chem. Soc. 1995, 117 (45), 11247–11253. 10.1021/ja00150a023. [DOI] [Google Scholar]
  8. Inoue K.; Iwahori F.; Iwamura H. Magnetic Properties of Bis(Hexafluoroacetylacetonato)Copper(II) Complex with 5-Bromo-1,3-Phenylenebis(N-Tert-Butyl-Aminoxyl) Having Polymeric Chain Structure. Chem. Lett. 1998, 27 (8), 737–738. 10.1246/cl.1998.737. [DOI] [Google Scholar]
  9. Ovcharenko V. I.; Maryunina K. Yu.; Fokin S. V.; Tretyakov E. V.; Romanenko G. V.; Ikorskii V. N. Spin Transitions in Non-Classical Systems. Russ. Chem. Bull. 2004, 53 (11), 2406–2427. 10.1007/s11172-005-0136-4. [DOI] [Google Scholar]
  10. Mautner F. A.; Cortés R.; Lezama L.; Rojo T. [N(CH3)4][Mn(N3)3]: A Compound with a Distorted Perovskite Structure through Azido Ligands. Angew. Chem., Int. Ed. Engl. 1996, 35 (1), 78–80. 10.1002/anie.199600781. [DOI] [Google Scholar]
  11. Dzyaloshinsky I. A Thermodynamic Theory of “Weak” Ferromagnetism of Antiferromagnetics. J. Phys. Chem. Solids 1958, 4 (4), 241–255. 10.1016/0022-3697(58)90076-3. [DOI] [Google Scholar]
  12. Moriya T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120 (1), 91–98. 10.1103/PhysRev.120.91. [DOI] [Google Scholar]
  13. Aizu K. Possible Species of Ferromagnetic, Ferroelectric, and Ferroelastic Crystals. Phys. Rev. B 1970, 2 (3), 754–772. 10.1103/PhysRevB.2.754. [DOI] [Google Scholar]
  14. Van Aken B. B.; Rivera J.-P.; Schmid H.; Fiebig M. Observation of Ferrotoroidic Domains. Nature 2007, 449 (7163), 702–705. 10.1038/nature06139. [DOI] [PubMed] [Google Scholar]
  15. Rao C. N. R.; Rao K.. Ferroics. In Solid State Chemistry: Compounds; Day P.; Cheetham A. K., Eds.; Oxford University Press: New York, 1992; pp 281–296. [Google Scholar]
  16. Schmid H. Multi-Ferroic Magnetoelectrics. Ferroelectrics 1994, 162 (1), 317–338. 10.1080/00150199408245120. [DOI] [Google Scholar]
  17. Kimura T.; Goto T.; Shintani H.; Ishizaka K.; Arima T.; Tokura Y. Magnetic Control of Ferroelectric Polarization. Nature 2003, 426 (6962), 55–58. 10.1038/nature02018. [DOI] [PubMed] [Google Scholar]
  18. Suzuki T.; Yoshizawa M.; Goto T.; Yamakami T.; Takahashi M.; Fujimura T. Structural Phase Transition of Layer Compound (C2H5NH3)2FeCl4. J. Phys. Soc. Jpn. 1983, 52 (5), 1669–1675. 10.1143/JPSJ.52.1669. [DOI] [Google Scholar]
  19. Nakajima T.; Yamauchi H.; Goto T.; Yoshizawa M.; Suzuki T.; Fujimura T. Magnetic and Elastic Properties of (CH3NH3)2FeCl4 and (C2H5NH3)2FeCl4. J. Magn. Magn. Mater. 1983, 31–34, 1189–1190. 10.1016/0304-8853(83)90857-0. [DOI] [Google Scholar]
  20. Ishihara T.; Takahashi J.; Goto T. Optical Properties Due to Electronic Transitions in Two-Dimensional Semiconductors. Phys. Rev. B 1990, 42 (17), 11099–11107. 10.1103/PhysRevB.42.11099. [DOI] [PubMed] [Google Scholar]
  21. Mitzi D. B.Synthesis, Structure, and Properties of Organic-Inorganic Perovskites and Related Materials. In Progress in Inorganic Chemistry.; Karlin K. D., Ed.; John Wiley & Sons: New York, 1999; pp 1–121. DOI: 10.1002/9780470166499.ch1. [DOI] [Google Scholar]
  22. Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131 (17), 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
  23. Ghalsasi P. S.; Inoue K. Distorted Perovskite Structured Organic–Inorganic Hybrid Compounds for Possible Multiferroic Behavior: [N-Alkyl]2FeCl4. Polyhedron 2009, 28 (9–10), 1864–1867. 10.1016/j.poly.2009.02.033. [DOI] [Google Scholar]
  24. Han J.; Nishihara S.; Inoue K.; Kurmoo M. On the Nature of the Structural and Magnetic Phase Transitions in the Layered Perovskite-Like (CH3NH3)2[FeIICl4]. Inorg. Chem. 2014, 53 (4), 2068–2075. 10.1021/ic402535u. [DOI] [PubMed] [Google Scholar]
  25. Han J.; Nishihara S.; Inoue K.; Kurmoo M. High Magnetic Hardness for the Canted Antiferromagnetic, Ferroelectric, and Ferroelastic Layered Perovskite-like (C2H5NH3)2[FeIICl4]. Inorg. Chem. 2015, 54 (6), 2866–2874. 10.1021/ic5030229. [DOI] [PubMed] [Google Scholar]
  26. Nakayama Y.; Nishihara S.; Inoue K.; Suzuki T.; Kurmoo M. Coupling of Magnetic and Elastic Domains in the Organic–Inorganic Layered Perovskite-Like (C6H5C2H4NH3)2FeIICl4 Crystal. Angew. Chem., Int. Ed. 2017, 129 (32), 9495–9498. 10.1002/ange.201703898. [DOI] [PubMed] [Google Scholar]
  27. Taniguchi K.; Nishio M.; Abe N.; Huang P.; Kimura S.; Arima T.; Miyasaka H. Magneto-Electric Directional Anisotropy in Polar Soft Ferromagnets of Two-Dimensional Organic–Inorganic Hybrid Perovskites. Angew. Chem., Int. Ed. 2021, 60 (26), 14350–14354. 10.1002/anie.202103121. [DOI] [PubMed] [Google Scholar]
  28. Jain P.; Dalal N. S.; Toby B. H.; Kroto H. W.; Cheetham A. K. Order–Disorder Antiferroelectric Phase Transition in a Hybrid Inorganic–Organic Framework with the Perovskite Architecture. J. Am. Chem. Soc. 2008, 130 (32), 10450–10451. 10.1021/ja801952e. [DOI] [PubMed] [Google Scholar]
  29. Xie Y.; Song R.; Singh A.; Jana M. K.; Blum V.; Mitzi D. B. Kinetically Controlled Structural Transitions in Layered Halide-Based Perovskites: An Approach to Modulate Spin Splitting. J. Am. Chem. Soc. 2022, 144 (33), 15223–15235. 10.1021/jacs.2c05574. [DOI] [PubMed] [Google Scholar]
  30. Fan C.-C.; Liu C.-D.; Liang B.-D.; Jin M.-L.; Ju T.-Y.; Chai C.-Y.; Han X.-B.; Zhang W. A Two-Dimensional Hybrid Lead Bromide Ferroelectric Semiconductor with an Out-of-Plane Polarization. Inorg. Chem. 2023, 62 (32), 12634–12638. 10.1021/acs.inorgchem.3c02057. [DOI] [PubMed] [Google Scholar]
  31. Park S.-H.; Oh I.-H.; Park S.; Park Y.; Kim J. H.; Huh Y.-D. Canted Antiferromagnetism and Spin Reorientation Transition in Layered Inorganic–Organic Perovskite (C6H5CH2CH2NH3)2MnCl4. Dalton Trans. 2012, 41 (4), 1237–1242. 10.1039/C1DT11544H. [DOI] [PubMed] [Google Scholar]
  32. Wei M.; Willett R. D. Crystal Structure of (3-Chloroanilinium)8NiCl10 and a Temperature-Dependent X-Ray Diffraction Study of the Jahn-Teller Distortion in (3-Chloroanilinium)8CuCl10. Inorg. Chem. 1995, 34 (14), 3780–3784. 10.1021/ic00118a027. [DOI] [Google Scholar]
  33. Aizu K. Possible Species of “Ferroelastic” Crystals and of Simultaneously Ferroelectric and Ferroelastic Crystals. J. Phys. Soc. Jpn. 1969, 27 (2), 387–396. 10.1143/JPSJ.27.387. [DOI] [Google Scholar]
  34. Zhang H.-Y.; Tang Y.-Y.; Shi P.-P.; Xiong R.-G. Toward the Targeted Design of Molecular Ferroelectrics: Modifying Molecular Symmetries and Homochirality. Acc. Chem. Res. 2019, 52 (7), 1928–1938. 10.1021/acs.accounts.8b00677. [DOI] [PubMed] [Google Scholar]
  35. Xiao X.; Zhou J.; Song K.; Zhao J.; Zhou Y.; Rudd P. N.; Han Y.; Li J.; Huang J. Layer Number Dependent Ferroelasticity in 2D Ruddlesden–Popper Organic-Inorganic Hybrid Perovskites. Nat. Commun. 2021, 12 (1), 1332. 10.1038/s41467-021-21493-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Zhao M.-M.; Zhou L.; Shi P.-P.; Zheng X.; Chen X.-G.; Gao J.-X.; Geng F.-J.; Ye Q.; Fu D.-W. Halogen Substitution Effects on Optical and Electrical Properties in 3D Molecular Perovskites. Chem. Commun. 2018, 54 (94), 13275–13278. 10.1039/C8CC07052K. [DOI] [PubMed] [Google Scholar]
  37. Rushbrooke G. S.; Wood P. J. On the Curie Points and High Temperature Susceptibilities of Heisenberg Model Ferromagnetics. Mol. Phys. 1958, 1 (3), 257–283. 10.1080/00268975800100321. [DOI] [Google Scholar]
  38. Lines M. E. The Quadratic-Layer Antiferromagnet. J. Phys. Chem. Solids 1970, 31 (1), 101–116. 10.1016/0022-3697(70)90291-X. [DOI] [Google Scholar]
  39. Ahmed M. A.; Radwan F. A.; El-Desoky M. M. Magnetic Susceptibility of the Compound (CH2)10(NH3)2FeCl4. J. Magn. Magn. Mater. 1987, 67 (3), 349–353. 10.1016/0304-8853(87)90194-6. [DOI] [Google Scholar]
  40. Chou F. C.; Cho J. H.; Lee Y. S. Magnetic Susceptibility Study of Hydrated and Nonhydrated NaxCoO2·yH2O Single Crystals. Phys. Rev. B 2004, 70 (14), 144526 10.1103/PhysRevB.70.144526. [DOI] [Google Scholar]
  41. Benner H. Experimental Proof of 2D Spin Diffusion by Frequency Dependence of ESR Linewidth. Phys. Lett. A 1979, 70 (3), 225–226. 10.1016/0375-9601(79)90214-7. [DOI] [Google Scholar]
  42. Bissey J.-C.; Filloleau N.; Chanh N.-B.; Berger R.; Flandrois S. Exchange Interaction as Studied by EPR in a Two-Dimensional Molecular Composite [NH3-(CH2)4-NH3]MnCl4. Solid State Commun. 1998, 106 (6), 385–389. 10.1016/S0038-1098(98)00041-6. [DOI] [Google Scholar]
  43. Stanley H. E.Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: New York, 1971. [Google Scholar]
  44. Taroni A.; Bramwell S. T.; Holdsworth P. C. W. Universal Window for Two-Dimensional Critical Exponents. J. Phys.: Condens. Matter 2008, 20 (27), 275233 10.1088/0953-8984/20/27/275233. [DOI] [PubMed] [Google Scholar]
  45. de Jongh L. J.Introduction to Low-Dimensional Magnetic Systems. In Magnetic Properties of Layered Transition Metal Compounds. de Jongh L. J., Ed.; 1990; pp 1–51. DOI: 10.1007/978-94-009-1860-3_1. [DOI] [Google Scholar]
  46. Weng D.-F.; Wang Z.-M.; Gao S. Framework-Structured Weak Ferromagnets. Chem. Soc. Rev. 2011, 40 (6), 3157. 10.1039/c0cs00093k. [DOI] [PubMed] [Google Scholar]
  47. Kahn O.Molecular Magnetism; VCH: New York, 1993. [Google Scholar]
  48. Sheldrick G. M. SHELXT – Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr., Sect. A 2015, 71 (1), 3–8. 10.1107/S2053273314026370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Sheldrick G. M. Crystal Structure Refinement with SHELXL. Acta Crystallogr., Sect. C 2015, 71 (1), 3–8. 10.1107/S2053229614024218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Dolomanov O. V.; Bourhis L. J.; Gildea R. J.; Howard J. A. K.; Puschmann H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Crystallogr. 2009, 42 (2), 339–341. 10.1107/S0021889808042726. [DOI] [Google Scholar]
  51. Bain G. A.; Berry J. F. Diamagnetic Corrections and Pascal’s Constants. J. Chem. Educ. 2008, 85 (4), 532. 10.1021/ed085p532. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao4c08297_si_001.pdf (1.6MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES