Understanding perspectives for mixed mode oscillations of the fractional neural network approaches to the analysis of neurophysiological data from the perspective of the observability of complex networks

Abstract

Using discrete fractional calculus, a wide variety of physiological phenomena with various time scales have been productively investigated. In order to comprehend the intricate dynamics and activity of neuronal processing, we investigate the behavior of a slow-fast FitzHugh-Rinzel (FH-R) simulation neuron that is driven by physiological considerations via the Caputo fractional difference scheme. Taking into account the discrete fractional commensurate and incommensurate mechanisms, we speculate on the numerical representations of various excitabilities and persistent activation reactions brought about by the administered stimulation. Furthermore, the outcomes concentrate on the variability of several time scales, encompassing mixed-mode oscillations and mixed-mode bursting oscillations formed by the canard occurrence. It is confirmed that the fast-analyzing component, which was isolated within this framework with the slow-fast evaluation process, is bistable, and the criterion for bistability is added as well. The architecture appears to be bistable based on this. The pertinent factors for examining time evolution, Poincaré maps, the bifurcation configuration of the system and chaos illustrations involve the inserted power stimulation using commensurate and incommensurate fractional-order values. We investigate the canards adjacent to the folded platforms using the folded node hypothesis. Additionally, we are employing mixed-mode oscillations to illustrate the homoclinic bifurcation and the resulting chaotic trajectory. Also, we determine our research results by computing the Lyapunov spectra as an expression of time in conjunction with the dominating factor ℑ to demonstrate the chaotic behavior in a particular domain. Besides that, we estimate intricacy employing the sample entropy (Sp-En) approach and ${\mathbb{C}}_0$ complexity. The emergence of chaos within the hypothesized discrete fractional FH-R system is verified using the $0-1$ criterion. Ultimately, we examine the prospective implications of mixed-mode oscillations in neuroscience and draw the inference that our observed outcomes could potentially be of great relevance. As a result, the predicted intricacy decreases while applying it to non-horizontal significant models. Finally, the simulation's characteristic phases, canards and mixed model oscillations are achieved statistically with the assistance of varying fractional orders.

Nomenclature

FH-R

FitzHugh-Rinzel

Sp-En

Sample Entropy

Ap-En

Approximate Entropy

C0

Complexity

FOs

Fractional orders

DF

Discrete fractional

NNs

Neural networks

DFO

Discrete fractional order

M-M-Os

Mixed mode oscillations

M-M-B-Os

Mixed mode bursting oscillations

FHN

FitzHugh-Naguma

MLE

Maximum Lyapunov exponents

1. Introduction

Over the past 20 years, chaotic discrete-time algorithms (maps) have drawn a lot of interest because of their extensive implications for oversight and image enhancement [1], [2]. These representations behave chaotically in this way because their respective positions heavily rely on the initial configuration of the framework. The investigations and practical implications of fractional discrete calculus have garnered greater enthusiasm within the scientific field in the last decade. Because of their limitless memory, fractional discrete algorithms offer a significant boost versus their associated object alternatives. This provides for greater modeling adaptability and increases the probability of chaotic behavior. Furthermore, fractional visualizations are more applicable in neural networks (NNs) since they typically show a chaos pattern throughout an assortment of fractional orders (FOs) (see [3], [4], [5], [6]). Recently, Abbas and Nazar [7] expounded the fractional analysis of unsteady MHD Jeffrey flow over an infinite vertical plate in the presence of Hall current. Abbas et al. [8] contemplated the effect of chemical reaction on MHD Casson natural convection flow over an oscillating plate in porous media using Caputo fractional derivative. Abbas et al. [9] explored the soret effect on MHD Casson fluid over an accelerated plate with the help of constant proportional Caputo fractional derivative. For more details see [10], [11] and the reference cited therein. A number of studies have tried to expand the robustness hypothesis underlying classical discrete calculus to encompass the fractional region while developing a comprehensive foundation for discrete fractional (DF) calculus [12], [13], [14], [15]. To the greatest extent of our comprehension, just a handful of FO chaotic visualizations have been identified and suggested throughout research, for example [16], [17], [18], [19], [20], because DF calculus remains an emerging area.

Furthermore, continuous-time fractional mathematical algorithms have prospective uses in an assortment of domains, including image processing, memory reconstruction, identification of patterns, and algorithmic optimization. An extensive number of researchers have recently focused on studying these systems' evolution. Nevertheless, discretizing continuous-time connections is crucial while they serve as instruments for technological device processing, creativity, or replication. This is especially true if continuous-time connections are constructed for these purposes. The continuous fractional model's counterpart's discretization process cannot maintain its unpredictable nature (see [21]). Consequently, it is essential to inquire about the structure of DF NNs. A few studies examining the unpredictable functioning of DF NN simulations have currently been published [22]. For example, Chen et al. [23] examined the chaos in DFO NNs with application to image encryption. Wu and Baleanu [24] contemplated the Jacobian matrix algorithm for Lyapunov exponents of the discrete fractional maps. Gafel and Rashid [25] contemplated the evolutionary approach for solving fractional difference recurrent NN systems. However, according to the most effective of our abilities, not much investigation has been executed to examine the evolving behaviors of DF NNs using discrete commensurate FO and incommensurate FOs [26], [27]. The overwhelming majority of the previously discussed DF NN inquiry focuses on algorithms via commensurate or incommensurate FOs. Thus, it is interesting to explore the chaotic nature of NN models founded on fractional differences involving commensurate and incommensurate variations in conjunction with associated statistical assessment.

Multi-timescale networks are frameworks that have numerous time dimensions [28], [29], [30]. Multi-timescale behavior is a ubiquitous trait shared by all three biological entities, particularly in neuronal representations. Due to the considerable differences in the progression of components in the multi-timescale mechanism, the setup is generally termed the slow-fast mechanism. The slow-fast behavioral structure of the fractional NNs and its properties, which typically show elliptical exploding, are covered extensively in this piece of information. It presents the method by which interconnected difference equations featuring slow-fast time frames in biological structures can produce diverse rhythms. We examine a single significant component within this structure; spiking changes happen while it fluctuates significantly. Certain neural pathways spontaneously fire at various points. One such phenomenon can be identified as exploding, and it is characterized by intervals of recurrent activation intermingled by inactive or motionless intervals. Certain neural pathways spontaneously fire at various moments, a phenomenon known as overflowing, which is composed of reserved or empty intervals between bursts of recurrent activation. It gradually exhibits an eruption throughout the dynamic segments, recovers gradually within the inactive stage, and becomes positioned to commence an additional explosion of shocks [31], [32]. The central nervous system's fundamental communication of knowledge technique hinges on electrical signals across the neuronal barrier; whenever these potentials elevate beyond a threshold, the network produces exploding and firing bursts through a variation in administered stimulus. Through the application of multiple nonlinear structures involving interconnected difference equations (as well as varying empirical characteristics), it is possible to theoretically represent the repetitive behavior of cellular potential [33], [34].

Mixed-mode oscillations (M-M-Os) are among the particularly fascinating, complicated, and unpredictable fluctuations that arise through neuronal electromagnetic responses [35], [37]. The alternate paths, which combine tiny and huge intensity rhythms, are referred to as M-M-Os. M-M-Os have complicated repetitive oscillations with distinct peaks and troughs of diverse intensities occurring during every loop. The hypothesis of M-M-Os involving canard algorithms has drawn a lot of attention from scholars lately [38], [39]. This type of M-M-O emerges thanks to its gradual-speed characteristics. Persistent current stimulation is provided to the neuron, which results in diverse flashing sequences capable of illustrating the functioning of the framework with respect to the reactions of the neurons. By applying instability concept and stabilization assessment, we are able to determine the enriched explosions involving M-M-Os/M-M-B-Os that are possibly triggered via the canard phenomena. M-M-B-Os: bursting can occasionally be seen in small intensity recurrent vibrations, the occurrence of M-M-Os and M-M-B-Os [40] might be either regular or irregular. Because of this, the representation is appealing, and the findings offer intriguing and possible implications for the context of both gradual and quick excitability realistic processes. The explosion behaviors of M-M-B-Os include bursts that include the greatest intensity oscillations as well as small intensity vibrations. A burst involving procedures is created in the architecture by the formation of M-M-B-Os.

However, the formation of small-intensity vibrations occurs when pathways pass close to a crumple and is caused by foldable strangeness. We must investigate the dynamics around foldable discontinuities and canard phenomena in order to comprehend the processes underlying M-M-Os. The Van der Pol equation's recurrent responses that continue adjacent to the repulsive weak continuum are represented by the canard phrase, which initially appeared [40]. The existence of canard phases within an enormously tiny range of attributes is their main characteristic. We refer to this stage of change as the “canard eruption” [41]. The canard systems connecting the gradual manifolds that embrace and repel are generated. Canard evolves robustly in nonlinear networks including multiple delayed variables, including small intensity rhythms approaching the fold discontinuity [42], [43]. The essential margin within our slow-fast mechanism possesses a cubic structure. When M-M-Os and M-M-B-Os are generated in the network, the supercritical Hopf-type bifurcation proceeds to a canard detonation, which causes shattering. M-M-Os are commonly seen at canard points, where slow-fast dynamics alternate between insignificant oscillations (near a stable manifold) and huge adventures (escape from the manifold).

Meanwhile, it has been discovered in earlier research that the behavior of M-M-Os resembles the neural and behavioral actions of inhalation or transpiration [44]. M-M-Os are additionally caused by disturbance and instability at various intervals in time [45], [46]. It has been identified in the electrocardiac and oxycontin signaling pathways [47]. We reveal the fact that canard occurrence via nonlinear structure techniques can be used to analyze the development of M-M-Os [48], [49]. The process underlying M-M-O fluctuations was investigated by Krupa et al. [50] employing a 2D representation of catecholamine neurons in the mammalian neural stems. The production of M-M-O according to the connected FitzHugh-Nagumo (FHN) framework was examined in [51]. A conductance-dependence simulation [49] was implemented to analyze the processes underlying these formations. M-M-Os may reportedly induce a sort of overflowing that appears in a biophysical representation of hypothalami lactotroph [52] and it is additionally perceived in constellation neurons of the lateral entorhinal cortical. The effects of current stimuli on calcium pathway resistance variations and a factor associated with the proportion of liberated cytoplasmic calcium levels in an activated simulation that influences neurological behavior that leads to the evolution via pseudo-plateau overflowing to M-M-Os have been studied lately [53]. The investigation by Bertram et al. [54] demonstrated that M-M-Os and M-M-B-Os could be additionally seen within the pancreatic beta-cell system. In addition to such investigations and endeavors, which include individual and coupling biophysics simulations, experts additionally delve into the electrical activity characteristics and aggregated behaviors of neurons interconnected in an intricate network framework [55], [56]. Pre-Botzinger intricate systems, a cortical area in animals that regulates inhalation, were found to contain M-M-Os [37]. Authors [57] investigated the formation of M-M-Os and rhythmic activity in an inconspicuous ensemble of disseminated connected Izhikevich neurons against a background of various capabilities. Xie et al. [58] just published a simulation study on the dual hybrid mode and twofold canard interactions with regard to the FH-R framework.

Adopting the aforesaid propensity, the behavior of a single neuronal layer is illustrated in this research employing the appropriate FH-R model [59], [60] using the Caputo-type difference operator, which is a variation of the conventional FH/N framework. We describe the differences between the FHN approach and the underlying interactions. It displays intriguing characteristics related to elevated production and physiological excitability using commensurate and incommensurate FOs. According to [61], [62], the algorithm is unable to produce a variety of sophisticated activation themes, particularly those observed in cortex-derived neurons using conventional techniques. In particular, in cortical code, the interaction involving firing and exploding reveals an intriguing physiological function in addition to a noteworthy phenomenon using commensurate FO values. The next factor causes explosive fluctuations and permits a repeated passage over the Hopf bifurcation. Both of the additional parameters are dependent on the initial contingent, ${\mathbf{u}}_1$. The intensity of the gradually altering electric stimulation and the fluctuations of the gradually shifting component determine the changeover stages via the incommensurate FO phenomenon. It can generate various activation patterns that are autonomous within a predetermined set of specifications. Both conceptual and computational examinations of the mathematical representation are conducted. Analysis is performed on the numerous characteristic configurations that match the significantly varied and unpredictable features of FOs. One intriguing aspect of curvilinear exploding is that the rhythms could possess an insignificant intensity when they occur, and the periodicity of activity spikes beginning and ending is nonzero [63]. This kind of explosion has been detected successfully within the trifacial muscles that regulate the articulation of mice's jaws [64], [65]. Furthermore, an analogous neuron with a variety of rhythms may operate in extensive systems with discrete patches. Researchers have examined the desingularized structure using the blowup approach. At this point, we investigate the FH-R framework using the geometric singleton disturbance technique convoluted with the DFO approach. We provide a variety of M-M-Os and M-M-B-Os that have not been thoroughly studied before. The current research can be considered advantageous as a beginning demonstration to explore broad-term NN structures by applying gradual and quick representations. We determine the bifurcations of various brusting/inactive areas contingent on setting collections. The simulation can generate inactive or fluctuating practices that can be captured via actual brain cells. A fascinating conventional representation of slow-fast interactions involves the 3D structure [42], [57]. It also displays the canard occurrence that is confirmed by the Shilnikov bifurcation hypothesis [66], [67] and illustrates substances that transition tremendously from an unalterable to a seemingly unpredictable manifold's for an extensive span in the convoluted framework timescale [51]. At this point, we demonstrate whether such rhythms and the development of M-M-Os and M-M-B-Os differentiate from various explosions having biophysically significant implications [68]. In addition to a thorough exploration of the dynamic attributes, a variety of FOs are employed to examine certain fundamental evolving features illustrated via this visualization, including Poincaré maps, bifurcation illustrations, and the maximum Lyapunov exponent (MLE) for the commensurate and incommensurate scenarios. Moreover, we provide sample entropy (Sp-En) evaluation, $0-1$ assessment and ${\mathbb{C}}_0$ complexities values in order to statistically quantify intricacy and verify the existence of chaos in the suggested FH-R model.

The article is composed as follows: We provide a few fundamental foundational ideas for DFC in Section 2. In Section 3, we provide an explanation of the hyperactive system's behavior, which displays the electric potential identified as spiking alongside certain essential information for the formation of the suggested framework. A detailed analysis of the DF FH-R model is constructed to qualitatively investigate the dynamics of the existence of canard in M-M-Os and M-M-B-Os, respectively. In Section 4, we employ the foldable network concept to show the canard response adjacent to the folding platforms, providing numerical findings, including both commensurate and incommensurate cases. Chaos, bifurcation schematics, phase equilibrium representation, and Lyapunov exponent evaluation aid in this investigation. We also explain the way the framework can experience the chaos of the Shilnikov diversity. In addition, we present our primary discoveries, which include a detailed discussion of the FH-R algorithm's dynamic expansion associated with the bifurcation outcomes. In Section 5, we quantify intricacy and confirm the occurrence of chaos in the representation using the ${\mathbb{C}}_0$ complexities, Sp-En test and $0-1$ analysis. Lastly, we wrap up the report with a summary of all of the substantial discoveries we found during the investigation.

2. Preliminaries

Here, the fundamental concepts in mathematics and theories needed for the article's quantitative evaluation are presented. Assume that ${\mathbb{N}}_{\tilde{a}}=\{\tilde{a},\tilde{a}+1,\tilde{a}+2,...\}$ such that $\tilde{a}\in \mathbb{R}$.

Definition 2.1

([12]) Assume that there is a mapping $\mathcal{F}:{\mathbb{N}}_{\tilde{a}}\mapsto \mathbb{R}$, then the χ-th order fractional sum defined as

$${\mathrm{\Delta }}_{\tilde{a}}^{-\chi }\mathcal{F}(\epsilon )=\frac{1}{\mathrm{\Gamma }(\chi )}\sum _{\nu =\tilde{a}}^{\epsilon -\chi }{(\epsilon -\nu -1)}^{(\chi -1)}\mathcal{F}(\nu ),$$ (2.1)

where $\epsilon \in {\mathbb{N}}_{\tilde{a}+\chi },\chi >0$.

Definition 2.2

([13]) For $\chi >0$ and there is a mapping $\mathcal{F}:{\mathbb{N}}_{\tilde{a}}\mapsto \mathbb{R}$, then the Caputo difference defined as

$${}^c\mathrm{\Delta }_{\tilde{a}}^{\chi }\mathcal{F}(\epsilon )={\mathrm{\Delta }}_{\tilde{a}}^{-(\zeta -\chi )}{\mathrm{\Delta }}^{\zeta }\mathcal{F}(\epsilon )=\frac{1}{\mathrm{\Gamma }(\zeta -\chi )}\sum _{\nu =\tilde{a}}^{\epsilon -(\zeta -\chi )}{(\epsilon -\nu -1)}^{(\zeta -\chi -1)}{\mathrm{\Delta }}^{\zeta }\mathcal{F}(\nu ),$$ (2.2)

where $\zeta =[\chi ]+1$ and $\epsilon \in {\mathbb{N}}_{\tilde{a}+\zeta -\chi }$.

Theorem 2.1

([17]) Assume that there is a discrete fractional difference system of order χ is

$${}^c\mathrm{\Delta }_{\tilde{a}}^{\chi }\mathcal{F}(\epsilon )=\mathcal{G}(\epsilon +\chi -1,\mathcal{F}(\epsilon +\chi -1)),{\mathrm{\Delta }}^{\zeta }\mathcal{F}(\epsilon )={\mathcal{F}}_{\zeta },\rho =\lceil \chi \rceil +1,\zeta =0,1,2,...,\rho -1,$$ (2.3)

hence the equivalent numerical representation is

$$\mathcal{F}(\epsilon )={\mathcal{F}}_0(\epsilon )+\frac{1}{\mathrm{\Gamma }(\chi )}\sum _{\nu =\tilde{a}+\rho -\chi }^{\epsilon -\chi }{(\epsilon -\nu +1)}^{(\chi -1)}\mathcal{G}(\nu +\chi -1,\mathcal{F}(\nu +\chi -1)),\epsilon \in {\mathbb{N}}_{\chi +\rho }$$ (2.4)

having

$${\mathcal{F}}_0(\epsilon )=\sum _{\zeta =0}^{\rho -1}\frac{{(\epsilon -\tilde{a})}^{(\zeta )}}{\mathrm{\Gamma }(\zeta +1)}{\mathrm{\Delta }}^{\zeta }\mathcal{F}(\tilde{a}).$$ (2.5)

Remark 2.1

Selecting the discrete kernel significance $\sum _{\nu =\tilde{a}+\rho -\chi }^{\epsilon -\chi }{(\epsilon -\nu +1)}^{(\chi -1)}$ as $\frac{\mathrm{\Gamma }(\epsilon -\nu )}{\mathrm{\Gamma }(\chi )\mathrm{\Gamma }(\epsilon -\nu -\chi +1)}$ considering the prerequisites that $\tilde{a}=0$ and $\nu +\chi =ȷ$, the numerical formulae for the case where $\chi \in (0,1)$ could potentially identified as

$$\mathcal{F}(\epsilon )=\mathcal{F}(0)+\frac{1}{\mathrm{\Gamma }(\chi )}\sum _{ȷ=1}^{\epsilon }\frac{\mathrm{\Gamma }(\epsilon -ȷ+\chi )}{\mathrm{\Gamma }(\epsilon -ȷ+1)}\mathcal{G}(ȷ-1,\mathcal{F}(ȷ-1)).$$ (2.6)

Lemma 2.1

( [69] ) For $\chi \in (0,1)$ and the fractional difference scheme can be expressed as follows:

$${\mathrm{\Delta }}^{\chi }\mathrm{\Xi }(\epsilon +1-\chi )=\mathrm{\Lambda }\mathrm{\Xi }(\epsilon ),{\varrho }_2=0,1,2,...,$$ (2.7)

where $\mathrm{\Lambda }\in {\mathbb{R}}^{\kappa \times \kappa }$ . Assume that

$${\mathcal{U}}^{\chi }=\{\upsilon \in \mathbb{C}:|\upsilon |<{(2\cos (\frac{|\arg (\upsilon )|-\pi }{2-\chi }\left)\right)}^{\chi }and|\arg (\upsilon )|>\frac{\chi \pi }{2}\},$$ (2.8)

where, $\arg (.)$ symbolizes the arguments for the result. Whenever all $\upsilon \in {\mathcal{U}}^{\chi }$ , then the mechanism (2.7) is systematically stable and whenever $\upsilon \in \setminus cl({\mathcal{U}}^{\chi })$ given certain υ therefore the mechanism (2.7) is unstable.

Remark 2.2

A wide variety of interpretations exist for DFO differences, including the Riemann-Liouvile and Caputo formulations. Of these, the Caputo fractional difference characterization is the most widely utilized in real-world situations for the explanations listed below. On the contrary, any constant's Caputo difference equals zero, and its existential significance is more obvious than that of other differences. However, the configuration of the initial settings of processes offered by the Caputo difference is identical to that of integer-order processes. In light of the aforementioned, this work adopts the Caputo fractional difference.

3. Construction of the slow–fast FH-R model

In what follows, we address the electrical processes of cortical cellular potential throughout a significant assortment of factor settings by focusing on the complex mechanisms of the responsive FH-R mechanism. The interactively diverse characteristics of the representation can be analyzed with computing efficiency and extensive significance. The subsequent collection of ordinary differential equations [59], [60] characterizes the temporal progression of the computational framework as

$$\{\begin{array}{c}\frac{d{\mathbf{u}}_1}{d\xi }={\mathbf{u}}_1-\frac{{\mathbf{u}}_1^3}{3}-{\mathbf{u}}_2+{\mathbf{u}}_3+\Im ,\hfill \\ \frac{d{\mathbf{u}}_2}{d\xi }=\rho ({\varsigma }_1+{\mathbf{u}}_1-{\varsigma }_2{\mathbf{u}}_2),\hfill \\ \frac{d{\mathbf{u}}_3}{d\xi }=\mu ({\varsigma }_3-{\mathbf{u}}_1-{\varsigma }_4{\mathbf{u}}_3),\hfill \end{array}$$ (3.1)

where ${\mathbf{u}}_1$, ${\mathbf{u}}_2$, and ${\mathbf{u}}_3$ stand for the protective membrane power, recuperation factor and gradual power variation, respectively. Component characteristics are ${\varsigma }_1,{\varsigma }_2,{\varsigma }_3,{\varsigma }_4,\rho$ and μ. The value ℑ quantifies the value of the exogenous infused voltage. Smaller factors, denoted by ρ and μ, control the rate at which the gradual process characteristics, ${\mathbf{u}}_2$ and ${\mathbf{u}}_3$, fluctuate. We choose $\mu ={\rho }^2$ [50] to create a framework containing three unique time frames, i.e., an explosive level that includes two slowing categories, the miniature factor μ, that occurs in $0<\mu \ll 1$. We consider the relatively small component ${\varsigma }_2>0$ [70]. The factor quantity ${\varsigma }_3$ in the FH-R paradigm and its value ${\varsigma }_1$ in the two-dimensional FHN paradigm coincide [60]. Additionally, there is a generally consistent period of exploding, but the time frames for bursting are greater whenever we diminish the significance of ${\varsigma }_1$. The interburst frequencies shorten, and recurrent exploding transforms into acute surging as ${\varsigma }_1$ approaches. The slow-fast compartments of the structure define it; the initially presented two formulae show the standard slow-fast FHN approach [42], [51], which only produces firing. “Superslow” is indicated by the attribute ${\mathbf{u}}_3$. More specifically, it results in barely noticeable intensity fluctuations and significant amplification surges in elliptical explosions given a predetermined collection of settings [60]. Following the quiescent period of exploding, it produces fluctuations with insignificant strength that diminish and increase slowly rather than being quickly dampened. Initially, we consider a neuron's membrane to be at the moment of blasting, and as the regulatory system being controlled changes cautiously, it exhibits spiking creation. We suggest a few fundamental explanations of canard and M-M-Os, which are noted within our observations of the oscillating structure transformation. The slow-fast mechanism is capable of being represented numerically [61] as:

$$\{\begin{array}{c}\dot{{\varkappa }_1}(\xi )=\mathcal{F}({\varkappa }_1,{\varkappa }_2),\hfill \\ \dot{{\varkappa }_2}(\xi )=\rho \mathcal{G}({\varkappa }_1,{\varkappa }_2),\hfill \end{array}$$ (3.2)

where $\dot{{\varkappa }_1}(\xi )=\mathcal{F}({\varkappa }_1,{\varkappa }_2)$ (gradual oscillation) and $\dot{{\varkappa }_2}(\xi )=\rho \mathcal{G}({\varkappa }_1,{\varkappa }_2)$ (rapid firing). The quickly moving factors are represented by ${\varkappa }_1\in {\mathbb{R}}^{{\varrho }_1}$ and the intermediary elements by ${\varkappa }_2\in {\mathbb{R}}^{{\varrho }_2}$, where $0<\rho \ll 1$ indicates the time frame separating parameter. The phase mechanism that comprises these interactions represents the singularity constraint that corresponds to $\rho =0$, and the gradually increasing factor ${\varkappa }_2$ exhibits an element in the confining structure [71], [72].

In the context of a slow-fast nonlinear framework, when the time dimension separating factor $\rho =0$, the threshold exponentially, represented by $\mathcal{C}=\{({\varkappa }_1,{\varkappa }_2)\in {\mathbb{R}}^{{\varrho }_1}\times {\mathbb{R}}^{{\varrho }_2}:\mathcal{F}({\varkappa }_1,{\varkappa }_2)=0\}$ correlates to each multilayered structure's stationary points.

Definition 3.1

Assuming the majority of the fixed points in ${\mathcal{C}}_1$ exhibit hyperbolicity conditions of the underlying framework, that is, ${\mathrm{\Delta }}_{{\varkappa }_1}\mathcal{F}$ possesses no eigenvalues containing zero real components, then any portion of ${\mathcal{C}}_1\subset \mathcal{C}$, which constitutes the critical exponentially, is designated as instinctively hyperbolic. In terms of dynamics, while eigenvalues are determined to comprise a greater or lesser real portion, ${\mathcal{C}}_1$ is said to be attracted (or repelled), whereas if they have neither, ${\mathcal{C}}_1$ constitutes a saddle.

Definition 3.2

([51], [72]) Let us assume the following: there is certainly one eigenvalue containing zero real component in the collection of points belonging to c the fact that it does not constitute transcendental points, that is., ${\mathrm{\Delta }}_{{\varkappa }_1}\mathcal{F}$ as

$${\mathcal{C}}_2=\{({\varkappa }_1,{\varkappa }_2)\in \mathcal{C}:\left(\begin{array}{c}\hfill rank({\mathrm{\Delta }}_{{\varkappa }_1}\mathcal{F}({\varkappa }_1,{\varkappa }_2))={\varrho }_1-1,\hfill \\ \hfill \ell ({\mathrm{\Delta }}_{{\varkappa }_1}^2\mathcal{F}({\varkappa }_1,{\varkappa }_2))(\nu ,\nu )\ne 0,\hfill \\ \hfill \ell ({\mathrm{\Delta }}_{{\varkappa }_2}\mathcal{F}({\varkappa }_1,{\varkappa }_2))\ne 0,\hfill \end{array}\right)\},$$

where constructed eigendirections of ${\mathrm{\Delta }}_{{\varkappa }_1}\mathcal{F}$ are indicated by ℓ and ν. The folded portion positions of the essential region $\mathcal{C}$ are displayed in ${\mathcal{C}}_2$. The threshold considerably $\mathcal{C}$ is selectively divided into portions that possess various stabilization by ${\mathcal{C}}_2$.

Definition 3.3

When a slow-fast dynamical approach $\dot{{\varkappa }_1}(\xi )=\mathcal{F}({\varkappa }_1,{\varkappa }_2)$ or $\dot{{\varkappa }_2}(\xi )=\rho \mathcal{G}({\varkappa }_1,{\varkappa }_2)$, remains inside $\theta (\rho )$ of a repulsive extend that forms the vital exponentially during an amount of time, i.e., $\theta (1)$ depending on the medium time frame interactions $\tau =\rho$, it is referred to being a canard.

Investigating the desingularized mechanism, which may be derived by considering delayed interactions by employing a specific temporal development, is necessary. The shape of the fold positions as well as the fixed positions of the slow-fast structure are surrounded by $\theta (\rho )$ environment that contains the stabilizing endpoints of the desingularized network. By implementing $\tau =\rho \xi$ to modify the expanded temporal category, we derive the slow-fast interactions in the following way:

$$\{\begin{array}{c}\rho \dot{{\varkappa }_1}(\xi )=\mathcal{F}({\varkappa }_1,{\varkappa }_2),\hfill \\ \dot{{\varkappa }_2}(\xi )=\mathcal{G}({\varkappa }_1,{\varkappa }_2),\hfill \end{array}$$ (3.3)

The simplified structure, which can be defined on the threshold exponentially, $\mathcal{C}$, is the exceptional restriction that describes $\rho =0$. It reflects the algebraic differential equations [50] correlating to the delayed component $\dot{{\varkappa }_2}(\tau )=\mathcal{G}({\varkappa }_1,{\varkappa }_2)$. The fixed points of the restricted interactions and the entire framework are identical. The differentiation $\mathcal{F}({\varkappa }_1,{\varkappa }_2)=0$ using (3.3) regarding to τ yields the resulting formulation, which we employ to figure out the desingularized structure [71], [72] as:

$${\mathbf{D}}_{{\varkappa }_1}\mathcal{F}\frac{d{\varkappa }_1}{d\tau }+{\mathbf{D}}_{{\varkappa }_2}\mathcal{F}\frac{d{\varkappa }_2}{d\tau }=0.$$ (3.4)

It is presently feasible to determine the transpose value for the cofactor matrix of ${\mathbf{D}}_{{\varkappa }_1}\mathcal{F}$ simply by dividing each component of (3.4) by adj$({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})$ as

$$-\det ({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})\frac{d{\varkappa }_1}{d\tau }=adj({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})({\mathbf{D}}_{{\varkappa }_2}\mathcal{F})\mathcal{G}({\varkappa }_1,{\varkappa }_2),$$ (3.5)

where the unique framework, often known as folding indications, is represented by $\det ({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})=0$. Within various indications, the usual presence and distinctiveness arguments are invalid. This is the process of obtaining the desingularized structure as

$$\{\begin{array}{c}\frac{d{\varkappa }_1}{d\tau }=adj({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})({\mathbf{D}}_{{\varkappa }_2}\mathcal{F})\mathcal{G}({\varkappa }_1,{\varkappa }_2),\hfill \\ \frac{d{\varkappa }_2}{d\tau }=-\det ({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})\mathcal{G}({\varkappa }_1,{\varkappa }_2).\hfill \end{array}$$ (3.6)

When ${\varrho }_1=1$, adj$({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})=1$ and ${\mathbf{D}}_{{\varkappa }_1}\mathcal{F}=\det ({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})=\frac{\mho \mathcal{F}}{\mho {\varkappa }_1}$ are scalars. In order to derive the component domain outflows associated with the simplified interactions resulting that the desingularized framework, one needs to change the pattern of the circulation of the desingularized mechanics on the freshly formed branches wherein $\det ({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})>0$, contingent on the newly introduced time duration $d\tau =-\det ({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})d\tau$. Currently, both kinds of stationary locations within the generalized configuration (3.6) are referred to as folding absurdities and standard anomalies, respectively, and we characterize them according to what follows:

Definition 3.4

([51], [72]) Assuming the fixed location that represents the desingularized mechanism (3.6) is equivalent to a point of reference of the simplified network and lies within the proximity $\theta (\rho )$ of the balance phase of the whole interactions, then such a point is referred to as being a conventional strangeness. The singularity's requirements are expressed as

$$\mathcal{G}({\varkappa }_1,{\varkappa }_2)=0,\det ({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})\ne 0,adj({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})({\mathbf{D}}_{{\varkappa }_2}\mathcal{F})\mathcal{G}({\varkappa }_1,{\varkappa }_2)\ne 0.$$

Definition 3.5

([51], [72]) Assuming a folding region of the simplified phase coincides with the balance point from the desingularized framework, it is referred to as a foldable absurdity. The following are the prerequisites to achieve a foldable singularity:

$$\det ({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})=0,adj({\mathbf{D}}_{{\varkappa }_1}\mathcal{F})({\mathbf{D}}_{{\varkappa }_2}\mathcal{F})\mathcal{G}({\varkappa }_1,{\varkappa }_2)=0.$$

3.1. Analysis of the DF FH-R model

In the recent investigation, we implement the Caputo difference operator to create a DFO FH-R model, extending the integer-order FH-R model. The FH-R's first-order difference can be represented by the following procedure:

$$\{\begin{array}{c}\mathrm{\Delta }{\mathbf{u}}_1(\eta +1)={\mathbf{u}}_1(\eta )-\frac{{\mathbf{u}}_1^3(\eta )}{3}-{\mathbf{u}}_2(\eta )+{\mathbf{u}}_3(\eta )+\Im ,\hfill \\ \mathrm{\Delta }{\mathbf{u}}_2(\eta +1)=\rho ({\varsigma }_1+{\mathbf{u}}_1(\eta )-{\varsigma }_2{\mathbf{u}}_2(\eta )),\hfill \\ \mathrm{\Delta }{\mathbf{u}}_3(\eta +1)=\mu ({\varsigma }_3-{\mathbf{u}}_1(\eta )-{\varsigma }_4{\mathbf{u}}_3(\eta )),\hfill \end{array}$$ (3.7)

where the commonly used difference operator is represented by $\mathrm{\Delta }{\mathbf{u}}_1(\eta )={\mathbf{u}}_1(\eta +1)-{\mathbf{u}}_1(\eta )$. A FO difference system is created in the previously stated procedure by replacing η by $\psi +\phi -1$ and Δ by substituting the Caputo difference operator ${}^c\mathrm{\Delta }_{\xi }^{\chi }$, then

$$\{\begin{array}{c}{}^c\mathrm{\Delta }_{\xi }^{\chi }{\mathbf{u}}_1(\psi )={\mathbf{u}}_1(\psi +\chi -1)-\frac{{\mathbf{u}}_1^3(\psi +\chi -1)}{3}-{\mathbf{u}}_2(\psi +\chi -1)+{\mathbf{u}}_3(\psi +\chi -1)+\Im ,\hfill \\ {}^c\mathrm{\Delta }_{\xi }^{\chi }{\mathbf{u}}_2(\psi )=\rho ({\varsigma }_1+{\mathbf{u}}_1(\psi +\chi -1)-{\varsigma }_2{\mathbf{u}}_2(\psi +\chi -1)),\hfill \\ {}^c\mathrm{\Delta }_{\xi }^{\chi }{\mathbf{u}}_3(\psi )=\mu ({\varsigma }_3-{\mathbf{u}}_1(\psi +\chi -1)-{\varsigma }_4{\mathbf{u}}_3(\psi +\chi -1)),\hfill \end{array}$$ (3.8)

where $\psi \in {\mathbb{N}}_{\zeta +1-\chi },\zeta$ is the starting value and $\chi \in (0,1]$ indicates the FO. Systems generated employing the Caputo formulation implement non-FO starting indications, but those formed using the Riemann-Liouville formulation necessitate FO initial conditions. This is the primary benefit of using the Caputo fractional difference formulation versus the Riemann-Liouville operator. Investigation on the subjective evaluation of such structures is continuing, and it is essential to understand whether the non-local nature of DF operators significantly affects network feedback, resulting in peculiar, unpredictable actions not noticed in continuous time-dependent processes.

Currently, considering fractional sum formulas for the commensurate FO, we determine the numerical solutions defined in Theorem 2.1 as

$$\{\begin{array}{c}{\mathbf{u}}_1(\psi )={\mathbf{u}}_1(0)+\sum _{\nu =1}^{\psi }\frac{\mathrm{\Gamma }(\psi -\nu -1+\chi )}{\mathrm{\Gamma }(\chi )\mathrm{\Gamma }(\psi -\nu )}({\mathbf{u}}_1(\nu )-\frac{{\mathbf{u}}_1^3(\nu )}{3}-{\mathbf{u}}_2(\nu )+{\mathbf{u}}_3(\nu )+\Im ),\hfill \\ {\mathbf{u}}_2(\psi )={\mathbf{u}}_2(0)+\sum _{\nu =1}^{\psi }\frac{\mathrm{\Gamma }(\psi -\nu -1+\chi )}{\mathrm{\Gamma }(\chi )\mathrm{\Gamma }(\psi -\nu )}\left(\rho \right({\varsigma }_1+{\mathbf{u}}_1(\nu )-{\varsigma }_2{\mathbf{u}}_2(\nu )\left)\right),\hfill \\ {\mathbf{u}}_3(\psi )={\mathbf{u}}_3(0)+\sum _{\nu =1}^{\psi }\frac{\mathrm{\Gamma }(\psi -\nu -1+\chi )}{\mathrm{\Gamma }(\chi )\mathrm{\Gamma }(\psi -\nu )}\left(\mu \right({\varsigma }_3-{\mathbf{u}}_1(\nu )-{\varsigma }_4{\mathbf{u}}_3(\nu )\left)\right),\psi =1,2,....\hfill \end{array}$$ (3.9)

Furthermore, the incommensurate version of the DFO FH-R system is defined as follows:

$$\{\begin{array}{c}{}^c\mathrm{\Delta }_{{\varsigma }_1}^{{\chi }_1}{\mathbf{u}}_1(\psi )={\mathbf{u}}_1(\psi +{\chi }_1-1)-\frac{{\mathbf{u}}_1^3(\psi +{\chi }_1-1)}{3}-{\mathbf{u}}_2(\psi +{\chi }_1-1)+{\mathbf{u}}_3(\psi +{\chi }_1-1)+\Im ,\hfill \\ {}^c\mathrm{\Delta }_{{\varsigma }_1}^{{\chi }_2}{\mathbf{u}}_2(\psi )=\rho ({\varsigma }_1+{\mathbf{u}}_1(\psi +{\chi }_2-1)-{\varsigma }_2{\mathbf{u}}_2(\psi +{\chi }_2-1)),\hfill \\ {}^c\mathrm{\Delta }_{{\varsigma }_1}^{{\chi }_3}{\mathbf{u}}_3(\psi )=\mu ({\varsigma }_3-{\mathbf{u}}_1(\psi +{\chi }_3-1)-{\varsigma }_4{\mathbf{u}}_3(\psi +{\chi }_3-1)),\hfill \end{array}$$ (3.10)

where $\psi \in {\mathbb{N}}_{{\varsigma }_1+1-{\chi }_{\iota }},{\varsigma }_1$ is the starting value and ${\chi }_{\iota }\in (0,1],\iota =1,2,3$ indicates the FO.

In view of Theorem 2.1, the incommensurate FO framework for the FH-R model evaluates the computational process for the aforesaid framework as follows:

$$\{\begin{array}{c}{\mathbf{u}}_1(\psi )={\mathbf{u}}_1(0)+\sum _{\nu =1}^{\psi }\frac{\mathrm{\Gamma }(\psi -\nu -1+{\chi }_1)}{\mathrm{\Gamma }({\chi }_1)\mathrm{\Gamma }(\psi -\nu )}({\mathbf{u}}_1(\nu )-\frac{{\mathbf{u}}_1^3(\nu )}{3}-{\mathbf{u}}_2(\nu )+{\mathbf{u}}_3(\nu )+\Im ),\hfill \\ {\mathbf{u}}_2(\psi )={\mathbf{u}}_2(0)+\sum _{\nu =1}^{\psi }\frac{\mathrm{\Gamma }(\psi -\nu -1+{\chi }_2)}{\mathrm{\Gamma }({\chi }_2)\mathrm{\Gamma }(\psi -\nu )}\left(\rho \right({\varsigma }_1+{\mathbf{u}}_1(\nu )-{\varsigma }_2{\mathbf{u}}_2(\nu )\left)\right),\hfill \\ {\mathbf{u}}_3(\psi )={\mathbf{u}}_3(0)+\sum _{\nu =1}^{\psi }\frac{\mathrm{\Gamma }(\psi -\nu -1+{\chi }_3)}{\mathrm{\Gamma }({\chi }_3)\mathrm{\Gamma }(\psi -\nu )}\left(\mu \right({\varsigma }_3-{\mathbf{u}}_1(\nu )-{\varsigma }_4{\mathbf{u}}_3(\nu )\left)\right),\psi =1,2,...,\hfill \end{array}$$ (3.11)

where the ICs are denoted by ${\mathbf{u}}_1(0),{\mathbf{u}}_2(0)$ and ${\mathbf{u}}_3(0)$. This FH-R mechanism is completely new and possesses “memory effects.” The results indicate that the factors ${\mathbf{u}}_1(\psi ),{\mathbf{u}}_2(\psi )$ and ${\mathbf{u}}_3(\psi )$ are interconnected with respect to each preceding component ${{\mathbf{u}}_1}_1(0),{{\mathbf{u}}_1}_2(0),...,{\mathbf{u}}_1(\psi -1),{{\mathbf{u}}_2}_1(0),{{\mathbf{u}}_2}_2(0),...,{\mathbf{u}}_2(\psi -1)$ and ${{\mathbf{u}}_3}_1(0),{{\mathbf{u}}_3}_2(0),...,{\mathbf{u}}_3(\psi -1)$. This can be observed in (3.10).

4. Dynamical analysis of FH-R system with external stimulus

The present portion intends to examine the stability and chaos of the previously proposed DFO FH-R models (3.9) and (3.11) in two scenarios: commensurate and non-commensurate FOs, respectively. A variety of mathematical approaches will be employed in this study, including phase visualization in multidimensional approximations and bifurcation diagrams. Furthermore, we will assess whether chaos exists in the analysis of FH-R models (3.9) and (3.11), respectively.

4.1. Commensurate fractional order

Here, the layering structure that corresponds to (3.9) and implements the relatively sluggish interactions (3.2) is initially derived in this subsection. In this instance, the slow component is 2D, whereas, as indicated by the two separate pairs carriers ${\varkappa }_1\equiv {\mathbf{u}}_1$ and ${\varkappa }_2\equiv ({\mathbf{u}}_2,{\mathbf{u}}_3)$, indicating the fast component. The gradually increasing ${\mathbf{u}}_2$ and extremely sluggish ${\mathbf{u}}_3$ parameters in scheme (3.8) have two distinct time frames, ρ and ${\rho }^2$, respectively. After viewing the slower factors $({\mathbf{u}}_{2}and{\mathbf{u}}_3)$ as parameters within the exceptional framework (4.1), the level framework is derived by assuming the exceptional restriction $\rho =0$ in the framework (3.8). The subsequent collection of FO difference equations describes the layer structure as

$$\{\begin{array}{c}{}^c\mathrm{\Delta }_{\xi }^{\chi }{\mathbf{u}}_1(\psi )={\mathbf{u}}_1(\psi +\chi -1)-\frac{{\mathbf{u}}_1^3(\psi +\chi -1)}{3}-{\mathbf{u}}_2(\psi +\chi -1)+{\mathbf{u}}_3(\psi +\chi -1)+\Im =\mathrm{\Upsilon }({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3),\hfill \\ {}^c\mathrm{\Delta }_{\xi }^{\chi }{\mathbf{u}}_2(\psi )=0,\hfill \\ {}^c\mathrm{\Delta }_{\xi }^{\chi }{\mathbf{u}}_3(\psi )=0.\hfill \end{array}$$ (4.1)

With mechanism (3.1) currently configured with the sluggish time frame ${\tau }_1=\rho \xi$, we get ${}^c\mathrm{\Delta }_{{\tau }_1}^{\chi }{\tau }_1=\rho {}^c\mathrm{\Delta }_{{\tau }_1}^{\chi }\xi$. The process (4.1) can be articulated as

$$\{\begin{array}{c}\rho {}^c\mathrm{\Delta }_{{\tau }_1}^{\chi }{\mathbf{u}}_1(\psi )={\mathbf{u}}_1(\psi +\chi -1)-\frac{{\mathbf{u}}_1^3(\psi +\chi -1)}{3}-{\mathbf{u}}_2(\psi +\chi -1)+{\mathbf{u}}_3(\psi +\chi -1)+\Im ,\hfill \\ {}^c\mathrm{\Delta }_{{\tau }_1}^{\chi }{\mathbf{u}}_2(\psi )=({\varsigma }_1+{\mathbf{u}}_1(\psi +\chi -1)-{\varsigma }_2{\mathbf{u}}_2(\psi +\chi -1)),\hfill \\ {}^c\mathrm{\Delta }_{{\tau }_1}^{\chi }{\mathbf{u}}_3(\psi )=\rho ({\varsigma }_3-{\mathbf{u}}_1(\psi +\chi -1)-{\varsigma }_4{\mathbf{u}}_3(\psi +\chi -1)).\hfill \end{array}$$ (4.2)

By assigning $\rho =0$ in (4.2), the equivalent simplified mechanism is produced. Therefore, the simplified process is capable of being represented as

$$\{\begin{array}{c}0={\mathbf{u}}_1(\psi +\chi -1)-\frac{{\mathbf{u}}_1^3(\psi +\chi -1)}{3}-{\mathbf{u}}_2(\psi +\chi -1)+{\mathbf{u}}_3(\psi +\chi -1)+\Im ,\hfill \\ {}^c\mathrm{\Delta }_{{\tau }_1}^{\chi }{\mathbf{u}}_2(\psi )=({\varsigma }_1+{\mathbf{u}}_1(\psi +\chi -1)-{\varsigma }_2{\mathbf{u}}_2(\psi +\chi -1)),\hfill \\ {}^c\mathrm{\Delta }_{{\tau }_1}^{\chi }{\mathbf{u}}_3(\psi )=0.\hfill \end{array}$$ (4.3)

It additionally carries out algebraic difference equations. Knowing the functioning of the entire structure (3.2) employing components (4.1) and (4.3) with $\rho >0$ is the most important objective of researching the patterned singularity disturbances theory. The behavior of the significant membrane ${\mathrm{\Psi }}_0$ is described by the algebraic formula of the aforementioned framework, which could potentially be written as follows:

$$\begin{gathered} {\mathrm{\Psi }}_0=\{\begin{array}{c}\{({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3):\mathcal{F}({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3)=0\},\hfill \\ \{({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3):{\mathbf{u}}_1(\psi +\chi -1)-\frac{{\mathbf{u}}_1^3(\psi +\chi -1)}{3}-{\mathbf{u}}_2(\psi +\chi -1)+{\mathbf{u}}_3(\psi +\chi -1)+\Im =0\},\hfill \\ \hfill \end{array} \\ =\{({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3):{\mathbf{u}}_2(\psi +\chi -1)={\mathbf{u}}_1(\psi +\chi -1)-\frac{{\mathbf{u}}_1^3(\psi +\chi -1)}{3}+{\mathbf{u}}_3(\psi +\chi -1)+\Im \}. \end{gathered}$$ (4.4)

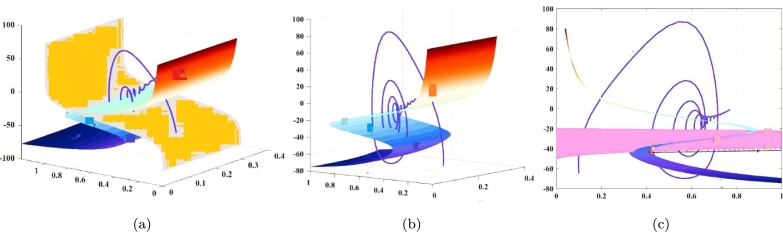
The geometry that defines tremendously ${\mathrm{\Psi }}_0$ is comparable to the configuration with the perceptible functioning, which describes the crucial network (see Fig. 1(a-b)). It additionally provides the component technique's assortment of fixed points (4.1). The factor ${\mathbf{u}}_3$ within ${\mathrm{\Psi }}_0$ is implemented as a constant since we can compute ${\mathrm{\Delta }}_{{\tau }_1}^{\chi }$ using (4.4). The folding perspectives $(\mathrm{\Phi }\pm )$ are the regions wherein ${\mathrm{\Psi }}_0$ no longer exhibits its typical hyperbolicity. Consequently, Φ± splits ${\mathrm{\Psi }}_0$ over three categories:

$${\mathrm{\Psi }}_0={\mathrm{\Psi }}_0^{{\varsigma }_1,-}\cup {\mathrm{\Phi }}^{-}\cup {\mathrm{\Psi }}_0^{\overline{s}}\cup {\mathrm{\Phi }}^{+}\cup {\mathrm{\Psi }}_0^{{\varsigma }_1,+},$$

where the magnetizing components of ${\mathrm{\Psi }}_0$ are represented as ${\mathrm{\Psi }}_0^{{\varsigma }_1,-}$ and ${\mathrm{\Psi }}_0^{{\varsigma }_1,+}$ and are specified as

$${\mathrm{\Psi }}_0^{{\varsigma }_1,-}\cup {\mathrm{\Psi }}_0^{{\varsigma }_1,+}=\{({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3)\in {\mathrm{\Psi }}_0:{\mathrm{\Delta }}_{{\mathbf{u}}_1}\mathcal{F}<0\}=\{({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3)\in {\mathrm{\Psi }}_0:{\mathbf{u}}_1<-1and{\mathbf{u}}_1>1\}.$$

Furthermore, the repulsive component of ${\mathrm{\Psi }}_0^{\overline{s}}$ is denoted by ${\mathrm{\Psi }}_0$ is described as

$${\mathrm{\Psi }}_0^{\overline{s}}=\{({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3)\in {\mathrm{\Psi }}_0:{\mathrm{\Delta }}_{{\mathbf{u}}_1}\mathcal{F}>0\}=\{({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3)\in {\mathrm{\Psi }}_0:-1<{\mathbf{u}}_1<1\}.$$

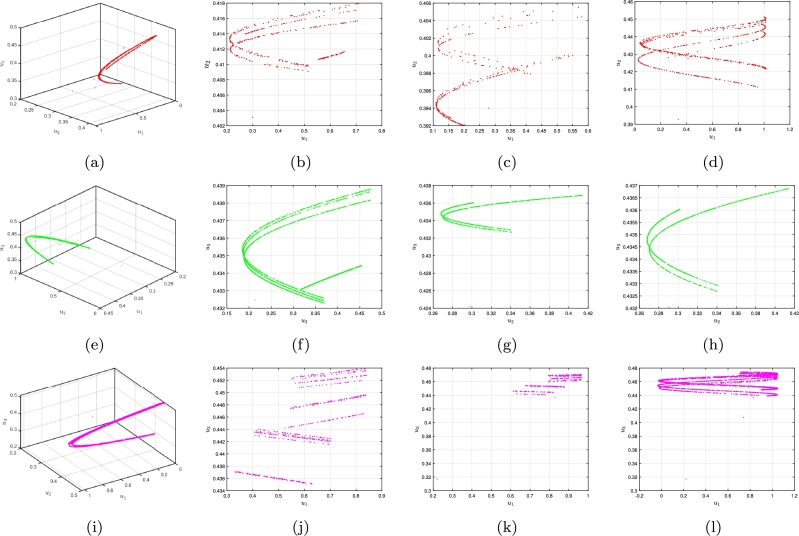
Fig. 1(a-b) shows the folded contours (${\mho }_{+}$ and ${\mho }_{-}$) within the commensurate FO FH-R mechanism. We additionally sketch the multidimensional components ${\mathrm{\Psi }}_0$ having a pattern in a multidimensional $({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3)$ region for improved visualization (see Fig. 1(c)). The overlapping patterns on the reverse side are ${\mho }_{+}$ and on the contrary, they are ${\mho }_{-}$. The attractive panels of ${\mathrm{\Psi }}_0$ reside on the exterior left portion of ${\mho }_{+}$ and the reverse edge of ${\mho }_{-}$. The paths pursue swift movement across the absorbing layer ${\mathrm{\Psi }}_0^{{\varsigma }_1,-}$, where they can intersect the folding path ${\mho }_{+}$ at an abrupt position ${\mathrm{\Phi }}^{+}$. At this moment, the pathways climb through the enticing layer, approaching the folded accordance ${\mho }_{-}$ and then leap back across the capturing strip ${\mathrm{\Psi }}_0^{{\varsigma }_1,+}$ closest to the collapse position ${\mathrm{\Phi }}^{-}$. The procedure can be represented as ${\mathrm{\Phi }}^{+}\mapsto {\mathrm{\Psi }}_0^{{\varsigma }_1,-}\mapsto {\mathrm{\Phi }}^{-}\mapsto {\mathrm{\Psi }}_0^{{\varsigma }_1,+}$. The recesses that comprise ${\mathrm{\Psi }}_0$ are represented by the values of ${\varphi }^{-}$ and ${\varphi }^{+}$ (see Fig. 1(a)), which are generated by meeting all of the requirements outlined in the specification of folded elements.

Figure 1.

Surfaces of the critical manifold ${\mathrm{\Psi }}_0^{\overline{s}}$ for the commensurate FO FH-R framework (3.9) having standard components (a) ℑ = 0.25, (b) ℑ = 0.375. (c) Plot of the manifold ${\mathrm{\Psi }}_0^{\overline{s}}$ for relaxing threshold process with ${\mathbf{u}}_1^{⁎}=1$, using identical assumptions that are shown in Fig. 1(a).

According to [36], considering a single faster and several sluggish components of such criteria, it decreases simply ${}^c\mathrm{\Delta }_{{\mathbf{u}}_1}\mathcal{F}{|}_{{\mathrm{\Phi }}^{\pm }}=0$, ${}^c\mathrm{\Delta }_{{\mathbf{u}}_1}^{\chi }{\mathrm{\Delta }}_{{\mathbf{u}}_1}^{-(\zeta -\chi )}\mathcal{F}{|}_{{\mathrm{\Phi }}^{\pm }}\ne 0$, and ${}^c\mathrm{\Delta }_{{\mathbf{u}}_1}^{\chi }{\mathrm{\Delta }}_{{\mathbf{u}}_2}^{-(\zeta -\chi )}\mathcal{F}{|}_{{\mathrm{\Phi }}^{\pm }}$ possesses complete rank one. The mechanism (3.8) has foldable indicates of ${\mathbf{u}}_1=\pm 1$ if the initial circumstance, ${}^c\mathrm{\Delta }_{{\mathbf{u}}_1}\mathcal{F}{|}_{{\mathrm{\Phi }}^{\pm }}=0$, is achieved. The subsequent criteria generate ${}^c\mathrm{\Delta }_{{\mathbf{u}}_1}^{\chi }{\mathrm{\Delta }}_{{\mathbf{u}}_1}^{-(\zeta -\chi )}\mathcal{F}{|}_{{\mathrm{\Phi }}^{\pm }}=2or-2$ and ${}^c\mathrm{\Delta }_{{\mathbf{u}}_1}^{\chi }{\mathrm{\Delta }}_{{\mathbf{u}}_2}^{-(\zeta -\chi )}\mathcal{F}{|}_{{\mathrm{\Phi }}^{\pm }}=(-1,1)$ having total rank a particular one, respectively. The mathematical formulas $\mathcal{F}({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3)=0$, regarding the value of ${\tau }_1$ have been decomposed in order to represent the gradual circulation as a function of the rapid factor ${\mathbf{u}}_1$. This yields ${\mathrm{\Delta }}_{{\mathbf{u}}_1}\mathcal{F}{\mathrm{\Delta }}_{{\tau }_1}{\mathbf{u}}_1+{\mathrm{\Delta }}_{{\mathbf{u}}_2}\mathcal{F}{\mathrm{\Delta }}_{{\tau }_1}{\mathbf{u}}_2+{\mathrm{\Delta }}_{{\mathbf{u}}_3}\mathcal{F}{\mathrm{\Delta }}_{{\tau }_1}{\mathbf{u}}_3=0$ or $(1-{\mathbf{u}}_1^2){\mathrm{\Delta }}_{{\tau }_1}{\mathbf{u}}_1-{\mathrm{\Delta }}_{{\tau }_1}{\mathbf{u}}_2=0$.

By replacing the default setting of ${\mathrm{\Delta }}_{{\tau }_1}{\mathbf{u}}_2$ in (4.3), we get

$$(1-{\mathbf{u}}_1^2(\varphi +\chi -1)){\mathrm{\Delta }}_{{\tau }_1}{\mathbf{u}}_1=({\varsigma }_1+{\mathbf{u}}_1(\varphi +\chi -1)-{\varsigma }_2({\mathbf{u}}_1(\varphi +\chi -1)-\frac{{\mathbf{u}}_1^3(\varphi +\chi -1)}{3}+{\mathbf{u}}_3(\varphi +\chi -1)+\Im \left)\right).$$

To convert the previous formula into a delayed-fast structure, one can typically add an inefficient module. Following a folding trajectory, the consequent 2D framework is unique. By reducing the temporal frame as ${}^c\mathrm{\Delta }_{{\varsigma }_1}^{\chi }{\tau }_1=-(1-{\mathbf{u}}_1^2(\varphi +\chi -1)){}^c\mathrm{\Delta }_{{\varsigma }_1}^{\chi }{\tau }_2$, it is possible to desingularize the gradual motion around the folding positions ${\mathbf{u}}_1^{⁎}=\pm 1$. Thus, the desingularized simplified scheme, which is represented as follows

$$\{\begin{array}{c}{}^c\mathrm{\Delta }_{\overline{{\varsigma }_1}}^{\chi }{\mathbf{u}}_1(\varphi )=-({\varsigma }_1+(1-{\varsigma }_2){\mathbf{u}}_1(\varphi +\chi -1)-{\varsigma }_2(-\frac{{\mathbf{u}}_1^3(\varphi +\chi -1)}{3}+{\mathbf{u}}_3(\varphi +\chi -1)+\Im \left)\right),\hfill \\ {}^c\mathrm{\Delta }_{\overline{{\varsigma }_1}}^{\chi }{\mathbf{u}}_3(\varphi )=-\rho (1-{\mathbf{u}}_1^2(\varphi +\chi -1))({\varsigma }_3-{\mathbf{u}}_1\varphi +\chi -1-{\varsigma }_4{\mathbf{u}}_3(\varphi +\chi -1)),\hfill \end{array}$$ (4.5)

confined to ${\mathrm{\Psi }}_0$. The collapsed absurdity is able to be categorized by the terms flipped concentration, pressed node, or collapsed saddle by considering the variety of eigenvalues present in the desingularized simplified scheme Jacobian matrix at this point in time. The foldable discontinuities, which are located on the overlapping edges ${\mho }_{\pm }$, are obtained as the state of stead-state with the structure (4.5). There are two different kinds of absurdities within the desingularized simplified scheme (4.5): foldable singularities and standard discrepancies. The distinct stability that remains on the folded point ${\mho }_{+}$ is ${\mathbf{u}}_2=\frac{{\varsigma }_1+1}{\overline{b}}$ having ${\mathbf{u}}_1^{⁎}=1$ and ${\mathbf{u}}_3^{⁎}=\frac{{\varsigma }_1}{{\varsigma }_2}-(2+3\Im )$. In the same manner, the solitary point of stability along the folding path ${\mho }_{-}$ is ${\mathbf{u}}_2=\frac{{\varsigma }_1-1}{\overline{b}}$ having ${\mathbf{u}}_1^{⁎}=-1$ and ${\mathbf{u}}_3^{⁎}=\frac{{\varsigma }_1}{{\varsigma }_2}-(2-3\Im )$. The desingularized simplified scheme's pushed extremes include two such stability positions, (4.5). By substituting the formulae ${\varsigma }_3-{\mathbf{u}}_1(\varphi +\chi -1)-{\varsigma }_4{\mathbf{u}}_3(\varphi +\chi -1)=0$ as well as $({\varsigma }_1+(1-{\varsigma }_2){\mathbf{u}}_1(\varphi +\chi -1)-{\varsigma }_2(-\frac{{\mathbf{u}}_1^3(\varphi +\chi -1)}{3}+{\mathbf{u}}_3(\varphi +\chi -1)+\Im \left)\right)=0$ for ${\mathbf{u}}_1$ and ${\mathbf{u}}_3$, respectively, the conventional equilibria solution can be established. The desingularized simplified scheme's Jacobian matrix enveloping the wrapped discontinuity is provided by

$$\mathcal{J}=\left(\begin{array}{cc}\hfill -1\hfill & \hfill {\varsigma }_2\hfill \\ \hfill 2\rho {\mathbf{u}}_1^{⁎}({\varsigma }_3-{\mathbf{u}}_1^{⁎}-{\varsigma }_4{\mathbf{u}}_3^{⁎})\hfill & \hfill 0\hfill \end{array}\right).$$ (4.6)

Currently, we are taking ${\mu }_1$ and ${\mu }_2$ to represent the intrinsic values of $\mathcal{J}$ for (4.5) over the position $({\mathbf{u}}_1^{⁎},{\mathbf{u}}_3^{⁎})$ that is constrained to ${\mathrm{\Psi }}_0$. Next, based upon the foldable discontinuities, we categorize the reference point $({\mathbf{u}}_1^{⁎},{\mathbf{u}}_3^{⁎})$ as described ${\mu }_1{\mu }_2>0,{\mu }_{1,2}\in \mathbb{R}$ signifies a folded node, and ${\mu }_1{\mu }_2>0$ with $Img({\mu }_{1,2})\ne 0$ indicates the folded focus.

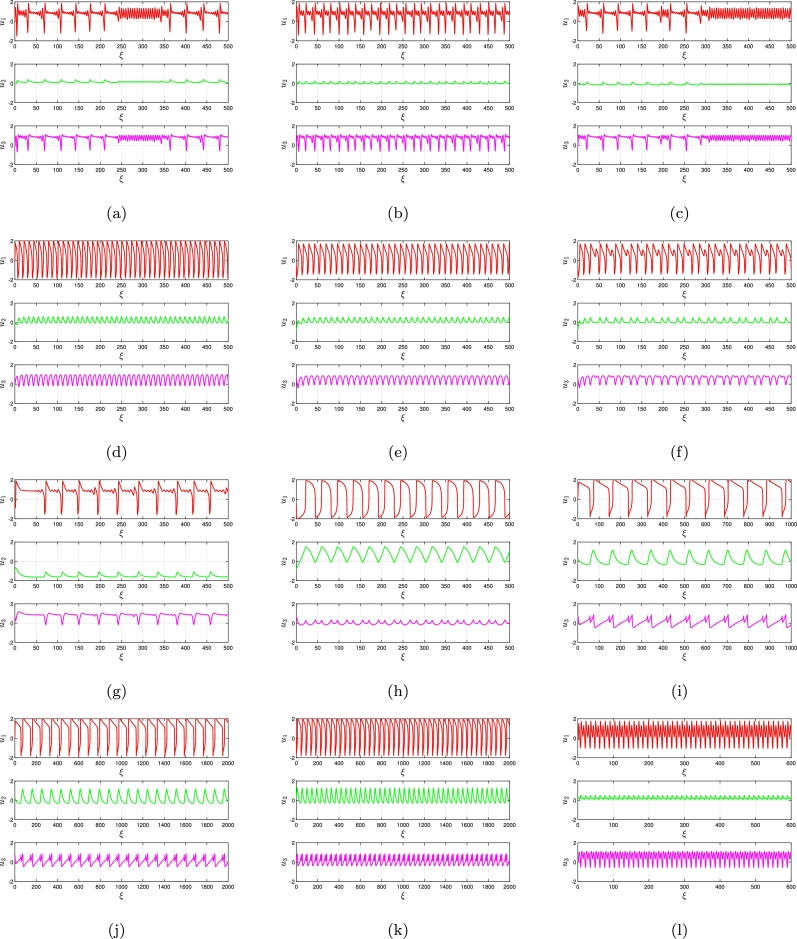
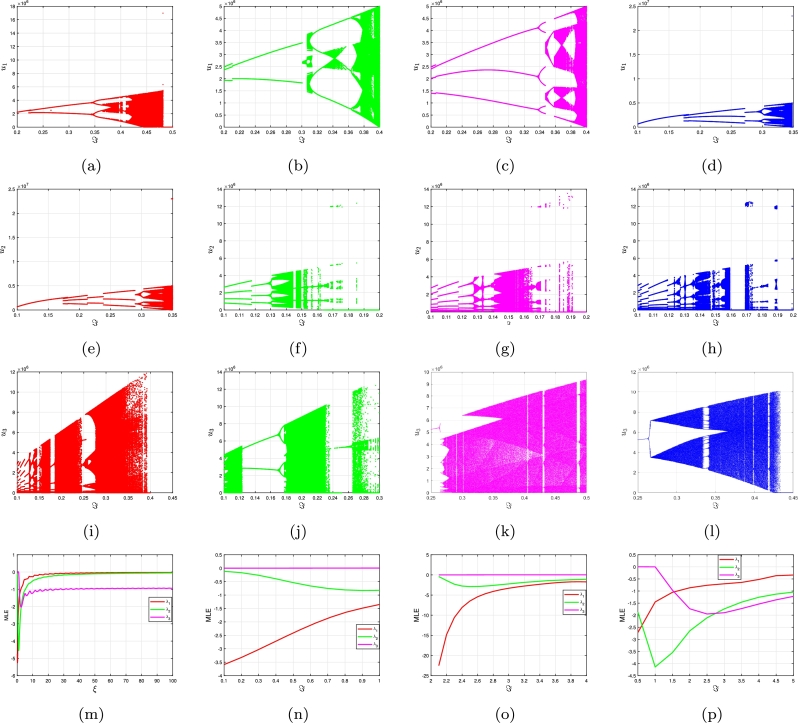
Matrix (4.6) demonstrates the eigenvalues ${\mu }_{1,2}=-0.856601\pm 0.887345\mathbf{i}$ and ${\mu }_{3,4}=-0.44785\pm 0.567892\mathbf{i}$. For $\chi =0.7$, we have ${(2\cos (\frac{|\arg ({\mu }_{1,2})|-\pi }{1.3}\left)\right)}^{0.7}=1.3985677$ and ${(2\cos (\frac{|\arg ({\mu }_{3,4})|-\pi }{1.3}\left)\right)}^{0.7}=1.4110981$. Therefore, criterion $|\mu |<{(2\cos (\frac{|\arg (\mu )|-\pi }{1.3}\left)\right)}^{\chi }$ has been met by (3.8) and (4.5). Furthermore, $|\arg (\mu )|>\frac{\chi \pi }{2}$ is valid. Two conjugate complex eigenvalues are present; therefore, it is necessary to confirm the subsequent requirements using Lemma 2.1. Consequently, it is apparent that the prerequisite $|\arg (\mu )|>\frac{\chi \pi }{2}$ meets the criteria with the result $|\arg ({\mu }_{1,2,3,4})|<1.210$. Mechanism (4.5) is exceptionally steady in the equilibrium phase, as shown in Fig. 2 (a-c) and quantitative assessment confirms the reliability criterion given in Lemma 2.1.

Figure 2.

Bursting reactions and adjustments of the commensurate FO FH-R system (3.8) via predetermined centered factors and the most prevalent value are taken into consideration for various FOs (a)χ = 0.67 and ℑ = 0.13, (b)χ = 0.75 and ℑ = 0.21, (c)χ = 0.85 and ℑ = 0.27, (d)χ = 0.78 and ℑ = 0.36, (e)χ = 0.80 and ℑ = 0.38, (f)χ = 0.81 and ℑ = 0.375, (g)χ = 0.85 and ℑ = 0.38, (h)χ = 0.89 and ℑ = 0.395, (i)χ = 0.93 and ℑ = 0.41, (j)χ = 0.95 and ℑ = 0.45, (k)χ = 0.98 and ℑ = 0.49, (l)χ = 0.99 and ℑ = 0.36.

In an architecture that displays M-M-Os, the extending network and foldable saddle-node transitions are typically observable [50]. In this instance, we will investigate various M-M-Os and exploding instabilities in mixed-mode phenomena in the framework of foldable nodes.

When $\rho >0$ is appropriate to accommodate the slow-fast scheme (3.9), the subsequent requirements are met:

• (i)If $\vartheta =\frac{{\mu }_{{\mathbf{u}}_2}}{{\mu }_{{\mathbf{u}}_1}}<1$ given a folding cluster is taken into consideration, therefore the singularity canard $\widehat{{\delta }_r}$, sometimes known as “the powerful canard,” necessarily impacts towards a peak performance canard ${\delta }_r$.
• (ii)The single canard $\widehat{{\delta }_m}$, sometimes known as “the inadequate canard,” exists whenever $\vartheta -1\in \mathbb{N}$. Furthermore, it disturbs a maximized canard ${\delta }_{\epsilon }$, wherein ${\delta }_m$ as well as ${\delta }_{\epsilon }$ stand for basic canards. Assume that within a foldable component, ${\varrho }_2>0$ represents a value that yields $\vartheta \ne 1/(2{\varrho }_2+2)$ as well as $2{\varrho }_2+3<\vartheta <2{\varrho }_2+1$. Following that, perhaps ${\varrho }_2$ additional extreme canards, designated as supplementary canards, exist along with ${\delta }_{m,\epsilon }$.
• (iii)There are currently no optimum canards regarding foldable concentration.

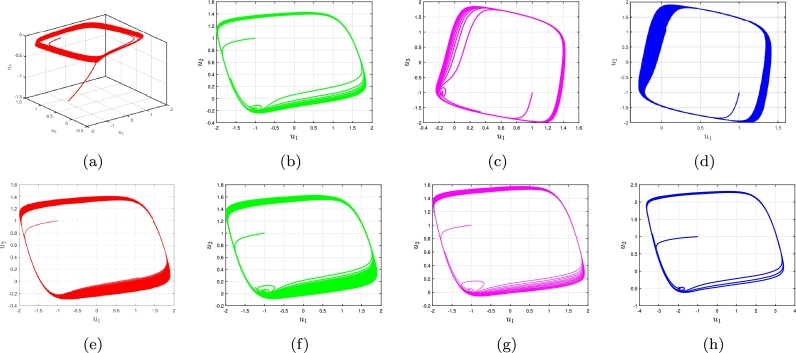
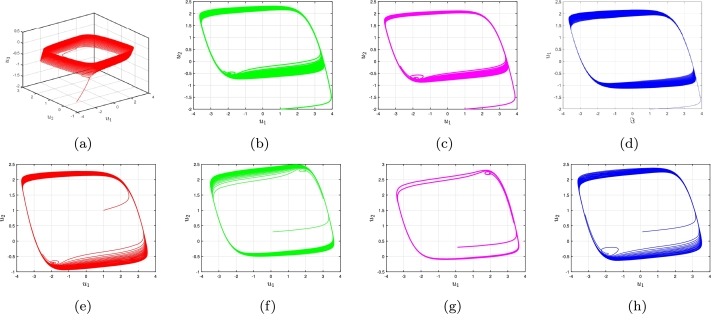
Numerous underlying foldings and stretchings of randomness are shown via homoclinic bifurcation in Fig. 3(a-d) for various ℑ and $\chi =0.7$. We present the data supporting M-M-Os having a pathway leading to homoclinic instability. The requirement for the framework's presence of simply one valid and two intricate corresponding components has been quantitatively deduced (4.6).

Figure 3.

Phase illustrations of the commensurate FO FH-R system (3.8) in the homoclinic chaos slow-fasts via predetermined centered factors and the most prevalent value are taken into consideration for (a) ℑ = 0.13, (b) ℑ = 0.21, (c) ℑ = 0.36, (d) ℑ = 0.395, (e) ℑ = 1.15, (f) ℑ = 2.13, (g) ℑ = 3.13, (h) ℑ = 3.157 for FO χ = 0.7.

The framework's (3.9) equilibrium boundaries are determined as ${\mathbf{u}}_2^{⁎}=({\mathbf{u}}_1^{⁎}+{\varsigma }_1)/{\varsigma }_2,{\mathbf{u}}_3^{⁎}=({\varsigma }_3-{\mathbf{u}}_1^{⁎})/{\varsigma }_4$ and ${{\mathbf{u}}_1^{⁎}}^3-3{\mathbf{u}}_1^{⁎}\nu =m$, where $\nu =\frac{{\varsigma }_2{\varsigma }_4-{\varsigma }_4-{\varsigma }_2}{{\varsigma }_2{\varsigma }_4}$ and $m=\frac{3\Im {\varsigma }_2{\varsigma }_4-3{\varsigma }_1{\varsigma }_4+3{\varsigma }_3{\varsigma }_2}{{\varsigma }_2{\varsigma }_4}$, respectively. The structure of (3.9) is capable of an optimal number of three equilibria of balance determined by the form of the exponent of the cubic formula: ${{\mathbf{u}}_1^{⁎}}^3-3{\mathbf{u}}_1^{⁎}\nu -m=0$. The aforementioned cubic polynomial's characteristic is provided by $-(4{\left(\frac{{\varsigma }_1}{{\varsigma }_2}\right)}^3+27{(3{\varsigma }_3+\frac{3{\varsigma }_1}{{\varsigma }_2}-3\Im )}^2)<0$ for ${\varsigma }_2>0$ and ${\varsigma }_4=1$, it demonstrates that a single, real-neutral situation prevails. After addressing the cubic formula aforesaid, we get ${\mathbf{u}}_1^{⁎}=\frac{3\sqrt{8}}{\mathcal{A}}-\frac{\mathcal{A}}{3\sqrt{8}}$, where $\mathcal{A}={(81{\varsigma }_1{\varsigma }_2^2-81{\varsigma }_2^3{\varsigma }_3-81{\varsigma }_2^3\Im +{({(81{\varsigma }_1{\varsigma }_2^2-81{\varsigma }_2^3{\varsigma }_3-81{\varsigma }_2^3\Im )}^2+2916{\varsigma }_2^3)}^{1/2})}^{1/3}$. Currently, we may acquire the variational matrix $\mathbb{J}$ produced by linearizing the framework (3.8) adjacent to its particular neutral position $({\mathbf{u}}_1^{⁎},{\mathbf{u}}_2^{⁎},{\mathbf{u}}_3^{⁎})$ as

$$\mathbb{J}({\mathbf{u}}_1^{⁎})=\left(\begin{array}{ccc}\hfill 1-{{\mathbf{u}}_1^{⁎}}^2\hfill & \hfill -1\hfill & \hfill 1\hfill \\ \hfill \rho \hfill & \hfill -\rho {\varsigma }_2\hfill & \hfill 0\hfill \\ \hfill -{\rho }^2\hfill & \hfill 0\hfill & \hfill -{\rho }^2\hfill \end{array}\right).$$ (4.7)

The matrix that represents $\mathbb{J}$'s characteristic polynomial is supplied by $P_1({\zeta }_1)={\zeta }_1^3-(1-{{\mathbf{u}}_1^{⁎}}^2-\rho {\varsigma }_2-{\rho }^2){\zeta }_1^2+(\rho -\rho {\varsigma }_2+{\varsigma }_2{\rho }^2+{\varsigma }_2\rho {{\mathbf{u}}_1^{⁎}}^2+{\rho }^2{{\mathbf{u}}_1^{⁎}}^2){\zeta }_1+({\rho }^3+{\varsigma }_2{\rho }^3{{\mathbf{u}}_1^{⁎}}^2)$.

The determinant of $\mathbb{J}$ can be derived simply as $det(\mathbb{J})=-{\rho }^3(1+{\varsigma }_2{{\mathbf{u}}_1^{⁎}}^2)<0$ signifying that at least one of the roots of $P_1({\zeta }_1)$ remains non-positive. The discriminant of the aforesaid system is as follows:

$$\mathcal{D}=\{\begin{array}{c}{({\varsigma }_2{\rho }^3-{\varsigma }_2\rho +{\varsigma }_2\rho {{\mathbf{u}}_1^{⁎}}^2+\rho +{\rho }^2{{\mathbf{u}}_1^{⁎}}^2)}^2{({\varsigma }_2\rho +{\rho }^2+{{\mathbf{u}}_1^{⁎}}^2-1)}^2\hfill \\ -4({\varsigma }_2{\rho }^3{{\mathbf{u}}_1^{⁎}}^2+{\rho }^3){({\varsigma }_2\rho +{\rho }^2+{{\mathbf{u}}_1^{⁎}}^2-1)}^3\hfill \\ +18({\varsigma }_2{\rho }^3-{\varsigma }_2\rho +{\varsigma }_2\rho {{\mathbf{u}}_1^{⁎}}^2+\rho +\rho {{\mathbf{u}}_1^{⁎}}^2)({\varsigma }_2{\rho }^3{{\mathbf{u}}_1^{⁎}}^2+{\rho }^3)({\varsigma }_2\rho +{\rho }^2+{{\mathbf{u}}_1^{⁎}}^2-1)\hfill \\ -{({\varsigma }_2{\rho }^3-{\varsigma }_2\rho +{\varsigma }_2\rho {{\mathbf{u}}_1^{⁎}}^2+\rho +{\rho }^2{{\mathbf{u}}_1^{⁎}}^2)}^3-27{({\rho }^3+{\varsigma }_2{\rho }^3{{\mathbf{u}}_1^{⁎}}^2)}^2.\hfill \end{array}$$ (4.8)

Assuming the eigenvalues of $\mathbb{J}$, assessed from the identical stability in this case, are ${\lambda }_1=\phi$ and ${\lambda }_{2,3}={{\zeta }_1}_1\pm \mathbf{i}{{\zeta }_1}_2$, whereby $\phi {{\zeta }_1}_1<0$ and ${{\zeta }_1}_2\ne 0$, then the state of equilibrium of the 3D structure (3.9) is referred to as an exponential saddle concentration. Thus, two corresponding imaginary eigenvalues, as well as the requirements from Lemma 2.1, must be confirmed. As a result, criterion $|\lambda |<{(2\cos (\frac{|\arg (\lambda )|-\pi }{1.3}\left)\right)}^{\chi }$ has been satisfied by (3.8) and (4.5). Also, $|\arg (\lambda )|>\frac{\chi \pi }{2}$ holds. As a consequence, we have ${(2\cos (\frac{|\arg ({\lambda }_1)|-\pi }{1.3}\left)\right)}^{0.7}=1.37001287$ and ${(2\cos (\frac{|\arg ({\lambda }_{2,3})|-\pi }{1.3}\left)\right)}^{0.7}=1.3906780$. Therefore, the condition of Lemma 2.1 is satisfied. As a result, the criterion $|\arg (\lambda )|>\frac{\chi \pi }{2}$ is fulfilled, and the value $|\arg ({\lambda }_{1,2,3})|<1.1$ is clearly noticeable. Considering a 3D continuous unsupervised nonlinear process with saddle concentration steady state for DFO χ, there is a Shilnikov-type homoclinic chaos [73]. If we take the technique's eigenvalues to be ${\lambda }_1=\phi$ and ${\lambda }_{2,3}={{\zeta }_1}_1+\mathbf{i}{{\zeta }_1}_{2,3}$, therefore the scenarios of $\phi <0$ as well as ${{\zeta }_1}_1>0$ or $\phi >0$ and ${{\zeta }_1}_1<0$ using $|\phi |>|{\zeta }_1|$ are those under which the Shilnikov chaos occurs (see Fig. 3 (e-h)), whereby paths that lie in the 2D eigenspace having $\phi <0$ as well as ${\zeta }_1>0$ pass through the saddle concentration stability in an inverted way following the steady eigenvector. We subsequently construct the saddle measure as ${\mathbf{u}}_1=|{{\zeta }_1}_1/\phi |$ and the overall saddle parameters as ${\phi }_1=\phi +{{\zeta }_1}_1$. When ${\phi }_1<0$ or ${\mathbf{u}}_1<1$, the processes of the structure (3.8) towards the saddle concentration are straightforward, and when ${\phi }_1>0or{\mathbf{u}}_1>1$, they are multifaceted [67]. While discussing the sequencing of M-M-Os and M-M-B-Os involving the changeover path to homoclinic instability and corresponding explosions in the sluggish and quicker biophysical framework, we concentrate the observations on the simplified criterion $|\phi |>|{{\zeta }_1}_1|$ regarding the appearance of Shilnikov chaos. According to the modeling findings [62], [63], the component settings having variable ℑ are regarded as ${\varsigma }_1=0.7,\rho =0.08,{\varsigma }_2=0.8,{\varsigma }_3=-0.775$ and ${\varsigma }_4=1$. Initially, we examine the steady states prior to the bifurcations to investigate the behavior of the framework. Using the method described in Theorem 2.1, mathematical computations of the DFO processes are carried out over extended time spans $\xi =10000$, while maintaining time steps of $\mathrm{\Delta }\xi =0.05$ or less. Important distinctions are not evident in the modeling outcomes obtained using a reduced time step. Employing the MatCont software programmer, the bifurcated graph illustrating the dynamics algorithm's stationary points is calculated [74].

Meanwhile, the framework for commensurate FO (3.9) phase illustrations investigation is demonstrated using the implanted voltage stimuli $\Im =0.375$ as the main component (see Fig. 4 (a-i)) for various FOs. Given ℑ, the mechanism possesses a real fixed point that falls within a predetermined region. For $\chi \in (0.65,1]$ steady and unsteady equilibria subdivisions are shown, respectively, in Fig. 2 (d-i). For $\chi =0.75$, there is simply a single steady state subdivision in the framework (a steady concentration node) under smaller electric stimulation values (ℑ < 0.13556). The structure demonstrates barely noticeable fluctuations when $\Im =0.13556$, wherein an insignificantly steady limiting process begins and a supercritical Hopf bifurcation (SHB) occurs with DFO $\chi =0.07,0.15,0.21,0.35,0.36,0.55,0.67,0.83,0.87,0.90.0.95,1$ (see Fig. 5 (a-j)). Considering $0.13556<\Im <3.26674$, the stable state abruptly disappears and an irregular restriction process attractor occurs in an alternating concentration phase. The architecture features an unchanging network for ℑ > 3.99945 with an additional robust concentration network with greater current stimulation $(3.26674<\Im <3.99945)$. For $\chi =0.9$, recurrent transitioning within the steady and unsustainable limitation cycles can be identified in the framework, which is a fascinating characteristic (see Fig. 5 (k)). Moreover, the framework (3.9) exhibits an additional SHB when $\Im =3.26674$, and an unsteady equilibrium point exhibiting robust limitation processes arises in Fig. 5 (l). A neuron, having been in a stable state, is triggered within the parabolic concentration domain and exhibits various forms of temporal and unpredictable repetitive behavior. It displays different kinds of M-M-Os and M-M-B-Os. Initially, followed by restorative surges. It is noteworthy to observe that as we boost the intensity of ℑ more thoroughly for $\chi =0.95$, the framework subsequently settles towards a passive condition within the SHB threshold and displays an entirely distinct M-M-Os configuration. Fig. 2 (a-i) displays the most extreme and least fluctuations of ${\mathbf{u}}_1$ via reference to ℑ. The equilibrium situation evolves within an unsteady region at $\Im =0.13342$, where commensurate FO (3.9) exhibits various instabilities. The structure's insignificant and enormously intensified fluctuations for $\chi =0.90$ (see Fig. 5 (j)), having different frequencies and resonances, are indicated by the dark zone containing subdivisions about ${\mathbf{u}}_1=\pm 1$. An intriguing observation has been made: the denseness of the zone adjacent to ${\mathbf{u}}_1=-1$ reduces while we progressively raise the level of ℑ when reducing the commensurate FO $\chi =0.95$. Fig. 4 (a-h) and Fig. 5 (m-p) demonstrates the chaotic domains exhibiting the MLEs. When χ approaches zero, the commensurate FH-R system (3.9) featuring FO demonstrates predictable behavior that transitions to chaos as χ increases gradually. As a result, this demonstrates that the result is a modification to activation sequences and a reduction in the aggregate amount of small amplitude oscillations in the framework (see Fig. 2 (a-f)). A comparable occurrence is noted for ${\mathbf{u}}_1=1$, but thanks to a declining ℑ level (see Fig. 2 (g-l)). Employing dispersed panels in the bifurcation diagram, Fig. 3 (a-f) illustrates the chaotic zone. Furthermore, Fig. 4 (a-l) describe phase illustrations of the commensurate FO FH-R system (3.8) via predetermined centered factors and the most prevalent value are taken into consideration for various FOs $\chi =0.07,\chi =0.15,\chi =0.21,\chi =0.35,\chi =0.36,\chi =0.55,\chi =0.67,\chi =0.83,\chi =0.87,\chi =0.90,\chi =0.95$ and $\chi =1$. As can be demonstrated by examining the MLEs in Fig. 5 (m-p)), the framework transforms into an area of stabilization whenever the χ rises. Figure 2, Figure 3, Figure 4, Figure 5 highlight an intriguing evaluation: the framework reveals an alteration in behavior from a steady helical phase plane to the development of complete loops when the χ is approaching 1.

Figure 4.

Phase illustrations of the commensurate FO FH-R system (3.8) via predetermined centered factors and the most prevalent value are taken into consideration for various FOs (a)χ = 0.07, (b)χ = 0.15, (c)χ = 0.21, (d)χ = 0.35, (e)χ = 0.36, (f)χ = 0.55, (g)χ = 0.67, (h)χ = 0.83, (i)χ = 0.87, (j)χ = 0.90, (k)χ = 0.95 and (l)χ = 1.

Figure 5.

Bifurcation illustrations of the commensurate FO FH-R system (3.8) via predetermined centered factors and the most prevalent value are taken into consideration for various FOs (a-I)χ:χ = 0.07, 0.15, 0.21, 0.35, 0.36, 0.55, 0.67, 0.83, 0.87, 0.90, 0.95 and 1 and ℑ ∈ [0.09356,0.55618]. Lyapunov spectra evolution for the subsequent system parameters: (m) time-dependent MLE for ℑ = 0.13 and χ = 0.67, (n) MLE for ℑ = 0.38 and χ = 0.95, (o-p) MLEs as an expression of ℑ in the domains ℑ = [2.0013,4] and ℑ = [0.45231,5.2001] for χ = 0.99, respectively.

4.2. Incommensurate fractional order

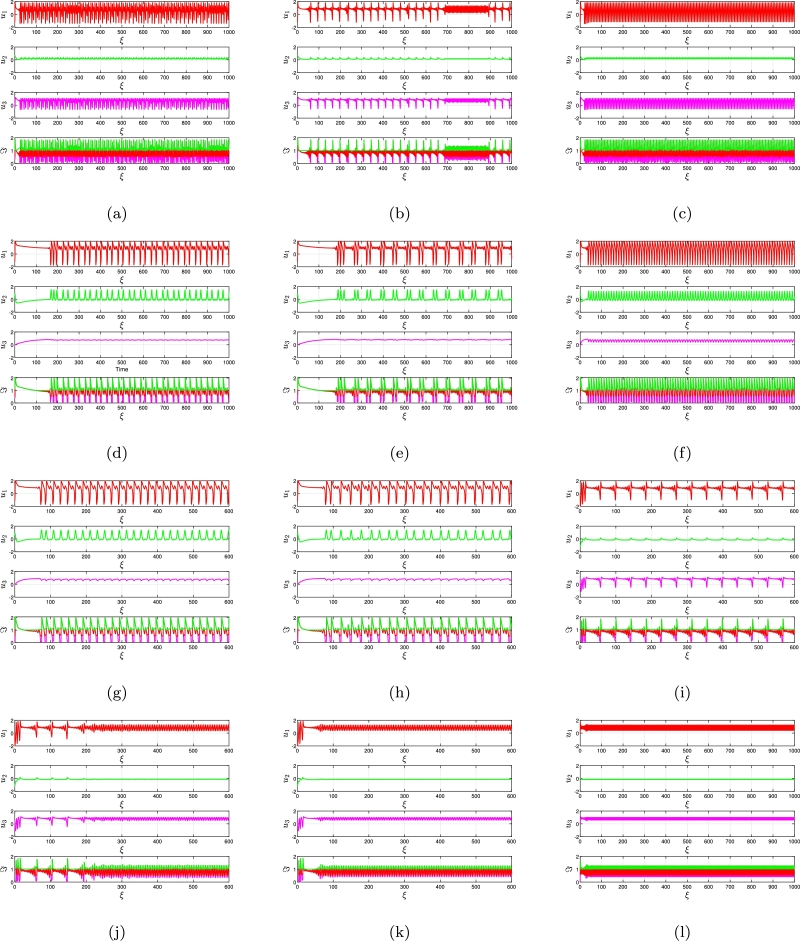
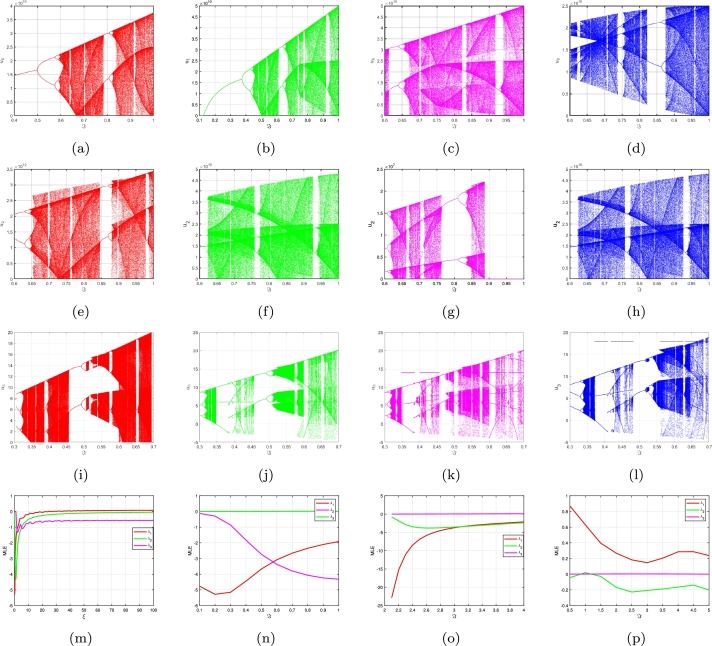
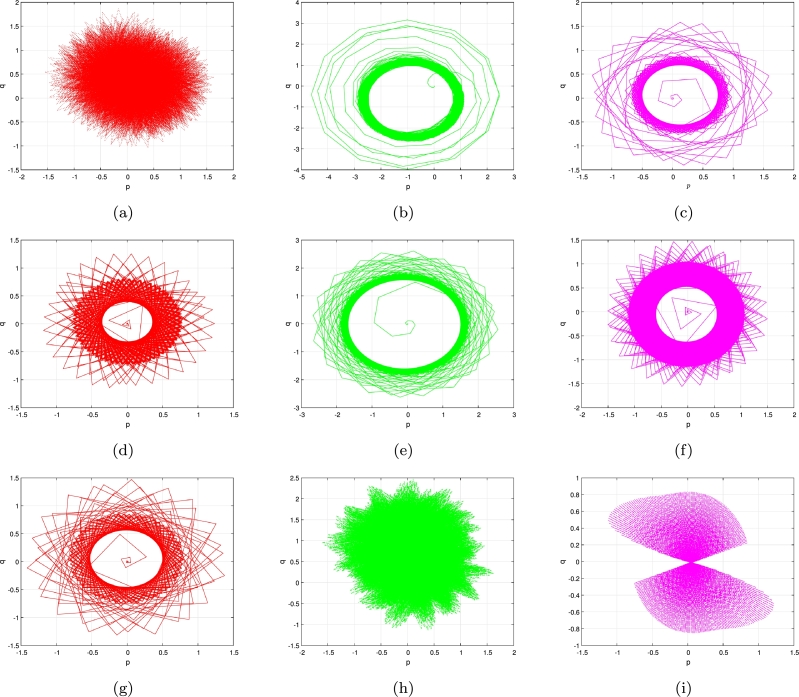
The objective of this portion is to explore the blasting characteristics displayed by the incommensurate FO FH-R model (3.11) architecture and the equilibria's transitioning behavior. To grasp the functioning of the framework comprehensively, the simulation is performed in several consecutive situations, each featuring unique factor selections. A vital point of contention is the type of equilibrium transition that can be detected in the current state parameters. Regarding all of the primary situations, the research additionally contrasts the impact of exterior influences. The article that follows is a comprehensive examination regarding the activation modifications through the inactive phase through the restriction process domain. The reported M-M-Os and M-M-MB-Os are formed up of spiked edges, or a ℘ quantity of small amplitude oscillations, and a ℓ quantity of large amplitude oscillations for ${\chi }_1=0.5$. The framework shows M-M-Os returning to the inactive phase ($\Im =0.15$; see Fig. 6(a-c)) with an estimated $\Im =0.25$. It consists of a limited quantity of slowly oscillating waves containing an individual large-amplitude oscillation surge and varying intensities. This study includes a 0.001 increment size variation from 0 to 1 for the orders ${\chi }_1$ (as shown in Fig. 6(a-c)), ${\chi }_2$ (as shown in Fig. 6(d-f)) and ${\chi }_3$ (as shown in Fig. 6(g-i)), respectively. As demonstrated in Fig. 7a, it has a structure of ${\ell }^{\wp }{\ell }^{\wp }{\ell }^{\wp }...=1^{{\varrho }_1}{1}^{{\varrho }_1}{1}^{{\varrho }_1}...,$ where $m={\varrho }_1$ is a real bounded integers. When $\Im =0.255$, an analogous class of M-M-Os is additionally detected (see Fig. 6(j-l)). The overall amount of small amplitude oscillations reduces while we elevate ℑ and ℘ the periodicity of the explosions varies according to various choices of ℘ and ℓ. With the exception of an extremely restricted domain ${\chi }_{\iota }\in [0.05,0.80],(\iota =1,2,3)$, where paths demonstrate chaotic behavior, Fig. 7(a) clearly shows that the condition of the incommensurate FH-R model (3.11) displays chaotic behavior throughout a wide range of ${\chi }_1$. This is demonstrated due to the existence of non-negative MLEs (see Fig. 9 (m)). A while analysis ($\xi =10000$) shows, for instance, that the pattern of M-M-Os, at $\Im =0.20$, resembles $1^{10}{1}^{10}....$ Other configurations are similarly feasible, including various amounts of small intensity oscillations and modifications in the intensity of small cycles (see Fig. 8 (a-d)). The incommensurate FO FH-R (3.11) has a nonlinear Hopf bifurcation with $\Im =0.13465$. Within the splitting point of view, a canard detonation is induce, while the mechanism approaches its explosive domain when ${\chi }_2$ is altered (see Fig. 9 (a-d)). A canard bursting is detected quantitatively at $\Im =0.15677$, wherein an enormous intensity unwinding process emerges involving an internal modification beyond cycles exhibiting small intensities.

Figure 6.

Time-dependent plots of the incommensurate FO FH-R model (3.11) for (a) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.15, (b) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.25, (c) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.35, (d) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.13465, (e) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.15676, (f) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.201, (g) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.13465, (h) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.15676, (i) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.201, (j) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.255, (k) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.3523, (l) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.3765.

Figure 7.

Phase profiles of the incommensurate FO FH-R model (3.11) for (a) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.15, (b) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.25, (c) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.35, (d) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.13465, (e) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.15676, (f) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.201, (g) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.13465, (h) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.15676.

Figure 9.

Bifurcation plots of the incommensurate FO FH-R model (3.11) for (a) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.15, (b) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.25, (c) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.35, (d) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.13465, (e) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.15676, (f) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.201, (g) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.13465, (h) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.15676, (i) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.201, (j) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.255, (k) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.3523, (l) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.3765. Also, MLEs depictions for (m) (χ₁,χ₂,χ₃)=(0.5,0.67,0.66) and ξ = 0.25 (n) (χ₁,χ₂,χ₃)=(0.5,0.67,0.95) and ℑ = 0.567, (o) (χ₁,χ₂,χ₃)=(0.5,0.67,0.97) and ℑ = [2.14,4.16], (p) (χ₁,χ₂,χ₃)=(0.5,0.67,0.97) and ℑ = [0.45,5.15].

Figure 8.

Poincaré plots of the incommensurate FO FH-R model (3.11) for (a) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.15, (b) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.25, (c) (χ₁,χ₂,χ₃)=(0.5,0.67,1) and ℑ = 0.35, (d) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.13465, (e) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.15676, (f) (χ₁,χ₂,χ₃)=(1,1,0.7) and ℑ = 0.201, (g) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.13465, (h) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.15676, (i) (χ₁,χ₂,χ₃)=(0.3,0.45,0.95) and ℑ = 0.201, (j) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.255, (k) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.3523, (l) (χ₁,χ₂,χ₃)=(0.8,0.75,0.05) and ℑ = 0.3765.

Additionally, the mechanism exhibits certain intriguing fluctuations, such as M-M-B-Os, which are symmetrical or irregular responses formed up of two distinct stages (see Fig. 8 (e-h)). Alternately, explosions or numerous substantial surges within the greatest intensity oscillations emerge in conjunction with small-intensity disturbances. The patterns of small intensity disturbances reveal in excess of a particular number of small intensity disturbances (varying from a single to indefinitely countless). We employ the foldable cluster static approach to the slow-fast network to examine the quantity of small intensity disturbances within the M-M-Os, which could be influenced by the dominating component ℑ. The disregularized configuration (3.11) at $\Im =0.201$ contains the following eigenvalues at the neutral aspects: (${\mathbf{u}}_1^{⁎}=-1,{\mathbf{u}}_3^{⁎}=0.11772$) and (${\mathbf{u}}_1^{⁎}=1,{\mathbf{u}}_3^{⁎}=1.37891$), respectively. It contains eigenvalues $(-0.9844556,-0.0265734)$ and $(-0.50000+\mathbf{i}0.37768,-0.50000+\mathbf{i}0.45678)$, as ${\chi }_2$ reduces and tends to 0, or when it boosts to 1, the states of the incommensurate fractional order FH-R (3.11) exhibits chaotic attractors (see Fig. 7 (b-d)), where the MLEs predict their greater value (see Fig. 9 (n). Also, it is simple to determine whether the subsequent amplitude is a foldable concentration, whereas the initial represents a foldable component. Throughout the other part of this range, the paths are perfectly consistent, in particular for ${\chi }_2\in [0.25,0.57]$. The resulting behavior highlights the framework's responsiveness to extremely small variations in the incommensurate FO ${\chi }_2$. Regarding the foldable network [36], using $\mathrm{\aleph }=|{\eta }_{\varpi }|/|{\eta }_{\wp }|=0.02453<1$ and ${\mathrm{\aleph }}^{-1}=70.0001\notin \mathbb{N}$. In addition, ${\mathrm{\aleph }}^{-1}=70.0001$ indicates that there is a 70.0001-fold difference in the strength of the insufficient eigenvector within the dominant one. At this point, the principal canards (${\delta }_{\wp }$ and ${\delta }_{\varpi }$, respectively) are the weakest and strongest canards that disrupt the highest possible canard. Additionally, we get ${\varrho }_2=32$, which satisfies the variant $2{\varrho }_2+3<\frac{1}{\mathrm{\aleph }}<2{\varrho }_2+1$ and ${\mathrm{\aleph }}^{-1}\ne 2{\varrho }_2+2$.

Furthermore, there are also an additional 32 extreme canards, referred to simply as supplementary canards, to be added to the existing fundamental canards ${\delta }_{\wp ,\varpi }$. As a result, 34 insignificant strength disturbances maxima are observable close to the collapsed terminal. Based on the numerical modeling, we determine 10 brief intensity disturbances, that correspond effectively with our analysis conclusions (see Fig. 6 (a-l)). When ρ is adequately appropriate, the estimation of the accurate assortment of resonances with small amplitudes is accurate. If $\mathrm{\aleph }\gg \sqrt{\rho }$ entails, the precise M-M-Os layout can be considered anticipated [59]. We determine that there definitely are no ultimate canards regarding foldable concentration, according to [66]. The total variety of small intensity oscillations in the M-M-Os decreases while exterior stimulation increases progressively. We discovered M-M-Os of category $1^6{1}^6...$ at $\Im =0.25$ and we notice an intriguing behavior while we change the dominating factor via $\Im =0.25$ to $\Im =0.322$. The algorithm is currently displaying M-M-Os with the pattern $1^4{1}^5{1}^4{1}^5...$ (see Fig. 6 (d-f)). Subsequently, assuming $\Im =0.34,0.35,0.36$ and 0.375, respectively, the order of operations shifts to $1^3{1}^4{1}^3{1}^4...,1^3{1}^3...,1^2{1}^3{1}^2{1}^3...,$ and $1^1{1}^2{1}^1{1}^2...$ (see Fig. 6 (g-i)). These graphs clearly show diverse characteristics, which suggest that the configurations of the incommensurate FO FH-R model (3.11) are greatly affected by an alteration in FOs $({\chi }_1,{\chi }_2,{\chi }_3)$ (see Fig. 7 (e-f)). For example, the structure's phases fluctuate between regular and chaotic behavior, exhibiting regular twofold bifurcation whenever the value of ℑ extends whenever $({\chi }_1,{\chi }_2,{\chi }_3)=(0.5,1,1)$ (see Fig. 8 (e-h)). The periodicity structure transforms once more to $1^1{1}^2{1}^1{1}^2...$ at $1^1{1}^1...$ at $\Im =0.31$ before transforming to $1^1{1}^1{1}^1...$ at $\Im =0.38$ (see Fig. 9 (e-h)). Here are two separate cycle stages, which include first, which is characterized by an immense supply of small intensity oscillations, immediately following a dual, or two enormous spiking in an identical explosion. This configuration duplicates itself for an extensive interval ($\xi =10000$) until $\xi =0.46$. According to Fig. 7 (g-h), the pattern is $2^1{2}^1....,$ wherein $\ell =2$ and $\wp =1$, respectively. Following that, when we boost $\Im =0.45$, the total assortment of large-intensity oscillations ℓ rises. The cycle generated alternately after $2^1{3}^1{2}^1{3}^1...$ having $\ell =2,3$ and $\wp =1$ Fig. 9 (i-l). The aggregate number component ℓ rises once more, while at $\Im =0.40$ (Fig. 6 (a-l)), we see M-M-B-Os containing characteristic $3^1{3}^1...$ in a comparable fashion. For each of the aforementioned scenarios, small intensity oscillations can be seen circling the foldable, demonstrating ${\mathbf{u}}_1^{⁎}=-1$, as shown by the critically important exponential as well as the framework's period series Fig. 8 (i-l).

Considering an unaltered threshold process, the activation crossover occurs in the mechanism at $\Im =0.4$, or resonant surging for $({\chi }_1,{\chi }_2,{\chi }_3)=(1,0.6,1)$ in Fig. 9 (a-l). During the halfway point periods, the periodic spiked behavior shifts to swift elevating pattern, which subsequently transforms across M-M-Os of an entirely distinct nature. It examines patterns that include a single large intensity oscillation containing several small oscillations (like $1^1{1}^2{1}^1{1}^2...$); when we boost a threshold of ℑ > 3.5, the pattern approaches $1^7{1}^7...$ at $\Im =3.5$ (Fig. 6 (a-b)). When $({\chi }_1,{\chi }_2,{\chi }_3)=(0.5,0.7,1)$, a transition trajectory is apparent, with overall pathways continuing consistent with relatively small amounts of ℑ and turning chaotic for significant amounts of $\Im \in [2.6,3]$ (see Fig. 7 (a-h)). The foldable cluster for ${\mathbf{u}}_1^{⁎}=1,{\mathbf{u}}_3^{⁎}=-1.74301$ as well as the foldable concentration for ${\mathbf{u}}_1^{⁎}=-1,{\mathbf{u}}_3^{⁎}=-2.90086$ have now appeared in the desingularized diminished framework (3.11). As seen in Fig. 6 (i-l), the small amplitude oscillations are formed within the foldable component, ${\mathbf{u}}_1^{⁎}=1$.

In view of (3.11), we determine $\mathrm{\aleph }=|{\eta }_{\varpi }/{\eta }_{\wp }|=0.026734<1$ and ${\mathrm{\aleph }}^{-1}=60.0034\notin \mathbb{N}$. In this instance, the predominant eigenvector outweighs the less powerful eigenvector by a factor of 60.0034. When ${\varrho }_2=27$, that is, when there are certainly a maximum of 27 supplementary canards added to the fundamental canards, the inequality is in acceptable harmony. As a result, there are 29 small-intensity oscillations surrounding the folding position. According to Fig. 6 (d-f), the mechanism is effectively simply seven small-intensity oscillations, which is within the prediction's range. After that, as ℑ increases even more, it enters the inactive domain. While we modify the intake potential stimulation, ℑ, we display the changes in the striking layouts for both separate settings corresponding to the temporal duration factor, ρ. In addition, Fig. 9 (a-l) displays the bifurcation diagram and the MLE that correlate to it when the values of ${\chi }_3$ are changed throughout the interval of 0 and 1. At this point, ${\chi }_1={\chi }_2=1$ is maintained to preserve the incommensurate ordering. The bifurcation visualization illustrates the fact that M-M-O processes are present within the transition from cyclic to chaotic regimes (see Fig. 7 (a-h)). By providing various repetitive transitions to Farey patterns, the M-M-Os are observable. We see the M-M-O crossover stages utilizing the Farey algorithm. When we change the prevalent factor ℑ, the incommensurate FO FH-R algorithm (3.11) displays a distinct series of recurring M-M-Os in addition to core and supplementary M-M-Os. This particular pattern for recurrent M-M-Os is designated as the Farey pattern [66], meaning whenever the regulating factor progressively approaches homoclinity, it resembles $1^0\mapsto {\infty }^1\mapsto {\Im }^1\mapsto 1^m\mapsto 1^{\infty }$. While ${\infty }^1$ represents an extended dominant spiked or repetitive resonances using a crossover from a moderate intensity cycle occurring the first time in the entire operational domain, 1⁰ signifies the big intensity restriction periods in the temporal region regarding dominant firing (see Fig. 6 (g-i)). After then, it moves to M-M-B-Os and M-M-Os that have distinct values of ℓ and ℘, either periodic or sporadic. One significant intensity fluctuation accompanied by a countably plenty of inconsistent lower intensity fluctuations constitutes homoclinic chaos authentication, or $1^{\infty }$ (see Fig. 7 (a-d)). The Farey pattern shown in this instance is $1^{{\varrho }_1}\mapsto ...1^{10}...\mapsto ...1^6...\mapsto ...1^4{1}^5...\mapsto 1^3{1}^4\mapsto ...1^0\mapsto ...1^7$ (see Fig. 7 (e-f)).

Next, we investigate the homoclinic chaos in the architecture (3.11) and attempt to identify the structure's tumultuous frames for ${\chi }_3$ within the interval of $(0,1)$. Considering an unchanged threshold of ${\varsigma }_3=-0.775$, the homoclinic chaos criterion is valid for $\Im \in [0.14,0.16]$ and $[3.21,3.26]$ (see Fig. 7 (g-h)). The distinctive realistic steady state is identified at $\Im =0.25$ and can be expressed as $({\mathbf{u}}_1^{⁎}=-0.97241,{\mathbf{u}}_3^{⁎}=-0.33659,{\mathbf{u}}_2^{⁎}=0.192345)$. Absolute values of the eigenvalues are $|(-0.0109013,0.00720096\pm \mathbf{i}0.285853)|$ and ${(2\cos (\frac{|\arg ({\lambda }_{1,2})-\pi |}{2-{\chi }_{\iota }}\left)\right)}^{{\chi }_{\iota }}=1.426783,\iota =1,2,3$. In other words, $\phi =-0.0110345<0,{\zeta }_1=0.009867>0$ and $|\phi /{\zeta }_1|=1.678901>1$ satisfy the requirements of homoclinic chaos (see Fig. 7 (a-h)). The results show that the saddle amplitude is ${\phi }_1=-0.00456099$ and the saddle factor is ${\mathbf{u}}_1=0.780032$. Regarding this case, we conclude ${\phi }_1<1$ and ${\mathbf{u}}_1<1$, indicating straightforward processes concerning the saddle concentration of the framework (3.11). Fig. 8 (a-l)) displays the phase images and accompanying data trends that represent the FH-R framework for various ℑ conditions in the homoclinic chaos domain ${\chi }_3\in [0.563,0.714)\cup (0.8341,0.9812]$. In each phase of perspective, we see the spiraling dynamics surrounding the saddle concentration for ${\chi }_2\in (0,1]$. In order to demonstrate the fractional chaotic dynamics of the framework (3.11), we additionally examine the MLEs over an expression of duration and the prevailing factor ℑ (see Fig. 9 (o-p)). Then, we depict the continuum assuming $\Im =0.25$ while taking into account the MLEs being an extension of delay. The Lyapunov factors that we discovered are $(0.000089,-0.000065,-0.067534)$. The structure is chaotic, as shown by the elevated fundamental Lyapunov factor in Fig. 9 (n). The spectra of MLEs within the range $\Im =[2.14,4.16]$ are shown in Fig. 9 (o-p), where it becomes apparent whether the primary MLE is non-negative within this region for $({\chi }_1,{\chi }_2,{\chi }_3)$. As can be shown in Figs. 6 (a-l), the framework (3.11) demonstrates M-M-Os characterized by one enormous and inevitably numerous asymmetrical small intensity fluctuations $1^{\infty }$ within this phase. Consequently, we see M-M-Os as a pathway leading to homoclinic chaos. The authentic steady state has been determined to be $({\mathbf{u}}_1^{⁎}=0.975612,{\mathbf{u}}_2^{⁎}=2.14523,{\mathbf{u}}_3^{⁎}=-1.800912)$ at $\Im =3.0092$ as well. As in the previous instance, we discovered that $(-0.0236701,0.01780098\pm \mathbf{i}0.3015672)$ being the respective eigenvalues of the fundamental framework, because the homoclinic chaos requirements are encountered, such as $\phi =-0.0236701<0,{\zeta }_1=0.01780098>0$ and $|\phi /{\zeta }_1|=1.2301>1$. At this point, the characteristics of the framework are straightforward adjacent to the saddle concentration, with ${\phi }_1<0$ and ${\mathbf{u}}_1<1$. Plotting the MLE continuum with regards to ℑ, where $\Im \in [0.45,5.15]$, we determined that the initial MLE is non-negative within this time period, suggesting that chaos is present in the framework (3.11) throughout this time frame (see Fig. 9 (p)).

5. Statistical tests for the DFO FH-R model

In this section, we analyze the fluctuating properties of the suggested 3D FH-R model by contemplating its complexities at both commensurate and incommensurate FOs. Higher levels of intricacy in an environment are frequently correlated with higher levels of chaos. In order to do this, we utilize the ${\mathbb{C}}_0$ complexity approach in addition to the sample entropy (Sp-En) approach. Furthermore, we employ the $0-1$ criterion to confirm that chaos exists in the FH-R system.

5.1. The Sp-En procedure

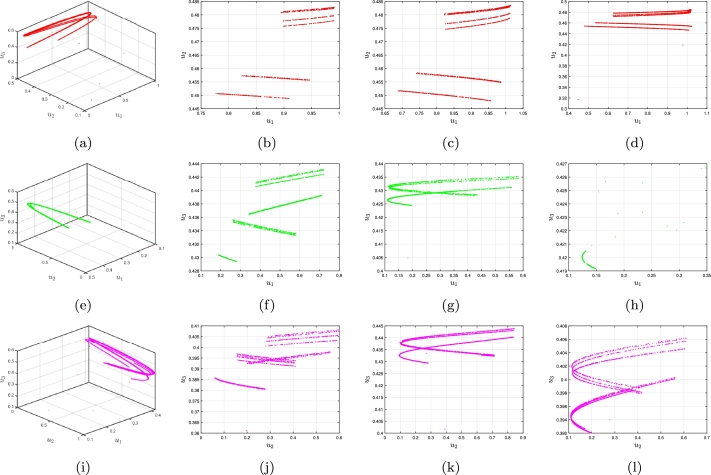
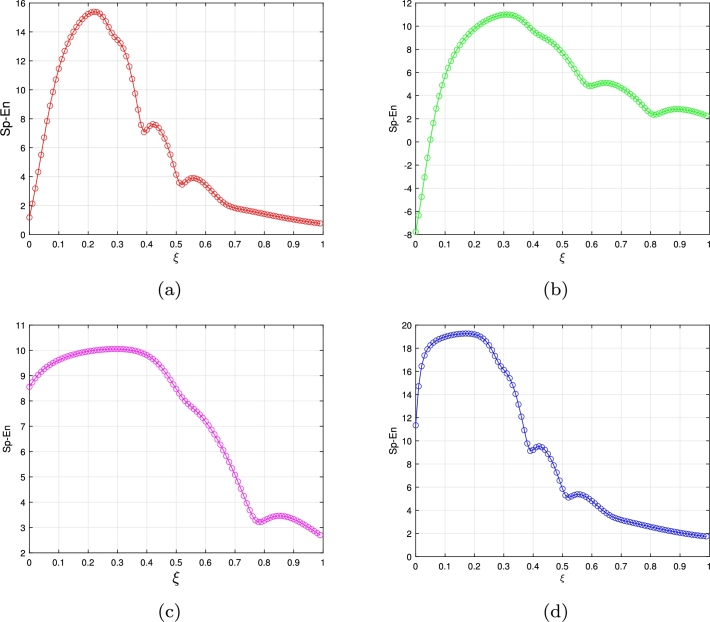
Here, we adopt the Sp-En technique as a tool to evaluate the intricacy of the 3D DFO FH-R model that is commensurate with (3.9) and its counterpart that is incommensurate with FO (3.11). In contrast to approximate entropy (Ap-En), Sp-En is able to quantify time series variability independent of both the comparison factor (φ) and its embedded level (ℓ). As a result, Sp-En supplies an increasingly scientific and accurate assessment than Ap-En [75]. The amount of the time sequence's difficulty is indicated by the Sp-En numbers, where larger numbers denote greater complexity [76]. The following procedure is used to calculate Sp-En:

$$SpEn=-\log \frac{{Ϝ}^{\eta +1}(\tau )}{{Ϝ}^{\eta }(\tau )},$$ (5.1)

where the mathematical formula for ${Ϝ}^{\eta }(\tau )$ is

$${Ϝ}^{\eta }(\tau )=\frac{1}{\ell -\eta +1}\sum _{\wp =1}^{\ell -\eta +1}\log {\mathcal{C}}_{\wp }^{\eta }(\tau )$$ (5.2)

and the acceptable range can be calculated as $\sigma =0.2\sqrt{Var(\mathcal{C})}$, with $Var(\mathcal{C})$ indicating for positive square root of variance. Fig. 10 (a-b) displays the Sp-En values for the commensurate FO FH-R model (3.9) as well as the incommensurate FO FH-R model (3.11) (see Fig. 10 (c-d)). More significant values suggest an increased degree of challenges in the measurement succession, as indicated by the calculated Sp-En outcomes. The findings show that the significantly higher Sp-En levels of the commensurate and incommensurate FO FH-R model (3.11) suggest more elevated sophistication. The produced outcomes additionally reinforce the unpredictable character of the processes in the suggested non-integer network and are consistent with the outcomes of the $MLEs$ study. The suggested incommensurate FO FH-R model (3.11)'s diverse variations are captured by fractional exponents, as seen by their chaotic performance and increased richness.

Figure 10.

Sample entropy plots for the commensurate FO FH-R model (3.9) when (a)χ = 0.9 with ℑ = 0.13465, (b)χ = 0.95 with ℑ = 0.13465. Also, sample entropy plots for the commensurate FO FH-R model (3.11) when (c) (χ₁,χ₂,χ₃)=(0.5,1,1) with ℑ = 0.13465, (d) (χ₁,χ₂,χ₃)=(1,0.6,1) with ℑ = 0.13465.

5.2. The ${\mathbb{C}}_0$ complexity

The ${\mathbb{C}}_0$ complexities procedure is employed to perform a complexity assessment [77], [78] for the purpose of investigating how the FO affects the dynamic features of the commensurate FO FH-R model (3.9) and the incommensurate FO FH-R model (3.11). The ${\mathbb{C}}_0$ intricacy is computed by the inverse Fourier transform.

We propose the ${\mathbb{C}}_0$ productivity approach for an ordered sequence $\{\epsilon (0),...,\epsilon (\mathcal{W}-1)\}$ in the following manner:

• It can be identified by the discrete Fourier transform of the sequence $\{\epsilon (0),...,\epsilon (\mathcal{W}-1)\}$ is:

$${\mathrm{\Xi }}_{\mathcal{U}}(\mathrm{\Theta })=\sum _{\mathbf{u}=0}^{\mathcal{W}-1}\epsilon (\mathbf{u})\exp \left(\frac{-2\pi \mathbf{i}d\mathbf{u}}{\mathcal{W}}\right),\mathrm{\Theta }=0,...,\mathcal{W}-1.$$ (5.3)

• This formula yields the mean square significance:

$${\mathcal{G}}_{\mathcal{W}}=\frac{1}{\mathcal{W}}\sum _{\mathrm{\Theta }=0}^{\mathcal{W}-1}|{\theta }_{\mathcal{W}}(\mathrm{\Theta }){|}^2.$$ (5.4)

• Adjusting:

$${\tilde{\theta }}_{\mathcal{W}}(\mathrm{\Theta })=\{\begin{array}{cc}{\theta }_{\mathcal{W}}(\mathrm{\Theta })\hfill & \text{if}|{\theta }_{\mathcal{W}}(\mathrm{\Theta }){|}^2>\phi {\mathcal{G}}_{\mathcal{W}},\hfill \\ 0\hfill & \text{if}|{\theta }_{\mathcal{W}}(\mathrm{\Theta }){|}^2\le \phi {\mathcal{G}}_{\mathcal{W}}.\hfill \end{array}$$ (5.5)

• The following is the inverse Fourier transform of ${\tilde{\theta }}_{\mathcal{W}}$:

$$\tilde{\epsilon }(\mathrm{\Theta })=\frac{1}{\mathcal{W}}\sum _{\mathbf{u}=0}^{\mathcal{W}-1}\tilde{\theta }(\mathbf{u})\exp \left(\frac{-2\pi \mathbf{i}d\mathbf{u}}{\mathcal{W}}\right),\mathrm{\Theta }=0,...,\mathcal{W}-1.$$ (5.6)

Furthermore, we examine the ${\mathbb{C}}_0$ complexity estimate by:

$${\mathbb{C}}_0=\frac{\sum _{\mathbf{u}=0}^{\mathcal{W}-1}|\epsilon (\mathbf{u})-\tilde{\epsilon }(\mathbf{u}){|}^2}{\sum _{\mathbf{u}=0}^{\mathcal{W}-1}|\epsilon (\mathbf{u}){|}^2}.$$ (5.7)

The ${\mathbb{C}}_0$ complexities of the commensurate FO FH-R model (3.9) and the incommensurate FO FH-R model (3.11) are presented in Fig. 11(a-d) with the following parameterized adjustment. These outcomes illustrate that the DFO FH-R model possesses greater complexity, which is compatible with the previously mentioned findings. This suggests that chaotic attractors could be produced by the DFO FH-R model, featuring commensurate and incommensurate fractional exponents.

Figure 11.

Graphical illustrations ${\mathbb{C}}_0$ complexity for the commensurate FO FH-R model (3.9) when (a)χ = 0.9 with ℑ = 0.13465, (b)χ = 0.95 with ℑ = 0.13465. Also, sample entropy plots for the commensurate FO FH-R model (3.11)(c) (χ₁,χ₂,χ₃)=(0.5,1,1) with ℑ = 0.13465, (d) (χ₁,χ₂,χ₃)=(1,0.6,1) with ℑ = 0.13465.

5.3. The 0-1 approach for chaos

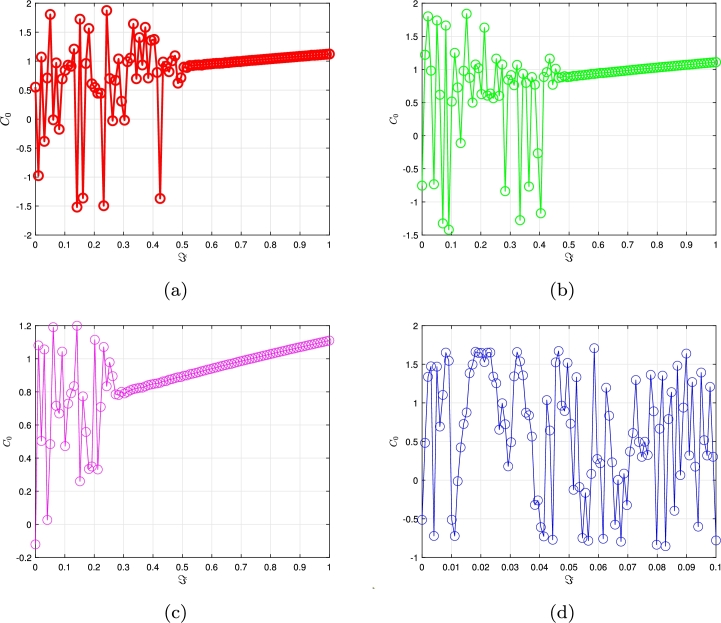
Specifically, we apply the 0-1 examination technique [79] for chaotic to determine if chaos exists in the commensurate fractional order FH-R model (3.9) and the incommensurate FO FH-R model (3.11). Letting $\{ħ(\mathrm{\Theta }),\mathrm{\Theta }=1,2,...,\mathcal{W}\}$ be an assortment of states, and notifying the transformation factors p and q be expressed as follows to illustrate this technique:

$$\mathbf{p}(\mathrm{\Theta })=\sum _{\wp =1}^{\mathrm{\Theta }}ħ(\wp )\cos (\wp \varsigma ),\mathbf{q}(\mathrm{\Theta })=\sum _{\wp =1}^{\mathrm{\Theta }}ħ(\wp )\sin (\wp \varsigma ),$$ (5.8)

where $\mathrm{\Theta }\in \{1,2,...,\mathcal{W}\}$ and $\varsigma \in (0,\pi )$. A helpful instrument for determining whether chaos exists in the suggested DFO FH-R model involves the $\mathbf{p}-\mathbf{q}$ diagram. Significant understanding of the fluctuations of the framework is possible to obtain through inspecting the progressions of the values of the p and q components. Assuming p and q's paths stay confined, it demonstrates that whatever dynamic features of the representation are periodic. On the other hand, assuming these pathways behave according to the Brownian framework, their interactions underlying the visualization are chaotic. At this point, the mean square eviction is determined using a specific algorithm that takes into consideration p and q.

$${\mathcal{U}}_{\varsigma }=\frac{1}{\mathcal{W}}\sum _{\wp =1}^{\mathcal{W}}({(\mathbf{p}(\wp +\mathrm{\Theta })-\mathbf{p}(\wp ))}^2+{(\mathbf{q}(\wp +\mathrm{\Theta })-\mathbf{q}(\wp ))}^2),\mathcal{W}>10\mathrm{\Theta }.$$ (5.9)

The asymptotic rate of expansion is computed in the following way:

$${\mathcal{K}}_{\varsigma }=\underset{\mathrm{\Theta }\mapsto \infty }{\lim }\frac{\log {\mathcal{U}}_{\varsigma }}{\log \mathrm{\Theta }}$$ (5.10)

and $\mathcal{W}=median({\mathcal{K}}_{\varsigma })$.

As a result, the framework behaves chaotically if $\mathcal{W}$ approaches 1, and periodically whenever $\mathcal{W}$ arrives at 0. The $0-1$ evaluation of the commensurate FO FH-R model (3.9) and the incommensurate FO FH-R model (3.11) are depicted in Figs. 12(a-c) and 12 (d-i). The network's periodicity is demonstrated by the restricted patterns that are evident in Figs. 12 (f) and 12 (h). Figs. 12(a) and 12 (i) demonstrate Brownian-like practices, which demonstrate the possibility of chaos and therefore confirm the occurrence of chaotic dynamics over either the commensurate as well as the incommensurate FH-R model. The results of the 0-1 assessment correspond closely to both the ${\mathbb{C}}_0$ complexities, the Sp-En technique and $MLEs$.

Figure 12.

Graphical depictions for (p − q) plots for the commensurate FO FH-R model (3.9) when (a)χ = 0.9 with ℑ = 0.13465, (b)χ = 0.95 with ℑ = 0.15, (c)χ = 0.99 with ℑ = 0.35. Also, (p − q) plots for the commensurate FO FH-R model (3.11) when (d) (χ₁,χ₂,χ₃)=(0.5,1,1) with ℑ = 0.13465, (e) (χ₁,χ₂,χ₃)=(1,0.6,1) with ℑ = 0.13465, (f) (χ₁,χ₂,χ₃)=(0.5,0.5,1) with ℑ = 0.15, (g) (χ₁,χ₂,χ₃)=(1,0.6,0.1) with ℑ = 0.35, (h) (χ₁,χ₂,χ₃)=(0.5,1,1) with ℑ = 0.13465, (i) (χ₁,χ₂,χ₃)=(0.2,0.6,1) with ℑ = 0.377.

6. Conclusion

In this article, we explore the phenomena that occur across numerous time scales within the slow-fast FH-R system, specifically focusing on M-M-Os and M-M-B-Os via discrete fractional calculus. Examining several categories of activation features, we have examined the evolution of the FH-R system using the main bifurcation factor, ℑ with the aid of commensurate and incommensurate FO. Meanwhile, we have demonstrated that Hopf bifurcations and the canard phenomenon are real. The fractional order has a considerable effect on the length and intensity of small and large oscillations in canard-type dynamics. Particularly, fractional differences incorporate memory impacts, resulting in greater complexity of dynamical behavior than integer-order derivatives. Our computational experiments entailed solving the dynamical framework of discrete fractional difference equations and we reveal the parameterized domain of canard phenomena wherein M-M-Os exist. Furthermore, we have employed folded network analysis to support the identification of the optimum amount of small-amplitude oscillations within two successive large-amplitude oscillations. Considering the simplified structure (4.1) and related significant manifolds, each of the steady-state evolution of the simulation has been examined. Remarkably, there are two separate classifications into which we may place the phases of M-M-Os and M-M-B-Os. Two classes exist: one where small-amplitude oscillations are formed close to the position ${\mathbb{k}}^{-}$ and the second where small amplitude oscillations develop close to the spot ${\mathbb{k}}^{+}$ for various FOs (see Figs. 2(a-l) and 6(a-l)), respectively.

Meanwhile, a detailed analysis has been conducted on the boundary between chaotic behavior and M-M-Os. M-M-B-Os are made up of small and large intensity oscillations and contain abrupt explosive fluctuations that include changeovers and crashes. Several spatiotemporal structures, including M-M-Os, inactivity, periodic exploding, etc., emerge at the threshold. In this regard, broad implications enabling multidimensional slow-fast networks accompanying the formation of M-M-Os have been developed; heterogeneity network features can potentially be incorporated for more research. Furthermore, an empirical basis for analyzing the fluctuating features of both functioning and malignant neurons revealed in research findings is provided by this sort of descriptive physiological approach [55]. We have studied in detail the behavioral attributes of this slow-fast dynamics of canard within both commensurate and incommensurate FOs. By utilizing diverse analytical methods such as bifurcations, homoclinical chaos, Poincaré maps, and Lyapunov exponent computations, the unique characteristics of the suggested fractional FH-R model were comprehensively investigated under a range of conditions. In addition, the Sp-En methodology and the ${\mathbb{C}}_0$ complexities approach were implemented to measure the M-M-O's and M-M-B-O's level of complexity, while the $0-1$ experiment has been applied to confirm that chaos exists on the visualization. The computational analyses executed revealed a number of fascinating and varied chaotic behaviors that were revealed by the mechanism's settings, commensurate FO and incommensurate FOs' substantial effect on the physical states of the fractional FH-R model. These factors are crucial in determining how the procedure interacts and how its functioning changes, resulting in various reactions and pathways in the configuration structure of the proposed fractional FH-R model. The understanding of chaos phenomena and nonlinear structures will be greatly enhanced by such results, which have great importance in clarifying the consequences of fractional NNs and memristive systems.

Under the implementation of M-M-Os and fractional formulations, synaptic activation is capable of being decreased to facilitate the removal of the activation prospective threshold to stable phases [56], [68]. Studies in [80], [81] examined the effects of barely noticeable vibrations, or small intensity oscillations, on various neural reactions. The small intensity oscillations have an intriguing function in the development of M-M-Os and in regulating spike aggregation [82], [83]. Additionally, small intensity oscillations affect how sensitive neurons are to changes in neural signals and how synchronized the system is for specific activation frequencies [84]. We addressed a variety of potential scientific hypotheses over the purposes of M-M-Os, which would be significant for scientists studying dynamical phenomena and computational modeling, both of which are important fields for comprehending the periodic actions of neurons. The present investigation of analogous M-M-Os and M-M-B-Os in physiological processes encompasses hypothetical, mathematical and behavioral techniques. In order to explore potential implementations in this domain, such types of investigations may also be expanded from interrelated processes to physiological platforms featuring various system topologies.

Funding

This research was funded by Taif University, Taif, Saudi Arabia (TU-DSPP-2024-127).

CRediT authorship contribution statement

Saima Rashid: Formal analysis, Data curation, Conceptualization. Ilyas Ali: Methodology, Investigation, Formal analysis. Sobia Sultana: Software, Resources, Methodology, Investigation. Zeemal Zia: Writing – original draft, Visualization, Validation. S.K. Elagan: Writing – original draft, Visualization, Validation.

Declaration of Competing Interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Dr. Saima Rashid reports was provided by Department of Computer Science and Mathematics, Lebanese American University, 11022801, Beirut, Lebanon. Dr. Saima Rashid reports a relationship with Department of Computer Science and Mathematics, Lebanese American University, 11022801, Beirut, Lebanon that includes: non-financial support. I am from Lebanon, and according to journal policy, I have a full waiver from Heliyon journal to publish the work. I am thankful to the editors and journal administration for this generous support. If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.