Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Nov 26;58(49):21536–21544. doi: 10.1021/acs.est.4c06702

Probability of Detection and Multi-Sensor Persistence of Methane Emissions from Coincident Airborne and Satellite Observations

Alana K Ayasse †,*, Daniel H Cusworth †, Katherine Howell †, Kelly O’Neill †, Bradley M Conrad ‡, Matthew R Johnson ‡, Joseph Heckler §, Gregory P Asner §, Riley Duren †
PMCID: PMC11636213  PMID: 39587769

Abstract

graphic file with name es4c06702_0007.jpg

Satellites are becoming a widely used measurement tool for methane detection and quantification. The landscape of satellite instruments with some methane point-source quantification capabilities is growing. Combining information across available sensor platforms could be pivotal for understanding trends and uncertainties in source-level emissions. However, to effectively combine information across sensors of varying performance levels, the probability of detection (POD) for all instruments must be well characterized, which is time-consuming and costly, especially for satellites. In August 2023, we timed methane-sensing aerial surveys from the Global Airborne Observatory (GAO) to overlap with observations from the NASA Earth Surface Mineral Dust Source Investigation (EMIT). We show how these coincident observations can be used to determine and verify the detection limits of EMIT and to develop and test a multisensor persistence framework. Under favorable conditions, the 90% POD at 3 for EMIT is 1060. We further derive a Bayesian model to infer probabilistically whether nondetected emissions were truly off, and we validate and show how this model can be used to assess the intermittency of emissions with GAO and EMIT. Time-averaged emission rates from persistent sources can be underestimated if POD is not characterized and if differences in POD across multisensor frameworks are not properly accounted for.

Keywords: methane, EMIT, remote sensing, point source emissions, persistence, probability of detection

Short abstract

In this study, we coordinated methane-sensing aerial surveys to overlap with observations from a similar satellite instrument in an area with large and frequent methane emissions. We use these data to show how these coordinated observations can be used to determine the detection limits of the satellite instrument and to develop and test a multisensor methane plume persistence framework.

Introduction

Reducing methane emissions has received increased attention for addressing global climate change, due to methane’s short lifetime and powerful radiative forcing.1,2 In 2021,150 nations signed the Global Methane Pledge with the goal to reduce emissions 30% by 2030.3 Reducing emissions by this magnitude is both ambitious and critical for achieving global climate targets and requires finding near-term mitigation solutions. In response, and in parallel, to the Global Methane Pledge, efforts to increase monitoring of methane emission sources have been proposed and prototyped, including the UN International Methane Emissions Observatory (IMEO) Methane Alert and Response System (MARS),4 the United States Environmental Protection Agency’s updated oil and gas rule,5 including provisions reporting for superemitting sources (localized emissions above 100 kg CH4 h–1), the European Union’s proposed new methane rule,6 the State of California’s new oil and gas rules,7 among other regulations and initiatives. Satellites have demonstrated the capability of detecting and quantifying methane emissions at the scales relevant to these initiatives.8 Understanding and assessing the performance of satellite technologies are therefore critical for evaluating their ability to address near-term climate goals.

Some passive remote sensing technologies use the short-wave infrared portion of the electromagnetic spectrum for column methane concentration quantification, which can then be used for methane detection for certain classes of high-emitting sources. In particular, one class of passive remote sensing technology, known as imaging spectrometers, measures reflected and backscattered radiance across visible to infrared wavelengths (typically 400–2500 nm) at a medium spectral resolution (typically 5–15 nm). There are many imaging spectrometers currently on orbit (PRISMA, EnMAP, EMIT, and GaoFen5) that have demonstrated methane sensing and localized superemitter detection capabilities.9−12 This paper will specifically focus on the NASA Earth Surface Mineral Dust Source Investigation (EMIT) instrument, onboard the International Space Station (ISS) that has been active since late 2022. Due to the ISS orbit, EMIT is capable of observing between 60° latitude north and south and to date has covered 94% of the US fossil fuel production. EMIT builds on decades of imaging spectrometer development at the NASA Jet Propulsion Laboratory, including the Next Generation Airborne Visible/Infrared Imaging Spectrometer (AVIRIS-NG) and the Global Airborne Observatory (GAO), both of which have been leveraged for large-scale surveys of superemitters across oil and gas, solid waste, and livestock sectors.13,14 EMIT, as well as any imaging spectrometer technology or any other passive remote sensing technology capable of methane detection (e.g., GHGSat, Sentinel-2, LandSat-8, and WorldView-3), is limited to detecting a subset of all emissions. This detection limit is characterized by an instrument’s signal-to-noise (SNR) ratio, its spectral resolution, its spatial resolution, and the environmental conditions (such as wind speed) at the time of observation. For this expanding suite of methane sensing technologies to be used together to understand and reduce methane emissions, the performance, and most importantly the detection limit, of these instruments must be well characterized.

Detection limits for remote sensing of methane are typically reported as the minimum detection limit (MDL) or the probability of detection (POD). The MDL can be estimated theoretically for an instrument of estimated column measurement precision, spatial resolution, or ground sampling distance, for certain environmental conditions.15 POD assigns probabilities of detection for an observing system at specific emission rate levels.16 The POD is best calculated from real observations, preferably controlled release experiments, in which detection for an observing system is evaluated against a wide range of known release rates. The derived POD models from empirical studies are more representative of the true performance of an observing system, including algorithms or manual processes deployed for CH4 plume detection. However, they require, at minimum, dozens of observations at known release rates, preferably across a set of real-world observing conditions. The controlled release experiments are time-consuming and costly to execute, especially for satellites, where observations are typically limited to a single overpass per day and repeat overpasses are set by an observing system’s sample revisit interval.

In addition to different instruments with different detection limits, multiple instruments are now being used in combined multiscale efforts to assess the total methane impact and persistence of individual facilities.17,18 Persistence is a metric of how frequently a source emits methane and is crucial for calculating the lifetime methane contribution of a source. By combining data from multiple instruments, we can increase the number of observations of a source and therefore improve persistence characterization. However, some instruments have a high detection limit, resulting in an inability to observe smaller plumes. If a sensor detection limit is too high to observe a plume, then the instrument should not be used to estimate persistence for that source. It can be difficult to identify which scenarios the detection limit is too high to observe a plume in and when the plume has truly stopped. In this study, we introduce a probabilistic model to solve this problem.

Here, we show how to generate a POD model for a satellite instrument (EMIT) efficiently using coincident airborne observation (GAO) under flights with an airborne instrument whose detection and quantification performance are well characterized. While these coincident observations are still difficult to coordinate, they result in more efficient acquisition of observation samples required to estimate a POD model. We demonstrate an EMIT POD model based on the GAO under flight to be consistent with theoretical estimates. We also show how a POD model can then be used to create a new multisensor persistence framework. We tested and validated this new model with EMIT and GAO observations in the Permian Basin in August of 2023. This framework allows for better probabilistic evaluation of nondetections for sources where airborne observations showed previous emission activity and shows the importance of POD when analyzing source trends using multiple sensors.

Results and Discussion

In this study, we use simultaneous data from the EMIT and GAO imaging spectrometers. We coordinated simultaneous acquisitions from both instruments, over the same target, on 2 days (see details below in the Materials and Methods section). We use the coincident data to derive a POD model for EMIT. The methods for deriving a POD model are detailed below in the methods and material section, and the results are discussed here. We then used the POD model for EMIT to show how data from two instruments with different detection limits can be combined to improve persistence estimates. We introduce this as the multisensor persistence; details on this algorithm are also found in the Materials and Methods section. We then apply and validate this new method with August 2023 EMIT and GAO data.

POD

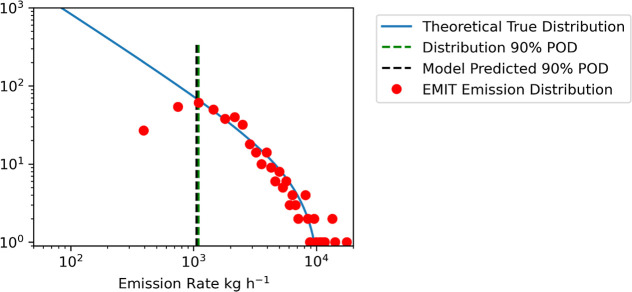
We find that at a 3 wind speed the 90% POD for EMIT is 1060 (Figure 1). This is consistent with what we have observed by analyzing a global distribution of emission rates quantified with EMIT. The most frequent emission rate range for wind speeds between 2 and 4 in all plumes collected and processed by Carbon Mapper from EMIT data is 900–1200 (Figure 2). If we assume that emission rates follow a power law,19 then we can assume that the point just past the peak distribution is the 90% POD and all emissions below the peak are not representative of the true distribution of emissions but rather the partial detection limit of the instrument. This is illustrated in Figure 2, where the blue line is a theoretical true distribution and the points are the EMIT distribution. Where the points diverge from the theoretical truth is the partial detection range. The good agreement between the modeled 90% POD and the observed emission peak indicates that the model is likely representative of the performance of the instrument. In addition, we can compare our model to a mass balance theoretical minimum detection.15 Using a mass balance MDL model introduced in Jacob et al. 2016, we predict the EMIT MDL to be 244 for a 3 wind speed.15 We find that this emission rate results in a 2% POD, which is to be expected, as the MDL represents the theoretical bottom limit. Our POD model aligns with two independent assessments of detection limits, which provides confidence that estimating POD from coincident observations can provide a representative model.

Figure 1.

Figure 1

Open in a new tab

POD heat map for EMIT, wind speed is on the x-axis, emission rate on the y-axis, and the colors represent the POD. The 90% POD and 10% POD line are displayed for reference on the figure.

Figure 2.

Figure 2

Open in a new tab

Distribution of all quantified methane emission from EMIT for wind speeds under 4 and over 2 at time of analysis (n = 422, bins = 50). The Model Predicated 90% POD is the 90% POD at 3 from the model in eq 4. The distribution 90% POD is where we estimate the EMIT distribution starts to diverge from a theoretical true distribution.

While this POD model aligns with independent methods, we do caution that the concentration and detection methods and the limited sample size may affect its global applicability. The POD presented here is applicable only within the methods presented in this paper; a different set of detection methods applied to the EMIT instrument could result in a different POD estimate. In addition, the small amount of data and the limited geography of these data may bias the results, and a larger and more diverse data set is crucial to creating a better constrained model. However, this analysis demonstrates how these types of data can be used to characterize the performance of satellite instruments when controlled release data are not available.

A representative POD model can help us integrate multiple data streams to better understand persistence trends, which we discuss in the next section; in addition, it can also help us to quantitively characterize how much of the total emission budget we can expect to observe with a given instrument. If we assume the true emissions can be represented by a power law (blue line in Figure 2), then we can also calculate what percent of the total emission budget EMIT should be able to observe by integrating under the power law curve. For example, we are interested in what percent of super emitters EMIT can observe (according to the EPA super emitter program, super emitters are defined as all plumes above 100),5 we integrate between 100 and 10,000 to get the super emitter total and then use the EMIT POD model to understand what percent of that total EMIT can observe. We find EMIT can observe between 29 and 36% of the total United States (US) oil and gas super emitter population, with the variation depending on how we define the total distribution. If we assume super emitters represent half of US oil and gas emission, then we can conclude that EMIT can see about 15% of all US oil and gas emissions. We caution that these assumptions are based on oil and gas emissions in the US and may not hold true for other sectors or countries. Future work will be needed to quantify whether this percentage holds true globally, but this highlights how a POD model can be used to assess the capabilities and performance of a sensor.

Assessing Persistence Using Multiple Sensors

Persistence, or plume detection frequency, at the source level is a key metric for understanding and quantifying methane emissions. Persistence provides information on how frequently a given source or area likely needs observation to reliably detect a plume, and it helps us to quantify the total methane contribution of a source. A large plume from a highly intermittent source may contribute less methane than a small but a persistent source over the sources’ lifetimes. In order to accurately calculate the persistence, we need as many observations of a source as possible. Multiple sensors can help provide a large sample, but calculating persistence becomes acutely difficult for multiple sensors with varying POD characteristics. For example, a persistently emitting facility at a low emission rate may be detected by a low detection limit instrument, but not a high detection limit instrument. Not accounting for instrument differences would bias persistence estimates for that theoretical facility. However, to get a statistically representative estimate of persistence, including high POD observations, when appropriate, can improve persistence estimates.

The new multisensor persistence method we introduce here (details in the Materials and Methods section below) uses a Bayesian framework to estimate the probability that a source is emitting when a high POD instrument, in this case EMIT, does not observe a plume. If the high POD instrument does not observe a plume and there is a high likelihood that the source is truly off, then the nondetect is included in the persistence estimate. If the high POD instrument does not observe a plume and there is a low likelihood that the source is off, then the nondetect is not included in the persistence estimate. We also introduce and compare two different prior choices and show how the prior choice can influence the probability. The multisensor persistence method is best illustrated in the example in Figure 3, where we take advantage of our coincident EMIT and GAO observations and use two examples where EMIT did not observe a plume. The first example is where the emission is below the detection limit, and the second is where the source is not emitting. We can then use the GAO data to validate that the multisensor persistence is accurately determining which case it is appropriate to include EMIT in the persistence and which case it is not appropriate.

Figure 3.

Figure 3

Open in a new tab

Time series of two example sources from the GAO/EMIT data set. Both include EMIT nondetects; however, for source 1 the EMIT nondetects are due to EMIT’s detection limit and for source 2 the EMIT nondetect is due to the source no longer emitting. This distinction is critical for understanding source/facility level methane emission dynamics.

In Figure 3, we show 2 sources observed by EMIT but where no plume was detected. One source is truly “off” (Figure 3, source 2) and the other is “on” but below the EMIT detection limit (Figure 3, source 1). Source 1 was observed 4 times by GAO between Aug 17 and Aug 21, and plumes were observed 3 of the 4 times, yielding a persistence of 75%. On Aug. 24th, if we assume EMIT was the only observation, a simple persistence would lead us recalculate the persistence to be 60%; however, if we consider the emission rate (227 kg h–1) from the previous airborne observations and the wind speed at the time of the EMIT observation (5 m s–1), we can determine that the POD for EMIT at this source is 1%. Given the POD and the prior persistence (75%), this yields a high probability that the source is on, but EMIT missed the detection. Therefore, this nondetect was not conclusive enough to make the determination that the source was truly not emitting, this results in the source persistence remaining at 75%. We can confirm this result with the GAO observations from Aug 24th that show the source was indeed emitting but below the EMIT detection limit. Source 2 shows an example of an airborne detection that had a higher emission estimate (4217 kg h–1), and if the source had been emitting, the POD for EMIT would be 99%. In this case, given the prior persistent is 25%, there is a high likelihood that the source was off and that EMIT truly captured a nondetect, so the persistence is incremented to 20%. Again, we can confirm this result with the GAO observations that shows the source was not emitting on this day. For the two examples described above, because they are extreme examples, the autocorrelation prior approach results in the same persistence as the standard simple prior Bayesian persistence.

Not accounting for POD when calculating persistence can also lead to an underestimation of total emissions when individual sources are aggregated to a basin or national scale. We highlight this with data from our study. To calculate the total emissions from a source (a source is a facility or piece of infrastructure that can have multiple associated plumes), we need to account for all plumes associated with the source as well as the nondetects, which we incorporate in the form of a persistence estimate. Here, we quantify the total emission by multiplying the mean emission rate from all plumes observed at the source by the persistence; this is known as the persistence adjusted emission rate. To scale to a basin level (or in this case to our study site level), we then sum all the persistence adjusted emission rates for the sources in the area of interest. If we do not account for POD, the persistence adjusted emission rate may have too many nondetects, which would be inaccurate if the source was still emitting but below the instrument detection limit and therefore have an underestimated persistence-adjusted emission rate.

The multisensor Bayesian approach (regardless of prior choice) for updating persistence will always result in a higher persistence estimation than using a straight detection frequency as some nondetects will be considered inconclusive. This is shown clearly in the right panel of Figure 4. However, the choice of prior information can also impact the persistence estimation across a large population of sources. The autocorrelation prior (Bayesian multisensor persistence with an autocorrelation weighted prior) approach results in a higher persistence across the whole population compared to the simple persistence approach (Figure 4). In general, the autocorrelation approach is less likely to assume confidence in the EMIT nondetects and, therefore, the autocorrelation prior approach is more likely to omit EMIT observations. However, where the autocorrelation approach has confidence in the EMIT nondetects, the sample size increases and provides more confidence in the persistence estimate than the aircraft data alone. The standard Bayesian simple prior (Bayesian multisensor persistence with a simple persistence prior) approach is more likely to assume confidence in the EMIT nondetects especially for prior intermittent sources and therefore has the largest effect on persistent sources.

Figure 4.

Figure 4

Open in a new tab

Left panel shows the simple persistence on the x-axis for all sources. On the y-axis are the two multisensor Bayesian models (simple prior and autocorrelation prior). The right panel shows the total persistence adjusted emission rate for all sources within the study using different persistence estimation methods from the left panel. For each bar, the total emission is broken out by intermittent (f < 0.5) and persistent (f > 0.5) sources.

In the left panel of Figure 4, we show the total persistence-adjusted emission rate for all sources in this study using the simple persistence approach and the multisensor persistence approaches. The simple persistence has a 11% underestimate compared the autocorrelation approach and a 6% underestimate compared to the standard Bayesian approach. Most of this underestimation comes from the persistent sources. This study only represents a short time period (<1 month); therefore, there are only 3 EMIT observations during this time, but if you extrapolate out quarterly or annually, and therefore include many more EMIT data, the underestimation would increase. Essentially, if POD is not taken into account more null detects will get added and this will falsely drive down the persistence and therefore cause an underestimation. Therefore, when assessing the facility or basin scale emissions using data from multiple sensors it is crucial that the POD for each sensor be well characterized, and the proposed multisensor persistence framework be adopted to characterize persistence. In addition, the true utility of this framework goes well beyond this example. This framework can be applied to different instrument combinations, different regions, other sectors, and other gas species. The POD model can be changed to better represent any instrument or any region. In addition, methods to determine the prior can also be changed. Here, we present two methods to determine the prior, but different regions, sectors, or gas species may require different methods to estimate the prior.

Our coincident data provided a unique data set with which to generate a POD model for EMIT and to test and verify the accuracy of the Bayesian persistence framework. We successfully derive an EMIT POD model and find that the 90% POD is around 1000. We then show that with a 1000 90% POD EMIT can observe roughly 30% of US oil and gas super emitters. We also show how a POD model can be used to integrate multiple instruments to better understand persistence. We introduce a new multisensor Bayesian approach to persistence estimates and demonstrate how it can be used to both increase the sampling for a better persistence estimate while also avoiding underestimating emissions, particularly for persistent emissions. Going forward, these methods could enable quantification of both basin and facility level emissions and persistence with multiple instruments, provided that each instrument has a well-characterized POD. This framework is increasingly necessary as the number of methane sensing instruments grow. In the coming year, more remote sensing technologies are scheduled to come online including Carbon Mapper and MethaneSat.20,21 In addition to satellites, there are, and will continue to be, airborne instruments mapping methane plumes. For this expanding suite of methane sensing technologies to be used together to understand and reduce methane emissions, the POD of these instruments must be well characterized and methods to accurately integrate the data, like the proposed multisensor persistence estimation method, must be adopted.

Methods and Materials

Data

This study is composed of data from two imaging spectrometers, EMIT and GAO. Both imaging spectrometers measure radiance between 400 and 2500 nm at roughly 5 nm spectral spacing for GAO and roughly 7 nm for EMIT. GAO has a swath width and pixel size that vary with the altitude of the aircraft; however, for this study, the swath width was ∼3 km and the pixel size was 5 m. EMIT orbits at about 400 km above the Earth’s surface. EMIT images are generally 80 km by 80 km, and it can collect continuous images along track. The pixel resolution of EMIT can vary depending on the height of the ISS, but it is generally 60 m.

On August 20th and 24th 2023, EMIT observed large areas of the Permian Basin, and we coordinated GAO observations to coincide with the EMIT overpasses. The Permian Basin is a target-rich environment that has reliably been observed with a high density of large superemitting methane plumes. It is also a relatively arid region with a homogeneous background, little urban development, and few heavily vegetated areas. These conditions make it a good area to test and compare the GAO and EMIT instruments for methane detection. In addition, these conditions are similar to the conditions where GAO was repeatedly evaluated against blinded controlled releases (Casa Grande, Arizona).22

The field deployment of GAO was designed to ensure that GAO and EMIT observed at least one plume at the same time. Many plumes in the Permian Basin are intermittent;17 however, there are a few exceptions, including persistent activity at some gas processing plants. To better ensure coincident observation of at least one plume, we targeted a large persistently emitting gas processing plant (31.845285, −101.77253°) as our primary target. For the hour surrounding the predicted EMIT observation, we repeatedly surveyed this gas processing plant. For the remainder of the flight day, the GAO surveyed additional high priority regions within the predicted EMIT observation area. The maximum time difference between the EMIT and GAO observations was 3 h. Beyond these coincident observations, GAO surveyed the same general areas on Aug. 16, 17, 19, and 21. The additional data helped us to identify persistent sources for the EMIT POD assessment described later. Figure 5 shows the EMIT and GAO coverage for 20th and 24th. In addition, we have detected and quantified plumes observed by EMIT across its observing record. Details on the EMIT and GAO quantification can be found in the supplement section.

Figure 5.

Figure 5

Open in a new tab

Map of EMIT and GAO coverage on August 20th 2023 (left panel) and August 24th 2023 (right panel) as well as detected plumes.

POD

POD is generally empirically estimated using a sampling of plumes that are above, at, and below the detection limit of the instrument using controlled emission releases.16 Though not a controlled test environment, on Aug 20th and 24th, GAO and EMIT were able to sample a distribution of plumes that were above and below EMIT’s detection limits (Figure 6). However, while we had very close to simultaneous acquisitions over our main target, for the rest of the area surveyed by GAO, there could be as much as a 3 h time difference between when a source was observed by GAO and EMIT. This time difference can make a direct comparison of emission rates challenging, but for POD, we can tolerate higher emission rate variability if the emissions are significantly above or below the detection limit. For observations near the detection limit, we may be incurring some error due to time variability, and this error will have to be corrected for as more data become available. Sources can also be highly intermittent even within a few hours; therefore, we selected sources where we had high confidence of continuous emission for the duration of the campaign. High confidence in source persistence is critical for classifying EMIT nondetections resulting from the detection limit and not due to potential short-duration emission events. To build this confidence in persistence, we used GAO data collected on August 16th, 17th, 19th, and 21st that covered roughly 1900 km2 or 15–30% of the EMIT area. If the source was emitting on all overpasses and has at least three overpasses, then we considered the source to be persistent and we assumed the source was emitting at the time of the EMIT acquisition. If the source was present in only one image, then we considered that source to be intermittent and excluded it from the POD analysis. Some sources had multiple overpasses by GAO on the 20th and 24th, for these sources we use the emission estimate that is the closest in time to the EMIT acquisition. This left us with a total of 55 detected plumes at sources identified by GAO, 8 of which were detected by EMIT and 46 were missed by EMIT (Figure 6).

Figure 6.

Figure 6

Open in a new tab

Detections and missed detections by EMIT from the coincident GAO/EMIT acquisition. The detects/missed detects are binned by the emission rate.

POD is the probability that an instrument, retrieval, and detection algorithm detect a methane plume given the emission rate, wind speed, solar, and albedo properties of the location and instrument properties. This can be summed up in the theoretical model developed by Conrad et al., 2023 (here after referred to as Conrad et al.) that takes the following form

graphic file with name es4c06702_m001.jpg 1
graphic file with name es4c06702_m002.jpg 2

where Q is the emission rate, h is the pixel resolution, and U is the wind speed. Φ is used to denote coefficients that will be optimized from the EMIT and GAO data. Signal-to-noise ratio (SNR), which is determined by a combination of instrument properties, solar zenith angle, and surface albedo, can be added to the denominator as Nϕ4. However, given that SNR did not vary in our study, this parameter is not used in the calculations. Equation 2 is the inverse link function, which is specified here as the Burr cumulative distribution function (CDF) but more generally could be the CDF of any distribution with a non-negative support.16 The inverse link function serves to translate x to a 0–1 probability (P).

We optimized the coefficients by minimizing l in the following equation

graphic file with name es4c06702_m003.jpg 3

where ϕ and θ are a pair of predictor and inverse link functions, respectively. In this case, ϕ is eq 1 and θ is eq 2. Di represents a successful detect (1) or a MD (0) by EMIT for every GAO observation (i). Fi is the output of the predictor and inverse link function for a given GAO observation (i). We used the SciPy minimization routine to minimize this equation. The final form of the POD model for EMIT resulted in the following equation with the inverse link function (eq 2)

graphic file with name es4c06702_m004.jpg 4

We also looked at alternative models from Conrad et al. and found little substantive difference in the predicted probabilities.

Multisensor Persistence

Traditionally, persistence is calculated as a straight detection frequency (f*); here, we refer to it as “simple persistence”, which takes the following form

graphic file with name es4c06702_m005.jpg 5

where N is the number of overpasses and M is the number of detections. While this approach can work for a single instrument, it does not work well for multiple instruments where there are different PODs. A high POD instrument may get many observations (N) but few detections (M) thereby deflating the persistence. Therefore, we propose a prototype multisensor persistence algorithm, based on empirical POD information using Bayesian inference. Calculating multisensor persistence requires decomposing the number of instrument overpasses (N) into two components: overpasses that can be used to conclusively calculate persistence (Nc) and overpasses that cannot be used to conclusively calculate persistence (NN), where N = Nc + NN. NN includes overpasses where observations may have been obscured (e.g., cloudy scenes) but may also include overpasses where one lacks confidence that a nondetection truly captured reality (i.e., the nondetect was due to detection limits rather that a source that stopped emitting). This lack of confidence can be estimated probabilistically: here, the goal is to estimate the probability that a source is emitting CH4 (on) given that an observation was made without a detection, also known as a MD, here written as p(on|MD). Using Bayes’s Theorem, this is explicitly estimated using the following form

graphic file with name es4c06702_m006.jpg 6

where p(MD|on) represents the probability of a MD given that the source is on. This value is estimated using an empirical POD curve derived for an instrument using eqs 1 and 2

graphic file with name es4c06702_m007.jpg 7

where PODI represents a unique POD function for instrument I, q* is a representative emission rate for the emitting source, and u is the windspeed. This value would ideally be the emission rate at the time of observation. However, in practice, it is impossible to estimate this value given that the observation resulted in no detection. Instead, one can assume this value by possibly using a distribution of previously estimated emission rates at that source. The value p(MD|off) represents the probability of not detecting a source given that it is off. This value can be estimated by the true negative rate, which is a function of true negative and false positive detections, derived from controlled release or other validation experiments

graphic file with name es4c06702_m008.jpg 8

The values p(on) and p(off) represent prior probabilities that an emission source is emitting or not, respectively.

Assumptions on prior probability distributions influence the estimation of p(on|MD). We show two applications of this framework under differing assumptions for p(on). First, we assume p(on) to be a simple emission persistence (f*) of that source derived from previous overflights, assuming at least 3 previous overpasses with GAO: f* = M/N, where M = number of detections and N = number of overpasses from previous airborne overpasses. We require N ≥ 3 in order to have a statistically robust enough sample to get a potential persistence less (or more) than 50%. The value p(off) is then estimated as 1 – f*. Using these assumptions, p(on|MD) reduces to the following form

graphic file with name es4c06702_m009.jpg 9

Multisensor persistence with a simple prior is then estimated using eq 9 and the following algorithm:graphic file with name es4c06702_0010.jpg

Second, we assume p(on) as the probability defined by the autocorrelative model. Here, this underlying assumption is that the most recent previous observation at that source is most predictive of the sources current on/off state. We assume an autocorrelative model of the following form

graphic file with name es4c06702_m010.jpg 10

where X represents the binary outcome of whether a plume was detected at some time of observation t∈[1, ...,N]. Values a, b, and c represent regression coefficients, and ⌊·⌉ represents a rounding operation. We fit the coefficients of this model using source-level observations from previous airborne campaigns in the Permian Basin.14 When trained on the entire data set, we find a fair predictive ability of this model to estimate the “on” state of a source, with precision of 0.73, recall of 0.79, and f – 1 score of 0.76. We assume p(on) to be the predicted probability from the logistic regression model. There are only 4 permutations of model states that exist in eq 11 given the state of the previous overpass (t–1) and overpasses prior to that (t–2+). Let φ(t–1,t–2+) be the function that maps previous overpass states to probabilities, and then φ(t–1,t–2+) takes the following form

graphic file with name es4c06702_m011.jpg 11

Therefore, the most recent previous overpass is the largest driver in the proximal state of the emission for the source. Using these explicit probabilities, the multisensor persistence algorithm with an autocorrelation prior takes the following form:graphic file with name es4c06702_0011.jpg

These priors are depended on prior observation from a low detection limit instrument, in this case, GAO. Here, we assume that GAO can detect everything, and therefore, the probability of an emission being under the detection limit is not possible. Therefore, the algorithms above are applied only to the EMIT observations. This is, of course, incorrect as there can be emission events under the GAO detection limit. However, for simplicity, we must adopt this assumption. If we are comparing instruments other than GAO and EMIT, then the lowest detection instrument could be used to estimate the prior. The lowest detection instrument may also suffer from missed plumes due to detection limits, and future work is needed to understand how best to use probabilities to assess persistence for a single instrument.

Acknowledgments

We would like to acknowledge the EMIT Science team including Philip Brodrick, Andrew Thorpe, and Clayton Elder for help with the EMIT forecast. From the Carbon Mapper team, we would like at acknowledge Andrew Aubrey, Ralph Jiorle, and Deja Newton for supporting the GAO flights and data. We would like to thank the GAO team for flight operations. The Global Airborne Observatory (GAO) is managed by the Center for Global Discovery and Conservation Science at Arizona State University. The GAO is made possible by support from private foundations, visionary individuals, and Arizona State University. Funding for flight operations and/or data analysis referenced in this paper was supported by NASA Carbon Monitoring System and the Earth Surface Mineral Dust Source Investigation (EMIT) Science and Applications Team. Lastly, the Carbon Mapper team acknowledges the support of their sponsors including the High Tide Foundation, Bloomberg Philanthropies, Grantham Foundation, and other philanthropic donors.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.4c06702.

  • Methane emission quantification, methane emission comparison, and source emission quantification (PDF)

The authors declare no competing financial interest.

Supplementary Material

es4c06702_si_001.pdf (381.1KB, pdf)

References

  1. Etminan M.; Myhre G.; Highwood E. J.; Shine K. P. Radiative Forcing of Carbon Dioxide, Methane, and Nitrous Oxide: A Significant Revision of the Methane Radiative Forcing. Geophys. Res. Lett. 2016, 43 (24), 614. 10.1002/2016GL071930. [DOI] [Google Scholar]
  2. Ocko I. B.; Sun T.; Shindell D.; Oppenheimer M.; Hristov A. N.; Pacala S. W.; Mauzerall D. L.; Xu Y.; Hamburg S. P. Acting Rapidly to Deploy Readily Available Methane Mitigation Measures by Sector Can Immediately Slow Global Warming. Environ. Res. Lett. 2021, 16 (5), 054042. 10.1088/1748-9326/abf9c8. [DOI] [Google Scholar]
  3. Global Methane Pledge, 2024. https://www.globalmethanepledge.org (accessed Feb 7, 2024).
  4. UNEP—UN Environment Programme . 4. UNEP. Methane Alert and Response System (MARS), 2024. https://www.unep.org/topics/energy/methane/international-methane-emissions-observatory/methane-alert-and-response-system (accessed May, 2024).
  5. Environmental Protection Agency. Standards of Performance for New, Reconstructed, and Modified Sources and Emissions Guidelines for Existing Sources: Oil and Natural Gas Sector Climate Review. Federal Register, 2024. https://www.federalregister.gov/documents/2024/03/08/2024-00366/standards-of-performance-for-new-reconstructed-and-modified-sources-and-emissions-guidelines-for (accessed May 9, 2024).
  6. European Commission. Communication on an EU strategy to reduce methane emissions COM(2020) 663 final. COMMUNICATION FROM THE COMMISSION TO THE EUROPEAN PARLIAMENT, THE COUNCIL, THE EUROPEAN ECONOMIC AND SOCIAL COMMITTEE AND THE COMMITTEE OF THE REGIONS on an EU strategy to reduce methane emissions, 2024. https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A52020DC0663 (accessed May 9, 2024).
  7. Greenhouse Gas Emission Standards for Crude Oil and Natural Gas Facilities, 2017. https://ww2.arb.ca.gov/resources/documents/oil-and-gas-regulation.
  8. Jacob D. J.; Varon D. J.; Cusworth D. H.; Dennison P. E.; Frankenberg C.; Gautam R.; Guanter L.; Kelley J.; McKeever J.; Ott L. E.; Poulter B.; et al. Quantifying methane emissions from the global scale down to point sources using satellite observations of atmospheric methane. Atmos. Chem. Phys. 2022, 22 (14), 9617–9646. 10.5194/acp-22-9617-2022. [DOI] [Google Scholar]
  9. Guanter L.; Irakulis-Loitxate I.; Gorroño J.; Sánchez-García E.; Cusworth D. H.; Varon D. J.; Cogliati S.; Colombo R. Mapping Methane Point Emissions with the PRISMA Spaceborne Imaging Spectrometer. Remote Sens. Environ. 2021, 265 (112671), 112671. 10.1016/j.rse.2021.112671. [DOI] [Google Scholar]
  10. Roger J.; Irakulis-Loitxate I.; Valverde A.; Gorroño J.; Chabrillat S.; Brell M.; Guanter L. High-Resolution Methane Mapping with the EnMAP Satellite Imaging Spectroscopy Mission. IEEE Trans. Geosci. Rem. Sens. 2024, 62, 1–12. 10.1109/TGRS.2024.3352403. [DOI] [Google Scholar]
  11. Thorpe A. K.; Green R. O.; Thompson D. R.; Brodrick P. G.; Chapman J. W.; Elder C. D.; Irakulis-Loitxate I.; Cusworth D. H.; Ayasse A. K.; Duren R. M.; Frankenberg C.; Guanter L.; Worden J. R.; Dennison P. E.; Roberts D. A.; Chadwick K. D.; Eastwood M. L.; Fahlen J. E.; Miller C. E. Attribution of Individual Methane and Carbon Dioxide Emission Sources Using EMIT Observations from Space. Sci. Adv. 2023, 9 (46), eadh2391 10.1126/sciadv.adh2391. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. He Z.; Gao L.; Liang M.; Zeng Z.-C. A Survey of Methane Point Source Emissions from Coal Mines in Shanxi Province of China Using AHSI on Board Gaofen-5B. Atmos. Meas. Tech. 2023, 17, 2937. 10.5194/egusphere-2023-3047. [DOI] [Google Scholar]
  13. Duren R. M.; Thorpe A. K.; Foster K. T.; Rafiq T.; Hopkins F. M.; Yadav V.; Bue B. D.; Thompson D. R.; Conley S.; Colombi N. K.; Frankenberg C.; McCubbin I. B.; Eastwood M. L.; Falk M.; Herner J. D.; Croes B. E.; Green R. O.; Miller C. E. California’s Methane Super-Emitters. Nature 2019, 575 (7781), 180–184. 10.1038/s41586-019-1720-3. [DOI] [PubMed] [Google Scholar]
  14. Cusworth D. H.; Thorpe A. K.; Ayasse A. K.; Stepp D.; Heckler J.; Asner G. P.; Miller C. E.; Yadav V.; Chapman J. W.; Eastwood M. L.; Green R. O.; Hmiel B.; Lyon D. R.; Duren R. M. Strong Methane Point Sources Contribute a Disproportionate Fraction of Total Emissions across Multiple Basins in the United States. Proc. Natl. Acad. Sci. U.S.A. 2022, 119 (38), e2202338119 10.1073/pnas.2202338119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Jacob D. J.; Turner A. J.; Maasakkers J. D.; Sheng J.; Sun K.; Liu X.; Chance K.; Aben I.; McKeever J.; Frankenberg C. Satellite Observations of Atmospheric Methane and Their Value for Quantifying Methane Emissions. Atmos. Chem. Phys. 2016, 16 (22), 14371–14396. 10.5194/acp-16-14371-2016. [DOI] [Google Scholar]
  16. Conrad B. M.; Tyner D. R.; Johnson M. R. Robust Probabilities of Detection and Quantification Uncertainty for Aerial Methane Detection: Examples for Three Airborne Technologies. Remote Sens. Environ. 2023, 288 (113499), 113499. 10.1016/j.rse.2023.113499. [DOI] [Google Scholar]
  17. Cusworth D. H.; Duren R. M.; Thorpe A. K.; Olson-Duvall W.; Heckler J.; Chapman J. W.; Eastwood M. L.; Helmlinger M. C.; Green R. O.; Asner G. P.; Dennison P. E.; Miller C. E. Intermittency of Large Methane Emitters in the Permian Basin. Environ. Sci. Technol. Lett. 2021, 8, 567–573. 10.1021/acs.estlett.1c00173. [DOI] [Google Scholar]
  18. Guanter L.; Roger J.; Sharma S.; Valverde A.; Irakulis-Loitxate I.; Gorroño J.; Zhang X.; Schuit B. J.; Maasakkers J. D.; Aben I.; Groshenry A.; Benoit A.; Peyle Q.; Zavala-Araiza D. Multi-Satellite Data Depicts Record-Breaking Methane Leak from a Well Blowout. Environ. Sci. Technol. Lett. 2024, 11, 825. 10.1021/acs.estlett.4c00399. [DOI] [Google Scholar]
  19. Sherwin E. D.; Rutherford J. S.; Zhang Z.; Chen Y.; Wetherley E. B.; Yakovlev P. V.; Berman E. S. F.; Jones B. B.; Cusworth D. H.; Thorpe A. K.; Ayasse A. K.; Duren R. M.; Brandt A. R. US Oil and Gas System Emissions from Nearly One Million Aerial Site Measurements. Nature 2024, 627 (8003), 328–334. 10.1038/s41586-024-07117-5. [DOI] [PubMed] [Google Scholar]
  20. Hamburg S.; Gautam R.; Zavala-Araiza D.. MethaneSAT - A New Tool Purpose-Built to Measure Oil and Gas Methane Emissions from Space; SPE: ADIPEC, Abu Dhabi, 2022. [Google Scholar]
  21. Zandbergen S. R.; Duren R.; Giuliano P. N.; Green R. O.; Haag J. M.; Moore L.; Shaw L.; Mouroulis P.. Optical Design of the Carbon Plume Mapper (CPM) Imaging Spectrometer. In Imaging Spectrometry XXV: Applications, Sensors, and Processing; Ientilucci E. J., Bradley C. L., Eds.; SPIE, 2022. [Google Scholar]
  22. El Abbadi S. H.; Chen Z.; Burdeau P. M.; Rutherford J. S.; Chen Y.; Zhang Z.; Sherwin E. D.; Brandt A. R. Technological Maturity of Aircraft-Based Methane Sensing for Greenhouse Gas Mitigation. Environ. Sci. Technol. 2024, 58 (22), 9591–9600. 10.1021/acs.est.4c02439. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

es4c06702_si_001.pdf (381.1KB, pdf)

Articles from Environmental Science & Technology are provided here courtesy of American Chemical Society

RESOURCES