REAL-TIME RECURSIVE ESTIMATION OF, AND UNCERTAINTY QUANTIFICATION FOR, BREATH ALCOHOL CONCENTRATION VIA LQ TRACKING CONTROL-BASED INVERSE FILTERING OF TRANSDERMAL ALCOHOL BIOSENSOR SIGNALS

Abstract

The utility of newly developed wearable biosensors for passively, non-invasively, and continuously measuring transdermal alcohol levels in the body in real time has been limited by the fact that raw transdermal alcohol data does not consistently correlate (quantitatively or temporally) with interpretable metrics of breath and blood across individuals, devices, and the environment. A novel method using a population model in the form of a random abstract hybrid system of ordinary and partial differential equations and linear quadratic tracking control in Hilbert space is developed to estimate blood or breath alcohol concentration from the biosensor-produced transdermal alcohol level signal. Using human subject data in the form of 270 drinking episodes, the method is shown to produce estimates of blood or breath alcohol concentration that are highly correlated and thus good predictors of breath analyzer measurements. Moreover, although the method requires some advanced offline training on a laptop or on the cloud, it produces the estimated blood or breath alcohol concentration recursively online in real time and requires only computations that could be carried out on either the biosensor’s built-in processor or on a portable mobile device such as a phone or tablet.

1. Introduction.

The two standard methods for monitoring alcohol use in naturalistic settings, the self-report and the breath analyzer, are plagued by a number of disadvantages. The self report is often hindered by lack of knowledge of alcohol content, quantity consumed, timing, variability in stomach content, metabolism, and body composition. This means that the amount of alcohol consumed does not easily translate into blood/breath alcohol concentration (BAC/BrAC). The Breath analyzer, typically considered the gold standard for measuring alcohol levels (i.e. BrAC) in the field, is often inaccurate when readings are taken by lay users due to not adequately rinsing their mouths before use [8], not taking deep lung breaths, and not allowing the device chamber enough time to clear. The resulting readings tend to be be either too high or too low. Both methods require active participation, which is burdensome and interferes with natural drinking. Thus, scientist and clinicians would benefit greatly from a means for passively obtaining accurate quantifiable alcohol data to study alcohol-related health outcomes, consumption patterns, drinking behavior, disease progression, treatment efficacy, and recovery. The National Institutes of Health (NIH) has been interested in, and has funded, the development of a wearable biosensor for monitoring blood-alcohol levels in real time. Such a device would also have consumer appeal as it could help individuals make better health choices.

The most promising technology for achieving this goal is a device that measures the ∼ 1% of body alcohol that is excreted from the surface of the skin in perspiration. Since the thirties [36] it has been known that the level of ethanol (the type of alcohol in alcoholic beverages) in sweat roughly correlates with BAC/BrAC and researchers have produced biosensors that exploit this observation [17, 57–60]. These biosensors produce a measurement known as transdermal alcohol concentration (TAC) (in fact, they do not measure concentration; but rather they count molecules of ethanol). The sensor is typically packaged in a bracelet that can be worn either on the wrist or ankle (Figure 1). They have a reservoir in which perspiration in the vapor state is collected and they then perform an oxidation-reduction (redox) reaction on the collected specimen that produces a fixed number of electrons for each molecule of ethanol processed. They are miniaturized ethanol sensitive and specific fuel cells.

FIGURE 1.

Left: Giner inc. WrisTAS 7 transdermal alcohol monitoring biosensor. Right: Alcohol Monitoring Systems Secure Continuous Remote Alcohol Monitor (SCRAM) transdermal alcohol biosensor system.

TAC biosensors were developed decades ago and have been used in research and the criminal justice system as abstinence monitors. Smartwatch-type TAC devices like Skyn by BACtrack and ION by Milo Sensors are also currently in development for commercial use. The utility of these devices as quantitative indicators of alcohol levels in the body, however, has been limited by the fact that, in contrast to breath analyzers which are relatively robust across individuals and ambient conditions [31], raw TAC data does not consistently correlate (quantitatively or temporally) with interpretable metrics of BAC/BrAC across individuals, devices, and the environment (see Figure 2). Unlike the relationship of BrAC to BAC, which is stable across people and conditions and are generally considered to be interchangeable, the diffusion of alcohol from the blood through the skin and into the TAC sensor varies across people and conditions. Addressing this variability in the TAC-BAC/BrAC relationship is critical for producing interpretable quantitative levels of alcohol from TAC.

FIGURE 2.

Variable TAC-BrAC relationship. Blue TAC has a delayed start from pink BrAC in all three drinking episodes, but TAC level is lower (left panel), the same (center panel), and higher (right panel) than BrAC across participants (left vs. center and right) and within individual participants across episodes (center vs. right).

We have developed several techniques for converting TAC biosensor measurements into an approximating equivalent BrAC signal, or eBrAC. Our schemes have two phases. First, models are trained with contemporaneous BrAC and TAC measurements. Then, the now trained model is used to convert the TAC test signal collected in the lab, clinic or in the field (but that was not used for training), into its BrAC equivalent. In our early studies [11,15,45] we assumed that the training data came from the same individual as the TAC test data. That is, the models were calibrated directly to the individual who supplied the test TAC. More recently,we developed schemes based on population models [1–4,24,25,52–56] that do not require calibration directly to the test participant and the testing environment; they produce eBrAC and uncertainty quantification (UQ) in the form of an error band.

TAC to BAC/BrAC conversion models by other researchers have included conventional linear regression models [12–14, 26, 27, 29], and more recently, machine learning-based schemes [16]. Our group has also looked at physics informed machine learning-based schemes using hidden Markov models [39], generative adversarial neural networks [38] and long short term memory neural networks [37].

All of our studies have been based on a first principles diffusion-based parabolic hybrid system of ordinary and partial differential equations in the form of a single input/single output (SISO) model in which the BAC/BrAC signal is the input and the TAC signal is the output. In this way, the BAC/BrAC estimation problem is an inverse problem. Given a TAC output signal, we want to estimate the BAC/BrAC input signal that produced it. By using a model that captures the essential physics of transdermal ethanol transport, we are able to greatly reduce the dimension of the space of unknown parameters that have to be fit to data. Our models which typically involve 2 to 8 unknown parameters, generalize well beyond the training set and are not plagued by over fitting (i.e. fitting noise rather than signal). In our population models we exploit an idea from [21, 50] in which the parameters are random variables and thereby making the models random evolution systems. In the training phase, we use population data to fit the distributions of the random parameters rather than their precise values. Our eBrAC UQ is then based on these fit population parameter distributions.

To be more precise concerning the uncertainty quantification in this treatment, we first note that there are several sources of uncertainty in the approach we take here. These include: 1. the uncertainty that results from the estimation of the distribution of the parameters in the population model from estimates of the parameters in an individual model fit to possibly not so random samples of drinking episodes, 2. the uncertainty that results from the fact that the estimation of the individual model parameters is based on a sampling of each drinking episode’s noisy BrAC and TAC signals, 3. the uncertainty that results from the fact that the inverse filtering problem we solve to obtain an estimate of the BAC or BrAC signal is based on the population model with random parameters and fit distributions; this would be the uncertainty across drinking episodes, and 4. the uncertainty that results from the fact that the resulting BrAC estimates are based on the population model involving random parameters and a noisy sampled TAC signal; this would be the uncertainty within a drinking episode. Taken all together, the result is an intractable mixed-effects estimation problem.

In this paper we are only interested in the uncertainty due to present, but largely un-measurable and un-modeled, 1) physiological differences across patients or participants, 2) environmental conditions, and 3) electro-chemical variations across different sensors. This uncertainty is captured in the distributions of the parameters that we consider to be random variables in a population model. In particular, we are interested in how these uncertainties propagate through to the BAC or BrAC estimates yielded by our LQ tracking-based approach. We quantify this uncertainty in the BAC/BrAC estimates with what we refer to as error bands. The fact that we call them error bands may suggest that they are deterministic, but they are not. They are also not statistical in any standard sense in that they are not confidence bands since they are in no way related to the many instances of sampling that occur throughout our approach, and they are also not credible bands since our approach is in no way Bayesian. We consider them to be probabilistic in the sense that since the output of our model (TAC) and the estimated input (BrAC), respectively $y(q)$ and $u(q)$, are deterministic functions of the random parameters, $q\in Q$, that appear in the population model, the error bands are quite simply obtained probabilistically from $P(y(Q))\ge P(Q)$ and $P(u(Q))\ge P(Q)$.

In addition, in this paper we refer to our underlying model as a random dynamical system, evolution equation, or hybrid system of ordinary and partial differential equations. We feel this is justified since our population model depends on deterministic parameters that are unknown, unmodeled, and unmeasurable, and assumed to be random across a population of different patients or participants, environmental conditions, and sensors. This is to distinguish them from stochastic evolution equations (which our model is not) that typically involve, and whose solutions are often considered to be, stochastic processes. In fact, by making use of the ideas in [21,50], we are able to transform our random evolution system into a deterministic one, the solution of which takes the form of an explicit function of the random parameters.

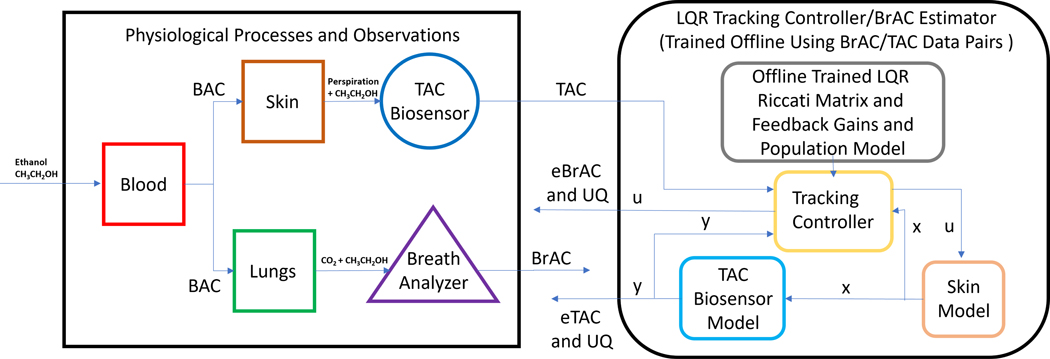
Our primary focus here is the development of a scheme based on linear quadratic (LQ) tracking control [30] that uses the trained population model to produce an eBrAC signal for a given TAC test signal. This is an inherently ill-posed problem; in our previous studies we used a Tikhonov regularized spline based non-negative least squares (NNLS) scheme (essentially, quadratic programming). This approach has a number of disadvantages. It is computationally intensive and time consuming; it requires specialized software and is not ideal for providing eBrAC in real time. Alternatively, what is desired is a scheme that provides eBrAC in real time, and aside from offline training, can be implemented on a Blue Tooth accessible mobile device such as a phone or tablet, or on the biosensor’s built-in processor. The scheme we develop here does precisely this via a non-standard application of LQ tracking control. It is non-standard in the sense that instead of using the model to design a controller for an actual process or plant, it is the model itself that we want to force to track the TAC test signal. The resulting closed loop system consisting of the population model, or state equation, and the feedback controller yield an eBrAC signal and its UQ in the form of a recurrence or recursion. Moreover, with a minor adaptation, the quadratic performance index serves to naturally introduce regularization thereby mitigating the effects of the ill-posedness of the inverse problem of estimating the BrAC input signal. A schematic diagram of our overall approach is shown in Figure 3.

FIGURE 3.

A signal-flow diagram of our LQ real time recursive tracking controller-based inverse filter, or BrAC estimator.

In Sections 2.1.1 - 2.1.3, we describe our underlying first principles diffusion-based mathematical model for the transdermal transport of ethanol, its discrete time formulation, and its reformulation in state space form as a random discrete time abstract evolution equation in Hilbert space. In Sections 2.2, 2.2.1, and 2.2.2 we explain how the distribution of the random parameters that appear in our population model are estimated from training data. In Sections 2.3 and 2.4 we provide, respectively, a brief summary of discrete time linear quadratic regulator (LQR) theory in Hilbert space [10,32–35,44,67] and the associated finite dimensional approximation theory and convergence results [6,7,19,20]. Uncertainty quantification is discussed in Section 2.5, while the modification to the LQR theory presented in 2.3 necessary to force the model to track the TAC test signal while regularizing the eBrAC signal is discussed in Section 2.6. A sampling of our numerical studies are presented in Section 3 including the details of our dosing and data collection protocols and the fitting of the distributions of the random parameters in the population model. A final Section 4 contains our statistical analysis and some discussion of the performance of our scheme across our entire testing data set of drinking episodes and a few concluding remarks.

2. Methods.

In the following subsections we review the construction of our first principles physics based individual and population models for the transdermal transport of ethanol from the blood to the TAC biosensor. We also explain the techniques we use together with population drinking episode data to estimate the distribution of the random parameters appearing in the population model. A more detailed description and discussion of these ideas can be found in [2]. We then briefly review the LQR control theory in Hilbert space and its finite dimensional approximation theory and convergence results. These ideas are presented in greater detail in [65,66]. We also discuss how the population model can be used to quantify the uncertainty in our eBrAC estimates and the modifications we make to the LQR theory so that it tracks a test TAC signal and so that it regularizes the eBrAC signal.

2.1. Individual and Population Models for the Transdermal Transport of Ethanol.

In this section we first derive the individual model in continuous time and then reformulate it in discrete or sampled time. We then consider its state space formulation and then use it as the basis for our population model.

2.1.1. The First Principles Individual Model.

Our basic underlying model for the transdermal transport of ethanol from the blood to the TAC biosensor on the surface of the skin takes the form of a linear single input single output (SISO) hybrid system consisting of ordinary and parabolic partial differential equations (ODE and PDE) together with boundary and initial conditions. The PDE captures the diffusion of ethanol molecules in the interstitial fluid in the epidermal layer of the skin, while the ODE describes the inflow/outflow dynamics of the sensor. There is no active blood supply to the combination of living and dead cells that make up the epidermal layer; they receive their nourishment from the blood vessels in the dermal layer and the interstitial fluid between the cells. For $t>0$ and $0<\eta <1$, we have

$$\begin{gathered} \frac{\partial x}{\partial t}(t,\eta )=q_1\frac{{\partial }^{2}x}{\partial {\eta }^2}(t,\eta ),\frac{dw}{dt}(t)=q_1\frac{\partial x}{\partial \eta }(t,0), \\ x(t,0)=w(t),x(t,1)=q_{2}u(t),y(t)=w(t), \end{gathered}$$ (1)

with initial conditions $w(0)=w_0$ and $x(0,\eta )={\varphi }_0(\eta )$. In (1), $x(t,\eta )$ is the ethanol concentration in the epidermal layer of the skin at time $t$ and dimensionless depth $\eta \in [0,1]$, $w(t)$ is the ethanol concentration in the biosensor’s collection reservoir and the system output, the TAC, $y(t)$ agrees with $w(t)$. The input is the BrAC or BAC, $u(t)$. The system has two essentially un-measurable subject, sensor hardware, and environmental dependent parameters, $\mathit{q}=\left[q_1,q_2\right]$. The parameter $q_1$ is essentially the diffusivity of ethanol in the interstitial fluid in the epidermal layer and the parameter $q_2$ is essentially the product of the alcohol impedance between the epidermal and dermal layers of the skin and the alcohol impedance between the epidermal layer and the membrane covering the collection chamber of the sensor where it comes into contact with the epidermal layer.

We convert the continuous time model given in (1) to discrete or sampled time by letting $\tau >0$ denote the length of the sensor’s sampling interval and assuming zero-order hold input, $u(t)=u_k$, $t\in [k\tau ,(k+1)\tau )$, $k=0,1,2,\dots ,K$, with a finite time horizon, $T>0$, where $K\tau =T$. We set $x_k=x_k(\eta )=x(k\tau ,\eta )$, $w_k=w(k\tau )$, and $y_k=y(k\tau )$, $k=0,1,2\dots ,K$. Making the change of variables $v(t,\eta )=x(t,\eta )-\xi (\eta )u_k$, with $\xi (\eta )=q_2\eta$, for $0<\eta <1$, and $k\tau \le t<(k+1)\tau$, each $k=0,1,2\dots ,K$, (1) becomes

$$\begin{gathered} \frac{\partial v}{\partial t}(t,\eta )=q_1\frac{{\partial }^{2}v}{\partial {\eta }^2}(t,\eta ),\frac{dw}{dt}(t)=q_1\frac{\partial v}{\partial \eta }(t,0)+q_2{u}_k, \\ v(t,0)=w(t),v(t,1)=0 \\ v(k\tau ,\cdot )=x(k\tau ,\cdot )-\xi (\cdot )u_k=x_k-\xi u_k. \end{gathered}$$ (2)

2.1.2. The State Space Formulation of the Individual Model.

Let $Q$ be a compact subset of the first quadrant of ${ℝ}^2$, let $H=ℝ\times L^2(0,1)$ be endowed with the inner product $\langle \left({\theta }_1,{\varphi }_1\right),\left({\theta }_2,{\varphi }_2\right)\rangle ={\theta }_1{\theta }_2+\underset{0}{\overset{1}{\int }}{\varphi }_1(\eta ){\varphi }_2(\eta )d\eta$, let $V=\{(\theta ,\varphi )\in H:\varphi \in H^1(0,1),\theta =\varphi (0),\varphi (1)=0\}$ be the Hilbert space with inner product given by

$${\langle \left({\varphi }_1(0),{\varphi }_1\right),\left({\varphi }_2(0),{\varphi }_2\right)\rangle }_V={\langle {\varphi }_1^{\prime },{\varphi }_2^{\prime }\rangle }_{L^2(0,1)},$$

where ${\langle \cdot ,\cdot \rangle }_{L^2(0,1)}$ denotes the standard $L^2(0,1)$ inner product, and let $|\cdot |$ and $\parallel \cdot \parallel$ denote respectively the norms induced by these two inner products on their respective spaces. Standard arguments yield the dense and continuous embeddings $V\mapsto H\mapsto V^{\ast }$.

Define the bilinear form $a(\mathit{q};\cdot ,\cdot ):V\times V\to ℝ$ for each $\mathit{q}\in Q$ by

$$a\left(q;{\widehat{\varphi }}_1,{\widehat{\varphi }}_2\right)=q_1\underset{0}{\overset{1}{\int }}{\varphi }_1^{\prime }(\eta ){\varphi }_2^{\prime }(\eta )d\eta$$

for ${\varphi }_1$, ${\varphi }_2\in V$ and with ${\widehat{\varphi }}_1=\left({\varphi }_1(0),{\varphi }_1\right)$, ${\widehat{\varphi }}_2=\left({\varphi }_2(0),{\varphi }_2\right)$. Standard arguments yield that the form $a(\mathit{q},\cdot ,\cdot )$ satisfies:

1. Boundedness There exists a constant ${\alpha }_0>0$ such that $\left|a\left(\mathit{q};{\widehat{\varphi }}_1,{\widehat{\varphi }}_2\right)\right|\le {\alpha }_0\Vert {\widehat{\varphi }}_1\Vert \Vert {\widehat{\varphi }}_2\Vert$, ${\widehat{\varphi }}_1$, ${\widehat{\varphi }}_2\in V$.

2. Coercivity There exist constant ${\lambda }_0\in ℝ$ and ${\mu }_0>0$ such that $a(\mathit{q},\widehat{\varphi },\widehat{\varphi })+{\lambda }_0|\widehat{\varphi }{|}^2\ge {\mu }_0\parallel \widehat{\varphi }{\parallel }^2$, $\widehat{\varphi }\in V$.

3. Continuity For all ${\widehat{\varphi }}_1$, ${\widehat{\varphi }}_2\in V$, we have that $\mathit{q}\to a\left(\mathit{q},{\widehat{\varphi }}_1,{\widehat{\varphi }}_2\right)$ is a continuous mapping from $Q$ into $ℝ$.

The fact that $Q$ is compact implies that the constants ${\alpha }_0$, ${\lambda }_0$ and ${\mu }_0$ in the above three properties do not depend on $\mathit{q}$ [24].

Define the operator $A(\mathit{q}):Dom(A(\mathit{q}))\subset H\to H$ by letting ${\langle A(\mathit{q})\widehat{\varphi },\widehat{\psi }\rangle }_{V^{\ast },V}=-a(\mathit{q};\widehat{\varphi },\widehat{\psi })$ with $Dom(A(\mathit{q}))=\left\{\widehat{\varphi }=(\varphi (0),\varphi )\in V:\varphi \in H^2(0,1)\right\}$. The domain, $Dom(A(\mathit{q}))$, does not depend on $\mathit{q}$, and for $\widehat{\varphi }\in Dom(A(\mathit{q}))$, we have $A(\mathit{q})\widehat{\varphi }=A(\mathit{q})(\varphi (0),\varphi )=\left(q_1{\varphi }^{\prime }(0),q_1{\varphi }^{″}\right)$. It follows that $A(\mathit{q})$ is densely defined on $H$, regularly dissipative and self-adjoint ( [5,61]). Hence, $A(\mathit{q})$ is the infinitesimal generator of a uniformly exponentially stable, self-adjoint, analytic semigroup of bounded linear operators, $\left\{e^{A(\mathit{q})t}:t\ge 0\right\}$, on $H$ ( [5,41,61]).

The system (2) can now be rewritten as $\frac{d\widehat{v}}{dt}(t)=A(\mathit{q})\widehat{v}(t)+q_1{q}_2(1,0)u_k$ where $\widehat{v}(k\tau )=\left(w_k,x_k-\xi u_k\right)$ in the interval $k\tau \le t<(k+1)\tau$. Letting $\widehat{x_k}=\left(w_k,x_k\right)$, and defining the operators $\widehat{A}(\mathit{q})=e^{A(\mathit{q})\tau }\in 𝓛(H,H)$, $B(\mathit{q})=q_1{q}_2(1,0)-A(\mathit{q})(0,\xi )\in 𝓛\left({ℝ}^1,H\right)$, and $\widehat{B}(\mathit{q})\in 𝓛\left({ℝ}^1,H\right)$ by

$$\begin{gathered} \widehat{B}(\mathit{q})=\underset{0}{\overset{\tau }{\int }}{e}^{A(\mathit{q})s}B(\mathit{q})ds=A{\left(\mathit{q}\right)}^{-1}{e}^{A(\mathit{q})s}B(\mathit{q}){|}_0^{\tau } \\ =(\widehat{A}(\mathit{q})-I)A{\left(\mathit{q}\right)}^{-1}B(\mathit{q}) \\ =(I-\widehat{A}(\mathit{q}))\left((0,\xi )-q_1{q}_{2}A{\left(\mathit{q}\right)}^{-1}(1,0)\right)\in 𝓛\left({ℝ}^1,H\right), \end{gathered}$$

the system (2) and the variation of constants formula yield the state space form of the individual model given by

$$\begin{gathered} {\widehat{x}}_{k+1}=\left(w_{k+1},x_{k+1}\right)=(w((k+1)\tau ),x((k+1)\tau ,\cdot )) \\ =\widehat{v}((k+1)\tau )+(0,\xi )u_k \\ =e^{A(\mathit{q})\tau }\left(w_k,x_k-\xi u_k\right)+q_1{q}_2\underset{0}{\overset{\tau }{\int }}{e}^{A(\mathit{q})s}(1,0)ds{u}_k \\ +(0,\xi )u_k \\ =\widehat{A}(\mathit{q}){\widehat{x}}_k+(I-\widehat{A}(\mathit{q}))(0,\xi )u_k \\ +q_1{q}_{2}A{\left(\mathit{q}\right)}^{-1}(\widehat{A}(\mathit{q})-I)(1,0)u_k \\ =\widehat{A}(\mathit{q}){\widehat{x}}_k+\widehat{B}(\mathit{q})u_k. \end{gathered}$$

The ellipticity of $A(\mathit{q})$ ensures that $A{\left(\mathit{q}\right)}^{-1}\in 𝓛(H,H)$ exists.

Then, setting the output operator $\widehat{C}\in 𝓛(H,ℝ)$ as $\widehat{C}(\theta ,\varphi )=\theta$ for $(\theta ,\varphi )\in H$, the discrete time model (2) becomes

$${\widehat{x}}_{k+1}=\widehat{A}(\mathit{q}){\widehat{x}}_k+\widehat{B}(\mathit{q})u_k,y_k=\widehat{C}{\widehat{x}}_k,k=0,1,2,\dots ,$$ (3)

with ${\widehat{x}}_0=\left(w_0,{\varphi }_0\right)$.

2.1.3. The Population Model.

We now assume that $\mathit{q}$ is a random vector denoted by $q$. We rely on ideas from [21,50]; the now random system (3) is converted to weak form as a deterministic system in a Gelfand triple of Bochner spaces [54]. We assume that $q$ is compactly supported in ${\times }_{i=1}^2\left[a_i,b_i\right]$ for some $-\infty <\overline{a}<a_i<b_i<\overline{b}<\infty$. Let $\mathit{a}=\left[a_1,a_2\right]$, $\mathit{b}=\left[b_1,b_2\right]$, and let $\text{Γ}$ be a compact subset of either a finite or infinite dimensional space. We assume that $q\sim F$ or equivalently $q\sim \pi$ where $F(q;[\mathit{a},\mathit{b},\gamma ])$ is an absolutely continuous cumulative distribution function and $\pi$ is a push forward measure $\pi =\pi ([\mathit{a},\mathit{b},\gamma ])$ for $\gamma \in \text{Γ}$. The parameter vector $\theta$, $\theta =(\mathit{a},\mathit{b},\gamma )\in \text{Θ},\text{Θ}$ a set of feasible parameters, defines the distribution of the random model parameters, $q$, and will have to be estimated from samples of $q$. How this is done will be discussed in greater detail in the next section. In what follows, we show this dependence on the estimated distribution defined by $\theta \in \text{Θ}$ by writing $\pi (\theta )\sim f(\theta )$ with $f(\theta )=f(\cdot ;\theta )$ being the corresponding density function.

We define the Bochner spaces $𝒱=L_{\pi }^2(Q;V)$ and $\mathscr{H}=L_{\pi }^2(Q;H)$ yielding the Gelfand triple $𝒱\mapsto \mathscr{H}\mapsto {𝒱}^{\ast }$ where ${𝒱}^{\ast }$ denotes the dual of $𝒱$. We define the bilinear form $a(\theta ;\cdot ,\cdot )$ on $𝒱\times 𝒱$ as a $\pi$-weighted version of $a(\mathit{q};\cdot ,\cdot )$ by

$$a(\theta ;\widehat{\varphi },\widehat{\psi })={\mathbb{E}}_{\pi }(a(\mathit{q};\widehat{\varphi }(\mathit{q}),\widehat{\psi }(\mathit{q})))=\underset{Q}{\int }a(\mathit{q};\widehat{\varphi }(\mathit{q}),\widehat{\psi }(\mathit{q}))d\pi (\mathit{q};\theta )$$

for $\widehat{\varphi }$, $\widehat{\psi }\in 𝒱$. Using properties (i)-(iii) it is not difficult to show [2] that $a(\cdot ;\cdot ,\cdot )$ is also a bounded and coercive bilinear form on $𝒱\times 𝒱$ with the same boundedness and coercivity constants as $a(\cdot ;\cdot ,\cdot )$.

We define the bounded linear map $𝒜(\theta ):𝒱\to {𝒱}^{\ast }$ By ${\langle 𝒜\widehat{\varphi },\widehat{\psi }\rangle }_{{𝒱}^{\ast },𝒱}=-a(\theta ;\widehat{\varphi },\widehat{\psi })$. The operator $𝒜$ can be either restricted or extended to being the infinitesimal generator of an analytic semigroup of bounded linear operators, $𝒯(t;\theta )=\left\{e^{𝒜(\theta )t}:t\ge 0\right\}$, on $𝒱$, $\mathscr{H}$ and ${𝒱}^{\ast }$, see [5,61].

Let $𝒰=L_{\pi }^2(Q;ℝ)$, and define the operator $ℬ(\theta )\in 𝓛(𝒰,\mathscr{H})$ by

$$\langle ℬ(\theta )u,\widehat{\psi }\rangle ={\mathbb{E}}_{\pi (\theta )}(\langle B(\mathit{q})u(\mathit{q}),\widehat{\psi }(\mathit{q})\rangle )=\underset{Q}{\int }\langle B(\mathit{q})u(\mathit{q}),\widehat{\psi }(\mathit{q})\rangle d\pi (\mathit{q};\theta )$$

for $u\in 𝒰$, and set $\widehat{𝒜}(\theta )=𝒯(\tau ;\theta )\in 𝓛(\mathscr{H},\mathscr{H})$, $\widehat{ℬ}(\theta )=𝒜{(\theta )}^{-1}(\widehat{𝒜}(\theta )-𝓘)ℬ(\theta )\in 𝓛(𝒰,\mathscr{H})$, where $𝓙$ is the identity on $\mathscr{H}$. The form $a(\cdot ;\cdot ,\cdot )$ being coercive, possibly together with a change of variables, yield that $𝒜{(\theta )}^{-1}$ exists and is bounded. Let the output operator $\widehat{𝒞}(\theta )$ be given by $\widehat{𝒞}(\theta )\widehat{\varphi }={\mathbb{E}}_{\pi (\theta )}(\widehat{C}\widehat{\varphi })\in 𝓛(\mathscr{H},ℝ)$.

With the dependence on the distribution parameters $\theta \in \text{Θ}$ now understood to be present but no longer explicitly displayed,the population model is then given by the discrete-time system

$${\widehat{x}}_{k+1}=\widehat{𝒜}{\widehat{x}}_k+\widehat{ℬ}{\widehat{u}}_k,{\widehat{y}}_k=\widehat{𝒞}{\widehat{x}}_k,k=0,1,2,\dots ,K,$$ (4)

with $u_k\in 𝒰$ and ${\widehat{x}}_0={\widehat{x}}_0=\left(w_0,{\varphi }_0\right)\in \mathscr{H}$.

2.2. Estimating the Distribution of the Random Parameters in the Population Model.

The ideas presented and discussed in this section were originally presented in our proceedings paper from the 2023 American Control Conference [2]. For completeness we include them here. The distribution of the random parameters in the population model can be estimated either parametrically or non-parametrically. We assume that BrAC and TAC data pairs, ${\left\{{\left\{u_{j,k}\right\}}_{k=0}^K,{\left\{y_{j,k}\right\}}_{k=0}^K\right\}}_{j=1}^M$ or M drinking episodes have been collected in the lab or clinic under the assumptions that $M$ is sufficiently large and that the population has adequate representation with respect to physiological characteristics of the cohort of subjects of interest (e.g. sex, age, BMI, race, etc.), variations in sensor devices (e.g. manufacturer, calibration, etc.), and environmental conditions (e.g. ambient temperature, humidity, etc.). We assume further that these BrAC/TAC data pairs are used to estimate values for the parameters $\mathit{q}=\left[q_1,q_2\right]$ that appear in the individual model (1) or (2) yielding the $M$ individual model parameter estimates, ${\left\{{\mathit{q}}_j=\left[q_{1,j},q_{2,j}\right]\right\}}_{j=1}^M$

2.2.1. Parametric Estimation of the Population Distribution.

In this section we discuss a method of moments [9,42] fit of a four parameter generalized beta distribution for the individual parameters $\mathit{q}=\left[q_1,q_2\right]$ appearing in the individual model (1) or (2). The population parameters are $\theta =[\mathit{a},\mathit{b},\gamma ]$, where $\mathit{a}=\left[a_1,a_2\right]$, $\mathit{b}=\left[b_1,b_2\right]$, and $\gamma =\left[{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2\right]\in {ℝ}^4$. Consequently, in this case $\text{Θ}$ is assumed to be a compact subset of ${ℝ}^8$. Other parametric techniques (e.g. maximum likelihood, Bayesian, etc.) and other distributions (e.g. normal, Gamma, etc.) yield similar results.

The probability density function (pdf) for the four parameter Beta distribution is given by $f(q;\alpha ,\beta ,a,b)=\frac{\text{Γ}(\alpha +\beta )}{\text{Γ}(\alpha )\text{Γ}(\beta )}\frac{{(q-a)}^{\alpha -1}{(b-q)}^{\beta -1}}{{(b-a)}^{\alpha +\beta -1}}$, $-\infty <a\le q\le b<\infty$ where the parameters are such that the interval $[a,b]$ is known as the support and $\alpha$ and $\beta$ are known as the shape parameters. We estimate the parameters using Pearson’s Method of Moments [23] wherein the population variance, skewness and excess kurtosis are equated with their population values. Although it is not required by our framework, in this case we assume that $q_1$ and $q_2$ are independent, and fit a four parameter beta distribution to samples of each of them and take the joint pdf to be the product of the two marginal pdfs.

For $i=1,2$, the sample mean, ${\overline{q}}_i$, variance, $s_i^2$, skewness, $G_{1,i}$, and excess kurtosis, $G_{2,i}$, are given by ${\overline{q}}_i=\frac{1}{n_i}{{\sum }_{j=1}^{n_i}q}_{i,j}$, $s_i^2=\frac{1}{n_i-1}{{\sum }_{j=1}^{n_i}\left(q_{i,j}-{\overline{q}}_i\right)}^2$, $G_{1,i}=\frac{n_i}{\left(n_i-1\right)\left(n_i-2\right)}\frac{{\sum }_{j=1}^{n_i}{\left(q_{i,j}-{\overline{q}}_i\right)}^3}{{\left(s_i^2\right)}^{\frac{3}{2}}}$, and $G_{2,i}=\frac{n_i\left(n_i+1\right)}{\left(n_i-1\right)\left(n_i-2\right)\left(n_i-3\right)}\frac{{\sum }_{j=1}^{n_i}{\left(q_{i,j}-{\overline{q}}_i\right)}^4}{{\left(s_i^2\right)}^2}-\frac{3{\left(n_i-1\right)}^2}{\left(n_i-2\right)\left(n_i-3\right)}$, respectively. On the other hand, the population mean, ${\mu }_i$, variance, ${\sigma }_i^2$, skewness, ${\gamma }_{1,i}$, and excess kurtosis, ${\gamma }_{2,i}$, are given by ${\mu }_i=a_i+\left(b_i-a_i\right)\frac{{\alpha }_i}{{\alpha }_i+{\beta }_i}$, ${\sigma }_i^2={\left(b_i-a_i\right)}^2\frac{{\alpha }_i{\beta }_i}{\left({\alpha }_i+{\beta }_i\right)\left(1+{\alpha }_i+{\beta }_i\right)}$, ${\gamma }_{1,i}^2=\frac{4{\left({\beta }_i-{\alpha }_i\right)}^2\left(1+{\alpha }_i+{\beta }_i\right)}{{\alpha }_i{\beta }_i{\left(2+{\alpha }_i+{\beta }_i\right)}^2}$, and ${\gamma }_{2,i}=\frac{6}{3+{\alpha }_i+{\beta }_i}\left(\frac{2+{\alpha }_i+{\beta }_i}{4}{\gamma }_{1,i}^2-1\right)$ respectively.

Setting ${\mu }_i={\overline{q}}_i$, ${\sigma }_i^2=s_i^2$, ${\gamma }_{1,i}=G_{1,i}$, and ${\gamma }_{2,i}=G_{2,i}$ then solving for ${\alpha }_i^{\ast }$, ${\beta }_i^{\ast }$, $a_i^{\ast }$, and $b_i^{\ast }$, we obtain estimated distributions for $q_i$ as $q_i\sim f\left(q_i;{\alpha }_i^{\ast },{\beta }_i^{\ast },a_i^{\ast },b_i^{\ast }\right)$, for $q_i\in \left[a_i^{\ast },b_i^{\ast }\right]$, $i=1,2$. Then with the assumption of independence, we obtain the joint distribution as $q=\left[q_1,q_2\right]\sim f\left(\mathit{q},{\theta }^{\ast }\right)=f\left(q_1;{\alpha }_1^{\ast },{\beta }_1^{\ast },a_1^{\ast },b_1^{\ast }\right)f\left(q_2;{\alpha }_2^{\ast },{\beta }_2^{\ast },a_2^{\ast },b_2^{\ast }\right)$ for $\mathit{q}=\left[q_1,q_2\right]\in \left[a_1^{\ast },b_1^{\ast }\right]\times \left[a_2^{\ast },b_2^{\ast }\right]$, where ${\theta }^{\ast }=\left[{\mathit{a}}^{\ast },{\mathit{b}}^{\ast },{\gamma }^{\ast }\right]$ with ${\mathit{a}}^{\ast }=\left[a_1^{\ast },a_2^{\ast }\right]$, ${\mathit{b}}^{\ast }=\left[b_1^{\ast },b_2^{\ast }\right]$, and ${\gamma }^{\ast }=\left[{\alpha }_1^{\ast },{\beta }_1^{\ast },{\alpha }_2^{\ast },{\beta }_2^{\ast }\right]$.

2.2.2. Non-Parametric Estimation of the Population Distribution.

In this section, we describe a non-parametric approach based on kernel density estimation [40, 46, 51, 63] and spline-based interpolation and re-sampling. Let ${\mathbf{\text{q}}}_1,{\mathbf{\text{q}}}_2,\dots ,{\mathbf{\text{q}}}_n$ be independent and identically distributed samples drawn from a bivariate distribution with an unknown density $f$. Then the kernel density estimate of $f$ at $\mathit{q}=\left[q_1,q_2\right]$ is given by $\widehat{f}(\mathit{q};\mathit{W})=\frac{1}{n}\sum _{i=1}^n{K}_{\mathit{W}}(\mathit{q}-{\mathbf{\text{q}}}_i)$, where $\mathit{q}=\left[q_1,q_2\right]$ and ${\mathbf{\text{q}}}_i=\left(q_{1,i},q_{2,i}\right)$, $i=1,\dots ,n$. Here $\mathit{W}\in {ℝ}^{2\times 2}$ is known as the bandwidth matrix; it is assumed to be positive definite symmetric. For $\mathit{x}\in {ℝ}^2$, $K_{\mathit{W}}(\mathit{x})=|\mathit{W}{|}^{-1/2}K\left({\mathit{W}}^{-1/2}\mathit{x}\right)$ is known as the kernel smoothing function, a non-negative, square integrable function whose integral over ${ℝ}^2$ is one. So, for example, the Matlab routine MVKSDENSITY takes $\mathit{W}=\text{diag}\left(h_1,h_2\right)$ with $h_i>0$, $i=1,2$ and $K$ to be a tensor product of one dimensional kernel smoothing functions, $K(\mathit{x})=k_1\left(x_1\right)k_2\left(x_2\right)$, $\mathit{x}\in {ℝ}^2$. In this case we have

$$\widehat{f}(\mathit{q};\mathit{W})=\frac{1}{n}\sum _{i=1}^n\frac{1}{\sqrt{h_1{h}_2}}{k}_1\left(\frac{q_1-q_{1,i}}{\sqrt{h_1}}\right)k_2\left(\frac{q_2-q_{2,i}}{\sqrt{h_2}}\right).$$ (5)

In addition, Matlab’s routine relies on kernel smoothing functions derived from standard normal densities which are then shifted to have means at the sample points and variances determined by the band width matrix. Once the estimated kernel has been fit, it can be evaluated at any desired resolution and, if its derivatives are needed, it can be interpolated with, for example, spline functions. Finally we note that under reasonable assumptions it can be argued that the kernel density estimator is consistent.

2.3. The Linear Quadratic Regulator (LQR) in Hilbert Space.

The discrete time linear quadratic regulator (LQR) problem for the individual model with the parameters $\mathbf{\text{q}}$ assumed random with $\mathbf{\text{q}}\sim \pi$ involves the minimization of the quadratic performance index

$$\widehat{J}(\widehat{u})={\mathbb{E}}_{\pi }\left\{\sum _{k=k_0}^{k_1-1}{\left|\widehat{C}{\widehat{x}}_k\right|}^2+\widehat{r}{\widehat{u}}_k^2+\widehat{\rho }{\left|\widehat{C}{\widehat{x}}_{k_1}\right|}^2\right\},$$

where $\widehat{r}>0$, $\widehat{\rho }\ge 0$, $k_1$ can be either finite or infinite (in the latter case, $\widehat{\rho }=0$) and when $\mathit{q}=q$, ${\widehat{x}}_k$ is given by

$${\widehat{x}}_{k+1}=\widehat{A}(\mathbf{\text{q}}){\widehat{x}}_k+\widehat{B}(\mathbf{\text{q}}){\widehat{u}}_k,k=k_0,1,2,\dots ,k_1-1,$$ (6)

with ${\widehat{x}}_0=(w(0),x(0,\cdot ))\in H$, $\widehat{A}(\mathbf{\text{q}})=e^{A(\mathbf{\text{q}})\tau }\in 𝓛(H,H)$ and, since $-A(q)$ is coercive, and hence either invertible or may be made so without loss of generality via a change of variable, that $\widehat{B}(\mathbf{\text{q}})=A{(\mathbf{\text{q}})}^{-1}(\widehat{A}(\mathbf{\text{q}})-I)B(\mathbf{\text{q}})\in 𝓛(ℝ,H)=H$ with $\widehat{B}(\mathbf{\text{q}})\in Dom(A(\mathbf{\text{q}}))$.

The discrete time LQR problem defined above in terms of the performance index $\widehat{J}$ given above can then be equivalently reformulated in $\mathscr{H}$ in terms of our population model (4). Let

$$\widehat{𝓙}(\widehat{u})=\sum _{k=k_0}^{k_1-1}{\left|\widehat{𝒞}{\widehat{x}}_k\right|}^2+\parallel \widehat{ℛ}{\widehat{u}}_k{\parallel }_u^2+\widehat{\rho }{\left|\widehat{𝒞}{\widehat{x}}_{k_1}\right|}^2,$$ (7)

where $\widehat{ℛ}\in 𝓛(𝒰,𝒰)$ is given by $\widehat{ℛ}u=\sqrt{\widehat{r}}u$, and

$$\begin{gathered} {\widehat{x}}_{k+1}=\widehat{𝒜}{\widehat{x}}_k+\widehat{ℬ}{\widehat{u}}_k,x_0={\widehat{\phi }}_0\in \mathscr{H}, \\ {\widehat{y}}_k=\widehat{𝒞}{\widehat{x}}_k,k=k_0,k_0+1,k_0+2,\dots , \end{gathered}$$ (8)

where $x=(w,x)\in \mathscr{H}$ with all components now functions of $q\in Q$. The quadratic performance index $\widehat{𝓙}$ given in (7) is equivalent to $\widehat{J}$ and the solution to (8) agrees with the solution to (6), $\pi$ almost surely on $Q$ [21,50].

2.3.1. Full State Feedback Solution to the Sampled-Time LQR Problem.

Since in the discrete or sampled time LQR formulation, all relevant operators are bounded (in particular, the state transition operator), the sampled time LQR theory on both the finite and infinite time horizons in Hilbert space is entirely analogous to the finite dimensional case [30] with the exception of the fact that the Riccati matrix equations, the expressions for the gains, and the matrices themselves are simply replaced by their operator counterparts. We briefly summarize the relevant results (see, for example, [20,30,33]) for both the finite and infinite time horizon problems. In a subsequent section we summarize the finite dimensional approximation and convergence theories upon which our computational schemes are based.

When $k_1<\infty$, for every initial value, $x_0$, the optimal input, $\overline{u}$ is unique and given by the following control law in the form of a linear feedback of the optimal trajectory $\widehat{x}$ as

$${\widehat{u}}_k=-{\widehat{ℱ}}_k{\widehat{x}}_k=-{\left({\widehat{ℬ}}^{\ast }{𝒦}_{k+1}\widehat{ℬ}+\widehat{ℛ}\right)}^{-1}{\widehat{ℬ}}^{\ast }{𝒦}_{k+1}\widehat{𝒜}{\widehat{x}}_k,k=k_0,k_0+1,\dots ,k_1-1,$$ (9)

where ${\widehat{ℱ}}_k={\left({\widehat{ℬ}}^{\ast }{𝒦}_{k+1}\widehat{ℬ}+\widehat{ℛ}\right)}^{-1}{\widehat{ℬ}}^{\ast }{𝒦}_{k+1}\widehat{𝒜}\in 𝓛(\mathscr{H},𝒰)$ with ${𝒦}_k$, computed backwards from $k_1$ to $k_0$ according to the Riccati difference equation given by

$${𝒦}_k={\widehat{𝒜}}^{\ast }\left[{𝒦}_{k+1}-{𝒦}_{k+1}\widehat{ℬ}{\left({\widehat{ℬ}}^{\ast }{𝒦}_{k+1}\widehat{ℬ}+\widehat{ℛ}\right)}^{-1}{\widehat{ℬ}}^{\ast }{𝒦}_{k+1}\right]\widehat{𝒜}+\widehat{𝒬},{𝒦}_{k_1}=\widehat{𝒢},$$ (10)

$k=k_1-1$, $k_1-2,\dots ,2,1,0$. In equations (9) and (10), $\widehat{𝒬}={\widehat{𝒞}}^{\ast }\widehat{𝒞}\in 𝓛(\mathscr{H},\mathscr{H})$, $\widehat{𝓙}=\widehat{\rho }{\widehat{𝒞}}^{\ast }\widehat{𝒞}\in 𝓛(\mathscr{H},\mathscr{H})$, and $\widehat{\Re }\in 𝓛(𝒰,𝒰)$ is positive definite and self adjoint as was given above.

When $k_1=\infty$, $\widehat{\rho }=0$. By Theorem 2.4 in [20] (see also [66]), $\widehat{𝒜}$ self adjoint and open loop stable, implies that the solution to the algebraic Riccati equation (ARE)

$$𝒦={\widehat{𝒜}}^{\ast }\left[𝒦-𝒦\widehat{ℬ}{\left({\widehat{ℬ}}^{\ast }𝒦\widehat{ℬ}+\widehat{\Re }\right)}^{-1}{\widehat{ℬ}}^{\ast }𝒦\right]\widehat{𝒜}+\widehat{𝒬}$$ (11)

exists, is unique, self-adjoint, and positive definite, and the efficacy of the linear state feedback controller

$${\widehat{u}}_k=-\widehat{ℱ}{\widehat{x}}_k=-{\left({\widehat{ℬ}}^{\ast }𝒦\widehat{ℬ}+\widehat{ℛ}\right)}^{-1}{\widehat{ℬ}}^{\ast }𝒦\widehat{𝒜}{\widehat{x}}_k,k=k_0,k_0+1,\dots$$ (12)

is guaranteed, where $\widehat{ℱ}={\left({\widehat{ℬ}}^{\ast }𝒦\widehat{ℬ}+\widehat{ℛ}\right)}^{-1}{\widehat{ℬ}}^{\ast }𝒦\widehat{𝒜}\in 𝓛(\mathscr{H},𝒰)$.

It is important to realize that with the model parameters, $q$ being random, necessarily the state, $\widehat{x}$, the TAC output $\widehat{y}$, and the BrAC input $\widehat{u}$ are all random as well. We assume that in practice researchers and clinicians will be most interested in the means of these quantities, $\overline{x}=E_{\pi }[\widehat{x}]$, $\overline{y}=E_{\pi }[\widehat{y}]$, and $\overline{u}=E_{\pi }[\widehat{u}]$, respectively.

In addition, typically in practice, the full state is not observed and consequently must be estimated via an observer; the most common choice taking the form of a Kalman filter. In addition, the state and output equations in the model are corrupted by noise. If the noise processes are zero-mean, stationary, Gaussian and white, the Kalman observer provides the minimum variance estimate of the state. The combined LQR controller and the Kalman observer is referred to a a linear quadratic Gaussian (LQG) compensator [19,65,66]. In the application of interest to us here where it is the model itself that we want to control, the full state is of course accessible and noise is not a factor.

2.4. Finite Dimensional Approximation and Convergence.

All of the expressions in previous section involve operators on infinite dimensional spaces. Actually computing the optimal output feedback tracking controller using these expressions requires finite dimensional approximation. Define the multi-index $N=\left(n,m_1,m_2\right)$, partition the interval $\left[a_i,b_i\right]$ into $m_i$ subintervals of equal width for $i=1,2$ and denote the characteristic function on the $j$-th subinterval by ${\chi }_j^{m_i}$ for $j=1,\dots ,m_i$. For $n=1,2,\dots$ let ${\left\{{\varphi }_j^n\right\}}_{j=0}^n$ be the standard linear B-splines (i.e. ”pup tent” or ”chapeau” functions on [0, 1] with respect to the uniform mesh $\left\{0,\frac{1}{n},\frac{2}{n},\dots ,1\right\}$ [49] and define ${\widehat{\varphi }}_j^n=\left({\varphi }_j^n(0),{\varphi }_j^n\right)\in V$.

Define the multi-index $J=\left(j_0,j_1,j_2\right)$ with $j_0\in \{0,1,\dots ,n\}$ and $j_i\in \left\{1,2,\dots ,m_i\right\}$, $i=1,2$. Let ${\text{Φ}}_J^N={\widehat{\varphi }}_{j_0}^n{\prod }_{i=1}^2{\chi }_{j_i}^{m_i}$, let ${𝒱}^N={\text{span}}_J\left\{{\text{Φ}}_J^N\right\}$, and let ${𝒰}^N=\text{span}\left\{{{\prod }_{i=1}^2\chi }_{j_i}^{m_i}\right\}$. Denoting the orthogonal projection of $\mathscr{H}$ onto ${𝒱}^N$ by ${𝒫}^N:\mathscr{H}\to {𝒱}^N$, it can be argued that ${𝒫}^N$ converges strongly to the identity in both $\mathscr{H}$ and $𝒱$, see [49]. Standard Galerkin approximation is used to define ${𝒜}^N$, an approximation to the operator $𝒜$ [54]. Then let ${\widehat{𝒜}}^N=\text{exp}\left({𝒜}^N\tau \right)\in 𝓛\left({𝒱}^N,{𝒱}^N\right)$, ${\widehat{ℬ}}^N={\left({𝒜}^N\right)}^{-1}\left({\widehat{𝒜}}^N-{𝓘}^N\right){𝒫}^Nℬ\in 𝓛\left({𝒰}^N,{𝒱}^N\right)$, and ${\widehat{𝒞}}^N=\widehat{𝒞}{𝒫}^N$.

With the above definitions of approximating subspaces and approximating operators, functional analytic arguments can be used to establish convergence. Ind eed, using the boundedness and coercivity assumptions, (i) and (ii), one can demonstrate resolvent convergence for the operators ${𝒜}^N$ to the resolvent of the operator $𝒜$. Since Galerkin approximation was used to define the operators ${𝒜}^N$, the the coercivity condition (ii) implies that the approximating semigroups, $\left\{\text{exp}\left({𝒜}^{N}t\right):t\ge 0\right\}$ are uniformly (in $N$) exponentially stable. It follows from the Trotter Kato Theorem from linear semigroup theory [41, 54]) that the operators ${\widehat{𝒜}}^N=e^{{𝒜}^N\tau }$ converge strongly to the operator $\widehat{𝒜}=e^{𝒜\tau }$. The definition of the operators ${\widehat{ℬ}}^N$ and ${\widehat{𝒞}}^N$ involving the orthogonal projections ${𝒫}^N$ and the strong convergence of the operators ${𝒫}^N$ to the identity are sufficient to conclude the convergence of $x_k^N$ to $x_k$ and $y_k^N$ to $y_k$, uniformly in $k$ on finite index sets.

Define ${\widehat{𝒬}}^N={\left({\widehat{𝒞}}^N\right)}^{\ast }{\widehat{𝒞}}^N$, ${\widehat{𝒢}}^N=\rho {\left({\widehat{𝒞}}^N\right)}^{\ast }{\widehat{𝒞}}^N$, and ${\widehat{ℛ}}^N=\widehat{ℛ}\in 𝓛\left({𝒰}^N,{𝒰}^N\right)$. Then, when $k_1<\infty$, the corresponding equations for the approximating controller are then given by

$${𝒦}_k^N={\left({\widehat{𝒜}}^N\right)}^{\ast }\left[{𝒦}_{k+1}^N-{𝒦}_{k+1}^N{\widehat{ℬ}}^N{\left({\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}_{k+1}^N{\widehat{ℬ}}^N+{\widehat{ℛ}}^N\right)}^{-1}{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}_{k+1}^N\right]{\widehat{𝒜}}^N+{\widehat{𝒬}}^N,$$ (13)

$k=k_1-1$, $k_1-2,\dots ,k_0$, with ${𝒦}_{k_1}^N={\widehat{𝒢}}^N$. The approximating optimal control, ${\widehat{u}}^N$, is given by ${\widehat{u}}_k^N=-{\widehat{ℱ}}_k^N{\widehat{x}}_k^N$, where ${\widehat{ℱ}}_k^N={\left[{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}_{k+1}^N{\widehat{ℬ}}^N+{\widehat{ℛ}}^N\right]}^{-1}{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}_{k+1}^N{\widehat{𝒜}}^N\in 𝓛\left({𝒱}^N,{𝒰}^N\right)$.

For the finite dimensional approximation scheme for the open-loop system (4) given in Section 2.1.3 and the convergence properties stated above, it is shown in, for example, [20], that ${𝒦}_k^N{𝒫}^N$ converges strongly to ${𝒦}_k$, $k\in \left[k_0,k_1\right]$, and ${ℱ}_k^N{𝒫}^N$ converges strongly to ${ℱ}_k$, $k=k_0$, $k_0+1,\dots ,k_1$. The approximating closed loop control, ${\widehat{u}}^N$, and closed loop state, ${\widehat{x}}^N$, converge to $\widehat{u}$ and $\widehat{x}$, respectively, in $l^2$, where the $l^2$ inner product and corresponding norm are defined by either ${\langle x,y\rangle }_{l^2(\mathscr{H})}={\sum }_{k=k_0}^{k_1}{\langle x_k,y_k\rangle }_{\mathscr{H}}$ for any $x$ and $y$ in $l^2\left(k_0,k_1;\mathscr{H}\right)$ or ${\langle u,v\rangle }_{l^2\left(𝒰\right)}={{\sum }_{k=k_0}^{k1}\langle u_k,v_k\rangle }_{𝒰}$ for any $u$ and $v$ in $l^2(k_0,k_1;𝒰)$. The approximating cost functions ${\widehat{𝓙}}^N\left({\widehat{u}}^N\right)$ also converge to $\widehat{𝓙}\left(\widehat{u}\right)$ as $N\to \infty$.

When $k_1=\infty$ and $\widehat{\rho }=0$, Theorems 3.9 and 3.10 in [20] yield that for each multi-index $N$ a positive semi-definite self-adjoint solution, ${𝒦}^N$, to the algebraic Riccati equation

$${𝒦}^N={\left({\widehat{𝒜}}^N\right)}^{\ast }\left\{{𝒦}^N-{𝒦}^N{\widehat{ℬ}}^N{\left[{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}^N{\widehat{ℬ}}^N+{\widehat{ℛ}}^N\right]}^{-1}{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}^N\right\}{\widehat{𝒜}}^N+{\widehat{𝒬}}^N,$$ (14)

exists, the approximating tracking controller, ${\widehat{u}}^N$, is

$${\widehat{u}}_k^N=-{\widehat{ℱ}}^N{\widehat{x}}_k^N=-{\left[{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}^N{\widehat{ℬ}}^N+{\widehat{ℛ}}^N\right]}^{-1}{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}^N{\widehat{𝒜}}^N{\widehat{x}}_k^N,$$ (15)

where ${\widehat{ℱ}}^N={\left[{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}^N{\widehat{ℬ}}^N+{\widehat{ℛ}}^N\right]}^{-1}{\left({\widehat{ℬ}}^N\right)}^{\ast }{𝒦}^N{\widehat{𝒜}}^N\in 𝓛\left({𝒱}^N,{𝒰}^N\right)$, and, analogous to the finite time horizon case, convergence of ${𝒦}^N$, ${ℱ}^N$, ${\widehat{u}}^N$, ${\widehat{x}}^N$, and ${\widehat{𝓙}}^N$ to their infinite dimensional counterparts, as $N\to \infty$, can be established [20, 65, 66].

We note that while the equations (13)–(15) are in fact finite dimensional, when actually carrying out the computations, one can not simply replace the operators and their adjonts with the corresponding matrix representations and their transposes to obtain standard matrix Riccati and gain formulas from the finite dimensional LQ theory [30]. Indeed, since the basis for our approximating subspaces ${𝒱}^N$ are not orthonormal, the Gram matrix is not equal to the identity. Consequently this fact must be taken into account when computing the matrix representations of the operator adjoints that appear in the equations. However, a simple change of variables involving the Gram matrix for the ${𝒱}^N$ basis does then yield the readily recognized equations from the finite dimensional LQ theory (see, for example, [18–20, 65, 66]).

2.5. Uncertainty Quantification.

The operators $\widehat{𝒜}$, $\widehat{ℬ}$, and $\widehat{𝓒}$ that define our model (8) and the quadratic performance index (7) all depend on the random parameters, $q$ and their distribution. Consequently, so too then does the solution the Riccati equations (10) and (11), and therefore the feedback gains as well. It follows that our estimated BrAC, or eBrAC, signal, $\widehat{u}=\widehat{u}(q)$ is also a function of the random parameters $q$ and their distribution. Moreover, the nature of our finite dimensional approximation scheme is that we actually determine the approximating Riccati operators, ${𝒦}_k^N$ or ${𝒦}^N$, feedback gains, ${\widehat{ℱ}}_k^N$ or ${\widehat{ℱ}}^N$, and therefore the approximating eBrAC signal, ${\widehat{u}}^N$ itself all as explicit functions of $\mathbf{\text{q}}$. Then by sampling our estimated distribution of the random parameters $q$, and then evaluating these explicit functions of $\mathit{q}$ at those samples, we can obtain conservative error bands for our estimates. More precisely, for example, in the case of the approximating eBrAC signal, ${\widehat{u}}^N$, the event $\{q\in 𝒬\}$ is contained in the event $\left\{{\widehat{u}}^N(q)\in {\widehat{u}}^N(𝒬)\right\}$, and consequently, therefore, $P\left(\left\{{\widehat{u}}^N(q)\in {\widehat{u}}^N(𝒬)\right\}\right)\ge P(\{q\in 𝒬\})$. We note that in our framework, these functions are $L_2$, so consequently, strictly speaking, pointwise evaluation at $\mathbf{\text{q}}$ is undefined. We have verified these UQ estimates via simulation, but we are also investigating ways to increase regularity by, for example, introducing $H^1$ coercivity into the population model.

2.6. An LQR and Population Model-Based Real-Time, Recursive, Regularized BrAC Estimator.

In this section we show how the infinite dimensional and finite dimensional approximating LQR control theory presented in Sections 2.3 and 2.4 can be adapted 1) to force the output of the model to track a given biosensor TAC signal with the resulting optimal control or input then serving as an approximation to the patient’s or participant’s BAC/BrAC, i.e. the eBrAC signal, and 2) to mitigate the effects of the ill-posedness of the inverse filtering of the biosensor’s TAC signal [54]. In fact, in both cases, the desired effect can be achieved by augmenting the infinite dimensional open loop stste space model with two additional difference equations and then appropriately adjusting the state transition, input, output, and penalty operators in the LQR formulation [22, 68, 69]. The new state variables introduced are effectively the input and output of the original system.

Let ${\left\{{\xi }_k\right\}}_{k=k_0}^{k_1}$ denote the given TAC signal to be inverse filtered and define the augmented SISO system in $\mathscr{H}\times ℝ\times 𝒰$ by

$$\begin{gathered} {\widehat{x}}_{k+1}=\widehat{𝒜}{\widehat{x}}_k+\widehat{ℬ}{\widehat{u}}_k,k=k_0,k_0+1,k_0+2,\dots ,k_1-1, \\ {\widehat{e}}_{k+1}={\widehat{e}}_k+\tau \left({\xi }_{k+\sigma }-\widehat{𝒞}{\widehat{x}}_k\right),k=k_0,k_0+1,k_0+2,\dots ,k_1-1, \\ {\widehat{u}}_{k+1}={\widehat{u}}_k+{\widehat{v}}_k,k=k_0,k_0+1,k_0+2,\dots ,k_1-1, \\ {\widehat{ℨ}}_k={\widehat{e}}_k,k=k_0,k_0+1,k_0+2,\dots ,k_1, \end{gathered}$$ (16)

with ${\tilde{x}}_0=\left({\widehat{x}}_0,{\widehat{e}}_0,{\widehat{u}}_0\right)=\left({\widehat{x}}_0,0,0\right)=(\left(\left(w_0,{\varphi }_0\right),0,0\right)\in \mathscr{H}\times ℝ\times 𝒰$ and $\sigma \ge 0$. We then rewrite the system (16) in state space form in the Hilbert space $\tilde{\mathscr{H}}=\mathscr{H}\times ℝ\times 𝒰$ as

$${\tilde{x}}_{k+1}=\widetilde{𝒜}{\tilde{x}}_k+\widetilde{ℬ}{\tilde{v}}_k+\tau \widetilde{𝒟}{\xi }_{k+\sigma },{\tilde{y}}_k=\widetilde{𝒞}{\tilde{x}}_k,k=k_0,k_0+1,k_0+2,\dots ,k_1-1,$$ (17)

where ${\tilde{x}}_k=\left({\widehat{x}}_k,{\widehat{e}}_k,{\widehat{u}}_k\right)$ $\in \tilde{\mathscr{H}}$, ${\tilde{v}}_k={\widehat{v}}_k$, $k=k_0$, $k_0+1$, $k_0+2,\dots ,k_1$, and

$$\widetilde{𝒜}=\left[\begin{array}{ccc}\widehat{𝒜}& 0& \widehat{ℬ}\\ -\tau \widehat{𝒞}& 1& 0\\ 0& 0& I\end{array}\right]\in 𝓛(\tilde{\mathscr{H}},\tilde{\mathscr{H}}),\widetilde{ℬ}=\left[\begin{array}{l}0\hfill \\ 0\hfill \\ I\hfill \end{array}\right]\in 𝓛(𝒰,\tilde{\mathscr{H}}),\widetilde{𝒟}=\left[\begin{array}{l}0\hfill \\ 1\hfill \\ 0\hfill \end{array}\right]\in 𝓛(ℝ,\tilde{\mathscr{H}}),$$ (18)

and $\widetilde{𝒞}=\text{diag}(\sqrt{\widehat{\delta }}\widehat{𝒞},\sqrt{\widehat{s}},ℛ)\in 𝓛\left(\tilde{\mathscr{H}},{ℝ}^2\times 𝒰\right)$, with $\widehat{\delta }$, $\widehat{s}\ge 0$. Then, defining the operators $\widetilde{ℛ}=[\sqrt{\widehat{p}}]\in 𝓛(𝒰,𝒰)$, with $\widehat{p}>0$, and $\widetilde{𝓔}=\left[\begin{array}{c}\sqrt{\widehat{\rho }}\widehat{𝒞}00\end{array}\right]\in 𝓛(\tilde{\mathscr{H}},ℝ)$, we consider the quadratic performance index

$$\widehat{𝓙}(\tilde{v})=\sum _{k=k_0}^{k_1-1}{\left|\widetilde{𝒞}{\tilde{x}}_k\right|}^2+{\Vert \widetilde{ℛ}{\tilde{v}}_k\Vert }_{𝒰}^2+{\left|\widetilde{𝓔}{\tilde{x}}_{k_1}\right|}^2,$$ (19)

with the goal of driving ${\widehat{e}}_k={\widehat{ℨ}}_k={\tilde{y}}_k\in ℝ$ to zero, while regularizing ${\widehat{u}}_k={\widetilde{ℬ}}^{\ast }{\tilde{x}}_k\in 𝒰$. If $k_1<\infty$, $\widehat{s}>0$, and $\widehat{\delta }\ge 0$, the LQR theory presented in Section 2.3.1 yields that the full state feedback controller

$${\tilde{v}}_k=-{\widetilde{ℱ}}_k{\tilde{x}}_k=-{\left({\widetilde{ℬ}}^{\ast }{\widetilde{𝒦}}_{k+1}\widetilde{ℬ}+\widetilde{ℛ}\right)}^{-1}{\widetilde{ℬ}}^{\ast }{\widetilde{𝒦}}_{k+1}\widetilde{𝒜}{\tilde{x}}_k,k=k_0,k_0+1,\dots ,k_1-1,$$ (20)

will force $y_k=\widehat{C}{\widehat{x}}_k=\widehat{𝒞}{\widehat{x}}_k$ to track ${\xi }_k$, $k=k_0$, $k_0+1,\dots ,k_1$ where ${\widetilde{ℱ}}_k=({\widetilde{ℬ}}^{\ast }{\widetilde{𝒦}}_{k+1}\widetilde{ℬ}+\widetilde{ℛ}{)}^{-1}{\widetilde{ℬ}}^{\ast }{\widetilde{𝒦}}_{k+1}\widetilde{𝒜}\in 𝓛(\tilde{\mathscr{H}},𝒰)$ with ${\widetilde{𝒦}}_k$, computed backwards from $k_1$ to $k_0$ according to the Riccati difference equation given by

$${\widetilde{𝒦}}_k={\widetilde{𝒜}}^{\ast }\left[{\widetilde{𝒦}}_{k+1}-{\widetilde{𝒦}}_{k+1}\widetilde{ℬ}{\left({\widetilde{ℬ}}^{\ast }{\widetilde{𝒦}}_{k+1}\widetilde{ℬ}+\tilde{\Re }\right)}^{-1}{\widetilde{ℬ}}^{\ast }{\widetilde{𝒦}}_{k+1}\right]\widetilde{𝒜}+\widetilde{𝒬},{\widetilde{𝒦}}_{k_1}=\widehat{𝒢},$$ (21)

$k=k_1-1$, $k_1-2,\dots ,2,1,0$, where $\widetilde{𝒬}={\widetilde{𝒞}}^{\ast }\widetilde{𝒞}\in 𝓛(\tilde{\mathscr{H}},\tilde{\mathscr{H}})$ and $\widetilde{𝒢}={\widetilde{𝓔}}^{\ast }\widetilde{𝓔}\in 𝓛(\tilde{\mathscr{H}},\tilde{\mathscr{H}})$.

On the other hand, in [69] it is shown that if $k_1=\infty$, $\widehat{\rho }=0$, $\widehat{s}>0$, and $\widehat{\delta }\ge 0$, the controller

$${\tilde{v}}_k=-\widetilde{ℱ}{\tilde{x}}_k=-{\left({\widetilde{ℬ}}^{\ast }\widetilde{𝒦}\widetilde{ℬ}+\widetilde{ℛ}\right)}^{-1}{\widetilde{ℬ}}^{\ast }\widetilde{𝒦}\widetilde{𝒜}{\tilde{x}}_k,k=k_0,k_0+1,\dots ,k_1-1,$$ (22)

with $\widetilde{ℱ}={\left({\widetilde{ℬ}}^{\ast }\widetilde{𝒦}\widetilde{ℬ}+\widetilde{ℛ}\right)}^{-1}{\widetilde{ℬ}}^{\ast }\widetilde{𝒦}\widetilde{𝒜}\in 𝓛(\tilde{\mathscr{H}},𝒰)$ and $\widetilde{𝒦}$, the solution to the ARE

$$\widetilde{𝒦}={\widetilde{𝒜}}^{\ast }\left[\widetilde{𝒦}-\widetilde{𝒦}\widetilde{ℬ}{\left({\widetilde{ℬ}}^{\ast }\widetilde{𝒦}\widetilde{ℬ}+\widetilde{ℛ}\right)}^{-1}{\widetilde{ℬ}}^{\ast }\widetilde{𝒦}\right]\widetilde{𝒜}+\widetilde{𝒬},$$ (23)

which is guaranteed to exist, will force $y_k=\widehat{C}{\widehat{x}}_k=\widehat{𝒞}{\widehat{x}}_k$ to track ${\xi }_k$, $k=k_0$, $k_0+1,\dots ,k_1$. Although, with the inclusion of the error equation in the system (16), the open loop system corresponding to (17) is no longer stabilizable, the requirement that $\widehat{\delta }>0$ guarantees that all unstable modes of the homogeneous open loop system corresponding to (17) are observable and this in turn implies that there will exist a unique self adjoint, positive definite solution to the ARE (23) (see, for example, [18, 20, 69].

In either case, $k_1<\infty$ or $k_1=\infty$, note that the Riccati operators ${\left\{{\widetilde{𝒦}}_k\right\}}_{k=k_0}^{k_1}$ or $\widetilde{𝒦}$ and the feedback gains ${\left\{{\widetilde{ℱ}}_k\right\}}_{k=k_0}^{k_1}$ or $\widetilde{ℱ}$ can be pre-computed offline and stored, and that

$${\tilde{u}}_k=\sum _{j=k_0}^{k-1}\text{Δ}{\tilde{u}}_j=\sum _{j=k_0}^{k-1}{\tilde{v}}_j={\widetilde{ℬ}}^{\ast }{\tilde{x}}_k,k=k_0,k_0+1,\dots ,k_1,$$ (24)

is our regularized, estimated, BrAC or eBrAC signal, where the closed loop state ${\left\{{\tilde{x}}_k\right\}}_{k=k_0}^{k_1}$ is given either by

$${\tilde{x}}_{k+1}=\left(\widetilde{𝒜}-\widetilde{ℬ}{\widetilde{ℱ}}_k\right){\tilde{x}}_k+\tau \widetilde{𝒟}{\xi }_{k+\sigma }k=k_0,k_0+1,k_0+2,\dots ,k_1-1,$$ (25)

if $k_1<\infty$, or by

$${\tilde{x}}_{k+1}=(\widetilde{𝒜}-\widetilde{ℬ}\widetilde{ℱ}){\tilde{x}}_k+\tau \widetilde{𝒟}{\xi }_{k+\sigma }k=k_0,k_0+1,k_0+2,\dots ,k_1-1,$$ (26)

if $k_1=\infty$, with ${\tilde{x}}_{k_0}=\left({\widehat{x}}_{k_0},{\widehat{e}}_{k_0},{\widehat{u}}_{k_0}\right)=\left({\widehat{x}}_0,0,0\right)=\left(\left(w_0,{\varphi }_0\right),0,0\right)\in \tilde{\mathscr{H}}$.

Of course, to actually compute ${\left\{{\tilde{u}}_k\right\}}_{k=k_0}^{k_1}$ the operators in the equations (16)–(26) must first be replaced by their finite dimensional approximations as in Section 2.4 and then by their equivalent matrix representations. Replacing the operators $\widehat{𝒜}$, $\widehat{ℬ}$ and $\widehat{𝒞}$ in equations (16)–(26) with their approximations as defined in Section 2.4 will entirely suffice for our convergence results to hold.

3. Results.

3.1. Experimental Data.

The results of our numerical studies that are presented in this section were carried out using two human subject data sets that we refer to as Trial 3 and Trial 4. These experiments were University of Southern California IRB approved and carried out in the Luczak Lab in the Department of Psychology on the USC campus in Los Angeles, California [47, 48]. The drinking episodes in Trial 3 were used for training data; they consisted of BrAC and TAC data from 40 participants, each of whom completed four drinking sessions. Each participant consumed an amount of alcohol designed (based on body water weight) for a maximum BrAC peak of .080. An Intoximeter IV breath analyzer (Intoximeters, Inc., St. Louis, MO) was used to obtain BrAC, and two SCRAM-CAM transdermal alcohol sensor bracelets (Alcohol Monitoring Systems, AMS, Littleton, CO) shown in Figure 1 worn on the upper arms measured TAC. BrAC and TAC measurements were taken at 10-minute intervals until BrAC reached .000. The TAC devices then continued to record automatically at 30-minute intervals until they also read .000. Some sets of BrAC-TAC data were excluded due to a change in the protocol. Each participant wore a sensor on each arm yielding two sets of TAC data recorded in each session. This resulted in 267 usable BrAC-TAC datasets [47]. Trial 4 consisted of drinking episodes involving 40 regular drinkers in the lab wearing a sensor on each arm, each drinking approximately 2 drinks in 15 minutes in two sessions and drinking ad libitum for 2–3 hours in two sessions [62, 64]. BrAC and TAC readings were taken every 15 minutes. This study resulted in simultaneous TAC and BrAC data for a total of 282 usable drinking episodes. With this experimental design, one may question whether or not the drinking episodes are independent. But rcall, the randomness in the parameters is intended to capture variations in skin physiology (which may vary on a single individuals right and left arms), environmental conditions, and different sensors.

3.2. Fitting the Population Model.

All training calculations were done on PC or Macbook Pro laptops in Matlab with Matlab codes that, whenever possible, used standard built-in functions such as the constrained optimization routine FMINCON and the non-negative least squares solver LSQNONNEG. In the left panel and right panels of Figure 4, are, respectively, histograms of the values for the individual model parameters $q_1$ and $q_2$ obtained using nonlinear least squares to fit the individual model (1), (2), or (3) to each of the BrAC/TAC data sets from the 267 training episodes in Trial 3. As an example to illustrate how well the two-parameter individual model captures the data once it has been fit, in the left panel of Figure 5 we plot the BrAC and TAC data from a Trial 4 episode, the eBrAC curve deconvolved from the TAC data using the fit individual model($q_1^{\ast }=1.2267$, $q_2^{\ast }=1.5739$) and regularized nonnegative least squares, and the eTAC signal obtained by inputing the deconvolved eBrAC signal back through the model. In the right panel of Figure 5, we plot the eBrAC signal obtained once again using the fit individual model and the LQ tracking scheme developed here.

FIGURE 4.

Fit values of individual model parameters $q_1$ (left panel) and $q_2$ (right panel) based on drinking episodes in Trial 3.

FIGURE 5.

eBrAC signal obtained using fit individual model and regularized nonnegative least squares (left panel) and eBrAC signal obtained using fit individual model and LQ tracking scheme (right panel).

In Figure 6, we plot the method of moments four parameter beta marginal distributions fit to the Trial 3 samples of the individual model parameters $q_1$ and $q_2$ shown in the histograms in Figure 4. The upper and lower left panels are the fit to $q_1\left(\alpha =2.357052,\beta =4.102699,a=0.248741,b=2.413776\right)$ while the right panels are the fit to $q_2\left(\alpha =3.878925,\beta =7.458199,a=-0.201485,b=3.543504\right)$. Note that the correlation coefficient of the Trial 3 fit values, or samples of $q_1$ and $q_2$ is −0.097 and the Pearson Chi-Square Test of Independence indicated that the null hypothesis that $q_1$ and $q_2$ are independent could not be rejected at the 5% level of significance. Consequently, in these Four Parameter Joint Beta Distribution Method of Moments fits we assumed that $q_1$ and $q_2$ are independent.

FIGURE 6.

Method of moments fit four parameter beta distributions for population model random parameters $q_1$ (left panel) and $q_2$ (right panel) based on fit values for individual model parameters $q_1$ and $q_2$ for Trial 3 drinking episodes.

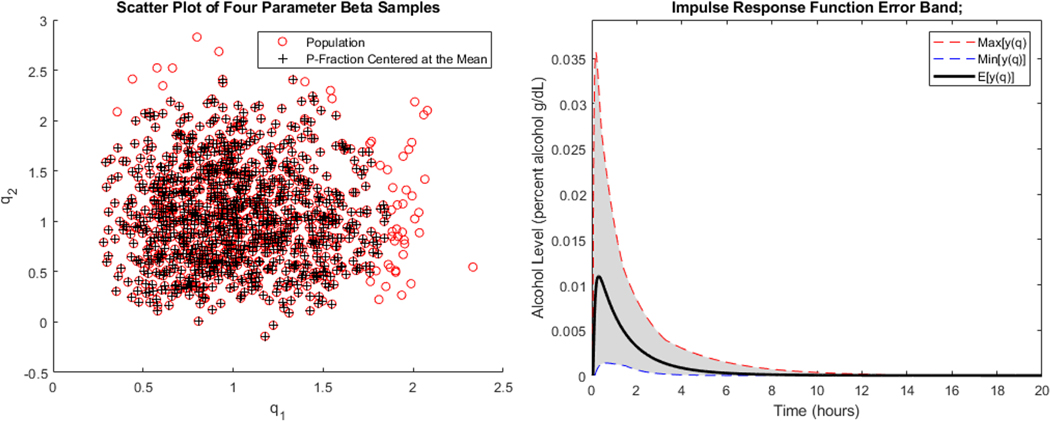
In the left panel of Figure 7 is a scatter plot of samples of $q$ generated using the joint probability density function obtained by taking the product of the marginals plotted in Figure 6. This plot also depicts the 95% elliptical region centered at the mean with the ratio of the semi major and minor axes determined by the fit supports of $q_1$ and $q_2$. Plotted in the right panel of Figure 7 is the impulse response function for the population model (4) obtained from an approximating system constructed using the joint distribution obtained as the product of the marginals plotted in Figure 6 together with the spline-based scheme described in Section 2.4 with $n=4$ and $m_1=m_2=8$, or $N=(4,8,8)$. The 95% error band is obtained using the samples in the 95% region in the scatter plot in left panel of Figure 7 and the approach outlined in Section 2.5.

FIGURE 7.

Samples generated by Trial 3 fit joint four parameter beta distribution and 95% region centered at mean (left panel). Corresponding population model impulse response function with conservative 95% error band.

The left and right panels of Figure 8 display respectively scatter plots of pre-cleaned and cleaned samples of the Trial 3 samples of the individual model fit parameters $q_1$ and $q_2$ as shown in the histograms in Figure 4. The width of our estimate error bands will depend on the variances of the population model’s random parameters. If these variances can be reduced, then the width of the error bands can also be reduced. If the test subject’s parameter values can be localized based on 1) covariates (e.g. sex, weight, BMI, hip to waist ratio, ambient temperature and humidity, etc.) and/or 2) a drinking episode for which both TAC and either actual or estimated ( [11, 43]) BrAC measurements are available, then the distribution of the parameters for the full population can be replaced in the population model with one that is conditioned on this localization and thus reduce the variance. We illustrate this in the Figures 8 and 10 below with a hypothetical conditioning sub-region enclosed in a red square. More on localized conditioning in Section 3.3 below.

FIGURE 8.

Scatter plot of pre-cleaned fit values of individual model parameters $q_1$ and $q_2$ based on drinking episodes in Trial 3. Region in red square shows potential conditioning region based on covariates (left panel). Scatter plot of pre-cleaned and cleaned fit values of individual model parameters $q_1$ and $q_2$ based on drinking episodes in Trial 3. Region in red square shows potential conditioning region based on covariates (right panel).

FIGURE 10.

Fit spline kernel joint density for $q_1$ and $q_2$ for Trial 3 drinking episodes with $q_1$ and $q_2$ assumed independent (left panel). Corresponding conditional joint density for $q_1$ and $q_2$ for Trial 3 drinking episodes conditioned on region in red square (right panel)

In the left and right panels of Figure 9, we have plotted spline kernel density estimates of the form given in (5) for the marginal distributions of $q_1$ (left panel) and $q_2$ (right panel) under the assumption of independence.

FIGURE 9.

Spline kernel fit distributions for population model random parameters $q_1$ (left panel) and $q_2$ (right panel) based on fit values for individual model parameters $q_1$ and $q_2$ for Trial 3 drinking episodes.

The joint distribution of $q$ is obtained by taking the product of the marginals. It is plotted in the left panel of Figure 10 along with the potential conditioning region inside the red boundary. The resulting conditional joint density is plotted in the right panel of Figure 10.

Plotted in the left panel of Figure 11 is the two dimensional spline kernel density estimate of the form given in (5) for the joint density of $q_1$ and $q_2$ when independence is not assumed. In the right panel of Figure 11, is the two dimensional spline kernel density estimate shown in the left panel, super-imposed over a three dimensional histogram of the $q_1$ and $q_2$ samples scatter plotted in the right panel of Figure 8.

FIGURE 11.

Fit spline kernel joint density for $q_1$ and $q_2$ for Trial 3 drinking episodes with $q_1$ and $q_2$ possibly dependent (left panel). Two dimensional spline kernel density estimate shown in the left panel super-imposed over a three dimensional histogram of the $q_1$ and $q_2$ samples shown in Figure 8 (right panel).

In the left panel of Figure 12 is a scatter plot of samples of $q$ generated using the joint probability density function shown in the left panel of Figure 10 (the case in which $q_1$ and $q_2$ were assumed to be independent) but conditioned to be in the region in the red rectangle with the resulting conditional joint density shown in the right panel of Figure 10. The left panel of Figure 12 also depicts the conditional 95% elliptical region centered at the mean with the ratio of the semi major and minor axes determined by the fit supports of $q_1$ and $q_2$. Plotted in the right panel of Figure 12 is the impulse response function for the population model (4) obtained from an approximating system constructed using the joint distribution plotted in the left panel of Figure 10 obtained as the product of the marginals plotted in Figure 9 and then conditioned on being in the region outlined in the red rectangle (the right panel of Figure 10), together with the spline-based scheme described in Section 2.4 with $n=4$ and $m_1=m_2=8$, or $N=\left(4,8,8\right)$. The 95% error band is obtained using the samples in the 95% region in the scatter plot in the left panel of Figure 12 and the approach outlined in Section 2.5. Comparing the right panels of Figure 7 and Figure 12, note how the conditioning significantly reduces the width of the 95% error band.

FIGURE 12.

Samples generated by Trial 3 fit joint spline kernel distribution conditioned on the region in the red rectangle in the left panel of Figure 10, and 95% region centered at mean (left panel). Corresponding population model impulse response function with conservative 95% error band (right panel).

3.3. Estimating BrAC: Inverse Filtering of the TAC Signal.

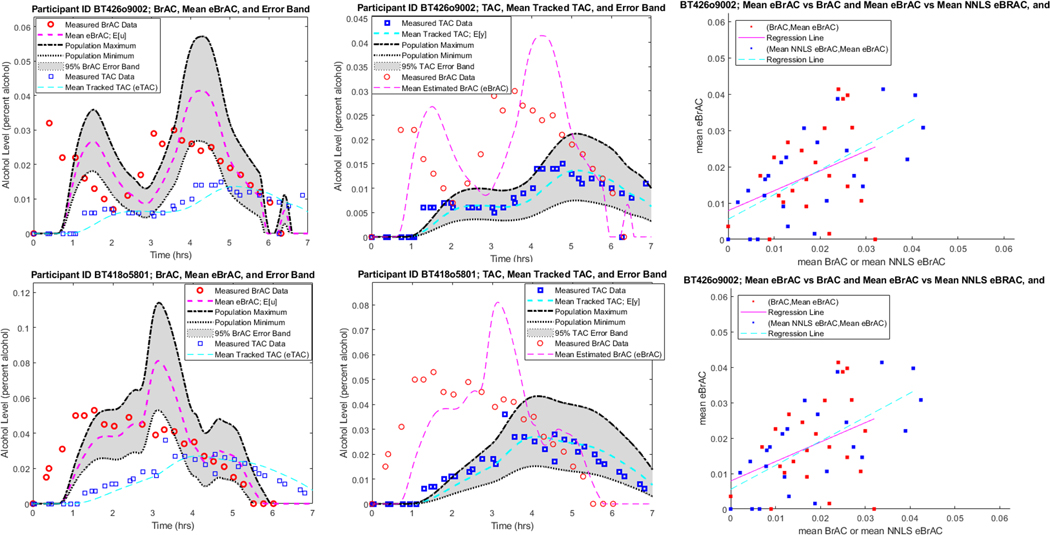
Following training based on the drinking episodes in Trial 3, we tested our LQ tracking inverse filtering scheme discussed in Section 2.6 on 270 of the 282 drinking episodes in Trial 4. Twelve of the drinking episodes in Trial 4 were eliminated because the BrAC and TAC were inconsistent; this is likely a result of issues occurring during data collection such as incorrect usage of the breath analyzer, a poorly fitting TAC sensor, presence of mouth alcohol when the breath measurement was taken, etc. Note that our training dataset, Trial 3, and our testing dataset, Trial 4, were completely separate, had no intersection, and followed different dosing and measurement protocols (for example, note the bi-modality in the BrAC signal in the upper left panel of Figure 13).

FIGURE 13.

Mean deconvolved BrAC signal (left panel) and mean tracked TAC signal (center panel) with conservative 95% error band. Upper panels: BrAC/mean eBrAC correlation: 0.93, Regression Slope: 1.10, Regression Intercept: 0.00. Lower panels: BrAC/mean eBrAC correlation: 0.98, Regression Slope: 0.99, Regression Intercept: 0.00. mean eBrAC vs BrAC and mean eBrAC vs mean NNLS BrAC together with regression lines (right panel).

In the examples we present here, based on the correlation coefficient and the Pearson Chi Squared Test for Independence for our training set, Trial 3, individual model fit values of $q_1$ and $q_2$, we continue to assume that the parameters $q_1$ and $q_2$ were independent and used a spline kernel density estimator (see Section 2.2.2) to estimate their marginal distributions, with the estimated joint density taken to be the product of the estimated marginals. For our testing set, Trial 4, the correlation coefficient of the individual model fit values, or samples, of $q_1$ and $q_2$ is −0.014 and the Pearson Chi-Square Test of Independence indicated that the null hypothesis that $q_1$ and $q_2$ are independent could also not be rejected at the 5% level of significance.

In our finite dimensional approximations we took $n=4$ and $m_1=m_2=8$, or $N=\left(4,8,8\right)$ with the resulting approximating LQ tracking system corresponding to (16) or (17) being of dimension $n{m}_1{m}_2+1+m^2=321$. We ran our codes with higher values for $n$ (6, 8, 10, and 16) and $m_i$, $i=1,2$, (8, 12, and 16) and did not notice any difference in the results other than that they took longer to run. In our LQ formulation we set $\widehat{r}=5.0\times {10}^0$, $\widehat{s}=1.5\times {10}^4$, $\widehat{\rho }=0.0$, $\widehat{p}=4\times {10}^2$, $\widehat{\delta }=0$, and used a sampling rate of 1/60 Hz or $\tau =1$ minute. We took the time horizon to be 6 or 7 hours or $k_0=0$ and $k_1=360$ or 420. Once again, the overall performance of our scheme was reasonably robust with respect to the choice of these optimization parameters. We used the steady state infinite time horizon solution to the matrix Riccati algebraic equation (23) rather than the finite time horizon solution to the matrix Riccati difference equation (21). We looked at both the finite and infinite time horizon solutions and did not detect any noticeable difference in the result. All offline LQ tracking calculations were carried out using the Matlab Control Systems Toolbox on a laptop, desktop, Mac or PC. The requisite online calculations, to wit, (24) and (26), can be done anywhere.

Hysteresis in both the blood-skin-biosensor system and the model put the regularization weight $\widehat{p}$ the tracking penalty $\widehat{s}$, and the sampling interval $\tau$ in tension. Indeed, increasing either $\tau$ or $\widehat{s}$ so as to cause the model to more closely track the TAC signal, the more oscillatory and consequently more unnatural the estimated BrAC or control input becomes. One could then increase the regularization penalty weight $\widehat{p}$, but then the less closely the TAC signal is tracked. In addition, increasing $\tau$ may render the zero-order hold assumption invalid. If on the other hand, we are willing to settle for a near-real time scheme, rather than one that is actually real time, if one takes $\sigma$ in 16 positive ($\sigma =0$ corresponds to real time), tracking is enhanced without introducing any undue oscillations in the eBrAC signal. Indeed, it is not surprising that introducing a peek into the future and forcing output or modeled TAC signal towards where it will be $\sigma$ sampling intervals in the future, mitigates the system’s and model’s inherent hysteresis. How many sampling intervals or how large to choose $\sigma$ tends to depend on the sampling interval $\tau$. For the results presented here with sampling rate 1/60 Hz or $\tau$ set to one minute, we found $\sigma =25$ minutes to be optimal.

A sampling of our results are shown in Figure 13 - Figure 15. Based on how well the resulting eBrAC signal mean is correlated with the BrAC signal data (with BrAC being known, but not used in the calculations), we show in Figure 13 two episodes with correlations close to 1.0, in Figure 14 two episodes with correlations close to the population median (0.83), and in Figure 15 two episodes with correlations among the lowest in the population of 270 drinking episodes. In each of the plots, the left panel is the mean estimated BrAC (eBrAC) and BrAC and the center panel is the mean tracked TAC signal. All of the left and center panels of the figures show the uncertainty quantification in the form of a 95% conservative error band afforded by our scheme and our population model as described in Section 2.5. For comparison purposes, in the BrAC plots we also include the TAC but without the error bands, and vice versa. Recall that the interpretation of the 95% error band is that if 1) the TAC data were generated by the individual model and 2) the estimated distribution of the random parameters used in the definition of the population model is in fact the distribution of parameters in the population, then there is at least a 95% conditional probability that the true BrAC (or TAC) signal lies in this region.

FIGURE 15.

Mean deconvolved BrAC signal (left panel) and mean tracked TAC signal (center panel) with conservative 95% error band. Upper panels: BrAC/mean eBrAC correlation: 0.46, Regression Slope: 0.63, Regression Intercept: 0.00. Lower panels: BrAC/mean eBrAC correlation: 0.72, Regression Slope: 0.88, Regression Intercept: 0.00. mean eBrAC vs BrAC and mean BrAC vs mean NNLS BrAC together with regression lines (right panel).

FIGURE 14.

Mean deconvolved BrAC signal (left panel) and mean tracked TAC signal (center panel) with conservative 95% error band. Upper panels: BrAC/mean eBrAC correlation: 0.83, Regression Slope: 0.89, Regression Intercept: 0.00. Lower panels: BrAC/mean eBrAC correlation: 0.83, Regression Slope: 0.80, Regression Intercept: 0.00. mean eBrAC vs BrAC and mean eBrAC vs mean NNLS BrAC together with regression lines (right panel).

In the right panel of all three figures are scatter plots of mean eBrAC vs the BrAC data and mean eBrAC vs the mean NNLS eBrAC or the mean eBrAC signal obtained using the open-loop nonnegative least squares technique and plots of the corresponding regression lines. In particular, in Figure 15, which contains two episodes for which our scheme did not perform particularly well, the fact that our mean eBrAC and the mean NNLS eBrAC signals are highly correlated and generally lie along the line $y=x$ indicated that both schemes obtained essentially the same result and that it’s likely that the reason for the poor showing in these two cases is that our model did not fit the BrAC/TAC data particularly well. Again, since there were relatively few drinking episodes in Trial 4 (approximately 23% with correlation less than 0.70) where our scheme performed relatively poorly, it is likely that the underlying reason for this was related to the data collection. A more complete discussion of the performance of our scheme across the entire Trial 4 population is given in the next Section, Section 4.

To illustrate our approach, we conditioned the population distribution of the random parameters by restricting the support to the sub-region (i.e. the region bounded by the red lines in Figure 10) $(1.0-\epsilon )q_i^{\ast }\le q_i\le (1.0+\epsilon )q_i^{\ast }$, $i=1,2$, where $\epsilon =0.1$ and $q_1^{\ast }$ and $q_2^{\ast }$ are the values of the parameters obtained by fitting the individual model to the test episode’s BrAC and TAC data. Now of course, in actual practice, this is not possible because the test episode’s BrAC data would not be available. However, if the very first time the biosensor is used, and in the user’s very first drinking episode, the wearer records the time at which they finish their drinks, the Widmark formula [12,43] can be used to obtain an estimated BAC curve for that drinking episode (covariates such as weight and total body water could be used to appropriately tune the parameters in the Widmark fomula). Estimates for$q_i^{\ast }$, $i=1,2$, could then be obtained offline by fitting our individual model to the TAC and Widmark estimated BAC data. Estimates for $\epsilon$, the variation in individual model parameters for the same subject but across different drinking episodes, can be obtained from the population training data. If the user is willing to repeat this procedure a number of times, a joint distribution for this individual’s parameters could be fit offline and then used in our population model in place of the parameter distribution for the entire population. We note that with no additional information at all, the population model could be trained using the parameter distribution for the entire population. Our research on this aspect of our approach is continuing. We also note that in practice, the LQ tracking parameters $\widehat{p}$, $\widehat{r}$, $\widehat{s}$, $\widehat{\rho }$, $\widehat{\delta }$ could be tuned using the training episodes for which both input (i.e.BrAC) and output (i.e. TAC) data are available. Indeed, it is conceivable that their optimal values could be determined by solving a straight forward optimization problem using the BrAC and TAC data from the same drinking episodes used to train the population model.

4. Discussion and Concluding Remarks.

In this section, we present and discuss summary population statistics for the performance of our scheme on the drinking episodes in Trial 4. In Table 1, we have tabulated the median correlations, regression line slopes, and regression line intercepts for the following three comparisons: 1) The mean eBrAC signal yielded by our LQ tracking scheme (eBrAC) and the re-sampled BrAC data acquired during the drinking session (BrAC), 2) the mean LQ tracked TAC signal, or eTAC, and the re-sampled TAC data acquired during the drinking session (TAC), and 3) our mean LQ tracking estimated BrAC signal (LQT eBrAC) and the estimated mean BrAC curve computed using regularized non-negative least squares optimization (NNLS eBrAC) as was done in, for example, [55]. We have also computed their means across the entire population of 270 drinking episodes along with 95% confidence intervals. For the correlations we used the Fisher z-Transformation [28] to mitigate the excessive skewness and obtain an improved central limit theorem-based approximation to the normal. The corresponding distributions of these three quantities across the 272 drinking episodes in Trial 4 are depicted in the form of histograms and box and whisker plots in Figure 16, Figure 17, and Figure 18, respectively. Ideally, in all cases, the correlations and regression line slopes should be 1.0 and the regression line intercepts should be 0.

TABLE 1.

Trial 4 drinking episode population median and mean correlations, regression line slopes, and regression line intercepts for eBrAC/BrAC, eTAC/TAC, and LQT/NNLS comparisons; n = 270.

Comparison (n=270 episodes)	Correlation	Regression Line Slope	Regression Line Intercept
eBrAC/BrAC	0.83	0.89	0.002
mean:95% CI	0.83:[0.81,0.85]	0.86:[0.84,0.88]	0.001:[0.001,0.002]
eTAC/TAC	0.96	0.94	0.001
mean:95% CI	0.97:[0.96,0.97]	0.91:[0.90,0.92]	0.001:[0.001,0.002]
LQT/NNLS	0.94	0.92	0.001
mean:95% CI	0.95 : [0.95,0.96]	0.90:[0.88,0.91]	0.002:[0.001,0.002]

FIGURE 16.

Trial 4 drinking episode population statistics; n= 270: left panels: mean eBrAC and BrAC correlations; center panels: mean eBrAC and BrAC regression line slopes; right panels: mean eBrAC and BrAC regression line intercepts. Upper panels are histograms and lower panels are box and whisker plots.

FIGURE 17.

Trial 4 drinking episode population statistics; n=270: left panels: mean eTAC and TAC correlations; center panels: mean eTAC and TAC regression line slopes; right panels: mean eTAC and TAC regression line intercepts. Upper panels are histograms and lower panels are box and whisker plots.

FIGURE 18.

Trial 4 drinking episode population statistics; n=270: left panels: mean LQT and mean NNLS eBrAC correlations; center panels: mean LQT and mean NNLS eBrAC regression line slopes; right panels: mean LQT and mean NNLS eBrAC regression line intercepts. Upper panels are histograms and lower panels are box and whisker plots.

Table 1 and Figure 16 reveal that our LQ tracking-based inverse filtering scheme does an excellent job at recovering the BrAC signal that yielded (in both the model and, more significantly, the body) the observed TAC signal. Although the median mean eBrAC/BrAC correlation across the entire Trial 4 population of drinking episodes is 0.83, almost one third have correlations greater than 0.9, nearly 60% have correlations greater than 0.8, and over three quarters have correlations greater than 0.7. And while the correlations close to 1.0 imply a linear relationship between mean eBrAC and BrAC, from the fact that the regression line slopes cluster about 1.0 and the regression line intercepts cluster around 0, one may reasonably conclude that our mean eBrAC signal is a strong predictor of the BrAC signal. We also note that upon closer inspection of the graphs of the mean eBrAC and BrAC signals, most of the differences between the two are very early in the episode and consequently may be the result of mouth alcohol [8]. Another confounding issue is that we necessarily only have relatively very sparse BrAC and TAC measurements upon which to base our estimates.

We also note that as one might expect, there is a measurable time delay between the start of the BrAC signal and the start of the TAC signal. Our model, on the other hand, is based on a linear parabolic diffusion equation and consequently exhibits infinite speed of propagation. We are investigating how our scheme performs when the parabolic diffusion model is replaced by a hyperbolic model that does not exhibit infinite speed of propagation. The model takes the form of a hyperbolic damped wave equation known as the telegraph equation. To wit, the telegraph equation includes a second derivative (in time) term that in effect provides the ethanol tracer molecules with inertia and hence yields a model that exhibits finite speed of propagation. This line of research is continuing.

The results in Table 1 and Figure 17 indicate that our LQ tracking control based BrAC estimation scheme does a very good job of tracking the test participants’ TAC signal across all the drinking episodes in Trial 4, while the results in Table 1 and Figure 18 indicate that our closed-loop recursive and real time LQ tracking control based scheme (LQT) produces essentially the same mean eBrAC signal as does the more conventional open-loop, non-negative least squares technique (NNLS) that we have used in many of our earlier studies (see, for example, [11,45,52–54,56].

Finally, in light of the results in Table 1 and Figure 18 comparing the performance of our closed-loop LQ tracking based scheme with the open-loop non-negative least squares deconvolution approach, we note that a significant benefit of the former is that the most data and computationally intensive parts of our method requiring highly specialized software is carried out offline on a laptop with the online estimation of BrAC is carried out in real time on a mobile device such as a phone or tablet or even on the senor’s micro-processor itself.

In actual practice, the process will work like this. A rectangular grid will be used to sub-divide the support of the random parameters $q$, supp $\left\{q\right\}$ (determined from fitting the population model to the samples obtained by fitting the individual model to each of the training drinking episodes), into sub-regions with mesh size $\epsilon$. Then using a technique from adaptive control known as gain scheduling, the random parameters will be conditioned on each sub-region. To wit, offline, with the discretization level, $N$ selected, for each conditioning sub-region of supp $\left\{q\right\}$, the operators ${\widetilde{𝒜}}^N$, ${\widetilde{ℬ}}^N$, ${\widetilde{𝒞}}^N$ and ${\widetilde{𝒬}}^N$ will be constructed, the ARE

$${\widetilde{𝒦}}^N={\widetilde{𝒜}}^{N\ast }\left[{\widetilde{𝒦}}^N-{\widetilde{𝒦}}^N{\widetilde{ℬ}}^N{\left({\widetilde{ℬ}}^{N\ast }{\widetilde{𝒦}}^N{\widetilde{ℬ}}^N+\widetilde{ℛ}\right)}^{-1}{\widetilde{ℬ}}^{N\ast }{\widetilde{𝒦}}^N\right]{\widetilde{𝒜}}^N+{\widetilde{𝒬}}^N,$$

will be solved for ${\widetilde{𝒦}}^N$, and the feedback gains, ${\widetilde{ℱ}}^N={\left({\widetilde{ℬ}}^{N\ast }{\widetilde{𝒦}}^N{\widetilde{ℬ}}^N+\widetilde{ℛ}\right)}^{-1}{\widetilde{ℬ}}^{N\ast }{\widetilde{𝒦}}^N{\widetilde{𝒜}}^N$ will be computed and stored. Then, using the test participant’s or patient’s covariates or Widmark estimated BrAC, their estimated individual model parameters will be used to identify the appropriate sub-region of supp $\left\{q\right\}$ and the corresponding feedback gains ${\widetilde{ℱ}}^N$ downloaded and stored on their mobile device or even on the sensor’s micro-processor. Then online, setting $k_0=0$, ${\tilde{x}}_0^N=\left({𝒫}^N{\widehat{x}}_0,0,0\right)=\left({𝒫}^N\left(w_0,{\varphi }_0\right),0,0\right)$, and ${\tilde{u}}_0^N=0$, at time $k\tau$, using the most recent sensor produced TAC measurement, ${\xi }_{k-1}$, and the stored most recent state, ${\tilde{x}}_{k-1}^N$, the next state, ${\tilde{x}}_k^N$, and the next mean eBrAC value, ${\tilde{u}}_k^N$, are generated recursively from

$${\tilde{x}}_k^N=\left({\widetilde{𝒜}}^N-{\widetilde{ℬ}}^N{\widetilde{ℱ}}^N\right){\tilde{x}}_{k-1}^N+\tau \widetilde{𝒟}{\xi }_{k-1+\sigma },{\tilde{u}}_k^N={\widetilde{ℬ}}^{\ast }{\tilde{x}}_k^N,k=1,2,\dots$$

Finally, we note that if there is no alcohol present at time $k=0$, it follows that

$${\tilde{u}}_k^N=\tau \sum _{j=0}^{k-1}{\widetilde{ℬ}}^{\ast }{\left({\widetilde{𝒜}}^N-{\widetilde{ℬ}}^N{\widetilde{ℱ}}^N\right)}^{k-1-j}\widetilde{𝒟}{\xi }_{j+\sigma }=\sum _{j=0}^{k-1}{\tilde{h}}_{k-j}^N{\xi }_{j+\sigma }={\left({\tilde{h}}^N\ast \tilde{\xi }\right)}_k,k=0,1,2,\dots ,$$

with the above expression taking the form of a discrete convolution where the kernel, or the TAC to BrAC inverse filter, is given by ${\tilde{h}}_j^N=\tau {\widetilde{ℬ}}^{\ast }{\left({\widetilde{𝒜}}^N-{\widetilde{ℬ}}^N{\widetilde{ℱ}}^N\right)}^{j-1}\widetilde{𝒟}\in ℝ$, $j=1,2,\dots$ and $\left\{{\tilde{\xi }}_j\right\}=\left\{{\xi }_{j+\sigma }\right\}$.

In Figure 19 we have plotted sample mean forward (i.e. BrAC to TAC) and mean inverse (i.e. TAC to BrAC) filter kernels with their population model-based 95% error bands. Note the difference in the amplitudes and time scales. Note also that the inverse filter is partially negative. Being the impulse response function with units of BrAC, this is, of course, not physical. However, this is not surprising in that the inversion process of estimating BAC or BrAC input from skin surface biosensor observations of TAC output is both non-physical and mathematically ill-posed.

FIGURE 19.

Forward or BrAC to TAC filter kernel or impulse response function with 95% error band (left panel), inverse or TAC to BrAC filter kernel or impulse response function with 95% error band (center panel), and for comparison, both the forward and inverse filter kernels with 95% error bands (right panel).