Quantifying the Corneal Nerve Whorl Pattern

Abstract

Purpose

The corneal nerves within the sub-basal nerve plexus (SBNP) display a distinctive whorl-like pattern, a highly dynamic structure that could be a marker of diseases. Previous studies have reported a decrease in whorl nerve density in patients with diabetes, indicating an avenue for noninvasive monitoring of diabetic neuropathy. However, conflicting results have since been reported, highlighting the need for improved quantitative analysis of the corneal whorl. We present an automated algorithm to characterize the whorl shape and test the hypothesis that the whorl organization is affected by diabetic neuropathy.

Methods

The SBNP whorl was analyzed as a vector field, from which seven whorl metrics were calculated. The efficacy of these whorl metrics was demonstrated in synthetic images, ex vivo mouse corneas, and in a publicly available dataset of wide-field in vivo confocal microscopy (IVCM) images of diabetic and control subjects. Linear discriminant analysis and the Peacock test were used to test for statistical differences. Our analysis code is made freely available.

Results

Using our whorl metrics, we were able to quantify different whorl patterns in our patient population and statistically compare cohorts. We determined that whorl patterns tend to present bilaterally in patients (P < 0.001), but there were no significant differences between whorl patterns in patients with diabetes and control subjects, nor between patients with or without neuropathy symptoms.

Conclusions

We present a generalizable framework to statistically compare corneal nerve patterns in cohorts of patients.

Translational Relevance

SBNP whorl patterns could serve as a noninvasive marker for ocular diseases, whereas few quantitative IVCM endpoints have been identified to date.

Introduction

The cornea is the most highly innervated tissue in the human body. Corneal nerves detect sensory inputs and help with maintaining corneal homeostasis by regulating tear production and inflammation.^1–3 The most recognizable corneal nerve structure is the sub-basal nerve plexus (SBNP), a thin but dense arrangement of fibers running from the periphery of the cornea toward the center. In humans, as well as in multiple animal models such as mice and rats, the SBNP forms a whorl-like pattern near the apex; in humans, this pattern is located approximately 1 to 2 mm inferonasal to the apex.^4–7 It is not entirely understood how this highly dynamic whorl pattern is formed,^6,8 but it undergoes major changes with age^9,10 and has recently been investigated as a potential landmark to study the effects of diseases on the cornea.^11–14

In vivo confocal microscopy (IVCM) enables the clinical imaging of the SBNP in patients. It holds great potential to assess corneal nerve health, and, more generally, to serve as a noninvasive tool for the early diagnosis and long-term monitoring of peripheral neuropathy.^15–18 However, IVCM imaging requires an experienced operator, contact between the eye and the instrument via an index-matching gel, which can be challenging for the patient, and images are limited in field-of-view (FOV), complicating navigation and leading to sampling biases.^19,20 The SBNP whorl is thus a convenient IVCM imaging location in patients: it is a recognizable imaging target that can be repeatedly found in patients over multiple imaging sessions,²¹ whereas also simplifying FOV identification when reporting results in the literature.

Promising studies in patients with diabetes have reported a reduction in nerve density at the whorl, and further decreases with diabetic neuropathy^22–25 and neuropathic pain.²⁶ Current clinical tools for the evaluation of small fiber neuropathy are invasive, lack sensitivity to the earliest disease stage, or rely on subjective testing. IVCM could thus play a powerful role in disease and treatment monitoring. However, contradicting results have also been reported in wide-field images of the SBNP where no reduction in nerve density was observed at the whorl in patients with diabetes.^27,28

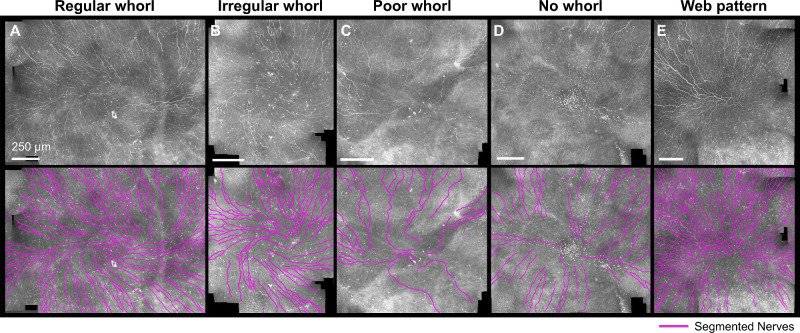
Limited work has been undertaken in quantifying the shape of the whorl pattern itself.^10,29 As can be seen in Figure 1, the human whorl region is highly heterogeneous, and quantification of the nerve density does not recapitulate the pattern in its entirety. Preliminary work focusing on the orientation of the whorl (clockwise, counterclockwise, or non-rotational) also failed to find a difference between patients with diabetes and nondiabetic patients.¹⁰ A more involved quantitative analysis of the whorl organization may be necessary to determine if diabetes has subtle effects on the appearance of the SBNP whorl, and if IVCM would be an appropriate tool for diagnosis of neuropathy and disease management.

Figure 1.

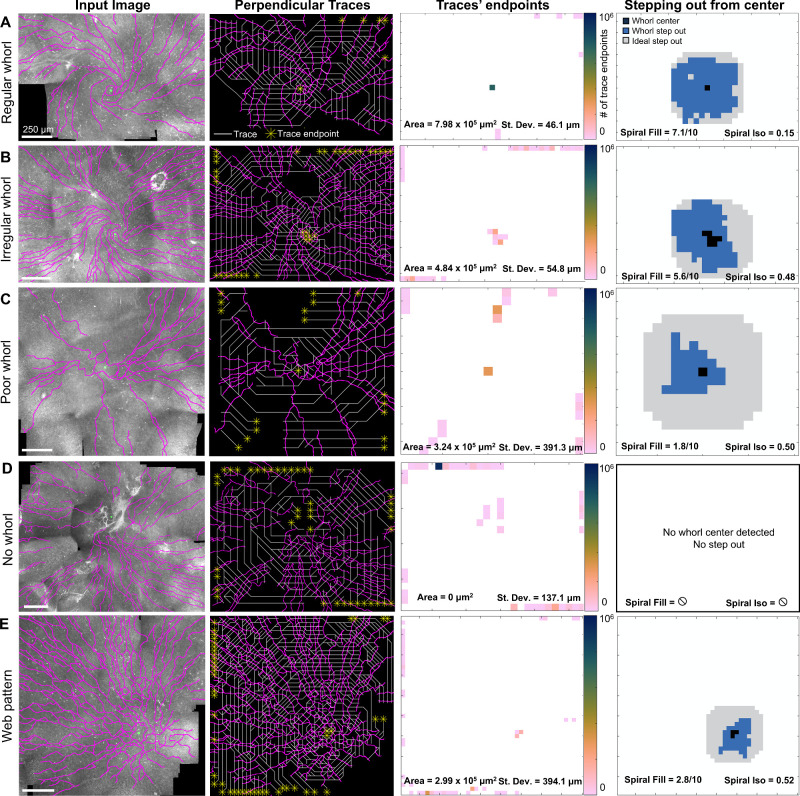
The diverse appearance of the whorl area in IVCM images. Representative wide-field IVCM images acquired in human subjects (top row) with nerves segmented (bottom row) for different whorl patterns qualitatively labeled as regular whorl, irregular whorl, poor whorl, no whorl, and a web-like non-spiraling pattern. Original images from Ref. 31.

We propose a quantitative approach to analyze the corneal whorl pattern using a series of whorl metrics that can be automatically calculated from segmented IVCM images and statistically tested for differences between patient cohorts. We demonstrate our metrics on synthetic images, mouse corneal images, and a publicly available dataset^30,31 of healthy subjects and patients with diabetes. Our method is easily transferrable to other patient cohorts or animal models and can be viewed as a general method for the quantitative analysis of ocular nerve patterns.

Methods

Quantifying the Whorl as a Vector Field

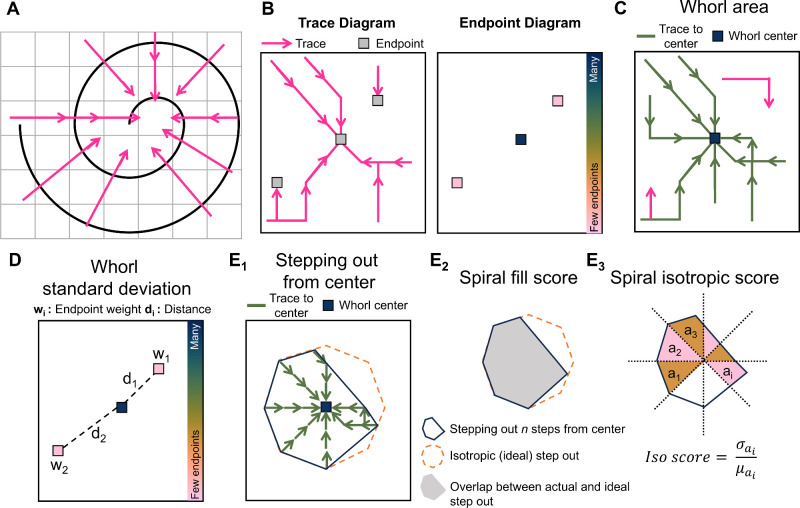
In a method inspired by hurricane detection,³² the whorl structure is analyzed as a vector field from which whorl metrics can be calculated. As seen in Figure 2A, when the nerves organize in a spiral shape, vectors perpendicular to the nerves will point toward the center of this spiral. This property is fundamental to our approach.

Figure 2.

Analyzing the corneal whorl pattern using whorl metrics. (A) Perpendicular vectors point toward the center of a spiral. (B) Creating traces by connecting the vectors and recording where traces end in the endpoint diagram. (C) The whorl area is the total image area that is connected by a trace to the whorl center. (D) The whorl standard deviation is calculated based on the distances (d_i) of each endpoint (with area w_i) with respect to the whorl center. (E) By following traces for n step outward from the center, the step-out area (E₁, blue) is compared to the ideal isotropic step-out (E₁, orange). The spiral fill score (E₂) is the overlap between the actual and ideal step-out. The spiral isotropic score (E₃) is the coefficient of variance calculated from 45 degree slices with area a_i of the step-out.

Whorl images are first divided into small square patches, and one average perpendicular vector is calculated per patch. Vectors are then assembled into long “traces” (Fig. 2B) by linking each patch to one neighbor-patch based on the vector orientation. Traces link patches until they reach an “endpoint.” The end points occur either when a vector extends beyond the image's boundaries or, if within the image, when a vector points to a patch already included in the trace. An “endpoint diagram” can be constructed (see Fig. 2B) based on how many traces end at each location. As seen in the endpoint diagram of Figure 2B, it would be expected for many traces to end at the whorl center, and for few traces to end at other locations in the image.

Whorl metrics are calculated for each whorl image based on the trace diagram and endpoint diagram. The “whorl area” (Fig. 2C) is the total area of the patches that traces back to the whorl center in the trace diagram (in units of µm²). The whorl center is defined as a single or adjacent group of endpoints whose associated traces total >10% of the image area, and which is situated within approximately 220 µm of a manually estimated location of where the whorl converges. The “whorl standard deviation σ” (Fig. 2D) is calculated as:

$$\begin{array}{c}\hfill \sigma =\sqrt{\frac{\sum _i\left(w_i*d_i\right)}{\left(\sum _i{w}_i\right)-1}}\end{array}$$ (1)

where for every endpoint i in the endpoint diagram, the weight w_i is the total area of the traces ending at endpoint i, and d_i is the Euclidian distance between endpoint i and the whorl center. End points at the edges of the image are excluded from the standard deviation calculation because they occur due to the cropping of the image, not the geometry of the whorl.

Two more whorl metrics are obtained by performing a “stepping out” operation (Fig. 2E₁): the “spiral fill score,” and the “spiral isotropic score.” A subsection of the trace diagram is identified by starting at the whorl center and by including all patches whose vectors are pointing directly at the whorl center, followed by all neighboring patches pointing to those first patches, repeating n times (n = 5 for this dataset). This operation creates a subset of patches (Fig. 2E₂), which can be compared to the ideal “step-out” from an ideal spiral, which would be isotropic. The spiral fill score is calculated as the overlap between the real and isotropic step-out areas (see Fig. 2E₂). The spiral isotropic score is a measure of the radial symmetry of the step-out area and is calculated as the coefficient of variance of the step-out area after it is divided into 45-degree slices. In the case where no whorl center can be identified (i.e. no connected group of patches totaling >10% of the image area and situated within approximately 220 µm of the manually indicated whorl convergence point), no spiral fill score and no spiral isotropic score are calculated.

Finally, three more whorl metrics are calculated: the “nerve density,” the “spiral score,” and the “isotropic endpoint score.” The nerve density sums the total nerve length in an area 730 × 730 µm² around the whorl center divided by the area (this nerve density provides comparable results to the nerve fiber length density provided by NeuronJ, an ImageJ plugin; see Supplementary Fig. S1). The spiral score is the spiral fill score divided by the spiral isotropic score and represents an overall measure of the spiral shape. Finally, the isotropic endpoint score determines if endpoints are equally distributed around the whorl center, because endpoints sometimes form a “ring” in the endpoint diagram (see Supplementary Fig. S2). A summary of the whorl metrics can be found in Table 1 (with full code implementation available, see Ref. 33).

Table 1.

Summary Description of the Whorl Metrics

Whorl Metrics	Description
Whorl area	Total image area that can be linked to the whorl center via perpendicular vectors
Whorl standard deviation	Spread of the trace endpoints around the whorl center
Spiral fill score	Image area which is connected to the whorl center via a trace using ≤ 5 patches, divided by the total image area within 5 patches of the center
Spiral isotropic score	A measure of the radial symmetry of the traces as they connect to the whorl center (≤5 patches radius)
Spiral score	Spiral fill score divided by spiral isotropic score
Nerve density	Total nerve length near the whorl center, divided by area
Isometric endpoint score	Detects the presence of “ring” endpoint pattern

Description of the Human Dataset

To demonstrate our algorithm, we analyzed a publicly available wide-field IVCM dataset^30,31 acquired in patients with type 2 diabetes and healthy control subjects. The dataset, which was acquired according to the tenets of the Declaration of Helsinki, has been described in more detail previously.^27,28,30,34 The dataset consists of large mosaics of registered IVCM images totaling 4 to 8 mm² in size showing the entire SBNP whorl region. For this study, images from the dataset were excluded only if the whorl region was not visible or if the nerve segmentation was not provided. In total 145 wide-field images from 78 subjects were analyzed (both eyes were included for 67/78 subjects). Subjects were divided between non-diabetic and diabetic groups, with further subdivision based on the results of an oral glucose tolerance test in the nondiabetic group (measurements at fasting and 2 hours post-glucose, with thresholds of <7 mM at fasting and <8.9 mM 2 hours post-glucose for the normal glucose tolerance group, and <7 mM and between 8.9 mM and 12.2 mM for the impaired glucose tolerance group) and based on years since diagnosis in the diabetic group (±10 years since diagnosis). The patients with diabetes were not assessed for diabetic retinopathy. The corneal sub-basal nerve fiber length density was measured at the whorl (wCNFL). All subjects also underwent a series of clinical assessments for neuropathy, including a measurement of intraepidermal nerve fiber density (IENFB) from a skin biopsy, evaluation of symptoms based on the Dyck Neuropathy Disability Score (NDS) and Neuropathy Symptom Score (NSS), measurements of the amplitude and conduction velocity of the sural nerve (SN) and the conduction velocity of the peroneal nerve (PN), and measurement of heat and cold perception thresholds in the foot (see Table 2 for full information).

Table 2.

Summary Information of the Publicly Available Human Dataset

	Normal Glucose Tolerance	Impaired Glucose Tolerance	Diabetic <10 Y	Diabetic 10+ Y	ANOVA P Value‡
# Patients (# images)	33 (62)	9 (17)	10 (18)	26 (48)
Age, y	69.2 ± 0.7	68.5 ± 0.5	68.8 ± 0.9	69.2 ± 1.8	0.37
Gender, M/F	16/16 (1*)	6/3	5/5	15/11
Smoker, Y/N	5/27 (1*)	3/6	2/8	8/18
BMI, kg/m2	25.5 ± 3.7	27.5 ± 6.3	27.8 ± 3.0	29.4 ± 4.5	0.01
HbA1c, mmol/mol	38.4 ± 2.6	39.4 ± 3.0	46.2 ± 4.9	57.8 ± 12.5	<0.001
IENFD, fibers/mm
Baseline, 10 y prior	3.17 ± 1.33	1.62 ± 1.41	2.14 ± 1.52	1.79 ± 0.98	<0.001
Follow up	0.92 ± 0.67	0.46 ± 0.64	0.78 ± 0.71	0.88 ± 1.02	0.54
NDS	6.2 ± 5.6	7.9 ± 6.1	8.1 ± 7.2	7.6 ± 6.0	0.70
NSS	1.3 ± 2.8	1.3 ± 1.6	1.4 ± 2.5	2.3 ± 3.4	0.63
Amplitude, SN, µV	7.2 ± 4.0	6.4 ± 4.7	5.8 ± 3.7	6.4 ± 4.3	0.77
Conduction velocity, SN, m/s	45.9 ± 4.9	45.1 ± 3.4	46.5 ± 5.5	44.0 ± 5.9	0.49
Conduction velocity, PN, m/s	47.0 ± 5.6	42.2 ± 2.9	44.7 ± 4.3	46.4 ± 11.0	0.40
Heat threshold
Left foot, °C	40.6 ± 3.6	42.9 ± 5.3	41.7 ± 4.1	41.7 ± 3.6	0.44
Right foot, °C	40.5 ± 3.9	42.3 ± 3.5	43.5 ± 3.2	42.4 ± 4.0	0.12
Cold threshold
Left foot, °C	29.1 ± 2.6	25.6 ± 3.8	26.0 ± 3.4	24.8 ± 5.7	0.04
Right foot, °C	27.3 ± 3.7	24.1 ± 5.5	26.4 ± 5.0	25.5 ± 5.0	0.23
wCNFL, mm/mm2	18.7 ± 4.7	17.6 ± 9.2	20.1 ± 4.3	19.2 ± 5.8	0.78

P < 0.05 in bold.

Data reported as mean ± standard deviation.

^*This information was not reported for one subject.

^‡ANOVA is used to compare the means of all four groups.

Analysis of the Human Dataset

All analysis of the human dataset, including the creation and testing of all whorl metrics was performed while blind to patient information and diabetic status. An initial qualitative label (regular whorl, irregular whorl, poor whorl, no whorl, and web-like pattern; see Table 3 for a full description) was assigned to every image to guide the creation process of the whorl metrics (see Fig. 1 for representative images). A whorl convergence location was manually identified on each image at the approximate center of the whorl, or at a central location where nerves centripetally approached from all directions if no whorl was visible. Images were then cropped around the whorl convergence point to maximize image size while minimizing the presence of unacquired FOVs (see the black areas in Fig. 1). Nerves in all images were already segmented as part of the publicly available dataset, but additional segmentation was performed in FIJI³⁵ using the NeuronJ³⁶ plugin if needed (<5% of images). All whorl metrics were calculated in MATLAB 2022a (Mathworks, Natick, MA, USA). Both a MATLAB and Python implementation of this code are made available as part of this study.³³ Patch size was dynamically calculated as the average distance between nerves inside a 417 × 417 µm² (400 × 400 pixels) window around the whorl center, with a fixed minimum patch size of 31 µm (30 pixels), and maximum patch size of 73 µm (70 pixels; minimum and maximum patch sizes were experimentally determined to account for images with unexpectedly high or low nerve densities, which could lead to impractical patch sizes to be calculated). Once perpendicular vectors were calculated for every patch in the image, the direction of each vector was kept as-is or rotated by 180 degrees so that vectors preferentially pointed either (1) in a counterclockwise direction (for clockwise whorls, or vice versa for counterclockwise whorls), and (2) toward the whorl center (see Supplementary Fig. S3). Orientation of the whorl (clockwise versus counterclockwise) was manually set based on user observation. If whorl orientation was ambiguous (for irregular, poor, no whorls, and web-like patterns), both orientations were attempted during analysis and the best results were recorded.

Table 3.

Description of Qualitative Whorl Labels to Guide the Development of the Whorl Metrics

Initial Qualitative Label	Labeling Criteria
Regular whorl	Clear spiral pattern expanding regularly from a central point, with either clockwise or counterclockwise orientation
Irregular whorl	Spiral-like pattern with irregular presentation, either from lack of a clear central point, asymmetric expansion around the central point, or presence of both clockwise and counterclockwise features
Poor whorl	No spiral pattern but presence of some nerves forming circular patterns, loops, curves, or other rotational shapes
No whorl	No spiral, circular, or rotational patterns
Web pattern	High nerve density and high branch point density with no visible spiral or rotational pattern

Synthetic Dataset

To demonstrate the whorl metrics on a typical spiral pattern, a non-rotational pattern or a web-like pattern, simple shapes were drawn in Microsoft Paint (Microsoft, Redmond, WA, USA) and analyzed using the same MATLAB code which was used to analyze the human whorl images.

Mouse Cornea Dataset

To demonstrate the whorl metrics in a commonly used animal model, two mouse corneas were imaged ex vivo and analyzed following the same algorithm as the human whorl images. All procedures were performed in accordance with relevant guidelines and regulations under the approval of the Case Western Reserve University Institutional Animal Care and Use Committee (IACUC). Corneas from two female C57BL/6 mice, aged 2 months, were fixed in 1.3% paraformaldehyde for 1 hour at 4°C, washed in 1× phosphate-buffered saline with 0.1% Tween-20 detergent (PBST), then kept in permeabilization buffer (1% Triton in 1× PBST) for 1 hour. Corneas were transferred to a blocking buffer (0.3% Triton X-100/0.1% Tween-20 in 5× PBST) with 20% bovine serum albumin (BSA) and kept at 25°C for 30 minutes. Corneas were then kept at 25°C with the neuron-specific marker beta-III tubulin NorthernLights NL557-conjugated antibody (1:200 dilution, Bio-Techne Corporation, Minneapolis, MN, USA) in the blocking buffer without BSA for 2 hours, and then at 4°C for 12 hours. The corneas were then washed in buffer (0.1% Tween-20 in 5× PBST).

The whorl region was imaged in three-dimensions using an Olympus SpinSR10 spinning disk confocal microscope (40×/1.4 NA oil immersion objective). Excitation light was 561 nm and emitted light was collected between 571 and 675 nm. A custom MATLAB code was used to segment the SBNP nerves using a series of adaptive intensity thresholds, morphological operations and the Skeleton3D package.³⁷ Each imaging FOV was 2304 × 2304 × 25 pixels (pixel size = 162.5 nm × 162.5 nm × 0.31 µm). After nerve segmentation, maximum intensity projections in 9 FOVs were registered to each other for a final image size of 1.06 mm × 1.06 mm. The whorl metrics were then calculated using the same MATLAB code as the human images, with an exception for the patch size which followed the same calculations but had a fixed minimum size of 24 µm (150 pixels) and maximum size of 33 µm (200 pixels).

Statistical Analysis

Linear discriminant analysis (LDA) was used to reduce the multi-dimensional distribution of whorl metrics into a low-dimension representation of the whorl shape. For this operation, each of the seven whorl metrics were first normalized to a mean of 0 and standard deviation of 1. To create a normal distribution, the logarithm of the spiral score was used. The isotropic endpoint score was treated as a binary input based on if it was greater than 0.5. A MATLAB implementation³⁸ of LDA was then used to obtain linear combinations of the whorl metrics that would best predict when a whorl belongs to one of the five qualitative labels (no whorl, poor, irregular, regular, and web). The resulting five axes are rating the likelihood for each data point to belong to one of these five qualitative labels. The fourth LDA axis (likelihood of regular whorl) and fifth LDA axis (likelihood of a web pattern) were then used to create a two-dimensional (2D) distribution of whorl shapes in the human dataset.

To test for statistically significant differences in whorl shape between different patient populations, a 2D extension of the Kolmogorov-Smirnov test, the Peacock's test,³⁹ was used on the LDA distributions. The Peacock's test determines the likelihood of two 2D samples being produced by the same 2D probability density function. The Peacock's test does not assume a normal distribution, and its accuracy has been found to be adequate with sample sizes as low as 10. We used a MATLAB implementation of the Peacock test.⁴⁰

Results

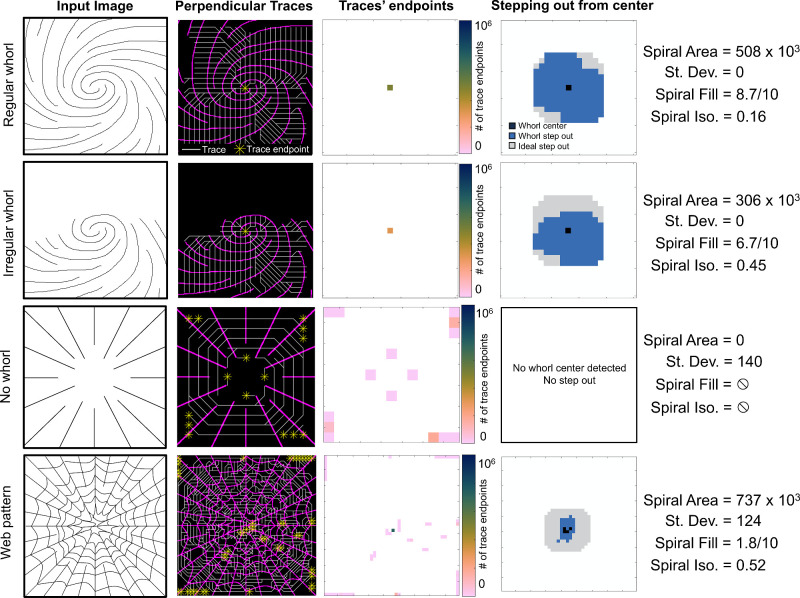
Demonstration of Whorl Metric Computations in a Synthetic Dataset

Whorl metrics were computed on hand-drawn images to illustrate how the metrics vary for different nerve patterns. Images representing a regular whorl (full spiral), an irregular whorl (half-spiral), no whorl (non-rotational radial pattern), and a web pattern (high density, highly connected, and non-rotational pattern) were analyzed, and the resulting perpendicular vector traces, endpoint diagrams and step-out diagrams can be seen in Figure 3. The regular whorl has a singular endpoint corresponding to the center of the whorl, which results in a large whorl area and low standard deviation. The step-out pattern from stepping out five times from the center covers a large area and is roughly isotropic, leading to a high spiral fill score and a small spiral isotropic score. The irregular whorl image also results in one trace endpoint; however, the area is reduced, the spiral fill score is smaller, and the spiral isotropic score is higher, indicating an asymmetric whorl pattern. When no whorl is present, multiple endpoints with low areas are obtained, and because none of the endpoints have >10% of the total area, no whorl center is identified, and the spiral fill and isotropic scores are not calculated. During analysis, the web pattern often leads to a medium-to-high whorl area but overall poor spiral fill and isotropic scores in addition to a potentially poor standard deviation. As seen in a Supplementary Figure S2, the web pattern can also lead to a “ring” of endpoints in the endpoint diagram, and the presence of such a ring is detected as a low isotropic endpoint score.

Figure 3.

Demonstration of whorl metrics on synthetic images of common nerve patterns. Traces (white) are drawn perpendicular to the nerves (magenta) and ending at endpoints (yellow). The number of endpoints at each location is used to calculate the spiral area and standard deviation. The whorl step-out is compared to the ideal (isotropic) step-out to calculate the spiral fill and spiral isotropic scores. For all images, patch size is proportional to the average distance between nerves.

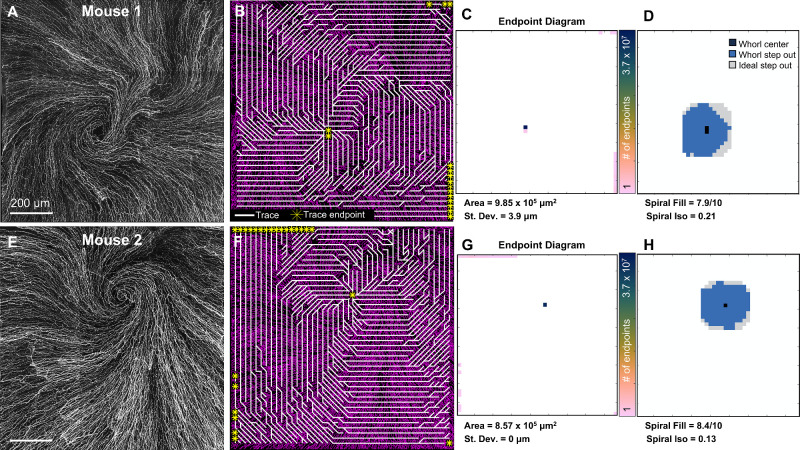
Demonstration of Whorl Metric Computations in Mouse Corneas

Corneal whorl images were acquired ex vivo in two mice and can be seen in Figure 4. In a clockwise whorl pattern (see Fig. 4A), perpendicular traces travel counterclockwise toward the center of the whorl, ending either at the center of the whorl or at the edges of the image (Fig. 4B). In the endpoint diagram (see Fig. 4C), a high number of endpoints are located at the whorl center, leading to a high whorl area and low standard deviation. Following all traces from the whorl center and stepping out for five patches results in a high spiral fill score and low spiral isotropic score (Fig. 4D). However, as can be seen in the second mouse with a counterclockwise whorl (Figs. 4E–H), a more regular spiral pattern led to a slightly higher spiral fill score and lower spiral isotropic score. The whorl area was similarly high, and the standard deviation similarly low.

Figure 4.

Whorl metrics in the mouse cornea. (A) Ex vivo confocal image of the sub-basal nerve whorl in a mouse. (B) Perpendicular traces (white) tend to have endpoints (yellow) at the center of the whorl. (C) Endpoint diagram displaying the number of trace endpoints at each location from which the whorl area and standard deviation are calculated. (D) Step-out diagram from which the spiral fill and spiral isotropic scores are calculated. (E) Whorl metrics calculated in a second mouse with (F) trace diagram, (G) endpoint diagram, and (H) step-out diagram. Size of the depicted field-of-view is the same for all visualizations on the same row.

Demonstration of Whorl Metric Computations in In Vivo Human Corneas

The whorl metrics were calculated for all 145 wide-field IVCM images. The MATLAB program took <3 seconds to perform all calculations for one cornea. Five representative examples of a regular whorl (Fig. 5A), an irregular whorl (Fig. 5B), a poor whorl (Fig. 5C), no whorl (Fig. 5D), or a web pattern (Fig. 5E) are shown. As previously demonstrated in the synthetic and mouse images, the regular whorl pattern (see Fig. 5A) resulted in a high whorl area, low whorl standard deviation, high spiral fill score, and low spiral isotropic score. These metrics degraded in the irregular whorl (see Fig. 5B) as less of the image area can be linked to the whorl center via the perpendicular traces (i.e. smaller whorl area), not all trace endpoints were at the whorl center (i.e. higher standard deviation), the whorl was overall smaller in radius (i.e. lower spiral fill score) and not as radially symmetric (i.e. larger spiral isotropic score). All metrics further degraded in the poor whorl (see Fig. 5C) and reached their worst when no whorl was present (see Fig. 5D). Even though many traces seemed to end at the same location in the web pattern (see Fig. 5E), the low spiral fill score and high spiral isotropic score confirmed that the image does not have a rotational whorl pattern and thus should not be classified as a type of whorl.

Figure 5.

Whorl metrics to quantify nerve patterns in human IVCM images, with typical results for (A) a regular whorl, (B) an irregular whorl, (C) a poor whorl shape, (D) no whorl visible, and (E) a high nerve-density, non-rotational web pattern. Segmented nerves (magenta) with manually identified whorl convergence points (green circles). Perpendicular traces (white) with trace endpoints (yellow stars). The endpoints diagram reports the number of endpoints at each image location from which the whorl area and standard deviation were calculated. The stepping out from the center operation follows all traces for five patches starting from the center and is compared to an ideal isotropic step-out to calculate the spiral fill score and the spiral isotropic score.

Quantifying a Wide Range of Whorl Patterns Using Whorl Metrics

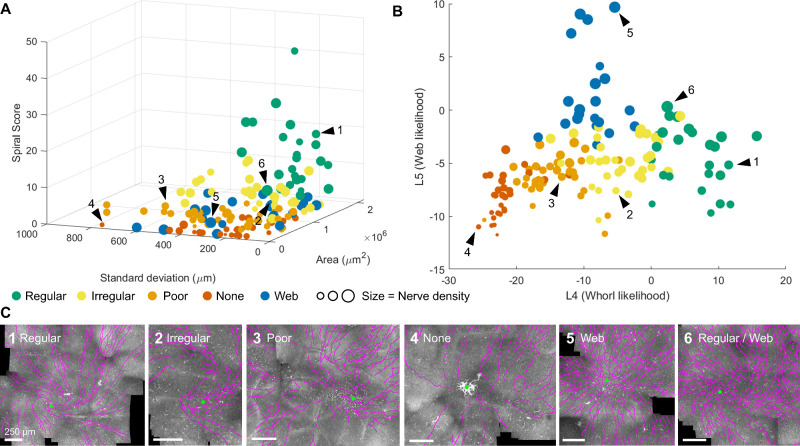
Even though the relationship between a few standard whorl images and their accompanying whorl metrics can be easy to predict (e.g. a regular whorl has a high whorl area), the heterogeneity of corneal nerve patterns observed in patients complicates the interpretation of the whorl metrics. To observe the variability in whorl metrics over the entire patient cohort, we plot the whorl area, whorl standard deviation, spiral score (spiral fill score divided by spiral isotropic score), and nerve density for all corneal images (see Fig. 6A).

Figure 6.

Multi-dimensional representation of the whorl metrics. (A) All 145 human corneas represented as a function of their whorl area, whorl standard deviation, spiral score, and nerve density (marker size). (B) All corneas as a function of a linear combinations of all whorl metrics obtained from linear discriminant analysis (LDA). L4 = 2.7 * nArea − 1.03 * nStDev + 1.08 * nDens + 6.4 * nSpF − 2.6 * nSpI + 0.6 * nSp + 9.5 * nIsoEnd − 9.7; L5 = 0.9 * nArea − 0.3 * nStDev + 3.0 * nDens − 3.5 * nSpF + 0.8 * nSpI + 2.2 * nSp + 9.0 * nIsoEnd − 5.1, with nArea, normalized whorl area; nStDev, normalized standard deviation; nDens, normalized density; nSpF, normalized spiral fill score; nSpI, normalized spiral isotropic score; nSp, normalized spiral score; nIsoEnd, normalized isotropic endpoint score. (C) Example IVCM images with segmented nerves (magenta) and whorl convergence point (green dot). The location of the example images 1 through 6 are indicated by black arrow heads in A and B.

Although some general trends can be observed in Figure 6A, such as regular whorls having a high spiral score and low standard deviation, or images with no whorls having low areas and low spiral scores, the multi-dimensionality of the metrics is an obstacle to data visualization and analysis. We used LDA to reduce the seven whorl metrics to two axes from which the distribution of whorl patterns can be more easily observed (Fig. 6B). In this LDA plot, position on the graph is meaningfully related to whorl appearance. As presented in six example images (Fig. 6C), the x-axis can be understood as the likelihood of a regular whorl pattern (i.e. regular whorls are positioned high on the axis, images with no whorls are positioned low on the axis), whereas the y-axis can be understood as the likelihood of a web pattern. Importantly, patterns that may have been labeled qualitatively as one pattern type, while potentially having minor characteristics of a different pattern type, will be positioned between those patterns. As an example, Figure 6C₆ shows a regular whorl with high nerve density and high nerve branch connectivity, both characteristics of a web pattern. Indeed, as seen in Figure 6B (arrow 6), this cornea is positioned midway between the regular and web pattern areas of the LDA plot.

Eyes Belonging to the Same Patient are More Likely to Have Similar Whorl Patterns

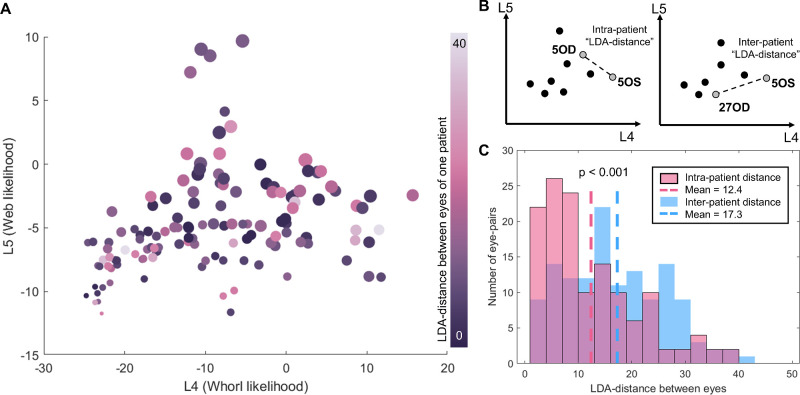
With the LDA plot, we can statistically test for similarities between whorl patterns among subjects. We first tested the hypothesis that the whorl pattern in one eye will resemble the whorl pattern in the contralateral eye of the same patient. We first calculated the LDA distance, the Euclidian distance between 2 points on the LDA plot, for all 67 patients where both eyes were part of the dataset (see Fig. 7A). In general, the LDA distance between the eyes of the same patient was low, indicating similar whorl patterns in both eyes. To formally test this, we compared the LDA distance between the eyes of the same patient (i.e. the intra-patient distance) to 67 random pairs of eyes belonging to different patients (i.e. inter-patient distance; see Fig. 7B). We found that the intra-patient distance is, on average, significantly smaller than the inter-patient distance (P < 0.001, Student t-test; see Fig. 7C). This finding confirmed that cornea whorl patterns are not varying randomly across human subjects and that patients are likely to have similar whorl patterns in both eyes. Additionally, we do not observe any correlation between whorl shape and LDA distance between the eyes. In other words, patients with regular whorls are no more likely than patients with poor whorls to have similarities or differences between eyes.

Figure 7.

Similarities of the whorl pattern between eyes. (A) Distance between eyes on the LDA graph for 67 patients where both eyes were available for analysis. (B) The intra-patient LDA distance is defined as the distance between both eyes of one patient, whereas the inter-patient LDA distance is between two eyes belonging to different patients. (C) The intra-patient distances for 67 patients are significantly smaller than the inter-patient distance tested on random combinations of the same 67 eye pairs. P < 0.001 Student t-test.

There are no Statistical Differences in Whorl Patterns Between Older Patients With Diabetes and Nondiabetic Patients

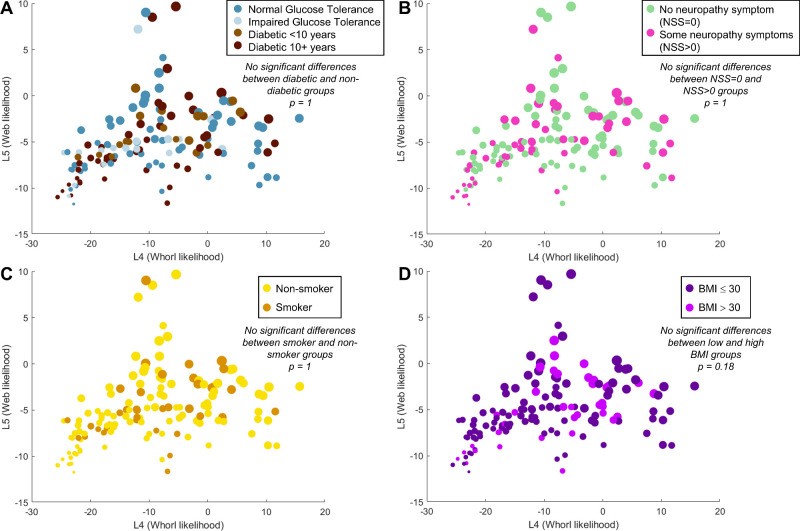
Using the whorl metrics and LDA plot as a quantitative and graphical representation of whorl shape, we tested the hypothesis that whorl shape is statistically different between a diabetic cohort and healthy controls. We labeled each analyzed cornea with their patient status, and the results can be seen in Figure 8A. No discernable patterns can be seen between the distribution of healthy patients and patients with diabetes and whorl shapes. Patients with diabetes can be found in areas of the LDA graph corresponding to regular, irregular, poor, and no whorls, in addition to web patterns. We used the Peacock's test to determine if the spatial distribution of the diabetic and non-diabetic corneas on the LDA graph could be obtained from the same probability density distribution (null hypothesis) and obtained a P value of 1, thus we could not reject the null hypothesis. We repeated this test to compare patients with or without neuropathy symptoms (as defined by a NSS > 0), which was again not statistically significant (Fig. 8B). No statistical differences in whorl shapes were found between smokers and nonsmokers (Fig. 8C), obese versus non-obese subjects (Fig. 8D), or any other patient characteristics (sex, HbA1c, other metrics of neuropathy, etc.; see Supplementary Figs. S4, S5). Additionally, combinations of factors such as “nondiabetic subjects with no symptoms of neuropathy” compared to “diabetic subjects with symptoms of neuropathy” also did not lead to statistical differences in whorl pattern (see Supplementary Fig. S4F). As this study used older age-matched subjects (age 69.1 ± 1.2 years), we could not test for a correlation between age and whorl shape.

Figure 8.

Testing for significant differences in whorl shape amongst patient populations. (A) Whorl shape distribution on the LDA graph based on diabetic status. No statistical differences as per the Peacock's test (P = 1). (B) No statistical differences in whorl shapes based on the neuropathy symptom score (NSS; Peacock's test P = 1). (C) No statistical differences in whorl shapes based on smoking status (Peacock's test P = 1). (D) No statistical differences based on subject's body-mass index (BMI) being within obesity range (Peacock's test P = 0.18).

Discussion

In this study, we present an algorithm to quantify the corneal whorl pattern and to statistically compare such patterns between experimental cohorts. Our method quickly grades a wide range of whorl shapes in IVCM images and does so without relying on an observer's subjective judgment and accompanying biases. As seen in the publicly available dataset that we analyzed, patients can present with highly variable nerve patterns which cannot be fully characterized by nerve density. Additionally, disease and old age lead to highly variable whorl patterns which are ambiguous in presentation and particularly difficult to describe qualitatively.^10,29 A multi-pronged quantitative approach that removes the user's judgment is thus more conducive to large clinical studies and to ensure accurate dissemination of results. We also release our analysis code in its original MATLAB format and in an equivalent Python implementation for easier adoption.³³

In our analysis, we found that neither diabetic status nor neuropathy are sufficient to explain the deterioration of the whorl pattern in older patients. There were no correlations between whorl shape and diabetic status, HbA1c measurements, body mass index (BMI), smoking status, sex, or multiple measures of neuropathy. Healthy patients with no whorls could be observed, whereas patients with diabetes with multiple neuropathy symptoms could have regular whorl patterns. These results corroborate a previous analysis of this dataset where no differences in nerve density at the whorl could be detected between patients with diabetes and control subjects.²⁷ However, our results do not match previously published studies where nerve density in younger patients was severely impacted by diabetes,^24–26 including some images showing a severe degradation of the whorl pattern with disease.^24,25 Age appears to be an important factor affecting the corneal nerves, with nerve density decreasing notably after the age of 60 years.⁹ Additionally, few studies have reported on the wide-field appearance of the whorl,^9,10,22,30 with many studies limited to small FOVs.

With our whorl analysis method, we present a generalizable framework to statistically compare experimental cohorts. It can be summarized in four steps: (1) treat the nerve pattern as a vector field, (2) create metrics that quantify this vector field, (3) reduce the dimensionality of the metric space to one or two dimensions (for example using LDA), and (4) use statistical tests such as Peacock's test to determine if statistically significant differences exist between patient populations. Here, this analysis pathway produced repeatable and interpretable results in synthetic, mice, and human datasets without major modifications. It is also easily adaptable to future needs because additional whorl metrics (e.g. branching density or nerve tortuosity) can be incorporated. Our approach is thus appropriate to study other medical situations where the whorl may be affected in humans or animal models, such as dry eye disease or following refractive surgery.

Whereas our whorl metrics quantify and automatize the process of evaluating whorl shape, some improvements could make our algorithm stronger. First, some manual inputs are still necessary for the analysis, such as identifying a whorl convergence location, cropping the image to roughly center the whorl, and identifying the whorl orientation. Although we attempted to reduce the influence of these inputs on the results, a more reliable algorithm would require no such manual interventions. In the same vein, the total image size can potentially affect the calculation of some metrics, although we do not believe this had a significant influence on our current analysis. For example, the whorl area may increase if the FOV size increases in cases of very regular whorl patterns (see, for example, Fig. 4), and very small FOVs could negatively affect the whorl area or spiral fill/isotropic scores. Finally, our analysis depends on the availability of wide-field images. In the current dataset, most images analyzed had an approximately 2 mm × 2 mm FOV, whereas in most other IVCM studies, the FOV is restricted to approximately 400 µm × 400 µm, which severely restricts the view of the whorl.

Future improvements in corneal nerve imaging, such as larger imaging FOVs and automated nerve segmentation, will lead to further demand for pattern analysis. As newer approaches (including deep learning)⁴¹ are tested for IVCM frame selection, image registration, and automated nerve segmentation, the resulting larger images will benefit from an automated analysis not limited by a qualitative assessment. Further demand for image analysis will also come from animal studies, where larger FOVs can be acquired ex vivo,^11,42 and from the field of technology development, where, for example, optical coherence microscopy has now successfully imaged corneal nerves and holds the promise of non-contact corneal imaging.⁴³