Tuning the physical properties of inorganic novel perovskite materials Ca₃PX₃ (X=I, Br and Cl): Density function theory

Abstract

In photovoltaic technology, inorganic perovskite solar cells formed from halide have developed into a noteworthy prospect, primarily attributable to their exceptional efficiency, cost-effectiveness, and straightforward manufacturing techniques. Lead-free A₃BX₃ inorganic perovskites have generated significant attention within the environmentally friendly solar industry thanks to their extraordinary characteristics encompassing thermoelectricity, optoelectronics, and elasticity. This research focuses on the attributes of the structural, electrical, and optical inorganic halide perovskites Ca₃PX₃ (X = I, Br, and Cl) using the first-principles density-functional theory (FP-DFT). According to the electronic band structures, Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ show semiconductor characteristics with a straight bandgap of 1.4909 eV, 1.9502 eV, and 2.2058 eV, respectively, at the Γ(gamma)-point. Whenever one takes consideration into account the spin-orbital coupling (SOC) effect, the bandgap of the Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ perovskites is minimized to 1.2382 eV, 1.6456 eV, and 1.9056 eV. All these structures' bandgaps are compressed under compressive strain while they expand with tensile strain. The optical properties indicate that these materials have outstanding visible light consumption capabilities due to their distinct band features, comprising functions of dielectric, consumption coefficient, and function of electron collapse. Observations indicate that the dielectric constant peaks of Ca₃PX₃ (where X represents I, Br, or Cl) exhibit a redshift, moving towards lower photon energy levels as compressive strain increases. Conversely, they show a blueshift behavior, shifting to a greater amount of photon energy levels by applying tensile strain. Therefore, these characteristics render Ca₃PX₃ perovskites highly suitable for optimizing light guidance for solar power and energy retention tools.

Highlights

• •Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ show semiconductor characteristics with a straight bandgap of 1.4909 eV, 1.9502 eV, and 2.2058 eV.
• •All these structures' bandgaps are compressed under compressive strain while they expand with tensile strain.
• •The optical properties indicate that these materials have outstanding visible light consumption capabilities.
• •These characteristics render Ca₃PX₃ perovskites highly suitable for optoelectronic devices.

1. Introduction

Solar power is an essential eco-friendly and sustainable energy source. Solar photovoltaic technology provides a remarkable alternative to conventional energy sources [1]. Photovoltaic cells can transform light energy into electrical power [2]. Perovskites made on organic-inorganic lead halide are highly desirable in photovoltaics due to their affordability in production. A broad spectrum of light can be absorbed and suitable bandgap for fabricating semiconductor devices [[3], [4], [5], [6], [7], [8]]. In the previous thirteen-year period of time, from 3.8% to 26.1%, the power conversion efficiency (PCE) increased [[9], [10], [11]]. Progress has been expedited in the prior decade by the improved characteristics of perovskite materials. Inorganic metal halide perovskites have drawn interest much interest as a consequence of their exceptional operational attributes, including their semiconducting solid-state nature, substantial absorption coefficients, reduced carrier recombination rates, and minimal reflection rates [[10], [11], [12], [13], [14]]. In the realm of optical purposes similar to solar cells, LED (light-emitting diodes), and green energy conversion devices, inorganic perovskites are often employed and processed [[12], [15], [16], [17]]. Regrettably, the predominant challenge facing the extended-term durability of organic-inorganic lead halide perovskites (OILHPs) lies in their vulnerability to environmental factors such as moisture, wind, sunlight, and temperature when deployed in practical settings [[18], [19], [20], [21], [22], [23], [24], [25], [26]]. Furthermore, the widespread applications and advancement of perovskite cells are hindered by the inherent instability of lead (Pb), device hysteresis, and toxicity. To achieve broad commercialization, three significant barriers must be resolved: the barter of toxic lead with non-fatal materials to address environmental concerns, mitigation of device hysteresis, and enhancement of perovskite material stability [[27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41]].

Recent studies indicate that cubic inorganic A₃BX₃ structure perovskites possess direct bandgaps and exhibit exceptional optical absorption properties, rendering them a promising choice for applications in LED, semiconductor, and solar energy technologies [[42], [43], [44]]. L. Zhang et al. findings revealed that nonliving halide perovskite solar cells can produce large open-circuit voltages repeatedly [45]. As a result, the expectation is that the limitations of OILHP materials could be overcome through the efficient utilization and manufacturing of perovskite materials composed of inorganic halides and related solar cells. Sr₃AsI₃, Ca₃PI_3, and Ca₃AsI₃ perovskite, categorized as an A₃BX₃ structure perovskite material, has garnered considerable attention within the market for solar technologies owing to its extraordinary optical, architectural, and electronic characteristics [[46], [47], [48]]. Notably, it is considered a novel substance, with its bandgap exclusively determined in a prior research paper [[48], [49], [50], [51]]. Remarkable optoelectronic characteristics of this perovskite include substantial light absorption, lengthy diffusion intervals of carriers, and efficient transmission of charges.

Furthermore, it can be manufactured cost-effectively and at scale through solution-based synthesis. Its suitability for mass manufacture of devices is attributed to its processability via solution methods, which has the potential to lead to cost-effective and widely accessible technology. Additionally, its highly tunable structure allows for doping, layout, and crystal form adjustments to tailor its properties as needed. A₃BX₃ exhibits promising applications in various devices, several samples of which include lasers, photodetectors, LEDs, and solar cells. Perovskite LEDs provide customizable and effective lighting techniques, although perovskite solar cells exhibit high-efficiency and cost-effective manufacturing processes. Additionally, perovskite-based photodetectors and lasers are characterized by their high sensitivity, rapid response times, and the ability to fine-tune emission wavelengths. As A₃BX₃ perovskites are auspicious novel materials, it is crucial for both inherent research and scientific petition, given the high potential of these materials.

In investigating semiconducting materials' electronic abilities, it is generally crucial to consider the influence of SOC. This outcome arises from the relativistic interaction between the orbital motion and spin orientation of orbiting electrons. The layout of the electronic bands is changed by the SOC and the states where electrons reside, leading to the potential narrowing or widening of material band gaps. The extent of SOC's impact is primarily contingent on atomic mass. Heavier atoms tend to induce more significant changes in the bandgap, while lighter atoms cause the bandgap to decrease in value. While numerous investigations have focused on the SOC effect in various materials over the past decade, there still needs to be a comprehensive examination regarding the SOC-induced physical properties of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ perovskite. Consequently, it is imperative to elucidate how the presence of SOC impacts the physical characteristics of Ca₃PX₃ (X = I, Br, and Cl) [48,[52], [53], [54]].

Strain engineering represents a powerful approach to altering perovskite components' crystal composition and attributes, rendering them well-suited for optoelectronic applications. Recent investigations into the impact of strain on material properties have unveiled an evident and unmistakable relationship between the material's structural properties and the applied strain [[55], [56], [57], [58], [59], [60], [61]]. Research has shown that applying slight pressure, typically below 0.3 GPa, can significantly prolong the carrier's entire lifespan of hybrid organic-inorganic lead halide perovskite compounds, increasing it by approximately 70%–100% [62] while concurrently reducing the bandgap [63]. Jing et al. established that the bandgap of CsPbI₃ could be adjusted throughout the field of 1.03–2.14 eV by manipulating strain levels from −5% to +5% [63].

Strain-induced alterations significantly enhance the photovoltaic potential of CH₃NH₃GeI₃ via enhancing the energy band gap, charge carrier vigor, and suction parameters [63]. According to Zhao et al. compressive strain significantly distorts the octahedral PbBr₆ arrangement of CsPbBr₃ [55]. Consequently, there is considerable ionic polarization due to the displacement of the core Pb²⁺ cations and Br⁻ anions. The structural, electrical, and optical guidings of CsGeI₃ perovskite are significantly affected by compressive and tensile strain. For instance, when the strain is adjusted from −3% to +3%, the Ge–I link elongation occurs, resulting in a bandgap of 1.36 eV [30,55]. Semiconductor materials with a bandgap within the 0.9–1.6 eV range are usually used in single-junction perovskite solar cell applications [[64], [65], [66]]. Consequently, the optimization of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃'s bandgap is of utmost importance, aiming to achieve a level that is well-suited for semiconductor applications while maintaining stability within an ideal range for the production of high-quality products [[67], [68]]. Nevertheless, until now, no extensive investigation has been conducted to examine the impact of strain on the optical, electrical, and mechanical characteristics of Ca₃PX₃.

This study aims to employ FP-DFT working out to interrogate the configurational, electronic, and optical peculiarity of cubic Ca₃PX₃ under different strain levels and the SOC effects. Our study utilizes two unconventional tactics to analyze the band configuration of Ca₃PX₃. In our investigation, we focused on investigating how variations in both strain and SOC affect the bandgap, together with instances where it increased or decreased. Consequently, conducting this research would be valuable in discerning the distinctive characteristics of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ inorganic materials under different SOC and strain conditions; this could have practical uses in upcoming solar cells and energy archiving gadgets.

2. Computational details

We employed FP-DFT along with norm-conserving (NC) pseudopotentials to investigate the electrical and optical characteristics [60,61]. The Generalized Gradient Approximation (GGA) incorporating the Perdew-Berke-Enzerhof (PBE) function of association as an exchange interaction was utilized for a more comprehensive understanding of these properties [69]. The DFT predictions were performed making use of the Quantum Espresso simulation package [[70], [71], [72]]. In our DFT computations, we employed the Quantum Espresso simulation package. We used a 50 Ry kinetic energy constraint and a 350 Ry charge density cutoff to enhance simulation performance and structural optimization. Geometrical optimization was carried out with stress calculations for individual atoms and the entire cell. During this computational analysis, we set the upper limit of acceptable force patience at 0.01 eV/Å. We used a self-consistent function threshold of roughly 10⁻⁶ atomic units to achieve high precision in our ground-state energy simulation. We used a convergence threshold for force calculations of 10⁻³ atomic units to optimize structural features and ionic relaxation. Additionally, we employed an 8 × 8 × 8 Monkhorst-Pack k-mesh grid to compute the electronic band layout and density of states (DOS) by inquiring over the first Brillouin Zone [72,73]. The biaxial strain is calculated by metamorohing the lattice element $a_{st}$ distinct by the ingredient, $\epsilon =\frac{a_{strained}-a_{relaxed}}{a_{relaxed}}\times 100\%$, where $\epsilon$ act for compressive and tensile strain. Inside the system of equations, $a_{relaxed}$ is seen to be the unstrained lattice perpetual, and the value of ε alters from −3% to +3% in units of 1%. In this context, negative strain utility denotes compressive strains, while positive strain values represent tensile strains. To investigate the dynamical solidity of compounds and explore their optical properties, we applied the FP-DET. We employed FP-DET to assess the exploration of the optical characteristics of materials and their dynamical stability [74]. Subsequently, we examined the photon energy (eV) range where the dielectric function is the convoluted band played to reach their highest absorption. We also didn't modify the Monkhorst-Pack k-mesh grid 8 × 8 × 8 for computing the optical characteristic with Gamma as its center. The complex dielectric function is the main correlation for the optical absorption coefficients. The equation is as follows:

$$\epsilon \left(\omega \right)={\epsilon }_1\left(\omega \right)+j{\epsilon }_2\left(\omega \right)$$ (1)

3. Results and discussion

3.1. Structural properties

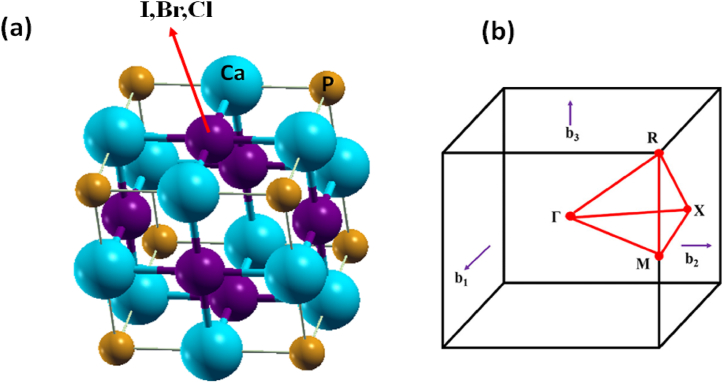
The crystal structure of Ca₃PX_3, a metal halide perovskite exhibiting cubic Pm-3m symmetry, consists of seven atoms inside the unit cell. As Fig. 1(a) illustrates, Ca²⁺ ions form octahedra by sharing edges and corners with two P³⁻ ions and four Br¹⁻ ions of equivalent sizes. It's important to note that the octahedra sharing corners in this structure are not tilted. The bond distances of Ca₃PI₃ for Ca–P and Ca–I are measured at 3.0610 Å and 3.0610 Å, of Ca₃PBr₃ for Ca–P and Ca–Br is measured at 2.9560 Å and 2.9560 Å and of Ca₃PCl₃ for Ca–P and Ca–Cl is measured at 2.8659 Å and 2.8659 Å respectively. P³⁺ ions create corner-sharing octahedral structures with six Ca²⁺ ions of uniform size, forming covalent bonds within the PCa₆ octahedra. It's worth noting that the octahedra sharing corners in this configuration remain undistorted.

Fig. 1.

(A), Ca₃PX₃ (X = I, Br, and Cl) optimized structure and (B) the first Brillouin zone's k-path to ascertain its electronic band configuration.

Additionally, Br¹⁻ ions arrange themselves in a planar square configuration, interacting with four Ca²⁺ ions of equal size. Fig. 1(b) represents the k-path corresponding to the first Brillouin zone. The electronic band layout of Ca₃PX₃ is determined by the locations of high symmetry within the Brillouin border (Γ, X, M, R, and Γ), and the band diagram repeats as it traverses these points. We explored the relationship between binding energy and lattice constant by conducting relax calculations within the PBE functional, thereby obtaining structural properties like the lattice parameter. The structural features have been established using PBE, and Table 1's demonstration of the lattice constant a($A°$) shows one such characteristic [75].

Table 1.

Ca₃PX₃ (X = I, Br, and Cl) lattice constant and energy bandgap were determined employing exploring data and previous DFT calculations [75].

Structure	Lattice constant ($A°$)		Bandgap Energy (eV)
	This work	Previous work	This work	Previous work
Ca3PI3	6.206	6.21	1.4909(PBE)	2.16(HSE) [69]
Ca3PBr3	5.923	5.91	1.9502(PBE)	2.63(HSE) [69]
Ca3PCl3	5.725	5.73	2.2058(PBE)	2.87(HSE) [69]

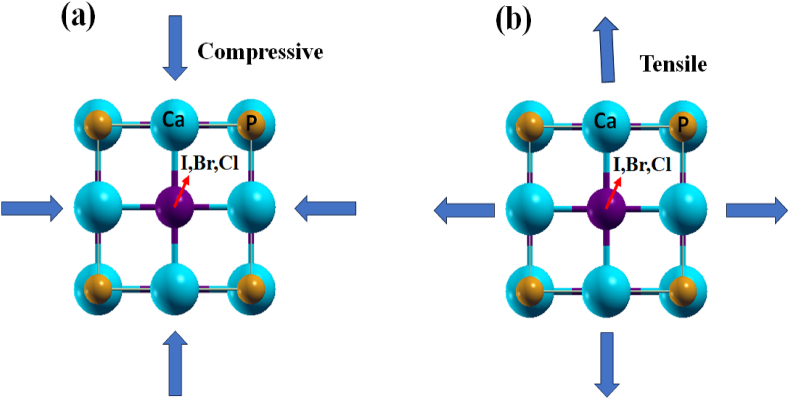
To determine the smallest ground state energy and ensure lattice stability, it is crucial to identify the lowest-energy-producing lattice constant in the earthly situation. Our optimized compound has a lattice constant for Ca₃PI₃ of 6.206 Å, Ca₃PBr₃ of 5.923 Å, and Ca₃PCl₃ of 5.725 Å, which aligns with prior findings [76]. Fig. 2(a) and (b) represent the effects of compressive and tensile strains on these compounds, respectively. It's important to highlight that the strain is applied in biaxial directions. The subsequent sections delve into the electronic and optical properties that can be derived from this category of strain-induced deformation.

Fig. 2.

The pictorial view of inorganic perovskite Ca₃PX₃ (X = I, Br and Cl) with (a) compressive and (b) tensile strain.

3.2. Electronic properties

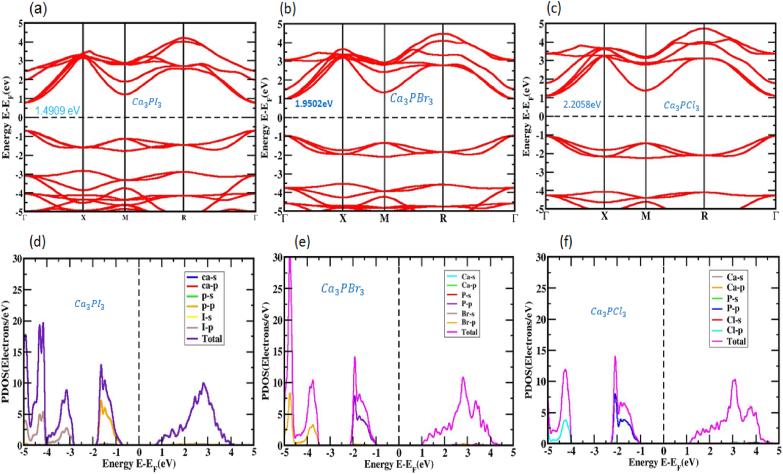
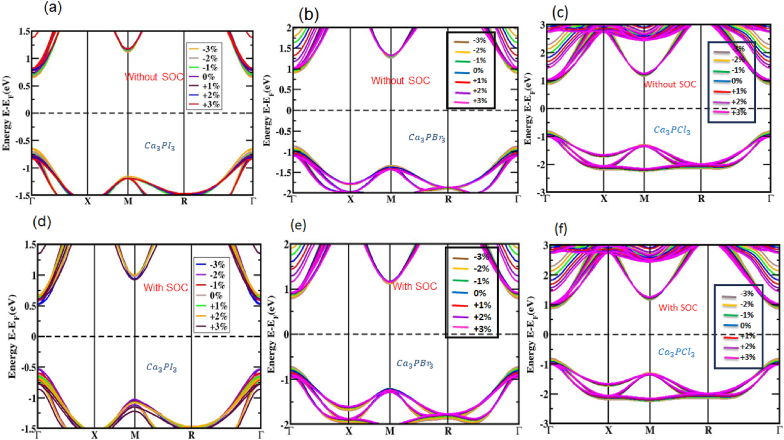
We analyzed its electronic band layout to better understand the optical properties of perovskite, an organic compound of Ca₃PX₃, in both strained and unstrained conditions. In Fig. 3 (a, b, and c), we observe the unstrained electronic band structures of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ configuration. The amount of bandgap in the figure is easily discernible by keeping the zero levels of the Fermi constant. Fig. 3 (a, b, and c) clearly shows that the valence band maximum (VBM) and the conduction band minimum (CBM) of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ are placed at the Г point, showing a configuration with a computed value of roughly a direct bandgap 1.4909 eV, 1.9502 eV and 2.2058 eV based on the PBE functional. It is evident that when employing the GGA approach to assess the bandgap, there is a tendency to underestimate the bandgap value, a common limitation associated with the GGA method.

Fig. 3.

(a, b, c) The electronic band formation and (d, e, f) PDOS of the Unstrained inorganic perovskite structure that has been optimized Ca₃PX₃ (X = I, Br, and Cl) without SOC.

Similarly, the depreciation of the bandgap constraint is also observed in the LDA + U and LDA approaches. To rectify this bandgap calculation error, scientists have devised several methods to tackle the issue, such as the GW approach and the hybrid operational. However, it's worth noting that these approaches come with their limitations [77]. Compared to the bandgap value calculated experimentally, the GGA + U method partially adjusts the bandgap as thought numerically. However, as noted by Nayak et al. [71,72] recent findings have demonstrated that the PBE method can yield reasonably reliable results, and the general pattern of alterations in the bandgap caused by strain is constant in the band structure regardless of the function used. This implies the PBE/GGA function is acceptable for investigating material responses to strain. Typically, the most suitable substance for photovoltaic power optoelectronic and photothermal purposes should have a straight bandgap in its crystalline state [47,[77], [78], [79]].

In general, the fractional DOS explains how specific atoms and their several regions are modulated by the bandgap energy of the Ca₃PX₃ formations. The PDOS ordination for the Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ arrangements can be observed in Fig. 3 (d, e, and f), covering an energy run from −5 to 5 eV. Significantly, the state hybridization involving Ca and P with I in Ca₃PI₃, Ca and P with Br in Ca₃PBr₃, Ca, and P with Cl in Ca₃PCl₃ cover the complete energy spectrum but do not encroach upon the bandgap. The bonding between Ca–I and P–I, Ca–Br and P–Br, Ca–Cl and P–Cl is primarily covalent. Furthermore, in the Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ structures (depicted in Fig. 3 (d, e, and f), there is a notable movement of electron charge from Ca and P to I, Ca, and P to Br, Ca, and P to Cl, a consequence of the substantial disparities in atomic states. Near the Fermi level, the role of Ca²⁺ atoms is relatively small. When we examine the cubic phase, we observe that the I-5p orbital primarily persuades the DOS near the valence band of Ca₃PX₃. In contrast, the navigation band is predominantly governed by the P-3p orbital, with the role of Ca-4s orbitals remaining lowest.

3.3. The effect of SOC on electronic structure

We merged the Hamiltonian combination that includes SOC to account for the influence of SOC on the electronic attributes of the Ca₃PX₃ perovskite.

$$H_{soc}=\frac{ħ}{4m_0{c}^2}\left(\overrightarrow{F}\times \overrightarrow{p}\right)·\overrightarrow{s}\text{.}$$ (2)

where H_soc relates to the SOC Hamiltonian operator, ħ is the scaled-down Planck's constant, p⃗ indicates the angular impetus of the orbit, F⃗ describes the force or potential energy, $m_0$ represents the weight of unbound electrons, and s⃗ demonstrates the spin angular pace.

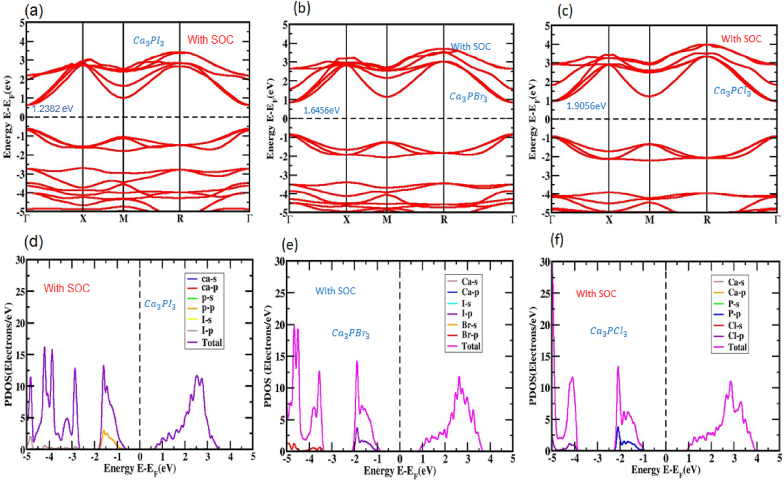
To conduct relativistic computations, we employed the PBE active procedure to evaluate the magnitude of relativity's impact and examine how the massive elements Ca and P influence the electronic structures of Ca₃PX₃ perovskites when SOC is considered. Both the conduction band area and the valence band field were significantly impacted by SOC, resulting in shifts in the places where the CBM and VBM were, as depicted in Fig. 4. The VBM underwent notable upward shifts, whereas the CBM experienced downward shifts addressing the Fermi level. However, the introduction of SOC resulted in a bandgap energy value of 1.2382 eV for Ca₃PI₃, 1.6456 eV for Ca₃PBr_3, and 1.9056 eV for Ca₃PCl₃ causing a reduction in the perovskite's bandgap. This alteration in the bandgap is visually revealed in Fig. 4 (a, b, and c).

Fig. 4.

(a, b, c) The electronic band layout and (d, e, f) PDOS of the Unstrained inorganic perovskite construction that was successfully optimized Ca₃PX₃ (X = I, Br, and Cl) with SOC.

A more thorough grasp of the cubic band structure Ca₃PX₃ can be gained by examining the PDOS while considering the influence of SOC. The connection of SOC results in modifications to the valence and transmission bands, owing to the distinct electron interactions compared to PDOS calculations without SOC consideration. The PDOS shown in Fig. 4 (d, e, and f) highlights that no recurring patterns in the influence of the Ca atom can be seen when SOC is considered. The splitting of I-5p, Br-5p, Cl-5p into p (j = 1/2) and I-5p, Br-5p, Cl-5p into p (j = 3/2) due to the SOC outcome does not lead to any differentiation in band edges at a high-symmetry locus. As depicted in Fig. 4 (d, e, and f), the primary contributions of I-5p, Br-5p, Cl-5p, (j = 1/2) and I-5p, Br-5p, Cl-5p, (j = 3/2) atoms mainly occupy the energy spectrum from −5 to −0.6 eV, −5 to −0.8 eV, −5 to −0.9 eV in the valence band (VB). Alternatively, the energy spectrum across 0.6 and 3.5 eV,0.8 and 3.7 eV, and 0.9 and 3.9 eV on the conduction band (CB) side is predominantly attributed to P-3p (j = 1/2) and P-3p (j = 3/2).

3.4. Strain-dependent electronic properties

We have investigated the influence of employed strain (in percentage) on the Ca₃PX₃ layout, both with and not in considering SOC's effects on tensile and compressive stresses. The compressive-to-tensile strain range investigated ranges from −3% to +3% with increments of 1%. For both Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ (as depicted in Fig. 5 (a, b, and c)) perovskites, we observed that the VBM and CBM exhibit shifts in the direction of the Fermi level according to compressive strain (varying from −3% to 0%). The band structures of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ addressing the SOC effect inside compressive strain are portrayed in Fig. 5 (d, e, and f), respectively. The compressive strain is exerted, which diminishes the bond width between Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ atoms, leading to increased orbital overlap, including and excluding the SOC effect. Under the employed compressive strain ranging from −3% to 0%, it's noteworthy that the VBM and CBM are positioned at the Γ-point.

Fig. 5.

Electronic bands of Ca₃PX₃ (X = I, Br, and Cl) under (a, b, c) compressive and tensile strains integrating lacking SOC effect; (d, e, f) compressive and tensile strains incorporating using SOC impact.

That being said, linear bandgap is achieved at the Γ-point, irrespective of whether or not the SOC effect is regarded. It has been noted that additional levels of compressive strain guided both in and out of the SOC effect in reducing the bandgap. The implementation of tensile strain (varying from 0% to +3%) also exerts an influence focusing on the electrical band structure. In these cases, the VBM and CBM have departed from the Fermi level, implying an expansion in the bandgap owing to the incorporation of tensile strain. This ascends in the bandgap results from the enlarged bond length and atomic separation between the Ca₃PX₃ atoms, decreasing the forces between them.

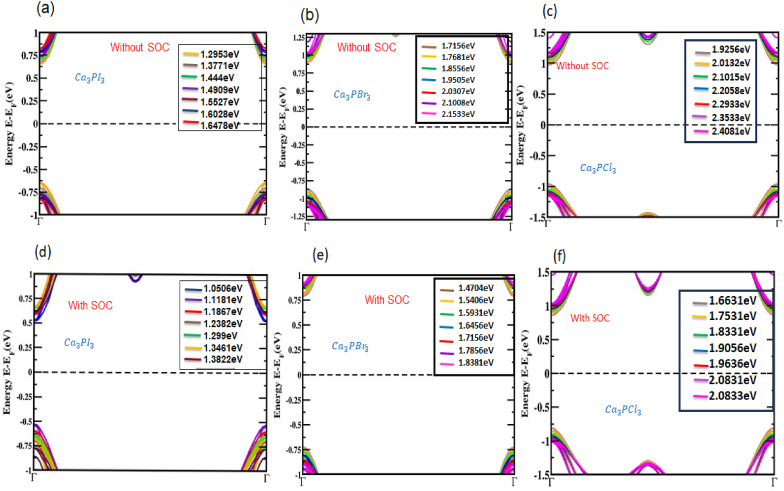
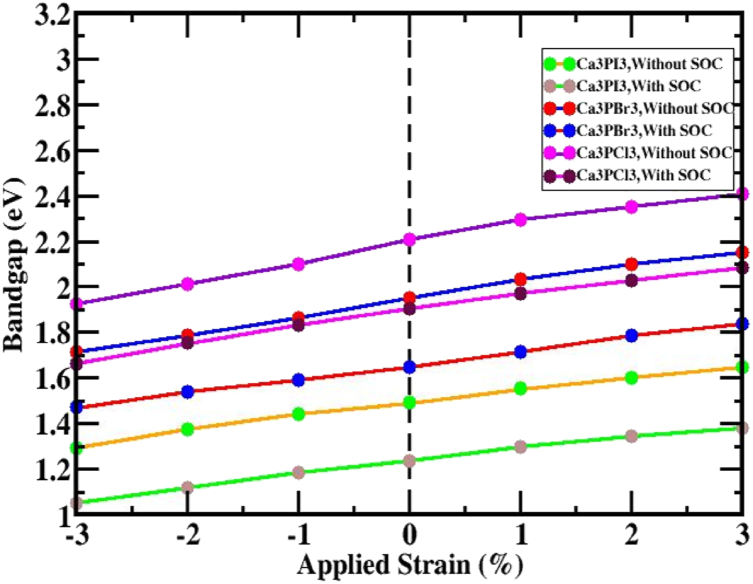
A band gap increase is seen in all the structures under tensile strain. It is noteworthy that a straight bandgap is seen at the Γ-point when tensile strain is employed, thinking about the SOC effect in the Ca₃PX₃ structures shown in Fig. 6. There is a straight bandgap in the electronic band layout in response to compressive and tensile strain employed on Ca₃PX₃ structures. Fig. 7 summarizes the fluctuations in bandgap for the Ca₃PX₃ frameworks under compressive and tensile loads, both in and out of considering the SOC effect, as well as in Table 2. In the utilized strain range of −3% to +3%, the bandgaps of Ca₃PI₃ exhibited variations, ranging from 1.2953 to 1.6478 eV (absent of SOC) and 1.0506–1.3822 eV (using SOC), Ca₃PBr₃ exhibited variations, ranging from 1.7156 to 2.1533 eV (lacking SOC) and 1.4704–1.8381 eV (employing SOC) and Ca₃PCl₃ exhibited variations, ranging from 1.9256 to 2.4081 eV (aside from SOC) and 1.6631–2.0833 eV (with SOC) correspondingly. Surprisingly, it has been noted that the direct bandgap characteristics remain unaltered during the entire applied strain limit. This signifies that this formation can potentially boost the solar cell's productivity by the principles outlined corresponding to the Shockley-Queisser theory [80].

Fig. 6.

Electronic bands of Ca₃PX₃ (X = I, Br, and Cl) under (a, b, c) enlarged view incorporating compressive and tensile strains not in SOC effect and (d, e, f) with SOC impact.

Fig. 7.

The variation of energy bandgap of the Ca₃PX₃ (X = I, Br, and Cl) response of the structure to the applied strain and integrating the without SOC and with SOC effect.

Table 2.

The calculated bandgap of cubic Ca₃PX₃ (X = I, Br, and Cl) perovskite within unique compressive and tensile strains.

	Ca3PI3				Ca3PBr3				Ca3PCl3
Applied Strain (%)	Compressive		Tensile		Compressive		Tensile		Compressive		Tensile
	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC
0	1.4909	1.2382	1.4909	1.2382	1.9502	1.6456	1.9502	1.6456	2.2058	1.9056	2.2058	1.9056
1	1.444	1.1867	1.5527	1.299	1.8656	1.5931	2.0307	1.7156	2.1015	1.8331	2.2933	1.9726
2	1.3771	1.1181	1.6028	1.3461	1.7881	1.5406	2.1008	1.7856	2.0132	1.7531	2.3533	2.0261
3	1.2953	1.0506	1.6478	1.3822	1.7156	1.4704	2.1533	1.8381	1.9256	1.6631	2.4081	2.0833

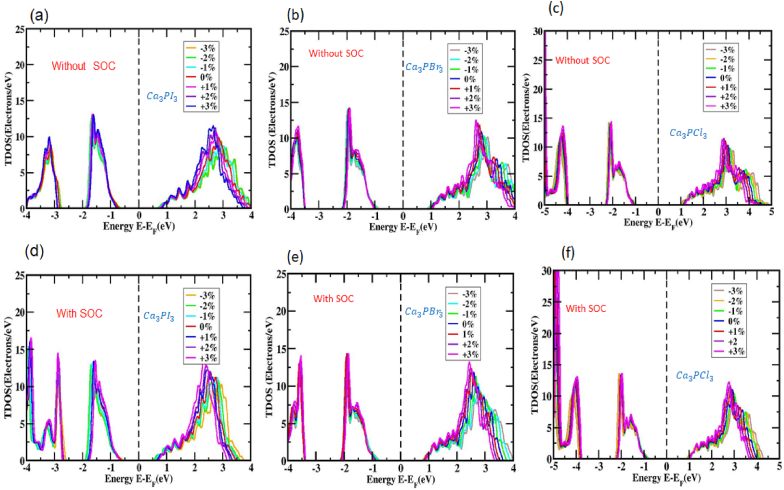
The exertion of strain also modifies the participation of the orbit of Ca₃PX₃ atoms. Figs. S1,2,3 illustrates the PDOS for Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ under both compressive Figs. S1, 2, and 3 (a, b, and c) and tensile Figs. S1, 2, and 3(d, e, and f) strains, disregarding the SOC effect. Since the strain fluctuates between −3% and +3%, it's observed that the PDOS attached to I atoms 5p orbital shifts approaching the valence band and positions itself behind the Fermi level. Within the conduction band, the total DOS is primarily affected by the 3p orbital of P atoms. The occupied DOS associated with the 3p orbital of P remains consistently located and conduction band side-structured, irrespective of variations in adapted strain; however, the overall influence of the DOS as the strain is adjusted within the extent of −3% to +3%. The figure shows that as the tensile strain increases, the Total Density of state (TDOS) for the Ca₃PX₃ structure experiences a notable increase, shifting from approximately 16 electrons/eV to around 29 electrons/eV.

Figs. S4, 5, and 6 depict the PDOS of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ under compressive Figs. S3, 4, and 5 (a, b, and c) and tensile Figs. S4, 5, and 6 (d, e, and f) strains while accounting for the effects of SOC. As the strain varies from −3% to +3% with the SOC effect considered, the PDOS associated using the I atom's 5p orbital reveals that it is discovered near the valence band and beneath the Fermi level. The total DOS is predominantly affected by the 3p orbital of the P atom in the vicinity of the conduction band. The incorporation of the SOC impact improves the overall DOS performance as the imposed strain is changed inside the variety of −3% to +3%. Figs. S4, 5, and 6 exhibit that, when the SOC effect is considered, the total DOS in the Ca₃PX₃ material changes from roughly 16 electrons/eV at a −3% strain to approximately 29 electrons/eV at a +3% strain.

Fig. 8 provides a visualization of the TDOS for Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ under varying degrees of both with (Fig. 10 (d, e, and f)) and without (Fig. 10 (a, b, and c)) the presence of biaxial compressive and tensile strain the influence of SOC. The analysis of TDOS can greatly enhance our understanding of the electronic band layout dynamics in Ca₃PX₃. In the unstrained Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ in TDOS, the band of valence beneath the Fermi level is primarily influenced through the I atom's orbitals, with minimal influence of the Ca-3p and P-3p orbitals, irrespective of SOC's existence. Similarly, the P atom's orbitals predominantly influence the TDOS of the conducting band more than the Fermi level, with negligible contributions from the Ca-3p and I-5p orbitals, at least of the presence of SOC. The semiconductor attributes of the material and the existence of a bandgap become obvious owing to the absence of a DOS near-proximity line to the Fermi level, in line with the observations made by Nayak et al. In a study involving MoS₂ [81], it was found that changes have a significant impact on the pressure about the band configuration and bandgap amplitude of MoS₂, and this effect did not show substantial dependence on the specific functional exchange-correlation used [82].

Fig. 8.

TDOS values of Ca₃PX₃ (X = I, Br, and Cl) very nearby Fermi levels across different strains (a, b, c) without and (d, e, f) with SOC consequence.

Fig. 10.

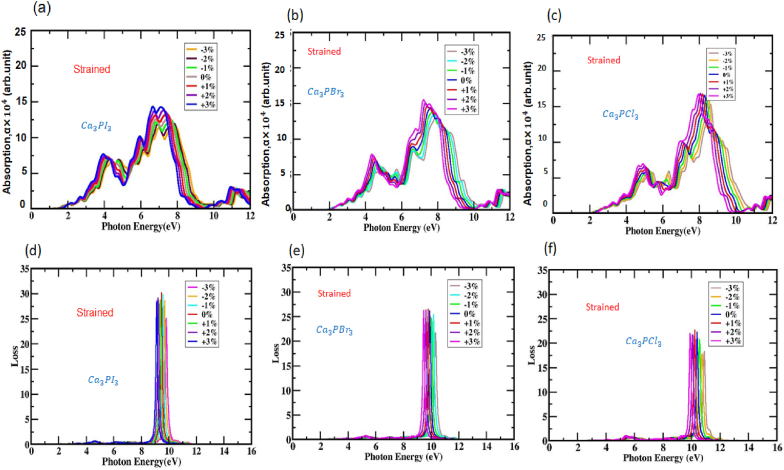
The alterations in the absorption coefficient resulting from varying photon energy levels with separate compressive and tensile strains are observed in (a, b, c) Ca₃PX₃(X = I, Br, and Cl) structures. The variations in the loss function can be noted as photon energy increases under distinct tensile and compressive strains in (d, e, f) Ca₃PX₃(X = I, Br, and Cl) structures.

The conductivity of Ca₃PX₃ materials experiences an enhancement because of the TDOS line swapping nearer to the Fermi level under compressive stresses within the range of 0% to −3%, whether the SOC effect is regarded as or not. As an alternative, the conductivity of Ca₃PX₃ materials decreases owing to the TDOS line that departs from the Fermi level when exposed to tensile strains ranging from 0% to +3%, whether or not the SOC influence is considered. Viewing the band structure in extensive detail and DOS of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ materials, a transition in the bandgap has been expected.

3.5. Optical properties

To assess the materials' appropriateness for optoelectronic applications, it's crucial to examine their optical properties, encompassing the analysis of factors like absorption, dielectric behavior, and loss function. We can enhance the material's optical characteristics by introducing biaxial strain to alter the lattice parameter. When a particular wavelength of light interacts with a material's surface, the absorption coefficients provide valuable insights into how far the light penetrates before being absorbed. These coefficients are essential in various applications, including their relevance in cellular systems. In this research, Ca₃PX₃ were examined for their diverse properties, and it was found that these properties could be altered by subjecting the material to both tensile strains in the extent of 0% to +3% and biaxial compression in the extent of 0% to −3%. Key material factors of utmost importance for optoelectronics and solar cell applications revolve around their optical properties, encompassing dielectric operations, extinction loss factor (EELF) reflectivity, and absorption coefficients.

We compute the complex dielectric activity, ε(ω) using Equation (1) [83].

The crucial element ${\epsilon }_1$ (ω) and the imagined portion ${\epsilon }_2$ (ω) of the dielectric performance depends on the incident light's frequency, denoted as ω. The true dielectric function was obtained via the Kramers-Kronig metamorphosis. At the same time, the parts of the momentum matrix were used to determine the unreal dielectric function as described in Ref. [83]. The crucial part of the dielectric function ${\epsilon }_1$ (ω) for the Ca₃PX₃ perovskite can be used to calculate the material's EELF and its absorption coefficient in Equation (3) [79,84]

$${\epsilon }_1\left(\mathit{\omega }\right)=1+\frac{2}{\pi }P\underset{0}{\overset{\infty }{\int }}\frac{{\epsilon }_2\left({\omega }^{\prime }\right){\omega }^{\prime }}{{\omega }^{\prime 2}-{\omega }^2}d\omega$$ (3)

where P is the absolute prime number.

Additionally, the hypothetical dielectric activity ${\epsilon }_2$ (ω) was obtained through Equation (4) [79,84]

$${\epsilon }_2\left(\mathit{\omega }\right)=\frac{V{e}^2}{2\pi \hslash m^2{\omega }^2}\times \int d^{3}k\sum |⟨{\phi }_c|p|{\phi }_v⟩\widehat{|}\left(2\right)\mathit{\delta }\left(E_c-E_v-\mathrm{\hslash }\mathit{\omega }\right)$$ (4)

where V reflects the unit cell's volume, ℏ is a compact form of Planck's constant, the motion is symbolized by the operator p, and the designations ${\phi }_c$ and ${\phi }_v$ are typically employed to specify the valence and conduction bands matching wave functions.

We can determine the absorption coefficient α(ω) by mixing the dielectric operation's real and unreal components. Estimating the absorption coefficient by Formula (5) [79,84].

$$\mathit{\alpha }\left(\mathit{\omega }\right)=\frac{\sqrt{2\omega }}{c}[\sqrt{{{\epsilon }_1\left(\omega \right)}^2+{{\epsilon }_2\left(\omega \right)}^2}–{\mathit{\epsilon }}_{\mathbf{1}}\left(\mathit{\omega }\right)\stackrel{{}^{1/2}}{]}$$ (5)

where c symbolizes the quickness of light.

Finally, the relationship (6) [83] was utilized to establish the ELF of Ca₃PX₃ perovskites:

$$L\left(\mathit{\omega }\right)=\frac{{\epsilon }_2\left(\omega \right)}{{\epsilon }_1^2\left(\omega \right)+{\epsilon }_2^2\left(\omega \right)}$$ (6)

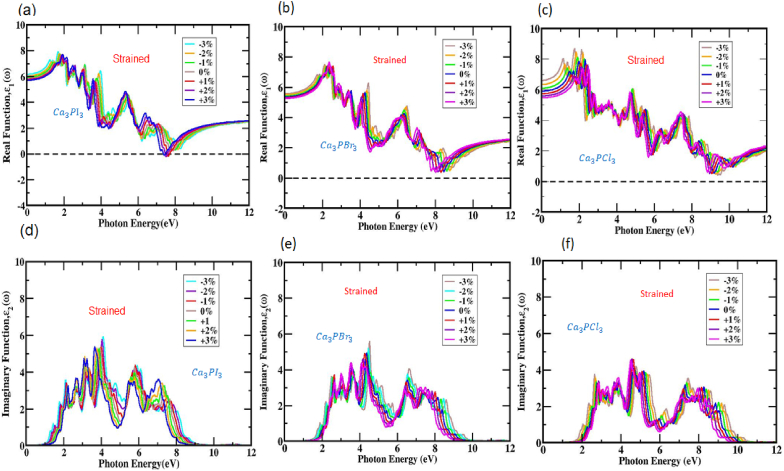
Polarization and dispersal phenomena become evident when exploring the real portion of the dielectric constant. The computation reveals a value of 5.91 for ${\epsilon }_1$ (0) in the cubic Ca₃PI₃ structure, 5.36 for ${\epsilon }_1$ (0) in the cubic Ca₃PBr₃ structure, and 5.97 for ${\epsilon }_1$ (0) in the cubic Ca₃PCl₃ structure. Notably, distinct absorption peaks emerge close photon energies of roughly 1.84 and 3.15 eV for Ca₃PI₃, 2.30 and 4.24 eV for Ca₃PBr_3, and 2.34 and 4.75 eV for Ca₃PCl₃ within the genuine portion ${\epsilon }_1$ (0) of the dielectric function, as pictorial in Figs. S7(a,b,c). The real part values of ${\epsilon }_1$ (ω) within the Ca₃PX₃ structure tend to expand initially from ${\epsilon }_1$ (0), reaching a peak and subsequently lowering, numerous peaks are created throughout the process. Changes in biaxial strain induce modifications in both the amplitude and origin of these peaks. Typically, materials with a large bandgap exhibit diminished peak values of the dielectric constant when compared to those with a small bandgap norm. In the case of compressive strain, as portrayed in Fig. 9 (a, b, and c), the dielectric constant's maximal within the Ca₃PX₃ structure shifts towards decreased photon energy due to a bandgap narrowing (redshift).

Fig. 9.

The actual element of the dielectric function within (a, b, c) Ca₃PX₃ (X = I, Br, and Cl) formation demonstrates changes as an execution of photon energy when subject to various tensile and compressive strains. The imaginary part of the dielectric execution in (d, e, f) Ca₃PX₃(X = I, Br, and Cl) shapes displays alterations in response to photon energy variations under varying tensile and compressive strains.

Conversely, under increasing tensile strain, the maximum dielectric constant within the Ca₃PX₃ structure experiences a lowering motion and a displacement toward more energetic photons (blueshift). The peaks discovered within the fictitious portion of the dielectric activity result from carrier transitions within the conduction and valence bands. A system's imaginary component ${\epsilon }_2$ (ω) and band structure are intertwined. Notably, the primary peaks in ${\epsilon }_2$ (ω) for cubic Ca₃PI₃ take place at a photon energy of 3.95 eV, Ca₃PBr₃ happens at a photon energy of 4.37 eV, and Ca₃PCl₃ takes place at a photon energy of 4.67 eV as shown in Fig. S7 (d, e, and f). Data collected from the Ca₃PX₃ compound indicates that its most significant peaks are anticipated to be between the observable and infrared ranges, possibly due to its narrower bandgap. Fig. 9 (d, e, and f) illustrates that the exertion of strain leads to an expansion and movement of the imaginary portion of the dielectric activity, particularly in the long-wavelength territory. Generally, the imaginary component Ca₃PX₃ spectrum can be separated into lower and higher-energy zones. This demonstrated that altering the biaxial compressive and tensile strains modified the broad energy span within the absorption range. Nevertheless, in the high-energy domain, the fictitious component of the dielectric constant remained at zero for all the Ca₃PX₃ samples inspired by strain. This outcome implies that all the samples subjected to strain presented excellent transparency, and in the high-energy zone, there is minimal absorption (over 9 eV).

The absorption peaks observed within the imaginary section of the spectrum play a significant role in shifting charge passing from the valence band to the conduction band. Variations in the bandgap and lattice constant are blamed for this maximum movement. As depicted in Fig. 9 (d, e, and f), the practice of both compressive and tensile strains led to shifts towards lower and higher photon energies, causing the fictitious peaks to redshift and blueshift, respectively. These research conclusions indicate that under investigation, the perovskite compound Ca₃PX₃ holds promise for exhibiting an adjustable absorption spectral range when subjected to two dimensions of compressive and tensile strains. Withal, it's noteworthy that the imaginary component of the dielectric behavior comes below zero with a photon energy threshold of 9 eV for Ca₃PI₃, 9.5 eV for Ca₃PBr_3, and 10.5 eV for Ca₃PCl_3, signifying that the compound possesses exceptional optical acuity while maintaining a minimal optical absorption.

The optical absorption coefficient, as presented in Fig. S8 (a, b, and c), represents the greatest depth that a certain amount of light energy can pass through a substance before being absorbed. Moreover, it provides valuable perspectives on solar energy conversion efficiency, a pivotal factor in determining a material's appropriateness for solar cell applications. Fig. S8 (a, b, and c) and 10 (a, b, and c) depict the coefficient of absorption varying with photon energy for both unstrained and strained structures of Ca₃PX_3, respectively. The location of the initial absorption peak holds paramount importance because it denotes the material's principal light suction range, making it exceptionally crucial in the context of solar cell operations. Consequently, Ca₃PX₃ exhibits lower absorption levels in the visible spectrum under unstrained conditions, as demonstrated in Fig. S8 (a, b, and c) and 10 (a, b, and c). As a result of tensile strain, the absorption edge of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ shifted to a higher energy range, causing a blueshift, while under compressive strain, it switched to a lower energy range, resulting in a redshift compared to its real state. Variations in biaxial compressive and tensile strain cause modifications in the cubic Ca₃PX₃ perovskites lattice constant.

Consequently, these alterations in the lattice constant have a direct impact on the bandgap, causing the absorption edge of the Ca₃PX₃ perovskite to go in the direction of the discernible and ultraviolet spectrum when subjected to, respectively, compressional stress and tensile stress. For solar cell technology, Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ materials under compressive tension seem to be the better choice. Furthermore, the broadest absorption spike under tensile tension was in the UV area, proposing that Ca₃PX₃ may be a successful substance for equipment utilized to disinfect medical tools. The electron loss function (EELF) measures the energy electrons lose through a dielectric material. Fig. S8 (d, e, and f) illustrates the EELF for unstrained Ca₃PI₃, Ca₃PBr₃, and Ca₃PCl₃. In the ELF plots for Ca₃PX₃ compounds, peaks were observed, indicating a decrease in energy when the event photon's vigor is above the bandgap of the molecule. Specifically, for Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl_3, the L(ω) peaks were evident in the cubic layouts and fell within the permissible range of 8.56–10.34 eV,8.91–10.80 eV, and 9.44–11.65 eV as depicted in Fig. 10 (d, e, and f). Notably, the data showed no dispersion within the bandgap energy. The predicted EELF [L(ω)] for Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ was relatively high at 1.31 eV,1.49 eV, and 1.20 eV. Furthermore, we have identified several strong EELF peaks, indicating that electron energy loss and resonance are taken in the case of the Ca₃PX₃ monolayer, particularly in the UV spectrum. The Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ material exhibited prominent peaks at 4.97 and 9.46 eV,5.44 and 9.85 eV, 5.21 and 10.30 eV. The limited impact of energy consumption under 4.7 eV positions our Ca₃PX₃ compound as highly responsive and efficient in both the infrared and visible spectrums of light absorption. Fig. 10 (d, e, and f) illustrates the calculated energy loss of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ under numerous biaxial compressive and tensile strain levels. As compressive strain grew for the Ca₃PX₃ frameworks, the EELF exhibited a notable modification towards greater photon energy, indicating a blueshift. An increase in tensile strain causes an inclination towards lower-energy regions, commonly called a redshift, leading to the opposite effect. The optical characteristics of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl_3, as calculated in this study, align well with previously established and published optical parameters [63,79,84,85]. Compounds with a bandgap of less than 3.1 eV are promising for developing devices that utilize visible light. The notable variations in the optical characteristics of Ca₃PX₃ perovskites within the energy spectrum of 1.2–12.3 eV make them appropriate for use cases such as LEDs or photodetectors suited for UV light and solar cells made for visible light.

3.6. Mechanical properties

Elastic constants for Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ metal halide were calculated to provide valuable information for characterizing the crystal's behavior under various strain conditions (Table 3, Table 4, Table 5). Specifically, calculations were performed for the elastic parameters C₁₁, C_12, and C₄₄ with consideration of applied strain. The outcomes of these DFT calculations and the mechanical properties are detailed in Table 3, Table 4, Table 5. The mechanical steadiness of Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ is typically assessed using the widely recognized Born stability parameters, which are presented below:

C₁₁ > 0, C₄₄ > 0, C₁₁ + 2C₁₂ > 0, C₁₁ − C₁₂ > 0 (7)

Table 3.

The calculated elastic and mechanical properties of cubic Ca₃PI₃ perovskite within unique compressive and tensile strains.

Strain (%)	C11	C12	C44	C12– C44	B (GPa)	G (GPa)	E (GPa)	B/G	$\vartheta$
−3	71.62	48.64	29.43	19.21	32.86	16.11	42.72	2.04	0.322
−2	67.33	43.81	24.74	19.07	30.98	15.65	40.61	1.98	0.316
−1	61.43	40.52	21.56	18.96	28.51	14.85	38.54	1.92	0.309
0	55.62	35.32	17.27	18.14	27.62	14.77	36.42	1.87	0.303
+1	49.74	31.22	13.67	17.55	24.99	13.66	34.34	1.83	0.294
+2	43.43	25.88	10.05	15.83	22.57	12.61	32.23	1.79	0.285
+3	38.64	22.16	7.92	14.24	20.96	11.91	30.12	1.76	0.278

Table 4.

The calculated elastic and mechanical properties of cubic Ca₃PBr₃ perovskite under particular compressive and tensile strains.

Strain (%)	C11	C12	C44	C12– C44	B (GPa)	G (GPa)	E (GPa)	B/G	$\vartheta$
−3	75.42	51.52	29.35	22.17	35.62	17.21	44.81	2.07	0.328
−2	71.61	48.63	27.46	21.17	32.85	16.10	42.78	2.03	0.322
−1	67.34	43.86	24.71	19.15	30.97	15.63	40.62	1.97	0.316
0	61.52	40.51	21.53	18.98	28.50	14.84	38.56	1.91	0.31
+1	55.58	35.34	17.24	18.10	27.61	14.76	36.43	1.86	0.304
+2	49.68	31.21	13.65	17.56	24.98	13.65	34.37	1.82	0.293
+3	43.38	25.86	10.12	15.74	22.56	12.60	32.26	1.78	0.284

Table 5.

The calculated elastic and mechanical properties of cubic Ca₃PCl₃ perovskite beneath distinct compressive and tensile strains.

Strain (%)	C11	C12	C44	C12– C44	B (GPa)	G (GPa)	E (GPa)	B/G	$\vartheta$
−3	78.22	55.38	31.50	23.88	38.85	18.24	46.37	2.13	0.333
−2	75.34	51.67	29.45	22.22	35.62	17.21	44.67	2.09	0.328
−1	71.45	48.65	27.47	21.18	32.86	16.11	42.52	2.03	0.323
0	67.35	43.83	24.78	19.05	30.98	15.65	40.67	1.96	0.314
+1	61.46	40.57	21.59	18.98	28.51	14.85	38.38	1.90	0.308
+2	55.53	35.32	17.23	18.09	27.62	14.77	36.28	1.85	0.304
+3	49.72	31.26	13.69	17.57	24.99	13.66	34.58	1.81	0.292

Table (III, IV, and V) reveals that Ca₃PX_3, a metal halide compound, meets the previously mentioned Born stability requirements, showcasing its impressive mechanical robustness even under substantial pressure variations. Additionally, applying external two-dimensional compressive strain leads to an augmentation in the values of C₁₁, C_12, and C₄₄. These elastic constants offer important information about the material's stiffness and stability. Table (III, IV, and V) displays the Pugh's ratio (B/G) and the Poisson's ratio (θ) of Ca₃PX₃ perovskites. Typically, a critical threshold for these ratios is established at 1.75 for Pugh's and 0.26 for Poisson's, serving as a demarcation between both brittle and ductile substances. Pugh's ratios greater (lesser) than 1.75 and Poisson's ratios greater (lesser) than 0.26 are used to categorize materials as ductile (brittle). Notably, Ca₃PI₃, Ca₃PBr_3, and Ca₃PCl₃ exhibit a more ductile behavior under compressive and tensile strains.

4. Conclusion

We employed first-principles DFT in our investigation calculations to investigate the inorganic substance Ca₃PX₃, primarily emphasizing its mechanical, optical, electrical, and structural characteristics. We determined that the direct bandgap of Ca₃PI₃ is 1.490 eV, Ca₃PBr₃ is 1.950 eV, and Ca₃PCl₃ is 2.205 eV; there was a smaller electronic bandgap after implementing the SOC impact into consideration of Ca₃PI₃ is 1.238 eV, Ca₃PBr₃ is 1.645 eV, and Ca₃PCl₃ is 1.905 eV. This reduction in bandgap is evident as compressive strain increases, despite the SOC impact under evaluation. In contrast, the bandgap widens when tensile strain is applied. Furthermore, applying compressive strain induces a redshift in the peak of the Ca₃PX₃ dielectric constant towards lower photon energies. In contrast, greater tensile tension causes a blueshift in the peak towards higher photon energies. These findings can potentially drive additional investigations into using Ca₃PX₃ for enhancing optoelectronic and photovoltaic (PV) devices.

CRediT authorship contribution statement

I.K. Gusral Ghosh Apurba: Writing – original draft, Investigation, Data curation. Md Rasidul Islam: Writing – review & editing, Validation, Supervision, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Md Shizer Rahman: Resources, Formal analysis, Data curation. Md Ferdous Rahman: Formal analysis, Data curation, Resources, Writing – review & editing. Jeongwon Park: Writing – review & editing, Validation, Funding acquisition.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: