Estimation curve of multivariate adaptive biresponse fuzzy clustering means regression splines approach to stunting and wasting cases in Southeast Sulawesi

Abstract

This article offers a new method of clustering data. This method is constructed by combining the multivariate adaptive regression spline biresponse continuous model (MARSBC) with the fuzzy clustering means (FCM) approach, called the multivariate adaptive biresponse fuzzy clustering means regression splines (MABFCMRS) model. This method uses patterns obtained from the MARSBC model to separate data into specific groups. Observing unobserved heterogeneity that has not been obtained from previous models. Unlike the classic fuzzy clustering methods that use euclid distances to determine the weight of the object, this method uses the total square of the massed residual distance generated by the MARSBC model. Theoretical studies were conducted to obtain predictions for the MABFCMRS model parameters. Furthermore, this method was applied to stunting and wasting cases in southeastern Sulawesi province. The results of the research show that in the case of stunting modeling and wasting in southeast Sulawesi province, the best clusters were obtained based on the criteria of partition coefficient (PC) and modification of PC (MPC). This research is able to show that the clustering process using the MABFCMRS model has been able to improve generalized cross-validation (GCV) values and determination coefficients.

• •This paper presents a new, effective method for clustering data based on unobserved heterogeneity.
• •This is applicable to sizable samples with 3 to 20 predictors.

Graphical abstract

Specifications table

Subject area:	Mathematics
More specific subject area:	Statistics: Non-parametric modeling
Name of your method:	Multivariate adaptive biresponse fuzzy clustering means regression splines (MABFCMRS)
Name and reference of original method:	•P. Ampulembang, B. W. Otok, A. T. Rumiati, and Budiasih, “Bi-responses non-parametric regression model using MARS and its properties,” Appl. Math. Sci., vol. 9, no. 29–32, pp. 1417–1427, 2015, https://doi.org/10.12988/ams.2015.5127 •Y. Pang, M. Shi, L. Zhang, X. Song, and W. Sun, “PR-FCM : A polynomial regression-based fuzzy C-means algorithm for attribute-associated data,” Inf. Sci. (Ny)., vol. 585, pp. 209–231, 2022. https://doi.org/10.1016/j.ins.2021.11.056
Resource availability:	Stunting and wasting prevalence data in southeastern Sulawesi province, along with predictor variables for 2021, came from the health service of Southeast Sulawesi province.

Background

One of the most popular mathematical models for explaining the relationship between a predictor and a response variable is regression. Regression curves describe these patterns of relationships and can be predicted using three types of approaches. The approaches used are parametric, non-parametric and semi-parameter regression approaches. A parametric regression approach is used when the shape of a regression curve is linear, quadratic, or cubic [1]. In cases where the regression curve's shape is unknown or nonexistent, the non-parametric regression approach applies [2]. If some forms of the regression pattern are known and some are unknown, then the semiparametric approach is used.

Non-parametric regression provides a versatile option for data modeling, particularly in the presence of non-linear and high-dimensional patterns. Typically, parametric regression is more inflexible than non-parametric regression because it is used when regression curves are predetermined. Some of the non-parametric regression approaches are spline methods [3], Fourier series estimator [2], kernel [4] and multivariate adaptive regression splines (MARS) [5]. MARS is a complex combination of truncated spline and recursive partition regression (RPR), capable of accommodating additive effects as well as predictor interactions, unlike truncated spline, which deals only with additive effects. With this flexibility, MARS is effective for regression analysis that includes the response variable of continuous data [6], categorical [7,8] and count data [[9], [10], [11], [12]]. MARS is capable of handling large-scale data and large data samples differently with a truncated spline, which is more suited for continuous response data. In addition, MARS produces a smooth model around the node based on the minimalization value of generalized cross-validation (GCV), showing his ability to reduce forecasting mistakes. The MARS model facilitates providing continuous answers with multiple good responses [13] neither category [14].

This research present the development of a multivariate adaptive regression splines biresponse continuous (MARSBC) model enchanced by a fuzzy clustering means (FCM) approach, termed the multivariate adaptive bisresponse fuzzy clustering means regression splines (MABFCMRS). The main objective of this model is to account for heterogeneity that was not included in the prior model and was not seen. This method differs from conventional fuzzy clustering methods that use Euclid distance since it bases cluster creation on the total square of the residual distance given the weight derived from the MARSBC model. A modification of these two processes offers results that differ from the prior model. Compared to the prior model, the resulting one has more complex basis functions and parameters. Based on the theoretical framework of information, this study suggests a total number of weighted sum-of-squared-errors criteria to determine an estimate of the MABFCMRS model.

Method details

Model specifications and estimation procedures

MARS Model

The model was first introduced by Friedman in 1991. MARS is a non-parametric regression model that incorporates many different types of regression, including recursive partitioning regression (RPR) and truncated spline regression, in a sophisticated way [5]. The modeling features of MARS allow it to consider factors in additive effects and interactions between predictors, which are challenges that spline cannot overcome. MARS versatility extends to a wide range of applications, encompassing both categorical [7,14,15] and continuous responses [[16], [17], [18], [19]], making it more powerful than a truncated spline. MARS, using an approach that is both effective and useful, can estimate models of high-dimensional datasets [5]. The model is produced in a continuous MARS on a node that cannot be obtained from RPR. Model formation is conducted in two stages, with stepwise procedures for forming basis functions (BF), maximum interactions (MI), and minimum observations. (MO). The first stage is a forward selection, which involves selecting all of the available basis functions derived with the highest feasible complexity. The second stage involves a backward selection, where the complexity of the formed basis function is reduced based on the smallest GCV value [5,6]. The form of the MARS model is seen in Eq. (1). Given the response variable:

$$y_i={\delta }_0+\sum _{m=1}^M{\delta }_m{B}_m\left({\mathbf{x}}_i\right)+{\epsilon }_i;\mathrm{i}=1,2,...,\mathrm{n}$$ (1)

where ${\mathbf{x}}_i=(x_{1i},x_{2i},...,x_{pi})$ represent the vector of predictor variables, with p indicating the total number of predictors, ${\epsilon }_i$ represents a random error that has a mean value of zero and a variance that remains constant, $n$ is the total number of observations. M denotes the number of non-constant basis functions. ${\delta }_0$ is a function parameter of a constant basis, ${\delta }_m$ is a non-constant-m basis function. $B_m\left(\mathbf{x}\right)$ is mth basis function that declared in Eq. (2).

$$B_m\left({\mathbf{x}}_i\right)=\prod _{k=1}^{K_m}{\left[s_{km}\left(x_{v(k,m)i}-t_{km}\right)\right]}_{+},$$ (2)

with $x_{iv(k,m)}\in {\left\{x_j\right\}}_{j=1}^p,t_{km}\in {\left\{x_{iv(k,m)}\right\}}_{i=1}^n$, $K_m$is the maximum interaction of mth basis function, $x_{v(k,m)}$ is the computation that involves multiplying the independent variables of the kth and mth basis function, $t_{km}$ is the value of the kth knot on interaction, the mth basis function, and $s_{km}=\pm 1$is the sign of the basis function.

MARSBC model

MARSBC is multivariate adaptive regression splines biresponse continuous, which builds upon the MARS paradigm [5] that was initially proposed in 2015 by Ampulembang [13]. A non-parametric regression model with biresponse continuous can get close to an unknown regression function of type $f$. This lets the relationship be written as an Eq. (3)

$$y_{\ell i}=f_{\ell }(x_{1i},x_{2i},...,x_{pi})+{\epsilon }_{\ell i};\ell =1,2;i=1,2,3,...,n$$ (3)

$\ell$ is the number of responses. When written in matrix format,

$$\mathbf{y}=\mathbf{B}(\mathbf{x},\mathbf{t})\delta +\epsilon$$ (4)

where $\delta$ is parameter of MARSBC, and

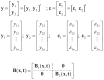(5)

assuming $\epsilon \sim N(\mathbf{0},\mathbf{W})$. The $\mathbf{W}$ is a covariance error matrix. The random errors $\epsilon$ in MARSBC equation follow a continuous normal distribution with mean $\mathbf{0}$ dan and covariance error matrices $\mathbf{W}$. $\mathbf{W}$ is a weight matrix used to accommodate the correlation between responses through an estimation of the model parameters. Model parameter estimates assume the $\mathbf{W}$ matrix is known (fixed variable). Eq. (6) illustrated the use of the maximum likelihood method to obtain parameter estimate for the MARSBC [13].

$$\widehat{\delta }={\left({\mathbf{B}}^{\prime }(\mathbf{x},\mathbf{t}){\mathbf{W}}^{-1}\mathbf{B}(\mathbf{x},\mathbf{t})\right)}^{-1}{\mathbf{B}}^{\prime }(\mathbf{x},\mathbf{t}){\mathbf{W}}^{-1}\mathbf{y}$$ (6)

Estimate the matrix covariance error $\mathbf{W}$ using the provided Eq. (7).

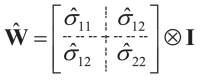(7)

with the Eq. (8):

$$\begin{array}{ccc}& & {\widehat{\sigma }}_{11}=\frac{{{\mathbf{y}}^{\prime }}_1{\left(\mathbf{I}-{\mathbf{H}}_1(.)\right)}^{\prime }\left(\mathbf{I}-{\mathbf{H}}_1(.)\right){\mathbf{y}}_1}{n},\hfill \\ & & {\widehat{\sigma }}_{22}=\frac{{{\mathbf{y}}^{\prime }}_2{\left(\mathbf{I}-{\mathbf{H}}_2(.)\right)}^{\prime }\left(\mathbf{I}-{\mathbf{H}}_2(.)\right){\underset{˜}{\mathbf{y}}}_2}{n},\hfill \\ & & {\widehat{\sigma }}_{12}=\frac{{{\mathbf{y}}^{\prime }}_1{\left(\mathbf{I}-{\mathbf{H}}_1(.)\right)}^{\prime }\left(\mathbf{I}-{\mathbf{H}}_2(.)\right){\mathbf{y}}_2}{n},\hfill \\ & & {\mathbf{H}}_1(.)={\mathbf{B}}_1(\mathbf{x},\mathbf{t}){\left({{\mathbf{B}}^{\prime }}_1(\mathbf{x},\mathbf{t}){\mathbf{B}}_1(\mathbf{x},\mathbf{t})\right)}^{-1}{{\mathbf{B}}^{\prime }}_1(\mathbf{x},\mathbf{t}),\hfill \\ & & {\mathbf{H}}_2(.)={\mathbf{B}}_2(\mathbf{x},\mathbf{t}){\left({{\mathbf{B}}^{\prime }}_2(\mathbf{x},\mathbf{t}){\mathbf{B}}_2(\mathbf{x},\mathbf{t})\right)}^{-1}{{\mathbf{B}}^{\prime }}_2(\mathbf{x},\mathbf{t}),\hfill \end{array}$$ (8)

Fuzzy clustering means

Fuzzy clustering means (FCM) is a non-hierarchical clustering method within fuzzy clusters, originally invented by Jim Bezdek in 1981 [20]. FCM is a method of clustering data in which the assigned position of each data point in a cluster is based on a membership value that fluctuates between 0 and 1 [21]. The iterative process known as FCM clustering uses the restrictions necessary to minimize objective functions. The grouping begins with the initialization of the center of the cluster, which is subsequently updated through iterations based on the objective function minimization in Eq. (9):

$$J_{FCM}(\mathbf{U},\mathbf{V})=\sum _{i=1}^n\sum _{c=1}^C{\left(u_{ci}\right)}^m{\parallel {\mathbf{x}}_i-{\mathbf{v}}_c\parallel }^2$$ (9)

let ${\mathbf{x}}_i={\left[{\mathbf{x}}_{1,i},{\mathbf{x}}_{2,i},...,{\mathbf{x}}_{p,i}\right]}^T$ is the data object, where ${\mathbf{x}}_{p,i}$denotes the value of the jth predictor variable, with j ranging from 1 to p. $v_c$ is the center of the cluster-$c$, is the degree of membership i on the data cluster-$c$. m is the weighted exponent of the fuzzifier, has the potential to influence FCM clustering performance. The membership value of an object $u_{ci}\in \left[0,1\right]$ achieve each aspect of the Eq. (10).

$$\sum _{c=1}^C{u}_{ci}=1;i=1,2,...,n$$ (10)

Optimizing $J_{FCM}(\mathbf{U},\mathbf{V})$ functions using iterative approaches. The Lagrange multiplier examination was used to derive the formula for minimizing Eq. (9), subject to the constraint in Eq. (10). This resulted in the iteration update formula for the prototype and the partition matrix [22]:

$$u_{ci}={\left[{\sum _{c^{*}=1}^C\left(\frac{{\parallel {\mathbf{x}}_i-{\mathbf{v}}_c\parallel }^2}{{\parallel {\mathbf{x}}_i-{\mathbf{v}}_{c^{*}}\parallel }^2}\right)}^{\frac{1}{m-1}}\right]}^{-1}$$ (11)

$${\mathbf{v}}_c=\frac{{\sum }_{i=1}^n{u}_{ci}^m{\mathbf{x}}_i}{{\sum }_{i=1}^n{u}_{ci}^m};c=1,2,...,C$$ (12)

Continue implementing the method outlined in Eqs. (11) and (12) to attain a value lower than the previous iteration, resulting in the lowest achievable value. The goal is to iteratively improve a series of sets on fuzzy clusters, and it should continue until no further improvements in $J_{FCM}(\mathbf{U},\mathbf{V})$ are possible [23].

Multivariate fuzzy clustering means membership

The degree of membership in the Multivariate Fuzzy Clustering Means (MFCM) algorithm varies between one response and another, as well as between different clusters. With the goal of performing this, it is essential to ascertain the proper representation of membership, in addition to the methodology for computing the effective distance between the cluster and its prototype [24]. Known multivariate membership degree matrix ${\mathbf{u}}_i=u_{\ell ci}(i=1,2,...,n)$, $u_{\ell ci}$ is the degree of membership from object-i to cluster-c, $(c=1,2,...,C)$ in respon tu-$\ell$ $(\ell =1,2,...,q)$. Now suppose that there is ${\mathbf{D}}_i=d_{\ell ci}$ a distance matrix of n where is the distance between patterns and prototype $y_{i\ell }$ the cluster with a goal to, $c(c=1,2,...,C)$ in response to-$\ell$ $(\ell =1,2,...,q)$. According to MFCM, the goal is to observe multivariate fuzzy partitions $\mathbf{V}=\left[\mathbf{u}{}_i\right](i=1,2,...,n)$ based on the data set $\Omega$, during the process of minimizing the objective function using Eq. (13).

$$F=\sum _{\ell }^q{\sum _{c=1}^C\sum _{i=1}^n\left(u_{\ell ci}\right)}^m{\parallel {\mathbf{x}}_{\ell i}-{\mathbf{v}}_{c\ell }\parallel }^2$$ (13)

where is the center of the cluster ${\mathbf{v}}_{c\ell }$ seen in Eq. (14):

$${\mathbf{v}}_{c\ell }=\frac{{\sum }_{i=1}^n{\left(u_{\ell ci}\right)}^m{x}_{\ell i}}{{\sum }_{i=1}^n{\left(u_{\ell ci}\right)}^m}$$ (14)

Index validity

Researchers primarily focus on identifying the optimal criterion for c that can reveal the data's structure. Most cluster methods require calculating c from the cluster. Working with the correct cluster size as an approach to determining the validity of the cluster is necessary to evaluate the size of a separate cluster [25]. The Partition Coefficient (PE) [[26], [27], [28]] were the first index validations linked to the FCM and Modification of PC (MPC) index, which Dave 1996 [29] presented. Eqs. (15) and (16) show the PC and MPC formulations appropriately.

$$\text{PC}\left(c\right)=\frac{1}{n}\sum _{i=1}^n\sum _{c=1}^C{u}_{ci}^2$$ (15)

where $\frac{1}{c}\le \text{PC}\left(c\right)\le 1$. Breaking ${\max }_{2\le c\le n-1}\text{PC}\left(\mathrm{c}\right)$ determines the optimal number of c* clusters to optimize the cluster's efficacy for X data sets. The performance of the MPC can reduce monotony and is distinguished by

$$\text{MPC}\left(c\right)=1-\frac{c}{c-1}\left(1-\text{PC}\left(c\right)\right)$$ (16)

with $0\le \text{MPC}\left(c\right)\le 1$. Generally, an optimal c* cluster will be obtained by breaking ${\max }_{2\le c\le n-1}\text{MPC}\left(\mathrm{c}\right)$ to produce the best cluster performance for the X data set.

MABFCMRS model

The MABFCMRS model is the development of the MARS Continuous Response model using the FCM approach. The MABFCMRS model can account for the variability of the process, resulting in a unique model for each cluster. The MABFCMRS model can be seen in the Eq. (17).

$$\begin{array}{ccc}& & y_{1\left(c\right)i}=f_{1\left(c\right)}(x_{1i},x_{2i},...,x_{pi})+{\epsilon }_{1\left(c\right)i}\hfill \\ & & y_{2\left(c\right)i}=f_{2\left(c\right)}(x_{1i},x_{2i},...,x_{pi})+{\epsilon }_{2\left(c\right)i}\hfill \end{array}$$ (17)

The Eq. (17) is represented as a matrix. The expression for the set of n observations is in Eq. (18).

$${\mathbf{y}}_{\left(c\right)}={\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}+{\epsilon }_{\left(c\right)};c=1,2,...,C$$ (18)

where

by assume ${\epsilon }_{\left(c\right)}\sim N(\mathbf{0},{\mathbf{W}}_{\left(c\right)})$. ${\delta }_{10\left(c\right)}$ is the parent basis's function parameter depending on the cluster's initial response and ${\delta }_{1M\left(c\right)}$ is a non-constant parameter to m in the initial response of the cluster to (c).

Parameter Estimation of MABFCMRS

The MBFCMRS parameter assumption determines the number of clusters in a data set using an objective function of the total number of square errors. This function is designed to identify a cluster partition that minimizes the objective function value, indicating the optimal cluster based on the provided parameters. The following theorem illustrates the MABFCMRS parameter.

Theorem 1

Given MABFCMRS model onEq. (18)with${\epsilon }_{\left(c\right)}$is the normal distribution, having a mean of 0 and a variance of${\mathbf{W}}_c$. The FCM goal function is defined byEq. (13)which uses the approach weighted least squares to define the FCM goal function and then determines a model parameter MABFCMRS based on theEq. (19).

$${\widehat{\delta }}_{\left(c\right)}={\left({\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t})\right)}^{-1}{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}$$ (19)

Proof of Theorem 1. The estimate of the MABFCMRS parameter is obtained by using the objective function of the total number of weighted sum-of-squared- errors criterion to find the number of clusters in the data set [30], as follows:

$$\begin{array}{ccc}\hfill F_{\ell }& =& \sum _{c=1}^C\sum _{i=1}^n{u}_{\left(c\right)i}^2{\epsilon }_{\ell \left(c\right)i}^2\hfill \\ & =& \sum _{c=1}^C\sum _{i=1}^n{\left(u_{\left(c\right)i}{\epsilon }_{\ell \left(c\right)i}\right)}^2\hfill \\ & =& \sum _{c=1}^C\left({\left(u_{\left(c\right)1}{\epsilon }_{\ell \left(c\right)1}\right)}^2+{\left(u_{\left(c\right)2}{\epsilon }_{\ell \left(c\right)2}\right)}^2+...+{\left(u_{\left(c\right)i}{\epsilon }_{\ell \left(c\right)i}\right)}^2+...+{\left(u_{\left(c\right)n}{\epsilon }_{\ell \left(c\right)n}\right)}^2\right);\ell =1,2\hfill \end{array}$$ (20)

$F_{\ell }$ is the objective function of MABFCMRS model and ${\sum }_{c=1}^C{u}_{ci}=1$ for every i. ${\epsilon }_{\ell \left(c\right)i}$ is residual of the MABFCMRS model associated with cluster observations ith in cluster cth. Objective function Eq. (20) if written in vector notation, the matrix will be Eq. (21):

$$F_{\ell }=\sum _{c=1}^C{\left({\mathbf{U}}_{\left(c\right)}{\epsilon }_{\left(c\right)}\right)}^T\left({\mathbf{U}}_{\left(c\right)}{\epsilon }_{\left(c\right)}\right);\ell =1,2$$ (21)

where

$$\begin{array}{ccc}& & {\epsilon }_{\left(c\right)}=\left[\begin{array}{c}{\epsilon }_{1\left(c\right)}\\ {\epsilon }_{2\left(c\right)}\end{array}\right];{\epsilon }_{1\left(c\right)}=\left[\begin{array}{c}{\epsilon }_{111}\\ {\epsilon }_{122}\\ ⋮\\ {\epsilon }_{1\left(c\right)n}\end{array}\right];{\epsilon }_{2\left(c\right)}=\left[\begin{array}{c}{\epsilon }_{211}\\ {\epsilon }_{222}\\ ⋮\\ {\epsilon }_{2\left(c\right)n}\end{array}\right];{\mathbf{U}}_{\left(c\right)}=\left[\begin{array}{c}{\mathbf{U}}_{1(\mathrm{c})}\\ {\mathbf{U}}_{2\left(\mathrm{c}\right)}\end{array}\right];\hfill \\ & & {\mathbf{U}}_{\mathbf{1}\left(c\right)}=\left[\begin{array}{cccc}{u}_{1\left(c\right)1}& 0& \cdots & 0\\ 0& u_{1\left(c\right)2}& \cdots & 0\\ ⋮& 0& \ddots & ⋮\\ 0& \cdots & 0& u_{1\left(c\right)n}\end{array}\right];{\mathbf{U}}_{2\mathbf{c}}=\left[\begin{array}{cccc}{u}_{2\left(c\right)1}& 0& \cdots & 0\\ 0& u_{2\left(c\right)2}& \cdots & 0\\ ⋮& 0& \ddots & ⋮\\ 0& \cdots & 0& u_{2\left(c\right)i}\end{array}\right]\hfill \end{array}$$

from Eq. (18) known that ${\epsilon }_{\left(c\right)}={\mathbf{y}}_{\left(c\right)}-\left({\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\right)$so

$$\begin{array}{ccc}\hfill F_{\ell }& =& \sum _{c=1}^C{\left({\mathbf{U}}_{\left(c\right)}\left({\mathbf{y}}_{\left(c\right)}-\left({\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\right)\right)\right)}^T\left({\mathbf{U}}_{\left(c\right)}({\mathbf{y}}_{\left(c\right)}-{\left({\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\right)}^T)\right)\hfill \\ & =& \sum _{c=1}^C\left({\mathbf{y}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}^T-{\left({\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\right)}^T{\mathbf{U}}_{\left(c\right)}^T\right)\left({\mathbf{U}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}-{\mathbf{U}}_{\left(c\right)}\left({\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\right))\right)\hfill \\ & =& \sum _{c=1}^C\left({\mathbf{y}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}^T-{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{U}}_{\left(c\right)}^T\right)\left({\mathbf{U}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}-{\mathbf{U}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\right)\hfill \\ & =& \sum _{c=1}^C({\mathbf{y}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}-{\mathbf{y}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}-{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{U}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}\hfill \\ & & +{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t})(\mathbf{x},\mathbf{t}){\mathbf{U}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)});{\mathbf{V}}_{\left(c\right)}={\mathbf{U}}_{\left(c\right)}^T{\mathbf{U}}_{\left(c\right)}\hfill \\ & =& \sum _{c=1}^C({\mathbf{y}}_{\left(c\right)}^T\mathbf{V}{\mathbf{y}}_{\left(c\right)}-{\mathbf{y}}_c^T{\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}-{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}+{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)})\hfill \\ \hfill F_{\ell }& =& \sum _{c=1}^C({\mathbf{y}}_{\left(c\right)}^T{\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}-2{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}+{\delta }_c^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)})\hfill \end{array}$$

by

$$\begin{array}{ccc}\hfill F_1& =& \sum _{c=1}^C({\mathbf{y}}_{\left(c\right)}^T{\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}-2{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}+{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)})\hfill \\ \hfill F_2& =& \sum _{c=1}^C({\mathbf{y}}_{\left(c\right)}^T{\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}-2{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}+{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)})\hfill \end{array}$$

Where vector ${\mathbf{y}}_{\left(c\right)}$of size $1\times n_{\left(c\right)}$, matrix ${\mathbf{V}}_{\left(c\right)}$ of size $n_{\left(c\right)}\times n_{\left(c\right)}$. ${\mathbf{B}}_{\left(c\right)}$ is a basis function matrix having size $n_{\left(c\right)}\times (M+1)$ and vector $\delta$ has a size of $(M+1)\times 1$. The parameter predictor for the MABFCMRS model uses the Lagrange multiplier approach. Eq. (22) represents the objective function:

$$\begin{array}{c}{F}_{\ell }=\sum _{c=1}^C({\mathbf{y}}_{\left(c\right)}^T{\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}-2{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}+{\delta }_{\left(c\right)}^T{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)})\hfill \\ +\lambda \left(\sum _{c=1}^C{\mathbf{U}}_{\left(c\right)}-1\right)\hfill \end{array}$$ (22)

To find the parameter of the MABFCMRS model, the Eq. (22) is the derivative against the ${\delta }_{\left(c\right)}$ where the function$F_{\ell }$ is equated with zero, until obtained.

$$\begin{array}{ccc}\hfill \frac{\partial F_{\ell }}{\partial {\delta }_{\left(c\right)}}& =& 0\left(\sum _{c=1}^C-2{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}+2{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\right)=0\hfill \\ & & -\sum _{c=1}^{C}2{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}=-\sum _{c=1}^{C}2{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\hfill \\ & & -2\sum _{c=1}^C{\mathbf{B}}_c^T(\mathbf{x},\mathbf{t})\mathbf{V}{\mathbf{y}}_c=-2\sum _{c=1}^C{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\hfill \\ & & \sum _{c=1}^C{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}=\sum _{c=1}^C{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\hfill \\ & & {\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}={\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t}){\delta }_{\left(c\right)}\hfill \\ & & {\widehat{\delta }}_{\left(c\right)}={\left({\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\left(c\right)}(\mathbf{x},\mathbf{t})\right)}^{-1}{\mathbf{B}}_{\left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\left(c\right)}\hfill \end{array}$$ (23)

with

$${\mathbf{V}}_{\left(c\right)\ell }=\left[\begin{array}{cccc}{u}_{c1}^2& 0& \cdots & 0\\ 0& u_{c2}^2& \cdots & 0\\ ⋮& 0& \ddots & ⋮\\ 0& \cdots & 0& u_{c{n}_{\left(c\right)}}^2\end{array}\right];\ell =1,2$$

Fuzzy membership values

Determines fuzzy membership values using the langrange multiplier method. Deduct the assumption from the Eq. (24):

$$F_{\ell }=\sum _{c=1}^C\sum _{i=1}^n{u}_{\left(c\right)i}^2{\epsilon }_{\left(c\right)i}^2+\lambda \left(\sum _{c=1}^C\sum _{i=1}^n{\mathbf{U}}_{\left(c\right)i}-1\right);\ell =1,2$$ (24)

With a formula of for ${\sum }_{c=1}^C{u}_{\left(c\right)i}=1$ by $i=1,2,..,n$. First derivative of $F_{\ell }$ relative to $u_{\left(c\right)i}$ then equate zero until obtained for $i$ and $c$ specific:

$$\begin{array}{ccc}& & \frac{\partial F_{\ell }}{\partial u_{\left(c\right)i}}=0;\hfill \\ & & \sum _{c=1}^C\sum _{i=1}^n{u}_{\left(c\right)i}^2{\widehat{\epsilon }}_{\left(c\right)i}^2+\lambda \left(\sum _{c=1}^C\sum _{i=1}^n{u}_{\left(c\right)i}-1\right)=0\hfill \\ & & 2u_{\left(c\right)i}\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]+\lambda =0\hfill \\ & & u_{\left(c\right)i\ell }=-\frac{\lambda }{2\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\hfill \end{array}$$ (25)

In contrast, following the summation of Eq. (25) for every c and specific i then

$$\begin{array}{ccc}& & \sum _{c=1}^C{u}_{\left(c\right)i\ell }=\sum _{c=1}^C-\frac{\lambda }{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\hfill \\ & & -\sum _{c=1}^C\left[\frac{\lambda }{\left[\sum _{C=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\right]=1\hfill \\ & & \lambda =\frac{1}{-\sum _{c^{*}=1}^C\left[\frac{1}{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\right]}\hfill \end{array}$$ (26)

Modify Eq. (26) with Eq. (25) and then acquire fuzzy membership values.

$$\begin{array}{ccc}& & u_{\left(c\right)i\ell }=-\frac{\frac{1}{\sum _{c^{*}=1}^C\left[-\frac{1}{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\right]}}{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\hfill \\ & & u_{\left(c\right)i\ell }=\frac{1}{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]\sum _{c^{*}=1}^C\left[\frac{1}{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\right]}\hfill \\ & & u_{\left(c\right)i\ell }=\frac{1}{\sum _{c^{*}=1}^C\left[\frac{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\right]}\hfill \\ & & u_{\left(c\right)i\ell }={\left[\sum _{c^{*}=1}^C\left[\frac{\left[\sum _{c=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}{\left[\sum _{C=1}^C\sum _{i=1}^n{\widehat{\epsilon }}_{\left(c\right)i}^2\right]}\right]\right]}^{-1}\hfill \end{array}$$ (27)

In order to obtain the MABFCMRS function meter, first it is necessary to substitute Eq. (23) into Eq. (18) then obtained function measurement MABFCMRS in Eq. (28).

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{f}}}_{\ell \left(c\right)}\left(\mathbf{x}\right)& =& \left[\begin{array}{c}{\widehat{\mathbf{f}}}_{1\left(c\right)}\left(\mathbf{x}\right)\\ {\widehat{\mathbf{f}}}_{\mathbf{2}\left(c\right)}\left(\mathbf{x}\right)\end{array}\right]={\mathbf{B}}_{\ell \left(c\right)}(\mathbf{x},\mathbf{t}){\widehat{\delta }}_{\ell \left(c\right)c}\hfill \\ & =& {\mathbf{B}}_{\ell \left(c\right)}(\mathbf{x},\mathbf{t}){\left({\mathbf{B}}_{\ell \left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\ell \left(c\right)}(\mathbf{x},\mathbf{t})\right)}^{-1}{\mathbf{B}}_{\ell c}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\ell c}\hfill \\ & =& {\mathbf{H}}_{\ell \left(c\right)}(.){\mathbf{y}}_{\ell \left(c\right)}\hfill \end{array}$$ (28)

where

$$\mathbf{H}(.)={\mathbf{B}}_{\ell \left(c\right)}(\mathbf{x},\mathbf{t}){\left({\mathbf{B}}_{\ell \left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\ell \left(c\right)}(\mathbf{x},\mathbf{t})\right)}^{-1}{\mathbf{B}}_{\ell \left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}$$

GCV for MABFCMRS

GCV is associated with the concept of reducing the residual sum of squares [31]. The most powerful MARS type is the one with the lowest GCV. GCV is employed to choose the most optimal basis function for constructing the MARS model [5]. GCV formula can be seen in the Eq. (29).

$$GCV\left(M\right)=\frac{\frac{1}{n}{{\sum }_{i=1}^n\left[y_i-\widehat{f}\left({\mathbf{x}}_i\right)\right]}^{{}_2}}{{\left[1-\frac{C\left(\tilde{M}\right)}{n}\right]}^2}=\frac{n{{\sum }_{i=1}^n\left[y_i-\widehat{f}\left({\mathbf{x}}_i\right)\right]}^{{}_2}}{{\left(n-C\left(\tilde{M}\right)\right)}^2}$$ (29)

with

$$C\left(\tilde{M}\right)=C\left(M\right)+\frac{d.M}{2}$$

$C\left(\tilde{M}\right)$is complex function, $C\left(M\right)$is the number of estimable parameters, d is the degree of interaction, indicating the additional contribution of each basis function to the overall complexity of the model resulting from the nonlinearity of the basis function parameters has been identified [32]. The optimum d value is in the interval $2\le d\le 4$, $M$ is the number of maximum nonconstant basis function and $\widehat{f}\left({\mathbf{x}}_i\right)$ is the estimated value of response variable. The GCV MABFCMRS formula can be seen based on the Eq.(30).

$$\begin{array}{ccc}\hfill GC{V}_{MABFCMRS}& =& \frac{n{{\sum }_{i=1}^n\left[y_i-\widehat{f}\left({\mathbf{x}}_i\right)\right]}^{{}_2}}{{\left(n-C\left(\tilde{M}\right)\right)}^2}\hfill \\ & =& \frac{n{\left[\mathbf{y}-{\mathbf{B}}_{\ell \left(c\right)}(\mathbf{x},\mathbf{t}){\left({\mathbf{B}}_{\ell \left(c\right)}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{B}}_{\ell \left(c\right)}(\mathbf{x},\mathbf{t})\right)}^{-1}{\mathbf{B}}_{\ell c}^T(\mathbf{x},\mathbf{t}){\mathbf{V}}_{\left(c\right)}{\mathbf{y}}_{\ell c}\right]}^2}{{\left(n-C\left(\tilde{M}\right)\right)}^2}\hfill \end{array}$$ (30)

Method validation

Application of MABFCMRS model

The MABFCMRS model obtained was applied to stunting and wasting prevalence data in Southeast Sulawesi province by 2021. Stunting is a length or lower height based on age, while wasting is a type of malnutrition that occurs when a child's weight is below the appropriate level of their height, according to the z-score according to the WHO nutritional status table [33]. The information that was collected comes from the health department of the southeastern province of Sulawesi, which has 222 subdistrict which is spread out in 17 districts and cities. There are two response variables and five predictor factors. The variable responses to this study are the prevalence of stunting $\left(y_1\right)$ and the prevalence of wasting $\left(y_2\right)$. The predictor variable used is: $x_1$ is the percentage of babies with a low birth weight, $x_2$ is the percentage of pregnant mothers who are anemic, $x_3$ is the percentage of infants exclusively receiving breast milk at six months of age, $x_4$ is the percentage of babies getting a complete basic immunization, $x_5$ is the percentage of toddler getting vitamin A and $x_6$ is the percentage of mothers getting vitamin A. Table 1 shows the descriptive statistics of each variable. The relationships between each predictor variable and each responder variable displayed in Fig. 1, Fig. 2. Data pairs illustrate the geometric structure of the unidentified forms. Non-parametric regression is the appropriate approach to use in this research. This study contrasts two non-parametric regression methodologies: MARSBC and MABFCMRS.

Table 1.

Descriptive statistics based on research variables.

Variable	Mean	StDev	Minimum	Maximum
$y_1$	15.01	11.85	0	51.91
$y_2$	4.34	5.07	0	45.09
$x_1$	3.53	3.35	0	23.1
$x_2$	43.68	37.4	0	101.4
$x_3$	52	26.12	0	98.6
$x_4$	85.82	30.48	0	201.7
$x_5$	74.13	25.19	0	168.1
$x_6$	86.51	18.89	17.9	157.1

Fig. 1.

Visualization of research variables of respon $y_1$_.

Fig. 2.

Visualization of research variables of respon $y_2$.

Table 1 presents the descriptive statistics for the dependent variables, prevalence of stunting $\left(y_1\right)$ and prevelance of wasting $\left(y_2\right)$ and the independent variables ($x_1$to $x_6$) employed in this research. The average value for $y_1$ is 15.01, with a standard deviation of 11.85, suggesting a moderate degree of variability from the average. This variable ranges from a minimum value of 0 to a maximum value of 51.91. $y_2$, the second dependent variable, has a mean of 4.34 and a standard deviation of 5.07. It also has a range of values from 0 to 45.09, suggesting a more uniform distribution in comparison to $y_1$. The independent variables $x_1$ through $x_6$ have significantly different mean values, ranging from 3.53 for $x_1$ to 86.51 for $x_6$. These standard deviations also indicate different levels of dispersion, suggesting that there is variation in the spread of data for each variable. Some variables, like $x_4$, show a much greater range of values, whereas $x_1$ shows limited oscillations in the range of minimum and maximum values, indicating significant disparities in the scale of measurement.

Fig. 1, Fig. 2 illustrate the distribution of predictor variables against response variables. The emerging pattern from these distributions lacks a clear form, suggesting that the Multivariate Adaptive Biresponse Fuzzy Clustering Means Regression Splines (MABFCMRS) model is suitable for further data analysis. Estimates of MARSBC models are shown in Table 2. The best model is obtained when the optimal BF= 22 MO =2 and MI= 3. Estimation of the MARSBC model resulted in 22 basis functions obtained for response 1 (prevelence of stunting) and response 2 (prevalence of wasting).

Table 2.

Model MARSBC.

Model in response 1		Model in response 2
Variables	Estimate	Variables	Estimate
(Intercept)	0.1317	(Intercept)	0.1264
bx_marsbc [, -1]h(X4-66.4)	0.0421	bx_marsbc [, -1]h(X3-56.9)	0.0352
bx_marsbc [, -1]h(66.4-X4)	-0.2614	bx_marsbc [, -1]h(56.9-X3)	-0.0281
bx_marsbc [, -1]h(X6-100)	0.0214	bx_marsbc [, -1]h(X4-124.1)	-0.2482
bx_marsbc [, -1]h(100-X6)	0.0056	bx_marsbc [, -1]h(124.1-X4)	0.2573
bx_marsbc [, -1]h(X2-97.2) *h(X6-100)	0.0107	bx_marsbc [, -1]h(X3-56.9) *h(X6-109.6)	0.6039
bx_marsbc [, -1]h(97.2-X2) *h(X6-100)	0.0010	bx_marsbc [, -1]h(X3-56.9) *h(109.6-X6)	0.0078
bx_marsbc [, -1]h(X1-1.1)	0.0433	bx_marsbc [, -1]h(X2-100) *h(56.9-X3)	0.8678
bx_marsbc [, -1]h(1.1-X1)	0.0042	bx_marsbc [, -1]h(100-X2) *h(56.9-X3)	0.0517
bx_marsbc [, -1]h(X1-3.8) *h(X4-66.4)	-0.0002	bx_marsbc [, -1]h(56.9-X3) *h(X5-42.7)	-0.0034
bx_marsbc [, -1]h(3.8-X1) *h(X4-66.4)	-0.0014	bx_marsbc [, -1]h(56.9-X3) *h(42.7-X5)	0.0275
bx_marsbc [, -1]h(1.1-X1) *h(X3-43)	0.3286	bx_marsbc [, -1]h(X1-3.3)	0.2782
bx_marsbc [, -1]h(1.1-X1) *h(43-X3)	0.5103	bx_marsbc [, -1]h(3.3-X1)	-0.0219
bx_marsbc [, -1]h(X2-81.8) *h(100-X6)	0.0319	bx_marsbc [, -1]h(X1-3.3) *h(X6-100)	-0.0026
bx_marsbc [, -1]h(81.8-X2) *h(100-X6)	-0.0012	bx_marsbc [, -1]h(X1-3.3) *h(100-X6)	-0.0007
bx_marsbc [, -1]h(X3-94.1) *h(100-X6)	0.1700	bx_marsbc [, -1]h(X2-3.4)	-0.1261
bx_marsbc [, -1]h(94.1-X3) *h(100-X6)	0.0698	bx_marsbc [, -1]h(3.4-X2)	-0.0019
bx_marsbc [, -1]h(1.1-X1) *h(X2-89.5)	-0.0004	bx_marsbc [, -1]h(X2-3.4) *h(X6-63.3)	0.7803
bx_marsbc [, -1]h(1.1-X1) *h(89.5-X2)	0.0000	bx_marsbc [, -1]h(X2-3.4) *h(63.3-X6)	-0.0712
bx_marsbc [, -1]h(1.1-X1) *h(X5-96.8)	-0.0021	bx_marsbc [, -1]h(X2-3.4) *h(X3-8.3)	0.4917
rbx_marsbc [, -1]h(X3-75.9)	-0.0064	bx_marsbc [, -1]h(3.3-X1) *h(X3-44.2)	0.3072
bx_marsbc [, -1]h(75.9-X3)	-0.0024	bx_marsbc [, -1]h(3.3-X1) *h(44.2-X3)	0.2318

The model for response 1, derived from Table 2, is presented in Eq. (31).

$$\begin{array}{ccc}\hfill y_1& =& 0.1317+0.0421bf1-0.2614bf2+0.0214bf3+0.0056bf4+0.0107bf5\hfill \\ & & +0.0010bf6+0.0433bf7+0.0042bf8-0.0002bf9-0.0014bf10\hfill \\ & & +0.3286bf11+0.05103bf12+0.0319bf13-0.0012bf14+0.1700bf15\hfill \\ & & +0.0698bf16-0.0004bf17-0.021bf19+0.0036bf20-0.0064bf21-0.0024bf22\hfill \end{array}$$ (31)

where

$$\begin{array}{ccc}& & bf1=h(x_4-66.4),bf2=h(66.4-x_4),bf3=h(x_6-100),bf4=h(100-x_6),\hfill \\ & & bf5=h(x_2-97.2)*(x_6-100),bf6=h(97.2-x_2)*(x_6-100),\hfill \\ & & bf7=h(x_1-1.1),bf8=h(1.1-x_1),bf9=h(x_1-3.8)*(x_4-66.4),\hfill \\ & & bf10=h(3.8-x_1)*h(x_4-66.4),bf11=h(1.1-x_1)*(x_3-43),\hfill \\ & & bf12=h(1.1-x_1)*h(43-x_3),bf13=h(x_2-81.8)*h(100-x_6),\hfill \\ & & bf14=h(81.8-x_2)*h(100-x_6),bf15=h(x_3-94.1)*h(100-x_6),\hfill \\ & & bf16=h(94.1-x_3)h(100-x_6),bf17=h(1.1-x_1)*h(x_2-89.5),\hfill \\ & & bf18=h(1.1-x_1)*h(89.5-x_2),bf19=h(1.1-x_1)*h(x_5-96.8),\hfill \\ & & bf20=h(1.1-x_1)*h(96.8-x_5),bf21=h(x_3-75.9),bf22=h(75.9-x_3)\hfill \end{array}$$ (32)

The Eq. (31) shows that all predictor variables have an impact on the response $y_1$. The interpretation of the model using basis function bf1 indicates that for values of $x_4$ greater than 66.4, there will be an increase in the prevalence of stunting by 0.0421, assuming all other predictor variables are held constant. But, if $x_1$ is less than 1.1 and $x_5$ is less than 96.8, the product of their interactions will make stunting more common by 0.0036, assuming that all other predictors stay the same. This is shown by the interaction term in basis function bf20. It is important to note that $x_1$ represents the percentage of babies born with low birth weight, x4 indicates the percentage of babies receiving complete basic immunization, and $x_5$ corresponds to the percentage of toddlers receiving vitamin A supplementation. These variables are critical because the model assumes linearity and interaction effects are specified.

$$\begin{array}{ccc}\hfill y_2& =& 0.11264+0.0352bf1-0.0281bf2-0.2482bf3+0.2573bf4+0.6039bf5\hfill \\ & & +0.0078bf6+0.8678bf7+0.0517bf8-0.0034bf9-0.0275bf10\hfill \\ & & +0.2782bf11-0.0219bf12-0.0026bf13-0.0007bf14-0.1261bf15\hfill \\ & & -0.0019bf16+0.7803bf17-0.0712bf18+0.4917bf19+0.0463bf20\hfill \\ & & +0.3072bf21+0.02318bf22\hfill \end{array}$$ (33)

where

$$\begin{array}{ccc}& & bf1=h(x_3-56.9),bf2=h(56.9-x_3),bf3=h(x_4-124.1),bf4=h(124.1-x_4),\hfill \\ & & bf5=h(x_3-56.9)*(x_6-109.6),bf6=h(x_3-56.9)*(109.6-x_6),\hfill \\ & & bf7=h(x_2-100)*h(56.9-x_3),bf8=h(100-x_2)*h(56.9-x_3),\hfill \\ & & bf9=h(56.9-x_3)*(x_5-42.7),bf10=h(56.9-x_3)*h(42.7-x_5),\hfill \\ & & bf11=h(x_1-3.3),bf12=h(3.3-x_1),bf13=h(x_1-3.3)*h(x_6-100),\hfill \\ & & bf14=h(x_1-3.3)*h(100-x_6),bf15=h(x_2-3.4),bf16=h(3.4-x_2),\hfill \\ & & bf17=h(x_2-3.4)*h(x_6-63.3),bf18=h(x_2-3.4)*h(63.3-x_6),\hfill \\ & & bf19=h(x_2-3.4)*h(x_3-8.3),bf20=h(x_2-3.4)*h(8.3-x_3),\hfill \\ & & bf21=h(33.1-x_1)*h(x_3-44.2),bf22=h(33.1-x_1)*(44.2-x_3)\hfill \end{array}$$ (34)

The Eq. (33) displays that all predictor variables have an impact on the response $y_2$. In the model utilizing basis function bf1, when $x_3$ exceeds 56.9, the prevalence of wasting increases by 0.0352, assuming all other predictor variables remain constant. On the other hand, if $x_1$ is less than 33.1 and $x_3$is greater than 44.2, their interaction within the basis function bf21 causes the prevalence of stunting to rise by 0.3072, assuming that all other variables stay the same. It is crucial to note that $x_1$ represents the percentage of babies born with low birth weight, while $x_3$ indicates the percentage of infants exclusively breastfed at six months of age. Both variables are essential, as the model assumes linearity and interaction effects among the variables.

After establishing the MARSBC model based on the optimal basis functions determined using the FCM approach, the MABFCMRS model was subsequently created. During this development phase, we validated the indices using PC and MPC, as outlined in Eq. (24). Table 3 displays the results of the clustering index validation using PC and MPC.

Table 3.

Validation index number of clusters.

Number of cluster	PC	MPC
2	0.76115117	0.52230234
3	0.51952332	0.27928498
4	0.39922768	0.19897024
5	0.33300297	0.16625371

The validation index calculation using PC and MPC indicates that the optimal number of clusters is 2. This is derived from the optimum PC and MPC values. The value of the fuzzy membership degree is shown in Appendix A. Appendix A displays the distribution of the incidence spreads that enter each cluster. Out of all the existing incidences, 102 were included in cluster 1 and 120 were included in cluster 2. The MABFCMRS model designed for cluster 1 is shown in Table 4. The best model is achieved when BF = 20, MO = 1, and MI = 2.

Table 4.

MABFCMRS Cluster 1 model.

Response 1
Model	Estimate
(Intercept)	30.0914
bx_mabfcmrs [, -1]h(X3-80)	-1.7595
bx_mabfcmrs [, -1]h(110.2-X4)	-0.3997
bx_mabfcmrs [, -1]h(X1-1.2) *h(X4-75.8) *h(X6-96.8)	0.0039
bx_mabfcmrs [, -1]h(X1-1.2) *h(75.8-X4) *h(X6-96.8)	0.0183
bx_mabfcmrs [, -1]h(1.2-X1) *h(29.7-X2)	-0.5832
bx_mabfcmrs [, -1]h(1.2-X1) *h(29.7-X2) *h(X3-68.2)	0.0270
bx_mabfcmrs [, -1]h(X3-79.1) *h(110.2-X4)	0.0240
bx_mabfcmrs [, -1]h(79.1-X3) *h(110.2-X4)	0.0049
Response 2
Model	Estimate
(Intercept)	7.2643
bx_mabfcmrs [, -1]h(X3-54.7)	-0.6118
bx_mabfcmrs [, -1]h(X4-91.3)	-0.1633
bx_mabfcmrs [, -1]h(63.3-X6)	0.5623
bx_mabfcmrs [, -1]h(39.1-X2) *h(54.7-X3)	0.0061
bx_mabfcmrs [, -1]h(99-X2) *h(91.3-X4)	-0.0017
bx_mabfcmrs [, -1]h(X2-94) *h(X3-54.7)	-0.0117
bx_mabfcmrs [, -1]h(94-X2) *h(X3-54.7)	0.0025
bx_mabfcmrs [, -1]h(X3-57.1)	-2.3486
bx_mabfcmrs [, -1]h(X2-4.2) *h(X3-54)	0.0279
bx_mabfcmrs [, -1]h(4.2-X2) *h(X3-54)	-0.0485
bx_mabfcmrs [, -1]h(94.6-X2) *h(X3-57.1)	0.0313

Table 4 MABFCMRS cluster 1 model for response 1 yields a model as depicted in Eq.(35). It is observed that out of the six predictor variables utilized, only five significantly influence the prevalence of stunting. These impactful variables are $x_1$, $x_2$, $x_3$, $x_4$and $x_6$ Eq. (35) describes the model where bf6 represents the interaction among three variables: $x_1$, $x_2$, $x_3$. This suggests that the prevalence of stunting will increase by 0.0270 if $x_1$ is less than 1.2, $x_2$ is less than 29.7, and $x_3$ is greater than 68.2, assuming all other variables remain constant.

$$\begin{array}{ccc}\hfill y_1& =& 30.0914-1.7595bf1-0.3997bf2+0.0039bf3+0.0183bf4-0.5832bf5\hfill \\ & & +0.0270bf6+0.0240bf7+0.0049bf8\hfill \end{array}$$ (35)

where

$$\begin{array}{ccc}& & bf1=h(x_3-80),bf2=h(110.2-x_4),bf3=h(x_1-1.2)*h(x_4-75.8)*h(x_6-96.8),\hfill \\ & & bf4=h(x_1-1.2)*h(75.8-x_4)*h(x_6-96.8),\hfill \\ & & bf5=h(1.2-x_1)*(29.7-x_2),bf6=h(1.2-x_1)*(29.7-x_2)*h(x_3-68.2),\hfill \\ & & bf7=h(x_3-79.1)*h(110.2-x_4),bf8=h(79.1-x_3)*h(110.2-x_4)\hfill \end{array}$$ (36)

Table 4 features the MABFCMRS model for response 2 in cluster 1 presents a model as shown in Eq. (37). Of the six predictor variables used, only four ($x_2$, $x_3$, $x_4$and $x_6$) have a significant impact. The interpretation of basis function bf11 indicates that if $x_2$ is less than 94 and $x_3$ is greater than 57.1, the prevalence of wasting will increase by 0.0313, assuming all other variables are held constant.

$$\begin{array}{ccc}\hfill y_2& =& 7.2643-0.6118bf1-0.1633bf2+0.5623bf3+0.0061bf4-0.0017bf5\hfill \\ & & -0.0117bf6+0.0025bf7-2.3486bf8+0.0279bf9-0.0485bf10+0.0313bf11\hfill \end{array}$$ (37)

where

$$\begin{array}{ccc}& & bf1=h(x_3-54.7),bf2=h(x_4-91.3),bf3=h(63.3-x_6)\hfill \\ & & bf4=h(39.1-x_2)*h(54.7-x_3),bf5=h(99-x_2)*(91.3-x_4),bf6=h(x_2-94)*(x_3-54.7),\hfill \\ & & bf7=h(94-x_2)*h(x_3-54.7),bf8=h(x_3-57.1),bf9=h(x_2-4.2)*h(x_3-54),\hfill \\ & & bf10=h(4.2-x_2)*h(x_3-54),bf11=h(94-x_2)*h(x_3-57.1)\hfill \end{array}$$ (38)

The MABFCMRS model designed for cluster 2 is shown in Table 5. The best model is achieved when BF = 22, MO = 3, and MI = 1.

Table 5.

MABFCMRS Cluster 2 model.

Response 1
Model	Estimate
(Intercept)	0.0008
bx_mabfcmrs [, -1]h(1.3-X1) *h(X3-47.4)	0.0008
bx_mabfcmrs [, -1]h(1.3-X1) *h(X2-89.5)	-0.0005
bx_mabfcmrs [, -1]h(1.3-X1) *h(89.5-X2)	0.0924
bx_mabfcmrs [, -1]h(X1-1.3) *h(X3-73.3)	-0.0008
bx_mabfcmrs [, -1]h(X1-1.3) *h(73.3-X3)	0.0412
bx_mabfcmrs [, -1]h(X1-1.3) *h(X2-57.1) *h(X3-73.3)	0.0030
bx_mabfcmrs [, -1]h(X1-1.3) *h(57.1-X2) *h(X3-73.3)	0.0027
bx_mabfcmrs [, -1]h(1.3-X1) *h(47.4-X3) *h(X4-95.5)	0.0032
bx_mabfcmrs [, -1]h(1.3-X1) *h(47.4-X3) *h(95.5-X4)	0.0093
bx_mabfcmrs [, -1]h(X6-100)	0.0075
bx_mabfcmrs [, -1]h(100-X6)	-0.0054
bx_mabfcmrs [, -1]h(1.3-X1) *h(X3-47.4) *h(X4-64.3)	0.0123
bx_mabfcmrs [, -1]h(1.3-X1) *h(X3-47.4) *h(64.3-X4)	0.0077
bx_mabfcmrs [, -1]h(X1-1.3) *h(73.3-X3) *h(111.3-X6)	-0.0005
bx_mabfcmrs [, -1]h(136.3-X4) *h(X6-111.7)	0.0480
bx_mabfcmrs [, -1]h(136.3-X4) *h(111.7-X6)	0.0014
Response 2
Model	Estimate
(Intercept)	0.0029
bx_mabfcmrs [, -1]h(X2-98.8) *h(X5-77)	0.0025
bx_mabfcmrs [, -1]h(X6-98)	-0.0333
bx_mabfcmrs [, -1]h(98-X6)	0.0649
bx_mabfcmrs [, -1]h(X6-49.3)	0.0443
bx_mabfcmrs [, -1]h(X3-87.4) *h(X6-98)	0.0784
bx_mabfcmrs [, -1]h(X3-71) *h(98-X6)	-0.0003
bx_mabfcmrs [, -1]h(71-X3) *h(X4-50.6) *h(98-X6)	0.0002
bx_mabfcmrs [, -1]h(3.7-X2) *h(X6-49.3)	-0.0076

Table 5 for response 1 presents the parameter estimates of the MABFCMRS model for cluster 2, as shown in Eq. (39) Of the six predictor variables used, only four significantly influence the prevalence of stunting: $x_1$, $x_2$, $x_3$, $x_4$, and $x_6$. The interpretation for basis function bf11 suggests that if $x_6$ is less than 100, the prevalence of stunting will decrease by 0.0054, assuming all other variables are held constant.

$$\begin{array}{ccc}\hfill y_1& =& 0.0008+0.0008bf1-0.0005bf2+0.0924bf3-0.0008bf4+0.0412bf5\hfill \\ & & +0.0030bf6+0.0027bf7+0.0032bf8+0.0093bf9+0.0075bf10-0.0054bf11\hfill \\ & & +0.0123bf12+0.0077bf13-0.0005bf14+0.0480bf15+0.0014bf16\hfill \end{array}$$ (39)

where

$$\begin{array}{ccc}& & bf1=h(1.3-x_1)*h(x_3-47.4),bf2=h(1.3-x_1)*h(x_2-89.5),\hfill \\ & & bf3=h(1.3-x_1)*(89.5-x_2),bf4=h(x_1-1.3)*h(x_3-73.3),\hfill \\ & & bf5=h(x_1-1.3)*(73.3-x_3),bf6=h(x_1-1.3)*(x_2-57.1)*h(x_3-73.3),\hfill \\ & & bf7=h(x_1-1.3)*h(57.1-x_2)*h(x_3-73.3),\hfill \\ & & bf8=h(1.3-x_1)*h(47.4-x_3)*h(x_4-95.5),\hfill \\ & & bf9=h(1.3-x_1)*h(47.4-x_3)*h(95.5-x_4),\hfill \\ & & bf10=h(x_6-100),bf11=h(100-x_6),bf12=h(1.3-x_1)*h(x_3-47.4)*h(x_4-64.3),\hfill \\ & & bf13=h(1.3-x_1)*h(x_3-47.4)*h(64.3-x_4),\hfill \\ & & bf14=h(x_1-1.3)*h(73.3-x_3)*h(111.3-x_6),bf15=h(136.3-x_4)*h(x_6-111.7),\hfill \\ & & bf16=h(136.3-x_4)*h(111.7-x_6)\hfill \end{array}$$ (40)

Table 5 for response 2 displays the parameter estimates of the MABFCMRS model for Cluster 2, as detailed in Eq. (41). Among the 6 predictor variables employed, only five significantly affect the prevalence of stunting: $x_2$, $x_3$, $x_4$, $x_5$and $x_6$. If $x_6$ does not exceeds 98, the basis function bf3 interpretation indicates a 0.0649 increase in the prevalence of wasting, assuming all other variables remain constant

$$\begin{array}{ccc}\hfill y_2& =& 0.0029+0.0025bf1-0.0333bf2+0.0649bf3+0.0443bf4+0.0784bf5\hfill \\ & & -0.0003bf6+0.0002bf7-0.0076bf8\hfill \end{array}$$ (41)

where

$$\begin{array}{ccc}& & bf1=h(x_2-98.8)*h(x_5-77),bf2=h(x_6-98),bf3=h(98-x_6),\hfill \\ & & bf4=h(x_6-49.3),bf5=h(x_3-87.4)*(x_6-98),\hfill \\ & & bf6=h(x_3-71)*(98-x_6),bf7=h(71-x_3)*h(x_4-50.6)*h(98-x_6),\hfill \\ & & bf8=h(3.7-x_2)*h(x_6-49.3)\hfill \end{array}$$ (42)

Comparison of the Goodness of fit model can be seen in Table 6. The MABFCMRS model in cluster 1 and cluster 2 has the smallest GCV and MSE value. Similarly, the R-square value shows a substantial rise from the MARSBC model to the MABFCMRS model.

Table 6.

Comparison of the goodness of fit model.

Model	Criteria			N
	MSE	R2	GCV
MARSBC	187.214596	0.32065947	211.099929	222
MABFCMRS Cluster1	54.9758835	0.67400923	134.91909	102
MABFCMRS Cluster 2	19.9363767	0.74444143	41.5878378	120

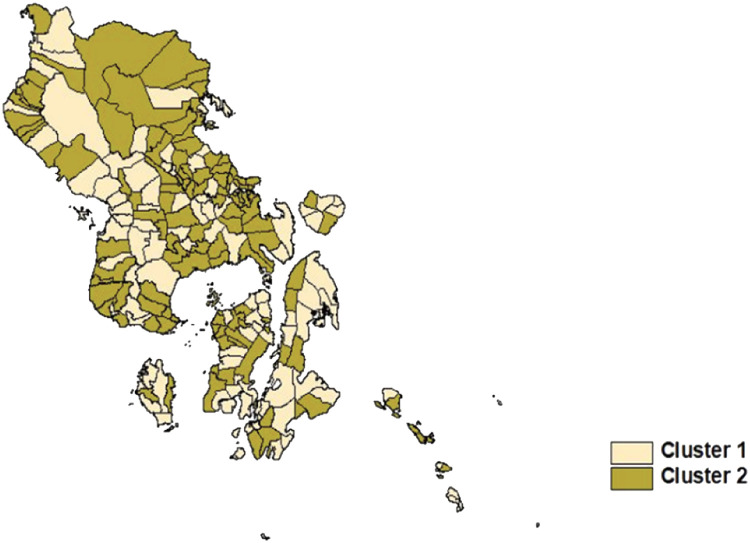
The MABFCMRS model in Fig. 3 categorizes the subdistricts based on the maximum validation values of the PC and MPC indices. The 222 subdistricts in Southeast Sulawesi province are divided into two clusters: the lighter color represents cluster 1, while the darker color represents cluster 2.

Fig. 3.

Southeast Sulawesi cluster distribution map.

Conclusion

This study developed a new MABFCMRS model that combines the MARSBC model and the FCM method. The MABFCMRS model is designed to involve unobserved heterogeneity. Creates a data cluster based on a previously established model cluster center. This makes the MABFCMRS model more complicated than the MARSBC model. The MABFCMRS model was applied to the prevalence of stunting and wasting in 222 subdistricts in the southeastern province of Sulawesi. Based on PC and MPC index validation values, there are two clusters. Cluster 1 groups 102 clusters, and cluster 2 groups 120. Based on the goodness of fit values, MSE, R2, and GCV show that the MABFCMRS model is better than the MARSBC model.

Limitations

In order to avoid the increased complexity and challenges associated with interpreting more extensive interactions, this study identified a limitation in the MABFCMRS model, restricting it to only include up to three interactions. Additionally, the current article does not include hypothesis testing for the proposed model, presenting an opportunity for future research to explore this aspect. The model's adaptability also allows for the inclusion of categorical and count data in subsequent studies.

CRediT authorship contribution statement

Mira Meilisa: Conceptualization, Methodology, Formal analysis, Writing – original draft, Visualization. Bambang Widjanarko Otok: Conceptualization, Methodology, Writing – review & editing, Supervision. Jerry Dwi Trijoyo Purnomo: Methodology, Validation, Writing – review & editing, Supervision.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A

Table A1. Degree of membership value for MABFCMRS to determine the sub-districts in Southeast Sulawesi province that belong to each cluster.

Table A1.

Degree of membership value for MABFCMRS.

No.	Subdistrict	Cluster 1	Cluster 2	Number of clusters	No.	Subdistrict	Cluster 1	Cluster 2	Number of clusters
1	Kapontori	0.7039	0.2961	1	112	Poleang Utara	0.9411	0.0589	1
2	Lasalimu	0.6803	0.3197	1	113	Rarowatu	0.0513	0.9487	2
3	Lasalimu Selatan	0.7895	0.2105	1	114	Rarowatu Utara	0.1195	0.8805	2
4	Pasar Wajo	0.9253	0.0747	1	115	Rumbia	0.0027	0.9973	2
5	Siontapina	0.4932	0.5068	2	116	Rumbia Tengah	0.1884	0.8116	2
6	Wabula	0.8059	0.1941	1	117	Tontonunu	0.0397	0.9603	2
7	Wolowa	0.0531	0.9469	2	118	Binongko	0.6248	0.3752	1
8	Batalaiworu	0.1612	0.8388	2	119	Kaledupa	0.2647	0.7353	2
9	Batukara	0.7274	0.2726	1	120	Kaledupa Selatan	0.0023	0.9977	2
10	Bone	0.1785	0.8215	2	121	Togo Binongko	0.6005	0.3995	1
11	Duruka	0.1249	0.8751	2	122	Tomia	0.9319	0.0681	1
12	Kabangka	0.2495	0.7505	2	123	Tomia Timur	0.4765	0.5235	2
13	Kabawo	0.9619	0.0381	1	124	Wangi-Wangi	0.9375	0.0625	1
14	Katobu	0.8793	0.1207	1	125	Wangi-Wangi Selatan	0.1604	0.8396	2
15	Kontukowuna	0.1144	0.8856	2	126	Uluiwoi	0.9999	0.0001	1
16	Kontunaga	0.9010	0.0990	1	127	Batu Putih	0.7517	0.2483	1
17	Lasalepa	0.7625	0.2375	1	128	Katoi	0.1286	0.8714	2
18	Lohia	0.8736	0.1264	1	129	Kodeoha	0.0074	0.9926	2
19	Maligano	0.0167	0.9833	2	130	Lambai	0.1037	0.8963	2
20	Marobo	0.0844	0.9156	2	131	Lasusua	0.2740	0.7260	2
21	Napabalano	0.9643	0.0357	1	132	Ngapa	0.0668	0.9332	2
22	Parigi	0.9334	0.0666	1	133	Pakue	0.5195	0.4805	1
23	Pasi Kolaga	0.9682	0.0318	1	134	Pakue Tengah	0.2492	0.7508	2
24	Pasir Putih	0.1287	0.8713	2	135	Pakue Utara	0.9225	0.0775	1
25	Tongkuno	0.0417	0.9583	2	136	Porehu	0.1555	0.8445	2
26	Tongkuno Selatan	0.9118	0.0882	1	137	Ranteangin	0.0020	0.9980	2
27	Towea	0.5925	0.4075	1	138	Tiwu	0.2740	0.7260	2
28	Wakorumba Selatan	0.8681	0.1319	1	139	Tolala	0.8487	0.1513	1
29	Watopute	0.9316	0.0684	1	140	Watunohu	0.7360	0.2640	1
30	Abuki	0.0837	0.9163	2	141	Wawo	0.7581	0.2419	1
31	Amonggedo	0.1121	0.8879	2	142	Bonegunu	0.2203	0.7797	2
32	Anggaberi	0.0016	0.9984	2	143	Kalisusu	0.7896	0.2104	1
33	Anggalomoare	0.2332	0.7668	2	144	Kambowa	0.9032	0.0968	1
34	Anggotoa	0.0238	0.9762	2	145	Kulisusu Barat	0.8953	0.1047	1
35	Asinua	0.6343	0.3657	1	146	Kulisusu Utara	0.0142	0.9858	2
36	Bandoala	0.5237	0.4763	1	147	Wakorumba Utara	0.1160	0.8840	2
37	Besulutu	0.0663	0.9337	2	148	Andowia	0.0762	0.9238	2
38	Kapoiala	0.4619	0.5381	2	149	Asera	0.0376	0.9624	2
39	Konawe	0.1399	0.8601	2	150	Landawe	0.0117	0.9883	2
40	Lalonggasumeeto	0.0676	0.9324	2	151	Langgikima	0.4067	0.5933	2
41	Lambuya	0.0397	0.9603	2	152	Lasolo	0.9994	0.0006	1
42	Latoma	0.0063	0.9937	2	153	Lasolo Kepulauan	0.2913	0.7087	2
43	Meluhu	0.8239	0.1761	1	154	Lembo	0.0500	0.9500	2
44	Morosi	0.2426	0.7574	2	155	Molawe	0.2367	0.7633	2
45	Onembute	0.0175	0.9825	2	156	Motui	0.8340	0.1660	1
46	Padangguni	0.2026	0.7974	2	157	Oheo	0.0838	0.9162	2
47	Pondidaha	0.4879	0.5121	2	158	Sawa	0.8952	0.1048	1
48	Puriala	0.9915	0.0085	1	159	Wawolesea	0.0720	0.9280	2
49	Routa	0.0109	0.9891	2	160	Wiwirano	0.7769	0.2231	1
50	Sampara	0.2058	0.7942	2	161	Aere	0.0292	0.9708	2
51	Soropia	0.0723	0.9277	2	162	Dangia	0.1693	0.8307	2
52	Tongauna	0.5509	0.4491	1	163	Ladongi	0.0085	0.9915	2
53	Tongauna Utara	0.7730	0.2270	1	164	Lalolae	0.9978	0.0022	1
54	Uepai	0.2092	0.7908	2	165	Lambandia	0.7515	0.2485	1
55	Unaaha	0.5181	0.4819	1	166	Loea	0.3561	0.6439	2
56	Wawotobi	0.0142	0.9858	2	167	Mowewe	0.6602	0.3398	1
57	Wonggeduku	0.0725	0.9275	2	168	Poli-Polia	0.9493	0.0507	1
58	Wonggeduku Barat	0.2465	0.7535	2	169	Tinondo	0.7566	0.2434	1
59	Baula	0.7151	0.2849	1	170	Tirawuta	0.9861	0.0139	1
60	Iwoimendaa	0.0410	0.9590	2	171	Uesi	0.7781	0.2219	1
61	Kolaka	0.9697	0.0303	1	172	Wawonii Barat	0.1286	0.8714	2
62	Latambaga	0.7456	0.2544	1	173	Wawonii Selatan	0.6112	0.3888	1
63	Polinggona	0.6074	0.3926	1	174	Wawonii Tengah	0.9911	0.0089	1
64	Pomalaa	0.6024	0.3976	1	175	Wawonii Tenggara	0.0065	0.9935	2
65	Samaturu	0.6327	0.3673	1	176	Wawonii Timur	0.6458	0.3542	1
66	Tanggetada	0.2852	0.7148	2	177	Wawonii Timur Laut	0.9826	0.0174	1
67	Toari	0.1782	0.8218	2	178	Wawonii Utara	0.9974	0.0026	1
68	Watubangga	0.3969	0.6031	2	179	Barangka	0.0946	0.9054	2
69	Wolo	0.2452	0.7548	2	180	Kusambi	0.0303	0.9697	2
70	Wundulako	0.5091	0.4909	1	181	Lawa	0.8350	0.1650	1
71	Andoolo	0.3676	0.6324	2	182	Maginti	0.1734	0.8266	2
72	Andoolo Barat	0.9353	0.0647	1	183	Napano Kusambi	0.7787	0.2213	1
73	Angata	0.0093	0.9907	2	184	Sawerigadi	0.0975	0.9025	2
74	Baito	0.6736	0.3264	1	185	Tiworo Kepulauan	0.9882	0.0118	1
75	Basala	0.0208	0.9792	2	186	Tiworo Selatan	0.4487	0.5513	2
76	Benua	0.5793	0.4207	1	187	Tiworo Tengah	0.1652	0.8348	2
77	Buke	0.1688	0.8312	2	188	Tiworo Utara	0.0466	0.9534	2
78	Kolono	0.0690	0.9310	2	189	Wa Daga	0.0107	0.9893	2
79	Kolono Timur	0.5351	0.4649	1	190	Gu	0.6983	0.3017	1
80	Konda	0.1088	0.8912	2	191	Lakudo	0.8179	0.1821	1
81	Laeya	0.9764	0.0236	1	192	Mawasangka	0.3564	0.6436	2
82	Lainea	0.3826	0.6174	2	193	Mawasangka Tengah	0.6652	0.3348	1
83	Lalembuu	0.1031	0.8969	2	194	Mawasangka Timur	0.9583	0.0417	1
84	Landono	0.8695	0.1305	1	195	Sangia Wambulu	0.0027	0.9973	2
85	Laonti	0.6962	0.3038	1	196	Talaga Raya	0.7931	0.2069	1
86	Moramo	0.0039	0.9961	2	197	Batauga	0.0358	0.9642	2
87	Moramo Utara	0.0039	0.9961	2	198	Batuatas	0.9899	0.0101	1
88	Mowila	0.6002	0.3998	1	199	Kadatua	0.9357	0.0643	1
89	Palangga	0.2098	0.7902	2	200	Lapandewa	0.9990	0.0010	1
90	Palangga Selatan	0.0733	0.9267	2	201	Sampolawa	0.2096	0.7904	2
91	Ranomeeto	0.8837	0.1163	1	202	Siompu	0.5026	0.4974	1
92	Ranometoo Barat	0.0695	0.9305	2	203	Siompu Barat	0.9971	0.0029	1
93	Sabulakoa	0.8121	0.1879	1	204	Abeli	0.1991	0.8009	2
94	Tinanggea	0.0211	0.9789	2	205	Baruga	0.0684	0.9316	2
95	Wolasi	0.0580	0.9420	2	206	Kadia	0.8064	0.1936	1
96	Kabaena	0.0537	0.9463	2	207	Kambu	0.0920	0.9080	2
97	Kabaena Barat	0.7824	0.2176	1	208	Kendari	0.2313	0.7687	2
98	Kabaena Selatan	0.7598	0.2402	1	209	Kendari Barat	0.1846	0.8154	2
99	Kabaena Tengah	0.9589	0.0411	1	210	Mandonga	0.3307	0.6693	2
100	Kabaena Timur	0.1982	0.8018	2	211	Nambo	0.2062	0.7938	2
101	Kabaena Utara	0.9564	0.0436	1	212	Poasia	0.2365	0.7635	2
102	Kep. Masaloka Raya	0.9776	0.0224	1	213	Puuwatu	0.8947	0.1053	1
103	Lantari Jaya	0.9652	0.0348	1	214	Wua-Wua	0.2462	0.7538	2
104	Mataoleo	0.0350	0.9650	2	215	Batupoaro	0.1842	0.8158	2
105	Matausu	0.8621	0.1379	1	216	Betoambari	0.6757	0.3243	1
106	Poleang	0.1038	0.8962	2	217	Bungi	0.7136	0.2864	1
107	Poleang Barat	0.4822	0.5178	2	218	Kokalukuna	0.6965	0.3035	1
108	Poleang Selatan	0.1768	0.8232	2	219	Lea-Lea	0.8083	0.1917	1
109	Poleang Tengah	0.9368	0.0632	1	220	Murhum	0.2156	0.7844	2
110	Poleang Tenggara	0.1081	0.8919	2	221	Sorawolio	0.0256	0.9744	2
111	Poleang Timur	0.7637	0.2363	1	222	Wolio	0.9955	0.0045	1

Data availability

• The authors do not have permission to share data.