Modelling and stability analysis of the dynamics of measles with application to Ethiopian data

Abstract

Measles, a highly contagious airborne disease, remains endemic in many developing countries with low vaccination coverage. In this paper, we present a deterministic mathematical compartmental model to analyze the dynamics of measles. We establish global stability conditions for both disease-free and endemic equilibria using the Lyapunov functional stability method. By using arbitrary parameters, we find that the proposed model exhibits forward bifurcation. To simulate the solution of the model for the forward problem, we perform numerical integration using MATLAB software. Moreover, we calibrate the model with real data from Ethiopia and estimate the parameters along with a 95 percent confidence interval (CI) by formulating an inverse problem. It is noteworthy that our model fits well with the actual data from Ethiopia. The estimated basic reproduction number ($R_0$) is determined to be $R_0=1.3973$, demonstrating the endemic status of the disease. Additionally, our local sensitivity analysis indicates that reducing the transmission rate and increasing vaccination coverage can effectively minimize $R_0$.

1. Introduction

Measles is an acute viral illness caused by the pathogen Morbillivirus whose only reservoir is the human host. Despite an extensive vaccination against measles, it is still endemic in many countries and is the main cause of morbidity and mortality in developing regions [1], [2]. Clinical symptoms of measles include: cough, runny nose, red eyes, sore throat, fever, and a widespread skin rash. If the virus is transmitted to the susceptible ones, they become exposed and pass the latent period within the first 6 to 9 days of exposure; after that, the infectious period follows and they are able to transmit the disease for 6 to 7 days [3], [4]. An individual once infected with measles becomes lifelong immune after running its entire course.

Mathematical modelling has been broadly used as a tool to understand the mechanisms by which infectious diseases spread, to decide on how to control the spread, and to minimize expenses in controlling disease outbreaks. [5], [6], [7], [8], [9], [10], [11], [12], [13], [14]. The predictive nature of these epidemic models, which aid in decision-making, is one of their key strengths. An optimal control theory plays an important role in epidemiological models. Authors in [14], [15] consider infectious disease models with optimal control strategies. Some other authors [16], [17], [18] studied disease models using fractional orders. One of the challenges in epidemic modelling is the analysis of the global stability of disease-free and endemic equilibria. So far, the most powerful method for global stability analyses of infectious diseases is the direct Lyapunov and the geometric methods [19], [20], [21], [22], [23], [24]. The authors [20], [21] studied the global stability analyses of SIS, SIR, and $SIRS$ epidemic models with constant recruitment, disease-induced death, and standard incidence rate using Lyapunov functions. However, constructing a Lyapunov function to establish the global stability of an $SEIR$ system with constant recruitment, standard incidence, and disease-induced death is still difficult. Moreover, an epidemic model must be validated to check if it is to be actually used [12], [25], [26], [27], [28], [29], [30], which contains comparing the real data with the model solutions in order to evaluate if the model proposed corresponds to reality. In most cases, the first model solutions fail to agree with the observed real data, probably due to the wrong choice of the initial parameters and a lack of adequate model assumptions. Even though the first model solution fails to agree with the observed real data, it can be adjusted through a process known as model calibration. Model calibration is the process whereby parameter values that promote a good agreement between the model solutions and observed real data are estimated.

Quite recently, studying the dynamics of the measles disease in the context of mathematics has become an important issue. [4], [16], [17], [19], [28], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39]. In [39] work, the global sensitivity analysis of the model parameters relative to the basic reproduction number and variables of the model has been investigated. This was performed using the partial rank correlation coefficient (PRCC). The result shows that individual protection, together with efficient treatment, could reduce the burden of the disease. Moreover, they further extend their model from integer to fractional-order derivatives. Some authors, such as [33], [35], [36] have studied the dynamics using constant and continuous controls. They have studied the global stability analyses of the disease-free and endemic equilibria. Other authors, for instance, [32] investigated the global stability analysis of the disease dynamics but failed to predict the disease dynamics in the context of a particular situation. There are also others, such as [34] who proposed a mathematical model of measles and predicted the disease situation in Bangladesh using double vaccination doses. However, the majority of previous $SEIR$ model studies have overlooked the assumption of standard incidence rates in disease transmission and have neglected to consider disease-induced death rates in their examination of disease dynamics. The study of the global stability of the disease-free and endemic equilibria using Lyapunov functions for this type of model is computationally difficult and quite rare. Furthermore, only a few researchers have delved into the estimation of parameters for the proposed model using real-world data. Consequently, it is crucial to investigate the global dynamics of the measles model by incorporating standard incidence assumptions in disease transmission and by estimating the model's parameters. Additionally, this research explores the impact of the transfer of exposed individuals to the infected class on the disease spread, which has not been previously investigated in the existing literature.

This work aims to propose a deterministic compartmental mathematical model for the dynamics of measles disease and calibrate the model to real data of measles outbreaks in Ethiopia. Particularly, we study the long-term global stability analyses of the disease-free and endemic equilibria using the Lyapunov stability method. We also investigate the bifurcation analysis. Next, the model is extended by assuming a fraction of the individuals recruited due to birth or immigration are vaccinated, and then model predictions are made to compare the model solutions with the real data using some plausible parameters as initial values. Then, a rigorous process of model calibration is done through the solution of an inverse problem to find the best parameter estimates. Finally, the local sensitivity analysis of the basic reproduction number to the estimated parameter values is done to check the robustness of the system proposed.

The work has seven sections: The measles model is formulated in Section 2. In Section 3, we study the mathematical analysis: The basic reproduction number, existence of equilibria, the local and global stability analysis of the equilibria, and following this, the bifurcation analysis is done in Section 4. The system parameters are estimated in Section 5. In Section 6, numerical simulation of the system is performed. Finally, we conclude the work in Section 7.

2. Mathematical model formulation

To formulate the mathematical model of measles, the population is divided into four mutually exclusive classes, with each class representing the health condition of an individual. Susceptible individuals (S), individuals carrying the pathogen transmitting the disease but showing no clinical symptoms of measles (E), individuals infected with measles, show the symptoms and can spread the disease (I). Finally, the members who recovered from measles (R) are not infected. The total human population is denoted by $N=S+E+I+R$.

Some of the main assumptions made in the formulation of the deterministic system (1) are: The population is homogeneously mixed. All susceptible individuals have the same probability of being infected. The incidence is assumed to be standard incidence based on the assumption that the rate of contact is constant. An individual infected with measles will either die or recover. There is life-long immunity for the measles disease survivors, and hence the model proposed is a $SEIR$. Diseases induced death rates exist for the members of the infected group. All parameters are non-negative.

The class of susceptible individuals is recruited by immigration or birth at a per capita rate Λ and decreased following infection with measles at a rate of $\frac{\beta I}{S+E+I+R}$. These populations are also decreased by natural death at a rate μ which is assumed to be the same for all classes. Hence, the first equation of system (1) is proposed. The population of humans exposed to measles (E) is generated at the rate $\frac{\beta I}{S+E+I+R}$. It is also decreased by the rate of progression to the infected class at a rate of ϵ and the natural death rate. Hence, the second equation of system (1) is proposed. The time elapsed in the exposed class is called the latent (or incubation) period. The population of humans infected with measles (I) is increasing at the rate of ϵ. These individuals recover naturally at a rate of γ. It is further diminished by the disease-induced death rate at a rate of d and the natural death rate. Hence, the third equation of system (1) is proposed. The population of measles recovered individuals (R) is generated at a rate of γ. It is also decreased by the natural death rate. Hence, the fourth equation of system (1) is developed.

The system model dynamics for the measles is given by the following deterministic system of nonlinear differential equations, and the parameter descriptions are given in Table 1, respectively.

$$\frac{dS}{dt}=\mathrm{\Lambda }-(\frac{\beta I}{S+E+I+R}+\mu )S,\frac{dE}{dt}=\frac{\beta IS}{S+E+I+R}-(\mu +ϵ)E,\frac{dI}{dt}=ϵE-(\mu +d+\gamma )I,\frac{dR}{dt}=\gamma I-\mu R,\frac{dN}{dt}=\mathrm{\Lambda }-\mu N-dI,S(0)>0,E(0)\ge 0,I(0)\ge 0,R(0)\ge 0.$$ (1)

Table 1.

Description of parameters of system (1).

Parameters	Interpretation	Units
Λ	Recruitment rate of susceptible population by immigration or birth	[Humans][week]−1
β	Effective contact rate of measles	[week]−1
μ	Natural death rate of humans	[week]−1
ϵ	Rate of progress from exposed to infectious class	[week]−1
d	Disease induced death rate of measles	[week]−1
γ	Natural recovery rate from measles	[week]−1

3. Model analysis

In this section, we examine the basic qualitative features which are useful in the subsequent sections.

3.1. Nonnegativity of solutions and the feasible region

Lemma 3.1

The solutions of system(1)with nonnegative initial data remain positive for all$t>0$.

Proof

Let $T=\sup \{t>0:S>0,E>0,I>0,R>0\}\in [0,t]$. The first equation of system (1) can be written as

$$\frac{dS}{dt}=\mathrm{\Lambda }-(\lambda +\mu )S,\text{where}\lambda =\frac{\beta I}{S+E+I+R}.$$ (2)

Eq. (2) is an initial value problem (IVP) with variable coefficients. It has a unique positive solution $S(t)$ given by

$$S(t)=S(0)\exp \{-A(t)\}+\exp \{-A(t)\}\underset{0}{\overset{t}{\int }}\mathrm{\Lambda }\exp \{A(s)\}ds,$$

where the function $A(t)={\int }_0^t(\lambda (s)+\mu )ds$ is a particular antiderivative of the function $(\lambda (s)+\mu )$.

Since T is the maximum of all the time in $[0,t]$, we have that $A(T)={\int }_0^T(\lambda (s)+\mu )ds$. So that the solution $S(T)$ is

$$S(T)=S(0)\exp \{-A(T)\}+\exp \{-A(T)\}\underset{0}{\overset{T}{\int }}\mathrm{\Lambda }\exp \{A(s)\}ds>0.$$

Likewise, it is easy to show that all other state variables of the system model remain positive for all $t>0$. □

Lemma 3.2

Every non-negative solution is bounded in$L^1$-norm by$max\{N(0),\frac{\mathrm{\Lambda }}{\mu }\}$.

Proof

The total dynamics of the system model obtained by adding all the equations of system (1) is:

$$\frac{dN}{dt}=\mathrm{\Lambda }-\mu N-dI.$$ (3)

Consequently, the total population $N(t)$ may vary in time. From Eq. (3), we also have $\frac{dN}{dt}\le \mathrm{\Lambda }-\mu N$. It is easy to show that

$$0\le N(t)\le (N(0)-\frac{\mathrm{\Lambda }}{\mu })e^{-\mu t}+\frac{\mathrm{\Lambda }}{\mu }.$$ (4)

Taking $t\to \infty$ in Eq. (4), we observe that $0<N(t)\to \frac{\mathrm{\Lambda }}{\mu }$.

The $L^1$-norm of each non-negative solution is N and satisfies $N^{\prime }\le \mathrm{\Lambda }-\mu N$ where $N^{\prime }$ represents the derivative of N. Consider a comparison differential equation $N_1^{\prime }=\mathrm{\Lambda }-\mu N_1$ where $N^{\prime }\le N_1^{\prime }$. Consider the solutions to the equation $N_1^{\prime }=\mathrm{\Lambda }-\mu N_1$. If $N_1(0)\le \frac{\mathrm{\Lambda }}{\mu }$ then ${\lim }_{t\to \infty }{N}_1(t)=\frac{\mathrm{\Lambda }}{\mu }$ and $\frac{\mathrm{\Lambda }}{\mu }$ is the upper bound. If $N_1(0)>\frac{\mathrm{\Lambda }}{\mu }$, then the solution will decrease to $\frac{\mathrm{\Lambda }}{\mu }$ as $t\to \infty$ and $N_1(0)=N_{10}$ is the upper bound of $N_1$. Since $N^{\prime }\le N_1^{\prime }$ the claim follows for $N(t)$ [40]. □

The biological feasible region for the system model (1) is given by

$$\mathrm{\Omega }=\left\{\right(S,E,I,R)\in {\mathbb{R}}_{+}^4|0\le S+E+I+R\le \frac{\mathrm{\Lambda }}{\mu }\}.$$ (5)

In the next subsection, we prove the positively invariant and attracting behavior of Eq. (5) with respect to system (1).

3.2. Positively invariant

Theorem 3.1

The non-negative orthant ${\mathbb{R}}_{+}^4$ is positively invariant for the system model (1) .

Proof

To prove this theorem, we first write the system (1) in the form $Y^{\prime }=\mathbf{\text{M}}Y+\mathbf{\text{K}}$, where

$$\mathbf{\text{M}}=\left[\begin{array}{cccc}\hfill -(\lambda +\mu )\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \lambda \hfill & \hfill -(\mu +ϵ)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill ϵ\hfill & \hfill -(\mu +d+\gamma )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill -\mu \hfill \end{array}\right]\mathrm{\text{and}}\mathbf{\text{K}}=\left[\begin{array}{c}\hfill \mathrm{\Lambda }\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right].$$

Clearly, the column vector $\mathbf{\text{K}}\ge 0$ and the matrix M have the properties of a Metzler matrix (all the off diagonal entries of M are non-negative). Following the results in [40], the system (1) is positively invariant in ${\mathbb{R}}_{+}^4$. □

3.3. Equilibria and the basic reproduction number

System (1) has a disease-free equilibrium $E_0=(\frac{\mathrm{\Lambda }}{\mu },0,0,0)$. In the study of disease dynamics mathematically, the basic reproduction number $R_0$ is the most important parameter to determine disease transmissibility. It determines the spread or die out of the infection with time [12]. Based on the next generation matrix approach developed by [41], the basic reproduction number of system (1) is given as:

$$R_0=\frac{\beta ϵ}{(\mu +ϵ)(\mu +d+\gamma )}.$$

It could be easily noticed that the basic reproduction number $R_0$ is independent of the fraction $\frac{\mathrm{\Lambda }}{\mu }$. The endemic equilibrium is given as $E_1=(S^{⁎},E^{⁎},I^{⁎},R^{⁎})$ with coordinates:

$$S^{⁎}=\frac{\mathrm{\Lambda }(\mu (\mu +\gamma +d)+ϵ(\mu +\gamma ))}{\mu ϵ(\beta -d)},E^{⁎}=\frac{\mathrm{\Lambda }(\mu +\gamma +d)(R_0-1)}{ϵ(\beta -d)},I^{⁎}=\frac{\mathrm{\Lambda }(R_0-1)}{\beta -d},R^{⁎}=\frac{\gamma \mathrm{\Lambda }(R_0-1)}{\mu (\beta -d)}.$$ (6)

It can be easily observed from Eq. (6) that the susceptible ($S^{⁎}$) is feasible only if $\beta >d$. So in what follows, we will assume that the effective contact rate (β) is always greater than the disease induced death rate (d).

3.4. Local stability analysis of disease-free equilibrium

Theorem 3.2

The disease-free equilibrium $E_0$ of the system (1) is locally asymptotically stable when $R_0<1$ , and unstable if $R_0>1$ .

Proof

The proof involves the evaluation of the Jacobian matrix of the system (1) at $E_0$, which is given by

$$J(E_0)=\left[\begin{array}{cccc}\hfill -\mu \hfill & \hfill 0\hfill & \hfill -\beta \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -(\mu +ϵ)\hfill & \hfill \beta \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill ϵ\hfill & \hfill -(\mu +d+\gamma )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill -\mu \hfill \end{array}\right].$$

The two negative eigenvalues are ${\lambda }_1={\lambda }_2=-\mu$, and the other eigenvalues are found from the submatrix:

$$A=\left[\begin{array}{cc}\hfill -(\mu +ϵ)\hfill & \hfill \beta \hfill \\ \hfill ϵ\hfill & \hfill -(\mu +d+\gamma )\hfill \end{array}\right].$$

Correspondingly, the other eigenvalues are the solutions of the quadratic equation

$${\lambda }^2-\mathrm{\text{trace}}(A)\lambda +\det (A)=0,$$

where

$$\mathrm{\text{trace}}(A)=-(2\mu +ϵ+d+\gamma )and\det (A)=(\mu +ϵ)(\mu +d+\gamma )-\beta ϵ=1-R_0.$$

It follows that $\det (A)>0$ when $R_0<1$ and $\mathrm{\text{trace(A)}}<0$. Hence, the quadratic equation, ${\lambda }^2-\mathrm{\text{trace(A)}}\lambda +\det (A)=0$ has negative eigenvalues [42]. Consequently, the system (1) is locally asymptotically stable at $E_0$ if $R_0<1$. □

3.5. Global stability of disease-free equilibrium

Theorem 3.3

The disease-free equilibrium,$E_0$, of system(1)is globally asymptotically stable in Ω if $R_0\le 1$.

Proof

To prove this, we define the Lyapunov function $L:\{(S,E,I,R)\in \mathrm{\Omega }:S>0\}\to \mathbb{R}$ by

$$L=ϵE+(\mu +ϵ)I.$$

Differentiating L with respect to time in the solutions of system (1) we get

$$\frac{dL}{dt}=ϵE^{\prime }+(\mu +ϵ)I^{\prime }.=ϵ(\frac{\beta IS}{S+E+I+R}-(\mu +ϵ)E)+(\mu +ϵ)(ϵE-(\mu +d+\gamma )I),=ϵ\left(\frac{\beta IS}{S+E+I+R}\right)-(\mu +ϵ)(\mu +d+\gamma )I,=\frac{I}{S+E+I+R}(ϵ\beta S-(\mu +ϵ)(\mu +d+\gamma )(S+E+I+R)),=\frac{I}{S+E+I+R}((\mu +ϵ)(\mu +d+\gamma )R_{0}S-(\mu +ϵ)(\mu +d+\gamma )(S+E+I+R)),=\frac{I(\mu +ϵ)(\mu +d+\gamma )}{S+E+I+R}(R_{0}S-(S+E+I+R)),=-\frac{I(\mu +ϵ)(\mu +d+\gamma )}{S+E+I+R}(-R_{0}S+(S+E+I+R)),=-\frac{I(\mu +ϵ)(\mu +d+\gamma )}{S+E+I+R}((1-R_0)S+(E+I+R)).$$

Then, if $R_0\le 1$, then $\frac{dL}{dt}\le 0$. Furthermore, $\frac{dL}{dt}=0$ if and only if $I=0$ or $E=I=R=0$ and $R_0=1$. Hence, L is a Lyapunov function on Ω. Thus, $(E,I,R)\to (0,0,0)$ as $t\to \infty$. Using $E=I=R=0$ in the first equation of system (1) we obtain $S\to \frac{\mathrm{\Lambda }}{\mu }$ as $t\to \infty$. Therefore, the largest compact invariant set in $\{(S,E,I,R)\in \mathrm{\Omega }:\frac{dL}{dt}(E,I)=0\}$ is the singleton $\left\{E_0\right\}$. It follows from LaSalle's-Lyapunov theorem [43] that $E_0$ is globally asymptotically stable in Ω. □

3.6. Local stability of endemic equilibrium

Theorem 3.4

The endemic equilibrium is locally asymptotically stable if $R_0>1$ .

Proof

Linearizing the system (1) around the endemic equilibrium $E_1$, gives the following Jacobian matrix

$$J(E_1)=\left(\begin{array}{cccc}\hfill -\frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}-\mu \hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill \frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}-(\mu +ϵ)\hfill & \hfill \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill ϵ\hfill & \hfill -(\mu +ϵ)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill -\mu \hfill \end{array}\right).$$

The characteristic equation of the matrix $J(E_1)$ evaluated at $E_1$ is

$$a_0{\lambda }^4+a_1{\lambda }^3+a_2{\lambda }^2+a_3\lambda +a_4=0,$$

where

$$a_0=1,a_1=x_1+x_2+x_3+x_4>0,a_2=x_3{x}_4+(x_1+x_2)(x_3+x_4)+x_1{x}_2>0,a_3=x_3{x}_4(x_1+x_2)+x_1{x}_2(x_3+x_4)>0,a_4=x_1{x}_2{x}_3{x}_4>0.$$

This directly follows from the condition $R_0>1$ for $\beta -d>0$.

Next remains to check if $D_i>0$, $i=1,2,3,4$ holds, where

$D_1=a_1$, $D_2=\left|\begin{array}{cc}\hfill a_1\hfill & \hfill a_3\hfill \\ \hfill a_0\hfill & \hfill a_2\hfill \end{array}\right|$, $D_3=\left|\begin{array}{ccc}\hfill a_1\hfill & \hfill a_3\hfill & \hfill a_5\hfill \\ \hfill a_0\hfill & \hfill a_2\hfill & \hfill a_4\hfill \\ \hfill 0\hfill & \hfill a_1\hfill & \hfill a_3\hfill \end{array}\right|$, $D_4=\left|\begin{array}{cccc}\hfill a_1\hfill & \hfill a_3\hfill & \hfill a_5\hfill & \hfill a_7\hfill \\ \hfill a_0\hfill & \hfill a_2\hfill & \hfill a_4\hfill & \hfill a_6\hfill \\ \hfill 0\hfill & \hfill a_1\hfill & \hfill a_3\hfill & \hfill a_5\hfill \\ \hfill 0\hfill & \hfill a_0\hfill & \hfill a_2\hfill & \hfill a_4\hfill \end{array}\right|$.

Using matrix manipulation we get

$$D_1=a_1=x_1+x_2+x_3+x_4>0,D_2=\left|\begin{array}{cc}\hfill a_1\hfill & \hfill a_3\hfill \\ \hfill a_0\hfill & \hfill a_2\hfill \end{array}\right|=\left|\begin{array}{cc}\hfill x_1+x_2+x_3+x_4\hfill & \hfill x_3{x}_4(x_1+x_2)+x_1{x}_2(x_3+x_4)\hfill \\ \hfill 1\hfill & \hfill x_3{x}_4+(x_1+x_2)(x_3+x_4)+x_1{x}_2\hfill \end{array}\right|,=x_3{x}_4(x_3+x_4)+{(x_1+x_2)}^2(x_3+x_4)+(x_1+x_2){(x_3+x_4)}^2+x_1{x}_2(x_1+x_2)>0,D_3=\left|\begin{array}{ccc}\hfill a_1\hfill & \hfill a_3\hfill & \hfill 0\hfill \\ \hfill a_0\hfill & \hfill a_2\hfill & \hfill a_4\hfill \\ \hfill 0\hfill & \hfill a_1\hfill & \hfill a_3\hfill \end{array}\right|=\left|\begin{array}{ccc}\hfill x_1+x_2+x_3+x_4\hfill & \hfill x_3{x}_4(x_1+x_2)+x_1{x}_2(x_3+x_4)\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill x_3{x}_4+(x_1+x_2)(x_3+x_4)+x_1{x}_2\hfill & \hfill x_1{x}_2{x}_3{x}_4\hfill \\ \hfill 0\hfill & \hfill x_1+x_2+x_3+x_4\hfill & \hfill x_3{x}_4(x_1+x_2)+x_1{x}_2(x_3+x_4)\hfill \end{array}\right|,=a_1(a_2{a}_3-a_1{a}_4)-a_3^2,=(x_1^2+x_2^2)(x_1+x_2)(x_3+x_4)x_3{x}_4+{(x_1+x_2)}^2{x}_1{x}_2{(x_3+x_4)}^2+(x_1+x_2){(x_1{x}_2)}^2(x_3+x_4),+{(x_3{x}_4)}^2(x_1+x_2)(x_3+x_4)+{(x_1+x_2)}^2{(x_3+x_4)}^2{x}_3{x}_4+(x_1+x_2)x_1{x}_2{(x_3+x_4)}^3>0,$$

$$D_4=\left|\begin{array}{cccc}\hfill a_1\hfill & \hfill a_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill a_0\hfill & \hfill a_2\hfill & \hfill a_4\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill a_1\hfill & \hfill a_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill a_2\hfill & \hfill a_4\hfill \end{array}\right|=a_1\left|\begin{array}{ccc}\hfill a_2\hfill & \hfill a_4\hfill & \hfill 0\hfill \\ \hfill a_1\hfill & \hfill a_3\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill a_2\hfill & \hfill a_4\hfill \end{array}\right|-a_3\left|\begin{array}{ccc}\hfill a_0\hfill & \hfill a_4\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill a_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill a_2\hfill & \hfill a_4\hfill \end{array}\right|,=a_4(a_1(a_2{a}_3-a_1{a}_4)-a_3^2),=a_4{D}_3>0.$$

Since $D_1$, $D_2$, $D_3$, $D_4$ are all positive, the Routh-Hurwitz criterion [44] for local stability holds. Therefore, the endemic equilibrium is locally asymptotically stable when it exists. □

3.6.1. Global stability of endemic equilibrium

To investigate the global stability of the system, we employ the geometric approach in [45].

Consider a bounded open set $D\subset R^n$ and the map $x\mapsto f(x)$ defined by $f:D\mapsto R^n$, where $f\in C^1(D)$ and x is a vector. Suppose that the solution $x(t)$ for the differential equation

$$x^{\prime }=f(x),$$ (7)

be uniquely determined by the initial condition $x(0,x_0)=x_0$, and denote the solution as $x(t,x_0)$. For any compact set $V\subset D$ and sufficiently large t, if $x(t,V)\subset K$, then K is an absorbing set in D. An open set D is then simply connected if every closed curve in D can be continuously deformed to a point within D. Consider the following assumptions hold for system (7):

• ($H_1$)D is simply connected.
• ($H_2$)there is a compact absorbing set $K\in D$.
• ($H_3$)there is a unique equilibrium $\overline{x}$ for system (7) in D.

Find conditions under which local stability of $\overline{x}$ in D leads to global stability of $\overline{x}$. Let $|.|$ refers to a vector norm in $R^n(n\in \mathbb{N})$ and the matrix norm which it induces matrices of size n. The Lozinskiĭ measure ${\mu }_1(B)$ of size n matrix B with respect to the norm $|.|$ is defined as

$${\mu }_1(B)=\underset{h\to 0^{+}}{\lim }\frac{|I+hB|-1}{h},\text{where}I\text{is a unit matrix of size}n.$$

Suppose the map $P(x):D\mapsto R^r$ is a $C^1$ and non-singular matrix valued function for all $x\in D$, where $r=({}_2^n)\times ({}_2^n)$, and assume the Lozinskiĭ measure with respect to the norm $|.|$ be ${\mu }_1$. Consider K is a compact absorbing set of system (7). Then define the quantity, $\overline{q}$ as

$$\overline{q}=\underset{t\to \infty }{\lim }\sup \underset{x_0\in K}{\sup }\frac{1}{t}\underset{0}{\overset{t}{\int }}{\mu }_1(B(x(s,x_0)))ds,$$ (8)

where $B=P_f{P}^{-1}+P{J}^{[2]}{P}^{-1}$, $P_f$ is derivative of P in the direction of f with $P_f=\frac{dP}{dt}$ and $J=\frac{\partial f}{\partial x}$.

Proposition 3.1

Consider the assumptions$(H_1),(H_2)$and$(H_3)$presented by[45]hold. Thus, the unique endemic equilibrium$\overline{x}$of system(7)is globally stable in D if the quantity$\overline{q}$in Eq.(8)is negative.

To show the existence of a compact set in the interior of Ω (${\mathrm{\Omega }}^{⁎}$), which is absorbing for system (1), is equivalent to proving the uniform persistence of the system (1). That is, there exists a positive number c such that every solution $(S,E,I,R)$ of system (1) with $(S(0),E(0),I(0),R(0))$ in ${\mathrm{\Omega }}^{⁎}$ satisfies

$$\min (\underset{t\to \infty }{\lim }\inf S(t),\underset{t\to \infty }{\lim }\inf E(t),\underset{t\to \infty }{\lim }\inf I(t),\underset{t\to \infty }{\lim }\inf R(t))\ge c.$$

We give the following theorem for a proof.

Theorem 3.5

If$R_0>1$, then system(1)in${\mathrm{\Omega }}^{⁎}$is uniformly persistent. This entails the existence of a constant$0<c<1$(independent of initial conditions), such that any solution$(S(t),E(t),I(t),R(t))$of system(1)satisfies$\lim {\inf }_{t\to +\infty }S(t)>c$,$\lim {\inf }_{t\to +\infty }E(t)>c$,${\lim }_{{\inf }_{t\to +\infty }}I(t)>c$, and$\lim {\inf }_{t\to +\infty }R(t)>c$.

Proof

We utilize methodologies employed by prior researchers [23], [46] to validate this Theorem. Assuming $X=\mathrm{\Omega },X_1={\mathrm{\Omega }}^{⁎},X_2=\partial \mathrm{\Omega }(\text{boundary of}\mathrm{\Omega })$, we can deduce $Y_1=\{(S,0,0,0):0<S\le \frac{\mathrm{\Lambda }}{\mu }\}$, ${\mathrm{\Omega }}_1={\bigcup }_{y\in Y_1}\omega (y)=\left\{E_0\right\}$, where $\left\{E_0\right\}$ represents an isolated compact invariant set in X. By defining $M=\left\{E_0\right\}$, we confirm M as acyclic isolated covering of ${\mathrm{\Omega }}_1$.

To show that $\left\{E_0\right\}$ is a weak repeller for $X_1$, suppose a positive orbit $(S(t),E(t),I(t),R(t))$ of system (1) exists such that

$$\underset{t\to +\infty }{\lim }N(t)=\frac{\mathrm{\Lambda }}{\mu },\underset{t\to +\infty }{\lim }S(t)=\frac{\mathrm{\Lambda }}{\mu },\underset{t\to +\infty }{\lim }E(t)=0,\underset{t\to +\infty }{\lim }I(t)=0,\underset{t\to +\infty }{\lim }R(t)=0.$$

Since $R_0>1$, we select $t_0>0$ sufficiently large such that when $t\ge t_0$, for small ε, system (1) implies $\frac{\mathrm{\Lambda }}{\mu }-\epsilon \le S(t),N(t)\le \frac{\mathrm{\Lambda }}{\mu }+\epsilon$, $0\le E(t)\le \epsilon$, $0\le I(t)\le \epsilon$, $0\le R(t)\le \epsilon$ for $t\ge 0$.

We also obtain the following inequality:

$$\frac{S}{N}\ge \frac{\frac{\mathrm{\Lambda }}{\mu }-\epsilon }{\frac{\mathrm{\Lambda }}{\mu }+\epsilon }.$$ (9)

From the second, third equations of system (1) and Eq. (9), we get

$$\frac{dE}{dt}\ge \frac{\beta (\frac{\mathrm{\Lambda }}{\mu }-\epsilon )I}{\frac{\mathrm{\Lambda }}{\mu }+\epsilon }-(\mu +ϵ)E,\frac{dI}{dt}=ϵE-(\mu +d+\gamma )I.$$ (10)

Following system (10), we consider the matrix $M_{\epsilon }$ defined by

$$M_{\epsilon }=\left(\begin{array}{cc}\hfill -(\mu +ϵ)\hfill & \hfill \frac{\beta (\frac{\mathrm{\Lambda }}{\mu }-\epsilon )}{\frac{\mathrm{\Lambda }}{\mu }+\epsilon }\hfill \\ \hfill ϵ\hfill & \hfill -(\mu +d+\gamma )\hfill \end{array}\right).$$

$M_{\epsilon }$ has a positive off-diagonal element, and the Perron-Frobenius Theorem gives a positive eigenvector $v=(v_1,v_2)$ for the maximum eigenvalue $R_0(\epsilon )$ of $M_{\epsilon }$. Let us consider the following system:

$$\frac{\mathrm{d}{z}_1}{\mathrm{d}t}=-(\mu +ϵ)z_1+\left(\frac{\beta (\frac{\mathrm{\Lambda }}{\mu }-\epsilon )}{\frac{\mathrm{\Lambda }}{\mu }+\epsilon }\right)z_2,\frac{\mathrm{d}{z}_2}{\mathrm{d}t}=ϵz_1-(\mu +d+\gamma )z_2.$$ (11)

Let $z(t)=(z_1(t),z_2(t))$ represent a solution of system (11) passing through $(l{v}_1,l{v}_2)$ at $t=t_0$, where $l>0$ is such that $l{v}_1<I\left(t_0\right),l{v}_2<E\left(t_0\right)$. Given that the semi-flow of system (11) is monotone and $M_{\epsilon }v>0$, we can deduce that $z_1(t)$ and $z_2(t)$ are strictly increasing and $z_1(t)\to +\infty$ and $z_2(t)\to +\infty$ as $t\to +\infty$, which contradicts the eventual boundedness of positive solutions of system (1). Therefore, $E_0$ acts as a weak repeller for $X_1$. This concludes the proof of the Theorem. □

Theorem 3.6

If $R_0>1$ , then the endemic equilibrium $E_1$ is globally asymptotically stable in ${\mathrm{\Omega }}^{⁎}$ provided that

$$\mu >\max \{2\beta ,\beta +ϵ,\beta +\gamma +d,\gamma +d\}.$$ (12)

Proof

Following Theorem 3.5 there is a compact absorbing set K in the interior of D which is absorbing for system (1). The proof of the theorem consists of choosing a suitable vector norm in $R^6$ and a $6\times 6$ matrix valued function $P(x)$ so that Proposition 3.1 is satisfied. The Jacobian matrix J of system (1) is given by:

$$J=\left(\begin{array}{cccc}\hfill -\frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}-\mu \hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill \frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}-(\mu +ϵ)\hfill & \hfill \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill ϵ\hfill & \hfill -(\mu +ϵ)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill -\mu \hfill \end{array}\right).$$

The second additive compound matrix $J^{[2]}$ is given by

$$J^{[2]}=\left(\begin{array}{cccccc}\hfill K_{11}\hfill & \hfill \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill 0\hfill \\ \hfill ϵ\hfill & \hfill K_{22}\hfill & \hfill 0\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill 0\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill \gamma \hfill & \hfill K_{33}\hfill & \hfill 0\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill \frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}\hfill & \hfill 0\hfill & \hfill K_{44}\hfill & \hfill 0\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}\hfill & \hfill \gamma \hfill & \hfill K_{55}\hfill & \hfill \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill ϵ\hfill & \hfill K_{66}\hfill \end{array}\right),$$

where

$$K_{11}=-\frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}-\frac{\beta SI}{{(S+E+I+R)}^2}-(2\mu +ϵ),K_{22}=-\frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}-(2\mu +ϵ),K_{33}=-\frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}-2\mu ,K_{44}=-\frac{\beta SI}{{(S+E+I+R)}^2}-2(\mu +ϵ),K_{55}=-\frac{\beta SI}{{(S+E+I+R)}^2}-(2\mu +ϵ),K_{66}=-(2\mu +ϵ).$$

Let

$$P=P(S,E,I,R)=\left(\begin{array}{cccccc}\hfill \frac{a_1}{E}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{a_1}{E}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a_1}{E}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a_2}{I}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a_2}{I}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a_2}{I}\hfill \end{array}\right),$$

where $a_1$ and $a_2$ are two undetermined positive constants, then $P_f{P}^{-1}=\mathrm{diag}(-\frac{\dot{E}}{E},-\frac{\dot{E}}{E},-\frac{\dot{E}}{E},-\frac{\dot{I}}{I},-\frac{\dot{I}}{I},-\frac{\dot{I}}{I})$. Let

$\mathrm{B}(S,E,I,R)=P_f{P}^{-1}+P{J}^{[2]}{P}^{-1}$,

$$=\left(\begin{array}{cccccc}\hfill K_{11}-\frac{\dot{E}}{E}\hfill & \hfill \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill 0\hfill \\ \hfill ϵ\hfill & \hfill K_{22}-\frac{\dot{E}}{E}\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{a_{1}I}{a_{2}E}\frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill \frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}\hfill & \hfill K_{44}-\frac{\dot{E}}{E}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a_{1}I}{a_{2}E}\frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill \frac{a_{2}E\gamma }{a_{1}I}\hfill & \hfill 0\hfill & \hfill K_{33}-\frac{\dot{I}}{I}\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill & \hfill -\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a_{2}E\gamma }{a_{1}I}\hfill & \hfill \frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}\hfill & \hfill K_{55}-\frac{\dot{I}}{I}\hfill & \hfill \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill ϵ\hfill & \hfill K_{66}-\frac{\dot{I}}{I}\hfill \end{array}\right).$$

The matrix $B(S,E,I,R)$ and be written in block matrix form:

$B(S,E,I,R)=\left(\begin{array}{cccc}{B}_{11}\hfill & B_{12}\hfill & B_{13}\hfill & B_{14}\hfill \\ B_{21}\hfill & B_{22}\hfill & B_{23}\hfill & B_{24}\hfill \\ B_{31}\hfill & B_{32}\hfill & B_{33}\hfill & B_{34}\hfill \\ B_{41}\hfill & B_{42}\hfill & B_{43}\hfill & B_{44}\hfill \end{array}\right)$, where

$$B_{11}=K_{11}-\frac{\dot{E}}{E},B_{12}=(\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2},-\frac{\beta SI}{{(S+E+I+R)}^2}),B_{14}=0,B_{13}=(\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2},-\frac{\beta SI}{{(S+E+I+R)}^2}),B_{21}={(ϵ,0)}^t,B_{22}=\left(\begin{array}{cc}\hfill K_{22}-\frac{\dot{E}}{E}\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill \frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}\hfill & \hfill K_{44}-\frac{\dot{E}}{E}\hfill \end{array}\right),B_{23}=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right),B_{24}={(-\frac{\beta SI}{{(S+E+I+R)}^2},-\frac{\beta SI}{{(S+E+I+R)}^2})}^t,B_{31}={(0,0)}^t,B_{32}=\left(\begin{array}{cc}\hfill \frac{a_{2}E\gamma }{a_{1}I}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{a_{2}E\gamma }{a_{1}I}\hfill \end{array}\right),$$

$$B_{33}=\left(\begin{array}{cc}\hfill K_{33}-\frac{\dot{I}}{I}\hfill & \hfill \frac{\beta SI}{{(S+E+I+R)}^2}\hfill \\ \hfill \frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}\hfill & \hfill K_{55}-\frac{\dot{I}}{I}\hfill \end{array}\right),B_{34}={(-\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2},\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2})}^t,B_{41}=0,B_{42}=(0,0),B_{43}=(0,ϵ),B_{44}=K_{66}-\frac{\dot{I}}{I}.$$

Let $\mathbf{v}=(v_1,v_2,v_3,v_4,v_5,v_6)$ be a vector in $R^6\cong R^{\left({}_2^4\right)}$. We then select a norm in $R^6$ as $\left|(v_1,v_2,v_3,v_4,v_5,v_6)\right|=\max \{\left|v_1\right|,\left|v_2\right|+\left|v_3\right|,\left|v_4\right|+\left|v_5\right|,\left|v_6\right|\}$ and let ${\mu }_1(B)$ be the Lozinskii measure of B with respect to the induced matrix norm $|\cdot |$ in $R^6$, defined by ${\mu }_1(B)={\lim }_{h\to 0^{+}}\frac{|I+hB|-1}{h}$.

Following the estimation approach as in [47], we then have

${\mu }_1(B)\le \sup \{h_1,h_2,h_3,h_4\}$, where

$h_1={\mu }_1(B_{11})+|B_{12}|+|B_{13}|+|B_{14}|,h_2={\mu }_1(B_{22})+|B_{21}|+|B_{23}|+|B_{24}|$,

$h_3={\mu }_1(B_{33})+|B_{31}|+|B_{32}|+|B_{34}|,h_4={\mu }_1(B_{4}4)+|B_{4}1|+|B_{42}|+|B_{43}|$.

$\left|B_{ij}\right|(i\ne j,i,j=1,2,3,4)$ are matrix norms with respect to the $l_1$ vector norm. We compute $h_i$ as follows:

$${\mu }_1(B_{11})=-\frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}-\frac{\beta SI}{{(S+E+I+R)}^2}-(2\mu +ϵ)-\frac{\dot{E}}{E},|B_{12}|=B_{13}=\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2},B_{14}=0.\text{Then},h_1=-\frac{\beta I(E+I+R)}{{(S+E+I+R)}^2}-\frac{\beta SI}{{(S+E+I+R)}^2}-(2\mu +ϵ)-\frac{\dot{E}}{E}+2\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}.$$

Furthermore, from the second and third equations of system (1), we have

$$\frac{\dot{E}}{E}=\frac{\beta SI}{E(S+E+I+R)}-(\mu +ϵ)\text{and}\frac{\dot{I}}{I}=\frac{ϵE}{I}-(\mu +\gamma +d).$$

Choosing $a_1=-a_2$, then we have

$$h_1\le 2\frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}-\mu \le 2\beta -\mu ,h_2\le \frac{\beta SI}{{(S+E+I+R)}^2}+ϵ-\mu \le \beta +ϵ-\mu ,h_3\le \frac{\beta S(S+E+R)}{{(S+E+I+R)}^2}+\gamma +d-\mu \le \beta +\gamma +d-\mu ,h_4\le \gamma +d-\mu .$$

The estimate ${\mu }_1(B)$ can be written as

$${\mu }_1(B)\le \sup \{h_1,h_2,h_3,h_4\}=-\text{min}\{-h_1,-h_2,-h_3,-h_4\}.\text{Let}h=\min \{\mu -2\beta ,\mu -(\beta +ϵ),\mu -(\beta +\gamma +d),\mu -(\gamma +d)\}.$$

Following condition (12), $h>0$, and then $-h<0$. As a result,

${\mu }_1(B)\le \sup \{h_1,h_2,h_3,h_4\}<-h$. It follows that ${\mu }_1(B)={\mu }_1(P_f{P}^{-1}+P_f{J}^{[2]}{P}^{-1})\le -h<0$.

Along each solution $(S,E,I,R)$ of system (1) with initial value $(S_0,E_0,I_0,R_0)\in K$ when $t>T$, we have

$$\frac{1}{t}\underset{0}{\overset{t}{\int }}{h}_{i}ds\le -h<0,i=1,2,3,4.$$

Averaging along each solution as $t\to \infty$, we get

$$\overline{q}=\underset{t\to \infty }{\lim }\sup \underset{x_0\in K}{\sup }\frac{1}{t}\underset{0}{\overset{t}{\int }}{\mu }_1(B(x(s,x_0)))ds\le -h<0.$$

 □

4. Bifurcation analysis

Theorem 4.1

The system (1) exhibits a forward bifurcation at $R_0=1$ .

Proof

Setting $x_1=S$, $x_2=E$, $x_3=I$, and $x_4=R$ we write system (1) as follows

$$\frac{d{x}_1}{dt}=\mathrm{\Lambda }-(\frac{\beta x_3}{x_1+x_2+x_3+x_4}+\mu )x_1:=f_1,\frac{d{x}_2}{dt}=\frac{\beta x_3{x}_1}{x_1+x_2+x_3+x_4}-(\mu +ϵ)x_2:=f_2,\frac{d{x}_3}{dt}=ϵx_2-(\mu +d+\gamma )x_3:=f_3,\frac{d{x}_4}{dt}=\gamma x_3-\mu x_4:=f_4.$$ (13)

Fix $R_0=1$ and let

$${\beta }^{⁎}:=\frac{(\mu +ϵ)(\mu +d+\gamma )}{ϵ}$$

be the bifurcation parameter. Jacobian of the linearized system (13) around the disease-free equilibrium $E_0$ when $\beta ={\beta }^{⁎}$ is

$$J(E_0)=\left(\begin{array}{cccc}\hfill -\mu \hfill & \hfill 0\hfill & \hfill -{\beta }^{⁎}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -(\mu +ϵ)\hfill & \hfill {\beta }^{⁎}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill ϵ\hfill & \hfill -(\mu +d+\gamma )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill -\mu \hfill \end{array}\right).$$

The eigenvalues of the characteristic polynomial are ${\lambda }_1={\lambda }_2=-\mu$, ${\lambda }_3=-(2\mu +d+\gamma +ϵ)$, and ${\lambda }_4=0$. We can observe that the three eigenvalues are real and negative, and one is 0 and simple.

To study the bifurcation analysis, we denote the right eigenvector corresponding to the zero eigenvalue ${\lambda }_4=0$ by w=${(w_1,w_2,w_3,w_4)}^T$. Computing $J(E_0)\mathbf{w}=\mathbf{0}\mathbf{w}$ gives

$$\begin{array}{c}\left(\begin{array}{cccc}\hfill -\mu \hfill & \hfill 0\hfill & \hfill -{\beta }^{⁎}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -(\mu +ϵ)\hfill & \hfill {\beta }^{⁎}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill ϵ\hfill & \hfill -(\mu +d+\gamma )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill -\mu \hfill \end{array}\right)\left(\begin{array}{c}\hfill w_1\hfill \\ \hfill w_2\hfill \\ \hfill w_3\hfill \\ \hfill w_4\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)\hfill \end{array}.$$

Direct calculation gives the right eigenvector

$$\mathbf{\text{w}}={(-\frac{\gamma (\mu +d+\gamma )}{ϵ\mu },\frac{\mu (\mu +d+\gamma )}{ϵ},\mu ,\gamma )}^T.$$

Next, we compute the left eigenvector v=$(v_1,v_2,v_3,v_4)$ associated with ${\lambda }_4=0$ by computing $\mathbf{v}J(E_0)=\mathbf{0}$ which is

$$\begin{array}{c}(v_1,v_2,v_3,v_4)\left(\begin{array}{cccc}\hfill -\mu \hfill & \hfill 0\hfill & \hfill -{\beta }^{⁎}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -(\mu +ϵ)\hfill & \hfill {\beta }^{⁎}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill ϵ\hfill & \hfill -(\mu +d+\gamma )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill -\mu \hfill \end{array}\right)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)\hfill \end{array}.$$

It follows that

$$\{\begin{array}{c}-\mu v_1=0,\hfill \\ -(\mu +ϵ)v_2+ϵv_3=0,\hfill \\ -{\beta }^{⁎}{v}_1+{\beta }^{⁎}{v}_2-(\mu +d+\gamma )v_3+\gamma v_4=0,\hfill \\ -\mu v_4=0.\hfill \end{array}$$

From the first and fourth equations, we have that $v_1=v_4=0$. Since v.w=1 one solution of the left eigenvector is $\mathbf{\text{v}}={(0,ϵ,\mu +ϵ,0)}^T$ by taking the expression of ${\beta }^{⁎}$ into account.

Based on theoretical results in [48], we have to compute the bifurcation coefficients a and b given by

$$\mathbf{\text{a}}=\sum _{k,i,j=1}^4{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k}{\partial x_i\partial x_j}(E_0,{\beta }^{⁎}),\mathbf{\text{b}}=\sum _{k,i=1}^4{v}_k{w}_i\frac{{\partial }^2{f}_k}{\partial x_i\partial \beta }(E_0,{\beta }^{⁎}).$$

Since the first and fourth components of v are zero, we do not need the derivatives of $f_1$ and $f_4$. From the derivatives of $f_2$ and $f_3$, the only nonzero values are:

$$\frac{{\partial }^2{f}_2}{\partial x_3^2}(E_0,{\beta }^{⁎})=-\frac{2\mu (\mu +ϵ)(\mu +d+\gamma )}{\mathrm{\Lambda }ϵ}\mathrm{\text{and}}\frac{{\partial }^2{f}_2}{\partial x_3\partial \beta }(E_0,{\beta }^{⁎})=1.$$

Which directly follows that,

$$\mathbf{\text{a}}=v_2{w}_3^2\frac{{\partial }^2{f}_2}{\partial x_3^2}(E_0,{\beta }^{⁎})=-\frac{2{\mu }^3(\mu +ϵ)(\mu +d+\gamma )}{\mathrm{\Lambda }},\mathbf{\text{b}}=v_2{w}_3\frac{{\partial }^2{f}_2}{\partial x_3\partial \beta }(E_0,{\beta }^{⁎})=\mu ϵ.$$

It is clear that $\mathbf{\text{a}}<0$ and $\mathbf{\text{b}}>0$ for all positive parameter values. Thus, the system (1) exhibits forward bifurcation at $R_0=1$. □

5. Model calibration with vaccination

Recently, great progress has been made towards measles elimination through constant vaccination against measles globally. Therefore, for any mathematical model regarding the measles epidemic to be realistic, it must include vaccination. In this section, we additionally assume that a fraction of the individuals recruited due to birth or immigration are vaccinated at a rate of θ and hence go to the recovered class. Vaccination and natural recovery from measles provide the same level of protection. The proportion of those vaccinated is represented by $\theta (0\le \theta \le 1)$ where $\theta =0$ represents vaccination is not applied and $\theta =1$ indicates all individuals recruited due to birth or immigration are vaccinated. The evolution of the system with the incorporation of vaccination is governed by the following nonlinear ordinary differential equations:

$$\frac{dS}{dt}=\mathrm{\Lambda }(1-\theta )-(\frac{\beta I}{S+E+I+R}+\mu )S,\frac{dE}{dt}=\frac{\beta IS}{S+E+I+R}-(\mu +ϵ)E,\frac{dI}{dt}=ϵE-(\mu +d+\gamma )I,\frac{dR}{dt}=\theta \mathrm{\Lambda }+\gamma I-\mu R.$$ (14)

The reproduction number of system (14) with the implementation of vaccination is given as

$$R_{0v}=\frac{\beta ϵ(1-\theta )}{(\mu +ϵ)(\mu +d+\gamma )}=(1-\theta )R_0.$$ (15)

It can be easily observed that $R_{0v}\le R_0$ and the equality holds when $\theta =0$. This shows that the vaccine will minimize the $R_0$. For measles eradication, we have obtained that $R_0\le 1$ (Theorem 3.3) and it follows from Eq. (15) that the critical vaccination for measles eradication is $\theta \ge 1-\frac{1}{R_0}={\theta }_c$.

5.1. Data

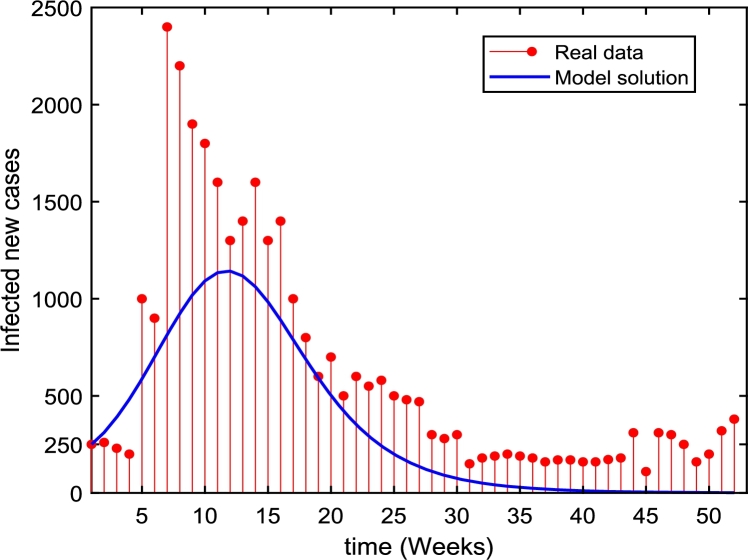
Ethiopia is one of the countries with a high measles mortality burden [31]. Measles is reported weekly by the Ministry of Health. According to the Ethiopian Weekly Epidemiological Bulletin [49] report, the national surveillance data summary of measles disease in 2015 is presented in Table 2, and graphically illustrated in Fig. 1. The real data points are represented by the red dot histogram.

Table 2.

Reported weekly measles cases in Ethiopia, 2015 [49].

Weeks	Infected	Weeks	Infected	Weeks	Infected	Weeks	Infected	Weeks	Infected
1	250	12	1300	23	550	33	190	43	180
2	260	13	1400	24	580	34	200	44	310
3	230	14	1600	25	500	35	190	45	110
4	200	15	1300	26	480	36	180	46	310
5	1000	16	1400	27	470	37	160	47	300
6	900	17	1000	28	300	38	170	48	250
7	2400	18	800	29	280	39	170	49	160
8	2200	19	600	30	300	40	160	50	200
9	1900	20	700	31	150	41	160	51	320
10	1800	21	500	32	180	42	172	52	380
11	1600	22	600

Figure 1.

Simulation of the model solution compared to the real data using the initial parameter and state values. Observed real data points are represented by the red dot histogram, and the best-fitting solution curve for the system model is shown by the blue curve.

5.2. Nominal parameters

In order to simulate the proposed measles model in the context of Ethiopian data, it is necessary to set all the parameter values. Some of the parameter values are obtained from national census databases. Among these are the natural birth and death rates and the total population. The natural mortality rate for Ethiopia is $\mu =1/(64\times 52){[weeks]}^{-1}$ [50]. Some others, such as the parameter rate of progress from exposed to infectious class (ϵ) and recovery rate (γ) are also found in measles infected patients' clinical studies. Considering the assumption that the latent period for measles ends in $6-9$ days and the infectious period as 5 days [51] we choose $ϵ=7.5/7{[weeks]}^{-1}$ and $\gamma =5/7{[weeks]}^{-1}$.

5.3. Forward problem

The system (14) can be given in vector form as:

$$\frac{d\mathbf{x}(t)}{dt}=\mathbf{f}(\mathbf{x}(t),\mathbf{p}),\mathbf{x}(t_0)={\mathbf{x}}_0,$$ (16)

where $\mathbf{x}(t)=(S,E,I,R)\in {\mathbb{R}}^4$ represents the state variables and ${\mathbf{x}}_0=(S(0),E(0),I(0),R(0))\in {\mathbb{R}}^4$ is the initial condition at the initial time $t_0$, the vector $\mathbf{p}=(p_1,p_2,p_3,p_4,p_5,p_6)=(\mathrm{\Lambda },\beta ,\mu ,ϵ,\gamma ,d)\in {\mathbb{R}}^6$ represents the model parameters and $\mathbf{f}:\mathbf{U}\subset {\mathbb{R}}^4\times {\mathbb{R}}^6\to {\mathbb{R}}^4$ is a nonlinear map representing the evolution law of the system defined on the open set:

$$\mathbf{U}=\{(\mathbf{x}(t),\mathbf{p})\in {\mathbb{R}}^4\times {\mathbb{R}}^6|x_i>0,fori=1,\dots ,4and{p}_i>0,fori=1,\dots ,6\}.$$ (17)

The solution to the forward problem in system (16) is obtained by numerical integration using a Runge-Kutta fourth and fifth orders (ode45) method. To simulate the forward problem, we assume the initial set of parameters as ${\mathbf{\text{p}}}_0=(500,2.59605,1/(64\times 52),7.5/7,5/7,0.168)$. Initially infected humans are assumed to be the number of confirmed measles cases in Ethiopia in 2015, which is $I(0)=250$ individuals. The exposed and infected groups are also equal, $E(0)=I(0)$. Moreover, initially recovered individuals are assumed to have $R(0)=1800$. The susceptible population is also assumed to be $S(0)=21000$. Accordingly, the initial state variables at the initial time $t_0$ are given as ${\mathbf{x}}_0=(21000,250,250,1800)$. It is also assumed that the proportion of vaccinated in 2015 was $\theta =0.65$.

Following the above initial assumptions, Fig. 1 depicts the $SEIR$ model solution compared with the real data reported weekly. Apart from the numerical variation between the model solution and the real data, there is agreement in the pattern of the model simulation and the real data. This characteristic pattern agreement and numerical disparity propose that the model solution may vary from the real data due to the use of improper initial parameter values or improper initial state variables in the numerical simulation. Therefore, it is important that model calibration be done to fit the model solution to the observed real data. Model calibration is a numerical simulation for the search of parameter values that make the model simulation fit well with the real data. It is discussed in the following subsection.

5.4. Inverse problem

In most cases, it is impractical the forward problem to reproduce the real data. This could be due to an error in data collection or registration or an error in model formulation caused by the wrong model assumptions. Therefore, model calibration consists of seeking a suitable set of parameters that, to a certain degree, makes the model solution as close as to the real data.

For the model calibration, the system contains $\mathit{p}=(p_1,p_2,p_3,p_4,p_5,p_6)$ unknown parameters to be estimated based on real data. For the purpose of comparison between the real data observations and model solutions, a discrete time set with $N=52$ weeks presented in Fig. 1 is used. The N time discrete real data points are represented by $\mathbf{\text{Z}}=(z_1,z_2,...,z_N)$ and the time discrete model solution $\mathit{y}(t_k)=(y_1,y_2,\dots ,y_N)$ is generated for the 4 outputs $y_1,y_2,y_3,y_4$ corresponding to N data points.

$$\begin{gathered} \mathit{y}(t_k)={[y_1(t_k),y_2(t_k),y_3(t_k),y_4(t_k)]}^{T}and \\ \mathit{y}={[y_1(t_1),\dots ,y_1(t_N),\dots ,y_4(t_1),\cdots ,y_4(t_N)]}^T(length4\cdot N). \end{gathered}$$

The model error (or the residual error) ${\mathit{e}}_k$ in (18) which is the difference between a column vector model solution y and a column vector real data points z is weighted in a quadratic criterion ${\mathit{J}}_N$ as:

$${\mathit{e}}_k=\mathit{z}(t_k)-\hat{\mathit{y}}(t_k,\hat{\mathit{p}}),k=1,\dots ,N,$$ (18)

$${\mathit{J}}_N=||\mathit{z}-\mathit{y}|{|}^2=\sum _{i=1}^M{\mathit{e}}_k^T\mathit{W}{\mathit{e}}_k.$$ (19)

In formal terms, given a real data observation vector z and a model solution vector y, the calibration aims at finding a vector of parameters $\stackrel{\mathbf{ˆ}}{\mathit{p}}$ such that

$$\stackrel{\mathbf{ˆ}}{\mathit{p}}=arg\underset{\stackrel{\mathbf{ˆ}}{\mathit{p}}\ge \mathbf{\text{0}}}{\min }{\mathit{J}}_N(\stackrel{\mathbf{ˆ}}{\mathit{p}}),$$ (20)

for a function Eq. (19). Here, $\stackrel{\mathbf{ˆ}}{\mathit{p}}$ in Eq. (20) is the optimal estimated parameter, and $\hat{\mathit{y}}$ is the model solution corresponding to the optimal $\stackrel{\mathbf{ˆ}}{\mathit{p}}$ value. W is a $4\cdot N\times 4\cdot N$ positive definite symmetric weighting matrix to be solved using the weighted least squares algorithm. For the optimal estimated parameter values, the functional ${\mathit{J}}_N$ reaches a minimum value [52].

For the implementation of the calibration, we used the least squares method using the Trust-Region

-Reflective method algorithm lsqnonlin from MATLAB's optimization toolbox. The parameters are estimated with lower and upper bounds. Global minimum convergence is not guaranteed in this case. However, to find the best optimal parameter estimates with the minimum functional value, the algorithm starts with different initial parameters and state values. The estimated parameter values are presented in Table 3 and the estimated basic reproduction number of measles for Ethiopia in the year 2015 is found to be $R_0=1.3973$.

Table 3.

Estimated parameter values for the proposed model.

Parameter	Lower bound	Upper bound	Reference	Estimated value(CI)
Λ	0	10000	Assumed	0.9289613942(-0.1423810 2.0003038) ×104
β	0	100	Assumed	0.0007107243(-0.0002338  0.0016552) ×104
μ	1/(70 × 52)	1/(60 × 52)	[50]	0.0000000275(-0.0000086 0.0000087) ×104
ϵ	6/7	9/7	[4], [51]	0.0001024338(-0.0000335 0.0002384) ×104
γ	6/7	1	[4], [51]	0.0001000000(-0.0009732 0.0011732) ×104
d	0	1	Assumed	0.0000779494(-0.0009738  0.0011297 ) ×104

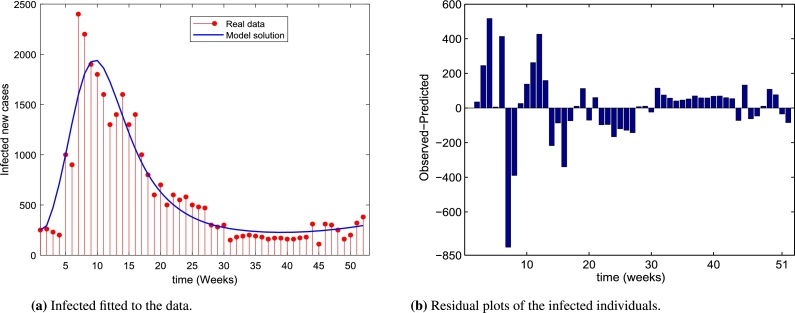
Fig. 2a depicts the proposed system model fitted to real data. We found that there are only a very few points that are poorly fitted with the model solution as compared. The fit of a system model to real data is also measured by its residuals, which are defined as the difference between the real data and the value predicted by the model. Following a similar approach [12], we computed the root mean squared error (RMSE) $1.413501277877855\times {10}^3$. The residual plots seem to be random, proving that the model is well calibrated (Fig. 2b). Moreover, we plotted the fitted model with a 95% confidence interval (CI), as can be seen in Fig. 3. The plot of the CI helps visualize the uncertainty in the estimated parameter values. In particular, the model is plotted using the estimated parameter values, and the 95% CIs are shown as error shaded areas around the fitted model. The confidence interval also helps to measure the model's performance. By examining the CIs over time, one can understand the stability and accuracy of the model's predictions. That is, if the CIs remain narrow and consistent, it suggests the model is performing well in capturing the underling dynamics of the epidemic. On the other hand, if the CIs widen or become inconsistent, it may indicate limitations or uncertainty in the model assumptions or data. The CIs remain narrow and consistent, as depicted in Fig. 3. Thus, it is evidence that the model fits well.

Figure 2.

The SEIR system fitted with the weekly reported real data. Observed real data points are represented by the red dot histogram, and the best-fitting solution curve for the system model is shown by the blue curve.

Figure 3.

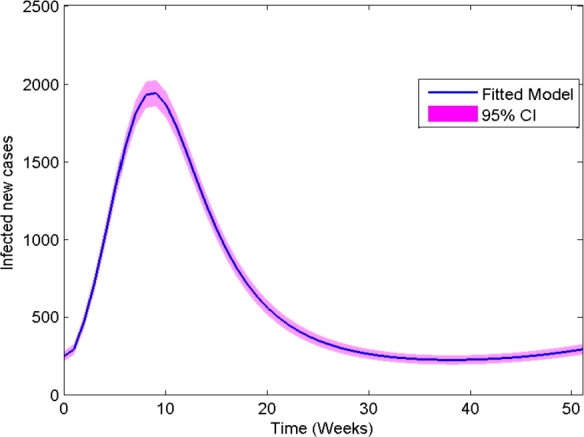
Infected new cases fitted to real data with 95% confidence interval.

5.5. Local sensitivity analysis

Studying the sensitivity of the basic reproduction number as model parameters change is important in system dynamics. It is used to determine the robustness of system predictions for parameter values. A highly sensitive parameter should be carefully estimated because a small variation in that parameter could lead to large quantitative changes. A less sensitive parameter does not require as much effort to estimate, since a small change in that parameter will not result in a big influence on the disease dynamics.

Definition 5.1

The normalized forward local sensitivity index of the basic reproduction number $R_{0v}$ that depends differentiably on a parameter ω is defined by

$${\mathrm{\Pi }}_{\omega }^{R_{0v}}=\frac{\partial R_{0v}}{\partial \omega }\frac{\omega }{|R_{0v}|}.$$ (21)

Notice that ${\mathrm{\Pi }}_{\omega }^{R_{0v}}$ has a maximum value of magnitude 1. ${\mathrm{\Pi }}_{\omega }^{R_{0v}}=1$ implies an increase (decrease) of ω by y% increases (decreases) $R_{0v}$ by y%. On the other hand, ${\mathrm{\Pi }}_{\omega }^{R_{0v}}=-1$ indicates an increase (decrease) of ω by y% decreases (increases) $R_{0v}$ by y%. Following Eq. (21), the normalized forward local sensitivity index of $R_{0v}$ with respect to $\beta ,\mu ,ϵ,\gamma ,d,\theta$ is given by

$${\mathrm{\Pi }}_{\beta }^{R_{0v}}=1,{\mathrm{\Pi }}_{\mu }^{R_{0v}}=-\frac{\mu (2\mu +ϵ+\gamma +d)}{(\mu +ϵ)(\mu +\gamma +d)},{\mathrm{\Pi }}_{ϵ}^{R_{0v}}=\frac{\mu }{\mu +ϵ},{\mathrm{\Pi }}_{\gamma }^{R_{0v}}=-\frac{\gamma }{\mu +\gamma +d},{\mathrm{\Pi }}_d^{R_{0v}}=-\frac{d}{\mu +\gamma +d},{\mathrm{\Pi }}_{\theta }^{R_{0v}}=-\frac{\theta }{1-\theta }.$$

It can be easily observed from Table 4 that the local sensitivity indices of the parameters β and ϵ are positive and the remaining are negative. Positive sensitivity indices have a positive effect on the increase of the basic reproduction number, and negative sensitivity indices have a reverse effect on the basic reproduction number. The effective contact rate of measles β and the rate of vaccination θ are the most sensitive parameters and significantly impact the disease dynamics. More importantly, decreasing the effective contact rate of measles β and increasing the vaccination rate θ decrease the basic reproduction number. On the other hand, the natural death rate of humans and the rate of progress from the exposed to the infectious class are less sensitive to the basic reproduction number.

Table 4.

Numerical value of the local sensitivity indices.

Parameters	Local sensitivity indices
β	${\mathrm{\Pi }}_{\beta }^{R_{0v}}=1$
μ	${\mathrm{\Pi }}_{\mu }^{R_{0v}}=-4.224877\times {10}^{-4}$
ϵ	${\mathrm{\Pi }}_{ϵ}^{R_{0v}}=2.681276111938502\times {10}^{-4}$
γ	${\mathrm{\Pi }}_{\gamma }^{R_{0v}}=-0.561870756205265$
d	${\mathrm{\Pi }}_d^{R_{0v}}=-0.437974883669988$
θ	${\mathrm{\Pi }}_{\theta }^{R_{0v}}=-1.857143$

6. Numerical simulations

6.1. The system without vaccination

In this subsection, numerical simulations of the forward bifurcation of the system (1) and the mesh and contour plots for the basic reproduction number are discussed.

6.1.1. Forward bifurcation

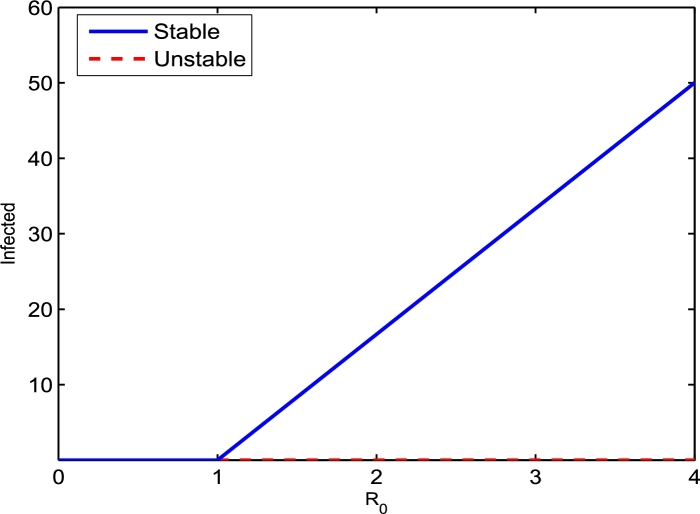
It is shown in Eq. (6) that the disease dies out if $R_0\le 1$ and is endemic if $R_0>1$ for $\beta >d$. These results further prove that the model exhibits forward bifurcation. The global stability of the disease free and endemic equilibria for $R_0\le 1$ and $R_0>1$ is also depicted graphically in Fig. 4. The dots colored red show that the disease free equilibrium is unstable if the reproduction number is greater than unity. On the other hand, the line segment colored blue shows that the disease free equilibrium is globally asymptotically stable if $R_0\le 1$ and the endemic equilibrium is globally stable if $R_0>1$. $R_0=1$ is the threshold value.

Figure 4.

The forward bifurcation graph for infected versus R₀ using the parameters Λ = 100, β = 6, μ = 0.00045662, ϵ = 0.01, d = 0.0015 and γ varies between 0.01 and 20, i.e., γ = 0.01:0.02:20.

6.1.2. Mesh and contour plots

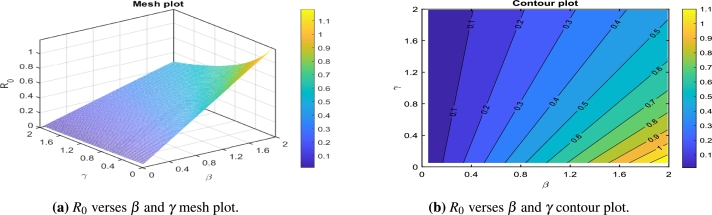
We draw the mesh and contour plots for the basic reproduction number dependence on the effective transmission rate β and the natural recovery rate γ. The mesh and contour plots show that the basic reproduction number increases significantly for higher values of β and lower values of γ (Figs. 5a and 5b). This result shows a good agreement with the local sensitivity indices depicted in Table 4. Thus, to control $R_0$, policymakers are recommended to work on reducing β and increasing γ. The variation of the basic reproduction number as well as the parameters effective transmission rate β and natural recovery rate γ are depicted in Fig. 5.

Figure 5.

Combined effects of the transmission rate β and the recovery rate γ on the basic reproduction number for the measles model. The parameters both vary in the interval β = 0.05:.02:2 and γ = 0.05:.02:2. The remaining parameters are given in Table 3.

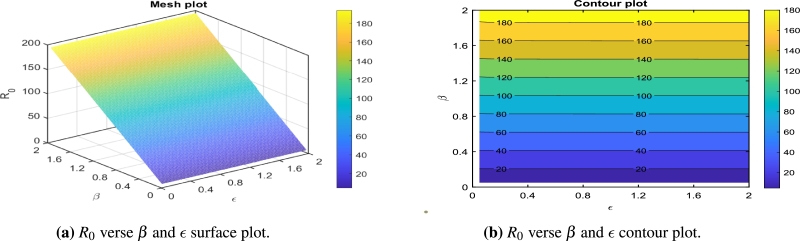
We also draw the mesh and contour plots for the basic reproduction number dependence on the effective transmission rate β and the rate of progression to the infectious class ϵ. The mesh and contour plots show that the basic reproduction number increases significantly for higher values of β, but ϵ has no significant value (Figs. 6a and 6b). In this case, to control $R_0$, policymakers are recommended to work on reducing β. The variation of the basic reproduction number as the parameters effective transmission rate β and the rate of progression to the infectious ϵ covary are depicted in Fig. 6.

Figure 6.

Combined effects of the effective transmission rate β and the rate of progression to the infectious class ϵ on the basic reproduction number for the measles model. The parameters β and ϵ vary in the interval β = 0.05:.01:2 and ϵ = 0.05:.01:2. The remaining parameters are given in Table 3.

6.2. The system with vaccination

In this subsection, numerical simulations of the proposed system (14) are done. We also validate the importance of the threshold parameter $R_0$ to show disease elimination and endemic cases. The simulations are done using the built-in MATLAB function ode45.

6.2.1. The disease extinction case

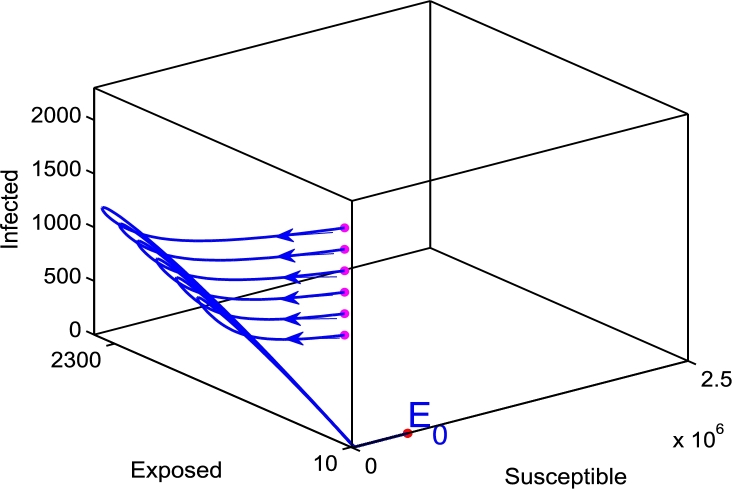
The measles disease extinction (Fig. 7). The starting points where the solution trajectories start are colored magenta, and the end point of the solution trajectories is colored red. The direction of the solution trajectories is shown by a forward arrow. In this case, the disease-free equilibrium $E_0=$(1690709,0,0,32123479) is globally stable. All solution values tend to move to the disease-free equilibrium, whatever the initial value is. The disease-free equilibrium is the plane containing the susceptible and recovered classes. From this graphical result, it could be concluded that the disease dies out in the community. The calculated value of the reproduction number is $R_0=0.1996$.

Figure 7.

Solution trajectories for the disease-free equilibrium. In this case, the assumed initial state value is (S(0),E(0),R(0))=(21000,250,18000) while varying the initial infected individuals between 1000 and 2000 with step size 200, the rate of vaccination is also assumed to be θ = 0.95, and the estimated parameter values are Λ = 9.289613942105396 × 10³, β = 0.007107 × 10³, ϵ = 0.001024 × 10³, μ = 0.0000002747 × 10³, γ = 1,  d = 0.0007795 × 10³.

6.2.2. The disease endemic case

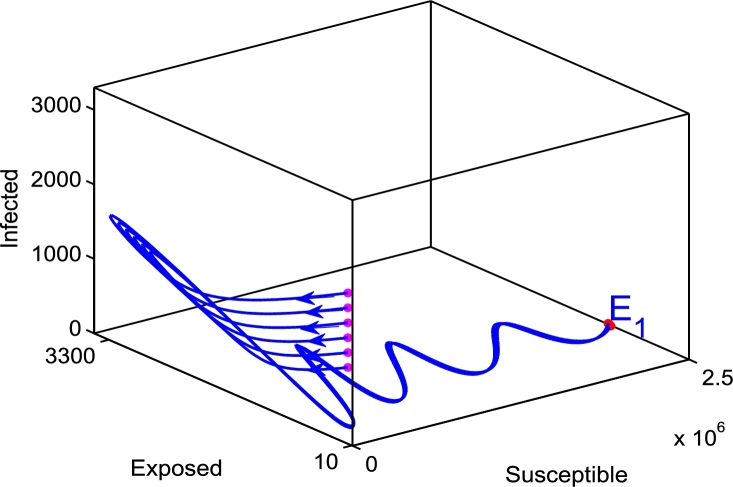
The measles disease endemic case (Fig. 8). The starting points where the solution trajectories start are colored magenta, and the end point of the solution trajectories is colored red. The direction of the solution trajectories is shown by a forward arrow. In this case, the endemic equilibrium $E^{⁎}=$(2250705,642,324,5601600) is globally stable. All solution values tend to move toward endemic equilibrium. From this graphical result, it could be concluded that the disease is endemic. The calculated value of the reproduction number is $R_0=1.3973$.

Figure 8.

Solution trajectories for the endemic equilibrium. In this case, the assumed initial state value is (S(0),E(0),R(0))=(21000,250,18000) while varying the initial infected individuals between 1000 and 2000 with step size 200, the rate of vaccination is assumed to be θ = 0.65, and the estimated parameter values are Λ = 9.289613942105396 × 10³, β = 0.007107 × 10³, ϵ = 0.001024 × 10³, μ = 0.0000002747 × 10³, γ = 1,  d = 0.0007795 × 10³.

6.2.3. The effects of vaccination and transmission rates

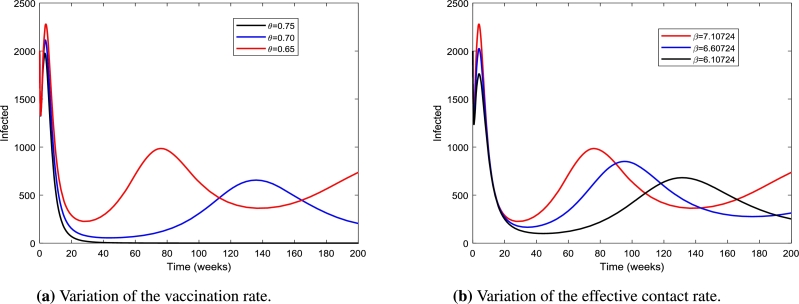
The effects of vaccination and transmission rates are discussed here. It is important to identify which one would be the most valid parameter for controlling disease spread since both are the most sensitive parameters. Fig. 9 shows the time series of the infected when the most sensitive parameters are changed. As the rate of vaccination increases from 0.65 to 0.75, it can be observed that the disease can be eradicated from the community (Fig. 9a). Compared to the impact of the vaccination rate, lowering the effective contact rate from 7.10724 to 6.10724 does not have a significant impact on the eradication of the disease (Fig. 9b). The epidemiological implication of this is that vaccination of the susceptible population is the best means for controlling the disease.

Figure 9.

Time series of the infected population by varying the vaccination and effective contact rates.

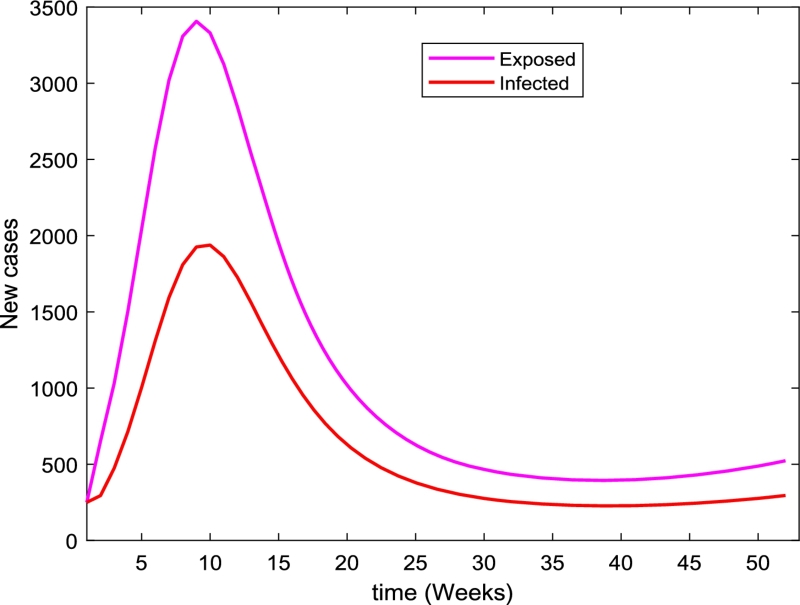
It is also worth noting that the $SEIR$ model assumption is not like the SIR in which it cannot be concluded that the disease dies out if the number of infected individuals is minimized. The time series of the exposed and infected individuals presented in Fig. 10 can prove this hypothesis. It can be observed that the number of individuals in the exposed class is enormous as compared to the infected ones. The exposed population rapidly grows and achieves its peak value of 3417 at the end of 9 weeks, whereas the infected population grows and reaches its peak value of 1938 at the end of 10 weeks. For the remaining periods, however, the number of both exposed and infected people decreased. Even though the infected individuals seem to decrease, which may ultimately cause the disease to die out, the disease may remain endemic due to the transfer of the exposed individuals to the infected class.

Figure 10.

The time series of the exposed and infected people. In this case the assumed initial state value is (S(0),E(0),I(0),R(0))=(21000,250,250,18000). The rate of vaccination is assumed to be θ = 0.65 and the estimated parameters values are Λ = 9.289613942105396 × 10³, β = 0.007107 × 10³, ϵ = 0.001024 × 10³, μ = 0.0000002747 × 10³, γ = 1,  d = 0.0007795 × 10³.

7. Discussions and conclusion

A deterministic $SEIR$ model to describe the dynamics of the measles outbreak in Ethiopia is analyzed and calibrated using weekly real data. The long-term dynamics of the system are analyzed. It is shown that the system is biologically feasible. It is also established that $R_0$ is a sharp threshold value, and it does completely determine the global stability of the disease-free equilibrium for $R_0<1$. And therefore, the system exhibits forward bifurcation. Furthermore, the global stability analysis of the endemic equilibrium is analyzed for $R_0>1$ using a suitable Lyapunov function by assuming the disease-induced death rate $d=0$. Based on our mathematical analysis, to eliminate the measles disease from a community, policymakers may work on reducing the basic reproduction number to less than unity. This result is different from the previous results on measles dynamics [4], [33], where reducing the basic reproduction number to less than one is not enough for measles eradication.

The calibration process is done through the solution of an inverse problem using the least squares method using the Trust-Region-Reflective method algorithm lsqnonlin from MATLAB's optimization Toolbox. Nominal initial parameter and range values are selected from the related literature studying measles disease dynamics. Estimated parameter values with 95% confidence intervals are presented. Furthermore, unlike the previous work by the authors [34] who studied the global sensitivity analysis of the basic reproduction number, local sensitivity analysis of the basic reproduction number to the estimated parameters is done to investigate the robustness of the model as parameters change. It is found that a decrease in the contact rate and an increase in the vaccination rate would cause the disease to die out.

The $SEIR$ model is not like the SIR in that we cannot say the epidemic is under control if the number of infected individuals drops. Definitely, in the $SEIR$ models, it may come about that temporarily the number of people in the infected class is small, though the exposed class is still enormous. Consequently, the epidemic may appear to have died out but will then be out of control again when the people in the exposed class transfer to the infected class and contaminate other people. Therefore, an effective strategy essentially takes into consideration the time necessary for the exposed class to transfer to the infected and will minimize to zero new infected cases throughout the period.

Like many epidemic models, the system studied has drawbacks. We calibrated the proposed model to weekly reported cases of measles to estimate the parameters of the model. Estimation of parameters is tedious work because a large part of the infectious process is missed in most cases [53]. One of the drawbacks is that we could obtain optimal parameter values that result in a local minimum. Therefore, to solve this problem, the recommendation is to simulate the system for several sets of initial parameter values and take the optimal parameters with the smallest error as the best parameter estimate. Moreover, it is still challenging to propose an appropriate Lyapunov function to study the stability of the endemic equilibrium when $d>0$. Therefore, further study using the Lyapunov function theory is needed to determine the global stability of the endemic equilibrium of an SEIR with a standard incidence and disease-induced death rate. However, the better way to deal with it so far is to use the geometric approach proposed in the works of [22].

Even though we used a comparatively simple model of measles to demonstrate our methodology, the method that we use can be functional on more complex models by incorporating additional information into the model. For instance, age structure would be very suitable when considering potential vaccination strategies for measles [10], [54]. Furthermore, parameter uncertainty will always exist during the estimation of the parameters and will always influence model predictions. Consequently, an age-structured measles model that incorporates uncertainty analysis in parameter estimation is essential to be investigated.

CRediT authorship contribution statement

Hailay Weldegiorgis Berhe: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Abadi Abay Gebremeskel: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Habtu Alemayehu Atsbaha: Writing – review & editing, Validation, Supervision, Investigation, Data curation. Yohannes Yirga Kefela: Writing – review & editing, Supervision, Investigation, Data curation. Abadi Abraha Asgedom: Writing – review & editing, Supervision, Investigation, Data curation. Woldegebriel Assefa Woldegerima: Writing – review & editing, Validation, Supervision, Investigation, Data curation. Shaibu Osman: Writing – review & editing, Supervision, Investigation, Data curation. Lamin Kabareh: Writing – original draft, Supervision, Investigation, Data curation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

All data relevant to this publication are within the paper.