Dataset for indoor air temperature measurements using ultrasonic travel-time tomography

Abstract

This dataset presents the indoor air temperature collections using the novel technique of Acoustic travel time TOMography (ATOM) in the ultrasonic frequency range. The presented measuring system employs early reflections as sound propagation paths in addition to the travel time of the direct path, effectively combining room acoustics with tomography techniques. The data was collected across various measurement scenarios within the climate chamber laboratory at the Building Physics Department at the Bauhaus-University Weimar. Additionally, the measurements data regarding the phase shift compensating of the utilized preamplifier in the setup are provided. These measurements served to assess the effectiveness of the new ultrasonic measurement system which was presented in the co-published article (Dokhanchi et al., 2024). The developed algorithms provided in this Dataset offers a valuable reference for researchers in the field of acoustic tomography especially those focusing on indoor applications, and the researchers involved in indoor climate monitoring where non-contact indoor air temperature measurements are required.

Specifications Table

Subject	Civil and Structural Engineering, Acoustics and Ultrasonics, Signal Processing,
Specific subject area	Indoor Climate Monitoring, Indoor Air Temperature Measurements, Ultrasonic Tomography, Room Acoustics and Room Impulse Response Calculations, Travel-Time Measurements of Signals
Data format	Raw, Formatted
Type of data	Table, Figure
Data collection	Empirical measurements were performed under various temperature conditions in a climate chamber to validate the developed ultrasound travel time tomography setup for indoor air temperature distribution. The setup comprised four sound sources and an omnidirectional microphone, positioned within the climate chamber based on calculated optimal locations. The temperatures derived from the ATOM system were compared against those recorded by highly accurate NTC thermistors as a benchmark. The measurements encompassed both steady state and transient conditions, and two distinct scenarios were considered: one with the preamplifier's switchable high-pass filter turned off, and another with it activated. The measurement data regarding the phase shift compensation of the utilized preamplifier are also provided.
Data source location	Institution: Bauhaus-University Weimar Chair of Building Physics City/Town/Region: Weimar Country: Germany
Data accessibility	Repository name: Dataset for Indoor Air Temperature Monitoring using Ultrasonic Travel-Time Tomography Data identification number: 10.17632/8kmtjnr47n.1 Direct URL to data: https://data.mendeley.com/datasets/8kmtjnr47n/1
Related research article	N. S. Dokhanchi, C. Othmani, J. Arnold, A. Vogel, S. Merchel, C. Voelker, M. E. Altinsoy, Indoor air temperature measurements using ultrasonic travel-time tomography, Applied Acoustics 218 (2024) 109,894, Doi: 10.1016/j.apacoust.2024.109894.

1. Value of the Data

• •The dataset contains the measuring programs and algorithms for travel times collections which are developed at the Chair of Building Physics at the Bauhaus-University Weimar for conducting indoor air temperature measurements utilizing Acoustic travel time TOMography (ATOM) in the ultrasonic frequency range. The developed measuring system combined tomography techniques with room acoustics for indoor applications.
• •The presented measurements dataset provides the assessment of the effectiveness of the novel ultrasonic tomography technique in monitoring indoor air temperature distribution across different thermal conditions. It offers a valuable comparison between indoor air temperatures measured using the ATOM system and those recorded by traditional NTC thermistors.
• •The dataset involves data acquisition and phase shift measurements which can serve as an exemplar for analogous scenarios in the field of signal processing.
• •The developed algorithms can serve as a reference point for researchers in the acoustic tomography field with a particular focus on indoor climate applications, and those involved in indoor climate monitoring, especially in cases where non-contact indoor air temperature measurements are essential.
• •Considering the widespread use and availability of climate chambers in the field of building physics, the conducted measurement data in the climate chamber under the defined conditions can effectively be used in a broader scientific community in the field.

2. Data Description

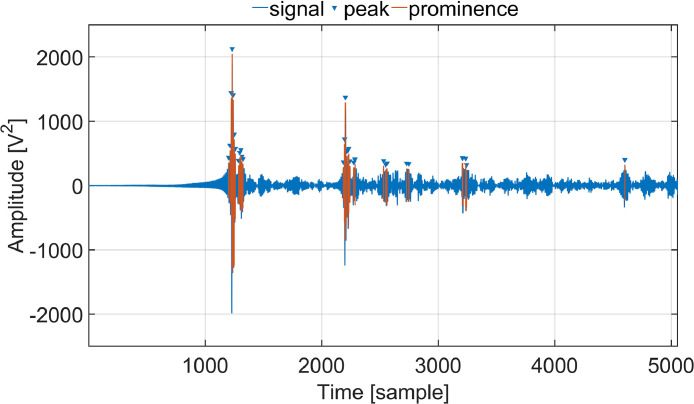
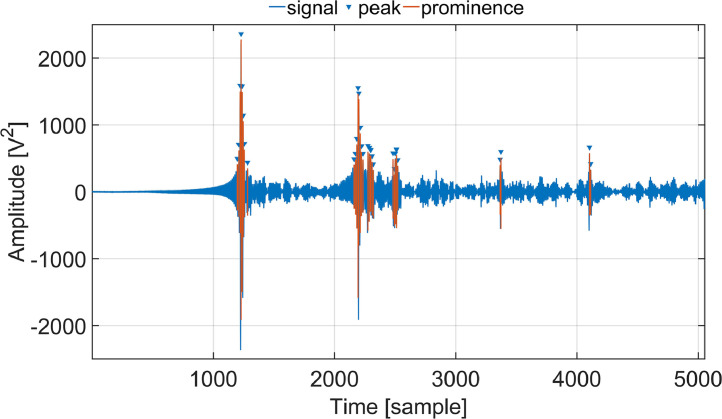
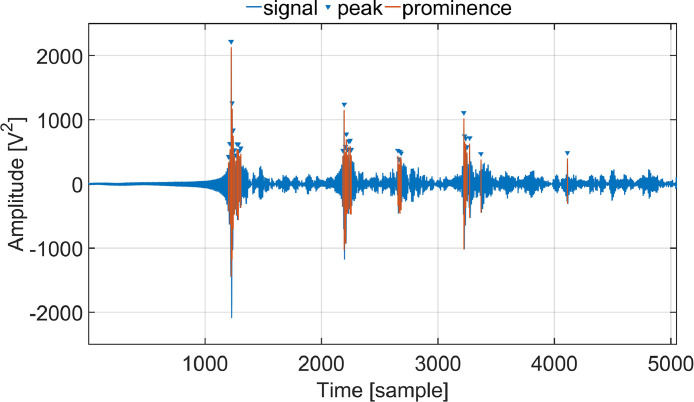
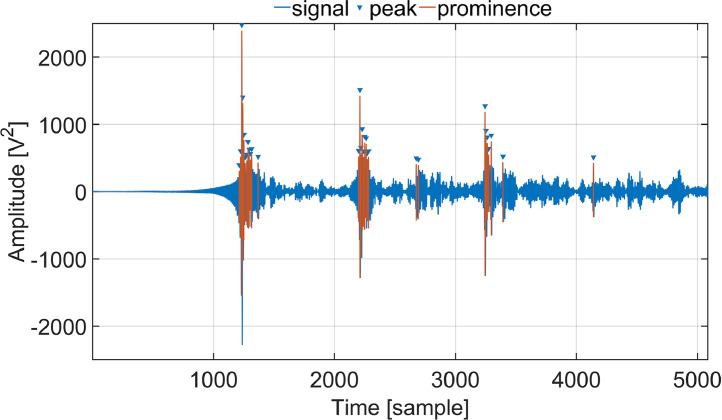
This article presents a comprehensive collection of indoor air temperature measurement data obtained through the utilization of an advanced Acoustic travel time TOMography (ATOM) system in the ultrasonic frequency range. In principle, traditional thermal sensors such as NTC thermistors provide localized point measurements, meaning they only capture data from specific installation locations. To map the distribution of air temperature, multiple thermal sensors must be strategically installed throughout the area of interest, which entails significant effort and expense. Moreover, depending on the distance between NTC thermistors and occupants in occupied spaces, the recorded climatic conditions at the thermistor points may differ from those experienced by users (e.g. at the workplace in office rooms), potentially impacting thermal comfort. This discrepancy can lead to unnecessary heating or cooling, resulting in increased energy consumption. ATOM presents an alternative to these conventional sensor networks by measuring transmission sound velocity signals. It enables the generation of a greater number of data points per sensor and facilitates non-contact, non-destructive measurements. The ATOM technique consists of two primary steps. Firstly, it involves measuring the signal travel times to measure the sound velocity along the sound propagation paths, and secondly, it employs tomography techniques to reconstruct the spatial temperature distribution across the entire test area, which in this case is the entire room [[2], [3], [4], [5]]. The development process of this system was previously described in the related article [1]. This article focuses on providing detailed reflectogram information for the room impulse responses (RIRs) measured in a climate chamber to collect the travel times of the direct paths and early reflections using four sound sources (S₁, S₂, S₃, and S₄ referred to the original paper [1]) within the measurement setup. The four sound sources are placed at each of the corners of the room at different calculated optimal locations. More information about the coordinates and arrangements of the four ultrasonic sound sources along with utilizing one omnidirectional ultrasonic microphone, can be found in the associated article [1]. The collected data is visualized in Fig. 1, Fig. 2, Fig. 3, Fig. 4 as examples. In these Figures, the utilized peak detection method is illustrated using the find local maxima command which returns a vector with the local maxima (peaks) of the input signal vector. The prominence of a peak measures how much the peak stands out due to its intrinsic height and its location relative to other peaks [6]. Because the climate chamber exhibits relatively symmetric dimensions, and the transducer's coordinates are fixed in the room geometry, it is evident from Figs. 1 to 4 that the distribution of early reflections for the four sound sources remains quite similar until approximately the early 24 ms (5, 090∕216, 000 ≈ 24 ms) of the impulse response reflectogram. The impulse responses in these examples are measured at a uniform temperature of 24 °C in which all the six surfaces of the climate chamber are tempered simultaneously. The algorithm for measuring the room impulse responses along with the method of travel times estimations are explained in Section 2.1 and the corresponding “. mat” files are provided in the data repository [7]. The noise reduction was achieved by time-averaged room impulse response reflectograms for each combination of sound source and receiver. The algorithm for the noise minimization is explained in section 2.1.6 and the corresponding raw data are provided in the data repository [7].

Fig. 1.

Room impulse response measurements for sound source number one (S₁) located in the climate chamber under a uniform temperature of 24 °C.

Fig. 2.

Room impulse response measurements for sound source number two (S₂) located in the climate chamber under a uniform temperature of 24 °C.

Fig. 3.

Room impulse response measurements for sound source number three (S₃) located in the climate chamber under a uniform temperature of 24 °C.

Fig. 4.

Room impulse response measurements for sound source number four (S₄) located in the climate chamber under a uniform temperature of 24 °C.

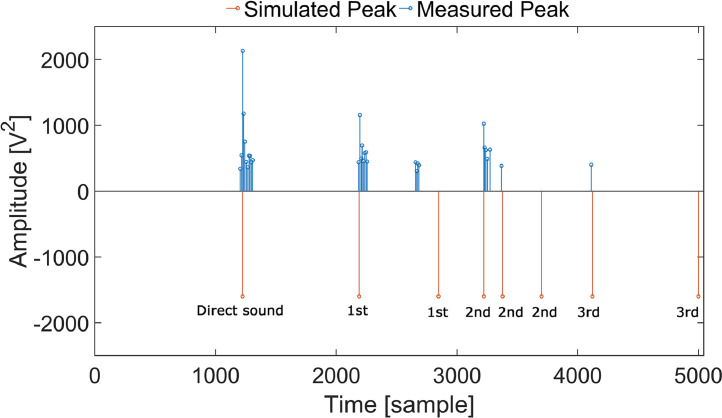
Moreover, the simulated and measured travel times are mapped together in Fig. 5 to enhance the clarity of the travel time detection as an example. It is evident that in addition to the travel time of the direct path, the travel times of the second-order and third-order reflections are aligned with the simulated ones. Due to the directivity angle of the utilized ultrasonic sound source, two of the early reflections lack corresponding peaks in the measured data.

Fig. 5.

The comparison of the measured and simulated peaks for the impulse response measured from the sound source one (S₁) located in the climate chamber under a uniform temperature of 24 °C. The simulation is performed using the Image Source Model (ISM). The simulated travel times involve the direct path, simulation of first-order reflections (1st), second-order reflections (2nd), and third-order reflections (3rd). The corresponding “. mat” file for ISM is also provided in the data repository [7].

2.1. Phase shift measurements of the preamplifier in the numeric computing platform

As described in the supported article [1], the developed ultrasonic setup contains a preamplifier with the type of "M208B" to enhance the power of the recorded signal. However, before determining the room impulse responses, it is essential to compensate for the additional phase shift introduced by this preamplifier in the received signal. This dataset provides a comprehensive account of these phase shift measurements. It covers two approaches: performing the complete measurements once in a numeric computing platform i.e. MATLAB which is described in this section and validating the measurements by conducting phase shift measurements using an oscilloscope which is described in 1.2. To assess the phase shift using the numeric computing platform, two scenarios are considered. In the initial scenario, the preamplifier's switchable high-pass filter, configured with a cutoff frequency of 15 kHz, is activated, whereas in the second scenario, it is deactivated. Phase responses were determined by measuring a single-tone chirp signal that covered a frequency range from 10,000 Hz to 40,000 Hz, using 1000 Hz intervals. The duration of the signal was 1 s plus 30 s segments of silence at the beginning of the signal. Table 1 presents the amount of phase shifts that occurs during the measurements for both scenarios. The measurement data is available in the data repository [7] as an ``.xlsx'' file, serving as a reference for users employing the “M208B” preamplifier with comparable configurations.

Table 1.

The phase shift measurements were carried out within the frequency range of 10,000 to 40,000 Hz, using 1000 Hz intervals, for both cases, with and without the high-pass filter.

Frequency interval [Hz]	High-pass filter deactivated [deg.]	High-pass filter activated [deg.]
1000	20.90	106.60
11,000	23.06	−98.71
12,000	25.05	−90.98
13,000	27.08	−83.42
14,000	29.26	−75.75
15,000	31.34	−68.35
16,000	33.33	−61.34
17,000	35.47	−54.43
18,000	37.63	−47.74
19,000	39.64	−41.53
20,000	41.70	−35.49
21,000	43.92	−29.64
22,000	45,10	−24.18
23,000	48.00	−18.96
24,000	50.20	−13.89
25,000	52.36	−9.04
26,000	54.37	−4.47
27,000	56.50	−0.023
28,000	58.72	4.32
29,000	60.79	8.44
30,000	62.85	12.38
31,000	65.08	16.34
32,000	67.25	20.15
33,000	69.28	23.65
34,000	71.46	27.23
35,000	73.72	30.75
36,000	75.78	34.20
37,000	77.90	37.53
38,000	80.19	40.89
39,000	82.34	44.15
40,000	84.41	47.30

2.2. Phase shift measurements of the preamplifier with oscilloscope

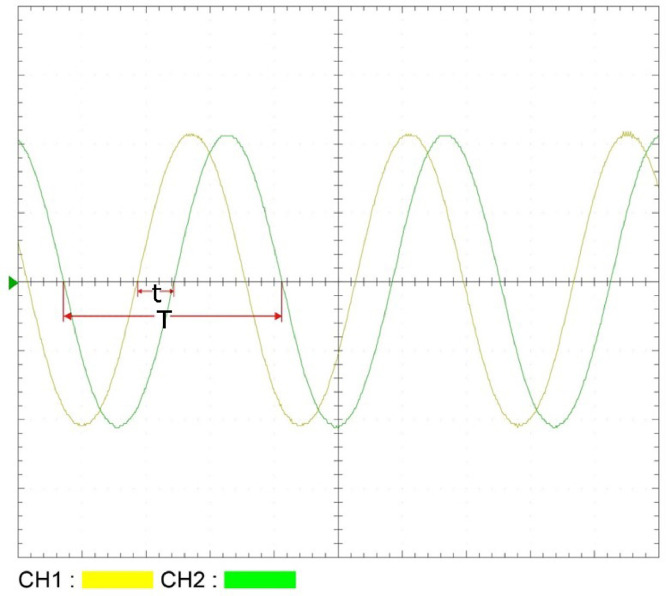
The phase shift between the reference signal, which passed through the DAQ device only, and the signal that traversed the preamplifier was determined for a single-tone sine sweep signal at frequencies of 10,000, 20,000, 30,000, and 40,000 Hz, utilizing a USB oscilloscope. Accordingly, channel one is set for the reference signal, and channel two is set for a signal passed through the preamplifier. The phase shift between the channels can be calculated as follows

$${\varnothing }^{\circ }=\frac{t}{T}\times {360}^{\circ }$$ (1)

where t is the horizontal distance of zero crossings and T is the horizontal distance for one period. Fig. 6 shows an example of the measured sign sweep signal with the frequency of 30000 Hz passing through channels one and two. Moreover, the results of the phase calculation are outlined in Table 2.

Fig. 6.

Phase shift measurements: dual channel operation using a single tone sine sweep signal with the frequency of 30,000 Hz using a USB oscilloscope.

Table 2.

The phase shift measurements were conducted with a USB oscilloscope for the frequency range of 10,000 to 40,000 Hz, using 10,000 Hz intervals, for both cases, with and without the high-pass filter.

Frequency interval [Hz]	High-pass filter deactivated [deg.]	High-pass filter activated [deg.]
10,000	14.40	−114.76
20,000	34.62	−36.00
30,000	55.64	11.65
40,000	77.56	47.52

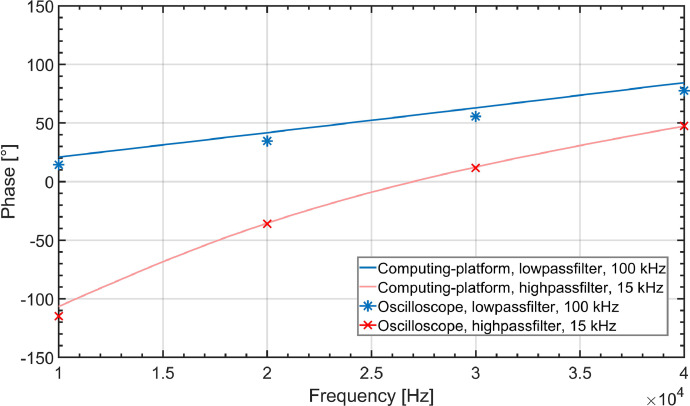
Fig. 7 illustrates the comparison between the two utilized approaches for measuring phase shifts: one involving the oscilloscope and the other involving the numeric computing platform. The phase measurements obtained are graphed in relation to the frequency.

Fig. 7.

Phase shift measurements: comparison of the measured data for both measuring methods namely using the USB oscilloscope and the numeric computing platform.

2.3. Phase shift compensation

The Phase shift compensation method is explained in the associated article [1]. To provide a clear explanation of the method, Table 3 compares the outcomes of applying the compensation method to a chirp signal with a 1 s duration which was excited in the climate chamber under the uniform temperature of 24 °C.

Table 3.

The comparison between the measured and compensated phase when a chirp signal with a frequency range of 10,000 to 40,000 Hz and duration of 1 s was excited into the room - high pass filter is activated in this example.

Frequency interval [Hz]	Compensated phase [deg.]	Measured phase [deg.]
20,000	57.36	57.36
21,000	77.90	83.75
22,000	135.31	146.83
23,000	102.37	119.37
24,000	48.42	70.72
25,000	80.56	107.97
26,000	82.95	115.29
27,000	153.29	−169.64
28,000	5–112.60	−70.97
29,000	−142.17	−96.17
30,000	53.88	104.05
31,000	−85.16	−30.98
32,000	−90.60	−32.62
33,000	1.57	63.17
34,000	−56.32	8.72
35,000	133.02	−158.69
36,000	−3.314	68.04
37,000	153.75	−132.01
38,000	130.37	−152.70
39,000	−99.61	−20.18
40,000	164.93	−113.30

2.4. Indoor air temperatures reconstruction

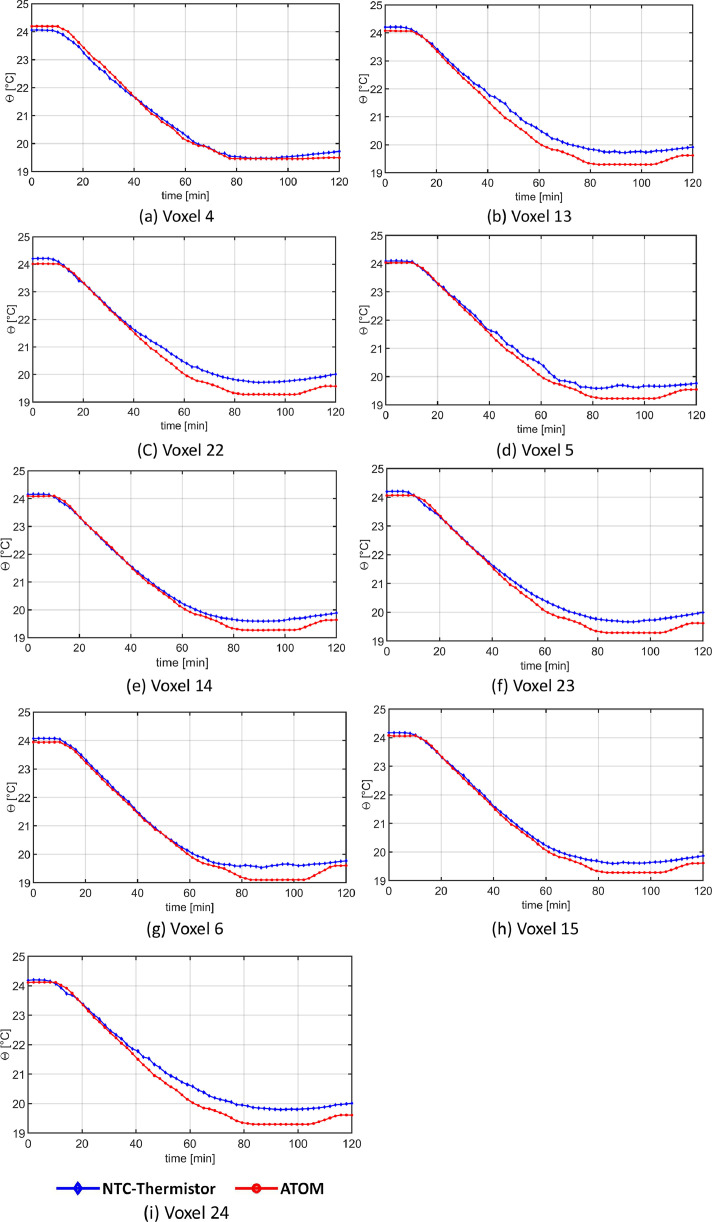
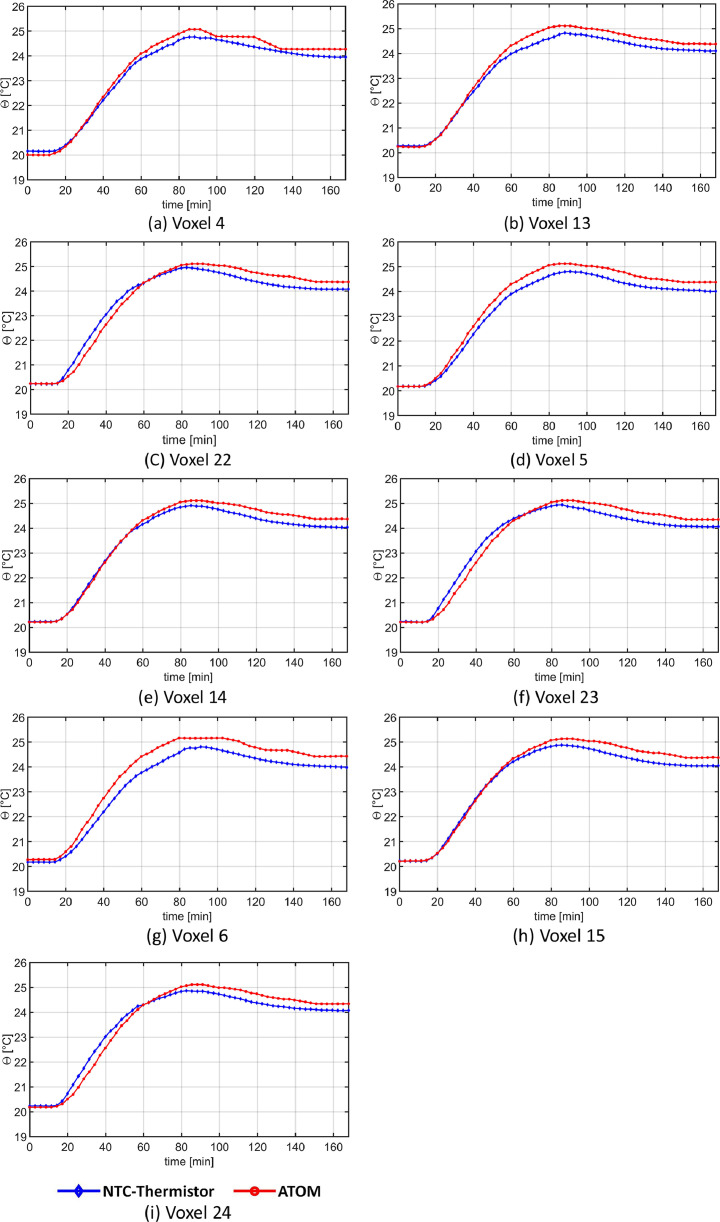
Regarding the tomography aspect, this paper presents the air temperature measurements obtained from tomographic reconstruction additionally for the entire set of selected voxels (volumetric grid cells). As explained in the associated article [1], for the tomography calculations, the climate chamber room was divided into 27 voxels in which 9 of the voxels are selected for evaluations. Accordingly, the monitoring of the air temperatures through all 9 voxels is outlined in Fig. 8, Fig. 9 in the following, which are extended the measurement data presented in Fig. 12, Fig. 13 in the original paper [1]. The measurements were conducted for both steady-state and transient conditions. Transient conditions were examined for both decreasing and increasing scenarios, during which all six surfaces of the climate chamber were simultaneously cooled from 24 °C to 20 °C and then heated from 20 °C to 24 °C, respectively.

Fig. 8.

The comparison of the indoor air temperatures measured with NTC-thermistors and ATOM within the nine selected voxels for the decreasing scenario from 24 °C to 20 °C in the climate chamber lab.

Fig. 9.

The comparison of the indoor air temperatures measured with NTC-thermistors and ATOM within the nine selected voxels for the increasing scenario from 20 °C to 24 °C in the climate chamber lab.

Fig. 12.

Defining the coordinates of the utilized transducers.

Fig. 13.

Setup the DAQ sessions and related input and output channels.

3. Experimental Design, Materials and Methods

The boundary conditions and measurement sessions of the experimental indoor air temperature monitoring using ATOM are summarized in Table 4.

Table 4.

Boundary conditions and measurement sessions.

Test area	Climate chamber of the Building Physics department at the Bauhaus-University Weimar
Dimension of the climate chamber	2.98 m in width, 2.99 m in length, and 2.41 m in height considering the non-ideality of the room geometry
Arrangement of the transducers	Placing an omnidirectional receiver at the center and distributing an array of four sound sources at each of the corners of the room. For more information please see Fig. 3, Fig. 10 in [1]
Type of receiver	MK-301-E (frequency range: 5 Hz-100 kHz)
Type of sound source	Kemo L010 (frequency range: 2–60 kHz)
Type of data acquisition device	DT 9847 (sampling frequency: 216 kHz)
Type of preamplifier	M208B with 8 IEPE channels and a switchable high-pass filter with a cutoff frequency of 15 kHz. When the filter is switched off, the unit operates with a preset low-pass filter with a cutoff frequency of 100 kHz
Type of sound source amplifier	PASCO CI-6552A
Type of NTC thermistors	Ahlborn with an accuracy of ±0.2 K of the measured value and a resolution of 0.01 K
Excitation signal	A chirp signal with a frequency range of 10,000 − 40,000 Hz and a duration of 1 s
Measurement scenario 1	A decreasing temperature scenario while the preamplifier's switchable highpass filter turned off
Measurement scenario 2	An increasing temperature scenario while the preamplifier's switchable high-pass filter turned on
Steady-state condition for the measurement scenario 1	All six surfaces of the chamber were adjusted to 24 °C and the chamber was left undisturbed overnight to reach a thermal steady state
Transient condition for the measurement scenario 1	The temperature of the six surfaces of the chamber was set to 20 °C simultaneously. This temperature reduction from 24 °C to 20 °C created a gradual air temperature drift in the chamber
Steady-state condition for the measurement scenario 2	All six surfaces of the chamber were adjusted to 20 °C and the chamber was left undisturbed overnight to reach a thermal steady state
Transient condition for the measurement scenario 2	The temperature of the six surfaces of the chamber was set to 24 °C simultaneously. This temperature reduction from 20 °C to 24 °C created a gradual air temperature drift in the chamber
Duration of the measurements	The entire course of measurement scenario 1 was 120 min considering 3 number of time-averaged RIR reflectograms for each loudspeaker-receiver combination for the noise minimization which resulted in a measurement interval of about ≈ 2 min. For the measurement scenario 2, the number of time-averaged RIR reflectograms was set to 5 which resulted in a measurement interval of about ≈ 2.8 min and a total duration of 168 min
Utilized tomography algorithm	The Simultaneous Iterative Reconstruction Technique (SIRT)
Number of tomography voxels	27 Voxels
The Utilized software package	MATLAB R2017b

3.1. Algorithm for room impulse response measurements

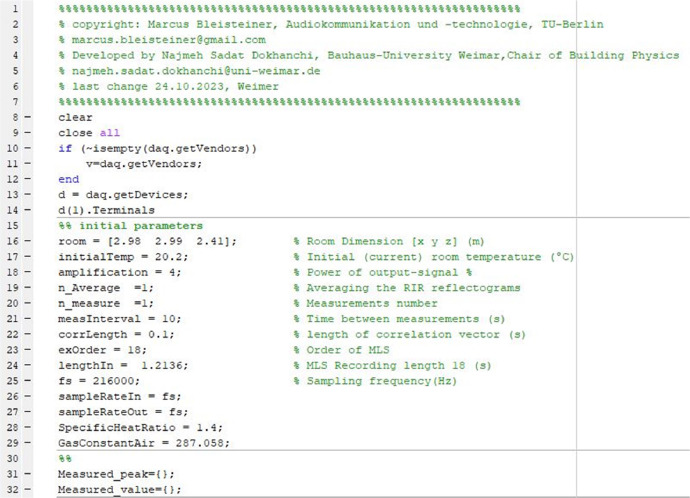
The MATLAB code ”ImpulseResponse.m” in the repository [7] is responsible for measuring the room impulse response and accordingly collecting the travel times of the direct paths and early reflections till third order reflections. The first step of the code is related to defining the initial parameters that are required during the measurements process (see Fig. 10). Among the parameters is “n_Average” which indicates the number of averaging the measured RIR reflectogram. This setting allows for multiple measurement repetitions to be configured for the purpose of noise minimization.

Fig. 10.

Defining the initial parameters that are required for the measurements process.

3.1.1. Designing the excitation signal and positioning the transducers

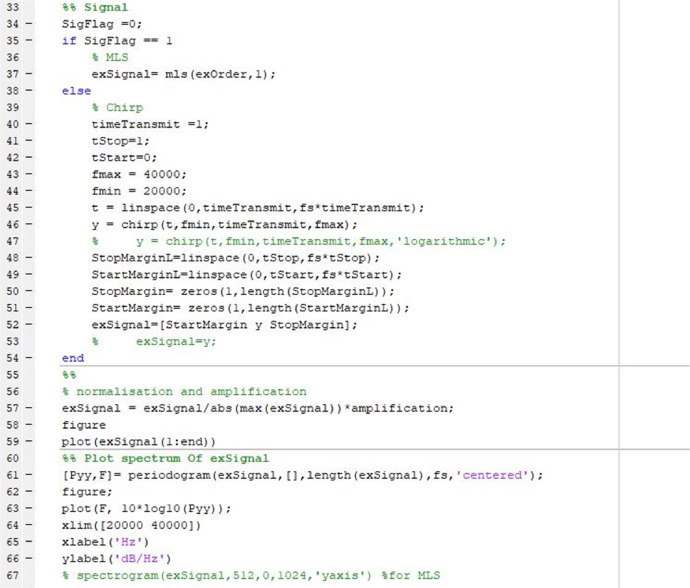
The next step is to define the type and parameters of the excitation signal. The excitation signals defined in the code are maximum length sequence (MLS) signal, linear and logarithmic chirp signals. For the current study, the linear chirp signal is used with the duration of 1 s and frequency range of 20–40 kHz. Regarding the chirp signals, a segment of silence of 1 s is added after each repeated input signal, referred as “tStop=1 s in the code, to avoid the time aliasing error. Accordingly, the StartMargin and StartMargin lengths are defined and added to the excitation signal referred as exSignal in the code (see Fig. 11).

Fig. 11.

Defining the type and parameters of the excitation signal.

Furthermore, the positions of the employed transducers are specified. Accordingly, the coordinates of four ultrasonic sound sources and one omnidirectional receiver are defined as illustrated in Fig. 12.

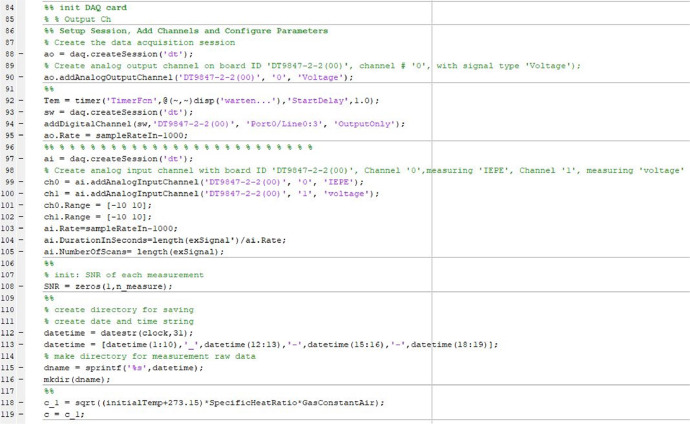
3.1.2. Configuring the data acquisition device

The following step involves configuring the data acquisition device (DAQ), namely the "DT9847–2–2(00)," and specifying the necessary input and output channels. One output channel is set up via channel “0″ of the DAQ, while two input channels are defined for both the loopback connection and the receiver (see Fig. 13). Moreover, the theoretical sound velocity referred as “c_1″ in the code is defined based on the given current temperature of the room which can be updated further based on the measured sound velocity along the direct paths.

3.1.3. Phase shift compensation of the preamplifier

Following the transmission of the signal into the test room and the reception of recorded data for both the room (data (:,1)) and the loopback (data (:,2)) as described in "ImpulseResponse.m," phase compensation can be applied. This involves calculating the phases of the recorded signal in the frequency range of 20–40 kHz, which corresponds to the excitation signal's frequency range. The main steps of the process of phase shift measurements are summarized in Table 5.

Table 5.

Phase shift measurement of the preamplifier.

Inputs: Sampling frequency of theDAQ-device =216 KHz, the amplification factor of the excitation signal= 0.8∕1000

1: for every excitation signal with one single frequency from 10 to 40 KHz with an interval of 1 KHz 2: Transmit the input signal (a chirp signal with a start margin of 30 s and duration of 1 s) 3: Record data that is directly received by the first input of the DAQ-device: dataDAQ = data (∶, 1) 4: Record data that is passed through the preamplifier and then received by the second input of the DAQ-device: dataPreamp = data (∶, 2) 5: Trim both data to remove the initial start margin of 30 s, thus focusing on the subsequent 1 s length of the transmitted signal: dataDAQCut=dataDAQ((length(StartMargin)):end); dataPreampCut=dataPreamp((length(StartMargin)):end); 6: Calculate the FFT of the both trimmed recorded data: D=fftshift(fft(dataDAQCut)); P=fftshift(fft(dataPreampCut)); 7: Calculate the Phase shift between the two signals: Phase=atan2(imag(D), real(D))*180/pi;

Output: Phase shift in angle

The compensation method is defined for both scenarios when the high pass filter of the preamplifier is switched off and when it is activated (see Fig. 14). The code contains compensation equations that were experimentally derived based on phase shift measurements explained in 2.2, 3.1.4.

Fig. 14.

Phase compensation method based on the phase shift measurements that are determined experimentally for the utilized preamplifier.

3.1.4. Room impulse response calculation

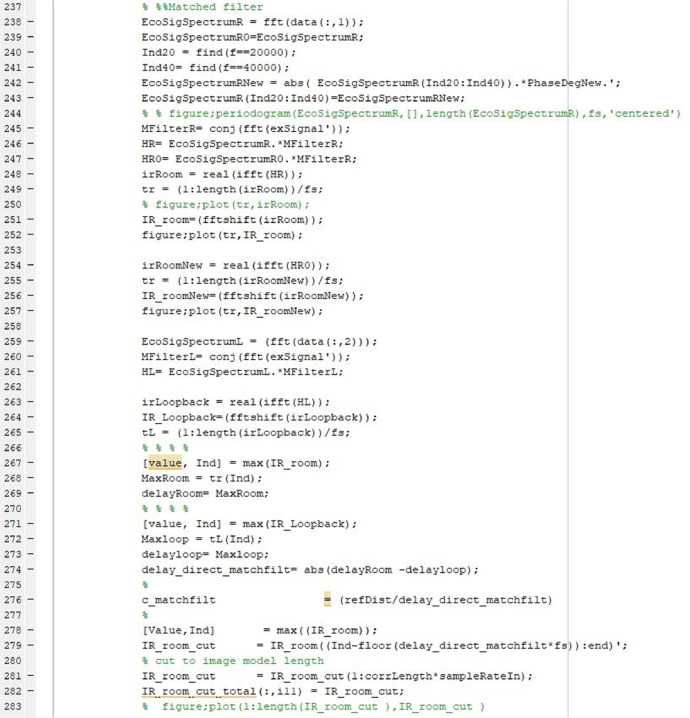
Subsequently, the impulse response of the room is computed using the ``matched filter'' method. To do this, the recorded data from the signal transmission into the test room (data (:,1)) is converted into the frequency domain using Fast Fourier Transform (FFT). The calculated phase of the desired frequency range, denoted as ``PhaseDegNew'' in the code, is then applied to the spectrum of the recorded signal (see Fig. 15). The impulse response of the room is determined by multiplying the transfer function of the conjugated excitation signal with the transfer function of the recorded signal, considering the phase compensation. Finally, by applying Inverse Fast Fourier Transform (IFFT), the impulse response of the room in the time domain is obtained. The “data.mat” available in the data repository [7] contains an example of the signal transmitted in the room and through loop back connection.

Fig. 15.

Room impulse response calculation to determine the travel time of the direct paths and early reflections.

Furthermore, the impulse response is also calculated for the loopback connection, where the transmitted signal is received directly by one of the DAQ inputs after passing through the sound source amplifier. A more detailed explanation of the measurement chain considering loopback connection can be found in the original paper [1]. Consequently, the accurate travel time of the direct path is determined by calculating the difference in travel time of the direct path between the loopback and the room. This calculation accounts for the delay introduced by the hardware and software through loopback connection. Thus, the sound velocity along the direct path, referred as “c_matchfilter” in the code, can be determined by dividing the measured travel times to the length of the direct path namely the distance between the sound source and receiver. Moreover, the calculated room impulse response is cut to the length of the simulated impulse response focusing specifically on the early portion of the reflectogram referred to as ``IR_room_cut,'' as illustrated in Fig. 15. Accordingly, by applying a proper peak detection method, the travel time of the early reflections can be selected. The corresponding “. mat” file for peak detection process is also provided in the data repository [7].

3.1.5. Noise minimization via time-averaged RIRs

For the purpose of noise minimization, the process of calculating the RIR described in the previous section namely the lines 164–318 in the MATLAB code ``ImpulseResponse.m'' [7], can be repeated to a certain number based on the specified number of averaging denoted as ``n-Average'' described in Section 2.1. Table 6 provides a summary of the averaging loop outlined in ``ImpulseResponse.m''.

Table 6.

The process of averaging the RIRs for the purpose of noise minimizations.

Input: Positioning the transducers inside the test room

1: for$i=1,\dots ,n_{avg}$do 2:   Signal transmission 3:   Apply phase shift compensation method described in Section 2.1.4 4:    t dir,i = troom-t loop Calculate the travel time of the direct path using loop-back connection 5:    c dir,i = D(s,r) /t dir,i Calculate the sound velocity along the direct path 6:   Calculate RIR namely $h_i\left(t\right)$ according to the codes described in Section 2.1.5 7: end for 8:$h\left(t\right)=\frac{1}{n{}_{avg}}\sum _{t=1}^{n_{avg}}{h}_i\left(t\right)$ Average the RIRs

Output: Time-averaged RIRs

As illustrated in the last line in Fig. 15, the obtained measurements data from RIRs are then stored in ``IR_room_cut_total''. Consequently, the ultimate RIR for each pair of sound source and receiver is determined by averaging the stored RIRs and denoted as ``IR_ cut''. Fig. 16 shows the calculation process of the ultimate averaging the measured RIRs. The MATLAB code ``ImpulseResponse.m'' available in the repository comprehensively outlines the calculation algorithms. Moreover, the “raw data” in the data repository [7] provides access to both data stored in ``IR_room_cut_total'' and the corresponding RIRs stored in "IR_cut" as an example.

Fig. 16.

The ultimate averaging the measured RIRs.

Limitations

‘Not applicable’.

Ethics Statement

No ethical issues are associated with this work.

CRediT authorship contribution statement

Najmeh Sadat Dokhanchi: Conceptualization, Methodology, Formal analysis, Software, Validation, Writing – original draft, Writing – review & editing. Joerg Arnold: Resources, Conceptualization, Methodology, Writing – review & editing. Albert Vogel: Methodology, Writing – review & editing. Conrad Voelker: Supervision, Conceptualization, Methodology, Writing – review & editing.

Data Availability

• Dataset for Indoor Air Temperature Monitoring using Ultrasonic Travel-Time Tomography (Original data) (Mendeley Data).