Entropy production associated with magnetohydrodynamics (MHD) thermo-solutal natural convection of non-Newtonian MWCNT-SiO₂-EG hybrid nano-coolant

Abstract

This article investigates the convective thermal and solutal exchange from the active walls of a trapezium chamber which is filled with multi-walled carbon nanotubes (MWCNT)-silicon dioxide (SiO₂)-ethylene glycol-water hybrid nano-coolant. The hybrid nano-coolant exhibits non-Newtonian shear-thinning rheology and is modeled by the power-law viscosity as per an exploratory report. The convection is generated by both the thermal and solutal buoyancy forces in the presence of a magnetic field. Thermophysical properties of the particular nano-coolants are estimated from the temperature-dependent empirical correlation. An in-house FORTRAN code based on the finite volume method (FVM) has been utilized to simulate the non-dimensional controlling equations representing the physical model. By systematically varying the strength of the magnetic field ($Ha=0-50$) and its direction (${\delta }_1=0-90$), the volume fraction of nano-coolant ($\varphi =0-0.04$) and solutal-to-thermal buoyancy ratio ($N=-2\text{ to }2$), we thoroughly analyzed their impact on the flow field, thermal, and solutal transmission behavior. Significant impacts arising from the shear-thinning nature ($n<1$) of the nano-coolant were observed, influencing both thermal and solutal transfer rates as reflected in the Nusselt number (Nu) and Sherwood number (Sh). The impact of Ha on Nu and Sh is more substantial for $n<1$ than the case $n=1$. The investigation exposed that when $Ha=30,{\delta }_1={30}^{\circ }$ the average Nu ($\overline{Nu}$) for nano-ccolants ($\varphi =2\text{\%}$) is maximally enhanced by 80% for $n=0.6$ compared to the case $n=1.0$. For the same nano-coolant with $Ha=30$ and ${\delta }_1={90}^{\circ }$, there is a 128% elevation in the average Sherwood number ($\overline{Sh}$) when $n=0.6$ compared to $n=1.0$. The entropy generation ($\bar{S}$) inherent to the heat and mass transfer process and hence a criterion ($\xi =\bar{S}/\overline{Nu}$) is computed to address the system thermal performance from the thermodynamics second law. $\bar{S}$ increased as n was reduced, indicating that the shear-thinning effect contributed strongly to the entropy generation.

Nomenclature

English Symbols

A

Aspect ratio of the enclosure $H/L$

$B_0$

Magnetic field kg A⁻¹ S⁻²

Be

Local Bejan number

C

Concentration of solutes kg m⁻³

$D_C$

Mass diffusivity m² s⁻¹

Cp

Specific heat in constant pressure J kg⁻¹ K⁻¹

H

Height of the cavity m

Ha

Hartmann number

k

Thermal conductivity W m⁻¹ K⁻¹

L

Width of the cavity m

$N_c$

Buoyancy ratio

Le

Lewis number

m

Consistency index N sⁿ m⁻²

n

Power-law index

n

Normal vector

Nu

Nusselt number

p

Pressure Pa

Pr

Prandtl number

Ra

Rayleigh number

Sh

Sherwood number

$S_D$

Entropy due to concentration gradient

$S_F$

Entropy due to thermal gradient

$S_M$

Entropy due to magnetic field

$S_S$

Total entropy

$S_T$

Entropy due to viscous dissipation

t

Time s

T

Temperature K

u,v

Dimensionless velocity along the horizontal and vertical directions

x,y

Dimensionless horizontal and vertical coordinate

Greek Symbols

α

Thermal diffusivity m² s⁻¹

${\mathit{\delta }}_0$

Angle between the inclined wall and horizontal surface

${\mathit{\delta }}_1$

Direction of the magnetic field

${\mathit{\beta }}_T$

Thermal expansion coefficient k⁻¹

${\mathit{\beta }}_C$

Concentration expansion coefficient kg⁻¹ m³

$\dot{\mathit{\gamma }}$

Dimensional shear rate s⁻¹

τ

Dimensional shear stress Pa

ϕ

Nanoparticles volume fraction

μ

Viscosity of fluid kg m⁻¹ s⁻¹

ρ

Density of fluid kg m⁻³

σ

Electric conductivity S m⁻¹

Upperscript

$\tilde{}$

Dimensional quantity

Subscripts

hbf

Hybrid nanofluid

f

Base fluid

eff

Effective properties

l

Left wall

r

Right wall

1. Introduction

The use of heat energy is becoming more attractive as scientists strive to develop the best heat transfer technologies for considerable energy savings in the industry. The fundamental cause of the problem is the poor showcase of heat conductance of typical liquids, e.g., water, oil, acetone, ethylene glycol (EG), and so on. Researchers engineered heat transfer (HT) fluids by combining various nanosized constituents having elevated thermal conductivity, named nanofluid (NF) as coined by Choi [1] in 1995, to enhance the thermal performance of functioning mediums. Numerous studies on NFs have been conducted using different geometries and boundary conditions, and the model has been modified to incorporate a porous effect or Lorentz effect. These nanoparticles (NPs) comprise oxide ceramics, metal oxides, metal carbides, chemically unstable metals, and other components [2]. Later, several researchers such as Das et al. [3], Minkowyez et al. [4], Neild and Bejan [5] and references in review paper [6] studied the influence of nanoparticles on various fluid models focusing on simulating natural convection and exploring the impacts of adding NFs displaying considerable HT increase in a closed enclosure. Among the many other prospects of nanoparticles, carbon nanotubes (CNTs) have received a broad engagement because of their unique structure, remarkable thermal properties, and high thermal conductivity [7]. Suspending CNTs in synthetic poly oil boosts thermal conductivity by 160% just for only 1% CNT in the nanofluid suspension. This phenomenon shows the great potential of CNT employment in preparing HNF. Furthermore, two of the most commonly used CNT are single-walled CNT (SWCNT) and multi-walled CNT (MWCNT), with thermal conductivity of 6000 W/(m.K) and 3000 W/(m.K), respectively, indicating that CNT-based NFs can be utilized to improve the thermal conductivity as well as HT phenomena of the regular fluids [8], [9], [10].

As for the choice of carrier fluids for NF preparation, engineers and researchers working in HT and coolant processes are paying close attention to the ethylene glycol (EG) based NF. Compared to water, EG works as an excellent mediator in the coolant process and HT in various engineering domains; as a result, it has an extended range of applications in process industries. Utilization of EG and water in a 60:40 mass ratio as an HT medium has become widespread for applications in building heating systems, vehicles, and heat exchangers, particularly in regions marked by frigid climates [11]. These heat transfer fluids, incorporating combinations of EG with varying proportions of H₂O, exhibit robust and reliable performance even under extremely low temperatures. They have found widespread application in diverse sectors, including baseboard heaters, heat exchangers, automobiles, and industrial facilities operating within cold environments [12]. In the pursuit of assessing thermal conductivity, Serebryakov et al. [13] utilized a blend of 90% EG and 10% water infused with Al2O3 nanoparticles. Similarly, Das [14] formulated NFs by suspending various NP in a 60-40 EG solution, exploring a temperature range of 298 Kelvin to 363 Kelvin. Yu et al. [15] delved into the thermal conductivity of ZnO NPs mixed in EG, highlighting the substantial influence of NP addition on thermal conductivity.

In continuance with NFs research, experimentalists have initiated the use of hybrid nanofluids (HNFs) in the last decade to obtain better thermal performance compared to the existing nanofluids. HNFs are regarded as engineered suspensions of dissimilar nanoparticles in a mixture with carrier fluids [16], [17], [18], [19]. In the realm of industrial applications, striking a balance among multiple properties often becomes imperative, and this is precisely where the versatility of HNFs shines. These innovative fluids have found utility in a range of industrial contexts, including micro-channels, heat exchangers, and air conditioning designs, among other applications [20], [21], [22]. Experimental studies [23], [24], [25] show that the thermal conductivity of HNF advances with nanoparticle addition and temperature growth. In the other study, the rheological characteristics of MWCNTs–SiO₂ additive Eg-Water based HNF with COOH functionalized are investigated by Eshgarf et al. [26]. Results claimed the Newtonian characteristics of the base fluid and the shear-thinning characteristics of the HNF with 0.0625 wt% to 2 wt% nanoparticles. The outcomes also revealed an escalation of apparent viscosity with adding more nano constituents, and the viscosity lessens with elevated temperatures. A separate study by Afrand et al. [27] showcased experimental findings regarding the impact of temperature and nanoparticle addition on the viscosity of an HNF, specifically a SiO₂-MWCNTs/engine oil (SAE40) combination. Their research established the Newtonian viscosity of the HNF for $0.0-1.0$ wt% nanoparticles at the wide range of temperatures $25-60$ ⁰C. From their exploratory research, a precise correlation for estimating the effective dynamic viscosity of the HNF for different volume fractions was provided. Another composition of MWCNT in solar glycol and water mixture with volume fractions 0.15 to 0.45 showed the non-Newtonian rheology as reported by Kumar et al. [28]. Fazeli et al. [29] explored the thermal properties of a brazed plate heat exchanger utilizing an HNF comprised of water and MWCNT-CuO (employed as the cold fluid). The investigation revealed that the most substantial HT enhancement is achieved under the conditions of a steady temperature of 35 °C.

Magnetohydrodynamics (MHD) has captivated the attention of numerous researchers owing to its extensive applicability across diverse sectors, including agriculture, physics, medicine, engineering, and the petroleum industry. Its presence contributes significantly to fluid motion regulation. Notably, the magnetic influence reshapes fluid concentration and transforms heat transmission outcomes within the flow, achieved through the manipulation of suspended nanoparticles [30]. Local magnetic effects can significantly impact the magnetic properties of nanoparticles, leading to various manifestations in nanoliquids. These include the formation of ferrohydrodynamic (FHD) fluids with sustained magnetism, magnetohydrodynamic (MHD) fluids with transient dynamic properties, or a hybrid combination of both [31], [32], [33]. Miroshnichenko et al. [34] conducted simulations to explore the free convective heat transfer of CuO nanofluid within a trapezoidal-shaped chamber, considering the impact of a consistent and directed magnetic field(MF). Their findings indicated that a reduction in the Hartmann number (Ha) and an augmentation in the nanoparticle concentration resulted in enhanced heat transmission effectiveness. Consequently, the behavior of nano liquids is intricately linked to MFs associated with heat transmission [35], [36], [37]. The effect of the MF on the entropy generation due to the thermal exchange in an irregular geometry filled with Ag-Mgo-water HNF was explored by Benzema et al. [38]. They evaluated a criterion from the second law of thermodynamics to explore the thermal performance of the vented system concerning the strength of the MF and the weight percentage of the nanoparticles. Aghaei et al. [39] aimed to employ a numerical model for simulating the irreversibility and HT phenomena with turbulent dynamics within a trapezium filled with oil-based MWCNT-CuO HNF with magnetic effect. Results exhibited that, for each Rayleigh number, the optimal approach for minimizing entropy generation (EGEN) involves utilizing a small amount of nanoparticles and strong MF. Another recent study reported by Parvin et al. [40] investigated the magnetic effect on the convective heat transfer of Al₂O₃-H₂O nanofluids within an irregularly shaped wavy chamber with an elliptic cylinder. They reported the exhibit of optimum heat transfer while the MF was directed vertically, and the fluid was considered non-Newtonian shear-thinning.

The aforementioned studies consider convection without solutal gradients; nevertheless, the addition of nano-constituents causes a significant impact on the HT and mass transfer (MT) with the associated advection subject to the concurrency of temperature and solutal gradients, known as double-diffusive convection (DDC). The presence of this phenomenon in various domains like oceanology, geoscience, life sciences, chemical processes, celestial studies, material engineering, and convective heat and solute transfer has sparked considerable attention in both experimental and theoretical explorations [41], [42], [43]. Esfahani and Bordbar [44] explored DDC inside a chamber of equal sides by employing NF. Their study revealed a notable trend: elevating the Lewis number (Le) amplified MT rates while concurrently diminishing heat transmission within the square cavity. The utilization of HNF subject to double-diffusive convection was studied by Toudja et al. [45] considering an irregular hexagon filled with MWCNT-MgO suspension. The base fluid of the suspension shows non-Newtonian shear-thinning behavior, and the results found that the elevated heat and mass transfer rate are found for the shear-thinning fluids with $n=0.8$ when the forced convection mode had dominated.

During the HT process in convection mode, NFs engage in intricate interactions with the boundaries of a structure. These structures can be tailored for efficient convection in various engineering contexts, taking on diverse geometrical shapes like cubes, triangles, squares, and trapezoids. Investigating HT in a convective process within an irregular geometry like a trapezium is notably more intricate than in regular chambers because of the presence of sloping walls. Trapezoidal configurations find applications in sectors like metal smelting (e.g., copper wire production) and the manufacturing of diverse heat exchangers. Notably, multiple studies have examined HT within trapezoidal enclosures, including works such as [46], [47], [48]. An exemplar in this domain is the work of Arian et al. [30], who examined the unsteady flow of Reiner-Rivlin NF confined between spinning circular dishes with a separation distance. This NF is characterized by traits of incompressibility and electrical conductivity. Their study comprehensively explored the impact of axial and tangential velocity, magnetic and temperature fields, concentration distribution, and the behavior of motile gyrotactic microorganisms within this complex system. In another investigation, Mebarek et al. [49] explored NF simulation within a trapezoidal cavity with an irregular boundary. The results indicated that augmenting the Ra and Ha improved thermal performance within the cavity. Amidst the existing body of research on trapezoidal enclosures, there remains a considerable knowledge gap concerning convective HT and MT due to both thermal and solutal diffusion within such enclosures when they are filled with HNF exhibiting non-Newtonian rheology. Furthermore, the literature lacks a comprehensive consensus on the entropy generation due to the convective flow of MWCNT-SiO₂-EG-water suspension to enhance convective heat transmission.

The objective of this paper is to comprehensively explore the unprecedented examination of natural convection subject to entropy generation within a trapezoidal enclosure filled with multi-walled CNT (MWCNT) and silicon dioxide (SiO₂) nanoconstituents within a binary mixture of water (70%) and EG (30%). Particularly, the investigation delves into the impact of distinct MF strengths and orientations at the forefront on free convection, featuring the unique inclusion of MWCNT-SiO₂-EG (30:70) HNF showcasing non-Newtonian shear-thinning rheology. By focusing on the thermal and fluid flow applications where the Newtonian or non-Newtonian nature of NF holds significant importance, this research seeks to contribute novel insights. Thermal and solutal gradients are established within the enclosure, with elevated temperatures and concentrations placed on the left inclined wall and lower counterparts on the right inclined wall. Through an in-depth exploration of governing parameters, the study scrutinizes the HT and MT rates quantified through its dimensionless engineering quantity named the Nusselt number (Nu) and Sherwood number (Sh), respectively. Additionally, the effectiveness of convective HT and MT is evaluated from a thermodynamic perspective, considering the entropy generation ($\bar{S}$) inherent to the heat and mass transfer process and hence quantify a criterion ($\xi =\bar{S}/\overline{Nu}$). Quantifying the ξ criterion can assist in improving thermal performance for industrial applications such as cooling systems, solar collectors, automobile radiators, etc.

2. Formulation of the physical problem

2.1. Physical model

Fig. 1(a) depicts the buoyancy-driven laminar two-dimensional (2D) heat and solute transfer flow in a trapezoidal container that contains MWCNT–SiO₂-EG ($30:70$) hybrid nanofluid (HNF). The enclosure is H in height and $L=2H$ in width with an aspect ratio of $A=H/L=0.5$. The left and right inclined wall is obtained by the relation $\tilde{x}=-\tilde{y}\cot {\delta }_0$ and $\tilde{x}=L+\tilde{y}\cot {\delta }_0$, respectively, where ${\delta }_0={110}^{\circ }$, and $0\le \tilde{y}\le H$. The top and bottom horizontal walls are maintained by adiabatic (${\tilde{T}}_{\tilde{y}}=\frac{\partial \tilde{T}}{\partial \tilde{y}}=0$) and impermeable (${\tilde{C}}_{\tilde{y}}=\frac{\partial \tilde{C}}{\partial \tilde{y}}=0$) conditions. The temperature of the left and the right side sloping wall is respectively at high (${\tilde{T}}_l$) and low (${\tilde{T}}_r$) temperature, thus generating a thermal buoyancy force. Analogously, the solutal concentrations are considered different in the left and the right inclined wall denoted by ${\tilde{C}}_l$ and ${\tilde{C}}_r$, respectively, thus generating a solutal buoyancy force. With the exception of density changes influenced by the temperature and solutal gradient in the horizontal direction, the fluid is presumed to be incompressible. This density variation is measured using the Boussinesq approximation. The volume fractions (ϕ) of nanoparticles (MWCNT + SiO₂) are considered very low ($<5\text{\%}$) to assure the fact of the homogeneous HNF model. The flow is supposed to be a single-phase HNF model, i.e., no-slip velocity exists in the interface of the host medium particles and the nanoparticles. The flow is thought of as influenced by a uniform magnetic field ${\mathbf{\text{M}}}_0=(M_0\cos ({\delta }_1),M_0\sin ({\delta }_1))$ of constant magnitude $M_0$ with oriented at an angle ${\delta }_1$ with the x-axis. Because of the electrically conductive HNF used within the container, this magnetic field (MF) creates the Lorentz force. The force term appearing in the momentum equations is obtained from $\mathbf{\text{F}}={\sigma }_{\mathrm{hbf}}(\mathbf{\text{V}}\times {\mathbf{\text{M}}}_0)\times {\mathbf{\text{M}}}_0$.

Figure 1.

(a) The physical model and (b) mesh configuration for the convective hybrid nanofluid fluid flow within the trapezoidal chamber with the associated boundary conditions.

2.2. Governing equations in dimensional form

The HNF submitted in the enclosure is considered laminar, two-dimensional, and incompressible with non-Newtonian characteristics. The non-linear partial differential equations (PDE) that regulate the development of mass, momentum, energy, and concentration for HNF within the enclosure under the magnetohydrodynamics (MHD) principle and Boussinesq approximation are stated in the following dimensional form [50], [51],

$$\frac{\partial \tilde{u}}{\partial \tilde{x}}+\frac{\partial \tilde{v}}{\partial y}=0$$ (1)

$${\rho }_{\mathrm{hbf}}[\frac{\partial \tilde{u}}{\partial \tilde{t}}+\tilde{u}\frac{\partial \tilde{u}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{u}}{\partial \tilde{y}}]=-\frac{\partial \tilde{p}}{\partial \tilde{x}}+\frac{\partial }{\partial \tilde{x}}\left[{\tilde{\tau }}_{\tilde{x}\tilde{x}}\right]+\frac{\partial }{\partial \tilde{y}}\left[{\tilde{\tau }}_{\tilde{x}\tilde{y}}\right]-{\sigma }_{\mathrm{hbf}}{M}_0^2[\tilde{u}{\sin }^2({\delta }_1)-\tilde{v}\sin ({\delta }_1)\cos ({\delta }_1)]$$ (2)

$${\rho }_{\mathrm{hbf}}[\frac{\partial \tilde{v}}{\partial \tilde{t}}+\tilde{u}\frac{\partial \tilde{v}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{v}}{\partial \tilde{y}}]=-\frac{\partial \tilde{p}}{\partial \tilde{y}}+\frac{\partial }{\partial \tilde{x}}\left[{\tilde{\tau }}_{\tilde{y}\tilde{x}}\right]+\frac{\partial }{\partial \tilde{y}}\left[{\tilde{\tau }}_{\tilde{y}\tilde{y}}\right]-{\sigma }_{\mathrm{hbf}}{M}_0^2[\tilde{v}{\cos }^2({\delta }_1)-\tilde{u}\sin ({\delta }_1)\cos ({\delta }_1)]+g[{\left(\rho {\beta }_{\tilde{T}}\right)}_{\mathrm{hbf}}(\tilde{T}-{\tilde{T}}_r)+{\left(\rho {\beta }_{\tilde{C}}\right)}_{\mathrm{hbf}}(\tilde{C}-{\tilde{C}}_r)]$$ (3)

$${(\rho C_p)}_{\mathrm{hbf}}[\frac{\partial \tilde{T}}{\partial \tilde{t}}+\tilde{u}\frac{\partial \tilde{T}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{T}}{\partial \tilde{y}}]=\frac{\partial }{\partial \tilde{x}}\left[k_{\mathrm{hbf}}\frac{\partial \tilde{T}}{\partial \tilde{x}}\right]+\frac{\partial }{\partial \tilde{y}}\left[k_{\mathrm{hbf}}\frac{\partial \tilde{T}}{\partial \tilde{y}}\right]$$ (4)

$$\frac{\partial \tilde{C}}{\partial \tilde{t}}+\tilde{u}\frac{\partial \tilde{C}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{C}}{\partial \tilde{y}}=\frac{\partial }{\partial \tilde{x}}\left[D_c\frac{\partial \tilde{C}}{\partial \tilde{x}}\right]+\frac{\partial }{\partial \tilde{y}}\left[D_c\frac{\partial \tilde{C}}{\partial \tilde{y}}\right]$$ (5)

where, ${\tilde{\tau }}_{\tilde{x}\tilde{x}}$, ${\tilde{\tau }}_{\tilde{x}\tilde{y}}$, ${\tilde{\tau }}_{\tilde{y}\tilde{x}}$, and ${\tilde{\tau }}_{\tilde{y}\tilde{y}}$ are the shear stress components defined by

$${\tilde{\tau }}_{\tilde{x}\tilde{x}}=2{\mu }_{\mathrm{eff}-\mathrm{hbf}}\frac{\partial \tilde{u}}{\partial \tilde{x}},{\tilde{\tau }}_{\tilde{x}\tilde{y}}={\mu }_{\mathrm{eff}-\mathrm{hbf}}(\frac{\partial \tilde{u}}{\partial \tilde{y}}+\frac{\partial \tilde{v}}{\partial \tilde{x}}),{\tilde{\tau }}_{\tilde{y}\tilde{x}}={\mu }_{\mathrm{eff}-\mathrm{hbf}}(\frac{\partial \tilde{v}}{\partial \tilde{x}}+\frac{\partial \tilde{u}}{\partial \tilde{y}}),{\tilde{\tau }}_{\tilde{y}\tilde{y}}=2{\mu }_{\mathrm{eff}-\mathrm{hbf}}\frac{\partial \tilde{v}}{\partial \tilde{y}}.$$

In the above equations, the velocity components $\tilde{u}$ and $\tilde{v}$ are taken into account along the $\tilde{x}$ and $\tilde{y}$ directions. The symbols $\tilde{p}$, T̃, and $\tilde{C}$ represent the fluid's dimensional pressure, temperature, and concentration. The HNF is characterized by parameters such as ${\rho }_{\mathrm{hbf}}$ for density, $k_{\mathrm{hbf}}$ for effective thermal conductivity, and $D_c$ for mass diffusivity. The term ${\mu }_{\mathrm{eff}-\mathrm{hbf}}$ represents the effective viscosity of the HNF, which is calculated using the equation below [50]:

$${\mu }_{\mathrm{eff}-\mathrm{hbf}}=m\left(\frac{{\mu }_{\mathrm{hbf}}}{{\mu }_{\mathrm{f}}}\right)|\dot{\tilde{\gamma }}{|}^{n-1}$$ (6)

where m (Nsⁿ/m²) stands for the consistency index and n is called the poser law index. The value of $n<1(n>1)$ determines the non-Newtonian shear-thinning (shear-thickening) characteristics of the hybrid-nanofluid of interest. It is noted that $m={\mu }_{\mathrm{f}}$ for Newtonian medium ($n=1$). Here, $|\dot{\tilde{\gamma }}|$ is called the shear rate defined by

$$|\dot{\tilde{\gamma }}|=\sqrt{2{\left(\frac{\partial \tilde{u}}{\partial \tilde{x}}\right)}^2+2{\left(\frac{\partial \tilde{v}}{\partial \tilde{y}}\right)}^2+{(\frac{\partial \tilde{u}}{\partial \tilde{y}}+\frac{\partial \tilde{v}}{\partial \tilde{x}})}^2}$$

2.3. Properties of hybrid-nanofluids

The equations for determining the thermophysical characteristics of the hybrid MWCNT-SiO₂-EG-Water HNF are outlined in this section. It's important to note that the experimental thermophysical quantities for the considered HNF in this study are not available in the existing literature. Therefore, this study relies on empirical correlations for two crucial effective thermal properties: thermal conductivity and dynamic viscosity. The effective thermal conductivity is estimated using an empirical correlation developed by Corcione through regression analysis based on a wide range of experimental data (14 sets from 10 independent research groups) relevant to water or ethylene glycol-based nanofluids with particle diameters ranging from 10 nm to 150 nm, nanoparticle volume fraction in the range from 0.02% to 9%, and temperature in the range between 294 K and 324 K. The standard deviations of effective thermal conductivity and effective dynamic viscosity are 1.86% and 1.84%, respectively [52], [53], [54], [55]. This validity is also confirmed by another experimental result of Ghanbarpour et al. [56]. These correlations are widely utilized in numerous published papers [57], [58], [59], [60], [61]. The effective mass density and specific heat at constant pressure are calculated using the mixing theory, which has been experimentally validated [20], [27], [28], [62], [63], [64], [65], [66], [67], [68], [69], [70]. Based on the model by Corcione et al. [53], the empirical correlations for dynamic viscosity and temperature-dependent thermal conductivity for the HNF of interest are defined in the study by Alsabery et al. [60] and explored here. It's worth noting that the subscripts “hbf”, “f”, “np1”, and “np2” are used throughout the study to represent the appropriate thermophysical properties of the HNF, base fluid, MWCNT, and SiO₂, respectively. Physical properties for hybrid nanoliquids used in the current numerical setup are detailed in Table 1 [31], [71]. In the empirical correlation of thermal conductivity, ${\tilde{T}}_{\mathrm{fr}}$ (=257 K) is the freezing temperature of the host medium, $R{e}_{np}=\frac{{\rho }_{\mathrm{f}}{u}_B(d_{np1}+d_{np2})}{{\mu }_{\mathrm{f}}}$ is defined as the Reynolds number of nanoparticles where $u_B=\frac{2k_b\tilde{T}}{\pi {\mu }_{\mathrm{f}}{(d_{np1}+d_{np2})}^2}$ determines the Brownian velocity of the suspended nanoparticles, $k_b=1.380648\times {10}^{-23}(J/K)$ determines the Boltzmann number and $d_f=0.1{[\frac{6M}{N_A\pi {\rho }_f}]}^{1/3}$ determines an approximation to the molecular diameter of the host liquid (30% Ethylene glycol+70% H₂O). Here the molecular weight of the base-fluid is $M=31.23$ g/mol, the Avogadro number is $N_A=6.022\times {10}^{23}$ mol⁻¹. ${\rho }_{\mathrm{f}}$ is the mass density of the base fluid calculated at temperature $T_0=300$ K. The necessary thermal properties of MWCNT and SiO₂ nanoparticles are mentioned in Table 2 to evaluate the thermophysical properties of HNF for further simulation process [27], [66], [72].

Table 1.

Thermal properties of hybrid nanofluids [31], [71].

Properties	Hybrid nanofluids
Density	ρhbf = ϕnp1ρnp1 + ϕnp2ρnp2 + (1 − ϕnp1 − ϕnp2)ρf
Heat capacitance	${(C_p)}_{\mathrm{hbf}}=\frac{{\varphi }_{np1}{(\rho C_p)}_{np1}+{\varphi }_{np2}{(\rho C_p)}_{np2}+(1-\varphi ){(\rho C_p)}_f}{{\rho }_{\mathrm{hbf}}}$
Dynamic viscosity	${\mu }_{\mathrm{hbf}}=\frac{{\mu }_{\mathrm{f}}}{1-34.87{(d_f)}^{0.3}{d}_{hp}}$ where, $d_{hp}={(d_{np1})}^{-0.3}{({\varphi }_{np1})}^{1.03}+{(d_{np2})}^{-0.3}{({\varphi }_{np2})}^{1.03}$
Thermal conductivity	$k_{\mathrm{hbf}}=k_{\mathrm{f}}[1+4.4R{e}_{np}^{0.4}P{r_f}^{0.66}{\left(\frac{\tilde{T}}{{\tilde{T}}_{fr}}\right)}^{10}{(k_{\mathrm{f}})}^{-0.03}{k}_{hp}]$ where, $k_{hp}={(k_{np1})}^{0.03}{({\varphi }_{np1})}^{0.66}+{(k_{np2})}^{0.03}{({\varphi }_{np2})}^{0.66}$
Electrical conductivity	${\sigma }_{\mathrm{hbf}}={\sigma }_{\mathrm{f}}\frac{1+3({\sigma }_{hp}/{\sigma }_{\mathrm{f}}-1){\sigma }_{\mathrm{hbf}}}{({\sigma }_{hp}/{\sigma }_{\mathrm{f}}+2)-({\sigma }_{hp}/\sigma \mathrm{f}-1){\sigma }_{\mathrm{hbf}}}$ where, ${\sigma }_{hp}=\frac{{\varphi }_{np1}{\sigma }_{np1}+{\varphi }_{np2}{\sigma }_{np2}}{{\varphi }_{np1}+{\varphi }_{np2}}$
Expansion coefficient	${({\beta }_{\tilde{T}})}_{\mathrm{hbf}}=\frac{{\varphi }_{np1}{({\rho }_{{\beta }_{\tilde{T}}})}_{np1}+{\varphi }_{np2}{({\rho }_{{\beta }_{\tilde{T}}})}_{np2}+(1-{\varphi }_{np1}-{\varphi }_{np2}){({\rho }_{{\beta }_{\tilde{T}}})}_{\mathrm{f}}}{{\rho }_{\mathrm{hbf}}}$

Table 2.

Thermophysical properties of MWCNT and SiO₂ nanoparticles at 27 ^∘C temperature. [27], [66], [72].

Properties	H20 + EG 30%	MWCNT	SiO2
Specific heat capacity, Cp (J/kg.K)	3736.2	711	765
Thermal conductivity, k (W/m.k)	0.48853	3000	36
Density, ρ (kg/m3)	1034	2100	3970
Viscosity, μ (kg/m.s)	1.7613×10−3	-	-
Thermal expansion coefficient, β (1/K)	3.3317 ×10−3	4.2×10−5	0.63×10−5
Electrical conductivity, σ (S/m)	5.03 × 10−4	1.9 × 10−4	1 × 10−10

2.4. Dimensionless formulations

The governing equations (1)-(6) in section 2.2 must be dimensionless in order to proceed with the numerical solution. In this regard, the following non-dimensional variables [50], [73] are used to non-dimensional governing equations mentioned above,

$$x=\frac{\tilde{x}}{L},y=\frac{\tilde{y}}{L},u=\frac{\tilde{u}L}{{\alpha }_f},v=\frac{vL}{{\alpha }_f},t=\tilde{t}\frac{{\alpha }_f}{L^2},p=\frac{\tilde{p}{L}^2}{{\rho }_f{\alpha }_f^2},\theta =\frac{\tilde{T}-{\tilde{T}}_r}{{\tilde{T}}_l-{\tilde{T}}_r},C=\frac{\tilde{C}-{\tilde{C}}_r}{{\tilde{C}}_l-{\tilde{C}}_r},Ha=\sqrt{\frac{{\sigma }_f{\alpha }_f^{1-n}}{m}}{M}_0{L}^n,Ra=\frac{g{\left(\rho {\beta }_{\tilde{T}}\right)}_f({\tilde{T}}_l-{\tilde{T}}_r)L^{2n+1}}{m{\alpha }_f^n},Pr=\frac{m{L}^{2-2n}}{{\rho }_f{\alpha }_f^{2-n}}.$$ (7)

Utilizing the transformation outlined in equation (7), we can derive the effective viscosity as follows:

$${\mu }_{\mathrm{eff}-\mathrm{hbf}}=m\left(\frac{{\mu }_{\mathrm{hbf}}}{{\mu }_{\mathrm{f}}}\right){\left(\frac{{\alpha }_f}{L^2}\right)}^{n-1}D$$ (8)

where, D denotes non-dimensional fluid viscosity [50] represented by

$$D=|\dot{\gamma }{|}^{n-1}={\left[\sqrt{2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})}^2}\right]}^{n-1}$$

Utilizing the above non-dimensional variables and parameters given in equation (7), the governing dimensional equations (1)-(5) can be formulated into its following non-dimensional form:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$ (9)

$$\frac{{\rho }_{\mathrm{hbf}}}{{\rho }_{\mathrm{f}}}[\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}]=-\frac{\partial p}{\partial x}+\frac{{\mu }_{\mathrm{hbf}}}{{\mu }_{\mathrm{f}}}Pr[\frac{\partial }{\partial x}\left(2D\frac{\partial u}{\partial x}\right)+\frac{\partial }{\partial y}(D\frac{\partial u}{\partial y}+D\frac{\partial v}{\partial x})]-\frac{{\sigma }_{\mathrm{hbf}}}{{\sigma }_{\mathrm{f}}}\cdot H{a}^2\cdot Pr[u{\sin }^2({\delta }_1)-v(\sin {\delta }_1)\cos ({\delta }_1)]$$ (10)

$$\frac{{\rho }_{\mathrm{hbf}}}{{\rho }_{\mathrm{f}}}[\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}]=-\frac{\partial p}{\partial y}+\frac{{\mu }_{\mathrm{hbf}}}{{\mu }_{\mathrm{f}}}Pr[\frac{\partial }{\partial x}(D\frac{\partial v}{\partial x}+D\frac{\partial u}{\partial y})+\frac{\partial }{\partial y}\left(2D\frac{\partial v}{\partial y}\right)]-\frac{{\sigma }_{\mathrm{hbf}}}{{\sigma }_{\mathrm{f}}}\cdot H{a}^2\cdot Pr[v{\cos }^2({\delta }_1)-u(\sin {\delta }_1)\cos ({\delta }_1)]+\frac{{\left(\rho {\beta }_{\tilde{T}}\right)}_{\mathrm{hbf}}}{{\left(\rho {\beta }_{\tilde{T}}\right)}_{\mathrm{f}}}\cdot Ra\cdot Pr(\theta +NC)$$ (11)

$$\frac{{\left(\rho C_p\right)}_{\mathrm{hbf}}}{{(\rho C_p)}_{\mathrm{f}}}[\frac{\partial \theta }{\partial t}+u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}]=\frac{\partial }{\partial x}\left(\frac{k_{\mathrm{hbf}}}{k_{\mathrm{f}}}\frac{\partial \theta }{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{k_{\mathrm{hbf}}}{k_{\mathrm{f}}}\frac{\partial \theta }{\partial y}\right)$$ (12)

$$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=\frac{1}{Le}(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2})$$ (13)

with the following non-dimensional boundary conditions:

$$\begin{gathered} u=v=0,\theta =C=1\text{on the left inclined wall}x=-y\cot {\delta }_0 \\ u=v=0,\theta =C=0\text{on the right inclined wall}x=1+y\cot {\delta }_0 \\ u=v=0,\frac{\partial \theta }{\partial y}=\frac{\partial C}{\partial y}=0\text{on the top and bottom horizontal walls} \end{gathered}$$ (14)

In equations (10) and (11), Pr, Ra, and Ha represent the Prandtl number, Rayleigh number, and the Hartmann number, respectively, for the carrier fluid with non-Newtonian properties. Also, $N=\frac{{\left({\beta }_{\tilde{C}}\right)}_{hbf}}{{\left({\beta }_{\tilde{T}}\right)}_{hbf}}\frac{{\tilde{C}}_l-{\tilde{C}}_r}{{\tilde{T}}_l-{\tilde{T}}_r}$ is referred to the buoyancy ratio, $Le=\frac{{\alpha }_f}{D_c}$ is the Lewis number, where, ${\alpha }_f=k_f/{\left(\rho C_p\right)}_f$ is the thermal diffusivity of the base fluid.

2.5. Heat and mass transfer rate

Exploring the rate of heat transfer (HT) and mass transfer (MT) due to the HNF flow from the left active wall, the local Nusselt number (Nu) and the local Sherwood number (Sh), two dimensionless quantities along the inclined wall are evaluated by

$$Nu=-\frac{k_{\mathrm{hbf}}}{k_{\mathrm{f}}}{\left[\frac{\partial \theta }{\partial \mathbf{\text{n}}}\right]}_{\mathrm{left}-\mathrm{wall}}\text{and}Sh=-{\left[\frac{\partial C}{\partial \mathbf{\text{n}}}\right]}_{\mathrm{left}-\mathrm{wall}},$$ (15)

where n denotes the plane's normal direction. The average quantities of these two dimensionless entities along the left inclined wall of length $l_w$ are given by,

$$\overline{Nu}=\frac{1}{l_w}\underset{\mathrm{left}-\mathrm{wall}}{\int }Nu\text{d}s\text{and}\overline{Sh}=\frac{1}{l_w}\underset{\mathrm{left}-\mathrm{wall}}{\int }Sh\text{d}s,$$ (16)

where ds indicates the differential element along the inclined wall.

2.6. Entropy generation (EGEN)

The existence of heat and concentration gradients between the sloping walls of the enclosure produces fluid motion that results in energy dissipation. This energy loss occurs in the processes of momentum, HT, and MT, and it is accompanied by the generation of entropy within a closed system. EGEN serves as a quantitative representation of the “quality” of the transfer process, indicating whether the process is reversible or irreversible (characterized by energy losses). In the context of magnetohydrodynamics convective HT and MT, EGEN or irreversibility is influenced by factors such as viscous effects, HT, MT, and the Lorentz force. Consequently, in this study involving the presence of an MF, the local EGEN can be calculated as the summation of the following components,

$${\tilde{S}}_{F,l}=\frac{{\mu }_{\mathrm{eff}-\mathrm{hbf}}}{T_0}[2{\left(\frac{\partial \tilde{u}}{\partial \tilde{x}}\right)}^2+2{\left(\frac{\partial \tilde{v}}{\partial \tilde{y}}\right)}^2+{(\frac{\partial \tilde{u}}{\partial \tilde{y}}+\frac{\partial \tilde{v}}{\partial \tilde{x}})}^2],{\tilde{S}}_{T,l}=\frac{k_{\mathrm{hbf}}}{T_0^2}[{\left(\frac{\partial \tilde{T}}{\partial \tilde{x}}\right)}^2+{\left(\frac{\partial \tilde{T}}{\partial \tilde{y}}\right)}^2],{\tilde{S}}_{C,l}=\frac{R{D}_c}{C_0}[{\left(\frac{\partial \tilde{C}}{\partial \tilde{x}}\right)}^2+{\left(\frac{\partial \tilde{C}}{\partial \tilde{y}}\right)}^2]+\frac{R{D}_c}{T_0}[\frac{\partial \tilde{T}}{\partial \tilde{x}}\frac{\partial \tilde{C}}{\partial \tilde{x}}+\frac{\partial \tilde{T}}{\partial \tilde{y}}\frac{\partial \tilde{C}}{\partial \tilde{y}}],{\tilde{S}}_{M,l}=\frac{{\sigma }_{\mathrm{hbf}}{M_0}^2}{T_0}{(\tilde{u}\sin {\delta }_1-\tilde{v}\cos {\delta }_1)}^2.$$ (17)

The dimensional form of the local EGEN can be expressed as ${\tilde{S}}_l={\tilde{S}}_{F,l}+{\tilde{S}}_{T,l}+{\tilde{S}}_{C,l}+{\tilde{S}}_{M,l}$. Using the non-dimensional transformations listed in Eq. (7) and typical characteristic scale $S_0=\frac{k_f{(\mathrm{\Delta }T)}^2}{T_0^2{L}^2}$ [74] for EGEN, one can obtain the local EGEN in non-dimensional form by

$$S_l=\frac{{\tilde{S}}_l}{S_0}=S_{F,l}+S_{T,l}+S_{C,l}+S_{M,l}$$ (18)

where

$$S_{F,l}={\lambda }_1\frac{{\mu }_{\mathrm{hbf}}}{{\mu }_{\mathrm{f}}}{[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})}^2]}^{\frac{n+1}{2}},S_{T,l}=\frac{k_{\mathrm{hbf}}}{k_{\mathrm{f}}}[{\left(\frac{\partial \theta }{\partial x}\right)}^2+{\left(\frac{\partial \theta }{\partial y}\right)}^2],S_{C,l}={\lambda }_2[{\left(\frac{\partial C}{\partial x}\right)}^2+{\left(\frac{\partial C}{\partial y}\right)}^2]+{\lambda }_3[\frac{\partial \theta }{\partial x}\frac{\partial C}{\partial x}+\frac{\partial \theta }{\partial y}\frac{\partial C}{\partial y}],S_{M,l}={\lambda }_1\frac{{\sigma }_{\mathrm{hbf}}}{{\sigma }_{\mathrm{f}}}H{a}^2{(u\sin {\delta }_1-v\cos {\delta }_1)}^2.$$ (19)

Here, the parameters ${\lambda }_1=\frac{T_{0}m{\alpha }_f^{n+1}}{k_f{(\mathrm{\Delta }T)}^2{L}^{2n}}$, ${\lambda }_2=\frac{R{D}_c{T}_0^2}{k_f{C}_0}{\left(\frac{\mathrm{\Delta }C}{\mathrm{\Delta }T}\right)}^2$, and ${\lambda }_3=\frac{R{D}_c{T}_0}{k_f}\left(\frac{\mathrm{\Delta }C}{\mathrm{\Delta }T}\right)$ are non-dimensional coefficients and called irreversibility distribution ratios. These ratios play a pivotal role in characterizing fluid friction and diffusive irreversibilities. Notably, the EGEN attributed to diffusion ($S_C$) can be dissected into distinct components. It's important to highlight that the EGEN in $S_C$ encompasses a pure term (1st term) dependent solely on the concentration gradient and a coupled term (2nd term) influenced by both thermal and concentration gradients. For a comprehensive perspective, the dimensionless average EGEN is derived through the integration of Equation (18) across the computational domain R, as expressed by the following equation:

$$\bar{S}=\frac{1}{R}\underset{\mathbf{\text{R}}}{\iint }{S}_l(x,y)d\mathbf{\text{R}},$$ (20)

where R is the area of the region of the enclosure. Another important dimensionless measure from the thermodynamics aspect is the local Bejan number $(B{e}_l)$, which was defined originally by $B{e}_l=\frac{S_{T,l}}{S_{F,l}+S_{T,l}}$. This definition of the $B{e}_l$ can only assess the relative dominance of EGEN owing to HT vs fluid friction in the absence of mass diffusion. In order to include the diffusive irreversibility, Oueslati et al. [75] proposed another version of Bejan number $(B{e}_l)$, which represents the relative dominance of HT and MT irreversibility to the total irreversibility $(S_L)$ and is defined by

$$B{e}_l=\frac{S_{T,l}+S_{C,l}}{S_{F,l}+S_{T,l}+S_{C,l}+S_{M,l}}.$$ (21)

Furthermore, the average Bejan number ($\overline{Be}$) is calculated by

$$\overline{Be}=\frac{1}{R}\underset{\mathbf{\text{R}}}{\iint }B{e}_l(x,y)d\mathbf{\text{R}}.$$ (22)

The Bejan number (Be) holds important physical implications based on its numerical values. Within the enclosure, when $Be>0.5$, it signifies that HT and MT irreversibility predominates over other forms of irreversibility. On the other hand, when $Be<0.5$, it indicates that irreversibility arising from the viscous effect (fluid friction) and the MF takes precedence.

3. Numerical implementation

3.1. Numerical method

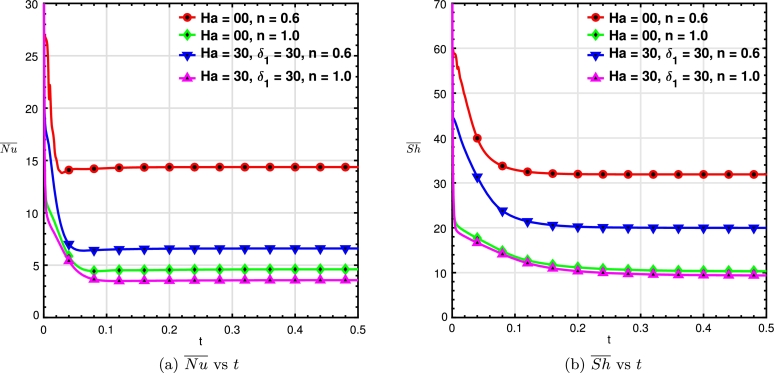
An in-house FORTRAN code based on the finite volume method (FVM) [76] alongside double-precision computation is used to numerically solve the dimensionless governing equations Eqs. (10) -(13) associated with the conditions Eq. (14) applied on the wall boundaries. For numerical simulations, the solution domain is first discretized into a finite number of control volumes (CVs) in a uniform fashion using the relationship $x=\xi +(2\xi -1)y\cot {\delta }_0$ where $0\le \xi \le 1$ and $0\le y\le A(=0.5)$. After that, the hyperbolic tangent (tanh) function has been utilized to transform the uniformly distributed mesh to a non-uniform distribution so that meshes appear densely near the walls and sparsely at the core region of the enclosure as illustrated in Fig. 1(b). Dense meshes near the walls can capture the complex fluid interaction within the thin boundary layer with the required accuracy and help to obtain higher accuracy in the overall numerical simulation. In the FVM, the dimensionless partial differential equations are discretized over the CVs and then integrated on CVs with four faces: north, west, south, and east around a node. In this method, the conservation of mass fluxes is maintained on the interface of CVs. The mass fluxes at individual cell faces are determined through linear interpolation based on the adjacent nodal values. The simulation progresses with a uniform time step interval of $\mathrm{\Delta }t={10}^{-5}$, and a 3-point backward difference method is applied to advance the simulation in the temporal domain. The second-order central-difference method is adopted to discretize the convective and diffusion terms. During the iterative process, pressure has been corrected using the most used SIMPLE algorithm [77], and the convergence criterion meets the requirement that the relative errors between two successive iterations in the field variables ($u,v,p,\theta ,C$) are less than ${10}^{-6}$. Once the field variables satisfy the convergence criterion, the value of the average Nusselt number $(\overline{Nu})$ and the average Sherwood number $(\overline{Sh})$ are calculated at each time step. The program runs until the steady state condition is obtained, i.e., the residual error of the quantities between two successive time steps is less than the ${10}^{-6}$ as illustrated for a few sample cases in Fig. 2(a,b). More details of the stability of the numerical simulation can be found in [50], [73]. The following sections illustrate grid independence tests and code validation to justify the precision and reliability of the numerical procedure utilized in the present study.

Figure 2.

Convergence feature for the average (a) Nusselt number ($\overline{Nu}$), and (b) Sherwood number ($\overline{Sh}$) for the case of Ra = 10⁵,N = 2.0,Le = 5.0,Pr = 13.470,ϕ = 0.02 while Ha = 0,30 and n = 0.6,1.0.

3.2. Grid sensitivity test

Table 3 demonstrates the impact of varying grid sizes on the numerical outcomes, specifically on the $\overline{Nu}$ and Sherwood number ($\overline{Sh}$). This sensitivity analysis is conducted considering both Newtonian fluids ($n=1.0$) and shear-thinning fluids ($n=0.6$), maintaining a constant ϕ of 2%. To ensure computational efficiency, the grid size denoted as $G_2$ has been selected for subsequent numerical simulations within this investigation.

Table 3.

Grid independence study at Pr = 13.470, Ra = 10⁵, N = 2.0, Le = 5.0, Ha = 0, and ϕ = 0.02.

Mesh Size	$\overline{Nu}(|\mathrm{\Delta }|\text{\%})$			$\overline{Sh}(|\mathrm{\Delta }|\text{\%})$
(x × y)	n = 0.6	n = 1.0		n = 0.6	n = 1.0
G1 = 41 × 41	13.66075 (5.10%)	4.40775 (4.64%)		30.36654 (5.00%)	9.88778 (4.24%)
G2 = 81 × 81	14.39592 (0.00%)	4.62242 (0.00%)		31.96785 (0.00%)	10.32517 (0.0%)
G3 = 161 × 161	14.76644 (2.57%)	4.72620 (2.24%)		32.84582 (2.75%)	10.54034 (2.08%)

3.3. Numerical validation

3.3.1. Justification for single-phase homogeneous nanofluid modeling

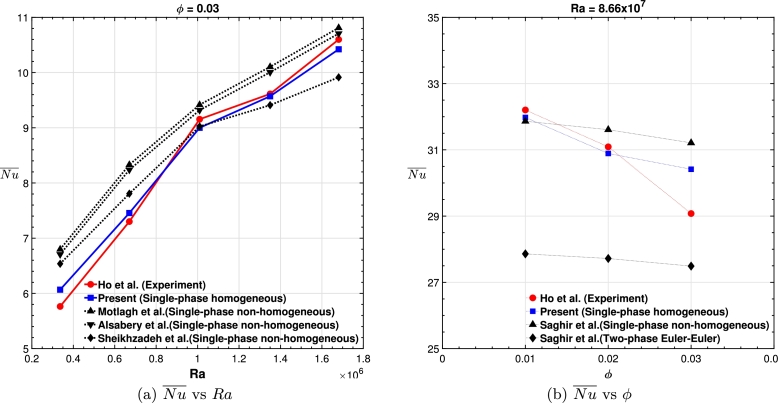
Numerical studies on nanofluid modeling typically follow two approaches. The first approach is the single-phase homogeneous or non-homogeneous model, where nanofluids are treated as pure fluids, assuming a local thermal equilibrium state occurs between the solid and liquid phases. In a homogeneous model, no-slip motion occurs between fluid molecules and nanoparticles. In contrast, in a non-homogeneous model, slip mechanisms occur between the solid and liquid phases due to Brownian diffusion and thermophoresis. Ongoing debates exist about the inclusion of Brownian diffusion and thermophoresis effects in the model, especially at low-volume fractions and small temperature gradients across the enclosure. Despite nanofluids being solid-liquid mixtures, most studies treat them as single-phase fluids due to the small sizes (<100 nm) and concentrations ($\le 4\text{\%}$) of suspended nanoparticles, assuming statistical homogeneity and isotropy. This means that nanofluids can be treated as pure fluids with further assumptions of local thermal equilibrium and no-slip motion between the solid and liquid phases. The second approach is the heterogeneous or two-phase model, which considers the effects of slip mechanisms between suspended particles and the base liquid, potentially leading to a non-uniform distribution of the solid phase concentration in the mixture. A significant amount of experimental and empirical research has been carried out to investigate the impact of nanoparticles on the characteristics of nanofluids. However, achieving a consensus on the validity of the results remains challenging due to the intricate nature of the experimental models. In this regard, Ho et al. [64] addressed this shortcoming by performing experiments on a simple cavity as model geometry to isolate the effect of material properties on the heat transfer characteristics.

To validate the applicability of the single-phase homogeneous model, a comparison of the average Nusselt number is made with experimental results from the natural convection of nanofluid in a square cavity conducted by Ho et al. [64], as well as numerical results from Motlag & Sotanipour [58], Alsabery et al. [59], Sheikhzadeh et al. [57] using a non-homogeneous single-phase model, as shown in the Fig. 3(a). In addition, a comparison between the present results and the two-phase model is provided in Fig. 3(b) to justify the relevance of the single-phase homogeneous model compared to the two-phase Euler-Euler model reported in Saghir et al. [78]. The present numerical results closely resemble the experimental data with an error of less than 5%, indicating that the single-phase approach predicts the heat transfer rate with better accuracy in contrast to other models, though other models provide deep insight into the liquid and solid phases in the mixture. Although the Euler-Euler two-phase model is the most versatile, it comes with a high computational expense. This suggests that employing the single-phase model with effective thermophysical properties would be both cost-effective and accurate in practical aspects as long as the nanoparticle volume fraction is considered low. Therefore, the present study is forwarded based on the concept that nanofluids act more like a single-phase fluid rather than a traditional solid-liquid mixture. This implies that convective heat transfer correlations used for single-phase flows can also be applied to nanoparticle suspensions, provided that the thermophysical properties used are the nanofluid effective properties calculated at the reference temperature.

Figure 3.

Comparison between present results with (a) the experimental results in [64], numerical results in Motlag & Sotanipour [58], Alsabery et al. [59], Sheikhzadeh et al. [57], (b) the results in Saghir et al. [78] to justify the relevance of the single-phase homogeneous model compared to the two-phase model with the experimental results.

3.3.2. Code validation for MHD double-diffusive convection

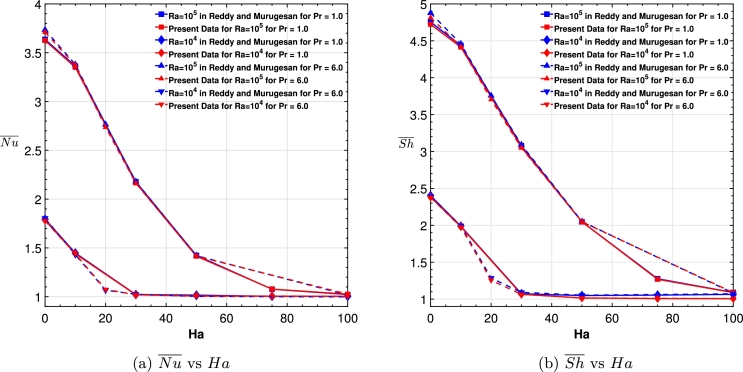
The validity of the present numerical code is established through a comparison with the study conducted by Reddy and Murugesan [79], which focused on a square enclosure. The consistency of the present numerical outcomes and their work is assessed in terms of the $\overline{Nu}$ and $\overline{Sh}$ across a range of Hartmann numbers ($Ha=0-100$) and Rayleigh numbers ($Ra={10}^4$, 10⁶). These validations are performed for a horizontal magnetic field (${\delta }_1=0$) with different values of Prandtl number such as $Pr=1$ and $Pr=6$ while keeping $Le=2.0$, $N=0.75$ and $\varphi =0$. The graphical representations as shown in Fig. 4(a,b) vividly indicate a strong agreement between the present code and the outcomes of the reference [79]. As a result, the internal computational code designed for studying double-diffusive convection influenced by an MF has been effectively validated, confirming its reliability for subsequent numerical simulations.

Figure 4.

Comparison of the present result with the results of Reddy and Murugesan [79] for the average (a) Nusselt number ($\overline{Nu}$) and (b) Sherwood number ($\overline{Sh}$) with Ha while Ra = 10⁴,10⁵ and Pr = 1,6.

3.3.3. Code validation for shear-thinning fluids and nanofluids(NF)

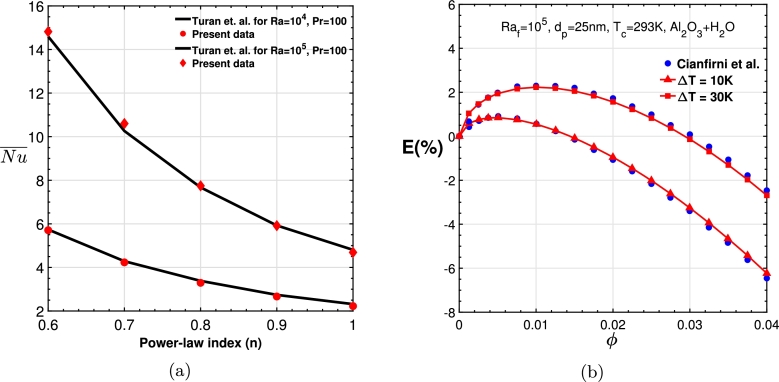
To justify whether the present numerical code is valid for the non-Newtonian shear-thinning fluids, we establish a comparison in Fig. 5(a) for the $\overline{Nu}$ with the corresponding outcomes reported in Turan et al. [80] for $n=0.6-1.0$ and $Ra={10}^4-{10}^5$. Furthermore, the present numerical solution regarding the usage of the temperature-dependent thermal properties towards the simulation of $\overline{Nu}$ followed by the heat transfer enhancement due to added nanoparticles is confirmed by comparing the present results to Cianfrini et al. [55]. Fig. 5(b) depicts a comparison of current numerical results to their work in terms of HT enhancement, $E\text{\%}=(\frac{\overline{Nu}-{\overline{Nu}}_{\varphi =0}}{{\overline{Nu}}_{\varphi =0}}\times 100)$ where, ${\overline{Nu}}_{\varphi =0}$ is the HT rate obtained using only base fluid, for various ϕ in the range $0-0.04$ by keeping $Pr=6.2$ and $Ra={10}^5$ fixed. As shown in the figure, the simulation results using the present numerical code are quite close to the previously reported numerical values.

Figure 5.

Comparison between present results with the results of (a) average Nusselt number ($\overline{Nu}$) for shear-thinning fluids in Turan et al. [80], and (b) heat transfer enhancement (E%) for nanofluids in Cianfrini et al. [55].

4. Results and discussion

This study aims to investigate the intricate relationships between thermo-solutal natural convection and EGEN driven by horizontal temperature and solutal gradients in a trapezoidal enclosure (${\delta }_0={110}^{\circ }$). The investigation encompasses fluids exhibiting a spectrum of rheological behaviors, ranging from shear-thinning ($n=0.6,0.8$) to Newtonian ($n=1$) fluids. The study's objective is to dissect the impact of various parameters, including magnetic field (MF) strength ($Ha=0-50$) with diverse angular directions (${\delta }_1=0^{\circ }-{90}^{\circ }$), and volume fraction ($\varphi =0\text{\%}-4\text{\%}$), on the intricate dynamics of thermal and solutal transfer processes. Furthermore, the research delves into the complexities of thermo-solutal convection in a non-Newtonian nanofluid flow, where both solutal and thermal buoyancy forces come into play, as quantified by buoyancy ratios ($N=-2,-1,0,1,2$). The ensuing sections of this study unravel insights into the intricate interplay of EGEN and thermal performance analysis within complex fluid systems, considering a constant $Ra={10}^5$ and $Le=5$.

4.1. Viscosity contours of non-Newtonian fluids

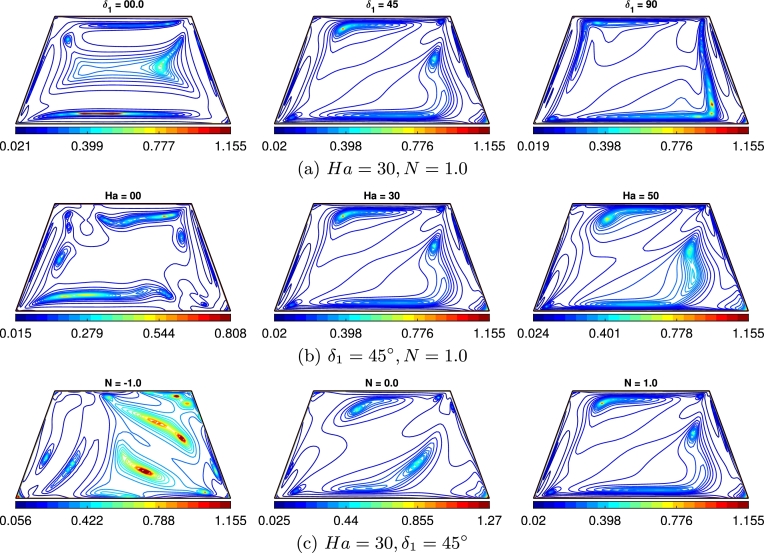
The numerical results obtained in this study begin by examining the non-Newtonian viscosity field within the enclosure. The non-Newtonian viscosity results for the chosen HNF are depicted in Fig. 6(a-c) for the shear-thinning fluid $n=0.6$, while the volume fraction is held constant at $\varphi =0.02$. The response of local viscosity with respect to the governing parameters is observed in this figure. The results indicate that changing the MF angle, as in Fig. 6(a), for a constant strength of a magnetic field does not significantly affect the global range of the viscosity variation within the enclosure. However, changing the MF orientation from horizontal to oblique reduces the viscosity within the boundary layer near the bottom wall. These results suggest strong convection can occur when the magnetic field is aligned at a ${45}^{\circ }$ angle. It is evident that increasing the MF strength leads to a reduction in flow strength, resulting in a decrement of shear rate along with an increase in viscous force, as demonstrated in Fig. 6(b). An interesting phenomenon is also observed when the buoyancy forces act in the opposite direction, as compared to the aided case. When $N=-1$, the buoyancy forces are of equal strength and directed in opposite directions, resulting in more bulk viscosity within the right half of the enclosure, leading to expectations of weak convection. In contrast, as illustrated in Fig. 6(c), lesser viscosity is observed in the case of aided buoyancy force $N=1.0$.

Figure 6.

Viscosity contours for the shear-thinning fluid (n = 0.6) in response to various governing parameters (a) Ha = 30,N = 1.0; (b) δ₁ = 45^∘,N = 1.0; and (c) Ha = 30,δ₁ = 45^∘ while the volume fraction is set ϕ = 0.02.

4.2. Flow field in terms of streamlines

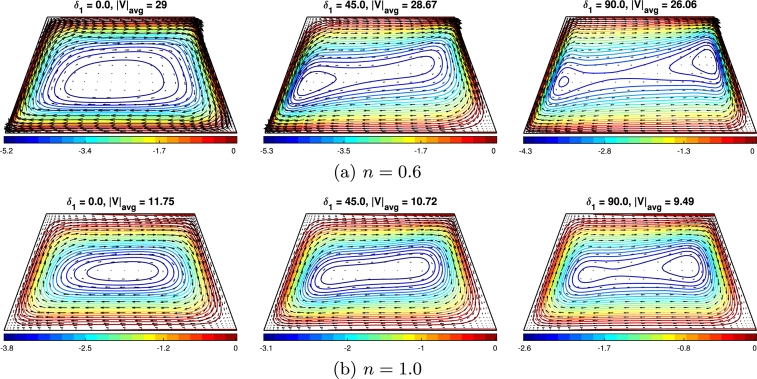
In this section, the flow of the fluid is observed when the parameters are varied. Fig. 7(a,b) displays the influence of MF angle (${\delta }_1$) on the streamlines featuring Newtonian ($n=1.0$) and shear-thinning ($n=0.6$) HNF when other parameters remained constant. When ${\delta }_1=0^{\circ }$, i.e., horizontal MF is applied, the streamlines appear more densely close to the walls, reducing the boundary layer thickness. With the MF's direction shifting, the flow gets weaker, and the inner vortex of the streamline stretches diagonally. With increasing MF angle, the magnitude of the stream functions decreases at all points within the enclosure, gradually weakening the fluid's flow circulation. The average velocity magnitude is observed to be lowered by 10% for the vertical magnetic field compared to the horizontal magnetic as applied to the shear-thinning fluid. However, for $n=0.6$, as the MF angle increases, the core region of the vortex tends to split out and slowly move toward the inclined wall of the trapezoidal enclosure. Simultaneously, the core region also inclines slightly with the MF angle, exhibiting complex and dynamic behavior. For a given MF angle (${\delta }_1$), the flow strength gets weakened when $n=1$ than $n=0.6$. The fluid's viscosity increases as the power law index decreases, resulting in higher fluid velocities and a thinner boundary layer.

Figure 7.

Effect of magnetic field direction (δ₁ = 0^∘,45^∘,90^∘) to the flow field (streamlines) for the (a) shear-thinning fluid (n = 0.6) and (b) Newtonian fluid (n = 1.0), where Ha = 30, N = 1.0 and ϕ = 0.02.

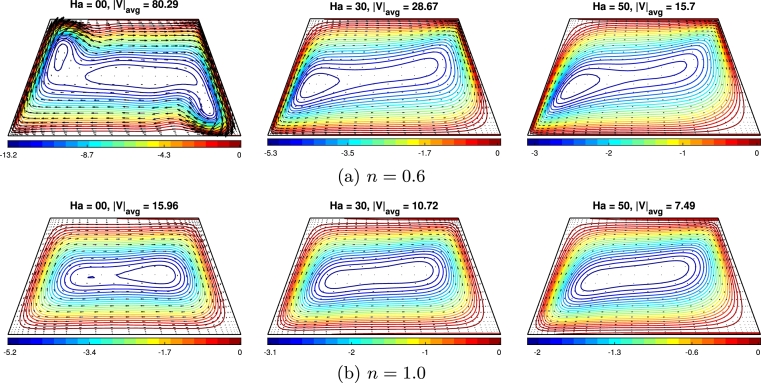
Fig. 8(a,b) depicted the impact of the non-dimensional number Hartmann number (Ha) representing the strength of the MF for n= 0.6 and 1,0. Results show that increasing Ha leads to a gradual reduction in the effectiveness of fluid flow circulation. It happens due to the strength of the Lorentz force, which acts as a resistive force against the flow and further weakens it, as can be seen by looking at the vector field. Augmenting the MF strength through an increment in Ha results in a decrement of the average velocity magnitude. Results show that the velocity magnitude gets lowered by 80% while applying MF with $Ha=50$ compared to $Ha=0$ for $n<1.0$. In the case of Newtonian fluids, the velocity magnitude decreases by 53% when MF is applied. In addition, increasing Ha reduces the contour size of streamlines, indicating a gradual decline in convection strength. Additionally, the boundary layer becomes thicker to the enclosure's side walls, and the vortex changes shape by elongating horizontally as Ha increases. In the case of Newtonian fluid, for $Ha=0$, two secondary vortexes are observed within the core region, which combine to form a single vortex as Ha increases. For the power law index of 0.6, two split vortexes are initially present within the core region for $Ha=0$, but they merge into a single core region as Ha increases ($Ha=30,50$). This behavior signifies a more substantial flow for $n=0.6$ than $n=1.0$ at a given Ha value. The reduced apparent viscosity associated with lower power law indices increases fluid velocity. Thus, increasing the power-law index represents the strengthening of the viscosity with the applied shear stress, resulting in a weaker version of the flow strength. Specifically, as n decreases, the vortex's core region expands and splits into two segments for $Ha=0$. However, as Ha increases ($Ha=30,50$), the vortex's core region tends to split out, forming a portion of the vortex moving toward the left inclined wall ($n=0.6$). Moreover, the momentum boundary layer becomes thinner with decreasing n. i.e., for shear-thinning fluids.

Figure 8.

Effect of Hartmann number (Ha=00, 30, 50) to the flow field (streamlines) for the (a) shear-thinning fluid (n = 0.6) and (b) Newtonian fluid (n = 1.0), where δ₁ = 45^∘, N = 1.0, and ϕ = 0.02.

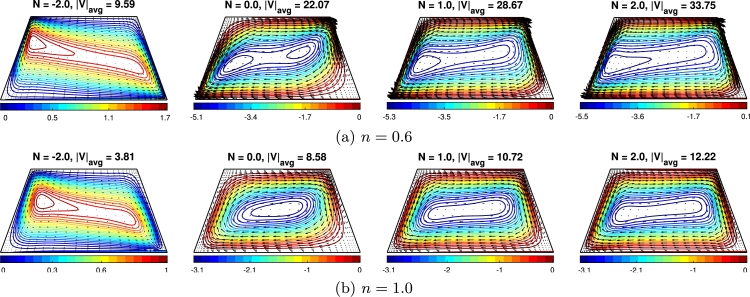
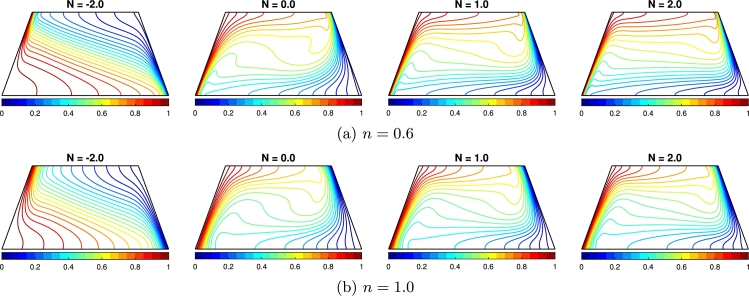
Fig. 9(a,b) shows how the buoyancy ratio (N) affects the flow field. In this chart, the impact of pure thermal convection ($N=0$) and thermo-solutal convection ($N\ne 0$) on the flow field is presented. The buoyancy ratio specifically marks which buoyancy force dominates during the convection process. Besides, the negative values of N indicate the opposite interactions of the two forces, while the positive value of N indicates the aiding interactions of the two buoyancy forces during the convection. The value $N=-1$ or 1 indicates that both forces are equally effective but opposing or aiding, respectively, in the convective heat and solutal transfer process. The magnitude of N exceeding one demonstrates that the solutal buoyancy force due to the solutal gradient becomes stronger than the thermal buoyancy force due to the temperature gradient. Results illustrate that when $N=-2$, the flow is anti-clockwise because of the opposite direction of the thermal and solutal gradient, and the solutal buoyancy force dominates. When $N>0$, the thermal and solutal gradients are in the same direction, aiding each other to enhance the convective flow within the enclosure. The flow exhibits clockwise unicellular motion for $N\ge 0$, the velocity magnitude increases and the boundary layer gets thinner with the increase of the value of N. The velocity magnitude for the shear-thinning coolant ($n=0.6$) is geared up by 53% for thermo-solutal convection ($N=2.0$) compared to pure thermal convection ($N=0$). A bone-shaped vortex core is observed for both the shear-thinning fluid and Newtonian ($n=1.0$) case. Also, a lower power index value ($n=0.6$) accelerates the flow than a higher power index value ($n=1.0$). For the negative buoyancy ratio, the core of the vortex cell is situated much closer to the left wall of the enclosure for shear-thinning fluids due to the low viscosity of the flow and the very thin boundary layer formed. For pure thermal convection and shear-thinning coolant, a vortex of a slightly oval shape is generated. For shear-thinning fluid, as circulation increases, the core region tends to split into two vortex cells. The effect of MF angle (${\delta }_1={45}^{\circ }$) is fixed for these figures. Due to this MF effect, the vortexes are slightly tilted and do not abide directly in the horizontal direction.

Figure 9.

Effect of buoyancy ratio (N = −2,0,1,2) to the flow field (streamlines) for the (a) shear-thinning fluid (n = 0.6) and (b) Newtonian fluid (n = 1.0), where Ha = 30, δ₁ = 45^∘ and ϕ = 0.02.

4.3. Temperature distribution in terms of isotherms

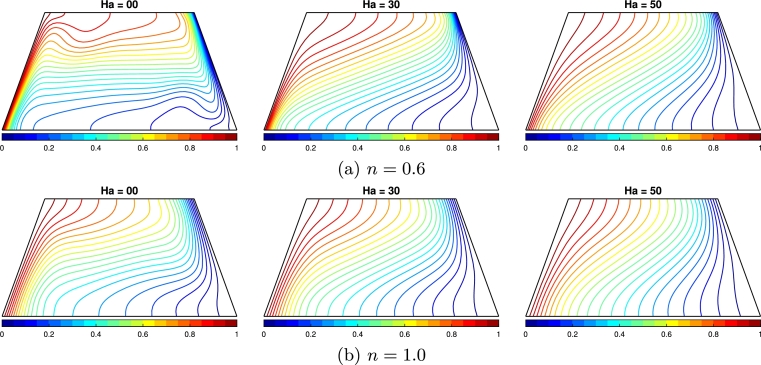
Isotherm is a crucial aspect of numerical analysis as it provides valuable information about temperature distribution within a system. Examining the isotherm can identify regions of HT, heat accumulation, and temperature gradients. This information aids in understanding the thermal behavior of the system, optimizing design parameters, and evaluating the effectiveness of cooling strategies. In Fig. 10(a,b), the Ha number is varied with Newtonian fluid and shear-thinning fluid with constant values of ${\delta }_1={45}^{\circ }$, $N=1$ and $\varphi =0.02$. The HT is maximum on both hot and cold inclined walls as buoyancy force is present. Hence, the flow initiates at the lower section of the hot wall and concludes in the upper region of the cold wall, where the isotherm lines are denser than other areas. The isotherm lines became sparse from the heated walls after applying the magnetic effect ($Ha=30,50$). When $n<1.0$, the HT is higher on the heated walls than in the case of $n=1.0$, indicating that shear-thinning fluid performs better than the Newtonian fluid in HT when Ha varies.

Figure 10.

Effect of Hartmann number (Ha = 00,30,50) to the temperature field (isotherms) for the (a) shear-thinning fluid (n = 0.6) and (b) Newtonian fluid (n = 1.0), where δ₁ = 45^∘, N = 1.0, and ϕ = 0.02.

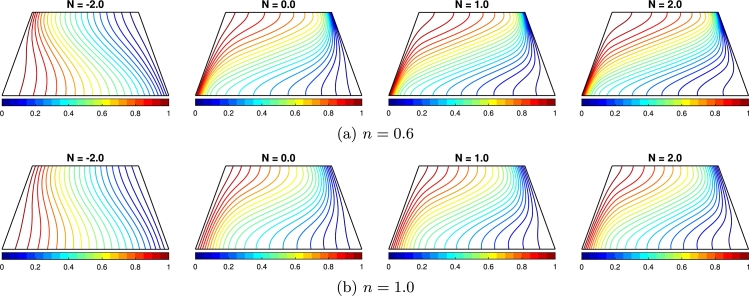
Fig. 11(a,b) shows that when both the buoyancy force is in the opposite direction ($N=-2$), isotherm lines are sparsely distributed, which indicates a lower HT rate. $N>0$ means the direction of both buoyancy forces is similar and aided by each other. In this regard, the HNF flow is directed by clockwise motion, and the isothermal lines are gathered more densely on the lower section of the hot wall and the upper region of the cold wall where the HT takes extremum. Fluids with shear-thinning behavior ($n=0.6,0.8$) show denser isothermal lines than Newtonian fluid, representing a higher heat exchange when applying a lower power law index.

Figure 11.

Effect of buoyancy ratio (N = −2.0,00,1.0,2.0) to the temperature field (isotherms) for the (a) shear-thinning fluid (n = 0.6) and (b) Newtonian fluid (n = 1.0), where Ha = 30, δ₁ = 45^∘ and ϕ = 0.02.

4.4. Solutal distribution in terms of isoconcentration

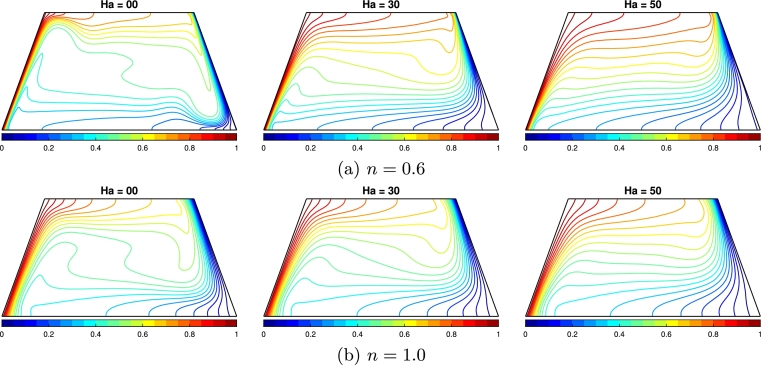
In this section, we focus on analyzing the MT characteristics of the choice of fluids using iso-concentration lines, which enable us to visualize concentration gradients in the fluid flow. To explore the influence of Ha and N, we systematically vary these factors to study their impact on MT phenomena within the enclosure. In Fig. 12(a,b), we observe distinct concentration patterns as we range Ha from 00 to 50. Notably, without a magnetic source ($Ha=0$), iso-concentration lines are densely packed towards the sloped walls and sparsely appeared in the enclosure's core. The meandering nature of iso-concentration is observed at the core region of the enclosure as the flow experiences no resistive force for $Ha=0$. However, when the magnetic field is introduced, the iso-concentration lines become less dense on the upper region of the hot wall and the lower section of the cold wall. Interestingly, shear-thinning fluids ($n=0.6$) exhibit a thinner boundary layer for solutal distribution compared to the Newtonian fluid ($n=1$). This comprehensive analysis sheds light on the intricate relationship between MT, fluid behavior, and the chosen parameters, offering valuable insights for diverse applications in fluid dynamics research. The buoyancy ratio (N) also significantly influences the iso-concentration lines, and the effect from the variation of N is observed in Fig. 13(a,b). For $N<0$, the lines exhibit similar characteristics to the isothermal lines due to the opposing direction of solutal and thermal buoyancy forces. Mass transfer in this scenario is notable in the upper region of the hot wall and the lower section of the cold wall. However, the situation changes when $N>0$, as the iso-concentration lines become denser on the lower section of the hot wall and the upper region of the cold wall. In the case of shear-thinning fluids, lower power law indices lead to coarser iso-concentration lines, indicating higher MT. Conversely, the iso-concentration lines are notably sparser for the Newtonian fluid ($n=1$). These observations highlight the intricate interplay between buoyancy effects, power law index, and fluid behavior, providing valuable insights for optimizing MT processes in various fluid systems.

Figure 12.

Effect of Hartmann number (Ha = 00,30,50) to the concentration field (iso-concentration) for the (a) shear-thinning fluid (n = 0.6) and (b) Newtonian fluid (n = 1.0), where δ₁ = 45^∘, N = 1.0, and ϕ = 0.02.

Figure 13.

Effect of buoyancy ratio (N = −2,0,1,2) to the concentration field (iso-concentration) for the (a) shear-thinning fluid (n = 0.6) and (b) Newtonian fluid (n = 1.0), where Ha = 30, δ₁ = 45^∘ and ϕ = 0.02.

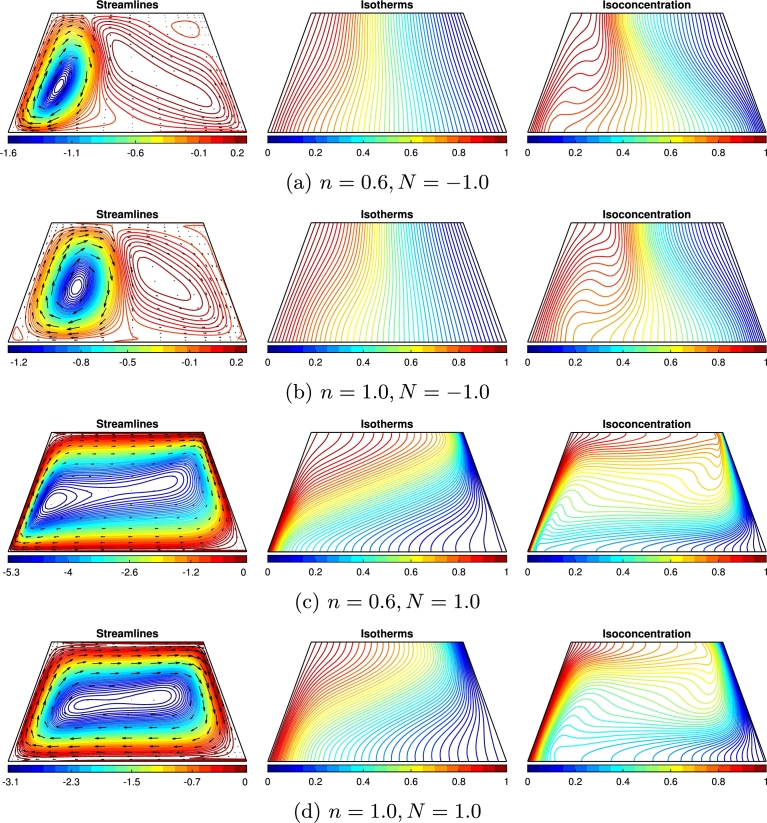
4.5. Effects from the equal order of opposite and aiding buoyancy forces

Fig. 14(a-d) exhibits the influences of the thermal and solutal buoyancy forces into the flow field, thermal field, and concentration field when the forces are in comparable order to each other but act opposite or cooperative. When the forces are in equal order but act in opposite directions ($N=-1.0$), the flow field distribution exhibits the counter-rotating vortices within the trapezoidal enclosure. The vortex on the left side rotates clockwise, but the right vortex rotates anti-clockwise due to the imposed thermal and solutal boundary conditions. The effect of inclined walls leads to creating a tertiary vortex to separate the fluid in the upper right corner. As a result, the thermal and solutal exchange between the active walls decreases significantly, as observed from the vertical stratification of isothermal and iso-concentration lines. Results show that increasing the power-law index while $N=-1.0$ transforms the two vortices into equal shapes, weakening the flow strength, but the thermal and solutal fields remain similar. When the forces act cooperatively with equal order of strength ($N=1.0$), the flow field shows a unicellular clockwise motion, thus resulting in increased thermal and solutal exchange, as observed from the thermal and solutal distribution. The isothermal and iso-concentration lines are oriented horizontally with the convective flow, indicating more heat and mass transfer rate than the case of equal strength of opposing buoyancy forces ($N=-1.0$).

Figure 14.

Effect of the equal power of buoyancy forces to the flow, thermal and concentration field for the (a,c) shear-thinning fluid (n = 0.6) and (b,d) Newtonian fluid (n = 1.0), where Ha = 30, δ₁ = 45^∘ and ϕ = 0.02.

4.6. Local heat and mass transfer rate

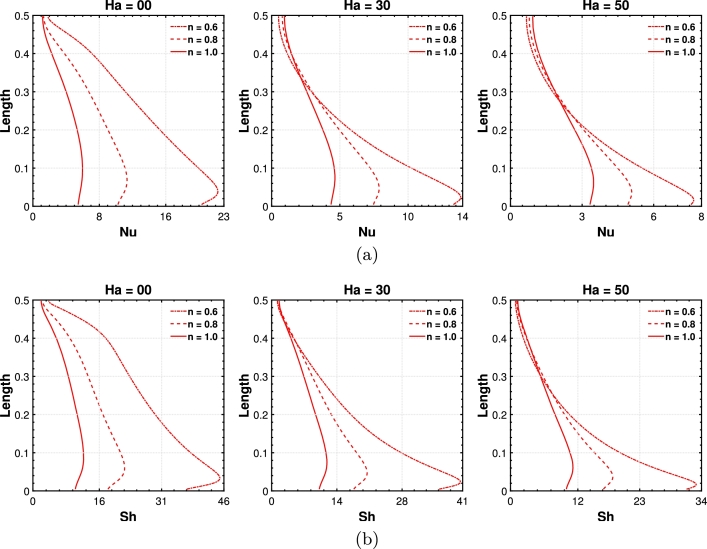
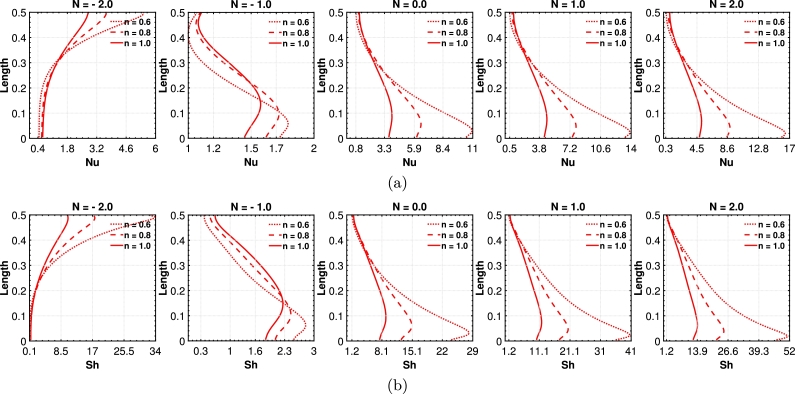
The local Nusselt number (Nu) and Sherwood number (Sh) are parameters that provide detailed information about HT and MT characteristics at the locations along a solid-fluid interface. HT and MT rates can vary significantly in complex fluid flow systems due to convective flow patterns and local property variations. By calculating the Nu and Sh, researchers can pinpoint regions with enhanced or reduced HT and MT, enabling targeted optimization of thermal and MT processes. Fig. 15(a,b) depicts the variation of local Nu and Sh in response to different $Ha=00,30,50$ for the nano-coolant with shear-thinning and Newtonian attributes. Here, the y-axis represents the length of the hot sloped wall of the trapezoidal enclosure, and the x-axis represents the local Nu or Sh. With increasing the Ha, the convective flow gets weakened due to the activation of the Lorentz force, resulting in a declination of Nu magnitudes and so for the HT rate. The HT rate is inferior at the top part of the inclined wall, whereas better HT is prominent in the lower section of the wall. The HT rate is lower for the Newtonian coolant ($n=1.0$) because of its more viscous force. The viscosity reduces with decreasing n, so the HT rate for the shear-thinning coolant will rise. We observe this kind of behavior when $Ha=00$. However, when $Ha=30,50$, the reverse phenomena are noticed in the top part of the hot wall. At the enclosure's upper region, the Newtonian fluid's HT rate ($n=1.0$) is more than the shear-thinning fluids ($n=0.6,0.8$). Nevertheless, at the lower portion of the enclosure, the HT rate of the shear-thinning fluid is always higher. Furthermore, the Sh is diminishing remarkably as the Ha rises. Thus, the rate of MT must also be declining. Due to their greater viscosity, Newtonian fluid ($n=1.0$) transmit mass at a slower pace. The mass diffusion rate from the hot wall to the cold wall will increase with a decrease in the power law index. As n is reduced, the mass diffusion rate from a hot wall to a cold wall tends to increase.

Figure 15.

Effect of Hartmann number on (a) local Nusselt number, and (b) local Sherwood number for the shear-thinning fluids (n = 0.6,0.8) and Newtonian fluid (n = 1.0), where δ₁ = 45^∘, N = 1.0 and ϕ = 0.02.

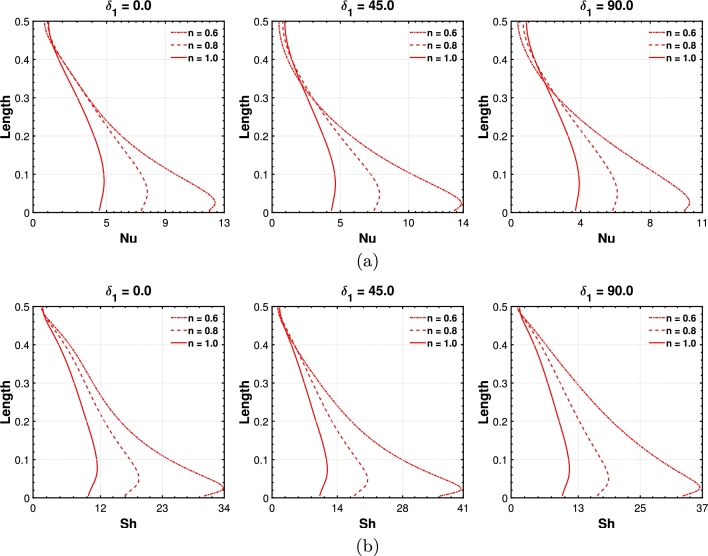
The fluctuation of the Nu and Sh with various MF directions (${\delta }_1=0^{\circ }-{90}^{\circ }$) is shown in Fig. 16(a,b). The Nusselt number (Nu) increases as the ${\delta }_1$ moves from $0^{\circ }$ to ${45}^{\circ }$, resulting in higher heat transmission within this range. However, HT decreases steadily as the ${\delta }_1$ increases beyond ${45}^{\circ }$. Heat transfer is less pronounced at the top of the inclined wall, while more heat is transferred at the enclosure's bottom side. Due to higher viscous forces, Newtonian fluids ($n=1.0$) exhibit a lower HT rate than shear-thinning fluids, which inherit lower viscosity with the applied shear rate. As n decreases, the HT rate for shear-thinning fluids increases due to reduced viscosity. However, an exciting reversal occurs at the top of the enclosure, where the HT rate of Newtonian fluid surpasses that of the shear-thinning fluid in a small area. Regarding MT, the Sherwood number (Sh) increases between $0^{\circ }$ and ${45}^{\circ }$, leading to a higher mass transmission rate. After ${\delta }_1={45}^{\circ }$, the MT rate decreases again as diffusion drives MT from areas of higher concentration to lower concentration. Overall, shear-thinning nano-coolants demonstrate a higher mass transmission rate than their Newtonian counterparts.

Figure 16.

Effect of magnetic field angle on (a) local Nusselt number, and (b) local Sherwood number for the shear-thinning fluids (n = 0.6,0.8) and Newtonian fluid (n = 1.0), where Ha = 30, N = 1.0 and ϕ = 0.02.

Fig. 17(a,b) illustrates the variation of the local Sh and Nu with different buoyancy ratios. For the negative buoyancy ratios of $N=-2.0$, when the thermal and solutal buoyancy forces are active in the opposite direction, but the thermal one dominates the solutal one, the fluid flow exhibits clockwise motion, resulting in more HT and MT at the upper part than the bottom region of the inclined active wall. When $N=-1.0$ represents equal strength but opposing buoyancy forces, two counter-rotating vortices result in lesser and higher quantities of HT and MT in the upper and lower parts, respectively. Conversely, for the purely thermal gradient with $N=0$ and the aiding condition of buoyancy forces with $N>0$, the fluid flow maintains anti-clockwise motion, and hence, the HT direction changes, with more evident HT at the lower side and less at the top of the inclined wall. The HT rate rises with increased buoyancy ratio, and higher positive buoyancy ratios result in better heat transmission. Additionally, the HT rate increases for shear-thinning fluids due to reduced viscosity. However, a reversal occurs, with the Newtonian fluid demonstrating higher HT rates at the upper left side of the enclosure. Mass transfer patterns also change with buoyancy ratios, with substantial MT occurring in the upper portion for positive balances.

Figure 17.

Effect of buoyancy ratio on (a) local Nusselt number, and (b) local Sherwood number for the shear-thinning fluids (n = 0.6,0.8) and Newtonian fluid (n = 1.0), where Ha = 30, δ₁ = 45^∘ and ϕ = 0.02.

4.7. Average heat and mass transfer rate

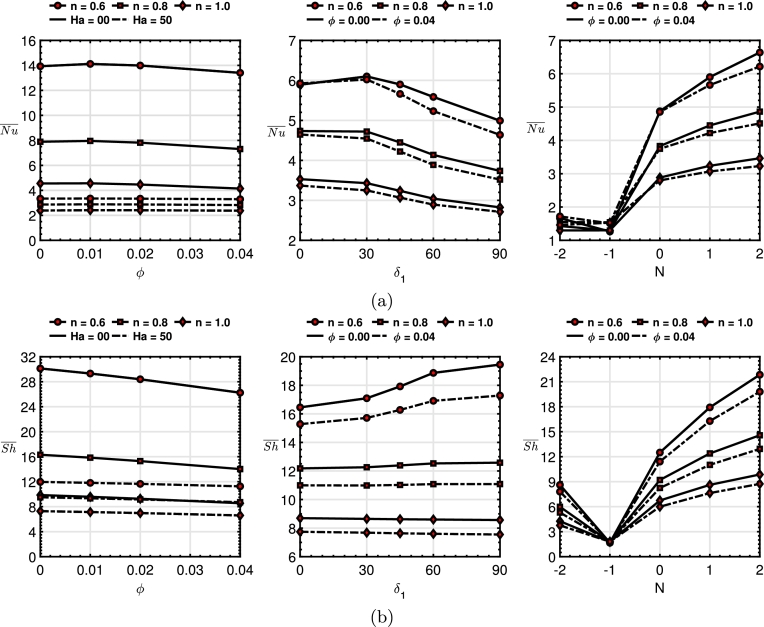
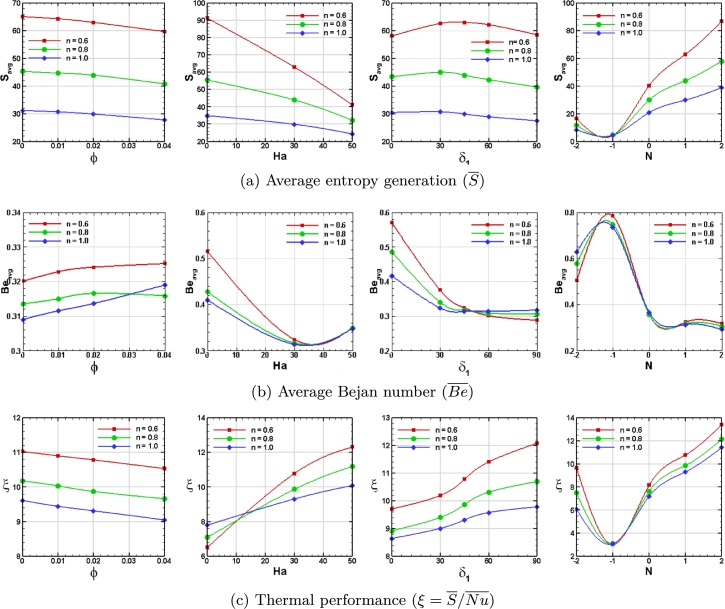
The average Nusselt number ($\overline{Nu}$) and Sherwood number ($\overline{Sh}$) are essential in convective HT and MT studies as they provide overall performance metrics for thermal and solutal transfer rates. These parameters help researchers quantify the efficiency of HT and MT within a system, providing insights into the system's overall thermal and mass transport capabilities. Fig. 18(a) visually presents the quantitative variation of $\overline{Nu}$ concerning the controlling parameters. Results show that for the absence of a magnetic field (MF) and having the equal strength of aiding forces ($Ha=00,N=1.0$), the shear-thinning coolants outperform the Newtonian coolant, and increasing the volume fraction leads to a decrease in the $\overline{Nu}$. However, applying an MF significantly affects the $\overline{Nu}$. For instance, a shear-thinning coolant of $n=0.6,\varphi =0.02$, $\overline{Nu}$ is reduced by 76.15% when MF is present ($Ha=50$) compared to $Ha=00$. Also, $\overline{Nu}$ shows a minor change with adding nanoparticles. This indicates that the existence of MF resists the effect of adding nanoparticles, i.e., volume fractions (ϕ), to increase the HT rate. Furthermore, keeping the MF strength constant ($Ha=30,N=1.0$) but varying the direction of MF shows that the shear-thinning characteristics of a nano-coolant perform better than the Newtonian counterpart. Changing the angle from horizontal to vertical leads to a decrease in the $\overline{Nu}$ by 21.72% for shear-thinning nano-coolant ($n=0.6,\varphi =0.04$) and that reduction is about 19.5% for Newtonian nano-coolant ($n=1.0,\varphi =0.04$). Results indicate that Newtonian fluids are less affected by the variation of ${\delta }_1$ as they inherit higher viscosity than the shear-thinning fluid with respect to the applied shear rate. With constant MF with a specific direction ($Ha=30,{\delta }_1={45}^{\circ }$), higher $\overline{Nu}$ is found for the case of aiding condition ($N>0$) than the cases of opposing condition ($N<0$). In the opposing condition ($N<0$), decreasing the magnitude of N leads to a decrease in the average thermal exchange rate ($\overline{Nu}$). In the aiding condition ($N>0$), increasing N leads to a rise $\overline{Nu}$, highlighting the superior performance of shear-thinning fluids over Newtonian fluids regardless of the addition of nanoparticles. However, the performance of the nano-coolant with $\varphi =4\text{\%}$ is loosened than the host fluid ($\varphi =0\text{\%}$) in these circumstances. Calculation found that $\overline{Nu}$ augmented by 36.2% and 28.0% for shear-thinning ($n=0.6$) coolant ($\varphi =00$) and nano-coolant ($\varphi =0.04$), respectively.

Figure 18.

Variation of (a) average Nusselt number ($\overline{Nu}$) and (b) average Sherwood number ($\overline{Sh}$) with the variation of governing parameters.

In Fig. 18(b), the response of the $\overline{Sh}$ against various controlling parameters is depicted. With the activation of an MF, the resistive Lorentz force is created, leading to a decrease in the convective MT rate. Results show that the $\overline{Sh}$ is higher with no MF than in the presence of it. Quantitatively, $\overline{Sh}$ is reduced by 60.28% for shear-thinning coolant ($n=0.6,\varphi =0.00$) when the MF becomes active ($Ha=50$) from inactive ($Ha=00$) and that reduction is about 57.10% for the nano-coolant case of $n=0.6,\varphi =0.04$. Moreover, adding nanoparticles also leads to a decline in the solutal transfer rate when the MF is absent. For instance, for $Ha=50$, an amount of 12.88% is found lesser for $\overline{Sh}$ in the case of nano-coolant ($\varphi =0.04$) than the coolant case ($\varphi =0.00$) which is happened due to higher viscosity of HNF than the base fluid. However, the declination graph is less steep with the MF, resulting in the more effective behavior of nano-coolant, and altering the direction of the MF from the horizontal to vertical leads to augmenting the solutal transfer rate by 18.21% for the shear-thinning coolant and 13.1% for the nano-coolant with $n=0.6$. The effect of MF direction has not been found prominent for the Newtonian coolant. It is worth mentioning that the effect of the buoyancy ratio is greater for the shear-thinning coolant than the Newtonian coolant. As for quantitative purposes, $\overline{Sh}$ increases by 153.5% if the buoyance force is changed from the opposing case ($N=-2.0$) to the aiding case ($N=2.0$) for the shear-thinning coolant or nano-coolant. For the Newtonian case, the amount is enhanced by 132%. It is notable to observe that the opposing buoyancy force condition with equal order of magnitude ($N=-1$) significantly reduces the non-Newtonian effect and the HNF effect on the overall HT and MT features within the trapezium enclosure. In all cases, non-Newtonian shear-thinning coolant outperforms the Newtonian one due to maintaining less viscosity during the convective thermo-solutal processes, which enhances both HT and the MT rate. These findings highlight the crucial role of the Buoyancy ratio, ϕ, and power law index in enhancing HT and MT efficiencies, guiding researchers in optimizing fluid systems for improved thermal and mass transport performance. The shear-thinning nano-coolant always shows better thermal and solutal transfer characteristics than the Newtonian coolant.

4.8. Entropy generation

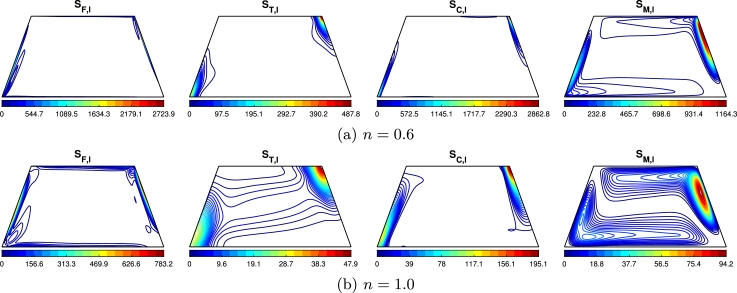
Entropy Generation (EGEN) is a thermodynamic concept that quantifies the irreversibility and inefficiency of a process or system. In any real-world process, energy conversions are never fully reversible, and some energy is inevitably lost during the physical transfer process and generates entropy in the form of heat. This energy loss leads to increased entropy, a measure of the system's disorder or randomness. This section illustrates EGEN over the trapezoid enclosure to look into the effect of different parameters ($Ha,{\delta }_1,N,n,\varphi$). Fig. 19(a,b) shows the contours of local entropy generations for Newtonian ($n=1.0$) and non-Newtonian shear-thinning ($n=0.6$) fluids when $Ha=30,N=2.0,\varphi =0.02$ and magnetization angle, ${\delta }_1={45}^{\circ }$. The EGEN, due to fluid friction, is found very high on the hot and cold walls of the enclosure as the nano-coolant experiences the motion and starts interacting with the hot wall. With the power law index increase, the isentropic lines expand from the active walls to the bulk region, recognizing the increasing momentum boundary layer with n. Local EGEN due to HT ($S_{T,l}$) and solutal transfer ($S_{C,l}$) are mostly localized on the bottom and top of the hot and cold inclined wall, respectively. Changing the nano-coolant rheology from non-Newtonian to Newtonian, the EGEN ($S_{T,l}$ and $S_{C,l}$) is expanded to the core of the enclosure from the active walls. This happens in association with the thermal and concentration boundary layer expansion with increasing the viscous force, i.e., increasing n. The particular geometry shape shows a high magnitude of $S_{T,l}$ and $S_{C,l}$ in the top right corner for all nano-coolant variations considered in the present study. Isentropic lines due to magnetization with $Ha=30,{\delta }_1={45}^{\circ }$ densely appear near the active walls. For shear-thinning nano-coolant, expanded isentropic lines are developed along the adiabatic walls. That development grows towards the center with an increased power law index for Newtonian nano-coolant. On the other hand, EGEN, due to magnetization, is more spread throughout the enclosure. Due to the MF orientation, the component-wise EGEN becomes larger near the right cold wall.

Figure 19.

Local entropy generation for the (a) shear-thinning fluid (n = 0.6) and (b) Newtonian fluid (n = 1.0), where Ha = 30,δ₁ = 45^∘,N = 2.0,ϕ = 0.02, and n = 0.6,1.0.

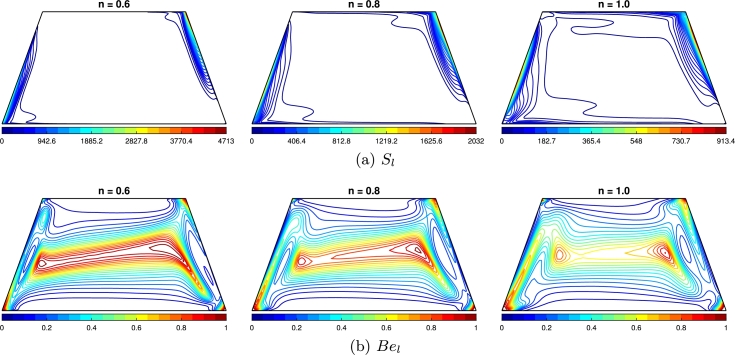
In Fig. 20(a,b), total localized EGEN ($S_l$) and local Bejan number ($B{e}_l$) are observed for nano-coolant with different rheological behavior under the presence of magnetization. The local EGEN due to MHD convective HT and MT process is lower for Newtonian nano-coolant than the shear-thinning one. The isentropic charts are observed symmetric about the center of the enclosure. The higher magnitude of irreversibility arises within the boundary layer thickness as the convection emanates from the wall boundary with fluid friction and thermal processes. Results are also displayed in terms of the contours of the $B{e}_l$ field. The higher values of $B{e}_l$ are observed on the lower-left and upper-right of the active walls. In this region, thermo-solutal convection plays a significant role, hence the irreversibility of HT and MT in contrast to the other components. The $B{e}_l$ gets lower with an increase in the power law index. Furthermore, a higher $B{e}_l$ is localized diagonally from the top of the hot wall to the bottom of the cold wall. The higher Be is concentrated at the center of the enclosure horizontally. The $B{e}_l$ weakens with an increased n. These findings provide valuable insights into the impact of flow direction and fluid properties on EGEN and $B{e}_l$, guiding researchers in optimizing energy-efficient designs and processes. Fig. 21(a-c) manifests the comprehensive impact of governing parameters on the average EGEN ($\bar{S}$), average Bejan number ($\overline{Be}$), and a criterion ($\xi =\bar{S}/\overline{Nu}$) to analyze the thermal performance of a closed system. Values of $\overline{Be}$ indicate whether the HT and MT irreversibility dominate over friction and magnetohydrodynamics irreversibility. The criterion ξ looked into the thermal systems performance by taking the ratio of the total energy losses to the total HT rate based on the second law of thermodynamics. The results provide significant insights into the overall system behavior. Notably, increasing nanoparticles to the coolant is accompanied by lower values of average EGEN and better thermal system performance, signifying reduced energy loss and improved system efficiency. Noteworthy, values of $\bar{S}$, $\overline{Be}$, and ξ are always found higher for the non-newtonian nano-coolant than the Newtonian version. In the case of considering the variation of magnetization (Ha), the overall entropy of the system gets reduced by strengthening the MF. The magnetohydrodynamics convection gets weakened by increasing the MF, resulting in the dominant mode of friction and magnetic irreversibility over the thermal and solutal ones. The feature is assured from the graph of the average Be number. When considering a constant magnetic strength, changing the magnetization angle (${\delta }_1$) leads to an increase followed by a decrease in the total energy losses. The HT and MT irreversibility dominates the other two for shear-thinning nano-coolant, while the MF is directed horizontally. The performance criterion also shows better thermal system efficiency for horizontal MFs than vertical ones. Intriguing findings are observed when considering the buoyancy ratio (N). Altering the buoyancy forces from the opposing condition ($N<0$) to the aiding condition $N>0$, more entropy generation ($\bar{S}$) is observed with losses of more energy. In the case of $N=-1$, the effect of the power-law index is not prominent. With the strength of the buoyancy force, the average Be number is decreasing. The case of $N=-1$ exhibits a significant decrease in the criterion ξ for HNF, declaring the efficiency of the thermal system as a reference value in other analysis.

Figure 20.

(a) Total localized entropy generation (S_l) and (b) local Bejan number (Be) for Ha = 30,δ₁ = 45^∘,N = 2.0,ϕ = 0.02, and n = 0.6,0.8,1.0.

Figure 21.

Effect of governing parameters on (a) average entropy generation ($\bar{S}$), (b) average Bejan number ($\overline{Be}$) and (c) thermal performance (ξ).

5. Conclusion

A computational investigation of thermal and solutal transmission subject to EGEN due to horizontal gradients of temperature and solutal within a trapezoidal enclosure has been reported. The enclosure contains an ethylene glycol (30:70) based MWCNT-SiO₂ nanoparticle solution that displays non-Newtonian rheology, and a magnetohydrodynamics effect was carried out. The side wall of the trapezoidal enclosure is tilted towards each other with an angle of ${20}^{\circ }$; hence ${\delta }_0={110}^{\circ }$. The left wall is thought to be the hot wall. Four variables were changed in order to conduct the investigation: the MF angle (${\delta }_1$), the Hartmann number (Ha), the volume fraction (ϕ), and the power law index (n). In the current work, the increased HT induced by the Brownian diffusion of nanoparticles in the base fluids is considered and incorporated with enhanced thermal conductivity. In this study, we are examining how irregularities can enhance HT. The influence of the non-Newtonian characteristics of NF on the rate of convective HT and MT from the heated inclined wall has also been examined. The numerical results have been depicted using graphical and tabular forms to provide a physical and numerical comprehension of the solutions discovered. A list of key findings from the current analysis is provided below:

• •convective strength of non-Newtonian nano-coolant gets weakened, and the size of the stream function associated with the velocity magnitude drops with an increase in the MF strength, direction, and power law index.
• •The flow strength and the magnitude of the streamline function reduced as the viscosity arose with the augmentation of the power law index and nanoparticles in addition to the base medium.
• •Local Nu and local Sh are observed to be higher on the lower region of the hot inclined wall than the upper region for all the variations of Hartman number(Ha), MF angle (${\delta }_1$) and Buoyancy ratio (N) except $N=-2.0$.
• •The shear-thinning characteristics of the non-Newtonian nano-coolant($n=0.6,0.8$), the efficacy of HT and MT rate is noticeably higher than Newtonian fluid($n=1$).
• •The non-Newtonian nano-coolant ($n=0.6,\varphi =0.2$) experiences a 76.15% reduction in $\overline{Nu}$ at $Ha=50$ compared to $Ha=0$. For the shear-thinning nano-coolant ($n=0.6,\varphi =0.04$), changing the angle from horizontal to vertical results in a 21.72% decrease. Additionally, varied phenomena with N exhibit a significant 36.2% augmentation in the observed heat transfer.
• •Average sherwood number ($\overline{Sh}$) reduced by 60.28% when $Ha=50$ activated for shear-thinning nano-coolant ($n=0.6,\varphi =0.00$). The angular variation (${\delta }_1$) from 0 to 90, augments $\overline{Sh}$ by 18.21%. The aided buoyancy ratio also enhanced the mass transfer rate by 153.5%.
• •Average EGEN is always higher for shear-thinning nano-coolant than the Newtonian one, as the convective strength is lower for the later one. EGEN shows higher magnitudes along the active walls, especially in the regions where the aiding buoyancy-driven convection leads.

CRediT authorship contribution statement

Tawsif Mahmud: Writing – original draft, Visualization, Investigation. Taha Chowdhury: Writing – original draft, Visualization. Preetom Nag: Writing – review & editing, Supervision, Methodology, Data curation, Conceptualization. Md. Mamun Molla: Writing – review & editing, Validation, Supervision, Software.

Declaration of Competing Interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Tawsif Mahmud reports financial support was provided by North South University. Taha Chowdhury reports financial support was provided by Ministry of Science and Technology, Government of the People's Republic of Bangladesh. Preetom Nag reports a relationship with North South University that includes: employment. If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

The data are available based on request.