Abstract
In pharmaceutical manufacturing, integrating model-based design and optimization can be beneficial for accelerating process development. This study explores the utilization of Machine Learning (ML) techniques as a surrogate model for the optimization of a three-unit wet-granulation based flowsheet model for solid dosage form manufacturing. First, a reduced representation of a wet granulation flowsheet model is developed, incorporating a granulation and milling process, along with a novel dissolution model that accounts for the effect of particle size, porosity, and microstructure on dissolution rate. Two optimization approaches are compared, including an autoencoder-based inverse design and a surrogate-based forward optimization. Both methods address the bi-objective problem of maximizing dissolution time and product yield by identifying the optimal granulation and mill process parameters. For this case study, both approaches were effective and incurred a similar computational cost, averaging under 4 s. However, the autoencoder approach offers an advantage through dimensionality reduction, a feature not available in surrogate-based optimization. Dimensional reduction is particularly beneficial for complex process designs with numerous inputs and outputs. The lower dimensional representation helps improve process understanding through enhanced visualization of the process design space and facilitates feasibility studies involving multiple constraints. The autoencoder-based inverse design introduced in this work showcases an implementation of AI and ML in pharmaceutical process development, demonstrating the potential to enhance process efficiency and product quality in complex manufacturing scenarios.
Keywords: Optimization, Granulation, Machine Learning, Autoencoders, Pharmaceuticals, Design
Graphical abstract
1. Introduction
The pharmaceutical industry has revolutionized itself significantly over the past decade, relying on highly innovative solutions to meet the ever-changing customer demands and strict regulatory requirements (Algorri et al., 2022). Notably, this evolution is characterized by a pivot from the development of batch to continuous manufacturing process, generalized to personalized medicines, and simple dosage forms to 3D printing and additive manufacturing (Am Ende, 2019). These transitions have been propelled by advancements in Internet of Things (IoT), Artificial Intelligence (AI), and advanced computing, which provide the tools necessary to transform the traditional approaches to the design and manufacture of pharmaceutical products (Venkatasubramanian, 2019; Arden et al., 2021). With the introduction of Industry 4.0, the future of pharmaceutical manufacturing aims to enhance productivity, to improve quality assurance, cost-effectiveness, and to increase flexibility to uncertainties, and agility to respond quickly changes (Arden et al., 2021; Litster and Bogle, 2019). Furthermore, the enthusiasm surrounding AI and machine learning (ML) is also reflected in the pharmaceutical industry, as evidenced by the US-FDA's release of articles outlining their perspective (Administration, 2021; Administration, 2023) and research studies have shown the benefits associated with the adoption of these technologies. In Research and Development (R&D), ML can be used for generative discovery of novel molecules with potential therapeutic effects (Sanchez-Lengeling and Aspuru-Guzik, 2018). Process development can also benefit from ML, particularly in determining process design spaces (Sampat and Ramachandran, 2022; Matsunami et al., 2023), and for the optimization of formulation and processing conditions of different drug products (Chen et al., 2023; Boukouvala and Ierapetritou, 2013; Sampat and Ramachandran, 2023). ML can also be applied to manufacturing systems for process monitoring and control (MacGregor et al., 2005), and for automation, enabling systems to operate with minimal human interaction (Arden et al., 2021).
Deep learning is a class of ML algorithms that utilize multiple processing layers (i.e. networks) to learn representation of data (LeCun et al., 2015; Sarker, 2021). Deep learning techniques have the capability of processing data in their raw form, and can handle various data types, such as numeric values, images, and text (Dargan et al., 2020). The benefit of deep learning lies in its abilities to extract intricate structures or patterns in high-dimensional data, which enables it to accomplish more complex tasks to a higher accuracy as compared to shallow networks or simpler models (LeCun et al., 2015). In the pharmaceutical industry, deep learning has been widely applied to drug discovery (Chen et al., 2018; Gupta et al., 2021; Gentile et al., 2020) and image analysis (Salami and Skomski, 2023; Preim and Botha, 2013; Zhang et al., 2020). Despite its potential, the use of deep learning in the process design and development is not yet widespread. Current industry practices in process design often rely on heuristics, first-principles, or physics-based process models to drive decision-making. Thus, there is an opportunity to innovate by incorporating ML and deep learning methodologies into workflows. More recently, there have been a few research studies that have started exploring the potential applications of deep learning in process development, including the use of Recurrent Neural Networks (RNN) or Long-Short Term Memory (LSTM) for time-series predictions of product quality (Aghaee et al., 2023), to support control and optimization of continuous processes (Sampat and Ramachandran, 2023; Wong et al., 2018), Autoencoders (AE) for dimensionality reduction (Sampat and Ramachandran, 2022) or fault detection (Agarwal et al., 2022), and Reinforcement Learning (RL) to optimize drug dosage and develop personalized treatment plans (Huo and Tang, 2022). Nevertheless, there are still many remaining applications for deep learning that can be developed which would benefit the design and development of drug products. In this work, we will the utilize an autoencoder-based model for inverse design optimization of a wet granulation manufacturing process, where the objective is to produce the targeted product quality.
The integration of model-based design and optimization has significantly contributed to the advancement in pharmaceutical process development and manufacturing, resulting in an improvement in process understanding, product quality, and productivity (Lakerveld et al., 2013; Gernaey and Gani, 2010). This is particularly evident in downstream pharmaceutical drug product manufacturing, which involves the processing of powders into tablets or capsules through a sequence of unit operations. Here, the handling of bulk powder materials often presents a complex and challenging environment, resulting in much of the processes being designed empirically due to the lack of scientific understanding (Boukouvala and Ierapetritou, 2013). However, in recent years, there has been a paradigm shift to the utilization of model-based strategies, such as process models to simulate several unit operations in powder processing, including mixing (Sen et al., 2012; Sen et al., 2013; Escotet-Espinoza et al., 2019), roller compaction (Reynolds et al., 2010), wet granulation (Chaudhury et al., 2014; Barrasso et al., 2015; Bellinghausen et al., 2022), milling (Barrasso et al., 2013; Dan et al., 2023; Reynolds, 2010; Metta et al., 2018; Bilgili and Scarlett, 2005) and tablet compaction (Matji et al., 2019; Escotet-Espinoza et al., 2018). The development of predictive process models enables the development of model-based flowsheet simulators, which can be used for dynamic simulation (Boukouvala et al., 2013; Rogers et al., 2013), sensitivity analysis (Metta et al., 2019; Boukouvala et al., 2012), and optimization (Chen et al., 2023; Boukouvala and Ierapetritou, 2013; Wang et al., 2017; Sampat et al., 2022) of integrated manufacturing processes. Process models commonly used to simulate particulate processes, such as population balance model (PBM) or discrete element model (DEM), are known to be computationally inefficient, thus are not suitable to be used for simulation-based optimization. To overcome the long simulation time, a common approach is to develop surrogate or reduced-order models for optimization purposes. Current literature in area of optimization of processes typically utilizes iterative optimization for objectives such as minimization of cost, or energy consumption while maintaining product quality (Chen et al., 2023; Boukouvala and Ierapetritou, 2013). However, when the objective is an end-goal in terms of product quality or performance, there is an alternative approach, known as the inverse design optimization, that could be more suitable. The inverse design optimization, widely applied in the area of material discovery, where the goal is to design a product that meets a specific desired properties or functionalities (Sanchez-Lengeling and Aspuru-Guzik, 2018). Unlike a traditional forward design method, which typically involves predicting the product quality based on the input parameters, the inverse design reverses this approach, by starting with a pre-defined target product quality and uses computational algorithms to generate the possible combinations of parameters to produce the final product with the specified output.
An example of a process where the adoption of inverse design could be useful is the pharmaceutical drug product manufacturing process via the wet granulation route, as it is complex and involves multiple unit operations including mixing, granulation, drying, milling and tableting to produce solid dosage forms. Solid dosage forms, such as tablets and capsules, designed for oral administration, works by releasing the drug substance, known as the active pharmaceutical ingredient (API) through the gastrointestinal (GI) tract (Zaborenko et al., 2019). While the determination of drug efficacy through in vivo mechanisms (i.e. drug release and drug absorption kinetics) is paramount, the successful in vivo drug absorption into the human body first requires efficient in vitro drug or API dissolution. This pre-requisite arises because drug substances need to be dissolved into its molecular or atomic entities before it can diffuse into living tissue (Siepmann and Siepmann, 2008). Thus, drug dissolution serves as a key indicator of drug bioavailability and the characterization of the therapeutic efficacy of a treatment (Siepmann and Siepmann, 2008). The key to understanding and predicting dissolution performance is to correlate formulation, process and equipment variables, to drug dissolution. It is common practice during development of a new product, that these factors are adjusted to obtain the targeted dissolution performance (Zaborenko et al., 2019; Maclean et al., 2024). In granulation processes, formulation and process variables affect the drug dissolution performance through its influence on intermediate granule quality attributes, such as granule size distribution, composition and microstructure. Here, the microstructure denotes the spatial distribution of different solid components (e.g. API, binder and excipients), and void space within the granule (Ansari and Stepanek, 2008). Numerous studies have observed the notable influence of these granule quality attributes on drug dissolution rates (Ansari and Stepanek, 2008; Hintz and Johnson, 1989).
Several studies have shown that granule attributes, such as the particle size had a significant impact on dissolution through its influence on the surface area and thickness of the diffusion layer (Hintz and Johnson, 1989; Ansari and Stepanek, 2007). The general approach taken to account for particle size distributions in dissolution modeling is to use a series of ordinary differential equations (ODEs) for each discretized particle size (Hintz and Johnson, 1989) or to use a population balance model (PBM), which are essentially a series of partial differential equations (PDEs) (Maclean et al., 2024; Djukaj et al., 2022; Wilson et al., 2012). Separately, studies have also observed through experimental dissolution and computer simulation of dissolution of single virtual granules, that the porosity and microstructure have a notable effect on dissolution rates and release profile (Ansari and Stepanek, 2008; Štěpánek, 2004; Kimber et al., 2011). However, to the best of our knowledge, there is not yet a mathematical model that can account for both the size distribution and microstructure. This gap in dissolution modeling motivates the objective of this study, which is to develop a model to predict dissolution rates while accounting for variation in feed PSD, composition and microstructure, resulting from heterogeneity in formulation and process parameters. It is important to note that this work involves modeling the dissolution process of granules and neglects the effect of tablet disintegration. Depending on the formulation, tablet disintegration can have a significant contribution to drug dissolution (Maclean et al., 2024; Wilson et al., 2012; Kalný et al., 2021). However, in this work, preliminary experiments that were conducted, showed that the granule dissolution is the rate limiting step of the dissolution process for this specific formulation, hence the disintegration kinetics were neglected for model simplification purposes. This assumption was also supported by Abdulla and Murtada, who observed that for an APAP and MCC formulation, the disintegration occurs in under 2 min, whereas the dissolution time takes up to 60 min.
This study will focus on the development of a simplified wet granulation flowsheet model, which accounts for the granulation and milling process. To determine the dissolution rate of the granules, a novel dissolution model which accounts for various intermediate granule properties, such as particle size, porosity and microstructure of the granules, will be developed. This dissolution model will be incorporated in the flowsheet model, as the dissolution rate is the key product quality metric. Sensitivity analysis will be used to determine the critical process parameters of the process affecting the dissolution rate and product yield. Two different optimization framework – surrogate-based forward optimization and the autoencoder-based inverse optimization will be designed to optimize the process parameters based on the multi-objective optimization problem consisting of product yield and dissolution time. The types of surrogate models evaluated in this work included Artificial Neural Networks (ANN), and Support Vector Regression (SVR), and the better performing model was used to represent the processes for the surrogate-based optimization. Additionally, since latent variables are generated via the autoencoder, the latent space will be used to visualize the process design space, and feasibility analysis with multiple constraints will be performed on the process design space.
2. Materials & methods
2.1. Flowsheet model
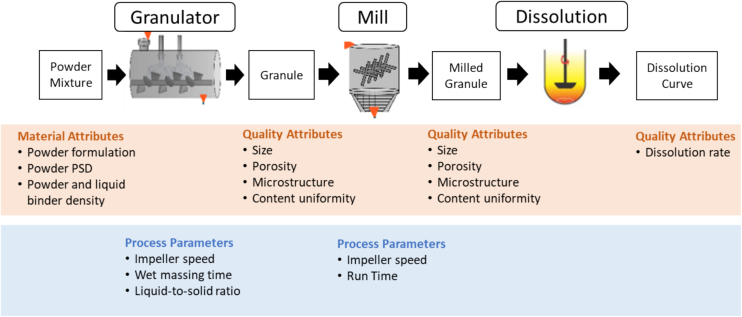
While a typical wet granulation manufacturing line includes processes such as feeder, mixer, granulator, dryer, mill, and a tablet press, as the focus of this study is to indicate a proof-of-concept of the inverse optimization framework, a reduced representation of a wet granulation process, as shown in Fig. 1, was used as the case study. The process was simplified to highlight the unit operations that have significant impact on the key intermediate granule properties – size, porosity and content uniformity, which in turn impacts the drug dissolution rate. For the specific formulation used in this study, assumptions were made to simplify the process, which includes the exclusion of the drying process, as we assume that the liquid content of the granule is the only properties that is changed during the drying process, and the exclusion of the tableting process, due to the assumption that the tablet disintegration process occurs very quickly, and granule dissolution is the rate limiting step of the process. So, only the granule dissolution process was considered here. The basis of the assumption on the drying process can be referred to in Sampat et al. (Sampat et al., 2022) and on the dissolution assumption can be supported by findings from Abdulla and Murtada (Abdulla and Oshi, 2024).
Fig. 1.
Schematic illustrating the transfer of information for the development of the flowsheet model.
A total of 7 granulator experiments and 12 Comil experiments were carried out, and these experimental results were used to validate the process models used to simulate the process and predict granule properties. For both the granulation and milling process, 3-dimensional population balance models were used to model the process.
2.2. Experimental setup and design
The formulation used in this study was a bi-component formulation of Acetaminophen, dense powder grade (Mallinckrodt Pharmaceuticals, North Carolina, USA) as the active pharmaceutical ingredient (API), and Micro-crystalline cellulose, Avicel PH102 grade (FMC Corporation, Pennsylvania, USA), as the excipient. Since this was a wet granulation process, and liquid binder was used, consisting of PVPK30 (Millipore Sigma, Missouri, USA), which was dissolved at 12.5 % w/w on Deionized water.
Granulation experiments were carried out in a bench-top high shear granulator (KEY International Inc., NJ), and milling experiments were conducted on a Comil (Quadro Engineering, Ontario, Canada), with a grater-type classification screen with 1016 μm opening. Experimental data used in this work were based on a previous publication (Dan et al., 2023; Dan et al., 2022), thus more comprehensive details on the equipment setup, experimental design and material characterization techniques used can be found in the authors' previous publications (Dan et al., 2023; Dan et al., 2022). A full factorial design of experiment with 3 factors and 2 levels with 1 additional center point, resulting in 9 total runs, was performed based on parameter ranges indicated in Table 1. These parameters are associated with the granulation process, and the batch of granules produced in each run was milled at two different screw speeds (1500 rpm and 3000 rpm) and was collected at various time points. The selection of the ranges for the parameters in Table 1 were determined based Sampat et al. (Sampat et al., 2022), which conducted granulation experiments on the same formulation and equipment, where the parameter boundaries were selected based on equipment constraints and the requirement to produce viable granules.
Table 1.
DOE variables and levels used in the experimental design.
| Unit Operation | Process Variables | Low Level | High Level |
|---|---|---|---|
| Granulation | Liquid-to-Solid Ratio | 0.65 | 0.8 |
| Wet Massing Time (Minutes) | 4 | 8 | |
| Impeller Speed (RPM) | 180 | 200 | |
| Mill | Impeller Speed (RPM) | 1500 | 3000 |
Characterization of the granules post-granulation and post-milling was done to determine the particle size distribution, porosity and drug (API) distribution across sizes after each process. Sieve analysis was performed to determine the particle size distribution, using a stack of sieves with mesh sizes ranging from 90 to 4000 μm, which was shaken for 15 min on an Endecotts shaker. The weights of granules in each sieve used was recorded to compute the cumulative size distribution, enabling the calculation of particle d10, d50 and d90. Granule porosity was measured using mercury intrusion porosimeter, where incremental intrusion of mercury was introduced to gauge pore size with diameters ranging from 10 to 100,000 nm. For composition analysis, the granule's drug or API content was determined using UV/VIS spectroscopy. The solution was prepared by dissolving 200 mg of the sample in 50 mL of methanol, sonicating for an hour, diluting with methanol, and analyzing via the UV/VIS spectroscopy at 248 nm wavelength. Methanol was selected as the solvent due Acetaminophen's solubility in methanol and Microcrystalline cellulose's insolubility.
Results of the experiments and granule characterization for both the granulation and mill run are listed in Table A1 and Table A2 in the Appendix section.
2.3. Process models
Process models for the granulation and milling process were developed for the purposes of predicting the key granule properties – particle size distribution, porosity and API content, and a dissolution model was developed to predict dissolution rates based on those key granule properties. The type of model used to simulate each process, as well as the model inputs and outputs are specified in Table 2. The material properties related inputs were used to initialize the model, which included the determination of the grid discretization, calculation of the number of particles and the distribution of particles into different bins on the discretized grids, whereas the process parameters were used as inputs to the kernel rate calculations.
Table 2.
Model type, inputs and outputs for each process model used to develop the flowsheet model.
| Unit Operation | Model | Inputs |
Outputs |
|
|---|---|---|---|---|
| Material Properties | Process Parameters | |||
| Granulation | 3-D Population Balance Model |
|
|
|
| Mill | 3-D Population Balance Model |
|
|
|
| Dissolution | ODE Model |
|
– |
|
2.3.1. Granulation
A population balance model (PBM), commonly used to model particulate processes, was used to model the granulation and milling processes. PBMs comprises of a series of partial differential equations (PDEs) used to track the number of entities as they evolve with time due to the occurrence of rate processes, such as nucleation, aggregation and breakage (Barrasso et al., 2015; Ramkrishna and Mahoney, 2002). In this study, a high shear wet granulation process is simulated using a 3-dimensional (3-D) PBM, where the internal coordinates consist of two solid components and one gas component. The use of a higher dimensional PBM was implemented despite it being more computationally expensive, because 1-D PBMs are limited in their abilities to accurately capture the process dynamics, as the model assume that a granule can be described sufficiently by size alone, and there are no considerable variations in other particle properties within a size class (Iveson, 2002; Barrasso and Ramachandran, 2012).
The 3-D PBM equation with lumped liquid component was used and is given by Eq. 1, where represents the number density and the internal coordinates used to characterizes the particle are represented by the API , excipient and gas volume. The lumped liquid volume component is represented by Eq. 2.
| (1) |
| (2) |
The formation and depletion of aggregation, represented by , is a function of aggregation rate, expressed as , which uses the Madec (Madec et al., 2003) kernel and incorporates the Matsuokas (Matsoukas et al., 2009) correction factor. In the Madec kernel, shown in Eq. 3, the aggregation rate is a function of liquid binder content (LC) and granule volume (V). Matsuokas correction factor was added to account for the composition dependencies, as the parameter indicates an attraction or repulsion that occurs between two solid components, and and indicates the fraction of API and excipient volume, respectively. The addition of the Matsuokas correction factor (Matsoukas et al., 2009) ensures that this aggregation kernel is size, liquid content and composition dependent.
| (3) |
| (4) |
The formation and depletion due to breakage (), is determined via the breakage rate kernel from Pandya and Spielman (Pandya and Spielman, 1983), shown in Eq. 5. The breakage rate is a function of impeller shear rate (), particle diameter , and estimated parameters . The impeller shear rate, , can be correlated to the diameter () and rotational speed () of the impeller using the equation (Chaturbedi et al., 2017).
| (5) |
The rates of particle transfer between bins are indicated by the rate of consolidation , and the rate of liquid addition , which are shown in Eqs. (6), (7), respectively. In Eq. 6, is the minimum granule porosity, and is a rate constant, and in Eq. 7, the liquid addition rate is indicated by . The amount of liquid received by each particle is dependent on the granule volume.
| (6) |
| (7) |
The ordinary differential equations (ODE) in the PBEs are solved simultaneously using a first-order explicit Euler integration technique. The selected time step satisfied the Courant-Friedrichs-Lewy (CFL) conditions (Ramachandran and Barton, 2010), ensuring that the steps were sufficiently small to prevent the number of particles leaving any given bin from exceeding the number of particles present in that bin during a single time step. All three internal coordinates were discretized into a volume-based non-linear grids of , to encompass a large range of sizes. Here, i represents the number of bins in the grid, and represents the volume of the smallest bin of each internal coordinate . A 3-dimensional cell average technique (Chaudhury et al., 2013) was used to redistribute particles that are formed in the intermediate range of two bins into the discretized bins.
The parameters present in the equations above, as well as the initial conditions of the model are listed in Table 3. Since the kernels utilized in this model were semi-empirical, some parameters were used as tuning parameters to calibrate the model to better match the experimental results. These tuning parameters include the aggregation kernel constants (, breakage kernel constants ), and consolidation constants . The estimation of the tuning parameters was conducted by minimizing the difference between the experimental data and the model prediction of the quality attributes. The optimization-based algorithm fminsearch on MATLAB was used to minimize the objective function, shown in Eq. 8, which is the sum of squared errors (SSE) for the particle average porosity and API fraction across the size fractions, average over the number of experiments, . A more detailed explanation of the model equations for a 3D, lumped liquid PBM, can be found in Barrasso and Ramachandran (Barrasso and Ramachandran, 2012).
| (8) |
Table 3.
Model parameters and initial conditions used in the granulation model.
| Parameters (Granulation) | Value | Units |
|---|---|---|
| Aggregation constant (ß0) | ||
| Aggregation constant (a) | 2.54 | – |
| Aggregation constant () | 0.01 | – |
| Breakage Kernel constant (P1) | 4.91 | |
| Breakage Kernel constant (P2) | 1.255 | – |
| Consolidation rate constant () | – | |
| Consolidate rate constant () | 8.51 | |
| Minimum granule porosity () | 0.1 | – |
| Initial particle radius (R) | 75 | μm |
| Diameter of impeller (D) | 0.203 | M |
| Total number of bins in each dimension | 10 | |
| Liquid binder spray interval | 120 < t < 300 | S |
| Volume of first bin, solid component 1 () | ||
| Volume of first bin, solid component 2 () | ||
| Volume of first bin, gas () | ||
| Initial particle count F in bin (1,1,1) | 3 × 10–13 | mol |
| Initial particle count F in bin (1,2,1) | 7 × 10–13 | mol |
2.3.2. Mill
Similar to the granulation model, a 3-D PBM with internal coordinates of the API , excipient and gas volume is used to simulate the mill model, and predict the key quality attributes, namely particle size distribution, porosity and composition, as shown in Eq. 9. In order to simulate the dynamics of the milling experiments, which are described in further detail in Dan et al. (Dan et al., 2022), was kept at 0, and was calculated based on particle exit classification model by Metta et al. (Metta et al., 2018).
| (9) |
In milling processes, the only rate process that is considered is breakage, and the rate of particle formation and depletion due to breakage is described by Eq. 9, where the first and second part of the equation denotes the rate of formation and depletion of particles, respectively. In Eq. 10, daughter particles are formed from parent particles at a rate of , shown in Eq. 11, and the daughter particles sizes follows a breakage distribution function, , which is based on a binominal and multivariate log-normal distribution, shown in Eq. 12 and Eq. 13. The binomial distribution was introduced to account for the two breakage modes, namely impact and attrition mode that are critical to the Comil process dynamics, whereas the multivariate was used to accommodate the three internal coordinates of this multi-dimensional model.
| (10) |
| (11) |
| (12) |
| (13) |
In Eq. 12, b1 and b2 represent the distribution function in relation to attrition mode and impact mode, respectively. Thus, z in the equation is indicative of the probability of occurrence attrition breakage mode. This probability varies with time, material properties and dynamic process conditions and is given by Eq. 14, which is determined at every timestep.
| (14) |
The particle outflow, , described by Eq. 15, is a function of a particle exit classification model and the particle retention ratio . is a linear piece-wise model developed by Metta et al. (Metta et al., 2018), which is dependent on the particle size , mill screen size and critical screen size .
| (15) |
| (16) |
| (17) |
Since the Comil operation was a starve-fed Comil, some amount of holdup materials are retained inside the mill at the end of the milling process. The amount of holdup in the mill is dependent on the feed properties and process parameters and is used to determine the yield of the process, as shown in Eq. 18.
| (18) |
A detailed explanation in of the model equations can be found in Dan et al. (Dan et al., 2023). The numerical method and discretization used to solve the mill PBM is similar to the granulation model discussed in the section earlier. Similar to the granulation model, the mill model is calibrated and validated against experimental data, by minimizing the normalized sum of square errors, as shown in Eq. 8. The relevant mill parameters and initial conditions of the model is listed in Table 4.
Table 4.
Model parameters and initial conditions used in the mill model.
| Parameters (Mill) | Value | Unit |
|---|---|---|
| Breakage constant () | 0.026 | |
| Breakage constant (a1) | 3 | – |
| Breakage constant (a2) | 1 | – |
| Breakage constant (a2) | 4 | – |
| Breakage distribution mean (n) | 0.795 | – |
| Breakage distribution standard deviation ( | 1.855 | – |
| Breakage distribution correlation coefficient ( | 0.6875 | – |
| Material retention ratio ( | 0.904 | – |
| Critical screen size parameter ( | 0.7405 | – |
| Critical screen size parameter ( | 0.2474 | – |
| Screen size | 1016 |
2.3.3. Dissolution
The granule dissolution process was modelled using the ordinary differential equation (ODE) model based on the Noyes-Whitney (Noyes and Whitney, 1897) and Nernst-Brunner (Nernst, 1904) equation, where the concentration balance of the bulk solute and the mass balance dissolving granule is denoted by Eq. 19 and Eq. 20, respectively.
| (19) |
| (20) |
Here, is the bulk concentration, is the saturation concentration, is the mass transfer coefficient, and is the surface area. The surface area , can be expressed in terms of the particle diameter .
The mass transfer coefficient , expressed as Eq. 21, is determined based on the size-dependent Sherwood number (Eq. 12) and material specific diffusion coefficient, , which was used as a tuning parameter. This correlation to determine was based on work by Djukaj et al. (Djukaj et al., 2022).
| (21) |
| (22) |
The Sherwood number (Eq. 22) is a function of the Reynolds (and Schmidt number . More details of these equations can be found in Djukaj et al. (Djukaj et al., 2022).
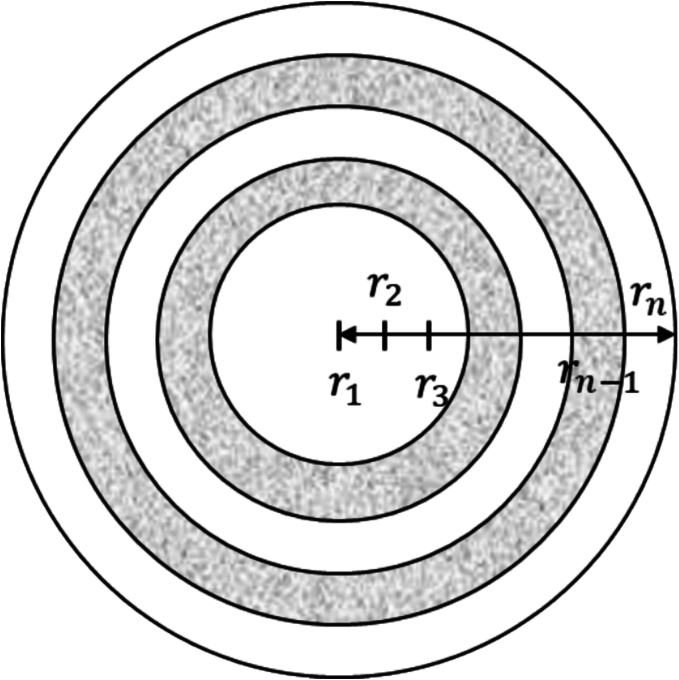
Since variation in granulation and milling process parameters leads to heterogeneity in particle size distribution, porosity, and composition, it is critical that the dissolution model account for these variations when predicting drug dissolution rates. Additionally, studies that have focused on understanding high shear granulation dynamics have found that the powder formulation and process parameters can affect the nucleation mechanisms that occur during granulation, resulting in a dominant formation of either a solid-spreading nuclei or immersion nuclei (Muthancheri and Ramachandran, 2020). The significance of nucleation mechanism is due to its effect on the corresponding granule growth mechanisms, which impacts the microstructure of the produced granules (Muthancheri and Ramachandran, 2020). Granule microstructure pertains to the spatial distribution of different solid components, binder, and void spaces within a granule (Ansari and Stepanek, 2008). Granule microstructure, along with particle size and porosity of the granule, has been shown to have significant effect on the drug dissolution profile (Ansari and Stepanek, 2008). To account for the size, porosity, composition, and microstructure of a granule in its prediction of dissolution rates, each granule is discretized by its radius, as shown in Fig. 2.
Fig. 2.
Radial discretization of a granule.
The spatial distribution of the active ingredient and excipient can be quantified by the radial distribution function (RDF) (Kataria et al., 2018). In this work, RDF indicates the volume fraction of each component, and is expressed as Eq. 23, where indicates the API, excipient and void spaces volume, respectively.
| (23) |
For this work, RDF is a pre-defined granule property, used to calculate the volume in each discretized radii layer of the granule, as shown in Eq. 24. Given that particle mass relates to volume by, , the volume in Eq. 24 can be altered into a mass to be used in the mass balance in Eq. 20.
| (24) |
In this proposed model, it is assumed that both solid components must be entirely dissolved from the outermost layer before materials in the next inner layer can begin dissolving. While this assumption is not entirely reflective of what occurs theoretically, it is useful in the process of developing this dissolution model, as it helps capture the significance of microstructure and dissolution rate differences between two components.
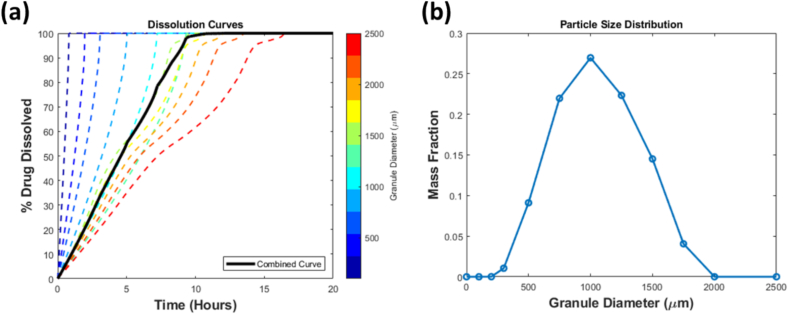
The methodology described above details a single-granule dissolution model. However, in a wet granulation process, a relatively large distribution of granule sizes can be generated, where the granules can range from 50 to 1000 . To incorporate different sizes in this model, granule sizes are discretized into multiple size bins, and the dissolution model is iterated over each bin, resulting in one dissolution curve generated for the granules of each bin. The representative dissolution curve based on the population of sizes is determined based on Eq. 25. An example of a PSD output from a granulation process, the corresponding dissolution curves of each discretized size bin, and the final dissolution curve is illustrated in Fig. 3. This dissolution model contains several parameters that were used as constants, which are listed in Table 5.
| (25) |
Fig. 3.
(a) Dissolution curve of each discretized granule size and the combined curve (black) based on (b) particle size distribution.
Table 5.
Model parameter values used for the dissolution model.
| Parameter | Value | Units |
|---|---|---|
| Solid density | 1500 | |
| Fluid density | 853 | |
| Saturation concentration | 2.935 | |
| API Diffusion coefficient | ||
| Excipient Diffusion coefficient | ||
| Energy dissipation per unit mass | 0.085 |
Since there were no experimental results available to validate the dissolution model, we used findings in the literature on dissolution studies to create a list of dissolution rules to verify that this dissolution model correctly captures the physical nature of the dissolution process, for a representative prediction. The dissolution model was verified using dissolution rules established based on literature studies on experimental and simulated granule dissolution process (Ansari and Stepanek, 2007; Štěpánek, 2004; Ansari and Stepanek, 2006). The categories of these rules include granule size, porosity, diffusion coefficients of each solid component, and microstructure.
A larger particle size has been associated with a lower dissolution rate due to the lower specific surface area which reduces the surface contact area of the granule to the liquid phase. Additionally, larger particles can create a thicker stagnant layer of solvent around them, known as the diffusion layer. This thicker layer increases the path length over which the drug must diffuse to be exposed to the bulk solution and this also contributes to the overall slower dissolution rate (Siepmann and Siepmann, 2008). A higher porosity, on the other hand is associated with faster dissolution. Assuming that pore saturation occurs quickly, a higher porosity attributes to a larger available contact area to the dissolution medium, resulting in a faster dissolution (Ansari and Stepanek, 2007).
When considering a bi-component or multi-component formulation, the dissolution rate of the granule is dependent on the composition and the dissolution rate of each component. For granules with a low drug composition, the drug dissolution is limited by the slower dissolving component, as they create a trapping effect on the faster dissolving component (Ansari and Stepanek, 2007). Whereas, for a higher drug composition granule, the drug dissolution is limited by the solvent saturation, because the driving force is lower as the solvent gets saturated (Ansari and Stepanek, 2007).
Granule microstructure, which denotes the spatial distribution of the active ingredient dictates the drug dissolution rate. When the drug is on the outer layer of the granule the drug dissolution occurs faster than if the active ingredient is in the inner layer (Ansari and Stepanek, 2008).
To ensure that the model captures the accurate dissolution dynamics as stipulated in the dissolution rules above, sensitivity analysis was conducted to determine the model outputs at different parameter variations. These parameters include size, porosity, diffusion coefficient of the active ingredient and the excipient, which was perturbed at three levels (−1, 0, +1). The input parameter values at each perturbation level are denoted in Table 6. The sensitivity is expressed as Eq. 26, where denotes the model output at the i-th perturbation of the j-th parameter, and is the base value for the model output at the j-th parameter.
| (26) |
Table 6.
Critical parameter values at different perturbations.
| Parameters/Levels | −1 | 0 | +1 |
|---|---|---|---|
| Size | 800 | 1000 | 1200 |
| Porosity | 0.1 | 0.3 | 0.5 |
| at low API % | |||
| at high API % |
2.4. Sensitivity analysis
A global sensitivity analysis was used to identify the critical inputs that have significant contributions to variations in the model outputs (Saltelli et al., 2008). In this case, the model outputs are the product yield and time taken for 10 %, 50 %, and 90 % of drug dissolution. A regression-based, partial rank correlation coefficient methodology was used to access the sensitivity of each input-output pair over the input range. PRCC is a variation of the Partial Correlation Coefficient (PRC) which utilizes rank transformed values instead of raw values for both the model inputs and outputs (Wang et al., 2017). This variation allows the PRCC method to be applicable to nonlinear and monotonic systems, as the rank transformation transfers nonlinear relationships into linear (Marino et al., 2008). The regression using the rank transformed values are indicated by Eq. (27), (28), and the correlations are calculated by Eq. (29), (30) (Marino et al., 2008). The PRCC output standardizes the measured correlation between each input-output variable into a − 1 to 1 range, with values closer to +1 and − 1 having the stronger positive and negative correlation, respectively.
| (27) |
| (28) |
| (29) |
| (30) |
Latin Hypercube Sampling (LHS) (McKay et al., 2000) was used to sample across the continuous space of the specified input parameter ranges while ensuring a uniform distribution is sampled. The ranges for the input parameters are listed in Table 1 and was based on the experimental process design, which was determined based on preliminary experiments which indicates the parameter boundaries necessary to produce viable granules.
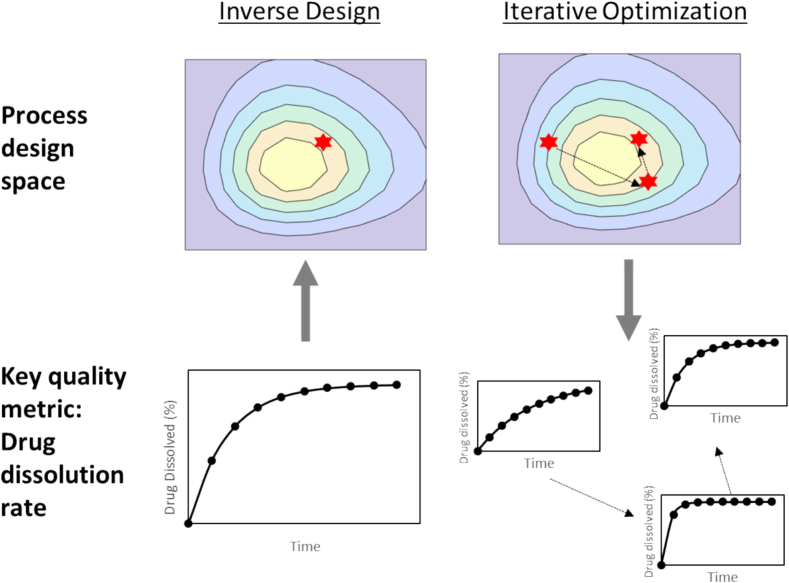
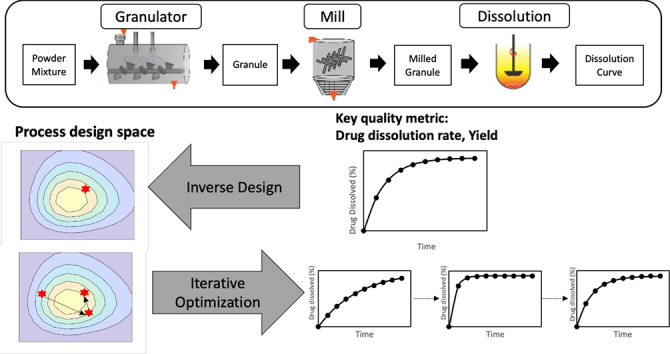
2.5. Optimization
Design optimization in process systems typically pertains to the determination of ideal operating conditions that maximize performance or productivity metrics under the specified constraints. Traditionally optimization can be carried out on iterative optimization on a forward model, however, an inverse design approach can also be a viable option for design optimization. Both approaches are illustrated in Fig. 4 and the implementation of both approaches will be discussed in this work.
Fig. 4.
Comparison of two different design optimization approaches - inverse design and forward (iterative) optimization.
2.5.1. Autoencoder-based inverse optimization
A deep learning based inverse optimization utilizes deep learning algorithms to generate potential optimal solutions for the objective function. One common algorithm that is used for inverse design is the autoencoder.
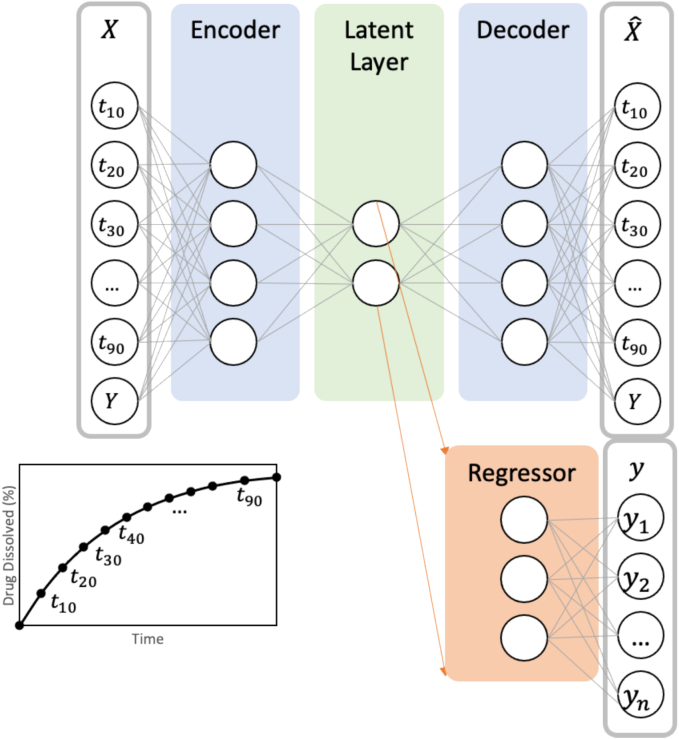
Autoencoders are a type of artificial neural network that are designed for representation learning, with the goal of mapping high-dimensional data into a lower-dimensional representation space, for the purposes of dimensionality reduction or feature extraction (Tschannen et al., 2018). Autoencoders consist of two main components: the encoder, which compresses the input data into a lower-dimensional latent space representation, and the decoder, which reconstructs the input or original data from the compressed representation. The training process of the autoencoder aims to minimize the error between the reconstructed data and input data (Kingma and Welling, 2013).
While autoencoders are traditionally implemented as unsupervised learning techniques, recent research has highlighted a trade-off between the degree of supervision and the usefulness of the learnt representation (Tschannen et al., 2018). Integrating supervised learning into the autoencoder framework has been shown to improve generalization and robustness of the model in various ML tasks (Le et al., 2018).In particular, supervised autoencoders are advantageous when the applications require both dimensionality reduction and accurate predictions. In the supervised autoencoder framework, the latent space layer is utilized not only for data reconstruction but also as input to a regressor for predicting the response variables.
The autoencoder model used was developed in Python v3.8.13 using Keras, which is an open-source neural network library written in Python that provides a high-level interface for building and training deep learning models. The autoencoder model developed consists of 10 input nodes (9 dissolution time metrics and yield), and the encoding step included 2 hidden layers and one dropout layer with 10 nodes each. The prediction of the last hidden layer is passed to a 3 node bottleneck layer, which is then used for decoding or reconstruction using the same number of layers and nodes as the encoding. The dropout layers were introduced at a dropout rate of 0.2, to add regularization which prevents the model from overfitting (Srivastava et al., 2014). The model was trained for 30 epochs at a batch size of 16, and the ‘Adam’ optimizer used to train the model at a learning rate of 0.01. The loss function used was the mean squared error of both the reconstruction and prediction variables.
In an inverse design framework, illustrated in Fig. 5, the inputs to the supervised autoencoder (SAE) are defined as the product outcome (i.e. dissolution time and yield). The dissolution time t10 to t90 indicates time taken for 10 % to 90 % of the granule to dissolve into the bulk solution. The autoencoder is trained to reproduce these inputs, through the encoding and decoding of a lower dimensional latent representation. The regressor attached to the latent layer will use the latent representation as inputs, to predict the critical process parameters for the granulation and milling process. The generation of the latent representation can serve as a lower dimensional process design space, which can be useful for design space visualization and feasibility studies.
Fig. 5.
Schematic detailing the supervised autoencoder architecture (Note: Y indicates yield)
2.5.2. Forward optimization
Forward optimization is a mathematical procedure where first an initial solution is provided to the problem and the objective function is evaluated. The solution is then improved through multiple iterations of function evaluation based on the defined criteria or algorithm. The process is completed, and the iteration stops when the convergence criteria is met either by the optimal solution being within the error tolerance or reaching the maximum iteration. SciPy, which is an open-source Python library was used for optimization, specifically the scipy.optimize.minimize function using the Nelder-Mean algorithm, which is a simplex transformation algorithm, was utilized to minimize the objective function. Eq. 31 shows an objective function example where the goal is to maximize both dissolution time and yield, to ensure that the formulation produces granules with extended-release properties within the design space. Since this is a bi-objective optimization the objective function that is minimized is a weighted sum of each function, with the weightages denoted by and .
| (31) |
2.5.2.1. Surrogate models
Due to the computational complexity and time-intensive nature of the differential equation-based process models within the flowsheet, surrogate models were developed as a computationally efficient replicates to the original models, for improved system analysis and optimization costs. The development of surrogate models first involves identifying an efficient sampling strategy to generate representative data points, which are later used to construct surrogate models. The effectiveness and accuracy of the surrogate model was assessed based on its ability to approximate the global optimum value. If necessary, the model can be refined through iterative adaptive sampling which improves the accuracy (Kim and Boukouvala, 2020).
For this work, the Latin Hypercube Sampling (LHS) method was chosen as the sampling design. LHS is a popular type of space-filling design that uniformly distributes samples across each variable axis, thereby preventing overlap and ensuring controlled randomness (McKay et al., 2000).This approach explores the full range of the input parameters in a representative manner while minimizing sampling bias (Gramacy, 2020). The sampled data points served as training data for developing the surrogate models. Two types of common machine learning (ML) based surrogate models were built, namely artificial neural network (ANN) and support vector regression (SVM). These models were compared to determine their accuracy and ability to represent the dynamic behaviors of the system.
Artificial neural networks (ANN) are efficient function approximations with capabilities of capturing non-linear effects between the inputs and outputs, and can be used for both regression and classification problems (Csáji, 2001). A standard neural network architecture consists of an input layer, hidden layer(s), and an output layer. These layers are connected using elements known as nodes or neurons, where the output of each neuron serves as the input of the corresponding neuron in the next layer. The mathematical representation of the output of a neuron can be shown by Eq. 32,
| (32) |
where, indicates the neuron in layer , are the weights for each input connected to the neuron, is the bias for the neuron and indicates the output of the neuron in the previous layer. The function is passed through an activation function, denoted by , which introduces non-linearity to the function approximation (Sharma et al., 2017). There are numerous activation functions that can be used depending on the nature of the problem and the dynamics of the system. Some examples include linear, sigmoid, Tanh, ReLU and softmax functions (Sharma et al., 2017).
The process of training a neural network model comprises of the tuning of weights and biases to minimize the prediction error. Another important element of building ML models is hyperparameter tuning, where configuration variables relating to the model architecture is tuned for optimized performance. For this work, hyperparameter tuning was conducted using grid search, which evaluates the model's performance at different combinations of hyperparameters to find the optimal configuration to minimize loss or error on the validation dataset. The range of values and the optimal value of the hyperparameters are tabulated in Table 7. The number of epochs was kept constant at 40, and the loss function used to train the model was the mean absolute error. Additionally, it is important to note that to ensure reduced model complexity, only a one hidden layer model architecture is considered for the ANN to ensure the model remains shallow.
Table 7.
Ranges and optimal value of hyperparameters of the surrogate models.
| ML Model | Hyperparameter | Range | Optimal value |
|---|---|---|---|
| Artificial Neural Network (ANN) | No. of neurons in the hidden layer | 1–10 | 9 |
| Learning rate | 0.001–1 | 0.01 | |
| Activation function | tanh, relu | relu | |
| Batch Size | 16, 32, 64, 128 | 16 | |
| L1 Regularization factors | 0.001–0.1 | 0.01 | |
| Support Vector Regression (SVR) | Kernel Type | linear, poly, rbf | rbf |
| Regularization parameter C) | 0.1–1000 | 10 | |
| Kernel Coefficient (Gamma) | 0.001–10 | 1 | |
| Epsilon | 0.01–1 | 0.1 |
The second surrogate model evaluated was the support vector regression (SVR),which is a variant of support vector machines (SVM) introduced by Drucker et al. (Drucker et al., 1996). SVR is designed for regression problems, while SVM is used for classification tasks. The basic principle of the SVR algorithm involves fitting a hyperplane or decision boundary that best fits the data while minimizing complexity. The regularization is done by introducing an error margin, also known as the , where zero prediction error is assigned to the points within the tube, while penalizing slack variables (i.e. variables outside the tube) by its distance () to the tube boundary (Awad and Khanna, 2015). A regularization parameter, C, is also introduced to handle the outliers more robustly, which helps controlling the trade-off between maximizing the margin and minimizing prediction error. SVR can also handle non-linear regressions by using kernel functions, which transforms the feature space into a higher-dimensional space, where the function, , can be solved. Some common kernel functions for the SVR include linear, polynomial, radial basis function (RBF) and sigmoid. The hyperparameter ranges and optimal values are for the SVR model development is tabulated in Table 7.
3. Results and discussion
3.1. Process model validation and verification
The granulation and mill process models were calibrated using 80 % of the experimental data, and the remainder of the 20 % was used to validate the model. The results for normalized outputs including d10, d50, d90, porosity and drug composition are indicated in parity plots, R2 and RMSE values. For the mill model, an additional output, which is the cumulative mass in the mill outlet, was also included in the parity plots.
Fig. 6, which shows the results for both granulation and mill model, indicates good predictive performance and accuracy on both the training and validation dataset.
Fig. 6.
Parity plots for the (a) Granulation PBM and (b) Mil PBM.
Since there was no experimental data available for validation of the dissolution model results, model verification was carried out based on sensitivities of various parameters following the dissolution rules listed in Section 2.3.3. These parameters were perturbed at three levels, as shown in Table 6, to ensure that the model physics is reflective of the experimental observations. The results of t90 (i.e. time taken for 90 % of drug to be dissolved) at each perturbation for size, porosity and diffusion coefficient are shown in Table 7.
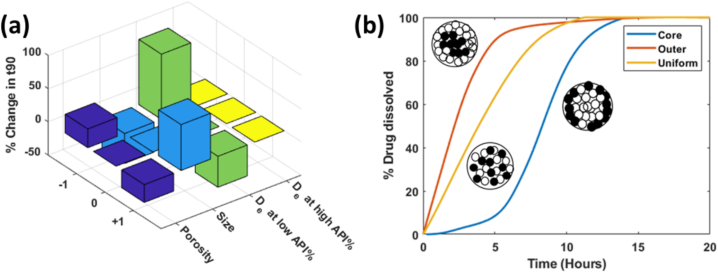
As shown in Fig. 7(a), t90 is inversely proportional to size and directly proportional to porosity, which is in agreement with the discussion in previous literature and in The next two columns in Fig. 7 (a) discusses the effect of diffusion coefficient of the excipient at low and high API content composition formulations. is fraction of the diffusion coefficient of the drug. Based on the figure, the parameter shows significant sensitivity at lower API content, but less so at higher API content. This is also in agreement with the discussion in the Section 2.3.3. We see that at low API content, the slower dissolving component is the limiting factor of drug dissolution.
Fig. 7.
Sensitivity of the dissolution t90 at different critical parameter values for (a) size, porosity, diffusion coefficients, and (b) granule microstructure.
The microstructure of granules significantly influences their dissolution behavior. In this part of the study, we consider three theoretical microstructures, where the active pharmaceutical ingredient (API) is concentrated in the core, the API in the outer layer, and the API uniformly distributed throughout the granule. These configurations are established by pre-defining the radial distribution function (RDF) of the drug components, to reflect these varied microstructures. The dissolution curves of each microstructure are illustrated in Fig. 7. Here, it is evident that the granules with the API in the core exhibit a noticeable time delay in dissolution. This delay is primarily due to the “trapping effect,” where excipient components surrounding the core must first dissolve before the API molecules are exposed to the dissolution medium. Consequently, the dissolution rate of the core API microstructure is initially slower compared to other structures. In contrast, granules with the API in the outer layer dissolve more rapidly, as the API is immediately available for dissolution upon contact with the solvent. The uniformly distributed API microstructure presents an intermediate dissolution profile, with the API dissolving steadily as the granule progressively shrinks in size. These findings highlight the critical role of microstructure in determining the dissolution kinetics of drug granules, which is essential for optimizing drug delivery and ensuring consistent therapeutic outcomes.
3.2. Sensitivity analysis
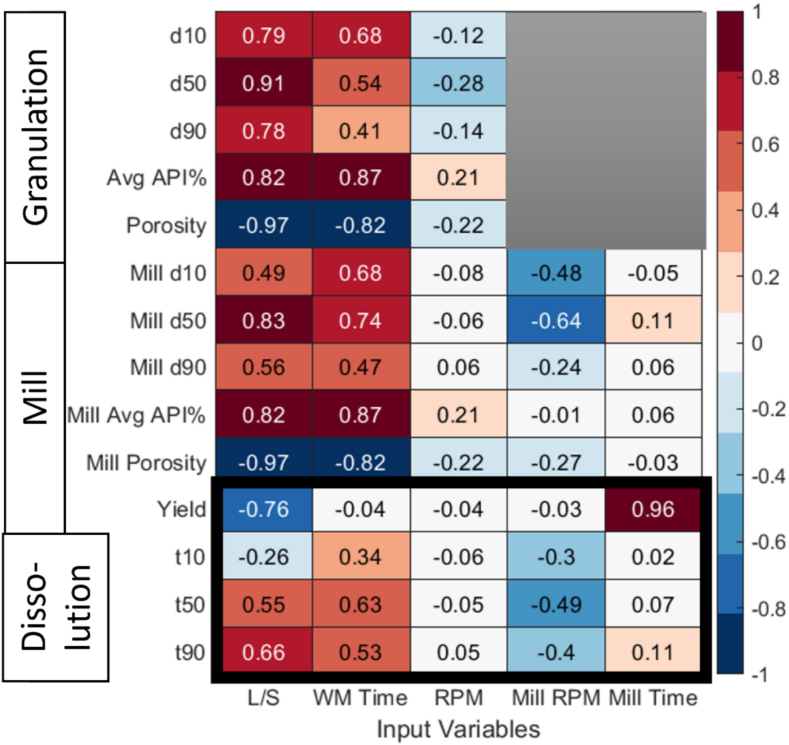
The PRCC method was used to evaluate the impact of the input variables on the outputs variables, and identify the critical process parameters, and the results of the sensitivity analysis was depicted in the intensity plots in Fig. 8. Fig. 8 represents the input and output variables in the x-axis and y-axis, respectively, and the coefficient is denoted by the values and the box color. Here, the darker red color indicates stronger positive correlation, while the darker blue color indicates stronger negative correlation. The output variables include intermediate quality attributes, such as size, porosity and API content from the granulation and milling process, and final quality attributes (highlighted in the black box), such as product yield and dissolution metrics . Yield is defined as the fraction of mass of material in the mill outlet over the feed.
Fig. 8.
Sensitivity analysis PRCC results of the model parameters in the flowsheet model.
The analysis above reveals that granulation L/S ratio and wet massing time exhibit the strongest positive correlations with dissolution metrics . Conversely, mill RPM shows a weaker negative correlation with the dissolution metrics. Granulation impeller speed (RPM) and mill time demonstrate a lower impact on dissolution metrics. However, mill time and L/S ratio notably correlated strongly with product yield, where the mill time denotes a positive correlation and L/S denotes a negative correlation. This is because as milling time increases, more material within the mill holdup undergoes breakage and exits the mill. On the other hand, the L/S ratio strongly influences the granule particle size and porosity. At a higher L/S ratio, a granule is formed with larger size and lower porosity, both of which contributes to a higher mill holdup, resulting in lower yield.
Additionally, in this process design space range, the granulation RPM is shown have minimal sensitivity to all final quality attributes, thus, to simplify the optimization problem dimension, granulation RPM was kept constant at 190 RPM.
3.3. Surrogate-based optimization
3.3.1. Surrogate model development
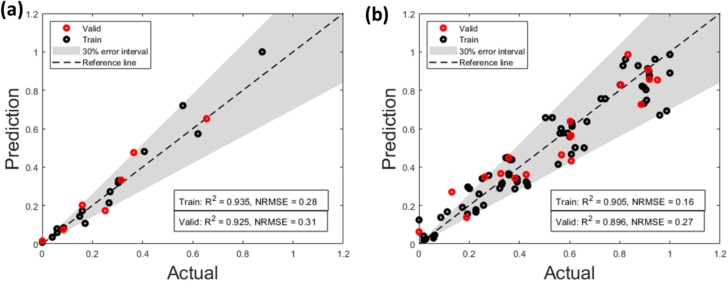
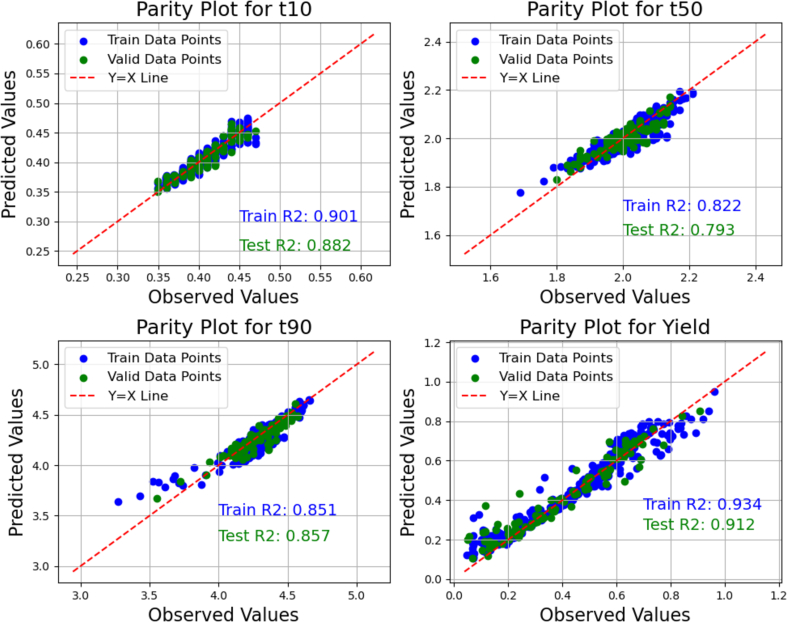
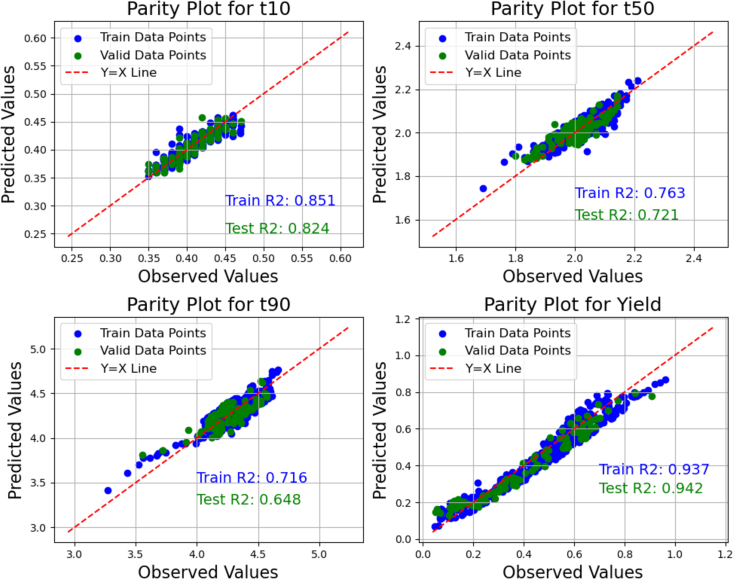
The effectiveness of the surrogate model was assessed using the model prediction performance, which can be indicated by parity plots and metrics such as the coefficient of determination ( which measures the goodness of fit of the model. Fig. 9 and Fig. 10 depicts the parity plots and values for both the optimized ANN and SVR models based on hyperparameters listed in Table 7. The comparison of both figures indicates that the NN model more effectively captures the pattern of data in this system, as indicated by the better model performance. This may be attributed to the more weights that can be tuned for better fit to the data in the ANN model. The computational time associated with training these models are minimal with the ANN requiring approximately 3 s and the SVR taking 0.4 s.
Fig. 9.
ANN model parity plot and prediction performance metrics.
Fig. 10.
SVR model parity and prediction performance metrics
3.3.2. Forward optimization
An optimization case study was designed to conduct forward optimization on the surrogate models. A bi-objective function based on maximizing both dissolution time (indicated by and yield is formulated. Both weighted sum optimization and pareto optimization methodology was compared. The results of the weighted sum are tabulated in Table 8, where the function weighted for the two objectives vary at the different cases. From Table 8 it is evident that as the weights for maximizing yield decreases and the weights for maximizing dissolution time increases (going from left to right), the optimal solution shows an increase in the L/S, wet massing time, and a decrease in milling time. The higher L/S and wet massing time results in a more significant densification and consolidation in the granulation mechanism, resulting in larger granules with lower porosity formed. These attributes contribute to a lower yield as they are more difficult to break during milling, but also contributes to a slower dissolution time.
Table 8.
Optimal solutions at different function weightages of the weighted sum multi-objective optimization.
| Function Weightage | Yield | 1 | 0.9 | 0.5 | 0.1 | 0 |
| 0 | 0.1 | 0.5 | 0.9 | 1 | ||
| Optimized Parameters | L/S | 0.68 | 0.68 | 0.72 | 0.765 | 0.8 |
| WMT | 240 | 281.8 | 309.5 | 240 | 480 | |
| Mill RPM | 2477.8 | 2276.4 | 1500 | 1500 | 1500 | |
| Mill Time | 15 | 15 | 14.93 | 13.74 | 0.5 | |
| Predicted Quality Metrics | Yield | 0.90 | 0.87 | 0.77 | 0.67 | 0.18 |
| 3.37 | 3.88 | 4.38 | 4.44 | 4.62 | ||
| 1.78 | 1.93 | 2.04 | 2.02 | 2.16 | ||
| 0.39 | 0.43 | 0.44 | 0.40 | 0.42 |
3.4. Autoencoder-based inverse design
3.4.1. Autoencoder model performance
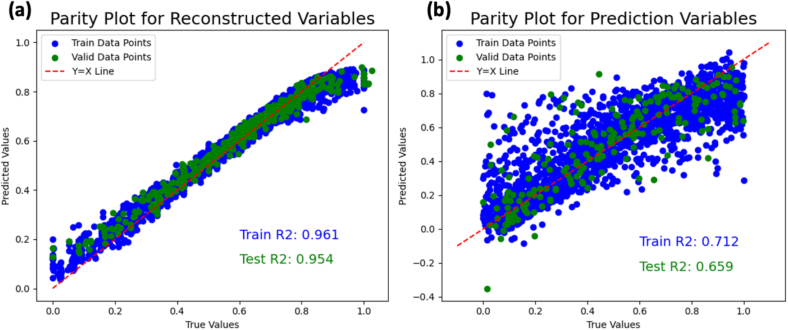
The supervised autoencoder training was based on minimizing the mean squared error (MSE) of both the reconstruction and prediction variables. The errors for the reconstruction and prediction variables were calculated based on difference to the process outcome (dissolution time and yield) and process parameters, respectively. The model performance is denoted by the normalized parity plots and (measure of the goodness of fit) values, illustrated in Fig. 11. Since the training and validation are quite similar, overfitting is concluded to be minimal as the model generalizes well to new inputs. Fig. 11 also shows that the performance for the prediction variables (process parameters) are poorer in comparison to the reconstruction variables (dissolution time and yield). This is because the process parameters have different level of sensitivity affecting the process outcome, as shown in Fig. 8. Thus, while the variables with higher sensitivity have good predictive performance, the variables with lower sensitivity have poorer performance. However, the goodness-of-fit is still within acceptable predictive performance required for this work. The computational cost of training this supervised autoencoder for 50 epochs at a batch size of 8 took 4.3 s.
Fig. 11.
Parity plots for the (a) reconstructed and (b) prediction variables of the supervised autoencoder.
3.4.2. Latent space representation
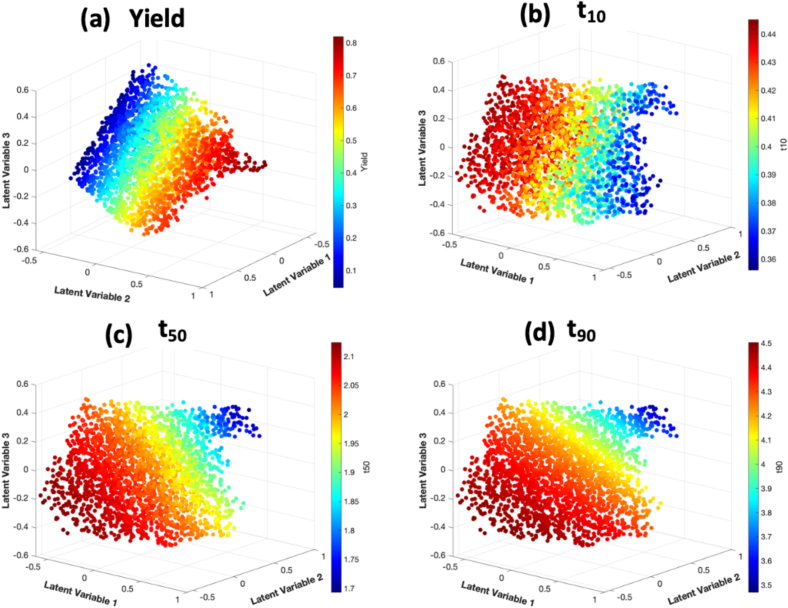
The latent space representation is represented by the three latent variables in the ‘bottleneck’ layer of the autoencoder. These latent variables are described as lower dimensional representation of the system. For this dataset, the minimum number of variables that was needed to explain the dynamics of the system was three, when one or two variable(s) was used in the latent layer, the reconstruction prediction was much poorer.
Fig. 12 shows the three latent variables in a 3-dimensional plot with each variable in one of the axes. In Fig. 12(a) the data points are colored by product yield values, where values closer to 1 indicates high yield and values closer to 0 indicates low yield. It is observed that yield is proportional to latent variable 2 and inversely proportional to latent variable 3. Yield is not significantly correlated to latent variable 1. Fig. 12(b,c,d) colors the data points by dissolution time . and was shown to be inversely correlated to latent variable 2, while was inversely correlated to variable 1.
Fig. 12.
Latent space representation, colored by (a) yield, (b) t10, (c) t50 and (d) t90.
The reduction of dimensionality of the autoencoder is similar to that of the PCA/PLS algorithms except that non-linear functions can be used in autoencoders, whereas PCA/PLS relies entirely on linear correlations.
3.4.3. Feasibility analysis
Feasibility analysis is a technique used for evaluating the ability of a process to satisfy all relevant operating, quality and production constraints (Grossmann et al., 2014). The goal of a feasibility analysis is to identify the feasible region, which denotes the range of conditions which a process can operate while satisfying all the relevant constraints (Rogers and Ierapetritou, 2015).
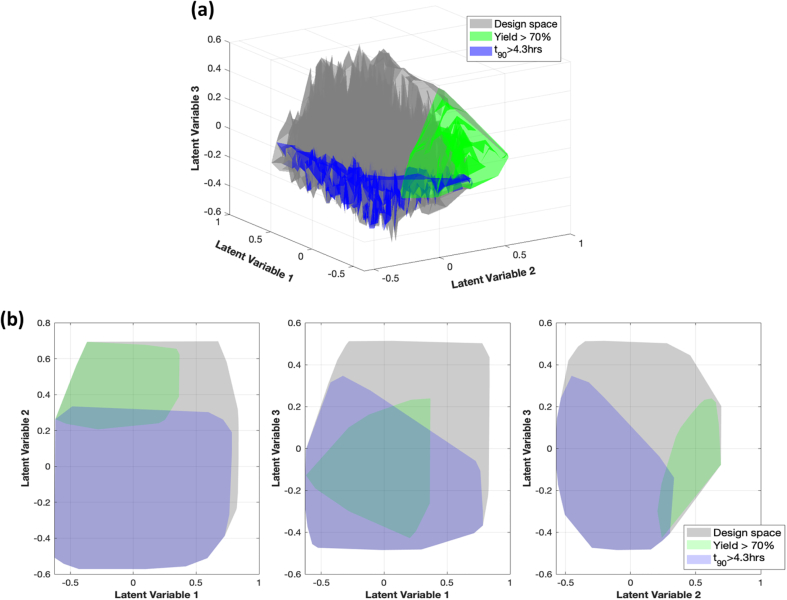
Eq. 33 describes the constraints on both the product quality and process parameters that were established for the problem. A surrogate-based feasibility analysis was conducted by utilizing the autoencoder as the surrogate model. The feasible region, which is represented by the autoencoder latent variables and determined based on the constraints established, are shown in Fig. 13. The gray shaded region indicates the feasible region denoted by the process design space (i.e. constraints only on L/S, WMT, Mill RPM and Mill Time), whereas the green region indicates additional constraint on yield and the blue region indicates additional constraint on t90. The overlap between the green and blue region indicates the feasible region where all the constraints listed in Eq. 33 are satisfied.
| (33) |
Fig. 13.
(a) 3-D representation and (2) 2-D representations of the feasible region.
Data generation was performed using the decoder and regressor components of the autoencoder. To generate data points, the encoded values, determined by the Latin Hypercube Sampling (LHS) algorithm, served as inputs. The outputs generated included both process parameters and product quality metrics. Initially, 5000 data points were sampled. After filtering for the process design space, 2500 data points remained. These 2500 data points were then used in the feasibility analysis. Out of the 2500 analyzed data points, 21 possible solutions were identified within the feasible region. The process parameter ranges within the feasibility region are, L/S ratio (0.7–0.74), wet massing time (4.1–7.2 Minutes), mill RPM (1507–2315 rpm), mill time (13.3–15 min). These results show similarity to those obtained from weighted sum optimization, indicating the applicability and consistency of both methods.
4. Conclusions
In conclusion, this study demonstrates the successful optimization of a three-unit flowsheet model using two distinct approaches: autoencoder-based inverse design and surrogate-based optimization. Both methods effectively addressed the multi-objective problem of maximizing dissolution time while maximizing yield to achieve target product quality.
The supervised autoencoder approach showed comparable results to the surrogate-based method, with the added benefit of dimensional reduction. This feature proves particularly advantageous for high-dimensional problems involving numerous process inputs and outputs. The lower-dimensional representation facilitates improved process understanding, enhanced visualization, and enables feasibility studies on latent variables. The inverse design capability of the supervised autoencoder makes it particularly well-suited for targeting specific product qualities, as demonstrated in this study.
In this case study, both the autoencoder and surrogate models (ANN/SVR) required comparable training times, each completing within seconds, and prediction accuracy with of 0.87 for the ANN and of 0.83 for the autoencoder. The surrogate-based optimization, which iterates over the surrogate model to find the optimal solution is also computationally efficient as it completes in under a minute. However, for more complex problems, the autoencoder training would likely take longer than training the ANN/SVR surrogate models, due to a larger number of tuning parameters in the autoencoder. Despite the initial time investment, the autoencoder method offers superior efficiency in the subsequent optimizations by allowing direct sampling from the latent space without the need for iterative model runs. As the problem complexity increases, the advantages of the autoencoder-based inverse design approach woule likely become more pronounced, because of the prolonged run time required to iterate over a forward optimization framework when searching for a solution to a complex optimization problem containing many inputs.
This research contributes to the field of process design and development by presenting a novel application of optimizing processes using supervised autoencoders to implement inverse design in pharmaceutical manufacturing. The findings suggest that this approach can be a powerful tool for efficiently optimizing complex multi-objective problems, and can be a great alternative option to the more common surrogate-based optimization, especially when targeting specific product qualities in complex process operations.
CRediT authorship contribution statement
Ashley Dan: Writing – original draft, Methodology, Investigation. Rohit Ramachandran: Writing – review & editing, Supervision, Project administration.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors would like to acknowledge Rutgers Research Council for funding this work. The work reported in this manuscript is also partially supported by the National Science Foundation (NSF) where R.R is on assignment as Program Director. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF.
Appendix A. Appendix
Table A1.
Experimental results for the granulation based on full factorial DOE design.
| Run | Label | L/S | W.M.T (min) | Impeller Speed (rpm) | d10 | d50 | d90 | Porosity (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | HHH | 0.8 | 8 | 200 | 538 | 876 | 2117 | 26.57 |
| 2 | HLL | 0.8 | 4 | 180 | 495 | 863 | 1927 | – |
| 3 | LHH | 0.65 | 8 | 200 | 133 | 390 | 1375 | – |
| 4 | HHL | 0.8 | 8 | 180 | 666 | 1356 | 2743 | – |
| 5 | LLL | 0.65 | 4 | 180 | 166 | 300 | 643 | 40.9 |
| 6 | LLH | 0.65 | 4 | 200 | 178 | 326 | 576 | – |
| 7 | LHL | 0.65 | 8 | 180 | 147 | 423 | 885 | – |
| 8 | MMM | 0.725 | 6 | 190 | 310 | 578 | 1347 | 32.82 |
Table A2.
Experimental results for the mill.
| Run | Feed Material - Granulation Run | Mill Impeller Speed (rpm) | Collection Time | d10 | d50 | d90 | Yield | Porosity (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | HHH | 1500 | 0.25 | 398 | 539 | 738 | 0.546 | – |
| 2 | HHH | 1500 | 0.5 | 401 | 543 | 745 | 0.601 | – |
| 3 | HHH | 1500 | 1 | 404 | 548 | 753 | 0.641 | – |
| 4 | HHH | 1500 | 5 | 407 | 556 | 771 | 0.695 | – |
| 5 | HHH | 1500 | 10 | 408 | 559 | 777 | 0.714 | – |
| 6 | HHH | 1500 | 15 | 406 | 560 | 783 | 0.727 | 31.07 |
| 7 | HHH | 3000 | 0.25 | 334 | 495 | 631 | 0.546 | – |
| 8 | HHH | 3000 | 0.5 | 337 | 497 | 636 | 0.601 | – |
| 9 | HHH | 3000 | 1 | 339 | 501 | 649 | 0.641 | – |
| 10 | HHH | 3000 | 5 | 340 | 510 | 694 | 0.695 | – |
| 11 | HHH | 3000 | 10 | 332 | 511 | 704 | 0.714 | – |
| 12 | HHH | 3000 | 15 | 319 | 510 | 708 | 0.727 | 33.46 |
| 13 | HLL | 1500 | 15 | 278 | 450 | 604 | 0.869 | – |
| 14 | HLL | 3000 | 15 | 254 | 419 | 586 | 0.941 | – |
| 15 | LHH | 1500 | 15 | 80 | 206 | 393 | 0.897 | – |
| 16 | LHH | 3000 | 15 | 76 | 197 | 379 | 0.919 | – |
| 17 | HHL | 1500 | 15 | 398 | 559 | 764 | 0.547 | – |
| 18 | HHL | 3000 | 15 | 276 | 529 | 735 | 0.691 | – |
| 19 | LLL | 1500 | 15 | 64 | 169 | 300 | 0.932 | – |
| 20 | LLL | 3000 | 15 | 60 | 155 | 288 | 0.926 | 38.7 |
| 21 | LLH | 1500 | 15 | 73 | 187 | 336 | 0.906 | – |
| 22 | LLH | 3000 | 15 | 68 | 177 | 305 | 0.927 | – |
| 23 | LHL | 1500 | 15 | 137 | 356 | 832 | 0.952 | – |
| 24 | LHL | 3000 | 15 | 125 | 305 | 780 | 0.967 | – |
| 25 | MMM | 1500 | 15 | 155 | 275 | 449 | 0.887 | – |
| 26 | MMM | 3000 | 15 | 145 | 262 | 421 | 0.932 | 36.29 |
Table A3.
List of possible solutions of in the feasible region.
| Optimized Outputs |
Process Parameters |
||||||
|---|---|---|---|---|---|---|---|
| Yield | LS | WMT | Mill RPM | Mill Time | |||
| 0.43 | 2.06 | 4.36 | 0.733 | 0.7 | 303.3 | 1535 | 14.3 |
| 0.44 | 2.06 | 4.32 | 0.733 | 0.72 | 253.5 | 2315 | 14.7 |
| 0.44 | 2.06 | 4.31 | 0.732 | 0.71 | 277.5 | 2301 | 14.7 |
| 0.44 | 2.06 | 4.32 | 0.728 | 0.72 | 268.4 | 2274 | 14.6 |
| 0.43 | 2.06 | 4.34 | 0.728 | 0.71 | 256.8 | 1940 | 14.1 |
| 0.44 | 2.07 | 4.34 | 0.724 | 0.72 | 250.3 | 2134 | 15 |
| 0.43 | 2.06 | 4.34 | 0.723 | 0.71 | 260.6 | 1963 | 14.1 |
| 0.43 | 2.05 | 4.33 | 0.722 | 0.7 | 289.4 | 1666 | 14 |
| 0.42 | 2.03 | 4.32 | 0.72 | 0.7 | 304.9 | 1507 | 13.8 |
| 0.44 | 2.06 | 4.36 | 0.72 | 0.72 | 246.9 | 2247 | 13.7 |
| 0.44 | 2.06 | 4.3 | 0.713 | 0.71 | 284.6 | 2315 | 13.7 |
| 0.44 | 2.07 | 4.34 | 0.71 | 0.72 | 255.6 | 2270 | 13.8 |
| 0.44 | 2.05 | 4.31 | 0.709 | 0.72 | 262.4 | 2266 | 13.3 |
| 0.43 | 2.04 | 4.31 | 0.709 | 0.71 | 284 | 1849 | 13.7 |
| 0.43 | 2.06 | 4.37 | 0.708 | 0.72 | 303.7 | 1834 | 14.6 |
| 0.45 | 2.07 | 4.34 | 0.708 | 0.7 | 316.3 | 1523 | 14.9 |
| 0.41 | 2.02 | 4.31 | 0.707 | 0.71 | 327.1 | 1533 | 13.8 |
| 0.41 | 2.05 | 4.39 | 0.703 | 0.7 | 434.3 | 1519 | 14.4 |
| 0.44 | 2.07 | 4.35 | 0.701 | 0.73 | 258.2 | 2111 | 13.9 |
| 0.4 | 2.03 | 4.37 | 0.7 | 0.71 | 408.2 | 1589 | 14.1 |
| 0.43 | 2.07 | 4.39 | 0.7 | 0.74 | 274.3 | 2189 | 15 |
Data availability
Data will be made available on request.
References
- Abdulla A.A., Oshi M.A. A simple approach to enhance dissolution of commercial paracetamol tablets for fast relief of pain. BrJP. 2024;7 [Google Scholar]
- Administration U.F.A.D. US Food & Drug Administration; Silver Spring, MD, USA: 2021. Artificial intelligence and machine learning in software as a medical device. [Google Scholar]
- Administration U.F.A.D. US Food & Drug Administration; Silver Spring, MD, USA: 2023. Artificial Intelligence and Machine Learning (AI/ML) in Drug Development. [Google Scholar]
- Agarwal P., Aghaee M., Tamer M., Budman H. A novel unsupervised approach for batch process monitoring using deep learning. Comput. Chem. Eng. 2022;159 [Google Scholar]
- Aghaee M., Krau S., Tamer M., Budman H. Unsupervised Fault Detection of Pharmaceutical Processes using Long Short-Term memory Autoencoders. Ind. Eng. Chem. Res. 2023;62:9773–9786. [Google Scholar]
- Algorri M., Abernathy M.J., Cauchon N.S., Christian T.R., Lamm C.F., Moore C.M. Re-envisioning pharmaceutical manufacturing: increasing agility for global patient access. J. Pharm. Sci. 2022;111:593–607. doi: 10.1016/j.xphs.2021.08.032. [DOI] [PubMed] [Google Scholar]
- Am Ende M.T. John Wiley & Sons; 2019. Chemical Engineering in the Pharmaceutical Industry: Drug Product Design, Development, and Modeling. [Google Scholar]
- Ansari M.A., Stepanek F. Design of granule structure: computational methods and experimental realization. AICHE J. 2006;52:3762–3774. [Google Scholar]
- Ansari M., Stepanek F. The evolution of microstructure in three-component granulation and its effect on dissolution. Part. Sci. Technol. 2007;26:55–66. [Google Scholar]
- Ansari M.A., Stepanek F. The effect of granule microstructure on dissolution rate. Powder Technol. 2008;181:104–114. [Google Scholar]
- Arden N.S., Fisher A.C., Tyner K., Lawrence X.Y., Lee S.L., Kopcha M. Industry 4.0 for pharmaceutical manufacturing: preparing for the smart factories of the future. Int. J. Pharmaceut. 2021;602 doi: 10.1016/j.ijpharm.2021.120554. [DOI] [PubMed] [Google Scholar]
- Awad M., Khanna R. Springer Nature; 2015. Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers. [Google Scholar]
- Barrasso D., Ramachandran R. A comparison of model order reduction techniques for a four-dimensional population balance model describing multi-component wet granulation processes. Chem. Eng. Sci. 2012;80:380–392. [Google Scholar]
- Barrasso D., Oka S., Muliadi A., Litster J.D., Wassgren C., Ramachandran R. Population balance model validation and predictionof CQAs for Continuous milling processes: toward QbDin pharmaceutical drug product manufacturing. J. Pharm. Innov. 2013;8:147–162. [Google Scholar]
- Barrasso D., El Hagrasy A., Litster J.D., Ramachandran R. Multi-dimensional population balance model development and validation for a twin screw granulation process. Powder Technol. 2015;270:612–621. [Google Scholar]
- Bellinghausen S., Gavi E., Jerke L., Barrasso D., Salman A.D., Litster J.D. Model-driven design using population balance modelling for high-shear wet granulation. Powder Technol. 2022;396:578–595. [Google Scholar]
- Bilgili E., Scarlett B. Population balance modeling of non-linear effects in milling processes. Powder Technol. 2005;153:59–71. [Google Scholar]
- Boukouvala F., Ierapetritou M.G. Surrogate-based optimization of expensive flowsheet modeling for continuous pharmaceutical manufacturing. J. Pharm. Innov. 2013;8:131–145. [Google Scholar]
- Boukouvala F., Niotis V., Ramachandran R., Muzzio F.J., Ierapetritou M.G. An integrated approach for dynamic flowsheet modeling and sensitivity analysis of a continuous tablet manufacturing process. Comput. Chem. Eng. 2012;42:30–47. [Google Scholar]
- Boukouvala F., Chaudhury A., Sen M., Zhou R., Mioduszewski L., Ierapetritou M.G., Ramachandran R. Computer-aided flowsheet simulation of a pharmaceutical tablet manufacturing process incorporating wet granulation. J. Pharm. Innov. 2013;8:11–27. [Google Scholar]
- Chaturbedi A., Bandi C.K., Reddy D., Pandey P., Narang A., Bindra D., Tao L., Zhao J., Li J., Hussain M. Compartment based population balance model development of a high shear wet granulation process via dry and wet binder addition. Chem. Eng. Res. Des. 2017;123:187–200. [Google Scholar]
- Chaudhury A., Kapadia A., Prakash A.V., Barrasso D., Ramachandran R. An extended cell-average technique for a multi-dimensional population balance of granulation describing aggregation and breakage. Adv. Powder Technol. 2013;24:962–971. [Google Scholar]
- Chaudhury A., Wu H., Khan M., Ramachandran R. A mechanistic population balance model for granulation processes: effect of process and formulation parameters. Chem. Eng. Sci. 2014;107:76–92. [Google Scholar]
- Chen H., Engkvist O., Wang Y., Olivecrona M., Blaschke T. The rise of deep learning in drug discovery. Drug Discov. Today. 2018;23:1241–1250. doi: 10.1016/j.drudis.2018.01.039. [DOI] [PubMed] [Google Scholar]
- Chen Y., Kotamarthy L., Dan A., Sampat C., Bhalode P., Singh R., Glasser B.J., Ramachandran R., Ierapetritou M. Optimization of key energy and performance metrics for drug product manufacturing. Int. J. Pharmaceut. 2023;631 doi: 10.1016/j.ijpharm.2022.122487. [DOI] [PubMed] [Google Scholar]
- Csáji B.C. Vol. 24. Faculty of Sciences, Etvs Lornd University; Hungary: 2001. Approximation with artificial neural networks; p. 7. [Google Scholar]
- Dan A., Kotamarthy L., Ramachandran R. Understanding the effects of process parameters and material properties on the breakage mechanisms and regimes of a milling process. Chem. Eng. Res. Des. 2022;188:607–619. [Google Scholar]
- Dan A., Vaswani H., Šimonová A., Ramachandran R. Multi-dimensional population balance model development using a breakage mode probability kernel for prediction of multiple granule attributes. Pharm. Dev. Technol. 2023;28:638–649. doi: 10.1080/10837450.2023.2231074. [DOI] [PubMed] [Google Scholar]
- Dargan S., Kumar M., Ayyagari M.R., Kumar G. A survey of deep learning and its applications: a new paradigm to machine learning. Arch. Comput. Methods Eng. 2020;27:1071–1092. [Google Scholar]
- Djukaj S., Kolář J., Lehocký R., Zadražil A., Štěpánek F. Design of particle size distribution for custom dissolution profiles by solving the inverse problem. Powder Technol. 2022;395:743–757. [Google Scholar]
- Drucker H., Burges C.J., Kaufman L., Smola A., Vapnik V. Support vector regression machines. Adv. Neural Inf. Proces. Syst. 1996;9 [Google Scholar]
- Escotet-Espinoza M.S., Vadodaria S., Singh R., Muzzio F.J., Ierapetritou M.G. Modeling the effects of material properties on tablet compaction: a building block for controlling both batch and continuous pharmaceutical manufacturing processes. Int. J. Pharmaceut. 2018;543:274–287. doi: 10.1016/j.ijpharm.2018.03.036. [DOI] [PubMed] [Google Scholar]
- Escotet-Espinoza M.S., Moghtadernejad S., Oka S., Wang Z., Wang Y., Roman-Ospino A., Schäfer E., Cappuyns P., Van Assche I., Futran M. Effect of material properties on the residence time distribution (RTD) characterization of powder blending unit operations. Part II of II: application of models. Powder Technol. 2019;344:525–544. [Google Scholar]
- Gentile F., Agrawal V., Hsing M., Ton A.-T., Ban F., Norinder U., Gleave M.E., Cherkasov A. Deep docking: a deep learning platform for augmentation of structure based drug discovery. ACS Cent. Sci. 2020;6:939–949. doi: 10.1021/acscentsci.0c00229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gernaey K.V., Gani R. A model-based systems approach to pharmaceutical product-process design and analysis. Chem. Eng. Sci. 2010;65:5757–5769. [Google Scholar]
- Gramacy R.B. Chapman and Hall/CRC; 2020. Surrogates: Gaussian Process Modeling, Design, and Optimization for the Applied Sciences. [Google Scholar]
- Grossmann I.E., Calfa B.A., Garcia-Herreros P. Evolution of concepts and models for quantifying resiliency and flexibility of chemical processes. Comput. Chem. Eng. 2014;70:22–34. [Google Scholar]
- Gupta R., Srivastava D., Sahu M., Tiwari S., Ambasta R.K., Kumar P. Artificial intelligence to deep learning: machine intelligence approach for drug discovery. Mol. Divers. 2021;25:1315–1360. doi: 10.1007/s11030-021-10217-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hintz R.J., Johnson K.C. The effect of particle size distribution on dissolution rate and oral absorption. Int. J. Pharmaceut. 1989;51:9–17. [Google Scholar]
- Huo L., Tang Y. Multi-objective deep reinforcement learning for personalized dose optimization based on multi-indicator experience replay. Appl. Sci. 2022;13:325. [Google Scholar]
- Iveson S.M. Limitations of one-dimensional population balance models of wet granulation processes. Powder Technol. 2002;124:219–229. [Google Scholar]
- Kalný M., Grof Z., Štěpánek F. Microstructure based simulation of the disintegration and dissolution of immediate release pharmaceutical tablets. Powder Technol. 2021;377:257–268. [Google Scholar]
- Kataria A., Oka S., Smrčka D., Grof Z., Štěpánek F., Ramachandran R. A quantitative analysis of drug migration during granule drying. Chem. Eng. Res. Des. 2018;136:199–206. [Google Scholar]
- Kim S.H., Boukouvala F. Surrogate-based optimization for mixed-integer nonlinear problems. Comput. Chem. Eng. 2020;140 [Google Scholar]
- Kimber J.A., Kazarian S.G., Štěpánek F. Microstructure-based mathematical modelling and spectroscopic imaging of tablet dissolution. Comput. Chem. Eng. 2011;35:1328–1339. [Google Scholar]
- Kingma D.P., Welling M. 2013. Auto-encoding variational bayes , arXiv preprint arXiv:1312.6114. [Google Scholar]
- Lakerveld R., Benyahia B., Braatz R.D., Barton P.I. Model-based design of a plant-wide control strategy for a continuous pharmaceutical plant. AICHE J. 2013;59:3671–3685. [Google Scholar]
- Le L., Patterson A., White M. Supervised autoencoders: improving generalization performance with unsupervised regularizers. Adv. Neural Inf. Proces. Syst. 2018;31 [Google Scholar]
- LeCun Y., Bengio Y., Hinton G. Deep learning. Nature. 2015;521:436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- Litster J., Bogle I.D.L. Smart process manufacturing for formulated products. Engineering. 2019;5:1003–1009. [Google Scholar]
- MacGregor J.F., Yu H., Muñoz S.G., Flores-Cerrillo J. Data-based latent variable methods for process analysis, monitoring and control. Comput. Chem. Eng. 2005;29:1217–1223. [Google Scholar]
- Maclean N., Armstrong J.A., Carroll M.A., Salehian M., Mann J., Reynolds G., Johnston B., Markl D. Flexible modelling of the dissolution performance of directly compressed tablets. Int. J. Pharmaceut. 2024;656 doi: 10.1016/j.ijpharm.2024.124084. [DOI] [PubMed] [Google Scholar]
- Madec L., Falk L., Plasari E. Modelling of the agglomeration in suspension process with multidimensional kernels. Powder Technol. 2003;130:147–153. [Google Scholar]
- Marino S., Hogue I.B., Ray C.J., Kirschner D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008;254:178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matji A., Donato N., Gagol A., Morales E., Carvajal L., Serrano D.R., Worku Z.A., Healy A.M., Torrado J.J. Predicting the critical quality attributes of ibuprofen tablets via modelling of process parameters for roller compaction and tabletting. Int. J. Pharmaceut. 2019;565:209–218. doi: 10.1016/j.ijpharm.2019.05.011. [DOI] [PubMed] [Google Scholar]
- Matsoukas T., Kim T., Lee K. Bicomponent aggregation with composition-dependent rates and the approach to well-mixed state. Chem. Eng. Sci. 2009;64:787–799. [Google Scholar]
- Matsunami K., Meyer J., Rowland M., Dawson N., De Beer T., Van Hauwermeiren D. T-shaped partial least squares for high-dosed new active pharmaceutical ingredients in continuous twin-screw wet granulation: granule size prediction with limited material information. Int. J. Pharmaceut. 2023;646 doi: 10.1016/j.ijpharm.2023.123481. [DOI] [PubMed] [Google Scholar]
- McKay M.D., Beckman R.J., Conover W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics. 2000;42:55–61. [Google Scholar]
- Metta N., Verstraeten M., Ghijs M., Kumar A., Schafer E., Singh R., De Beer T., Nopens I., Cappuyns P., Van Assche I. Model development and prediction of particle size distribution, density and friability of a comilling operation in a continuous pharmaceutical manufacturing process. Int. J. Pharmaceut. 2018;549:271–282. doi: 10.1016/j.ijpharm.2018.07.056. [DOI] [PubMed] [Google Scholar]
- Metta N., Ghijs M., Schäfer E., Kumar A., Cappuyns P., Van Assche I., Singh R., Ramachandran R., De Beer T., Ierapetritou M. Dynamic flowsheet model development and sensitivity analysis of a continuous pharmaceutical tablet manufacturing process using the wet granulation route. Processes. 2019;7:234. [Google Scholar]
- Muthancheri I., Ramachandran R. Mechanistic understanding of granule growth behavior in bi-component wet granulation processes with wettability differentials. Powder Technol. 2020;367:841–859. [Google Scholar]
- Nernst W. Theorie der Reaktionsgeschwindigkeit in heterogenen Systemen. Z. Phys. Chem. 1904;47:52–55. [Google Scholar]
- Noyes A.A., Whitney W.R. The rate of solution of solid substances in their own solutions. J. Am. Chem. Soc. 1897;19:930–934. [Google Scholar]
- Pandya J., Spielman L. Floc breakage in agitated suspensions: effect of agitation rate. Chem. Eng. Sci. 1983;38 [Google Scholar]
- Preim B., Botha C.P. Newnes; 2013. Visual Computing for Medicine: Theory, Algorithms, and Applications. [Google Scholar]
- Ramachandran R., Barton P.I. Effective parameter estimation within a multi-dimensional population balance model framework. Chem. Eng. Sci. 2010;65:4884–4893. [Google Scholar]
- Ramkrishna D., Mahoney A.W. Population balance modeling. Promise for the future. Chem. Eng. Sci. 2002;57:595–606. [Google Scholar]
- Reynolds G.K. Modelling of pharmaceutical granule size reduction in a conical screen mill. Chem. Eng. J. 2010;164:383–392. [Google Scholar]
- Reynolds G., Ingale R., Roberts R., Kothari S., Gururajan B. Practical application of roller compaction process modeling. Comput. Chem. Eng. 2010;34:1049–1057. [Google Scholar]
- Rogers A., Ierapetritou M. Feasibility and flexibility analysis of black-box processes part 1: Surrogate-based feasibility analysis. Chem. Eng. Sci. 2015;137:986–1004. [Google Scholar]
- Rogers A.J., Hashemi A., Ierapetritou M.G. Modeling of particulate processes for the continuous manufacture of solid-based pharmaceutical dosage forms. Processes. 2013;1:67–127. [Google Scholar]
- Salami H., Skomski D. Building confidence in deep Learning-based image analytics for characterization of pharmaceutical samples. Chem. Eng. Sci. 2023;278 [Google Scholar]
- Saltelli A., Ratto M., Andres T., Campolongo F., Cariboni J., Gatelli D., Saisana M., Tarantola S. John Wiley & Sons; 2008. Global Sensitivity Analysis: The Primer. [Google Scholar]
- Sampat C., Ramachandran R. Risk assessment for a twin-screw granulation process using a supervised physics-constrained auto-encoder and support vector machine framework. Pharm. Res. 2022;39:2095–2107. doi: 10.1007/s11095-022-03313-y. [DOI] [PubMed] [Google Scholar]
- Sampat C., Ramachandran R. 2023. Optimizing Energy Efficiency of a Twin-Screw Granulation Process in Real-Time Using a Long Short-Term Memory (LSTM) Network, ACS Engineering Au. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sampat C., Kotamarthy L., Bhalode P., Chen Y., Dan A., Parvani S., Dholakia Z., Singh R., Glasser B.J., Ierapetritou M. Enabling energy-efficient manufacturing of pharmaceutical solid oral dosage forms via integrated techno-economic analysis and advanced process modeling. J. Adv. Manuf. Process. 2022;4 [Google Scholar]
- Sanchez-Lengeling B., Aspuru-Guzik A. Inverse molecular design using machine learning: generative models for matter engineering. Science. 2018;361:360–365. doi: 10.1126/science.aat2663. [DOI] [PubMed] [Google Scholar]
- Sarker I.H. Deep learning: a comprehensive overview on techniques, taxonomy, applications and research directions. SN Comput. Sci. 2021;2:420. doi: 10.1007/s42979-021-00815-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen M., Singh R., Vanarase A., John J., Ramachandran R. Multi-dimensional population balance modeling and experimental validation of continuous powder mixing processes. Chem. Eng. Sci. 2012;80:349–360. [Google Scholar]
- Sen M., Dubey A., Singh R., Ramachandran R. Mathematical development and comparison of a hybrid PBM-DEM description of a continuous powder mixing process. J. Powder Technol. 2013;2013 [Google Scholar]
- Sharma S., Sharma S., Athaiya A. Activation functions in neural networks. Towards Data Sci. 2017;6:310–316. [Google Scholar]
- Siepmann J., Siepmann F. Mathematical modeling of drug delivery. Int. J. Pharmaceut. 2008;364:328–343. doi: 10.1016/j.ijpharm.2008.09.004. [DOI] [PubMed] [Google Scholar]
- Srivastava N., Hinton G., Krizhevsky A., Sutskever I., Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014;15:1929–1958. [Google Scholar]
- Štěpánek F. Computer-aided product design: granule dissolution. Chem. Eng. Res. Des. 2004;82:1458–1466. [Google Scholar]
- Tschannen M., Bachem O., Lucic M. 2018. Recent advances in autoencoder-based representation learning. arXiv preprint arXiv:1812.05069. [Google Scholar]
- Venkatasubramanian V. The promise of artificial intelligence in chemical engineering: is it here, finally? AICHE J. 2019;65:466–478. [Google Scholar]
- Wang Z., Escotet-Espinoza M.S., Ierapetritou M. Process analysis and optimization of continuous pharmaceutical manufacturing using flowsheet models. Comput. Chem. Eng. 2017;107:77–91. [Google Scholar]
- Wilson D., Wren S., Reynolds G. Linking dissolution to disintegration in immediate release tablets using image analysis and a population balance modelling approach. Pharm. Res. 2012;29:198–208. doi: 10.1007/s11095-011-0535-1. [DOI] [PubMed] [Google Scholar]
- Wong W.C., Chee E., Li J., Wang X. Recurrent neural network-based model predictive control for continuous pharmaceutical manufacturing. Mathematics. 2018;6:242. [Google Scholar]
- Zaborenko N., Shi Z., Corredor C.C., Smith-Goettler B.M., Zhang L., Hermans A., Neu C.M., Alam M.A., Cohen M.J., Lu X. First-principles and empirical approaches to predicting in vitro dissolution for pharmaceutical formulation and process development and for product release testing. AAPS J. 2019;21:1–20. doi: 10.1208/s12248-019-0297-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H., Zhao M., Liu L., Zhong H., Liang Z., Yang Y., Zhou X., Wu Q.J., Wang Y. Deep multimodel cascade method based on CNN and random forest for pharmaceutical particle detection. IEEE Trans. Instrum. Meas. 2020;69:7028–7042. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.