ABSTRACT
Identifying interventions that are optimally tailored to each individual is of significant interest in various fields, in particular precision medicine. Dynamic treatment regimes (DTRs) employ sequences of decision rules that utilize individual patient information to recommend treatments. However, the assumption that an individual's treatment does not impact the outcomes of others, known as the no interference assumption, is often challenged in practical settings. For example, in infectious disease studies, the vaccine status of individuals in close proximity can influence the likelihood of infection. Imposing this assumption when it, in fact, does not hold, may lead to biased results and impact the validity of the resulting DTR optimization. We extend the estimation method of dynamic weighted ordinary least squares (dWOLS), a doubly robust and easily implemented approach for estimating optimal DTRs, to incorporate the presence of interference within dyads (i.e., pairs of individuals). We formalize an appropriate outcome model and describe the estimation of an optimal decision rule in the dyadic‐network context. Through comprehensive simulations and analysis of the Population Assessment of Tobacco and Health (PATH) data, we demonstrate the improved performance of the proposed joint optimization strategy compared to the current state‐of‐the‐art conditional optimization methods in estimating the optimal treatment assignments when within‐dyad interference exists.
Keywords: dWOLS, dyadic network, interference, joint optimization, PATH, precision medicine
Abbreviations
- DTR
dynamic treatment regime
- dWOLS
dynamic weighted ordinary least squares
1. Introduction
Treatment of a chronic disease or condition often involves a series of decisions for which multiple long‐term strategies are possible. The decision of which regime of treatments to pursue is often made by a medical professional, who chooses an appropriate treatment regime based on metrics that, historically, emphasize the illness. Precision medicine is an approach that aims to improve upon the traditional method of treatment selection by taking into account additional relevant factors. The basic idea is that the efficacy of a particular treatment may be influenced by certain individual‐level characteristics of each person, such that the effectiveness of the treatment will vary across individuals with different values of these characteristics. By incorporating relevant information into the treatment decision, precision medicine enables clinicians to select the most suitable treatment for each individual with greater precision. The focus on individual‐level characteristics is why precision medicine is sometimes also known as personalized medicine [1].
The relationship between treatments and individual‐level characteristics may be explored through dynamic treatment regimes (DTRs). A DTR is a sequence of decision rules each of which considers individual‐level information thought to impact the effectiveness of the treatments under consideration [2]. A central focus of DTR researchers is devising methodologies for the estimation of optimal DTRs [3]. What is meant by optimal is contextual, but a typical approach is to consider it in terms of the individual's expected health outcome under the estimated regime.
Different methods of estimating optimal DTR have been proposed in the literature [4]. Among these methods, some focus on modeling the conditionally expected outcome to derive and optimize DTRs, with Q‐learning as a notable example [5, 6]. Q‐learning is relatively straightforward to implement, but in its traditional form, it suffers from a lack of robustness to model misspecification. An approach that improves on this shortcoming of Q‐learning is G‐estimation [7]. G‐estimation is similar to Q‐learning in many ways (see, e.g., Chakraborty, Murphy, and Strecher [8]), but provides double robustness against misspecification of nuisance models. The robustness of G‐estimation, and the flexibility to accommodate nonlinear modeling strategies, makes it an attractive method for estimating optimal DTR, but relatively more complex to implement compared to Q‐learning. Building on the foundations laid by Q‐learning and G‐estimation, new methods have been developed to address model misspecification. One such significant advancement is the data‐driven robust Q‐learning approach introduced by Ertefaie et al. [9] to reduce the risks of model misspecification in DTR. Of particular interest for our purposes is the dynamic weighted ordinary least squares (dWOLS) approach, another method that integrates a key strength of G‐estimation, that is, robustness to nuisance model misspecification, and Q‐learning, which is simple to implement. The dWOLS method is adaptable to continuous treatments and time‐to‐event outcomes [10, 11, 12].
Most of the foregoing methods for estimating optimal DTRs assume that the treatment of one individual has no impact on the outcome of any other individual under consideration. This is the so‐called no interference assumption of classical causal inference, a crucial component of the stable unit treatment value assumption (SUTVA) [13]. However, no interference assumption may not hold true in all scenarios. For example, interference arises in the study of infectious diseases, where the treatment status (i.e., vaccination) of people around an individual could impact their likelihood of getting infected [14]. Ignoring interference, when it exists, could bias the causal estimates of interest [15]. Moreover, estimating the effect of the treatment of others on an individual's outcome may itself be of intrinsic interest in some settings [16]. While various studies have addressed interference in different causal inference contexts [17, 18, 19, 20, 21], it remains underexplored in the context of DTR.
Recently, attempts have been made to extend DTRs to situations in which the no interference assumption is relaxed. One of the first works on estimating an optimal treatment regime in the presence of interference with a regression‐based population model was proposed by Su, Lu, and Song [22]. The authors characterize network interference by including neighbors' covariates and treatment status in each individual's outcome model. However, the model is only for a single‐stage treatment decision and does not assume any interaction between individuals' treatments. That leads to an optimal decision rule that ultimately does not depend on the treatment status of one's neighbors. A more recent study considers a DTR framework utilizing dWOLS, in which the treatment status and covariate values of the neighbors of individuals of interest are gathered into a scalar‐valued exposure interference term, which is then incorporated at the modeling stage [23]. However, the treatments of the neighbors are considered constant and are not included in the optimization stage; that is, the optimization employs a conditional optimization approach. Therefore, the estimation of optimal treatment for an individual could potentially proceed with the usual dWOLS algorithm.
In this work, we propose a methodology for the estimation of optimal DTRs within a population in which interference among those being considered for treatment exists. In particular, we consider the context of a patient population exhibiting a dyadic‐network structure, where each individual in the sample forms a dyad (i.e., pair) with another individual in the sample. Interference is then permitted to exist among those patients belonging to the same dyad, but not between dyads. In a population with such an interference structure, each individual is influenced by two treatments: their own prescribed treatment and the treatment of their dyad cohabitant. It follows that each treatment is then associated with two individuals, and therefore optimal value of the treatment can only be obtained when the resulting ramifications on both parties are considered. Estimation of the optimal treatment regime then proceeds through, without loss of generality, maximization of a dyad outcome through the dyad‐health function, a contextual measure of the health status of those comprising a dyad. The model, therefore, accounts for the interference of treatment statuses within the population in estimation, and, to our knowledge, is the first model to do so in the DTR literature. In addition, the introduction of the dyad‐health function provides practitioners with the flexibility to accommodate concerns, such as prioritizing marginalized groups or individuals within dyads who suffer from more serious health problems.
To demonstrate the importance of the innovations provided by the proposed model, we focus on nicotine exposure. Studies show that smoking behaviors tend to cluster within families [24], and that the effectiveness of smoking cessation interventions for an individual can be influenced by social factors such as the concordance of smoking tendencies between family members [25, 26, 27]. Through a detailed analysis of the Population Assessment of Tobacco and Health (PATH) data set, we investigate the impact of adoption of e‐cigarettes in households with two tobacco users. We assess whether the adoption of e‐cigarettes by an individual impacts their nicotine exposure, and whether there exists an interference effect, that is, when one member of a tobacco using household adopts e‐cigarette use, does it impact the nicotine exposure in the other member of the dyad?
The remainder of this work is structured as follows: Section 2 provides the methodological and theoretical background, including notation, and sets up the modeling framework for a K‐stage DTR on a dyadic‐network population. In Section 3, we discuss the details of estimating the proposed model, including the treatment and outcome models, as well as the optimal treatment decisions for the dyadic‐network DTR. Section 4 contains three simulation studies. The first demonstrates that the proposed methodology retains the double‐robustness property of dWOLS, while the second compares the performance of the proposed model with existing methodologies on data sampled from a dyadic‐network population structure. The third simulation explores the impact of different dyad‐health functions on the resulting DTR within a dyadic‐network context. Section 5 contains our analysis of the PATH data set, and Section 6 concludes the paper with some discussion.
2. Methodology
2.1. Notation
In the framework of DTR, it is assumed that patients undergo multiple stages of treatment. This process begins with the initiation of treatment, followed by subsequent treatment decisions, taking into account the current and past information available for the patients. A K‐stage treatment regime is a sequence of decision rules that specify how to assign treatments over K time points based on a patient's evolving history.
In accordance with the established DTR literature, consider a sample of individuals who have completed a ‐stage treatment regime. We assume that interference takes a special form, specifically of a dyadic network, which is to say, each individual in the sample forms a dyad (i.e., pair) with another individual in the sample, with whom they interact. Under this assumption, interference is restricted to occur only within these dyads. Hence, the sample may be considered analogously as a sample of independent dyads. We index the members of a given dyad using . In general, when the member of interest is member we use the notation to represent the measurements corresponding to their dyadic partner. For simplicity, we will define quantities in terms of Member when the quantity is member‐specific. The analogous quantity for Member can be found by simply replacing all the s with s in these definitions, and vice versa.
We let index the treatment stages, and we will let index the sampled dyads (rather than individuals). Consider an arbitrary dyad at an arbitrary stage . We use to denote the set of treatment options available at stage . Typically, binary treatments are considered, hence is isomorphic to and we will, without loss of generality, use this representation going forward. The random variable denotes the treatment of dyad at stage . This consists of , the treatment of the members of a dyad at stage , that is, and .
We assume that a set of covariate measurements are taken on each individual prior to treatment at stage . We denote these covariates by . Additionally, we let denote the vector of shared covariates among the dyad members as of stage . This shared vector may contain, for example, household income, living conditions, geographic location and so on. Although covariates are assumed to be measured at each stage , any measurements preceding treatment at that stage can also be used to inform the decision. Accordingly, we define to be the history of measurements relevant for informing the treatment decision of dyad member at stage , through the current stage itself. The history may consist of current and past stage covariates of either member of the dyad, previous treatment values of either, the shared covariates, or functions thereof. We use to analogously denote history at the dyad level at stage .
Following the th stage, that is, after the treatment regime has finished, we assume a measurement is made on each individual to assess the efficacy of the treatment regime. We refer to this measurement simply as the outcome, and it is denoted by for the outcome associated with member . It is assumed throughout that the outcome is continuous and that, without loss of generality, larger values are preferable, in the sense that this indicates a more efficacious regime.
Before the outcome is actually observed, we call it a “potential” outcome because its value depends on the sequence of administered treatments and the history. When we talk about a specific individual's outcome in this context, we call it “individual‐level” to distinguish it from any group or dyad outcomes. In situations where interference is present in the form of a dyadic network, the individual‐level potential outcome depends on the full sequence of dyad treatments, denoted , rather than only the individual treatments. Sometimes, it will be necessary to make the dependence of the potential outcome on the treatments and history explicit, which we do using the notation .
Thus, for a given dyad , represents the outcome of member that would be observed if, over the stages of the regime, the history is observed to be and the dyadic treatments over the stages follow the sequence . Note that this function is defined for all possible dyad treatment sequences in the space , meaning it accounts for every potential treatment assignment among the dyad pair, not just the observed ones.
Let be a bivariate function which takes as its argument a dyad outcome , and, based on this input, returns a value summarizing the overall health of the dyad in a contextually relevant manner. We call this the dyad‐health function. It follows from this definition that we may obtain our desired dyad‐level optimal treatment regime by maximizing over . Specifically, let be the set of decision rules comprising the dyadic DTR, where determines the prescribed dyad treatment at stage given the dyad history . We call a treatment regime, and in this case more specifically, a ‐stage treatment regime. Let be some class of ‐stage treatment regimes of interest. The general goal in the given context would be to find the ‐stage treatment regime that maximizes the expected dyad health,
As an example, consider choosing to be the average of the elements of , that is, . By averaging and , we're essentially specifying that both individuals' outcomes contribute equally to the dyad's health. Under the proposed framework, this choice of recovers the oft‐used maximization of the population expected value, with the caveat that it now accounts for dyad‐level interaction (because it technically maximizes the average of pairwise averages). Although averaging is a simple and easily understood choice, it may not always be a contextually appropriate one, and we will discuss this point further in the experiment in Section 4.3.
2.2. Causal Framework
To allow for the estimation of causal effects in the presence of interference at the dyad level, updates to the typical causal inference assumptions of positivity, consistency, and no unmeasured confounders, are required. In this section, we specify the required changes in turn. Note that each assumption is specified at the dyad level and is assumed to hold for all dyads in the population. We hence drop the subscript denoting an arbitrary dyad in the following assumption definitions.
For any stage , and any observable dyad history , we propose a generalization of the consistency assumption to the dyadic network context as follows: Let be the space of all sequences of dyad‐level treatments over a ‐stage regime and be the associated set of potential outcomes for member with observed history . We assume that the observed outcome can be specified as, , where denotes the indicator function of the event .
For an analog to the no unmeasured confounders assumption in the dyadic network context, define as the set of dyad‐level potential outcomes, and as the space of observable histories over a ‐stage treatment regime. We must assume that, conditional on an observed sequence of histories , the observed sequence of dyad treatments is assigned independently of the set of potential outcomes of that dyad. That is, .
To adapt the standard positivity assumption, we need to ensure that within each level of the shared or unshared covariates, any possible dyad‐level treatments can occur. Specifically, for dyad treatment at stage , we assume that for all and for every observable history in support of , the probability of assigning is greater than 0. Formally, this is expressed as: for all and all observable histories .
We can sometimes also impose a symmetry assumption called exchangeability. If exchangeability holds, the joint distribution of outcomes and histories for the dyad members is identical. Formally, this means . Under this assumption, the dyad members are statistically indistinguishable in terms of their outcome and history distributions within any given dyad. This symmetry allows for the analysis and interpretation of dyad‐level interactions without differentiating between specific members of the dyad.
We first introduce the underlying assumptions for interference modeling. The causal framework outlined in Section 2.2 facilitates the development of causal models that enable the estimation and optimization of treatment effects within a dyadic‐network population. The most general formulation of our modeling assumptions is represented succinctly in the leftmost causal diagram in Figure 1. All arrows in Figure 1 represent dependence; however, colors have been used to distinguish between dependence structures of different contextual or modeling importance. For example, blue‐directed arrows have been used to show the causal impact of the individual covariates of one member of the dyad on the treatment or outcome of the other, while green arrows pertain to treatment interference. Finally, red arrows have been used to signify association, which can occur between the treatments or the outcomes of the dyad members due to some common cause. Dashed lines were used to emphasize that these common causes are assumed unobserved.
FIGURE 1.
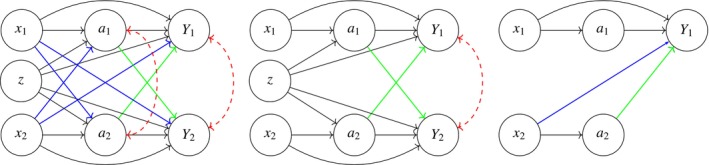
Combined models: This figure integrates three models illustrating varying degrees of interference and independence between members of a dyad. On the left, Model 1 (General Interference Model) represents a scenario where treatments and covariates of each member can influence both their own and the other member's treatment and outcome, with dashed‐bidirectional arcs indicating potential unobserved shared causes. The middle, Model 2 (Restricted Model), simplifies this by assuming no causal impact of a member's covariates on the other member and conditional independence of treatments given observed covariates. On the right, Model 3 (Independent Treatment Model) isolates the focus on Member 1, where only the treatment and covariates of Member 2 influence the outcome of Member 1. Model 3 was used by Jiang, Wallace, and Thompson [23]. Colors are used to differentiate dependence structures across models.
In practice, there are scenarios that can be represented by simpler interference structures. For example, we might assume that the individual covariates of one member do not have an impact on the treatment or outcome of the other member, and that the treatment assignment of dyad members is independent of each other, given their shared and individual covariates. The middle graph in Figure 1 illustrates the causal graph representing such a scenario. Adoption of the simplest causal diagram which adequately reflects the data context can lead to savings at estimation time. This is discussed in more detail in Section 3.2.
For comparison purposes, we also present the causal model assumed by Jiang, Wallace, and Thompson [23], which is shown in the rightmost graph of Figure 1. In their model, they only explicitly model Member 1 from each dyad, under the assumption that individual covariates and the treatment of Member 2 might have a potential causal impact on the outcome of Member 1. Furthermore, the treatment of Member 1 is regarded as independent of the treatment of the other member. In contrast, we extend their model to encompass both members of a dyad in both the modeling and optimization stages (as detailed in Section 3), thereby allowing for the consideration of potential interference from the covariates and treatment of both members on each other's outcomes.
2.3. Modeling a K‐Stage DTR in a Dyadic Network
To formalize the dyadic‐network DTR model, we start by considering the final treatment decision, which is made at stage . The goal at this stage is to select the treatment that optimizes the dyad outcome (or some function thereof, see Section 3.3). In the general case, we assume that the expected outcome for each dyad member, given all available information at stage , can be expressed as a two‐component parametric model:
| (1) |
where represents a so‐called treatment‐free component for individual at stage , parameterized by , and denotes a so‐called blip component at stage , parameterized by . Equation (1) is a general model specification broadly used in the DTR literature and here we adapt it to the context of dyadic‐network interference [23]. Note that although the definitions of the expected values are independent of the dyad outcomes, this does not exclude the possibility that they are correlated as random variables.
Both components of the model serve a particular purpose, which can be understood intuitively within the framework of personalized medicine. The treatment‐free component, , can be intuitively understood as the part of dyad member 's outcome that would occur regardless of the treatment assigned at the th stage. Moreover, serves as an untreated baseline expected outcome against which the effects of assigning treatment to the dyad can be evaluated.
The blip component, , captures the expected change in outcome due to the treatment assigned at stage . Interference among the dyad members implies that this blip model should consider both dyad members' treatments. From the model's perspective, this is equivalent to assuming that individual is exposed to a bivariate treatment, which reflects the treatment status of both dyad members. It follows that we can interpret the blip component as the relative change in the expected outcome of dyad member , with respect to the baseline scenario where no treatment is assigned to either member of the dyad, due to the dyad receiving treatment . This subtle but important change is a key feature that distinguishes the dyadic‐network DTR from earlier methodologies. To emphasize this point, we refer to the blip component in this context as the dyadic‐blip component.
Utilizing the outcome model of Equation (1), our goal is to identify an optimal DTR. Traditionally, an optimal treatment refers to that treatment that maximizes over all possible treatment assignments, where this expected value is taken over the dyad superpopulation distribution. However, because the dyad‐level potential outcome is vector‐valued, the concept of maximization is ambiguous. To proceed, it is necessary to impose some constraints.
Constraints can be implemented by introducing a real‐valued function that maps the outcome space onto the real line. This function allows us to express the optimization problem in a mathematically well‐defined way: we seek the treatment regime that maximizes . The choice of the function is context‐dependent, reflecting the specific goals and priorities of the intended analysis.
In our context, the function can be understood as defining a measure of overall dyad health that is of particular interest. Hence, we refer to as the dyad‐health function. By specifying , we impose a constraint on the optimization problem, directing it to focus on the aspects of the dyad outcome that are most relevant to the health of the dyad. The selection of is therefore not unique, and different plausible choices may lead to different optimal treatment regimes. We will discuss these ideas further in Section 3.3.
Under this framework, the optimal decision rule at stage is found by solving,
| (2) |
where optimization takes place over the space of vector‐valued dyad treatments. Previous methods that assume interference or interacting pairs, such as Su, Lu, and Song [22] and Jiang, Wallace, and Thompson [23], do not optimize the outcome, or treatment, of interfering members. This partial optimization can lead to only a conditional maximum, rather than a global one, which risks overlooking the broader impact on the dyad population. In particular, such approaches may inadvertently worsen outcomes for the population as a whole. Our model addresses this limitation by jointly optimizing the treatments for all dyad members, ensuring that the global maximum is pursued and that the overall health of the population is not compromised.
Once the optimal treatment at stage is obtained, the next step is to evaluate how much the expected dyad outcome would be improved under this potentially counterfactual treatment assignment. From the assumed model in Equation (1), the expected outcome for each dyad member under the optimal treatment assignment at the final stage can be expressed as,
| (3) |
Intuitively, we are correcting for the effect of the observed treatment, which was potentially suboptimal, by subtracting off its effect while simultaneously adding on the effect of the optimal treatment. If the optimal treatment and the observed treatment coincide, the added quantity is identically 0. The bracketed term in Equation (3) is therefore sometimes referred to as the regret, since it quantifies, in terms of the individual's health, how much we regret treating them suboptimally.
The quantity is also known as the pseudo‐outcome, and is a crucial component of the model [10]. Indeed, as we will see in Section 3.2, having finished modeling of the th stage and ascertaining the th stage decision rule, we then move backward to stage and repeat the process: define a model for the outcome, fit the parameters, and maximize the dyad‐health function. The difference between fitting at stage and stage is that the latter needs to account for the fact that more treatments will be assigned in the future. However, due to the backward nature of our estimation algorithm, we already know how to treat optimally at the stage . We can account for this at stage by fitting the outcome model on the pseudo‐outcomes rather than the observed outcomes . This process continues for each in until all stages have been addressed, after which we will have obtained decision rules with which we may inform treatment decisions of future patients at each stage of the regime.
As an example, suppose one chooses as the dyad health function. The optimal decision rule at stage given in Equation (2) can now be expressed as,
In this case, the optimal treatment for the dyad is the one that maximizes the sum of the respective members' individual expected outcomes, given the observed history . To interpret what this means, first consider the individual‐level population expected outcome, which is given by,
Using our sample of dyads, we could estimate this as,
| (4) |
The summands in Equation (4) are exactly the terms being optimized by the decision rule corresponding to this choice of . It follows that this choice recovers the traditional objective of maximization of the individual‐level expected outcome. It should be clear from the above derivation that it was necessary to consider the correct interference structure to recover this objective. For comparison, the model of Jiang, Wallace, and Thompson [23] would propose the following decision rule:
This will in fact not recover the objective, because it considers only half the population and does not address interference in its optimization. Indeed, by ignoring the outcome of Member 2 when making the decision about , this approach risks choosing an optimal treatment assignment that is suboptimal for Member 2. Furthermore, by treating as another covariate rather than as part of the individual's treatment, this approach does not even maximize the individual‐level expected outcome for the half of the population that it does consider. These shortcomings are demonstrated in Section 4.2 with a simulation study.
3. Estimation and Determination of Optimal Treatment Regime
It is clear that the dyadic‐blip component of the model is crucially linked to identification of the optimal treatment regime. It is therefore imperative that the estimation procedure used to fit the proposed model offers desirable properties in terms of the resulting estimates for at each stage . One such approach is the (generalized) dWOLS procedure [10, 11]. Indeed, assuming that we can specify balancing weights that eliminate any dependence between the history and the treatment at a given stage, the dWOLS framework will provide consistent estimation of the dyadic‐blip parameters. Along with specifying these weights, implementation of this estimation framework additionally requires modeling of the propensity score of the treatments. An important property of this procedure is that it is doubly‐robust with respect to nuisance model misspecification—consistent estimation of the dyadic‐blip parameters is still guaranteed if one of either the propensity score model or the treatment‐free model component is misspecified. This is a desirable property, and motivates our use of this estimation procedure for fitting the proposed model.
3.1. Balancing Weights
For each treatment stage, the algorithm fits the specified model using a weighted data set. The weights need to be specified such that they remove any dependence between the history and the observed treatment assignment, that is, they must offset any differences in the treatment assignment mechanism that are due to the value of the measured dyad history.
We denote the th stage weights by to emphasize that the weights are a function that depends on the history and observed treatment assignment. To find weights that achieve the desired effect, it is common to specify that they satisfy a particular balancing condition. In the seminal dWOLS work [10], a balancing condition for the case of a binary treatment was presented. Later, in the development of the generalized dWOLS methodology [11], the balancing condition was extended to the case of continuous and categorical treatments. When dyadic‐interference exists, each individual is exposed to a bivariate treatment. We now present a theorem detailing a balancing condition for treatments arising in this form.
Theorem 1
A weighted ordinary least‐squares regression based on the model,
will give consistent estimates for the dyadic‐blip parameters provided that the weights satisfy,
(5) for any , where is the joint propensity score.
A proof of this theorem is provided in Appendix A.2. Details on the different types of weights satisfying this balancing condition, and their estimation methods, are presented in Appendix A.3. In particular, under the restricted interference model (the middle graph of Figure 1), we extend the “absolute value weights”, defined by introduced by Wallace and Moodie [10], to the dyadic‐network settings. We call these new weights dyadic‐absolute value weights, and they have the form,
| (6) |
where is the expected probability that member of dyad receives treatment, given their observed history , for each . Intuitively, these weights assign greater importance to individuals whose own observed treatments or their dyadic partners' observed treatments significantly differ from what is expected according to the treatment model.
3.2. Estimation of Model Parameters
Having decided on an appropriate weight function, we proceed with estimation of the model parameters. Estimation takes place in stages, one for each stage of treatment. The algorithm we employ, dWOLS [10], proceeds similarly to Q‐learning, which works by sequentially estimating the optimal decision rules for each stage starting from the final stage , and moving backward through the stages to the initial stage. The procedure at each stage is fundamentally the same, so we will outline the details of how it may be carried out at an arbitrary stage , which necessarily includes how we take this information backward to allow for the completion of the same steps at stage .
We specify a linear model for the outcome which takes the form,
| (7) |
where we have specified the treatment‐free model as , and the dyadic‐blip as,
| (8) |
We have assumed for simplicity of presentation that each component of the blip depends on the entire history , although this is not strictly a requirement. We specify to be the concatenation of all the dyadic‐blip component parameters. We have also added a tilde on the outcome here to reflect the fact that, unless we are at stage , we are regressing on the pseudo‐outcome of Equation (3) discussed in Section 2.3.
Under this formulation, the dyadic‐blip is decomposed into three sub‐components: the sub‐component corresponding to the treatment of member , which we call the direct blip; which corresponds to the treatment of the dyadic partner, which we call the indirect blip; and which corresponds to the interaction between both treatments, which we call the interaction blip. With this form, the components of are directly interpretable in terms of understanding the relationship between the history and dyad‐level treatment as it pertains to the expected outcome.
With the weights from Section 3.1 we estimate the stage model parameters using the following weighted generalized estimating equation:
| (9) |
Here, we have used the notation to represent the score vector of the specified outcome model with respect to the model parameters, which in the case of the model presented in Equation (7), takes the form,
Since our chosen model is linear, solving this GEE is equivalent to estimation via weighted ordinary least‐squares regression. We choose to present estimation in the more general GEE framework, however, to demonstrate that alternative outcome models can be accommodated.
Solving Equation (9), we obtain model parameter estimates, which we denote by . Plugging these estimates into the model of Equation (7) defines our estimated model, and then plugging the estimated model into Equation (2) defines our optimal decision rule for stage . We then evaluate the estimated decision rule on each dyad in the sample to get the estimated optimal treatment,
Having obtained our estimated optimal treatments, we are finished with stage and ready to move on to estimation at stage . To proceed, the pseudo‐outcomes need to be computed. This can be done according to,
where we let the observed outcome of individual in dyad . Thus, the pseudo‐outcome is defined recursively, where, at each stage, we “add back” the individual level regret to account for the potentially suboptimal treatment decision that was initially observed at that stage. Estimation of the next stage, then begins by formulating the outcome model for these new pseudo‐outcomes. The full estimation algorithm is illustrated in Algorithm 1. We also prove in Appendix A that the proposed algorithm inherits the double‐robustness property of dWOLS. It is worth noting that dWOLS assumes that the blip model is correctly specified and its doubly‐robustness property is with respect to nuisance model (i.e., treatment‐free model and treatment model) misspecification.
ALGORITHM 1. Dyadic dWOLS estimation procedure.
Require: Data
, dyad‐health function
, weight function
, and number of stages
.
1: for
do
2: Define the stage
treatment model
and the stage
outcome model
.
3: Fit the treatment model
using the stage
data.
4: Use the estimated treatment model of step 3 to compute the GEE weights
.
5: Solve the weighted GEE,
to obtain parameter estimates .
6: Use the estimated model parameters of step 5 to define the optimal stage
decision rule and compute the estimated optimal treatments
7: if
then
8: Compute the pseudo‐outcome for the next stage:
9: end if
10: end for
11: Return the estimated parameters
and the optimal decision rules
.
3.3. Optimal Treatment Assignment and the Dyad‐Health Function
In the classic optimal DTR scenario, we seek the regime such that,
for all possible regimes . For example, in a two‐stage regime, the optimal regime can be found by solving
iteratively, starting with the inner most maximization problem and working outward. This is the approach of Q‐learning, which can be extended to an arbitrary number of stages by further breaking down the inner most conditional expected value appropriately; see, for example, the textbook by Tsiatis et al. [4]
As discussed in Section 2.3, we cannot directly apply this approach when the outcome of interest is vector‐valued, since the maximization of a vector is not well‐defined. This motivates the introduction of the dyad‐health function , which we assume takes the outcome values of a particular dyad and returns a value that is to be interpreted as a measure of the dyad's overall health. Without loss of generality, it is assumed that larger values of are associated with greater dyad health. It follows that in the case of a dyadic‐network population structure, the associated optimal treatment regime can be found according to,
| (10) |
At first glance, this might suggest that modeling the random variable directly is required to estimate the optimal treatment regime. Indeed, nothing in our model setup prohibits the modeling of rather than itself. If can be expressed in a form amenable to estimation via generalized estimating equations (GEE), then we can accommodate this approach within our existing framework. Specifically, the weighted‐GEE methodology outlined in Algorithm 1 provides a flexible tool for parameter estimation, even when the outcome of interest is a transformation of the individual health outcomes, such as .
However, there are limitations to this approach. One of the more critical arguments against the modeling of directly is that the impact of the optimal treatment on the health of each individual in the dyad often becomes unidentifiable in such scenarios. For example, consider the choice , which we can model directly using a parametric linear model, that is, . This approach seems very natural, and in such a case, we may indeed still proceed to find the optimal dyad‐level treatment regime without issue. However, we will not be able to say anything about how the optimally assigned treatment impacts the individual health levels of the dyad members, as these are not identifiable under the assumed model. Hence, such an approach moves away from the ethos of personalized medicine, in which optimal treatment regime estimation is rooted. Further, such an approach may lead to ethical concerns, as outright maximization of may lead to an “optimal” regime in which the health of one dyad member is sacrificed for a sufficiently large gain in the health of the other to increase . We therefore do not pursue this approach here, instead proceeding with a model for .
By focusing on the modeling of we run the risk that the conditional expected value of is difficult to handle in practice. Indeed, one needs to derive the distribution of from the distribution of to compute the conditional expectations of Equation (10). Since no distributional assumptions are made on the error term in the specification of , this distribution cannot be determined in general. One could proceed by addressing exactly this issue, that is, by making distributional assumptions of the errors. This may unnecessarily restrict the scope of the model, hence we prefer to make some restrictions on the form of . We suppose that is such that it is monotonic (non‐decreasing) in both of its arguments. That is, for we have,
With this assumption, and the modeling assumption for given in Equation (1), it is straightforward to show that maximization of the conditional expected value of is equivalent to the maximization of composed with the conditional expected value of . That is, . For any such choice of , we find our optimal decision rule at stage by maximizing over all possible dyad treatment decisions .
While the assumption of monotonicity in the dyad‐health function provides a straightforward path to optimizing the treatment regime, another interesting approach is to impose convexity on . In so doing, we align the optimization process with a more cautious and ethically sound philosophy, particularly within the framework of personalized medicine.
To understand the implications of choosing a convex , recall Jensen's inequality, which states that for any convex function ,
This inequality reveals that the expected value of provides a lower bound on the true population‐level health improvement under any treatment regime. In other words, by maximizing with convex , we ensure that our model's predictions are conservative and do not overestimate the actual gains in dyad or individual health that might be realized under the implemented policy.
From an ethical standpoint, the use of a convex dyad‐health function serves to mitigate the risk of overly optimistic treatment decisions. In personalized medicine, where the goal is to tailor interventions to maximize individual and group health outcomes, it is important to avoid scenarios where the model suggests an inflated potential benefit that may not materialize in practice. Convexity in ensures that the policy derived from our model does not inadvertently favor treatments that could lead to marginal or even detrimental effects. Practically, the adoption of a convex simplifies the interpretation of our model's predictions. When is convex, the policy derived from can be interpreted as a reliable lower bound on the true health benefits that the dyad will experience under the optimal treatment regime. This aligns well with clinical practices where conservative estimates are often preferred, especially in the face of uncertainty.
In summary, while the weighted‐GEE approach used in our model is sufficiently flexible to accommodate the direct modeling of we prefer to model instead. This preference stems from our emphasis on preserving the interpretability of the treatment regime at the individual level. By focusing on , we maintain the ability to assess treatment effects for each dyad member, ensuring that the derived policies are both effective and fair. However, we maintain that modeling is a completely viable approach and may be appropriate or preferred in certain scenarios, such as when the dyads being studied are not comprised of people (e.g., different components of a machine), or when health is not the primary outcome of interest. In Section 4.3 we investigate the proposed dyadic‐network under different choices for the dyad‐health function, and discuss the differences in the analysis when modeling vs. modeling .
4. Simulation Study
We illustrate key properties of the dyadic‐network DTR approach through three simulation studies. Specifically, we investigate the purported double robustness property of the estimated coefficients, and the ability to obtain an improved optimal treatment regime with respect to the conditional optimization approach in the first simulation, for both a single‐stage and a two‐stage model. The first simulation demonstrates these results for a single‐stage model, while the second simulation presents the same results for a two‐stage model. We present the results of the single‐stage model simulation in this section. The results of the two‐stage model simulation can be found in Appendix B.2. In the second simulation, we compare the method of Jiang, Wallace, and Thompson [23] with our proposed dyadic‐network DTR approach. In the third simulation, we explore the impact of different dyad‐health functions on the resulting DTR within a dyadic‐network context.
4.1. Simulation I: Double Robustness
First, we illustrate the double robustness property regarding consistent estimation of the dyadic‐blip parameters. We do this for varying sample sizes, and under different specifications of the treatment‐free, and dyadic‐blip model. Second, we compare the performance of the dyadic‐network DTR with existing DTR methodologies on data exhibiting a dyadic‐network interference structure. This illustrates the necessity of the joint optimization approach in contexts where interference exists.
Since consistency is an asymptotic property, we choose sample size as our simulation parameter. We use the sample sizes n = 200, 1000, and 5000 dyads. For each sample size, we generate data sets, fit the model on the data, and record the observed bias of the estimated dyadic‐blip parameters. For each data set, we also find optimal treatments according to the conditional optimization approach, so that we can compare those results with the proposed methodology.
Our baseline model is generated as follows: for each dyad and each member , we generate the patient information, , according to a uniform distribution on the interval . The treatment model is a logit model on the patient information, . Finally, we define the dyad outcome model to be , where . In alignment with Equation (7), the outcome model decomposes into treatment‐free model and dyadic‐blip model , with the dyadic‐blip parameters as for each member .
To show double robustness, we show that the model obtains consistent estimators of the dyadic‐blip parameters even when one of the model components is misspecified. Hence, we perform four analyses, one for each possible combination of specifying or misspecifying the treatment‐free and treatment models. Analysis 1 denotes the case in which neither component of the model is correctly specified, Analysis 2 denotes the case in which only the treatment‐free component is misspecified, Analysis 3 denotes the case where only the treatment model is misspecified, and Analysis 4 denotes the case in which both models are correctly specified. To misspecify the treatment‐free component, we omit the terms involving nonlinear functions of the patient information ( and ). Therefore, the misspecified treatment‐free model will be an intercept model. The treatment model is misspecified through the removal of the intercept term, that is, .
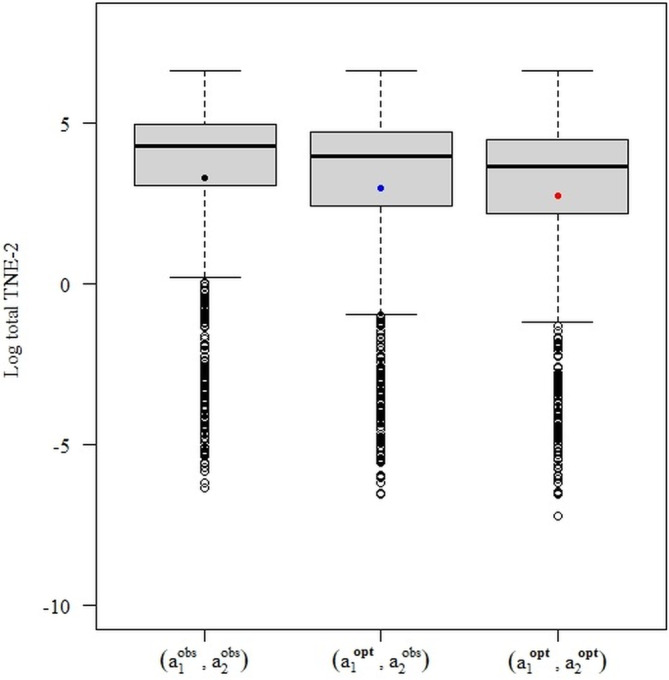
The results of the simulation are provided in Figure 2. This figure shows three sets of boxplots, which correspond to our three chosen sample size settings, for the estimation of the dyadic‐blip parameter with the true value of 2. Each boxplot in one subfigure corresponds to one of the four analysis scenarios. From these plots, we can see that the model appears to provide doubly‐robust estimation as expected. When at least one of the model components is correctly specified, the dyadic‐blip parameter estimates appear to be consistent, which can be surmised from their central tendency of zero and their shrinking variance as the sample size increases. The results of parameter estimation for the rest of the dyadic‐blip parameters are provided in Appendix B.
FIGURE 2.
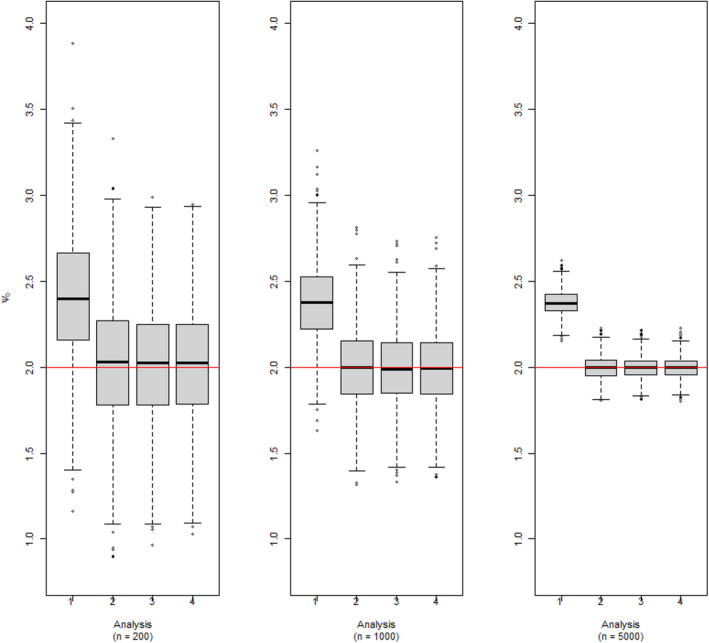
Dyadic‐blip function parameter estimates for 1000 simulated data sets via our dyadic‐dWOLS approach when neither (Analysis 1), one (Analyses 2 and 3), or both (Analysis 4) treatment and treatment‐free outcome models are correct. True value of = 2.
For the second part of this simulation, within the same simulation setting, we compare the results of the conditional optimization approach previously proposed by Jiang, Wallace, and Thompson [23] with our proposed dyadic‐network DTR approach, which utilizes a joint optimization strategy. Under the conditional optimization, members of a dyad were randomly labeled as Member 1 and they received the optimal treatment based on the observed treatment of the other members in the dyad. In contrast, under the dyadic‐network DTR approach, the treatment of both members of the dyad is jointly optimized in a way to maximizes the average outcome of the dyad. To compare the performance of these two optimization approaches, we estimate the optimized expected outcomes for the population assuming both treatment and treatment‐free models are correctly specified (Analysis 4).
There are a couple of important features to discuss in Figure 3. First, comparing only the boxplots of Member 1, we see that the conditional approach appears superior in terms of improving the health of these members. However, the cost of ignoring interference in the population can be seen in the boxplots of the second members, where these members are seen to be suffering relative to their dyadic partners who received the optimal treatment. In contrast, under the dyadic‐network DTR approach, both Members 1 and 2 boxplots seem to be similarly improved.
FIGURE 3.
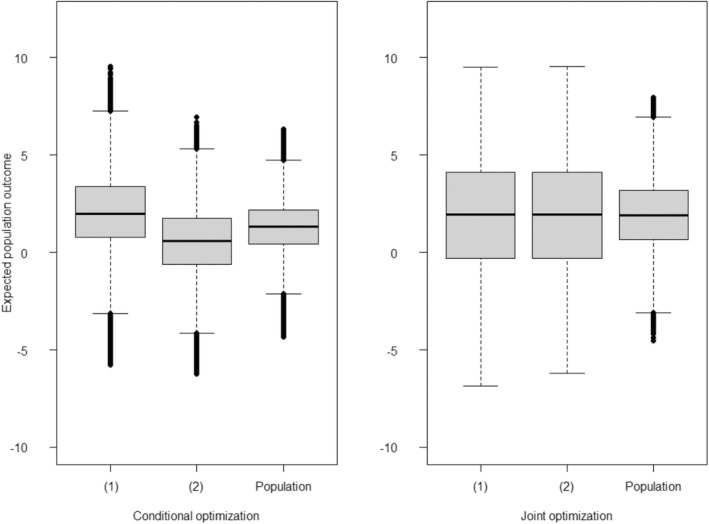
Boxplots of the estimated expected outcomes under the Simulation I setting, where both treatment and treatment‐free models are correctly specified (Analysis 4). Each boxplot associated with two different optimization strategies. Left: Results under conditional optimization methods, previously proposed by Jiang, Wallace, and Thompson [23]. In this approach, Member receives an optimal treatment conditioned on the observed treatment of the other member of the dyad (Member ). Right: Results under the dyadic‐network DTR approach, where treatments for both members of a dyad are optimized jointly (joint optimization). The label “(1)” denotes the expected outcome for those labeled Member , “(2)” denotes the expected outcome for individuals labeled Member , and “Population” denotes the expected outcome for the entire population of both members of a dyad following an optimization strategy.
4.2. Simulation II: Comparison With Conditional Approach
In this section, we apply the method of Jiang, Wallace, and Thompson [23] and the proposed method on simulated data. We assumed a single‐stage DTR and a dyadic‐network with non‐exchangeable members in a sample of 1000 dyads. The data are generated according to a model where the covariates are drawn from , and from the absolute value of a normal distribution, . The binary treatments and are then generated using a logit model based on the patient information, .
The outcome model was defined as for and for , with for both members. Hence, the treatment‐free model of Member 1, , is and their dyadic‐blip model is defined as . Therefore, the corresponding dyadic‐blip parameters are . As for Member 2, treatment‐free model is and the dyadic‐blip model is defined as . The dyadic‐blip parameters for Member 2 are then, . The dyadic‐blip parameters were estimated assuming the correct specification of both the treatment‐free and treatment models.
We consider the dyad health outcome of interest to be the average of dyad members' outcomes', . With this dyad health function, the goal is to maximize the expected health outcome of the population, while taking interference within dyads into account. This specification also allows the dyadic‐network approach, that is, joint optimization, to be directly compared to the method of Jiang, Wallace, and Thompson [23], which can be viewed as using , thereby maximizing the expected outcome of Member 1 only.
Figure 4 compares the outcomes of a simulated population based on the conditional optimization proposed by Jiang, Wallace, and Thompson [23] with our proposed method of joint optimization. The top panel contrasts the originally observed outcomes for the population, outcomes under conditional optimization treatment where in each dyad, only the member labeled as Member 1 received their optimal treatment conditioned on the observed treatment of Member 2, and outcomes under a joint optimization strategy for the treatments implemented to optimize the dyadic health outcome (here, the average). Red lines between box plots indicate a decrease in the outcome for an individual in comparison to the optimization strategy, whereas gray lines suggest an improvement. The expected outcome of the population has increased more significantly as a result of joint optimization compared to conditional optimization, with differences highlighted in the last box.
FIGURE 4.
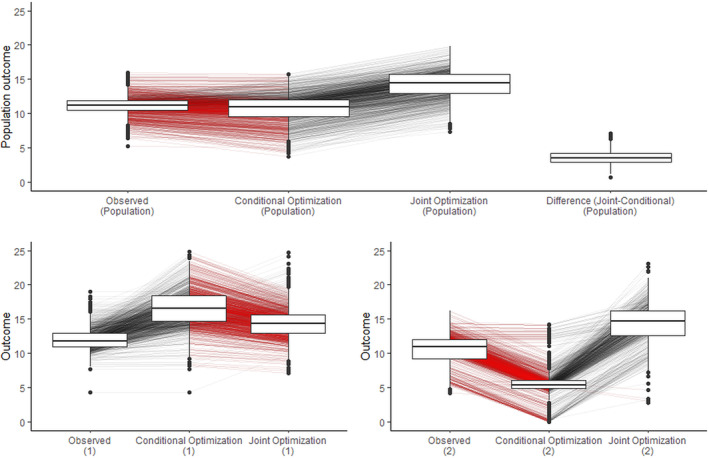
Simulation results comparing conditional optimization [23] with the proposed method of joint optimization for a dyadic‐health outcome. Top: Population outcomes. Bottom: Outcomes based on different members of a dyad. The label (1) denotes the outcome for those labeled as Member 1 and label (2) denotes the outcome for individuals labeled as Member 2. Red lines between box plots indicate a decrease in the outcome for an individual compared to the optimization strategy, whereas gray lines suggest an improvement. The members of these dyads in this example are not exchangeable.
The bottom panel demonstrates the impact of conditional optimization for Member 1 and joint optimization on the outcomes for Members 1 and 2 in the population, analyzed separately. The left plots reveal that the outcome for Member 1 has increased as a result of both conditional and joint optimization, with a more pronounced improvement observed in conditional optimization. However, as demonstrated in the right panel, conditional optimization for Member 1 has a deteriorating effect on the outcome for Member 2. In contrast, joint optimization results in improvements for both individuals. As a result, the true change in the population outcome is presented in the middle box of the top panel. The critical insight here is that reporting the expected outcome of the population, as shown in conditional optimization (1) in the bottom panel, instead of reporting it as conditional optimization (population) in the top panel, would be incorrect.
4.3. Simulation III: Impact of Dyad Health Function
In this section, we explore the impact of different dyad‐health functions on the resulting DTRs within a dyadic‐network context. Our objectives are twofold: first, to demonstrate how varying a dyad‐health function influences the health outcomes of the dyad members; second, to illustrate the interpretability benefits of modeling the individual outcomes directly, rather than through the dyad‐health function .
We assumed a single‐stage DTR and a dyadic‐network with non‐exchangeable members in a sample of 2500 dyads. The data are generated according to a model where the covariates and are independently drawn from a standard normal distribution. The binary treatments are generated using logit models based on the covariates as for both members. The outcomes are generated according to , and where and are normally distributed with mean 0 and standard deviation 0.5.
Different dyad‐health functions, , were employed. The selected functions, along with their mathematical formulations, are presented in Table 1. The Log‐Sum‐Exp functions, LSE‐m and LSE‐M, serve as convex approximations of the minimum and maximum of a set of outcomes, respectively. In optimization stage, LSE‐m prioritizes the treatment that maximizes the minimum outcome within the dyad. Conversely, LSE‐M prioritizes maximizing the largest outcome within the dyad. The parameter controls the sharpness of the approximation; larger values of yield a closer approximation to the true minimum or maximum, resulting in a stricter policy that more closely mirrors the extremum of interest.
TABLE 1.
Summary of functions and their parameter settings.
| Function name | Mathematical formula | Parameter settings | ||
|---|---|---|---|---|
| Log‐Sum‐Exp: Minimum (LSE‐m) |
|
|
||
| Weighted p‐Norm (wp‐norm) |
|
|
||
| Log‐Sum‐Exp: Maximum (LSE‐M) |
|
|
||
| Quadratic Form (Q‐form) |
|
|
||
|
|
The weighted p‐Norm prioritizes the members of the dyad, through the use of the weights, and . Finally, the quadratic form, that is, Q‐form, although similar in appearance to the weighted p‐Norm, distinguishes itself through its inclusion of interactions between the outcomes and . The off‐diagonal element of the symmetric matrix governs the degree, and the nature, of these interactions. A positive encourages both outcomes to be simultaneously high, and therefore favors treatments that increase both and simultaneously. In contrast, a negative discourages treatments that lead to simultaneous improvements in both outcomes, potentially penalizing cases where both members' outcomes rise together.
For each dyad‐health function listed in Table 1, we selected specific parameter settings to explore their impact on the resulting treatment regimes. These settings are detailed in the “Parameter Settings” column of the table. For instance, the LSE‐m function was tested with and , reflecting different degrees of approximation to the true minimum. Similarly, the weighted p‐Norm function was applied with varying weights and to assess how the prioritization of one dyad member's health over the other influences the treatment decisions. The Q‐form was explored with two different interaction matrices , highlighting how positive and negative correlations between dyad outcomes affect the optimized treatment strategies.
Figure 5 illustrates scenarios, assuming s are modeled directly. It compares the corresponding dyad‐health outcomes before and after receiving optimal treatments based on dyadic‐network DTR optimization approach, joint optimization. As shown, the value of the dyad‐health function increases across the sampled dyads under dyadic treatment regime, indicating an overall improvement in dyad‐health outcomes as defined by each function. However, as illustrated in Figure 5, each dyad‐health function imposes a different unit of measure, and a direct comparison of the impact of the optimal treatment strategy on the population outcome is not possible. While direct modeling allows for estimating the effect of the optimal regime strategy on the dyad‐health outcome , it does not provide a direct estimate of its effect on the individuals outcomes and .
FIGURE 5.
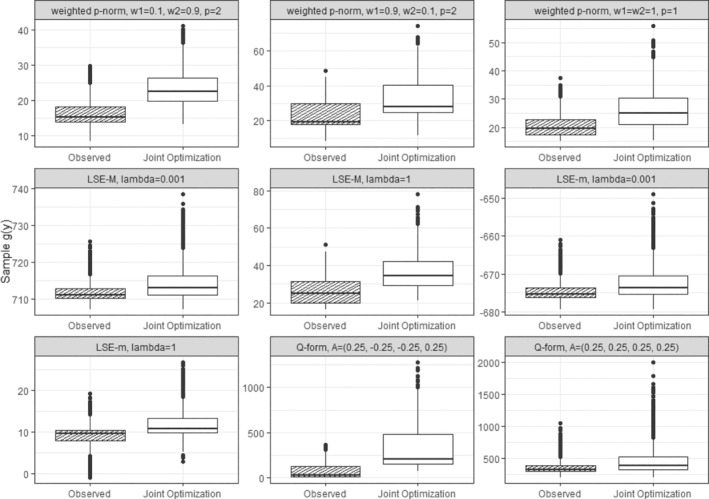
Boxplots of the dyad‐health function values across sampled dyads for nine different dyad‐health functions, each corresponding to a distinct set of parameter settings as summarized in Table 1. The observed values are shown before and after fitting the optimal treatment regime using the dyadic‐network DTR. Across all configurations, the fitted treatment regime leads to higher values of the dyad‐health function, reflecting an improvement in dyad health under the corresponding measure.
Figure 6 presents the observed individual‐level outcomes alongside their expected outcomes under optimal regime strategy for each of the chosen dyad‐health functions. This detailed view is made possible by modeling and directly, rather than modeling . The figure demonstrates how each dyad‐health function results in a distinct distribution of individual outcomes under the treatment regime dictated by the dyadic‐network DTR strategy, joint optimization.
FIGURE 6.
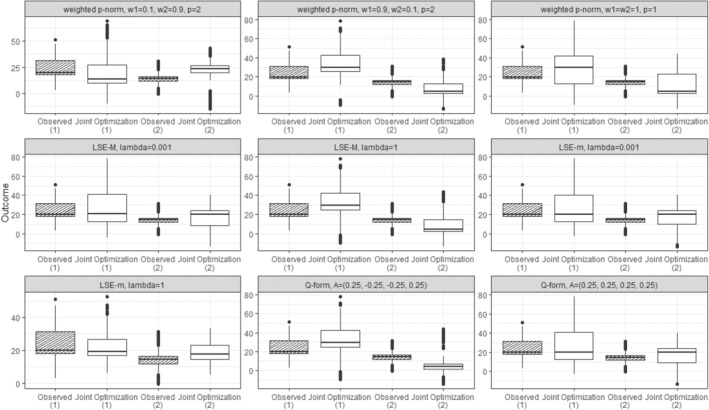
Boxplots of the outcome values for members across sampled dyads are presented for nine different dyad‐health functions, each associated with a unique set of parameter settings, as summarized in Table 1. The observed values are depicted both before and after applying the optimal treatment regime derived from the dyadic‐network DTR.
As expected by the structure of the applied dyad‐health functions, most of these optimizations prioritized the outcome of one member. For example, the weighted p‐Norm with a large weight on one member significantly improves that member's outcome. In contrast, the weighted p‐Norm with equal weights leads to a more balanced improvement between the two members. The LSE‐M function favors Member 1, who has a higher potential for marginal health improvement, while the LSE‐m tends to favor Member 2, who typically has lower overall health. The Q‐form with negative interaction favors Member 1 and generates an optimal treatment regime resembling those of the LSE‐M and the weighted p‐Norm with a large weight on Member 1. Finally, the Q‐form with positive interaction produces a balanced outcome, and indeed finds an optimal treatment policy identical to that of the weighted p‐Norm with balanced weights. The boxplots comparing the outcome values of both members for different dyad‐health function optimizations, are provided in Appendix B.3.
These results highlight the flexibility of modeling the individual outcomes and optimization of a dyad‐health function in defining what constitutes an “optimal” treatment regime. By allowing the dyad‐health function to specify the criteria for optimality, the dyadic‐network optimization strategy can yield a diverse range of treatment regimes, each reflecting the unique properties of the chosen dyad‐health function. Moreover, modeling the individual‐level outcome, we can compare the effects of the fitted regimes and select the dyad‐health function that aligns with desired treatment goals, something that would be more challenging if we only modeled . While we can intuitively predict the general impact of these dyad‐health functions on the treatment regime, the exact details of their impact on individual outcomes remain unclear without explicit modeling of and . Our approach allows us to choose a dyad‐health function that not only meets our dyad‐level objectives but also aligns with the individual‐level effects we are comfortable with.
5. Application: Path Study
The addictive properties of tobacco products are well‐established, with nicotine being the primary compound responsible [28, 29]. In light of this, it is of interest to investigate the extent to which e‐cigarette adoption may reduce total nicotine exposure among pairs of tobacco product users in the United States. To this end, we will analyze data from the PATH study [30], which provides a rich source of information on various tobacco‐related behaviors and outcomes. The PATH study is a longitudinal cohort study that was undertaken with the broad aim of accruing information to aid in the assessment of longitudinal patterns of tobacco‐use behaviors in the United States. A nationally representative sample of households was undertaken using a four‐stage, stratified area probability sample design. Sampling began in 2013, with consenting members of each sampled household forming the “Wave 1” cohort. From each of the consenting households, a maximum of two adults and two youths were assessed. Members of the cohort who chose to remain in the study were then contacted annually for further data collection, with the results forming subsequent waves. A replenishment sample was added to the cohort at the outset of Wave 4 and in total, six waves have been measured. More details regarding the logistics of this study can be found in the report of Hyland et al. [30]
Measurements collected consist of answers to a survey regarding tobacco‐use behaviors, and biospecimens taken from blood and urine samples of study participants who provided the additional requisite consent. The survey can be roughly divided into three main sections. The first section captures various socio‐demographic characteristics of each participant, including age, sex, ethnicity, education, employment status, and annual income. The second section focuses on tobacco use, inquiring about the types of products used and frequency of use. Finally, the third section aims to provide context by asking questions about health status, quality of life, and the perceived social role of tobacco among the participants' social circles. Biospecimen samples were used to measure biomarkers of tobacco exposure, such as tobacco‐specific nitrosamines, and diseases purported to be associated with tobacco use.
We utilize the data from the PATH study to fit a two‐stage dyadic network DTR. We restrict our focus to households where two adults were identified as current users of any tobacco product at Wave 1. A current user is defined as any adult who has ever used a tobacco product and now uses it with some degree of regularity [31]. Among these households, we retain for analysis only those households in which both adult members provided survey responses and biospecimen samples at Wave 2. These conditions yield a sample consisting of 516 households, or 1032 individuals. We randomly assign the labels of Member 1 and Member 2 to each individual in a household.
Our intended response is nicotine exposure, which we propose to quantify using total nicotine equivalents. Total nicotine equivalents involve the sum of molar concentrations of nicotine and its various metabolites. Total nicotine equivalents have been shown to be highly correlated with true nicotine intake, and robust to metabolic differences among individuals [32, 33]. The PATH data provides measurements of total cotinine and total trans‐3‐hydroxycotinine, which can be summed together to give the measure known as TNE‐2 [29]. We choose the log‐transformed sum of TNE‐2 values at Wave 1 and Wave 2 to be the continuous response for our model. We call this outcome as log total TNE‐2.
Our treatment designation is based on e‐cigarette use. To be more specific, we consider any adult reported as an e‐cigarette user within the year prior to Wave 1 as having received initial treatment (Stage 1). Similarly, individuals who are recorded as e‐cigarette users between Wave 1 and Wave 2 are considered to have been treated at Stage 2. With this setup, PATH study waves correspond to model stages, as defined in Section 2. Consequently, our model is a two‐stage DTR. For the purpose of comparison, we implement both our joint optimal treatment model and a conditional optimal treatment model as done in previous literature [23].
At each stage, we fit a dyadic‐blip model of the form . For the tailoring covariates, at Stage 1, is comprised of biological sex (binary), age (continuous), non‐Hispanic (binary), reported heart disease (binary), cigarette smoking status of the individual (every day, some days, and not a current smoker), and average cigarettes smoked per day (numeric). If someone is a non‐smoker, their average number of cigarettes is 0 [34]. The covariate is the same at both stages and is comprised of dyad cohabitant 's cigarette smoking status and average number of cigarettes per day.
Since there is no meaningful way to assign membership labels within the path data set, we assign labels within each dyad randomly. As a result, member exchangeability is satisfied in this analysis. Accordingly, we fit the outcome and the treatment model on a stacked data set, combining the member data to fit a single outcome regression.
In each stage, the weights were estimated under two interference settings, which we have called M under the restricted model and M
under the restricted model and M under the independent treatment model, respectively (see Appendix A.3). The propensity for receiving treatment in each stage exhibits acceptable overlap, and the balance of covariates has been achieved, as indicated by the standardized mean difference of weighted covariates being below 0.1, with the exception of age, which has a standardized mean difference of 0.21.
under the independent treatment model, respectively (see Appendix A.3). The propensity for receiving treatment in each stage exhibits acceptable overlap, and the balance of covariates has been achieved, as indicated by the standardized mean difference of weighted covariates being below 0.1, with the exception of age, which has a standardized mean difference of 0.21.
5.1. Results
The dyadic‐blip model estimates at each stage for each model are presented in Table 2. Recall that our outcome in this case is log‐transformed sum of TNE‐2 for Waves 1 and 2, and hence, in this setting, lower values correspond to a better health outcome. From this reference point, it is possible to interpret negative blip coefficients as relating to those factors that increase the efficacy of the treatment, while positive coefficients show the opposite relationship. Also, recall that in joint optimization, we optimize the sum of the blips, so cigarette smoking by either member will appear in the optimization equation in two capacities. For example, at Stage 1 for Model 2, if both are someday‐cigarette smokers, the terms corresponding to cigarette smoking in the blip sum given . It follows that, when both members are everyday cigarette smokers, treatment is more likely to be effective. Additionally, if either member is of non‐Hispanic origin and is a male, the treatment is more likely to be effective. As an example, suppose Member 1 is a 30‐year‐old non‐Hispanic female with no heart issues, who is not a current smoker. She is in a dyad with Member 2, a 35‐year‐old non‐Hispanic male with no heart issues, who is a current “someday” smoker averaging 5 cigarettes per day. At Stage 2, recommending e‐cigarettes to both members increases the total log sum of TNE‐2. The dyadic‐optimal decision rule at Stage 2 for this dyad is to recommend e‐cigarettes only to Member 2.
TABLE 2.
Dyadic‐blip estimates.
| Tailoring covariate | Coefficients (standard error) | |||||
|---|---|---|---|---|---|---|
| Stage 1 | Stage 2 | |||||
| M3 | M2 | M3 | M2 | |||
|
|
E‐cigarette1 | −0.084 (0.529) | 0.367 (0.422) | −0.746 (0.546) | −0.701 (0.579) | |
|
|
E‐cigarette1: Age1 | −0.001 (0.011) | −0.008 (0.012) | 0.007 (0.011) | 0.012 (0.011) | |
|
|
E‐cigarette1: Sex1 (female) | 0.124 (0.271) | 0.078 (0.300) | 0.293 (0.262) | 0.134 (0.271) | |
|
|
E‐cigarette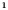 : Non‐Hispanic : Non‐Hispanic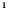
|
−0.010 (0.320) | −0.177 (0.432) | −0.135 (0.468) | 0.027 (0.545) | |
|
|
E‐cigarette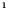 : Heart disease : Heart disease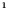 (no) (no) |
−0.839 (0.346) | −0.684 (0.409) | 0.189 (0.349) | 0.241 (0.373) | |
|
|
E‐cigarette : Cigarette : Cigarette (not a current smoker) (not a current smoker) |
1.715 (0.562) | 1.831 (0.611) | 1.257 (0.566) | 1.023 (0.604) | |
|
|
E‐cigarette : Cigarette : Cigarette (some day) (some day) |
0.689 (0.405) | 0.372 (0.464) | −0.187 (0.356) | −0.368 (0.317) | |
|
|
E‐cigarette : Average cigarette : Average cigarette per day per day |
0.015 (0.011) | 0.011 (0.013) | 0.031 (0.020) | 0.019 (0.018) | |
|
|
E‐cigarette
|
−0.498 (0.270) | −0.502 (0.246) | −0.383 (0.289) | −0.316 (0.293) | |
|
|
E‐cigarette : Cigarette : Cigarette (not a current smoker) (not a current smoker) |
1.811 (0.544) | 1.723 (0.561) | 0.550 (0.507) | 0.582 (0.509) | |
|
|
E‐cigarette : Cigarette : Cigarette (some day) (some day) |
0.313 (0.362) | 0.325 (0.261) | 0.150 (0.296) | 0.152 (0.291) | |
|
|
E‐cigarette : Average cigarette : Average cigarette per day per day |
0.013 (0.011) | 0.014 (0.011) | 0.006 (0.017) | 0.005 (0.017) | |
|
|
E‐cigarette : E‐cigarette : E‐cigarette
|
0.170 (0.339) | 0.152 (0.311) | 0.569 (0.339) | 0.491 (0.331) | |
Note: The sample consists of 516 dyads. Weights were estimated under two interference settings, M under the restricted model and M
under the restricted model and M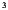 under the independent treatment Model 2.3. Standard errors were estimated using 1000 bootstrap samples. Bold indicates statistical significance at the 10 level.
under the independent treatment Model 2.3. Standard errors were estimated using 1000 bootstrap samples. Bold indicates statistical significance at the 10 level.
Figure 7 gives an assortment of boxplots related to the models and their outcomes under optimal treatment. In particular, the first boxplot shows the joint total TNE‐2 for all couples as observed in the data set, while the second and third boxplots show the new outcomes under conditional and dyadic‐network DTR modeling, respectively. From the plot, it is clear that the dyadic‐network model appears to show an improvement in total TNE‐2 values among the sampled households, which can be seen by its noticeably lower central tendency, and skewness toward negative values. The boxplot of the outcomes under the conditional models' optimal treatment rule also shows a general decrease in total TNE‐2 values across the sample, although its central tendency and skewness toward negative values are noticeably less.
FIGURE 7.
Boxplots of log total TNE‐2 values in the observed data (Left), under conditional optimization (middle), and under joint optimization (right). In this case, both approaches seem to have generally decreased population TNE‐2 values, with the dyadic‐DTR approach performing slightly better.
Specifically, under the conditional approach, which only optimizes treatments based on the first dyad member, the expected log total TNE‐2 values decreased by 0.46 on average across the optimized members. This also indirectly led to a decrease of 0.20 in the non‐optimized members. Overall, the population expected log total TNE‐2 values decreased on average by 0.33 under this approach, from 3.33 to 3.01. The joint optimization approach of the dyadic‐DTR methodology, on the other hand, results in 0.58 reduction in the mean of sum of TNE‐2 of each member and the total of 0.58 reduction for the population of dyads. It is worth noting that these analyses rely on the assumption that linear dyadic‐blip models are correctly specified.
6. Discussion
The proposed methodology extends the estimation of DTRs to account for interference when the population arises in the form of a dyadic network. This is done by modification of the dWOLS algorithm's optimization step through introduction of the dyad‐health function. This function takes the outcome values of a particular dyad's members, and uses them to produce a value which, ostensibly, corresponds to dyad health—a value we intend to maximize through treatment assignment. The dyad‐health function is specified by the practitioner, and may take multiple forms. In particular, when the dyad‐health function is the average of the outcome of the individuals of a dyad, the joint optimization will optimize the population's expected outcome. This is in contrast to the conditional optimization methodology introduced previously in the literature which cannot promise this result. Additionally, this feature provides the practitioner flexibility in defining what is meant by optimal as it relates to the outcome of a treatment decision. This is an important point, because the typical choice of maximizing the populations expected outcome can potentially result in undesirable repercussions for certain population members at the individual level, and may therefore be undesirable to implement in practice.
The dyadic‐network DTR can be implemented by directly modeling the dyad‐health function or by modeling the individuals' outcomes. In this paper, we advocate for the latter due to the fact that it provides the detailed information needed to evaluate treatment effects at the individual level.
When modeling the dyad‐health outcome directly, the dyad‐health function serves as the primary tool for evaluating a dyadic‐network DTR strategy on the population. This approach effectively treats the dyads as single units during both the estimation and optimization stages, collapsing individual‐level outcomes into a single scalar value. Consequently, the analysis, which focuses solely on the dyad‐level health outcome, is not able to provide direct insight into the effects of the treatment strategy on individuals' outcomes. This limitation is particularly significant in personalized medicine, where understanding individual responses to treatment is typically of interest.
Moreover, when considering multiple dyad‐health functions, comparing the impact of different choices becomes challenging. While directly modeling the dyad‐health function can provide valuable insights, it lacks the granularity needed to fully understand the effects of a treatment strategy on individual‐level outcomes, and it complicates comparisons across different dyad‐health functions.
The proposed methodology was implemented through a simulation study and an analysis of the data from the PATH study. Through these examples, we were able to demonstrate how the models perform. Specifically, under the dWOLS assumption, when the dyad‐health function is chosen to be the average of the dyad outcomes, the proposed joint optimization approach consistently identifies an optimal treatment assignment that is at least as effective as, and potentially better than, the conditional optimization previously proposed by Jiang, Wallace, and Thompson [23], as it explores the entire dyadic treatment space. Note that demonstrating this was the sole purpose of the analysis of the PATH data set—the decision rule estimated therein should not be understood as a serious policy suggestion. In particular, the completed analysis has a few simplifying assumptions that may not hold in practice. For example, it was assumed that dyad members within the PATH study were exchangeable, but the existence of a variable that makes the dyad members distinguishable should be considered and analysis run accordingly and compared. The assumption that the behavior of individuals observed at each wave remained homogeneous, so that they did not undergo any significant changes throughout the one‐year interval between waves, is also unlikely to be true generally. While this assumption facilitated our analysis, it is important to recognize that individual behaviors can be influenced by various factors that may evolve or fluctuate over time. Therefore, the generalizability of our findings may be affected, as unaccounted changes in behavior patterns between waves could potentially impact the observed results.
Furthermore, while we were able to showcase the application of the dyadic dWOLS method in a multistage setting using two waves of data, it is important to note that the inclusion of additional waves would have provided a more comprehensive understanding of the dynamic nature of the phenomenon under investigation. We were unable to incorporate a larger number of waves into the analysis, due to the limitations imposed by the sample size, notwithstanding any consideration of missing data adjustment, which could be a consideration in future work.
Moreover, our analysis relied on the assumption of correct specification of the linear dyadic‐blip model. However, as these models are prone to misspecification, the correct specification of the treatment model becomes crucial to achieve the double‐robustness property. Some methods have been proposed for model selection in the traditional DTR setting [35, 36]. Exploring the validity and extension of these methods in the presence of interference represents an interesting avenue for future research.
In terms of potential future work in the area of intersection between DTRs and interference, our study motivates several intriguing possibilities. The most natural next step would be to allow for interference among groups consisting of two or more individuals. This, along with allowing for groups of various sizes within the population would extend the model to much more realistic scenarios.
While much of the existing literature on causal inference and interference has primarily focused on binary treatment, exploring interference in the context of continuous treatment could lead to the development of more effective DTR and interference methods. This avenue of investigation would allow for the development of tailored methods specifically designed for use in continuous treatment scenarios.
Another potential extension that merits exploration in the intersection between DTRs and interference involves cases where different sources or types of measurement from one outcome are available. In a more general context, this extension would also encompass situations where a treatment and its potential interference have an impact on multiple health outcomes of an individual. Investigating the effects of interference in such complex scenarios would undoubtedly be challenging, but the insights gained would be valuable in developing more effective intervention strategies that target multiple health outcomes simultaneously. The development of sophisticated analytical approaches that can accommodate the interplay between different health outcomes and the various factors that influence them would enable more personalized and tailored treatment plans, leading to improved patient outcomes and quality of life. One interesting extension would be to adapt other robust methods, such as robust Q‐learning and G‐estimation methods, to account for interference effects [7, 9].
Conflicts of Interest
The authors declare no conflicts of interest.
Supporting information
Data S1. Supporting Information.
Appendix A. Double Robustness
We give a proof for the consistency and double‐robustness of dyadic dWOLS following Wallace and Moodie [10] and Simoneau and Moodie [12]. The proof is concerned with the dyadic‐blip estimators . To estimate the parameters, we solve the following weighted generalized estimating equation,
| (A1) |
Here, we have used the notation to represent the score vector of the specified outcome model with respect to the model parameters, which in the case of the model presented in Equation (A1), takes the form,
For simplicity, the proof is detailed for a single‐stage DTR. It is straightforward to extend the reasoning to more than one stage.
Treatment‐Free Model Correctly Specified, Treatment Models Misspecified
Assuming that the dyadic blip model is correctly specified, when the treatment‐free model is correctly specified, . With the expectation taken with respect to , we have
When the treatment‐free model is correctly specified, then
such that consistently estimates the blip parameters when the treatment‐free model is correctly specified.
Treatment‐Free Model Misspecified, Treatment Models Correctly Specified
Let the treatment model be correctly specified, that is, . We show that finding the root of the estimating function yields consistent estimators of if the weights satisfy the following balancing property.
Theorem 2
(Balancing property) A weighted ordinary least‐squares regression based on the model,
will give consistent estimates for the dyadic‐blip parameters provided that the weights satisfy,
(A2) for any , where is the joint propensity score. In case of binary treatment, this condition translates to
Proof. The estimates of in an ordinary least‐squares regression will be biased unless we at least have for all in . Hence, it is sufficient to find weights such that, in the weighted data set, this condition holds. Specifically, using subscripts to denote the weighted data, we require weights such that .
A sufficient condition to give us this result is that the conditional distribution of the dyad history in the weighted data set is equal to the marginal, . Expressing the left‐hand side in terms of the joint weighted distribution, we find that this condition is equivalent to
It follows that we require weights such that,
| (A3) |
Having the numerators and the denominators equal in Equation (A3) is sufficient for it to hold. Let denote the weight function. Beginning with the numerators, the weighting scheming means we can write each numerator as,
where . It follows immediately that when Equation (A2) holds, the numerators will all be equal.
Similarly, for any in the denominators we may written as,
where we have defined . We can now see that when Equation (A2) holds, we will also have the numerators being equal. This concludes the proof.
Interference Models and Weights Estimation
We intend to discuss possible weight specifications satisfying the balancing conditions, and how they may simplify under different modeling casual graphs. Commonly, weights are a function of the joint propensity score, , which is generally unknown and must be estimated from the data. We have called this model the treatment model. Under the causal framework explained in Section 2.2, the dyad‐level treatment can be considered as a categorical treatment which takes one of four values: or , which we collect into the set . For multiple nominal treatments, the generalized propensity scores are frequently modeled by a multinomial logistic regression. In the case of within‐dyad interference, where each individual is exposed to a bivariate binary treatment, we can also implement a bivariate logistic model to estimate the weights. In another approach we can fit the marginal distributions and , then model the association between the exposures via a Dale model [37].
The formulation of the dyad treatment as a categorical variable allows weights previous devised in the literature to be used in this dyadic‐network context. The balancing weights proposed for categorical treatment proposed in Li et al., for example, will satisfy the balancing property [38]. In their most general form these weights can be expressed as,
which can be interpreted as a Boltzmann distribution over the treatment space where the energy of each treatment is defined to be the negative log of the propensity score for that treatment.
Sometimes we estimate and to form joint treatment model. Under this the balancing condition of A3 can be written as,
such that . Additionally, the weights can be written specifically in terms of this model formulation as,
As we have already mentioned, under simpler causal graphs than the most general case, as presented in Figure 1 (Model 3), the formulation of the treatment model, and hence the weights may be simplified. For example, under a model specified according to Figure 1 (Model 1), the treatment of each dyad member is independent of the other condition on their individual and shared covariates. In such a case, and therefore . The balancing condition in Equation (A3) simplifies in this case to the same condition for each set of marginal distributions, that is,
for indexing the dyad treatments. Therefore,
It follows that in such a case, any weights previously satisfying the balancing condition provided in, for example, Wallace and Moodie [10], can be used on each member of the dyad individually and multiplied together to form a dyad weight [10].
Appendix B. Simulation
Single‐Stage Regime
In this section, we present additional results regarding the analysis presented in Section 4.1. These are provided in Figure B1 and Table B1.
FIGURE B1.
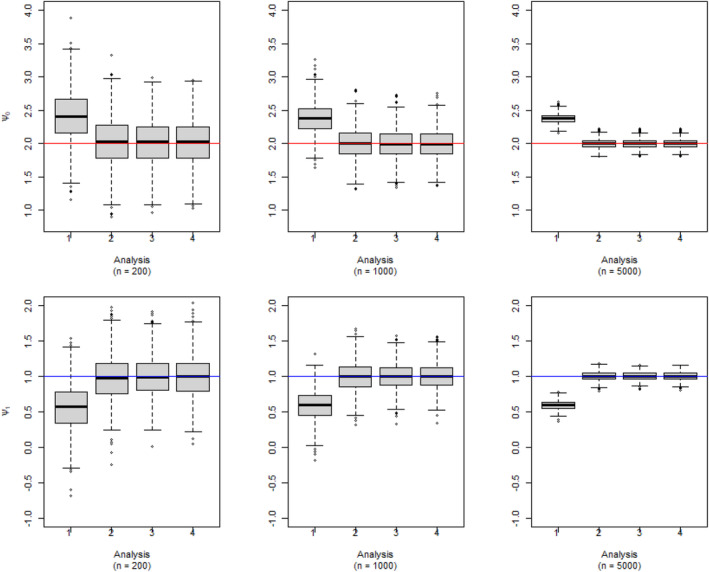
Dyadic‐blip function parameter estimates for 1000 simulated data sets via our dyadic‐dWOLS approach when neither (Analysis 1), one (Analyses 2 and 3), or both (Analysis 4) treatment and treatment‐free models are correct for single‐stage simulation. n is the sample size of dyads. True value of = 2 and = 1.
TABLE B1.
Mean, standard error, bias, and root mean squared error of the blip estimators with sample size n = 1000 dyads across four scenarios for the single‐stage simulation.
| Scenario | Mean | Standard error | Bias | RMSE | |||
|---|---|---|---|---|---|---|---|
|
|
1 | 2.402 | 0.021 |
|
0.555 | ||
| 2 | 2.026 | 0.012 |
|
0.372 | |||
| 3 | 2.011 | 0.011 |
|
0.346 | |||
| 4 | 2.013 | 0.011 |
|
0.347 | |||
|
|
1 | 0.567 | 0.010 |
|
0.541 | ||
| 2 | 0.967 | 0.010 |
|
0.322 | |||
| 3 | 0.990 | 0.009 |
|
0.286 | |||
| 4 | 0.989 | 0.007 |
|
0.291 | |||
|
|
1 | −2.004 | 0.007 |
|
0.225 | ||
| 2 | −2.005 | 0.007 |
|
0.234 | |||
| 3 | −1.977 | 0.007 |
|
0.208 | |||
| 4 | −1.996 | 0.008 |
|
0.214 | |||
|
|
1 | 0.988 | 0.013 |
|
0.403 | ||
| 2 | 0.988 | 0.012 |
|
0.392 | |||
| 3 | 0.993 | 0.011 |
|
0.353 | |||
| 4 | 0.989 | 0.011 |
|
0.361 | |||
|
|
1 | −1.994 | 0.009 |
|
0.284 | ||
| 2 | −1.991 | 0.009 |
|
0.277 | |||
| 3 | −2.001 | 0.008 |
|
0.242 | |||
| 4 | −1.997 | 0.008 |
|
0.252 |
Note: True value of = 2, = 1, = −2, = 1, and = −2.
Two‐Stage Regime
Here, we investigate the performance of the proposed model with two stages of treatment. For each dyad and each member we generate the patient information at Stage 1, , according to a normal distribution with mean of 2 and standard deviation of 1. Patient information at the second stage, , is generated according to a uniform distribution on the interval . The treatment model at stage is defined as , for . The outcome model is where , where the dyadic‐blip model at stage is Model misspecification for the treatment model, at each stage, is done by exclusion of the nonlinear term. The treatment‐free model at Stage 2 is misspecified by eliminating , and at Stage 1 by excluding .
Figure B2 shows boxplots of the estimated dyadic‐blip parameters for the first stage, while Figure B3 plots the same for the second‐stage estimates for the specific case of dyads. Blue horizontal lines have been drawn at the true value of each parameter. The Label 1 denotes the case in which neither component of the model is correctly specified, Label 2 denotes the case in which only the treatment‐free component is misspecified, Label 3 denotes the case where only the treatment model is misspecified, and Label 4 denotes the case in which everything is correctly specified. Consistent estimates of dyadic‐blip parameters are achieved when at least one of the treatment model or treatment‐free model is correctly specified.
FIGURE B2.
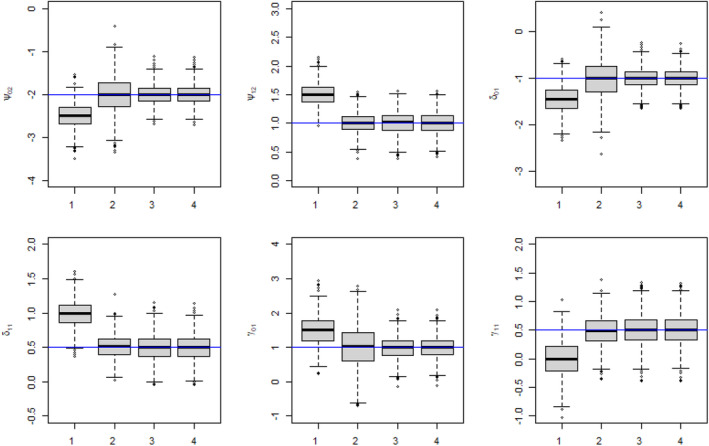
First‐stage dyadic‐blip parameter estimates for simulated data sets via the dyadic‐dWOLS approach for a two‐stage DTR, when both (Analysis 1), one (Analyses 2 and 3), or neither (Analysis 4) treatment and treatment‐free models are misspecified. True value of = −2, = 1, = −1, = −0.5, = 1, and = 0.5.
Simulation III: Dyadic‐Health Functions
FIGURE B3.
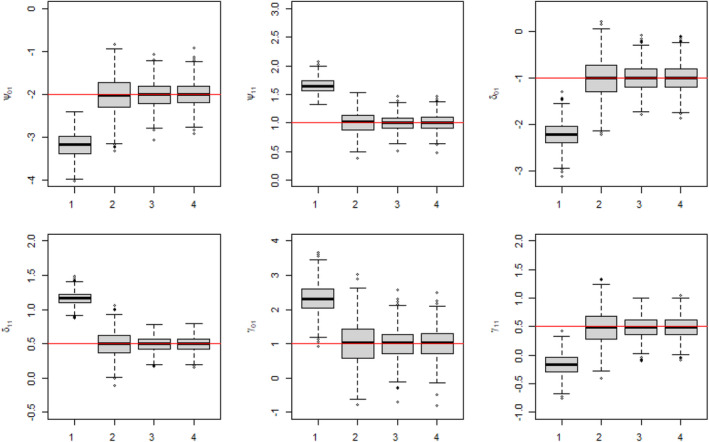
Second‐stage dyadic‐blip parameter estimates for simulated data sets via the dyadic‐dWOLS approach for a two‐stage DTR, when both (Analysis 1), one (Analyses 2 and 3), or neither (Analysis 4) treatment and treatment‐free outcome models are misspecified. rue value of = −2, = 1, = −2, = 0.5, = 1, and = 0.5.
FIGURE B4.
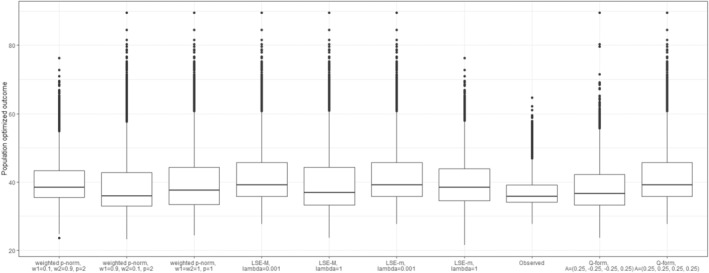
Boxplots of the outcome values for both members across sampled dyads are presented for nine different dyad‐health functions, each associated with a unique set of parameter settings, as summarized in Table 1.
FIGURE B5.
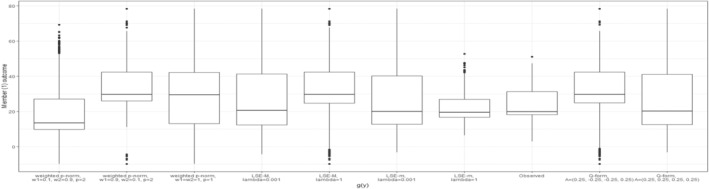
Boxplots of Member 1's outcomes for nine different dyad‐health functions and the observed values.
FIGURE B6.
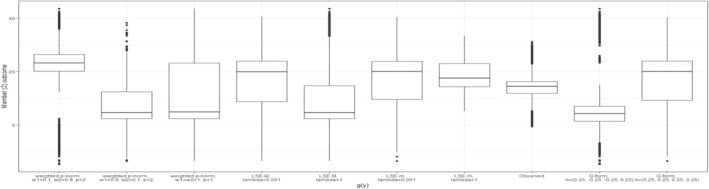
Boxplots of Member 2's outcomes for nine different dyad‐health functions and the observed values.
Funding: The authors received no specific funding for this work.
Data Availability Statement
The data that support the findings of this study are available from ICPSR. Restrictions apply to the availability of these data, which were used under license for this study. Data are available from https://www.icpsr.umich.edu/web/ICPSR/series/606 with the permission of ICPSR.
References
- 1. Kosorok M. R. and Laber E. B., “Precision Medicine,” Annual Review of Statistics and Its Application 6, no. 1 (2019): 263–286, 10.1146/annurev-statistics-030718-105251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Chakraborty B. and Moodie E. E. M., Statistical Methods for Dynamic Treatment Regimes: Reinforcement Learning, Causal Inference, and Personalized Medicine (New York, NY: Springer, 2013), 10.1007/978-1-4614-7428-9. [DOI] [Google Scholar]
- 3. Murphy S. A., Arjas E., Jennison C., et al., “Optimal Dynamic Treatment Regimes,” Journal of the Royal Statistical Society, Series B: Statistical Methodology 65, no. 2 (2003): 331–355, 10.1111/1467-9868.00389. [DOI] [Google Scholar]
- 4. Tsiatis A. A., Davidian M., Holloway S. T., and Laber E. B., Dynamic Treatment Regimes: Statistical Methods for Precision Medicine (Boca Raton, FL: Chapman and Hall/CRC, 2020), 10.1201/9780429192692. [DOI] [Google Scholar]
- 5. Moodie E. E. M., Chakraborty B., and Kramer M. S., “Q‐Learning for Estimating Optimal Dynamic Treatment Rules From Observational Data,” Canadian Journal of Statistics 40, no. 4 (2012): 629–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Moodie E. E. M., Dean N., and Sun Y. R., “Q‐Learning: Flexible Learning About Useful Utilities,” Statistics in Biosciences 6, no. 2 (2014): 223–243, 10.1007/s12561-013-9103-z. [DOI] [Google Scholar]
- 7. Robins J. M., “Optimal Structural Nested Models for Optimal Sequential Decisions,” in Proceedings of the Second Seattle Symposium in Biostatistics: Analysis of Correlated Data, eds. Lin D. Y., and Heagerty P. J. (New York, NY: Springer, 2004), 189–326, 10.1007/978-1-4419-9076-1_11. [DOI] [Google Scholar]
- 8. Chakraborty B., Murphy S., and Strecher V., “Inference for Non‐Regular Parameters in Optimal Dynamic Treatment Regimes,” Statistical Methods in Medical Research 19, no. 3 (2010): 317–343, 10.1177/0962280209105013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Ertefaie A., McKay J. R., Oslin D., and Strawderman R. L., “Robust Q‐Learning,” Journal of the American Statistical Association 116, no. 533 (2021): 368–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Wallace M. P. and Moodie E. E. M., “Doubly‐Robust Dynamic Treatment Regimen Estimation via Weighted Least Squares,” Biometrics 71, no. 3 (2015): 636–644. [DOI] [PubMed] [Google Scholar]
- 11. Schulz J. and Moodie E. E. M., “Doubly Robust Estimation of Optimal Dosing Strategies,” Journal of the American Statistical Association 116, no. 533 (2021): 256–268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Simoneau G., Moodie E. E. M., Nijjar J. S., Platt R. W., and Investigators SERAIC , “Estimating Optimal Dynamic Treatment Regimes With Survival Outcomes,” Journal of the American Statistical Association 115, no. 531 (2020): 1531–1539. [Google Scholar]
- 13. Rubin D. B., “Randomization Analysis of Experimental Data: The Fisher Randomization Test Comment,” Journal of the American Statistical Association 75, no. 371 (1980): 591–593. [Google Scholar]
- 14. Halloran M. E. and Struchiner C. J., “Causal Inference in Infectious Diseases,” Epidemiology 16, no. 2 (1995): 142–151, 10.1097/00001648-199503000-00013. [DOI] [PubMed] [Google Scholar]
- 15. Sobel M. E., “What Do Randomized Studies of Housing Mobility Demonstrate? Causal Inference in the Face of Interference,” Journal of the American Statistical Association 101, no. 476 (2006): 1398–1407. [Google Scholar]
- 16. Tchetgen E. J. T. and VanderWeele T. J., “On Causal Inference in the Presence of Interference,” Statistical Methods in Medical Research 21, no. 1 (2012): 55–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Campbell M. J., Donner A., and Klar N., “Developments in Cluster Randomized Trials and Statistics in Medicine,” Statistics in Medicine 26, no. 1 (2007): 2–19. [DOI] [PubMed] [Google Scholar]
- 18. Rosenbaum P. R., “Interference Between Units in Randomized Experiments,” Journal of the American Statistical Association 102, no. 477 (2007): 191–200. [Google Scholar]
- 19. Hudgens M. G. and Halloran M. E., “Toward Causal Inference With Interference,” Journal of the American Statistical Association 103, no. 482 (2008): 832–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Aronow P. M. and Samii C., “Estimating Average Causal Effects Under General Interference, With Application to a Social Network Experiment,” Annals of Applied Statistics 11, no. 4 (2017): 1912–1947. [Google Scholar]
- 21. Ogburn E. L. and VanderWeele T. J., “Vaccines, Contagion, and Social Networks,” Annals of Applied Statistics 11, no. 2 (2017): 919–948. [Google Scholar]
- 22. Su L., Lu W., and Song R., “Modelling and Estimation for Optimal Treatment Decision With Interference,” Stat 8, no. 1 (2019): e219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Jiang C., Wallace M. P., and Thompson M. E., “Dynamic Treatment Regimes With Interference,” Canadian Journal of Statistics 51 (2023): 469–502. [Google Scholar]
- 24. Manning M., Wojda M., Hamel L., Salkowski A., Schwartz A. G., and Harper F. W., “Understanding the Role of Family Dynamics, Perceived Norms, and Lung Cancer Worry in Predicting Second‐Hand Smoke Avoidance Among High‐Risk Lung Cancer Families,” Journal of Health Psychology 22, no. 12 (2017): 1493–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Cooley M. E., Sarna L., Brown J. K., et al., “Tobacco Use in Women With Lung Cancer,” Annals of Behavioural Medicine 33 (2007): 242–250. [DOI] [PubMed] [Google Scholar]
- 26. Di Castelnuovo A., Quacquaruccio G., Donati M. B., Gaetano D. G., and Iacoviello L., “Spousal Concordance for Major Coronary Risk Factors: A Systematic Review and Meta‐Analysis,” American Journal of Epidemiology 169, no. 1 (2008): 1–8. [DOI] [PubMed] [Google Scholar]
- 27. Jackson S. E., Steptoe A., and Wardle J., “The Influence of Partner's Behavior on Health Behavior Change: The English Longitudinal Study of Ageing,” JAMA Internal Medicine 175, no. 3 (2015): 385–392. [DOI] [PubMed] [Google Scholar]
- 28. “The Health Consequences of Smoking: Nicotine Addiction: A Report of the Surgeon General,” 1988, Report.
- 29. Benowitz N. L., Hukkanen J., and P. Jacob, III , “Nicotine Chemistry, Metabolism, Kinetics and Biomarkers,” in Nicotine Psychopharmacology, eds. Stolerman I. M. P., and Price L. H. (Berlin, Heidelberg: Springer, 2009), 29–60, 10.1007/978-3-540-69248-5_2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Hyland A., Ambrose B. K., Conway K. P., et al., “Design and Methods of the Population Assessment of Tobacco and Health (PATH) Study,” Tobacco Control 26, no. 4 (2017): 371–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Strong D. R., Pearson J., Ehlke S., et al., “Indicators of Dependence for Different Types of Tobacco Product Users: Descriptive Findings From Wave 1 (2013–2014) of the Population Assessment of Tobacco and Health (PATH) Study,” Drug and Alcohol Dependence 178 (2017): 257–266. [DOI] [PubMed] [Google Scholar]
- 32. Benowitz N. L., Dains K. M., Dempsey D., Yu L., and Jacob P., “Estimation of Nicotine Dose After Low‐Level Exposure Using Plasma and Urine Nicotine Metabolites,” Cancer Epidemiology, Biomarkers & Prevention 19, no. 5 (2010): 1160–1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Benowitz N. L., St Helen G., Nardone N., Cox L. S., and Jacob P., “Urine Metabolites for Estimating Daily Intake of Nicotine From Cigarette Smoking,” Nicotine & Tobacco Research 22, no. 2 (2020): 288–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Goniewicz M. L., Smith D. M., Edwards K. C., et al., “Comparison of Nicotine and Toxicant Exposure in Users of Electronic Cigarettes and Combustible Cigarettes,” JAMA Network Open 1, no. 8 (2018): e185937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Wallace M. P., Moodie E. E., and Stephens D. A., “Model Selection for G‐Estimation of Dynamic Treatment Regimes,” Biometrics 75, no. 4 (2019): 1205–1215. [DOI] [PubMed] [Google Scholar]
- 36. Bian Z., Moodie E. E., Shortreed S. M., and Bhatnagar S., “Variable Selection in Regression‐Based Estimation of Dynamic Treatment Regimes,” Biometrics 79, no. 2 (2023): 988–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Dale J. R., “Global Cross‐Ratio Models for Bivariate, Discrete, Ordered Responses,” Biometrics 42, no. 4 (1986): 909–917. [PubMed] [Google Scholar]
- 38. Li F., Morgan K. L., and Zaslavsky A. M., “Balancing Covariates via Propensity Score Weighting,” Journal of the American Statistical Association 113, no. 521 (2018): 390–400. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Supporting Information.
Data Availability Statement
The data that support the findings of this study are available from ICPSR. Restrictions apply to the availability of these data, which were used under license for this study. Data are available from https://www.icpsr.umich.edu/web/ICPSR/series/606 with the permission of ICPSR.


