Review Highlights
-
•
A new dataset transformation method has been presented using wPCA and FastICA.
-
•
An effective feature selection method has been introduced using new binary exponential henry solubility optimization algorithm.
-
•
Efficient use of data transformation approaches has been depicted for optimal feature selection.
Method name: A new feature selection approach with binary exponential henry gas solubility optimization and hybrid data transformation.
Keywords: Metaheuristic, Feature selection, Weighted principal component analysis, Fast independent component analysis, Hybrid data transformation
Abstract
In the common classification practices, feature selection is an important aspect that highly impacts the computation efficacy of the model, while implementing complex computer vision tasks. The metaheuristic optimization algorithms gain popularity to obtain optimal feature subset. However, the feature selection using metaheuristics suffers from two common stability problems, namely premature convergence and slow convergence rate. Therefore, to handle the stability problems, this paper presents a fused dataset transformation approach by joining weighted Principal Component Analysis and Fast Independent Component Analysis Techniques. The presented method solves the stability issues by first transforming the original dataset, thereafter newly proposed variant of Henry Gas Solubility Optimization is employed for obtaining a new feature's subset. The proposed method has been compared with other metaheuristic approaches across seven benchmark datasets and observed that it selects better features set which improves the accuracy and computational complexity of the model.
Graphical abstract
Specifications table
| Subject area: | Computer Science |
| More specific subject area: | Image processing and Pattern Recognition |
| Name of the reviewed methodology: | A New Feature Selection Approach with Binary Exponential Henry Gas Solubility Optimization and Hybrid Data Transformation Methods |
| Keywords: | Metaheuristic, Feature Selection, Weighted Principal Component Analysis, Fast Independent Component Analysis, Hybrid Data Transformation |
| Resource availability: | Machine of 1.80 GHz Intel Core i5 processor, UCI Machine Learning Repository http://archive.ics.uci.edu/ml |
| Review question: |
Q1. Why classification-based learning models often suffers with overfitting and scalability challenges, especially in high-dimensional spaces.? Q2. Why learning-based models have high computational costs? Q3. How data dimensionality reduction may be applied through the application of data transformation methods and metaheuristic algorithms in high-dimensional datasets. |
Introduction
In recent few years, the prevalence of images and videos on various social media platforms and sensors have surged which resulted in an exponential increase in the production of high-dimensional data. Unfortunately, this rapid growth in data dimensionality has also led to an increase in irrelevant, redundant, and noisy features. As a result of high dimensionality, low-quality features can become more prevalent and this can propagate to fast growth in the time-space complexities in the image processing techniques. This can negatively impact the performance of machine learning approaches in image classification tasks [1]. Therefore, feature selection techniques are generally playing a vital role in avoiding unnecessary and irrelevant features, and selecting relevant and compact feature subsets from high dimensional feature sets which can boost the performance in different computer vision tasks [2].
Generally, finding specific features set through a brute force approach can be highly resource-intensive and time-consuming. With k features, there can be as many as possible feature combinations, making it impractical to compare and evaluate all these subsets [3]. Therefore, this paper aims to find a concise feature's subset from the high dimensional feature's set using an appropriate assessment criterion. This reduction of features can improve the accuracy and computational expenses of the classification systems [4] and also enhance interpretability in the considered models [5]. In the literature, the feature selection (FS) methods are majorly classified into three classes, namely filter methods (FMs), wrapper methods (WMs), and embedded methods (EMs). The FMs refer to the techniques that are evaluated the relevance of individual features by their statistical characteristics or other non-parametric measures [6]. Hence, the correlation coefficient (CRC), mutual information (MI), variance thresholding, or chi-squared test (CST) are usually employed for the score-based feature evaluation [4]. The statistical scores are then sorted to find the top (k) features and the top (k) features are considered relevant features for further analysis. These methods exhibited less time-space complexity as compared to WMs and EMs feature selection approaches [7]. Therefore, FMs can be utilized as pre-processing methods to reduce computational expenses [5].
The WMs evaluate the predictive power of the feature's subset using a learning-based approach. These methods find the optimal feature's subset by using a recursive feature addition or elimination methodology that maximizes the performance of the algorithm in classification task [8]. Moreover, WMs are more sensitive to the choice of these learning approaches and the quality of the training data. However, for the multidimensional large datasets, these methods require high computing expenses for the performance evaluation of the classification methods [9]. Embedded methods for the feature selection are employed in some specific techniques, namely gradient boosting and decision tree (DT). The selection process of features embedded within the used approaches and carried out simultaneously with the model training process. EMs can be computationally inexpensive as compared to WMs [10]. As none of the feature selection methods within these categories alone appear to guarantee optimal outcomes in terms of predictive performance, robustness, and stability, hence the researchers have investigated the efficacy of hybrid approaches that incorporate a combination of diverse selectors. Zhou et al. [11] reported a hybrid FS (HFS) approach for the image classification, where a relief algorithm is applied at the initial stage for the elimination of irrelevant feature set and employed a wrapper-based feature section method named SVM-RFE for computing the quality of each feature vector. Further, Aguilera et al. [12] described another HFS approach by using two FMs, namely Chi2 and Anova along with two EMs, namely Random Forest and Extra-tree in the binary classification models.
Recently, WMs-based feature selection methods have used various deep learning techniques, both implicitly and explicitly, to automate feature selection in image classification tasks [30,32]. Vivekanandan et al. [28] introduced a WMs-based feature selection method employing a modified differential evolution (DE) algorithm and fuzzy Analytic Hierarchy Process (AHP) in conjunction with a feed-forward neural network to predict heart disease. Canayaz et al. [30] proposed the integration of deep learning models such as AlexNet, VGG19, GoogleNet, and ResNet, along with metaheuristic methods to automatically select features in COVID-19 datasets. Doğan et al. [14] employed CNN-based models, specifically MobileNetv1, MobileNetv2, and NASNetMobile, for feature extraction, combined with linear support vector classification (SVC) to perform feature selection in vehicle classification tasks. However, these approaches were computationally demanding, necessitating substantial computational resources for training [13]. A brief description of various feature selection methods has been depicted in Table 1.
Table 1.
Description of state-of-the-art methods used for feature selection in the literature.
| S.No. | Methods | Algorithm and Tools | Datasets | Results | Authors |
|---|---|---|---|---|---|
| 1 | HFS (FMs) | reliefF-SVM-RFE | Caltech-256 | Accuracy: 96.14 % Run time:1715s | Zhou et al. [11] |
| 2 | HFS (FMs) | Chi2 and Anova, RF and Extra-tree RF, LR, KNN, and SVM. | HER2 image | Recall: 93.9 %, Specificity: 86.6 %, Accuracy: 90.3 %, Precision: 87.5 %, F1-score 90.6 %. | Aguilera et al. [12] |
| 3 | WMs | PCA and SGbSA (GbSA-PCA) | UCI (Iris and E. coli) | Run time: 81.38 s and 653.83 s for respective datasets | Hosseini et al. [49] |
| 4 | WMs | wPCA based MRbTA and SVM | Wisconsin diagnostic breast cancer, wine, Leukemia microarray |
Accuracy: 92.27 %, 93.79 %, 90.29 % for respective datasets | Kim et al. [50] |
| 5 | HFS | IPCA, Gaussian and Super Gaussian | Liver Toxicity, Prostate cancer, Yeast metabolomic | Average of correctly identified non-zero loadings: 86.7 %, 87.7 %, 80.80 % | Yao et al. [50] |
| 6 | HFS | IPC, ICA, naıve Bayes and SVM | Wisconsin Breast Cancer, Wine, Crabs | Accuracy: 96.85 %, 98.90 %, 99.50 % for respective datasets | Reza et al. [51] |
| 7 | HFS (FMs) | ReliefF, Chi square, and Symmetrical techniques, GA, SVM | Microstructural images: Annealing twin, Brass/bronze, Ductile cast iron, gray cast iron, Malleable cast iron, Nickel-based superalloy, White cast iron | Overall Accuracy: 90.1 % | Khan et al. [19] |
| 8 | EMs | Tree-based genetic program (GP-FER) | DISFA, DISFA+, CK+, MUG | Average accuracy: 94.2 % | Ghazouani et al. [21] |
| 9 | WMs | HHBBO and SVM | RADARSAT 2 (NLCD 2006) | Overall accuracy: 96.01 %, Average accuracy: 93.37 % | Rostami et al. [3] |
| 10 | WMs | bPSO and bGWO, SVM, AlexNet, Vgg19, GoogleNet and ResNet. | COVID-19, normal, pneumonia X-ray images | Overall accuracy: 99.38 % | Canayaz et al. [30] |
| 11 | WMs | ACO, GA and TS, Fuzzy Rough set (ACTFRO) and GATFRO) | SRBCT, DLBCL, Breast, Leukemia, Swarm behaviour | Accuracy: 90.48 %, 97.41 %,83.33 %, 94.74 %, 86.68 % for respective datasets | Meenachi et al. [31] |
| 12 | WMs | GA and PSO with bagging, SVM and DT | NASA Metrics Data (MDP) | Accuracy: 84.4 %, 87.2 % respective methods | Wahono et al. [32] |
| 13 | WMs | GWO, Adaptive PSO and MLP, SVM, DT, KNN, NBC, RFC, LR. | UCI Machine Learning Repository | Accuracy: 96 % and 97 % respective methods | Le et al. [25] |
| 14 | WMs | Rough set and Scatter search, LR, DT and NN | Australian dataset, UCI Repository | Accuracy: 90.5 %, 83.4 % and 87.9 % | Wang et al. [26] |
| 15 | HFS (FMs) | Chi-Square, PCC, MI, NDS and GA | IDS dataset | Accuracy (99.48 %) | Dey et al. [33] |
| 16 | WMs | Modified DE, fuzzy approach and CNNs | University of California, Irvine (UCI) | Accuracy 83 % | Vivekanandan et al. [28] |
| 17 | WMs | Binary encoded SSA based on PCA-fastICA | 11 datasets from UCI | Overall accuracy: 94.73 % | Shekhawat et al. [29] |
| 18 | WMs | MAF and CNN, HGSO algorithm, RF, SVM | ISIC 2017 and HAM10000 datasets | Overall accuracy: 92.22 % and 99.34 % respectively | Obayya et al. [39] |
| 19 | WMs | MobileNetv1, MobileNetv2, NASNetMobile, linear SVC, SVM | Real traffic scenes | Accuracy:87.4 % | Doğan et al. [14] |
| 20 | WMs | Binary BCS based on PCA-fastICA | 11 datasets from UCI | Highest accuracy: 95.2 % | Pandey et al. [17] |
Generally, any feature selection method aimed to grow the classifier efficacy and remove the unimportant or unrelated features, which also required a trade-off between these two objectives. To eliminate redundant features, enhance the classifier's performance, and reduce computational time, optimization algorithms are often useful in solving classification problems [3,18]. Many metaheuristic optimization algorithms, namely particle swarm optimization (PSO) [23], grasshopper optimization algorithm (GOA) [24], grey wolf optimization (GWO) [25], artificial bee colony (ABC) [3], scatter search (SC) [26], binomial cuckoo search (BCS) [17], tabu search (TS)[30], Non-dominated sorting (NDS) [33], henry gas solubility optimization (HGSO) [27], differential evolution (DE) [28], biogeography-based optimization (BBO) [3], and salp swarm algorithm (SSA) [29] have been employed for the optimization issues in the FS approaches and applied in various computer vision applications. Rostami et al. [3] proposed a combination of two metaheuristic algorithms, namely BBO and ABC along with an SVM classifier for the selection of optimal features. Canayaz et al. [30] combined binary PSO and binary GWO for the selection of optimal features and obtained the best efficacy among the considered method with the SVM classifier.
In the existing literature, binary-encoded metaheuristic algorithms have been designed specifically for binary problems. Several researchers have used binary-encoded versions of various metaheuristic algorithms to simultaneously achieve the multi objectives in different applications. Moreover, the binary encoded algorithms have been utilized to achieve single objectives and multi-objectives in different computer vision applications. These algorithms include binary GWO [34], binary PSO [23], chaotic binary coded GSA [35], improved binary PSO [36], binary-embedded GSA [37], binary GOA [24]}, and binary quantum-inspired GSA [38]. Furthermore, Pandey et al. [17] introduced binary encoded BCS for solving binary objective problems in feature selection approaches. This method aims to enhance the efficacy of classification by utilizing binary encoding. Similarly, Shekhawat et al. [29] presented binary encoded SSA for designing a feature selection approach. The objective of this method is to identify non-redundant subsets of features, thereby improving the efficacy of classification methods while reducing the size of the feature sets. Recently, Neggaz et al. [41] proposed a binary HGSO algorithm-based approach in dimensionality reduction and selection of the most significant features and thereby improving classification accuracy. Since the current position update mechanism in the binary HGSO algorithm is linearly related to the previous position of the solutions, this relationship may encourage a lack of intensification of the HGSO algorithm, resulting in slow convergence precision [40].
Although metaheuristic-based FS methods have made progress in solving binary objective and multi-objective problems, there are still some challenges in the feature selection process. A study by Akinola et al. [44] reported scalability and stability problems when these algorithms were applied to higher-dimensional datasets. These methods do not consistently yield the same optimal feature subset after each run [44]. To mitigate these problems, researchers have employed various data transformation methods (DTMs) within the FS approach. Principal component analysis (PCA [23], linear discriminant analysis (LDA) [46], independent component analysis (ICA) [47] and fast independent component analysis [48] are popular DTMs mentioned in the literature to eliminate irrelevant and redundant features in FS methods. The PCA and LDA are statistical-based transformation technique that identifies all the interrelated features and reduces the size of the original feature's subset. Hosseini et al. [49] proposed an optimization approach for feature selection that combines the Spiral Galaxy-Based Search Algorithm (SGbSA) with PCA. The SGbSA algorithm efficiently explores the search space and identifies relevant features, while PCA is employed for dimensionality reduction, validating the effectiveness of the SGbSA algorithm. Kim et al. [52] addressed the interpretability problem arising from PCA. Hence, they proposed a variant of PCA named weighted PCA (wPCA) in combination with the moving range-based thresholding (MRBT) meta-heuristic algorithm. The MRBT algorithm is used for optimal feature selection, and wPCA assigns weights to original features to enhance interpretability. However, Chattopadhyay et al. [47] reported that PCA identifies linear correlations between data points but may not effectively capture higher-order correlations, and the features identified by PCA are not necessarily independent. In contrast, ICA identifies mutually uncorrelated variables and can be a more versatile technique for data analysis.
Yao et al. [50] noted that a single DTM does not effectively rectify the challenges of reducing high dimensionality in unsupervised methods. To overcome this limitation, they proposed Independent PCA, which combines the strengths of both PCA and ICA to reduce dimensionality while identifying independent and uncorrelated components within the dataset. This approach shows promise in addressing the challenges of high dimensionality in unsupervised learning methods. Further, Reza et al. [51] introduced a hybrid FS (HFS) approach, using DTMs namely IPCA and ICA for classification problems. This HFS approach identified significant optimal feature sets that improved classification accuracy. However, the existing DTMs were ineffectively minimizing the correlation and top-order dependency simultaneously.
To overcome the various above-mentioned limitation of existing DTMs, this work introduces the new HFS approach wPCA-FastICA based DTMs that combines two DTMs, namely wPCA and FastICA before the FS process. Furthermore, this paper introduces an enhanced binary exponential HGSO (EHGSO) algorithm to avoid early premature convergence and encourage population diversity in the standard HGSO. Finally, to overcome the challenges in the feature selection for the high dimensional datasets, the HFS approach named wPCA-FastICA based bEHGSO-FS is employed to discover the best feature's subset in the different benchmark datasets. The work has been analyzed and compared with state-of-the-art techniques.
In the rest of the paper, Section 2 to Section 5 are structured as follows: Section 2 gives a description of the standard HGSO method. The newly proposed method is detailed in Section 3, while Section 4 depicts experimental results and outcomes. Finally, Section 5 presents the conclusion and the future scope.
Standard HGSO method
The standard HGSO algorithm mimics Henry's law of gases [27]. The algorithm majority stated the impact of temperature and pressure on the solubility of gases. It uses the gas particle's population to generate the optimal solution [41]. The various steps of the standard algorithm are presented below.
Initialization of candidate solution and constants: In this step, HGSO population gas particles is randomly initialized using Eq. (1).
| (1) |
In this equation, denotes the initial position of the gas particle, while and denote the low and high limits of the search area respectively. The term rand (0,1) generates random numbers.
Moreover, initial partial pressure of gas particles in group, Henry's constant and constants of group are defined by Eq. (2).
| (2) |
Grouping of gas particles
The grouping process categorizes the population of gas particles based on their gas type. Within each group, all gas particles have a similar value.
Evaluation process
This step is carried out by fitness function to identify the most appropriate gas within each group which achieves the highest equilibrium. A ranking mechanism is also utilized to determine the best agent.
Upgrading henry's constant
The Henry's constant for the iteration, denoted as iteration, denoted as is calculated based on the Henry constantfrom the iteration, using Eq. (3).
| (3) |
Here, equals to, T represents the temperature, while indicates the highest number of iterations.
Improving solubility
The formula for updating the solubility of each gas particle is presented in Eq. (4).
| (4) |
Here, the variables and are solubility and partial pressure respectively of the gas particle in the group at the iteration. Additionally, the variable K represents a fixed value in the formula for updating solubility.
Upgrading location
The updated location gas particle in the group of the population is denoted as and is computed using the following formula, as shown in Eq. (5).
| (5) |
Here, flagging parameter F is utilized to monitor the search movements of the search particle. The location of the best local search particle in group at iteration is denoted by and represents the location of the global best particle at repetition . The represents the strength of a search particle with respect to gas groups, and represents the degree of influence that other search particles have on the search particle. The fitness value of search particle n group is shown by and represents the fitness function in the whole population.
Avoiding local optimum
The formula in Eq. (6) is used to prevent the local optima situation.
| (6) |
Here, represents the worst search particles and M is the population of particles. The worst-performing search particle location is reinitialized by using Eq. (1). The complete procedure of HGSO may be referred in Neggaz et al. [41].
Proposed methodology
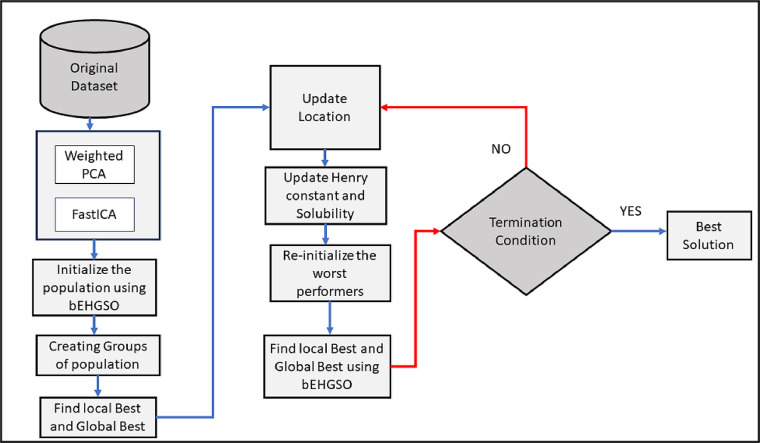
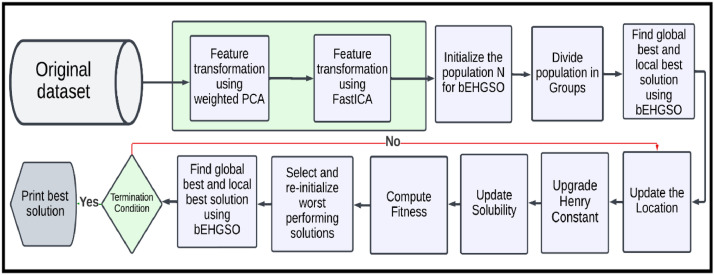
This paper presents a new bEGHSO and wPCA-FastICA-based bEGHSO feature selection (bEGHSO-FS) method. The complete approach is depicted in Fig. 1. As shown in the figure, the initial set of features passes through wPCA-FastICA-based DTM. The transformed feature's subset is given to bEHGSO for the selection of the optimal subset of features. The various phases used in the proposed method, namely wPCA-FastICA based DTM, bEHGSO, and new FS method are described in the below sections.
Fig. 1.
Flow chart of the proposed feature selection method using Binary Exponential HGSO and wPCA-FastICA Data transformation method.
Weighted PCA and fastica based dataset transformation method
The weighted PCA (wPCA) is a widely used statistical method for analyzing datasets and reducing their dimensionality [52]. The primary aim of wPCA is to capture the maximum amount of variance in the dataset by identifying a group of linear non-correlated features named principal components (PCs) [49]. This is achieved using an orthogonal transformation approach that converts the correlated feature's subset into a reduced uncorrelated feature's subset. The number of PCs in wPCA is always less than features in the original standardized dataset [46].
Mathematical equations of wPCA on the considered number of d-dimensional features is described in the following steps [16].
Standardization
This step involves scaling the original data to ensure the normalization of variables which helps to avoid biased outcomes. To transform the d-dimensional features X into a standardized format, compute the mean of X using Eq. (7).
| (7) |
Compute covariance
The covariance matrix is a square matrix that provides correlation (co-variances) and dependencies among the features in the dataset. Its diagonal elements contain the variances of the individual feature, while the off-diagonal elements represent the correlation between each pair of feature sets. This step finds the covariance matrix of features using Eq. (8).
| (8) |
here, T denotes transpose of a matrix and is a diagonal matrix of weights.
Decomposition
In this step, the covariance matrix is spectrally decomposed to calculate the eigenvalues and eigen vectors . To obtain lower d-dimensional features, sort the eigenvalues and eigenvectors such that and .
In this step, the lower dimensional features consisting of principal components (PCs), is computed. The transformed lower d-dimensional features are obtained using Eq. (9).
| (9) |
here, is transpose matrix and is mean of .
The weighted PCs are obtained by sorting all PCs according to their assigned weights and adding top k PCs, where the value of the k is decided on the basis of the contribution of the corresponding feature. This allows for a more interpretable representation of the features [52].
Independent components generation
The weighted PCs are utilized in the generation of independent components by using FastICA. FastICA is a fast convergence method for converting a diversified signal into diversified non-Gaussian signals [20]. The algorithm employs the standard kurtosis approach to generate components that are unrelated to each other from the source signal [22]. The weighted PCs features are considered as the observed signal and can represent a combination of an actual and mutually independent source of signal as shown in Eq. (10).
| (10) |
where, denotes expectation.
The optimum value of that yields the optimal solution for function Y is determined through the application of stochastic gradient in the kurtosis method. The transformed value of the source signal () is calculated using Eq. (11).
| (11) |
Proposed binary exponential HGSO
Once the dataset has transformed, an efficient metaheuristic method can be utilized to extract the suitable features from the transformed datasets. Therefore, in this section, an improved variant of HGSO called Binary Exponential Henry Gas Solubility Optimization (bEHGSO) is presented for selecting the optimal feature subset by incorporating two modifications into the standard HGSO. In the modified approach, HGSO initialized a population of M search particles where each search particle represents a feature's subset to be evaluated in the FS approach. The effectiveness of this step is crucial for achieving convergence and improving the quality of the desired solution [41]. The continuous values of the initial solution are converted into binary values represented as before evaluating the fitness of every search particle. The following formula in Eq. (12) is used to compute value of
| (12) |
In the standard HGSO algorithm, the position upgrade of search particles is linearly related to its previous position, which lacks nonlinearity in the position update equation. This results in slow intensification in the search space and premature convergence [42]. Hence, the position upgrade of search particles is crucial in computing the global best solution. Therefore, as the second modification step of HGSO, an exponential function [15] is incorporated into Eq. [13] to increase nonlinearity in the position update of each search particle, thus reducing premature convergence using fast intensification [43].
| (13) |
here, is an exponential function, k is the iteration constant, is the highest number of iterations, and is the controlling parameter to adjust the speed of the convergence behavior.
The new bEHGSO-FS methodology
The proposed bEHGSO-FS approach relies on the WMs methodology which requires a classifier to validate the effectiveness of selected features. Therefore, the new bEHGSO method integrates a K-nearest neighbor (KNN) classifier to ensure the quality of the selected features. In the initial step, the wPCA-FastICA-based DTM is utilized to transform the extracted input features. In the subsequent step, the bEHGSO methodology leverages these transformed feature sets, dynamically navigating the search space to maximize feature assessment in conjunction with the KNN classifier. The overall working of proposed method is described below.
-
1.Initialize the population, consisting of N solutions. Represent each solution as a d-dimensional feature vector, obtained after applying the wPCA-FastICA method. Therefore, the solution, denoted as in the population, can be expressed as shown in Eq. (14).
(14) -
2.
Convert each solution into binary values using Eq. (12).
-
3.Compute the fitness value for each solution by considering the features whose value is one. To achieve this, bEHGSO utilizes a weighted multi-objective function outlined in Eq. (15).
where, is the number of selected solutions, denotes total number of solutions, and A is the accuracy denoted by using Eq. (16).(15)
where, and denote true-positive, true-negative, false-positive, and false-negative values respectively.(16) -
4.
After computing the fitness value for each solution, bEHGSO updates Henry's constant, upgrades solubility and updates the location for each solution.
-
5.
Identify the weak performing solutions and re-initialize the worst performing solutions.
-
6.
Repeat steps 2 through 6 until the termination condition is met.
-
7.
After meeting the termination criteria, the bEHGSO algorithm returns the solutions with the best fitness value. These fittest solutions represent the optimal set of features determined by the bEHGSO algorithm. Subsequently, these features are utilized by the KNN classifier.
Experimental results
The performance of the proposed method has been analyzed in two phases. In the first phase, the proposed variant of HGSO (EHGSO) has been tested on the twenty-six established benchmark problems [27]. In the second phase, the efficiency of the wPCA-FastICA-based bEHGSO-FS method has been evaluated using seven standard datasets of the UCI repository [45]. All simulations have been conducted using MATLAB 2018 on a machine of 1.80 GHz Intel Core i5 processor to ensure fairness in comparison. The subsequent sections provide results and performance discussion of the proposed EHGSO and a novel wPCA-FastICA-based bEHGSO-FS method.
Performance evaluation of EHGSO
The performance of EHGSO is compared with five existing meta-heuristic methods, namely GSA [37], GWO [25], HGSO [27], SSA [29], and BCS [17] against 26 benchmark problems. The optimal values for all considered benchmark problems are presented in Table 2. These methods are randomized in nature hence, all the benchmark problems in Table 2 are executed 30 times to reduce this effect. Each method was implemented with a population of value 45 and the highest number of iterations were set at 1000. The parameter configuration for considered algorithms is presented in Table 3. Table 4 display the comparative performance using the metrics, namely average fitness value and standard deviation for both the considered and proposed metaheuristic algorithms.
Table 2.
Multimodal, Unimodal, and Fixed Dimensional Multimodal (FDMM) Benchmark Problems [27].
| S. No. | Category | Problem | Dim | Limit | Fmin |
|---|---|---|---|---|---|
| 1 | Multimodal | Ackley | 30 | [−35,35] | 0 |
| 2 | Multimodal | Alpine | 30 | [−10, 10] | 0 |
| 3 | Multimodal | Brown | 30 | [−10, 10] | 0 |
| 4 | Unimodal | Schwefel 2.21 | 30 | [−100,100] | 0 |
| 5 | Unimodal | Schwefel 2.22 | 30 | [−100,100] | 0 |
| 6 | FDMM | Ackley 2 | 2 | [−32,32] | −200 |
| 7 | FDMM | Cross-in-Tray | 2 | [−10,10] | −2.06 |
| 8 | Unimodal | Schwefel 2.20 | 30 | [−100,100] | 0 |
| 9 | Multimodal | Mishra 1 | 30 | [0,1] | 2 |
| 10 | Multimodal | Mishra 2 | 30 | [0,1] | 2 |
| 11 | FDMM | Hartman | 6 | [0,1] | −3.32 |
| 12 | FDMM | Matyas | 2 | [−10,10] | 0 |
| 13 | FDMM | Trecanni | 2 | [−5,5] | 0 |
| 14 | Multimodal | Cigar | 30 | [−100,100] | 0 |
| 15 | Unimodal | Schwefel 2.23 | 30 | [−10,10] | 0 |
| 16 | Unimodal | Sum Squares | 30 | [−10,10] | 0 |
| 17 | Multimodal | Xin-She Yang 3 | 30 | [−20,20] | 0 |
| 18 | Multimodal | Quartic | 30 | [−1.28,1.28] | 0 |
| 19 | FDMM | Periodic | 2 | [−10,10] | 0.9 |
| 20 | Multimodal | Schwefel 2.25 | 30 | [0,10] | 0 |
| 21 | FDMM | Rump | 2 | [−500,500] | 0 |
| 22 | FDMM | Egg Crate | 2 | [−5,5] | 0 |
| 23 | FDMM | ScCrossLegTable | 2 | [−10,10] | −1 |
| 24 | Multimodal | Xin-She Yang 2 | 30 | [−2pi, 2pi] | 0 |
| 25 | Multimodal | Griewank | 30 | [−10, 10] | 0 |
| 26 | Multimodal | Zakharov | 30 | [−5,10] | 0 |
Table 3.
Parameter configuration for each considered algorithm.
| PA | EHGSO | HGSO | SSA | GSA | BCS | GWO |
|---|---|---|---|---|---|---|
| M | 45 | 45 | 45 | 45 | 45 | 45 |
| khigh | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
| G0 | 100 | |||||
| AC | 20 | |||||
| SD | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] |
| Pa | [0.05,0.5] | |||||
| α | 1 | 1 | 1 | 0.99 | ||
| β | 1 | 1 | 1 | 0.01 | ||
| SC | [0.01,0.5] | |||||
| GS | 7 | 7 | 7 | 7 | 7 | 7 |
| C1 | [0,1] | [0,1] | [0,1] | |||
| C2 | [0,1] | [0,1] | [0,1] | |||
| R | 30 | 30 | 30 | 30 | 30 | 30 |
PA, M, khigh, G0, AC, SD, P0, SC, GS, and R stand for Parameters, Population Size, Maximum Iterations, Gravitational constant, Acceleration Coefficient, Probability, Step scaling coefficient, Group Size and Runs respectively, C1 and C2 are controlling parameters respectively.
Table 4.
Comparison of the proposed method with existing methods based on statistical results obtained for the benchmark problems. Bold values represent the best result.
| Prob. | GSA |
GWO |
SSA |
BCS |
HGSO |
EHGSO |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AFV | STD | AFV | STD | AFV | STD | AFV | STD | AFV | STD | AFV | STD | |
| 1 | 6.7E-135 | 7.3E-130 | 1.23E+02 | 2.31E+02 | 2.3E-144 | 6.5E-139 | 9.2E-135 | 2.1E-112 | 4.9E-147 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 2 | 2.38E+00 | 7.88E+13 | 1.35E+00 | 8.80E+16 | 6.77E-01 | 8.74E+13 | 7.44E-06 | 6.74E+15 | 1.46E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 3 | 1.42E-08 | 2.52E-09 | 2.64E-22 | 5.73E-23 | 8.8E-249 | 0.00E+00 | 2.6E-210 | 0.00E+00 | 1.2E-146 | 2.2E-147 | 0.00E+00 | 0.00E+00 |
| 4 | 3.62E-08 | 4.50E-09 | 8.60E-53 | 1.54E-53 | 2.6E-256 | 0.00E+00 | 2.1E-226 | 0.00E+00 | 6.2E-185 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 5 | 8.72E-87 | 2.27E-87 | 4.6E-287 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 6 | −2.4E+02 | 4.33E+07 | −2.2E+02 | 6.75E+06 | −2.0E+02 | 6.59E+05 | −2.0E+02 | 6.74E+06 | −2.0E+02 | 5.44E+07 | −2.0E+02 | 5.64E+06 |
| 7 | −2.6E+00 | 6.74E-10 | −2.1E+00 | 5.68E+06 | −2.5E+00 | 5.64E+06 | −2.3E+00 | 6.74E+08 | −3.9E+00 | 5.67E+09 | −2.0E+00 | 6.44E+05 |
| 8 | 3.92E-09 | 5.65E-10 | 4.00E-52 | 1.15E-52 | 3.5E-261 | 0.00E+00 | 1.3E-233 | 0.00E+00 | 4.1E-289 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 9 | 2.45E+00 | 1.24E+04 | 2.13E+00 | 2.13E+05 | 3.54E+00 | 9.84E+04 | 2.32E+00 | 4.33E+03 | 2.57E+00 | 3.45E+06 | 1.91E+00 | 2.34E+06 |
| 10 | 4.46E+00 | 5.68E+10 | 2.52E+00 | 4.55E+04 | 4.34E+00 | 6.79E+08 | 3.54E+00 | 5.13E+09 | 2.46E+00 | 4.35E+07 | 1.89E+00 | 4.52E+07 |
| 11 | −3.8E+00 | 1.28E-03 | −3.4E+00 | 7.89E-03 | −3.6E+00 | 2.36E-03 | −3.4E+00 | 4.16E-02 | −3.3E+00 | 4.26E-02 | −3.3E+00 | 4.56E-02 |
| 12 | −2.9E+67 | 7.52E+31 | −9.0E+49 | 9.76E+33 | −8.4E+42 | 4.01E+44 | −3.7E+48 | 3.13E+48 | −8.9E+49 | 4.33E+44 | −7.9E+42 | 4.33E+44 |
| 13 | 9.38E+22 | 1.87E+28 | 9.02E+42 | 1.49E+34 | 9.01E+42 | 5.66E+48 | 5.23E+42 | 3.66E+46 | 7.01E+42 | 1.35E+21 | 9.00E+47 | 4.39E+44 |
| 14 | 9.61E-02 | 1.65E-02 | 2.50E-03 | 5.84E-04 | 5.68E-04 | 4.82E-05 | 3.45E-04 | 7.82E-05 | 2.68E-02 | 7.01E-05 | 2.00E-06 | 4.50E-05 |
| 15 | 2.13E-40 | 5.69E-67 | 7.84E-27 | 9.76E-63 | 2.14E-50 | 1.22E-40 | 2.84E-09 | 1.88E-53 | 2.44E-32 | 3.99E-67 | 0.00E+00 | 0.00E+00 |
| 16 | 7.2E-112 | 1.8E-113 | 1.0E-107 | 5.6E-108 | 3.3E-111 | 2.5E-126 | 1.3E-110 | 1.2E-124 | 3.0E-117 | 2.1E-124 | 0.00E+00 | 0.00E+00 |
| 17 | 3.8E-114 | 3.5E-116 | 3.5E-156 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 18 | 1.1E-132 | 6.7E-148 | 5.2E-32 | 1.25E-52 | 7.6E-175 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 1.4E-211 | 6.44E-45 | 6.4E-209 | 0.00E+00 |
| 19 | 9.59E+01 | 1.45E-15 | 9.8E-01 | 3.13E-15 | 9.67E-01 | 4.98E-15 | 9.56E-01 | 6.45E-15 | 9.00E-01 | 3.23E-15 | 9.00E-01 | 4.88E-16 |
| 20 | 4.97E-08 | 1.87E-01 | 2.8E+00 | 1.35E-02 | 0.00E+00 | 3.27E-13 | 2.34E+01 | 4.57E-02 | 6.74E-03 | 1.01E-07 | 0.00E+00 | 0.00E+00 |
| 21 | 3.21E-08 | 9.03E-16 | 8.91E-07 | 1.67E-06 | 2.71E-05 | 8.53E-06 | 6.26E-04 | 8.73E-05 | 1.5E-281 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 22 | 5.73E-05 | 3.22E-03 | 1.76E-04 | 4.07E-03 | 9.96E-02 | 1.12E-07 | 7.76E-07 | 1.72E-04 | 1.79E-10 | 4.07E-05 | 0.00E+00 | 0.00E+00 |
| 23 | −6.8E-01 | 4.54E-02 | −5.7E-01 | 4.09E-02 | −7.89E-01 | 2.39E-02 | −5.64E-01 | 3.43E-02 | −9.9E-02 | 5.67E-05 | −9.9E-02 | 8.90E-04 |
| 24 | 4.25E-05 | 0.00E+00 | 2.68E-04 | 0.00E+00 | 8.70E-04 | 0.00E+00 | 2.35E-06 | 0.00E+00 | 9.01E-03 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 25 | −2.1E+00 | 3.91E-22 | −1.52E+00 | 1.17E-06 | −1.9E+00 | 1.22E-07 | −1.3E+00 | 8.13E-05 | −1.6E+00 | 3.42E-07 | −1.0E+00 | 1.24E-07 |
| 26 | 3.20E-03 | 1.26E-06 | 2.67E-05 | 5.17E-17 | 1.24E-05 | 4.44E-16 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
In the results, Problem denoted by (prob.), the average fitness value (AFV), and the corresponding standard deviation (STD) for each method.
From Table 4, it is evident that the minimum average fitness value for the set of unimodal problems (4, 5, 8, 15, 16) is zero. Only the EHGSO algorithm was able to attain this minimum average fitness value of zero for all the unimodal problems in the set. Moreover, HGSO, BCS, and SSA could also achieve the minimum average fitness value of zero for the set of problems (4, 15), (4), and (4, 16) respectively. Consequently, EHGSO proves to be the best method among all the considered algorithms for unimodal problems. For all the multimodal set of problems (1, 2, 3, 9, 10, 14, 17, 18, 20, 24, 25, 26) the EHGSO algorithm attains the best average fitness value except for problem (18). Moreover, HGSO, BCS, and SSA achieve the best average fitness value for the set of problems (26), (18), and (20) respectively. Regarding the fixed-dimensional multimodal set of problems (6, 7, 11, 12, 13, 19, 21, 22, 23), EHGSO once again demonstrates the best average fitness value for all BMPs. For these problems, HGSO, BCS, and SSA also achieve the best average fitness value for the set of problems (6, 19, 23), (6) and (6) respectively. The proposed EHGSO achieves the highest average fitness value in the major benchmark problems of different modularity. Therefore, depicted average fitness value of the EHGSO on different benchmark problems validates its superior balance between exploration and exploitation. Consequently, these experiments affirm that EHGSO exhibits better search performance with a higher precision value.
Performance evaluation of wPCA-FastICA based bEHGSO-FS method
The effectiveness of the wPCA-FastICA-based bEHGSO-FS method was evaluated on various classification benchmark datasets [45]. Table 5 provides details about these classification datasets, including quantity features, classes, and instances. For measuring the classification accuracy of the proposed feature selection method, a KNN classifier (K = 5) has been utilized in this study. Five binary encoded metaheuristic methods, namely bGSA [42], bGWO [34], bHGSO [41], bSSA [29], and bBCS [17] were considered for the feature selection. Therefore, the proposed bEHGSO-FS method using DTMs and without using DTMs are evaluated against bGSA-FS, bGWO-FS, bHGSO-FS, bSSA-FS, and bBCS-FS for the comparative analysis. Each method was executed 30 times to mitigate the impact of the random behaviour of metaheuristic methods. Various metrics were considered to assess performance, namely average number of selected features, accuracy value, and average computational time.
Table 5.
Description of considered UCI classification datasets [45].
| S. No. | Applied Dataset | Features | Classes | Instances |
|---|---|---|---|---|
| D1 | Mushroom | 22 | 2 | 8124 |
| D2 | Molecular-Biology | 58 | 2 | 106 |
| D3 | Soybean (L) | 35 | 19 | 307 |
| D4 | Chess (KRKPA7) | 36 | 2 | 3196 |
| D5 | BC-DS | 9 | 2 | 286 |
| D6 | Statlog-IS | 19 | 7 | 2310 |
| D7 | Lgraphy | 18 | 4 | 148 |
In the table BC-DS, IS, Lgraphy, and KRKPA7 are standing for Breast cancer dataset, Image segmentation, Lymphography and King-Rook vs. King-Pawn respectively.
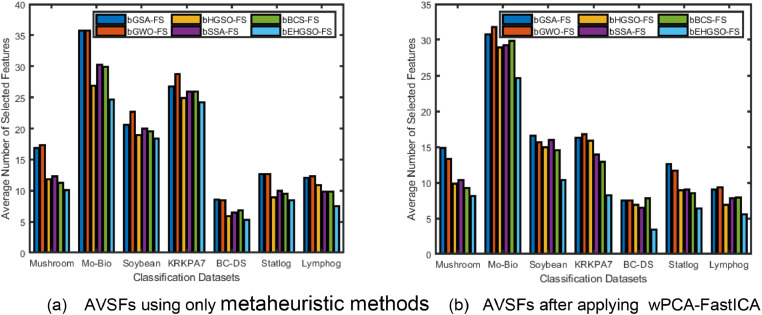
The bar chart in Fig. 2 illustrates the average number of selected features for all the methods on each dataset. Fig. 2(a) displays the average number of selected features which are selected by the considered metaheuristic-based FS methods and bEHGSO based FS method without applying the DTMs. Fig. 2(b) shows the average number of selected features for the transformed datasets using the wPCA-FastICA based metaheuristic methods. It is evident from the bar chart that the bEHGSO-FS method consistently achieves the minimum average number of selected features among all the considered FS methods for both the original and transformed datasets. This confirms the bEHGSO-FS based meta-heuristic method performs the best in terms of average number of selected features.
Fig. 2.
Bar chart (a) represents the average number of selected features (AVSFs) using considered metaheuristic methods without using DTMs (b) represents AVSFs using wPCA-FastICA and considered metaheuristic methods.
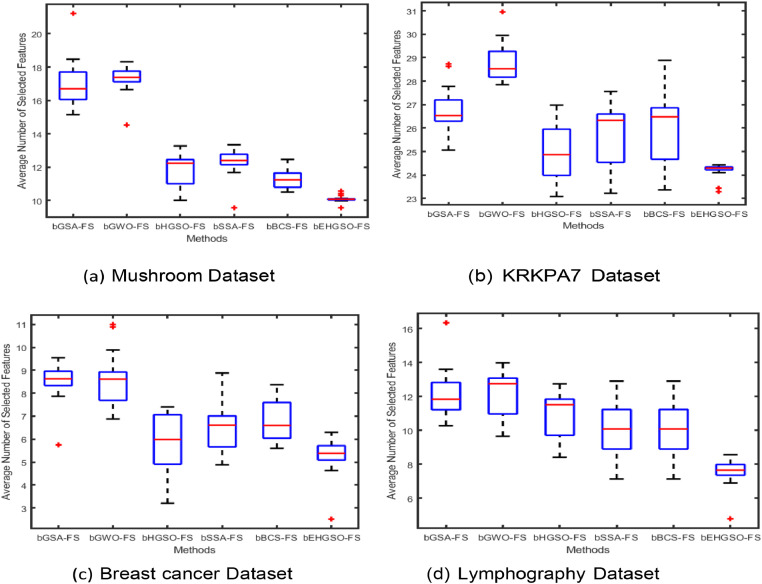
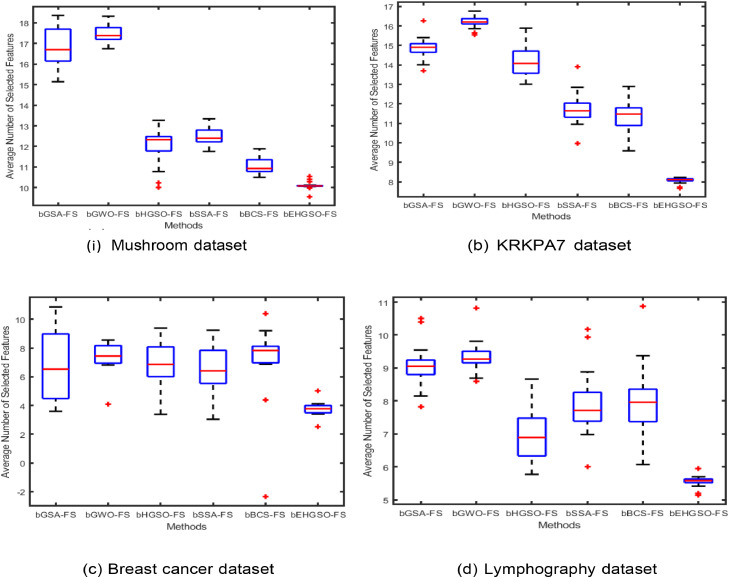
Furthermore, the Box plot graphs analysis was done to establish consistency and stability study of the approaches under consideration. Box plot graphs were generated for both the initial datasets and the PCA-FastICA transformed datasets. Fig. 3, Fig. 4 display the box plot analysis of four classification datasets, namely Mushroom, chess King-Rook vs. King-Pawn (KRKPA7), Breast cancer (BC), and Lymphography for the original dataset and PCA-FastICA transformed dataset respectively. These figures show that the proposed bEHGSO-FS method exhibits minimal variation in the transformed dataset using wPCA-FastICA, which emphasizes its superiority in minimizing average number of selected features as validated through experimental analysis.
Fig. 3.
Box Plot Graph analysis for the average number of selected features using the considered metaheuristic methods and bEHGSO in the original datasets.
Fig. 4.
Box Plot Graph analysis for average number of selected features using wPCA-FastICA based considered metaheuristic FS methods.
To see effect of considered wPCA and FastICA based transformation methods, Table 6, Table 7, Table 8, Table 9 are presented. Table 6 shows the accuracy value produced by the considered metaheuristic methods and proposed bEHGSO method. Table 7 exhibits accuracy value on transformed datasets using wPCA, while Table 8 displays accuracy value for transformed dataset using FastICA. Finally, Table 9 summarizes the accuracy results for the metaheuristic approaches based on wPCA-FastICA DTMs. From Table 6, it is evident that the bEHGSO-based FS method outperforms all other considered metaheuristic methods without the use of any DTMs. Furthermore, as observed in Tables 7 and Table 8, the bEHGSO-based DTMs exhibit superior performance compared to other considered metaheuristic methods after applying DTMs.
Table 6.
The comparative analysis of the accuracy value of original datasets and metaheuristic-based methods.
| Without FS Methods in the original Datasets | ||||||
|---|---|---|---|---|---|---|
| Dataset | bGSA | O | bHGSO | bBCS | bSSA | bEHGSO |
| Mushroom | 86.42 | 83.7 | 90.62 | 89.96 | 87.6 | 90.89 |
| Mol-Bio | 92.34 | 92.3 | 93.56 | 94.78 | 94.6 | 95.89 |
| Soybean | 90.22 | 90.3 | 91.23 | 91.15 | 91.1 | 92.4 |
| KRKPA7 | 74.28 | 73.4 | 78.13 | 77.97 | 78.1 | 78.31 |
| BC-DS | 94.11 | 93.2 | 93.44 | 94.85 | 95.4 | 96.98 |
| Statlog-IS | 89.98 | 88.3 | 90.56 | 89.45 | 89.6 | 91.68 |
| Lymphography | 95.78 | 94.7 | 96.98 | 95.69 | 96.3 | 97.29 |
| Average | 89.02 | 88 | 90.65 | 90.55 | 90.4 | 91.92 |
| With metaheuristic-based FS Methods in the original Datasets | ||||||
|---|---|---|---|---|---|---|
| Dataset | bGSA | bGWO | bHGSO | bBCS | bSSA | bEHGSO |
| Mushroom | 85.42 | 83.67 | 89.62 | 88.96 | 87.56 | 91.95 |
| Mol-Bio | 95.86 | 95.80 | 96.06 | 96.28 | 96.14 | 96.40 |
| Soybean | 91.34 | 91.50 | 93.43 | 93.36 | 92.31 | 93.79 |
| KRKPA7 | 76.98 | 75.40 | 81.09 | 81.76 | 82.56 | 82.88 |
| BC-DS | 95.71 | 94.89 | 94.74 | 94.55 | 95.98 | 98.09 |
| Statlog-IS | 92.10 | 91.45 | 93.56 | 92.67 | 93.45 | 93.68 |
| Lymphography | 96.89 | 96.79 | 97.21 | 96.23 | 96.65 | 98.39 |
| Average | 90.61 | 89.93 | 92.24 | 91.97 | 92.09 | 93.60 |
Bold values represent the best result.
Table 7.
The comparative analysis of the accuracy value for the wPCA-based metaheuristic and FastICA-based metaheuristic methods.
| Using wPCA based Metaheuristic FS methods | ||||||
|---|---|---|---|---|---|---|
| Dataset | bGSA | bGWO | bHGSO | BC-DS | bSSA | bEHGSO |
| Mushroom | 91.34 | 90.45 | 96.64 | 94.03 | 92.61 | 97.90 |
| Mol-Bio | 95.96 | 96.01 | 96.23 | 96.36 | 96.14 | 96.79 |
| Soybean | 92.34 | 91.89 | 93.89 | 93.56 | 94.75 | 94.01 |
| KRKPA7 | 77.99 | 76.21 | 81.56 | 82.76 | 82.99 | 83.34 |
| BC-DS | 95.90 | 95.34 | 95.04 | 95.98 | 95.08 | 98.69 |
| Statlog-IS | 92.38 | 91.90 | 93.89 | 92.90 | 93.64 | 94.18 |
| Lymphography | 97.39 | 96.97 | 97.29 | 96.78 | 96.98 | 98.69 |
| Average | 91.90 | 91.25 | 93.51 | 93.20 | 93.17 | 94.80 |
| Using FastICA based Metaheuristic FS methods | ||||||
|---|---|---|---|---|---|---|
| Dataset | bGSA | bGWO | bHGSO | BC-DS | bSSA | bEHGSO |
| Mushroom | 91.98 | 90.70 | 96.81 | 94.23 | 95.11 | 98.11 |
| Mol-Bio | 96.12 | 96.13 | 96.43 | 96.88 | 96.24 | 96.78 |
| Soybean | 92.87 | 92.39 | 93.98 | 93.78 | 92.89 | 94.45 |
| KRKPA7 | 78.28 | 76.34 | 81.67 | 82.88 | 83.11 | 83.56 |
| BC-DS | 96.22 | 95.67 | 96.14 | 96.12 | 95.13 | 98.72 |
| Statlog-IS | 92.56 | 92.15 | 93.99 | 93.12 | 93.78 | 94.56 |
| Lymphography | 97.54 | 97.15 | 97.34 | 96.83 | 96.99 | 98.70 |
| Average | 92.22 | 91.50 | 93.77 | 93.41 | 93.32 | 94.98 |
Bold values represent the best result.
Table 8.
The comparative analysis of the accuracy value for the wPCA-FastICA based metaheuristic methods.
| Using wPCA-FastICA based Metaheuristic FS methods | ||||||
|---|---|---|---|---|---|---|
| Dataset | bGSA | bGWO | bHGSO | bBCS | bSSA | bEHGSO |
| Mushroom | 92.56 | 90.89 | 96.90 | 94.45 | 95.23 | 98.67 |
| Mol-Bio | 96.65 | 96.34 | 96.78 | 97.65 | 96.98 | 98.45 |
| Soybean | 94.12 | 93.78 | 95.32 | 95.34 | 93.12 | 97.98 |
| KRKPA7 | 78.91 | 76.49 | 83.67 | 82.93 | 83.23 | 84.12 |
| BC-DS | 96.78 | 95.90 | 98.93 | 97.45 | 97.34 | 99.40 |
| Statlog-IS | 93.76 | 93.54 | 95.32 | 94.45 | 94.98 | 96.76 |
| Lymphography | 97.78 | 97.56 | 97.56 | 96.90 | 97.19 | 99.36 |
| Average | 92.94 | 92.07 | 94.93 | 94.17 | 94.01 | 96.39 |
Bold values represent the best result.
Table 9.
The Overall average accuracy values of different considered methods.
| Overall Average Accuracy value for all considered methods | ||||||
|---|---|---|---|---|---|---|
| Methods | bGSA | bGWO | bHGSO | bBCS | bSSA | bEHGSO |
| Without FS | 89.02 | 87.99 | 90.65 | 90.55 | 90.38 | 91.92 |
| With Metaheuristic FS | 90.61 | 89.93 | 92.24 | 91.97 | 92.09 | 93.45 |
| wPCA based Metaheuristic FS | 91.90 | 91.25 | 93.51 | 93.20 | 93.17 | 94.80 |
| FastICA based Metaheuristic FS | 92.22 | 91.50 | 93.77 | 93.41 | 93.32 | 94.98 |
| wPCA-FastICA based Metaheuristic FS | 92.94 | 92.07 | 94.93 | 94.17 | 94.01 | 96.39 |
Bold values represent the best result.
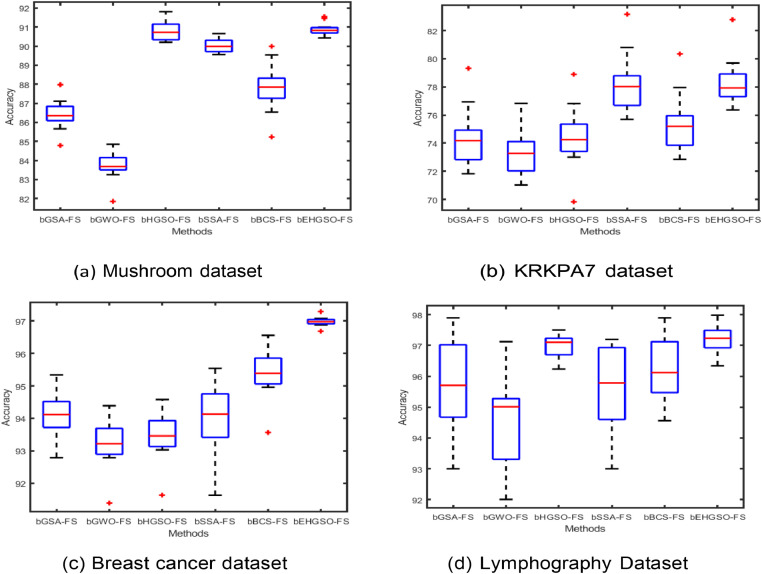
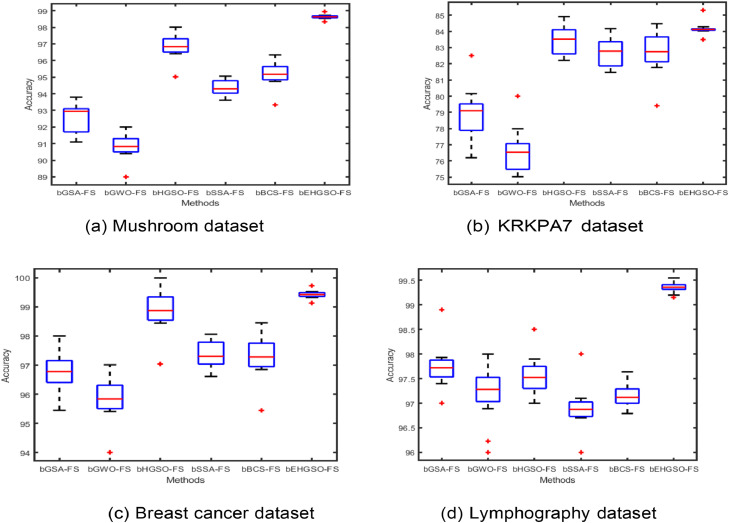
Moreover, to ensure the consistency and stability of the accuracy value metric analysis for the methodologies under consideration in the initial dataset and the wPCA-FastICA-based transformed datasets, box plot graphs were constructed. Fig. 5 displays the box plot analysis for the original datasets and the wPCA-FastICA-based transformed datasets are shown in Fig. 6. These figures reveal that the proposed bEHGSO-FS method exhibits minimal variation in the wPCA-FastICA-based transformed datasets, emphasizing its superiority in maximizing classification accuracy value as validated through experimental analysis.
Fig. 5.
Box plot graph analysis of accuracy using metaheuristic methods in the original datasets.
Fig. 6.
Box plot graph analysis of accuracy using wPCA-FastICA based metaheuristic methods in the transformed datasets.
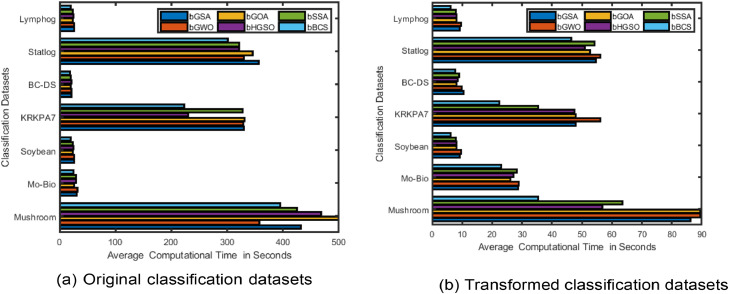
For the comparative analysis of average computational time the bar chart has bee shown in the Fig. 7. Fig. 7(a) illustrates the average computational time for the original classification datasets, while Fig. 7(b) shows the average computational time after applying PCA-FastICAs-based metaheuristic methods. From the figures, it is evident that the average computational time for the bEHGSO method is minimum for both the original datasets and the PCA-FastICAs-based transformed datasets, indicating that the bEHGSO-FS method has the lowest average computational time among all the considered methods.
Fig. 7.
Bar chart (a) represents average computational time on the original datasets (b) represents average computational time using wPCA-FastICA based considered metaheuristic FS methods in the transformed datasets.
Conclusion
In this study, a new binary exponential Henry gas solubility optimization approach was developed for choosing the best feature sets from large dimensional datasets. Three modularity levels were used to evaluate the performance of the bEHGSO on 26 benchmark problems. The bEHGSO employed wPCA and FastICA as data transformation methods to identify the best feature set. The aim of the feature selection technique was to reduce the presence of irrelevant, correlated, and higher-order dependent features while selecting pertinent, non-redundant data. To accomplish this, the method first used a hybrid data transformation technique called wPCA-FastICA to modify the dataset. The best features were then chosen using the bEHGSO-FS methodology. The performance of the wPCA-FastICA-based bEHGSO-FS approach was evaluated on seven common benchmark classification datasets. The evaluation was based on three parameters, namely average number of selected features, accuracy value, and average computational time. Comparing the wPCA-FastICA-based bEHGSO-FS approach to current metaheuristic feature selection methods indicated that it achieves the greatest classification average accuracy (96.39) along with the fewest feature subsets of all the methods studied. Both statistical and empirical evaluations indicated that the proposed wPCA-FastICA-based bEHGSO-FS approach outperforms the existing methods.
Future research endeavours might explore leveraging deep learning techniques to enhance the performance metrics of the proposed method through meticulous adjustment of the controlling parameters. Furthermore, the suggested technique may be expanded to accommodate multi-objective fitness functions, enabling testing in real-time applications.
CRediT authorship contribution statement
Nand Kishor Yadav: Conceptualization, Methodology, Software, Writing – original draft, Visualization, Investigation. Mukesh Saraswat: Supervision, Writing – review & editing.
Declaration of competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Ethics statements
Not applicable
Acknowledgements
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability
Data will be made available on request.
References
- 1.Qi Y., Su B., Lin X., Zhou H. A new feature selection method based on feature distinguishing ability and network influence. J. Biomed. Inform. 2022;128 doi: 10.1016/j.jbi.2022.104048. [DOI] [PubMed] [Google Scholar]
- 2.Venkatesh B., Anuradha J. A review of feature selection and its methods. Cybern. Inform. Technol. 2019;19(1):3–26. [Google Scholar]
- 3.Rostami O., Kaveh M. Optimal feature selection for sar image classification using biogeography-based optimization (bbo), artificial bee colony (abc) and support vector machine (svm): a combined approach of optimization and machine learning. Comput. Geosci. 2021;25:911–930. [Google Scholar]
- 4.Tang J., Alelyani S., Liu H. Feature selection for classification: a review. Data Classific.: Algorith. Appl. 2014:37. [Google Scholar]
- 5.Saraswat M., Arya K. Feature selection and classification of leukocytes using random forest. Med. Biol. Eng. Comput. 2014;52:1041–1052. doi: 10.1007/s11517-014-1200-8. [DOI] [PubMed] [Google Scholar]
- 6.Chandra B., Gupta M. An efficient statistical feature selection approach for classification of gene expression data. J. Biomed. Inform. 2011;44(4):529–535. doi: 10.1016/j.jbi.2011.01.001. [DOI] [PubMed] [Google Scholar]
- 7.Wang J., Zhou S., Yi Y., Kong J. An improved feature selection based on effective range for classification. Sci. World J. 2014;2014 doi: 10.1155/2014/972125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xue B., Zhang M., Browne W.N., Yao X. A survey on evolutionary computation approaches to feature selection. IEEE Trans. Evol. Comput. 2015;20(4):606–626. [Google Scholar]
- 9.Li S., Wu H., Wan D., Zhu J. An effective feature selection method for hyperspectral image classification based on genetic algorithm and support vector machine. Knowl. Based Syst. 2011;24(1):40–48. [Google Scholar]
- 10.Uysal A.K. An improved global feature selection scheme for text classification. Expert Syst. Appl. 2016;43:82–92. [Google Scholar]
- 11.Zhou X., et al. Feature selection for image classification based on a new ranking criterion. J. Comput. Commun. 2015;3(03):74. [Google Scholar]
- 12.Aguilera A., Pezoa R., Rodr´ıguez-Delherbe A. A novel ensemble feature selection method for pixel-level segmentation of her2 overexpression. Complex Intell. Syst. 2022;8(6):5489–5510. [Google Scholar]
- 13.Athanasios V., Doulamis N., Anastasios Doulamis, and Eftychios Protopapadakis Deep learning for computer vision: a brief review. Comput. Intell. Neurosci. 2018 doi: 10.1155/2018/7068349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Doğan G., Ergen B. A new approach based on convolutional neural network and feature selection for recognizing vehicle types. Iran J. Comput. Sci. 2023;6(2):95–105. [Google Scholar]
- 15.Chen S.-C., Huang W.-C., Hsueh M.-H., Pan C.-Y., Chang C.-H. A novel exponential-weighted method of the antlion optimization algorithm for improving the convergence rate. Processes. 2022;10(7):1413. [Google Scholar]
- 16.Omuya E.O., Okeyo G.O., Kimwele M.W. Feature selection for clas- sification using principal component analysis and information gain. Expert Syst. Appl. 2021;174 [Google Scholar]
- 17.Pandey A.C., Rajpoot D.S., Saraswat M. Feature selection method based on hybrid data transformation and binary binomial cuckoo search. J. Ambient. Intell. Humaniz. Comput. 2020;11(2):719–738. [Google Scholar]
- 18.O.H. Babatunde, L. Armstrong, J. Leng, D. Diepeveen, A genetic algorithm-based feature selection (2014).
- 19.Khan A.H., Sarkar S.S., Mali K., Sarkar R. A genetic algorithm-based feature selection approach for microstructural image classification. Exp. Tech. 2022:1–13. [Google Scholar]
- 20.Matin A., Bhuiyan R.A., Shafi S.R., Kundu A.K., Islam M.U. 2019 Joint 8th International Conference on Informatics, Electronics Vision (ICIEV) and 2019 3rd International Conference on Imaging, Vision Pattern Recognition (icIVPR) IEEE; 2019. A hybrid scheme using PCA and ICA based statistical feature for epileptic seizure recognition from EEG signal; pp. 301–306. [Google Scholar]
- 21.Ghazouani H. A genetic programming-based feature selection and fusion for facial expression recognition. Appl. Soft. Comput. 2021;103 [Google Scholar]
- 22.Du N., Zhang Z., Xiao Y., Jiang L., et al. Fast independent component analysis algorithm-based functional magnetic resonance imaging in the diagnosis of changes in brain functional areas of cerebral infarction. Contrast Media Mol. Imag. 2021:2021. doi: 10.1155/2021/5177037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chuang L.-Y., Tsai S.-W., Yang C.-H. Improved binary particle swarm optimization using catfish effect for feature selection. Expert Syst. Appl. 2011;38(10):12699–12707. [Google Scholar]
- 24.Hichem H., Elkamel M., Rafik M., Mesaaoud M.T., Ouahiba C. A new binary grasshopper optimization algorithm for feature selection problem. J. King Saud. Univ.-Comput. Inform. Sci. 2022;34(2):316–328. [Google Scholar]
- 25.Le T.M., Vo T.M., Pham T.N., Dao S.V.T. A novel wrapper– based feature selection for early diabetes prediction enhanced with a metaheuristic. IEEE Access. 2020;9:7869–7884. [Google Scholar]
- 26.Wang J., Hedar A.-R., Wang S., Ma J. Rough set and scatter search metaheuristic-based feature selection for credit scoring. Expert Syst. Appl. 2012;39(6):6123–6128. [Google Scholar]
- 27.Hashim F.A., Houssein E.H., Mabrouk M.S., Al-Atabany W., Mir- jalili S. Henry gas solubility optimization: a novel physics-based algorithm. Future Gener. Comput. Syst. 2019;101:646–667. [Google Scholar]
- 28.Vivekanandan T., Iyengar N.C.S.N. Optimal feature selection using a modified differential evolution algorithm and its effectiveness for pre- diction of heart disease. Comput. Biol. Med. 2017;90:125–136. doi: 10.1016/j.compbiomed.2017.09.011. [DOI] [PubMed] [Google Scholar]
- 29.Shekhawat S.S., Sharma H., Kumar S., Nayyar A., Qureshi B. BSSA: binary SALP swarm algorithm with hybrid data transformation for feature selection. IEEE Access. 2021;9:14867–14882. [Google Scholar]
- 30.Canayaz M. Mh-covidnet: diagnosis of covid-19 using deep neural networks and meta-heuristic-based feature selection on x-ray images. Biomed. Signal. Process. Control. 2021;64 doi: 10.1016/j.bspc.2020.102257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Meenachi L., Ramakrishnan S. Metaheuristic search-based feature selection methods for classification of cancer. Pattern Recognit. 2021;119 [Google Scholar]
- 32.Wahono R.S., Suryana N., Ahmad S. Metaheuristic optimization-based feature selection for software defect prediction. J. Softw. 2014;9(5):1324–1333. [Google Scholar]
- 33.Dey A.K., Gupta G.P., Sahu S.P. Hybrid meta-heuristic based feature selection mechanism for cyber-attack detection in iot-enabled networks. Procedia Comput. Sci. 2023;218:318–327. [Google Scholar]
- 34.Emary E., Zawbaa H.M., Hassanien A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing. 2016;172:371–381. [Google Scholar]
- 35.Wang M., Wan Y., Ye Z., Gao X., Lai X. A band selection method for airborne hyperspectral image based on chaotic binary coded gravitational search algorithm. Neurocomputing. 2018;273:57–67. [Google Scholar]
- 36.Chuang L.-Y., Chang H.-W., Tu C.-J., Yang C.-H. Improved binary pso for feature selection using gene expression data. Comput. Biol. Chem. 2008;32(1):29–38. doi: 10.1016/j.compbiolchem.2007.09.005. [DOI] [PubMed] [Google Scholar]
- 37.Joshi S.K., Bansal J.C. 2021. arXiv preprint. [Google Scholar]
- 38.Nezamabadi-Pour H. A quantum-inspired gravitational search algorithm for binary encoded optimization problems, engineering applications of. Artif. Intell. 2015;40:62–75. [Google Scholar]
- 39.Obayya M., Alhebri A., Maashi M., Salama A.S., Mustafa Hilal A., Alsaid M.I., Osman A.E., Alneil A.A. Henry gas solubility optimization algorithm-based feature extraction in dermoscopic images analysis of skin cancer. Cancers (Basel) 2023;15(7):2146. doi: 10.3390/cancers15072146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vishnoi E.S., Jain A.K. An improved henry gas solubility optimization- based feature selection approach for histological image taxonomy. Int. J. Intell. Syst. Technol. Appl. 2021;20(1):58–78. [Google Scholar]
- 41.Neggaz N., Houssein E.H., Hussain K. An efficient henry gas solubility optimization for feature selection. Expert Syst. Appl. 2020;152 [Google Scholar]
- 42.Zhu H., Huang B., Hao H. 2020 7th International Conference on Information Science and Control Engineering (ICISCE) IEEE; 2020. A new chaotic binary gravitational search algorithm and its algorithm test; pp. 65–69. [Google Scholar]
- 43.Agarwal R., Shekhawat N.S., Luhach A.K. Automated classification of soil images using chaotic henry's gas solubility optimization: smart agricultural system. Microprocess. Microsyst. 2021 [Google Scholar]
- 44.Akinola O.O., Ezugwu A.E., Agushaka J.O., Zitar R.A., Abualigah L. Multiclass feature selection with metaheuristic optimization algorithms: a review. Neural Comput. Appl. 2022;34(22):19751–19790. doi: 10.1007/s00521-022-07705-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.D. Dua, C. Graff, UCI machine learning repository (2017). http://archive.ics.uci.edu/ml
- 46.V.P. Rathi, S. Palani, Brain tumor MRI image classification with feature selection and extraction using linear discriminant analysis, arXiv preprint arXiv:1208.2128 (2012).
- 47.Chattopadhyay A.K., Mondal S., Biswas A. Independent component analysis and clustering for pollution data. Environ. Ecol. Stat. 2015;22:33–43. [Google Scholar]
- 48.Spurek P., T J., Struski U. Fast independent component analysis algorithm with a simple closed-form solution. Knowl. Syst. 2018;161:26–34. [Google Scholar]
- 49.Shah-Hosseini H. Principal components analysis by the galaxy-based search algorithm: a novel metaheuristic for continuous optimisation. Int. J. Comput. Sci. Eng. 2011;6(1–2):132–140. [Google Scholar]
- 50.Yao F., Coquery J., Lˆe Cao K.-A. Independent principal component analysis for biologically meaningful dimension reduction of large biological data sets. BMC Bioinformatics. 2012;13:1–15. doi: 10.1186/1471-2105-13-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Reza M.S., Ma J. 2016 IEEE 13th International Conference on Signal Process- ing (ICSP) IEEE; 2016. Ica and PCA integrated feature extraction for classification; pp. 1083–1088. [Google Scholar]
- 52.Kim S.B., Rattakorn P. Unsupervised feature selection using weighted principal components. Expert Syst. Appl. 2011;38(5):5704–5710. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.