Relating visual and pictorial space: Integration of binocular disparity and motion parallax

Abstract

Traditionally, perceptual spaces are defined by the medium through which the visual environment is conveyed (e.g., in a physical environment, through a picture, or on a screen). This approach overlooks the distinct contributions of different types of visual information, such as binocular disparity and motion parallax, that transform different visual environments to yield different perceptual spaces. The current study proposes a new approach to describe different perceptual spaces based on different visual information. A geometrical model was developed to delineate the transformations imposed by binocular disparity and motion parallax, including (a) a relief depth scaling along the observer's line of sight and (b) pictorial distortions that rotate the entire perceptual space, as well as the invariant properties after these transformations, including distance, three-dimensional shape, and allocentric direction. The model was fitted to the behavioral results from two experiments, wherein the participants rotated a human figure to point at different targets in virtual reality. The pointer was displayed on a virtual frame that could differentially manipulate the availability of binocular disparity and motion parallax. The model fitted the behavioral results well, and model comparisons validated the relief scaling in the form of depth expansion and the pictorial distortions in the form of an isotropic rotation. Fitted parameters showed that binocular disparity renders distance invariant but also introduces relief depth expansion to three-dimensional objects, whereas motion parallax keeps allocentric direction invariant. We discuss the implications of the mediating effects of binocular disparity and motion parallax when connecting different perceptual spaces.

Introduction

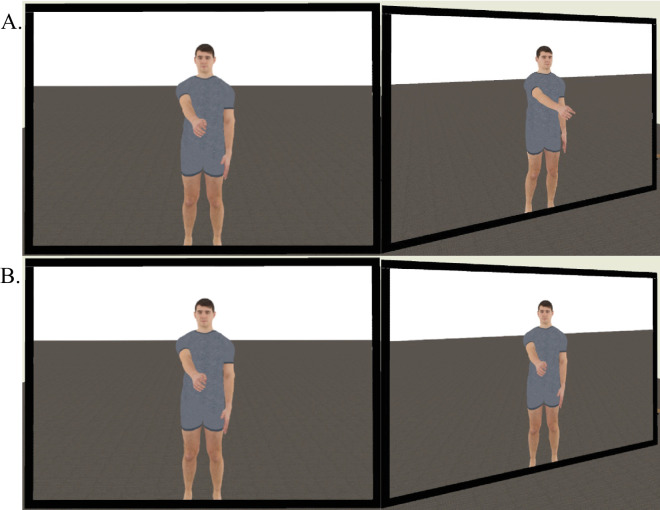
The visual experience of looking at an object or a person in the physical environment is different from that of looking at the image of the object or person. Figure 1 demonstrates this distinction (see also Koenderink, van Doorn, Pinna, & Pepperell, 2016). In Figure 1A, the observer sees a three-dimensional (3D) person pointing forward. As the observer shifts from a frontal to an oblique view, the person is still perceived to be pointing in the original direction. In contrast, Figure 1B shows the image of the same pointer. While the image appears identical to the 3D person when viewed head-on, as the observer moves to an oblique angle, the image itself remains unchanged, and the pointer continues to be perceived as pointing directly at the observer. This effect is also famously illustrated in paintings such as the Mona Lisa, where her gaze always follows the spectator (Hecht, Boyarskaya, & Kitaoka, 2014; Rogers, Lunsford, Strother, & Kubovy, 2003).

Figure 1.

An illustration of the effect of changing the observer's vantage point on looking at (A) a person and (B) the image of the person.

Conceptually, these unique perceptual experiences can be categorized using different perceptual spaces. Visual space emerges from the visual experience associated with “open[ing] one's eye in broad daylight” (Koenderink & van Doorn, 2012, p. 1213), which can be construed as seeing in the physical, unmediated environment. Pictorial space, on the other hand, corresponds to “looking into” a picture or image, where the observer experiences the depicted 3D content of the picture, instead of the two-dimensional (2D) surface on which the pictorial content is depicted (Koenderink & van Doorn, 2003). Researchers have suggested that visual and pictorial spaces are qualitatively different (Koenderink & van Doorn, 2003; Koenderink & van Doorn, 2012; Linton, 2017; Linton, 2023; Vishwanath, 2014; Vishwanath, 2023). According to Koenderink and van Doorn (2012), this qualitative difference emerges because visual space is perspectival while pictorial space is not. In this context, being perspectival means that the perceptual experience depends on the observer's instantaneous position relative to what is being observed (see Natsoulas, 1990). In the physical environment, the eye receives optical stimulation from a particular vantage point. As the observer moves, the optical stimulation received by the eye also changes, reflecting the evolving spatiotemporal relationship between the vantage point and the environment (Figure 1A). In contrast, the depicted scene on a static picture bears no immediate relation to the observer's vantage point (i.e., the eye is not in pictorial space; Koenderink & van Doorn, 2008; Wagemans, van Doorn, & Koenderink, 2011). As such, regardless of the observer's location, the pictorial space remains constant (Figure 1B).

Visual and pictorial spaces have been traditionally considered qualitatively different, and as a result, inquiries have been primarily focused on delineating their respective geometrical properties (e.g., for visual space, see Cuijpers, Kappers, & Koenderink, 2000; Foley, Ribeiro-Filho, & Silva, 2004; Koenderink & van Doorn, 2008; for pictorial space, see Farber & Rosinski, 1978; Wagemans et al., 2011; Koenderink & van Doorn, 2003; Vishwanath, Girshick, & Banks, 2005). While this distinction was straightforward when comparing visual perception in the physical environment with that of a 2D image, advances in modern technology have increasingly obscured this difference. Notably, head-mounted display (HMD)–based virtual reality (VR) presents visual environments via 2D digital displays, a feature normally associated with pictorial space. However, through stereoscopic displays and head-tracking, the HMD also presents unique views to different eyes and updates the rendered content based on the observer's real-time location in the virtual environment. These features, in turn, render visual perception in VR perspectival, a requirement for visual space. Consequently, it is difficult to unequivocally argue whether the perceptual space associated with VR is visual or pictorial space solely based on how VR's visual environment is conveyed.

Exocentric pointing

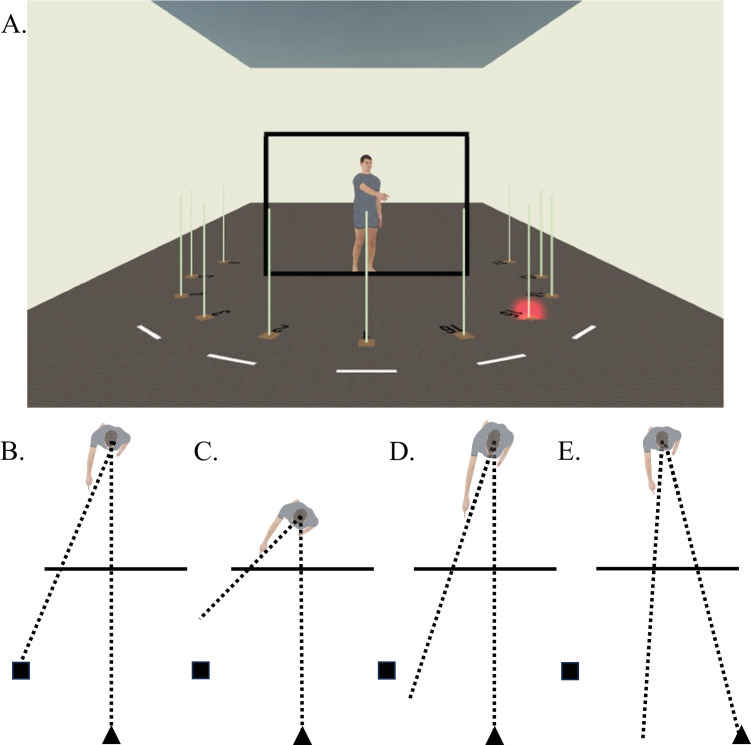
Building on the complexities introduced by modern technology, we sought in an earlier study to move beyond the traditional distinctions between visual and pictorial space by investigating their spatial connection in terms of different spatial properties, including distance, direction, and 3D shape (Wang & Troje, 2023; see also Wijntjes, 2014). We used HMD-based VR to present a virtual environment in which the observers stood in front of a picture frame surrounded by a series of targets (Figure 2A). The observers were asked to perform an exocentric pointing task, where they would need to adjust the orientation of a pointer displayed on the frame so that he is pointing directly at the target with a blinking light. This task requires the observer to utilize different perceived spatial properties of the pointer from a specific vantage point (Figures 2B–E).

Figure 2.

(A) Illustration of the virtual environment for the exocentric pointing task used in both Wang and Troje (2023) and the present study. (B–E) Illustrations of the exocentric pointing task, where the observer (triangle) adjusts the pointer to a specific target (square). (B) The observer accurately perceives the pointer's distance and his 3D shape in visual space, resulting in the pointer pointing directly at the target. However, if the observer (C) underestimates the pointer's distance, (D) perceives the pointer as expanded in depth, or (E) is at an oblique viewing angle, angular deviations occur between the pointer's pointing direction and the target.

Binocular disparity and motion parallax

Given the various spatial properties required to perform the task, it is important to understand how different types of visual information specify these properties. We primarily focused on binocular disparity and motion parallax. Binocular disparity arises from the lateral separation of the two eyes, resulting in slightly different optic array picked up by each eye. In a natural viewing environment, two eyes rotate to fixate on an object (a process called vergence). The retinal images corresponding to the fixation point coincide in the two eyes, yielding zero disparity. Relative to the fixation point, other points in the environment have nonzero disparity, and the magnitude of the disparity is modulated by the points’ distance relative to the fixation point (Backus, Banks, Van Ee, & Crowell, 1999; Banks, Hooge, & Backus, 2001). Therefore, when combined with oculomotor information (e.g., vergence angle) and the observer's interpupillary distance (IPD), binocular disparity can be an effective source of distance information (Cutting & Vishton, 1995; Renner, Velichkovsky, & Helmert, 2013). Moreover, studies have also suggested that binocular disparity may elicit an unknown relief depth scaling along the observer's line of sight, rendering the perceived 3D object to be either compressed or expanded in depth (Todd, Oomes, Koenderink, & Kappers, 2001; Wang, Lind, & Bingham, 2018; Wang, Lind, & Bingham, 2020a; Wang, Lind, & Bingham, 2020b; Wang, Lind, & Bingham, 2020c). Crucially, this relief scaling only affects the perceived 3D shape of the object but not its perceived distance (Bingham, 2005; Bingham, Crowell, & Todd, 2004).

On the other hand, motion parallax emerges from observer motion: As the observer moves, the optic array picked up by the observer also changes, reflecting the observer's spatial relationship with the surrounding environment. As the distance between the observer and a point in the environment increases, the magnitude of the optical motion decreases (Nakayama & Loomis, 1974), and, therefore, motion parallax could also be a source of depth information (Ono, Rogers, Ohmi, & Ono, 1988; Rogers et al., 2009; Rogers & Graham, 1979; Rogers & Graham, 1982). Nevertheless, it is worth noting that motion parallax may only be effective in specifying relative depth since additional, extraretinal information (e.g., the velocity of observer motion) is needed to obtain absolute depth (Ono et al., 1988). Importantly, because motion parallax allows the view of the visual environment to be dynamically updated based on the observer's vantage point inside the visual environment, it also provides allocentric direction information, that is, the position or direction of an object in space relative to external references, independent of the observer's position. Without motion parallax, the observer's view of the visual environment remains static, unresponsive to the observer's changing vantage point, as in looking into a picture. This would result in allocentric directions varying based on the spectator's position (Figure 1B). However, if the view of the visual environment systematically changes as the spectator moves, the allocentric direction would remain invariant relative to the environment regardless of the observer's location (Figure 1A). In this regard, motion parallax helps to situate the observer inside the visual environment and directionally connects the observer with objects in the environment.

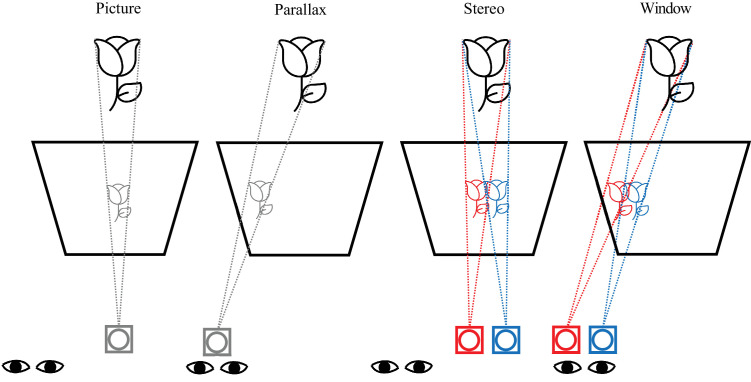
To manipulate binocular disparity and motion parallax, our previous study presented the pointer using a picture frame called the Alberti Frame (Troje, 2023a; Wang & Troje, 2023), named after Leon Batista Alberti, who first presented principles of perspective projection during the Renaissance period (Alberti, 1967). Figure 3 offers a detailed description of the Alberti Frame. The Alberti Frame could present the pointer as a picture, where the image was generated based on a single, static center of projection (CoP) that renders zero binocular disparity and no motion parallax (picture condition). Alternatively, the frame could also present the pointer as if the observer is looking through a window by rendering the content via a pair of stereoscopic cameras that follows the observer's real-time location, which, as a result, provides binocular disparity and motion parallax information of the pointer and his surrounding environment (window condition). Two additional viewing conditions were also used, including one in which the depicted pointer was constantly updated based on the observers’ vantage point, but it contained zero binocular disparity (parallax condition), and the other in which the pointer was depicted using nonzero binocular disparity but rendered from a static viewpoint (stereo condition).

Figure 3.

An illustration of the four modes of the Alberti Frame. The isosceles trapezoids represent the Alberti Frame, and the gray/red/blue squares with a circle represent the virtual cameras. The black rose is in the visual environment captured by the virtual camera(s), which uses perspective projection to present the image(s) of the rose on the frame based on the camera's center of projection. The display mode of the frame is dictated by the behaviors of the camera(s) in relation to the observer (a pair of eyes). Picture mode: The depicted scene is captured by a single camera at a fixed location. The depth of the depicted visual environment is only conveyed through pictorial information (e.g., linear perspective). The visual experience is akin to looking at a picture. The resulting perceptual space is not perspectival and is considered pictorial space. Note that even under picture mode, the observer still viewed the display biocularly. Window mode: The depicted scene is captured by a pair of stereoscopic cameras that follow the observer's real-time location, where the image from each camera is presented to its corresponding eyes. The resulting perceptual space is conveyed through binocular disparity and motion parallax and is perspectival in nature. As a result, the observer can obtain different views of the depicted scene, and the visual experience is akin to looking through an empty window frame or a portal. Parallax mode: There is one camera placed at the observer's cyclopean eye that follows the observer's real-time location. The depicted scene provides motion parallax but not binocular disparity. Stereo mode: There is a pair of stereoscopic cameras at a fixed location. The depicted scene provides binocular disparity but not motion parallax. Note: An offset to the camera(s) and the observer's eyes was introduced in the Window and Parallax modes for clarity, while in practice, the locations of the camera(s) and the observer's eyes coincide.

Relating visual and pictorial space

In a series of two experiments, Wang and Troje (2023) showed that while the observers struggled to accurately relate the pointer in pictorial space to targets in visual space, the inclusion of binocular disparity and motion parallax helped to specify the necessary spatial properties and mitigate this issue. Experiment 1 focused on the role of binocular disparity in specifying distance and 3D shape by varying the pointer's location relative to the targets. To control for potential perturbations to allocentric direction due to pictorial distortions, the observers stood at the same location as the Alberti Frame's camera(s) so that their vantage point always coincided with the frame's CoP. A trigonometry-based model was developed that uses the pointer's adjusted pointing angle to derive the pointer's perceived distance and 3D shape, conceptualized as a relief scaling factor along the observer's line of sight. Model fitting revealed that the perceived distance under the window and stereo conditions was accurate, whereas there was a noticeable distance underestimation in the picture and parallax conditions. Moreover, the results also showed a relief depth expansion to the perceived pointer in the window and stereo conditions.

Experiment 2 examined allocentric direction by varying the observer's location around the Alberti Frame while fixing the pointer's location. In the picture and stereo conditions, because the frame's CoP remains at a fixed location, changing the observer's vantage would result in pictorial distortions, including magnification/minification and/or shearing of the perceived pictorial content (Farber & Rosinski, 1978; Sedgwick, 1991). The shearing component of the pictorial distortions is the basis of the Mona Lisa effect discussed earlier (Hecht et al., 2014; Maruyama, Endo, & Sakurai, 1985; Rogers et al., 2003), which also applies to stereoscopic displays in the absence of motion parallax (Gao, Hwang, Zhai, & Peli, 2018; Woods, Docherty, & Koch, 1993). By evaluating the angular deviations between the target and pointing angles, we found that the perceived orientation of the pointer remained invariant regardless of the observer's location in the window and parallax conditions but not in the picture or stereo conditions. Although we did not apply the geometrical model from Experiment 1 to this experiment, the results of the window and stereo conditions still demonstrated the pattern that one would expect from relief depth scaling.

A surprising finding of Experiment 2 is that the perceptual distortion observed in the picture and stereo conditions failed to conform to the pictorial distortions that other studies have suggested (Cutting, 1988; Gournerie, 1859; Rosinski, Mulholland, Degelman, & Farber, 1980). Conventionally, the shearing component of the pictorial distortions is contingent upon the pictorial content's orientation relative to the image plane. If the content is perpendicular to the image plane, shearing would render the perceived content to always follow the observer's vantage point, resulting in maximum perceptual distortion. However, if the pictorial content is parallel to the image plane, the orientation of the perceived content would remain constant, always parallel to the image plane regardless of the location of the observer's vantage point. Goldstein (1979) and Goldstein (1987) called this contrast the differential rotation effect (see also Todorović, 2005; Todorović, 2008). However, our results revealed an isotropic rotation to the entire pictorial space, where the perceived direction of the pointer is uniformly rotated by an amount proportional to the observers’ viewing angle. Importantly, the magnitude of this isotropic rotation differs for different viewing conditions. While the window condition yielded almost zero distortion, the picture and stereo conditions produced the highest rotation of around −0.8 times the viewing angle. In this context, the negative gain indicates that the perceived orientation of the pictorial content is uniformly rotated in the same direction as the observer's change in viewing angle: If the observer moves clockwise, the perceived pointer will also rotate clockwise around the center of the frame. In other words, this negative gain effectively renders the perceived pointer to always follow the observer, as in the Mona Lisa effect. More interestingly, for the parallax condition, the rotation was around 0.2 times the viewing angle, suggesting that the pictorial content was also uniformly rotated based on the observer's vantage point but in the opposite direction as the observer's change in viewing angle. In other words, if the observer were to move in a clockwise direction, the perceived pointer would move in a counterclockwise direction. This effectively yields a faster optical motion from motion parallax, which was also observed in an earlier study (Wang, Thaler, Eftekharifar, Bebko, & Troje, 2020).

The geometry of perceptual spaces

Findings from Wang and Troje (2023) suggest that visual and pictorial space may not be categorically different as many thought. Instead, transitioning one from the other may simply entail introducing different types of visual information to specify different spatial properties of the visual environment. This idea resonates with a classical framework for studying human visual perception that leverages the geometrical comparison between a 3D visual environment and the resulting 3D percept of the environment (Koenderink & van Doorn, 2008; Todd, Oomes, Koenderink, & Kappers, 1999):

$$\begin{array}{c}\hfill \Psi =f\left(\Phi \right)\end{array}$$

where properties of a visual environment (Φ) are mapped onto a perceptual space (Ψ) over the transformation f(Φ). Following Felix Klein's Erlangen Programm (Klein, 1893), the geometry of perceptual space can be specified by properties of the visual environment that remain invariant after a certain set of transformations. Therefore, by identifying the group of transformations that leave certain spatial properties unchanged, one can systematically classify and study different perceptual spaces, such as visual and pictorial space. For instance, Euclidean geometry entails rigid motion, such as rotations, reflections, and translations, that preserves parallelism of lines, collinearity of points, distance, and angle. Euclidean geometry underlies the structure of the physical environment and is the most constrained type of geometry as it maintains the exact properties of shapes and figures. In contrast, affine geometry focuses on properties that remain invariant under affine transformations, which include linear transformations (e.g., scaling and shearing) and translations. Affine geometry is less strict than Euclidean geometry, only preserving properties such as parallelism, collinearity, and ratios of segment lengths along parallel lines, whereas properties such as distance and angle can vary. Pictorial space can be described using affine geometry, where distance is weakly specified and changing the observer's vantage point perturbs allocentric direction (i.e., angles).

Given the above framework, we propose that perceptual spaces should be categorized based on the specific visual information available within a given visual environment, instead of their corresponding visual environments. Then, following Ψ = f(Φ), the characteristics of a perceptual space Ψ can be described using the invariant properties after the transformation f(Φ) associated with each type of visual information. Following this approach, pictorial space can be defined as the perceptual space resulting from visual information derived from perspective projection through a fixed CoP in the visual environment, such as linear perspective, relative size, and occlusion. Crucially, the visual information that underlies pictorial space is independent of the observer's vantage point (i.e., there is no motion parallax), resulting in a disconnect between the observer and the depicted visual environment. Therefore, pictorial space is not perspectival, and the spatial relationship between the observer and the depicted visual environment is undetermined except when the observer's vantage point coincides with the CoP. In contrast, visual space entails additional types of visual information (i.e., binocular disparity and motion parallax) that enable the observer to be spatially connected with the visual environment and is perspectival in nature.

With this updated approach, we can reinterpret findings from Wang and Troje (2023) to categorize different perceptual spaces using binocular disparity and motion parallax. Specifically, the transformations driven by binocular disparity preserve distance while scaling the 3D object along the observer's line of sight in the resulting perceptual space. In comparison, the transformations associated with motion parallax maintain allocentric direction but do not preserve distance in the resulting perceptual space. Crucially, pictorial space can transform into visual space through binocular disparity and motion parallax and their respective transformations.

Extending this line of inquiry, the current study aims to achieve two primary objectives. First, we present a geometrical model that describes the transformations underlying binocular disparity and motion parallax. As an adaptation of the trigonometry-based model in Experiment 1 of Wang and Troje (2023), this model incorporates a series of linear transformations specific to each type of visual information (see “An updated model” section). Unlike the original, the new model introduces an additional component that accounts for the transformation imposed by motion parallax, capturing how the discrepancy between the display's CoP and the observer's vantage point influences perceived allocentric direction. For initial validation, we fitted the model to the results of Experiment 2 of Wang and Troje (2023). Using this reformulated model, the second objective is to examine the interactions between binocular disparity and motion parallax. Previous experiments have independently manipulated the pointer's distance and the observer's vantage point, highlighting the distinct contributions of binocular disparity and motion parallax in specifying distance, 3D shape, and allocentric direction. In the “Behavioral experiment” section, we present a new experiment that simultaneously manipulated the pointer's distance and the observer's vantage point to assess whether changes in the observer's vantage point affect binocular disparity's effectiveness in specifying distance and whether changes in the pointer's distance impact motion parallax's effectiveness in specifying direction. The results from the model fitting underscore the model's robustness, providing a more comprehensive account of how binocular disparity and motion parallax transform the visual environment and establish connections between different perceptual spaces.

An updated model

Model description

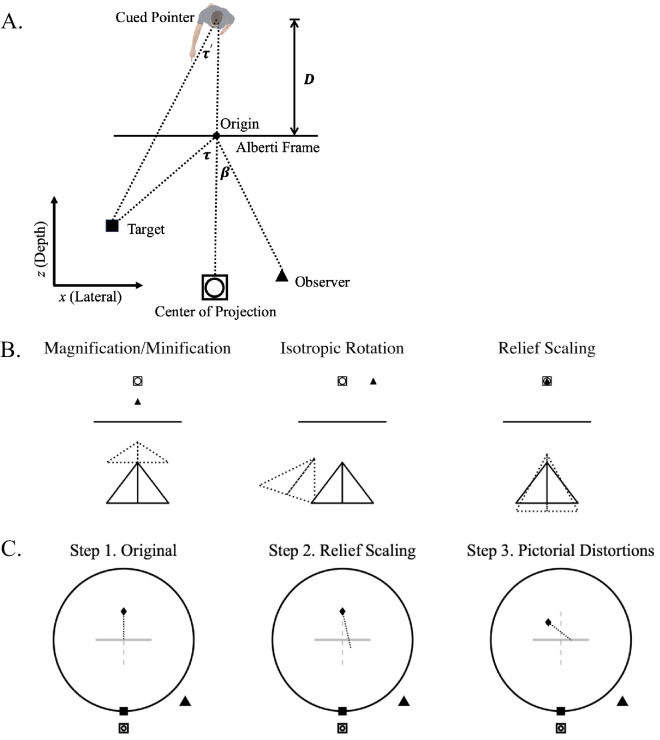
The updated model uses a series of linear transformations to describe how spatial properties of the visual environment are mapped to yield the adjusted pointer direction in an exocentric pointing task (Figure 4A). The task requires the observer to rotate the pointer such that the pointer is perceived to be pointing at the target (see Figure 2). The pointer is cued at a distance D from the Alberti Frame. The observer's vantage point is defined as the viewing angle β and the target location is defined using target angle τ, both relative to the Alberti Frame's normal. The adjusted target angle τ′ denotes the pointer's orientation relative to the Albert Frame's normal direction when he is directly pointing at the target. The distinction between target angle τ and adjusted target angle τ′ is due to the offset between the pointer's location to the center of the Alberti Frame. The task measures the pointer's adjusted pointing direction $\widehat{\alpha }$. The model applies different transformations to the spatial properties of the visual environment (i.e., target angle τ, viewing angle β, and pointer's cued distance d) to derive the pointer's adjusted pointing direction $\widehat{\alpha }$. There are two key transformations: (a) the pictorial distortions resulting from the displacement between the observer's vantage point and the image's CoP and (b) the relief depth scaling.

Figure 4.

(A) An illustration of the model environment as a 2D xz-plane, where the x-axis is parallel and the z-axis is perpendicular to the plane of the Alberti Frame, and the origin is centered at the Alberti Frame. See text for details. (B) Illustrations of the effects of magnification/minification (perpendicular displacement; Equation 3 with ω = 1), isotropic rotation (lateral displacement; Equation 4 with ω = 1), and relief scaling on the perceived object (dashed triangles; Equation 5 with C = 1.4). The solid triangles represent the observer's vantage point, whereas open squares and circles represent the image's center of projection. (C) A step-by-step illustration of the linear transformations. Step 1: In the original visual environment, the pointer (filled diamond) is cued behind the Alberti Frame (gray horizontal line) and pointing at the 0° target (filled square). Step 2: Because of relief scaling, the pointer's perceived dimensions are expanded along the observer's (filled triangle) line of sight, which slightly perturbs the pointer's perceived pointing direction. Step 3: The discrepancy between the observer's vantage point (filled triangle) and the image's center of projection (open square and circle) leads to pictorial distortions, which rotate the entire perceptual space of the pointer around the center of the frame by an amount proportional to the observer's viewing angle. Note: (1) because the pointer is not perceived to be at the center of the frame, its perceived location is also rotated around the frame, and (2) the transformed pointing direction does not exactly coincide with the observer's location due to the relief scaling in Step 2.

For the pictorial distortions, two relevant transformations are magnification/minification, λ, and isotropic rotation, σ. Let the image's $\mathrm{CoP}=\left[\begin{array}{c}0\\ Co{P}_z\end{array}\right]$ and the observer location $O=\left[\begin{array}{c}{O}_x\\ O_z\end{array}\right]$. If the displacement between the CoP and the observer location is perpendicular to the image plane, then magnification/minification of the perceived pictorial content would occur (Figure 4B), which can be expressed as (for proof, see Farber & Rosinski, 1978; Sedgwick, 1991):

$$\begin{array}{c}\hfill \lambda =\left[\begin{array}{cc}\hfill 1& \hfill 0\\ \hfill 0& \hfill \frac{O_z}{Co{P}_z}\end{array}\right]\end{array}$$ (1)

Another type of displacement between the CoP and the vantage point is in a direction parallel to the image plane. Traditionally, this type of displacement would result in shearing (Farber & Rosinski, 1978):

$$\begin{array}{c}\hfill \sigma =\left[\begin{array}{cc}\hfill 1& \hfill \frac{O_x}{Co{P}_z}\\ \hfill 0& \hfill 1\end{array}\right]\end{array}$$ (2)

However, as pointed out earlier, behavioral results indicated an isotropic rotation to the entire pictorial space. Therefore, with β as the viewing angle, we define the isotropic rotation as a 2D rotation matrix (Figure 4B):

$$\begin{array}{c}\hfill \sigma =\left[\begin{array}{cc}\hfill cos\beta & \hfill -sin\beta \\ \hfill sin\beta & \hfill cos\beta \end{array}\right]\end{array}$$

The magnification/minification and the isotropic rotation are deterministic to the extent that their effects on the resulting perceptual space can be uniquely determined given the observer's vantage point and the image's CoP. However, our previous study (see Figure 6C of Wang & Troje, 2023) suggested that the relationship between the viewing angle and the magnitude of the isotropic rotation is not scaled by a factor of 1. For instance, for the picture condition, a viewing angle of 45° would lead to a 36° isotropic rotation to the pictorial space, scaled at a factor of approximately 0.8. This could be attributed to the inconsistencies across different visual information in different visual conditions. To capture this effect, we introduced an additional variable, pictorial distortion strength ω:

$$\begin{array}{c}\hfill \lambda =\left[\begin{array}{cc}\hfill 1& \hfill 0\\ \hfill 0& \hfill \omega ·\left(\frac{O_y}{Co{P}_y}-1\right)+1\end{array}\right]\end{array}$$ (3)

$$\begin{array}{c}\hfill \sigma =\left[\begin{array}{cc}\hfill cos\left(\omega ·\beta \right)& \hfill -sin\left(\omega ·\beta \right)\\ \hfill sin\left(\omega ·\beta \right)& \hfill cos\left(\omega ·\beta \right)\end{array}\right]\end{array}$$ (4)

When ω = 0, λ and σ return the identity matrix, indicating a lack of pictorial distortions. When ω = 1, the amount of pictorial distortions can be strictly predicted by the difference between the observer's vantage point and the CoP. Importantly, when ω is neither 0 nor 1, the magnitude of the pictorial distortions is weaker than what the perceptual geometry would predict.

Figure 6.

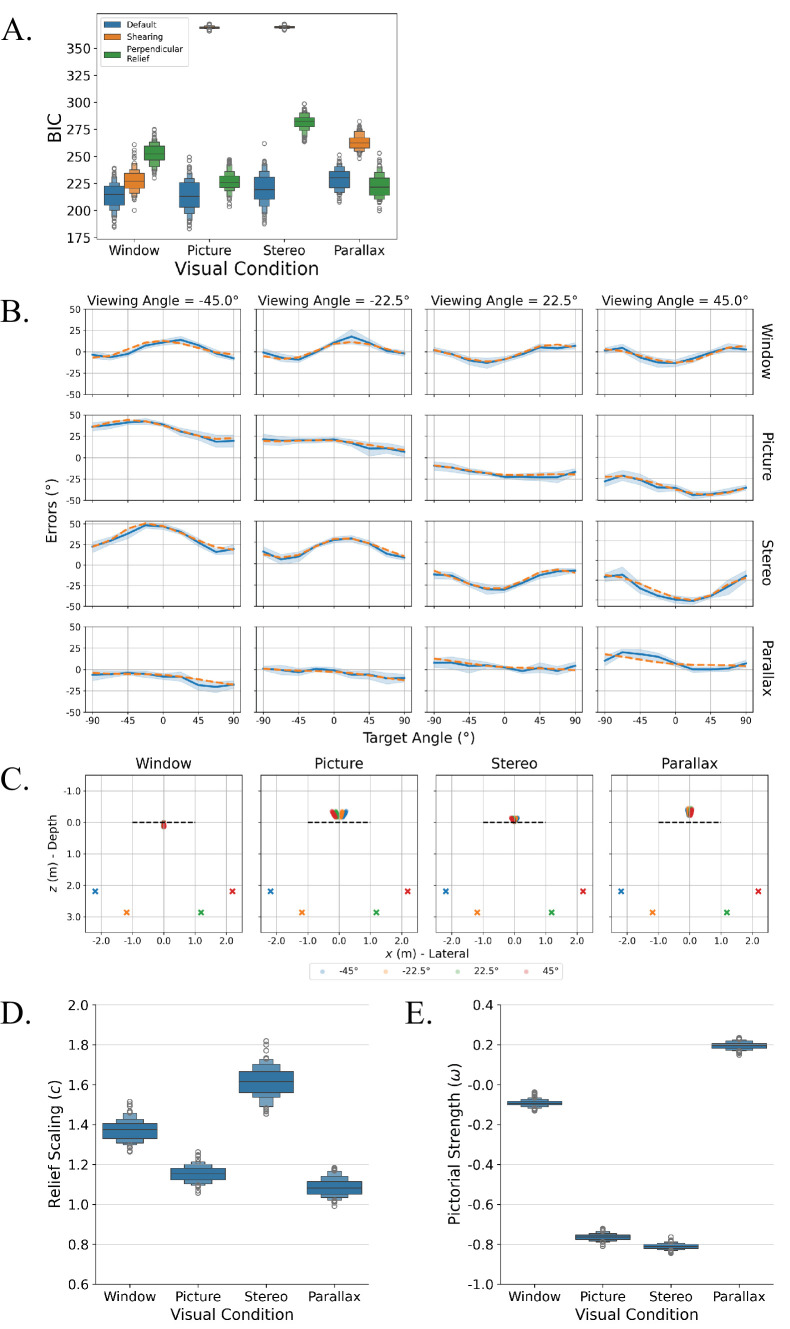
(A) BIC scores for the default (blue), shearing (orange), and perpendicular relief (green) versions of the updated geometrical model for different visual conditions. The model is considered more appropriate for fitting the data when it has the lowest BIC score. (B) Comparisons between behavioral and model prediction results. The blue solid lines represent the mean errors between set and target angle (behavioral results), whereas the orange dashed lines represent deviations between predicted set and target angle (model predictions based on the bootstrapped test data set). Different rows correspond to different visual conditions and different columns, different viewing angles. Shaded error bars represent 95% confidence intervals. (C) Perceived pointer locations (circles) for different viewing angles for different visual conditions. The crosses indicate the corresponding viewing locations, whereas the black dashed line indicates the Alberti Frame. (E–D) Optimized model parameters, including (D) relief scaling factor (c) and (E) pictorial distortion strength (ω), for different visual conditions. Error bars represent 95% confidence intervals.

For relief depth scaling, let the scaling factor be c, and the relief scaling matrix ρ can be expressed as (Figure 4B)

$$\begin{array}{c}\hfill \rho =\left[\begin{array}{cc}\hfill 1& \hfill 0\\ \hfill 0& \hfill 1/c\end{array}\right]\end{array}$$ (5)

This matrix expands (c > 1) or contracts (c < 1) the dimension along the z-axis. Because relief scaling occurs along the observer's line of sight, we need to rotate perceptual space based on the observer's viewing angle β, apply the relief transformation, and rotate the space back. The corresponding rotation matrix R is

$$\begin{array}{c}\hfill \mathbf{R}=\left[\begin{array}{cc}\hfill cos\beta & \hfill -sin\beta \\ \hfill sin\beta & \hfill cos\beta \end{array}\right]\end{array}$$ (6)

Given various components of the linear transformations, Figure 4C shows the order through which the transformations are applied. The targets are on a concentric circle with radius r around the frame's center. Their coordinates are $r·\left[\begin{array}{c}sin\tau \\ cos\tau \end{array}\right]$. Given the pointer distance d, the initial pointer location is $\left[\begin{array}{c}0\\ d\end{array}\right]$. If the pointer is pointing directly at the target, we can describe his location and pointing direction as (Figure 4C, Step 1):

$$\begin{array}{c}\hfill \mathbf{P}=\left[\begin{array}{cc}\hfill 0& \hfill r·sin\tau \\ \hfill d& \hfill r·cos\tau \end{array}\right]\end{array}$$ (7)

First, the perceived pointer goes through relief scaling (Figure 4C, Step 2):

$$\begin{array}{c}\hfill {\mathbf{P}}^{\text{'}}={\mathbf{R}}^{-1}·\rho ·\mathbf{R}·\mathbf{P}\end{array}$$

Second, the perceived pointer goes through pictorial distortions (Figure 4C, Step 3):

$$\begin{array}{c}\hfill {\mathbf{P}}^{\text{'}\text{'}}=\sigma ·\lambda ·{\mathbf{P}}^{\text{'}}\end{array}$$

Note that the pictorial distortions also changed the pointer's perceived location. The overall transformation can be expressed as

$$\begin{array}{c}\hfill {\mathbf{P}}^{\text{'}\text{'}}=\sigma ·\lambda ·{\mathbf{R}}^{-1}·\rho ·\mathbf{R}·\mathbf{P}\end{array}$$ (8)

The perceived pointer location is $\left[\begin{array}{c}{\mathbf{P}}_{11}^{{}^{\text{'}\text{'}}}\\ {\mathbf{P}}_{21}^{{}^{\text{'}\text{'}}}\end{array}\right]$. We can also derive the pointer's pointing direction, $\widehat{\alpha }$:

$$\begin{array}{c}\hfill \widehat{\alpha }=\arctan \left(\frac{{\mathbf{P}}_{22}^{{}^{\text{'}\text{'}}}-{\mathbf{P}}_{21}^{{}^{\text{'}\text{'}}}}{{\mathbf{P}}_{12}^{{}^{\text{'}\text{'}}}-{\mathbf{P}}_{11}^{{}^{\text{'}\text{'}}}}\right)\end{array}$$ (9)

Combining Equation 3 with Equation 9, we can derive the predicted set angle using two trial-dependent input variables, target angle τ and viewing angle β, and three unknown parameters, pointer distance d, relief scaling c, and pictorial distortion strength ω:

$$\begin{array}{c}\hfill \widehat{\alpha }=f\left(\tau ,\beta ;d,c,\omega \right)\end{array}$$

Model fitting for Experiment 2 from Wang et al.

Compared to the original geometrical model, the updated model introduces pictorial distortions due to the discrepancy between the observer's vantage point and the visual environment's CoP. As an initial evaluation of its effectiveness, the model was fitted to the behavioral results of Experiment 2 in Wang and Troje (2023).

Experiment summary

The experiment was conducted in a virtual environment presented through an HTC VIVE Pro HMD. Figure 5 shows the layout of the virtual environment. Inside the virtual environment, an Alberti Frame was centrally located, and a series of nine targets was placed around a circle with a 2.5-m radius. The center of the target circle coincided with the center of the Alberti Frame. Target angles were defined relative to the Alberti Frame's normal, ranging from −90° to 90° with a 22.5° increment and the 0° target being presented twice (10 target angles). The participants stood at one of five potential locations, 3.1 m away from the center of the frame, with the resulting viewing angle ranging from −45° to 45° with a 22.5° increment. Because the 0° viewing angle did not produce pictorial distortions, the pictorial distortion strength ω would not be adequately constrained during the model-fitting process. Therefore, we excluded trials with a 0° viewing angle (four viewing angles). A male pointer was presented at the center of the Alberti Frame (i.e., cued distance = 0 m). As mentioned previously, the Alberti Frame rendered the pointer in one of four visual conditions: picture, window, stereo, and parallax. In the picture and stereo conditions, the frame's CoP was always 3.1 m away from the center of the frame along its normal. In the window and parallax conditions, the CoP always followed the observer's vantage point. Regardless of the visual condition, the participants always viewed the display biocularly. For each trial, the participants were asked to rotate the pointer to point at a target with a blinking red light (Figure 2A), and the pointer's adjusted orientation was measured (set angle). The angular deviations were derived as the difference between the set and target angle. We blocked the trials by visual condition and viewing angle. There were 4 (visual conditions) × 4 (viewing angles) × 10 (target angles; 0° target was repeated) = 160 trials and 12 participants.

Figure 5.

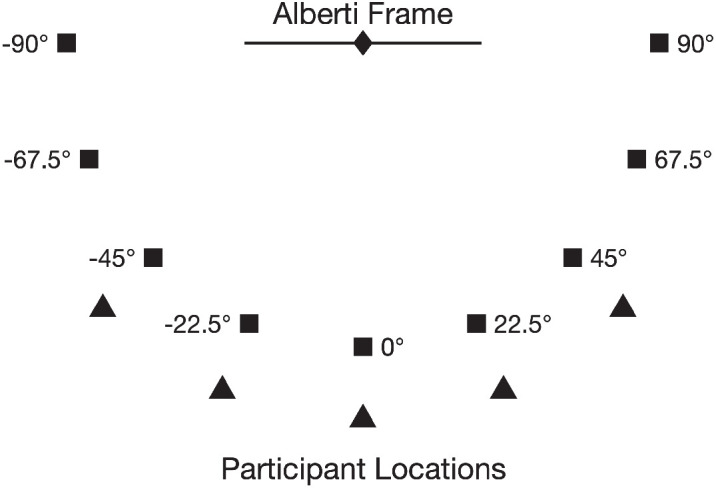
An illustration of the setup of Experiment 2 in Wang and Troje (2023). A schematic illustration of the virtual environment. Filled squares: targets; filled diamond: pointer location; filled triangles: possible participant locations.

Model fitting

Model comparison was used to evaluate the key assumptions in the updated geometrical model. We will refer to the model described in the “Model description” section as the default version. First, the model assumes that the pictorial distortions yield an isotropic rotation to the entire perceptual space whose magnitude is modulated by a pictorial distortion strength ω. This contrasts with the conventional way of characterizing pictorial distortions as shearing, and the discrepancy between the observer's vantage point and the image's CoP should uniquely determine the amount of shear. To evaluate this assumption, an alternative model was constructed such that the pictorial distortions follow Farber and Rosinski's (1978) formulation as magnification/minification (Equation 1) and shearing (Equation 2). Moreover, because of its deterministic nature, this model does not require the pictorial distortion strength as in the default version. We refer to this version as the shearing version. Second, the relief depth scaling is assumed to occur along the participant's line of sight instead of the CoP's line of sight, perpendicular to the frame. As a result, a rotation is applied to the perceptual space based on the viewing angle before and after the relief transformation (Equation 6). This assumption is reasonable for the window and parallax conditions since the participant's line of sight coincides with that of the CoP. However, it is unclear whether the same would also apply to the picture and stereo conditions since the CoP is at a fixed location different from the observer's vantage point. To evaluate this assumption, an alternative model could simply omit the rotational components for relief scaling, indicating that the direction of relief depth scaling is perpendicular to the frame. We refer to this version as the perpendicular relief version.

We fitted three versions of the model (default, shearing, and perpendicular relief) to the behavioral results and optimized the unknown parameters using a least squares method with the Levenberg–Marquardt algorithm (Moré, 1978) in Python's LMFIT package (Newville et al., 2024). Because of a lack of repetition in the experimental design and the relatively small sample size, we employed a participant-level bootstrap method. This allowed us to validate various model versions through a train–test split approach. For each bootstrap iteration, nine participants’ data were randomly selected (with replacement) for training. For each bootstrapped sample, the mean set angle was calculated for each visual condition, viewing angle, and target angle. Within each sample, parameter optimization was performed separately for each visual condition, which contains 40 data points (4 viewing angles × 10 target angles). The default and perpendicular relief versions of the model have three unknown parameters (pointer distance, relief scaling, and pictorial distortion strength), whereas the shearing version has two (pointer distance, relief scaling). The optimization algorithm searched for the unknown parameter values that minimize the sum of squared differences between the predicted set angle $\widehat{\alpha }$ and the mean set angle α:

$$\begin{array}{c}\hfill \underset{d,c,\omega }{\arg \min }\sum {\left(\widehat{\alpha }-\alpha \right)}^2\end{array}$$

For the test set, three participants’ data were randomly selected (with replacement), and the mean set angle was calculated. The predicted set angle from the trained model parameters was compared to the mean set angles from the test set. Model selection was performed using the Bayesian information criterion (BIC), which evaluates whether the model is the true model for the data:

$$\begin{array}{c}\hfill \mathrm{BIC}=nln\left(\frac{\mathrm{SSE}}{n}\right)+kln\left(n\right)+nln\left(2\pi \right)+n\end{array}$$

where SSE is the sum of squared errors between the model prediction and behavioral results, n is the number of observations used for the fit, and k is the number of estimated parameters in the model. The bootstrap was iterated 100 times, and the model with the smallest BIC values was preferred. For the selected model, we compared the 95% confidence intervals (CIs) of the fitted relief scaling factor and pictorial strength between different visual conditions. We also computed the perceived pointer location using Equation 8, which was compared to the pointer's cued location.

Model comparison

Figure 6A shows the BIC scores for the default, shearing, and perpendicular relief versions of the updated model for different visual conditions. While the default and perpendicular relief versions of the model had three unknown parameters (pointer distance, relief scaling, and pictorial distortion strength), the shearing version had two unknown parameters (pointer distance and relief scaling; see the “Model fitting” section for details). Overall, the default version of the model yielded the lowest BIC scores across all visual conditions. Noticeably, the BIC scores for the shearing version were drastically higher in the picture and stereo conditions than in the other conditions. As reasoned by Wang and Troje (2023), if the picture and stereo conditions yield pictorial shearing, the angular deviations between the set and target angles should be 0° for ±90° target angles. Instead, results revealed an overall shift in the angular deviation as a function of the viewing angle, suggesting an isotropic rotation to the entire perceptual space. The model comparison provides evidence that the isotropic rotation is more appropriate in describing the pictorial distortions in the picture and stereo conditions.

Moreover, for relief scaling, the window and stereo conditions showed that BIC scores for the default version were lower than the perpendicular relief version. Because the window and stereo conditions are more susceptible to relief depth scaling, the lower BIC scores for the default version indicate that the relief scaling is best formulated to be along the observer's line of sight. This is particularly interesting for the stereo condition, where there was a discrepancy between the observer's vantage point and the stereo cameras’ CoPs. The binocular disparity rendered on the frame was specified based on the cameras’ projective geometry and their CoPs. From the observer's vantage point, however, the rendered disparity on the frame is distorted. If the relief scaling still occurs along the observer's line of sight, this scaling would therefore be applied to the distorted perceived pointer. This observation suggests a potential interaction between pictorial distortions and relief scaling, which will be explored in detail in a subsequent experiment (see “Behavioral experiment” section).

Overall, the model comparison suggests that the default version of the geometrical model is more suitable to describe the behavioral data. Therefore, the fitted parameters and the model fitting results from the default version were used to examine the effects of different visual conditions on pictorial distortions and relief scaling.

Fitting results

Figure 6B compares the mean behavioral results and model predictions from the default version for each unique combination of visual condition and viewing angle. Our model predicted the behavioral results well. Notably, our model captures the vertical shift in angular deviations as a function of viewing angle for the picture and stereo conditions, conceptualized as an isotropic rotation of the pictorial space (Equation 4). Additionally, our model also accurately predicted the effect of relief scaling on set angles in the window and stereo conditions. In these conditions, angular deviations produced a curvilinear pattern, oscillating as a function of the target angle, and changes in viewing angle laterally shifted this pattern. Together, these observations further confirmed that the relief depth scaling occurred along the observer's line of sight and justified the rotations applied before and after the relief depth scaling (Equation 5).

Figure 6C shows the perceived pointer locations based on model fitting. For the window condition, the pointer's perceived distance was close to the frame (mean = 0.085 m, CI = [0.080, 0.091]). Combined with weak pictorial distortions, the pointer was perceived to be at around where he was cued, and more importantly, there was no impact of the viewing angle on his perceived location. In contrast, for the picture condition, the pointer was perceived to be noticeably behind the frame (mean = −0.24 m, CI = [−0.25, −0.23]), and with strong pictorial distortions, the pointer's perceived location distinctively varied as a function of the viewing angle. As Figure 6C shows, not only was the pointer perceived to be behind the frame, but his perceived location also rotated in the same direction as the viewing angle. For the stereo condition, the binocular disparity specified distance relatively well, where the pointer's perceived distance to the frame was closer to his cued distance (mean = −0.071 m, CI = [−0.077, −0.066]). However, due to relatively strong pictorial distortions, the pointer's perceived location rotated around the center of the frame in the same direction as the participants’ viewing angle, similar to the picture condition. Finally, for the parallax condition, the pointer's perceived distance to the frame was comparable to that in the picture condition (mean = −0.32 m, CI = [−0.33, −0.31]). More interestingly, there was an isotropic rotation of the pictorial space in the opposite direction to the participant's viewing angle, suggesting the presence of pictorial distortions in the reverse direction compared to those observed in the picture and stereo conditions.

As for the fitted parameters, the relief scaling factor (Figure 6D) for the parallax condition (mean = 1.09, CI = [1.08, 1.09]) was the closest to 1, followed by the picture condition (mean = 1.15, CI = [1.15, 1.16]). In contrast, the window (mean = 1.37, CI = [1.36, 1.38]) and stereo (mean = 1.62, CI = [1.60, 1.63]) conditions had relief scaling factors that are much greater than 1, indicating relief depth expansion along the observer's line of sight. Figure 6E shows the distributions of pictorial distortion strength across different visual conditions. The picture (mean = −0.76, CI = [−0.77, −0.76]) and stereo (mean = −0.81, CI = [−0.81, −0.81]) conditions had the largest pictorial strength in terms of magnitude, whereas the window condition had the lowest (mean = −0.09, CI = [−0.10, −0.09]). Finally, the pictorial strength for the parallax condition also had a nonzero relief scaling (mean = 0.19, CI = [0.19, 0.20]) but in the direction opposite of the picture and stereo conditions.

Discussion

Overall, fitting the updated model to results from Experiment 2 of Wang and Troje (2023) demonstrated the model's effectiveness in accounting for the invariant properties associated with binocular disparity and motion parallax and how these two types of visual information can be leveraged to spatially connect different perceptual spaces.

First, the model confirmed that binocular disparity retains distance information while introducing relief scaling along the observer's line of sight. Although the present experiment did not vary the pointer’s cued location, Figure 6C still shows that as soon as binocular disparity is rendered, the pointer is perceived to be where it was cued. Without binocular disparity, however, the pictorial content is always perceived to be slightly behind the image plane. Additionally, binocular disparity also independently scales the perceived extent of 3D objects along the observer's line of sight. The magnitude of the relief scaling in the current analysis is comparable to that observed in Experiment 1 of Wang and Troje (2023): The stereo condition produced the largest depth expansion of 1.6, followed by the window condition at around 1.4. The picture condition had slightly expanded scaling at around 1.1, and finally, the parallax condition had a scaling factor of around 1. The depth expansion in the first two conditions and the lack of it in the latter two suggest that binocular disparity also elicits relief scaling along the observer's line of sight.

Second, the model also showed that that motion parallax retains allocentric direction. Without motion parallax, the entire perceptual space is subject to an isotropic rotation proportional to the observer's viewing angle. This isotropic rotation was the most prominent in the picture and stereo conditions due to the discrepancy between the observer's vantage point and the camera's CoP. This highlighted the importance of motion parallax in keeping directional information invariant in the resulting perceptual space. Importantly, this finding challenges the conventional conceptualization of pictorial distortions as an affine transformation in which lateral shearing is differentially applied to the depicted objects depending on the objects’ relative orientation to the image plane. This finding is rather surprising because, to the best of our knowledge, none of the previous studies have reported similar results despite decades of research (Cutting, 1988; Farber & Rosinski, 1978; Gournerie, 1859; Koenderink & van Doorn, 2012; Sedgwick, 1991). For images, shearing is a reasonable way to describe the perceived orientation of a pictorial object (Figure 7A). When the depicted cylinder is perpendicular to the image plane, the perceived orientation of the object would always follow the spectator's vantage point. When the depicted object is parallel to the image plane, the perceived object would also remain in the image plane regardless of the observer's viewing angle. The reason behind this phenomenon is rather trivial: The pigments/pixels on the image plane that depict the object do not change. Because the observer cannot perceive what is not depicted, as the observer moves relative to the image plane, the perceived object would always be based on what is depicted. When the cylinder is perpendicular to the image plane, for instance, the frontal view of the cylinder would always indicate that the observer is looking at the depicted object head-on, regardless of the observer's location. Therefore, the perceived cylinder would appear to be following the observer. Alternatively, for the perceived cylinder to not follow the observer's vantage point, the side of the object should start revealing itself as the observer moves, which is impossible for a static image.

Figure 7.

(A) A cylinder that is perpendicular (top) or parallel (bottom) to the image plane. Readers may try to change their viewing perspective of the images by moving their heads laterally. The perceived orientation of the top cylinder would always follow the observer's vantage point, whereas that of the bottom cylinder would remain stationary. (B) Illustrations of the perceived pointer in the picture condition when the pointer is pointing perpendicular (top) or parallel (bottom) to the image plane and when the observer is looking at the pointer from the image's center of projection (left) or at 45° to the side (right).

Unexpectedly, we did not observe this pattern in the current study. As Wang and Troje (2023) reasoned, the present experimental setup enabled the observers to actively rotate the pointer while standing at an oblique angle to the image plane. If a component of the pictorial distortions is shearing, then the pointer would appear to be rotating at varying angular velocity based on its relative orientation to the image plane. Since the pointer was always rotated at a constant velocity, this would have calibrated the pictorial space and transformed the shearing into isotropic rotation. Additionally, even with static images of the pointer viewed from different angles (Figure 7B), readers could still perceive the effect of the isotropic rotation. In the top row, the pointer is pointing perpendicular to the image plane. Therefore, as the observer changes the viewing angle, the pointer naturally follows. In the bottom row, the pointer is pointing parallel to the image plane. However, at an oblique viewing angle, the pointer does not appear to be pointing in the same direction anymore: Instead of being parallel to the image plane, the perceived pointer is pointing slightly behind the image. It is not readily apparent why the pointer's orientation is perceived as such, and identifying the source of this distortion may require further experimentation.

Another interesting aspect of the pictorial distortions is the positive distortion strength (i.e., ω in Equation 4) in the parallax condition. Between the stereo and window conditions, introducing motion parallax eliminated pictorial distortions. However, between the window and parallax conditions, not rendering binocular disparity produces pictorial distortions of a lesser magnitude and in the opposite direction as in the picture and stereo conditions. Model fitting yielded a distortion strength of 0.19, comparable to 0.2 derived using linear regression from Experiment 2 of Wang and Troje (2023). Originally, this phenomenon was attributed to the perceived slant of the image plane interacting with the perceived direction of the pointer. However, the present model fitting only computationally confirmed the earlier observations without providing additional data to elucidate the geometrical origin of such distortions.

In the subsequent experiment, we simultaneously manipulated the participants’ viewing angle and the depicted pointer's location relative to the image plane. This additional experiment would not only help to further validate our model but may also provide additional insights into any potential interactions between relief scaling, pictorial distortions, and the depicted pictorial object's distance relative to the image plane. For continuity with Wang and Troje (2023), we will refer to this experiment as Experiment 3.

Behavioral experiment

Methods

Participants

Thirteen adults (3 males and 10 females; age mean = 20.62, SD = 3.82) participated in this experiment in exchange for course credits. All participants had normal or corrected-to-normal vision. Prior to participating in the experiment, all participants provided their informed consent. This study was approved by York University's Office of Research Ethics.

Stimuli and apparatus

This experiment used the same stimuli and apparatus as in Wang and Troje (2023). A virtual environment was developed using Unity3D and presented through an HTC VIVE Pro HMD (1,440 × 1,600 pixels per eye, 110° field of view, and 90 Hz refresh rate) connected to a computer with an Intel Core i7 CPU, 16 GB RAM, and an NVIDIA GTX 1080Ti GPU. Figure 8 shows the layout of the virtual environment. The pointer was cued at three different depth locations: in the plane of the frame (0 m) or 1 m or 2 m behind it. Nine targets were presented around a circle of radius 2.5 m, concentric with the frame. Target angles were measured relative to the frame's normal through its center, between ±90° with a 22.5° increment. As in the previous study, participants stood 3.1 m away from the center of the frame with two possible viewing angles, −45° or −22.5°. Finally, the pointer was presented on the Alberti Frame with four visual conditions (window, picture, parallax, and stereo; see Figure 3). Regardless of the visual condition, the participants always viewed the display biocularly. A detailed description of the implementation of the Alberti Frame can be found in Figure 3 and our earlier study (Wang & Troje, 2023).

Figure 8.

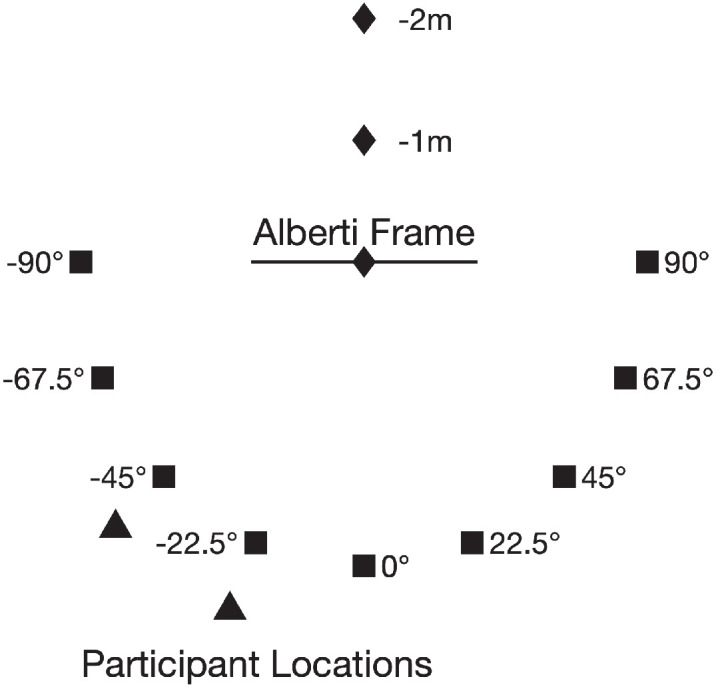
An illustration of the experimental setup. Filled squares: targets; filled diamond: possible cued pointer locations; filled triangles: possible participant locations. See text for details.

Procedure and design

After providing their informed consent, the participants were told to stand upright to have their eye height captured via the HMD, which was subsequently used to specify the height of the Alberti Frame's camera(s). This procedure was used to minimize the vertical displacement between the observer's vantage point and the frame's CoP. Participants stood in an upright posture while holding a VIVE Controller. In each trial, a male virtual character would appear in the middle of the Alberti Frame in a random orientation with his right arm extending forward, and the base of one target would emit a blinking red light (Figure 2A). The participants were instructed to use the controller to rotate the pointer to point at the target, and the pointer's orientation (set angle) was recorded. Trials were blocked by viewing angle (two levels) and visual condition (four levels), yielding eight blocks presented in a counterbalanced order. Within each block, there were three cued pointer distances (−2, −1, and 0 m) and nine target locations (between ±90° with a 22.5° increment). Trial orders were randomized within each block. In total, there were 4 (visual conditions) × 2 (viewing angles) × 3 (cued pointer distance) × 9 (target angles) = 216 trials. Finally, because the target angle was measured relative to the center of the frame while the pointer may have been behind the frame, the target angle needed to be adjusted based on the pointer's location to identify the orientation of the pointer that would allow him to be pointing directly at the target (Figure 4A; for derivations, see Appendix 1 of Wang & Troje, 2023).

Model fitting

An identical optimization method was used to fit the data to the model (see the “Model fitting” section). Training was performed using the bootstrapped means of nine randomly selected participants (with replacement) while testing was performed using the bootstrapped means of four participants’ data. The input for both training and testing contains 54 data points (2 viewing angles × 3 cued pointer distance × 9 target angles). Given three cued pointer distances, the optimization algorithm searched for the values of five unknown parameters (three pointer distances d, one for each cued distance; one relief scaling c; and one pictorial distortion strength ω) to minimize the sum of squared differences between the predicted and mean set angles.

Previous model comparisons confirmed that the pictorial distortions should be best described as an isotropic rotation and that relief scaling occurs along the observer's line of sight. The current experiment introduced variations of the cued pointer's distance to the frame in addition to changes in the viewing angle. This setup could help to test additional assumptions about the model. For instance, Wang and Troje (2023) assumed a single relief scaling factor for the same visual condition for pointers cued at different locations relative to the frame. To validate this assumption, an alternative model was created in which relief scaling varies as a function of cued pointer distance, which yields seven unknown parameters (three pointer distances, three relief scaling factors, and one pictorial strength). This version of the model will be referred to as different relief. Similarly, it is also unclear whether the magnitude of pictorial distortions is mediated by the pointer's distance to the image plane. Therefore, another alternative model, the different pictorial version, was created in which the pictorial strength varies with pointer distance (seven parameters with three pointer distances, one relief scaling factor, and three pictorial strength). Finally, a third alternative model was tested that varies both relief scaling and pictorial distortion strength as a function of cued distance (nine parameters with three pointer distances, three relief scaling factors, and three pictorial strength), which will be referred to as the different relief and pictorial version. Using 100 bootstrap samples, the BIC scores for different versions of the model were compared to identify the most suitable version to fit the data. The selected model's fitted parameters were evaluated using 95% CI.

Results

Model comparison

Figure 9A shows the BIC scores for four versions of the model across different visual conditions. Unlike the model comparisons in the “Model comparison” section, different model versions exhibit varying levels of fit to different visual conditions. For the window condition, all four versions of the model yielded comparable BIC scores, with the default version having the lowest score. This outcome suggests that the additional parameters introduced in other versions did not significantly improve the model's fit. That is, the relief scaling factor and pictorial distortion strength are not influenced by cued distance in the window condition. For the picture condition, the default and different pictorial versions of the model had the lowest BIC scores, with the default being slightly lower. Because the picture condition did not exhibit significant relief depth scaling, the additional relief scaling in the different relief and different relief and pictorial versions do not contribute to the model's goodness of fit. Furthermore, since the default version's score is slightly lower, it implies that the added pictorial strengths in the latter version did not significantly improve the model's fit, suggesting consistent pictorial distortions across different cued distances. However, the same did not apply to the stereo and parallax conditions. The BIC scores for these conditions indicate that both the default and different relief versions of the model yielded a notably worse fit, whereas the different pictorial version provided a better fit to the data despite the additional parameters. This observation implies that pictorial distortion strength, but not relief scaling, is modulated by the cued pointer's distance to the frame in the stereo and parallax conditions. Moreover, because the different relief and pictorial versions contain additional relief scaling factors but did not yield a noticeable improvement in the model's goodness of fit, the different pictorial version is the most appropriate model for data from the stereo and parallax conditions.

Figure 9.

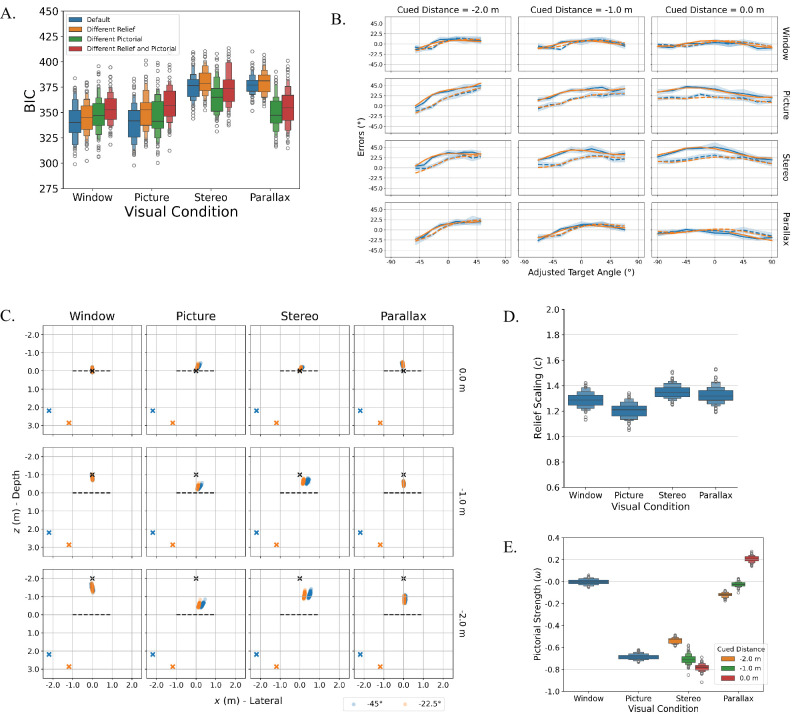
(A) BIC scores for the default (blue), different relief (orange), different pictorial (green), and different relief and pictorial (red) versions of the updated geometrical model for different visual conditions. (B) Mean errors from the behavioral results (blue lines) and model predictions (orange lines) as a function of the adjusted target angle for different viewing angles (solid lines: −45°; dashed lines: −22.5°), cued distances (columns), and visual conditions (rows). The window and picture conditions were fitted using the default version of the model, whereas the stereo and parallax conditions were fitted using the different pictorial version. Shaded error bars represent standard errors. (C) Perceived pointer locations for different viewing angles, visual conditions (columns), and cued distances (rows). Black crosses represent cued pointer location, and the black dashed line represents the Alberti Frame. (D, E) Optimized model parameters, including mean (D) relief scaling factor for different visual conditions and (E) pictorial distortion strength for different visual conditions and cued pointer distances.

Overall, model comparisons showed that different visual conditions require different versions of the model. Therefore, model fit analysis will use the parameters from the default version for the window and picture conditions and those from the different pictorial version for the stereo and parallax conditions.

Fitting results

Figure 9B compares model predictions with behavioral results for errors between set angle and adjusted target angle. The model fits behavioral data relatively well, especially given the complex interactions among relief scaling, pictorial distortions, cued pointer distance, and viewing angle. For 0° adjusted target angle, the window and parallax conditions’ errors were at around 0°, whereas the picture and stereo conditions’ errors were at around the values of the viewing angles. This is similar to the findings shown in Figure 6B and is a result of pictorial distortions. The curvilinear pattern indicative of relief scaling was not as pronounced in any of the visual conditions as observed earlier, suggesting the potential absence of a strong relief scaling. Instead, there is a noticeable positive linear trend modulated by the cued distance across almost all visual conditions, especially when the pointer was cued to be 2 m behind the frame. This trend is attributed to the pointer being perceived to be closer to the frame. The further away the pointer is cued, the smaller the adjusted target angle would be (i.e., the angle between the midsagittal plane and the pointer's orientation). If the pointer is perceived to be closer to the frame, the magnitude of the error would increase as the target angle increases, resulting in the observed linear trend.

Figure 9C shows the perceived pointer location derived from model fitting. For the window condition, the pointer was generally perceived to be at around his cued locations. The farther the pointer is from the frame, the more underestimated and variable his perceived distance to the frame was (at 0 m: mean = 0.059 m, CI = [−0.071, −0.046]; at −1 m: mean = −0.84 m, CI = [−0.85, −0.82]; at −2 m: mean = −1.46 m, CI = [−1.48, −1.44]). A linear regression showed that the pointer's perceived distance was approximately 70% of his cued distance. Because of this increased inaccuracy, angular errors also increased as the cued distance increased (Figure 9B). Importantly, because of the absence of pictorial distortions, changes in viewing angle did not affect the perceived pointer location (the mean distance to the frame's normal was at around 0.00 m for all cued distances). In contrast, for the picture condition, the pointer was always perceived to be slightly behind the frame regardless of where the pointer was cued (at 0 m: mean = −0.21 m, CI = [−0.22, −0.20]; at −1 m: mean = 0.32 m, CI = [−0.33, −0.31]; at −2 m: mean = −0.54 m, CI = [−0.55, −0.52]), where the perceived distance was approximately 16% of the cued distance. Importantly, the perceived pointer location also shifted laterally, reflecting the isotropic rotation component of pictorial distortions. For the stereo condition, the perceived pointer location varied as a function of the pointer's cued distance (at 0 m: mean = −0.12 m, CI = [−0.13, −0.11]; at −1 m: mean = −0.63 m, CI = [−0.64, −0.62]; at −2 m: mean = −1.11 m, CI = [−1.13, −1.09]), and the pointer's perceived distance to the frame is still more compressed than the window condition where the perceived distance was about 49% of the cued distance. Moreover, because of pictorial distortions, changes in viewing angle also impacted the pointer's perceived location, diminishing as a function of the cued pointer distance to the frame. Finally, the parallax condition was similar to the picture condition, where the cued pointer was always perceived to be slightly behind the frame (at 0 m: mean = −0.34 m, CI = [−0.35, −0.33]; at −1 m: mean = −0.50 m, CI = [−0.51, −0.49]; at −2 m: mean = −0.85 m, CI = [−0.87, −0.83]), or an equivalent of a 26% compression of the cued distance. What is interesting is the effect of the cued pointer distance on the relief distortion strength. When the pointer's location was cued to be in the plane of the frame (0 m), the pointer's perceived location was shifted to the same side as the participants (distance to the frame's normal mean = −0.041 m, CI = [−0.044, −0.039]). This is in the opposite direction as the picture and stereo conditions. However, as the pointer moved farther back, the strength of pictorial distortions diminished, allowing the participants to perceive the pointer to be along the frame's midsagittal line as where the pointer was cued to be.

 Figure 9D shows the distributions of relief scaling factors for different visual conditions. Unlike the apparent difference between different visual conditions from earlier experiments (e.g., Figure 6D), the magnitudes of relief scaling were comparable across visual conditions. The stereo condition had the largest relief scaling (mean = 1.35, CI = [1.34, 1.36]), closely followed by the parallax (mean = 1.32, CI = [1.31, 1.34]) and window (mean = 1.29, CI = [1.28, 1.30]) conditions. The picture condition has the smallest relief scaling, but it is still noticeably greater than 1 (mean = 1.20, CI = [1.19, 1.21]). Together, these findings confirmed a lack of strong relief depth scaling indicated by the error patterns.

Figure 9E shows the distributions of pictorial distortion strength for different visual conditions. First, the window and picture conditions used the default version of the model with a single pictorial strength for all cued distances. As expected, the window condition did not exhibit any pictorial distortions (mean = −0.002, CI = [−0.007, 0.002]), while the picture condition showed strong pictorial distortions (mean = −0.69, CI = [−0.69, −0.68]). This finding replicated earlier findings (Figure 6E). More interesting results emerge in the stereo and parallax conditions, which had unique pictorial distortion strengths for different cued distances. For the stereo condition, when the pointer was cued at the frame (0 m), the pictorial distortions (mean = −0.78, CI = [−0.79, −0.78]) was comparable to what was reported earlier (mean = −0.81). However, as the pointer moved further behind the frame, the strength of the distortion became weaker (−1 m: mean = −0.71, CI = [−0.72, −0.70]; −2 m: mean = −0.54, CI = [−0.54, −0.53]). A similar trend also applies to the parallax condition. When the pointer was cued at 0 m, the pictorial distortion strength (mean = 0.21, CI = [0.20, 0.21]) was similar to that reported earlier (mean = 0.19). Then, as the depicted pointer moved further behind the frame, the pictorial distortions became negligible (at −1 m: mean = −0.02, CI = [−0.03, −0.02]) and even switched to the opposite direction (at −2 m: mean = −0.12, CI = [−0.12, −0.11]).

Discussion

Compared to the previous experiments, the current experiment manipulated the pointer's cued distance and the observer's viewing angle at the same time. With this manipulation, model comparison and model fitting revealed additional caveats concerning the interaction between binocular disparity and motion parallax and how this interaction affected distance, 3D shape, and allocentric direction information. When the two types of visual information are congruent, as in the window and picture conditions, both relief scaling and pictorial distortions were similar to those in the previous experiments. When they are incongruent, as in the stereo and parallax conditions, increasing the pointer's cued distance while at an oblique viewing angle would ameliorate the effects of pictorial distortions and relief scaling.

Overall, this experiment presented two main findings. First, we showed that the magnitude of the pictorial distortion is modulated by the pointer's cued distance to the image plane in the stereo and parallax conditions. For the stereo condition, there was a noticeable reduction in the overall strength of the pictorial distortion as the depicted pointer moved farther away from the image plane. For the parallax condition, although the increase in the cued distance also reduces the magnitude of the pictorial strength (at −1 m), the pictorial distortions reversed to the opposite direction as the depicted pointer moved farther back (at −2 m). Together, the results of these two conditions suggest two potential outcomes for the pictorial distortions based on the distance of the depicted pointer to the image plane. First, the effect of pictorial distortions could diminish as a function of distance. This may reflect the trend in the stereo condition where the magnitude of the pictorial strength would eventually reduce to around 0. Second, increasing distance may strengthen the pictorial distortions in the opposite direction. This could be the case for the parallax condition, where the pictorial strength may further decrease in value, arriving at a level observed in the picture condition. The results of the current study do not provide adequate evidence to discern the two alternatives, and future studies are needed.

Second, we also showed that relief scaling is affected by the depicted pointer distance at an oblique viewing angle. The picture and window conditions yielded comparable levels of relief scaling to the previous experiments, at around 1.2 (picture) and 1.3 (window). For the stereo condition, relief depth expansion was attenuated to around 1.3, as compared to 1.6 in the earlier experiments. In contrast, the parallax condition produced an increased relief depth expansion, from 1 to around 1.3. Our previous results showed that the source of relief depth expansion is binocular disparity, which also facilitates the perception of the pointer's distance. As the depicted pointer moved farther away from the observer, the magnitude of binocular disparity decreased, leading to reduced sensitivity to the depth specified by disparity (Patterson et al., 1995). Consequently, if relief scaling was attenuated, the overall influence of binocular disparity on perceptual judgment would also diminish. This reduction in binocular disparity's effectiveness should also result in increased inaccuracy in the pointer's perceived distance. This was indeed the case as we compared the perceived pointer locations between the window and stereo conditions (Figure 9E), where the pointer was perceived to be closer to the frame in the stereo condition than in the window condition. Curiously, although the parallax condition did not contain any disparity information of the pointer, this condition also yielded a more noticeable relief depth expansion compared to our previous experiments. This suggests that motion parallax might have become more similar to binocular disparity with a longer distance and an oblique viewing angle. If this was the case, the parallax condition should also yield a more accurate perceived distance, which was again confirmed by Figure 9E, where the perceived pointer distance is less compressed compared to the picture conditions.

The above reasoning suggests that changes in the fitted relief scaling factor (and the perceived pointer distance) in the stereo and parallax conditions could share a common underlying mechanism introduced to the current experiment. Compared to the previous experiments, the present experiment simultaneously varied the pointer's cued distance and the participant's viewing angle, and hence, it could be the interaction between the cued distance and viewing angle that contributed to the changes in relief scaling. However, how the interaction between the two factors produced such behavioral outcomes is beyond the scope of the current study. More experiments are needed to further delineate the underlying mechanism of such perceptual distortions. Finally, it should also be acknowledged that the current study used an exocentric pointing task and model fitting to infer behaviors related to relief scaling and pictorial distortions. While model fitting provides valuable insights, it is difficult to isolate the impact of individual factors, such as the pointer's cued distance and the participant's viewing angle, from these gross results alone. Future studies should therefore adopt psychophysical experiments to systematically measure how relief scaling and pictorial distortions—particularly isotropic rotation—vary with specific factors like cued distance and viewing angle. These experiments would provide a more direct, quantitative comparison to the parametrized predictions and further validate our findings.

General discussion

The current study presented a geometrical model that describes the perceptual spaces corresponding to binocular disparity and motion parallax in terms of their invariant spatial properties. We first fitted the model to Experiment 2 of Wang and Troje (2023), where we only manipulated the participant's viewing angle. We showed that motion parallax alone retains allocentric direction and 3D shape information while introducing distance compression, whereas binocular disparity alone keeps distance invariant while introducing relief depth expansion along the observer's line of sight and an isotropic rotation of the perceptual space. Subsequently, we presented an additional experiment that simultaneously manipulated the participant's viewing angle and pointer's cued distance to the image plane. In this context, motion parallax is required to offset the effect of changing the viewing angle to keep allocentric direction invariant, while binocular disparity is required to counter changing cued distance to keep distance invariant. Results showed that without either visual information (i.e., picture condition), distance was compressed and allocentric direction followed the observer's vantage point. With both types of visual information (i.e., window condition), distance and allocentric direction were preserved, but the 3D shape was expanded along the observer's line of sight. Interestingly, the invariant properties of each type of visual information were modulated when there was a mismatch between binocular disparity and motion parallax. When only binocular disparity was available (i.e., stereo condition), the absence of motion parallax not only rendered allocentric direction ambiguous but also reduced the effectiveness of binocular disparity in specifying distance and eliciting relief scaling. Similarly, with only motion parallax (i.e., parallax condition), the absence of binocular disparity yielded distance compression and perturbed allocentric direction.

The modulation of invariant properties highlights the crucial impact of interacting visual information. For instance, combining static disparity with motion parallax also yields stereomotion information, including change of disparity over time (CDOT) and interocular velocity difference (IOVD; Harris, Nefs, & Grafton, 2008; Himmelberg, Segala, Maloney, Harris, & Wade, 2020; Nefs, O'Hare, & Harris, 2010; Shioiri, Saisho, & Yaguchi, 2000). While CDOT takes the temporal derivatives of static disparity to yield information regarding motion in depth, IOVD first takes the temporal derivatives of monocular motion for velocity and then derives the difference between the velocities from each eye. Therefore, it is possible that the synergistic improvement in task performance when both binocular disparity and motion parallax are available compared to when only one is available could be attributed to the emergence of additional types of visual information that specify depth and allocentric direction.

Under an updated approach to conceptualizing different perceptual spaces, the current study assumed that the perceptual experience in VR is equivalent to that in a physical environment, where both yield visual space due to their perspectival nature. However, this assumption is solely based on retinal information, that is, motion parallax and binocular disparity. It is important to note that VR perturbs other sources of information, such as extraretinal (e.g., accommodation; Wang et al., 2024b) and proprioceptive (e.g., HMD weight; Buck, Young, & Bodenheimer, 2018) information. For instance, VR HMDs place the stereoscopic displays at a fixed distance, and even with specialty lenses that modify the displays’ focal distance (e.g., Fresnel lens for HTC VIVE), images of the displays are still perceived at a fixed distance (e.g., around 70 cm for HTC VIVE; Batmaz, et al., 2023; Krajancich, Kellnhofer, & Wetzstein, 2020; Yeh, Liu, Sun, Chi, & Hwang, 2021). In other words, the eyes always accommodate to a fixed distance in HMD. In a normal viewing condition, vergence (simultaneous rotation of the two eyes to point at a target) and accommodation are tightly coupled where changes in one would drive the other (Eadie, Gray, Carlin, & Mon-Williams, 2000; Hung, 1992; Hung, Ciuffreda, & Rosenfield, 1996). Because VR HMDs restrict accommodation, the vergence–accommodation conflict would occur, which perturbs the stereoscopic viewing geometry and, consequently, depth perception (Wang et al., 2024b) and sensorimotor control (Wang et al., 2024a; Wang, Nitsche, Resch, Mazalek, & Welsh, under review). In other words, while the visual space of VR and that of the physical world are both perspectival, there could be quantitative differences between the two due to the contributions from extraretinal information.

With rapid technological development and the ever-evolving display technologies, different visual information that was painstaking to re-create in a laboratory can now be easily implemented and even readily available in the consumer market. For instance, implementing motion parallax on a computer monitor could be challenging because the algorithm needs to track the metric position of the user's eyes relative to the display and render the images based on the relative locations between the eyes and the virtual objects. This could become more challenging if the target display is a real person, instead of a virtual rendering of the person, where the algorithm needs to predictively render different views of the person even when the view is not captured by the camera. However, with deep neural networks, hand and eye tracking could be easily accomplished through a consumer-level webcam (Lugaresi et al., 2019), and the recent development in computer vision also enables controllable realistic avatars with extremely high fidelity (Zielonka et al., 2023). Therefore, with the advance in display technologies, it is important to delineate the geometry of the perceptual space corresponding to different visual information. This way, applications can be specifically tailored to the unique perceptual geometry corresponding to the display to fully take advantage of the display. For example, since motion parallax provides direction information, it was suggested that implementing motion parallax could facilitate screen-based social interactions (Troje, 2023a; Troje, 2023b). Because we showed that motion parallax without binocular disparity would yield slight pictorial distortions that would make the perceived objects move faster (Wang et al., 2020), an 80% gain should be added to the mapping of user motion and the motion of the virtual camera with which the image is rendered to improve the visual fidelity of the display.