State Readout of a Trapped Ion Qubit Using a Trap-Integrated Superconducting Photon Detector

Abstract

We report high-fidelity state readout of a trapped ion qubit using a trap-integrated photon detector. We determine the hyperfine qubit state of a single ⁹Be⁺ ion held in a surface-electrode rf ion trap by counting state-dependent ion fluorescence photons with a superconducting nanowire single-photon detector fabricated into the trap structure. The average readout fidelity is 0.9991(1), with a mean readout duration of $46\mu \text{s}$, and is limited by the polarization impurity of the readout laser beam and by off-resonant optical pumping. Because there are no intervening optical elements between the ion and the detector, we can use the ion fluorescence as a self-calibrated photon source to determine the detector quantum efficiency and its dependence on photon incidence angle and polarization.

Qubit state readout is an essential part of quantum computing and simulation [1,2], including most quantum error correction protocols [3,4]. Trapped ion qubits are typically read out by driving an optical cycling transition with laser light and observing the presence or absence of ion fluorescence [5]. A fraction of the fluorescence photons from the ion are collected, usually with an objective, and imaged onto a photon-counting detector or camera; the number of photons counted over the duration of the readout process indicates the projected state of the qubit. In general, counting just a few percent of the total fluorescence photons from the ion is sufficient to provide readout fidelities in excess of 0.99 [6], and readout fidelities at or approaching 0.9999 have been reported [7–10]. Trapped-ion readout can also be accomplished using state-dependent interactions with a second ion followed by fluorescence readout of that ion, as in quantum logic spectroscopy [11].

Increasing the number of qubits in trapped-ion quantum processors and simulators can boost computational power, but presents the challenge of reading out the individual states of multiple ions in parallel. One solution is to employ spatially resolved detection, where each ion’s fluorescence is ideally imaged onto a separate active detector region. Fluorescence cross talk, where photons from one ion are counted by a detector region dedicated to a different ion, can be tolerated to some degree before the readout fidelity is degraded [8,12,13]. Alternatively, multi-ion readout can be achieved without spatially resolved detection through time-domain-multiplexed illumination of individual ions, for example, by separating ions into different locations in the trap and reading them out in series [14]. This increases the duration of readout in proportion to the number of qubits, limiting utility for many-ion systems.

A number of groups use microfabricated surface-electrode traps [15], which can hold many ions and feature complex designs with multiple trapping zones [16–19], asa path toward large-scale trapped-ion quantum computing. The separate trapping zones can be used for different algorithmic tasks, such as memory, readout, or gate operations [6,19,20]. A natural method for simultaneous readout in such traps is to integrate on-chip photon collection features into the readout zones, such as optical fibers [21], high-numerical-aperture (NA) micro-optics [22–24], or high-reflectivity trap surfaces [25,26]. However, these solutions all rely on separate photon detectors or cameras, and some still require external objectives made with bulk optics. Alternatively, spatially resolved detectors fabricated directly into a surface-electrode trap could perform parallel qubit readout without external collection optics or detectors, with readout signals coupled out of the trap chip as electrical pulses [27–29]. Such a readout architecture frees up the space and optical access used by bulk optics objectives and cameras and potentially enables surface-electrode traps to be tiled in the third dimension, especially when combined with integrated photonics for light delivery [30–32]. It also eliminates the need for imaging system alignment and can, in principle, be scaled to ion traps with many trap zones.

In this Letter, we report the first use of a trap-integrated photon detector for high-fidelity state readout of an ion qubit. We use a superconducting nanowire single-photon detector (SNSPD) cofabricated with a surface-electrode ion trap to detect fluorescence photons at 313 nm from a single ⁹Be⁺ ion, achieving qubit state readout with fidelity 0.9991(1) in an average of $46\mu \text{s}$ using an adaptive Bayesian readout scheme [7,33]. Using the ion as a tunable, self-calibrating source of photons with known flux and polarization, we characterize the detection efficiency of the SNSPD as a function of incidence angle and polarization, finding agreement with theoretically predicted values. We also study the effect of the trapping rf fields on the SNSPD performance and characterize motional heating of an ion confined over the SNSPD.

SNSPDs are a class of photon detectors with high quantum efficiency [34,35], low dark counts [36,37], and picosecond timing jitter [38]. Recent experiments have shown quantum efficiencies in the UV of 75%–85% at operating temperatures up to 4 K, a parameter regime relevant for ion trap applications [29,36]. Ion fluorescence photons collected with traditional high-NA bulk optics have been counted by a fiber-coupled SNSPD in a stand-alone cryostat to perform fast, high-fidelity qubit readout [39]. However, surface-electrode ion traps present a challenging electromagnetic and thermal environment for integrated SNSPDs: SNSPDs requiring low-noise bias currents of a few microamperes must be placed close to trap electrodes with rf potentials of tens to hundreds of volts oscillating at up to ~100 MHz. Furthermore, the superconducting transition temperature $T_c$ of the SNSPD should be at least ~25% higher than the temperature at the surface of the trap (typically ≳4 K) to achieve the best detection efficiency [36,40,41]. Combining the separate microfabrication processes for SNSPDs and ion traps while maintaining high device yield and good performance is also a challenge [42]. However, previous work has demonstrated successful integration and operation of SNSPDs on a test chip simulating the thermal and electromagnetic environment of an ion trap [29].

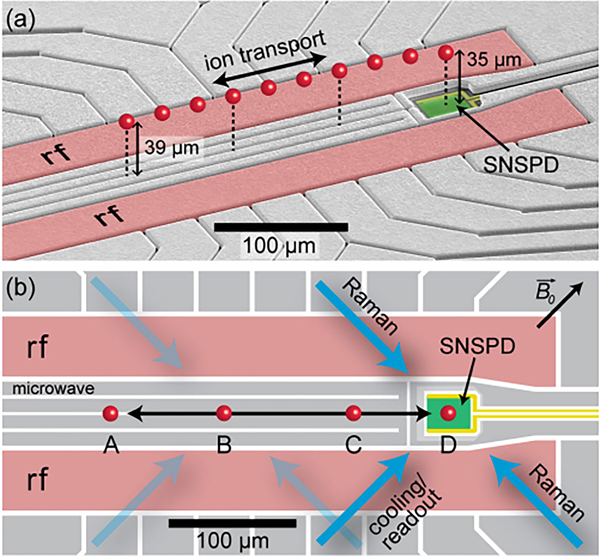
The trap used in this Letter, shown in false color in Fig. 1, is a linear rf (Paul) surface-electrode trap with a SNSPD (green) fabricated on the trap substrate. The rf electrodes (pink) provide confinement transverse to the trap axis [shown as a double-headed black arrow in Fig. 1(b)], while the surrounding segmented electrodes (gray) confine the ion at adjustable positions along the rf null line, from directly over the SNSPD (zone $D$) to 264 μm away from the SNSPD center (zone $A$). The ion is held ≈39 μm above the top surface plane of the trap electrodes, dropping by design to a smaller distance of ≈29 μm above this plane when centered over the SNSPD, which is recessed another 6 μm below this plane. The SNSPD consists of a meandered nanowire of 110 nm width on a 170 nm pitch, covering a total active area of 22 × 20 μm. When the ion is in zone $D$, this gives an effective NA of 0.32 for the SNSPD; accounting for the dipole emission pattern of the ion fluorescence with the quantization axis as shown in Fig. 1(b), 2.0(1)% of the emitted photons will strike the SNSPD active region [42]. An integrated current-carrying electrode running along the length of the trap between the rf electrodes generates microwave-frequency magnetic fields for qubit control. The trap electrodes are made of electroplated Au on an intrinsic Si substrate, while the SNSPD is made of amorphous Mo_0.75Si_0.25 and has a superconducting transition temperature of 5.2 K [42]. The trap is installed in an ultrahigh-vacuum low-vibration closed-cycle cryostat operated at a temperature of ≈3.5 K [56].

FIG. 1.

Trap configuration. (a) False-color scanning electron micrograph of the ion trap showing the rf electrodes (pink), SNSPD (green), and SNSPD bias leads (yellow). A trapped ion (red sphere, shown in multiple positions along the rf null line) can be transported along the trap axis by applying appropriate time-varying potentials to the outer segmented electrodes (gray). (b) Top view scale diagram showing four labeled trapping zones $A-D$ along the trap axis (double-headed black arrow), as well as the geometry of the laser beams (blue solid arrows, here shown directed at zone $D$) and quantization magnetic field ${\overrightarrow{B}}_0$, which all lie in the plane of the trap at 45° angles to the trap axis. The laser beams can be translated horizontally to follow the ion as it is transported between zones, as indicated by the faint laser beam arrows directed at zone $B$.

We trap a single ⁹Be⁺ ion with typical motional frequencies of ~2 MHz in the axial direction and 5–10 MHz in the radial directions (normal to the trap axis). The potential on the trap rf electrodes has a peak amplitude of 8.8 V at a frequency of 67.03 MHz. A magnetic field of 0.56 mT, in the plane of the trap electrodes and oriented at 45° relative to the trap axis [see Fig. 1(b)], lifts the degeneracy between hyperfine sublevels and defines the quantization axis. This field had no discernible effect on SNSPD performance, consistent with other studies at higher fields [57–59]. We use the $\left|F=2,m_F=-2\right.⟩\equiv |\downarrow ⟩$ and $\left|F=1,m_F=-1\right.⟩\equiv |\uparrow ⟩$ and $\left|F=1,m_F=-1\right.⟩\equiv |\uparrow ⟩$ states within the $2{}^{2}S_{1/2}$ hyperfine manifold as our qubit, which has a transition frequency of ${\omega }_0/2\pi \approx 1.260\mathrm{G}\mathrm{H}\mathrm{z}$. We prepare $|\downarrow ⟩$ by optical pumping on the $2{}^{2}S_{1/2}\leftrightarrow 2{}^{2}P_{3/2}$ transitions at 313 nm with ${\sigma }^{-}$ polarized light. The qubit is read out by detecting fluorescence from the laser-driven $|\downarrow ⟩\leftrightarrow \left|2^2{P}_{3/2},F=3,m_F=-3\right.⟩$ cycling transition [42]. Before detection, microwave current pulses on the trap-integrated microwave electrode are used to transfer (“shelve” [5]) population from $|\uparrow ⟩$ to the $|\mathrm{a}\mathrm{u}\mathrm{x}⟩\equiv \left|2^2{S}_{1/2},F=1,m_F=1\right.⟩$ state for improved readout fidelity. A pair of counterpropagating laser beams detuned 80 GHz blue of the $2{}^{2}S_{1/2}\leftrightarrow 2{}^{2}P_{1/2}$ transition at 313 nm are used to drive stimulated Raman transitions on the first-order secular motional sidebands, enabling sideband cooling and motional heating rate measurements [60].

One terminal of the SNSPD is grounded close to the trap chip, while the other is connected via a 50 Ω coaxial cable to room temperature bias and readout electronics [42]. The SNSPD bias current is applied only during readout and is off at other times. The output signal is amplified and filtered to remove parasitic pickup of the trap rf drive before being digitized by a high-speed Schmitt-trigger comparator. The digital pulses are counted and time stamped with 1 ns resolution.

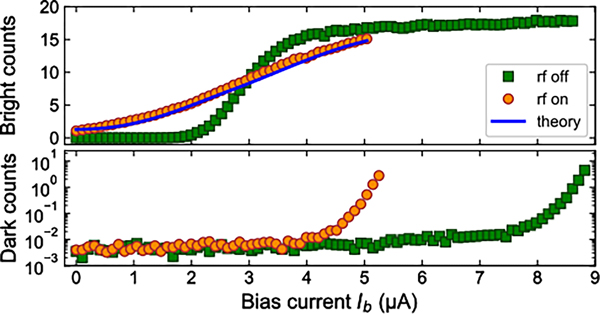
The performance of the SNSPD at 3.45 K was evaluated with the trap rf both off and on. Because an ion cannot be held without trap rf, these measurements were carried out using a simulated ion fluorescence signal generated by laser beam scatter. The beam position and intensity were chosen to give SNSPD count rates similar to those from a single ion in the trap. Figure 2 plots the bright counts (laser on) and dark counts (laser off) during a $200\mu \text{s}$ detection window as a function of the applied SNSPD bias current $I_b$, both with and without trap rf. The $I_b$ at which the critical current density of the superconducting nanowire is exceeded, known as the switching current, is ≈8.9 μA. The trap rf decreases the maximum dc bias current $I_m$ that can be applied without driving the SNSPD to the normal (nonsuperconducting) state. We attribute this reduction to induced rf currents modulating the bias current of the SNSPD [29,42]; a two-parameter fit to a theoretical model for induced rf currents, shown as the blue line, agrees quantitatively with experimental data [42]. Despite the reduction in $I_m$, the maximum bright counts with the trap rf on are only 17% lower than the maximum bright counts with the rf off. The mean dark counts per detection, both with and without rf, remain below 10⁻² for $I_b$ at least ~1 μA below the rf-dependent $I_m$. We emphasize that the dark counts in Fig. 2 are measured in the absence of laser light and are due to residual stray room light or intrinsic detector dark counts [61]. In the experiments described below, the dark count rate is dominated by stray laser light. Qubit control pulses on the microwave electrode with peak power of ~100 mW drive the SNSPD to the normal state even in the absence of bias current, but the SNSPD recovers within a few microseconds of turning off the microwave pulses.

FIG. 2.

Impact of trap rf on SNSPD performance. We plot bright (top) and dark (bottom, log scale) counts in a $200\mu \text{s}$ detection window versus SNSPD bias current, with trap rf either off (green squares) or on (orange circles), using laser scatter to simulate ion fluorescence for the bright counts. The blue line is a fit to a theoretical model accounting for induced rf currents in the SNSPD. The bright counts are background-corrected by subtracting the measured dark counts at each bias current. The 68% confidence intervals on the reported values are smaller than the plot symbols.

Ion loading occurs in trap zone $A$, 264 μm from the SNSPD center, and the trapped ion is transported to the detector (zone $D$) using time-varying potentials on the segmented outer electrodes. When the ion is held above the SNSPD, the detector count rates from ion fluorescence can be combined with knowledge of the excited state lifetime $1/\Gamma =8.850\left(2\right)\text{ns}$ [62] of the ion and the ion-detector geometry (including the ion dipole radiation pattern) to provide an absolute calibration of the system detection efficiency (SDE) of the SNSPD. The SDE is defined as the fraction of photons incident on the SNSPD that register as counts in the readout electronics. We vary the intensity of the readout laser beam and fit the corresponding count rates to determine the count rate when the atomic fluorescence transition is driven with a saturation parameter $s\gg 1$ [63]. The background count rate, arising from stray laser scatter not due to the ion, can be subtracted by preparing the ion in a nonfluorescing state and measuring the count rate. Using this technique, we extract a SDE of 48(2)% with the trap rf on and $I_b=4\mu \mathrm{A}$; accounting for the effects of rf and $I_b<I_m$, this would correspond to a maximum SDE of 65 (5)% without rf [42]. This number is slightly lower than the theoretical design SDE of 72%, potentially due to nanowire oxidation [42].

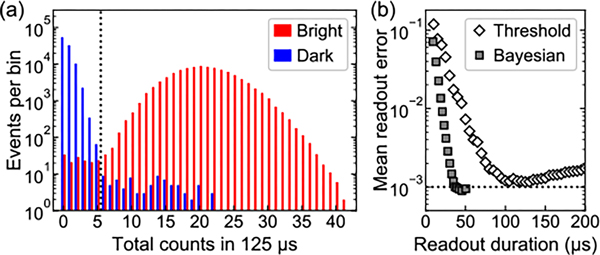
To characterize the fidelity of the qubit state readout, we prepare the ion in either the fluorescing “bright” $|\downarrow ⟩$ state or the shelved “dark” $|\text{aux}⟩$ state and apply the readout laser beam for $500\mu \text{s}$. We record the time stamps of all photons counted during this period, which enables us to vary the readout duration in postprocessing. We use heralding to improve the state preparation fidelity. We define the first $50\mu \text{s}$ of the data as the heralding period and retain for further analysis only those trials with zero photon counts in this period as prepared in the dark state and those trials with eight or more photon counts as prepared in the bright state. This method reduces the contribution of state preparation error to the total measurement error. We then analyze the readout fidelity for these trials, using only photon count data from after the heralding period, whose end defines the start of the readout period. Figure 3(a) shows histograms of measured photon counts for both states using a readout duration of $125\mu \text{s}$ after the heralding period, with a dotted line showing the threshold number of counts for optimal discrimination of bright and dark states [42]. The fidelity is limited by non-Poissonian tails that cross this threshold, arising from off-resonant pumping of $|\text{aux}⟩$ into $|\downarrow ⟩$ and from imperfections in the $|\downarrow ⟩\leftrightarrow \mid 2^2{P}_{3/2},F=3,m_F=-3⟩$ cycling transition due to polarization impurity and trap-rf-induced state mixing [42]. The minimum readout error with the thresholding method is 1.2(1) × 10⁻³ at a readout duration of $125\mu \text{s}$. We also analyze the measured state using a variant of the adaptive Bayesian method from Ref. [7]; details are given in the Supplemental Material [42]. As shown in Fig. 3(b), the mean readout duration to reach a given error level is shorter than for the threshold method, and the minimum readout error of 9(1) × 10⁻⁴, achieved with an average readout duration of $46\mu \text{s}$, is smaller than can be achieved with thresholding. The corresponding maximum readout fidelities are 0.9988(1) and 0.9991(1) for the thresholding and Bayesian methods, respectively.

FIG. 3.

Counts and readout error. (a) Count histograms (log scale) for 10⁵ trials each of preparing the bright (red) and dark (blue) states, using a $125\mu \text{s}$ detection window. The dashed vertical line indicates the optimal threshold for state discrimination. (b) Mean readout error for 2 × 10⁵ trials, half prepared dark and half prepared bright, using either standard thresholding or adaptive Bayesian methods for state determination. For the Bayesian method, the horizontal axis is the mean readout duration before reaching a given state determination confidence level. The dashed horizontal line indicates 10⁻³ mean readout error. Statistical uncertainty in the mean readout error at the 68% confidence level is smaller than the plot symbols.

The motional heating rate of the axial mode was measured in trap zone $B$, away from the SNSPD, to be 63(6) quanta/s at a frequency of $\omega /2\pi =2\mathrm{M}\mathrm{H}\mathrm{z}$, scaling with frequency as ${\omega }^{-1.7\left(7\right)}$. When centered directly over the SNSPD in zone $D$, the axial mode heating rate was measured to be 113(14) quanta/s at $\omega /2\pi =5.3\mathrm{M}\mathrm{H}\mathrm{z}$. Assuming heating rate distance scaling of $d^{-4}$ [64,65] and the measured frequency scaling from zone $B$, the scaled electric field noise over the SNSPD is estimated to be roughly 6 times higher than that over the gold electrodes, but is still on par with state-of-the-art values reported in cryogenic ion traps [65]. It is unclear whether this increase is due to noise from the wideband SNSPD bias line, to materials properties of the SNSPD, or to some other mechanism.

When the SNSPD outputs a pulse, some portion of the nanowire will stay at ground potential, while the remainder will track the output voltage. This causes a brief impulsive electric field “kick” to the ion, exciting its motion. During readout, this effect can be neglected, as the ion temperature is determined primarily by the scattering of the resonant readout laser beam from the ion. However, during operations such as stimulated Raman transitions when the ion does not spontaneously emit many photons, SNSPD pulses from stray laser light can become the dominant source of heating. Even when the bias current is off, the SNSPD will occasionally pulse in response to photons when the trap rf is on, as seen in Fig. 2. We measure the resulting heating rate on the 5.3 MHz axial mode in zone $D$ to be 0.009(5) quanta per SNSPD count. This effect limited our ability to perform Raman sideband cooling of an ion held over the SNSPD, due to stray light from the Raman laser beams. In a large-scale processor, operations with high-power Raman beams could be carried out in other trap zones, with the ion(s) transported to the readout zone(s) afterward. The addition of optically transparent SNSPD shielding electrodes may permit operations with high-power Raman beams to be performed in trap zones with integrated SNSPDs, while also reducing induced rf currents in the SNSPDs.

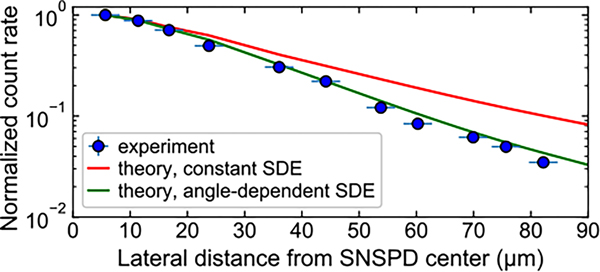
Cross talk from ions in neighboring readout zones will impact the fidelity of parallel readout with trap-integrated SNSPDs. We characterized the cross talk strength by measuring the SNSPD count rate as a function of the ion position along the trap axis. In Fig. 4, we plot the background-subtracted SNSPD count rate when the ion transition is driven with $s\gg 1$, normalized to the highest measured value, as a function of ion distance from the SNSPD center (zone $D$) along the trap axis [42]. The red curve shows the numerically calculated value assuming constant detector SDE, while the green curve uses a polarization- and incidence-angle-dependent SDE derived from finite element analysis of the SNSPD [42]. The improved agreement between the data and the angle-dependent SDE (versus constant SDE) provides, to the best of our knowledge, the first experimental measurement of the dependence of SNSPD SDE on photon incidence angle. Both theory curves are normalized to the leftmost experimental data point; this overall scaling accounts for experimental reductions in the SDE due to bias currents below $I_m$ and rf pickup [42]. The angle dependence of the SDE would help reduce cross talk errors for parallel qubit readout below the level predicted simply from the solid angle and dipole emission pattern.

FIG. 4.

Count rate spatial dependence. Moving the ion along the trap axis away from the SNSPD reduces the count rate (blue circles) more strongly than is expected based on detector solid angle and ion dipole radiation pattern alone (red line). Including the calculated angular dependence of SNSPD SDE improves agreement (green line). The 68% confidence intervals on the count rates are smaller than the symbols; those on the theoretical calculations are narrower than the plotted lines.

Our results provide a path for scalable qubit readout in ion traps. By combining multipixel SNSPD readout [66,67] with trap-integrated photonic waveguides for laser light delivery [30–32], it would be possible to create an ion trap without any free-space optical elements, potentially bringing substantial stability and performance improvements. Such traps could be used not only for large-scale quantum computing, but also for field-deployable quantum sensors, quantum network nodes, or multi-ion optical clocks. Finally, this Letter demonstrates the usefulness of individual trapped ions as well-characterized, tunable, high-precision photon sources for absolute calibration of single-photon detectors.