SUMMARY
Inference of causal transcriptional regulatory networks (TRNs) from transcriptomic data suffers notoriously from false positives. Approaches to control the false discovery rate (FDR), for example, via permutation, bootstrapping, or multivariate Gaussian distributions, suffer from several complications: difficulty in distinguishing direct from indirect regulation, nonlinear effects, and causal structure inference requiring “causal sufficiency,” meaning experiments that are free of any unmeasured, confounding variables. Here, we use a recently developed statistical framework, model-X knockoffs, to control the FDR while accounting for indirect effects, nonlinear dose-response, and user-provided covariates. We adjust the procedure to estimate the FDR correctly even when measured against incomplete gold standards. However, benchmarking against chromatin immunoprecipitation (ChIP) and other gold standards reveals higher observed than reported FDR. This indicates that unmeasured confounding is a major driver of FDR in TRN inference. A record of this paper’s transparent peer review process is included in the supplemental information.
In brief
Cataloging the structure of causal gene regulatory networks is fundamental to systems-level models of cells. Kernfeld et al. study the false discovery rate of network inference methods, employing new statistical tools to correctly account for nonlinear and indirect effects. In three examples across separate species, findings indicate unmeasured confounding that will make false discovery rate control impossible via many current approaches, indicating that new data or methods are needed.
Graphical abstract
INTRODUCTION
A transcriptional regulatory network (TRN) is the set of direct regulatory relationships between transcription factors (TFs) and their target genes in a given biological system. Inferring TRNs has been a high priority because they enable systems-based approaches to study complex biological processes. For example, TRNs can predict the effects of genetic perturbations during differentiation and development,1 reveal the genetic architecture of complex traits,2–4 and aid in drug development.5–8 These are just a few of the many applications across diverse fields of biological research in which accurate TRN models would yield useful advances.9–13
Since the advent of gene expression profiling,14,15 much effort has been dedicated to the development of computational methods to infer TRNs from transcriptomic data based on statistical association between TFs and putative target gene expression (reviewed in Nguyen et al.16 and Sanguinetti and Huynh-Thu17). As the interpretation of TRNs depends on their accuracy, evaluation of TRN inference method performance is vital. In a seminal TRN benchmarking study using gold standards ranging from simulation ground truth to yeast motif- and chromatin immunoprecipitation (ChIP)-based networks,18 the best-performing methods reached a maximum precision of roughly 0.5, meaning that even for the top approaches, roughly half of the inferred edges were incorrect. In more recent benchmarks on mammalian data, early precision with respect to cell type-specific ChIP data is at most 1.7 times better than random19 or no better than random.20 These results are not uncommon, and the high rate of false positives is widely recognized as one of the most difficult obstacles to realizing the potential of TRN inference methods.21
A general strategy for handling a preponderance of false positives is to statistically filter TRN outputs to achieve a user-specified precision, typically expressed in terms of false discovery rate (FDR) control.22–27 In brief, the FDR is the proportion of significant predictions that are expected to be false positives, and there are various ways to estimate the FDR of TRN inferences (see Box 1). If FDR estimates are accurate, then the user can generate a TRN in which only a specified fraction of edges are false positives. This makes it much more likely that the downstream uses of the TRN (e.g., predicting transcriptional effect of perturbations) will be fruitful and that experimental follow-up will be efficient.
Box 1. False discovery rate control.
Given a collection of hypothesis test results, FDR is defined as the expected proportion of false positives among the significant findings.28 If 100 tests are conducted with a p value cutoff of 0.05, and 15 discoveries are made, a reasonable estimate of the FDR is 5/15. Eliding certain technicalities, a slightly modified FDR equals one minus the expected precision, and it also equals the posterior probability that a randomly chosen positive result is a false positive.29,30 FDR control has become standard in many fields, including differential gene expression analysis31 and neuroimaging,32 due to its simple interpretation and useful balance between stringency and power.28
Most TRN methods, including widely used methods such as GENIE3 and ARACNE,33,34 do not report FDR at all. For those that do, FDR estimation typically begins by independently permuting expression values within each column of a samples-by-genes matrix.22,23,27 Then, any measure of association can be computed to yield a statistic for each gene-gene pair in the original and permuted data (Box 1 Figure A). For true relationships, the original, unpermuted data should give a stronger association (Box 1 Figure A, red). For a given significance cutoff, a common estimate of the raw number of false discoveries is the fraction of findings arising from the permuted data. As an alternative, some TRN FDR control methods rely on bootstrapping or multivariate Gaussian assumptions.24,35 In the STAR Methods, we summarize assumptions of FDR control methods used in this study.
How can we be sure that the FDR reported by a TRN inference method is accurate? Ideally, reported FDR is compared with the observed FDR, which is computed by counting the fraction of false discoveries emerging from inferring a TRN in a biological context in which the true TRN is known (Box 1 Figure B).
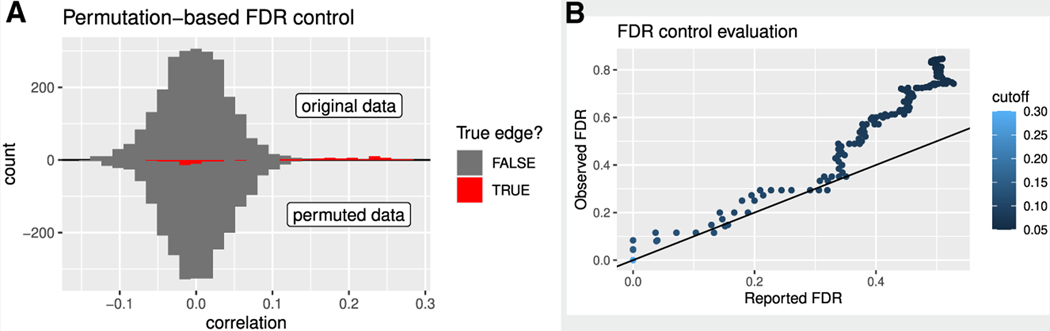
Box 1 Figure. Evaluating permutation-based FDR control in a simple example network.
(A) Correlations before and after permuting. This analysis is from a simulated network with 25 regulator-target pairs and n = 1,000 observations. Color indicates whether the edge is truly present in the network.
(B) For various correlation cutoffs (colorscale, unitless), the observed FDR from the known network structure (y axis) and the FDR reported by the permutation procedure based on the fraction of gene pairs that are permuted (x axis).
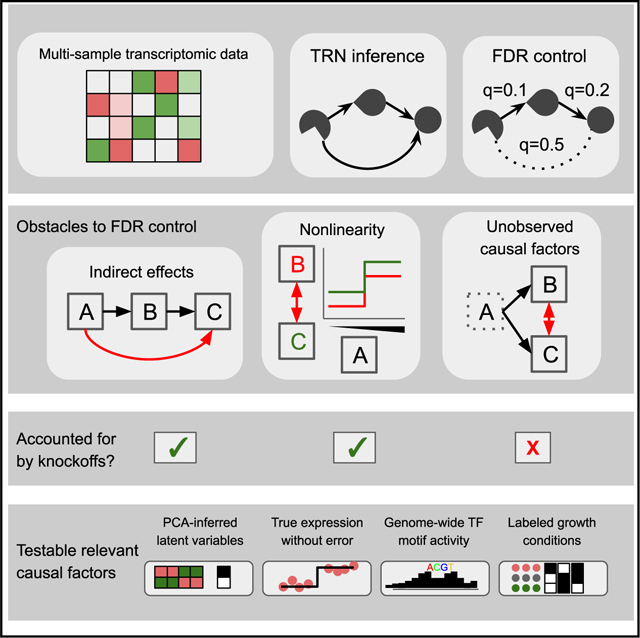
Unfortunately, FDR-controlled TRN inference faces distinctive and challenging obstacles. First, permutation tests cannot account for indirect effects.36,37 Second, methods allowing indirect effects typically make strong assumptions of linear and Gaussian data,25,38 whereas responses to TFs are neither fully understood nor empirically linear.39,40 Third, some TRN inference methods do not estimate the causal graph structure; instead, they infer a closely related undirected graph called the Markov random field (MRF) structure. Though the nodes of the MRF are identical to the nodes of the causal graph, the MRF counterpart to a causal graph structure has additional edges necessary to capture dependencies between nodes with shared downstream effects.41 Fourth, TRN inference depends on a crucial assumption known as causal sufficiency,41,42 which requires all relevant causal factors to be measured. However, transcriptomic data are heavily affected by unobserved confounders that may include batch effects or post-transcriptional regulation. Finally, gold standard data are incomplete, biased toward specific well-studied regulators, and lacking in high-confidence curated negative results, so that reported and observed FDR are not directly comparable. Indeed, prior work on FDR-controlled TRNs has not systematically compared reported FDR on real datasets against gold standards.22–27,43
We develop gold standards and approaches for a fair empirical evaluation of FDR control across a variety of methods and assumptions. In order to directly test or completely avoid certain modeling assumptions, we contribute a computationally efficient adaptation of the model-X knockoff filter, which has distinctive advantages for TRN inference36,44 (Box 2). By applying this approach and others to benchmark FDR control in TRN inference on simulated and real data, we find that the reported FDR underestimates the observed FDR, leading to inflated confidence in the resulting TRN. After systematically eliminating other sources of error, we find that transcriptomic data do not satisfy causal sufficiency, even when certain likely confounders are included in the models. Because this is an inherent limitation of the datasets we study, FDR control is unlikely to be achievable by any TRN inference method. Because our approach should be useful to diagnose obstacles to causal network inference across a variety of domains and data types, we have made our software and documentation freely available (STAR Methods).
Box 2. The model-X knockoff filter.
The model-X knockoff filter was designed for supervised machine learning problems with a target Y and features X. The knockoff filter is a class of algorithms that control FDR while selecting a relevant subset of features from X. Here, a feature is defined to be relevant if it is dependent on Y conditional on all other features. This notion of relevance exactly matches many TRN inference methods.34,45,46
Given a target Y and a set of features X, the procedure begins by constructing knockoffs K that act as negative controls for each feature in X. We use a specific type of knockoffs, called model-X knockoffs, that are based on a probability model for X. Valid model-X knockoffs must obey a specific mathematical criterion: any set of features S can be swapped with the corresponding original features while preserving the joint distribution of the data and the knockoffs. Formally, [XS,XSc,KS,KSc] and [KS,XSc,XS,KSc] are equal in distribution, where Sc denotes the complement of S, meaning Sc contains the indices of the features that are not swapped with their knockoffs.36,44 Model-X knockoff construction relies on an assumed probability model for the features X, and different software implementations have enabled knockoff construction from different families of distributions.47,48 In this work, we use Gaussian knockoffs36,44 or Gaussian mixture model knockoffs.49
Given the knockoffs, the analyst may measure feature relevance via any “knockoff statistic” as long as it obeys a key symmetry property: the absolute value of the knockoff statistic must remain the same when any set of features is swapped with its knockoffs. The feature importance should be positive whenever the feature is more important than its knockoff and negative otherwise. We typically use a LASSO regression including both X and its knockoffs. We record the maximum penalty parameter at which a feature or its knockoff is still selected into a LASSO regression. If the knockoff enters before the original feature, we make it negative. This statistic is a common choice with good power in simple settings.50 Tree-based or other statistics could also be used.
Under the null hypothesis of conditional independence, the knockoff statistics are symmetric about zero, so the left and right tails of the sampling distribution are identical.44 For a given cutoff t, the estimated FDR is the number of statistics below —t divided by the number above t. The threshold t can be raised or lowered to control the FDR at the desired level.
The model-X knockoff filter has two distinctive advantages for TRN inference. First, even when using a linear model internally, maintaining error control requires no assumptions about . Second, assumptions about P(X) are directly testable and can be customized to each dataset.
RESULTS
Efficient generation of model-X knockoffs enables computationally tractable genome-wide TRN inference
Our approach centers on a recent innovation in high-dimensional statistics: model-X knockoffs.36,44 Model-X knockoffs were originally intended to be applied to individual regression problems, not network inference. Here, we use model-X knockoffs to build a network by regressing each gene on all other genes. If done naively, this process requires time proportional to the fourth power of the number of genes. We derived methods to re-use portions of the calculations to improve runtime and memory consumption for high-dimensional data, and our approach saves considerable computational resources (Figures S1A and S1B). Rather than running the whole procedure independently for each gene, which would control FDR separately in many subsets of the network, we pool the symmetric statistics and use the same threshold t across all regressions. This method has no theoretical guarantee, but per-target FDR control and global FDR control are not equivalent (STAR Methods), and simulations indicate that pooling improves global FDR control (Figure S1C).
Model-X knockoffs approximately control FDR in TRN inference from simulated data
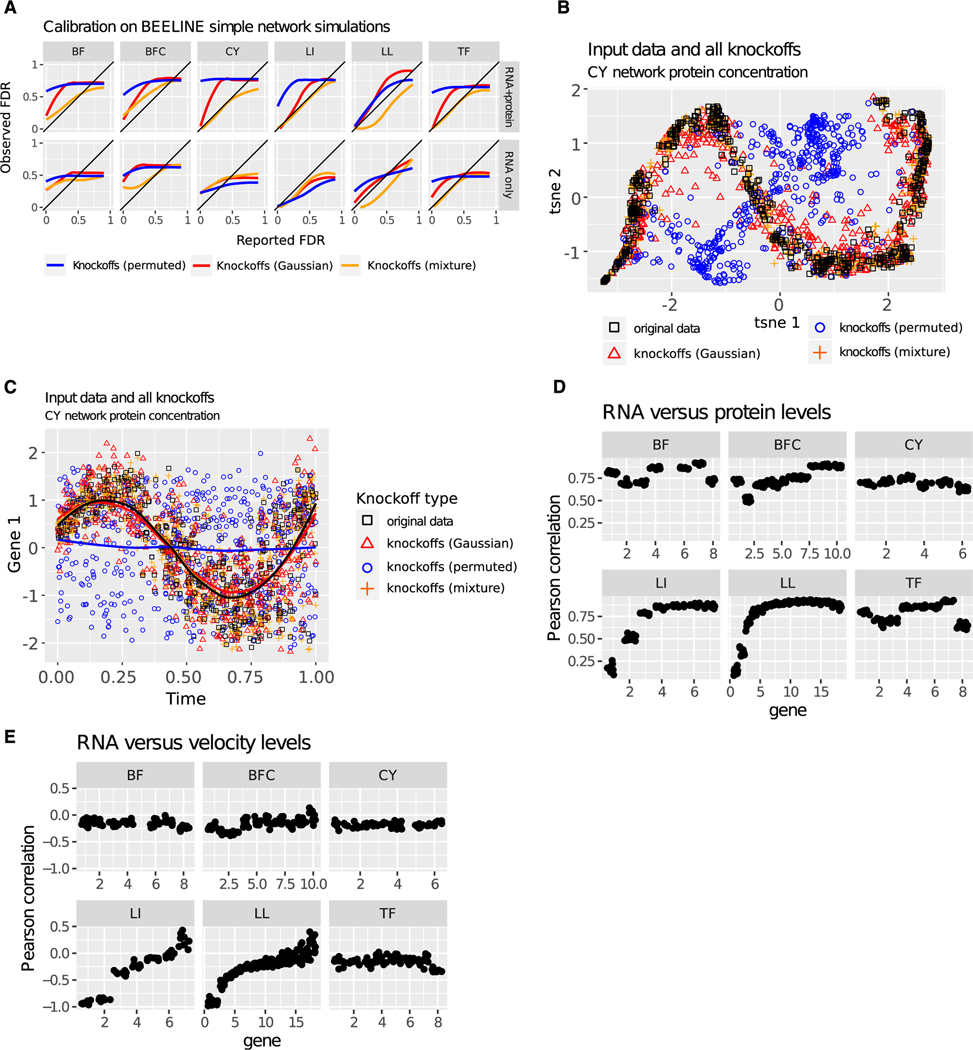
To test the reliability of model-X knockoffs in a controlled setting, we used the previously published simulated network data from the BEELINE TRN inference benchmarking framework.19 BEELINE evaluates TRN inference on a variety of datasets simulated from nonlinear stochastic differential equations, with various known network structures giving rise to different types of developmental trajectories. We generated knockoffs with three different methods that reflect different modeling assumptions. The first method, labeled “Gaussian,” used Gaussian knockoffs with covariance equal to the sample covariance matrix. Though the data are not Gaussian, Gaussian knockoffs are simple to construct, and they may be adequate given that the knockoff filter is somewhat robust to mis-specification.51,52 The second method, “mixture,” used a Gaussian mixture model,49 which is again mis-specified, but provides more flexibility than Gaussian knockoffs for cases where the data are nonlinear or multimodal. The third method, “permuted,” randomly permutes samples within each gene (independent of the permutation applied to the other genes). Independently permuting the entries of each feature yields valid knockoffs, but only if all features are independent.53 Genes in this simulation are not independent, as the simulation is specifically meant to reflect regulatory cascades.19 Thus, permutation is not expected to yield adequate knockoffs; however, we include this method due to the popularity of permutation methods for error control in TRN inference.22,23,26,27,54 We provided the simulated data to the knockoff filter using only RNA expression levels (“RNA only”) or revealing RNA expression, RNA production rate, and protein levels (“RNA + protein”). The latter captures the full state of the simulation. Using networks capable of generating a variety of temporal trajectories, these experiments provide a baseline expectation for the behavior of the knockoff filter in TRN inference.
Results show that FDR control depends on testing the correct null hypothesis, choosing an adequate model for knockoff construction, and obtaining causally sufficient data. When using permutation to test the incorrect null hypothesis that all genes are independent, excess false positives are observed in 10/12 evaluations (Figure 1A, blue trend lines). When testing the correct null hypothesis, but using Gaussian knockoffs on these non-Gaussian data, excess false positives are observed in 10/12 evaluations (Figure 1A, red trend lines). When testing the correct null hypothesis using a flexible mixture model for knockoff construction, excess false positives are observed in only 5/12 evaluations (Figure 1A, orange trend lines). When considering tests where the correct null is tested via flexible knockoffs on causally sufficient data with protein concentration and RNA production rate revealed, only 2/6 tests show slight excess FDR (Figure 1A, orange trend line, top row). When protein levels and transcription rates are revealed, proteins are assumed to regulate transcripts and not vice versa, so non-oriented edges from the knockoff filter can be oriented, and backward edges are counted as false positives (Figure 1A, bottom row). With RNA only, static methods cannot infer directionality, so edge direction was not considered when calculating FDR (Figure 1A, bottom row). This difference in evaluation may account for better performance in the RNA-only condition for some experiments.
Figure 1. FDR control with model-X knockoffs using simulated data.
(A) Reported FDR versus observed FDR for knockoff-based hypothesis tests used to infer TRNs based on data simulated with the BEELINE framework in which the ground truth TRN is known.19 The “reported FDR” represents the target false discovery rate (FDR) that is reported by the algorithm. The “observed FDR” is calculated by comparing inferred TRN to the ground truth TRN. The six networks are listed across the top margin: bifurcating (BF), bifurcating converging (BFC), cyclic (CY), linear (LI), linear long (LL), and trifurcating (TF). In the top row (RNA + protein), RNA concentrations, protein concentrations, and RNA production rates are all revealed, and edges in the wrong direction are counted as incorrect. In the bottom row (RNA only), RNA concentrations are used as input to the algorithm, following Pratapa et al. In the bottom row, edges in the wrong direction are counted as correct. The colors indicate three methods of knockoff construction: independent permutation of all features (permuted), second-order knockoffs (Gaussian), and Gaussian mixture model knockoffs (mixture).49 Results are averaged over 10 independent simulations, each with 500 cells. A line below the diagonal indicates a conservative method: observed FDR is lower than reported. A line above the diagonal indicates an overconfident method: observed FDR is higher than reported. A diagonal line indicates a well-calibrated method.
(B) Protein expression for all genes in a realization of the BFC network (n = 500), along with three types of knockoffs (n = 500 each), all jointly reduced to two dimensions via t-stochastic neighbor embedding (t-SNE).55 The colors indicate three different methods of knockoff construction.
(C) Protein concentration and corresponding knockoff features for gene 1 n = 500 cells simulated from the CY network model, plotted against time. No cell is measured twice, and each dot is the terminus of an independent trajectory. Time is not used as input for generating knockoffs. The colors indicate three different methods of knockoff construction.
(D) Pearson correlation between RNA concentration and protein levels for each gene across all simulations used. Each dot summarizes one gene in n = 500 simulated cells.
(E) Pearson correlation between RNA concentration and RNA production rate for each gene across all simulations used. Each dot summarizes one gene in n = 500 simulated cells.
Figure 1A highlights that the specific model used to generate model-X knockoffs must be chosen carefully. Fortunately, goodness-of-fit can be assessed even without gold-standard data on network structure. For example, trends over time or joint embeddings can directly test the swap condition that defines valid knockoffs (Box 2). Applied to protein concentrations from the cyclic network structure, these comparisons reveal a complete lack of structure in permuted knockoffs and subtle deviations from the original data distribution in Gaussian knockoffs. Mixture-model knockoffs are visually indistinguishable from the original data (Figures 1B and 1C).
Figure 1A also highlights how FDR control relies on observation of all causal factors, which in this simulation include protein concentrations. Correlations between protein and RNA levels or RNA production rate and RNA levels were sometimes low or negative (Figures 1D and 1E) and can also be poor in real data.56 Failure of FDR control despite using a model that yields plausible knockoffs is a sign that some causal factors were not measured.
Model-X knockoffs control FDR in testing conditional independence on a large, diverse E. coli dataset
Next, we tested the extent to which standard knockoff construction methods can match the distribution of real data. We chose the Many Microbe Microarrays Database, which is comprised of gene expression data for 4,511 genes, including 334 TFs, across 805 E. coli samples.57 As with the BEELINE data, we constructed knockoffs using three approaches: a Gaussian distribution based on the sample covariance matrix, a Gaussian mixture model (cluster assignments are shown in Figure S2A), and independent permutation of each gene. However, because the Many Microbe Microarrays dataset is higher dimensional than the BEELINE data, the sample covariance matrix may be a poor estimator.35 Therefore, we tested four additional sets of Gaussian knockoffs based on established methods for high-dimensional covariance estimation. For the “shrinkage” method, we used an adaptive shrinkage method.35 For the “glasso_0.01,” “glasso_0.001,” and “glasso_1e—4” methods, we used graphical LASSO with penalty parameters 10−2, 10−3, and 10−4.58 Stronger regularization may lead to estimates that fit the data worse and also to worse-fitting knockoffs. Because setting the strength of shrinkage parameters is not fully understood in the context of knockoff construction, we tested a range of options empirically.
We evaluated the resulting knockoffs using three types of diagnostics. The first diagnostic used high-dimensional visualization to determine how well each knockoff construction method preserved qualitative properties of the data. We concatenated the TF expression matrix with all TF expression knockoffs and jointly reduced to two dimensions via t-stochastic neighbor embedding (t-SNE)55 (Figure S2A). Most methods appeared similar to the original data, but in the permuted method, the distribution of the knockoffs has very little overlap with the distribution of the original data. Based on this diagnostic, permuted knockoffs will not control FDR.
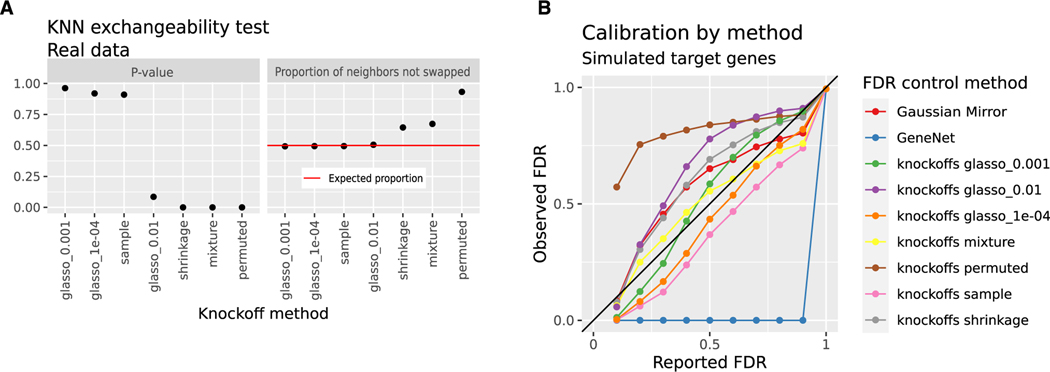
The second diagnostic is a swap test based on k-nearest neighbors (KNN) that is sensitive to any violation of the key exchangeability criterion that valid knockoffs must satisfy.47 For data with N observations and D variables, this test creates a matrix of size 2N by 2D, including original features in the upper left, knockoffs in the upper right, and original features randomly swapped with knockoffs in the bottom half. For any row in the top (unswapped) half of this matrix, the expected proportion of nearest neighbors that is in the bottom (swapped) half is 50%, and Romano et al. describe how to test this 50% proportion as a null hypothesis. Low p values indicate evidence that knockoffs are invalid. Most knockoff generation methods failed this test, but the sample, glasso_0.001, and glasso_1e—04 methods showed no evidence of poor fit (Figure 2A). Based on this test, the sample, glasso_0.001, and glasso_1e—04 model-X knockoff constructions should control FDR in testing for conditional independence.
Figure 2. Model-X knockoffs control FDR in testing conditional independence.
(A) KNN-based swap test with k = 20. This diagnostic swaps all variables with their knockoffs, then compares each observation to its unswapped counterpart, measuring how many nearest neighbors are swapped or unswapped.47 Low p values (left) and proportions of non-swapped neighbors far from 50% (right) indicate a poor fit. For ideal knockoffs, the expected proportion of non-swapped neighbors is 50%. There are n = 805 samples in the DREAM5 E. coli data.
(B) Reported and observed FDR of various methods used to select regulators for each of 1,000 simulated E. coli target genes. Real regulator expression is used to simulate target genes as shown in Algorithm 1. The colors indicate different methods for FDR control. The x axis displays the FDR reported by the method, while the y axis shows the observed fraction of false discoveries based on what is known from the simulation. Data above the diagonal indicate excess FDR. GeneNet returns no findings except at an FDR cutoff of 1.
See also Figure S2.
In the third diagnostic, we followed a commonly used simulation scheme that uses real TF expression and simulated target gene expression (Algorithm 1). Using real regulator data and simulated targets adequately tests the assumptions of model-X knockoff construction, which only requires a correct model for regulators and not targets. Using the same simulated targets, we also benchmarked two methods that assume target genes follow a linear relationship with their regulators: we tested the GeneNet R package25 and the Gaussian mirror.59 GeneNet is conservative, returning no discoveries except at an FDR of 1. The Gaussian mirror and most knockoff-based methods failed to control FDR, with permuted knockoffs performing worst. The sample and glasso_1e—04 knockoff constructions yielded slightly lower observed than reported FDR (Figure 2B).
These three diagnostics characterized several attempts at FDR control in tests of conditional independence using real TF expression data. Based on the combined results, we conclude that the sample and glasso_1e—04 knockoff constructions are valid model-X knockoffs and can control FDR in testing conditional independence.
A modified knockoff filter allows FDR calibration with incomplete gold standards
The preceding section addressed fitting the distribution of knockoffs to real data, for example, using real regulator data with simulated target genes. However, tests on real target genes are also necessary, which raises an additional complication: gold standard data from ChIP or literature curation are incomplete. Below, we will describe gold standards based on direct binding data (ChIP-chip, ChIP sequencing [ChIP-seq], and ChIP-exo) and genetic perturbations followed by transcriptomics. When direct binding data and perturbation data both support the presence of a TF-target edge, it will be included in our gold standard positives, and likewise, when neither support an edge, it will be included in our negatives. Where the two sources disagree, edges will be annotated as unknown. These gold standards may contain disproportionately more positive or negative examples because they include only the most confident conclusions and they measure only a small fraction of active regulators. Because the base rate of positive examples does not match the network as a whole, even perfect methods run on ideal data would not report the same FDR that is observed relative to the gold standard.
Algorithm 1.
Measuring FDR control with synthetic target genes
| Input: |
| - TF expression (matrix, observations by genes) |
| - , , and will denote expression for a given sample and/or gene . |
| - A desired FDR level |
| - The number of simulations |
| - Sets of indices indicating the true regulators in each simulation. We select the number of regulators as max(M, 1), where M is Poisson with mean 2. Then we select regulators randomly without replacement. |
| - Dose-response curves dictating the true response to the regulator in each simulation. We set if for all in and otherwise. |
| Procedure: |
| - For : |
| - For : |
| - Generate . |
| - Run the knockoff filter to obtain pairs at FDR . |
| - For : |
| - If is in , count as correct. |
| - If is not in , count as a false discovery. |
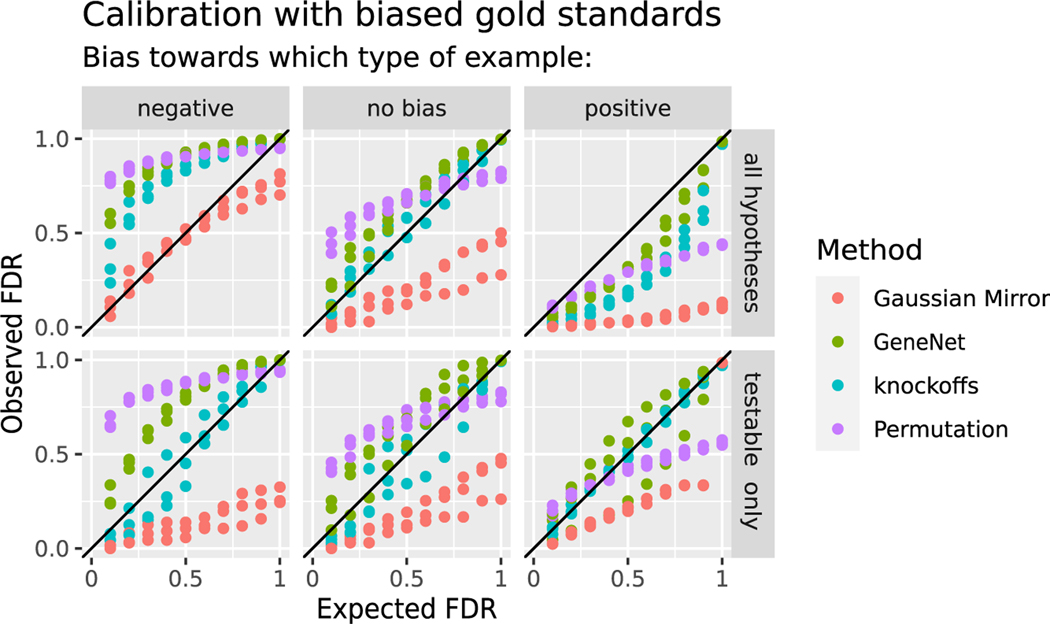
To account for bias in FDR checks using incomplete gold standards, we designed a simulation study where gold standards are purposefully biased toward positive or negative examples (STAR Methods). We tested FDR control by partitioning the TF-target relationships from each gold standard into three sets: a set of positives P, a set of negatives N, and a set of unknowns U. Each hypothesis was considered testable if it was in P or N. We carried out the final step of the knockoff filter (the selective SeqStep procedure36) either on all hypotheses as usual or on only testable hypotheses. Focusing the analysis on testable hypotheses correctly calibrated the reported FDR from the knockoff filter to match the observed FDR from incomplete gold standards, whereas including all hypotheses failed to align the reported and observed FDR (Figure 3, blue). This simulation suggests that the knockoff filter will control FDR as measured by gold standards consisting of high-confidence positive and negative TF-target relationships, as long as the final step is applied to testable hypotheses only.
Figure 3. Model-X knockoffs allow direct comparison of predicted FDR to incomplete gold standards.
Reported FDR versus observed FDR on fully synthetic data with n = 805 samples. Although the data are simulated and all causal relationships are known, the evaluation uses biased gold standards in which 80% of causal relationships are marked as unknown (left) or 80% of gene pairs with no causal relationship are marked as unknown (right). In the top row, we applied the final step in each FDR control method to all hypotheses, while in the bottom row, we applied the final step only to hypotheses that are testable given the remaining gold standard data. The colors indicate different methods for FDR control.
We applied the same tactic using permuted knockoffs and using the Gaussian mirror, which also uses selective SeqStep as the final step. We attempted to use GeneNet in a similar way by applying its final step, a mixture model with a parametric null distribution, to testable hypotheses only. The Gaussian mirror had lower observed than reported FDR and, in fact, was overly conservative, except when testing all hypotheses against negatively biased gold standards. Effects of gold standard bias were greatly reduced by using testable instead of all hypotheses (Figure 3). GeneNet and the permutation-based knockoffs had elevated observed FDR except on positively biased gold standards (Figure 3), and for GeneNet and permuted knockoffs, benchmarking testable hypotheses did not fully remove bias due to incomplete gold standards. We also attempted to benchmark BINCO, which is promising due to its ability to accommodate nonlinear indirect effects.24 But, as in prior reports,23 we encountered software errors because BINCO requires a U-shaped distribution of test statistics, which our data did not produce.
In summary, no alternative method was as successful as model-X knockoffs in matching observed and reported FDR in the presence of incomplete gold standard data. The Gaussian mirror may be a usable conservative alternative, but GeneNet or permutation-based benchmarks on positively biased gold standards are likely to be too optimistic.
Reported FDR underestimates observed FDR in the DREAM5 E. coli expression data
The preceding tests address nonlinear responses, indirect effects, and incomplete gold standards as sources of excess FDR. However, all TRN inference methods used in this work also assume causal sufficiency, meaning they assume all factors affecting transcript levels have been measured. Causal factors that are unmeasured present a fundamental issue in network inference, yielding statistical relationships among observed variables where no causal connection exists.41,42 For example, if a TF and a gene that is not a direct target are both controlled by retinoic acid levels, unmeasured variation in retinoic acid levels could lead to a correlation between the TF and the non-target gene. Simple measurement error also would violate the causal sufficiency assumption, as would compositional effects (Simpson’s paradox) or experimental batch effects. We discuss this further and show simulations in the STAR Methods. It is unclear a priori whether measuring mRNA levels of candidate regulators, along with metadata on cell types or culture conditions, is enough to approximate causal sufficiency in typical TRN inference tasks. This motivated us to test FDR control on real data.
To test FDR on real data, we developed two gold standards based on convergent results of distinct experimental designs. For a TF-target relationship to be included as a testable hypothesis, we required concordant evidence from both ChIP data and genetic perturbation followed by transcriptomic analysis rather than a replicated result between similar experiments (e.g., multiple ChIP experiments). For one gold standard, we collected ChIP targets and knockout data from RegulonDB v10.9,60 and for the other, we combined RegulonDB ChIP data with all genetic perturbation outcomes from the Many Microbe Microarrays Database (except where genetic effects were confounded by differences in growth medium). To check the reliability of these sources, we compared each dataset against the others and against RegulonDB v10., which is a manually curated collection supported by evidence from binding motif occurrences, binding assays, site mutation, or gene expression assays. We also compared against a small number of validation experiments from the DREAM5 competition.18 The various sources were well-supported by one another, except for RegulomeDB knockout data, which frequently did not support hypotheses from other sources and thus may be under-powered (Figure S2B). These two gold standards contained 754 positive and 8,496 negative examples across 6 TFs (8% edge density), with each example having two types of concordant evidence. We note that these gold standards’ edge density is likely much higher than the true network density, as an 8% edge density with roughly 300 total TFs would imply roughly 24 TFs directly regulating the average target gene. The true network density is unknown, but other bacteria provide perspective: in Mycobacterium tuberculosis, ChIP and perturbation of hundreds of TFs found 7,248 DNA-binding locations in the presumed promoters of 2,520 unique genes (roughly 3 TF binding sites per gene),61 and in Bacillus subtilis, TRN inference has found 4,516 regulatory relationships across 3,086 genes (roughly 1.5 per gene).62 This is evidence that the TFs featured in available E. coli ChIP and knockout data are more promiscuous than average, underscoring the importance of FDR assessment methods that tolerate imbalanced gold standards.
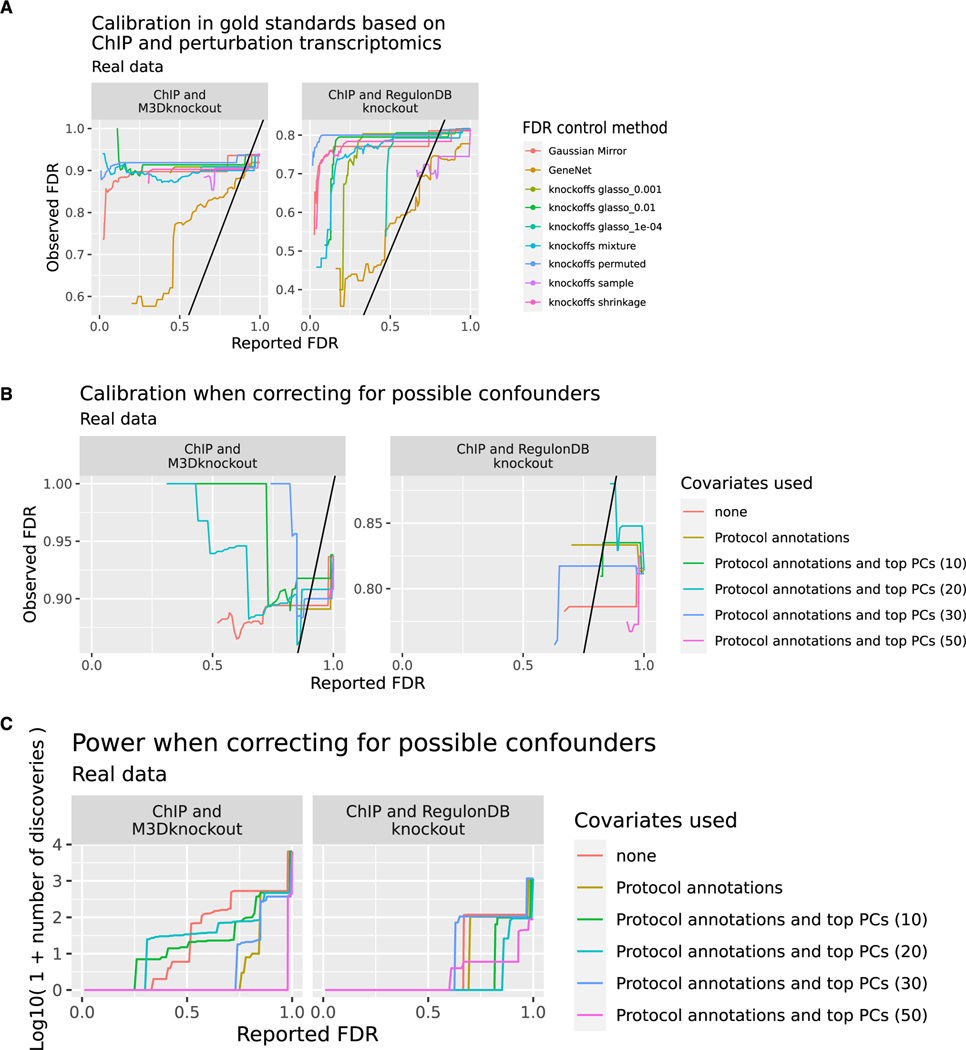
Combined with our method for testing FDR control on unbalanced gold standards, this resource provides a tractable method to check FDR control on a real TRN task. We performed knockoff-based TRN inference using GeneNet, the Gaussian mirror, and a variety of model-X knockoff constructions, fully described in the STAR Methods. We then checked results on the testable hypotheses from the two gold standards. No method successfully controlled FDR on real data (Figure 4A; Table S2). Notably, the glasso_1e—04 knockoffs, which successfully controlled FDR on simulated data (Figure 2B), failed to control FDR when applied to real target genes. The sample method displayed very low power on real data, with almost no testable discoveries below q = 0.5, so we were unable to assess observed FDR for sets of hypotheses with low reported FDR (Table S2). GeneNet was closest to controlling FDR on real data, but its observed FDR often exceeded its reported FDR.
Figure 4. Diverse methods do not control FDR in TRN inference.
(A) Comparison of FDR reported by each method (x axis) and observed FDR (y axis) across different methods and gold standards. The observed FDR is calculated across hypotheses that are testable using an intersection of target gene sets from ChIP and perturbation transcriptomics experiments. M3DKnockout refers to the genetically perturbed samples from the Many Microbe Microarrays Database57 while RegulonDBKnockout refers to genetically perturbed samples downloaded from RegulonDB. When fewer than 10 testable hypotheses are returned below a given reported FDR, the observed FDR is highly uncertain, and we leave the left part of the plot blank. The colors indicate different methods of FDR control. Analysis is based on n = 805 microarray profiles.
(B) Reported and observed FDR when correcting for labeled and unlabeled indicators of confounding. Knockoffs are constructed using the glasso_1e—04 method conditioning on no covariates, on labeled perturbations, or on both labeled perturbations and the top (10, 20, 30, 50) principal components of the full expression matrix. When fewer than 10 testable hypotheses are returned below a given reported FDR, the observed FDR is highly uncertain, and we leave the left part of the plot blank. The colors indicate which confounders were controlled for. Analysis is based on n = 805 microarray profiles.
(C) Power (number of discoveries) in the same analysis shown in (B). The colors indicate which confounders were controlled for. Analysis is based on n = 805 microarray profiles.
Permutation procedures test the overly strong null hypothesis that each gene is independent of all other genes, and permutation tests will thus mistake indirect effects for direct effects.36,37 As an example of how these findings can affect biological interpretation, consider the melibiose regulator melR, which was shown by DNase footprinting, ChIP-chip, and knockout transcriptomics to have a total of 3 or 4 target genes.63,64 Analyses using permuted knockoffs yielded 131 predicted targets of melR. These discoveries were nominally significant at a reported FDR of 0.01, but the only known target among the 131 results was melA. The spurious targets detected by permutation-based FDR control span diverse biological functions, and if taken literally, these findings would massively revise the field’s perception of melR’s function. By contrast, GeneNet, knockoffs with glasso_1e—04 covariance estimation, and knockoffs based on the sample covariance do not discover any melR targets at 0.01 FDR. For GeneNet, at reported FDR of 0.2, a total of six findings include two known targets, melA and melB. These results show that using calibrated conditional independence tests in place of permutation tests to estimate FDR can reduce the volume and perhaps the rate of false discoveries on a real TRN task, with meaningful improvement in interpretation.
Causal factors that are unmeasured present a fundamental issue in causal statistics, yielding conditional dependence relationships among observed variables where no causal connection exists. One problem falling under this umbrella is confounding by technical factors.65,66 Another is exogenous perturbations: for example, repressor proteins can be activated by binding to a ligand, and this does not require altered mRNA levels.67 We sought to address these possibilities with a combination of labeled perturbations present in the data and estimation of unobserved confounders via unsupervised machine learning. Unsupervised methods such as principal-component analysis (PCA) can estimate unwanted variation from transcriptome data, for example, cleanly separating batches.68 Similar methods have been used to remove batch effects prior to network inference.65,66
To address possible confounding, we tested against gold standards while conditioning on labeled perturbations and principal components. Combined with the glasso_1e—04 knockoff construction method, this approach effectively removed associations with all factors explicitly conditioned upon, producing very high q-values that indicate no evidence for conditional dependence (Figure S2C). Conditioning on labeled perturbations and principal components did not restore FDR control relative to either gold standard (Figure 4B). Observed FDR was volatile (Figures 4A and 4B), likely because very few discoveries contributed to the observed FDR estimates (Figure 4C). It remains unclear whether accounting for principal components or surrogate variables in transcriptome data alone could mitigate the false discoveries driven by unmeasured confounders. Furthermore, use of PCA as a proxy for unmeasured confounders may limit power by removing useful signal.66
In principle, conditional independence tests do not directly estimate the causal graph structure; instead, they infer a closely related undirected graph called the MRF structure. Though the nodes of the MRF are identical to the nodes of the causal graph, the MRF has extra edges.41 Specifically, the neighbors of a node Y in the MRF consist of the parents, the children, and the spouses (parents of children) of node Y in the causal graph. The spouses may manifest as excess false discoveries, even if the MRF structure is otherwise learned with controlled FDR. We accounted for spouses by treating all TF-TF edges as unknown and excluding them from the real-data calibration estimates described above. Thus, spousal relationships cannot explain the excess FDR we observe, and failure of causal sufficiency remains the likely culprit.
Reported FDR underestimates observed FDR in mouse and human RNA-seq data with paired chromatin state
Statistical assumptions that work or fail for TRN inference in E. coli may not work or fail the same way in eukaryotes.18 Furthermore, modern multi-omic methods merge mRNA measurements with much more molecular information, and this may suffice to capture influences missed in mRNA data. In particular, genome-wide averages of downstream transcription or accessibility near known TF binding motifs may contain information about TF activity that is not present in counts of any individual TF transcript.69 To evaluate knockoff filter FDR control on multi-omic data, we turned to a mouse skin and hair follicle dataset consisting of paired RNA and chromatin measurements on 34,774 single cells from an unknown number of female mice70 and a dataset of 10,691 human peripheral blood mononuclear cells (PBMCs) from a single donor, generated using 10x Genomics’ simultaneous RNA sequencing (RNA-seq) and ATAC-seq.71 We first applied our models to the RNA portions of these datasets to explore FDR control, and then we incorporated various types of information from the ATAC portion.
Single-cell sequencing suffers from large measurement error. In theory, measurement error can cause false positives in network inference (STAR Methods). To reduce the effect of measurement error, we averaged the data across cells within 100 k-means clusters and discarded any cluster with <10 cells, producing 57 clusters (skin) or 46 clusters (PBMCs). This is a reasonable method for separating biological and technical variation since a similar approach has been shown to yield groups of cells that are consistent with an identical expression profile perturbed by multinomial measurement error.72 For the skin data, most clusters had at least 80% of their cells sharing the same annotation from prior analysis.70 We generated permuted knockoffs and Gaussian knockoffs for the resulting TF expression matrix (57 clusters by 1,972 TFs, skin, and 46 clusters by 1,108 TFs, PBMCs). Since there are more TFs than expression profiles, we could not construct Gaussian knockoffs using the sample method as done in the E. coli analyses; instead, we used a positive-definite optimal shrinkage estimator.35
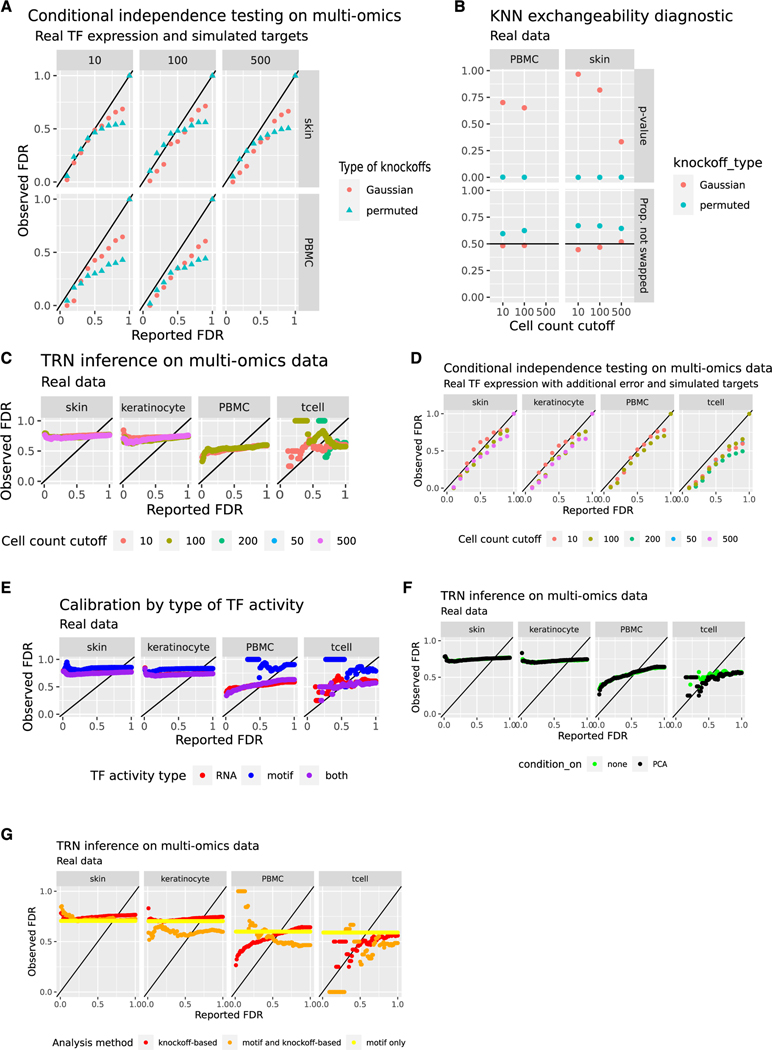
We used two diagnostics to evaluate conditional independence tests prior to addressing questions of causality: simulated target genes and the swap-based KNN test. For simulated target genes, both types of knockoffs controlled FDR (Figure 5A). The KNN swap test found no evidence against Gaussian knockoffs but strong evidence for failure of permuted knockoffs, suggesting that genes in natural data are not all statistically independent (Figure 5B). This demonstrates that permutation-based methods are unlikely to control FDR in TRN inference or in the simpler subtask of conditional independence testing, but Gaussian knockoffs can control FDR in conditional independence tests.
Figure 5. FDR calibration is not improved by including TF activity inferred from single nucleus multiomics data.
This figure contains a mixture of real and simulated data.
(A) Error control in detecting regulators based on simulated target gene expression. Simulation uses real TF RNA data from the PBMC (n = 10,691 cells) and mouse skin (n = 34,774 single cells) multi-omics datasets. Targets are simulated as described in Algorithm 1. Knockoffs are constructed via independent permutation of each gene’s values (permuted) or Gaussian model-X knockoffs using an optimal shrinkage estimator35 for the covariance matrix. 1,000 target genes are simulated. The x axis displays the FDR reported by the method to the user, while the y axis shows the observed fraction of false discoveries based on the ground truth from the simulation setup. The colors indicate different methods for knockoff construction.
(B) KNN swap test with k = 5 and swapping all variables (“full”, not “partial”).47 Low p values (vertical axis) and high proportions of non-swapped neighbors (horizontal axis) indicate a poor fit. Results are shown for permuted and Gaussian knockoffs deployed on SHARE-seq TF expression data. The colors indicate different methods for knockoff construction.
(C) Reported FDR from the knockoff filter versus observed FDR relative to ChIP-seq data when using the knockoff filter to infer regulators of each gene in the SHARE-seq data. Gaussian knockoffs are used. The color scale shows cell count cutoffs: clusters with fewer than the indicated number of cells are omitted. The x axis displays the FDR reported to the method by the user, while the y axis shows the observed fraction of false discoveries based on ChIP-seq data. Points above the black line (y = x) indicate excess false discoveries.
(D) Variant of (A) where covariates are contaminated with additional Poisson error prior to construction of knockoffs. The cell count cutoff is indicated in the color scale. Gaussian knockoffs are used.
(E) Variant of (C) where global accessibility of JASPAR human and mouse motifs is used as a measure of TF activity instead of, or in addition to, TF RNA levels. The cell count cutoff is 10. Colors indicate which measure of TF activity is used.
(F) Variant of (C) where knockoffs are constructed conditional on the top 5 principal components of the RNA matrix and the ATAC matrix. These experiments use both RNA and global accessibility as measured of TF activity, as in (E) (purple). The cell count cutoff is 10. Colors indicate whether the analysis controlled for principal components or not.
(G) Variant of (C) where specific hypotheses are removed from consideration unless they are supported by a TF binding motif in a nearby region whose chromatin accessibility correlates with transcript levels of the putative target gene. This strategy is used alone, where it does not have a specific reported FDR (yellow), or in combination with knockoff-based FDR control (orange). These experiments use both RNA and global accessibility as measured of TF activity, as in (E) (purple), and they condition on the top principal components, as in (F) (bright green). The cell count cutoff is 10. Colors indicate whether the analysis used knockoffs, motif matching, or both to filter out false positives.
To test FDR on real gold standards, we selected all TFs from ChIP-atlas with skin or PBMC ChIP-seq data.73 The skin ChIP data covered 65 TFs and 19,882 unique targets with 315,143 total edges. The PBMC ChIP data covered 13 TFs and 15,784 unique targets with 116,590 total edges. We used Gaussian knockoffs to infer regulators of all genes passing a minimum expression cutoff. We generated q-values for hypotheses that are testable via ChIP. Additional variants of the analysis used only T cells or only the keratinocyte lineage for network inference. The results showed poor enrichment and many false positives with highly confident results, with 37,155 findings (skin) or 9,247 findings (PBMCs) at an FDR of 0.1 (Figure 5C; Table S3). Conditional independence testing via knockoffs does not control FDR in TRNs inferred from these datasets.
One potential explanation for this issue is measurement error (STAR Methods). To reduce the effect of measurement error, we increased the cutoff to 100 cells or 500 cells per cluster. Too few PBMC clusters remained at 500 cells per cluster, so only the skin data are analyzed at that cutoff. Fewer discoveries were made (3,711 in PBMCs and 8,345 in skin at FDR 0.1 and at least 100 cells per cluster), but FDR was controlled only in the T cell analysis (Figure 5C; Table S3). Aggregating more cells in this way does not eliminate all measurement error, so we devised an independent method to estimate the degree to which measurement error increases false discoveries. We simulated measurement error starting from the cluster-aggregated data. Specifically, we resampled each TF expression count Xij by replacing it with a Poisson random variable whose expectation equals Xij.74 We constructed knockoffs based on the resampled TF expression. We tested the results on real target genes and on target genes that were simulated prior to resampling. Resampling caused slight deleterious effects in simulations, especially at high reported FDR, but had a weak effect on ChIP-seq benchmarks (Figure 5D; Table S3). Based on these analyses, measurement error could not explain the degree of miscalibration we observed.
Aside from transcript quantification errors, another possible driver of false positives is the inability of transcriptomics to directly measure TF activity. A better measure of TF activity might be a summary of gene or enhancer targets rather than the mRNA level of the TF.75–78 There are many similar methods reviewed and benchmarked by DoRothEA.79 As a measure of TF activity, we used ChromVAR to calculate per-motif differential accessibility scores.80 We repeated our mouse and human multi-omics experiments using motif activity alone, or both motif activity and TF RNA levels, as predictive features (Figure 5E; Table S3). We also attempted to remove unmeasured confounding by conditioning on the top 5 principal components of both the gene expression matrix and the ATAC counts matrix during knockoff construction (Figure 5F; Table S3). Neither approach reported an FDR matching the observed FDR, suggesting that these metrics of TF activity based on global chromatin accessibility do not contain enough additional information to satisfy causal sufficiency.
Finally, it is possible to screen each individual hypothesis by requiring support from a TF binding motif located in the promoter of the relevant target gene or in a co-accessible enhancer candidate—this is done (for example) by CellOracle and SCENIC+.1,81 To check whether this strategy could facilitate FDR control by enriching for relevant edges, we created a motif-based TF-target network. We paired each gene with correlated ATAC peaks within 50 kilobases (kb) of the gene and searched for JASPAR TF binding motifs in each peak via motifmatchr.82 For a cell count cutoff of 10, the portion of the PBMC motif-based network that was testable using our collection of ChIP data included 4 regulators and 13,271 target genes with 33,680 edges. The testable portion of the skin motif-based network included 23 regulators and 12,802 target genes with 164,932 edges. However, intersecting knockoff-based results with the results of motif analysis did not improve FDR control (Figure 5G).
DISCUSSION
False positives have been a persistent problem in TRN inference.21 Statistical FDR control has become indispensable in closely related domains, such as differential expression analysis.31 But FDR control has seen limited use in TRN inference. TRN inference presents several stubborn and poorly characterized obstacles, with recommendations about the source of false discoveries and recommendations about possible solutions differing heavily depending on the dataset under study.18,19,65,83,84 In this work, we provided tools and approaches to systematically diagnose and address several of these obstacles in a dataset-specific way.
Specifically, model-X knockoffs can control FDR even when targets respond to regulators in a way that is nonlinear, unlike many alternatives,25,38,85 model-X knockoffs can correctly discriminate between direct and indirect effects unlike permutation tests,36 and a modification of the knockoff filter allows FDR estimation on an incomplete set of testable hypotheses. Furthermore, we excluded TF-TF edges from our analyses, so differences between directed and undirected graphical models are unlikely to explain the excess FDR, and for analyses using single-cell sequencing data, Poisson resampling experiments showed that measurement noise is unlikely to explain excess FDR.
Despite these improvements, FDR remained inflated in an E. coli transcriptome application and in mammalian multi-omics applications using either RNA levels or global motif accessibility as proxies for TF activity. These results cast doubt on a considerable amount of TRN work making explicit causal interpretations of conditional dependence structure.43,45,86–90
Our observation of poor FDR control via permutation also has implications for common practice. FDR control in TRN inference often relies on permuted genes as negative controls,22,23,26,27 which we demonstrate does not yield good control. As an example, in the E. coli analysis, permuted knockoffs yielded 131 melR targets spanning diverse biological functions. This conflicts with ChIP and perturbation experiments showing three or four targets of melR, almost all located in the melibiose operon.64,91 If melR were not already well studied, follow-up experiments based on these findings could have wasted considerable resources.
A natural continuation of our work is to identify specific reasons for failure of causal sufficiency, and we emphasize that nearly any type of error or incompleteness could eventually be revealed as an obstacle. A simple possibility is the unit of observation and the source of variation: since bulk RNA data can be subject to Simpson’s paradox or variable cell type composition, it is possible that the main source of variation across bulk samples does not reflect mechanisms operating in each cell. Even in single-cell data, local averaging of cells to estimate a pseudo-time trajectory is inferior to dynamic information at a single-cell level.45 Another plausible source of unmeasured causes is batch effects or poor normalization.65,66,84 It is possible that better normalization,92 better controls for quantitation,93,94 or more standardized experiments95 may improve FDR control. However, our analyses using PCA to infer and remove surrogate variables were largely unsuccessful. For a third possible source of unmeasured causes, recent reports based on multi-layered simulations attribute TRN inference errors to non-mRNA layers of cell state96,97 such as protein abundance. By that logic, new multi-omics technologies may yield improvements, especially by directly measuring proteins or by measuring transcription rate instead of RNA levels.45,98–100 Even in the same multi-omics data we use, improved attribution of motif accessibility to TFs could potentially improve our results. For example, many families of TFs share motifs, and TF affinity depends on cellular context.
For new datasets, our approach could be applied to assess causal sufficiency. Though we recommend knockoff constructions be separately validated on each dataset they are applied to, we find that Gaussian knockoffs with regularized covariance estimates are a sensible initial choice for -omics data with low sample size and high dimension.
If careful analyses of data from improved experimental methodologies continue to indicate lack of causal sufficiency, then the field should pursue analytical approaches that do not require causal sufficiency. Some causal structure inference methods allow for unobserved causal factors, and they have been deployed for TRN inference, but they lack finite-sample FDR control.54,101 If these methods could be equipped with realistic guarantees on FDR control, this would help facilitate further methodological refinement or yield high-confidence regulatory relationships for end users. Meanwhile, thoughtful external evaluation will be critical for understanding the performance of TRN methods.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Patrick Cahan (patrick.cahan@jhmi.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
This paper analyzes publicly available data. We list the source URLs for the datasets in the key resources table. We have also made all data available as a collection via Zenodo with DOIs listed in the key resources table.
We have deposited all original code at GitHub as of May 2023 (https://github.com/ekernf01/knockoffs_paper), with DOIs for relevant releases minted by Zenodo. DOIs are listed in the key resources table.
Any additional information required to repeat the analyses reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Deposited data | ||
|
| ||
| All data used in this study | Zenodo | DOI: https://doi.org/10.5281/zenodo.6573413 |
| DREAM5 E. coli data | Sage Bionetworks | https://dreamchallenges.org/dream-5-network-inference-challenge/ |
| Mouse transcription factors | AnimalTFDB | https://guolab.wchscu.cn/AnimalTFDB#!/ |
| Human transcription factors | Lambert et al.102 | http://humantfs2.ccbr.utoronto.ca/download.php |
| SHARE-seq data | Ma et al.70 | GEO: GSM4156608 and GEO: GSM4156597 |
| 10X multiomics data | 10x Genomics website | https://www.10xgenomics.com/datasets/pbmc-from-a-healthy-donor-no-cell-sorting-10-k-1-standard-2-0-0 |
| Human and mouse transcription factor targets | ChIP-atlas | http://dbarchive.biosciencedbc.jp/kyushu-u/metadata/experimentList.tab |
| E. coli high-throughput gold standards | RegulonDB v10.9 | https://regulondb.ccg.unam.mx/ht |
| E. coli curated gold standards | RegulonDB v10.9 | https://regulondb.ccg.unam.mx/releasesNote/date=2021-04-02&version=10.9 |
|
| ||
| Software and algorithms | ||
|
| ||
| Modification of the BoolODE framework | This paper | DOI: https://doi.org/10.5281/zenodo.10063178 |
| Modification of the BEELINE framework | This paper | DOI: https://doi.org/10.5281/zenodo.10063174 |
| E. coli analysis | This paper | DOI: https://doi.org/10.5281/zenodo.10063164 |
| Multi-omics analysis | This paper | DOI: https://doi.org/10.5281/zenodo.10688721 |
| Demonstration of knockoff construction speedups and calibration on incomplete gold standards | This paper | DOI: https://doi.org/10.5281/zenodo.10063183 |
| Faster implementation of the Gaussian mirror (R package) | This paper | DOI: https://doi.org/10.5281/zenodo.10063192 |
| Faster implementation of knockoff construction (limited Julia interface) | This paper | DOI: https://doi.org/10.5281/zenodo.10063198 |
| Faster implementation of knockoff construction (limited Python interface) | This paper | DOI: https://doi.org/10.5281/zenodo.10063196 |
| Faster implementation of knockoff construction (R package) | This paper | DOI: https://doi.org/10.5281/zenodo.10063187 |
METHOD DETAILS
Hardware and software used
We ran speed/memory tests in Figures 2 and S1 on a Dell XPS 13 with 8GB RAM and an Intel Core i5 processor. We ran BoolODE in a virtual environment according to the maintainers’ instructions, with minimal changes made to export protein concentrations and RNA rates of change. We ran BEELINE within a conda environment according to the maintainers’ instructions (https://github.com/Murali-group/Beeline). We made minimal modifications in order to test multiple sets of parameters (https://github.com/Murali-group/Beeline/issues/59) and to benchmark directed and undirected FDR. E. coli and multiomics experiments ran on Amazon Web Services EC2 t2.2xlarge instances based on the Ubuntu 20.04 image or on a Dell XPS15 running Ubuntu 20.04. Experiments used R version 4.1.2. R package versions were installed from either Bioconductor 3.14 or were explicitly pinned and installed from CRAN. We set seeds and automated package installation for repeatability, checking certain key figures and md5 checksums of certain intermediate outputs. BEELINE results may vary due to randomness in BoolODE simulations. E. coli analyses are exactly repeatable. SHARE-seq analyses are exactly repeatable up to knockoff generation but may yield slightly different symmetric statistics and calibration results.
E. coli datasets and gold standard processing
We downloaded E. coli microarray data from the DREAM5 challenge website at https://www.synapse.org/#!Synapse:syn2787211. The DREAM5 competition contains decoy genes with values chosen at random from the rest of the dataset.103 These are absent from all gold standards, but we left them unchanged to facilitate comparison with previous work. We downloaded E. coli transcriptional units from the Biocyc smart table “All transcription units of E. coli K-12 substr. MG1655,” available at https://biocyc.org/group?id=:ALL-TRANSCRIPTION-UNITS&orgid=ECOLI. We collected gold standard data as follows.
“dream5 validation”: we manually extracted interactions from Data S7 of Marbach et al.18
“M3Dknockout” includes all single-knockout samples and their controls from the DREAM5 training data, downloaded from https://www.synapse.org/#!Synapse:syn2787211. We excluded experiments with aliased effects; e.g., if the knockout was accompanied by a change in growth conditions relative to the controls. We removed any sample used in this gold standard from the training data prior to knockoff construction whenever we used this gold standard for evaluation.
“regulondb10_9” consists of manually curated regulatory interactions, which we downloaded from https://regulondb.ccg.unam.mx/menu/download/full_version/files/10.9/regulonDB10.9_Data_Dist.tar.gz on 2022 Jan 28.
“chip” and “regulonDB knockout”: we downloaded ChIP-based and knockout-based TF-target pairs from RegulonDB version 10.9; a complete list of accessions is given in Table S1. In E. coli ChIP data, IHF targets were regarded as targets of both IHF genes (ihfA and ihfB). The MelR targets melA and melB were added manually, since they were missing despite having high-quality ChIP evidence (Grainger et al. 2005). ChIP-chip and ChIP-seq studies lacking loss-of-function controls were excluded to reduce risk of false positives104; otherwise, all datasets listed were included, including ChIP-exo without loss-of-function controls.
E. coli targets are often determined at the level of a transcription unit, which may contain multiple genes.105,106 We thus augment E. coli ChIP and knockout-based gold standards to include any gene sharing a transcriptional unit with a target gene listed in the RegulonDB high-throughput downloads. For figures mentioning "chip and M3Dknockout" or "chip and RegulonDB_knockout," we marked a regulatory relationship as positive if it was consistent with both ChIP data and knockout data. We treated a relationship as negative if it was missing from both. Additionally, if the target or the regulator did not appear at least once in both datasets, we marked the example as unknown.
QUANTIFICATION AND STATISTICAL ANALYSIS
Designating analyses that use real and simulated data
We use real data, simulated data, and hybrid data with real regulators and simulated target genes. To clarify, each figure or figure panel states “real data,” “simulated data,” or “Real TF expression with simulated target genes.”
Knockoff filter usage
We constructed knockoffs via the R package rlookc, which is released along with this paper. We applied the knockoff filter using the same measure of variable importance throughout unless otherwise noted. It is the signed max lasso coefficient at entry (stat.lasso_lambdasmax from the R package knockoff) with one computational speedup: we fitted LASSO paths by glmnet with dfmax=21, corresponding to the assumption that no gene has over 20 direct regulators. Where we sought FDR control for a collection of discoveries from separate runs of the knockoff filter, for example, across multiple E. coli target genes, we estimated FDR after pooling the symmetric knockoff statistics.
Speed and memory tests
We measured runtime using the microbenchmark R package and peak memory usage using the peakRAM R package (Figures S1A and S1B).
Threshold selection tests
In Figure S1C, we simulated covariates with the same mean, covariance, and sample size as the E. coli TF expression data. We constructed knockoffs using the exact mean and covariance (not an estimate from the simulated dataset). We set responses equal to the covariates, so each column has a single relevant feature. We applied the knockoff filter using the difference in linear model coefficients as the variable importance measure. We selected thresholds separately for each target (“separate”) or using a single shared threshold (“merged”). We calculated FDR as the number of false discoveries across all targets divided by the number of discoveries over all targets.
BEELINE benchmarking
For Figure 1, we constructed Gaussian knockoffs using the sample mean and covariance. We inferred Gaussian mixture model parameters using mclust.107 We used 100 clusters, all having equal, spherical covariance. BoolODE does not separate production from decay, so we inferred RNA decay rates using piecewise quantile regression of RNA rates of change on RNA levels. Our method cannot reliably infer self edges, and we ruled these out a priori.
E. coli analysis
For the 334 TFs in the E. coli microarray data, we constructed knockoff features under multivariate Gaussian or Gaussian mixture model assumptions. When n>=p, we used the semidefinite program implementation in the R package knockoff to determine optimal valid correlations of knockoff features with the original features. When p>n, we used a new method (STAR Methods). For mixture models, we set hard cluster assignments using the k-means clusters described below, and per-cluster covariance was estimated using the method for p>n.
We constructed each simulated target gene by randomly selecting a set S containing max(1,M) TFs, where M is Poisson with a mean of 2. We set the target expression to 1 if all regulators were greater than their mean expression and 0 otherwise. We performed 1,000 simulations, and experiments cycled through 10 independently generated sets of knockoffs.
For each gene in turn, we selected TF regulators via the knockoff filter. To find regulators of TFs, we created new knockoffs omitting the TF in question, and otherwise we inferred regulators in the same way. For GeneNet, we used the GeneNet R package to compute all partial correlations, and we used the fdrtool package to fit mixture models to only the partial correlations involving the target. For the Gaussian Mirror, we used a fork of the GM R package implementing simultaneous mirrors.
To adjust for confounders, we computed knockoffs after appending columns (features) to the TF expression matrix containing either non-genetic perturbations or non-genetic perturbations and the top principal components (Figure 4B). We computed the principal components using the full expression matrix as input, scaled and centered. These knockoffs thus violate the dictum to construct knockoffs without influence of the target variable, but the effect is to make the results more conservative. We tested association with the confounding variables (Figure S2C) using the Pearson correlation as the measure of variable importance inside the knockoff filter.
We computed t-SNE embeddings using the R package tsne with default settings, using as input the 334 by 805 TF expression matrix concatenated with many 334 by 805 matrices of knockoffs (yielding a a 334 by 805*(k+1) matrix). We computed K-means clusters using the kmeans function from the R package stats with the entire expression matrix (TFs and non-TF genes) as input. The t-SNEs in the supplement are from the analysis with no adjustment for confounders and no special handling of genetic perturbations.
Since the knockoff filter tests conditional independence, not the direction of causality, we marked backwards edges confirmed by a given gold standard as correct. To rule out spouses as a source of false positives (appearing in MRF structure but not gold standards), we marked all TF-TF edges as unknown, even if they appear to be ruled in or out by a given gold standard.
Incomplete gold standard simulations
For Figure 3, we simulated data and computed knockoff statistics as in Figure S1C. We marked gold standard positives (negatives) as unknown with 80% probability in the negative (positive) bias trials. We computed Q-values via Selective SeqStep36 on all hypotheses (top row of Figure 4), or only hypotheses that were testable with the remaining gold standard data (bottom row). We computed observed FDR using the remaining gold standard data. We performed ten independent replicates.
Multi-omics analysis
We downloaded SHARE-seq skin count matrices from GEO accessions GSM4156608 and GSM4156597 and reformatted them as 10x-format HDF5 matrices using the DelayedArray and HDF5Array R packages. To successfully merge ATAC read counts with cell metadata, we subtracted 48 from the number in the final barcode associated with each cell in the count data. We acquired PBMC multi-omics data from the 10x Genomics website on Aug 21, 2023.71
We clustered the cells in each dataset using the Bioconductor packages scran, scater, and mbkmeans. For PBMCs only, we removed droplets with 2,000 or fewer total RNA counts. For both datasets, we normalized the RNA data by dividing by total counts per cell. We selected 2,000 highly variable transcripts as input for PCA. We selected 50 principal components as input for mbkmeans. For keratinocyte-only experiments, we used existing cell-type annotations, and we retained cells with the following labels: ahighCD34+ bulge, alowCD34+ bulge, Basal, Hair Shaft-cuticle.cortex, Infundibulum, IRS, K6+ Bulge Companion Layer, Medulla, ORS, Spinous, TAC-1, TAC-2. For T cell-only experiments, we annotated clusters using the following markers – CD4 T Cell: IL7R, CCR7, CD3E; CD8 T Cell: CD8A, CD3E, NKG7; CD16 Monocyte: FCGR3A, MS4A7; CD14 Monocyte: CD14, LYZ; B cell: MS4A1, CD19; NK cell: GNLY, NKG7, NCR1; Dendritic cell: FCER1A, CST3. We summed raw RNA and ATAC counts within each of the 100 clusters determined by mbkmeans, conducting all downstream analysis with the “pseudo-bulk” data.
We normalized “pseudo-bulk” RNA profiles by dividing by total counts and multiplying by 1,000,000. We excluded genes below 1CPM. We centered and scaled each gene to have mean 0 and variance 1. We replaced genes with constant expression with standard Gaussian random draws. We downloaded human TFs curated iby Lambert et al.102 from http://humantfs.ccbr.utoronto.ca/download.php on March 18, 2022. We downloaded mouse TFs and cofactors from AnimalTFDB 3.0108 on October 14, 2021. We used cofactors in addition to TFs since they can alter the effect of the TFs on downstream expression. We constructed knockoffs for the centered, scaled TF expression matrix using the “permuted” method (permuting samples within each gene independently) or using the scalable Gaussian knockoff implementation in the function “createHighDimensionalKnockoffs” released in the rlookc package accompanying this paper. In cases where we test independence conditional on principal components of the ATAC or RNA data, we computed these using all genes/features, and we concatenated them onto the TF expression data prior to knockoff construction. We generated simulated target genes as in the E. coli analysis.
We constructed motif-based networks by pairing ATAC peaks with any promoter within 50kb whose RNA levels correlated with the peak’s ATAC signal (Pearson correlation > 0.2), then finding motifs in the promoter or linked ATAC peaks via motifmatchr. Correlation was measured on the pseudo-bulk data.
We downloaded ChIP-seq peaks within 10kb of any promoter from ChIP-atlas73 on September 7, 2023. We selected files with “blood” or “epidermis” in the metadata. We retained each column of each file only if the cell type descriptions included the substrings “skin”, “hair”, “epiderm”, “keratinocyte", “blood”, or “pbmc". We averaged the signal within each TF. The signal distribution was heavily skewed with many small values, so we filtered peaks to exclude any peak with less than the mean signal strength.
Leave-one-out knockoff construction (LOOKC)
Network inference on N genes usually requires running N regression models, where each gene in turn is treated as the target. In this derivation, a method is developed for fast construction of Gaussian-X knockoffs when each variable is omitted in turn, so that we can condition on every variable except the one omitted.
To provide complete published documentation of our software, we include derivations of certain additional features not used in our study of TRN inference.
From Candes et al.,44 Gaussian knockoffs are constructed such that the centered, scaled data and the knockoffs have joint covariance
This ensures the correct exchangeability properties that lead to proper FDR control. Since the mean is 0 and the distribution is Gaussian, this covariance matrix completely specifies the distribution. Here, is the covariance of or an estimate thereof. is a diagonal matrix that can be specified by the user. There is one constraint on (it must yield a positive-definite ), but otherwise can be chosen freely. The specific choice can affect the method’s power, and existing software can determine a good option for that is compatible with the methods described herein.
Since is known but must be generated, a sample is drawn not from but from . This distribution can be derived with standard techniques and is given in the model-X knockoffs paper. The exact formulas in terms of , , and are reproduced below as needed.
We now describe how to reduce the computational cost. Generating knockoffs involves matrix operations of order and where is the number of variables and Nis the number of observations. In general, knockoffs must depend on but must not depend on , so whenever a new variable is treated as , the construction would need to be repeated with that variable left out. If done naively, this would add a factor of to the runtime (where is the number of variables).
Instead, it is possible to generate all leave-one-out knockoffs (LOOKs) within a constant factor of the original computation time. The method is:
For a first approximation, generate knockoffs for and omit column .
Update the knockoffs to remove the residual influence of column kon the remaining variables.
The exact updates are derived below. They can be done by adding two rank-one matrices to the initial approximation. We define terminology as follows:
Without loss of generality, assume we wish to omit the final column of Xprior to knockoff generation, and call this variable .
Let denote the joint covariance of features and knockoffs as in Candes et al.44 Let denote but omitting variables and . Both rows and columns are omitted. is never formed explicitly, but it is important mathematically because it specifies a joint covariance for the distribution of our leave-one-out knockoffs . To obtain valid knockoffs, one requirement is that must remain positive definite. This is satisfied because for a positive definite matrix, any principal submatrix is also positive definite. also satisfies the knockoff exchangeability criterion. Thus, no change is needed in the choice of .
- Let and be the mean and covariance of with no variables omitted. From Candes et al.,44
- .
- Let , , , , , , and denote the obvious matrices but with variable omitted. ( is the “first approximation” mentioned above.) For , , and , omitting a variable means omitting the column and the row. For and , only the column is omitted. For , the inverse is computed first, and row and column are omitted later. This implies
and - Let and be the desired mean and covariance of the distribution we need to sample from: . It yields almost the same result as and , but note that variable must be omitted before computing the inverse of , not after:
A reasonable guess would be to pre-compute knockoffs with all variables and omit portions of them at each iteration. This method is not quite correct on its own, because
. Another way to understand this is to note that
But, these initial guesses are very close, and they can be corrected efficiently, which we will now show by comparing to and to . Before that comparison, there is one preliminary to discuss. Partition and as
and
In general, , but this can be resolved with a standard rank-one update:
This is useful in correcting both the mean and the covariance.
Without loss of generality, assume we are omitting the final variable, at index k. The mean can be partitioned to isolate the variable to be removed:
The relevant block is
This is the mean of the naive procedure (generate knockoffs first, then omit). By contrast, we need the result as if variable k were removed *before* knockoff generation:
The necessary correction is of rank 1. It is:
For the covariance, the desired matrix (again removing variable k *before* generating knockoffs) is
Thus, the covariance of the precomputed knockoffs can be corrected by adding a random vector where . This must be done times, once per observation in . These derivations have been implemented in our R package rlookc and tested for correctness against the reference implementation in the R package knockoff.
Efficient leave-one-out knockoffs with groups of variables
In a dataset with a correlated set of variables in , it may be impossible to distinguish among the different options, yet it may be clear that at least one of them is in the active set. In this scenario it is desirable to test the null hypothesis (where indexing by – denotes omission of the whole set). In Sesia et al.,48 model-X knockoffs are extended to composite hypotheses of this type. Their framework assumes variables are partitioned into (disjoint) groups . Error control is similar to the un-grouped knockoff framework, but the exchangeability criterion
no longer needs to be met for all sets of variables . Rather, exchangeability is only required for swaps where grouped variables stay together, i.e. is the union of any of the .
A method for constructing such knockoffs is described in Sesia et al.,48 but it only applies to a specific HMM used on genotype data. Constructing grouped model-X knockoffs for Gaussian is discussed by Katsevich and Sabatti109 as an extension of prior work done under the more restrictive assumptions of fixed-X knockoffs.110 The method is reasonably simple: the diagonal matrix can be replaced with a block-diagonal matrix where the blocks correspond to the variable groups. As before, the only other constraint on is that must remain positive definite. Dai and Barber110 give a fast, simple scheme for choosing .
Given knockoffs obeying the correct exchangeability criterion, test statistics may be constructed arbitrarily as long as they are symmetric under the null. For example, the maximum (or mean) importance measure within each group can be subtracted from the maximum (or mean) over the corresponding knockoff importance measures, or the test could use the likelihood ratio
, or LASSO-based methods could use grouped LASSO. Grouped hypothesis tests are implemented in ‘rlookc‘ and unit-tested successfully, with checks for error control, power, and positive definiteness of . The computational cost of sampling group knockoffs is similar to the cost of sampling individual knockoffs.
For efficient leave-one-out knockoffs, the strategy outlined above applies with slight modifications. Partition as
Since is no longer 0,
The terms on the left are as above, but the rightmost term is new. The desired quantity has the same formula as before, though may not be diagonal:
The necessary correction is still of rank 1, and the algebra strongly resembles the case above.
Similarly, the last three terms (which we will denote ) are new in
, and the correction becomes
For brevity, we have introduces some new names above: and . To convert a Gaussian random vector with covariance into one with covariance , it suffices to add a standard Gaussian times the square root of the increment, which is
These results reduce to the updates for non-grouped LOOKs whenever . Grouped LOOKs are successfully unit tested against the slower reference implementation for mean, covariance, and correlation with held-out variables.
Gaussian mixture knockoffs and the efficient leave-one-out knockoffs (LOOKs)
Compared to Gaussian knockoffs, Gaussian mixture models can provide more flexibility and extend the applicability of this framework. If an observation is drawn from a mixture of Gaussians with PDF
then Gimenez et al.49 showed that a joint density for and a knockoff could be
where is defined separately for each cluster as above. If is the (latent) cluster chosen for , we can generate a knockoff by choosing a cluster at random from and drawing knockoffs from ; Gimenez et al.49 show that this preserves the necessary exchangeability property.
For mixture-model leave-one-out knockoffs (LOOKs), it is necessary to sample from , meaning almost the same posterior but without knowledge of one coordinate. Fast methods for doing this are outlined in the next paragraph. Then can be drawn from as described above. Beware: cluster assignments may vary across leave-one-out iterations even within the same observation, and the low-rank updates should not be applied to a knockoff observation sampled from the wrong cluster. It is thus necessary to maintain multiple initial guesses for the knockoffs, one per cluster, and always select the correct one to update.
To sample from , suppose the estimates of the cluster proportions remain unchanged. From Bayes’ Theorem,
If cluster has mean and covariance , then computation is dominated by the cost of
The term inside the exponent can be cheaply obtained from the rank-one correction used earlier:
The determinant can be computed from a Cholesky decomposition: if and is triangular, then
One way to update the determinant cheaply is via the Cholesky factors. If
, then
By a well-known matrix determinant lemma,
Given a precomputed of size , this update can be computed in time via forward and backward substitution, compared to if done naively.
Gaussian mixture model knockoffs are implemented and unit-tested in our software, but leave-one-out Gaussian mixture model knockoffs are not yet implemented at time of writing.
Efficient high-dimensional Gaussian knockoffs
RNA-seq and ATAC-seq commonly measure 20,000 to hundreds of thousands of features. The original model-X knockoffs paper44 includes a GWAS demo with 71,145 SNPs. But, the SNPs are distributed over 23 chromosomes with each chromosome treated separately, and the biggest matrix operations are on the order of a 10k by 10k block. Since RNA-seq and ATAC-seq can far exceed the 10,000 variables included in the original demonstration of model-X knockoffs, we envision the need for more computationally efficient high-dimensional Gaussian knockoff generation. Here, we develop an efficient method for Gaussian knockoff generation in settings with p>>n, where the dominant cost is that of a singular value decomposition (SVD).
The sample covariance matrix will be singular and a poor estimate of the true covariance. We instead begin with the optimal shrinkage method of Schaefer and Strimmer,35 which yields a positive definite estimate as well as better mean squared error than the sample covariance.
We assume throughout that X has mean 0, variance 1 for each feature. If needed, knockoffs can be constructed on centered, scaled data and then transformed back to match the original mean and scale. Let , , and denote the same matrices that were used in the leave-one-out derivations.
The first task in generating Gaussian knockoffs for large : it is hard to find such that
is positive definite. The memory requirements of the reference implementation appear to scale with the square of the dimension. But, the shrinkage estimator above suggests a much easier way to obtain a valid . It returns an estimate of the form
where is the sample covariance matrix and is determined from the data by ‘corpcor::estimate.lambda‘. Since a sufficient condition for to be positive definite is to be positive definite, can be set to for 0 , and then
which is positive definite.
It is useful to discuss certain computational tricks prior to the rest of the derivation. The sample covariance is
Let UTV be a full SVD of with singular values . Then the column of is an eigenvector of many related matrices:
with eigenvalue
with eigenvalue
with eigenvalue
with eigenvalue
Thus, the product where is any of these matrices can be computed as:
where returns a diagonal matrix with the appropriate transformation applied piecewise to the eigenvalues in . For , , so anything orthogonal to the top columns of has the same eigenvalue. Partition accordingly as . The product can be written
This can be computed with just O(np) memory because
The knockoffs must be created with mean . The reference implementation in the R package “knockoff” forms and computes the inverse explicitly, which incurs prohibitive memory requirements. Instead, we apply the third bullet point above, with chosen for . Likewise, the knockoffs must be created with covariance . To do this, the reference implementation in the R package ‘knockoff‘ performs an inverse and a Cholesky factorization, both of them having memory requirements. Instead, we use the fourth bullet point above to efficiently multiply by the square root of .
Merging sets of FDR-control results
Material in this section is adapted from one author’s comments on a public question and answer forum, licensed under a Creative Commons CC-by-SA 4.0 license and available at https://stats.stackexchange.com/a/536311/86176. The knockoff filter involves a choice of threshold, which is varied based on the user’s desired FDR and which is applied to a set of intermediate statistics produced as part of the knockoff filter. Here we motivate the choice to use a single threshold across all target genes, rather than running the whole knockoff filter procedure for each gene separately and later combining the discoveries.
Consider merging two disjoint sets of discoveries, each generated by a method that controls FDR at level . Let and be the number of false discoveries in the first and second set respectively. Let and be the total number of discoveries. Let . “FDP” will refer to the false discovery proportion observed in the data (with the convention for cases with no discoveries), and “FDR” will mean .
The combined FDP is a convex combination of the individual FDPs.
It is tempting to conclude
where is the FDR of the two input sets, but since is random and not independent of ;;;, this equality does not hold in general. A counterexample can be constructed as follows. Let , let , let , let , and let equal 0 or 100 with 50% probability. Then, is in fact slightly less than 50%, but is 1/3 or 101/103 with equal probability, and its expected value exceeds 0.5. When the number of true hypotheses is limited, as we expect in a sparse gene regulatory network, the mixture proportion is dominated by sets that happen to yield more false discoveries. Thus, in practice, FDR is inflated when measured across the combined set. In our implementation, we do not control FDR independently for selecting regulators of each target gene. Rather, we choose a threshold jointly across all target genes. Joint choice of threshold is not mathematically guaranteed to our knowledge, but in simulations, it seems to resolve this issue.
Causal sufficiency and false discoveries in TRN inference
This note describes how TRN inference methods ideally work with complete measurements and how incomplete measurements lead to false discoveries. Our concept of causal TRNs begins by reducing the cell to a list of numbers—usually, one number for each gene, representing the abundance of its mRNA. Obviously, information is lost between the cell and the numerical representation, especially about isoforms, miRNAs, DNA methylation, chromatin state, extracellular signals, and proteins (amount, phosphorylation, intracellular localization). But there is a well-developed mathematical theory of causal structure inference for complex systems that are partially observed and represented as a list of numbers. We offer a brief introduction to this theory following the Carnegie Mellon school of causal statistics.41 We also refer readers to two excellent expositions of the TRN inference problem that mostly align with our view.111,112
As a building block, imagine a future technology that can measure and exert fine-grained control over all aspects of molecular state that affect transcription. We assume transcription at locus j is controlled by a limited number of direct regulators, and we suppose for now that observations are causally sufficient: all factors affecting transcription are observed. Formally, we define the "direct regulators" to be the smallest set of factors such that if the direct regulators are experimentally held constant, no intervention on other factors will alter transcription at j. The causal graph structure we hope to infer is a graph with one node for each number in the cell state representation and with a directed edge connecting each node to any node that it is a direct regulator of.
Although the end goal of our TRN analysis is specified in terms of causation, the means to this end are described in terms of conditional dependence tests. Causal relationships and conditional dependence relationships are closely related, and conditional independence relations can be read from a causal graph via a graphical criterion called d-separation.41 Two nodes are independent conditional on a set S whenever they are d-separated by S in the causal graph. A general definition of d-separation can be found in Spirtes et al.,41 sections 2.3.4 or 3.7.1, but for unidirectional chains, d-separation is just separation: the ends are d-separated by any variable linking them. The implication is that upstream regulators are independent of downstream targets conditional on mediators.
If a given set of measurements lacks causal sufficiency, the relationship between conditional dependence and causal structure is much less straightforward. It is conceptually useful to imagine a bigger set of measurements that is causally sufficient, then study d-separation on the bigger causal graph, then determine what conditional dependence structures can arise among the observed variables.
For example, in a unidirectional chain , if the mediator is observed with error, we can add a new node for the observed value.
 |
The ends are d-separated conditional on the true value , but not the observed value . Below, we include simple simulations with measurement error to demonstrate that measurement error can cause excess false discoveries when using conditional dependence to discover causal structure.
A non-causal correlation between two transcript levels can also be driven by an unobserved shared cause such as a batch effect or an unmeasured extracellular signal. This topic is discussed in section 6.3 of Spirtes et al.,41 “Mistakes,” with a key example describing a simple chemical reaction. Below, we describe causal graphs and simulations showing excess false discoveries driven by failure of causal sufficiency with three distinct mechanisms: measurement noise; variable growth conditions; and poor normalization.
We first discuss measurement noise. Consider a causal network where regulates regulates . To reduce mathematical complexity, suppose the data are generated from the following linear and Gaussian model.
We test for a direct relationship between and using a t-test (cutoff p< 0:05) of the regression coefficient in a model . There is no direct relationship between and , so the true value of is 0, and the expected rate of false positives is 0.05. The following R code can be used to verify that the false positive rate is indeed 0.05.
| set.seed(0)p = list() |
| for(i in 1:1000){ |
| X1 = rnorm(100, 0, 1) |
| X2 = 0.5*(X1 + rnorm(100, 0, 1)) |
| X3 = 0.5*(X2 + rnorm(100, 0, 1)) |
| p[[i]] = coef(summary(lm(X3 ~ X1 + X2)))[2,4] |
| } |
| mean(unlist(p)<0.05) |
We now repeat these experiments, but before running the t-test, we add measurement error to each variable. Formally, we define , where , and we run the regression . Because of the measurement error, the false positive rate is roughly tripled (the following code prints 0.162).
| set.seed(0)p = list() for(i in 1:1000){ |
| X1 = rnorm(100, 0, 1) |
| X2 = 0.5*(X1 + rnorm(100, 0, 1)) |
| X3 = 0.5*(X2 + rnorm(100, 0, 1)) |
| Y1 = X1 + rnorm(100, 0, 1) |
| Y2 = X2 + rnorm(100, 0, 1) |
| Y3 = X3 + rnorm(100, 0, 1) |
| p[[i]] = coef(summary(lm(Y3 ~ Y1 + Y2)))[2,4] |
| } |
| mean(unlist(p)<0.05) # 0.162 |
These examples follow an E-shaped causal model:
 |
Because the true expression blocks the path from to , and are d-separated by and are independent conditional on . Because the measured expression+noise does not block this path, and are not d-separated by and are dependent conditional on .
Unmeasured confounding can also cause tests of conditional independence to produce excess false positives relative to a ground-truth causal network. Using the same base model as above, we can show what would happen if a normalization issue caused expression values to decrease by 50%, affecting half of the observations. In the normalization artifact scenario, the following R code shows that the false positive rate climbs from 5% (reported) to 8.3% (observed).
| set.seed(0)p = list() |
| for(i in 1:1000){ |
| X1 = rnorm(100, 0, 1) |
| X2 = 0.5*(X1 + rnorm(100, 0, 1)) |
| X3 = 0.5*(X2 + rnorm(100, 0, 1)) |
| has_bad_normalization = 1:50 |
| X1[has_bad_normalization] = X1[has_bad_normalization]*0.5 |
| X2[has_bad_normalization] = X2[has_bad_normalization]*0.5 |
| X3[has_bad_normalization] = X3[has_bad_normalization]*0.5 |
| p[[i]] = coef(summary(lm(X3 ~ X1 + X2)))[2,4] |
| } |
| mean(unlist(p)<0.05) # 0.083 |
This example reflects the following structure, in which C provides an alternate path between and that is not blocked by .
 |
Another possible source of unmeasured confounding is extracellular conditions or signals. In the next example, we use the same true causal structure, but additionally we simulate an unmeasured change in growth media present in 50% of samples that increases the values of A and C by 50%. Due to the altered growth condition, the false positive rate climbs from 5% (reported) to 6.2% (observed).
| set.seed(0)p = list() |
| for(i in 1:1000){ |
| X1 = rnorm(100, 0, 1) |
| X2 = 0.5*(X1 + rnorm(100, 0, 1)) |
| X3 = 0.5*(X2 + rnorm(100, 0, 1)) |
| growth_condition_differs = 1:50 |
| X1[growth_condition_differs] = X1[growth_condition_differs]*1.5 |
| X3[growth_condition_differs] = X3[growth_condition_differs]*1.5 |
| p[[i]] = coef(summary(lm(X3 ~ X1 + X2)))[2,4] |
| } |
| mean(unlist(p)<0.05) # 0.062 |
This example reflects the following structure, in which C provides an alternate path between and that is not blocked by .
 |
Methods for FDR control in subset selection
The following table summarizes the statistical assumptions made by methods used in this study.
We also wish to clarify a few points.
First, although our knockoff constructions typically assume the model for X is Gaussian, that assumption can be modified, for example, using mixture models or generative neural networks.
Second, BINCO24 provides a formal definition of “U-shaped” as well as some guidance on what procedures yield U-shaped selection frequencies (albeit only in the limit of infinite data). If is the selection frequency distribution under the null hypothesis and is the distribution under the alternative, they define U-shaped as “There exist V1 and V2, 0, such that as , on and is monotonically decreasing on (V1, 1].” They also provide the following guidance. “Lemma 1: A selection procedure [is U-shaped] if, as the sample size increases, [selection probability] tends to one uniformly for all true edges and has a limit superior strictly less than one for all null edges.”
Third, permutation tests can be viewed in two different ways. The typical viewpoint is that, without any assumptions, they can test if any two variables are marginally independent. Our objective is to test conditional independence, not marginal independence. Permuted variables can also be viewed as conditional independence tests because they are valid model-X knockoffs, but only under the assumption that all features are independent.53
Supplementary Material
Highlights.
FDR control in statistical TRN inference despite nonlinear and indirect effects
Methods to accurately assess FDR despite incomplete gold standard data
The major remaining obstacle is unmeasured confounding
Growth conditions, noise, and latent variables tested as potential confounders
ACKNOWLEDGMENTS
Many thanks to Prashanthi Ravichandran, Da (Dan) Peng, Ashton Omdahl, Alexander Chen, and Joshua Weinstock for helpful discussions and again to Joshua Weinstock for testing parts of the code. A.B. was funded by NIH grant R35GM139580. P.C. was funded by NIH grant R35GM124725.
Footnotes
DECLARATION OF INTERESTS
A.B. is a stockholder for Alphabet, Inc.; has consulted for Third Rock Ventures; and is a founder of CellCipher, Inc.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.cels.2024.07.006.
REFERENCES
- 1.Kamimoto K, Stringa B, Hoffmann CM, Jindal K, Solnica-Krezel L, and Morris SA (2023). Dissecting cell identity via network inference and in silico gene perturbation. Nature 614, 742–751. 10.1038/s41586-022-05688-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Boyle EA, Li YI, and Pritchard JK (2017). An expanded view of complex traits: from polygenic to omnigenic. Cell 169, 1177–1186. 10.1016/j.cell.2017.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Freimer JW, Shaked O, Naqvi S, Sinnott-Armstrong N, Kathiria A, Garrido CM, Chen AF, Cortez JT, Greenleaf WJ, Pritchard JK, and Marson A. (2022). Systematic discovery and perturbation of regulatory genes in human T cells reveals the architecture of immune networks. Nat. Genet 54, 1133–1144. 10.1038/s41588-022-01106-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Krishnan A, Zhang R, Yao V, Theesfeld CL, Wong AK, Tadych A, Volfovsky N, Packer A, Lash A, and Troyanskaya OG (2016). Genome-wide prediction and functional characterization of the genetic basis of autism spectrum disorder. Nat. Neurosci 19, 1454–1462. 10.1038/nn.4353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Baca SC, Takeda DY, Seo J-H, Hwang J, Ku SY, Arafeh R, Arnoff T, Agarwal S, Bell C, O’Connor E, et al. (2021). Reprogramming of the FOXA1 cistrome in treatment-emergent neuroendocrine prostate cancer. Nat. Commun 12, 1979. 10.1038/s41467-021-22139-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Reddy J, Fonseca MAS, Corona RI, Nameki R, Segato Dezem F, Klein IA, Chang H, Chaves-Moreira D, Afeyan LK, Malta TM, et al. (2021). Predicting master transcription factors from pan-cancer expression data. Sci. Adv 7, eabf6123. 10.1126/sciadv.abf6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Amrute JM, Lai L, Ma P, Koenig AL, Kamimoto K, Bredemeyer A, Shankar TS, Kuppe C, Kadyrov FF, Schulte LJ, et al. (2022). Defining cardiac recovery at single cell resolution. Preprint at BioRxiv. 10.1101/2022.09.11.507463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee H-Y, Jeon Y, Kim YK, Jang JY, Cho YS, Bhak J, and Cho K-H (2021). Identifying molecular targets for reverse aging using integrated network analysis of transcriptomic and epigenomic changes during aging. Sci. Rep 11, 12317. 10.1038/s41598-021-91811-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Parfitt D-E, and Shen MM (2014). From blastocyst to gastrula: gene regulatory networks of embryonic stem cells and early mouse embryogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci 369, 20130542. 10.1098/rstb.2013.0542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Singh AJ, Ramsey SA, Filtz TM, and Kioussi C. (2018). Differential gene regulatory networks in development and disease. Cell. Mol. Life Sci. 75, 1013–1025. 10.1007/s00018-017-2679-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fernandez-Valverde SL, Aguilera F, and Ramos-Díaz RA (2018). Inference of Developmental Gene Regulatory Networks Beyond Classical Model Systems: New Approaches in the Post-genomic Era. Integr. Comp. Biol 58, 640–653. 10.1093/icb/icy061. [DOI] [PubMed] [Google Scholar]
- 12.Ben Guebila M, Lopes-Ramos CM, Weighill D, Sonawane AR, Burkholz R, Shamsaei B, Platig J, Glass K, Kuijjer ML, and Quackenbush J. (2022). GRAND: a database of gene regulatory network models across human conditions. Nucleic Acids Res. 50, D610–D621. 10.1093/nar/gkab778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weighill D, Ben Guebila M, Glass K, Platig J, Yeh JJ, and Quackenbush J. (2021). Gene targeting in disease networks. Front. Genet 12, 649942. 10.3389/fgene.2021.649942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Duggan DJ, Bittner M, Chen Y, Meltzer P, and Trent JM (1999). Expression profiling using cDNA microarrays. Nat. Genet 21, 10–14. 10.1038/4434. [DOI] [PubMed] [Google Scholar]
- 15.Liang S, Fuhrman S, and Somogyi R. (1998). Reveal, a general reverse engineering algorithm for inference of genetic network architectures. Pac. Symp. Biocomput 18–29. [PubMed] [Google Scholar]
- 16.Nguyen H, Tran D, Tran B, Pehlivan B, and Nguyen T. (2021). A comprehensive survey of regulatory network inference methods using single cell RNA sequencing data. Brief. Bioinform 22, bbaa190. 10.1093/bib/bbaa190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sanguinetti G, and Huynh-Thu VA, eds. (2019). Gene regulatory networks: methods and protocols (Springer; ). 10.1007/978-1-4939-8882-2. [DOI] [Google Scholar]
- 18.Marbach D, Costello JC, Ku€ffner R, Vega NM, Prill RJ, Camacho DM, Allison KR, DREAM5 Consortium, Kellis M, Collins JJ, and Stolovitzky G. (2012). Wisdom of crowds for robust gene network inference. Nat. Methods 9, 796–804. 10.1038/nmeth.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pratapa A, Jalihal AP, Law JN, Bharadwaj A, and Murali TM (2020). Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat. Methods 17, 147–154. 10.1038/s41592-019-0690-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Djordjevic D, Yang A, Zadoorian A, Rungrugeecharoen K, and Ho JWK (2014). How difficult is inference of mammalian causal gene regulatory networks? PLoS ONE 9, e111661. 10.1371/journal.pone.0111661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Diaz LPM, and Stumpf MPH (2022). Gaining confidence in inferred networks. Sci. Rep 12, 2394. 10.1038/s41598-022-05402-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chasman D, Iyer N, Fotuhi Siahpirani A, Estevez Silva M, Lippmann E, McIntosh B, Probasco MD, Jiang P, Stewart R, Thomson JA, et al. (2019). Inferring Regulatory Programs Governing Region Specificity of Neuroepithelial Stem Cells during Early Hindbrain and Spinal Cord Development. Cell Syst. 9, 167–186.e12. 10.1016/j.cels.2019.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Morgan D, Tjärnberg A, Nordling TEM, and Sonnhammer ELL (2019). A generalized framework for controlling FDR in gene regulatory network inference. Bioinformatics 35, 1026–1032. 10.1093/bioinformatics/bty764. [DOI] [PubMed] [Google Scholar]
- 24.Li S, Hsu L, Peng J, and Wang P. (2013). Bootstrap inference for network construction with an application to a breast cancer microarray study. Ann. Appl. Stat 7, 391–417. 10.1214/12-AOAS589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schäfer J, and Strimmer K. (2005). An empirical Bayes approach to inferring large-scale gene association networks. Bioinformatics 21, 754–764. 10.1093/bioinformatics/bti062. [DOI] [PubMed] [Google Scholar]
- 26.Kimura S, Fukutomi R, Tokuhisa M, and Okada M. (2020). Inference of Genetic Networks From Time-Series and Static Gene Expression Data: Combining a Random-Forest-Based Inference Method With Feature Selection Methods. Front. Genet 11, 595912. 10.3389/fgene.2020.595912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lu J, Dumitrascu B, McDowell IC, Jo B, Barrera A, Hong LK, Leichter SM, Reddy TE, and Engelhardt BE (2021). Causal network inference from gene transcriptional time-series response to glucocorticoids. PLoS Comput. Biol 17, e1008223. 10.1371/journal.pcbi.1008223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Benjamini Y, and Hochberg Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289–300. 10.1111/j.2517-6161.1995.tb02031.x. [DOI] [Google Scholar]
- 29.Käll L, Storey JD, MacCoss MJ, and Noble WS (2008). Posterior error probabilities and false discovery rates: two sides of the same coin. J. Proteome Res. 7, 40–44. 10.1021/pr700739d. [DOI] [PubMed] [Google Scholar]
- 30.Storey JD (2003). The positive false discovery rate: a Bayesian interpretation and the q-value. Ann. Statist 31, 2013–2035. 10.1214/aos/1074290335. [DOI] [Google Scholar]
- 31.Korthauer K, Kimes PK, Duvallet C, Reyes A, Subramanian A, Teng M, Shukla C, Alm EJ, and Hicks SC (2019). A practical guide to methods controlling false discoveries in computational biology. Genome Biol. 20, 118. 10.1186/s13059-019-1716-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Genovese CR, Lazar NA, and Nichols T. (2002). Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage 15, 870–878. 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- 33.Huynh-Thu VA, Irrthum A, Wehenkel L, and Geurts P. (2010). Inferring regulatory networks from expression data using tree-based methods. PLOS One 5. 10.1371/journal.pone.0012776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Margolin AA, Nemenman I, Basso K, Wiggins C, Stolovitzky G, Dalla Favera R, and Califano A. (2006). ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics 7, S7. 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schäfer J, and Strimmer K. (2005). A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Mol. Biol 4, 32. 10.2202/1544-6115.1175. [DOI] [PubMed] [Google Scholar]
- 36.Barber RF, and Candès EJ (2015). Controlling the false discovery rate via knockoffs. Ann. Statist 43, 2055–2085. 10.1214/15-AOS1337. [DOI] [Google Scholar]
- 37.Fithian W, and Lei L. (2020). Conditional calibration for false discovery rate control under dependence.Preprint at arXiv. [Google Scholar]
- 38.Kim S. (2015). ppcor: An R package for a fast calculation to semi-partial correlation coefficients. Commun. Stat. Appl. Methods 22, 665–674. 10.5351/CSAM.2015.22.6.665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Domingo J, Minaeva M, Morris JA, Ziosi M, Sanjana NE, and Lappalainen T. (2024). Non-linear transcriptional responses to gradual modulation of transcription factor dosage. Preprint at bioRxiv. 10.1101/2024.03.01.582837. [DOI] [Google Scholar]
- 40.Eck E, Liu J, Kazemzadeh-Atoufi M, Ghoreishi S, Blythe SA, and Garcia HG (2020). Quantitative dissection of transcription in development yields evidence for transcription-factor-driven chromatin accessibility. eLife 9, e56429. 10.7554/eLife.56429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Spirtes P, Glymour C, and Scheines R. (1993). Causation, Prediction, and Search (Springer; ). 10.1007/978-1-4612-2748-9. [DOI] [Google Scholar]
- 42.Scheines R. (1997). An Introduction to Causal Inference (Carnegie Mellon University; ). 10.1184/r1/6490904.v1. [DOI] [Google Scholar]
- 43.Opgen-Rhein R, and Strimmer K. (2007). From correlation to causation networks: a simple approximate learning algorithm and its application to high-dimensional plant gene expression data. BMC Syst. Biol 1, 37. 10.1186/1752-0509-1-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Candès E, Fan Y, Janson L, and Lv J. (2018). Panning for gold: ‘model-X’knockoffs for high dimensional controlled variable selection. J. R. Stat. Soc. B 80, 551–577. 10.1111/rssb.12265. [DOI] [Google Scholar]
- 45.Qiu X, Rahimzamani A, Wang L, Ren B, Mao Q, Durham T, McFaline-Figueroa JL, Saunders L, Trapnell C, and Kannan S. (2020). Inferring Causal Gene Regulatory Networks from Coupled Single-Cell Expression Dynamics Using Scribe. Cell Syst. 10, 265–274.e11. 10.1016/j.cels.2020.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Meinshausen N, and Bühlmann P. (2010). Stability selection. J. R. Stat. Soc. B 72, 417–473. 10.1111/j.1467-9868.2010.00740.x. [DOI] [Google Scholar]
- 47.Romano Y, Sesia M, and Candès E. (2020). Deep Knockoffs. J. Am. Stat. Assoc 115, 1861–1872. 10.1080/01621459.2019.1660174. [DOI] [Google Scholar]
- 48.Sesia M, Katsevich E, Bates S, Candès E, and Sabatti C. (2020). Multi-resolution localization of causal variants across the genome. Nat. Commun 11, 1093. 10.1038/s41467-020-14791-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gimenez JR, Ghorbani A, and Zou J. (2019). Knockoffs for the mass: new feature importance statistics with false discovery guarantees. In The 22nd International Conference on Artificial Intelligence and Statistics, pp. 2125–2133. [Google Scholar]
- 50.Weinstein A, Barber R, and Candes E. (2017). A Power and Prediction Analysis for Knockoffs with Lasso Statistics. Preprint at arXiv. 10.48550/arXiv.1712.06465. [DOI] [Google Scholar]
- 51.Barber RF, Candès EJ, and Samworth RJ (2020). Robust inference with knockoffs. Ann. Statist 48, 1409–1431. 10.1214/19-AOS1852. [DOI] [Google Scholar]
- 52.Zhou J, Li Y, Zheng Z, and Li D. (2022). Reproducible learning in large-scale graphical models. J. Multivar. Anal 189, 104934. 10.1016/j.jmva.2021.104934. [DOI] [Google Scholar]
- 53.Huang D, and Janson L. (2020). Relaxing the assumptions of knockoffs by conditioning. Ann. Statist 48, 3021–3042. 10.1214/19-AOS1920. [DOI] [Google Scholar]
- 54.Verny L, Sella N, Affeldt S, Singh PP, and Isambert H. (2017). Learning causal networks with latent variables from multivariate information in genomic data. PLoS Comput. Biol 13, e1005662. 10.1371/journal.pcbi.1005662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.van der Maaten L, and Hinton G. (2008). Visualizing Data using t-SNE. J. Mach. Learn. Res 9, 2579–2605. [Google Scholar]
- 56.de Sousa Abreu R, Penalva LO, Marcotte EM, and Vogel C. (2009). Global signatures of protein and mRNA expression levels. Mol. Biosyst 5, 1512–1526. 10.1039/b908315d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Faith JJ, Driscoll ME, Fusaro VA, Cosgrove EJ, Hayete B, Juhn FS, Schneider SJ, and Gardner TS (2008). Many Microbe Microarrays Database: uniformly normalized Affymetrix compendia with structured experimental metadata. Nucleic Acids Res. 36, D866–D870. 10.1093/nar/gkm815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Friedman J, Hastie T, and Tibshirani R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9, 432–441. 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Xing X, Zhao Z, and Liu JS (2019). Controlling False Discovery Rate Using Gaussian Mirrors. Preprint at arXiv. 10.48550/arxiv.1911.09761. [DOI] [Google Scholar]
- 60.Santos-Zavaleta A, Salgado H, Gama-Castro S, Sánchez-Pérez M, Gómez-Romero L, Ledezma-Tejeida D, García-Sotelo JS, Alquicira-Hernández K, Muñiz-Rascado LJ, Peña-Loredo P, et al. (2019). RegulonDB v 10.5: tackling challenges to unify classic and high throughput knowledge of gene regulation in E. coli K-12. Nucleic Acids Res. 47, D212–D220. 10.1093/nar/gky1077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Turkarslan S, Peterson EJR, Rustad TR, Minch KJ, Reiss DJ, Morrison R, Ma S, Price ND, Sherman DR, and Baliga NS (2015). A comprehensive map of genome-wide gene regulation in Mycobacterium tuberculosis. Sci. Data 2, 150010. 10.1038/sdata.2015.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Arrieta-Ortiz ML, Hafemeister C, Bate AR, Chu T, Greenfield A, Shuster B, Barry SN, Gallitto M, Liu B, Kacmarczyk T, et al. (2015). An experimentally supported model of the Bacillus subtilis global transcriptional regulatory network. Mol. Syst. Biol 11, 839. 10.15252/msb.20156236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Belyaeva TA, Wade JT, Webster CL, Howard VJ, Thomas MS, Hyde EI, and Busby SJ (2000). Transcription activation at the Escherichia coli melAB promoter: the role of MelR and the cyclic AMP receptor protein. Mol. Microbiol 36, 211–222. 10.1046/j.1365-2958.2000.01849.x. [DOI] [PubMed] [Google Scholar]
- 64.Grainger DC, Overton TW, Reppas N, Wade JT, Tamai E, Hobman JL, Constantinidou C, Struhl K, Church G, and Busby SJW (2004). Genomic studies with Escherichia coli MelR protein: applications of chromatin immunoprecipitation and microarrays. J. Bacteriol 186, 6938–6943. 10.1128/JB.186.20.6938-6943.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Parsana P, Ruberman C, Jaffe AE, Schatz MC, Battle A, and Leek JT (2019). Addressing confounding artifacts in reconstruction of gene co-expression networks. Genome Biol. 20, 94. 10.1186/s13059-019-1700-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Cote AC, Young HE, and Huckins LM (2022). Comparison of confound adjustment methods in the construction of gene co-expression networks. Genome Biol. 23, 44. 10.1186/s13059-022-02606-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Semsey S, Jauffred L, Csiszovszki Z, Erdossy J, Stéger V, Hansen S, and Krishna S. (2013). The effect of LacI autoregulation on the performance of the lactose utilization system in Escherichia coli. Nucleic Acids Res. 41, 6381–6390. 10.1093/nar/gkt351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sprang M, Andrade-Navarro MA, and Fontaine J-F (2022). Batch effect detection and correction in RNA-seq data using machine-learning-based automated assessment of quality. BMC Bioinformatics 23, 279. 10.1186/s12859-022-04775-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Pemberton-Ross PJ, Pachkov M, and van Nimwegen E. (2015). ARMADA: using motif activity dynamics to infer gene regulatory networks from gene expression data. Methods 85, 62–74. 10.1016/j.ymeth.2015.06.024. [DOI] [PubMed] [Google Scholar]
- 70.Ma S, Zhang B, LaFave LM, Earl AS, Chiang Z, Hu Y, Ding J, Brack A, Kartha VK, Tay T, et al. (2020). Chromatin Potential Identified by Shared Single-Cell Profiling of RNA and Chromatin. Cell 183, 1103–1116.e20. 10.1016/j.cell.2020.09.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.10x Genomics (2021). PBMC from a Healthy Donor - No Cell Sorting (10k). https://www.10xgenomics.com/resources/datasets/pbmc-from-a-healthy-donor-no-cell-sorting-10-k-1-standard-2-0-0. [Google Scholar]
- 72.Baran Y, Bercovich A, Sebe-Pedros A, Lubling Y, Giladi A, Chomsky E, Meir Z, Hoichman M, Lifshitz A, and Tanay A. (2019). MetaCell: analysis of single-cell RNA-seq data using K-nn graph partitions. Genome Biol. 20, 206. 10.1186/s13059-019-1812-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Oki S, Ohta T, Shioi G, Hatanaka H, Ogasawara O, Okuda Y, Kawaji H, Nakaki R, Sese J, and Meno C. (2018). ChIP-Atlas: a data-mining suite powered by full integration of public ChIP-seq data. EMBO Rep. 19, e46255. 10.15252/embr.201846255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Sarkar A, and Stephens M. (2021). Separating measurement and expression models clarifies confusion in single-cell RNA sequencing analysis. Nat. Genet 53, 770–777. 10.1038/s41588-021-00873-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Balwierz PJ, Pachkov M, Arnold P, Gruber AJ, Zavolan M, and van Nimwegen E. (2014). ISMARA: automated modeling of genomic signals as a democracy of regulatory motifs. Genome Res. 24, 869–884. 10.1101/gr.169508.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Madsen JGS, Rauch A, Van Hauwaert EL, Schmidt SF, Winnefeld M, and Mandrup S. (2018). Integrated analysis of motif activity and gene expression changes of transcription factors. Genome Res. 28, 243–255. 10.1101/gr.227231.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Ma CZ, and Brent MR (2021). Inferring TF activities and activity regulators from gene expression data with constraints from TF perturbation data. Bioinformatics 37, 1234–1245. 10.1093/bioinformatics/btaa947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Liao JC, Boscolo R, Yang Y-L, Tran LM, Sabatti C, and Roychowdhury VP (2003). Network component analysis: reconstruction of regulatory signals in biological systems. Proc. Natl. Acad. Sci. USA 100, 15522–15527. 10.1073/pnas.2136632100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Garcia-Alonso L, Holland CH, Ibrahim MM, Turei D, and Saez-Rodriguez J. (2019). Benchmark and integration of resources for the estimation of human transcription factor activities. Genome Res. 29, 1363–1375. 10.1101/gr.240663.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Schep AN, Wu B, Buenrostro JD, and Greenleaf WJ (2017). chromVAR: inferring transcription-factor-associated accessibility from single-cell epigenomic data. Nat. Methods 14, 975–978. 10.1038/nmeth.4401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Bravo González-Blas C, De Winter S, Hulselmans G, Hecker N, Matetovici I, Christiaens V, Poovathingal S, Wouters J, Aibar S, and Aerts S. (2022). SCENIC+: single-cell multiomic inference of enhancers and gene regulatory networks. Preprint at bioRxiv. 10.1101/2022.08.19.504505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Schep A. (2023). motifmatchr: Fast Motif Matching in R. Bioconductor. 10.18129/b9.bioc.motifmatchr. [DOI] [Google Scholar]
- 83.Saint-Antoine M, and Singh A. (2023). Benchmarking gene regulatory network inference methods on simulated and experimental data. Preprint at bioRxiv. 10.1101/2023.05.12.540581. [DOI] [Google Scholar]
- 84.Faith JJ, Hayete B, Thaden JT, Mogno I, Wierzbowski J, Cottarel G, Kasif S, Collins JJ, and Gardner TS (2007). Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 5, e8. 10.1371/journal.pbio.0050008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Mukhopadhyay ND, and Chatterjee S. (2007). Causality and pathway search in microarray time series experiment. Bioinformatics 23, 442–449. 10.1093/bioinformatics/btl598. [DOI] [PubMed] [Google Scholar]
- 86.Mohan K, London P, Fazel M, Witten D, and Lee S-I (2014). Node-Based Learning of Multiple Gaussian Graphical Models. J. Mach. Learn. Res 15, 445–488. [PMC free article] [PubMed] [Google Scholar]
- 87.Wang Y, Solus L, Yang K, and Uhler C. (2017). Permutation-based causal inference algorithms with interventions. Adv. Neural Inf. Process. Syst 30. [Google Scholar]
- 88.Buschur KL, Chikina M, and Benos PV (2020). Causal network perturbations for instance-specific analysis of single cell and disease samples. Bioinformatics 36, 2515–2521. 10.1093/bioinformatics/btz949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.van Duin L, Krautz R, Rennie S, and Andersson R. (2022). Transcription factor expression is the main determinant of variability in gene co-activity. Preprint at bioRxiv. 10.1101/2022.10.11.511770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Mahmoodi SH, Aghdam R, and Eslahchi C. (2021). An order independent algorithm for inferring gene regulatory network using quantile value for conditional independence tests. Sci. Rep 11, 7605. 10.1038/s41598-021-87074-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Wade JT, Belyaeva TA, Hyde EI, and Busby SJ (2000). Repression of the Escherichia coli melR promoter by MelR: evidence that efficient repression requires the formation of a repression loop. Mol. Microbiol 36, 223–229. 10.1046/j.1365-2958.2000.01850.x. [DOI] [PubMed] [Google Scholar]
- 92.Zhao Y, Wong L, and Goh WWB (2020). How to do quantile normalization correctly for gene expression data analyses. Sci. Rep 10, 15534. 10.1038/s41598-020-72664-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Marquina-Sanchez B, Fortelny N, Farlik M, Vieira A, Collombat P, Bock C, and Kubicek S. (2020). Single-cell RNA-seq with spike-in cells enables accurate quantification of cell-specific drug effects in pancreatic islets. Genome Biol. 21, 106. 10.1186/s13059-020-02006-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Ziegenhain C, Hendriks G-J, Hagemann-Jensen M, and Sandberg R. (2022). Molecular spikes: a gold standard for single-cell RNA counting. Nat. Methods 19, 560–566. 10.1038/s41592-022-01446-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Lamoureux CR, Decker KT, Sastry AV, McConn JL, Gao Y, and Palsson BO (2021). PRECISE 2.0: an expanded high-quality RNA-seq compendium for Escherichia coli K-12 reveals high-resolution transcriptional regulatory structure. Preprint at bioRxiv. 10.1101/2021.04.08.439047. [DOI] [Google Scholar]
- 96.Erbe R, Stein-O’Brien G, and Fertig EJ (2023). A mechanistic simulation of molecular cell states over time. Preprint at bioRxiv. 10.1101/2023.02.23.529720. [DOI] [Google Scholar]
- 97.Mahajan T, Saint-Antoine M, Dar RD, and Singh A. (2022). Limits on inferring gene regulatory networks from single-cell measurements of unstable mRNA levels. In 2022 IEEE 61st Conference on Decision and Control (CDC) (IEEE), pp. 3884–3889. 10.1109/CDC51059.2022.9992359. [DOI] [Google Scholar]
- 98.Chen AF, Parks B, Kathiria A, Ober-Reynolds B, Goronzy J, and Greenleaf W. (2021). NEAT-seq: Simultaneous profiling of intra-nuclear proteins, chromatin accessibility, and gene expression in single cells. Preprint at bioRxiv. 10.1101/2021.07.29.454078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Specht H, Emmott E, Petelski AA, Huffman RG, Perlman DH, Serra M, Kharchenko P, Koller A, and Slavov N. (2021). Single-cell proteomic and transcriptomic analysis of macrophage heterogeneity using SCoPE2. Genome Biol. 22, 50. 10.1186/s13059-021-02267-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Chung H, Parkhurst C, Magee EM, Phillips D, Habibi E, Chen F, Yeung B, Waldman JA, Artis D, and Regev A. (2021). Simultaneous single cell measurements of intranuclear proteins and gene expression. Preprint at bioRxiv. 10.1101/2021.01.18.427139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Zhang J, Squires C, Greenewald K, Srivastava A, Shanmugam K, and Uhler C. (2023). Identifiability Guarantees for Causal Disentanglement from Soft Interventions. Preprint at arXiv. 10.48550/arXiv.2307.06250. [DOI] [Google Scholar]
- 102.Lambert SA, Jolma A, Campitelli LF, Das PK, Yin Y, Albu M, Chen X, Taipale J, Hughes TR, and Weirauch MT (2018). The human transcription factors. Cell 172, 650–665. 10.1016/j.cell.2018.01.029. [DOI] [PubMed] [Google Scholar]
- 103.Cokelaer T, Bansal M, Bare C, Bilal E, Bot BM, Chaibub Neto E, Eduati F, de la Fuente A, Gö nen, M., Hill, S.M., et al. (2015). DREAMTools: a Python package for scoring collaborative challenges. F1000Res 4, 1030. 10.12688/f1000research.7118.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Waldminghaus T, and Skarstad K. (2010). ChIP on Chip: surprising results are often artifacts. BMC Genomics 11, 414. 10.1186/1471-2164-11-414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Kim D, Seo SW, Gao Y, Nam H, Guzman GI, Cho B-K, and Palsson BO (2018). Systems assessment of transcriptional regulation on central carbon metabolism by Cra and CRP. Nucleic Acids Res. 46, 2901–2917. 10.1093/nar/gky069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Nonaka G, Blankschien M, Herman C, Gross CA, and Rhodius VA (2006). Regulon and promoter analysis of the E. coli heat-shock factor, sigma32, reveals a multifaceted cellular response to heat stress. Genes Dev. 20, 1776–1789. 10.1101/gad.1428206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Scrucca L, Fop M, Murphy TB, and Raftery AE (2016). mclust 5: Clustering, Classification and Density Estimation Using Gaussian Finite Mixture Models. R J. 8, 289–317. 10.32614/RJ-2016-021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Hu H, Miao Y-R, Jia L-H, Yu Q-Y, Zhang Q, and Guo A-Y (2019). AnimalTFDB 3.0: a comprehensive resource for annotation and prediction of animal transcription factors. Nucleic Acids Res. 47, D33–D38. 10.1093/nar/gky822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Katsevich E, and Sabatti C. (2019). Multilayer knockoff filter: controlled variable selection at multiple resolutions. Ann. Appl. Stat 13, 1–33. 10.1214/18-AOAS1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Dai R, and Barber R. (2016). The knockoff filter for FDR control in group-sparse and multitask regression. In International Conference on Machine Learning. [Google Scholar]
- 111.Oates CJ, and Mukherjee S. (2012). Network Inference and Biological Dynamics. Ann. Appl. Stat 6, 1209–1235. 10.1214/11-AOAS532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Wagner A. (2001). How to reconstruct a large genetic network from n gene perturbations in fewer than n(2) easy steps. Bioinformatics 17, 1183–1197. 10.1093/bioinformatics/17.12.1183. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This paper analyzes publicly available data. We list the source URLs for the datasets in the key resources table. We have also made all data available as a collection via Zenodo with DOIs listed in the key resources table.
We have deposited all original code at GitHub as of May 2023 (https://github.com/ekernf01/knockoffs_paper), with DOIs for relevant releases minted by Zenodo. DOIs are listed in the key resources table.
Any additional information required to repeat the analyses reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Deposited data | ||
|
| ||
| All data used in this study | Zenodo | DOI: https://doi.org/10.5281/zenodo.6573413 |
| DREAM5 E. coli data | Sage Bionetworks | https://dreamchallenges.org/dream-5-network-inference-challenge/ |
| Mouse transcription factors | AnimalTFDB | https://guolab.wchscu.cn/AnimalTFDB#!/ |
| Human transcription factors | Lambert et al.102 | http://humantfs2.ccbr.utoronto.ca/download.php |
| SHARE-seq data | Ma et al.70 | GEO: GSM4156608 and GEO: GSM4156597 |
| 10X multiomics data | 10x Genomics website | https://www.10xgenomics.com/datasets/pbmc-from-a-healthy-donor-no-cell-sorting-10-k-1-standard-2-0-0 |
| Human and mouse transcription factor targets | ChIP-atlas | http://dbarchive.biosciencedbc.jp/kyushu-u/metadata/experimentList.tab |
| E. coli high-throughput gold standards | RegulonDB v10.9 | https://regulondb.ccg.unam.mx/ht |
| E. coli curated gold standards | RegulonDB v10.9 | https://regulondb.ccg.unam.mx/releasesNote/date=2021-04-02&version=10.9 |
|
| ||
| Software and algorithms | ||
|
| ||
| Modification of the BoolODE framework | This paper | DOI: https://doi.org/10.5281/zenodo.10063178 |
| Modification of the BEELINE framework | This paper | DOI: https://doi.org/10.5281/zenodo.10063174 |
| E. coli analysis | This paper | DOI: https://doi.org/10.5281/zenodo.10063164 |
| Multi-omics analysis | This paper | DOI: https://doi.org/10.5281/zenodo.10688721 |
| Demonstration of knockoff construction speedups and calibration on incomplete gold standards | This paper | DOI: https://doi.org/10.5281/zenodo.10063183 |
| Faster implementation of the Gaussian mirror (R package) | This paper | DOI: https://doi.org/10.5281/zenodo.10063192 |
| Faster implementation of knockoff construction (limited Julia interface) | This paper | DOI: https://doi.org/10.5281/zenodo.10063198 |
| Faster implementation of knockoff construction (limited Python interface) | This paper | DOI: https://doi.org/10.5281/zenodo.10063196 |
| Faster implementation of knockoff construction (R package) | This paper | DOI: https://doi.org/10.5281/zenodo.10063187 |