Postoperative recurrence prediction model for atrial fibrillation: a meta-analysis

Abstract

Objective: To systematically evaluate a recurrence risk prediction model for patients with Atrial Fibrillation (AF) following ablation, and to provide a reference for the model establishment and optimization. Methods: Literature retrieval was conducted in databases including PubMed, Cochrane Library, EMbase, and Web of Science to collect studies on recurrence risk prediction models for AF patients following ablation. Study quality was assessed using Prediction Model Risk of Bias Assessment Tool, and a meta-analysis was performed using MedCalc statistical software. Results: A total of 17 studies were included, with 4 of high risk of bias, 9 of unknown risk of bias, and 4 of low risk of bias. Across all studies, forest plots and logistic regression models were the most used prediction models. The area under the receiver operating characteristic curve (AUC) values of the prediction models ranged from 0.667 to 0.920, with a median AUC of 0.852. Through the calculation of the weighted summary of the AUC, the meta-analysis yielded a total AUC of 0.815 (0.780-0.850), indicating that the prediction models have good overall discrimination for the risk of recurrence in AF patients after ablation. After excluding studies with extreme AUC values, the adjusted AUC was 0.817 (0.786-0.849), suggesting that these extreme values did not significantly affect the overall combined results. Further subgroup analysis revealed that factors such as study design, follow-up time, sample size, and data set partitioning may significantly influence model performance and heterogeneity. Meta-analysis of predictive factors referenced in at least three studies showed that gender (OR = 0.862), atrial fibrillation type (OR = 0.660), and left atrial diameter (OR = 0.094) were predictive factors for postoperative recurrence in atrial fibrillation patients (P < 0.05). Results of Egger’s test and Begg’s test did not find evidence of publication bias in the studies. Conclusion: Current predictive models can be used as clinical decision support tools, but due to certain heterogeneity and risk of bias, they are recommended to be used cautiously in clinical practice and combined with other clinical information for comprehensive judgments.

Introduction

With the increase in the average life span of the global population and the extension of the survival period for chronic diseases, atrial fibrillation (AF) has become a major cardiovascular concern in the 21st century [1]. Currently, AF affects approximately 0.51% of the global population, marking a 33% increase over the past 20 years [2]. It is reported that by 2050, at least 72 million people in Asia will be diagnosed with AF [2]. The rise in AF prevalence is closely related to the increase in diseases such as coronary heart disease, hypertension, and heart failure [3]. AF can induce thrombosis and embolism, leading to stroke, hemiplegia, and even death; besides, it can also cause peripheral arterial embolism and pulmonary embolism [4,5].

Ablation therapy has a significant therapeutic effect on AF, and most patients can undergo ablation therapy. A systematic review covering 5 clinical trials with a total of 994 patients showed that catheter ablation therapy is significantly more effective than antiarrhythmic drug therapy in reducing the recurrence of atrial tachyarrhythmia, symptomatic AF, and hospitalization [6]. However, despite the use of the latest technologies and multiple repeat procedures, the recurrence of AF remains a concern. Statistics indicate that the risk of AF recurrence within one year after undergoing radiofrequency ablation therapy can be as high as 50% [7]. Therefore, a thorough understanding of the risk factors for postoperative AF recurrence, detailed stratification of patients’ recurrence risks, identification of appropriate patient populations for radiofrequency catheter ablation therapy, and implementation of personalized treatment strategies, are crucial for improving procedural success rates and reducing patients’ economic burden. Some researchers have developed predictive factors, scoring systems, or prediction models for postoperative recurrence in different AF study cohorts [8,9]. However, there is still controversy regarding the reliability and applicability of these prediction models, with variations in research quality. As a result, we conducted a systematic review of prediction models for post-ablation recurrence risk in AF patients, aiming to provide reference basis for the establishment and optimization of these models.

Data and methods

This study was registered in PROSPERO (CRD42024572954).

Inclusion and exclusion criteria

Inclusion criteria: (1) Study subjects were AF patients aged ≥ 18 years; (2) Studies focused the construction and/or validation of predictive models for postoperative AF recurrence, risk stratification, etc.; (3) Study design was either retrospective or prospective; (4) Outcome indicator was postoperative recurrent AF, diagnosed using methods such as electrocardiogram, Holter monitoring, or telemetry devices, and/or a comprehensive judgment based on clinical characteristics; (5) English and Chinese literature. Exclusion criteria: (1) Duplicated published literature; (2) Reviews, case reports, conference abstracts, or other similar literature; (3) Literature with only an abstract or where the full text cannot be obtained; (4) Literature that only analyzed risk factors without constructing a risk prediction model; (5) Literature with incomplete model construction process or lacking details; (6) Literature providing risk prediction models based on systematic reviews/Meta-analyses.

Literature search strategy

A comprehensive search was conducted for studies on the construction of postoperative recurrence prediction models for AF patients published in PubMed, Embase, Web of Science and Cochrane Library databases. The search period spanned from January 2000 to May 2024. Relevant references were traced and supplemented. The search terms include “Atrial Fibrillation”, “Auricular Fibrillation”, “Persistent Atrial Fibrillation”, “Familial Atrial Fibrillation”, “Paroxysmal Atrial Fibrillation”, “Catheter Ablation”, “Radiofrequency Ablation”, “Cryoballoon Ablation”, “Recurrence”, “Postoperative Recurrence”, “Clinical Prediction Model”, “Risk Prediction”, “Risk Assessment”, “Risk Prediction Model”, “Model”, “Risk Stratification”, and “Predictor”.

A combination of ree-text and MeSH terms (Medical Subject Headings) was used for retrieval. Taking PubMed as an example, the search mode was (((((((((“Atrial Fibrillation”[Mesh]))) OR (Auricular Fibrillation[Title/Abstract])) OR (Persistent Atrial Fibrillation[Title/Abstract])) OR (Familial Atrial Fibrillation[Title/Abstract])) OR (Paroxysmal Atrial Fibrillation[Title/Abstract])) AND ((((((“Catheter Ablation”[Mesh]) OR (Transvenous Electrical Ablation[Title/Abstract])) OR (Electric Catheter Ablation[Title/Abstract])) OR (Catheter Abla-tion, Percutaneous[Title/Abstract])) OR (Radiofrequency Catheter Ablation[Title/Abstract])) OR (Transvenous Catheter Ablation[Title/Abstract]))) AND ((((“Recurrence”[Mesh]) OR (Relapse[Title/Abstract])) OR (Relapses[Title/Abstract])) OR (Recrudescence[Title/Abstract]))) AND (((((“Nomograms”[Mesh]) OR (Nomogram[Title/Abstract])) OR (Partin Tables[Title/Abstract])) OR (Partin Nomograms[Title/Abstract])) OR (Partin Table[Title/Abstract])).

Literature selection

Two researchers (Chaofeng Chen, Yanyan Guo) independently screened the literature based on inclusion and exclusion criteria and cross-checked their selections. In case of disagreements, they first discussed the issue to reach a resolution. If consensus could not be reached, a third-party opinion was sought for consultation.

Data extraction

Two researchers (Chaofeng Chen, Yanyan Guo) developed a data collection form to extract information, including the first author, country, type of study, sample size, number of models built, methods of model construction, area under the receiver operating characteristic curve (AUC), model performance and validation methods, and model presentation methods.

Quality evaluation

Based on the Prediction model Risk of Bias Assessment Tool (PROBAST) [10], two researchers (Chaofeng Chen, Yanyan Guo) assessed the risk of bias in the collected literature. The assessment covered key areas such as the study population, predictive variables, outcomes, and analysis methods, as well as overall bias risk and applicability. Each area was categorized into low, unknown, or high levels of bias based on the degree of risk identified.

Model evaluation

Model evaluation is measured by two key indicators: discrimination and calibration. Discrimination reflects the model’s ability to distinguish between events that are likely to occur and those that are not, with the AUC being the primary metric. The AUC ranges from 0.5 to 1, where 0.5 indicates no discriminative ability, 0.5-0.6 indicates poor discrimination; 0.6-0.7 indicates limited discrimination; 0.7-0.8 indicates moderate discrimination; 0.8-0.9 indicates good discrimination; and 0.9-1 indicates excellent discrimination. Calibration, on the other hand, reflects the consistency between the model’s predicted outcomes and actual observed outcomes, serving as a measure of predictive accuracy. Calibration can be assessed through calibration curves or statistical tests. Calibration curves show the relationship between predicted probabilities and actual occurrence probabilities, where strong calibration means predicted probabilities align closely with actual occurrence.

Meta analyses

If the literature only reports the model’s AUC and its 95% confidence interval (CI), the standard error should be calculated using Newcombe RG [11]. For literature that only reports the AUC value without 95% CI or standard error, the method developed by Hanley and McNeil [12] was used to estimate the standard error. The AUC, standard error, 95% CI, and other data were then entered into the MedCalc software for meta-analysis. The meta-analysis of predictive factors for postoperative recurrence in AF patients was conducted using Stata 17. The I² statistic was used to assess the heterogeneity among studies. I² value > 50% or P < 0.1 indicates significant heterogeneity, and a random effects model was applied to calculate the combined effect size, including the odds ratio (OR) and its 95% CI. I² ≤ 50 or P > 0.1 indicates acceptable heterogeneity, and a fixed effects model was used.

Publication bias

Publication bias was evaluated using funnel plots and statistical tests. In addition, subgroup analyses were performed to determine whether specific study characteristics, such as study type, follow-up duration, data set partitioning, and sample size, contributed to heterogeneity.

Results

Literature screening process

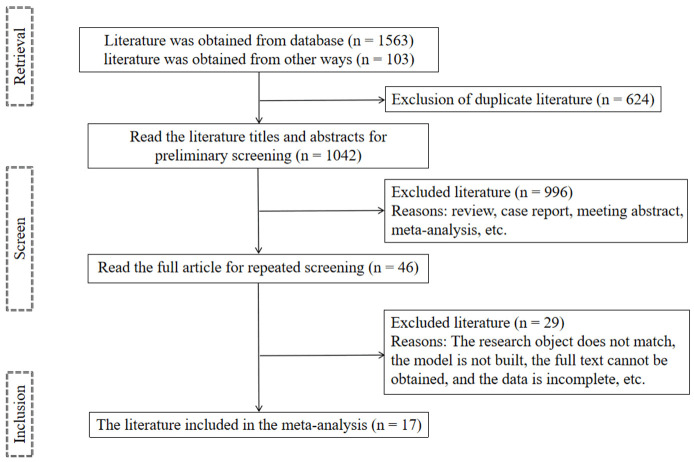
A total of 1,666 relevant articles were retrieved. After initial screening, 624 duplicate articles were excluded. Upon reviewing the titles and abstracts of the remaining articles, 996 articles were excluded for not meeting the inclusion criteria. A full-text review of the remaining 46 articles identified 17 articles [13-29] for final meta-analysis. Figure 1 illustrates the detail literature screening process.

Figure 1.

Flow chart of literature screening.

Description of literature features

Most of the studies (13 articles) were conducted in China. The recurrence rate of AF after surgery ranged from 8.70% to 48.57%. The number of predictive factors in the risk prediction models ranged from 3 to 19, with most models developed using logistic regression (Table 1).

Table 1.

Basic features of the included literature

Study	Year	Region	Research type	Sample size		Follow-up time	Number of predictors	Modeling approach
				Non-recurrence	Recurrence
Ruan ZB et al. [13]	2022	China	F	162	59	NA	4	Multivariate Cox regression
Budzianowski J et al. [14]	2023	Poland	F	144	57	1 year	12	XGBoost
Zheng D et al. [15]	2023	China	R	232	100	1 year	4	Multivariate Cox regression
Zhao Z et al. [16]	2022	China	R	278	207	1 year	4	Logistic egression
Zhou XJ et al. [17]	2021	China	F	233	79	1 year	6	Logistic egression
Liu M et al. [18]	2023	China	R	89	47	3 months	4	Logistic egression
Dong Y et al. [19]	2022	China	F	342	107	1 year	5	Multivariate Cox regression
Jia S et al. [20]	2021	China	R	144	56	1 year	5	Logistic egression
Lee DI et al. [21]	2022	China	R	130	47	1 year	11	Multilayer Perceptron
Baalman SWE et al. [22]	2021	Netherlands	F	258	188	24 months	12	Logistic egression
Saglietto A et al. [23]	2023	Italy	F	2331	797	1 year	19	Random forest
Sun S et al. [24]	2023	China	R	298	61	1 year	6	XGBoost
Yang Z et al. [25]	2021	China	R	160	55	3-6 months	4	Logistic egression
Sheng J et al. [26]	2022	China	R	252	24	3-6 months	4	Logistic egression
Ma XX et al. [27]	2021	China	R	83	41	12±9 months	4	Logistic egression
Tang S et al. [28]	2022	Canada	R	112	44	1 year	6	Deep neural network
Ma Y et al. [29]	2023	China	R	336	135	13-36 months	15	Random forest

Notes: NA: Not described; F: foresight study; R: retrospective study.

Basic characteristics of risk prediction model

Among the included studies, only six provided specific information on handling missing data. Three studies employed K-fold cross-validation for dataset partitioning, while eight studies performed a single random split, with the remaining studies not describing their approach. In terms of model performance, most studies assessed the model’s discrimination and calibration. For validation, 11 studies described an internal validation process, while only three conducted external validation. The prediction models were mainly presented in the form of a nomogram (Table 2).

Table 2.

The basic characteristics of the risk prediction model

Study	Data set partitioning	Missing value handling method	Efficiency of model		Verification of model		Model presentation
			Distinction	Calibration degree	Internal verification	External verification
Ruan ZB et al. [13]	NA	NA	AUC, Sensitivity, Specificity	Calibration curve	Bootstrap	NA	Nomograph
Budzianowski J et al. [14]	Cross verification	NA	AUC	NA	NA	NA	SHAP
Zheng D et al. [15]	7:3	NA	AUC	Calibration curve, Decision curve	Bootstrap	Yes	Nomograph
Zhao Z et al. [16]	7:3	NA	C-index	Calibration curve	NA	NA	Nomograph
Zhou XJ et al. [17]	NA	NA	AUC, Sensitivity, Specificity	Calibration curve, Hosmer-Lemeshow	Bootstrap	NA	Nomograph
Liu M et al. [18]	NA	NA	AUC	Hosmer-Lemeshow, Decision curve	Bootstrap	NA	Nomograph
Dong Y et al. [19]	NA	Mean filling	AUC	Calibration curve, Decision curve	Bootstrap	Yes	Nomograph
Jia S et al. [20]	7:3	NA	AUC, Accuracy	Calibration curve, Decision curve	NA	NA	β coefficient plots the risk scoring formula
Lee DI et al. [21]	Cross verification	NA	AUC, Sensitivity, Specificity	NA	Cross verification	NA	Deep learning model based on multi-layer Perceptron architecture
Baalman SWE et al. [22]	NA	Iterative interpolation is performed by MissForest method	AUC	NA	Cross verification	NA	SHAP
Saglietto A et al. [23]	8:2	K-nearest Neighbor interpolation technique	AUC	Hosmer-Lemeshow	NA	Yes	Line computer
Sun S et al. [24]	8:2	NA	AUC, Sensitivity, Specificity	Calibration curve	Cross verification	NA	SHAP
Yang Z et al. [25]	NA	NA	AUC	Calibration curve	Bootstrap	NA	Nomograph
Sheng J et al. [26]	75:25	NA	AUC, Sensitivity, Specificity	Calibration curve	NA	NA	Nomograph
Ma XX et al. [27]	NA	NA	AUC	Calibration curve	Bootstrap	NA	Nomograph
Tang S et al. [28]	NA	Mean filling	AUC	Brier score	Cross verification	NA	Rank the importance of clinical features
Ma Y et al. [29]	7:3	Median filling	AUC, Accuracy, Recall, F1 rating	Decision curve	NA	NA	SHAP

Notes: NA: Not described; SHAP: Shapley additive explanations.

Bias assessment results

We conducted bias risk assessment using the PROBAST tool. Among the 11 retrospective studies, the risk of bias in the study population was assessed as “unknown risk”. In the study by Zheng D et al. [15], due to potential technical or operational errors in the radiomics feature extraction process, the bias risk for the predictive variables was also assessed as “unknown risk”. The outcomes of 5 articles were rated as “unknown risk”, while the rest were rated as “low risk”. Most articles exhibited some level of “unknown risk” and “high risk” in the analysis methods, mainly due to the lack of handling missing data, issues related to data complexity, and insufficient description of model validation. The common presence of “unknown risk” and “high risk” across these four domains led to an overall bias risk being categorized as “unknown risk” or “high risk” in most cases. In terms of overall applicability, 13 studies were rated as having “unknown risk” (Table 3).

Table 3.

Results of bias risk assessment

Study	Study population	Predictive variables	Outcomes	Analysis methods	Overall bias risk	Overall applicability
Ruan ZB et al. [13]	+	+	?	?	?	?
Budzianowski J et al. [14]	+	+	+	-	-	+
Zheng D et al. [15]	+	?	+	+	?	?
Zhao Z et al. [16]	?	+	+	-	-	?
Zhou XJ et al. [17]	?	+	+	?	+	?
Liu M et al. [18]	?	+	?	+	?	?
Dong Y et al. [19]	+	+	+	+	+	+
Jia S et al. [20]	?	+	+	-	-	?
Lee DI et al. [21]	?	+	+	?	?	?
Baalman SWE et al. [22]	+	+	+	+	+	+
Saglietto A et al. [23]	+	+	+	+	+	+
Sun S et al. [24]	?	+	+	?	?	?
Yang Z et al. [25]	?	+	?	?	?	?
Sheng J et al. [26]	?	+	?	-	-	?
Ma XX et al. [27]	?	+	?	?	?	?
Tang S et al. [28]	?	+	+	+	?	?
Ma Y et al. [29]	?	+	+	+	?	?

Notes: +: Low risk; -: High risk; ?: Unknown Risks.

Results of meta-analysis of AUC for predictive models

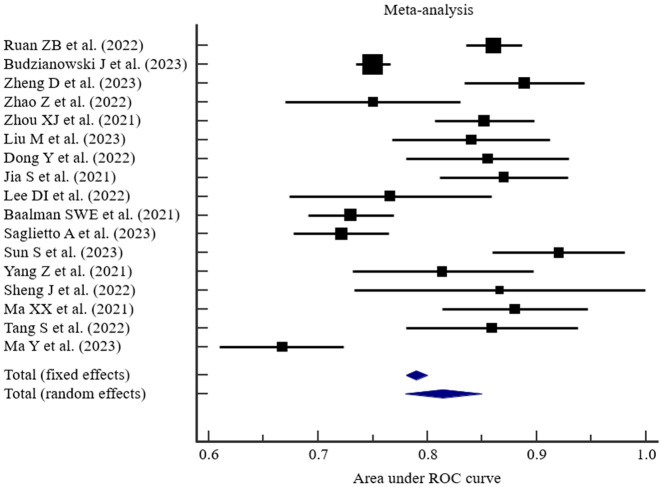
The AUC values for the predictive models established in the 17 studies [13-29] ranged from 0.667 to 0.920, with a median AUC of 0.852. The results of the random-effects meta-analysis are shown in Figure 2, with heterogeneity I² = 89.59%, P < 0.001. The pooled AUC was 0.815 (0.780-0.850).

Figure 2.

Results of meta-analysis of AUC for predictive models.

Subgroup analysis

To determine if specific study characteristics (such as study type, follow-up duration, method of data partitioning, and sample size) contribute to heterogeneity, we conducted subgroup analyses. The summary results are shown in Table 4.

Table 4.

Subgroup analysis

Subgroup	N	AUC (95% CI)	I2	P
All studies	17	0.815 (0.780-0.850)	89.59%	< 0.001
Research type
R	11	0.829 (0.784-0.874)	81.84%	< 0.001
F	6	0.793 (0.743-0.842)	93.75%	< 0.001
Follow-up timea
< 1 year	3	0.834 (0.784-0.884)	0%	< 0.001
1 year	10	0.822 (0.780-0.865)	89.29%	< 0.001
> 1 year	3	0.757 (0.659-0.855)	91.50%	< 0.001
Sample size
< 300	9	0.830 (0.795-0.866)	89.40%	< 0.001
≥ 300	8	0.797 (0.737-0.857)	91.02%	< 0.001
Data set partitioningb
Single random partition	7	0.809 (0.740-0.879)	91.02%	< 0.001
K-fold cross-validation	2	0.750 (0.735-0.766)	0%	< 0.001

Notes: F: foresight study; R: retrospective study;

^aRuan ZB et al. [13]. The follow-up time was not mentioned in the study and was not analyzed.

^bEight studies did not mention the data set partitioning method and were not analyzed.

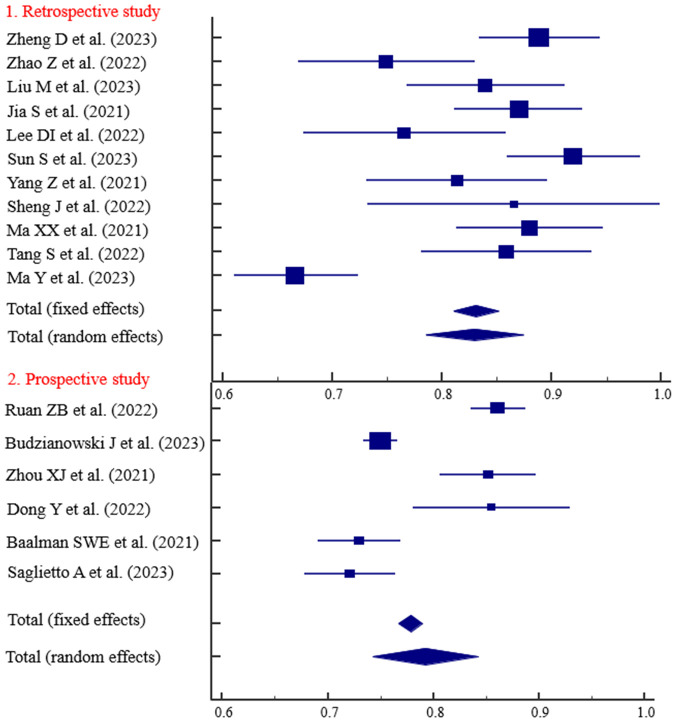
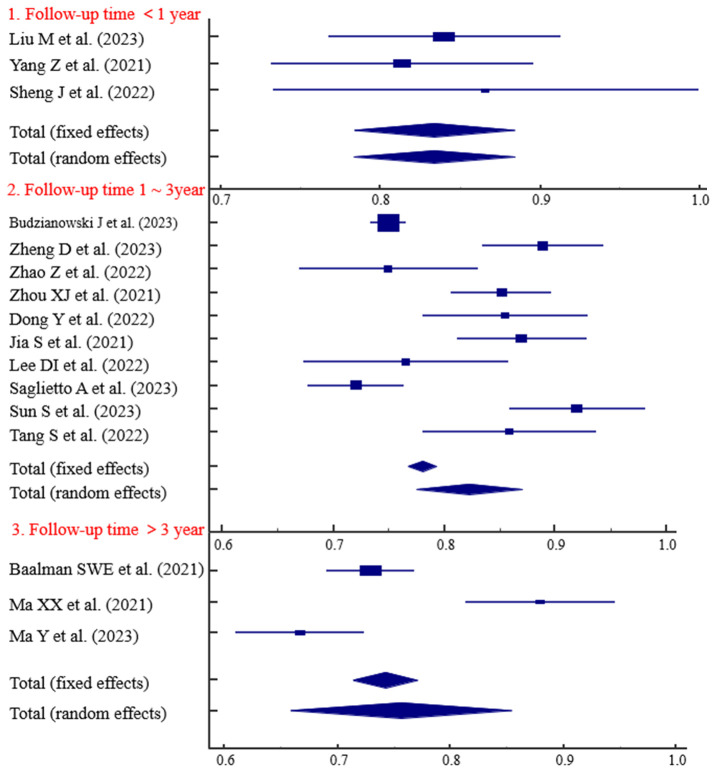
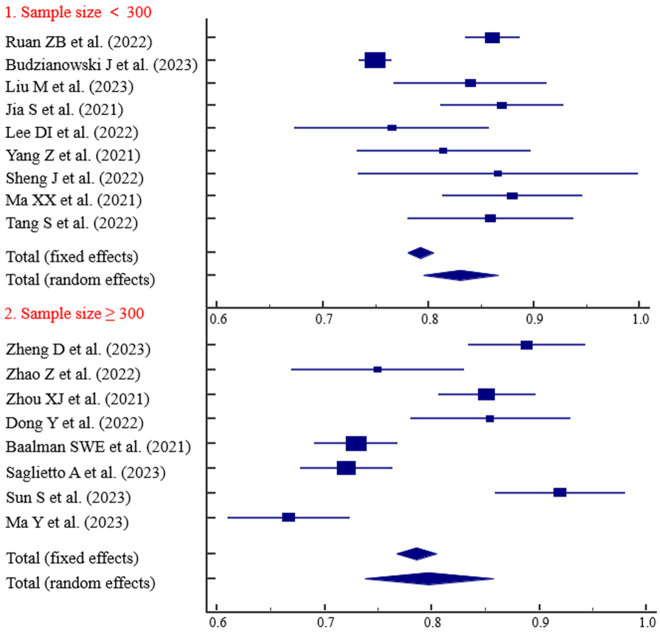
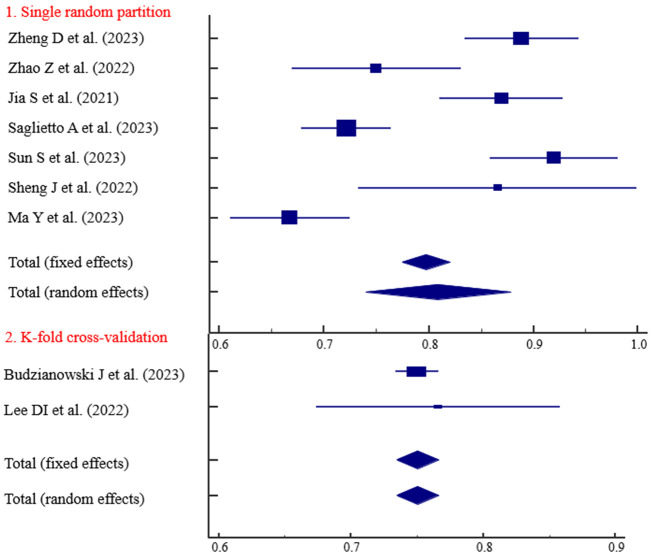
The predictive ability of the models based on retrospective studies was slightly higher than those based on prospective studies, with AUC values of 0.829 and 0.793, respectively (Figure 3). Three studies with follow-up durations of less than 1 year demonstrated strong predictive ability (AUC = 0.834) (Figure 4). The predictive ability of models with sample sizes < 300 (AUC = 0.830) was significantly higher than those with sample sized ≥ 300 (AUC = 0.797) (Figure 5). Predictive results obtained through random data set partitioning (AUC = 0.809) were better compared to predictive results obtained through cross-validation method (AUC = 0.750) (Figure 6).

Figure 3.

Subgroup analysis of research types.

Figure 4.

Subgroup analysis of follow-up time.

Figure 5.

Subgroup analysis of sample size.

Figure 6.

Subgroup analysis of dataset partitioning method.

Analysis of predictors of postoperative recurrence in AF patients

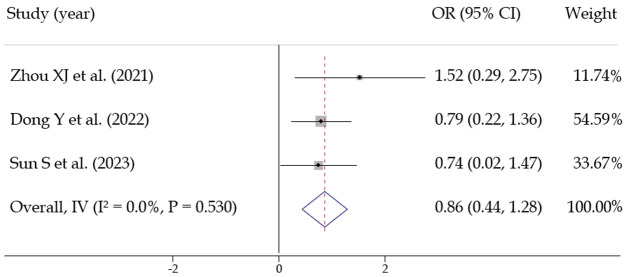
(1) Gender: Three studies [17,19,24] assessed the effect of gender on postoperative recurrence. No statistical heterogeneity was observed among the studies (I² = 0%, P = 0.530), allowing for the use of a fixed-effects model. The pooled effect size was OR = 0.862 [0.441, 1.284], with statistical significance Z = 4.011, P < 0.001, suggesting that gender is a predictive factor for postoperative recurrence in AF patients (Figure 7).

Figure 7.

Meta analysis of predictors of postoperative recurrence in patients with atrial fibrillation (gender).

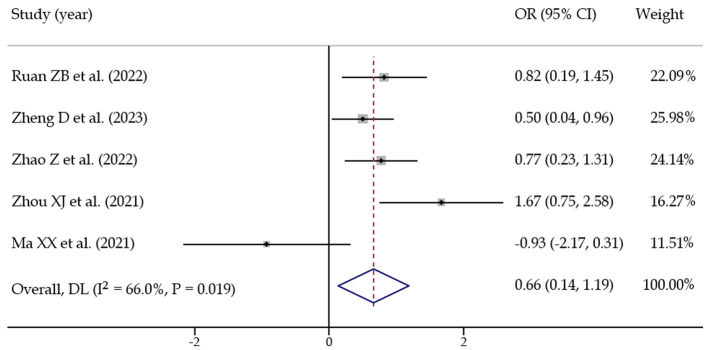
(2) AF type: Five studies [13,15-17,27] assessed the impact of atrial fibrillation type on recurrence. Statistical heterogeneity was present among the studies (I² = 66.0%, P = 0.019), so a random-effects model was used. The pooled effect size was OR = 0.660 [0.135, 1.185], with statistical significance (Z = 2.465, P = 0.014), suggesting that AF type is a significant predictor for postoperative recurrence (Figure 8).

Figure 8.

Meta analysis of predictors of postoperative recurrence in patients with atrial fibrillation (atrial fibrillation type).

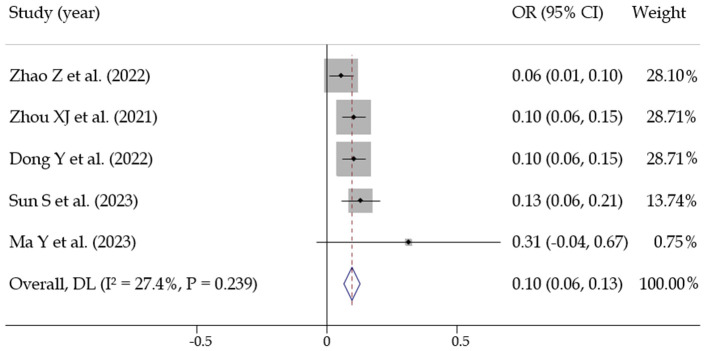
(3) Left atrial diameter: Five studies [16,17,19,24,29] assessed the relationship between left atrial diameter and recurrence. No statistical heterogeneity was observed among the studies (I² = 27.4%, P = 0.239). A fixed-effects model was then used, yielding a pooled effect size of OR = 0.094 [0.069, 0.119], with statistical significance (Z = 7.476, P < 0.001). This suggests that left atrial diameter is a significant predictive factor for postoperative recurrence in atrial fibrillation patients (Figure 9).

Figure 9.

Meta analysis of predictors of postoperative recurrence in patients with atrial fibrillation (left atrial diameter).

Publication bias

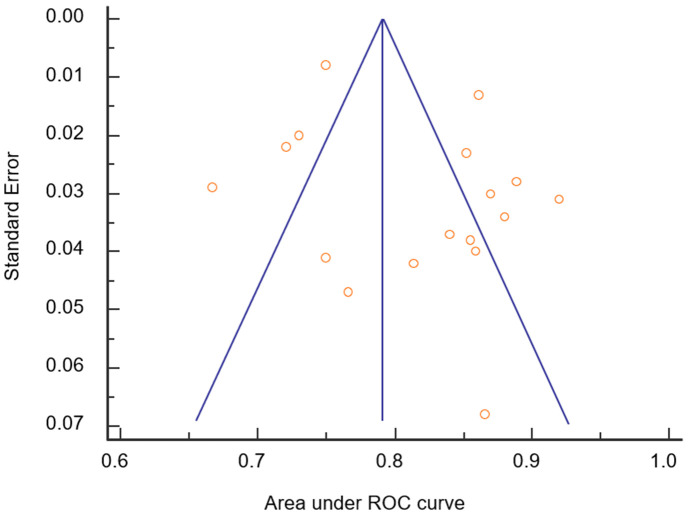
Most of the studies had AUC values outside the 95% CI of the weighted summary AUC, but the distribution was relatively symmetric. Egger’s test (P = 0.138) and Begg’s test (P = 0.621) showed that the publication bias did not significantly impact the results (Figure 10).

Figure 10.

Publication of bias assessment results.

Discussion

Patients with AF face a relatively high risk of recurrence within one year after ablation surgery. Accurate risk prediction models can identify high-risk patients early, enabling timely medical intervention, preventive measures, and a reduction in the recurrence rate. This study comprehensively analyzed 17 predictive models for postoperative AF recurrence, revealing that the logistic regression was the primary modeling method, with most models presented as nomograms. These models generally demonstrated good predictive efficacy, with a high AUC value (> 0.7). However, several limitations were identified, including insufficient information on variable selection, missing data processing, comprehensive assessment of model calibration, rigorous model validation, and result reporting. A complete model construction process usually includes determining research objectives, selecting data sources, performing variable screening, and carrying out data preprocessing, among other key steps [30,31]. In this study, among the 17 predictive models included, 11 were based on retrospective studies, which may carry the risk of data bias. To improve the accuracy and reliability of the model, it is recommended that in future model optimization work, prospective studies or registry study data should be prioritized. Prospective studies, due to their rigorous design, can reduce bias in data collection and processing.

In terms of variable selection, we found that most studies relied on univariate logistic regression analysis during the variable selection stage. Although this method is simple, it may lead to incorrect inclusion or exclusion of certain predictive factors, thus impacting the accuracy and reliability of the model. To improve the accuracy of variable selection, more advanced methods such as Least Absolute Shrinkage and Selection Operator (LASSO) regression, Ridge regression, and ElasticNet regression [32,33] can be applied. These methods introduce regularization terms to minimize the risk of overfitting in the model. We suggest that in future variable selection, new methods should be combined with clinical practice to improve the accuracy of selection, thereby developing more reliable and effective models for predicting the risk of postoperative AF recurrence.

In this study, 12 risk prediction models did not mention the handling of missing data, which could affect the stability of the models and potentially lead to overfitting. In statistical modeling and the development of prediction models, validation is a crucial step for ensuring both the accuracy and reliability of the models. Debray TP et al. [34] emphasized the importance of validation studies for prediction models, highlighting that validation is essential for assessing the model’s performance in new patient populations. Internal validation, which involves splitting the dataset into training and testing sets, allows for fitting the model on the training set and validating it on the testing set. This helps detect whether the model generalizes well to unseen data or overfits the training data. External validation further enhances the model’s generalizability [35]. By testing the model on a completely different dataset from the one used to develop it, external validation evaluates the model’s performance on new samples, confirming its practicality and stability.

In this study, 11 risk prediction models underwent internal validation. However, only 3 models underwent external validation, which raises concerns about overfitting and overestimation of the models’ predictive performance. Dretzke J et al. [35] conducted a systematic review of the literature, including 33 studies that developed or validated 13 different prediction models. Using the PROBAST tool to assess the risk of bias, they found that most models lacked external validation, potentially leading to overly optimistic estimates of model performance. Future research should prioritize incorporating more external validation techniques, such as cross-validation and independent cohort validation, to better evaluate the predictive performance and extrapolation ability of the models.

Through meta-analysis, we calculated a pooled AUC value of 0.815 (0.780-0.850) across all included models, indicating that these predictive models have good efficacy in distinguishing the risk of AF recurrence after ablation in patients and hold practical value in clinical applications. However, heterogeneity exists among the studies. Subgroup analyses revealed that factors such as study design, follow-up time, sample size, modeling methods, and data partitioning methods may significantly impact both the performance and heterogeneity level of predictive models.

Subgroup analysis showed that models based on retrospective studies had better predictive ability than those based on prospective studies, with AUC values of 0.829 and 0.793, respectively. Retrospective studies benefit from advantages in sample size and data completeness but may also be associated with potential selection bias and information bias. Predictive models for post-AF ablation recurrence risk demonstrated different predictive ability under different follow-up times and sample size conditions. Specifically, models with follow-up period of less than 1 year exhibited higher predictive accuracy than those with sample sizes greater than 300. Shorter follow-up times may allow researchers to more accurately monitor and record postoperative recurrence events, as patients may undergo more frequent evaluations, enabling the model to capture recurrence risk factors faster. However, shorter follow-up times may not fully account for long-term recurrence risks, as some patients may experience recurrence after the end of the follow-up period. Models with shorter follow-up times may struggle to accurately assess the efficacy of long-term effectiveness of treatment strategies and patient prognosis. Small sample sizes may lead to model overfitting, especially in the presence of noise in the data, impacting the model’s generalizability to a broader patient population [36]. Additionally, we found that predictive results obtained through random data set partitioning (AUC = 0.809) were superior to those obtained through cross-validation method data set partitioning (AUC = 0.750). While K-fold cross-validation offers a more robust evaluation of model performance, single random partitioning can yield different results due to the inherent randomness of the process.

When exploring the application of machine learning to predict AF recurrence after catheter ablation, Fan et al. [37] revealed that logistic regression is a widely used machine learning algorithm. Our research results are consistent with those of Fan et al. [37], as both identified logistic regression as the most used predictive model. This may be because logistic regression can handle linear relationships in clinical data and is easy to interpret, making it popular choice in medical research. Fan et al. [37] identified age, left atrial diameter, and type of AF as key variables. We conducted a meta-analysis on predictive factors referenced in at least three studies, and found that gender, type of AF, and left atrial diameter are key factors influencing postoperative recurrence in AF patients. This inconsistency may be due to differences in dataset characteristics, sample size, or radiomics feature extraction and analysis methods. An important variable in Fan et al.’s [37] model was radiomics features, which were not significant in our study. Additionally, Fan et al. included the duration of AF as a key variable, but in our analysis, it did not emerge as a significant independent predictor. This could be due to differences in study design, patient populations, or multicollinearity between AF duration and other variables. Studies indicate significant differences between males and females in hormonal levels, cardiac structure, and function, which may have an impact on the onset and recurrence of atrial fibrillation [38,39]. Paroxysmal AF and persistent AF also show differences in clinical presentation, disease progression, and treatment strategies. Particularly, persistent AF may indicate significant changes in cardiac structure and electrophysiological characteristics, potentially increasing the risk of postoperative recurrence [40]. Left atrial enlargement, an indicator of AF severity, is closely correlated with AF duration and recurrence risk after surgery [17,27]. Moreover, left atrial enlargement may be associated with atrial fibrosis and electrophysiological disturbances, both of which heighten the risk of AF recurrence [41].

Inevitably, several limitations should be noticed: (1) No meta-analysis was conducted on predictive factors; (2) In calculating the combined AUC, the lack of direct reporting of standard errors in most studies required the use of indirect methods, potentially affecting accuracy; (3) Due to the absence of clear guidelines for establishing prognostic prediction models, many studies lacked sufficient methodological details, further affecting the reliability of the research results.

Conclusion

At present, predictive models for the risk of AF recurrence after ablation surgery demonstrate good predictive efficacy, but there is still significant room for improvement, especially in terms of data processing, model calibration, and validation. Future research needs to focus on improving the handling of missing values, enhancing model calibration, and improving model quality by considering sample size, follow-up time, and types of study design.

Disclosure of conflict of interest

None.