Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Dec 3;128(49):10498–10506. doi: 10.1021/acs.jpca.4c05408

Advancing 19F NMR Prediction of Metal-Fluoride Complexes in Solution: Insights from Ab Initio Molecular Dynamics

Sahil Gahlawat †,‡, Kathrin H Hopmann †, Abril C Castro §,*
PMCID: PMC11647890  PMID: 39626023

Abstract

graphic file with name jp4c05408_0008.jpg

19F NMR parameters are versatile probes for studying metal-fluoride complexes. Quantum chemical calculations of 19F NMR chemical shifts enhance the accuracy and validity of the resonance signal assignments in complex spectra. However, the treatment of solvation effects in these calculations remains challenging. In this study, we establish a successful computational protocol using ab initio molecular dynamics simulations for the accurate prediction of 19F NMR chemical shifts in square-planar nickel-fluoride complexes. In particular, we have studied in detail the trans-[NiF(2,3,4,5-C6F4I)(PEt3)2] complex in a benzene solution. Our computations revealed that accounting for the dynamic conformational flexibility of the complex, including intramolecular interactions, is crucial for obtaining reliable 19F NMR chemical shifts. Overall, this study advances the understanding of employing state-of-the-art quantum chemistry methods to accurately model 19F NMR chemical shifts of nickel-fluoride complexes, emphasizing the importance of addressing solvation effects in such calculations.

1. Introduction

Metal-fluoride complexes have gained significant interest owing to their unique and interesting catalytic properties, which are of high importance in the pharmaceutical, agrochemical, and advanced materials industries.1,2 Their reactivity patterns are remarkably different from those of their more well-known alkoxy, chloro, bromo, and iodo counterparts, influenced by the distinctive properties of fluorine.3,4 Fluoride’s tendency to form stronger bonds with early transition metals or metals in high oxidation states is primarily attributed to its small size and high electronegativity. It can also act as a π-donor, enhancing activation by both the metal and the fluoride. In addition, fluoride’s ability to form strong hydrogen bonds and halogen bonds can facilitate further coordination of substrates near the metal atom, enhancing both the stability and reactivity of metal-fluoride complexes.5

Nuclear magnetic resonance (NMR) parameters of fluorine serve as highly versatile experimental probes for the molecular structure and chemical bonding of metal-fluoride complexes.6−8 The spin-1/2 19F nucleus, being 100% naturally abundant, exhibits a NMR span range of ∼1300 ppm9 in general and ∼300 ppm for organofluoride compounds.10,11 Moreover, metal-fluorides are particularly intriguing because they exhibit a 19F NMR resonance that lies upfield of most signals derived from carbon-bound fluorine. However, the sensitivity of 19F NMR shifts to the chemical environment means that even slight variations in the metal’s coordination sphere can significantly change the observed spectra, complicating the assignment of the resonance signals.12 The effectiveness and accuracy of 19F NMR analysis can therefore be enhanced by theoretical calculations, particularly when the spectra exhibit multiple resonances that are difficult to interpret in a straightforward manner.

Overall, the accuracy of 19F NMR chemical shift calculations is influenced by many factors, including the level of theory, geometry optimization, rovibrational corrections, and relativistic effects.9,13−16 However, few studies have addressed the influence of the solvation effects. Recent investigations confirmed that specific solute–solvent interactions significantly impact the 19F NMR shifts of fluoride-type anions, where fluoride exhibits strong hydrogen bonding interactions with the CH bonds of organic solvents.17,18 Notably, these strong interactions are not covered by implicit solvent models and become evident only with explicit solvation treatment.

Since 19F NMR is sensitive to halogen bonding interactions, it has proven to be particularly useful in detecting these types of interactions, both in solution19 and in the solid state.20 By detecting and studying halogen bonding, we gain valuable insights into molecular interactions and the formation of stable structures, as demonstrated in the pioneer study of NiII-fluoride complexes that form self-complementary networks held by a NiF···I(C) halogen bond.21 To understand how the 19F NMR resonances of the nickel-bonded fluoride are affected by the halogen bonds formed in the network, a computational study was performed in the square-planar trans-[NiF(2,3,4,5-C6F4I)(PEt3)2] (1oF), trans-[NiF(2,3,5,6-C6F4I)(PEt3)2] (1pF), and trans-[NiF(C6F5)(PEt3)2] (3F) complexes (Figure 1).22 The 19F NMR chemical shifts of these complexes were calculated in both the solution and the solid state to investigate the origin of the shielding. Preliminary density functional theory (DFT) calculations, including a continuum solvent model for benzene, reproduced the 19F NMR shifts of the nickel-bonded fluorine in 1pF and 3F in excellent agreement with the experimental data23 (within −0.1 and −2.1 ppm, respectively). However, the chemical shift of 1oF was not accurately reproduced. In this case, the calculation at the 2c-ZORA-PBE/TZ2P level showed a shift value of ∼23 ppm more shielded than that in the experiment.

Figure 1.

Figure 1

Open in a new tab

Nickel-fluoride complexes were examined in this work. The labels used in refs (21) and (22) are kept for easier connection with this work.

As relativistic effects were found to be small,22 and such discrepancies clearly exceed the expected margin of error for the functional and basis set,24 it was suspected that specific solvent interactions in the experimentally used benzene, which are not adequately covered by the standard implicit solvent model used, are responsible for the differences. Moreover, functional groups may also influence the 19F shielding, either through direct noncovalent interactions or through conformation alteration.11 Therefore, the influence of both the ortho iodine on the nickel-bonded fluoride resonance, which could significantly depend on the motion of the aryl group, and the intramolecular interactions between the fluoride and the phosphine groups is unlikely to be properly represented by the single structure retained for the calculation. In this work, we will demonstrate these factors by employing ab initio molecular dynamics (AIMD) simulations.

2. Methods

2.1. Structure Optimization

We conducted geometry optimization calculations for 1oF, 1pF, and 3F at the PBE0/TZ2P level of theory.25−27 Scalar and spin–orbit relativistic effects at the two-component (2c) level were included using the zeroth-order regular approximation (ZORA) Hamiltonian.28−32 To address dispersion effects, we employed Grimme’s D3 approach.33 Core electrons were represented using an effective core potential that integrates a small core, as implemented in the ADF program, version 2022.34,35 Furthermore, we incorporated the COSMO implicit solvent model for benzene during the optimization process.36−38

2.2. Ab Initio Molecular Dynamics Simulations

Ab initio molecular dynamics (AIMD)39 simulations of complex 1oF were performed in explicit benzene solvation according to the Born–Oppenheimer approximation using the CP2K program package.40 The starting model system for AIMD simulations was produced using the Packmol program.41 The model consists of complex 1oF surrounded by 50 benzene molecules in a cubic box of edge 20.4 Å, reproducing the solvent density of 0.87 g/mL. The simulation cell was treated under periodic boundary conditions using a time step of 0.25 fs. The simulation was performed with Kohn–Sham DFT (PBE exchange-correlation functional)25,26 and a combined DZVP Gaussian and auxiliary plane-wave (250 Ry cutoff) basis set.42 The pure functional PBE was used instead of the hybrid functional PBE0 (used for geometry optimizations) to reduce the computational cost of the AIMD simulations. The core electrons were accounted for using pseudopotentials of the Goedecker–Teter–Hutter (GTH) type.43 The dispersion correction was considered with Grimme’s D3 model.33

The equilibration of the initial model conformation was performed using a microcanonical ensemble (NVE) until an average temperature of 298 K was reached. After the equilibration, a production trajectory of 30 ps was generated using a canonical (NVT) ensemble with a temperature of 298 K regulated with the CSVR algorithm.44 From the simulation of 30 ps, a total of 180 snapshots were taken randomly. Identical snapshots were used for modeling dynamic NMR with and without explicit solvents. The geometries from the AIMD simulation were not optimized further because we are interested in the chemical shifts of the thermodynamic ensemble of structures.

2.3. 19F NMR Chemical Shift Calculations

We computed the NMR shielding tensors and chemical shifts of the nickel-bound fluorine on different systems, namely, (1) 1oF, 1pF, and 3F complexes, (2) 1oF with an explicit benzene molecule, (3) snapshots of 1oF from AIMD simulations without benzene molecules, and (4) snapshots of 1oF from AIMD simulations with three explicit benzene molecules chosen through noncovalent interaction (NCI) analysis. For the snapshots from AIMD simulations, we computed the final chemical shift value by averaging the values across an ensemble of structures.

The 19F NMR calculations were performed with the PBE functional25,26 along with the all-electron Slater-type orbitals (STO) TZ2P basis set.27 The shielding tensors were computed with an implicit COSMO solvent model for benzene.36−38 Relativistic effects were considered using the 2c-ZORA approach,28−32 as implemented in the ADF program.34,35 The gauge-origin problem was treated using the gauge-invariant atomic orbital (GIAO) approach.45 Additional static δ(19F) calculations were performed for 1oF, 1pF, and 3F complexes using two approaches: (1) at the 2c-ZORA-PBE/TZ2P level in the gas phase to evaluate the performance of the COSMO model and (2) using a nonrelativistic (NR) method at the PBE/TZ2P level to examine the relativity dependence of the 2c-ZORA results. All calculated shieldings σ(19F) were converted to chemical shifts δ(19F) (in ppm) relative to the shielding of trichlorofluoromethane, computed at the same level of theory (CFCl3, calculated σ(19F) = 144.0 (2c-ZORA)solv, 144.6 (NR)solv, 141.6 (2c-ZORA)gas).

2.4. Noncovalent Interactions Analysis

The noncovalent interactions between 1oF and explicit solvent molecules were analyzed with the NCIPLOT 4.0 program.46 The density and gradient files generated by the program were used to draw the isosurface, displaying the interactions. The VMD program47 was used for drawing the isosurface and selecting the solvent molecules interacting closely with 1oF. The gradient isosurfaces (s = 0.3 au) are colored on a blue-green-red scale analogous to the values of sign(λ2)ρ ranging from −3.0 to 3.0 au.

A data set collection of the computational results is available in the ioChem-BD repository48 and can be accessed via 10.19061/iochem-bd-6-422.

3. Results and Discussion

3.1. Static Approach for 19F NMR Chemical Shifts in Solution

As a first approximation, the 19F NMR chemical shifts δ(19F) of the nickel-bonded fluoride in complexes 1pF, 1oF, and 3F (Figure 1) were calculated based on static (fully optimized) structures using the PBE0 functional, including an implicit COSMO solvation model for benzene; see the Computational Methods section for more details. The structural parameters of the computed structures show minor variations compared to the previously reported values obtained with a PBE0/SMD approach.22 For instance, the Ni–F bond distances in 1pF and 3F are slightly larger than the ones reported earlier, with differences of 0.014 and 0.015 Å, respectively (Table S1). These differences can be attributed to the modified computational protocol used in this work, which includes changes to the basis set, implicit solvent model, and the consideration of relativistic effects. However, the calculated Ni–F bond distance in 1oF (1.837 Å) is only 0.003 Å longer than the one obtained at the PBE0/SMD level. Overall, the structural parameters obtained from both methodologies are consistent, allowing us to employ the selected 2c-ZORA-PBE0/TZ2P approach combined with the COSMO model for further calculations of the 19F NMR chemical shifts.

For the static δ(19F) shift calculations, the performance of the COSMO model vs gas phase was assessed, and the role of relativity was analyzed by comparing the nonrelativistic (NR) approach and the two-component SO relativistic zeroth-order regular approximation (2c-ZORA); see the Computational Methods section for more details. The resulting 19F NMR chemical shifts, reported as deviations from the experimental values (Δδ), are shown in Table 1. The sole mismatch in the case of 1oF is clearly observed in our calculations; at the 2c-ZORA level, the Δδ values are −18.2 (gas phase) and −19.5 ppm (benzene solution). By contrast, 1pF and 3F show good agreement with the experimental values. Notably, the computed δ(19F) values in the solution phase, particularly those including relativistic effects, outperformed the gas-phase calculations. Moreover, the δ(19F) values at the 2c-ZORA level show an improvement of ∼2 and ∼5 ppm over their nonrelativistic values. Although this improvement is relatively modest, the importance of including both scalar and spin–orbit relativistic contributions at the 2c-ZORA level is evident.

Table 1. Static 19F NMR Chemical Shifts (in ppm) for 1oF, 1pF, and 3F Computed in the Gas Phase and in Benzene Solution, Comparing Both Nonrelativistic (NR) and Two-Component (2c-ZORA) Methods with the Experimental Values.

    calculations in gas phasea
 calculations in benzene solutiona
complex Exp (δ)b NR (δ) Δδc 2c-ZORA (δ) Δδc NR (δ) Δδc 2c-ZORA (δ) Δδc
1oF –397.9 –414.6 –16.7 –416.1 –18.2 –413.4 –15.5 –417.4 –19.5
1pF –388.3 –376.4 11.9 –379.2 9.1 –378.6 9.7 –383.7 4.6
3F –394.3 –386.4 7.9 –388.9 5.4 –387.9 6.4 –392.7 1.6
Open in a new tab
a

See Computational Methods section for more details.

b

Values reported in ref (21).

c

Δδ = δ(calc) – δ(exp).

As a second step in the treatment of the solvation process, we analyzed the effect of adding explicit solute–solvent interactions to the 19F chemical shift of 1oF. To achieve this, we examined the inclusion of a benzene molecule in three different positions around 1oF (Figure 2): (a) near the nickel-bonded fluoride, (b) near the iodine atom of the substituted phenyl ligand, and (c) near one of the triethyl phosphine ligands. The δ(19F) values were calculated at the 2c-ZORA-PBE/TZ2P level. These calculations were based on static (fully optimized) structures using an implicit COSMO solvation model for benzene (see the Computational Methods section).

Figure 2.

Figure 2

Open in a new tab

19F NMR chemical shifts of complex 1oF interacting with an explicit benzene molecule in three different positions: (a) near the nickel-bonded fluoride, (b) near the iodine atom of the substituted phenyl ligand, and (c) near one of the triethyl phosphine ligands. The benzene molecule is shown in blue for clarity. The calculated Δδ values (ppm) give the difference between the calculated and experimental chemical shifts.

When comparing the δ(19F) values of 1oF with and without an explicit benzene molecule, the effect of adding a benzene molecule near the iodine atom or the P(Et)3 ligand (Figure 2b,c) is rather small (differences up to 3.5 ppm). In contrast, the inclusion of a benzene molecule near the nickel-bonded fluoride (Figure 2a) significantly improved the δ(19F) value, reducing the error from −19.5 to −6.5 ppm. This finding corroborates the importance of explicit solute–solvent interactions on the 19F NMR chemical shifts, particularly highlighting the need to consider the interaction between fluoride and benzene in the present case.

3.2. Influence of Dynamics on the 19F NMR Chemical Shifts

To move beyond a static description and provide a more realistic representation of the system’s behavior,49−56 we performed AIMD simulations where complex 1oF was surrounded by solvent molecules (benzene) and followed over time (see Computational Methods section for more details). From these simulations, samples of snapshots were taken and used to obtain dynamically averaged 19F NMR chemical shifts. Since these δ(19F) values are derived from an ensemble of structures, they can be referred to as dynamic19F NMR chemical shifts.

We first computed the dynamic δ(19F) chemical shifts for the solute alone (complex 1oF), i.e., removing the solvent molecules from the snapshots before computing the chemical shifts. Thus, these calculations capture only the effect of dynamic motion on the δ(19F) values. To ensure convergence in the δ(19F) values and avoid bias in the NMR calculations due to an insufficient number of snapshots, we implemented a systematic approach. Thus, from a production NVT trajectory of 30 ps, we first used a sample of 20 random snapshots to calculate the dynamically averaged δ(19F) value. We then repeated this procedure, increasing the sample size by 20 snapshots each time until we reached a total of 180 snapshots (Figure 3 and Table S2). These calculations were performed at the 2c-ZORA-PBE/TZ2P level, including the implicit COSMO model for benzene.

Figure 3.

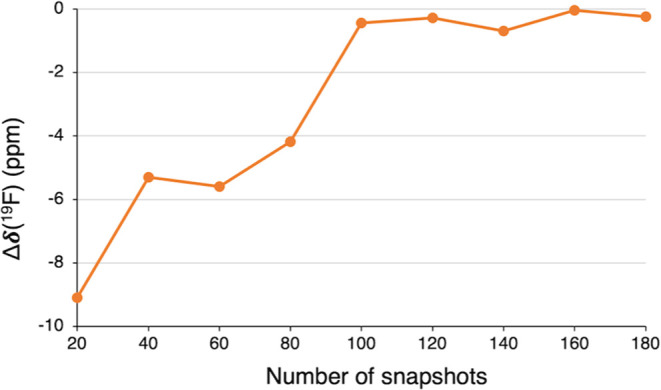
Figure 3

Open in a new tab

Dynamic 19F NMR chemical shift error (Δδ, in ppm) for 1oF, calculated using different numbers of snapshots along a NVT trajectory of 30 ps. The Δδ values (in ppm) give the difference between calculated and experimental chemical shifts.

As shown in Figure 3, the convergence behavior of the δ(19F) values clearly indicates that a large number of snapshots must be taken into account. The dynamic 19F NMR chemical shift value reasonably converges to a value of ca. −398 ppm after the first 100 snapshots, with a small error of −0.4 ppm. Beyond this point, only insignificant fluctuations were observed. Notably, the accuracy is drastically improved from a static (−19.5 ppm) to a dynamic approach (−0.4 ppm) using a total of 100 snapshots. Therefore, it is evident that considering the structural flexibility of 1oF is crucial to obtaining a good agreement with the experimental value.

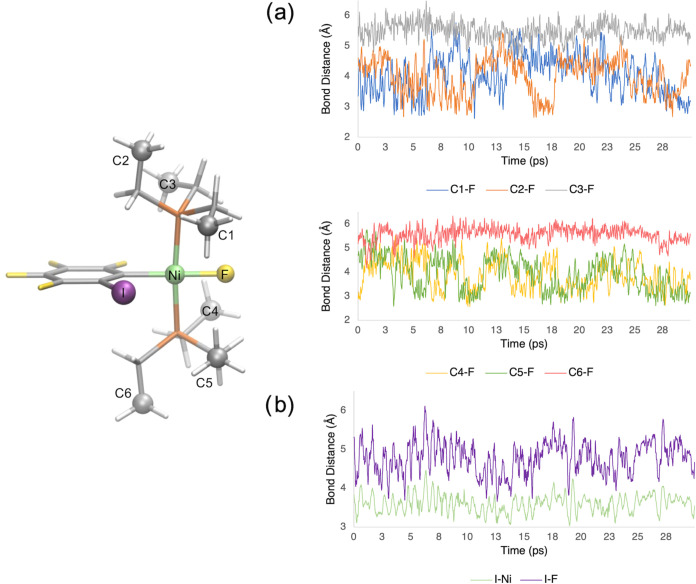
To understand the reasons behind this improved accuracy, we analyzed the molecular dynamics of the 1oF complex along its trajectory. Notably, the triethyl phosphine (PEt3) ligands were demonstrated to be highly fluxional, exhibiting conformational changes that are not considered in the static optimized structures. By analyzing the F···C distances between the nickel-bonded fluoride and the terminal carbon atoms of the ethyl arms (C1–C6) in the PEt3 ligand (Figure 4a), we can gain a reasonable description of the intramolecular interactions between the Ni-bonded fluoride and the hydrogen atoms of the PEt3 ligands. The large variation in the F···C distances reveals that the carbon atoms, specifically C1, C2, C4, and C5, exhibit significant flexibility and frequently approach the nickel-bonded fluoride, with a minimum F···C distances of around 2.6 Å (Figures 4a, S1a and Table S3).

Figure 4.

Figure 4

Open in a new tab

Evolution of distances between (a) the fluoride ligand and the carbon atoms of the PEt3 ligands, and (b) the iodine atom on the phenyl ligand with either the nickel metal or the fluoride ligand, along the NVT trajectory of 1oF complex.

Furthermore, we observed significant flexibility in the iodine atom on the phenyl ligand during the AIMD trajectory. Notably, this flexibility allows interactions between the iodine atom and both the fluoride ligand and the metal center. To further analyze these interactions, we examined the I···F and I···Ni distances along the trajectory (Figures 4b, S1b, and Table S3). The iodine atom can approach fluorine with a minimum distance of 3.7 Å and an average distance of 4.8 Å. The nickel metal center can make even closer contact with the iodine atom, with a minimum distance of 3.0 Å and an average distance of 3.6 Å. This indicates the presence of short I···Ni interactions, where the distance between atoms is less than the sum of Bondi’s van der Waals radii (3.61 Å).57 Such interactions may be identified as boundary noncovalent interactions.58 Thus, these findings highlight the significant role of noncovalent interactions, attributed to the considerable flexibility of both the phenyl ring and the two phosphine ligands in the complex, in determining the 19F NMR chemical shifts of 1oF. It is worth noting that a similar flexibility for phosphine ligands is also observed in the 1pF complex (Figure S2 and Table S4). However, in 1pF, the iodine atom is in the para position to Ni, restricting interactions between I···F and I···Ni, which reduces the phenyl ring’s flexibility compared to 1oF. This suggests fewer dynamic effects on 1pF and aligns with the results of the static NMR calculations, as they successfully reproduced the chemical shifts of 1pF and 3F but not 1oF. We will consider a dynamic NMR approach for 1pF and 3F in future studies to gain deeper insights into how these interactions affect the shift values.

To further enhance our understanding of the intramolecular interactions that are present in 1oF, we carried out a detailed analysis of the noncovalent interactions using the NCIPLOT program (see more details in the Computational Methods section). Specifically, we selected random snapshots where close interactions were observed in the nickel-bonded fluoride or in the iodine atom (Figure 5). This allowed us to identify attractive and repulsive interactions between fluoride and the phosphine ligands (Figure 5a, represented by blue and red colors), agreeing with the earlier observation that the PEt3 ligands closely approach fluoride. Comparatively, weak van der Waals interactions are observed between PEt3 and fluoride ligands in the optimized geometry of 1oF, which was used for static NMR calculations (Figure S3a).

Figure 5.

Figure 5

Open in a new tab

Noncovalent interactions of 1oF identified close to (a) the nickel-bonded fluoride and (b) the iodine atom on the phenyl ligand. Regions in blue/green indicate strong, attractive interactions, and regions in red indicate strong nonbonded overlap.

The NCI analysis also reveals considerable strong interactions of iodine with the phosphine ligands and the nickel metal center (Figure 5b). The phosphine ligands mainly form weak van der Waals interactions (in green), whereas the nickel engages in strong, attractive interactions (in blue) and some strong repulsive interactions (in red). In contrast, the static optimized geometry of 1oF shows relatively weaker interactions between the nickel and iodine atoms (Figure S4a). These findings highlight the necessity of a dynamic treatment of the 1oF complex to capture these significant noncovalent interactions.

3.3. Specific Solute–Solvent Interactions on the Dynamic 19F NMR Chemical Shifts

As an additional step in the solvation process, we examined the impact of incorporating explicit benzene molecules on dynamic 19F NMR chemical shift calculations. To achieve this, we selected three benzene molecules per snapshot. This approach allowed us to focus on solvent molecules that directly interact with 1oF while maintaining computational efficiency. The identification of which solvent molecules to include is, however, not straightforward and we resorted to the NCIPLOT program. We gave priority to the solvent molecules surrounding the fluoride atom based on our static NMR results, where the inclusion of one explicit solvent molecule yielded the best accuracy when interacting with the fluoride ligand (Figure 2). For each snapshot, we manually selected the three benzene molecules that exhibited the most substantial noncovalent interactions (see Figure 6; strong interactions are indicated in blue, and weaker dispersion interactions in green).

Figure 6.

Figure 6

Open in a new tab

AIMD snapshot of complex 1oF with three explicit benzene molecules identified based on the noncovalent interaction regions using the NCIPLOT program. Regions in blue/green indicate strong, attractive interactions, and regions in red indicate strong nonbonded overlap. The selected three benzene molecules are shown in blue for clarity.

The dynamically averaged 19F NMR chemical shifts of 1oF with three explicit benzene molecules were calculated using the systematic approach described in Section 3.2. Thus, we collected samples of 20 random snapshots, increasing the sample size by 20 snapshots each time until we reached a total of 180 snapshots (Figure 7 and Table S5). The dynamic 19F NMR chemical shift value reasonably converges to a value of ca. −385.5 ppm after the first 120 snapshots, having an error of 12.4 ppm, with minor fluctuations observed beyond this point. The inclusion of explicit benzene molecules in the dynamic approach causes a large deshielding on the nickel-bonded fluoride, resulting in an increase of approximately 13 ppm in the δ(19F) value. As a result, this leads to a larger deviation from the experimental value by 12.4 ppm, which is less accurate compared to the dynamic NMR calculations performed without explicit solvent molecules (Figure 3 and Table S2). Hence, these findings suggest that the inclusion of explicit benzene molecules appears to deteriorate the dynamic δ(19F) results. It is known that variables such as the number of explicit solvent molecules and their strategic placement can critically influence the precision of computational outcomes.59−62 Thus, it appears that our approach has been adversely affected by the limited selection of only three benzene molecules, which may not adequately account for the solute–solvent interactions affecting the computed chemical shift values. Moreover, the selection of explicit solvent molecules only around the fluoride ligand appears to overestimate the deshielding effect. These interpretations need to be assessed by considering a larger selection of solvent molecules to complete the first full solvation shell around the complex. However, this approach was not implemented due to the high associated computational cost.

Figure 7.

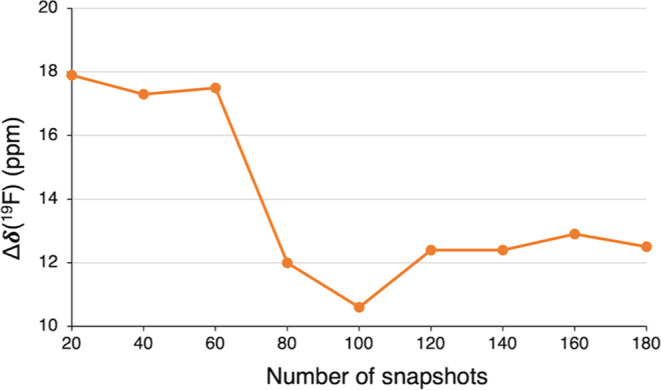
Figure 7

Open in a new tab

Dynamic 19F NMR chemical shift error (Δδ, in ppm) for 1oF interacting with three benzene solvent molecules, calculated using a different number of snapshots along a NVT trajectory of 30 ps. The Δδ values (in ppm) give the difference between calculated and experimental chemical shifts.

3.4. Static vs Dynamic Treatment

After the detailed examination of the solvation effects, a general comparison of the results can be made to determine the most effective approach for the prediction of δ(19F) in the 1oF complex (Table 2). Our first static approach, considering an isolated 1oF complex in the gas phase, showed a change of −18.2 ppm when compared to the experimental value. The inclusion of the COSMO model resulted in minor changes, indicating that the electronic solute–solvent interactions cannot be properly modeled with a continuum model. However, such a model is useful for describing bulk solvent effects. Notably, the addition of an explicit solvent benzene molecule near the fluoride ligand has a direct effect on the δ(19F) value, resulting in a deviation of −6.5 ppm. However, it is important to mention that this improvement in accuracy was not observed when considering interactions between benzene and iodine or P(Et)3 ligands.

Table 2. Summary of Computed 19F NMR Chemical Shifts (in ppm) for the Nickel-Bonded Fluoride in 1oF, Using Both Static and Dynamic Approaches and Comparing with the Experimental Value.

    chemical shift (δ) Δδa
experimental shift valueb   –397.9  
static-gas phase isolated 1oF complex –416.1 –18.2
static-COSMO isolated 1oF complex –417.4 –19.5
static-COSMO 1oF + 1 benzenec –414.5 –16.6
static-COSMO 1oF + 1 benzened –413.8 –15.9
static-COSMO 1oF + 1 benzenee –404.4 –6.5
dynamic isolated 1oF complex –398.1 –0.2
dynamic 1oF + 3 benzene –385.4 12.5
Open in a new tab
a

Δδ = δ(calc) – δ(exp).

b

Value reported in ref (21).

c

Interaction of benzene with I.

d

Interaction of benzene with P(Et)3 ligand.

e

Interaction of benzene with fluoride ligand.

In the dynamic approach, it is crucial to emphasize the importance of including dynamic averaging in the calculation of the 19F NMR chemical shift. This involves calculating an averaged δ(19F) value by taking snapshots from the AIMD trajectory and considering the isolated 1oF complex as the basis for δ(19F) calculations. Both the vibrational averaging over the molecule’s degrees of freedom at room temperature and the indirect effect induced by the presence of the solvent molecules in the AIMD simulations contribute to understand this phenomenon. The effect of dynamical averaging directly affects the chemical shift, which increases by approximately 19 ppm when compared with the static-COSMO approach (Table 2). Furthermore, the addition of explicit solvent molecules enhances this effect. The δ(19F) value is further increased but shows a higher error of about 12.5 ppm. As mentioned previously, this is likely due to the inappropriate selection of the benzene molecules from the snapshots. Hence, the best match to the experimental value, with a difference of only −0.2 ppm, is obtained by employing a dynamic approach without including explicit solvent molecules.

4. Conclusions

In this study, we examined the reliability of various levels of theory for modeling the 19F NMR chemical shifts in solution for square-planar nickel-fluoride complexes. The calculation of these chemical shifts presents a challenge in computational chemistry, mainly due to solvent effects, which complicates the establishment of a simple protocol for conducting such studies. Particularly, we focused on the trans-[NiF(2,3,4,5-C6F4I)(PEt3)2] (1oF), trans-[NiF(2,3,5,6-C6F4I)(PEt3)2] (1pF), and trans-[NiF(C6F5)(PEt3)2] (3F) complexes. The modeling of the δ(19F) values for 1pF and 3F species was successful by using a static approach with an implicit solvation model. However, this approach failed for the 1oF complex, which showed a large discrepancy (∼20 ppm) compared with the experimental signal. To address this discrepancy, we first investigated a static protocol, including specific solute–solvent interactions on the 19F NMR calculations. Notably, the interaction of a benzene molecule with the nickel-bonded fluoride caused a large deshielding effect, significantly improving the description of the δ(19F) value.

More advanced dynamic protocols were also employed to calculate the δ(19F) values. These protocols involved AIMD simulations of the complex 1oF surrounded by explicit benzene solvent molecules. In these calculations, we initially selected random snapshots and considered the isolated 1oF complex to calculate an averaged (19F) value. Subsequently, we introduced the inclusion of three benzene molecules to examine their impact. A careful monitoring of the number of snapshots was crucial to ensure convergence of the (19F) values. The convergence of the dynamic 19F NMR chemical shifts was achieved at 100 snapshots for the approach using the isolated 1oF complex and at 120 snapshots for the approach including 1oF and three explicit benzene molecules.

The inclusion of dynamic averaging using AIMD simulations resulted in a significant improvement in the 19F NMR chemical shift. This improvement can be attributed to the large flexibility exhibited by both the phenyl and the two P(Et)3 ligands within the complex, which results in significantly noncovalent interactions around the fluoride ligand and nickel metal center during the AIMD trajectory. Including these interactions with molecular dynamics resulted in the precise calculation of the chemical shift for 1oF. Notably, these interactions are missing in 1pF and 3F, as the iodine is too far from nickel in the former and absent in the latter. In contrast, the inclusion of three explicit benzene molecules on the dynamic NMR calculations caused a large deshielding of 12.5 ppm. This deshielding was likely caused by the interactions between benzene and fluoride, which were the focus when selecting the three explicit benzene molecules, potentially skewing the averaged chemical shift value. Overall, our study demonstrates that accounting for dynamic conformational flexibility using AIMD simulations can result in accurate 19F NMR chemical shift calculations, rationalizing the use of advanced quantum chemical methods for calculating NMR resonances. Hence, this study reports an important protocol for the 19F NMR characterization of nickel-fluoride complexes in solution.

Acknowledgments

We thank the Research Council of Norway (grants no. 300769 and 325231, and Centre of Excellence grant no. 262695), the Sigma2 – National Infrastructure for High Performance Computing and Data Storage in Norway (nn9330k and nn4654k), NordForsk (grant no. 85378), and the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 859910.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.4c05408.

  • Additional computational data of static and dynamic 19F NMR chemical shifts; histogram plots of distances; additional figures of noncovalent interactions (PDF)

  • Cartesian coordinates (XYZ)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry Aspecial issue “Trygve Helgaker Festschrift”.

Supplementary Material

jp4c05408_si_001.pdf (1.2MB, pdf)
jp4c05408_si_002.xyz (1.4MB, xyz)

References

  1. Pagenkopf B. L.; Carreira E. M. Transition Metal Fluoride Complexes in Asymmetric Catalysis. Chem. - Eur. J. 1999, 5 (12), 3437–3442. 10.1002/(sici)1521-3765(19991203)5:123.3.co;2-5. [DOI] [Google Scholar]
  2. Nikiforov G. B.; Roesky H. W.; Koley D. A survey of titanium fluoride complexes, their preparation, reactivity, and applications. Coord. Chem. Rev. 2014, 258–259, 16–57. 10.1016/j.ccr.2013.09.002. [DOI] [Google Scholar]
  3. Pauling L.The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry; Cornell University Press, 1960. [Google Scholar]
  4. Clark H. C. S.; Holloway J. H.. Advanced Inorganic Fluorides; Elsevier: Oxford, 2000. [Google Scholar]
  5. Fagnou K.; Lautens M. Halide Effects in Transition Metal Catalysis. Angew. Chem., Int. Ed. 2002, 41 (1), 26–47. . [DOI] [PubMed] [Google Scholar]
  6. Leclerc M. C.; Bayne J. M.; Lee G. M.; Gorelsky S. I.; Vasiliu M.; Korobkov I.; Harrison D. J.; Dixon D. A.; Baker R. T. Perfluoroalkyl Cobalt(III) Fluoride and Bis(perfluoroalkyl) Complexes: Catalytic Fluorination and Selective Difluorocarbene Formation. J. Am. Chem. Soc. 2015, 137 (51), 16064–16073. 10.1021/jacs.5b12003. [DOI] [PubMed] [Google Scholar]
  7. Pike S. J.; Hunter C. A.; Brammer L.; Perutz R. N. Benchmarking of Halogen Bond Strength in Solution with Nickel Fluorides: Bromine versus Iodine and Perfluoroaryl versus Perfluoroalkyl Donors. Chem. - Eur. J. 2019, 25 (39), 9237–9241. 10.1002/chem.201900924. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Joksch M.; Agarwala H.; Ferro M.; Michalik D.; Spannenberg A.; Beweries T. A Comparative Study on the Thermodynamics of Halogen Bonding of Group 10 Pincer Fluoride Complexes. Chem. - Eur. J. 2020, 26 (16), 3571–3577. 10.1002/chem.201904863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fedorov S. V.; Krivdin L. B. Computational Protocols for the 19F NMR Chemical Shifts. Part 1: Methodological Aspects. J. Fluor. Chem. 2020, 238, 109625 10.1016/j.jfluchem.2020.109625. [DOI] [Google Scholar]
  10. Kasireddy C.; Bann J. G.; Mitchell-Koch K. R. Demystifying fluorine chemical shifts: electronic structure calculations address origins of seemingly anomalous 19F-NMR spectra of fluorohistidine isomers and analogues. Phys. Chem. Chem. Phys. 2015, 17 (45), 30606–30612. 10.1039/C5CP05502D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lu Y.; Sun M.; Xi N. 19F NMR chemical shifts are sensitive to remote functional group variations. J. Mol. Struct. 2023, 1283, 135273 10.1016/j.molstruc.2023.135273. [DOI] [Google Scholar]
  12. Dahanayake J. N.; Kasireddy C.; Karnes J. P.; Verma R.; Steinert R. M.; Hildebrandt D.; Hull O. A.; Ellis J. M.; Mitchell-Koch K. R.. Progress in Our Understanding of 19F Chemical Shifts. In Annual Reports on NMR Spectroscopy; Webb G. A., Ed.; Academic Press, 2018; Chapter 5, Vol. 93, pp 281–365. [Google Scholar]
  13. Zheng A.; Liu S.-B.; Deng F. 19F Chemical Shift of Crystalline Metal Fluorides: Theoretical Predictions Based on Periodic Structure Models. J. Phys. Chem. C 2009, 113 (33), 15018–15023. 10.1021/jp904454t. [DOI] [Google Scholar]
  14. Saielli G.; Bini R.; Bagno A. Computational 19F NMR. 1. General features. Theor. Chem. Acc. 2012, 131 (3), 1140 10.1007/s00214-012-1140-z. [DOI] [Google Scholar]
  15. Saunders C.; Khaled M. B.; Weaver J. D. III; Tantillo D. J. Prediction of 19F NMR Chemical Shifts for Fluorinated Aromatic Compounds. J. Org. Chem. 2018, 83 (6), 3220–3225. 10.1021/acs.joc.8b00104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Rusakova I. L.; Ukhanev S. A.; Rusakov Y. Y. On the relativistic effects on 19F nuclear magnetic resonance chemical shifts in the presence of iodine atoms. J. Fluor. Chem. 2023, 271, 110188 10.1016/j.jfluchem.2023.110188. [DOI] [Google Scholar]
  17. Pröhm P.; Schmid J. R.; Sonnenberg K.; Voßnacker P.; Steinhauer S.; Schattenberg C. J.; Müller R.; Kaupp M.; Riedel S. Improved Access to Organo-Soluble Di- and Tetrafluoridochlorate(I)/(III) Salts. Angew. Chem., Int. Ed. 2020, 59 (37), 16002–16006. 10.1002/anie.202006268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kaupp M.; Schattenberg C. J.; Müller R.; Reimann M. Unusually Large Effects of Charge-assisted C–H···F Hydrogen Bonds to Anionic Fluorine in Organic Solvents: Computational Study of 19F NMR Shifts versus Thermochemistry. ChemistryOpen 2022, 11 (12), e202200146 10.1002/open.202200146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. von der Heiden D.; Vanderkooy A.; Erdélyi M. Halogen bonding in solution: NMR spectroscopic approaches. Coord. Chem. Rev. 2020, 407, 213147 10.1016/j.ccr.2019.213147. [DOI] [Google Scholar]
  20. Vioglio P. C.; Chierotti M. R.; Gobetto R. Solid-state nuclear magnetic resonance as a tool for investigating the halogen bond. CrystEngComm 2016, 18 (48), 9173–9184. 10.1039/C6CE02219G. [DOI] [Google Scholar]
  21. Thangavadivale V.; Aguiar P. M.; Jasim N. A.; Pike S. J.; Smith D. A.; Whitwood A. C.; Brammer L.; Perutz R. N. Self-complementary nickel halides enable multifaceted comparisons of intermolecular halogen bonds: fluoride ligands vs. other halides. Chem. Sci. 2018, 9 (15), 3767–3781. 10.1039/C8SC00890F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Castro A. C.; Cascella M.; Perutz R. N.; Raynaud C.; Eisenstein O. Solid-State 19F NMR Chemical Shift in Square-Planar Nickel–Fluoride Complexes Linked by Halogen Bonds. Inorg. Chem. 2023, 62 (12), 4835–4846. 10.1021/acs.inorgchem.2c04063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Cronin L.; Higgitt C. L.; Karch R.; Perutz R. N. Rapid Intermolecular Carbon–Fluorine Bond Activation of Pentafluoropyridine at Nickel(0): Comparative Reactivity of Fluorinated Arene and Fluorinated Pyridine Derivatives. Organometallics 1997, 16 (22), 4920–4928. 10.1021/om9705160. [DOI] [Google Scholar]
  24. Benassi E. An inexpensive density functional theory-based protocol to predict accurate 19F-NMR chemical shifts. J. Comput. Chem. 2022, 43 (3), 170–183. 10.1002/jcc.26780. [DOI] [PubMed] [Google Scholar]
  25. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  26. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 1997, 78, 1396 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]
  27. van Lenthe E.; Baerends E. J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
  28. Chang C.; Pelissier M.; Durand P. Regular Two-Component Pauli-Like Effective Hamiltonians in Dirac Theory. Phys. Scr. 1986, 34, 394 10.1088/0031-8949/34/5/007. [DOI] [Google Scholar]
  29. Lenthe E. v.; Baerends E. J.; Snijders J. G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. 10.1063/1.466059. [DOI] [Google Scholar]
  30. Schreckenbach G.; Ziegler T. Calculation of NMR Shielding Tensors Using Gauge-Including Atomic Orbitals and Modern Density Functional Theory. J. Phys. Chem. A 1995, 99, 606–611. 10.1021/j100002a024. [DOI] [Google Scholar]
  31. Wolff S. K.; Ziegler T.; van Lenthe E.; Baerends E. J. Density functional calculations of nuclear magnetic shieldings using the zeroth-order regular approximation (ZORA) for relativistic effects: ZORA nuclear magnetic resonance. J. Chem. Phys. 1999, 110, 7689–7698. 10.1063/1.478680. [DOI] [Google Scholar]
  32. Autschbach J. The role of the exchange-correlation response kernel and scaling corrections in relativistic density functional nuclear magnetic shielding calculations with the zeroth-order regular approximation. Mol. Phys. 2013, 111, 2544–2554. 10.1080/00268976.2013.796415. [DOI] [Google Scholar]
  33. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  34. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
  35. Baerends E. J.; Ziegler T.; Atkins A. J.; Autschbach J.; Baseggio O.; Bashford D.; Bérces A.; Bickelhaupt F. M.; Bo C.; Boerrigter P. M.. et al. ADF 2022.1, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands. [Google Scholar]
  36. Klamt A.; Schüürmann G. COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc., Perkin Trans. 2 1993, 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]
  37. Klamt A. Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. A 1995, 99, 2224–2235. 10.1021/j100007a062. [DOI] [Google Scholar]
  38. Klamt A.; Jonas V. Treatment of the outlying charge in continuum solvation models. J. Chem. Phys. 1996, 105, 9972–9981. 10.1063/1.472829. [DOI] [Google Scholar]
  39. Iftimie R.; Minary P.; Tuckerman M. E. Ab initio molecular dynamics: Concepts, recent developments, and future trends. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6654–6659. 10.1073/pnas.0500193102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Kühne T. D.; Iannuzzi M.; Del Ben M.; Rybkin V. V.; Seewald P.; Stein F.; Laino T.; Khaliullin R. Z.; Schütt O.; Schiffmann F.; et al. CP2K: An electronic structure and molecular dynamics software package -Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103 10.1063/5.0007045. [DOI] [PubMed] [Google Scholar]
  41. Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  42. Godbout N.; Salahub D. R.; Andzelm J.; Wimmer E. Optimization of Gaussian-type basis sets for local spin density functional calculations. Part I. Boron through neon, optimization technique and validation. Can. J. Chem. 1992, 70 (2), 560–571. 10.1139/v92-079. [DOI] [Google Scholar]
  43. Goedecker S.; Teter M.; Hutter J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703 10.1103/PhysRevB.54.1703. [DOI] [PubMed] [Google Scholar]
  44. Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  45. Ditchfield R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. 10.1080/00268977400100711. [DOI] [Google Scholar]
  46. Boto R. A.; Peccati F.; Laplaza R.; Quan C.; Carbone A.; Piquemal J. P.; Maday Y.; Contreras-Garcĺa J. NCIPLOT4: Fast, Robust, and Quantitative Analysis of Noncovalent Interactions. J. Chem. Theory Comput. 2020, 16, 4150–4158. 10.1021/acs.jctc.0c00063. [DOI] [PubMed] [Google Scholar]
  47. Humphrey W.; Dalke A.; Schulten K. VMD: Visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  48. Álvarez-Moreno M.; de Graaf C.; López N.; Maseras F.; Poblet J. M.; Bo C. Managing the Computational Chemistry Big Data Problem: The ioChem-BD Platform. J. Chem. Inf. Model. 2015, 55 (1), 95–103. 10.1021/ci500593j. [DOI] [PubMed] [Google Scholar]
  49. Piana S.; Sebastiani D.; Carloni P.; Parrinello M. Ab Initio Molecular Dynamics-Based Assignment of the Protonation State of Pepstatin A/HIV-1 Protease Cleavage Site. J. Am. Chem. Soc. 2001, 123 (36), 8730–8737. 10.1021/ja003145e. [DOI] [PubMed] [Google Scholar]
  50. Sebastiani D.; Parrinello M. A New ab-Initio Approach for NMR Chemical Shifts in Periodic Systems. J. Phys. Chem. A 2001, 105 (10), 1951–1958. 10.1021/jp002807j. [DOI] [Google Scholar]
  51. Sebastiani D.; Parrinello M. Ab-initio Study of NMR Chemical Shifts of Water Under Normal and Supercritical Conditions. ChemPhysChem 2002, 3 (8), 675–679. . [DOI] [PubMed] [Google Scholar]
  52. Li D. W.; Brüschweiler R. Certification of molecular dynamics trajectories with NMR chemical shifts. J. Phys. Chem. Lett. 2010, 1, 246–248. 10.1021/jz9001345. [DOI] [Google Scholar]
  53. Robustelli P.; Stafford K. A.; Palmer A. G. Interpreting protein structural dynamics from NMR chemical shifts. J. Am. Chem. Soc. 2012, 134, 6365–6374. 10.1021/ja300265w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Bandaru S.; English N. J.; Macelroy J. M. D. Implicit and explicit solvent models for modeling a bifunctional arene ruthenium hydrogen-storage catalyst: A classical and ab initio molecular simulation study. J. Comput. Chem. 2014, 35, 683–691. 10.1002/jcc.23514. [DOI] [PubMed] [Google Scholar]
  55. Torchia D. A. NMR studies of dynamic biomolecular conformational ensembles. Prog. Nucl. Magn. Reson. Spectrosc. 2015, 84–85, 14–32. 10.1016/j.pnmrs.2014.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Maste S.; Sharma B.; Pongratz T.; Grabe B.; Hiller W.; Erlach M. B.; Kremer W.; Kalbitzer H. R.; Marx D.; Kast S. M. The accuracy limit of chemical shift predictions for species in aqueous solution. Phys. Chem. Chem. Phys. 2024, 26, 6386–6395. 10.1039/D3CP05471C. [DOI] [PubMed] [Google Scholar]
  57. Bondi A. van der Waals Volumes and Radii of Metals in Covalent Compounds. J. Phys. Chem. A 1966, 70 (9), 3006–3007. 10.1021/j100881a503. [DOI] [Google Scholar]
  58. Bikbaeva Z. M.; Ivanov D. M.; Novikov A. S.; Ananyev I. V.; Bokach N. A.; Kukushkin V. Y. Electrophilic–Nucleophilic Dualism of Nickel(II) toward Ni···I Noncovalent Interactions: Semicoordination of Iodine Centers via Electron Belt and Halogen Bonding via σ-Hole. Inorg. Chem. 2017, 56 (21), 13562–13578. 10.1021/acs.inorgchem.7b02224. [DOI] [PubMed] [Google Scholar]
  59. Sterzel M.; Autschbach J. Toward an Accurate Determination of 195Pt Chemical Shifts by Density Functional Computations: The Importance of Unspecific Solvent Effects and the Dependence of Pt Magnetic Shielding Constants on Structural Parameters. Inorg. Chem. 2006, 45 (8), 3316–3324. 10.1021/ic052143y. [DOI] [PubMed] [Google Scholar]
  60. Truflandier L. A.; Sutter K.; Autschbach J. Solvent Effects and Dynamic Averaging of 195Pt NMR Shielding in Cisplatin Derivatives. Inorg. Chem. 2011, 50 (5), 1723–1732. 10.1021/ic102174b. [DOI] [PubMed] [Google Scholar]
  61. Sure R.; el Mahdali M.; Plajer A.; Deglmann P. Towards a converged strategy for including microsolvation in reaction mechanism calculations. J. Comput. Aided Mol. Des. 2021, 35 (4), 473–492. 10.1007/s10822-020-00366-2. [DOI] [PubMed] [Google Scholar]
  62. Fehér P. P.; Stirling A. Assessment of reactivities with explicit and implicit solvent models: QM/MM and gas-phase evaluation of three different Ag-catalysed furan ring formation routes. New J. Chem. 2019, 43 (39), 15706–15713. 10.1039/C9NJ04003J. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp4c05408_si_001.pdf (1.2MB, pdf)
jp4c05408_si_002.xyz (1.4MB, xyz)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES