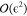Abstract

Hybrid nanoplasmonic structures composed of subwavelength apertures in metallic films and nanoparticles have recently been demonstrated as ultrasensitive plasmonic sensors. This work investigates the electrokinetically driven propagation of the assembly mechanism of the metallic nanoparticles through nanoapertures. The Debye–Hückel approximation for a symmetric electrolyte solution with overlapping electrical double layers (EDLs) is used to obtain an analytical solution to the problem. The long-term silver nanoparticle concentration response is derived using the homogenization method and a multiscale analysis. The results indicate that uncharged nanoparticles will flow through the nanohole array if the nanochannel height is larger than the Debye length (h0 > λD), while a trapping mechanism occurs, due to the overlapping of the EDL, when h0 ∼ 3.8λD. For charged nanoparticles, the response to the electric field occurs locally with the walls of the nanochannel, regardless of its height. For a critical value of the nanochannel length, the leading order of the concentration field becomes purely diffusive.
Introduction
Optofluidics, the emergent field arising from the synergistic combination of photonics and microfluidics, has enabled the development of ultracompact devices with applications in different fields, such as label-free sensing.1 Ordered arrays subwavelength apertures, known as nanohole arrays (NHAs), have been demonstrated as nanoplasmonic sensors that can be fabricated with accurate periodicities and aperture shapes due to recent advances in nanofabrication techniques.2 NHAs feature relatively long channels (in the order of 101 to 102 nm)3,4 with customizable pore sizes.5,6 These nanoapertures have been used for fluidic transport of considerably small volumes, and the enrichment of electrocharged analytes results in improved sensor response7−12 and controllable nanoinjection across the nanostructured substrate. Unlike microfluidics, nanofluidics involve nanostructures where the solid boundaries are extremely close, and overlapping of electrical double layers (EDLs) is possible,13 which invalidates the use of Boltzmann distribution for ionic charge density.
Recent studies have presented analytical models for overlapped EDLs. Qu and Li14 derived a model to determine the electrical potential and ionic concentration distributions between two infinitely large flat plates, establishing corrected boundary conditions for these distributions. Golovnev and Trimper15 obtained an analytical solution for the Poisson–Nernst–Planck equation when Faradaic processes are discarded, revealing different ion concentration behaviors in both the short- and the long-time regimes. Zachariah et al.16 analyzed the repulsive forces that appear during the collapse of the EDLs using the DLVO theory, concluding that the hydration force is due to multiple layering of hydrate ions, which subsequently undergo transitions between different confined adsorbed ion states. Such a case occurs when a microchannel is connected to a nanochannel, and a micro–nano interface is formed, leading to charge transport and ion concentration polarization (ICP).17 ICP enables the enrichment of charged particles, such as biomarkers and ions, as well as rectification effects on ionic current.18,19 In this regard, Mani et al.20 and Yaroshchuk and Bondarenko21 established transport analytical models considering the area average for ICP, with emphasis on the dominance of axial diffusion in determining the extent of diffuse layers at micro-to-nanochannel interfaces when the ion reservoir is large. In the context of sensing, the transport and placement of metallic nanoparticles within and around NHAs to construct hybrid nanoplasmonic structures with improved sensitivity have been demonstrated experimentally.11,22,23 However, the reported analytical work has focused on ionic concentration and does not address the transport scenarios with charged colloidal systems.
In this work, we investigate the role of the EDL overlapping on both charged and uncharged metallic nanoparticles in nanoconfinement using an analytical approach. The analysis is focused on the creation of hybrid nanostructures as surface-enhanced Raman scattering (SERS) substrates, as previously reported experimentally.11 The investigation involves flow-through metallic nanoapertures that support surface plasmon resonance and metallic nanoparticles that naturally exhibit localized surface plasmon resonance, within a microfluidic environment under an applied electric field. We analyze the significance of the field distribution and the influence of the overlapping EDL on it, elucidating the critical impact of some parameters leading to novel perspectives on the physics of nanoparticle transport.
Hydrodynamic Formulation
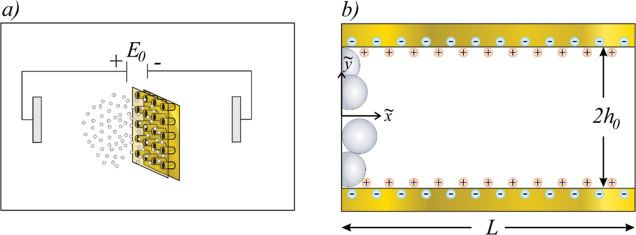
The system used in this study
encompasses a microfluidic chip assembly
with an embedded metallic NHA under the influence of a direct current
(DC) electric field applied externally, as shown in Figure 1a. A Newtonian fluid is assumed
to contain small ions (average size ∼1 Å) and large silver
nanoparticles (Ag NPs), flowing through an NHA. Both the ionic and
Ag NP concentrations are initially uniform throughout the system.
An electroosmotic flow (EF) emerges from an externally imposed electric
field 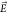 and the induced field in the EDL. The imposed
external field yields the transference of electrons to particles,
resulting in the acquisition of a net negative surface electric charge.
Some particles may undergo polarization while retaining their electrical
neutrality; in this manner, consideration of both charged and uncharged
nanoparticles in the present analysis is warranted. Figure 1b depicts a cross-sectional
view of a single nanohole within the NHA. Notably, silver nanoparticles
exhibit a distinct Gaussian distribution concentration close to the
nanohole’s entrance, a phenomenon attributed to the localized
enhancement of the electric field.8 The
effect of the electric field gradient at the rim of the nanoholes
on both the ions and the Ag NPs is of particular interest for producing
hybrid nanostructures that enable SERS. This system, along with the
assumption of NHA axis symmetry regarding electrokinetic phenomena,
is the main domain for the analytical solution presented in this work.
The nanohole is modeled as an isothermal flat nanochannel of height h0 and length L. A 2D Cartesian
system of coordinates
and the induced field in the EDL. The imposed
external field yields the transference of electrons to particles,
resulting in the acquisition of a net negative surface electric charge.
Some particles may undergo polarization while retaining their electrical
neutrality; in this manner, consideration of both charged and uncharged
nanoparticles in the present analysis is warranted. Figure 1b depicts a cross-sectional
view of a single nanohole within the NHA. Notably, silver nanoparticles
exhibit a distinct Gaussian distribution concentration close to the
nanohole’s entrance, a phenomenon attributed to the localized
enhancement of the electric field.8 The
effect of the electric field gradient at the rim of the nanoholes
on both the ions and the Ag NPs is of particular interest for producing
hybrid nanostructures that enable SERS. This system, along with the
assumption of NHA axis symmetry regarding electrokinetic phenomena,
is the main domain for the analytical solution presented in this work.
The nanohole is modeled as an isothermal flat nanochannel of height h0 and length L. A 2D Cartesian
system of coordinates 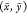 is adopted at the nanochannel left inlet,
where · indicates that the variable has dimensional units. The
extension of the model to cylindrical coordinates is trivial, as reported
by Pennathur and Santiago.3
is adopted at the nanochannel left inlet,
where · indicates that the variable has dimensional units. The
extension of the model to cylindrical coordinates is trivial, as reported
by Pennathur and Santiago.3
Figure 1.
(a) Schematic representation of the microfluidic chip assembly connected to a DC source containing multiple silver nanoparticles and an NHA embedded in a gold film. (b) Close-up view of a nanohole from the NHA where silver nanoparticles respond to the induced electrical potential in the overlapped EDL.
Governing Equations
The governing equations that serve as a starting point to investigate the EF in this study are the continuity equation
| 1 |
and the Navier–Stokes equations
| 2 |
where ρm is the fluid density, considered constant, 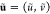 is the velocity vector,
is the velocity vector, 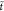 is the time,
is the time, 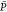 is the pressure, ∇ is the Nabla
operator defined as
is the pressure, ∇ is the Nabla
operator defined as 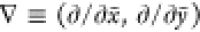 , and
, and 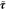 is the stress tensor for a Newtonian fluid,
given by
is the stress tensor for a Newtonian fluid,
given by
| 3 |
where μ is the dynamic viscosity of the fluid. The hydrodynamic boundary conditions related to the impermeability and no-slip condition at the walls are given by
| 4 |
and
| 5 |
respectively. n represents the unit vector normal to the microelectrode surface
pointing toward the fluid. The pressure is 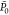 at
at 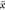 = 0,L. The electrical
body force in eq 2 consists
of the electric charge density ρe and the total electrical potential
= 0,L. The electrical
body force in eq 2 consists
of the electric charge density ρe and the total electrical potential 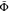 , which is governed by Poisson’s
equation
, which is governed by Poisson’s
equation
| 6 |
where ϵm denotes the dielectric permittivity of the medium. Here, 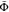 is split into the induced nonuniform equilibrium
potential in the EDL,
is split into the induced nonuniform equilibrium
potential in the EDL, 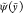 , and the potential describing the external
electric field
, and the potential describing the external
electric field 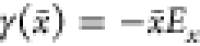 , where Ex = ϕ0/L and ϕ0 is the voltage provided by the generator. The boundary condition
for
, where Ex = ϕ0/L and ϕ0 is the voltage provided by the generator. The boundary condition
for 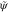 at the walls is
at the walls is 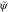 = ζ, where ζ is the zeta potential.
The electrical charge density ρe is proportional to the local concentration difference between the
cations and anions. For a symmetric (z/z) electrolyte solution, the charge density can be defined as
= ζ, where ζ is the zeta potential.
The electrical charge density ρe is proportional to the local concentration difference between the
cations and anions. For a symmetric (z/z) electrolyte solution, the charge density can be defined as
| 7 |
where z is the valence of
the electrolyte, e represents the fundamental charge
of an electron, and 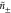 represents the concentration of cations
and anions, respectively. Transport of ions in a dilute solution is
described by the Nernst–Planck equation24
represents the concentration of cations
and anions, respectively. Transport of ions in a dilute solution is
described by the Nernst–Planck equation24
| 8 |
where Di is the diffusion coefficient of the ions, kB is the Boltzmann constant, and T is the absolute temperature. Equation 8 is subject to the following boundary conditions14
| 9 |
The concentration field 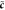 of the diffusing charged NPs is governed
by the convective diffusion equation25
of the diffusing charged NPs is governed
by the convective diffusion equation25
| 10 |
where the molecular diffusion coefficient of nanoparticles, denoted as D, is determined through the Stokes–Einstein equation26
| 11 |
where Rp is the hydrodynamic radius of the nanoparticles. In eq 10, the second right-hand term corresponds to an electromigration phenomenon, which consists of nanoparticle motion under the influence of Coulomb force. The Coulomb force appears between the gradient of the total electrical potential and the electrically charged NPs. Therefore, this term should only be considered for charged NPs. The boundary and initial conditions associated with eq 10 are
| 12 |
| 13 |
| 14 |
where 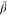 is the rate of disappearance of NPs due
to an irreversible first-order reaction between the solution and the
walls,27C* is the initial
concentration of NPs,
is the rate of disappearance of NPs due
to an irreversible first-order reaction between the solution and the
walls,27C* is the initial
concentration of NPs, 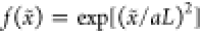 , and a is a constant.
In boundary conditions 12 we consider two cases:
(i) the nonpenetration boundary for uncharged nanoparticles and (ii)
the so-called perfect-sink model for charged nanoparticles. The nonpenetration
boundary is obtained when
, and a is a constant.
In boundary conditions 12 we consider two cases:
(i) the nonpenetration boundary for uncharged nanoparticles and (ii)
the so-called perfect-sink model for charged nanoparticles. The nonpenetration
boundary is obtained when 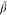 = 0, which specifies that there is no penetration
of the particles at the boundary, ensuring that any change in concentration
at the wall is solely due to diffusion and not advection.28 The boundary acting as a perfect sink, which
is used in theories of diffusion of charged particles,29 is obtained when
= 0, which specifies that there is no penetration
of the particles at the boundary, ensuring that any change in concentration
at the wall is solely due to diffusion and not advection.28 The boundary acting as a perfect sink, which
is used in theories of diffusion of charged particles,29 is obtained when 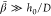 . This model assumes that all particles
arriving at the wall will be irreversibly adsorbed immediately and
subsequently disappear from the system.30
. This model assumes that all particles
arriving at the wall will be irreversibly adsorbed immediately and
subsequently disappear from the system.30
Nondimensional Mathematical Model
The governing equations
together with their corresponding boundary conditions can be written
in a nondimensional form by introducing the dimensionless variables x = 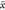 /L,
/L, 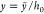 ,
, 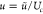 ,
, 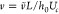 ,
, 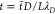 ,
, 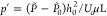 ,
, 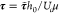 , ψ =
, ψ = 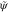 /ζ,
/ζ, 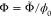 ,
, 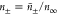 , and
, and 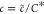 . Here, Uc = ϵmζ2/μL
is the characteristic velocity,31tc = LλD/D is the harmonic time,32
. Here, Uc = ϵmζ2/μL
is the characteristic velocity,31tc = LλD/D is the harmonic time,32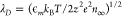 is the Debye length, and n∞ is the ionic number in the concentration in the
bulk solution. When defining the nondimensional pressure p′, we have introduced the useful definition P = p′ – (1/2)(dψ/dy)2 introduced by Ajdari,33 which serves to eliminate the electric terms in the momentum
equation in the y direction. Therefore, the expanded
nondimensional forms of the hydrodynamic, electric, and concentration
governing eqs 1–3, 6–8, and 10 are as follows
is the Debye length, and n∞ is the ionic number in the concentration in the
bulk solution. When defining the nondimensional pressure p′, we have introduced the useful definition P = p′ – (1/2)(dψ/dy)2 introduced by Ajdari,33 which serves to eliminate the electric terms in the momentum
equation in the y direction. Therefore, the expanded
nondimensional forms of the hydrodynamic, electric, and concentration
governing eqs 1–3, 6–8, and 10 are as follows
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
In eqs 15–20, ϵ = λD/L, η = h0/L, k = h0/λD, α = −ζ/ϕ0, δ = −ζze/kBT, DT = D/Di, Pe = UcλD/D is the Péclet number, and Re = ρmUch0/μ is the Reynolds numbers. The dimensionless boundary conditions of eqs 15–20 are
| 21 |
| 22 |
| 23 |
| 24 |
| 25 |
| 26 |
and
| 27 |
where
| 28 |
and 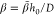 . In conditions 22, the induced potential gradient is zero at x =
0,1 due to symmetry. In nanofluidic systems, typical values of the
parameters ϵ, DT, and Re are very small (λD = 10
nm, L = 200 nm, Di = 10–9 m2/s, D = 8.5844 × 10–12 m2/s, Uc = 0.002 m/s, ϵ = 0.05, DT = 10–3,
and Re = 2.5 × 10–4), while
η < 1 (η = 0.5). Therefore, a simplified version of
the nondimensional governing equations, as well as a regular perturbation
technique,34 can be used to solve the set
of mentioned equations for small values of the parameter ϵ.
Thus, a regular expansion is proposed for each dependent variable
(say, X) in the following form
. In conditions 22, the induced potential gradient is zero at x =
0,1 due to symmetry. In nanofluidic systems, typical values of the
parameters ϵ, DT, and Re are very small (λD = 10
nm, L = 200 nm, Di = 10–9 m2/s, D = 8.5844 × 10–12 m2/s, Uc = 0.002 m/s, ϵ = 0.05, DT = 10–3,
and Re = 2.5 × 10–4), while
η < 1 (η = 0.5). Therefore, a simplified version of
the nondimensional governing equations, as well as a regular perturbation
technique,34 can be used to solve the set
of mentioned equations for small values of the parameter ϵ.
Thus, a regular expansion is proposed for each dependent variable
(say, X) in the following form
| 29 |
where X = u, v, P, ψ. Substituting the expansion eq 29 into the nondimensional
governing eqs 15–19, and collecting terms of 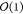 , we obtain the following problems
, we obtain the following problems
| 30 |
| 31 |
| 32 |
| 33 |
| 34 |
From eq 32, P0 = P0(x) should be determined as a part of the hydrodynamics problem together with u0 and v0. The solution of Nernst–Planck eq 34 is given by14
| 35 |
and
| 36 |
where ψc is the unknown electrical potential at the center of the nanochannel. In eqs 35 and 36 it is assumed that the concentrations of cations and anions at the center are the same (n0,+ = n0,– = 1 at y = 0). Further applying the Debye–Hückel approximation yields
| 37 |
and
| 38 |
Substituting eqs 37 and 38 in 33 returns
| 39 |
The 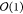 solution of Poisson eq 39, considering the boundary conditions [eq 23], is given by
solution of Poisson eq 39, considering the boundary conditions [eq 23], is given by
| 40 |
To recover the Boltzmann equation (ψ = 0 at y = 0 and k ≫ 1), we have assumed that ψc = ζ/k, obtaining the following simplification
| 41 |
The general hydrodynamic solution of eq 31 is obtained by substituting eq 41 in the momentum equation and integrating the result twice with respect to y; considering eq 21 as the boundary condition, we obtain that the velocity profile in the lowest order is given as
| 42 |
In the above equation, the pressure gradient is unknown and can be obtained using the continuity equation, eq 30. The suggested procedure is to substitute eqs 42 into 30, obtaining a solution for v0 and P0. However, one should find that the leading order for the variables v0 and P0 is zero. Therefore, the above physically means that there are no induced pressure terms in this order and that the velocity field is hydrodynamically developed. Therefore, substituting eqs 41 in 42 yields
| 43 |
The next step is to assess the 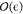 solutions for ψ1, u1, v1, and P1. In this order, the ion concentration does
not get affected by convection, thus making the
solutions for ψ1, u1, v1, and P1. In this order, the ion concentration does
not get affected by convection, thus making the 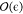 Poisson equation to yield ψ1 = 0, leading to u1 = v1 = P1 = 0 due to its role
as the primary force in the momentum equations.
Poisson equation to yield ψ1 = 0, leading to u1 = v1 = P1 = 0 due to its role
as the primary force in the momentum equations.
Homogenization Method
To obtain an analytical solution for the concentration field of Ag NPs, the homogenization method35 is proposed to derive an expression that allows us to solve the convective diffusion equation. Thus, three distinct time scales are involved in the analysis of Ag NPs, which are as follows: the harmonic time,32t0 ∼ LλD/D, the transverse diffusion time, t1 ∼ 4h02/D, and the longitudinal diffusion time, t2 ∼ L2/D.
From typical values of the previous times (L = 200 nm, h0 = 100 nm, t0 = 2 × 10–4 s, and t1 = t2 = 4 × 10–3 s), the following two time scales can be introduced
| 44 |
and using eq 29 to expand for the dimensionless concentration
| 45 |
where cj = cj(x,y,t0,t2) and j = 0,1,2. The original time derivate becomes, according to the chain rule
| 46 |
Substituting eqs 45 and 46 in 20 yields
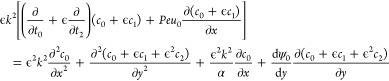 |
47 |
At order 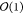 , the governing equation is given by
, the governing equation is given by
| 48 |
To obtain a solution for eq 48, we consider two cases: uncharged nanoparticles, which neglect the electromigration term (second left-hand term) in eq 48, and charged nanoparticles. In addition, both cases must satisfy the following boundary condition due to the symmetry of the nanochannel
| 49 |
In both cases, the solution at 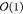 is c0 = Cx(x,t0,t2). The procedure
that determines the function Cx is given in the lines below. Taking the
is c0 = Cx(x,t0,t2). The procedure
that determines the function Cx is given in the lines below. Taking the 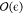 from eq 47 yields the governing equation for c1
from eq 47 yields the governing equation for c1
| 50 |
The next step is to take the cross-sectional
average of eq 50, defined
as 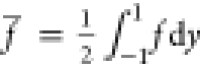 for any function f, where
· will indicate the averaged function. In this context, the first
right-hand term in eq 50 becomes zero as a consequence of its symmetry with respect to the y-axis, which is known from the inflection point at y = 0 [eq 49]. Similarly, the second right-hand term becomes zero due to the
product of two odd functions. Thus, the cross-sectional average of eq 50 is
for any function f, where
· will indicate the averaged function. In this context, the first
right-hand term in eq 50 becomes zero as a consequence of its symmetry with respect to the y-axis, which is known from the inflection point at y = 0 [eq 49]. Similarly, the second right-hand term becomes zero due to the
product of two odd functions. Thus, the cross-sectional average of eq 50 is
| 51 |
where
| 52 |
Substituting eqs 51 into 50 yields
| 53 |
Considering the linearity of eq 53, the solution c1 can be expressed as
| 54 |
and its substitution in eq 53 leads to a second-order ordinary differential equation for B(y) as follows
| 55 |
where
| 56 |
First, eq 55 is solved for uncharged nanoparticles using boundary condition 25 considering β = 0 as follows
| 57 |
Solving eq 55 for uncharged NPs, neglecting the electromigration term (second left-hand term) in eq 55, yields
| 58 |
For charged nanoparticles (β ≫ 1), eq 55 was solved using the fourth-order Runge–Kutta method with the aid of the shooting approach together with the following boundary condition [eq 25]
| 59 |
| 60 |
Substituting eqs 51 and 54 in 60 returns
| 61 |
Taking the cross-sectional average of eq 61, the following governing equation is obtained
| 62 |
where
| 63 |
For uncharged nanoparticles, 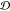 was calculated by substituting eqs 56 and 58 in 63, obtaining the following equation
was calculated by substituting eqs 56 and 58 in 63, obtaining the following equation
| 64 |
For charged nanoparticles, 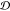 was calculated by using numerical methods.
Finally, eq 51 is added
to 62, where the artifice of two times is no
longer needed and can be removed35
was calculated by using numerical methods.
Finally, eq 51 is added
to 62, where the artifice of two times is no
longer needed and can be removed35
| 65 |
where
| 66 |
The second right-hand term in eq 66 is part of electromigration and should only be considered for charged nanoparticles. First, we propose a solution for Cx that eliminates the convective term in eq 65, i.e., the first right-hand term, as follows
| 67 |
Substituting eqs 67 into 65 yields
| 68 |
The initial and boundary conditions of eq 68 are taken from eqs 26–28 as follows
| 69 |
and
| 70 |
The general solution for the leading order, using the Fourier method for eqs 68 and substituting 67, is
| 71 |
Results and Discussion
In the Nondimensional
Mathematical Model and Homogenization Method sections, the
nondimensional potential in the EDL, velocity vector, and concentration
field of silver nanoparticles, subjected to the electromigration effect,
were calculated. To estimate the values of dimensionless parameters
involved in the analysis, we consider values of physical and geometrical
parameters that have been reported in previous work:11h0 = 100 nm, L = 200 nm, Rp = 25 nm, T = 293 K, ϵm = 7.8 ×
10–10 C/V m, ρm = 997 kg/m3, μ = 1 × 10–3 kg/ms, ϕ0 = 3 V, ζ = −25.4 ×
10–3 V, z = 1, n∞ = 6.022 × 1023 m–3, λD = 10 nm, Uc = 2.5 × 10–3 m/s, D = 8.58 × 10–12 m2/s, and Di = 1.65 × 10–9 m2/s. With the previous physical domain, the dimensionless
parameters for the calculations assume the following values: ϵ
= 0.05, k = 10, η = 0.5, α = 8.4 ×
10–3, δ = 1, Re = 2.5 ×
10–4, Pe = 2.93, and 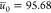 . For the analytical process, we consider
uncharged and charged Ag NPs, obtaining
. For the analytical process, we consider
uncharged and charged Ag NPs, obtaining 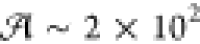 and
and 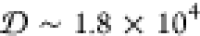 at k = 10. Besides, the
nondimensional concentration field is governed by the following equation
at k = 10. Besides, the
nondimensional concentration field is governed by the following equation
| 72 |
In Figure 2c, the
nondimensional concentration field [eq 72] is shown for both charged and uncharged Ag NPs at k = 10. The selected times are determined using the time-dependent
diffusive component in eq 71 to counteract the condition 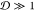 . As t increases beyond
these selected values, the nondimensional concentration field converges
to a constant value, i.e.,
. As t increases beyond
these selected values, the nondimensional concentration field converges
to a constant value, i.e., 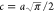 . The first noticeable effect in Figure 2a is the propagation
of NPs from their initial concentration at t = 0,
which occurs rapidly throughout the entire system. This phenomenon
is primarily attributed to diffusion, and notably, it conserves the
original distribution of NPs but elongates along the system. The concentration
distribution at x = 0.2 at this initial time is exclusively
influenced by the initial boundary condition [eq 70]. Figure 2b shows the concentration field for uncharged nanoparticles
at t = 10–5, where a distinctive
negative concentration is observed at the walls of the nanochannel.
This negative concentration indicates a deficit of nanoparticles close
to the walls. On the other hand, positive concentration values at
the entrance, middle, and exit of the nanochannel indicate that uncharged
nanoparticles, initially located near the entrance, are driven toward
the center of the channel, flow through it, and are eventually expelled
at the opposite end. Figure 2d shows that the concentration field for charged nanoparticles
is presented at t = 10–5. In this
case, a concentration value of c = 0 indicates the
occurrence of the reaction of NPs with the walls, as can be appreciated
from eqs 13 and 59. This outcome suggests that most charged NPs react
primarily at the entrance and exit regions of the nanochannel, while
the excess of NPs that cannot react at the walls is concentrated at
the central region. Furthermore, the coefficient
. The first noticeable effect in Figure 2a is the propagation
of NPs from their initial concentration at t = 0,
which occurs rapidly throughout the entire system. This phenomenon
is primarily attributed to diffusion, and notably, it conserves the
original distribution of NPs but elongates along the system. The concentration
distribution at x = 0.2 at this initial time is exclusively
influenced by the initial boundary condition [eq 70]. Figure 2b shows the concentration field for uncharged nanoparticles
at t = 10–5, where a distinctive
negative concentration is observed at the walls of the nanochannel.
This negative concentration indicates a deficit of nanoparticles close
to the walls. On the other hand, positive concentration values at
the entrance, middle, and exit of the nanochannel indicate that uncharged
nanoparticles, initially located near the entrance, are driven toward
the center of the channel, flow through it, and are eventually expelled
at the opposite end. Figure 2d shows that the concentration field for charged nanoparticles
is presented at t = 10–5. In this
case, a concentration value of c = 0 indicates the
occurrence of the reaction of NPs with the walls, as can be appreciated
from eqs 13 and 59. This outcome suggests that most charged NPs react
primarily at the entrance and exit regions of the nanochannel, while
the excess of NPs that cannot react at the walls is concentrated at
the central region. Furthermore, the coefficient 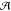 , as defined in eq 66, may become zero for charged nanoparticles
implying that, under certain nanochannel dimensions, no convective
transport can take place for the leading order of the concentration
field. An analytical expression for the critical nanochannel length,
denoted as Lcrit, is derived by eq 66, yielding Lcrit = 12πRpλD3n∞f(k), where
, as defined in eq 66, may become zero for charged nanoparticles
implying that, under certain nanochannel dimensions, no convective
transport can take place for the leading order of the concentration
field. An analytical expression for the critical nanochannel length,
denoted as Lcrit, is derived by eq 66, yielding Lcrit = 12πRpλD3n∞f(k), where 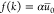 [eq 52]. For instance, at k = 10, this results
in Lcrit = 474 nm. However, it is noteworthy
to mention that for the current ratio
[eq 52]. For instance, at k = 10, this results
in Lcrit = 474 nm. However, it is noteworthy
to mention that for the current ratio 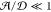 , no significant changes in the concentration
fields are discernible even at the critical length Lcrit. To improve the concentration field with convection,
it is necessary to increase the
, no significant changes in the concentration
fields are discernible even at the critical length Lcrit. To improve the concentration field with convection,
it is necessary to increase the 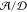 ratio. Our analysis, using eqs 64–66, reveals that this can only be achieved by increasing the parameter
α and/or decreasing k = h0/λD. The parameter α = −ζ/ϕ0 can be increased by subjecting the system to an external
heat flux,36 or by reducing the applied
voltage from the generator. Caution must be exercised when decreasing
ϕ0 since this would cause a quadratic reduction in
the dielectrophoretic force and thus is not recommended. Considering
the reduction of h0, a lower limit of k = 2.5 is deduced. This requirement ensures that the height
of the nanochannel allows the passage of at least one nanoparticle
through it, i.e., h0 = Rp = 25 nm.
ratio. Our analysis, using eqs 64–66, reveals that this can only be achieved by increasing the parameter
α and/or decreasing k = h0/λD. The parameter α = −ζ/ϕ0 can be increased by subjecting the system to an external
heat flux,36 or by reducing the applied
voltage from the generator. Caution must be exercised when decreasing
ϕ0 since this would cause a quadratic reduction in
the dielectrophoretic force and thus is not recommended. Considering
the reduction of h0, a lower limit of k = 2.5 is deduced. This requirement ensures that the height
of the nanochannel allows the passage of at least one nanoparticle
through it, i.e., h0 = Rp = 25 nm.
Figure 2.
Nondimensional concentration field c for uncharged nanoparticles at k = 10, evaluated at the nondimensional time (a) t = 0 and (b) t = 10–5. Nondimensional concentration field c for charged nanoparticles at k = 10 and (c) t = 0 and (d) t = 10–5.
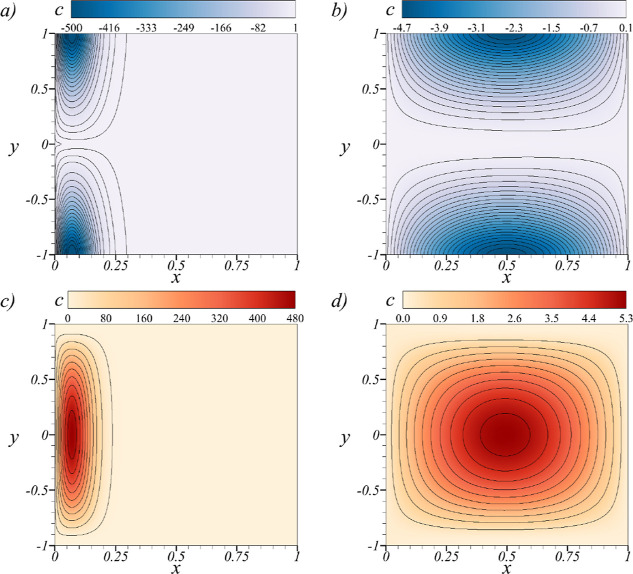
In Figure 3, the nondimensional concentration field at k = 2.5 is shown. In Figure 3a, a pronounced trapping mechanism for uncharged nanoparticles is evident, whereby a significant quantity of Ag NPs becomes trapped near the center of the nanochannel. This change in behavior is governed by the variable B(y), which, in return, is a consequence of the overlap within the EDL. This phenomenon can be elucidated by considering the representation of eqs 58 with 39 and 42, as follows
| 73 |
Figure 3.
Nondimensional concentration field c at the nondimensional time t = 10–4 and k = 2.5 for (a) uncharged nanoparticles and (b) charged nanoparticles.
The trapping mechanism is observed to manifest when tanh(k) < 0.999 which is obtained when k = 3.8. In Figure 3b, the concentration field for charged Ag NPs is depicted, where it is observed that these nanoparticles undergo electrical reactions predominantly at the exit of the nanochannel while filling the nanohole in a counter-flow manner. For the specified value of k = 2.5, the critical length is calculated to be Lcrit = 212 nm.
Conclusions
Propagation of uncharged and charged nanoparticles due to an EF and electromigration in a nanochannel with overlapping EDLs has been studied by deriving an analytical expression for the ionic distribution, hydrodynamic forces, and Ag NP concentration. From the current analysis, the following major points are obtained: (i) for charged nanoparticles, colloidal transport convection is countered by electromigration, where a critical length of the nanochannel will produce a pure diffusion process for the leading concentration field solution; (ii) for uncharged nanoparticles, a trapping mechanism can be achieved due to overlapping of the EDL at k = 3.8; and (iii) in addition to modifying the nanochannel dimension, the propagation of colloids can be achieved by increasing the surface potential ζ through an external heat source. This last finding requires that the energy equation be coupled with the governing equations. Further studies on the propagation of colloids in nanoconfinement would be required to investigate, experimentally, the nanoaperture dimension and the variation in zeta potential. The latter could be achieved by using an external heat source36 or by modifying the ionic concentration of the solvent,14 as both approaches invalidate the Debye–Hückel approximation.
Acknowledgments
C.V. acknowledges the support from the DGAPA program for a postdoctoral fellowship at UNAM. Carlos Escobedo gratefully acknowledges the financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC), from the Canada Foundation for Innovation (CFI), and from Queen’s University for a FEAS Excellence in Research Award.
Author Contributions
The manuscript was written through all the contributions of all authors. All authors have approved the final version of the manuscript.
Natural Sciences and Engineering Research Council of Canada (NSERC), no. RGPIN-201-05138. Canada Foundation for Innovation (CFI), no. 31967. Queen’s University FEAS Excellence in Research Award.
The authors declare no competing financial interest.
References
- Wang J.; Maier S. A.; Tittl A. Trends in Nanophotonics-Enabled Optofluidic Biosensors. Adv. Opt. Mater. 2022, 10, 2102366. 10.1002/adom.202102366. [DOI] [Google Scholar]
- Escobedo C. On-chip nanohole array based sensing: a review. Lab Chip 2013, 13, 2445–2463. 10.1039/c3lc50107h. [DOI] [PubMed] [Google Scholar]
- Pennathur S.; Santiago J. G. Electrokinetic Transport in Nanochannels. 1. Theory. Anal. Chem. 2005, 77, 6772–6781. 10.1021/ac050835y. [DOI] [PubMed] [Google Scholar]
- Pennathur S.; Santiago J. G. Electrokinetic transport in nanochannels. 2. Experiments. Anal. Chem. 2005, 77, 6782–6789. 10.1021/ac0508346. [DOI] [PubMed] [Google Scholar]
- Striemer C. C.; Gaborski T. R.; McGrath J. L.; Fauchet P. M. Charge- and size-based separation of macromolecules using ultrathin silicon membranes. Nature 2007, 445, 749–753. 10.1038/nature05532. [DOI] [PubMed] [Google Scholar]
- Mukaibo H.; Wang T.; Perez-Gonzalez V.; Getpreecharsawas J.; Wurzer J.; Lapizco-Encinas B.; McGrath J. L. Ultrathin nanoporous membranes for insulator-based dielectrophoresis. Nanotechnology 2018, 29, 235704. 10.1088/1361-6528/aab5f7. [DOI] [PubMed] [Google Scholar]
- Eftekhari F.; Escobedo C.; Ferreira J.; Duan X.; Girotto E. M.; Brolo A. G.; Gordon R.; Sinton D. Nanoholes as nanochannels: Flow-through plasmonic sensing. Anal. Chem. 2009, 81, 4308–4311. 10.1021/ac900221y. [DOI] [PubMed] [Google Scholar]
- Escobedo C.; Brolo A. G.; Gordon R.; Sinton D. Optofluidic Concentration: Plasmonic Nanostructure as Concentrator and Sensor. Nano Lett. 2012, 12, 1592–1596. 10.1021/nl204504s. [DOI] [PubMed] [Google Scholar]
- Ertsgaard C. T.; McKoskey R. M.; Rich I. S.; Lindquist N. C. Dynamic placement of plasmonic hotspots for super-resolution surface-enhanced Raman scattering. ACS Nano 2014, 8, 10941–10946. 10.1021/nn504776b. [DOI] [PubMed] [Google Scholar]
- Larson S.; Luong H.; Song C.; Zhao Y. Dipole Radiation-Induced Extraordinary Optical Transmission for Silver Nanorod-Covered Silver Nanohole Arrays. J. Phys. Chem. C 2019, 123, 5634–5641. 10.1021/acs.jpcc.9b00477. [DOI] [Google Scholar]
- Bdour Y.; Beaton G.; Gomez-Cruz J.; Cabezuelo O.; Stamplecoskie K.; Escobedo C. Hybrid plasmonic metasurface as enhanced Raman hot-spots for pesticide detection at ultralow concentrations. Chem. Commun. 2023, 59, 8536–8539. 10.1039/D3CC01015E. [DOI] [PubMed] [Google Scholar]
- Khosravi B.; Gordon R. Accessible Double Nanohole Raman Tweezer Analysis of Single Nanoparticles. J. Phys. Chem. C 2024, 128, 15048–15053. 10.1021/acs.jpcc.4c03536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Leebeeck A.; Sinton D. Ionic dispersion in nanofluidics. Electrophoresis 2006, 27, 4999–5008. 10.1002/elps.200600264. [DOI] [PubMed] [Google Scholar]
- Qu W.; Li D. A model for overlapped EDL Fields. J. Colloid Interface Sci. 2000, 224, 397–407. 10.1006/jcis.1999.6708. [DOI] [PubMed] [Google Scholar]
- Golovnev A.; Trimper S. Analytical solution of the Poisson-Nernst-Planck equations in the linear regime at an applied dc-voltage. J. Chem. Phys. 2011, 134, 154902. 10.1063/1.3580288. [DOI] [PubMed] [Google Scholar]
- Zachariah Z.; Espinosa-Marzal R. M.; Spencer N. D.; Heuberger M. P. Stepwise collapse of highly overlapping electrical double layers. Phys. Chem. Chem. Phys. 2016, 18, 24417–24427. 10.1039/c6cp04222h. [DOI] [PubMed] [Google Scholar]
- Yeh L.-H.; Zhang M.; Qian S.; Hsu J.-P.; Tseng S. Ion concentration polarization in Polyelectrolyte-modified nanopores. J. Phys. Chem. C 2012, 116, 8672–8677. 10.1021/jp301957j. [DOI] [Google Scholar]
- Lapizco-Encinas B. H. Microscale electrokinetic assessments of proteins employing insulating structures. Curr. Opin. Chem. Eng. 2020, 29, 9–16. 10.1016/j.coche.2020.02.007. [DOI] [Google Scholar]
- Wu Z.-Q.; Li Z.-Q.; Ding X.-L.; Hu Y.-L.; Xia X.-H. Influence of Asymmetric Geometry on the Ion Transport of tandem nanochannels. J. Phys. Chem. C 2021, 125, 24622–24629. 10.1021/acs.jpcc.1c06884. [DOI] [Google Scholar]
- Mani A.; Zangle T. A.; Santiago J. G. On the propagation of concentration polarization from microchannel-nanochannel interfaces Part I. Analytical model and characteristic analysis. Langmuir 2009, 25, 3898–3908. 10.1021/la803317p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaroshchuk A.; Bondarenko M. P. Current-Induced concentration polarization of nanoporous media: Role of electroosmosis. Small 2018, 14, 1703723. 10.1002/smll.201703723. [DOI] [PubMed] [Google Scholar]
- Chen L.; Hu C.; Dong Y.; Li Y.; Shi Q.; Liu G.; Long R.; Xiong Y. Tunable Layered Gold Nanochips for High Sensitivity and Uniformity in SERS. J. Phys. Chem. C 2023, 127, 8167–8174. 10.1021/acs.jpcc.3c01359. [DOI] [Google Scholar]
- Sakamoto M.; Saitow K. Large-Area Plasmon Mapping via an Optical Technique: Silver Nanohole Array and Nano-Sawtooth Structures. J. Phys. Chem. C 2023, 127, 13105–13111. 10.1021/acs.jpcc.3c01919. [DOI] [Google Scholar]
- Hille B.Ionic Channels of Excitable Membranes; Sinauer Associates Inc., 1992. [Google Scholar]
- Probstein R. F.Physicochemical Hydrodynamics; Wiley-Interscience, 2005. [Google Scholar]
- Philipse A. P.Brownian Motion. Elements of Colloid Dynamics; Springer, 2018. [Google Scholar]
- Vacík J.Electrophoresis a Survey of Techniques and Applications; Elsevier, 1979. [Google Scholar]
- Elimelech M.; Gregory J.; Jia X.; Williams R. A.. Particle Deposition and Aggregation. Measurement, Modelling and Simulation; Butterworth-Heinemann, 1995. [Google Scholar]
- Leonard G.; Mitchner M.; Self S. A. Particle transport in electrostatic precipitators. Atmos. Environ. 1980, 14, 1289–1299. 10.1016/0004-6981(80)90230-9. [DOI] [Google Scholar]
- Adamcyzk Z. Particle deposition from flowing suspensions. Colloids Surf. 1989, 39, 1–37. 10.1016/0166-6622(89)80176-3. [DOI] [Google Scholar]
- Miloh T.; Boymelgreen A. Travelling wave dipolophoresis of ideally polarizable nanoparticles with overlapping electric double layers in cylindrical pores. Phys. Fluids 2014, 26, 072101. 10.1063/1.4884956. [DOI] [Google Scholar]
- Bazant M. Z.; Thornton K.; Ajdari A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys. 2004, 70, 021506. 10.1103/PhysRevE.70.021506. [DOI] [PubMed] [Google Scholar]
- Ajdari A. Electro-osmosis on Inhomogeneously charged surfaces. Phys. Rev. Lett. 1995, 75, 755–758. 10.1103/PhysRevLett.75.755. [DOI] [PubMed] [Google Scholar]
- Bender C. M.; Orzag S. A.. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer Science and Business, 2013. [Google Scholar]
- Mei C. C.; Vernescu B.. Homogenization Methods for Multiscale Mechanics; World Scientific Publishing Co., 2010. [Google Scholar]
- Vargas C.; Bautista O.; Méndez F. Effect of temperature-dependent properties on electroosmotic mobility at arbitrary zeta potentials. Appl. Math. Model. 2019, 68, 616–628. 10.1016/j.apm.2018.11.050. [DOI] [Google Scholar]