A multiscale brain map derived from whole-brain volumetric reconstructions

Abstract

Animal nervous system organization is crucial for all body functions and its disruption can manifest in severe cognitive and behavioral impairment¹. This organization relies on features across scales, from nanoscale localization of synapses, through multiplicities of neuronal morphologies and their contribution to circuit organization, to stereotyped connections between different regions of the brain². The sheer complexity of this organ means that, to date, we have yet to reconstruct and model the structure of a complete nervous system that is integrated across all these scales. Here, we present a complete structure-function model of the nematode C. elegans main neuropil, the nerve ring, which we derive by integrating the volumetric reconstruction from two animals with corresponding³ synaptic and gap junctional connectomes. Whereas previously the nerve ring was considered a densely packed tract of neural processes, we uncover internal organization and show how local neighborhoods spatially constrain and support the synaptic connectome. We find that the C. elegans connectome is not invariant, but that a precisely wired core circuit is embedded in a background of variable connectivity, and propose a corresponding reference connectome for the core circuit. Based on this reference, we propose a modular network architecture of the C. elegans brain that supports sensory computation and integration, sensorimotor convergence and brain-wide coordination. These findings point to scalable and robust features of brain organization that are likely universal across phyla.

A primary goal of systems neuroscience is to understand how the brain’s structure and function combine to generate behavior. Since the discovery of neurons and their connections through synapses and gap junctions, a major effort has focused on characterizing these units and the micro- and macro-circuits that they comprise, culminating in a growing body of high-resolution nanoconnectomic data across species^3–12. Naturally, data, however rich, cannot on their own provide explanatory power to address the computation within circuits or to determine how these circuits communicate and coordinate information flow to generate behavior. Indeed, constructing a comprehensive brain map will require a meaningful strategy for integrating structure and function across scales. Achieving this feat in even a small animal can provide a useful model for postulating principles of brain organization across scales².

The free-living nematode C. elegans has a small, compact nervous system^3,5,7,13 while exhibiting a range of complex, individualized behaviors, making it an ideal model system for studies of whole brain organization². All 302 C. elegans neurons have been anatomically characterized based on serial sectioned electron micrographs (EM)⁵ to produce a whole animal connectome^3,5,13. This animal’s invariant cell-lineage¹⁴ and anatomy⁵ might suggest that its connectome too is invariant¹⁵. Unfortunately, the small sample size of available reconstructions has precluded a reliable estimate of reproducibility and variability of the synaptic connectome. Furthermore, while the synaptic wiring has been exhaustively characterized^3,5,13,16,17, the spatial proximity of neurons is only partially determined^18,19. Thus, it remains to be determined whether lessons about whole brain organization in C. elegans can inform questions and approaches for other systems.

We provide two complete volumetric reconstructions of the C. elegans nerve ring from legacy EMs⁵, from one adult and one larval stage 4 (L4) animal (Methods, Supplementary Table 1, Supplementary Videos 1–3, Supplementary Information 1). The two EM series (with roughly 300 sections in the L4 and 400 in the adult) span approximately the same 36 μm long volume, starting in the anterior and ending in the ventral ganglia (Fig. 1a). Our reconstructions provide the first contactome: a complete, nanoresolution dataset of all neuronal membrane contacts in the nerve rings of these two animals. We define two neurons as immediate neighbors if the membranes along their neural processes are physically adjacent in at least one EM section¹⁸. To characterize synaptic pathways within a spatial context, we integrated our volumetric reconstructions with our recent rescoring of synapses on the same L4 and adult animals³ (for validation and comparison with other datasets^5,20, see Methods).

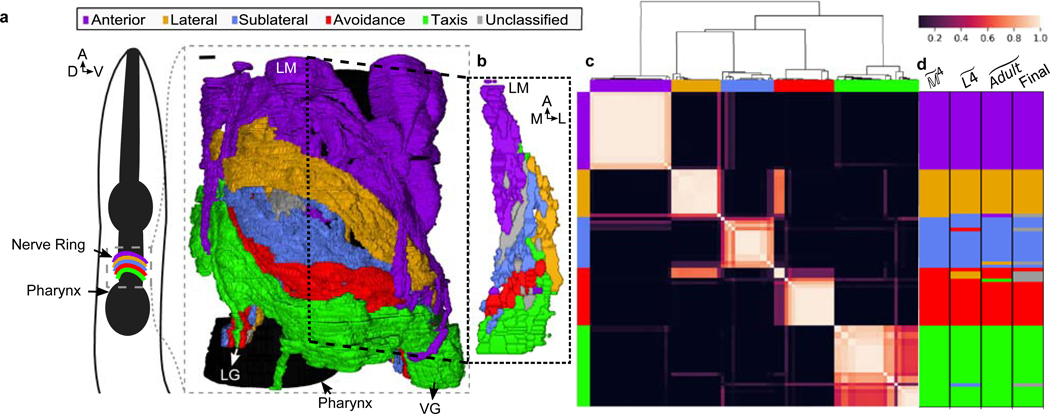
Fig. 1. Five densely connected neurite clusters comprise the nerve ring neuropil.

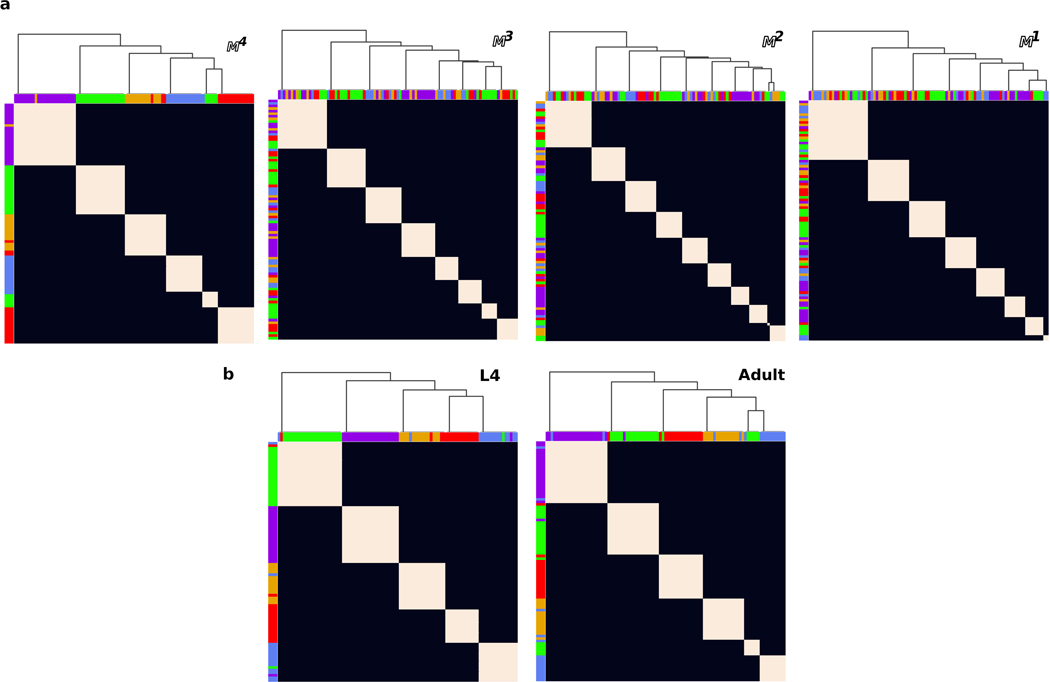
a, The nerve ring neuropil (<4% of the worm’s body length and most synaptically dense region of the nervous system) includes neurites of 181 L4 (185 adult ) neurons. Complete volumetric reconstruction of the L4 neuropil spans 36 μm (Supplementary Video 3). 15 μm -long region (inset): left view, superficial neurons removed. D: dorsal, V: ventral, A: anterior. b, A 250 nm oblique volumetric slice at approximately the lateral midline (LM) rendered with no processes removed (right). A/P: anterior/posterior, M/L: medial/lateral, LG/VG: lateral/ventral ganglia. Scale bar: 1 μm Neurites with relatively high spatial affinity (but no physical boundaries) form spatially ordered clusters along anterior-posterior axis. c, Cluster matrix: frequency that cells $i$ and $j$ cluster together across the population $\widetilde{{\mathbb{M}}^4}$: Row and column order minimized frequency variance along the diagonal. Clusters were then ordered to visually match AP ordering (original ordering in Extended Data Fig. 5i). Top: Dendrogram of the hierarchical clustering. d, Clustering results of model $\widetilde{{\mathbb{M}}^4}$, $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$ populations (Extended Data Fig. 5i) and consensus cluster assignment across the 3 populations. Row and column order same as rows in c. 7 cell classes (ADE, ALN, AVA, RID, RIR, RMD, URX) with discrepant cluster assignments among the 3 populations are unclassified (gray). $n=1000$ perturbed datasets per population (Methods).

Conserved and variable circuits overlap

Consistent with White et al.⁵, our volumetric reconstructions show that neural processes are bilaterally (left/right) conserved (Supplementary Results, Supplementary Videos 4–7). We hypothesized that the bilateral symmetry of C. elegans processes extends to the nanoscale to support a homology of membrane contacts and synapses between cells. Homologous processes exhibit statistically high overlaps in the size and composition of their immediate neighborhood (Extended Data Fig. 1a–c) and in membrane contact locations along their processes (Methods, Extended Data Fig. 1d–f, Supplementary Information 2). In contrast, the smallest 35% of membrane contacts (< 0.4 μm²) are not reproducible (Extended Data Fig. 2a), account for only 2% of total membrane contact area between all neurons (Extended Data Fig. 2b,c) and contain predominantly nonreproducible synaptic contacts (Extended Data Fig. 2e). As such, we exclude them from our analysis. We conclude that the reproducibility of neuronal processes and their immediate neighborhoods supports a stereotyped pattern of cell-cell membrane contacts.

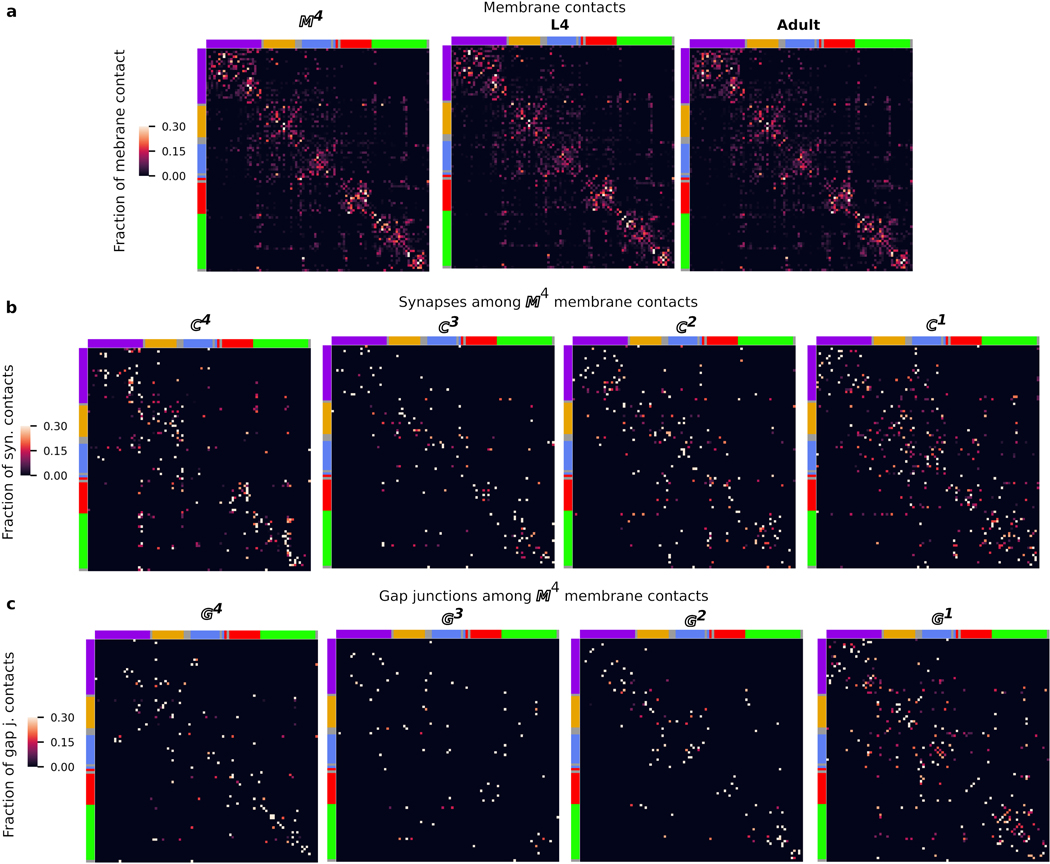
The availability of two reconstructions, combined with the bilateral homology of the nerve ring, naturally lends itself to establishing a reference dataset that is more likely conserved across animals, providing a basis to address mechanistic questions about precision and variability of the connectome at nanoscale resolution. We defined the adjacency graph, ${\mathbb{M}}^{\text{δ}}$, of membrane contacts across 4 datasets (adult left, adult right, L4 left and L4 right), where $\text{δ}$ labels the number of datasets in which a membrane contact occurs (Supplementary Information 3). The ${\mathbb{M}}^4$ reference dataset, i.e. the most reproducible membrane contacts, comprises ~40% of all membrane contacts (Extended Data Fig. 2g) and exhibits above average membrane contact area (Extended Data Fig. 2h). Adjacency graphs of chemical synapse, ${\mathbb{C}}^{\text{δ}}$, and gap junction, ${\mathbb{G}}^{\text{δ}}$, contacts are similarly defined (Supplementary Information 3). We define ${\mathbb{M}}^4$, ${\mathbb{C}}^4$ and ${\mathbb{G}}^4$ contacts as reference datasets and hypothesize that the ${\mathbb{M}}^4$ set of membrane contacts is representative of the conserved membrane contacts across individuals in C. elegans and is more likely to support a conserved synaptic connectome.

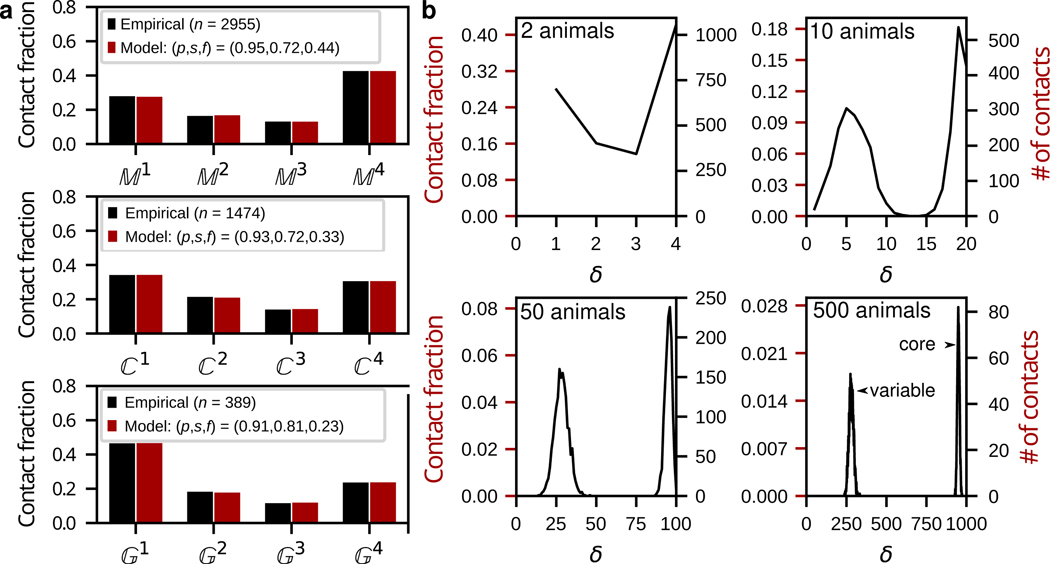
To examine this hypothesis, we exploit the combined spatial and synaptic information across datasets over the entire neuropil. We assume that stereotyped wiring patterns require precision to find target neurons and specificity to avoid off-target neurons, and formulate statistical models of membrane and synaptic contacts to capture their relative propensity to occur in 1, 2, 3 or all 4 of the datasets (Methods). We find that a minimal model with three parameters suffices (Methods); these are the fraction of target contacts, $f$, the precision, $p$, for target contacts, and the frequency to avoid off-target contacts or specificity, $s$. Despite their parsimony, these models yield good fits for the distribution of membrane, synaptic and gap junctional contacts across the 4 datasets (Methods, Fig. 2a). The high reproducibility of membrane contacts across datasets (${\mathbb{M}}^4$ count) is consistent with our model prediction that less than half of membrane contacts are actively targeted ($f=0.44$, Fig. 2a) with high precision $(p=0.95)$. The significant variability across datasets is accounted for by a non-negligible basal membrane contact rate ($1-s$ ~25-30%). Therefore, high precision combined with basal connectivity are required to account for the reproducibility and variability of membrane contacts across datasets (Fig. 2a; Supplementary Results, Extended Data Fig. 3).

Fig. 2. The nerve ring is comprised of a core circuit embedded in a variable background.

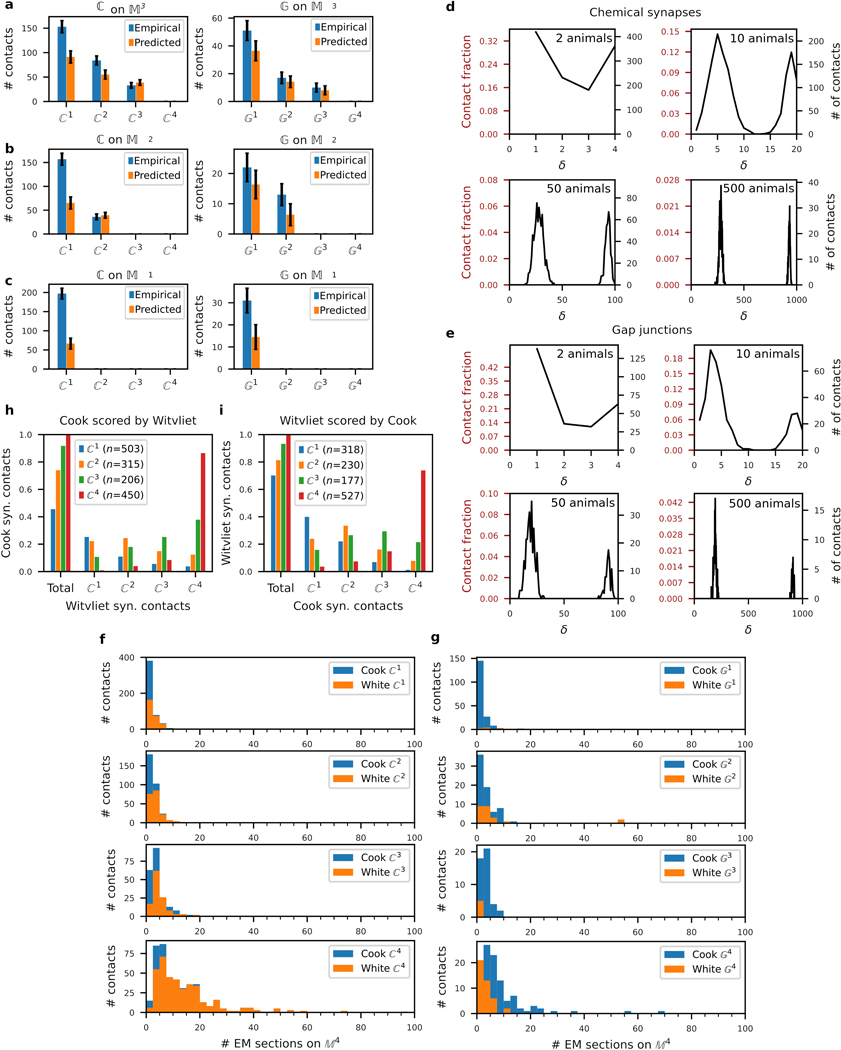
a, Empirical data and model fits for the reproducibility, across $\delta$ datasets, of membrane, ${\mathbb{M}}^{\delta }$ (top), synaptic, ${\mathbb{C}}^{\delta }$ (middle) and gap junction, ${\mathbb{G}}^{\delta }$ (bottom) contacts. Empirical and model frequency distributions normalized by the total empirical contact count, $n$ (e.g. for membrane contacts, $n={{\sum }_{\delta =1}^4\mathbb{M}}^{\delta }$). b, Surrogate data for 4, 20, 100, 1000 datasets (2, 10, 50 and 500 model animals). 4 datasets suffice to deduce that the distribution is bimodal. 20 datasets (10 animals) would suffice to completely distinguish between the core and variable subcircuits. No contact is expected to occur across 1000 datasets (500 animals). Target contacts comprise ~73% of each dataset.

How useful is the ${\mathbb{M}}^4$ reference in predicting conserved membrane contacts? Our model predicts that ~99% of the ${\mathbb{M}}^4$ contacts and 68% of the ${\mathbb{M}}^3$ contacts together constitute the vast majority (≳98%) of the core neuronal membrane adjacency matrix of the C. elegans nerve ring (Methods). Furthermore, above average membrane contacts (>1.77μm²) comprise more than 80% of ${\mathbb{M}}^4$ contacts (Extended Data Fig. 2h) and are more reproducible (with higher precision, $p=0.98$, and larger fraction, $f=0.77$, Extended Data Fig. 3a–b). We conclude that the ${\mathbb{M}}^4$ dataset offers an excellent candidate set of conserved membrane contacts. While highly reproducible, core membrane contacts are not easily distinguished from variable ones. Our model predicts that ~50% of membrane contacts are variable across animals. Using model-generated surrogate datasets (Methods), we estimate that 20 datasets (from 10 animals, with 2 datasets per bilateral reconstruction) would suffice to identify all core membrane contacts in the C. elegans nerve ring (Fig. 2b).

To model synaptic and gap-junctional precision, we re-fit the model to ${\mathbb{C}}^{\delta }$ and ${\mathbb{G}}^{\delta }$ (Methods). To control for synaptic variability due to differences in process placement, we restricted our analysis to ${\mathbb{M}}^4$ contacts (for a more general treatment, see Extended Data Fig. 4a–c). Even among reproducible membrane contacts, our model predicts that high precision (p > 0.90) combined with basal connectivity ($1-s~20-30\%$) are required to account for the reproducibility and variability of synaptic and gap junctional contacts across datasets (Fig. 2a; Supplementary Results, Extended Data Fig. 4d–e). For the bilateral worm, a synaptic precision of 93% implies a ~99% probability of a core synaptic contact occurring at least once per animal (on the left, right or both sides), and ≳97% chance to occur in at least 3 of 4 datasets (across 2 animals). Conversely, we predict that ~98% of ${\mathbb{C}}^4$ and ${\mathbb{G}}^4$ are good representatives of the core circuit (as well as >60% of ${\mathbb{C}}^3$ and ${\mathbb{G}}^3$), lending further confidence to the usefulness of the reference connectome. However, the placement of the most reproducible synapses along the process is not restricted to reproducible membrane contact sites (Extended Data Fig. 1g–h). Thus, location along the process cannot be used to distinguish core from variable synapses. Taken together, these results demonstrate that each dataset can be divided into a common, precisely targeted core circuit and a variable component, and that, given additional connectomes, it should be possible to distinguish between them (Extended Data Fig. 4d,e).

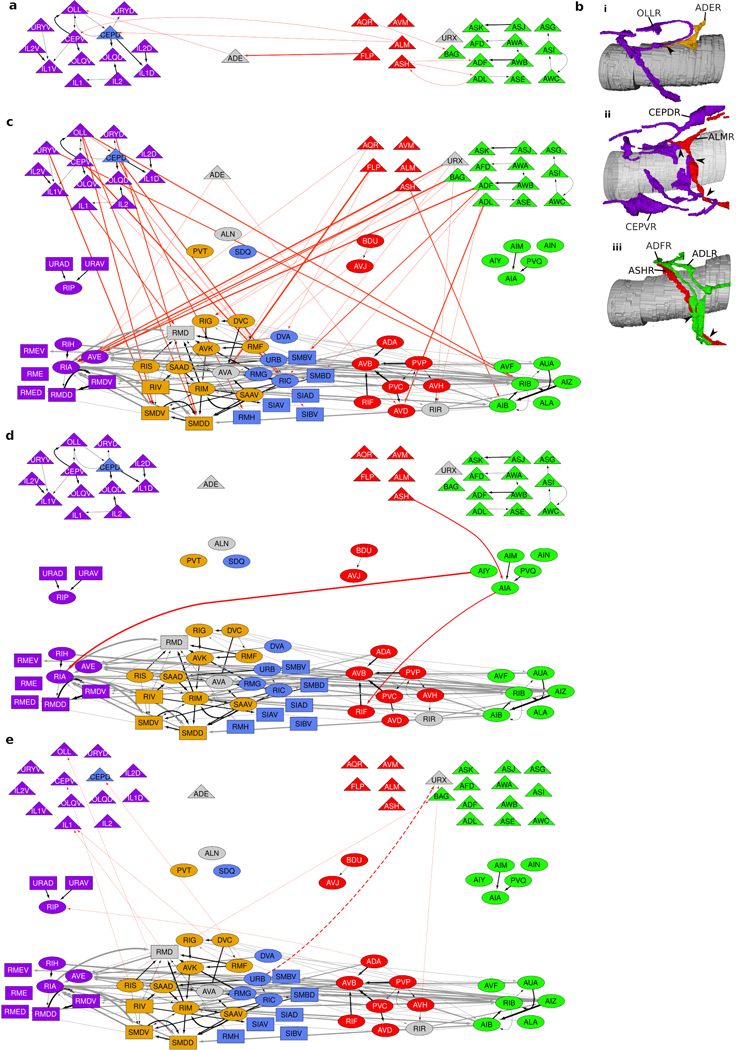
We next asked what principles of spatial organization support the reproducible, highly specified neuronal placement in the nerve ring. To address this question, we noted that the observed variability of membrane contacts suggests that no one animal is representative of the population at large and even core contacts likely vary across individuals (Extended Data Fig. 4h,i). Hypothesizing that conserved membrane contacts form the basis of the neuropil organization, we estimated the expected variability in our reference contacts across a population of animals by computing the variability in ${\mathbb{M}}^4$ contact areas across the four datasets at our disposal. We used the reference membrane contact distributions and their associated membrane contact area variability across the datasets to generate stochastic population models of core membrane contacts from the L4 and adult bilateral datasets and the ${\mathbb{M}}^4$ reference dataset (Methods, Extended Data Fig. 5). To group together neurites with high spatial affinity, we used a multi-level graph clustering algorithm²¹ on each individual in our population model (Methods). We find that 5 subgroups of neurons consistently emerge from the data whose processes are spatially ordered along the anterior-posterior axis of the nerve ring (Fig. 1a, Supplementary Information 4). We label these clusters anterior, lateral, sublateral, avoidance and taxis (Supplementary Results). Regionalization of processes in the nerve ring into the anterior circuit (associated with mechanosensation), the posterior, amphid neural circuit (associated with chemosensation and navigation) and lateral and sublateral neurons (associated primarily with head motor control) has previously been highlighted⁵. Our quantitative analysis is consistent with the above description but our focus on the core nanostructure reveals finer organization of the nerve ring that may not be apparent from the raw volumetric data (Methods, Extended Data Fig. 6).

We asked whether the cluster organization of the nerve ring is indicative of modularization of synaptic pathways^{3,13,18,19,22}. We find that most neurons have strong membrane and synaptic contacts within a single cluster, whereas others physically and synaptically contact neurons across multiple clusters (Fig. 3a-b, Extended Data Fig. 7). However, synaptically sparse lateral neurons and a number of neurons that closely link across the lateral and sublateral neighborhoods suggest that lateral and sublateral clusters may be merged for purposes of information processing analysis.

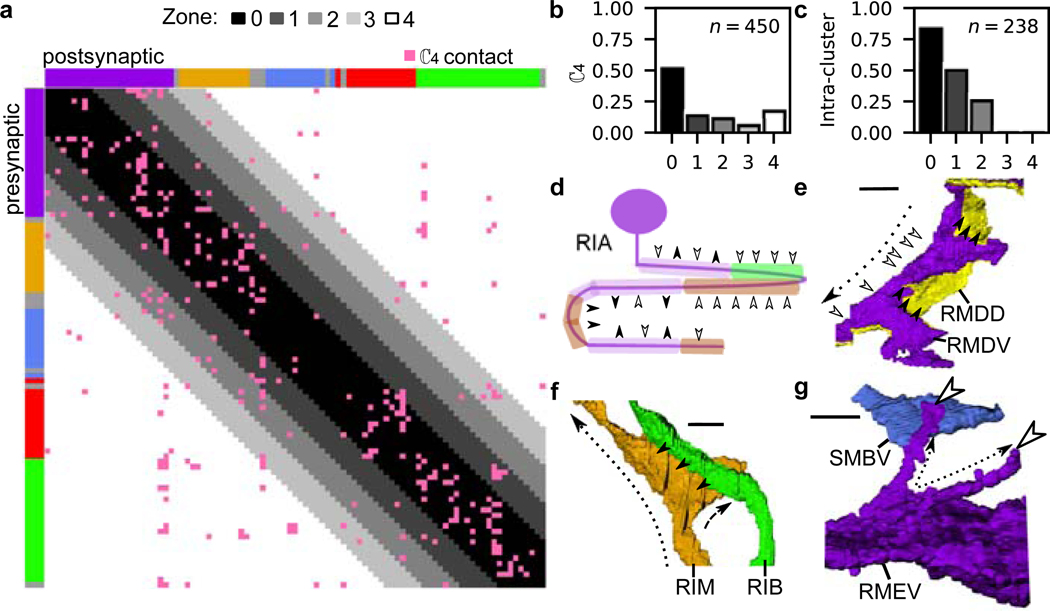
Fig. 3. Nano-, micro- and meso-scale process structure supports local and nonlocal connectivity.

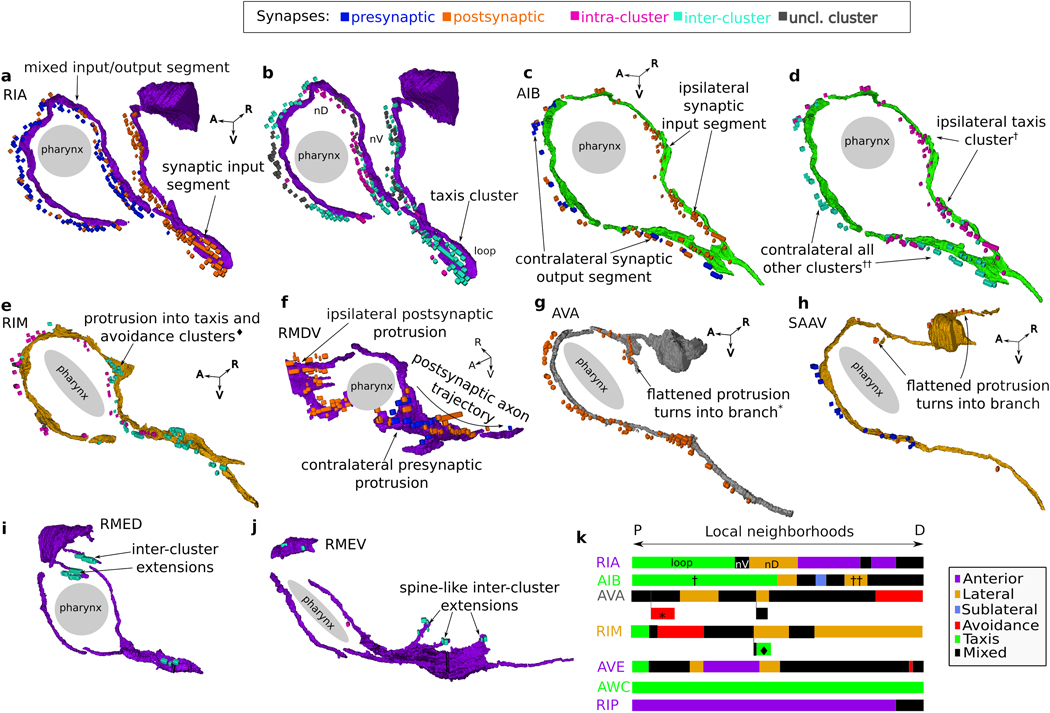
a, Matrix of ${\mathbb{C}}^4$ synaptic contacts (pink). Rows/Columns: pre-/post-synaptic cells. 4 zones around the main diagonal delineate growing neighborhoods around each cell with: Zone 0: average immediate neighborhood sizes in ${\mathbb{M}}^4$. Zones 1-3: Zone 0 plus 1, 2 and 3 standard deviations, respectively; Zone 4: remaining ${\mathbb{C}}^4$ contacts not in Zones 0-3. b, 75% of ${\mathbb{C}}^4$ synaptic contacts form locally within Zones 0-2. $n$: empirical count of ${\mathbb{C}}^4$ synaptic contacts. c, Fraction of intra-cluster and intra-zone ${\mathbb{C}}^4$ contacts (total, $n$). Many nonlocal (Zones 3–4) synaptic contacts occur with neurons that traverse different neighborhoods, exhibit flattened protrusions and/or exhibit synaptic compartmentalization. d, Synaptic compartmentalization: RIA synaptic polarity varies with changes in cluster assignment of neighboring cells. White/black arrows label synaptic polarity (inputs/outputs). e-g, Volumetric rendering of selected processes shows local structures that support localized, reproducible synapses. e, RMDV flattened protrusions support synapses onto RMDD, diversifying synaptic polarity. f, RIM protrusions support synapse onto RIB. g, Spine-like extensions (dashed black arrows) from RMEV cell body support synapses from SMBVL (not shown) and SMBVR. All examples observed bilaterally in L4 and adult (Extended Data Fig. 9, additional examples in Supplementary Information 4). Row/Column (a) and cell (d-g) colors denote cluster assignment except e, RMDD (anterior cluster, yellow). Scale bar: 1 μm.

Neurons that synapse across clusters are often characterized by processes that change neighborhood along their trajectories (Fig. 3c-e, Extended Data Fig. 8k). We identified 33 cell classes whose processes synapse across different regions of the nerve ring (Methods). These cell classes use two principal strategies: synapse compartmentalization (19/33 cell classes, Supplementary Information 4, Fig. 3e) and flattened protrusions (23/33 cell classes, Supplementary Information 4). We hypothesize that a subset of neurons synaptically link different neighborhoods of the nerve ring to support brain-wide coordinated activity²³. Consistent with our hypothesis, these specialized spatial features and the synapses they support are largely conserved across our 4 datasets. In summary, we find that the nerve ring obeys a consistent set of spatial organization principles across scales, including a macroscopic modular neighborhood organization which supports the mesoscopic organization along neurites, microscopic precision of membrane contacts and nanoscopic morphological features, that together support conserved synaptic wiring.

A C. elegans brain map

We integrate the knowledge gained to map the architecture of the C. elegans brain: The high-level spatial organization (Fig. 1a) – the ‘macro-connectome’² – suggests modular circuits, with distinct functional roles. Neuronal organization within and across spatial regions, comprising predominantly local and some cross-cutting neurons (Fig. 3a-c) that exhibit micro- and nanoscale structures (Fig. 3e-h), allows us to map the coordination across the nerve ring. Our reference connectome allows us to focus on reliable, likely conserved connectivity (Fig. 2). Finally, classification of neurons as sensory, interneuron and motoneuron allows us to trace sensorimotor pathways within and across these modules. By combining these features in the data, we set out to construct a brain map of the C. elegans nerve ring.

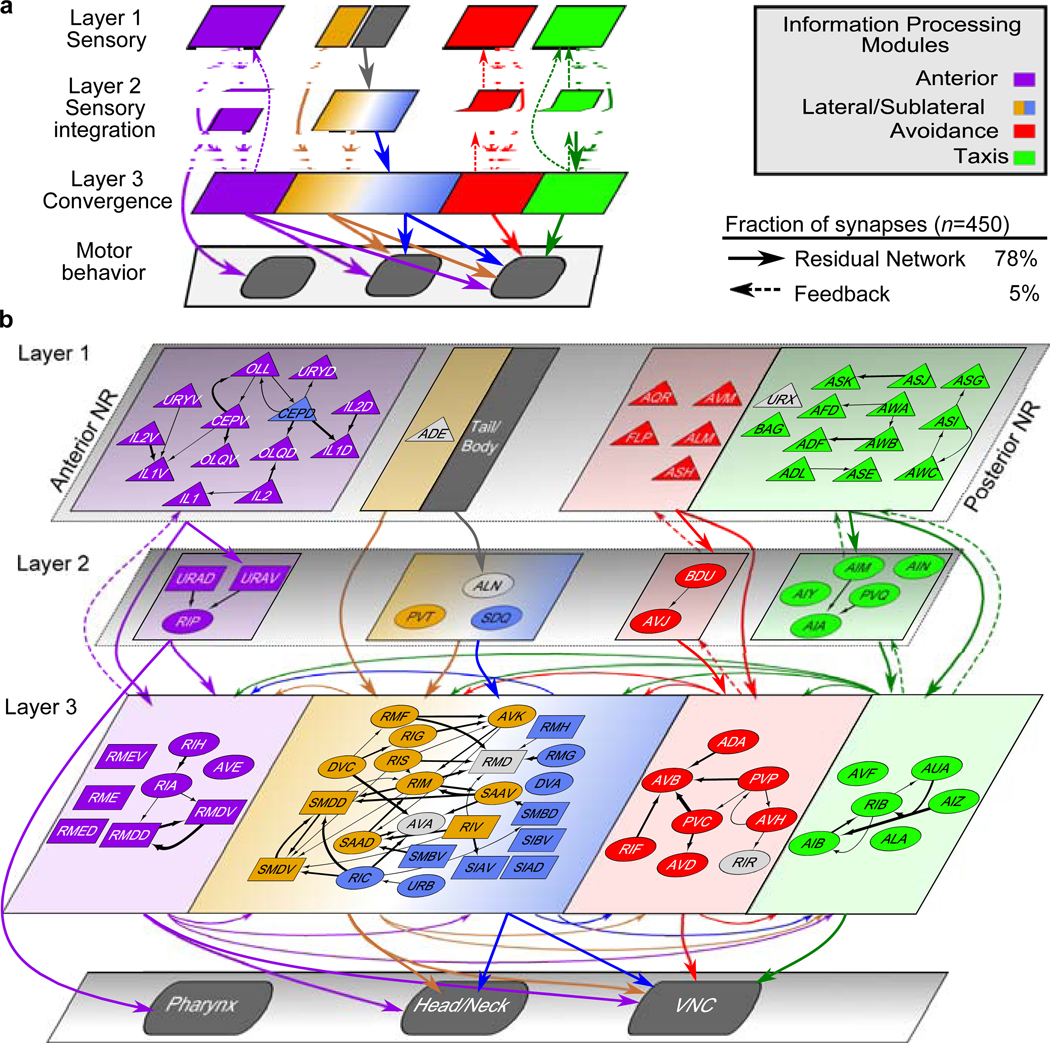
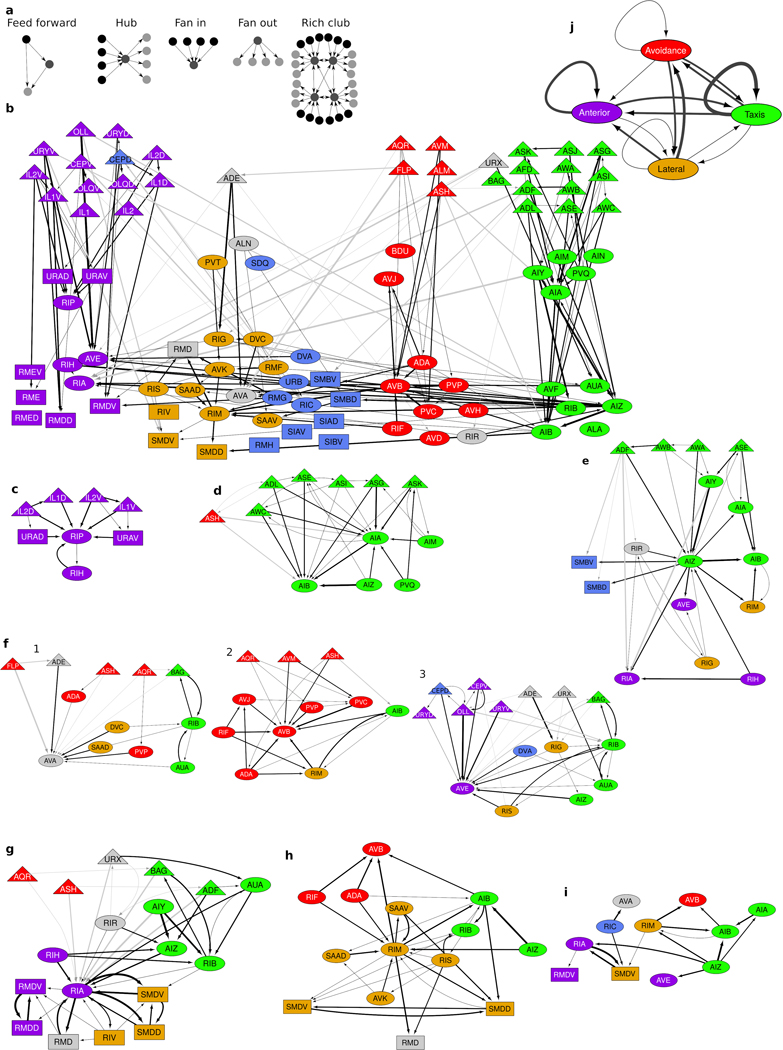
We posit a parsimonious 3-layer architecture with parallel information processing modules and assign every neuron of the nerve ring into a layer roughly corresponding to the 5 neuron clusters (Methods). To achieve overall feed-forward pathways, sensory neurons all occupy the first layer whereas spatially cross-cutting neurons dominate layer 3 (Methods, Fig. 4). Connectomic features, identified from network analysis of the C. elegans connectome (such as highly connected ‘hub’ neurons, high assortativity hubs known as ‘rich-club neurons’^24,25, network motifs^13,26 and the small-world organization¹³ as well as new features such as fan-in and fan-out motifs¹³ (characterized by higher in- or out-degrees, respectively, Extended Data Fig. 9a) can now be interpreted within the context of modular, brain-wide computation and information flow (Supplementary Results, Extended Data Fig. 9b–j). In particular, the feed-forward loop motif, previously identified in the C. elegans connectome^3,13,26, reappears in our map as the skeleton of the layered synaptic pathways within each module (>50% of all ${\mathbb{C}}^4$ contacts; Fig. 4a, Extended Data Fig. 10 shows additional contacts). This system-wide feed-forward connectivity is reminiscent of the layered connectivity of pyramidal neurons in the mammalian cortex and its biologically inspired analogue – Residual Networks (ResNets)²⁷. Such architectures have been conjectured to enhance the resilience of synaptic pathways and to support flexibility and plasticity²⁷.

Fig. 4. The C. elegans brain map.

a, A 3-layer, modular Residual Network architecture²⁷ (solid arrows and recurrent connectivity in layer 3) captures 78% of ${\mathbb{C}}^4$ synaptic contacts in the nerve ring: parallel feed-forward loop motifs converge onto layer 3, supporting functional sensorimotor pathways. Layer-3 interneurons and motoneurons (with ${\mathbb{C}}^4$ contacts across multiple zones, Fig. 3a) form a distributed circuit across all modules. Dashed arrows: intra-module feedback (5% of ${\mathbb{C}}^4$). $n$: empirical count of ${\mathbb{C}}^4$ synaptic contacts. b, All 80 bilateral neuron classes and 11 single neurons (AVL and RID lack ${\mathbb{C}}^4$ contacts) overlaid on the network architecture (a). Sensory neurons (triangles, layer 1); interneurons (ovals); motoneurons (rectangles). Except CEPD, module assignment matches cluster. CEPD (anterior module, sublateral cluster) shares the same process looping trajectories as and synapses more extensively with anterior sensory cells (Extended Data Fig. 10). Unclassified cells (gray) module placement based on process trajectory. Black arrows: intra-module synaptic contacts (thickness proportional to synapse size, aggregate number of EM sections where synapses were scored).

Examination of the C. elegans brain map (Fig. 4b) reveals a number of features. Layer 1 separates the modules (with a few notable and functional exceptions, Extended Data Fig. 10). The intra-module, intra-layer connectivity indicates that sensory neurons likely perform limited sensory computation in addition to sensory encoding of environmental cues, and allows the identification of sensory hub (high-degree) neurons (Supplementary Results). Layer 2 largely maintains the modular synaptic information flow. Convergence of sensory neurons onto this sparser layer reveals a fan-in architecture, supporting modular sensory integration (Supplementary Results, Extended Data Fig. 9c–d). Layer 3 contrasts with the above. Inputs are received from all three layers: Synapses from layers 1 and 2 comprise the core of each module, whereas layer-3 synapses interlink and couple the modules, forming a recurrent, highly distributed circuit, consistent with the dominance of spatially complex neurons in this layer and suggestive of brain-wide coordination roles (Extended Data Fig. 9e–j). Outputs from the nerve ring control the pharynx, head and neck muscles and the motor circuit of the ventral nerve cord (VNC). The taxis and avoidance modules support distinct information pathways (Fig. 4b) despite responding to overlapping sensory cues and both synapsing onto the VNC command interneurons. In contrast, the sublaterals highlight cross-connectivity within the nerve ring, with all but two neuron classes occupying layer 3. Pharyngeal output is mediated by layer-2 anterior neurons, indicating that the pharyngeal control is independent of the distributed layer-3 circuit. In contrast, head and neck muscles are controlled by layer-3 anterior, lateral and sublateral neurons and the VNC is controlled by all layer-3 modules, revealing the convergence of sensory pathways and associated modular subcircuits into a small number of highly coordinated motor programs.

Discussion

The C. elegans connectome has been available for over 30 years, and yet the delineation of functions within its main neuropil is still incomplete. By characterizing the spatial embedding of its connectome, we sought insight into the structures that could support a hierarchical, modular and nested architecture in the C. elegans brain. Previous analyses of the C. elegans connectome identified a common feed-forward loop motif among triplets of neurons^3,26. Our brain map recasts this local motif as an architectural motif, reminiscent of layered cortical architectures²⁸ and their artificial analogue, Residual Networks²⁷. Such a ‘connectionist’ description of a biological brain provides a promising methodology for identifying parallel and distributed circuits.

While there are no physical boundaries within the nerve ring, our analysis points to spatial clustering of neural processes into five neighborhoods. The parallel pathways in our brain map largely fall into this modular neighborhood organization, linking spatial and functional organization. The spatial organization may also reflect developmental roles of nerve ring pioneers²⁹ and constraints on synaptic and neuromuscular connectivity for motor coordination and control functions. Within the Residual-Network template are intra-layer local circuits, whose neurons by-and-large lack structural or functional compartmentalization. Thus, consistent with the neuron doctrine, within local subcircuits, neurons represent the basic unit of computation. However, the modular architecture converges within the final layer to achieve brain-wide coordination of behavior. In this distributed circuit, the nanoconnectome rules: specialized subcellular structures give rise to compartmentalized dynamics and interlink distant regions of the C. elegans brain. Similar subcellular structures performing analogous functions, found in thalamic local interneurons³⁰, reveal a richness of subcellular computation. Thus, brain-wide coordination may be achieved by designated processes that interface between or thread across multiple subcircuits to underpin sensory convergence and sensorimotor transformations. the C. elegans brain map and its nested architecture might suggest a much closer analogy between the C. elegans neuropil and the coordination between the nano- and macro-connectomes of other invertebrates and even vertebrates³¹.

The concept of a reference connectome was key to our brain map and the modeling framework we used to establish this reference can easily be extended to accommodate future connectomes. In vertebrates, nanoscale organization underpinning individual synapses is variable, supporting individual wiring, plasticity and adaptability. In C. elegans, the proportion of conserved synapses was unknown. We found that the connectome consists of a core, conserved circuit that is embedded in a significant variable background. While pinning down the extent of the variable circuit is challenging due to the technical limitations of synaptic scoring and will therefore require multiple further connectomes, it is noteworthy that conserved synapses, like most variable ones, are constrained by the same contactome. Thus, if the core circuit represents the baseline functionality of the animal, the variable component could support redundancy, individuality³² and plasticity⁶.

The large number of cell classes, so densely packed in the nerve ring, presents a challenge to physically achieving stereotyped connectivity. Our finding of finely orchestrated organization across scales imposes spatial constraints on neurite and synaptic placement, thus restricting each neuron’s connectivity problem to a local neighborhood. This scalable solution is robust across a large population and naturally generalizes to much larger nervous systems. Viewed differently, the spatial organization reduces the required capacity for cell-cell molecular recognition machinery, while increasing the complexity of mechanisms producing the cell’s morphology and relative positioning in the tissue. But how is the neighborhood organization developmentally orchestrated? Previous models of neuropil development have proposed that pioneer neurites guide follower neurons³³. While such models could be generalized to identify the pioneers of each neihborhood³⁴, the highly reproducible pattern of membrane contacts indicates a more elaborate developmental mechanism. In complementary models, some guidance molecules would coordinate the relative neighborhood placement and others – the placement of neurites³³. Identifying key guidance molecules in early nerve ring formation may help to address such predictions^29,33. Whatever the developmental mechanisms may be, the brain map of C. elegans requires that these mechanisms too are nested and coordinated across scales to guide and support the modular, scalable and flexible neural architecture that produces the mind and behavior of the nematode C. elegans.

Methods

Anatomical and neuron-class nomenclature

The anatomy of the C. elegans nerve ring, associated ganglia and the delineation of 6 nerve bundles entering the nerve ring, was described in detail by Ware et al.³⁵. Early observations, e.g. the distinction between papillary and amphid sensory specializations and their postulated mechano- and chemo-sensory roles have been validated since. Individual cell classes were identified and named by White et al.⁵. Each neuron name consists of either two or three uppercase letters indicating class and in some cases a number indicating the neuron number within one class (e.g. IL1, IL2). Bilaterally symmetric neurons (cell pairs) have a three letter/number class name followed by L (left) or R (right). Radially symmetrical neurons (with either 4 or 6 members) have a three-letter name followed by D (dorsal), or V (ventral), L (left) or R (right) (e.g. SIADL, SIADR, SIAVL, SIAVR and RMDL, RMDR, RMDDL, RMDDR, RMDVL, RMDVR). Unless otherwise noted, we use the term class synonymously with bilateral cell pair for radially symmetric cell classes (e.g. SIAV and SIAD are treated as separate classes). Additionally, 17 nerve ring neurons constitute the only members of their class (ALA, ALM, ALN, AQR, AVL, AVM, DVA, DVC, PVT, PVR, RID, RIH, RIR, RIS, RMED, RMEV and SABD). A small number of VNC motoneurons also enter the nerve ring. These VNC motoneurons names consists of two uppercase letters indicating muscle innervations (V: ventral, D: dorsal) and class (A-C) and a number indicating the neuron within one class (counted from anterior to posterior). Neurons are designated as sensory neurons, interneurons or motoneurons following their primary descriptions in WormAtlas³⁶ (excluding proprioception from the sensory designation). We note, however, that in C. elegans, these designations are not exclusive. Our use of the term neighborhood to describe processes that run closely together in the nerve ring follows White et al.^5,18. We use the stronger term immediate neighborhood to designate neural processes that make physical contact.

Electron micrograph (EM) preparation

The two legacy electron micrographs (EM) series used in this study were constructed in the MRC Laboratory of Molecular Biology (Cambridge, UK) during the 1970s. Both series are of hermaphrodite worms of the wild-type N2 (Bristol) strain. Worms were fixed in 1% osmium tetroxide in 0.1 M sodium phosphate, pH 7.5 for 1 h at 20°C before embedding, sectioning and post-staining⁵. This method was previously determined to best bring out cell membranes and synaptic structures at the expense of features within the cytoplasm. The EM series are transverse to the longitudinal axis of the worm; estimated section thickness is 70–90 nm, judged by silver color³⁷. The original 55 cm × 60 cm montaged prints covering the nerve ring commissure and 30 cm × 40 cm covering the posterior lobe of the nerve ring have since been digitized, archived in the Hall Laboratory and available at www.wormimage.org.

The two series reconstructed for this study include the synaptically dense nerve ring neuropil and ventral ganglia regions of the anterior nervous system. One series is from a larval stage 4 (L4) worm and the other series is from an adult (estimated three days from adulthood³), referred to as JSH and N2U, respectively. The JSH series extends from just anterior of the nerve ring to the excretory pore. The N2U series is substantially longer, extending from just anterior of the nerve ring to the vulva. We only considered the section of the N2U series that physically corresponds to the JSH series. This resulted in 302 sections in the N2U series compared to 410 sections in the JSH series. In N2U, starting at the nerve ring posterior lobe, only every other EM section was imaged (N2U EM sections 183–302). Additionally, it is speculated that the JSH images may have slightly smaller section thickness. To correct for this when making comparisons between the L4 and the adult, data from this region in N2U was scaled by a factor of 2.

EM segmentation

EMs were manually segmented using TrakEM2 software³⁸. The software provides GUI tools to facilitate the segmentation of cells across an EM stack. Within the EM series, we segmented all neuronal cell bodies and processes that extend into the nerve ring (Supplementary Videos 1 and 2). Cell bodies were then removed from our membrane contact analysis, because their large sizes skew the cell contact distribution. We also segmented the portion of the pharynx in the nerve ring, which serves as both a visual reference and spatial reference for the cylindrical coordinates. We did not segment dendrites of sensory neurons, because dendrites have very few synapses and therefore were not of interest for our analysis. We also did not reconstruct the sublateral cells SABVL and SABVR whose anterior processes leave the ventral nerve cord via the amphid commissure⁵. Measurements of the membrane contact between neurons were taken directly from the TrakEM2 XML data. We estimated each pixel to be ~5 nm², based on size measurements of cell bodies which are estimated to be 2–3 μm wide. In all, we segmented 181 and 185 cells that innervate the L4 and adult nerve rings, respectively (the “complete dataset”).

Extracting adjacency data

We developed custom software (parsetrakem2, https://github.com/cabrittin/parsetrakem2) to quantify the pairwise membrane contacts between TrakEM2 segmented processes. In each EM, TrakEM2 stores each segmented cell as a set of boundary points. For each segmented cell, $i$, our software defines a search radius that is proportional to the diameter of the segmented cell $i$. Any immediately neighboring segmented cell, $j$, that has a boundary point within the search radius is checked for adjacency to $i$. We define adjacency for the pair ($i$, $j$) as the number of boundary points of $j$ that are less than 10 pixels (~50 nm) from the boundary points of $i$. We found that a radius of 10 pixels was sufficiently large to ensure that adjacencies were not missed. Any cell pairs erroneously identified as adjacent could easily be screened out in downstream analysis based on membrane contact area.

To check the accuracy of the algorithm, for two EM sections, we compared the contacts scored by our software to those obtained from manual scoring of membrane contacts (Supplementary Table 2). For manual scoring of membrane contacts, we used the connector feature in TrakEM2 to generate a connectivity graph of adjacent cells. An EM section with $n$ cells has $n(n-1)/2$ possible cell pairings that were then classified as either adjacent (if the cells touch) or non-adjacent (if the cells do not touch). We assume the manually scored contacts to be the ‘ground truth’, which we use to define true positives $(TP)$, false positives $(FP)$, true negatives $(TN)$ and false negatives $(FN)$ in our automated classification. Sensitivity, defined as $TP/(TP+FN)$, measures how likely two physically touching cells are classified by our software as adjacent. Specificity, defined as $TN/(TN+FP)$, measures how likely two separate cells are classified by our software as non-adjacent. Aggregating results from the two manually scored EM sections (JSH001 and JSH040), the sensitivity and specificity of our classification algorithm are 0.974 and 1.00, respectively (Supplementary Table 2). In other words, the algorithm will miss ~2.5% of adjacent cell pairs within an EM section and a negligible number (<0.05%) of separate cell pairs will be incorrectly classified as adjacent. We assessed the missed adjacent cells in our test set and found that these adjacencies were small (tens of nanometers) and resulted primarily from poor segmentation (the manual cell segmentation did not extend completely to the cell membrane). Furthermore, all 11 cell pairs incorrectly classified as non-adjacent in the two test EM sections were correctly classified as adjacent in subsequent EM sections. As adjacent cell pairs missed in one EM section are likely to be correctly classified as adjacent in subsequent EM sections, and because most of our analyses aggregate adjacencies across EM sections, any missed adjacencies within a single EM section is likely to have negligible impact on our results.

As an additional test, we compared the adjacent cells extracted by our algorithm to the adjacent cells previously reported for a small subset of neurons based on a sparse analysis of physical adjacency in the L4¹⁸. White et al. determined the neighborhoods of cells AIAR, AIBR and AQR in the L4 (JSH) EM series. Our algorithm was able to find all but 1 adjacent cell pair in the White et al.¹⁸ neighborhoods (Supplementary Information 5). Closer inspection revealed that the cell pair does not make physical contact and was thus mis-scored by White et al. as adjacent. Furthermore, we found an additional 69 adjacent cell pairs not included in the White et al. neighborhoods (Supplementary Information 5). Therefore, our volumetric dataset is more extensive than those previously reported.

EM annotation for synaptic connectivity

We used our previously published connectivity data for chemical synapses and gap junctions and refer the reader to Cook et al.³ for details on how synapses were annotated. Briefly, we used custom software³⁹ to aid manual annotation of chemical synapses and gap junctions. For chemical synapses, presynaptic cells are identified by the presence of a presynaptic density while postsynaptic cells are identified as the cells directly apposed to the presynaptic density. Most synapses are polyadic – multiple postsynaptic partners are assigned to a single presynaptic cell. Gap junctions are recognized as a straightened or slightly curving region of apposed membranes with increased staining and a uniform small gap. For the purpose of the current study, we restrict the synaptic and gap junctional dataset to those in our volumetric reconstruction (i.e. those scored in EMs that were segmented for this study). In all, the numbers of synapses and gap junctions scored is larger than in the original connectome⁵, with a notable increase in synapses that were scored in only 1 EM section. Within our reference ${\mathbb{C}}^{\delta }$ dataset (see Generating reference graphs below), Cook et al. (2019)³ scored an additional 489 synaptic contacts to the White et al. (1986)⁵ connectome, of which 249 (49%) synaptic contacts only occur in 1 EM section. To control for the possibility of false positives in this annotation, more restricted datasets were constructed for validation (see Validation against test datasets, below).

Generating reference graphs

In order to control for variations in connectivity, we found it useful to map the data to a novel data structure, which we call a reference graph. Reference graphs classify contacts (defined as the aggregate pairwise connections over all EM sections within a dataset) based on their degree of reproducibility across datasets. We took advantage of the bilateral symmetry of the worm to effectively double our sample size. We therefore generated 4 datasets (adult left/right and L4 left/right) from the two reconstructed nerve rings. For a sample size of $n=4$, simply averaging across datasets is not a useful way to build a reference model of the data. Instead, we segregate the contacts into 4 separate categories based on their reproducibility. To this end, we removed from our analysis a number of neurons that exhibit appreciable differences in synaptic connectivity or process morphology laterally (PLN, PVN, HSN), between the L4 and adult (HSN, PVR, SABD), or those that make minimal membrane contact in the nerve ring (in VB, VC and VD classes), leaving 173 cells in 93 cell classes (the “restricted dataset”, Supplementary Information 3). The restricted dataset excludes HSNR, PLNL, PLNR, PVNL, PVR, SABD, VB01 and VD01 neurons – in both L4 and adult – and HSNL, PVNR, VB02 and VC01 – in the adult.

We generate reference graphs as follows. We first threshold membrane contacts by eliminating the smallest 35% of contacts in each of the adult and L4 datasets (Extended Data Fig. 2). From these, we then generate 4 datasets of membrane contacts: adult left, adult right, L4 left and L4 right. Each dataset was converted to a graph, where vertices are neurons and edges denote membrane contacts between a pair of adjacent neurons. The reference graphs ${\mathbb{M}}^1$, ${\mathbb{M}}^2$, ${\mathbb{M}}^3$ and ${\mathbb{M}}^4$ represent the set of membrane contacts found in $\delta =1,2,3$ and all 4 datasets (see explicit calculation of reproducibility degree, $\delta$, below). Reference graphs for chemical synapses $\left(\mathbb{C}\right)$ and gap junctions $(\mathbb{G})$ were generated similarly, but with slightly different edge thresholding. Whereas for $\mathbb{M}$, we thresholded based on the magnitude of membrane contact, for $\mathbb{C}$ and $\mathbb{G}$ we only included edges that correspond to ${\mathbb{M}}^4$ contacts (or from ${\mathbb{M}}^3$ or ${\mathbb{M}}^2$ where explicitly mentioned). By only including edges in ${\mathbb{M}}^4$, we effectively eliminate differences in synaptic connectivity due to differences in process placement. Each edge in the membrane reference graph $\left({\mathbb{M}}^{\delta }\right)$ has an associated normalized mean contact area (across the 4 datasets). To control for slight differences in cell sizes between the larva and adult series, we normalize all membrane contact areas within each of the 4 datasets by the sum of all membrane contacts within that dataset. The normalized membrane contact area between neurons ($i$, $j$) in ${\mathbb{M}}^{\delta }$ is then the mean normalized contact area across the $\delta$ datasets in which the contact is present.

For bilateral cell classes, let indices, e.g. $i$ and $j$, each denote some side of an animal (left or right) and let $\overline{l}$, $\overline{\gamma }$, etc. denote the respective contralateral side. For a contact $\left\{{\text{X}}_i^1,{\text{Y}}_j^1\right\}$ made between cell ${\text{X}}_i$ in class $\text{X}$ to ${\text{Y}}_j$ in class $\text{Y}$ in animal 1, $\delta$ is defined as the number of contacts among $\left(\left\{{\text{X}}_i^1,{\text{Y}}_j^1\right\},\left\{{\text{X}}_{\overline{l}}^1,{\text{Y}}_{\overline{J}}^1\right\},\left\{{\text{X}}_i^2,{\text{Y}}_j^2\right\},\left\{{\text{X}}_{\overline{l}}^2,{\text{Y}}_{\overline{J}}^2\right\}\right)$ where the superscript 2 labels the other animal. For intra-class connections, $\delta$ is the number of contacts among $\left(\left\{{\text{X}}_i^1,{\text{X}}_{\overline{l}}^1\right\},\left\{{\text{X}}_{\overline{l}}^1,{\text{X}}_i^1\right\},\left\{{\text{X}}_i^2,{\text{X}}_{\overline{l}}^2\right\},\left\{{\text{X}}_{\overline{l}}^2{\text{X}}_i^2\right\}\right)$, and for single cell classes, e.g. DVA connecting to some class Y (or vice versa), $\delta$ is counted among $\left(\left\{{\text{DVA}}^1,{\text{Y}}_j^1\right\},\left\{{\text{DVA}}^1,{\text{Y}}_{\overline{J}}^1\right\},\left\{{\text{DVA}}^2,{\text{Y}}_j^2\right\},\left\{{\text{DVA}}^2,{\text{Y}}_{\overline{J}}^2\right\}\right)$ (or vice versa).

Population spatial models

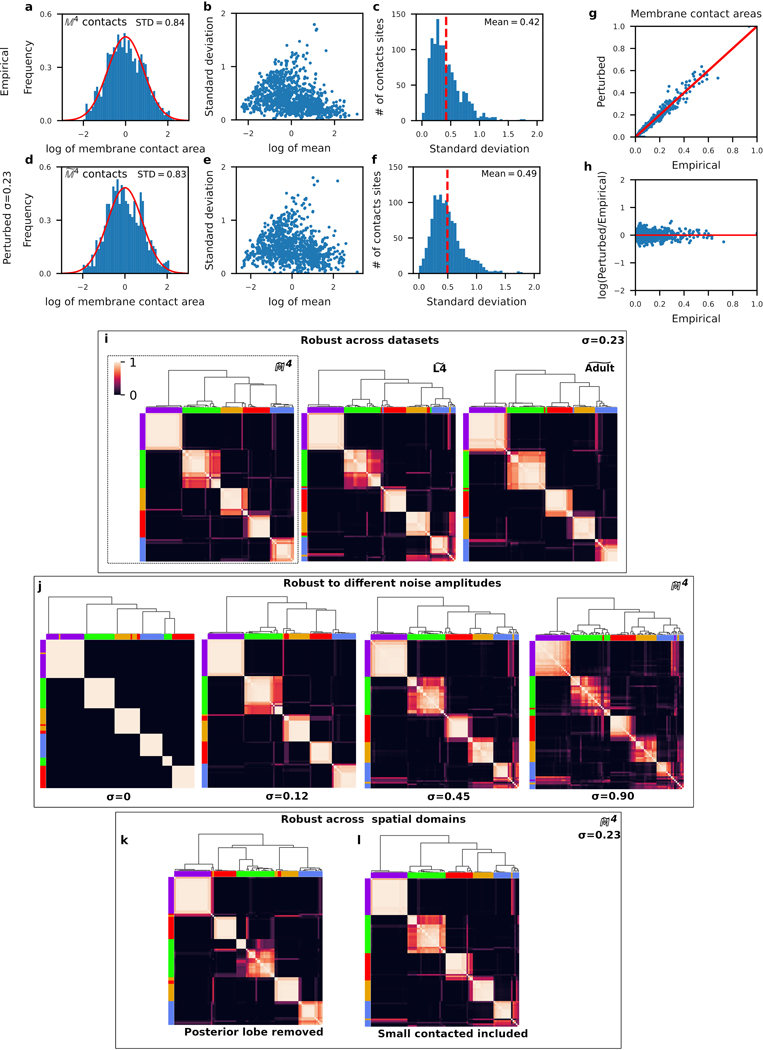
The observed variability in membrane contacts, both bilateral and across the two animals, indicates that it is unlikely that any one animal is representative of the population at large. We generated a population model of all membrane contacts, by stochastically perturbing the area associated with each membrane contact, such that the overall distribution of mean membrane contact areas is preserved and that the variability in membrane contact areas across datasets is also preserved. To establish the baseline variability across the 4 datasets, we considered the log-normalized distribution of ${\mathbb{M}}^4$ membrane contact areas (Extended Data Fig. 6a). For each contact in ${\mathbb{M}}^4$, we computed the normalized mean membrane contact area (see Generating reference graphs) and the standard deviation of membrane contact areas across the 4 datasets. We observed no correlation between the normalized mean membrane contact area and standard deviation (Extended Data Fig. 5b), indicating that the variability in membrane contact areas does not depend strongly on membrane contact area (similar to immediate neighborhood sizes in Extended Data Fig. 1a). Therefore, we estimated the variability in the membrane contact area by the mean variability among ${\mathbb{M}}^4$ membrane contacts (Extended Data Fig. 5c).

To perturb each dataset, we applied multiplicative white noise to each membrane contact area, which we derived from the distribution of membrane contact areas, as follows. A log-transformed (un-skewed) and standardized (mean 0 and variance 1) membrane contact area $y$ is computed from membrane contact area $x$ by

$$y=\frac{log(x)-\widehat{\text{μ}}}{\widehat{\text{ϕ}}},$$ (1)

where $\widehat{\text{μ}}$ and $\widehat{\text{ϕ}}$ denote the geometric mean and standard deviations of the membrane contact areas (i.e. the arithmetic mean taken in the log domain), across the 4 datasets, per cell pair. Rearranging terms gives

$$x=e^{\widehat{\text{μ}}}{e}^{y\widehat{\text{Φ}}}.$$ (2)

To perturb membrane contact areas $\left(x\to x^{\prime }\right)$, we add white noise $\epsilon$ in the log domain, i.e.,

$$x^{\prime }=e^{\widehat{\text{μ}}}{e}^{(y+\text{ε})\widehat{\text{Φ}}}=e^{\widehat{\text{μ}}}{e}^{y\widehat{\text{Φ}}}{e}^{\text{ε}\widehat{\text{Φ}}}=x{e}^{\text{ε}\widehat{\text{Φ}}}.$$ (3)

Hence, we scale each membrane contact by $e^{\text{ε}\widehat{\text{ϕ}}}$, where $\widehat{\text{ϕ}}$ is determined by the membrane contact area distribution of the dataset and the distribution $\epsilon$ is drawn randomly from a normal distribution with mean 0 and standard deviation $\sigma$.

The standard deviation, $\sigma$, of the $\epsilon$ distribution sets the amplitude of the perturbation. We determined the appropriate noise amplitude by comparing the distributions of perturbed and empirical datasets. We found that a noise amplitude of $\sigma =0.23$ – roughly half of the mean standard deviation of membrane contact areas (Extended Data Fig. 5c) – yields perturbed membrane contact area distributions (Extended Data Fig. 5d–f) that are qualitatively similar to the empirical dataset (Extended Data Fig. 5a–c). Moreover, the perturbed membrane contact areas scale linearly with membrane contact area (Extended Data Fig. 5g) and variability as a fraction of membrane contact area is uniform (Extended Data Fig. 5h).

Perturbed populations are denoted $\widetilde{{\mathbb{M}}^{𝟜}}$, $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$. For $\widetilde{{\mathbb{M}}^4}$, we perturb contacts conserved across the 4 datasets (L4 left, L4 right, adult left, adult right). For $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$, we perturb bilaterally conserved contacts in the L4 and adult, respectively. Each population consists of 1000 perturbed datasets.

Spatial modularity analysis

To identify groups of neurites with high spatial affinity in the nerve ring, we performed a graph modularity analysis of the membrane contact areas. Since spatial adjacencies between neurons consist of both conserved and variable membrane contacts, we applied our clustering analysis to $\widetilde{{\mathbb{M}}^{𝟜}}$, $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$ population models (unless otherwise stated). For clustering purposes, we reduced contralateral left/right homologue vertices to a single vertex class. For example, vertices ASHL and ASHR were reduced to the single vertex, ASH. The algorithm was then applied to each individual in the population.

The multilevel community detection algorithm yields a number of clusters of neuron classes whose neurites exhibit high spatial affinity. Topological clustering methods such as modularity optimization^21,40 are well suited for characterizing the organization of a complex system from pairwise undirected linked relationships^40,41, as is the case for characterizing spatial organization from membrane contacts between neural processes. In particular, algorithms of this class are appropriate when the organization sought is static^40,41. Other, random-walk based algorithms^34,41 assume or impose a flow on the network and are often ill-suited for characterizing spatial (i.e. static) organization, as they can introduce bias in the clustering or miss static features in the organization of the system⁴¹. We applied the Louvain method, a multilevel community detection algorithm using the igraph software package⁴². This topological clustering algorithm is a bottom-up heuristic method based on modularity optimization²¹. Initially, every vertex is placed in a separate community. Vertices are then iteratively moved between communities in a way that maximizes the vertex’s local contribution to the overall modularity score (the ratio of the number of intra- to inter-community edges). When no vertex movement increases the modularity score, communities are shrunk to a single vertex and the process is repeated.

Cluster assignment and validation

The graph clustering algorithm (see above) was applied to each individual in each population model. For each population, we generated a cluster frequency matrix that counts the number of times each pair of neurons is clustered together. We then sorted the rows and columns of the frequency matrix so as to minimize the variance along the main diagonal of the matrix (Extended Data Fig. 5i). Sorting was achieved using a hierarchical matrix clustering algorithm²¹. The resulting dendrogram assigns neurons to a cluster. We obtained a set of 5 largely overlapping clusters for each of the $\widetilde{{\mathbb{M}}^4}$, $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$ population models (Extended Data Fig. 5i). Cell classes whose cluster assignment agreed across the 3 population models were assigned to the consensus cluster. Seven neuron pairs (ADE, ALN, AVA, RID, RIR, RMD and URX) were classified differently across the different population models, and were designated ‘unclassified’ accordingly. To evaluate the robustness of the clusters to empirical variability between the L4 and adult series, we compared clusters obtained from population models of $\widetilde{{\mathbb{M}}^4}$, $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$ (see Population spatial model, Fig. 1b,c, Extended Data Fig. 5i and 6b).

We performed four sets of validation experiments using our population models to confirm the robustness of our neuron clusters. (1) As discussed above, we compared cluster assignments across $\widetilde{{\mathbb{M}}^4}$, $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$ (Fig. 1b,c, Extended Data Fig. 5i). (2) We generated cluster assignments for $\widetilde{{\mathbb{M}}^4}$ populations that were perturbed with different noise amplitudes ($\sigma =0,0.12,0.23,0.45,0.9$; see Population spatial models, Extended Data Fig. 5j). (3) We generated a new $\widetilde{{\mathbb{M}}^4}(\sigma =0.23)$ population from membrane contacts in a more restricted volume recently used in Moyle et al. (2020)³⁴ which consists of the anterior ~60% of our nerve ring neuropil volume (Extended Data Fig. 5k). (4) We generated a new $\widetilde{{\mathbb{M}}^4}(\sigma =0.23)$ population that also includes the smallest 35% membrane contact areas (Extended Data Fig. 5l; recall smallest contacts were removed from our analysis, Extended Data Fig. 2). All of our validation experiments resulted in largely similar cluster assignments (Supplementary Information 4). A handful of neuron classes were assigned to different clusters in different population models, but the gross structure of the 5 main neuron clusters, as defined by the cluster assignments of a large majority of the neurons, was consistent across the populations. Thus, our cluster assignments are robust across model population datasets, the L4 and adult, a wide range of noise amplitudes, well above the observed inter-animal variability, and different spatial domains.

Next, we validated our population model by repeating the clustering analysis on the unperturbed ${\mathbb{M}}^4$ reference dataset as well as on the unperturbed adult and L4 bilateral datasets (Extended Data Fig. 5k, $\sigma =0$ and Extended Data Fig. 6b). We find small differences between these datasets, but those are not robust to small perturbation in our population models ($\sigma =0.12$, i.e. below our estimated level of expected biological variability in core contacts). We also validate our core assumption that the conserved structure of the nerve ring requires analysis of the reproducible membrane contacts by comparing clusters from unperturbed ${\mathbb{M}}^1-{\mathbb{M}}^4$ datasets. We find that whereas the reproducible membrane contact datasets consistently give rise to a small number of clusters, with largely similar composition, ${\mathbb{M}}^1-{\mathbb{M}}^3$ membrane contacts fail to reproduce these results (Extended Data Fig. 6a), suggesting that variable membrane contacts may be masking the core, conserved spatial organization of the nerve ring neuropil.

Mesoscale analysis of synaptic connectivity

Given that the organization of the neuropil is modular, with most neurons spatially clustering within local neighborhoods and others spatially interconnecting different neighborhoods, we wanted to determine if synapses form local subcircuits, or to what extent synaptic circuits also span different neighborhoods of the nerve ring. To assess the spatial organization of synaptic circuits, we considered the distribution of conserved ${\mathbb{C}}^4$ synaptic contacts (Fig. 3a). Using the ${\mathbb{M}}^4$ dataset, we calculated the mean ($\overline{N}=17$ cells) and standard deviation ($\text{Δ}N=8$ cells) of immediate neighborhood sizes (Anatomical and neuron-class nomenclature). We order the cells as in Fig. 1b so as to maximize the amount of physical $\left({\mathbb{M}}^4\right)$ contact along the diagonal of the matrix.

We define 5 zones based on the size distribution of immediate neighborhoods. Each zone refers to regions between two diagonals above and below the main diagonal of the ${\mathbb{M}}^4$ matrix. The inner zone (labeled 0) consists of neighborhoods of size $\overline{N}$ for each cell around the main diagonal. The next zone (1) extends from the edges of the inner zone to diagonals $\text{Δ}N$ further away from the main diagonal, and zones 2–3 similarly extend by $\text{Δ}N$. The outermost zone (4) extends from the previous zone (3) to encompass cells in the remainder of the matrix. (Formally, zones are defined by their inner and outer diagonals, with the inner diagonal defined by $\overline{N}/2+(k-1)\text{Δ}N$ from the main diagonal for zones 1 to 4 and the outer diagonals defined by $\overline{N}/2+k\text{Δ}N$ from the main diagonal for zones 0 to 3.) We counted the number of ${\mathbb{C}}^4$ contacts in each Zone (Fig. 3b). Finally, we counted ${\mathbb{C}}^4$ contacts between pre- and postsynaptic neurons that have been assigned to the same cluster (Fig. 3c). For this purpose, synapses between two unclassified neurons are not considered intra-cluster.

Contact localization analysis

While some membrane contacts appear to be reproducible (our ${\mathbb{M}}^4$ reference dataset), contacts are aggregate measures (along the entire process). To assess the reproducibility in the location of individual instances of membrane adjacencies along a neurite, we assigned each EM in each process a discrete coordinate, $\widehat{z}$, from the anterior $(\widehat{z}=0)$ to the posterior $(\widehat{z}=1)$ of the process. This allows us to compare relative locations of a contact across the four datasets (L4 left/right, adult left/right). Different discretizations of $\widehat{z}$ (0.7 μm, 1.4 μm, 3.6 μm) define different resolution for the reproducibility of contacts along the process. For each ${\mathbb{M}}^4$ contact, we define the spatial reproducibility count as the number of datasets where the contact was observed at a given position, $\widehat{z}$. We further define the maximum spatial reproducibility count, $\text{max}{(\delta )}_{\widehat{z}}$, as the highest reproducibility count across all locations, $\widehat{z}$, per cell pair (i.e. given an ${\mathbb{M}}^4$ contact exists between two immediate neighbors, the highest reproducibility count of instances of membrane adjacencies between the two cells). To assess synaptic localization, we similarly measured the spatial reproducibility counts (and their maxima) for all ${\mathbb{C}}^4$ contacts. See also Supplementary Results.

Synapse compartmentalization and subcellular structures

Identification of synaptic compartmentalization and subcellular structures was performed by visually inspecting the volumetric reconstruction of the processes of 173 neurons (the restricted dataset) in both the adult and L4 datasets (346 cells in total). To visualize synapses, we imported synapse locations³ (http://wormwiring.org) into the reconstructed TrakEM2 datasets. To facilitate visual identification, we colored synapses based on whether the cell is presynaptic or postsynaptic and whether the synapses occurs between cells of the same cluster or not. For each cell, we required synapse compartmentalization and/or subcellular structures to be bilaterally conserved in both the L4 and the adult (Supplementary Information 4). The one exception are the RMF cells, where there is clear branching in the L4 (both left and right) that is not observed in the adult. However, because we are limited to 2 samples, we cannot determine if these are developmental, individual differences or reconstruction error⁵.

We identified two types of synaptic compartmentalization: compartmentalization of synaptic inputs and outputs and compartmentalization of synapses with different clusters. To identify compartmentalization of inputs (outputs), we required neural segments to have ≥3 synaptic inputs (outputs) that are spatially distinct from segments with synaptic outputs (inputs) or neural segments with mixed synaptic inputs and outputs (Extended Data Fig. 9).

We identified flattened protrusions by looking for points along the neural processes with increased surface area. We further identified flattened protrusions with mixed synaptic inputs and outputs, which we interpret to be local points with diverse synaptic polarity. In some instances (Supplementary Information 4), these flattened protrusions appear to extend to branches or spine-like structures (Extended Data Fig. 8). Note that synaptic compartmentalization and flattened protrusions are not mutually exclusive. We observed 9 cells that exhibit co-localized synaptic compartmentalization and flattened protrusions. In these instances, the flattened protrusions appear to be used to compartmentalize reproducible (${\mathbb{C}}^4$) synapses (Extended Data Fig. 8).

Mapping neighborhood changes of neurites

We observe that some neuron processes extend into multiple neighborhoods (Fig. 3 and Extended Data Fig. 8). We manually mapped neighborhood changes along process trajectories for selected L4 left neurons (as representatives of their cell class). Starting at the proximal end of the process (closest to cell body), we followed the process trajectory through the EM stack. At each EM, we visually noted the cluster assignments of the neighboring neurites and assigned the neighborhood of that segment of the neurite accordingly. If the neighboring neurites comprised two or more clusters then we labeled the local neighborhood as ‘mixed’. The sequence of local neighborhood segments along the neurite was then scaled by the total length of the neurite so that all positions along the neurite range between 0 and 1. In the case of AVA and RIM, which have protrusions that branch out from the main process trajectory, we scaled the protrusion length by the same factor as the main neurite trajectory.

Brain map construction

We posited a 3-layer architecture as the minimal number of layers needed to capture the organizing principles of the connectome. Classifications of neurons as sensory neurons, interneurons or motoneurons followed WormAtlas³⁶. All sensory neurons were assigned to the first layer. SDQ, BDU and ALN have been postulated to have sensory functions^44,45 but were classified as interneurons as they are not ciliated and physiological evidence for sensory function is lacking. Reclassifying them as sensory neurons would not alter the high-level connectivity of the brain map. With the exception of AIY and AIA, all neurons that make at least one ${\mathbb{C}}^4$ inter-cluster contact were placed in layer 3, with the remainder of neurons assigned to layer 2. Placing AIY and AIA in layer 2 is consistent with functional and ablation studies suggesting that these cells are first-layer amphid interneurons^22,46. Furthermore, AIY and AIA each only make 1 inter-cluster ${\mathbb{C}}^4$ synaptic contact (Extended Data Fig. 10). AIY synapses onto the multi-compartment cell RIA which traverses multiple neighborhoods (Extended Data Fig. 8a). AIA synapses onto RIF whose neurite is at the interface of taxis and avoidance cells in the nerve ring posterior lobe. We confirmed that our map is robust to small changes in which neurons with relatively few inter-cluster synaptic contacts between layers are shifted to layer 2. However, the configuration adopted here optimizes the feed-forward directionality of the synaptic circuit (from the sensory layer to layer 3).

Our information processing modules roughly correspond to the 5 spatially identified clusters. The sublateral and lateral clusters were merged into a single module. With one exception (CEPD), cell classes in the same cluster are placed within the same module. Because CEPD neurons follow the same looping neurite trajectories as other papillary sensory neurons, CEPD cells, which are assigned to the sublateral cluster, are more sensibly placed in the anterior module. Unclassified cells are difficult to cluster because they exhibit high spatial affinity with cells from different clusters. To place the 7 unclassified cell classes on the brain map, we relied on the relative placement of their process trajectories among the clusters. We identified representative cells from each cluster to serve as fiducial points for process placement (Anterior: RIH, Lateral: AVK and RIV, Sublateral: SIAD, Avoidance: AVB, Taxis: ASJ). Each unclassified cell was then added to the module of the representative cells whose neurite most closely aligned with the neurite of the unclassified cell.

Statistical connectivity models

We asked whether stochastic processes could account for the reproducibility and variability of contacts across the 4 datasets. For parsimony, we treat all potential contacts, or graph edges, as identical and allow for all-to-all connectivity. The empirical contact distributions (${\mathbb{M}}^{\delta }$ for membrane contacts, ${\mathbb{C}}^{\delta }$ for synapses and ${\mathbb{G}}^{\delta }$ for gap junctions, Fig. 2a) are all bimodal. Therefore, within the above assumptions, a single stochastic process (for making, or equivalently suppressing) contacts cannot account for these distributions.

We therefore constructed a minimal 3-parameter model combining two stochastic processes – precision and specificity. Precise targeting of contacts and active avoidance of others both require us to distinguish between the set of candidate target contacts and the remainder (non-targets). Accordingly, we define a fraction of target contacts $(f)$, the probability to form a target contact (precision, $p$) and the probability to avoid an off-target contact (specificity, $s$).

This model suffices to define the distribution 0, 1, 2, 3 and 4 contacts. For $\mathbb{A}\in \{\mathbb{M},\mathbb{C},\mathbb{G}\}$, the probability of ${\mathbb{A}}^{\delta }$ is given by:

$$\text{Pr}\left[{\mathbb{A}}^{\delta }\right]={\sum }_{\delta =0}^4(\begin{array}{c}4\\ \delta \end{array})\left(f{p}^{\delta }{(1-p)}^{4-\delta }+(1-f){(1-s)}^{\delta }{s}^{4-\delta }\right),$$ (4)

where the parameters $f$, $p$ and $s$ may take on different values for different instances of $\mathbb{A}\in \{\mathbb{M},\mathbb{C},\mathbb{G}\}$. In the absence of empirical data for estimating the physically accessible subset of contacts, we distribution 0, 1, 2, 3 and 4 contactsto $\delta \in \{1,2,3,4\}$, or in general, for $K$ datasets, using Bayes’ theorem:

$$\text{Pr}\left[{\mathbb{A}}^{\delta }\mid \delta >0\right]=\frac{\text{Pr}\left[{\mathbb{A}}^{\delta },\delta >0\right]}{\text{Pr}[\delta >0]}=\frac{\text{Pr}\left[{\mathbb{A}}^{\delta }\right]}{{\sum }_{\delta =1}^k\text{P}r\left[{\mathbb{A}}^{\delta }\right]}.$$ (5)

Model fits

We used a greedy search of the entire parameter space (with 1% resolution) to find the 3 parameter values ($f$, $p$ and $s$) that minimize the $L^1$-norm between the predicted and empirical distributions. Due to the symmetry of the equations, the model has two solutions that are equivalent up to relabeling of the nodes (and given by $f\to 1-f$, $p\to 1-s$, $s\to 1-p$) such that target and non-target populations are swapped both in size and in the probability of contacts. We choose the solution in which the target fraction, $f$, corresponds to the solution with $p>1-s$, such that precisely targeted contacts are synonymous with higher reproducibility across datasets.

A further equivalent reparametrization exists that replaces a specificity mechanism (acting only on non-target edges) with a uniform basal connectivity (that applies to both target and non-target edges). This variant of the model provides an alternative interpretation, in which the three parameters are the target fraction, $\tilde{f}$, precision, $\tilde{p}$, and basal activity level, $\tilde{b}$. The solution can be obtained with the reparametrization: $f=\tilde{f}$, $s=1-\tilde{b}$, $p=\tilde{p}+\tilde{b}-\tilde{p}\tilde{\text{b}}$. Imposing the condition $0\le \tilde{p}\le 1$ eliminates one of the two solutions for all our model fits.

Empirical data for fits and bias control

For membrane, synaptic and gap junction contacts, we found no evidence of higher reproducibility of edges between the left sides of the L4 and adult datasets, or between the right sides of the L4 and adult, as compared to L4 left and adult right, or vice versa (Supplementary Table 3). However, for membrane contacts, development leads to an overall increase of edges between the L4 and adult (Supplementary Table 1). We considered all neuron pairs in our complete dataset (3203 edges with membrane contact areas ≥35 percentile, Extended Data Fig. 4b) as well as the restricted dataset (see above, 2955 edges). Models of the complete and restricted datasets yielded quantitatively similar results (Extended Data Fig. 3e).

Our restricted dataset consists of 173 neurons. In the absence of spatial constraints, all-to-all connectivity would, in principle, allow for up to 173×172/2 = 14,878 edges. Conversely, using the model fit, the sum ${\sum }_{\delta =0}^K{\mathbb{M}}^{\delta }$ could provide an estimate for the size of the pool of physically accessible membrane contacts in the nerve ring. The above estimate (≈ 3500 edges for the restricted set of contacts) is about 23% of the all-to-all number. This model estimate points to the strong role that spatial constraints play in the actual circuit.

The space of possible synaptic and gap junction contact is restricted by the existence of a physical membrane contact. Unless otherwise noted, all fits were performed on ${\mathbb{C}}^{\delta }$ and ${\mathbb{G}}^{\delta }$ that were restricted to edges from the set of ${\mathbb{M}}^4$ membrane contacts. To control for possible bias due to the subselection of ${\mathbb{M}}^4$ contacts, validation plots were generated by considering ${\mathbb{M}}^j$ contacts and scaling the counts ${\mathbb{C}}^{\mathrm{\delta }}{|}_{{\mathbb{M}}^{\text{j}}}\to \frac{\mathbb{C}{|}_{{\mathbb{M}}^{\text{j}}}}{\mathbb{C}{|}_{{\mathbb{M}}^4}}{\mathbb{C}}^{\mathrm{\delta }}{|}_{{\mathbb{M}}^4}$ for $j=1,\dots ,\delta$, where $\mathbb{C}={\sum }_{\delta =0}^j{\mathbb{C}}^{\delta }$ and ‘${|}_{{\mathbb{M}}^{\text{j}}}$’ denotes synaptic contacts occurring on the domain of membrane contact ${\mathbb{M}}^{\text{j}}$ (scaling was performed in the same way for gap junction contacts, $\mathbb{G}$; Extended Data Fig. 4a–c). For chemical synapses, we find good agreement with ${\mathbb{C}}^3$ when scaled by ${\mathbb{M}}^3$ and ${\mathbb{C}}^2$ when scaled by either ${\mathbb{M}}^3$ or ${\mathbb{M}}^2$. Rescaling systematically underestimated ${\mathbb{C}}^1$ across all datasets, possibly due to a subset of small synapses not accounted for by the model. Indeed, consistent with Hall and Russell⁶, we find that both ${\mathbb{C}}^1$ synapses and ${\mathbb{G}}^1$ gap junctions are significantly smaller (Extended Data Fig. 4f,g) and occur at smaller membrane contacts (Extended Data Fig. 2i, see also Validation against test datasets, below).

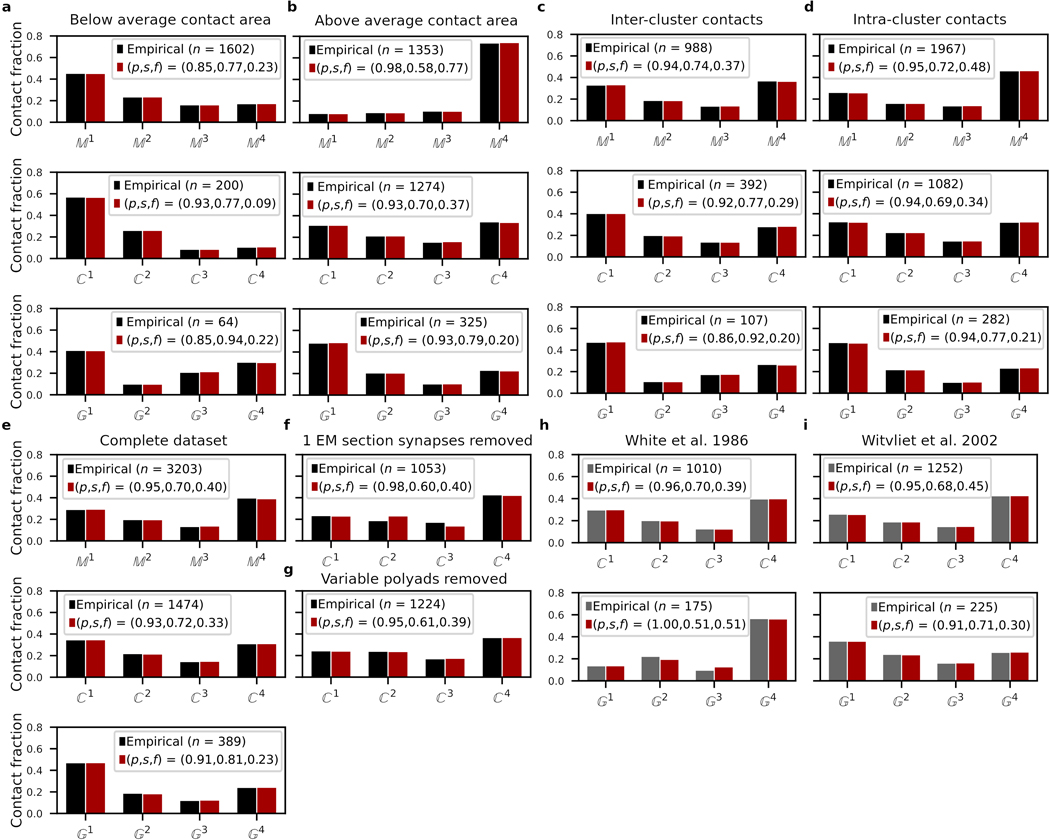
To estimate the fraction of target edges (for $\delta =1\dots 4$), we used Eq. (5). For example, the probability of observing $\delta =4$ target membrane contacts is given by $f{p}^4=0.44\times {0.95}^4=36\%$, whereas the probability of finding 4 variable membrane contacts, $(1-f){(1-s)}^4$, is negligible. Thus, the estimated fraction of ${\mathbb{M}}^4$ membrane contacts in the core circuit is estimated as $f{p}^4/\left[f{p}^4+(1-f){(1-s)}^4\right]>.99\%$, whereas, the estimated fraction of ${\mathbb{M}}^3$ contacts in the core circuit is only $4f{p}^3(1-p)/[4f{p}^3(1-p)+4(1-f)s{(1-s)}^3]=68\%$. Finally, we estimate that in two animals (4 datasets) one would expect $p^4+4p^3(1-p)$ of core edges to occur in at least 3 datasets (corresponding to ~99% of core membrane contacts and ~97% of core synaptic edges). Additionally, we separately fit the model to intra-cluster and inter-cluster edges. For each set of membrane contacts, ${\mathbb{M}}^{\delta }$, we separated the contacts that occur between neurons with the same cluster identity (intra-cluster) and contacts between neurons with different cluster identities (inter-cluster). We then separately fit the model to the sets of intra- and inter-cluster edges, corresponding to membrane contacts, synapses and gap junctions (Extended Data Fig. 3c–d).

Simulation and generation of surrogate data

To construct each surrogate dataset, $k$, we set the size of the dataset, $n$ (e.g. 2955 for membrane contacts) and created an ordered list $𝓛(k)$ of edges. We generated a binary target list (the first round $(fn)$ elements in the list, ${𝓛}_{\text{T}}(k)$ and a binary non-target list ${𝓛}_{\text{NT}}(k)$; among target edges, contact, i.e. 1, occurs with probability $p$ and among off-target edges, contact occurs with probability $1-s$. We then aggregate the counts across $k$ surrogate datasets, ${\delta }_i={\sum }_{k=1}^K{𝓛}_i(k)$, where ${\delta }_i$ corresponds to the number of datasets in which edge $i$ forms a contact. The list of ${\delta }_i$ then forms a surrogate dataset for the reproducibility of contacts, e.g. $\mathbb{M}$.

Validation against test datasets

As additional connectomes are generated and technologies change, we expect slight differences in scoring of different datasets generated from different EM sets^{3,6,7,17,18,39}. These could arise from slightly different demarcation of the volume being scored, different EM sectioning (or sections scored) and different scoring criteria. In the absence of functional (molecular of physiological) data, it is difficult to avoid some false positives (scored synapses that are not fully developed and functional) and false negatives (missed synapses). Often, smaller synapses fare harder to score accurately. Furthermore, most C. elegans synapses are polyadic and present particular challenges, especially when one of the targets occurs with a considerably smaller membrane contact area. Methods and validation of synaptic scoring for the dataset used here have been described by Cook et al.³. Here, we address complementary aspects, relating to reproducibility of scores and implications for our model of core and variable circuits (Extended Data Fig. 3e–i).

Cook et al.³ (the dataset used here) scored a greater number of small synapses than White et al.⁵ (Extended Data Fig. 4f). Furthermore, while this paper was under submission, additional connectomes have been reported for eight hermaphrodite C. elegans nerve rings, including two adults²⁰. We therefore validated our main results on synaptic reproducibility against the connectomes of White et al.⁵ and the two adults in Witvliet et al.²⁰ (hereafter, ‘test datasets’, denoted with the subscript test). As the volumetric reconstruction and hence membrane contact analysis is only available for our study, we used the ${\mathbb{M}}^4$ edges identified here as a common basis for comparison and validation.

Size dependence of synaptic reproducibility has previously been noted^3,6,7,39. Consistently with these earlier results, Extended Data Fig. 4f shows that ${\mathbb{C}}^4$ synapses, and less so ${\mathbb{C}}^3$ synapses, have a considerably higher fraction of edges associated with higher EM section counts: 87% of ${\mathbb{C}}^4$ and 37% of ${\mathbb{C}}^3$ edges are observed in ≥ 5 EM sections, as compared to 13% and 21% in ${\mathbb{C}}^1$ and ${\mathbb{C}}^2$, respectively. That said, a comparison with the White et al. test dataset⁵ shows that the additionally scored synaptic edges are evenly distributed across ${\mathbb{C}}^1-{\mathbb{C}}^4$ (Extended Data Fig. 4f). To check whether different scoring criteria leading to different counts of small synapses affect our conclusions, we re-fit our model to a more restricted synaptic dataset in which all 1-EM section synapses were excluded. While this substantially suppresses ${\mathbb{C}}^1$ counts (hence affecting the relative core and variable fractions), its effect on our model precision and specificity is minor (Extended Data Fig. 3f). The scoring of polyadic synapses is also potentially challenging, if synapses are formed with only a subset of co-localized postsynaptic neighbors. To check whether excessive scoring of polyadic synapses might affect our results, we constructed a synaptic dataset in which for every polyadic pre-synaptic site, we excluded any postsynaptic partner that is in ${\mathbb{C}}^1$. Re-fitting our model to this restricted synaptic dataset, we again find similar precision and specificity.

Next, we reasoned that to be reliable, our statistical model should be robust across datasets. To validate this, we re-fit our model to the two test datasets (Extended Data Fig. 3h–i). Both test datasets show a qualitatively similar bimodal distribution of synaptic reproducibility (${\mathbb{C}}^1-{\mathbb{C}}^4$) that is well fitted to our 3-parameter model. Model fit parameters varied only slightly from our results (Fig. 2): a synaptic edge precision of 92-96% and a specificity of 68-74%. For each synaptic edge scored by Cook et al.³, we then counted the number of edges scored in the test dataset. All but 1 of our ${\mathbb{C}}^4$ edges and 93% of our ${\mathbb{C}}^3$ edges were scored at least once by Witvliet et al.²⁰ (Extended Data Fig. 4h), suggesting that some small synapses are in fact highly reproducible. While slight differences in our model fits preclude automatic merging of the datasets (or models), their similarity implies that it should be possible to quantitatively validate the two extremes, namely non-reproducible and entirely reproducible edge counts, as those are almost certain to come from the variable and core circuits, respectively.

To validate the scoring of postulated variable synapses, we use our model parameters and Eq. (4) to estimate what number of synaptic edges in our dataset would be statistically expected to be absent from two independent animals,

$$n\frac{\text{Pr}\left[{\mathbb{C}}^0\right]}{\text{Pr}\left[{\mathbb{C}}^{\delta }\mid \delta >0\right]}=n\left(\frac{1}{1-(1-f)s^4-f{(1-p)}^4}-1\right).$$

This expression yields an estimated number of ~330 synaptic edges. Empirically, we find that 374 of our synapses were not scored in the Witvliet et al. test dataset²⁰ (Extended Data Fig. 3i; difference not statistically significant under binomial counting statistics). This result adds confidence to the scoring of variable and in particular, small synapses in our dataset. To examine the consistency of postulated conserved synapses, we estimated the number of ${\mathbb{C}}^4$ synaptic edges scored by Cook et al.³ that would also be expected to be found in two independent animals (i.e. in a new set of ${\mathbb{C}}^4$). Of our 450 ${\mathbb{C}}^4$ synaptic edges, we expect a test dataset to include $\frac{n_{\text{test}}}{n}450~380$ as ${\mathbb{C}}^4$ (also equivalent to $n_{\text{test}}f{p}^4\text{Pr}\left[{\mathbb{C}}^{\delta }>0\right])$. Empirically, Witvliet et al.²⁰ score 389 ${\mathbb{C}}^4$ of our ${\mathbb{C}}^4$ contacts, consistent with our model predictions.

Statistics and reproducibility

Membrane contact datasets are derived from the EM reconstructions of the nerve rings from 2 animals at different developmental stages. Each animal in our restricted dataset consists of 80 pairs of bilateral homologous cells. Extended Data Fig. 1 and 2 established that bilateral homologous cells are sufficiently similar. Accordingly, for the purposes of generating reference graphs and for our core-variable and population models, we assume the two sides of each animal may be treated as independent, yielding 4 independent datasets (L4 left, L4 right, adult left and adult right) each consisting of 93 cells classes. As further measures of reproducibility, we validated our core-variable synaptic and gap junction contact models against data scored by different experts on the same EM series⁵ and on different EM datasets²⁰ (in both cases, limited to our ${\mathbb{M}}^4$ contacts). Our models yielded qualitatively similar results for the different scorings and datasets (Extended Data Fig. 3h,i). Spatial population model data were drawn from distributions that matched the empirical distributions of ${\mathbb{M}}^4$ membrane contact areas across the 4 datasets.

Extended Data

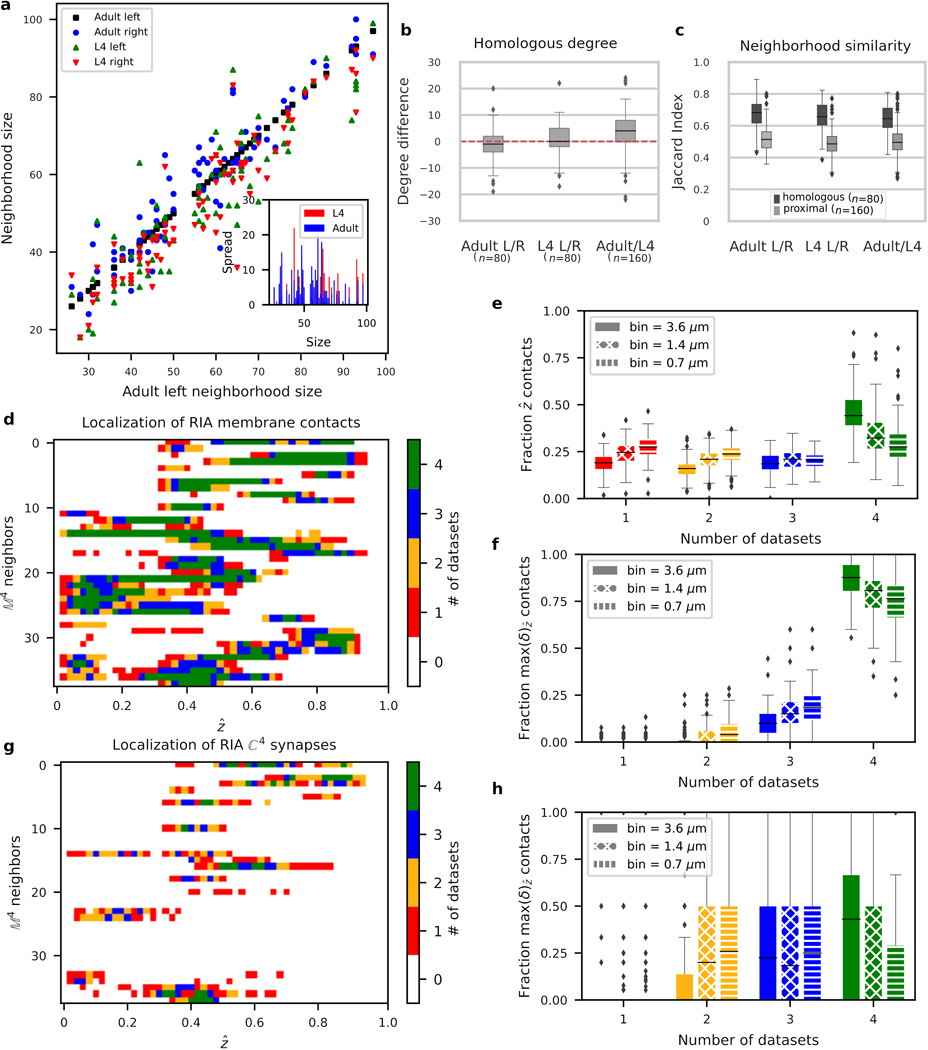
Extended Data Fig. 1. Neuron neighborhoods are bilaterally conserved in size, composition and membrane contact positions.

a, Variability in immediate neighborhood size (adjacency degree) does not vary with immediate neighborhood size. Immediate neighborhood sizes for each neuron in each dataset (adult left, adult right, L4 left, L4 right, $n=80$ bilateral cell classes common to L4 and adult) plotted against the immediate neighborhood size of the corresponding neuron in the adult left. The inset shows the immediate neighborhood size difference between homologous left/right neurons (vertical spread) as a function of neighborhood size for the L4 (red) and adult (blue). b, Distribution of immediate neighborhood size differences between homologous contralateral neurons in the same animal (adult L/R and L4 L/R) are statistically indistinguishable from 0 (two-sided Wilcoxon signed-rank test derived p-values: 0.07 and 0.29, respectively, $n=80$ cell classes). Immediate neighborhood size differences between homologous adult and L4 neurons on the same side of the body are statistically distinguishable from 0 (two-sided Wilcoxon signed-rank test, p-value 9.2×10⁻¹¹, $n=160$ cells), but the difference is small (mean degree difference 3.6). c, Similarity between immediate neighborhood compositions as quantified by the Jaccard index (Supplementary Results), shows higher compositional similarity between homologous contralateral neighborhoods ($n=80$ cell classes) than between proximal ipsilateral neighborhoods (Supplementary Results, $n=160$ cells). d-f, Membrane contact placement along processes is highly reproducible bilaterally and across the adult and L4 datasets. For each process, we mapped each ${\mathbb{M}}^4$ contact to a position along the anterior-posterior (AP) axis, $\widehat{\text{z}}$, (see Methods and Supplementary Results). For each ${\mathbb{M}}^4$ contact, we then counted the number of datasets where the contact was observed at a given $\widehat{\text{z}}$ (reproducibility count). d, Demonstration of reproducibility count for a single cell class (RIA): RIA has the longest process in the nerve ring and among the highest average reproducibility counts. A raster plot of reproducibility counts as a function $\widehat{\text{z}}$ of all ${\mathbb{M}}^4$ contacts made with RIA. Neighboring processes: rows in alphabetical order. Color: reproducibility count. We define the maximum spatial reproducibility count, $\text{max}{\left(\delta \right)}_{\widehat{z}}$, as the highest reproducibility count across all locations, $\widehat{\text{z}}$, per cell pair (i.e. for every row in the raster). For rasters of all other cell classes, see Supplementary Information 2. e, Fraction of ${\mathbb{M}}^4$ membrane contact sites co-localized in $\delta$ datasets (distribution over $n=80$ cell classes). f, For each cell class, the fraction of membrane contacts achieved with a maximum spatial reproducibility count, $\text{max}{(\delta )}_{\widehat{z}}$ (distribution over $n=80$ cell classes). g-h, Comparatively, ${\mathbb{C}}^4$ synaptic contact placement is less reproducible than physical adjacency. For each process, we mapped each ${\mathbb{C}}^4$ contact along the AP axis, $\widehat{\text{z}}$. g, Demonstration of synaptic spatial reproducibility count for RIA. h, For each cell class, the fraction of ${\mathbb{C}}^4$ synaptic contacts achieved with a maximum spatial reproducibility count, $\text{max}{(\delta )}_{\widehat{z}}$ (distribution over $n=80$ cell classes). Box plots: center line, median; box limits, upper and lower quartiles; whiskers, 1.5x interquartile range; points, outliers.

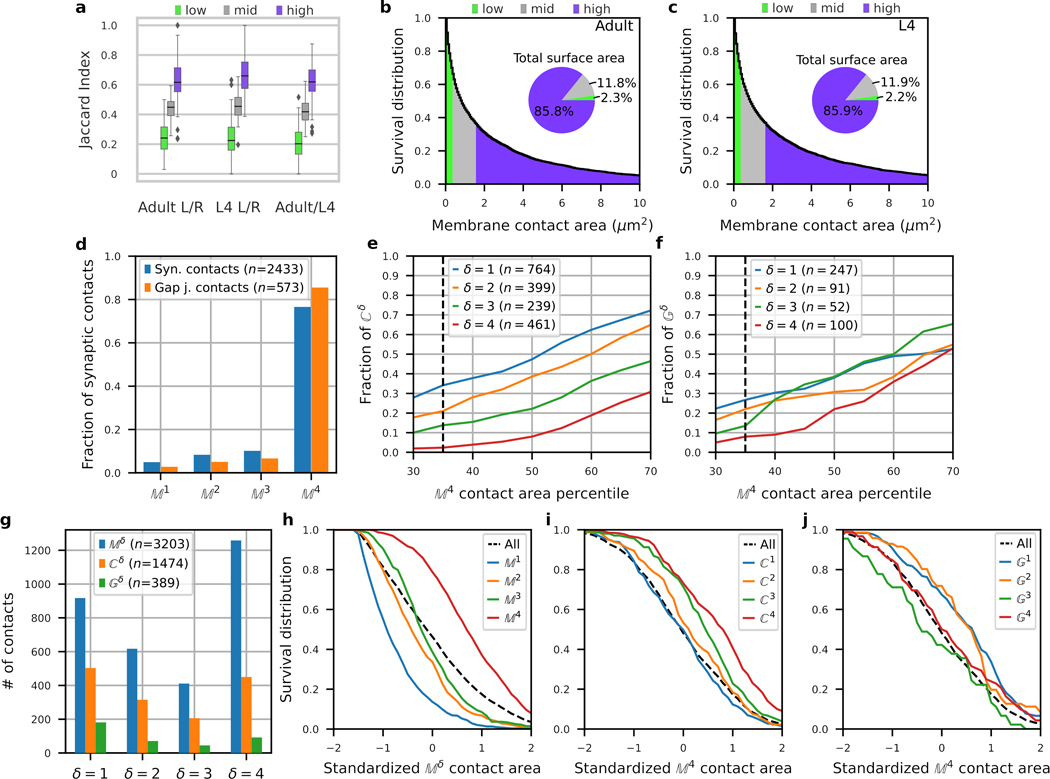
Extended Data Fig. 2. Contact sizes and reproducibility.

a-f, Small membrane contact areas are less likely to be bilaterally conserved. Membrane contacts were divided into three groups (‘low’, ‘mid’ and ‘high’) based on their membrane contact areas (35% low, 31% mid, 34% high), see Supplementary Results). a, Similarity of homologous (L4 bilateral; adult bilateral; L4 and adult – same side) immediate neighborhood compositions for low, middle and high membrane contact groups, as measured by the Jaccard index (Supplementary Results, $n=80$ cell classes). Box plot: center line, median; box limits, upper and lower quartiles; whiskers, 1.5x interquartile range; points, outliers. b,c, Survival (i.e. complementary cumulative) distribution of membrane contacts in b, the adult ($n=5,179$) and c, the L4 ($n=4,744$). The pie charts show the fraction of total membrane area contact between all processes accounted for by each group. d, Empirical frequency distribution of synaptic ($n=2,433$) and gap junctional (n=573) contacts broken down by the reproducibility of membrane contacts. The majority of synaptic contacts (77% and 85% of synaptic and gap junction contacts, respectively) occur at ${\mathbb{M}}^4$ contacts. e,f, Cumulative distribution of e, ${\mathbb{C}}^{\delta }$ synaptic contacts and f, ${\mathbb{G}}^{\delta }$ gap junction contacts for $\delta =1,2,3,4$ as a function of membrane contact area (in percentiles). To control for differences in neurite placement, we restrict ${\mathbb{C}}^{\delta }$ and ${\mathbb{G}}^{\delta }$ to contacts that occur on ${\mathbb{M}}^4$ membrane contacts. The smallest 35% of membrane contacts (dashed line) comprises ~3% of ${\mathbb{C}}^4$ synaptic contacts and ~9% of ${\mathbb{G}}^4$ gap junction contacts (on ${\mathbb{M}}^4$) with growing fractions for smaller $\delta$ (up to ~33% and ~27% of the more variable ${\mathbb{C}}^1$ and ${\mathbb{G}}^1$ contacts). g, Empirical frequency distribution of membrane, synaptic and gap junctional contacts across the 4 datasets ($\delta =1$ to 4). h-j, Survival distribution of contacts as a function of membrane contact area for ${\mathbb{M}}^{\delta }$, ${\mathbb{C}}^{\delta }$ and ${\mathbb{G}}^{\delta }$ graphs ($n$ given in g), plotting the probability that a membrane/synaptic/gap junction contact occur with membrane contact area > some value). Membrane contact areas have been log-normalized and standardized so that the distribution is centered about 0, i.e. log-transformed, standardized (by subtracting the mean) and normalized (by dividing by the standard deviation), such that a range of ±1 corresponds to ±1 standard deviation of the distribution of log(membrane contact area).

Extended Data Fig. 3. Core and variable model validations.

a,b, Model fits for reproducibility of ${\mathbb{M}}^{\delta }$ contacts, with membrane contact areas a, below and b, above the log-normalized mean (after thresholding, Methods, Extended Data Fig. 2h). c,d, Reproducibility model fits of c, inter-cluster and d, intra-cluster ${\mathbb{M}}^{\delta }$ contacts. e, Reproducibility model fits for complete ${\mathbb{M}}^{\delta }$, ${\mathbb{C}}^{\delta }$ and ${\mathbb{G}}^{\delta }$ datasets including membrane contact areas <35% (results qualitatively similar to restricted dataset model fit in Figure 2a; Methods: Generating reference graphs). f, Reproducibility model fits for ${\mathbb{C}}^{\delta }$ excluding synaptic contacts scored in only 1 EM section (Methods). g, Reproducibility model fits for ${\mathbb{C}}^{\delta }$ excluding synaptic contacts derived from non-reproducible post-synaptic partners of polyadic synapses (Methods). h,i, Reproducibility model fits for synaptic and gap junction contact datasets scored by h, White et al. (1986)⁵ and i, Witvliet et al. (2020)²⁰ limited to our ${\mathbb{M}}^4$ contacts. $\mathbb{M}$: membrane, $\mathbb{C}$: chemical synapse and $\mathbb{G}$: gap junction contacts. Black bars: empirical distributions used in this study. Gray bars: other empirical distributions^5,20. Red bars: Model fits for the empirical distributions. All fractions of the total empirical counts ($n$).

Extended Data Fig. 4. Validation of core-variable model and contact scoring.

a-c, Core-variable model reliably predicts the empirical synaptic and gap junction contact reproducibility (${\mathbb{C}}^{\delta }$ and ${\mathbb{G}}^{\delta }$) on ${\mathbb{M}}^2$ and ${\mathbb{M}}^3$. To predict synaptic/gap junctional contact counts on ${\mathbb{M}}^{j<\mathit{4}}$ contacts, ${\mathbb{C}}^{\delta }$ (or ${\mathbb{G}}^{\delta }$) contact counts on ${\mathbb{M}}^4$ are scaled by the ratio of all $\mathbb{C}(\mathbb{G})$ on ${\mathbb{M}}^j$ count : all $\mathbb{C}(\mathbb{G})$ on ${\mathbb{M}}^{\mathit{4}}$ count (Methods). E.g. in a, the model predicts a ${\mathbb{C}}^3$ count on ${\mathbb{M}}^3$ contacts as 206×285/1474 = 40 where 206 is the empirical ${\mathbb{C}}^3$ count on ${\mathbb{M}}^4$ contacts, 285 is the total empirical synaptic contact count, $\mathbb{C}$, on ${\mathbb{M}}^3$ and 1474 is the total empirical count of synaptic contacts on ${\mathbb{M}}^4$. The model prediction is consistent with the empirical ${\mathbb{C}}^3$ on ${\mathbb{M}}^3$ count (43). Error bars: $\pm \surd n$, where $n$ is the empirical or predicted count (see Source Data for precise $n$ values). d, Chemical synapses and e, gap junctions also consist of a core and variable circuit. Surrogate model data for ${\mathbb{C}}^{\delta }$ and ${\mathbb{G}}^{\delta }$, generated as in Fig. 2b. Across each dataset, ~62% of synaptic contacts and ~59% of gap junction contacts consist of target contacts (given by $fp/\left[fp+\left(1-f\right)\left(1-s\right)\right]$, Methods). f,g, Core synaptic contacts are typically larger than variable ones in both Cook et al. (2019)³ and White et al. (1986)⁵. Distribution of f, ${\mathbb{C}}^{\delta }$ and g, ${\mathbb{G}}^{\delta }$ contact counts by EM sizes (the total number of EM sections in which a contact was observed)^3,7. To check for biases in contact size due to possible differences in synaptic/gap junction scoring criteria, we compare the distributions of EM sizes for contacts identified by White et al. (1986)⁵ (orange) and those identified by Cook et al. (blue). Because White et al. (1986)⁵ does not provide EM sizes, we used the EM sizes from Cook et al. (2019)³ for all contacts. Although many additional synapses identified by Cook et al. (2019)³ occur only in 1 EM section, we find no systematic bias towards smaller synaptic contacts by Cook et al. (2019)³. h,i, Bidirectional comparison of Cook et al. (2019)³ and Witvliet et al. (2020)²⁰ synaptic contact reproducibility. h, Fraction of Cook et al. (2019)³ synaptic contacts scored by Witvliet et al. (2020)²⁰. i, Fraction of Witvliet et al. (2020)²⁰ synaptic contacts scored by Cook et al. (2019)³. h,i, Fractions of the total empirical count of synaptic contacts $(n)$.

Extended Data Fig. 5. Robust clustering of nerve ring processes from ${\mathbb{M}}^4$ spatial population models.

The variability of membrane contacts (Fig. 2, Extended Data Fig. 2) suggest that no single animal is representative of the population. We estimated the variability among membrane contact areas. a, The log-normalized empirical distribution of ${\mathbb{M}}^4$ membrane contact areas (mean centered at 0, STD: standard deviation, red line: normal distribution with empirical mean and standard deviation, $n=1,258$ membrane contacts). We estimated the variability across the four datasets (L4 left, L4 right, adult left and adult right). For each conserved ${\mathbb{M}}^4$ contact, we computed the mean and standard deviation of the membrane contact area across the four datasets (see Methods). b, Plot of the standard deviation versus mean contact area across the datasets, where each point is one ${\mathbb{M}}^4$ contact. Similar to Extended Data Fig. 1a, we find no dependence of the variability on membrane contact area. Therefore, we estimate membrane contact area variability by the mean variability among all membrane contact areas. c, The distribution of standard deviations of membrane contact area for all ${\mathbb{M}}^4$ contacts. Red dashed line: mean standard deviation. d-i, A stochastic spatial population model matches the above distributions by randomly perturbing membrane contact areas in the four datasets with multiplicative white noise with standard deviation ($\sigma$) of 0.23 (Methods). d-f, Spatial population data perturbs the membrane contact areas while maintaining contact area and variability distributions that are similar to the empirical ${\mathbb{M}}^4$ contact area distributions. g, Perturbed contact areas scale linearly with the empirical contact areas. h, The spread of perturbed contact areas (log of the perturbed contact area as a fraction of the empirical contact area) is mostly uniform across membrane contact areas. i-l, Neurite clusters obtained from a population of 1,000 $\widetilde{{\mathbb{M}}^4}$ perturbed individuals and 1,000 $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$ perturbed individuals (perturbing left/right conserved contacts in the L4 and adult datasets). For each perturbed individual in each population we used a multi-level graph clustering algorithm to identify spatial clusters. Across each population, we computed the frequency that cell pairs cluster together, represented as an $n\times n$ cluster frequency matrix ($n=93$). A hierarchical clustering algorithm is used to sort the rows and columns of the cluster frequency matrix in order to minimize variation along the diagonal. Hence, cells pairs that frequently cluster together are sorted together on the cluster frequency matrix (Methods). Five largely overlapping subgroups of neurons emerge across different perturbations (see main text). i, Consensus subgroups are robust across datasets. $\widetilde{\text{L}4}$ and $\widetilde{\text{Adult}}$ clusters visualized using row and column colors of the $\widetilde{{\mathbb{M}}^4}$ population cluster assignments (dashed box). j, The consensus subgroups are robust across different noise amplitudes. Clustering applied to populations generated by perturbations to ${\mathbb{M}}^4$ using white noise with standard deviations 0 (empirical data), 0.12, 0.45 and 0.9. k,l, The consensus subgroups are robust across different spatial domains. k, Clustering applied to $\widetilde{{\mathbb{M}}^4}$ populations generated from the more spatially restricted subset of the neuropil considered by Moyle et al. (2020)³⁴, which excluded the posterior lobe of the neuropil. l, Clustering applied to populations generated by perturbations to all reproducible membrane contact areas after restoring the smallest 35% contact areas to each of the L4, adult and ${\mathbb{M}}^4$ datasets (Extended Data Fig. 2). For all cluster frequency matrices: Matrix element ($i$, $j$) corresponds to the frequency that cells $i$ and $j$ cluster together across the 1000 perturbed individuals. Row and column orders minimize variance along the diagonal (Methods). Cell cluster assignments (color) follow the perturbed $\widetilde{{\mathbb{M}}^4}$ dataset (Figure 1b reproduced in dashed box). Top: dendrogram of the hierarchical clustering.

Extended Data Fig. 6. Variable contacts obscure the organization of the nerve ring.

a, Cluster analysis of unperturbed membrane contact datasets ${\mathbb{M}}^1$, ${\mathbb{M}}^2$, ${\mathbb{M}}^3$ and ${\mathbb{M}}^4$. Clustering results for membrane contacts predicted to combine core and variable contacts (${\mathbb{M}}^3$) and overwhelmingly variable contacts (${\mathbb{M}}^2$, ${\mathbb{M}}^1$) significantly and increasingly diverge from 5 consensus clusters, indicated by large numbers of small clusters. b, Cluster analysis of (unperturbed) L4 and adult datasets. Both the unperturbed ${\mathbb{M}}^4$ and adult datasets yield 6 clusters rather than the 5 clusters found in the perturbed population models (Figure 1c and Extended Data Fig. 5). The additional cluster results from a split of the taxis cluster into two. This split of the taxis cluster is not observed in either the perturbed ${\mathbb{M}}^4$ or the perturbed Adult dataset, even with half the noise levels observed empirically, indicating that the split is unlikely to be robust across a population of animals. For all cluster frequency matrices: Row and column ordering and colors are the same as the perturbed $\widetilde{{\mathbb{M}}^4}$ population dataset (Extended Data Figure 5i). Matrix element ($i$, $j$) is 1 if cells $i$ and $j$ cluster together and 0 otherwise. Top: dendrogram of the hierarchical clustering.

Extended Data Fig. 7. Distribution of core and variable synapses among neighborhoods.

a, Membrane contacts of the L4, adult and reference ${\mathbb{M}}^4$ datasets demonstrate that all three datasets have similar membrane contact profiles. For L4 and adult datasets, only bilaterally conserved contacts are included. b, Synaptic contacts on ${\mathbb{M}}^4$ membrane contacts broken down by degree of synaptic contact reproducibility (${\mathbb{C}}^1$, ${\mathbb{C}}^2$, ${\mathbb{C}}^3$ and ${\mathbb{C}}^4$). Most (56%) of conserved synapses (${\mathbb{C}}^4$) occur within clusters near the main diagonal, while variable synapses (${\mathbb{C}}^1$) are spread across clusters. c, Gap junction contacts on ${\mathbb{M}}^4$ membrane contacts broken down by degree of reproducibility (${\mathbb{G}}^1$, ${\mathbb{G}}^2$, ${\mathbb{G}}^3$ and ${\mathbb{G}}^4$). For all matrices: Row and column ordering is the same as the perturbed $\widetilde{{\mathbb{M}}^4}$ dataset (Extended Data Fig. 5i). Row and column colors correspond to final clusters assignments (Fig. 1c), where unclassified cells are colored gray. Matrix element ($i$, $j$) corresponds to the fraction of cell $i$’s membrane contact with cell $j$, with rows normalized to sum to 1.

Extended Data Fig. 8. Subcellular structures support local and nonlocal connectivity; RIA and AIB processes demonstrate synaptic compartmentalization.

a,b, Volumetric rendering of RIAL and its synapses (cuboids) colored by a, synaptic polarity or b, intra-/inter-cluster. Combining a and b: synaptic input and output segments correspond to changes in neighborhood composition. Changes in RIA neighborhood correspond to the 3 neurite segments (nV, nD and loop) which exhibit independent calcium dynamics that encode head movement⁶². c,d, AIB processes change neighborhood at the lateral midline¹⁸. The ipsilateral segment (†) of the AIB process is surrounded by cells in the taxis cluster while the contralateral segment (††) makes contact with cells in every other cluster. c, AIB process segments alternate between synaptic inputs on the ipsilateral side and synaptic outputs on the contralateral side. d, The alternating synaptic inputs and outputs correspond to a change in neighborhood occurring at the dorsal midline. e-h, Flattened protrusions link processes to adjacent cells in adjacent clusters. e, The flattened protrusion strategy as demonstrated by RIM processes (♦). f, The RMDV processes demonstrate how flattened protrusions are used to locally expand synaptic polarity. On the contralateral side, the main process trajectory is postsynaptic while the contralateral protrusion is presynaptic. Both g, AVA and h, SAAV exhibit flattened protrusions that appear to turn into small branches. The small AVA branch extends into a neighborhood comprised of cells from a different cluster (*). SAAV ipsilateral branches receive synaptic inputs while its main process trajectory on the contralateral side is mostly pre-synaptic. RMEV/D processes spine-like features extend to cells in a different cluster. i, 2 longer RMED extensions and j, 3 shorter RMEV spine-like extensions are postsynaptic to the sublateral cluster. In all images, the pharynx is shown for a spatial reference. R: right, A: anterior, V: ventral. Note: for visual clarity, synapses have been offset from the cell process. k, Schematic of neighborhood changes of selected cells (labeled in color of cluster assignment). P: proximal and D: distal to cell body. Each trajectory scaled to the length of the reconstructed left L4 process. Black boxes denote sections in which the process makes contact with at least two clusters.

Extended Data Fig. 9. Network features of the brain map.

a, Schematics of network features (from left to right): Feed-forward loop motif (FF) defined by a triplet of nodes with connectivity: Source → Intermediary → Target and Source → Target; network hub (high degree node, H); fan-in (high in-degree node, FI); fan-out (high out-degree node, FO); and rich club (highly connected hubs, RC). b, FF triplets within the brain map support the ResNet architecture of the nerve ring. All 101 FF instances among ${\mathbb{C}}^4$ synaptic contacts (all edges in Fig. 4, Extended Data Fig. 10) are shown. Black arrows: FF synaptic contacts within the ResNet architecture (Fig. 4). Gray arrows: additional FF synaptic contacts (Extended Data Fig. 10). 72/93 cell classes participate in at least one FF motif. Prominent FF targets include: AIA, AIB, AIZ, AVA, AVB, AVE, RIA, RIC, RIM, RIP, RMDV and SMDV. Additional contacts superimposed on the ResNet come mostly from cross-sensory module connectivity (Extended Data Fig. 10b). c, RIP, the only synaptic link between the somatic and pharyngeal nervous systems, is a major FF target cell for papillary sensory source cells and URA intermediaries. d, AIA are a major taxis Layer-2 intermediary cell pair regulating information flow from Layer-1 Taxis sensory cells onto the Layer-3 AIB Taxis target cell. e, AIZ, major Layer-3 cells that supports nonlocal connectivity (Fig. 3a), serve both to integrate information flow from Layers-1 and 2 Taxis source cells (FI) and as an intermediary to various Layer-3 target cells in other modules (FO). f, Primary locomotion regulating interneurons – AVA, AVB and AVE – are major Layer-3 FF targets and connect extensively onto motoneurons of the ventral nerve cord. Connectivity among these cells occurs in the ventral nerve cord (but not observed in the nerve ring), suggesting that the regulation of locomotion down the body occurs posteriorly to the nerve ring. g, RIM, a major hub that support nonlocal connectivity, triples as source, intermediary and target FF cell pair within Layer-3. h, The nonlocal supporter, multi-compartment pair RIA are a major FF target for Layer-1 sensory (primarily Avoidance) source cells and Layer-2/3 (Taxis and Avoidance) intermediary cells as well as intermediaries that control Layer-3 head motoneurons. Additionally, RIA are major targets for feedback from lateral (RMD, RMDD, RMDV) and sublateral (SMDD, SMDDV) head motoneurons, consistent with their roles in spatially encoding dorso-ventral head movement to coordinate turning behaviors.⁴⁷ i, Major FF targets (11 neuron classes acting as a target of > 3 FF motifs, including 5 RC classes) form a highly interconnected subnetwork. Note the frequent representation of some cells in multiple motifs (c-i). j, Layer-3 aggregated FF synaptic contacts within and among the modules shows strong recurrence and no clear feed-forward directionality or hierarchy of Layer-3 connectivity, consistent with highly distributed computation. Sublaterals are merged into the Lateral module node. Layer-3 anterior cells form FF connectivity with only one other module (Taxis). All network schematics were generated with Cytoscape 3.7.1.

Extended Data Fig. 10. 17% of ${\mathbb{C}}^4$ contacts are not accounted for by the ResNet model.

a, Layer-1 synaptic connectivity across information processing modules in ${\mathbb{C}}^4$ could support distributed sensory computation and integration. 8 (2% of ${\mathbb{C}}^4$) contacts occur between sensory cells across different modules. These contacts include: (i) ADE→OLL, (ii) ALM→CEPD/V, (iii) reciprocal contacts between ASH, ADL and AFD. (i) Mechanosensitive^48,49 anterior cell OLL loops around intermediate processes, while the processes of ADE extend toward the OLL loop, suggesting a functional role for the more elaborate loop morphology. (ii) Both CEPD and CEPV processes loop around intermediate processes and extend flattened protrusions to meet the ALM processes, where ALM are postsynaptic. CEPD and CEPV respond to head touch⁵⁰, while ALM respond to both gentle⁵¹ and harsh⁵² body touch, inhibit backward locomotion⁵³ and have been implicated in the habituation of tap response⁵⁴. (iii) Nociception: ASH, ADE and ADF may coordinate avoidance behaviors between the taxis and avoidance modules⁵⁵. b, Layer-1 to Layer-3 inter-module feed-forward synaptic connectivity in ${\mathbb{C}}^4$. 54 (12% of ${\mathbb{C}}^4$) contacts are inter-module, originate in Layer 1 and target Layer 3 neurons directly. A small number of taxis and avoidance sensory neurons (ADF and ADL, ASH, URX and BAG) project to all but Laterals in Layer 3; this contrasts with extensive anterior sensory neuron projections that almost exclusively target (sub)lateral Layer-3 interneurons and motoneurons, likely mediating rapid sensorimotor transformations. c, Layer-2 and inter-module feed-forward ${\mathbb{C}}^4$ synaptic connectivity. 3 contacts (1% of ${\mathbb{C}}^4$) are inter-module and originate in Layer 2. Notably, Layer-2 taxis AIY neurons synapse onto Layer-3 anterior multi-compartment neurons RIA. d, Inter-module feedback synaptic connectivity in ${\mathbb{C}}^4$. 9 (3% of ${\mathbb{C}}^4$) contacts provide inter-module feedback. Black arrows: synaptic contacts between cells in the same neighborhood. Grey arrows: synaptic contacts between layer 3 cells in different neighborhoods. Red arrows: synaptic contacts not accounted for by the ResNet model. Solid arrows: feed-forward or recurrent (intra-layer) synaptic contacts. Dashed arrows: feedback synaptic contacts.

Data Availability

The volumetric datasets generated during the current study, associated connectivity databases and associated analysis are available at https://doi.org/10.5281/zenodo.4383277 and http://wormwiring.org/. The raw data for volumetric reconstructions for Figs. 1 and 3, Extended Data Fig. 8 and all Supplementary Videos is available at https://doi.org/10.5281/zenodo.4383277. Extracted adjacency data is available in Supplementary Information 1. The reference datasets are available in Supplementary Information 3. The Cytoscape files use to generate the brain map (Fig. 4 and Extended Data Fig. 10) and network motifs (Extended Data Fig. 10) are available at https://doi.org/10.5281/zenodo.4383277. See associated Source Data for the data used to generate plots. The collection of C. elegans nervous system electron micrographs are also available at https://www.wormatlas.org/ and https://wormimage.org.