Significance
Complex systems can often be conceptualized at both a microlevel (for example, molecules of a gas) and a macrolevel (for example, pressure and temperature of the gas). Bottom–Up, agent-based mechanistic modeling and Top–Down, statistical inference are the two dominant approaches to modeling such systems. Despite the frequently made assumption that causation flows only upward from the micro- to the macrolevel, many complex systems exhibit bidirectional cross-scale causation or “scale entwinement.” We present an approach for predicting the dynamic behavior of such systems, explicitly incorporating upward and downward causation, and combining information-theoretic statistical inference with agent-based process modeling. Examples of possible applications in nonequilibrium chemical thermodynamics, epidemiology and public health, economics, and ecology illustrate the potential multidisciplinary scope of our proposed approach.
Keywords: complex systems, maximum entropy, non-equilibrium
Abstract
In many complex systems encountered in the natural and social sciences, mechanisms governing system dynamics at a microscale depend upon the values of state variables characterizing the system at coarse-grained, macroscale (Goldenfeld and Woese, 2011, Noble et al., 2019, and Chater and Loewenstein, 2023). State variables, in turn, are averages over relevant probability distributions of the microscale variables. Neither inferential Top–Down nor mechanistic Bottom–Up modeling alone can predict responses of such scale-entwined systems to perturbations. We describe and explore the properties of a dynamic theory that combines Top–Down information-theoretic inference with Bottom–Up, state-variable-dependent mechanisms. The theory predicts the functional form of nonstationary probability distributions over microvariables and relates the trajectories of time-evolving macrovariables to the form of those distributions. Analytic expressions for the time evolution of Lagrange multipliers from Maxent solutions allow for rapid calculation of the time trajectories of state variables even in high dimensional systems. Examples of possible applications to scale-entwined systems in nonequilibrium chemical thermodynamics, epidemiology, economics, and ecology exemplify the potential multidisciplinary scope of the theory. A worked-out low-dimension example illustrates the structure of the theory and demonstrates how scale entwinement can result in slowed recovery from perturbations, reddened time series spectra in response to white-noise input, and hysteresis upon parameter displacement and subsequent restoration.
“It is advisable to look from the tide pool to the stars and then back to the tide pool again.”—John Steinbeck, The Log from the Sea of Cortez
Many physical, biological, and social systems can be described at two well-differentiated levels: the microscale and the macroscale. In statistical mechanics, for example, the kinetic energy of an individual gas molecule is a microvariable, while pressure, volume, and temperature are macrovariables (also referred to as state, or macrostate, variables). Wages of individual workers are a microvariable in economics; the total annual output of the economy is a state variable. And in ecology, the metabolic rate of an individual organism and the abundance of a species are microvariables; the total productivity and total number of individuals and species in an ecosystem are state variables.
The dynamics of such systems are especially complex if the microscale and the macroscale are “entwined” in the specific sense that there is cross-scale, bidirectional causation. In such cases, the equations governing microscale dynamics depend explicitly upon both the microvariables and one or more time-dependent state variables (1–3). In epidemiology, for example, the rate constant governing disease transmission between individuals can be influenced by the incidence of the disease in the larger population if individuals heed public health warnings when that disease incidence is high. In economics, knowledge about the changing state of the macroeconomy can influence the economic decisions individuals and firms make. In ecosystems, the reproductive and growth rates of individuals can depend upon the total number of species and individuals in a region via crowding and competition.
Cross-scale, bidirectional causation represents feedback but it differs from the kind of feedback that is typically modeled in complex systems analysis. The latter, exemplified by ice-albedo feedback in climate models, describes two-way causation between two same-level, subsystems of a larger system. The theory advanced here describes feedback across hierarchical levels, rather than subsystems at the same level of a complex system.
Analysis of the dynamics of multilevel systems rarely attempts to capture downward causation. Instead, models are generally either Top–Down and statistical (4–6) or, more frequently, Bottom–Up and mechanistic (7, 8). In the Bottom–Up approach, interactions among microlevel “agents” control larger-scale outcomes; state variables are appropriate sums or averages over microvariables. Under the assumption that top–down causation is absent, probability distributions over microvariables are often derived using a master equation approach in which transition rates do not depend upon mathematical moments of the distributions. Because causal influence is often best understood mechanistically at the microlevel, Bottom–Up approaches can be useful. Alone, however, they fail to capture important top–down causal influences.
In the Top–Down approach, state variables and other macrolevel information provide constraints that allow inference of the functional forms of the probability distributions over microvariables. Here, a powerful inference method is maximizing information entropy (Maxent). The least-biased probability distribution over microvariables is determined by maximizing information entropy (9) of the distribution subject to the constraints imposed on the distribution by prior knowledge at the macrolevel (4–6). Maximization of information entropy is carried out using the method of Lagrange multipliers (10, 11). We emphasize that the term entropy as used here refers to Shannon information entropy and should not be conflated in every case with thermodynamic entropy.
The Top–Down approach to inference often yields accurate predictions of probability distributions over microvariables when the constraints imposed by the state variables are relatively constant in the time period under consideration (12). An example in physics is the derivation of the Maxwell–Boltzmann distribution of molecular kinetic energies from the constraints of total energy and total number of molecules in an ideal gas in thermal equilibrium (4). Other examples include image reconstruction in medicine and forensics (13–16), protein folding (17, 18), and a variety of applications in neuroscience (19), ecology (20, 21), climate (22), and economics (23).
If state variables are changing relatively rapidly in time, however, as is in a non-steady-state thermodynamic system, during a pandemic, a growing or shrinking economy, or in a highly disturbed or disrupted ecosystem, the Top–Down Maxent procedure, alone, may fail to reliably predict instantaneous distributions over microvariables. In thermodynamics this has long been noted (24, 25) but in other fields as well, such as ecology (26–34), application of Maxent inference often fails in rapidly changing systems.
Here, we present and explore a scale-entwined theory of the dynamics of two-tiered systems in which state variables influence microscale dynamics and in turn can be calculated by averages over derived probability distributions of microvariables. This theory of Dynamic Maxent across Entwined Scales, or DyMES, combines the Maxent Top–Down inference procedure with state-variable-dependent mechanisms governing agents at the microlevel, to predict the time evolution of both the state variables and the probability distributions over the microvariables.
In a previous specific model application (34) of DyMES, we showed that a static Maxent-based theory of ecology (20, 21) could be extended to an ecosystem in which state variables were changing over time. We showed that the time-evolving shapes of both state variables and probability distributions over microvariables were consistent with the predictions of DyMES. However, because of the inevitable uncertainties in census data from whole ecosystems, the data used in ref. 34 cannot cleanly validate or invalidate DyMES. One goal of this research, then, is to establish a broader framework so that other model realizations may be constructed and the theory can be more definitively tested. Hence, here we generalize that exploratory effort and provide a more comprehensive explanation and analysis of the structure, types of predictions, and possible applications and tests of DyMES.
In applications of Maxent to static systems, the information entropy of probability distributions over microvariables is maximized under the constraints derived from knowledge of static macrostate variables. This process produces Lagrange multipliers that solve the constraints and characterize the resulting microvariable distributions. To construct a dynamic theory, we enlarge the set of constraints to include time derivatives of the state variables. The set of Lagrange multipliers is correspondingly increased. Explicit equations that generate the time dependence of both the state variables and the probability distributions over microvariables are derived. Remarkably, the Lagrange multipliers that result can be shown to obey time-differential equations. This both eliminates the task of having to search numerically for entropy-maximizing values at every iteration in time and allows for more rapid calculation of dynamics in high-dimensional systems.
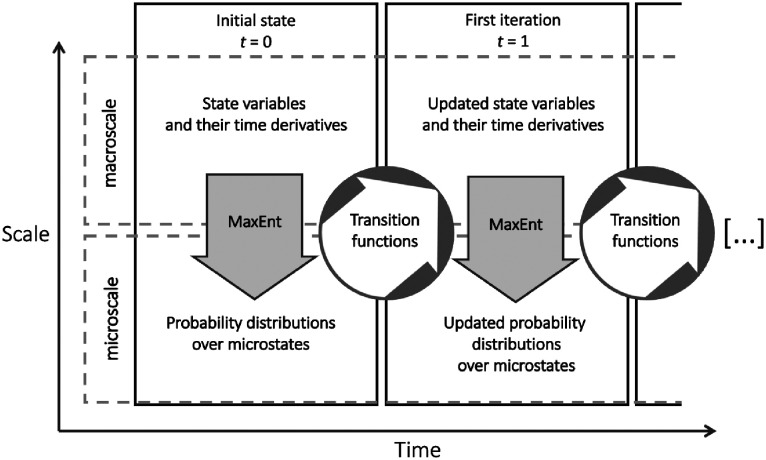
Central to DyMES is the notion of transition functions, which govern microvariable dynamics. Scale entwinement, and in particular, downward causation, is captured by explicit dependence of transition functions on state variables as well as on microvariables. Each choice of state variables and the form of the transition functions corresponds to different model realizations of DyMES. Eqs. 1-9 that follow describe the general theory. The architecture of DyMES is shown in Fig. 1.
Fig. 1.
The essential concepts in Dynamic Maxent across Entwined Scales (DyMES). Maxent imposes constraints derived from the time-evolving macroscale state variables on the probability distributions of the microstates of the system, and mechanistic microstate dynamics are expressed using transition function that can depend upon state variables as well as upon microvariables. Macroscale variables are updated in time by suitable averages of state variables and their time derivatives over the probability distributions. This results in a theory that hybridizes mechanism and Maxent.
The General Theory
Some Notation.
We consider a system that is characterized by m macroscale state variables, , and up to m corresponding microscale variables . For example, in thermodynamics the state variables might be total thermal energy and total number of molecules in a gas, while the microscopic variable could be the kinetic energy of a randomly selected molecule. We also denote by R(x) the joint probability distribution over the microscale variables.
To determine R(x), the Shannon information entropy of R(x) is maximized subject to constraints imposed by and . We denote these constraints as , where the are functions of the state variables. As in the example of classical thermodynamics, where a constraint on the distribution of molecular kinetic energies is total thermal energy divided by the total number of molecules, the are often ratios of the Xi.
The functions whose averages over R yield those constraints are denoted by . For the are functions of the . In the thermodynamic example, the f corresponding to the constraint of total energy divided by total number of molecules would just be the microvariable the kinetic energy of a randomly selected molecule, but in more complex cases, the for , can be functions of more than one microvariable (34). Scale entwinement arises because for the , which are the transition functions, can depend on macrovariables as well as upon microvariables . We assume, for simplicity in what follows, that the transition functions do not depend explicitly on the time derivatives of the X nor explicitly on time. We can then write all the constraint conditions as:
| [1] |
where , the sum denotes a sum over each of the xi, and the conditionality of R on X is explicit. In what follows, we often reexpress this sum over microvariables using the notation “< >” to denote the average, as .
The Maxent Solution.
Maximizing the Shannon information entropy, , of R we obtain (4–6)
| [2] |
where are the Lagrange multipliers (4, 10) obtained by solving the constraint conditions, and is a normalization constant. Although each term, F, f, R, and in Eqs. 1 and 2 can be time dependent, the time variable is not written explicitly. The x are summation variables and are not time-dependent.
Updating the Xi and their Time Derivatives.
A defining assumption of DyMES is the procedure for updating constraints. If the X and dX/dt are known at time t, then the are determined by the Maxent condition at time t. To obtain the at time t + dt, we have to update the constraints. X(t + dt) is calculated directly using dX(t)/dt:
| [3] |
To update dX/dt, Eq. 1 is modified by evaluating the transition functions both where they multiply R and where they appear in the second exponent in Eq. 2, with the value of X at t + dt. The , however, are evaluated at time t. In equation form, and for :
| [4] |
Eq. 4 can be contrasted with the constraint equations at time t + dt which, from Eq. 1, read:
| [5] |
The Lagrange multipliers in the constraint Eq. 5 are evaluated at t + dt, while in the updating Eq. 4, they are evaluated at time t. In both, the transition functions, f, are calculated using the value of X at t + dt. This updating procedure is the only consistent one that we could define and implement, but proof of its uniqueness within the overall DyMES framework is lacking.
Core Differential Equations for the and the Xi.
Subtracting Eq. 4 from Eq. 5, and making use of the form of R in Eq. 2, we obtain (SI Appendix, SI I for a derivation):
| [6] |
where the index i ranges from 1 to m, and Cov(A, B) = <AB> − <A><B>. Eq. 6 provides m relationships among the 2m time derivatives of the Lagrange multipliers. To proceed, we make use of an identity that is valid for any probability distribution of the form of Eq. 2 (SI Appendix, SI I for a derivation):
| [7] |
where A is any differentiable function of the xi and the Xi. Letting A = in Eq. 7 results in:
| [8] |
Eqs. 6 and 8 can be solved rapidly by matrix inversion to determine the time derivatives of the . We can then iterate the Lagrange multipliers as .
An additional set of equations can be derived for the time evolution of the Xi. Letting A in Eq. 7 equal , then for i = 1, …, m:
| [9] |
The Force-Free Limit of DyMES.
If all the transition functions are independent of the Xi but are arbitrary function of the xi, then their time derivatives obey , and so from Eq. 9, d 2Xi/dt2 = 0 in every case. Thus, if downward causation in the form of dependence of transition functions on state variables is completely absent, systems are effectively force free (zero acceleration of the state variables). In that case, only exogenous macrolevel forcing mechanisms can accelerate state variables. Additional examples of analytically solvable, closed form, solutions to model realizations of DyMES are given in SI Appendix, SI III.
A Single-Variable Illustrative Model System.
To provide a more intuitive understanding of DyMES, and show examples of applications and potential tests of its predictions, we present a model-system realization with a single microvariable, a single state variable, and a single transition function. Specifically, consider a system with N individual entities divided among S, mutually exclusive categories. For simplicity, we assume that S is a fixed number, and thus not a state variable, whereas N is a time-dependent state variable. Entities could be, for example, molecules of a gas, people in a pandemic or an economy, or individual trees in a forest. Categories could be energy levels of molecules, social clusters in a pandemic, income brackets in an economy, or species of trees.
Let the microscale variable, n, be the number of entities in a randomly selected category. We define P(n) to be the probability that if a category is selected at random at time, t, then it contains n individuals. The Shannon information entropy of P(n), , is maximized at every moment in time subject to the constraints imposed by the instantaneous values of the macrovariable N(t) and its time derivative. Eq. 1 now take the form:
| [10] |
and
| [11] |
where all quantities are evaluated at a common time, t. In Eq. 11, f(n, N) is the single transition function describing dynamics at the microscale; with scale entwinement, it is a function of N, as well as of n. Eq. 2 now becomes:
| [12] |
The Lagrange multipliers, and the normalization constant, z, will be functions of the time-dependent state variable, N.
In this simple model, Eqs. 6 and 8 provide two relationships between the time derivatives of the two Lagrange multipliers, which can be solved to give:
| [13] |
| [14] |
and for the time evolution of the state variable, N, Eq. 9 gives:
| [15] |
where . These expressions are derived in SI Appendix, SI II, along with an analytic expression for the time derivative of the Shannon entropy. The explicit procedure for solving DyMES iteratively, using the illustrative model as an example, is given in SI Appendix, SI III.
Applications of the Simple Model.
The Table 1 shows four examples of single-state-variable applications of DyMES. After a brief description of the first three examples, we explore in more detail the ecological example, focusing on some unexpected responses of the state variable, N, and distribution, P(n), to several types of perturbation from steady state. We argue in the Discussion section that these responses are interrelated and are likely to be pervasive outcomes in many applications of DyMES.
Table 1.
Potential applications of the single-variable illustrative model of DyMES
| Model Structure | State Variable | Microlevel Variable | Probability Distribution | Transition Function | Goal of Application |
|---|---|---|---|---|---|
| Application | |||||
| Chemical reaction | Thermal energy of mixture, E | Molecular kinetic energies, ε | Kinetic energies across molecules | Predict nonequilibrium distribution of molecular energies | |
| Pandemic | Total incidence of disease, I | Incidences within social clusters, n | Incidence across multiple social clusters |
f (n, I) = r0 (1-I/M)m-n)n – d0n |
Determine influence of publicizing disease prevalence on incidence |
| Wealth distribution | Gross domestic income, I | Incomes of individuals, n | Income over individuals |
|
Determine effect of policy on relationship between inequality and GDP growth |
| Multispecies ecological community | Total community population size, N | Abundances of species, n | Abundances over species |
|
Determine effect of perturbation on abundance |
The transition functions shown here are explained in more detail in the main text, SI Appendix, SI IV and SI V.
The first application and potential test of DyMES in Table 1 is to nonequilibrium chemical thermodynamics. The system consists of two gases, chosen to react exothermically but not explosively at low concentration within an inert gas in a calorimeter. We can use DyMES to address the question: At what rate does the temperature in the vessel increase as the reaction proceeds? Before the reaction commences, the Maxwell–Boltzmann distribution characterizes the equilibrium distribution of molecular kinetic energies. As the reaction proceeds the average kinetic energy of the molecules will increase, the reaction will accelerate, and the nonequilibrium distribution P will acquire an term as in Eq. 12, where E and are defined in Table 1 and the former is now time-dependent. The transition function can be calculated by first letting N(t) equal the number of molecules of whichever gas is limiting the reaction, and writing:
| [16] |
where c0 is a reaction rate constant, is the activation energy for the reaction, and is a step function equal to 0 for and 1 for . By writing the transition function as in Eq. 16, rather than using the Arrhenius expression, we avoid having to assume a Maxwell–Boltzmann distribution for a system out of equilibrium. To replace the state variable N in Eq. 16 with the more convenient state variable, E, we let be the heat produced by a single molecular reaction, so that:
| [17] |
Eq. 17 results in the expression for the transition function given in Table 1. A derivation of the transition function and more detailed description of the proposed experiment are given in SI Appendix, SI IV. By solving DyMES for E(t), the time dependence of the temperature can be calculated using E = (3/2)NTkT, where NT is the total number of molecules, and compared with the observed rate of temperature increase to provide a test of DyMES.
Another potential application is to the spread of pandemics in circumstances in which, at the microlevel, human behavior that spreads disease among individuals within social clusters is influenced by information about the overall incidence of disease in the greater population (macrolevel). For example, consider a nation with, at the macrolevel, M individuals of whom I are infected and upon recovery are again susceptible. The microlevel consists of social clusters, for example communities, that in the simplest case each contain m individuals, of whom n are infected. If individual behavior within groups is, for example, influenced by information from the media regarding the magnitude of I, then we could write dI/dt = (M/m) < f(n, m, I, M)>, where a plausible form for the transition function might be f = r0((1 − I/M)m − n)n − d0n. The term (1 − I/M)m is the effective group size, with meff < m as a consequence of some individuals within groups responding to information about overall infection rates by avoiding exposure to others. The term r0(meff − n)n replaces the traditional term r0SI in the expression for dI/dt in an SIR model (7). Application of DyMES will predict a time-dependent distribution P(n) across groups as well as the time trajectory of the total number of infected individuals, I. The above is easily generalized to the case in which infected individuals die or become immune, and in which group size varies across groups, resulting in a time-dependent distribution P(n,m).
In one of many possible economics applications, DyMES could predict a pattern-process linkage between income inequality across income earners and the growth trajectory of an economy. Assume, for example, a transition function f(n, I) where I is national income and n is individual share of I. Consider a very simple transition function of the form describing personal income growth, where a and b could be greater or less than 1. The exponent a reflects how fast individual wealth begets more wealth (the larger is a, the faster the rich get richer). The exponent b reflects the priority given to investing national tax revenue into wealth creation. As seen in Eqs. 12 and 15, both parameters will influence, and thus interconnect, the shape of the income distribution, P(n), and the rate of growth of national income, dI/dt.
The last application of the illustrative DyMES model in Table 1 is to the population dynamics of a multispecies ecological community. We explore here a transition function that generalizes the classic logistic model describing the growth or decline of an isolated population of size n in a closed environment (8). It includes both the nonlinear dependence of the rate of change of a population of a randomly selected species on n, as in the logistic model, and also a scale entwinement arising from causal dependence of the transition function on the size of the total community population, N:
| [18] |
SI Appendix, SI V further motivates Eq. 18 and describes its relationship to both the classical logistic equation for a single species and the Lotka–Volterra Eq. 8 for a community of species.
We examine the responses of N(t) and P(n) to a variety of perturbations to gain insight into the nature, distinctiveness, and potential value, of predictions made by DyMES. We look at displacement from steady state of N, and fixed, periodic, and stochastic changes in a rate constant. For purposes of numerical analysis, we choose parameter values that are plausible for a mature forest (SI Appendix, SI V for details).
Following an initial increase in the death rate parameter d2 in the transition function, Eq. 18, the state variable N decreases and asymptotes to a new steady state very slowly compared to equilibration in the comparable logistic model: (Fig. 2A). Moreover, the displacement of N from its original steady state is much greater in DyMES than in the logistic model. The Lagrange multiplier increases from its initial value of 0 and approaches a new steady state with (http://www.pnas.org/lookup/doi/10.1073/pnas.2408676121#supplementary-materialsSI Appendix, Fig. SI VII.a). Thus, DyMES admits of two classes of steady state: those in which the Lagrange multipliers associated with the transition functions are zero and nonzero. This same conclusion was reached in a more complex application (34) of DyMES with three dynamic state variables.
Fig. 2.
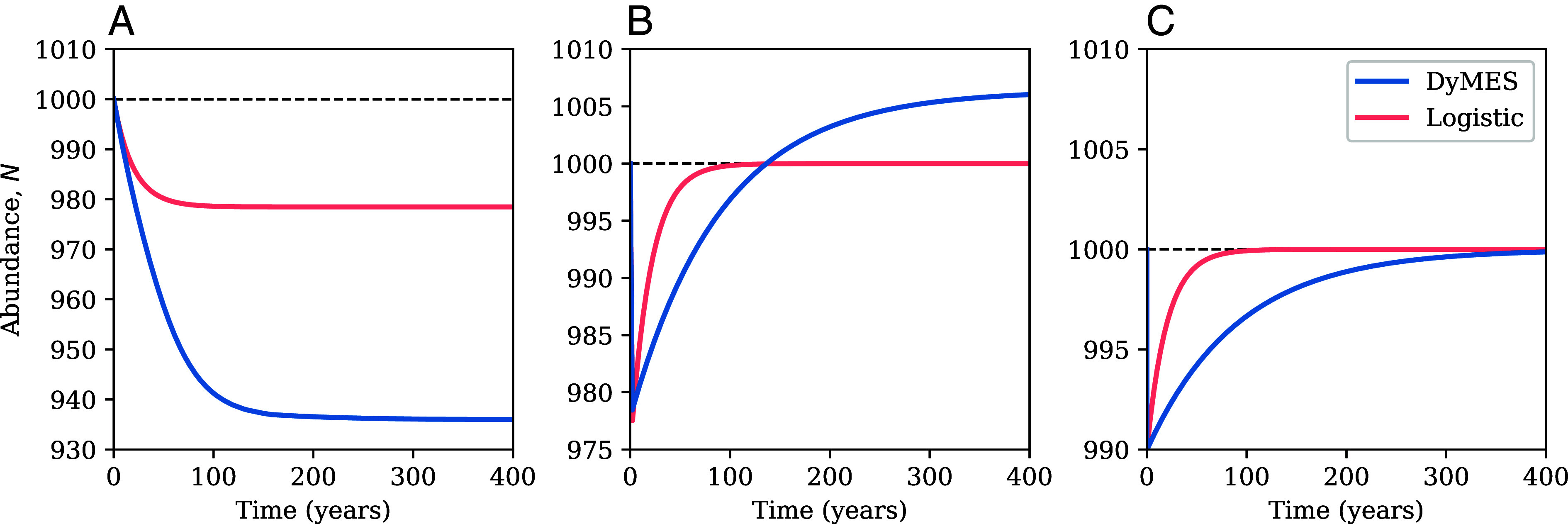
Responses to perturbations in the DyMES illustrative model. (A) Response of the total abundance, N, to a 10% increase in d2 in Eq. 18, and a comparable increase in d0 in the logistic model. (B) Response of the total abundance, N, to a doubling of the death rate parameter d2, followed 2 y (20 iterations) later by restoration to the original value, and a comparable increase (SI Appendix, SI V) and recovery of d0 in the logistic model. (C) Response of the total abundance, N, to a decrease in the initial value of N from 1,000 to 990 in the illustrative model realization of DyMES and in the logistic model.
If d2 is subsequently returned to its original value, then N overshoots its original steady state (Fig. 2B) and does not return to zero (http://www.pnas.org/lookup/doi/10.1073/pnas.2408676121#supplementary-materialsSI Appendix, Fig. SI VII.b). The longer the delay before restoration of d2, the larger the initial drop in the value of N, the faster its rate of recovery and the larger its eventual steady state (SI Appendix, Fig. SI VII.c). This hysteresis effect increases with the magnitude of the initial perturbation as well as with its duration before restoration. Hysteresis also arises in the more complex model (34) and appears to be a pervasive phenomenon predicted by DyMES. The perturbed logistic model, in contrast, exhibits more rapid recovery and no hysteresis (Fig. 2B).
If d2 oscillates around its original steady-state value then N oscillates around a mean that trends slowly toward a value above its initial steady-state value (http://www.pnas.org/lookup/doi/10.1073/pnas.2408676121#supplementary-materialsSI Appendix, Fig. SI VII.d). Under the same perturbation in the logistic model, N recovers more rapidly than in DyMES and to a state of oscillation around a mean that is equal to its original steady-state value.
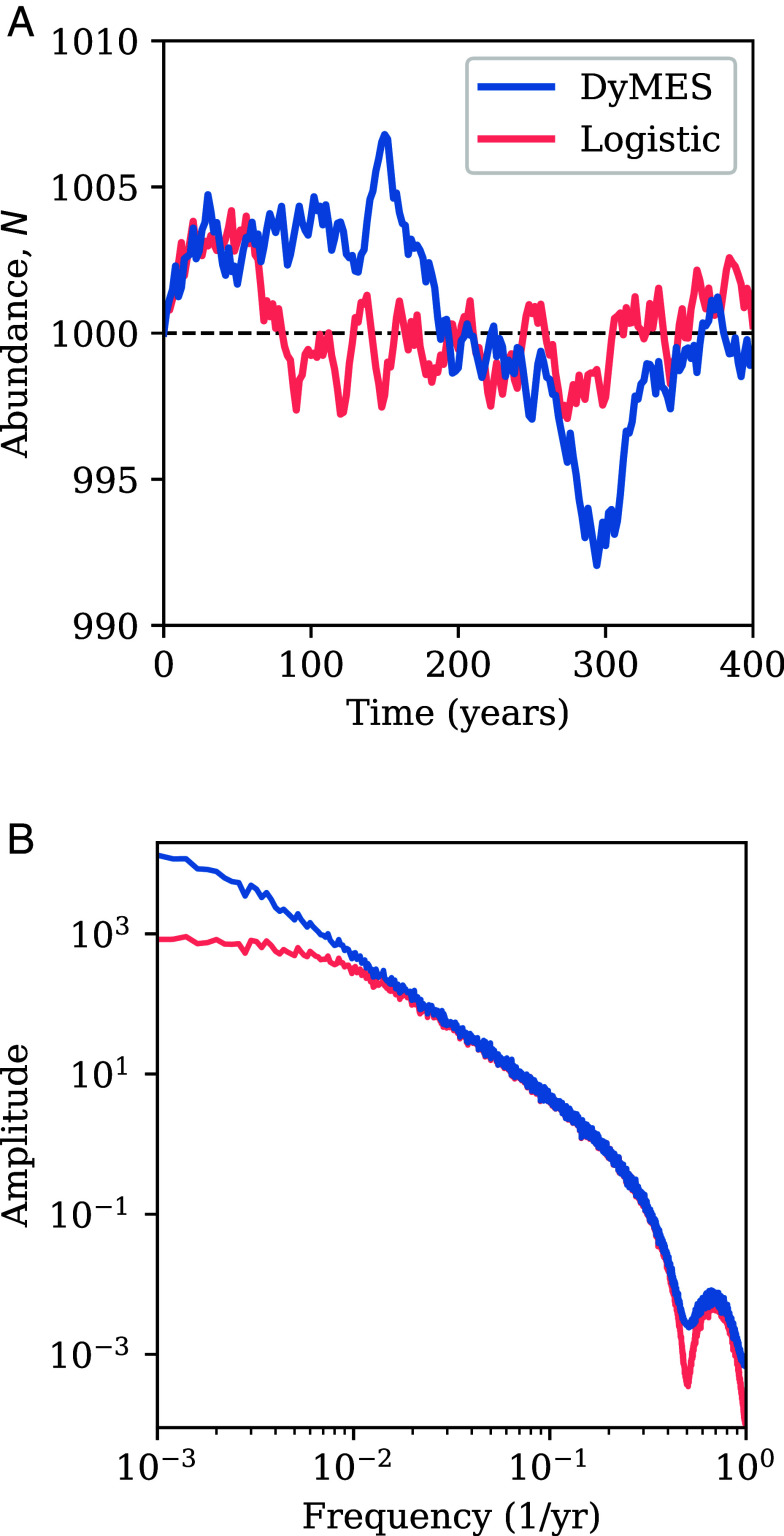
In response to white noise, biennial variation in d2, DyMES exhibits much more variability at low frequency (for example, ~0.01/y) than does the logistic model (Fig. 3 A and B). The reddened time series spectrum highlights low frequencies that correspond to neither the time scale of the stochastic fluctuations nor the intrinsic time scale associated with birth and death processes (1/r0 = 20 y) in the model.
Fig. 3.
Response to a stochastic death rate. (A) Response of the total abundance, N, to uniform stochastic variation every two years in the death rate constant, d2 in the illustrative model realization of DyMES, in the interval d2 ± 5%, and a comparable stochastic variation in the logistic model death rate parameter, d0, in the interval d0 ± 1.1%. (B) Power spectrum of the spectral density function (sdf) of N(t) under the same perturbation as in A. Shown is the average sdf over 100 model runs, each over 5,000 y, using an iteration interval of 0.1 y.
Following an initial perturbation in which N is reduced in value from its initial steady state, N recovers to the original steady state, but again much more slowly in DyMES than in the logistic model (Fig. 2C). Moreover, also returns to zero, its original steady-state value (SI Appendix, Fig. SI VII.e).
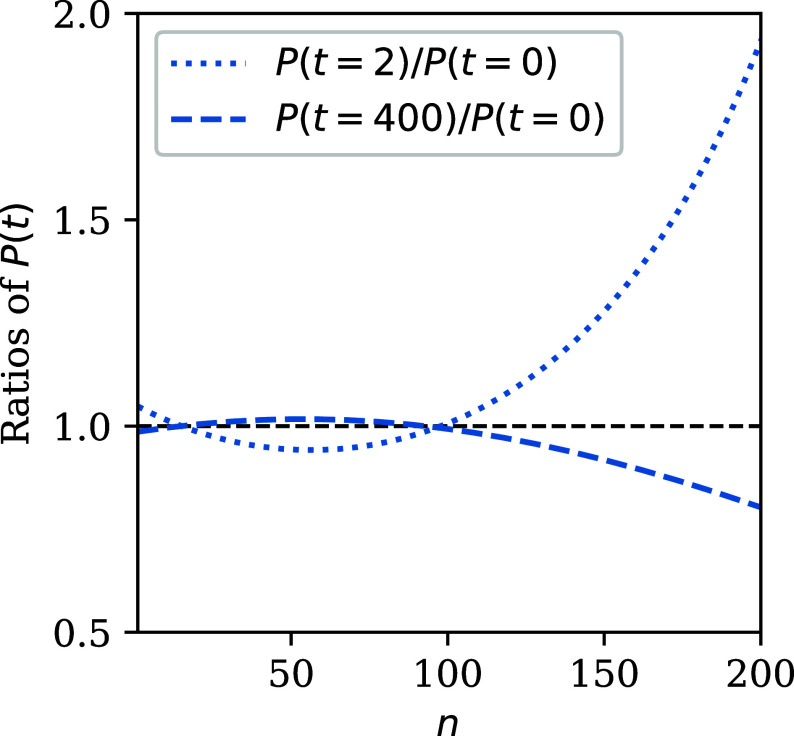
A general feature of DyMES is that it predicts a relationship between the form of distributions over microvariables, R(x, X) and the transition functions governing dynamics. Because in many systems such distributions are measurable (20), insight can be obtained into the nature of a perturbation from the signature provided by the distribution (34). In the illustrative ecological model, we examine the effect on P(n) of initially doubling d2 at t = 0 (equivalent to a 22% increase in total death rate in eq. 18) when the system was in steady state, and then restoring d2 to its original value at t = 2 y. At t = 2 y, when N is rapidly changing immediately prior to restoration of the death rate, the distribution deviates considerably from the steady-state distribution at t = 0, while at t = 400 y when the system has approached a new steady state, the distribution is practically indistinguishable from that at t = 0 before the perturbation was imposed (Fig. 4). The deviation at t = 2 is a consequence of the term in Eq. 12. The pattern of departure of the distribution from its equilibrium form is clearly case-specific because the perturbed distribution depends explicitly upon the transition functions; different types of perturbations will result in different forms of the probability distributions.
Fig. 4.
Response of P(n) to an initial doubling of the parameter d2 in Eq. 18, followed two years later by restoration of d2 to its original value. P(n) is plotted at t = 0, at t = 2 y when N is changing rapidly, and at t = 400 y when the system has approached a new steady state.
Discussion
DyMES is a theory of scale-entwined systems in which macroscale state variables explicitly influence processes governing microscale variables and constrain the probability distributions over those variables. By including time derivatives of state variables in the constraint set, an iterative procedure is defined which allows calculation of both the state variable trajectories over time and the changing shape of the microvariable distributions. The functional form of the latter is determined by the dynamics as expressed in transition functions that can depend upon both micro- and macrovariables. DyMES hybridizes mechanism with Maxent, effectively linking finer-scale phenomena to coarser-scale outcomes via an inferential tool that predicts finer-scale distributions from coarser-scale knowledge. DyMES predicts the time evolution of both the state variables and the probability distributions over microvariables.
Relationship to Other Dynamical Models.
Several dynamical modeling approaches in complex systems theory bear at least some similarities to DyMES.
Incorporation of state variables in transition functions can be compared to using a mean field approximation. For example, our illustrative DyMES model with transition function given by Eq. 18 superficially resembles a mean field approximation to the Lotka–Volterra Eq. 8 used in ecology to describe the dynamics of populations of a multispecies community. By hybridizing Maxent with mechanism, however, dynamics in our theory obey time-evolution rules for both state variables and probability distributions over microvariables that differ from those in mean field models.
Another class of models describes time evolution of probability distributions as a Markov process (35) using a master equation approach. Unlike DyMES, in most master equation models, the transition functions do not depend upon the distributions over microvariables. In one Markov model application (12), however, such dependence can be incorporated and Maxent is used to infer the form of a transition function using observed time series data as constraints. DyMES, in contrast, predicts the time evolution of state variables and distributions over microvariables based on the assumed dependence of transition functions on micro- and macrolevel variables.
Maximum entropy production and maximum caliber (6, 36) extend the use of Maxent from distributions over microstates to the distribution of paths through phase space during thermodynamically irreversible transitions. Maximum caliber predicts the final state to in a nonequilibrium process to be that state to which the most paths through phase space that begin at the initial state lead. DyMES, too, predicts the trajectory of the macrostate and also the time-dependent probability distribution over microvariables throughout the process. An analytic expression for the time rate of change of Shannon entropy in DyMES is readily calculated (SI Appendix, Eqs. SI–S20), but whether the rate of change of information entropy in DyMES obeys an extremum principle in nonstationary processes remains to be investigated. Thus, for now, possible connections between DyMES and either maximum entropy production or maximum caliber are open questions.
Another theory (25) of nonequilibrium thermodynamic systems with constant gradients invokes the notion of “second entropy,” a dynamic analog of entropy in equilibrium systems. Whether this promising approach can be applied to the variety of scale-entwined, nonthermodynamic systems, with dynamic gradients and no well-defined thermodynamic entropy, is unclear.
A recent proposal (37) to extend Maxent from the static to the dynamic domain combines Maxent with explicit stochastic forcing in a quasi-stationary approximation. In contrast to DyMES, this approach does not address bidirectional causation and does not include among the constraint set the rates of change of state variables.
Time derivatives of state variables as constraints in a Maxent application have been utilized previously in atmospheric science (38), although only for an equilibrium configuration with zero average velocity. DyMES is a formulation of a more general theory of dynamical systems using arbitrary velocity constraints.
Finally, an elegant coarse-graining method (39) of Mori and Zwanzig calculates the dynamics of macroscopic variables from coarse-grained, multivariate microscopic dynamics. In contrast to DyMES, it does not incorporate downward causation in the form of explicit dependence of microvariable dynamics on macrovariables.
Linking Pattern to Process with DyMES.
DyMES predicts the changing shapes of probability distributions over microscale variables and, in particular, their deviation from steady state or equilibrium when specific processes described by the transition functions cause the deviations from steady state. The reason is seen in Eq. 2, in which the appearance of the explicit mechanisms at the microlevel captured by the , appear in R, the distribution over microvariables. In a more complex ecological model (34) than our single-variable model above, with three dynamic state variables, DyMES relates the empirically changing shape of the species abundance distribution in a disrupted ecosystem to specific processes that could be causing the perturbation. In a warming thermodynamic system, DyMES relates the changing functional form of the distribution over molecular kinetic energies to specific processes, such as exothermic chemical reactions, driving departure from equilibrium.
DyMES also allows additional information about disruption mechanisms to be extracted from observation of the time evolution of the state variables (34). An example of this is seen in Fig. 2; the existence of hysteresis distinguishes a transient perturbation in a rate constant from an initial displacement of a state variable.
Responses to perturbations.
Four signature responses to perturbations were observed in the illustrative DyMES model output when contrasted with a comparable model lacking bidirectional causation:
-
i)
Relatively slowed response and recovery (decreased resilience) and larger magnitude response (decreased resistance) of state variables to perturbations (Figs. 2 and 3 and SI Appendix, SI VII.e).
-
ii)
Hysteresis in the response of state variables to displacement, followed by restoration, of a rate constant in a transition function (Fig. 2B and SI Appendix, Fig. SI VII.b).
-
iii)
Two classes of steady state, characterized by Lagrange multipliers associated with transition functions that are either zero (class 1) or nonzero (class 2), and under perturbations in rate constants, systems transition from class 1 to class 2 but not vice versa (SI Appendix, Fig. SI VII.b).
-
iv)
Considerably reddened time series of a state variable in response to white-noise stochastic variation in a rate constant in a transition function (Fig. 3 A and B).
Time series analysis of long-term population census data reveals, at least qualitatively, such a spectral reddening (40). While it has been speculated that this observed reddening can be attributed to environmental long waves (41), we suggest such reddened spectra arise even in the absence of long-wave exogenous noise.
Hysteresis, irreversible transitions between the classes of steady state, and slower responses to perturbations were also observed in the output from a more complex higher-dimensional DyMES model (34) and are plausibly a consequence of both state variable dependence of transition functions and the feedback arising from the iteration procedure in which Top–Down and Bottom–Up causation alternate. An eigenvalue analysis provides insight into the interconnections among these observed outputs. A comparison (SI Appendix, SI VI) of dominant eigenvalues for the logistic model (−r = −0.05) and for the illustrative ecological DyMES application (−d2<n> = −0.011) reveals the latter is smaller in magnitude than the former and thus the recovery time constant is longer.
That analysis may also explain the more reddened response to stochastic input in DyMES compared to the logistic model. The spectrum of output fluctuations in a dynamical system subjected to stochastic input is determined by the form of the spectral transfer function relating the covariance density function of the input to that of the output (42). That transfer function is typically a function of frequency and of the magnitude of the dominant eigenvalue, which we have seen differs between the logistic model and the DyMES population model. Smaller dominant eigenvalues tend to correspond to enhanced transfer of long waves (42). For the above reasons, and because the observed signature output behaviors are not unique to our simple illustrative model system (34), we find it plausible that the observed suite of response signatures will characterize DyMES output more widely. Further case-by-case analysis, however, is warranted.
The Value of Analytic Expressions for the Time Evolution of the Lagrange Multipliers.
In applications of DyMES, each iteration requires finding the maximum of Shannon entropy and as a result multiple iterations can be computationally slow. For the illustrative single-state-variable DyMES models in Table 1, the time saved using Eqs. 13 and 14, or more generally using Eqs. 6 and 8 to update the Lagrange multipliers, compared to the straightforward method of “brute force” calculations for finding the maximum of Shannon entropy, is small (SI Appendix, Fig. SI VII.f). But in more complex models, including DynaMETE (34) with five Lagrange multipliers, the computational time using Eqs. 6 and 8 is reduced by an order of magnitude compared to brute force maximization.
Future Tasks.
Scale entwinement need not be restricted to only a pair of scales, nor to bidirectional causality only acting across adjacent scales. A remaining theoretical task is to derive explicit analytic generalizations of Eqs. 1-9 for the time evolution of the state variables and the probability distributions over microvariables in such systems. Another direction for future work is to examine the applicability of other information measures besides Shannon’s. Given the central role in DyMES of top–down causation, quantification of the relative magnitude of such causation using transfer entropy could be of interest. In many complex systems, causality can be difficult to disentangle; DyMES may provide a means of quantifying direction and magnitude of causal links. Finally, a critical future task will be to test the ability of DyMES to accurately predict the trajectories of macrovariables and the time evolution of probability distributions over microvariables in nonstationary complex systems; the ecological application in ref. 34 is a step toward this goal but much more testing is needed.
Conclusion
In a pertinent commentary, Goldenfeld and Woese (1) posed a challenge to the scientific community. In complex systems, they noted, the equations governing dynamics at the microscale can depend upon and evolve with the changing macrostate of the system; at the same time, the state variables are sums or averages over suitable distributions of the microvariables. Thus the simple picture of top–down inference, alone, in which macrolevel constraints determine distributions over microvariables, or of Bottom–Up inference, alone, in which the consequences of mechanisms acting at the microlevel can be aggregated to determine macrolevel properties of the system, may no longer be useful for predicting the dynamics of complex systems. The challenge they posed, and that we have responded to here, was to develop theory suitable for addressing the complexity of scale entwinement.
The general theory presented here, and the illustrative model realization, incorporate scale entwinement by hybridizing Top–Down Maxent with bottom–up mechanism. Simulations of DyMES here and in previous work (34) suggest that the theory has the potential to enrich our understanding of perturbed complex systems and to allow attribution of perturbative processes from knowledge of distributions over microvariables and trajectories of state variables. Examples of applications and tests provided here, along with others which we hope readers will envision, can determine how widely applicable DyMES will be to understanding the dynamics of complex scale-entwined systems across many fields of inquiry.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We thank Keon Abedi, Joshua Cal, George Greenstein, Alexis Harte, Alejandro Maass, Roya Safaeinili, Sharanya Sahu, and Meilin Yen for useful discussions and comments on earlier drafts. JH acknowledges support from grant DEB 1751380 from the US National Science Foundation. MB acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), [PGSD2-517114-452018].
Author contributions
J.H. designed research; J.H., M.B., K.U., P.M., and E.A.N. performed research; J.H., M.B., K.U., P.M., and E.A.N. analyzed data; and J.H., M.B., K.U., and E.A.N. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
There are no data underlying this work.
Supporting Information
References
- 1.Goldenfeld N., Woese C., Life is physics: Evolution as a collective phenomenon far from equilibrium. Annu. Rev. Condens. Matter Phys. 2, 375–399 (2011). [Google Scholar]
- 2.Noble R., Tasaki K., Noble P. J., Noble D., Biological relativity requires circular causality but not symmetry of causation: So, where, what and when are the boundaries? Front. Physiol. 10, 827 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chater N., Loewenstein G., The i-frame and the s-frame: How focusing on individual-level solutions has led behavioral public policy astray. Behav. Brain Sci. 46, e147 (2023). [DOI] [PubMed] [Google Scholar]
- 4.Jaynes E. T., Information theory and statistical mechanics. Phys. Rev. 106, 620–630 (1957). [Google Scholar]
- 5.Jaynes E. T., On the rationale of maximum-entropy methods. Proc. IEEE 70, 939–952 (1982). [Google Scholar]
- 6.Pressé S., Ghosh K., Lee J., Dill K. A., Principles of maximum entropy and maximum caliber in statistical physics. Rev. Mod. Phys. 85, 1115–1141 (2013). [Google Scholar]
- 7.Murray J. D., “Mathematical biology: I. An introduction” in Interdisciplinary Applied Mathematics (Springer, New York, NY, 2002), vol. 17. http://link.springer.com/10.1007/b98868. [Google Scholar]
- 8.May R. M., Stability and Complexity in Model Ecosystems (Princeton University Press, 2019). [Google Scholar]
- 9.Shannon C. E., A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948). [Google Scholar]
- 10.Arfken G. B., Weber K. A., Mathematical Methods for Physicists, ed. 6, 2005).
- 11.Brummer A. B., Newman E. A., Derivations of the core functions of the maximum entropy theory of ecology. Entropy 21, 712 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Golan A., Harte J., Information theory: A foundation for complexity science. Proc. Natl. Acad. Sci. U.S.A. 119, e2119089119 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Frieden B. R., Restoring with maximum likelihood and maximum entropy. J. Opt. Soc. Am. 62, 511–518 (1972). [DOI] [PubMed] [Google Scholar]
- 14.Gull S. F., Newton T. J., Maximum entropy tomography. Appl. Opt. 25, 156–160 (1986). [DOI] [PubMed] [Google Scholar]
- 15.Roussev V., “Data fingerprinting with similarity digests” in Advances in Digital Forensics VI, Chow K.-P., Shenoi S., Eds. (Springer, Berlin, Heidelberg, 2010) IFIP Advances in Information and Communication Technology, pp. 207–226. [Google Scholar]
- 16.Skilling J., “Theory of maximum entropy image reconstruction” in Maximum Entropy and Bayesian Methods in Applied Statistics: Proceedings of the Fourth Maximum Entropy Workshop University of Calgary, 1984, Justice J. H., Ed. (Cambridge University Press, Cambridge, 1986), pp. 156–178. [Google Scholar]
- 17.Steinbach P. J., Ionescu R., Matthews C. R., Analysis of kinetics using a hybrid maximum-entropy/nonlinear-least-squares method: Application to protein folding. Biophys. J. 82, 2244–2255 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mora T., Walczak A. M., Bialek W., Callan C. G., Maximum entropy models for antibody diversity. Proc. Natl. Acad. Sci. U.S.A. 107, 5405–5410 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Meshulam L., Gauthier J. L., Brody C. D., Tank D. W., Bialek W., Collective behavior of place and non-place neurons in the hippocampal network. Neuron 96, 1178–1191.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Harte J., Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics (OUP Oxford, 2011). [Google Scholar]
- 21.Harte J., Newman E. A., Maximum information entropy: A foundation for ecological theory. Trends Ecol. Evol. 29, 384–389 (2014). [DOI] [PubMed] [Google Scholar]
- 22.Laurent R., Cai X., A maximum entropy method for combining AOGCMs for regional intra-year climate change assessment. Clim. Change 82, 411–435 (2007). [Google Scholar]
- 23.Golan A., Foundations of Info-Metrics: Modeling, Inference, and Imperfect Information (Oxford University Press, 2018). [Google Scholar]
- 24.Grandy W. T., Entropy and the Time Evolution of Macroscopic Systems (Oxford University, Press, Oxford UK, 2008), p. 209. [Google Scholar]
- 25.Attard P., Theory for non-equilibrium statistical mechanics. Phys. Chem. Chem. Phys. 8, 3585–3611 (2006). [DOI] [PubMed] [Google Scholar]
- 26.Kempton R. A., Taylor L. R., Log-series and log-normal parameters as diversity discriminants for the Lepidoptera. J. Anim. Ecol. 43, 381–399 (1974). [Google Scholar]
- 27.Carey S., Harte J., Del Moral R., Effect of community assembly and primary succession on the species-area relationship in disturbed ecosystems. Ecography 29, 866–872 (2006). [Google Scholar]
- 28.Supp S. R., Xiao X., Ernest S. K. M., White E. P., An experimental test of the response of macroecological patterns to altered species interactions. Ecology 93, 2505–2511 (2012). [DOI] [PubMed] [Google Scholar]
- 29.Rominger A. J., et al. , Community assembly on isolated islands: Macroecology meets evolution. Glob. Ecol. Biogeogr. 25, 769–780 (2016). [Google Scholar]
- 30.Newman E. A., et al. , Disturbance macroecology: A comparative study of community structure metrics in a high-severity disturbance regime. Ecosphere 11, e03022 (2020). [Google Scholar]
- 31.Franzman J., et al. , Shifting macroecological patterns and static theory failure in a stressed alpine plant community. Ecosphere 12, e03548 (2021). [Google Scholar]
- 32.Brush M., Matthews T. J., Borges P. A. V., Harte J., Land use change through the lens of macroecology: Insights from Azorean arthropods and the maximum entropy theory of ecology. Ecography 2022, e06141 (2022). [Google Scholar]
- 33.Xu M., Allen M. R. B., Newman E. A., Earthquake disturbance shifts metabolic energy use and partitioning in a monodominant forest. Glob. Ecol. Biogeogr. 32, 1575–1590 (2023). [Google Scholar]
- 34.Harte J., Umemura K., Brush M., DynaMETE: A hybrid MaxEnt-plus-mechanism theory of dynamic macroecology. Ecol. Lett. 24, 935–949 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Costa A. C., Ahamed T., Jordan D., Stephens G. J., A Markovian dynamics for C. elegans behavior across scales. bioRxiv [Preprint] (2023). 10.1101/2023.10.19.563098 (Accepted 22 October 2023). [DOI] [PMC free article] [PubMed]
- 36.Bolhuis P. G., Brotzakis Z. F., Vendruscolo M., A maximum caliber approach for continuum path ensembles. Eur. Phys. J. B 94, 188 (2021). [Google Scholar]
- 37.Bud’ova K., Szep E., Barton N., Dynamic maximum entropy provides accurate approximation of structured population dynamics. PLoS Comput. Biol. 17, e1009661 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Verkley W. T. M., Severijns C. A., The maximum entropy principle applied to a dynamical system proposed by Lorenz. Eur. Phys. J. B 87, 7 (2014). [Google Scholar]
- 39.te Vrugt M., Wittkowski R., Projection operators in statistical mechanics: A pedagogical approach. Eur. J. Phys. 41, 045101 (2020). [Google Scholar]
- 40.Pimm S., Redfearn A., The variability of population densities. Nature 334, 613–614 (1988). [Google Scholar]
- 41.Lawton J. H., More time means more variation. Nature 334, 563–563 (1988). [Google Scholar]
- 42.Roughgarden J., A simple model for population dynamics in stochastic environments. Am. Nat. 109, 713–736 (1975). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
There are no data underlying this work.