Abstract
This review provides a comprehensive overview of ultrasonic wave propagation, with a primary focus on high-power ultrasound systems where cavitation bubbles are likely to occur. The review is structured to guide readers through the historical development of cavitation models, from early works such as the Rayleigh-Plesset equation to more advanced numerical approaches. It explores the dynamics of cavitation bubbles, their physical effects, and the key factors influencing bubble formation, growth, and collapse. In addition to bubble-induced cavitation, the review addresses nonlinear wave propagation in the absence of bubbles, highlighting phenomena such as harmonic generation and shock wave formation. A detailed discussion on the numerical modelling of ultrasonic systems follows, covering linear and nonlinear approaches, boundary conditions, and the challenges of accurately simulating cavitating systems. The review concludes with an analysis of recent developments, emerging trends, and future directions in computational modelling for ultrasonic applications. By presenting a structured overview of both the theoretical and practical aspects of ultrasonic wave propagation, this work aims to provide a foundation for future research and design improvements in sonochemical and acoustic systems.
1. Introduction
Ultrasound has managed to attract significant attention in the scientific community due to its potential application in many fields, for example sonochemistry, water treatment, sonoluminecence, polymer engineering and biotechnology. A large part of the attention is focused on the acoustic cavitation effect which involves the generation and subsequent collapse of bubbles as a response to the application of an acoustic pressure to a body of liquid. The formation of these high energy bubbles can be exploited in many fields, such as in medicine [10] and in chemical reactions [4]. In sonochemistry, ultrasound is used to affect chemical reactions in such a way that the reaction pathway can be changed to obtain an increase in yield or conversion. However, one key disadvantage of ultrasound enhanced reactions in large scales is the inefficient generation of ultrasound, leading to high operating expenditures. However, it is still potentially an economically viable or even a preferred option in cases where it enables operation of reactors at milder conditions, reduces the use of solvents, or simplifies the overall synthesis process [127]. This has put sonochemistry in a promising spot in the high-value chemical and pharmaceutical industry.
As of today, the computational modelling of acoustic cavitation systems remains a formidable challenge due to the complexity arising from the interactions between multiple physical systems. To improve the accuracy of the model, one would usually have to generate a system which considers fluid dynamics, heat and mass transfer, acoustic fields and chemical reaction kinetics. The complexity of the system is further enhanced when multiple phases are to be simulated, such as in heterogeneous systems. Due to its complex nature, enormous number of experiments, characterisation and optimisation work has been carried out by researchers on their respective acoustic cavitation systems.
Whilst these were deemed to be useful, they often lack the fundamentals of bubble dynamics, acoustical behaviour and the underlying theories contributing to a generalised sonochemical behaviour. As such, an alternative to overcome the shortcomings of acoustic cavitation systems is to investigate in depth the theoretical fundamentals of bubble interactions towards acoustical systems.
Recent advancements in the computational modelling of acoustic cavitation systems have made significant strides in incorporating complex physical interactions, including fluid dynamics, heat transfer, and chemical reaction kinetics. Early models, such as the Rayleigh-Plesset equation, provided the foundation for understanding bubble dynamics, but their limitations in simulating multi-phase and heterogeneous systems became evident as the field advanced. Current models aim to improve the accuracy of predicting cavitation behaviour by integrating more sophisticated approaches, such as non-linear wave propagation and bubble–bubble interactions. This review seeks to provide a comprehensive overview of these developments, placing the state of the art in the context of the challenges and opportunities for optimizing acoustic systems in various industrial applications, such as sonochemistry and ultrasonic cleaning. The review also aims to highlight gaps in current methodologies and propose future directions for advancing the field.
2. Brief History on the modelling of acoustic systems
In the case of mathematical models, the first model depicting the cavitation phenomena in incompressible fluids was presented by [113]. The equation which initially ignored the effect of viscosity and surface tension, was later improved upon by [108] by considering these parameters to give the well-known Rayleigh-Plesset equation which describes the dynamics of a spherical bubble. The discovery of the beneficial effects of ultrasound on chemical systems took place in a similar period, where it was first found to show an enhancement in reaction rates in in a chemical system [114] and a biological system [146]. Since then, many important discoveries related to the field of sonochemistry have been published. The concept of rectified diffusion, which refers to the bubble growth due to unequal mass transfer across the bubble boundary during cavitation, has also been introduced by [49]. The first computational modelling on cavitation was carried out by [4] who have modelled the motion of a cavitation bubble using a differential analyser. Another important acoustic phenomenon – acoustic microstreaming, also occurs [20].
Acoustic microstreaming was identified to be the main factor responsible for the observation of ultrasonic cleaning in heterogeneous systems, which led to the development of ultrasonic cleaning baths. Another important development in the field comes in the form of a hypothesis proposed by [102], which states that a bubble which collapses in contact with a solid boundary may cause the collapsing bubble wall to strike the solid before the minimum bubble volume is reached, leading to physical damage to the solid boundary. This hypothesis, which is proposed under the assumption that the bubble is non-hemispherical but axially symmetrical is still an important concept in explaining the pitting and size reduction of solids in heterogeneous systems. Cavitation can be classified into two main categories, transient cavitation and stable cavitation, both which are still very important in describing cavitation activity today [44].
3. The acoustic system
An acoustic system in this paper refers to a system that is produced by propagating an ultrasonic acoustic wave through a liquid medium, generally using a sound wave emitter such as an ultrasonic transducer. When the sound wave propagates through the system, it both causes and experiences various phenomena which have been studied and even applied in various fields. One particularly useful phenomenon that arises from this system is the generation of cavitation bubbles.
3.0.1. Bubble formation and dynamics
Early studies have found out that propagating ultrasound through a medium containing chemical reactant positively affected the reaction yields [114]. Ultrasound, with wavelengths spanning from above 20 kHz, produces acoustic wavelengths ranging from around 10 cm to 1 µm when sound velocities are generally around 1500 m/s, such as in water. These wavelengths are a few orders of magnitude larger than the molecular level. This indicates that instead of a direct coupling between the acoustic field and chemical species, some other phenomenon is responsible for these observations. This phenomenon was determined to be acoustic cavitation [79], [91], [122]. Propagating ultrasonic waves across a liquid medium generates bubbles which are formed via nucleation upon pre-existing gas bubbles dissolved in the system, particles of solid impurities or even nucleation sites on surfaces [91]. The generated bubble is not a perfect vacuum, but only a region with relatively low gas pressure. Below critical size, the bubble would be subjected to dissolution back into the liquid due to the Laplace pressure in the bubble as well as due to surface tension. Above critical size, the bubble would be able to resist dissolution.
During the rarefaction cycle of the acoustic system, the bubbles can grow to an unstable size whereby they would subsequently collapse, particularly when they are subjected to high acoustic pressures of around 1 bar or more [110]. The time frame of the collapse of the bubble is very small. Modelling works of [101] showed that the bubble collapse occurs in timeframes less than 5 µs. Due to this short timeframe, it is common for models that assume the bubble collapse to be an adiabatic process [127].
The hot spot theory which postulates that cavitation generates local hot spots which can reach extreme temperatures and pressures, has been used to explain sonochemical and sonoluminescent observations. While another theory known as the “electrical theory” has been proposed by [88] as an argument against the hot spot, it has been completely discounted as a mechanism behind sonoluminescence and sonochemistry [89], [127]. As of now, the hot spot theory is still generally accepted in the as the mechanism behind sonochemistry [155]. The theory states that the potential energy stored within the expanding gas bubble is concentrated into a energy dense core when the bubble undergoes implosion [122]. For a single bubble, this can be calculated by performing an energy balance across a model describing the bubble dynamics such as the Rayleigh-Plesset equation and has the findings have also been validated using empirical methods [77]. In practical applications, the reactions do not occur in a single isolated bubble but in a multi-bubble system or a cavitation cloud, which may limit the efficiency of the system and result in less extreme conditions compared to a single isolated bubble [72].
Generation of bubbles using ultrasound is particularly useful in many fields of study. For example, in chemical synthesis of specific products or sonochemistry, where the generation of cavitation bubbles facilitates the reactions at extreme thermodynamic conditions locally. These extreme conditions, often referred to as hot spots, can exhibit high temperatures (up to 5000 K), high pressures (around 1000 atm) and high temperature changes (above 1010 K/s), allowing the reaction of chemical species in a body of liquid with low temperature [5], [122], [148]. The amount of energy generated for a single collapsing bubble can be up to 13 eV [53]. In this energy dense core, the extreme thermodynamic conditions can cause ionisation and plasma formation [39], leading to the observations of sonoluminescence as well as the generation of ions and free radicals based on the chemical species in the system [50], [85], [122].
Upon nucleation, the bubble is further subjected to the compression (high hydrodynamic pressure) and rarefaction (low hydrodynamic pressure) cycles generated by the applied acoustic field, which causes the bubble to contract and expand respectively. When the bubble undergoes expansion, the lower pressure within the bubble drives mass transport into the bubble. On the other hand, when the bubble is compressed, its higher interior pressure drives mass transport outwards. However, since the rate of mass diffusion across the surface boundary of a bubble is dependent on its surface area, there may be a net positive in mass transfer into the bubble, which induces bubble growth. This is also known as the “area effect”. On a similar note, the thickness of the liquid–air boundary which affects mass transfer in and out of the bubbles is also affected by the acoustic pressure cycles and can also induce positive bubble growth [23]. This is known as the “shell effect”. Both the “area effect” and “shell effect” primarily contribute to the phenomenon known as rectified diffusion, which is used to describe bubble growth in acoustic systems [74]. Bubble stability is found to be dependent on a critical size [72].
In the case where a bubble can oscillate around a mean radius for many acoustic cycles, this observation is termed stable cavitation. On the other hand, if a bubble only exists for a relatively short time scale followed by the subsequent collapse of the bubble, it is called transient cavitation [3]. These terms were first coined by the works of [40] to classify the difference in behaviour between the two types of cavitation. Today, the terms stable and transient cavitation are also referred to as non-inertial and inertial cavitation respectively, following the works which provided a more in-depth understanding on the mechanisms involved in these phenomena [19]. In general, stable/ non-inertial cavitation is observed at low acoustic pressures. Increasing the acoustic pressure can cause a transition into the state of transient/ inertial cavitation [141]. As a general rule, transient/ inertial cavitation can be said to occur when the maximum radius of the expanding bubble is equal to or greater than twice its equilibrium radius [41]. The bubble radius which is twice the equilibrium radius of the bubble is also referred to as the inertial cavitation threshold [141].
3.0.2. Physical effects of cavitation bubbles
The cavitation effect also causes notable physical phenomena in the system which could be exploited for certain applications. It is this physical effect that is responsible for many observations such as ultrasonic cleaning, erosion, pitting and enhancement of surface chemistry [5]. Studies have reported that when a cavitating bubble collapses near a significantly larger surface, the collapse would occur asymmetrically, generating high velocity liquid jet that smashes into the surface [103], [117]. It has been known since a long time ago that cavitation is the culprit behind pitting deformation of boat propellers [128]. A cavitation bubble can release a significant amount of kinetic energy towards its surroundings when it implodes or explodes. The energy is released in the form of microjets and shockwaves (Pokhrel, et al., 2016). The microjets and shockwaves can drive a significant degree of micromixing in the system, greatly enhancing mass transfer [33]. Studies have also shown that these jets and shockwaves which can have speeds up to 4000 m/s can be used to induce high velocity collisions between micro particles in the system [111]The high energy shockwaves and microjets can also be used to create structural changes in solid–liquid systems, where brittle solids can be broken down into smaller fragments in the process referred to as sonofragmentation [154].
3.1. Factors affecting cavitation
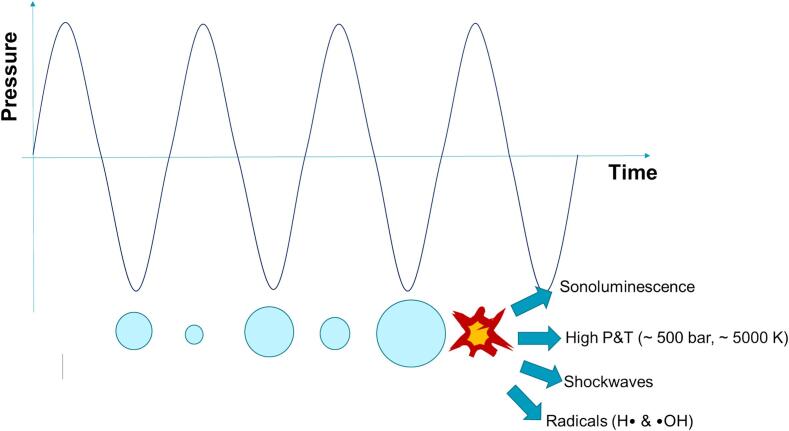
The conditions of the system can greatly affect the intensity of the cavitation phenomenon. The intensity of cavitation depends on how the system affects the bubbles throughout their lifetimes, including nucleation, growth and collapse. In this section, these factors affecting the intensity of cavitation are discussed. Fig. 1 illustrates the acoustic pressure cycle in a liquid medium, with the formation, expansion and contraction of cavitation, which eventually leads to the implosion of the bubbles. As seen in Fig. 1, the collapse of the cavitation leads to immense formation of shockwaves, production of light called sonouminescence, formation of radicals and generating high local temperature and pressure. These were the main contributing factors to the overall sonochemical activities in an ultrasonic system; hence the further sections below describe the individual factors contributing to the cavitation profiles.
Fig. 1.
Schematic of acoustic pressure cycle when ultrasound is subjected in a liquid medium, forming the growth, expansion, and contraction of cavitation.
3.1.1. Presence of dissolved gases
Dissolved gases which exist as small microbubbles in the medium, are often the primary nucleation site for cavitation activity. Dissolved gases also influence bubble growth as they diffuse into the bubble. As the presence of dissolved gases greatly affects cavitation activity, it is a common practice to bubble gases through the medium in studies and applications involving cavitation. The species and characteristics of the dissolved gas also play a role in influencing cavitation and studies have been done on this topic [37]. A general rule often followed in that a gas with a higher specific heat ratio shall offer a greater cavitation effect than that with a lower specific heat ratio. This implies that monoatomic gases provide more efficient energy release compared to diatomic gases. Other parameters include the solubility and thermal conductivity of the dissolved gas [127]. In systems where the formation of radicals through cavitation are important, the reaction undergone by the dissolved gas species is crucial and studies are often conducted on the effect of various gas species on sonochemical applications.
3.1.2. Temperature and pressure
In sonochemistry, bubbles generated through acoustic cavitation play a pivotal role in chemical reactions by creating localized extreme conditions. As ultrasonic waves propagate through a liquid, alternating compression and rarefaction cycles cause microbubbles to form, grow, and collapse violently. During collapse, the temperature inside the bubble can reach up to 5,000 K, with pressures around 1,000 atm, triggering endothermic dissociation of vapor molecules, such as water (H2O →H2 + ½ O2). This dissociation absorbs heat, moderating the peak temperature inside the bubble and altering its internal dynamics. The breakdown of vapor into smaller molecules also produces reactive free radicals, such as hydroxyl (OH•) and hydrogen (H•), which enhance chemical reactivity in the surrounding liquid. By influencing energy distribution and promoting radical formation, endothermic dissociation contributes to the efficiency of sonochemical processes, making it essential in applications like cleaning, wastewater treatment, and chemical synthesis.
Thermodynamic properties of temperature and pressure also affect cavitation. In the case of temperature, higher temperature leads to an increase in equilibrium vapour pressure of the system, which in turn leads to easier cavitation (lower cavitation threshold). However, from a sonochemical standpoint, this leads to a less energy being released during bubble collapse since the vapour in the bubble not only provides resistance to the bubble collapse, but also causes part of the implosion energy to be used for the condensation of the vapour. In short, while higher system temperature lowers the cavitation threshold, it also lowers the effects of bubble collapse and other effects related to it [54]. In temperature sensitive reaction systems, one would need to optimise the system temperature to balance the effect of reaction kinetics and sonochemical effectiveness [140], [153].
On the other hand, increasing the overall system pressure results in a decrease of equilibrium vapour pressure. This in turn causes the initiation of cavitation to be more difficult (cavitation threshold is increased) but allows for a more intense energy release when cavitation occurs. Therefore, it is common for the overall system pressure to be optimised to balance the cavitation threshold and the cavitation effectiveness to obtain the best results [71].
3.1.3. Physical properties of the liquid medium
The ease of bubble generation as well as the intensity of bubble collapse is also influenced by physical properties of the liquid medium such as the vapour pressure, viscosity and surface tension. In theory, for liquids with higher vapour pressure, lower viscosity and lower surface tension, the cavitation threshold would be lower. However, the intensity of bubble collapse in the liquid would also be reduced. For example, [78] have found that the intensity of cavitation is the highest in solvents with higher viscosity. [28] found that for very volatile solvents, the cavitation effect is not observed.
3.1.4. Ultrasonic frequency and acoustic power
The ultrasonic frequency of a system influences the cavitation effect in a few ways. From the modelling of bubble dynamics, it is known that the system frequency plays an influential role in determining the critical size of the cavitation bubbles. Usually, increasing the frequency of the system would reduce the cavitation effect. This can be attributed to two explanations. Firstly, increasing the frequency would cause the compression and rarefaction cycle to occur at higher frequency. If the timescale of the rarefaction cycle is too short, the bubbles would not have sufficient time to grow for the full cavitation effect to take place. On the other hand, the compression cycle can also occur faster than the collapse of the bubble and inhibiting the cavitation effect, resulting in the formation of stable cavitation bubbles which remain in the system for a longer duration compared to the violent transient cavitation bubbles. A significant number of studies is reported on this matter for different acoustic cavitation systems. [37] reported that changing the frequency as no effect on the dissociation of carbon disulphide. In another study, [36] found that increasing the frequency improved the oxidation of iodide. Other similar studies have also reported similar effects in reactions requiring free radicals [51], [68], [92]. The consensus supports the hypothesis that higher frequencies produce more stable cavitation bubbles, leading to less violent transient bubble collapse, which results in less efficient chemical reactions due to the reduced production of radicals during transient cavitation. In general, while increasing the system frequency decreases the intensity of transient cavitation, it also increases the rate of bubble generation, which may be beneficial to certain systems.
The effect of acoustic power supplied to the system was reported to depend on the ultrasonic frequency used [144]. Some studies suggest that there exists an optimal system power that maximises sonochemical effects [46]. A possible explanation is that as the power increases over a certain threshold, the higher intensity bubble generation near the probe tip can limit the transmission of energy to the rest of the system, reducing the overall sonochemical effect [22].
In their study on a multi-bubble system using pulsed ultrasound method, Brotchie, et al. (2009) found that the mean bubble size increases with increasing acoustic power and decreased with increasing ultrasonic frequency. On a similar note, [93] performed a numerical modelling of a single bubble system and reported similar results for the effect of frequency but claimed that increasing the ultrasonic amplitude increases the range of bubble radius instead. In acoustic cavitation systems, controlling the mean bubble size is important, as not all bubbles contribute to sonochemical effects. A mean bubble diameter of approximately 40–50 µm is considered ideal for generating sufficient acoustic pressure to facilitate chemical reactions [151].
4. Numerical modelling of ultrasonic systems
The availability of commercial finite element method (FEM) solvers which offer acoustic modules has greatly encouraged the modelling of acoustic pressure systems. Modelling of acoustic systems has been widely employed in many fields, most notably in sonobiology, nanotechnology and sonochemistry. One key advantage of numerical modelling of acoustic systems is that it provides insights into acoustic intensity distribution, which is often difficult to determine from methods such as calorimetry [157], erosion testing [112], reaction rate analysis [106] and probe analysis [38], [90]. Modelling these systems enables theoretical analysis and optimisation without the need for experimental methods, greatly reducing the resources required for developing and designing new technologies. For example, in the field of sonoreactor design, models often focus on the intensity and distribution of cavitation activity as well as the acoustic field structure to allow for scale-up and optimisation of reactors [45].
The following sections explore and review various methods of modelling and simulating ultrasonic systems using numerical and computational models. Literature review results showed that two main types of studies on acoustic systems are commonly published. The first type involves the use of models to study phenomena within an acoustic system, such as identifying cavitating regions, and analysing temperature, pressure, and velocity profiles, along with the effects of operating parameters (geometry, power, frequency, etc.) on the system. Some studies also involve coupling multiple models, for example, in fluid–structure interaction studies and multiphase acoustic systems. These studies often employ finite element method (FEM) solvers to obtain the acoustic pressure field.
The second type of study is more common in sonochemistry, where models simulate single or multiple cavitating bubbles. In these models, based on equations of bubble dynamics, significant emphasis is placed on coupling acoustic phenomena with mass and energy balances and reaction rate equations to predict the conditions within cavitating bubbles.
4.1. Description of the problem
The phenomena taking place within an acoustic system can be dauntingly complex when scrutinised in detail. In general, the system mainly comprises a few major components. The first component is the medium through which sound propagates. The medium can be a single liquid phase or a multiphase system consisting of two or more liquid phases or a liquid phase containing one or more solid objects. The second component is the source of the ultrasonic wave source or emitter, often comprising one or more transducers. The third major component of the system is the solid vessel walls surrounding the liquid medium, which significantly affect the acoustic properties of the system. In many cases, the boundary conditions are crucial for the resolution of the models, and therefore must be appropriately represented.
Considering a simple system where a transducer is placed in a body of water within a vessel, the boundary conditions of the vessel walls, transducer surfaces and the water–air interface is required. The propagating sound waves in the system can then be described based on the wave equation, such as the Helmholtz equation for linear systems. If the transducer frequency is fixed, a time-harmonic study can be conducted. Solving the model would allow the acoustic pressure field to be obtained. The acoustic pressure field can then be coupled with other models, such as transport equations, to calculate the velocity and flow profiles in the system to study acoustic streaming.
However, the complexity of an acoustic system greatly increases when cavitating bubbles are considered. In systems where cavitation is significant, propagating acoustic waves can be modified by the bubble field through refraction, reflection, diffusion, diffraction and absorption. Abrupt and unpredictable pressure changes due to shockwaves and streaming further increase the difficulty of developing an accurate model [24].
4.2. Linear models for the acoustic system
The availability of commercial FEM solvers has led to many studies being conducted using linear models. The key advantage of using linear models is their simplicity and its availability in many commercial FEM software. Calculations involving linear models are less resource intensive while also providing relatively satisfactory results that offer significant insights into problems involving acoustic systems.
4.2.1. Helmholtz equation for wave propagation
The basic three dimensional model for wave propagation in a liquid can be written as the wave partial differential equation as a function of space and time dependant acoustic pressure, P(r,t) as:
| (1) |
In the case where the liquid is homogeneous and the density is constant, it can be written:
| (2) |
If the system is time harmonic, which is often true for cases using transducers with a single frequency, the equation can be written as:
| (3) |
where , is defined as the spatial variable, . The time-independent acoustic pressure, , is most obtained from the Helmholtz equation, which was a common partial differential equation applicable in many fields [52]. In the case of acoustic modelling, the equation, which was derived from the wave equation, represents the linear, time-independent form of sound propagation in a medium. By writing the equation in the terms of time-independent pressure amplitude, p, the following equation is obtained.
| (4) |
is known as the wave number which depends on the angular frequency, ω and the speed of sound in the liquid medium, . The equation is derived based on the four key assumptions: linear propagation of sound, negligible shear stress, constant liquid density and compressibility as well as the acoustic pressure is time harmonic. The model can then be solved using methods such as the finite element method [56]. Despite its limitations in address key problems such as non-linear dissipation by cavitating bubbles, the Helmholtz equation remains valuable tool since it is easy to solve, as well as allows the use of harmonic response simulations.
One notable study based on the linear Helmholtz models is published by [116], where FEMLAB simulations were carried out to characterise the ultrasonic field to study the distribution of cavitation activity. The simulation results were compared to experimental data from calorimetry, foil erosion test and thermal measurements. Similarly, [67] also used FEMLAB for their study. Their results showed that for a probe operating in a “free field”, high acoustic intensities can only be found in close vicinity to the horn, with a given example shown in Fig. 2. They also reported that by varying various parameters, such as the dimensions of the walls as well as horn size and depth, the amount of volume with high acoustic intensity can be maximised. By comparing their results to experimental data, while the position of the pressure maxima was justified, the simulated magnitude was found to be too high and not possible, due to the use of simplifying assumptions.
Fig. 2.
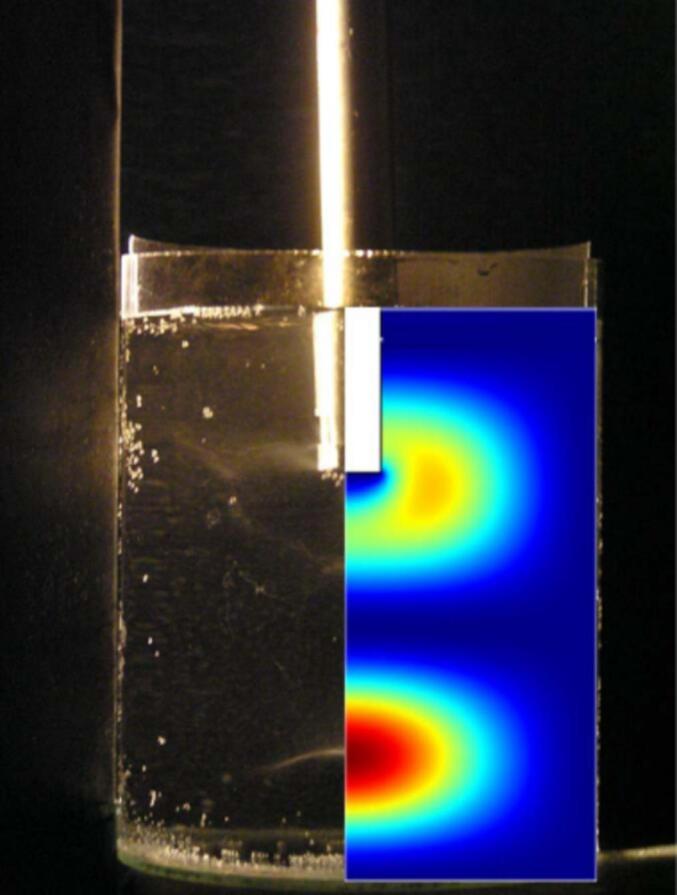
Photograph of a cavitating liquid (left) compared to the simulated results by [67] (Reproduced with author’s permission).
[65] used the Helmholtz model in their study to predict the energy density of various solvents. COMSOL Multiphysics simulations were carried out using the acoustic and heat transfer modules. The Helmholtz equation is solved along with heat transfer equations to give the pressure and temperature fields of the system. The simulation was then carried out using different solvent properties and varying ultrasonic power and irradiation times. In their study on numerically modelling ultrasonic agglomeration for treating magnesium alloy melts, [120] used the Helmholtz model to describe the standing waves formed from the ultrasonic field. After resolving for the acoustic pressure field, they performed particle modelling to find out the spatial distribution of free particles based on the calculated acoustic field. In a subsequent study, they coupled cavitation behaviour and bubble dynamics with the Helmholtz ultrasound field model and performed experimental validation to support the numerical data [120].
Solving acoustic systems using the linear Helmholtz equation does present certain limitations, such as not taking non-linear wave propagation into account as well as ignoring the effects of shear waves [116]. Additionally, the solution of the model is also sensitive to the wavenumber used, where higher wavenumbers may result in higher oscillatory results [48]. Also, as discussed in previous sections, while there are proposed methods for linear models to be able to provide satisfactory results accounting for energy losses for certain cases, non-linear models are often better at representing the various energy losses experienced by the system at the cost of higher complexity and larger resource requirements.
4.2.2. Boundary conditions
Using appropriate boundary conditions is crucial for the accuracy of the numerical models with respect to the system that is being studied. In this section, different boundary conditions and their respective justifications in employing them are discussed. In studies involving the resolution of the Helmholtz equation, the common boundary conditions used to represent the system boundaries are shown in Table 1 [132], 2014).
Table 1.
Common boundary conditions for solving the Helmholtz equation in linear models.
| Boundary Condition | Description |
|---|---|
| (5) | This condition is used for infinitely soft (free) boundaries. |
| (6) | This condition is used for infinitely hard (fixed) boundaries. Where n is a normal vector pointing outward. |
| (7) | This condition is commonly applied at the surface of the emitting ultrasonic transducer. |
4.2.2.1. Boundary conditions for vessel walls
Earlier FEM studies on linear acoustic models often treated the vessel boundaries as either infinitely rigid walls (Sáez, Frías-Ferrer, et al., 2005; [118], [120], or specified them as infinitely soft boundaries [67], [125], [123], [134]. The use of infinitely hard boundaries to represent the vessel walls is set on the basis that the walls are rigid and do not deform upon interacting with propagating acoustic waves, while the representation using infinitely soft boundaries assumes that the walls are thin enough to vibrate and deform. This is often done as a simplification to the model, as representing the vessel walls as infinitely hard or soft, is realistically inaccurate unless there is no propagation of sounds through the walls [133]. To validate the different boundary conditions set for vessel walls in previous studies, [152] studied the effect of the thickness of the vessel walls in an acoustic system and reported that for a thin glass wall (2 mm), the boundary is similar to that of a free (soft) boundary, while for a thick glass wall (7 mm), the boundary is similar to a rigid (hard) boundary. However, further studies conducted by researchers on this matter have found that the impact of reducing the effect of the vessel walls into a single boundary condition is significant, especially in systems with more complex wall geometries. The fluid–structure interaction models used in the studies of [84] and [132] coupled the acoustic field in the medium to the structural deformation of the vessel walls. It is found that the resonance frequencies and antinode locations of a system where the structural deformations are simulated vary significantly compared to systems where the vessel walls are represented as infinitely hard or soft boundaries.
Besides the boundary conditions, other types of boundary conditions have also been used to represent the walls of the vessels. In their study, [148] represented the walls of the quartz glass container using an impedance boundary condition. In another study, [60] used a plane wave radiation boundary to represent the inner walls of a microchannel reactor while defining the outer walls of the reactor as infinitely soft.
4.2.2.2. Boundary conditions for emitter surfaces
Another common over-simplified boundary condition for simulations of acoustic systems is the boundary representing the surfaces of the transducers. This simplification is often used because in order to correctly represent the vibrating transducer, one would otherwise have to model all the parts of the transducer, including the piezo ceramics as well as develop appropriate coupling equations with the fluid [84].
In many works, the transducer is usually defined as a pressure source, and the transducer boundary is defined in the form of acoustic pressure amplitude of the emitted wave, such as in the works of [67], [116], [120], [125].
| (8) |
The acoustic pressure amplitude defined for the transducer surface is often obtained experimentally by measuring the power dissipated into the system. The transducer pressure boundary can also be written in the following form, as a function of power dissipated in the system, [60].
| (9) |
Recently, it is also common to represent the vibrating transducer using its amplitude for normal displacement as shown [84], [132]:
| (10) |
[118]decided to represent their transducer boundary condition as a time dependant velocity which is a function of maximum transducer amplitude, written as:
| (11) |
4.2.2.3. Boundary conditions for liquid surfaces
There is currently a lack of discussion on the boundary conditions used for liquid surfaces which are not in contact with vessel walls, such as open liquid–air surfaces. Many past studies have represented liquid–air interfaces as infinitely sound soft boundaries [67], [116], [120]. In their study, [148] represented the air–water interface an impedance boundary condition.
4.3. Energy balance and dissipation effects
Considering an acoustic system for a volume of liquid, from the Euler equations.
| (12) |
| (13) |
The energy balance for a system with volume and its boundary can be written as
| (14) |
| (15) |
| (16) |
Which describes the relation between the energy density within the volume (W/m3) to the acoustic intensity of its surface boundaries (W/m3). By comparing the above energy balance to the theorem of kinetic energy, [84] presented for a volume of liquid excited by the surface of a sonotrode, the following energy conservation equation for a mono-harmonic system.
| (17) |
| (18) |
| (19) |
| (20) |
is the active power supplied into the system from the sonotrode surface, , while represents the power loss into the surroundings through the boundary surfaces, , and lastly the dissipated power within the liquid, , which is related to the attenuation coefficient .
4.3.1. Attenuation of sound waves and the damping factor
The attenuation of acoustic waves within the liquid can occur through many reasons, such as through reflection, refraction, scattering and thermo-viscoelastic losses within the liquid. Propagating waves can also lose energy to bulk loss mechanisms such as bulk shear effects and heat conduction. Besides that, in real systems, the interaction of propagating waves and the vessel walls also result in loss of wave energy, such as the loss of heat to the walls and energy dissipation due to viscous forces due to the interaction with the no-slip condition at wall boundaries. However, the significance of these losses greatly depends on the medium properties, wavelength and the domain size. It is known that thermo-viscoelastic losses are a lot more significant for the propagation of acoustic waves through gaseous media such as air [6]. In the case of liquid acoustic systems, the major dissipation effects arise from cavitation bubbles, where the bubbles can induce viscous friction, bubble heat diffusion and even acoustic radiation [21], [84].
It is known that as waves propagate away from the transducer, the intensity is observed to decrease with increasing distance. In the case of a linear, mono-harmonic system, the attenuation coefficient can be defined as follows:
| (21) |
Early studies reported by [66] attempted to quantify the effects of thermal conduction on the attenuation of sound waves as shown:
| (22) |
Where K is the thermal conductivity, is the gas constant and Cp is the specific heat capacity. In another work, [35]tried to quantify the attenuation factor of a sound wave propagating through a liquid as a function of the shear and bulk viscosity, where.
| (23) |
b* is constant ( for water containing cavitating bubbles) and C is the speed of sound in liquid. The author noted that the equation is limited to applications for low frequencies.
[98] reported that the attenuation can be written as a function of physiochemical properties of the liquid medium, velocity of sound in the medium and the operating frequency.
| (24) |
However, the use of the above equations is difficult especially when bubbles are formed within the acoustic system. As the attenuation is dependent on the properties of the medium, the attenuation factor is not spatially uniform and constant, but instead dependant on many spatial–temporal variables. The main challenges include accurately predicting the spatial and size distribution of bubbles across time.
4.4. Representing damping effects in linear models
In their study on cavitation activity in sonoreactors, [124] have modified the Helmholtz equation to account for damping effects and solved the linear model using COMSOL Multiphysics. A similar approach is also later used by [148] in their linear modelling of a sonochemical reactor.
The modification is done by changing the density and speed of sound terms to give a modified form of Helmholtz equation:
| (25) |
Where the complex parameters of density, speed of sound, wave number and impedance can be represented as follows:
| (26) |
| (27) |
| (28) |
| (29) |
While the above method provides a rather simple way of considering acoustic damping in linear models, the author noted that the above method neglects any effect of temperature and is only limited to systems with low cavitation intensities. This is because in systems with intense cavitation, shielding effects by bubble clouds and the introduction on non-homogeneity may show vastly different behaviour of that predicted by the model.
4.5. Linear models with presence of bubbles
As it was previously mentioned a cavitating acoustic system is rather complex. Especially in systems with intense cavitation, it is important to account for the effects of cavitation bubbles clouds. This is because the presence of bubbles in the system significantly affects wave propagation. During cavitation, a homogeneous liquid can show non-homogeneity as the single-phase liquid continuum is transformed into two phases. Cavitation clouds can amplify acoustic dispersion and attenuation while also altering the velocity of acoustic waves in the liquid. As an example, the sound velocity in water is around 1500 ms−1 while in a bubbly liquid, it can drastically decrease to around 20 ms−1 [118]. Moreover, the bubbly medium exhibits a significant degree of compressibility which greatly increases the nonlinearity in sound propagation. However, to account for bubbles in the system would significantly increase the degree of non-linearity of the model. While non-linear methods may provide an accurate representation of the system, it is often difficult to incorporate into acoustic simulations due to its complexity and the requirement of large computational power.
In 1989, a paper published by [21] presented a linear model base on the linearization of the Caflisch equations [14] which directly incorporated the wave attenuation from bubble clouds using a complex wave number. Further discussion on the Caflisch equations can be found in subsequent sections on the topic of non-linear models. The linearised Caflisch equations can be easily incorporated into the Helmholtz model, further improving the linear models used in many FEM. A summary of the proposed model is given in Table 2.
Table 2.
Parameters for the linear model accounting for wave propagation in bubbly liquid systems.
| Model Parameter | Mathematical Representation |
|---|---|
| Complex wave number, | (30) |
| Damping factor, | (31) |
| Complex dimensionless parameter, | (32) |
| Dimensionless parameter, | (33) |
| Bubble resonance frequency, | (34) |
| Volume fraction of bubbles, | (35) |
In the model, is the number of bubbles per unit volume, is the resonance frequency of the bubbles, is the monodisperse bubble equilibrium radius, is the damping factor, is the liquid viscosity, is the undisturbed pressure at bubble location, and are both imaginary parts of the complex dimensionless parameter , is the specific heat ratio of the gas inside the bubbles, the thermal diffusivity of the gas, which is used to calculate the dimensionless parameter , is the resonance frequency of the bubble, is the surface tension of the liquid and is the volume fraction of bubbles.
[26] was one of the earlier studies which applied the above model in their studies. In one of their earlier works on modelling the acoustic field of a 3D sonochemical reactor by determining the three-dimensional, time-independent pressure field. By applying the works of [21] in their model, they were able to model acoustic propagation in a system with a non-homogeneous distribution of bubble density by relating the propagating acoustic waves and the cavitating bubbles. The model is based on a stepwise calculation of a propagating wave, with the bubble density distribution calculated stepwise based on the phase velocity and attenuation coefficient. From their study, they noticed a few key findings. Notably, they reported that most of the acoustic energy is focused near the vicinity of the transducer due to the significant damping effects. They also concluded that the damping effects of the cavitating bubbles are significant and greatly affect the acoustic fields. In subsequent studies, they improved the developed model by considering the time dependent wave equation, which allows for a more realistic prediction on the cavitation event [27]. In subsequent studies, the time-dependent model was further developed by solving it using the finite difference approach [27] and compared to experimental results reported by [121] as well as being investigated for sonoreactors with different geometries [27].
The linearized model for acoustic systems with bubbles is also adapted in the works of other authors. In their study, [59] first solved the homogeneous linear model, and subsequently investigated the effect of bubbles on the system by manually varying the bubble volume fraction assuming the distribution is homogeneous. In the same study, they also resolved the model by defining a linear relationship between the pressure and volume fraction, based on previous works [25], [119].
| (36) |
Similarly, [60] in their simulation of a microchannel reactor also applied the linearized Caflisch model in their COMSOL Multiphysics simulation. Their simulation used an acoustic pressure model similar to that of [59]. The calculated acoustic pressure field is then used to resolve the flow profile and chemical reaction kinetics in the reactor.
While certainly offering a more rigorous approach compared to the simple Helmholtz model in modelling ultrasonic systems, the linearized Caflisch equations are not without limitations. In their comprehensive review, [133] provided a comprehensive discussion on this matter. Namely, the implementation of the linearised model is often based on an arbitrary Gaussian bubble size distribution which is often larger than those experimentally observed. Another highlighted problem lies with the Caflisch equations themselves, from which the linearized model is derived. The model is developed based on the assumptions where the fluid velocity is small enough for convection to be neglected, as well as very small volume fractions of bubbles. This issue is also discussed by [21] who noted that the linearised model is only accurate up to bubble fractions of 1–2 %.
4.6. Non-Linear models for the acoustic system
The main contributor to non-linearity in acoustic systems is the phenomenon of cavitation. While the simple linear Helmholtz equation may show a certain degree of agreement when subjected to experimental validation, this is often valid for systems where cavitation intensity is low or the cavitating regions are limited. Nonetheless, linear models can still offer a good prediction of pressure antinodes where cavitation could occur. Non-linearity is introduced into the system once cavitation begins. The degree of non-linearity subsequently increases as the bubbles expand, vibrate and collapse in the medium, causing various effects such as shockwaves and microjets that interacts with propagating acoustic waves. The bubbles themselves also affect propagating waves through reflections, refractions and other energy dissipation effects. Generation and migration of bubbles clouds changes the physical properties of the system and forms an interdependent relationship with the acoustic pressure field. This creates a very complex system which requires the consideration of many phenomena spanning various spatial and temporal scales [133].
4.6.1. Bubble motion in acoustic fields
The bubble density or bubble fraction term is often a key parameter in many models accounting for presence of bubbles. The bubble density was known to not be homogeneous across a medium. The cavitation bubbles also show translational motion and self-organisation behaviours [94]. This knowledge on the spatial evolution of the bubble distribution is crucial in the development of models to properly describe wave propagation in bubbly liquids.
There have been studies aimed to investigate the non-linear effect of the acoustic pressure on the cavitation bubbles, particularly on the topic of bubble migration and formation of bubble clouds. The Bjerknes forces are believed to be the primary cause of the translational motion of radially vibrating bubbles. A study on this effect has been extensively studied in the context of non-linear inertial radial oscillations and travelling waves by Mettin and coworkers [1], [95]. Experimental observations have revealed that bubbles in ultrasonic fields tend to form bubble clouds with certain geometries such as cones [99] and branches [96]. There are also efforts to model these observations using particle modelling, where the forces exerted on the bubbles by their surroundings are calculated directly using their non-linear dynamics [2].
To account for the motion of a single bubble, one would have to perform a force balance on the bubble. Essentially, one should account not only the driving forces such as the Bjerknes forces, but also viscous drag and added mass forces. Ideally, the motion of the bubbles should be calculated by simultaneously resolving the radial bubble dynamics and the translational bubble motion. This idea was first brought up by [142] and has since been improved upon by [29], [30], [31].
4.6.1.1. The Bjerknes force
The Bjerknes force [8] is the main contributor to bubble translational motion in an acoustic field [1], [158]. It can be defined as the generalized buoyancy force exerting on a body in an accelerating liquid, averaged over one oscillation period [87].
| (37) |
The bracket of the right-hand side term is used to represent the average over one acoustic period. is the bubble volume and is the acoustic pressure. In an acoustic cycle, the bubble would translationally move in the direction of the pressure gradient. However, the forward and backward motion of the bubble may not compensate. This is due to the possibility that the bubble may be larger when it is moving forward compared to when it is moving backward. The effect of the Bjerknes force on a bubble has been comprehensively discussed by [83].
In systems with standing waves, it is known that bubbles smaller than the resonant size are attracted to pressure antinodes, while bubbles larger than resonant sizes migrate towards pressure nodes instead [150]. This observation has been confirmed in early experimental works [23]. It is also found that the in cases where the antinode pressure exceeds a certain threshold, the bubbles would be repulsed instead. This effect is found to be nonlinear [1] has have also been confirmed in experiments [9]. In the case of travelling waves, it was known that the Bjerknes forces exerted by travelling waves are negligible when the amplitudes are small. However, large amplitude travelling waves can result in significant Bjerknes forces on the bubbles [83], [94], leading to observations like bubbles being repelled by ultrasonic sources generating a travelling wave.
4.6.1.2. Coupling bubble motion to the acoustic field
[83]conducted a study which aims to study the effect of travelling waves on bubble motion in an acoustic field. In their model, they represented the Bjerknes force for a mono-harmonic pressure field as a function of space and time as:
| (38) |
Where the bubble volume in the equation is obtained by simultaneously solving the bubble dynamics equation:
| (39) |
The equations are further modified to allow for the Bjerknes force to be calculated as an average over an acoustic period. This is done by fixing the phase of the pressure function by expressing certain equations in a dimensionless form. This representation of the Bjernes force can be now written as
| (40) |
| (41) |
| (42) |
A key advantage of the model proposed is that the contributions of standing waves and travelling waves on the Bjerknes force can be individually calculated.
4.6.2. Wave propagation in bubbly liquids
Likewise, there are also studies which aims to explore the non-linear effects of cavitating bubbles on the acoustic pressure of the system. Many works have tried to further develop a model for acoustic propagation in bubbly liquids by further studying the many factors of non-linearity. There is a significant number of studies published on the theoretical description of wave propagation in liquid systems containing bubbles. Examples include works by [43], [55], [61]; [145]. Publications are also done in the field of biomedicine, where ultrasound is used for therapeutic and diagnostic applications [32], [75]. Classical references such as the works of [47] and [104] have also reported good physical understanding of the phenomenon based on analytic perturbation techniques. Approximation models were proposed for nonlinear incoherent scattering [57], [104]. Non-linearity presented by encapsulated microbubbles have been presented by [86] while shielding effects of bubble layers were studied by [76]. In their work, [76] also described a technique on generation of bubble walls in spatial control therapy and highlighted the importance of understanding non-linear behaviour of ultrasound for applications in medicine. [63] used the linear pressure theory to study the non-homogeneous bubble distribution. A comprehensive discussion on coupling the acoustic field with bubble dynamics was also given in relevant review papers [62], [133].
4.6.3. Non-linear models with the presence of bubbles
In the topic of non-linear models with the presence of bubbles, the early work of [42] laid an important foundation for many studies to come. In their work, they developed a model which describes the linear scattering of waves based on an arbitrary distribution of scatterers. In the case of propagating linear sounds waves, the scatterers in context would be the cavitating bubbles, as applied in the study by [16]. Further development on the model for the consideration of non-linear dispersive waves was contributed by the work of (van Wijngaarden, 1968) and later by other authors [69], [109].
Another important development on the topic is the Caflisch model [15]which is essentially a rigorous generalisation of Foldy’s model for non-linear cases. In the model, the bubbly liquid is described as a continuum, where the mass and momentum conservation of the bubbly liquid can be written as:
| (43) |
| (44) |
The non-homogeneous equation for the conservation of mass is responsible for the non-linearity of the system of equations. The non-homogeneous term is then related to the local bubble dynamics using the inviscid Rayleigh-Plesset equation.
[21] reduced the Caflisch model using a linear approximation, reducing it to the dispersion relation of Foldy. The model was widely used in studies using the Helmholtz equation to couple the wave propagation and cavitating bubbles. Subsequently, [73] proposed a model to study the non-linear acoustic effects associated with bubble dynamics on wave propagation. Their model considered bubble motion under the action of primary and secondary Bjerkness forces. In the same year, [97] studied the transmission of an acoustic wave through a single layer of bubbles using the non-linear Caflisch equations. They noted that when the frequency used is close to the resonance frequency of the bubbles, reflection greatly dominates and wave transmission through the bubbly layer is greatly decreased. They also noted that for systems where the wavelength is much greater than the bubbly later thickness, the bubbly region can be replaced by an effective boundary condition for velocity and pressure.
While the fully non-linear form of the Caflisch equations is powerful, solving these equations is challenging, as it requires extremely complex temporal integration to obtain the solution [133], and is also difficult to apply to cases with complex geometries. Efforts to solve the Caflisch equations also found that the model presents convergence problems when applied to inertial cavitation, even when solved in one dimension [80], [137].
[82] considered the realistic estimation of power dissipation by bubble oscillations an important aspect for correctly estimation wave attenuation in bubbly liquid. They have proposed a model by simplifying the Caflisch equations. In their study, they developed a simple yet powerful model which couples a non-linear Helmholtz equation with the bubble field. The model calculates the wave attenuation directly from the energy dissipated by a single bubble using non-linear bubble dynamics, accounting for thermal diffusion and viscous friction. The model also considers energy conservation in the medium as well as non-linear attenuation of acoustic waves. The basis of the proposed model is the non-linear Helmholtz equation, which is given as:
| (45) |
The non-linear equation is then solved by using the derived relations of.
(46So)
and.
| (47) |
Where the terms and which corresponds to the thermal and viscous losses from the bubbles can be estimated from non-linear bubble dynamics. As for the real part of the wave number k, it can be obtained from the classic linear dispersion relation as:
| (48) |
A key finding obtained from the study is that the model can predict the commonly observed cavitation phenomena of conical bubble structures under ultrasonic horns [99], where linear based models often fail to predict. Results obtained from the models showed strong attenuation caused by cavitation, as well as significant energy dissipation caused by cavitating bubbles, which greatly affected the resulting acoustic pressure profile. They noted that the viscous friction losses calculated were around 4 orders of magnitude higher than the linear dispersion relation. The strong attenuation also found to cause the formation of travelling waves in the system, even when perfectly reflecting wall boundaries are specified. In a review by [133], they commented that while the model provides a better approximation than previous linear models, notably the amplitude calculations, it does possess certain limitations such as being based on unproven approximations in the derivation of the non-linear Helmholtz equations. Simulations are also conducted using an arbitrary choice of bubble radius as well as the assumption that the bubble distribution is homogeneous when the pressure is above the Blake threshold. In the study, 5 µm bubbles are considered based on experimental data by [13].
4.6.4. Wave propagation in the absence of bubbles
While it is notable that a significant amount of research has focused on wave propagation and the non-linearity caused by acoustic cavitation bubbles, there are also cases where ultrasonic waves propagate non-linearly in the absence of bubbles. Such instances occur particularly in diagnostic ultrasound, where the ultrasonic frequencies are in the MHz range, making the acoustic cycle too short to induce cavitation bubbles. In these cases, the non-linear propagation arises from the distortion of the wave as the compressional phase moves faster than the rarefaction phase, leading to the generation of harmonics and the formation of shock waves. These effects contribute to localized heating, acoustic streaming, and enhanced energy transfer, which can facilitate molecular interactions even without cavitation. These findings were well reported by the earlier works of [7] and [47].
Building on these insights, [34] demonstrated that the nonlinearity of wave propagation in the absence of bubbles could be quantified by the shock parameter, σ. In general, the value of σ represents the extent of waveform distortion during propagation, where higher values indicate stronger non-linear effects. Specifically, when σ < 1, the wave behaves linearly, with minimal distortion. At σ = 1, a shock wave begins to form, and as σ increases further, the wave evolves into a sawtooth shape, generating multiple harmonics and exhibiting advanced nonlinearity. The behaviour of σ is influenced by factors such as source pressure, frequency, and medium properties, with higher values reflecting faster wave distortion, enhanced harmonic content, and increased energy transfer within the system.
In the context of this review, the focus is on ultrasonic waves in high-power ultrasonic regions, where cavitation bubbles are highly likely to occur. Therefore, the discussion will center on wave propagation and its characteristics in the presence of acoustic cavitation bubbles.
5. Notable studies and discoveries in acoustic system modelling
[120] performed numerical simulation with experimental validation in their study on ultrasonic agglomeration for treating magnesium alloy melts. Initially, the Helmholtz model was employed to model the ultrasonic field. Once the acoustic field is established, particle modelling was carried out through force balance accounting for the acoustic radiation force, fluid drag, buoyancy and particle momentum [131].
[120] investigated the treatment of AZ80 alloy melts using ultrasound by modelling cavitation behaviour and bubble dynamics coupled with the Helmholtz ultrasound field model. Experimental validation is carried out to support the numerical data. [65] utilized COMSOL Multiphysics simulations using the acoustic and heat transfer modules to study the temperature and pressure profiles in an acoustic system for different solvents.
[147] developed a one-dimensional model to study the mechanism of bubble transport in a standing wave field for experimental validation. Their numerical model represented the bubble dynamics using the Keller-Miksis equation [64] equation for radial oscillations and modifying it to account for translational motion [11], [12], [29], [142]
[60] performed a computational simulation using COMSOL Multiphysics with further experimental validation for a microchannel sonochemical reactor set-up. Their simulation integrated four key modules: the Pressure Acoustic Module for the simulation of solid walls, the Helmholtz model for acoustic pressure in liquid, the Laminar Flow Module for flow velocity simulations, and the Chemical Reaction Module to account for sonochemical reactions.
[118] performed a computational simulation for an acoustic system with presence of bubbles using a non-linear model developed based on the Catflisch equations and solved using the Aquilon code after certain modifications. In their work, formation of bubbles is based on an assumed cavitation threshold, while bubble radii distribution is represented following the work published by [21]. The Catlisch equations which relates wave propagation and bubble dynamics are used and solved together with the Navier-Stokes equations. The entire system was modelled using the Eulerian two-fluid approach, where two Eulerian and Navier-Stokes models for both the liquid and bubble phase can be coupled together using interfacial transfer terms. The model not only accounted for bubble generation sites, but also bubble movement towards pressure nodes, time averaged bubble velocity, as well as fluid flow. In their subsequent work, the model is further improved by introducing a linear relationship between the time-dependant bubble density to the acoustic pressure amplitude [119].
[149] aimed to study the formation of an ultrasonic fountain using numerical simulation to improve the performance of ultrasonic atomization. Their model involves using the inhomogeneous Helmholtz equation and included complex parameters to account for attenuation, pressure as transducer boundary, liquid–air interface set as impedance boundary. Additionally, the liquid flow field was calculated using the transport and continuity equations. The liquid surface was modelled as an external fluid interface with free deformation to simulate the fountain formation, with the boundary condition being a function of surface tension.
6. Computational software and codes for numerical modelling
Earlier efforts in numerically solving the acoustic pressure field were often done using computational algorithms. [27] performed a three-dimensional modelling on various reactor geometries by solving the Helmholtz integral and Kirchhoff integral using Riemann integration with their FORTRAN 90 codes.
Solving models such as the Helmholtz equation is frequently accomplished using the finite element method (FEM) or finite element analysis (FEA). A literature review indicates that many recent computational studies of ultrasonic systems favour the use of the commercial simulation software COMSOL Multiphysics (previously known as FEMLAB) in their studies. This software enables users to solve of the Helmholtz equation through its built-in acoustic module and facilitates the coupling of multiple physics models within a system. COMSOL is often employed for time-harmonic studies (time-independent) of the acoustic pressure fields with results typically validated against experimental data [67]; Sáez, Frías-Ferrer, et al., 2005).
In addition to COMSOL Multiphysics, other FEM solvers, although less common, have also been used for the modelling of ultrasonic systems. For example, the ATILA code is used by [107] to investigate the ultrasonic pressure field in a textile treatment bath. [100] studied the ultrasonic fields in cylindrical reactors using the PZflex code. As one of the earlier studies of acoustic modelling, [24] studied the coupling of the acoustic pressure field and the velocity field (streaming) by using the Sysnoise code to solve for the acoustic pressure then transferring it to the commercial software Fluent to solve for flow fields.
Another earlier work reported by [70] took the approach of solving the acoustic field using Euler equations by using the Eole code, and then coupling it to the Navier-Stokes equation with energy balance using the Aquilon code. It was reported that the accuracy of this method was limited to high frequency-low power systems, where the less intense cavitation would generate less non-linearity in the system. In the works of [118], a Eulerian two-fluid approach is used to model the acoustic field in a two-phase system comprising the liquid phase and the bubble phase. In their study, they used the CFD code Estet-Astrid which is commonly used to study bubbly fluid flows to obtain solutions for the model [105].
6.1. Recent developments and future trends
There have been significant recent developments in the field of acoustical modelling in the past decade. Some notable highlights include Louisnard’s research group, who has focused on developing non-linear collapse of cavitation bubbles to predict the acoustic attenuation caused by the presence of cavitation collapse. Their model concludes a simplified method based on the principle of primary Bjerknes force provides a better representation of the real-life acoustic environment [81], [83]. Other notable researchers in this field include Vanhille and co-workers, where they have included numerous studies, including stationary and transient phase simulations on non-linear acoustic waves, some of which considered the presence and effect of heat on the overall acoustic simulation system [126], [135], [136], [138], [139].
Most of the time, the issue with numerical simulations lies within the comparison and compatibility with real-life experimental data. Example such as [143] demonstrated a classic piece of work to map the acoustic simulation studies to their pilot-scale sonoreactors. Other classic works of comparing between experimental and pilot-scale reactors include [59], [58], [132], [133], [156], who have provided notable information regarding to the improvement of numerical simulations, mainly focusing on the improvements of mathematical model equations to represent the actual complex bubble dynamics. Additionally, some recent developments performed by a research group led by the author have demonstrated significant improvements in incorporating multi-phase and multiple-frequency models [18], [17], [130], [129], with an example result of multi-frequency simulation shown in Fig. 3. These works have successfully, for the first time, simplified the semi-empirical bubbly liquid models to be used in a multiple-frequency set-up. The main outcome from the research has provided insightful findings for simplified, organised and systematic numerical simulations to represent various acoustic systems, which can further enhance future sonochemical reactor designs and developments.
Fig. 3.
Comparison of simulated acoustic pressure fields in a multi-frequency reactor, using semi-empirical bubbly liquid models (Commander Prosperetti and Non-linear Helmholtz equation) and the experimental data [17].
7. Concluding Remarks
The field of acoustic cavitation modelling has evolved significantly, offering crucial insights into the behaviour of sonochemical systems. From early models like the Rayleigh-Plesset equation to more complex approaches such as the Commander-Prosperetti and non-linear Helmholtz models, advancements have steadily improved the accuracy of simulations, bridging the gap between theoretical predictions and experimental data. These developments have enhanced the scalability and design of sonochemical reactors, enabling more effective industrial applications. However, challenges remain in optimizing models for multi-phase systems and capturing non-linear effects, which are critical for achieving further improvements in the efficiency and scalability of these systems.
This review has successfully provided a comprehensive overview of the key advancements in acoustic cavitation modelling, highlighting both the progress made and the areas that require further exploration to optimize sonochemical reactor designs and applications.
CRediT authorship contribution statement
T.Joyce Tiong: Writing – review & editing, Supervision, Project administration, Investigation. Jin Kiat Chu: Writing – original draft, Investigation, Conceptualization. Khang Wei Tan: Validation, Resources, Project administration.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors are grateful to Xiamen University Malaysia Research Fund (XMUMRF/2022-C10/IENG/0048), Industry Grant (EENG/0059) and the Ministry of Higher Education (MOHE) Malaysia under the Fundamentals Research Grant Scheme (FRGS/1/2023/STG04/UNIM/02/1) for funding this research work.
Contributor Information
T.Joyce Tiong, Email: joyce.tiong@nottingham.edu.my.
Khang Wei Tan, Email: khangwei.tan@xmu.edu.my.
Data availability
No data was used for the research described in the article.
References
- 1.Akhatov I., Mettin R., Ohl C.D., Parlitz U., Lauterborn W. Bjerknes force threshold for stable single bubble sonoluminescence. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat Interdiscip. Topics. 1997;55(3):3747–3750. doi: 10.1103/PhysRevE.55.3747. [DOI] [Google Scholar]
- 2.Appel J., Koch P., Mettin R., Krefting D., Lauterborn W. Stereoscopic high-speed recording of bubble filaments. Ultrason. Sonochem. 2004;11(1):39–42. doi: 10.1016/S1350-4177(03)00111-1. [DOI] [PubMed] [Google Scholar]
- 3.Authier O., Ouhabaz H., Bedogni S. Modeling of sonochemistry in water in the presence of dissolved carbon dioxide. Ultrason. Sonochem. 2018;45:17–28. doi: 10.1016/j.ultsonch.2018.02.044. [DOI] [PubMed] [Google Scholar]
- 4.Noltingk B.E., Neppiras E.A. Cavitation produced by Ultrasonics. Proc. Phys. Soc. London, Sect. B. 1950;63(9):674. doi: 10.1088/0370-1301/63/9/305. [DOI] [Google Scholar]
- 5.Bang J.H., Suslick K.S. Applications of ultrasound to the synthesis of nanostructured materials. Adv. Mater. 2010;22(10):1039–1059. doi: 10.1002/adma.200904093. [DOI] [PubMed] [Google Scholar]
- 6.Berggren M., Bernland A., Noreland D. Acoustic boundary layers as boundary conditions. J. Comput. Phys. 2018;371:633–650. doi: 10.1016/j.jcp.2018.06.005. [DOI] [Google Scholar]
- 7.Beyer R.T. Acoustical Society of America; 1997. Nonlinear acoustics. [Google Scholar]
- 8.Bjerknes V.F.K. Fields of Force. In Columbia University Press; Colombia University Press: 1906. Bjerknes. [Google Scholar]
- 9.Blake J.R., Keen G.S., Tong R.P., Wilson M. Acoustic cavitation: The fluid dynamics of non-spherical bubbles. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1999;357(1751):251–267. doi: 10.1098/rsta.1999.0326. [DOI] [Google Scholar]
- 10.Brennen C.E. Cavitation in medicine. Interface Focus. 2015;5(5):1–12. doi: 10.1098/rsfs.2015.0022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brotchie A., Grieser F., Ashokkumar M. Effect of power and frequency on bubble-size distributions in acoustic cavitation. Phys. Rev. Lett. 2009;102(8):84302. doi: 10.1103/PhysRevLett.102.084302. [DOI] [PubMed] [Google Scholar]
- 12.Brotchie A., Mettin R., Grieser F., Ashokkumar M. Cavitation activation by dual-frequency ultrasound and shock waves. PCCP. 2009;11(43):10029–10034. doi: 10.1039/B912725A. [DOI] [PubMed] [Google Scholar]
- 13.Burdin F., Tsochatzidis N.A., Guiraud P., Wilhelm A.M., Delmas H. Characterisation of the acoustic cavitation cloud by two laser techniques. Ultrason. Sonochem. 1999;6(1–2):43–51. doi: 10.1016/S1350-4177(98)00035-2. [DOI] [PubMed] [Google Scholar]
- 14.Caflisch R.E., Miksis M.J., Papanicolaou G.C., Ting L. Effective equations for wave propagation in bubbly liquids. J. Fluid Mech. 1985;153:259–273. doi: 10.1017/S0022112085001252. [DOI] [Google Scholar]
- 15.Caflisch R.E., Miksis M.J., Papanicolaou G.C., Ting L. Wave propagation in bubbly liquids at finite volume fraction. J. Fluid Mech. 1985;160:1–14. doi: 10.1017/S0022112085003354. [DOI] [Google Scholar]
- 16.Carstensen E.L., Foldy L.L. Propagation of Sound Through a Liquid Containing Bubbles. J. Acoust. Soc. Am. 1947;19(3):481–501. doi: 10.1121/1.1916508. [DOI] [Google Scholar]
- 17.Chu J.K., Tiong T.J., Chong S., Asli U.A. Investigation on different time-harmonic models using FEM for the prediction of acoustic pressure fields in a pilot-scale sonoreactor. Chemical Engineering Science. 2022;247 doi: 10.1016/j.ces.2021.116912. [DOI] [Google Scholar]
- 18.Chu J.K., Tiong T.J., Chong S., Asli U.A., Yap Y.H. Multi-frequency sonoreactor characterisation in the frequency domain using a semi-empirical bubbly liquid model. Ultrason. Sonochem. 2021;80 doi: 10.1016/j.ultsonch.2021.105818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Church C.C., Carstensen E.L. “Stable” inertial cavitation. Ultrasound Med. Biol. 2001;27(10):1435–1437. doi: 10.1016/S0301-5629(01)00441-0. [DOI] [PubMed] [Google Scholar]
- 20.Collis J., Manasseh R., Liovic P., Tho P., Ooi A., Petkovic-Duran K., Zhu Y. Cavitation microstreaming and stress fields created by microbubbles. Ultrasonics. 2010;50(2):273–279. doi: 10.1016/j.ultras.2009.10.002. [DOI] [PubMed] [Google Scholar]
- 21.Commander K.W., Prosperetti A. Linear pressure waves in bubbly liquids: Comparison between theory and experiments. J. Acoust. Soc. Am. 1989;85(2):732–746. doi: 10.1121/1.397599. [DOI] [Google Scholar]
- 22.Contamine R.F., Wilhelm A.M., Berlan J., Delmas H. Power measurement in sonochemistry. Ultrason. Sonochem. 1995;2(1):S43–S47. doi: 10.1016/1350-4177(94)00010-P. [DOI] [Google Scholar]
- 23.Crum L.A., Eller A.I. Motion of Bubbles in a Stationary Sound Field. J. Acoust. Soc. Am. 1970;48(1B):181–189. doi: 10.1121/1.1912115. [DOI] [Google Scholar]
- 24.Dahlem O., Reisse J., Halloin V. The radially vibrating horn: A scaling-up possibility for sonochemical reactions. Chem. Eng. Sci. 1999;54(13–14):2829–2838. doi: 10.1016/S0009-2509(98)00356-X. [DOI] [Google Scholar]
- 25.Dähnke S., Swamy K.M., Keil F.J. A comparative study on the modeling of sound pressure field distributions in a sonoreactor with experimental investigation. Ultrason. Sonochem. 1999;6(4):221–226. doi: 10.1016/S1350-4177(99)00011-5. [DOI] [PubMed] [Google Scholar]
- 26.Dähnke S., Swamy K.M., Keil F.J. Modeling of three-dimensional pressure fields in sonochemical reactors with an inhomogeneous density distribution of cavitation bubbles. Ultrason. Sonochem. 1999;6(1–2):31–41. doi: 10.1016/s1350-4177(98)00026-1. [DOI] [PubMed] [Google Scholar]
- 27.Dähnke S.W., Keil F.J. Modeling of linear pressure fields in sonochemical reactors considering an inhomogeneous density distribution of cavitation bubbles. Chem. Eng. Sci. 1999;54(13–14):2865–2872. doi: 10.1016/S0009-2509(98)00340-6. [DOI] [PubMed] [Google Scholar]
- 28.Dickens M.J., Luche J.-L. Further evidence for the effect of ultrasonic waves on electron transfer processes - the case of the kornblum-russell reaction. Tetrahedron Lett. 1991;32(36):4709–4712. doi: 10.1016/S0040-4039(00)92288-3. [DOI] [Google Scholar]
- 29.Doinikov A.A. Translational motion of a spherical bubble in an acoustic standing wave of high intensity. Phys. Fluids. 2002;14(4):1420–1425. doi: 10.1063/1.1458597. [DOI] [Google Scholar]
- 30.Doinikov A.A. Mathematical model for collective bubble dynamics in strong ultrasound fields. J. Acoust. Soc. Am. 2004;116(2):821–827. doi: 10.1121/1.1768255. [DOI] [Google Scholar]
- 31.Doinikov A.A. Equations of coupled radial and translational motions of a bubble in a weakly compressible liquid. Phys. Fluids. 2005;17(12):1–4. doi: 10.1063/1.2145430. [DOI] [Google Scholar]
- 32.Doinikov A., Novell A., Bouakaz A., Calmon P. The Westervelt equation for nonlinear propagation: Numerical simulations and experimental validation of ultrasonic fields produced by array transducers. IEEE International Ultrasonics Symposium (IUS) 2013;2013:608–610. doi: 10.1109/ULTSYM.2013.0157. [DOI] [Google Scholar]
- 33.Doktycz S.J., Suslick K.S. Interparticle collisions driven by ultrasound. Science. 1990;247(4946):1067–1069. doi: 10.1126/science.2309118. [DOI] [PubMed] [Google Scholar]
- 34.Duck F.A. Nonlinear acoustics in diagnostic ultrasound. Ultrasound in Med. & Biol. 2002;28(1):1–18. doi: 10.1016/S0301-5629(01)00463-X. [DOI] [PubMed] [Google Scholar]
- 35.Eckart C. Vortices and streams caused by sound waves. Phys. Rev. 1948;73(1):68–76. doi: 10.1103/PhysRev.73.68. [DOI] [Google Scholar]
- 36.Entezari M.H., Kruus P. Effect of frequency on sonochemical reactions II. Temperature and Intensity Effects. Ultrasonics Sonochemistry. 1996;3(1):19–24. doi: 10.1016/1350-4177(95)00037-2. [DOI] [PubMed] [Google Scholar]
- 37.Entezari M.H., Kruus P., Otson R. The effect of frequency on sonochemical reactions III: dissociation of carbon disulfide. Ultrason. Sonochem. 1997;4(1):49–54. doi: 10.1016/s1350-4177(96)00016-8. [DOI] [PubMed] [Google Scholar]
- 38.Faïd F., Romdhane M., Gourdon C., Wilhelm A.M., Delmas H. A comparative study of local sensors of power ultrasound effects: Electrochemical, thermoelectrical and chemical probes. Ultrason. Sonochem. 1998;5(2):63–68. doi: 10.1016/S1350-4177(98)00008-X. [DOI] [PubMed] [Google Scholar]
- 39.Flannigan D.J., Suslick K.S. Inertially confined plasma in an imploding bubble. Nat. Phys. 2010;6(8):598–601. doi: 10.1038/nphys1701. [DOI] [Google Scholar]
- 40.Flynn H.G. Physics of Acoustic Cavitation. In Academic Press. Doi. 1964;10(1121/1):1930333. [Google Scholar]
- 41.Flynn H.G. Cavitation dynamics: II. Free pulsations and models for cavitation bubbles. J. Acoust. Soc. Am. 2005;58(6):1160–1170. doi: 10.1121/1.380799. [DOI] [Google Scholar]
- 42.Foldy L.L. The multiple scattering of waves. I. General theory of isotropic scattering by randomly distributed scatterers. Phys. Rev. 1945;67(3–4):107–119. doi: 10.1103/PhysRev.67.107. [DOI] [Google Scholar]
- 43.Fuster D., Conoir J.M., Colonius T. Effect of direct bubble-bubble interactions on linear-wave propagation in bubbly liquids. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014;90(6):63010. doi: 10.1103/PhysRevE.90.063010. [DOI] [PubMed] [Google Scholar]
- 44.Gielen B., Jordens J., Janssen J., Pfeiffer H., Wevers M., Thomassen L.C.J., Braeken L., van Gerven T. Characterization of stable and transient cavitation bubbles in a milliflow reactor using a multibubble sonoluminescence quenching technique. Ultrason. Sonochem. 2015;25:31–39. doi: 10.1016/j.ultsonch.2014.08.013. [DOI] [PubMed] [Google Scholar]
- 45.Gogate P.R., Sutkar V.S., Pandit A.B. Sonochemical reactors: Important design and scale up considerations with a special emphasis on heterogeneous systems. Chem. Eng. J. 2011;166(3):1066–1082. doi: 10.1016/j.cej.2010.11.069. [DOI] [Google Scholar]
- 46.Gutiérrez M., Henglein A. Nanometer-Sized Bi Particles in Aqueous Solution: Absorption Spectrum and Some Chemical Properties. J. Phys. Chem. 1996;100(18):7656–7661. doi: 10.1021/jp953774o. [DOI] [Google Scholar]
- 47.Hamilton M.F., Blackstock D.T. Academic Press; 1998. Nonlinear Acoustics. [Google Scholar]
- 48.Harari I., Shalom R., Barbone P.E. Higher-order boundary infinite elements. Comput. Methods Appl. Mech. Eng. 1998;164(1):107–119. doi: 10.1016/S0045-7825(98)00049-8. [DOI] [Google Scholar]
- 49.Harvey E.N., McElroy Wm.D., Whiteley A.H. On Bubble Formation in Water. J. Appl. Phys. 1947;18(2):162–172. doi: 10.1063/1.1697598. [DOI] [Google Scholar]
- 50.Hatanaka S.-I., Mitome H., Yasui K., Hayashi S. Single-bubble sonochemiluminescence in aqueous luminol solutions. J. Am. Chem. Soc. 2002;124(35):10250–10251. doi: 10.1021/ja0258475. [DOI] [PubMed] [Google Scholar]
- 51.Hoffmann M.R., Hua I., Hoechemer R.H. Application of Ultrasonic Irradiation for the Degradation of Chemical Contaminants in Water. Ultrason. Sonochem. 1996;3:168–172. [Google Scholar]
- 52.Huttunen T., Malinen M., Kaipio J.P., White P.J., Hynynen K. A full-wave Helmholtz model for continuous-wave ultrasound transmission. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005;52(3):397–409. doi: 10.1109/TUFFC.2005.1417262. [DOI] [PubMed] [Google Scholar]
- 53.Hyman S.D., Lazio T.J.W., Kassim N.E., Ray P.S., Markwardt C.B., Yusef-Zadeh F. A powerful bursting radio source towards the Galactic Centre. Nature. 2005;434(7029):50–52. doi: 10.1038/nature03400. [DOI] [PubMed] [Google Scholar]
- 54.Ibisi, V. •, & Brown, B. (1967). Variation of the Relative Intensity of Cavitation with Temperature. doi: 10.2.
- 55.Ida M., Naoe T., Futakawa M. Suppression of cavitation inception by gas bubble injection: A numerical study focusing on bubble-bubble interaction. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007;76(4):46309. doi: 10.1103/PhysRevE.76.046309. [DOI] [PubMed] [Google Scholar]
- 56.Ihlenburg F., Babuška I. Finite element solution of the Helmholtz equation with high wave number Part I: The h-version of the FEM. Comput. Math. Appl. 1995;30(9):9–37. doi: 10.1016/0898-1221(95)00144-N. [DOI] [Google Scholar]
- 57.Ilinskii Y.A., Zabolotskaya E.A. Cooperative radiation and scattering of acoustic waves by gas bubbles in liquids. J. Acoust. Soc. Am. 1992;92(5):2837–2841. doi: 10.1121/1.404403. [DOI] [Google Scholar]
- 58.Jamshidi R., Brenner G. Dissipation of ultrasonic wave propagation in bubbly liquids considering the effect of compressibility to the first order of acoustical Mach number. Ultrasonics. 2013;53(4):842–848. doi: 10.1016/j.ultras.2012.12.004. [DOI] [PubMed] [Google Scholar]
- 59.Jamshidi R., Pohl B., Peuker U.A., Brenner G. Numerical investigation of sonochemical reactors considering the effect of inhomogeneous bubble clouds on ultrasonic wave propagation. Chem. Eng. J. 2012;189–190:364–375. doi: 10.1016/j.cej.2012.02.029. [DOI] [Google Scholar]
- 60.Jordens J., Honings A., Degrève J., Braeken L., van Gerven T. Investigation of design parameters in ultrasound reactors with confined channels. Ultrason. Sonochem. 2013;20(6):1345–1352. doi: 10.1016/j.ultsonch.2013.03.012. [DOI] [PubMed] [Google Scholar]
- 61.Kargl S.G. Effective medium approach to linear acoustics in bubbly liquids. J. Acoust. Soc. Am. 2002;111(1):168–173. doi: 10.1121/1.1427356. [DOI] [PubMed] [Google Scholar]
- 62.Karpov S., Prosperetti A., Ostrovsky L. Nonlinear wave interactions in bubble layers. J. Acoust. Soc. Am. 2003;113(3):1304–1316. doi: 10.1121/1.1539519. [DOI] [PubMed] [Google Scholar]
- 63.Keil F.J., Dähnke S. Numerical calculation of pressure fields in sonochemical reactors - Linear effects in homogeneous phase. Period. Polytech., Chem. Eng. 1996;41(1):41–55. [Google Scholar]
- 64.Keller J.B., Miksis M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1998;68(2):628–633. doi: 10.1121/1.384720. [DOI] [Google Scholar]
- 65.Kim H.J., Chi M.H., Hong I.K. Effect of ultrasound irradiation on solvent extraction process. J. Ind. Eng. Chem. 2009;15(6):919–928. doi: 10.1016/j.jiec.2009.09.025. [DOI] [Google Scholar]
- 66.Kirchhoff G. Ueber den Einfluss der Wärmeleitung in einem Gase auf die Schallbewegung. Ann. Phys. 1868;210(6):177–193. doi: 10.1002/andp.18682100602. [DOI] [Google Scholar]
- 67.Klíma J., Frias-Ferrer A., González-García J., Ludvík J., Sáez V., Iniesta J. Optimisation of 20 kHz sonoreactor geometry on the basis of numerical simulation of local ultrasonic intensity and qualitative comparison with experimental results. Ultrason. Sonochem. 2007;14(1):19–28. doi: 10.1016/j.ultsonch.2006.01.001. [DOI] [PubMed] [Google Scholar]
- 68.Kohno M., Mokudai T., Ozawa T., Niwano Y. Free radical formation from sonolysis of water in the presence of different gases. J. Clin. Biochem. Nutr. 2011;49(2):96–101. doi: 10.3164/jcbn.100130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kuznetsov V.v., Nakoryakov V.E., Pokusaev B.G., Shreiber I.R. Liquid with gas bubbles as an example of a Korteweg-de Vries-Burgers medium. J. Exp. Theor. Phys. Lett. 1976;23:172–176. [Google Scholar]
- 70.Laborde J.L., Bouyer C., Caltagirone J.P., Gérard A. Acoustic cavitation field prediction at low and high frequency ultrasounds. Ultrasonics. 1998;36(1–5):581–587. doi: 10.1016/S0041-624X(97)00106-6. [DOI] [Google Scholar]
- 71.Lafond M., Watanabe A., Yoshizawa S., Umemura S.I., Tachibana K. Cavitation-threshold Determination and Rheological-parameters Estimation of Albumin-stabilized Nanobubbles. Sci. Rep. 2018;8(1) doi: 10.1038/s41598-018-25913-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Leighton T. The Acoustic Bubble. in Journal of the Acoustical Society of America - J ACOUST SOC AMER. 1994;Vol. 96 doi: 10.1121/1.410082. [DOI] [Google Scholar]
- 73.Leighton T.J., Walton A.J., Pickworth M.J.W. Primary Bjerknes forces. Eur. J. Phys. 1990;11(1):47. doi: 10.1088/0143-0807/11/1/009. [DOI] [Google Scholar]
- 74.Leong T.S.H., Martin G.J.O., Ashokkumar M. Ultrasonic encapsulation – A review. Ultrason. Sonochem. 2017;35:605–614. doi: 10.1016/j.ultsonch.2016.03.017. [DOI] [PubMed] [Google Scholar]
- 75.Liu Y., Sugiyama K., Takagi S., Matsumoto Y. Numerical study on the shape oscillation of an encapsulated microbubble in ultrasound field. Phys. Fluids. 2011;23(4):41904. doi: 10.1063/1.3578493. [DOI] [Google Scholar]
- 76.Lo A.H., Kripfgans O.D., Carson P.L., Fowlkes J.B. Spatial control of gas bubbles and their effects on acoustic fields. Ultrasound Med. Biol. 2006;32(1):95–106. doi: 10.1016/j.ultrasmedbio.2005.09.009. [DOI] [PubMed] [Google Scholar]
- 77.Löfstedt R., Barber B.P., Putterman S.J. Toward a hydrodynamic theory of sonoluminescence. Phys. Fluids A. 1992;5(11):2911–2928. doi: 10.1063/1.858700. [DOI] [Google Scholar]
- 78.Lorimer J.P., Mason T.J. Sonochemistry. Part 1 - The physical aspects. Chem. Soc. Rev. 1987;16:239–274. doi: 10.1039/CS9871600239. [DOI] [Google Scholar]
- 79.Lorimer J.P., Mason T.J. Sonochemistry. Part 1—The physical aspects. Chem. Soc. Rev. 1987;16:239–274. doi: 10.1039/CS9871600239. [DOI] [Google Scholar]
- 80.Louisnard, O. (1998). Contribution à l’étude de la propagation des ultrasons en milieu cavitant..
- 81.Louisnard O. Nonlinear attenuation of sound waves by inertial cavitation bubbles. Phys. Procedia. 2010;3(1):735–742. doi: 10.1016/j.phpro.2010.01.093. [DOI] [Google Scholar]
- 82.Louisnard O. A simple model of ultrasound propagation in a cavitating liquid. Part I: Theory, nonlinear attenuation and traveling wave generation. Ultrason. Sonochem. 2012;19(1):66–76. doi: 10.1016/j.ultsonch.2011.06.007. [DOI] [PubMed] [Google Scholar]
- 83.Louisnard O. A simple model of ultrasound propagation in a cavitating liquid. Part II: Primary Bjerknes force and bubble structures. Ultrason. Sonochem. 2012;19(1):56–65. doi: 10.1016/j.ultsonch.2011.06.007. [DOI] [PubMed] [Google Scholar]
- 84.Louisnard O., Gonzalez-Garcia J., Tudela I., Klima J., Saez V., Vargas-Hernandez Y. FEM simulation of a sono-reactor accounting for vibrations of the boundaries. Ultrason. Sonochem. 2009;16(2):250–259. doi: 10.1016/j.ultsonch.2008.07.008. [DOI] [PubMed] [Google Scholar]
- 85.Luo X., Cao J., Gong H., Yan H., He L. Phase separation technology based on ultrasonic standing waves: A review. Ultrason. Sonochem. 2018;48:287–298. doi: 10.1016/j.ultsonch.2018.06.006. [DOI] [PubMed] [Google Scholar]
- 86.Ma J., Yu J., Fan Z., Zhu Z., Gong X., Du G. Acoustic nonlinearity of liquid containing encapsulated microbubbles. J. Acoust. Soc. Am. 2004;116(1):186–193. doi: 10.1121/1.1760792. [DOI] [Google Scholar]
- 87.Magnaudet J., Eames I. The Motion of High-Reynolds-Number Bubbles in Inhomogeneous Flows. In Annual Review of Fluid Mechanics (vol. 2000;32, Issue 1) doi: 10.1146/annurev.fluid.32.1.659. [DOI] [Google Scholar]
- 88.Margulis M.A. Sonoluminescence and sonochemical reactions in cavitation fields. A Review. Ultrasonics. 1985;23(4):157–169. doi: 10.1016/0041-624X(85)90024-1. [DOI] [Google Scholar]
- 89.Margulis M.A. Fundamental problems of sonochemistry and cavitation. Ultrason. Sonochem. 1994;1(2):S87–S90. doi: 10.1016/1350-4177(94)90003-5. [DOI] [Google Scholar]
- 90.Martin C.J., Law A.N.R. The use of thermistor probes to measure energy distribution in ultrasound fields. Ultrasonics. 1980;18(3):127–133. doi: 10.1016/0041-624X(80)90026-8. [DOI] [PubMed] [Google Scholar]
- 91.Mason T.J. Sonochemistry: Current Uses and Future Prospects in the Chemical and Processing Industries. Philosophical Transactions: Mathematical, Physical and Engineering Sciences. 1999;357(1751):355–369. http://www.jstor.org/stable/55004 [Google Scholar]
- 92.Mason T.J. Large scale sonochemical processing: aspiration and actuality. Ultrason. Sonochem. 2000;7(4):145–149. doi: 10.1016/S1350-4177(99)00041-3. [DOI] [PubMed] [Google Scholar]
- 93.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Energy analysis during acoustic bubble oscillations: Relationship between bubble energy and sonochemical parameters. Ultrasonics. 2014;54(1):227–232. doi: 10.1016/j.ultras.2013.04.014. [DOI] [PubMed] [Google Scholar]
- 94.Mettin R. In Modern Trends and Applications; Research Signpost: 2005. Bubble structures in acoustic cavitation. [Google Scholar]
- 95.Mettin R., Akhatov I., Parlitz U., Ohl C.D., Lauterborn W. Bjerknes forces between small cavitation bubbles in a strong acoustic field. In. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat Interdiscip. Topics. 1997;Vol. 56, Issue 3 doi: 10.1103/PhysRevE.56.2924. [DOI] [Google Scholar]
- 96.Mettin R., Luther S., Ohl C.D., Lauterborn W. Acoustic cavitation structures and simulations by a particle model. Ultrason. Sonochem. 1999;6(1–2):25–29. doi: 10.1016/S1350-4177(98)00025-X. [DOI] [PubMed] [Google Scholar]
- 97.Miksis M.J., Ting L. Effects of bubbly layers on wave propagation. J. Acoust. Soc. Am. 1989;86(6):2349–2358. doi: 10.1121/1.398442. [DOI] [Google Scholar]
- 98.Moholkar V.S., Sable S.P., Pandit A.B. Mapping the cavitation intensity in an ultrasonic bath using the acoustic emission. In AIChE Journal (vol. 2000;46, Issue 4) doi: 10.1002/aic.690460404. [DOI] [Google Scholar]
- 99.Moussatov A., Granger C., Dubus B. Cone-like bubble formation in ultrasonic cavitation field. Ultrason. Sonochem. 2003;10(4–5):191–195. doi: 10.1016/S1350-4177(02)00152-9. [DOI] [PubMed] [Google Scholar]
- 100.Mutasa T., Gachagan A., Nordon A., O’Leary R.L. Ultrasonic wave propagation in cylindrical vessels and implications for ultrasonic reactor design. IEEE International Ultrasonics Symposium. 2010;2010:1470–1473. doi: 10.1109/ULTSYM.2010.5935906. [DOI] [Google Scholar]
- 101.Naidu G.M., Prasad V.K. In Caves; Kogut: 1984. Predictors of Export Strategy and Performance of Small-and Medium-Sized Firms Review of Literature. [Google Scholar]
- 102.Naudé C.F., Ellis A.T. On the Mechanism of Cavitation Damage by Nonhemispherical Bubbles Collapsing in Contact With a Solid Boundary. J. Basic Eng. 1961;83:648–656. [Google Scholar]
- 103.Naudé C.F., Ellis A.T. On the Mechanism of Cavitation Damage by Nonhemispherical Bubbles Collapsing in Contact With a Solid Boundary. J. Basic Eng. 2011;83(4):648. doi: 10.1115/1.3662286. [DOI] [Google Scholar]
- 104.Naugolnykh K., Ostrovsky L. Cambridge University Press; 1998. Nonlinear Wave Proecesses in Acoustics. [Google Scholar]
- 105.Nguyen V.-T., Bae B.-U., Euh D.-J., Song C.-H., Yun B.-J. The Effect of Bubble-Induced Turbulence on the Interfacial Area Transport in Gas-Liquid Two-Phase Flow. The Journal of Computational Multiphase Flows. 2012;4(3):327–340. doi: 10.1260/1757-482X.4.3.327. [DOI] [Google Scholar]
- 106.Nomura H., Koda S., Yasuda K., Kojima Y. Quantification of ultrasonic intensity based on the decomposition reaction of porphyrin. Ultrason. Sonochem. 1996;3(3):S153–S156. doi: 10.1016/S1350-4177(96)00020-X. [DOI] [Google Scholar]
- 107.Perincek S., Uzgur A.E., Duran K., Dogan A., Korlu A.E., Bahtiyari I.M. Design parameter investigation of industrial size ultrasound textile treatment bath. Ultrason. Sonochem. 2009;16(1):184–189. doi: 10.1016/j.ultsonch.2008.06.003. [DOI] [PubMed] [Google Scholar]
- 108.Plesset M.S., Pasadena C. The Dynamics of Cavitation Bubbles. In. J. Appl. Mech.. 1949 [Google Scholar]
- 109.Prosperetti A. The thermal behaviour of oscillating gas bubbles. In. J. Fluid Mech. 1991;222 doi: 10.1017/S0022112091001234. [DOI] [Google Scholar]
- 110.Prosperetti A. The speed of sound in a gas–vapour bubbly liquid. Interface. Focus. 2015;5(5) doi: 10.1098/rsfs.2015.0024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Prozorov T., Prozorov R., Suslick K.S. High velocity interparticle collisions driven by ultrasound. J. Am. Chem. Soc. 2004;126(43):13890–13891. doi: 10.1021/ja049493o. [DOI] [PubMed] [Google Scholar]
- 112.Pugin B. Qualitative characterization of ultrasound reactors for heterogeneous sonochemistry. Ultrasonics. 1987;25(1):49–55. doi: 10.1016/0041-624X(87)90012-6. [DOI] [Google Scholar]
- 113.Rayleigh L. VIII. On the pressure developed in a liquid during the collapse of a spherical bubble. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of. Science. 1917;34(200):94–98. doi: 10.1080/14786440808635681. [DOI] [Google Scholar]
- 114.Richards W.T., Loomis A.L. THE CHEMICAL EFFECTS OF HIGH FREQUENCY SOUND WAVES I. A PRELIMINARY SURVEY. J. Am. Chem. Soc. 1927;49(12):3086–3100. doi: 10.1021/ja01411a015. [DOI] [Google Scholar]
- 116.Sáez V., Frías-Ferrer A., Iniesta J., Gonález-zGarcía J., Aldaz A., Riera E. Characterization of a 20 kHz sonoreactor. Part II: analysis of chemical effects by classical and electrochemical methods. Ultrason. Sonochem. 2005;12(1):67–72. doi: 10.1016/j.ultsonch.2004.06.010. [DOI] [PubMed] [Google Scholar]
- 117.Sander J.R.G., Zeiger B.W., Suslick K.S. Sonocrystallization and sonofragmentation. Ultrason. Sonochem. 2014;21(6):1908–1915. doi: 10.1016/j.ultsonch.2014.02.005. [DOI] [PubMed] [Google Scholar]
- 118.Servant G., Caltagirone J.P., Gérard A., Laborde J.L., Hita A. Numerical simulation of cavitation bubble dynamics induced by ultrasound waves in a high frequency reactor. Ultrason. Sonochem. 2000;7(4):217–227. doi: 10.1016/S1350-4177(00)00059-6. [DOI] [PubMed] [Google Scholar]
- 119.Servant G., Laborde J.L., Hita A., Caltagirone J.P., Gérard A. Spatio-temporal dynamics of cavitation bubble clouds in a low frequency reactor: Comparison between theoretical and experimental results. Ultrason. Sonochem. 2001;8(3):163–174. doi: 10.1016/S1350-4177(01)00074-8. [DOI] [PubMed] [Google Scholar]
- 120.Shao Z.W., Le Q.C., Cui J.Z., Zhang Z.Q. Numerical simulation of standing waves for ultrasonic purification of magnesium alloy melt. Transactions of Nonferrous Metals Society of China (english Edition) 2010;20(SUPPL. 2):s382–s387. doi: 10.1016/S1003-6326(10)60502-X. [DOI] [Google Scholar]
- 121.Soudagar S.R., Samant S.D. Semiquantitative characterization of ultrasonic cleaner using a novel piezoelectric pressure intensity measurement probe. Ultrasonics - Sonochemistry. 1995;2(1):S49–S53. doi: 10.1016/1350-4177(94)00012-H. [DOI] [Google Scholar]
- 122.Suslick, K. S., Didenko, Y., Fang, M. M., Hyeon, T., Kolbeck, K. J., McNamara, W. B., Mdleleni, M. M., & Wong, M. (1999). Acoustic cavitation and its chemical consequences.
- 123.Sutkar V.S., Gogate P.R. Design aspects of sonochemical reactors: Techniques for understanding cavitational activity distribution and effect of operating parameters. Chem. Eng. J. 2009;155(1–2):26–36. doi: 10.1016/j.cej.2009.07.021. [DOI] [Google Scholar]
- 124.Sutkar V.S., Gogate P.R. Mapping of cavitational activity in high frequency sonochemical reactor. Chem. Eng. J. 2010;158(2):296–304. doi: 10.1016/j.cej.2010.01.051. [DOI] [Google Scholar]
- 125.Sutkar V.S., Gogate P.R., Csoka L. Theoretical prediction of cavitational activity distribution in sonochemical reactors. Chem. Eng. J. 2010;158(2):290–295. doi: 10.1016/j.cej.2010.01.049. [DOI] [Google Scholar]
- 126.Tejedor Sastre M.T., Vanhille C. Numerical models for the study of the nonlinear frequency mixing in two and three-dimensional resonant bubbles filled with a bubbly liquid. Ultrason. Sonochem. 2017;39:597–610. doi: 10.1016/j.ultsonch.2017.05.009. [DOI] [PubMed] [Google Scholar]
- 127.Thompson L.H., Doraiswamy L.K. Sonochemistry: Science and Engineering. Ind. Eng. Chem. Res. 1999;38(4):1215–1249. doi: 10.1021/ie9804172. [DOI] [Google Scholar]
- 128.Thornycroft J.I., Barnaby S.W. Torpedo-Boat Destroyers. Minutes of the. Proc. Inst. Civ. Eng. 1895;122:51–69. [Google Scholar]
- 129.Tiong T.J., Chu J.K., Lim L.Y., Tan K.W., Hong Yap Y., Asli U.A. A computational and experimental study on acoustic pressure for ultrasonically formed oil-in-water emulsion. Ultrason. Sonochem. 2019;56:46–54. doi: 10.1016/j.ultsonch.2019.03.026. [DOI] [PubMed] [Google Scholar]
- 130.Tiong T.J., Liew D.K.L., Gondipon R.C., Wong R.W., Loo Y.L., Lok M.S.T., Manickam S. Identification of active sonochemical zones in a triple frequency ultrasonic reactor via physical and chemical characterization techniques. Ultrason. Sonochem. 2017;35:569–576. doi: 10.1016/j.ultsonch.2016.04.029. [DOI] [PubMed] [Google Scholar]
- 131.Townsend R.J., Hill M., Harris N.R., White N.M. Investigation of two-dimensional acoustic resonant modes in a particle separator. Ultrasonics. 2006;44:e467–e471. doi: 10.1016/j.ultras.2006.05.025. [DOI] [PubMed] [Google Scholar]
- 132.Tudela I., Sáez V., Esclapez M.D., Bonete P., Harzali H., Baillon F., González-García J., Louisnard O. Study of the influence of transducer-electrode and electrode-wall gaps on the acoustic field inside a sonoelectrochemical reactor by FEM simulations. Chem. Eng. J. 2011;171(1):81–91. doi: 10.1016/j.cej.2011.03.064. [DOI] [Google Scholar]
- 133.Tudela I., Sáez V., Esclapez M.D., Díez-García M.I., Bonete P., González-García J. Simulation of the spatial distribution of the acoustic pressure in sonochemical reactors with numerical methods: A review. Ultrason. Sonochem. 2014;21(3):909–919. doi: 10.1016/j.ultsonch.2013.11.012. [DOI] [PubMed] [Google Scholar]
- 134.Vanhille C., Campos-Pozuelo C. Numerical simulation of two-dimensional nonlinear standing acoustic waves. J. Acoust. Soc. Am. 2004;116(1):194–200. doi: 10.1121/1.1760798. [DOI] [Google Scholar]
- 135.Vanhille C., Campos-Pozuelo C. Three Time-Domain Computational Models for Quasi-Standing Nonlinear Acoustic Waves, Including Heat Production. J. Comput Acoust. 2006;14(02):143–156. doi: 10.1142/s0218396x06002986. [DOI] [Google Scholar]
- 136.Vanhille C., Campos-Pozuelo C. Nonlinear Ultrasonic Propagation in Bubbly Liquids: A Numerical Model. Ultrasound Med. Biol. 2008;34(5):792–808. doi: 10.1016/j.ultrasmedbio.2007.11.004. [DOI] [PubMed] [Google Scholar]
- 137.Vanhille C., Campos-Pozuelo C. Nonlinear ultrasonic waves in bubbly liquids with nonhomogeneous bubble distribution: Numerical experiments. Ultrason. Sonochem. 2009;16(5):669–685. doi: 10.1016/j.ultsonch.2008.11.013. [DOI] [PubMed] [Google Scholar]
- 138.Vanhille C., Campos-Pozuelo C. Numerical simulation of nonlinear ultrasonic standing waves in bubbly liquid. International Journal of Nonlinear Sciences and Numerical Simulation. 2009;10(6):751–757. doi: 10.1515/IJNSNS.2009.10.6.751. [DOI] [Google Scholar]
- 139.Vanhille C., Campos-Pozuelo C. Nonlinear ultrasonic standing waves: Two-dimensional simulations in bubbly liquids. Ultrason. Sonochem. 2011;18(2):679–682. doi: 10.1016/j.ultsonch.2010.09.002. [DOI] [PubMed] [Google Scholar]
- 140.Wang D., Yan L., Ma X., Wang W., Zou M., Zhong J., Ding T., Ye X., Liu D. Ultrasound promotes enzymatic reactions by acting on different targets: Enzymes, substrates and enzymatic reaction systems. Int. J. Biol. Macromol. 2018;119:453–461. doi: 10.1016/j.ijbiomac.2018.07.133. [DOI] [PubMed] [Google Scholar]
- 141.Wang M., Zhou Y. Numerical investigation of the inertial cavitation threshold by dual-frequency excitation in the fluid and tissue. Ultrason. Sonochem. 2018;42:327–338. doi: 10.1016/j.ultsonch.2017.11.045. [DOI] [PubMed] [Google Scholar]
- 142.Watanabe T., Kukita Y. Translational and radial motions of a bubble in an acoustic standing wave field. Phys. Fluids A. 2002;5(11):2682–2688. doi: 10.1063/1.858731. [DOI] [Google Scholar]
- 143.Wei Z., Weavers L.K. Combining COMSOL modeling with acoustic pressure maps to design sono-reactors. Ultrason. Sonochem. 2016;31:490–498. doi: 10.1016/j.ultsonch.2016.01.036. [DOI] [PubMed] [Google Scholar]
- 144.Whillock G.O.H., Harvey B.F. Ultrasonically enhanced corrosion of 304L stainless steel II: The effect of frequency, acoustic power and horn to specimen distance. Ultrason. Sonochem. 1997;4(1):33–38. doi: 10.1016/S1350-4177(96)00015-6. [DOI] [PubMed] [Google Scholar]
- 145.van Wijngaarden L., Kapteyn C. Concentration waves in dilute bubble/liquid mixtures. J. Fluid Mech. 1990;212:111–137. doi: 10.1017/S0022112090001896. [DOI] [Google Scholar]
- 146.Wood R.W., Loomis A.L. XXXVIII. The physical and biological effects of high-frequency sound-waves of great intensity. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of. Science. 1927;4(22):417–436. doi: 10.1080/14786440908564348. [DOI] [Google Scholar]
- 147.Xi X., Cegla F.B., Lowe M., Thiemann A., Nowak T., Mettin R., Holsteyns F., Lippert A. Study on the bubble transport mechanism in an acoustic standing wave field. Ultrasonics. 2011;51(8):1014–1025. doi: 10.1016/j.ultras.2011.05.018. [DOI] [PubMed] [Google Scholar]
- 148.Xu Z., Yasuda K., Koda S. Numerical simulation of liquid velocity distribution in a sonochemical reactor. Ultrason. Sonochem. 2013;20(1):452–459. doi: 10.1016/j.ultsonch.2012.04.011. [DOI] [PubMed] [Google Scholar]
- 149.Xu Z., Yasuda K., Liu X. Simulation of the formation and characteristics of ultrasonic fountain. Ultrason. Sonochem. 2016;32:241–246. doi: 10.1016/j.ultsonch.2016.03.016. [DOI] [PubMed] [Google Scholar]
- 150.Yasui K. 1st ed. Springer International Publishing; 2018. Acoustic Cavitation and Bubble Dynamics. doi: 10.1007/978-3-319-68237-2. [Google Scholar]
- 151.Yasui K., Iida Y., Tuziuti T., Kozuka T., Towata A. Strongly interacting bubbles under an ultrasonic horn. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2008;77(1):16609. doi: 10.1103/PhysRevE.77.016609. [DOI] [PubMed] [Google Scholar]
- 152.Yasui K., Kozuka T., Tuziuti T., Towata A., Iida Y., King J., Macey P. FEM calculation of an acoustic field in a sonochemical reactor. Ultrason. Sonochem. 2007;14(5):605–614. doi: 10.1016/j.ultsonch.2006.09.010. [DOI] [PubMed] [Google Scholar]
- 153.Yu H., Zhong Q., Liu Y., Guo Y., Xie Y., Zhou W., Yao W. Recent advances of ultrasound-assisted Maillard reaction. Ultrason. Sonochem. 2020;64 doi: 10.1016/j.ultsonch.2019.104844. [DOI] [PubMed] [Google Scholar]
- 154.Zeiger B.W., Suslick K.S. Sonofragmentation of molecular crystals. J. Am. Chem. Soc. 2011;133(37):14530–14533. doi: 10.1021/ja205867f. [DOI] [PubMed] [Google Scholar]
- 155.Zhang Y., Zhang Y. Chaotic oscillations of gas bubbles under dual-frequency acoustic excitation. Ultrason. Sonochem. 2018;40:151–157. doi: 10.1016/j.ultsonch.2017.03.058. [DOI] [PubMed] [Google Scholar]
- 156.Zhang Z., Gao T., Liu X., Li D., Zhao J., Lei Y., Wang Y. Influence of sound directions on acoustic field characteristics within a rectangle-shaped sonoreactor: Numerical simulation and experimental study. Ultrason. Sonochem. 2018;42:787–794. doi: 10.1016/j.ultsonch.2017.12.024. [DOI] [PubMed] [Google Scholar]
- 157.Zieniuk J., Chivers R.C. Measurement of ultrasonic exposure with radiation force and thermal methods. Ultrasonics. 1976;14(4):161–172. doi: 10.1016/0041-624X(76)90048-2. [DOI] [PubMed] [Google Scholar]
- 158.Zwick S.A. Behavior of Small Permanent Gas Bubbles in a Liquid: Part I. Isolated Bubbles. J. Math. Phys. 1958;37(1–4):246–268. doi: 10.1002/sapm1958371246. [DOI] [Google Scholar]
Further reading
- 115.Sáez V., Frías-Ferrer A., Iniesta J., González-García J., Aldaz A., Riera E. Chacterization of a 20 kHz sonoreactor. Part I: Analysis of mechanical effects by classical and numerical methods. Ultrason. Sonochem. 2005;12(1–2 SPEC. ISS.):59–65. doi: 10.1016/j.ultsonch.2004.06.011. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data was used for the research described in the article.