Abstract
Proteins are exposed to hydrostatic pressure (HP) in a variety of ecosystems, as well as in processing steps such as freeze-thaw, cell disruption, sterilization, and homogenization, yet pressure effects on protein-protein interactions (PPIs) remain underexplored. With the goal of contributing towards the expanded use of HP as a fundamental control parameter in protein research, processing, and engineering, small-angle X-ray scattering was used to examine the effects of HP and ionic strength on ovalbumin, a model protein. Based on an extensive data set, we develop an empirical method for scaling PPIs to a master curve by combining HP and osmotic effects. We define an effective pressure parameter, shown to successfully apply to other model protein data available in the literature, with deviations evident for proteins that do not follow the apparent Hofmeister series. The limitations of the empirical scaling are discussed in the context of the hypothesized underlying mechanisms.
Graphic Abstract
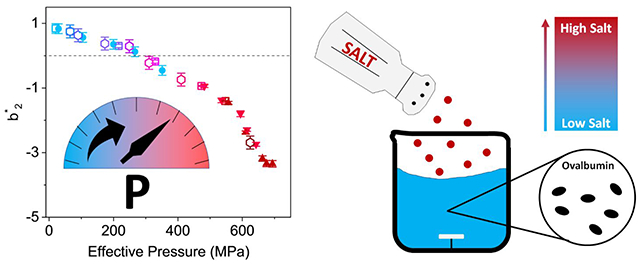
Schematic representation of how protein-protein interactions can be scaled for data collected at various salt and hydrostatic pressure conditions.
1. INTRODUCTION
Protein solutions can experience a variety of natural and artificial environments, spanning ranges of temperature, pressure, ionic strength, and pH 1. Due to limitations of the instrumentation available, high hydrostatic pressure (HP) is arguably the least used parameter to manipulate biomolecular structures and colloidal stability, despite its common application in microbial inactivation of heat-sensitive foods and drug formulations 2, 3. There are, nonetheless, recent and ongoing efforts towards expanding measurement capabilities in the range of 100 MPa-1000 MPa, including, e.g., small angle X-ray and neutron scattering, NMR, crystallography, and fluorescence. These advances reflect an increasing awareness of the advantages of pressure beyond its prevalent use in sterilization 4. In situ data are essential to support the development of predictive tools for existing and novel applications, such as pressure-assisted precipitation and crystallization, or the design of cost-effective alternatives to chromatographic downstream protein processing at industrial scale 5, 6.
High pressure increases the density of pure water through a distortion of the near-tetrahedral local structure of liquid water 7. HP applied to aqueous solutions of proteins increases the overall system density through a water-mediated process: the density of the protein hydration layer increases and the volume of regions or domains containing internal cavities is reduced, due to changes in the water structure under pressure that weaken the hydrophobic effect. The effects of salt ions on protein solubility and protein-protein interactions (PPIs) have also been described for many years as a function of their ability to alter water structure, reflected by the Hofmeister series 8. The lyotropic series effectively orders the potential of ions according to their ability to weaken (chaotropic) or strengthen (kosmotropic) the hydrogen-bond network of water. Studies of HP effects on pure water and electrolyte solutions have used neutron diffraction data to show that the structure of water is affected similarly by salt or pressure 9, 10: both have the ability of water structure making or breaking. Recent studies have, however, shown that the similarity of the effects from adding salt or applying pressure is restricted to the first ionic solvation shell; ion hydration impacts orientation correlations in bulk water, but the tetrahedral structure is not distorted beyond the first solvation shell 11. It has also been shown that the combined effects of salt and pressure cannot be separated from the direct effects of ion-binding to the protein, as well as interactions with the protein hydration shell 8. Ion-specific effects can, for example, help to explain why the solubility of some positively charged proteins, such as lysozyme, follow a reverse Hofmeister series 12.
Synergistic effects of pressure and salt on macroscopic protein solution and gel properties have been well-documented 13–15. Motivated by this synergism, we investigated the possibility of a relatively simple empirical screening of protein behavior to capture the combined effects of pressure and ionic concentration on PPIs. A model protein, ovalbumin, was studied in the presence of a kosmotrope at near neutral pH. The dilute limit regime was chosen so that the studies could be applied to a single-phase solution, and to simplify the calculation of interaction parameters based on the assumption that the protein tertiary structure is stable in the range of pressure and salt concentrations chosen 16. The choice of salt and protein were guided by the existence of numerous studies on the structure and solubility of ovalbumin, the hen egg white albumin previously studied in the presence of ammonium sulfate 17. The monomeric form of ovalbumin is a 45 kDa phosphoglycoprotein with an isoelectric point (pI) reported in the literature between 4.5 and 4.8 18, 19. Ovalbumin solutions have rich phase behavior with crystals, gels, and dense particles appearing at moderate-to-high salt concentrations with relatively low protein concentrations (< 50 mg/mL) 17. At neutral pH and ambient temperature, dense ovalbumin phases appear at concentrations above 1.4 M ammonium sulfate (where M represents the SI units mol/L). Pressure denaturation of ovalbumin was first reported near 600 MPa, as identified by the seminal work of Bridgman on the pressure-induced coagulation of egg white 20.21,22. Subsequent studies revealed complex behavior under pressure; for example, a pH-dependent baroresistance study highlighted that the secondary structure of ovalbumin remains largely unchanged at pressures up to 400 MPa in a range of pH, although the pressure effects depend on the pressure holding time 23.
The present study explores the influence of dissolved salt and applied hydrostatic pressure on ovalbumin interactions in relatively dilute solutions. Small-angle X-ray scattering data were collected for multiple pressure and salt concentration conditions and fitted to calculate the osmotic second virial coefficient, , a broadly used parameter to characterize PPIs 16 and, by extension, to correlate and predict protein crystallization conditions 24 (observed to often occur at values from to ). Data were successfully collapsed via an empirical scaling for both ovalbumin in ammonium sulfate and for data for other proteins from the literature.
2. MATERIALS AND METHODS
2.1. Sample Preparation
Ammonium sulfate (AS) and sodium phosphate monobasic anhydrous were purchased from Fisher Scientific (Pittsburgh, PA). Sodium deuteroxide from Cambridge Isotope Laboratories (Andover, MA) was used to adjust the measured pH in solutions (taken as directly equivalent to the pD). Lyophilized ovalbumin powder was purchased from Sigma-Aldrich (A5503; St. Louis, MO) with 98% purity, as assessed by gel electrophoresis, and used without further purification. Protein samples were prepared in with the goal of expanding the reported work to future studies using small-angle neutron scattering (SANS), to take advantage of the non-destructive nature of the technique to investigate hysteresis, pressure holding time effects, and their reversibility. shifts the phase boundaries with respect to the same conditions in , but the present study was performed in the single-phase regime. Ovalbumin was solubilized in 5 mM sodium phosphate buffer (pD 7).
Stock solutions of 2.4 M AS were prepared by dissolving ammonium sulfate in 5 mM phosphate buffer (pD 7). The pD of all solutions was remeasured after mixing protein and salt solutions: the observed pD was in the full range of salt and protein concentrations used. All samples were prepared immediately prior to data collection. Protein concentrations were measured via absorbance at 280 nm, using the ovalbumin solution extinction coefficient of 25.
2.2. Small-Angle X-Ray Scattering (SAXS)
SAXS measurements at atmospheric pressure were performed on protein solutions at various concentrations using the 18-ID BioCAT beamline of the Advanced Photon Source, Illinois, USA. Data were collected at room temperature (), on a Pilatus3 1M pixel detector (Dectris). SAXS was measured using an X-ray wavelength of across a momentum-transfer -range of to , where
| (1) |
and is the scattering angle. In-line size-exclusion chromatography SEC-SAXS data were also collected to assess the protein oligomerization state: samples were loaded onto a Superdex 200 Increase 5/150 GL column on an Äkta Pure chromatography system and eluted using 5 mM phosphate buffer (pD 7, with the corresponding AS concentration) at a flow rate of . Eluted samples were analyzed by UV absorbance, prior to flowing into a continuous co-flow through the X-ray beam to minimize radiation damage during data collection 26. SEC-SAXS data were collected as an elution profile, using exposure times of 0.24 s per image. 20-30 images were averaged using BioXTas ; the buffer contributions were subtracted as an average of the background data before the elution peak 27. The elution profile of the AS-free solution of ovalbumin shows a dominance of the monomeric form of the protein with a radius of gyration of (Figure S1).
HP static SAXS measurements were performed on the ID7A BioSAXS beamline at the Cornell High Energy Synchrotron Source with 9.8 keV X-rays. Prior to data collection, the beam attenuation and the optimal number and length of exposures were determined by using sacrificial samples of ovalbumin solution to assess radiation damage (measured as the onset of a shift from the average scattering profile). Data collected after depressurization do not overlap with the starting atmospheric conditions (1 atm MPa), but radiation damage effects cannot be excluded. Sample volumes of were loaded into a Kapton sample-holder and subjected to the desired hydrostatic pressure using the HP-SAXS cell available at the beamline 28. SAXS was measured at pressures up to 350 MPa after 5 minutes of equilibration at each pressure setpoint. Twenty exposures of 0.5 seconds each were collected for each sample condition. Buffer data collected at equivalent pressure steps were subtracted from the corresponding ovalbumin solution data using BioXTAS RAW27.
2.3. Dynamic Light Scattering
Dynamic light scattering (DLS) data were collected on 1 mg/mL ovalbumin in 5 mM sodium phosphate buffer (pD 7). Data were collected at 23°C using a DynaPro Nanostar II DLS instrument from Wyatt Corporation (Santa Barbara, CA), at a wavelength of 658 nm. A refractive index was measured for 5 mM phosphate buffer (pD 7) using an Abbemat 300 digital refractometer from Anton Paar (Graz, Austria). The protein autocorrelation function (Figure S2) was collected with a counting time of 5 minutes, and the hydrodynamic radius was determined from the Stokes-Einstein-Sutherland relation as 29
| (2) |
where is the solvent viscosity, T is the solution temperature, is Boltzmann’s constant, and is the protein diffusivity in solution. The measured hydrodynamic radius for ovalbumin solution in the absence of ammonium sulfate is consistent with the measured by SEC-SAXS for the monomeric protein at .
2.4. Circular Dichroism Spectroscopy (CD)
Room temperature far-UV CD data were collected on 0.9 mg/mL ovalbumin solutions in 5 mM phosphate buffer (pD 7) with varying AS concentrations. A Chirascan Applied Photophysics spectrometer was used with a bandwidth of 1 nm to measure the mean residue ellipticity in the range 175 nm – 260 nm, with a sample path length of 0.1 mm, a step size of 0.5 nm and 3 seconds per step. Three scans were averaged per sample. Buffer CD data were subtracted from the protein solution data. The CD spectra (Figure S3) were deconvoluted using the CONTILL algorithm available on Dichroweb and the Reference set SP175 30–32. The CD curves overlap well up to 1.2 M ammonium sulfate concentration, consistent with no measurable effects of the salt concentration on the protein secondary structure in the range measured. Higher salt concentrations were not measured by CD due to strong absorbance by the buffer at lower wavelengths.
2.5. SAXS Data Fitting and Analyses
The SAXS intensities were modeled as 33
| (3) |
where is the volume fraction of ovalbumin in solution, and is the difference between the X-ray scattering length densities (SLDs) of the protein and the buffer, respectively. is the specific volume of the protein, is the single particle form factor and is an effective structure factor. X-ray SLDs were calculated for varying AS buffers via the online tool SASSIE, and used as input parameters for the form factor fits to the SAXS data 34. All ovalbumin solutions were modeled using SasView 35 with a triaxial ellipsoid form factor averaged over all orientations 36 as
| (4a) |
| (4b) |
where the ellipsoid volume is a function of the polar radius and the equatorial radii and . The effective particle radius is a function of the ellipsoid radii, and the projection vectors are e-f-g respectively.
The decoupling approximation was applied to the structure factor models to account for both polydispersity and anisotropy of the solution structure 37, so that an effective structure factor is defined as
| (5a) |
| (5b) |
where is the structure factor for a monodisperse isotropic protein solution, and is the structure factor corrected for non-sphericity. The correction factor is a function of the form factor , where the brackets represent both ensemble and angular averages of the complex scattering amplitudes.
2.5.1. Structure Factors for AS-Free Protein Solutions
The structure factors of the AS-free 15 mg/mL ovalbumin solution at various pressures were calculated directly from the experimental data using Equation 3: the measured scattering intensities were divided by those of the 5 mg/mL ovalbumin sample at room pressure, and normalized by the corresponding volume fractions to obtain an experimental structure factor. This calculation is premised on the assumptions that contributions of the structure factor to the measured scattering intensity for the AS-free 5 mg/mL ovalbumin solution are negligible, and that the form factor remains approximately constant between 5 mg/mL and 15 mg/mL protein concentrations, for applied pressures up to 350 MPa.
Although effects from sample preparation protocols and measurement inconsistencies cannot be excluded - such as buffers, protein concentration or pressure holding time - the assumption of a constant average form factor for AS-free 15 mg/mL ovalbumin solutions under pressure is consistent with existing literature that reports the baroresistance of the ovalbumin tertiary structure at ambient temperature. For example, neutron scattering studies on a 10 mg/mL ovalbumin solution in a salt-free buffer, at neutral pH, report no shifts of up to 21. The quality of the fits to the scattering data for the AS-free ovalbumin SAXS data reported here, using only the triaxial ellipsoid form factor model (Figure S4), and the agreement between the from the Guinier and distance distribution analyses (Table S2), are consistent with a constant form factor and negligeable structure factor contributions to the scattering profile of ovalbumin solutions up to concentration. The measured from 5 mg/mL ovalbumin solution data, and the measured by DLS on a more dilute protein solution (Figure S2), are also consistent with the aspect ratio expected for globular proteins.
A comparative analysis of the HP-SAXS data was carried out to monitor potential effects of pressure on the form factor of ovalbumin in the conditions measured: no significant shifts in Kratky plots or on normalized scattering intensities were observed for the ovalbumin solutions measured at various AS concentrations up to 350 MPa (see Figures S6A–B). The calculated for the AS-free solution was therefore considered a sufficient approximation of the average form factor for all solutions measured by HP-SAXS. As will be described in section 3.3, the resulting calculations and the master curve analysis successfully scale data collected by different authors on different samples and by different techniques, further supporting that the empirical approach is self-consistent and that the assumption of an approximately constant form factor for ovalbumin up to 350 MPa is valid.
The reduced osmotic second virial coefficient was then estimated from the zero-angle structure factor (0) using 38
| (6) |
where is the protein concentration, is Avogadro’s number, and are the osmotic second virial coefficient for the protein and for non-interacting hard spheres, respectively, and is the protein molar mass. The hard sphere diameter can be approximated as twice the hydrodynamic radius as determined via DLS (31.3 Å ± 3.3 Å, Figure S2). Positive values of indicate net repulsive interactions and negative values indicate net attractive interactions. The calculated for the AS-free solution matches well with prior measurements of ovalbumin 39. Mapping interaction data in terms of the reduced coefficient rather than allows for a comparison of interaction strength with data in the literature for other protein systems 39, 40.
2.5.2. Interaction Parameters for AS-Containing Protein Solutions
HP-SAXS data for dilute protein concentrations at the various salt concentrations – which would be required to directly calculate the structure factors from the experimental data as described in section 2.5.1 - were not collected. This choice was motivated by concerns that the sensitivity of SAXS contrast to AS concentration could potentially introduce errors from inconsistencies between samples at different protein concentrations, as well as beamtime limitations.
Calculations of the structure factor assumed that the form factor does not significantly change between the AS-free and AS-containing protein solutions up to 1.36M AS, and that it does not significantly change with pressure as described in the previous section. Atmospheric pressure CD data collected for 0.9 ovalbumin solutions at different salt concentrations (Figure S3) show no evidence of significant changes in secondary structure, consistent with this assumption. Kratky plots calculated from the HP-SAXS data for the AS-containing 15 mg/mL ovalbumin solutions also show no significant shifts up to 350 MPa, as expected if the protein tertiary structure remains unchanged (Figure S6A–B). Therefore, the form factor for AS-containing ovalbumin solutions was calculated from the triaxial ellipsoidal fit to the AS-free solution data (Table S1). An effective structure factor was then calculated using the decoupling approximation and assuming applicability of a ‘sticky’ hard-sphere model to AS-containing solutions only – based on the assumption that repulsive interactions are screened by counterions so that the Percus-Yevick (PY) closure, an adequate closure for an attractive interparticle potential applies. The ‘stickiness’ was approximated using a modified Baxter model 41 by
| (7a) |
| (7b) |
where and are the interaction potential energy well depth and width respectively, is the hard sphere diameter, and is a perturbation parameter. The interaction potential is defined as
| (8) |
The hard sphere diameters used in the analyses and fitted parameters are tabulated in the Supporting Information (Tables S3–S4). The stickiness is related to the reduced second osmotic virial coefficient for solutions at the dilute limit 42 as
| (9) |
2.6. Thermodynamic Master Curve
Using the osmotic coefficient to account for non-idealities for concentrated electrolytes solutions, the osmotic pressure can be defined from 43
| (10) |
where is the salt concentration, is the solution temperature, is the gas constant and is the number of moles of counterion per mole of salt. For salt concentrations above 100 mM, the empirical Pitzer correlations can be used to calculate thermodynamic properties such as the osmotic coefficient for different salts (Figure S7) 44, 45. Following the original Pitzer and modified models, for a binary mixture of a cation M and anion X can be expressed as 45
| (11) |
where is the solute molality, is the molality-based ionic strength defined as and are the cation and anion stoichiometric coefficients, and and are the corresponding ion charges. is the Debye-Hückel coefficient for the osmotic function defined as 46
| (12) |
is Avogadro’s number, is the pressure-dependent density of the solvent (Equations S5 and S6), is the charge of an electron and is the pressure-dependent dielectric constant of the solvent. The dielectric constants of light and heavy water were previously measured up to and the data were fitted to the Tait equation 47. The Tait equation connects the liquid density to hydrostatic pressure following the relation and was used in the present study to estimate the solvent dielectric constants at various conditions 48. At and in and in . The second coefficient is a function of ionic strength and the empirical parameters , and relations can be found in the associated references; values are tabulated in the Supporting Information for several common salts in the protein literature (Table S5).
To combine the effects of salt and HP, a total effective pressure on the protein in solution and pressure-dependent interaction parameter is defined as
| (13) |
where is the applied hydrostatic pressure for the in situ HP-SAXS measurements, and is an empirical weighting parameter on the osmotic pressure contributions. was determined by fitting as a function of and using a numerical approach (empirical) to parameterize the data (see Supporting Information). The parameters and were estimated using the MATLAB Curve Fitter. The goodness of fit was taken as the coefficient of determination , where RSS is the sum of the squares of the deviation between experimental and fitted values using a linear regression analysis. was taken as an acceptable fit and as a good fit.
3. RESULTS AND DISCUSSION
3.1. Dependence of Protein Scattering on Ionic Strength at Atmospheric Pressure
In-line SEC-SAXS data were used to monitor oligomerization in the absence of ammonium sulfate at pD 7. The corresponding elution profile (Figure S1) shows that, in a AS-free buffer, the protein is essentially monomeric, consistent with repulsive PPI interactions in the phosphate buffer. Dimeric forms of ovalbumin solution have been reported at neutral pH at low ionic strength in various buffers. SAXS analyses of ovalbumin over a range of phosphate buffer capacities reported in the literature do, however, support a stabilization of the monomeric form 49, 50.
Fitting parameters for the ovalbumin form factor can be found in Table S1, and the fit to the data for an AS-free ovalbumin solution is shown in Figure S4. The fitted ellipsoid dimensions yield an aspect ratio of approximately 2.5, as expected for the monomeric protein. Theoretical scattering profiles were calculated from the online tool FoXS 51 using the Protein Data Bank (PDB) structure 1OVA 52–54 for the monomeric and dimeric structures, and compared with a triaxial ellipsoidal fit. The calculated monomeric PDB scattering profile agrees relatively well with the experimental scattering data. A Guinier fit to the data for the AS-free ovalbumin solution results in a calculated radius of gyration of , consistent with the calculated from the 1OVA crystal structure for an ovalbumin monomer (), and considerably smaller than that of a crystallographic dimer ().
Figure 1a shows SAXS data collected for ovalbumin solutions at various AS concentrations, at atmospheric pressure. Differences between profile shapes are attributed to a dominant effect of the AS-induced structure factor, , as shown in Figure 1b. The structure factor shown for 0 M AS is the experimental as described in section 2.5.1, while all other profiles are effective structure factors using the sticky hard sphere model. A deviation of the effective structure factor from 1 is particularly noticeable below , showing a shift towards increasingly attractive interactions as the AS concentration increases. This behavior is consistent with screening electrostatic repulsion and an increasing role for the kosmotropic nature of AS in promoting net attractive PPIs 55. This trend is also reflected in the stickiness parameter (Table S4), which shows the transition from net repulsion to attraction () occurring between 0.5 M and 0.8 M AS concentrations. As the salt concentration increases from 0.2 M to 0.8 M AS, a shallow peak – slightly above 1 – shifts from to a higher Q value that approximately matches correlation distances similar to the ovalbumin polar radius, suggesting that screening of electrostatic repulsions may favor protein-protein interactions in a specific orientation. As shown in Figure 1b, the effective structure factors correlate with relatively short-range attractive PPIs ( and strong long-range attractive PPIs (). The long-range PPIs shift towards positive effective structure factors with increasing AS concentration.
FIGURE 1.
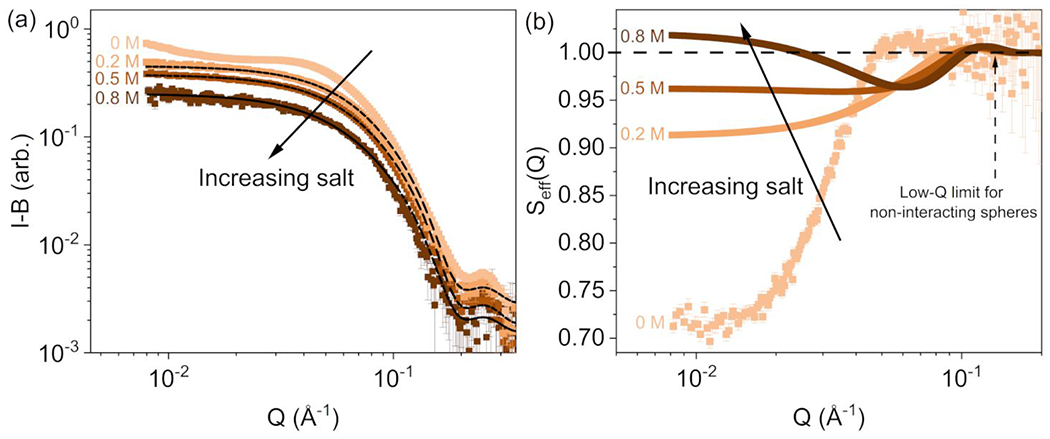
a: Buffer subtracted SAXS profiles for 15 mg/mL ovalbumin solutions over a range of AS concentrations. The fit lines to the scattered intensities from the AS-containing solutions are shown, using the sticky hard sphere structure factor combined with the triaxial ellipsoid form factor model. b: Calculated for SAXS profiles. The 0 M AS solution corresponds to the experimental structure factor. Error bars are standard errors from counting statistics, and where not apparent are smaller than the symbols.
3.2. Dependence of Protein Scattering on Applied Pressure
HP-SAXS profiles for data collected on AS-free solutions, at applied hydrostatic pressures up to 350 MPa, are shown in Figure 2a. The measured intensities decrease with increasing pressure; this effect is known for HP-SAXS data and results from a change in scattering contrast, mostly due to an increase in water density 28. The structure factors (Figure 2b) show an intensity maximum centered around and an intensity minimum around for near-atmospheric pressure (10 MPa). The increase in with increasing pressure suggests an increasing interprotein attraction. The shapes of the profiles flatten as the behavior shifts towards net attractive interactions under increasing pressures, with the structure factor for rising above between 265 MPa and 350 MPa. Although the dependence on AS concentration in Figure 1b shows a similar trend to that on applied hydrostatic pressure, neither the magnitude nor the Q-dependence of the structure factors are the same.
FIGURE 2.
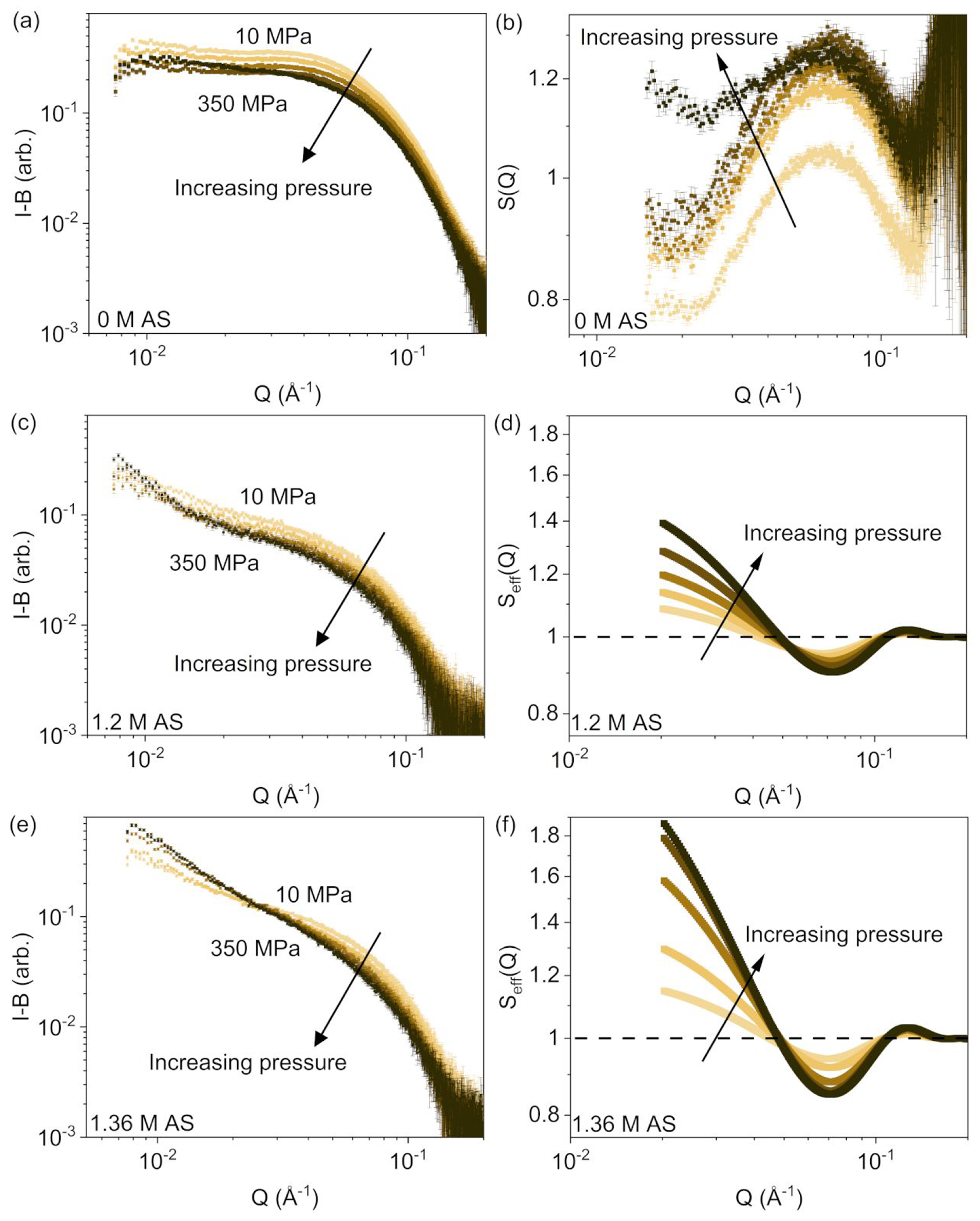
HP-SAXS profiles (buffer subtracted) of 15 mg/mL ovalbumin solutions (left panels) and corresponding effective structure factors (right panels) containing a, b: 0 M AS; c, d: 1.2 M AS; e, f: 1.36 M AS. The applied hydrostatic pressure steps were 10 MPa, 98 MPa, 195 MPa, 265 MPa, and 350 MPa. The 0 M AS solution structure factors were experimentally determined ; structure factors for AS-containing solutions are from sticky hard sphere model fits. Error bars are standard errors from counting statistics, and where not apparent are smaller than the symbols.
Figures 2c–d and 2e–f show the additional effect of salt, via measured SAXS profiles and corresponding structure factors for ovalbumin solutions containing 1.2 M AS and 1.36 M AS, respectively. The structure factor profiles in the presence of AS show a shallow minimum centered around , and the effective structure factors rise above 1 with an increasingly sharp Q dependence for as the applied hydrostatic pressure increases. The latter correspond well to the scattered intensity profiles, where the low-Q upturn characteristic of scattering contributions from aggregated protein is clearly present. As the applied hydrostatic pressure increases, the stickiness parameter decreases (Table S4), consistent with the more attractive interactions.
3.3. Collapsing Protein Interaction Data to a Master Curve
The scattering data were used to determine values of as a measure of PPIs. The variation of the profiles for ovalbumin solutions in different AS concentrations is shown in Figure 3. At atmospheric pressure, decreases with increasing AS concentration, with a transition from repulsive (positive) to attractive (negative) values near 0.7 M AS (Figure 3a). SAXS data collected on ovalbumin solutions containing 0.7 M AS, which were never included in the experimental data points used to fit the master curve, overlay very well with SAXS data on dilute ovalbumin in the absence of AS (Figure S8), providing cross-validation for the results. Values in the literature, where was measured via self-interaction chromatography (SIC) 56 for ovalbumin solutions, display a similar dependence with a transition to negative at 0.85 M AS. As shown in Figure 3b, also decreases with increased applied hydrostatic pressure, and the AS-free solution transitions into the attractive regime near 275 MPa. In the presence of AS, also decreases and the PPIs remain attractive throughout the pressure range.
FIGURE 3.
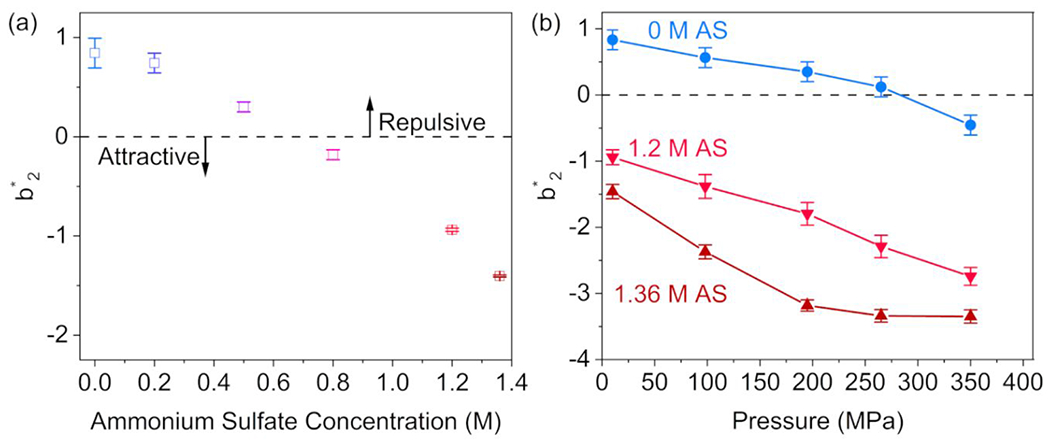
a: The reduced second virial coefficients as a function of AS concentration for ovalbumin solutions at atmospheric pressure, calculated from SAXS data. Increasing salt concentration is color coded from light blue (0 M AS) to dark red (1.36 M AS). b: Reduced second virial coefficients as a function of applied hydrostatic pressure for ovalbumin solutions in 0 M, 1.2 M, and 1.36 M AS. The lines are guides for the eye. Error bars in both plots are estimated from the uncertainty in hard sphere diameter (AS-free solutions, using Equation 6) or are estimated from the fitting error in the stickiness (AS-containing solutions, using Equation 9).
The data were collapsed together following Equation 13 for all of the pressure series at various AS concentrations, in addition to ovalbumin-AS data from the literature 56, to construct the master curve shown in Figure 4. The calculated osmotic pressure scales linearly with total ion concentration (Figure 4, inset). All data were collected in phosphate buffer at pD 7, at least 2 pH units above the protein pI, where the protein is expected to remain negatively charged (net charge ca. −11 at pH 7) 57. Given the known poor resistance of phosphate buffer to hydrostatic pressure-driven shifts in 58, negative pD shifts of less than 1 pH unit are expected.
FIGURE 4.
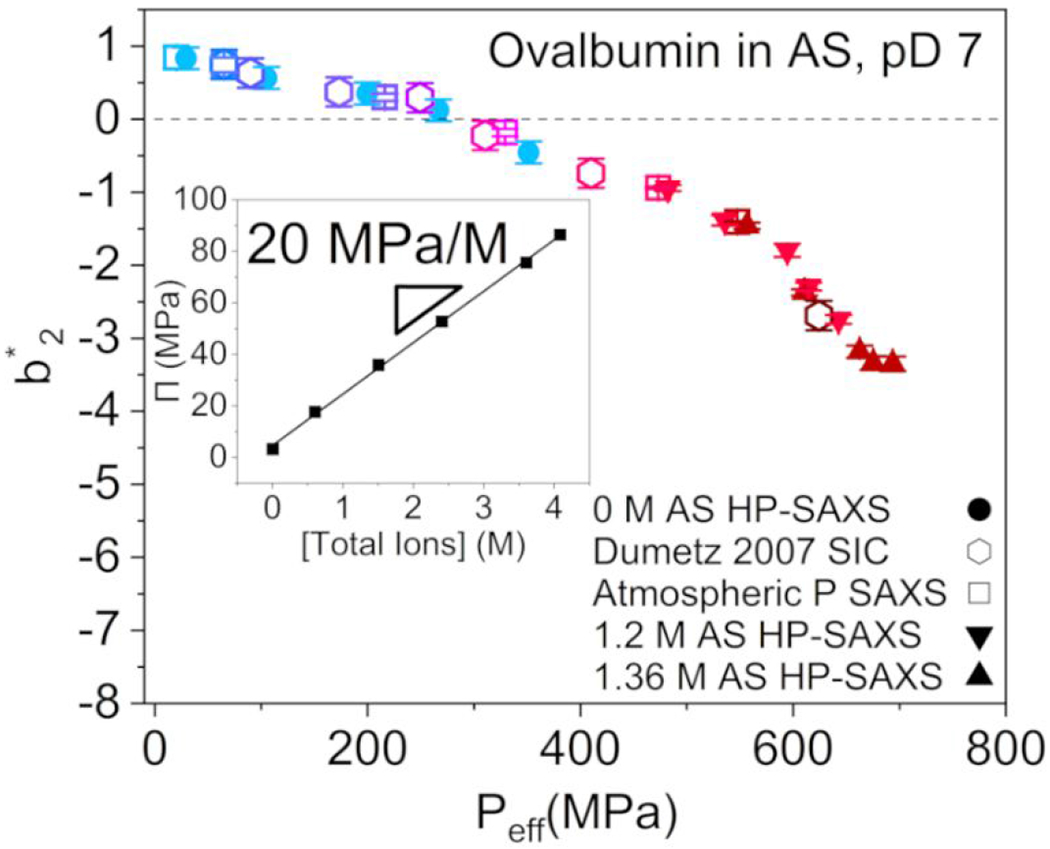
Master curve of ovalbumin as a function of the effective pressure, , with ). AS concentration is denoted by color consistent with Figure 3, with a range of 0 M AS (light blue) to 1.36 M AS (dark red). Sample composition and experimental conditions for each data point can be found in Table S6 in the Supporting Information. Inset: Dependence of the osmotic pressure on total ion concentration, with . Error bars for the literature data are estimated from known experimental uncertainties 56.
The master curve shows a transition from repulsion to attraction at 275 MPa effective pressure, with the rate of decrease accelerating at high . The transition pressure corresponds to 0.77 M AS at atmospheric pressure, calculated from Equation 13, approximately matching the corresponding applied hydrostatic pressure for the AS-free solution data (Figure 3b). The -dependency of follows a negative slope that changes at the transition from repulsion to attraction, and again at . The most attractive points – i.e., with the most negative – reflect solutions under applied hydrostatic pressure in the presence of AS (Figure S11). Although the range of applied pressures is non-denaturing, the of 575 MPa is close to the known 600 MPa denaturation hydrostatic pressure in the absence of salt 20 and may indicate the onset of measurable conformational effects.
To investigate the applicability of this empirical approach to other protein-salt systems, the master curve scaling was applied to interaction data available from the literature for two additional globular proteins: lysozyme 24, 59–63 and β-lactoglobulin (β-LG) 64–68. Data plotted for each protein were chosen to have consistent protein concentration and solution conditions. Figure 5a shows the master curve for β-LG (pI ≈ 5.2, molar mass 18.4 kDa) from static light scattering (SLS) and HP-SANS data, measured at neutral pH in a relatively baroresistant 3-(N-morpholino)propanesulfonic acid (MOPS) buffer. Positive pH shifts of less than 1 pH unit are expected in the pressure range studied in MOPS buffer, so that the net protein charge remains negative in a salt-free solution (cf. net charge at pH 7) 69. The pressure range used for the master curve of β-LG in NaCl is non-denaturing (up to 140 MPa applied hydrostatic pressure). The β-LG master curve fits most data points well: HP-SANS data collected in the absence of NaCl, as well as osmometry and SLS data collected in the presence of salt at atmospheric pressure, scale well to a single profile, consistent with synergistic effects of salt and pressure on β-LG PPIs. becomes negative at 30 MPa – corresponding to 75 mM NaCl.
FIGURE 5.
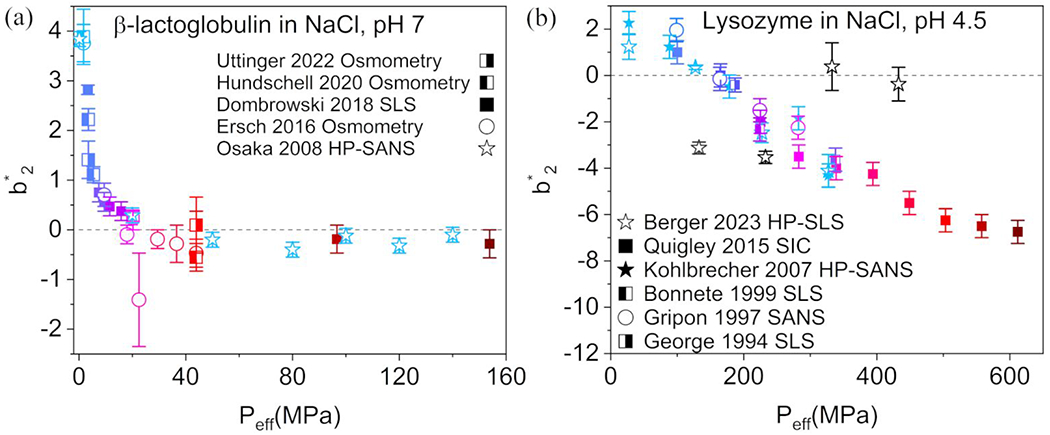
a: Master curve of β-lactoglobulin, based on data from the literature (Table S7) 64–68 with . The NaCl concentration is denoted by color, with a range of 0 M (light blue) to 0.3 M (dark red). b: Master curve of lysozyme, based on data from the literature (Table S8) 24, 59–63 with . NaCl concentration is denoted by color, from 0 M (light blue) to 1 M (dark red). Black open star symbols correspond to data collected at different pressures for solutions of lysozyme containing 59. Error bars for both plots are reproduced from the literature data, estimated from the normalization by (Tables S3 and S5) when available, or from the error in the calculation using Equation 6 (NaCl-free SANS data).
At atmospheric pressure and in the absence of salt, is significantly larger for β-LG than for ovalbumin, suggesting that β-LG displays inherently stronger repulsive interactions despite closer proximity to the protein pI. The effects of the known anisotropic charge distribution on the β-LG surface residues 70 are a potential driver of the strong repulsive interactions in the absence of salt, and of the sharp drop in with low added quantities of NaCl. Hydrostatic pressure induces a similar effect on salt-free β-LG PPIs: relatively low applied pressures neutralize .
Figure 5b shows the master curve from data on lysozyme solutions measured by HP-SLS, self-interaction chromatography (SIC), SLS, and SANS. The range of pressure data used for the master curve of lysozyme in NaCl are non-denaturing (up to 300 MPa applied hydrostatic pressure). All solutions were measured in acetate buffer at acidic pH (4.4 to 4.6), significantly below the isoelectric point ( 71, so that the net charge of lysozyme in a salt-free solution is expected to remain positive, even taking into consideration potential negative pH shifts from the poor baroresistance of acetate buffers. While HP-SLS data 59 in the absence of NaCl fit well with a master curve, in the presence of 150 mM NaCl (black open stars) the HP-SLS data points are significant outliers from the overall trend of the variation as a function of . Lysozyme, possessing a strong positive charge (cf. net charge of +11 at pH 4.8) 71, has been reported to follow two distinct Hofmeister behaviors in the presence of salt 8: a reverse series at relatively low salt concentrations, and a direct series at relatively high salt concentrations 72. The master curve in Figure 5b does reflect at least two different behaviors. A bias of towards salt-related effects, however, cannot be excluded, and this master curve should be revisited as more experimental data under high-pressure conditions become available.
A large fraction of the data in Figure 5b do collapse well to a master curve: NaCl-containing solution at atmospheric pressure, and pressurized NaCl-free solution. A scaling factor of for the osmotic pressure contributions was found to produce a master curve with a significantly different profile from those found for ovalbumin and β-LG. becomes negative at 140 MPa, corresponding to 175 mM NaCl as determined from Equation 13 at atmospheric pressure. The repulsive PPIs in the absence of salt for lysozyme are weaker than those of β-LG despite being much farther from the isoelectric point ). This is a clear indication of the presence of other factors than simple electrostatic mechanisms. Prior studies of the second osmotic virial coefficient of lysozyme do show very different dependences of salt concentration for AS and NaCl, where the AS-containing solutions are all characterized by negative second virial coefficients 56. As more in situ HP data collected for protein solutions become available in the future, the compressibility and expansibility properties of specific salts can potentially be analyzed in terms of their effect on the rate at which interactions become more attractive 73.
4. CONCLUSIONS
The present study of pressure- and salt-dependent PPIs is, to the best of our knowledge, the first reported attempt to collapse the combined PPI effects of hydrostatic pressure and ionic strength to a single curve. Although provides a robust measure of PPIs, specific protein-salt interactions, common-ion effects (salt partitioning between the solution and the hydrated protein), and particularly patchy surface charge distributions may factor into unaccounted mechanisms that alter the effective pressure felt by proteins in solution 74. It was previously suggested that a combined analysis of the preferential-interaction coefficient as a function of effective pressure can provide an improved description of protein solution behavior 75.
Future work will benefit significantly from experimental data to account for effects of the pressurizing rate, pressure steps, and the holding time per pressure on the effective pressures calculated. For the empirical approach described here, no weight or time-dependent parameters were used for since most hydrostatic pressure data were measured for relatively short holding times. HP-SAXS data are relatively limited by the propagation of radiation damage through the sample, and equilibration times of 5 minutes or less are typical. In this context, both HP-SLS and HP small angle neutron scattering (SANS) are ideal techniques to provide relevant data on colloidal stability at a broad range of structural and PPI length scales.
Supplementary Material
ACKNOWLEDGEMENTS
This work was prepared under cooperative agreement #70NANB20H133 from NIST, U.S. Department of Commerce. We acknowledge the support of the National Institute of Standards and Technology, U.S. Department of Commerce, in providing the research facilities used in this work. This work utilized facilities supported in part by the National Science Foundation under Agreement No. DMR-0944772.
We would like to thank Jessie Hopkins and Max Watkins at the BioCAT beamline (APS) for useful discussions and guidance during data collection. The research used resources of the Advanced Photon Source, a US Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. BioCAT was supported by grant P41 GM103622 from the National Institute of General Medical Sciences of the National Institutes of Health. Use of the Pilatus 3 1M detector was provided by Grant 1S10OD018090 from NIGMS.
We would like to thank Richard Gilillan and Qingqiu Huang at the HP Bio-beamline (CHESS) for useful discussions and guidance during data collection. Research conducted at the Cornell High Energy Synchrotron Source (CHESS) is supported by the National Science Foundation under NSF award DMR-0936384, using the Macromolecular Diffraction at CHESS (MacCHESS) facility. This work benefitted from use of the SasView software, which was originally developed by the DANSE project under NSF award DMR-0520547.
ABBREVIATIONS
- AS
ammonium sulfate
- β-LG
β-lactoglobulin
- CD
circular dichroism
- DLS
dynamic light scattering
- HP
high hydrostatic pressure
- LYS
lysozyme
- MOPS
3-(N-morpholino)propanesulfonic acid
- OVA
ovalbumin
- pI
isoelectric point
- PPIs
protein-protein interactions
- RSS
residual sum of squares
- SANS
small-angle neutron scattering
- SAXS
small-angle x-ray scattering
- SEC
size-exclusion chromatography
- SIC
self-interaction chromatography
- SLD
scattering length density
- SLS
static light scattering
Footnotes
Supporting Information
Example SEC-SAXS chromatogram, UV-Vis profiles; correlation function from dynamic light scattering; circular dichroism spectra, deconvolution of secondary structure fractions; tabulated triaxial ellipsoidal form factor parameters, fitted SAXS profile; Guinier analyses and Inverse Fourier Transform analyses; structure factor for dilute ovalbumin solution; hard sphere diameters of proteins studied; Baxter stickiness and of ovalbumin in AS and under pressure; Kratky analysis of pressure-series SAXS data; normalized scattering intensities to room pressure data for each HP-SAXS profile; Pitzer empirical parameters, osmotic coefficients for several binary electrolytes; comparison of dilute solution data and solution data with via addition of AS; pressure dependence of water density; empirical equation for master curve determination; master curves with empirical fit lines; osmotic components of ovalbumin-AS master curve; tabulated solution conditions for master curves.
The following files are available free of charge: SupportingInformation.pdf
Certain instruments and software are identified to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the instruments and software identified are necessarily the best available for the purpose. The statements, findings, conclusions and recommendations are those of the authors and do not necessarily reflect the view of NIST, the National Institute of General Medical Sciences, the National Institutes of Health, or the U.S. Department of Commerce. The authors declare no competing financial interest.
REFERENCES
- (1).Knop J-M; Mukherjee S; Jaworek MW; Kriegler S; Manisegaran M; Fetahaj Z; Ostemieier L; Oliva R; Gault S; Cockell CS; Winter R Life in Multi-Extreme Environments: Brines, Osmotic and Hydrostatic Pressure—A Physicochemical View. Chem. Rev 2023, 123 (1), 73–104. DOI: 10.1021/acs.chemrev.2c00491. [DOI] [PubMed] [Google Scholar]
- (2).Sehrawat R; Kaur BP; Nema PK; Tewari S; Kumar L Microbial inactivation by high pressure processing: principle, mechanism and factors responsible. Food Sci. Biotechnol 2021, 30(1), 19–35. DOI: 10.1007/s10068-020-00831-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Barroso SPC; Vicente Dos Santos AC; Souza Dos Santos P; Dos Santos Silva Couceiro JN; Fernandes Ferreira D; Nico D; Morrot A; Lima Silva J; Cheble de Oliveira A Inactivation of avian influenza viruses by hydrostatic pressure as a potential vaccine development approach. Access Microbiol. 2021, 3(4), 000220. DOI: 10.1099/acmi.0.000220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Khaliq A; Chughtai MFJ; Mehmood T; Ahsan S; Liaqat A; Nadeem M; Sameed N; Saeed K; Rehman JU; Ali A High-Pressure Processing; Principle, Applications, Impact, and Future Prospective. In Sustainable Food Process. Eng. Challenges, Elsevier, 2021; pp 75–108. [Google Scholar]
- (5).Collins MD; Kim CU; Gruner SM High-Pressure Protein Crystallography and NMR to Explore Protein Conformations. Annu. Rev. Biophys 2011, 40(1), 81–98. DOI: 10.1146/annurev-biophys-042910-155304. [DOI] [PubMed] [Google Scholar]
- (6).Azevedo AM; Rosa PA; Ferreira IF; Aires-Barros MR Optimisation of aqueous two-phase extraction of human antibodies. J. Biotechnol 2007, 132(2), 209–217. DOI: 10.1016/j.jbiotec.2007.04.002. [DOI] [PubMed] [Google Scholar]
- (7).Russo D; Laloni A; Filabozzi A; Heyden M Pressure effects on collective density fluctuations in water and protein solutions. Proc. Natl. Acad. Sci 2017, 114 (43), 11410–11415. DOI: 10.1073/pnas.1705279114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Zhang Y; Cremer PS Interactions between macromolecules and ions: The Hofmeister series. Curr. Opin. Chem. Biol 2006, 10(6), 658–663. DOI: 10.1016/j.cbpa.2006.09.020. [DOI] [PubMed] [Google Scholar]
- (9).Leberman R; Soper AK Effect of high salt concentrations on water structure. Nature 1995, 378 (6555), 364–366. DOI: 10.1038/378364a0. [DOI] [PubMed] [Google Scholar]
- (10).Tromp RH; Neilson GW; Soper AK Water structure in concentrated lithium chloride solutions. J Chem. Phys 1992, 96(11), 8460–8469. DOI: 10.1063/1.462298. [DOI] [Google Scholar]
- (11).Zhang C; Yue S; Panagiotopoulos AZ; Klein ML; Wu X Dissolving salt is not equivalent to applying a pressure on water. Nat. Commun 2022, 13(1), 882. DOI: 10.1038/s41467-022-28538-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Dahal YR; Schmit JD Ion Specificity and Nonmonotonic Protein Solubility from Salt Entropy. Biophys. J 2018, 114(1), 76–87. DOI: 10.1016/j.bpj.2017.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Ma F; Chen C; Sun G; Wang W; Fang H; Han Z Effects of high pressure and CaCl2 on properties of salt-soluble meat protein gels containing locust bean gum. Innov. Food Sci. Emerg. Technol 2012, 14, 31–37. DOI: 10.1016/j.ifset.2011.12.001. [DOI] [Google Scholar]
- (14).Zhao Z-K; Mu T-H; Zhang M; Richel A Effect of salts combined with high hydrostatic pressure on structure and gelation properties of sweet potato protein. Food Sci. Technol 2018, 93, 36–44. DOI: 10.1016/j.lwt.2018.03.007. [DOI] [Google Scholar]
- (15).Saalfeld D; Riegel I; Kulozik U; Gebhardt R The Combined Effect of High Hydrostatic Pressure and Calcium Salts on the Stability, Solubility and Gel Formation of beta-Lactoglobulin. Foods 2015, 4(2), 229–239. DOI: 10.3390/foods4020229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Blanco MA; Perevozchikova T; Martorana V; Manno M; Roberts CJ Protein-protein interactions in dilute to concentrated solutions: alpha-chymotrypsinogen in acidic conditions. J. Phys. Chem. B 2014, 118(22), 5817–5831. DOI: 10.1021/jp412301h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Greene DG; Modla S; Wagner NJ; Sandler SI; Lenhoff AM Local Crystalline Structure in an Amorphous Protein Dense Phase. Biophys. J 2015, 109, 1716–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Abeyrathne ED; Lee HY; Ahn DU Egg white proteins and their potential use in food processing or as nutraceutical and pharmaceutical agents--a review. Poult. Sci 2013, 92 (12), 3292–3299. DOI: 10.3382/ps.2013-03391. [DOI] [PubMed] [Google Scholar]
- (19).Spada A; Emami J; Tuszynski JA; Lavasanifar A The Uniqueness of Albumin as a Carrier in Nanodrug Delivery. Mol. Pharm 2021, 18(5), 1862–1894. DOI: 10.1021/acs.molpharmaceut.1c00046. [DOI] [PubMed] [Google Scholar]
- (20).Bridgman PW The coagulation of albumen by pressure. J. Biol. Chem 1914, 19(4), 511–512. [Google Scholar]
- (21).Gomes DC; Teixeira SCM; Leão JB; Razinkov VI; Qi W; Rodrigues MA; Roberts CJ In Situ Monitoring of Protein Unfolding/Structural States under Cold High-Pressure Stress. Mol. Pharm 2021, 18(12), 4415–4427. DOI: 10.1021/acs.molpharmaceut.1c00604. [DOI] [PubMed] [Google Scholar]
- (22).Smith D; Galazka VB; Wellner N; Sumner IG High pressure unfolding of ovalbumin. Int. J. Food Sci. Technol 2000, 35(4), 361–370. DOI: 10.1046/j.1365-2621.2000.00395.x. [DOI] [Google Scholar]
- (23).Tedford LA; Smith D; Schaschke CJ High pressure processing effects on the molecular structure of ovalbumin, lysozyme and β-lactoglobulin. Food Res. Int 1999, 32(2), 101–106. DOI: 10.1016/s0963-9969(99)00062-9. [DOI] [Google Scholar]
- (24).George A; Wilson WW Predicting protein crystallization from a dilute solution property. Acta Crystallogr., Sect. D. Biol. Crystallogr 1994, 50(4), 361–365. DOI: 10.1107/s0907444994001216. [DOI] [PubMed] [Google Scholar]
- (25).Lundblad RL Handb. Biochem. Mol. Biol:, CRC Press, 2018. [Google Scholar]
- (26).Kirby N; Cowieson N; Hawley AM; Mudie ST; McGillivray DJ; Kusel M; Samardzic-Boban V; Ryan TM Improved radiation dose efficiency in solution SAXS using a sheath flow sample environment. Acta Crystallogr., Sect. D: Struct. Biol 2016, 72 (12), 1254–1266. DOI: 10.1107/s2059798316017174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Hopkins J; Gillilan R; Skou S BioXTAS RAW 2.0: the latest in SAXS data analysis. Acta Crystallogr., Sect. A: Found Adv 2020, 76(a1), a27–a27. DOI: 10.1107/s0108767320099729. [DOI] [Google Scholar]
- (28).Rai DK; Gillilan RE; Huang Q; Miller R; Ting E; Lazarev A; Tate MW; Gruner SM High-pressure small-angle X-ray scattering cell for biological solutions and soft materials. J. Appl. Crystallogr 2021, 54 (Pt 1), 111–122. DOI: 10.1107/S1600576720014752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Hansen J; Egelhaaf SU; Platten F Protein solutions close to liquid–liquid phase separation exhibit a universal osmotic equation of state and dynamical behavior. Phys. Chem. Chem. Phys 2023, 25(4), 3031–3041. DOI: 10.1039/d2cp04553b. [DOI] [PubMed] [Google Scholar]
- (30).Miles AJ; Ramalli SG; Wallace BA DichroWeb, a website for calculating protein secondary structure from circular dichroism spectroscopic data. Protein Sci. 2022, 31 (1), 37–46. DOI: 10.1002/pro.4153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Lees JG; Miles AJ; Wien F; Wallace BA A reference database for circular dichroism spectroscopy covering fold and secondary structure space. Bioinformatics 2006, 22(16), 1955–1962. DOI: 10.1093/bioinformatics/btl327. [DOI] [PubMed] [Google Scholar]
- (32).Provencher SW; Gloeckner J Estimation of globular protein secondary structure from circular dichroism. Biochemistry 1981, 20(1), 33–37. DOI: 10.1021/bi00504a006. [DOI] [PubMed] [Google Scholar]
- (33).Feigin, Dmitri LS, Struct. Anal Small-Angle X-Ray Neutron Scattering, Spring Science, 1987. [Google Scholar]
- (34).Sarachan KL; Curtis JE; Krueger S Small-angle scattering contrast calculator for protein and nucleic acid complexes in solution. J. Appl. Crystallogr 2013, 46 (6), 1889–1893. DOI: 10.1107/s0021889813025727. [DOI] [Google Scholar]
- (35).Doucet M; Cho JH; Alina G; Attala Z; Bakker J; Bouwman W; Bourne R; Butler P; Cadwallader-Jones L; Campbell K; Cooper-Benun T; Durniak C; Forster L; Gilbert P; Gonzalez M; Heenan R; Jackson A; King S; Kienzle P; Krzywon J; Maranville B; Murphy R; Nielsen T; O’Driscoll L; Potrzebowski W; Prescott S; Ferraz Leal R; Rozyczko P; Snow T; Washington A; Wolf C SasView version 5.0.5 2022. DOI: 10.5281/zenodo.6331344. [DOI] [Google Scholar]
- (36).Finnigan JA; Jacobs DJ Light scattering by ellipsoidal particles in solution. J. Phys. D: Appl. Phys 1971, 4, 72–77. [Google Scholar]
- (37).Kotlarchyk M; Chen SH Analysis of small angle neutron scattering spectra from polydisperse interacting colloids. J. Chem. Phys 1983, 79(5), 2461–2469. DOI: 10.1063/1.446055. [DOI] [Google Scholar]
- (38).Goldenberg DP; Argyle B Self Crowding of Globular Proteins Studied by Small-Angle X-Ray Scattering. Biophys. J 2014, 106(4), 895–904. DOI: 10.1016/j.bpj.2013.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Dumetz AC; Chockla AM; Kaler EW; Lenhoff AM Effects of pH on protein-protein interactions and implications for protein phase behavior. Biochim. Biophys. Acta 2008, 1784 (4), 600–610. DOI: 10.1016/j.bbapap.2007.12.016. [DOI] [PubMed] [Google Scholar]
- (40).Sibanda N; Shanmugam RK; Curtis R The Relationship between Protein-Protein Interactions and Liquid-Liquid Phase Separation for Monoclonal Antibodies. Mol. Pharm 2023, 20 (5), 2662–2674. DOI: 10.1021/acs.molpharmaceut.3c00090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Menon SV; Manohar C; Rao SK A new interpretation of the sticky hard sphere model. J. Chem. Phys 1991, 95(12), 9186–9190. [Google Scholar]
- (42).Matsarskaia O; Roosen-Runge F; Lotze G; Möller J; Mariani A; Zhang F; Schreiber F Tuning phase transitions of aqueous protein solutions by multivalent cations. Phys. Chem. Chem. Phys 2018, 20 (42), 27214–27225. DOI: 10.1039/c8cp05884a. [DOI] [PubMed] [Google Scholar]
- (43).Ullner M; Qamhieh K; Cabane B Osmotic pressure in polyelectrolyte solutions: cell-model and bulk simulations. Soft Matter 2018, 14(28), 5832–5846. DOI: 10.1039/c8sm00654g. [DOI] [PubMed] [Google Scholar]
- (44).Temoltzi-Avila J; Iglesias-Silva GA; Ramos-Estrada M Comparison Among Pitzer Model and Solvation Models. Calculation of Osmotic and Activity Coefficients and Dilution Enthalpy for Single-Electrolyte Aqueous Solutions. Ind. Eng. Chem. Res 2018, 57 (31), 10684–10700. DOI: 10.1021/acs.iecr.8b00699. [DOI] [Google Scholar]
- (45).May PM; Rowland D; Hefter G; Königsberger E A Generic and Updatable Pitzer Characterization of Aqueous Binary Electrolyte Solutions at 1 bar and 25 °C. J. Chem. Eng. Data 2011, 56(12), 5066–5077. DOI: 10.1021/je2009329. [DOI] [Google Scholar]
- (46).Ananthaswamy J; Atkinson G Thermodynamics of concentrated electrolyte mixtures. 4. Pitzer-Debye-Hueckel limiting slopes for water from 0 to 100.degree.C and from 1 atm to 1 kbar. J. Chem. Eng. Data 1984, 29(1), 81–87. DOI: 10.1021/je00035a027. [DOI] [Google Scholar]
- (47).Huang YK; Chow CY The generalized compressibility equation of Tait for dense matter. J. Phys. D: Appl Phys 2021, 7, 158–160. [Google Scholar]
- (48).Srinivasan KR; Kay RL Pressure dependence of the dielectric constant of H2O and D2O. J. Chem. Phys 1974, 60(9), 3645–3648. DOI: 10.1063/1.1681584. [DOI] [Google Scholar]
- (49).Matsumoto T; Inoue H Association State, Overall Structure, and Surface-Roughness of Native Ovalbumin Molecules in Aqueous-Solutions at Various Ionic Concentrations. J. Colloid Interface Sci 1993, 160(1), 105–109. DOI: DOI 10.1006/jcis.1993.1373. [DOI] [Google Scholar]
- (50).Bucciarelli S; Midtgaard SR; Nors Pedersen M; Skou S; Arleth L; Vestergaard B Size-exclusion chromatography small-angle X-ray scattering of water soluble proteins on a laboratory instrument. J. Appl. Crystallogr 2018, 51(6), 1623–1632. DOI: 10.1107/s1600576718014462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Schneidman-Duhovny D; Hammel M; Tainer JA; Sali A FoXS, FoXSDock and MultiFoXS: Single-state and multi-state structural modeling of proteins and their complexes based on SAXS profiles. Nucleic Acids Res. 2016, 44 (W1), W424–429. DOI: 10.1093/nar/gkw389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Stein PE; Leslie AG; Finch JT; Carrell RW Crystal Structure of Uncleaved Ovalbumin at 1.95 Å Resolution. J. Mol. Biol 1991, 221 (3), 941–959. DOI: 10.2210/pdb1ova/pdb. [DOI] [PubMed] [Google Scholar]
- (53).Berman HM; Westbrook J; Feng Z; Gilliland G; Bhat TN; Weissig H; Shindyalov IN; Bourne PE The Protein Data Bank. Nucleic Acids Res. 2000, 28(1), 235–242. DOI: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Berman H; Henrick K; Nakamura H Announcing the worldwide Protein Data Bank. Nat. Struct. Mol. Biol 2003, 10(12), 980–980. DOI: 10.1038/nsb1203-980. [DOI] [PubMed] [Google Scholar]
- (55).Beck C; Grimaldo M; Braun MK; Bühl L; Matsarskaia O; Jalarvo NH; Zhang F; Roosen-Runge F; Schreiber F; Seydel T Temperature and salt controlled tuning of protein clusters. Soft Matter 2021, 17(37), 8506–8516. DOI: 10.1039/d1sm00418b. [DOI] [PubMed] [Google Scholar]
- (56).Dumetz AC; Snellinger-O’brien A M; Kaler EW; Lenhoff AM Patterns of protein protein interactions in salt solutions and implications for protein crystallization. Protein Sci. 2007, 16 (9), 1867–1877. DOI: 10.1110/ps.072957907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Ianeselli L; Zhang F; Skoda MWA; Jacobs RMJ; Martin RA; Callow S; PréVost S; Schreiber F Protein–Protein Interactions in Ovalbumin Solutions Studied by Small-Angle Scattering: Effect of Ionic Strength and the Chemical Nature of Cations. J. Phys. Chem. B 2010, 114 (11), 3776–3783. DOI: 10.1021/jp9112156. [DOI] [PubMed] [Google Scholar]
- (58).Quinlan RJ; Reinhart GD Baroresistant buffer mixtures for biochemical analyses. Anal. Biochem 2005, 341 (1), 69–76. DOI: 10.1016/j.ab.2005.03.002. [DOI] [PubMed] [Google Scholar]
- (59).Berger JE; Teixeira SCM; Sloey CJ; Qi W; Roberts CJ High Pressure Light Scattering of Therapeutic Proteins To Probe Aggregation and Protein-Protein Interactions. J. Phys. Chem. B 2023, 127 (26), 5742–5754. DOI: 10.1021/acs.jpcb.2c09118. [DOI] [PubMed] [Google Scholar]
- (60).Quigley A; Williams DR The second virial coefficient as a predictor of protein aggregation propensity: A self-interaction chromatography study. Eur. J. Pharm. Biopharm 2015, 96, 282–290. DOI: 10.1016/j.ejpb.2015.07.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Bonnete F; Finet S; Tardieu A Second virial coefficient: variations with lysozyme crystallization conditions. J. Cryst. Growth 1999, 196, 403–414. [Google Scholar]
- (62).Gripon C; Legrand L; Resenman I; Vidal O; Robert MC; Boue F Lysozyme-lysozyme interactions in under- and super-saturated solutions: a simple relation between the second virial coefficients in H20 and D20. J. Cryst. Growth 1997, 178, 575–584. [Google Scholar]
- (63).Kohlbrecher J; Bollhalder A; Vavrin R; Meier G A high pressure cell for small angle neutron scattering up to 500 MPa in combination with light scattering to investigate liquid samples. Rev. Sci. Instrum 2007, 78(12), 125101. DOI: 10.1063/1.2817632. [DOI] [PubMed] [Google Scholar]
- (64).Uttinger MJ; Hundschell CS; Lautenbach V; Pusara S; Bäther S; Heyn TR; Keppler JK; Wenzel W; Walter J; Kozlowska M; Wagemans AM; Peukert W Determination of specific and nonspecific protein–protein interactions for beta-lactoglobulin by analytical ultracentrifugation and membrane osmometry experiments. Soft Matter 2022, 18 (35), 6739–6756. DOI: 10.1039/d2sm00908k. [DOI] [PubMed] [Google Scholar]
- (65).Hundschell CS; Bäther S; Drusch S; Wagemans AM Osmometric and viscometric study of levan, β-lactoglobulin and their mixtures. Food Hydrocolloids 2020, 101, 105580. DOI: 10.1016/j.foodhyd.2019.105580. [DOI] [Google Scholar]
- (66).Dombrowski J; Gschwendtner M; Saalfeld D; Kulozik U Salt-dependent interaction behavior of β-Lactoglobulin molecules in relation to their surface and foaming properties. Colloids Surf., A 2018, 558, 455–462. DOI: 10.1016/j.colsurfa.2018.09.015. [DOI] [Google Scholar]
- (67).Ersch C; Meijvogel LLC; van der Linden E; Martin A; Venema P Interactions in protein mixtures. Part I: Second virial coefficients from osmometry. Food Hydrocolloids 2016, 52, 982–990. DOI: 10.1016/j.foodhyd.2015.07.020. [DOI] [Google Scholar]
- (68).Osaka N; Takata S.-i.; Suzuki T; Endo H; Shibayama M Comparison of heat- and pressure-induced gelation of β-lactoglobulin aqueous solutions studied by small-angle neutron and dynamic light scattering. Polymer 2008, 49(12), 2957–2963. DOI: 10.1016/j.polymer.2008.04.055. [DOI] [Google Scholar]
- (69).Mercadante D; Melton LD; Norris GE; Loo TS; Williams MA; Dobson RC; Jameson GB Bovine beta-lactoglobulin is dimeric under imitative physiological conditions: dissociation equilibrium and rate constants over the pH range of 2.5-7.5. Biophys. J 2012, 103 (2), 303–312. DOI: 10.1016/j.bpj.2012.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Lošdorfer Božič A; Podgornik R Anomalous multipole expansion: Charge regulation of patchy inhomogeneously charged spherical particles. J. Chem. Phys 2018, 149 (16), 163307. DOI: 10.1063/1.5037044. [DOI] [PubMed] [Google Scholar]
- (71).Chiu H-T; Lin J-M; Cheng T-H; Chou S-Y; Huang C-C Direct purification of lysozyme from chicken egg white using weak acidic polyacrylonitrile nanofiber-based membranes. J. Appl. Polym. Sci 2012, 125(S2), E616–E621. DOI: 10.1002/app.36764. [DOI] [Google Scholar]
- (72).Boström M; Parsons DF; Salis A; Ninham BW; Monduzzi M Possible Origin of the Inverse and Direct Hofmeister Series for Lysozyme at Low and High Salt Concentrations. Langmuir 2011, 27 (15), 9504–9511. DOI: 10.1021/la202023r. [DOI] [PubMed] [Google Scholar]
- (73).Naseem B; Arif I; Jamal MA Kosmotropic and chaotropic behavior of hydrated ions in aqueous solutions in terms of expansibility and compressibility parameters. Arab. J. Chem 2021, 14 (11), 103405. DOI: 10.1016/j.arabjc.2021.103405. [DOI] [Google Scholar]
- (74).Annunziata O; Payne A; Wang Y Solubility of lysozyme in the presence of aqueous chloride salts: common-ion effect and its role on solubility and crystal thermodynamics. J. Am. Chem. Soc 2008, 130(40), 13347–13352. DOI: 10.1021/ja804304e. [DOI] [PubMed] [Google Scholar]
- (75).Garajova K; Balogova A; Dusekova E; Sedlakova D; Sedlak E; Varhac R Correlation of lysozyme activity and stability in the presence of Hofmeister series anions. Biochim. Biophys. Acta 2017, 1865 (3), 281–288. DOI: 10.1016/j.bbapap.2016.11.016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


