Physics Informed Neural Networks for Estimation of Tissue Properties from Multi-echo Configuration State MRI

Abstract

This work investigates the use of configuration state imaging together with deep neural networks to develop quantitative MRI techniques for deployment in an interventional setting. A physics modeling technique for inhomogeneous fields and heterogeneous tissues is presented and used to evaluate the theoretical capability of neural networks to estimate parameter maps from configuration state signal data. All tested normalization strategies achieved similar performance in estimating $T_2$ and $T_2^{\mathrm{*}}$. Varying network architecture and data normalization had substantial impacts on estimated flip angle and $T_1$, highlighting their importance in developing neural networks to solve these inverse problems. The developed signal modeling technique provides an environment that will enable the development and evaluation of physics-informed machine learning techniques for MR parameter mapping and facilitate the development of quantitative MRI techniques to inform clinical decisions during MR-guided treatments.

1. Introduction

Magnetic resonance imaging (MRI) has been a critical tool for gathering clinical information about soft tissues within the body. Conventionally, MRI has offered radiologists qualitative insights into the identities and properties of biological tissues. Quantitative measurements of MR-sensitive parameters have shown substantial clinical value for the evaluation and monitoring of cancer [10, 12, 14]. As the use of MRI to guide interventional procedures increases, quantitative MRI (qMRI) has the potential to substantially impact oncology interventions. Clinical adoption of qMRI has been limited by the requirements for collecting and processing the data needed to make these measurements [5, 6]. Advances in MRI acquisition and reconstruction, together with modern deep learning techniques, have the potential to address time and computing constraints that have impeded the clinical deployment of qMRI. Deep learning techniques must first overcome several technical challenges posed by this context.

Large, diverse training datasets are typically required to achieve reliable performance of deep learning models. In qMRI, such datasets are not available and are costly to create [6]. Additionally, varying imaging parameters and system imperfections across scanners and protocols adversely impact current deeplearning models in MRI [11, 13]. These inconsistencies are exacerbated in the interventional context. Finally, for any qMRI technique to achieve the desired clinical impact, the uncertainty and repeatability must be adequately understood to inform clinical decisions [2]. Physics-informed neural networks (PINNs) have the potential to address data and generalization challenges faced by current machine learning approaches in qMRI [6, 18]. To support the development of new PINN approaches to quantitative MRI, this work develops physics modeling techniques for inhomogeneous fields and heterogeneous tissues with protons bound to water and to fat contributing to the received signal. This modeling technique is then used to evaluate the theoretical capability of neural networks to estimate parameter maps from simulated configuration state imaging data.

Unbalanced steady-state sequences have the capacity to sample multiple configuration states that uniquely encode both tissue properties and field maps [8, 15]. For this work, a multi-echo configuration state imaging sequence previously developed for brain imaging was evaluated [4], with monopolar readout gradients to facilitate imaging fat. Gradients are balanced along the phase encoding directions and unbalanced along the frequency encoding direction. The unbalanced frequency encoding gradient results in many configuration states in steady-state, which are sampled as each pathway becomes coherent during readout (Fig. 1a). The different encoding of flip angle and $T_1$ information in various configuration states (Fig. 1b) suggests that a mapping could be learned to separate flip angle and $T_1$ information from a single set of configuration state signals at a single nominal flip angle. The resulting data enable the creation of quantitative $T_1,T_2$, and $T_2^{\mathrm{*}}$ maps from a single acquisition while also reconstructing anatomically meaningful and interpretable source images. Analytical models estimating these parameters from configuration state imaging often necessitate making many assumptions that cannot be satisfied in the real imaging environment or require the acquisition of additional information [1, 9]. The potential for neural networks to relax these assumptions in a data-informed way and extract relevant additional information (explicitly or implicitly) provides an alternative approach for solving these inverse problems.

Fig.1.

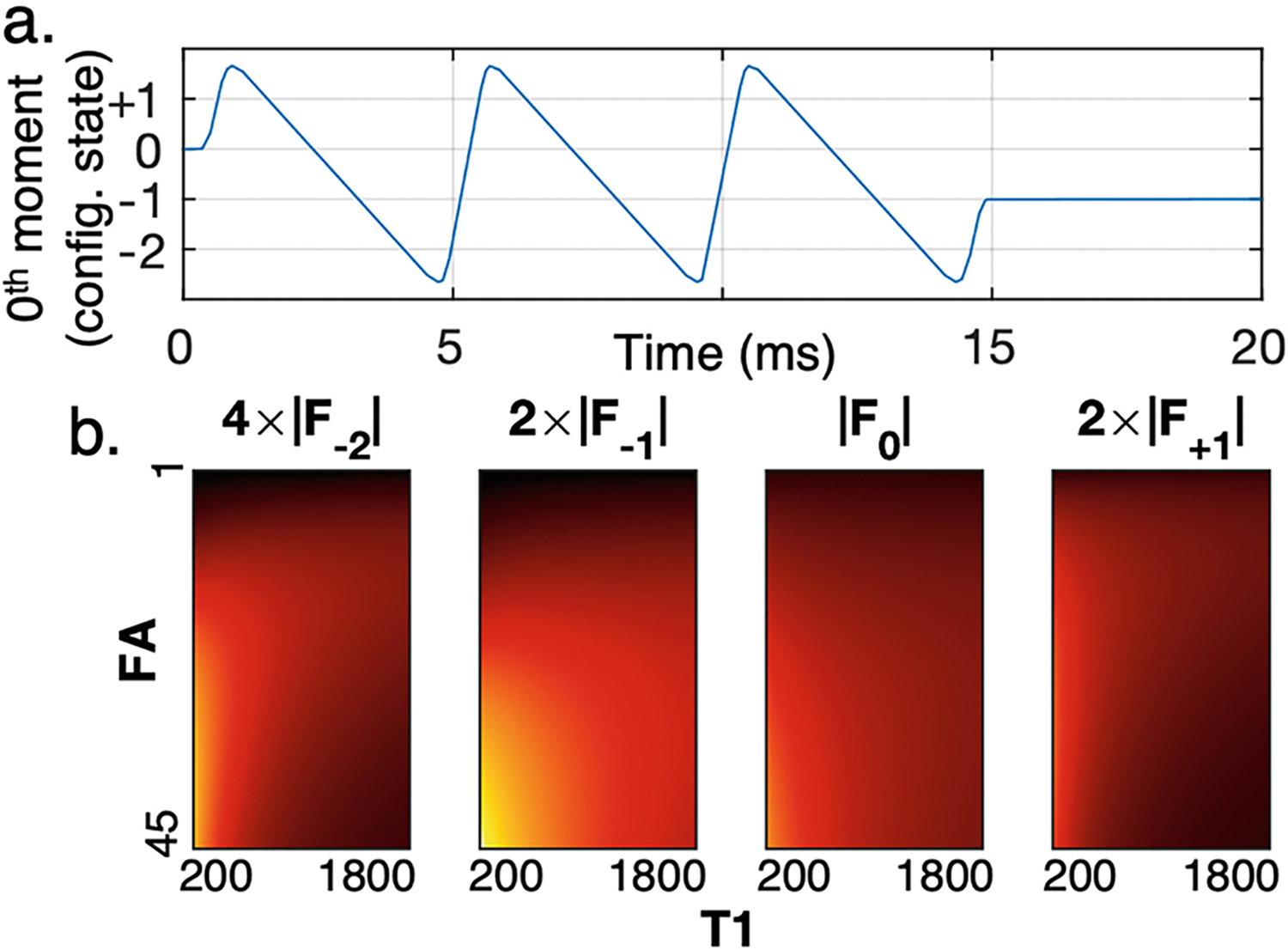
Configuration state imaging encodes different information in each configuration state. a) Plot of the 0th moment under the frequency encoding gradient over time for a single repetition of the sequence sampling 4 configuration states at 3 echo times with monopolar readout gradients. As area accumulates under the frequency encoding gradient, different configuration states become coherent and measurable. b) Simulated signal magnitude for configuration states −2, −1, 0, +1 for varying combinations of flip angle and $T_1$ in water protons (scale adjusted for visualization).

2. Methods

2.1. MR Forward Model

The Bloch Equation.

For an isolated population of hydrogen spins, the behavior of the bulk nuclear magnetic moment, $\mathit{M}=M_x\hat{i}+M_y\hat{j}+M_z\hat{k}$, in the presence of an external magnetic field is defined by the Bloch equation,

$$\frac{d\mathit{M}}{dt}=\gamma \mathit{M}\times \mathit{B}-\frac{M_x\hat{i}+M_y\hat{j}}{T_2}-\frac{M_z-M_0}{T_1}\hat{k},$$ (1)

where $\gamma$ is the gyromagnetic ratio, $\mathit{B}$ is the external magnetic field, $T_1$ and $T_2$ are the longitudinal and transverse relaxation times, respectively, and $M_0$ is the equilibrium magnetization in the direction of the main magnetic field.

To enable the modeling of a heterogeneous environment where signal may originate from many spin populations with varying local magnetic fields and resonance frequencies, we developed a technique for simulating MR signal evolution for samples with arbitrary NMR spectra and parameters in the presence of typical field inhomogeneities.

Bloch Solver.

The on-resonance frequency for a particular spin population is proportional to the strength of the external magnetic field, ${\omega }_0=\gamma B_0$, where the proportionality constant is also the gyromagnetic ratio $\gamma$. Depending on their local chemical environment, spins of the same type of nucleus may exhibit different resonance frequencies, described by their chemical shift, $\delta =\frac{\omega -{\omega }_0}{{\omega }_0}$. For example, the primary peak of the NMR spectra for lipid-bound protons has a chemical shift of ${\delta }_{\text{fat}}=-3.5\mathrm{p}\mathrm{p}\mathrm{m}$ relative to water protons.

We allow tissue-specific parameters $T_1,T_2$, and the population resonance frequency $\omega ={\omega }_0(1+\delta )$ to be spatially varying, while the external field $\mathit{B}$ may vary over space and time. Different system features are considered along the longitudinal and transverse directions of the external magnetic field. Longitudinally, the external field consists of the main magnetic field, $B_0$, magnetic gradient fields, $B_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}}(\mathit{r},t)$, and main field spatial inhomogeneity, $\Delta B_0\left(\mathit{r}\right)$. The x- and y -components of the external field are defined by the applied radio-frequency excitation field, $B_1$, which can be considered as a separable function of the time-varying excitation envelope (on-resonance frequency demodulated), $B_1^{\mathrm{e}}\left(t\right)$, and the spatially-varying excitation efficiency, $B_1^{\text{map}}\left(\mathit{r}\right)$.

Equation 1 can be written as the combination of two operations on $\mathit{M}$: precession with angular velocity $\mathit{\omega }=\gamma (1+\delta )\mathit{B}$ and relaxation governed by $T_1$ and $T_2$. Demodulating the effects of on-resonance precession about the main magnetic field, precessional angular velocity is given by

$$\mathit{\omega }=\gamma (1+\delta )\mathit{B}=\gamma \left(\begin{array}{c}(1+\delta )B_{1,x}^e{B}_1^{\text{map}}\\ (1+\delta )B_{1,y}^e{B}_1^{\text{map}}\\ \delta B_0+(1+\delta )\left(\Delta B_0+\mathit{G}\cdot \mathit{r}\right)\end{array}\right).$$ (2)

The solution was approximated using a symmetric operator splitting technique [7], where a piecewise constant field was assumed (10μs resolution when temporally varying) and the new magnetic moment obtained by sequential application of rotation and relaxation operators. Specifically, the magnetic moment after an interval $\Delta t$ is approximated by applying half the total rotation, applying relaxation and recovery, and then applying the remaining rotation:

$$\mathit{M}[t+\Delta t]\approx \mathbf{R}[t;\Delta t/2]\left(\mathbf{A}\right[\Delta t\left]\mathbf{R}\right[t;\Delta t/2]\mathit{M}+\mathit{b}[\Delta t\left]\right).$$ (3)

$\mathbf{R}[t;\Delta t/2]$ is the axis-angle rotation matrix for rotation about the unit vector $\mathit{u}=\frac{\mathit{\omega }}{\parallel \mathit{\omega }\parallel }$ by the angle $\theta =\parallel \mathit{\omega }[t]\parallel \frac{\Delta t}{2}$. The relaxation components are given by

$$\mathbf{A}\left[\Delta t\right]=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\mathrm{e}\mathrm{x}\mathrm{p}\left\{-\Delta t/T_2\right\},\mathrm{e}\mathrm{x}\mathrm{p}\left\{-\Delta t/T_2\right\},\mathrm{e}\mathrm{x}\mathrm{p}\left\{-\Delta t/T_1\right\}\right),$$ (4)

$$\mathit{b}[\Delta t]={\left(0,0,M_0\left(1-\mathrm{e}\mathrm{x}\mathrm{p}\left\{-\Delta t/T_1\right\}\right)\right)}^{\mathrm{\top }}.$$ (5)

Signal Model.

The Bloch equation alone is inadequate to model some practical NMR phenomena, such as spin echoes [17]. In practice, the measured MR signal demonstrates a reversible decay of signal due to local variations in resonance frequency and dephasing due to nonzero gradients, in addition to irreversible $T_2$ decay. This is modeled by the collective evolution of a population of spins with varying chemical shifts and positions along the readout direction (a 2D grid of spectroscopic axis and position). Reversible decay due to inhomogeneous broadening is observed as a monoexponential decay following $\mathrm{e}\mathrm{x}\mathrm{p}\left\{-t/T_2^{\prime }\right\}$. Because different phase coherence pathways are known to have varying levels of gradient-echo- and spin-echo-like properties, the adopted technique must be able to independently model each of these components. This is achieved by solving the Bloch equation for spins with varying chemical shift and adding them together with a Lorentzian weighting ($\mathrm{f}\mathrm{u}\mathrm{l}\mathrm{l}-\mathrm{w}\mathrm{i}\mathrm{d}\mathrm{t}\mathrm{h}\mathrm{h}\mathrm{a}\mathrm{l}\mathrm{f}-\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}={\left(\pi T_2^{\prime }\right)}^{-1}$). Along this spectroscopic axis, the resonance frequency increment must be small enough to prevent time-domain aliasing. This limit can be expressed as

$$\Delta f\le \mathrm{m}\mathrm{i}\mathrm{n}\left(\frac{1}{2T_{\mathrm{m}\mathrm{a}\mathrm{x}}},\frac{1}{T_{\mathrm{m}\mathrm{a}\mathrm{x}}-ϵT_2^{\mathrm{*}}}\right),$$ (6)

where $T_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the total simulated duration, $ϵ$ is the maximum allowed relative error (in this work, 10⁻³), and $T_2^{\mathrm{*}}$ is the combined rate including the effects of both irreversible and reversible signal decay,

$$\frac{1}{T_2^{\mathrm{*}}}=\frac{1}{T_2}+\frac{1}{T_2^{\prime }}.$$ (7)

After simulation, the signal at a given readout time was computed as the weighted sum of the magnetization vectors of all the spins for that voxel, the spectroscopic axis added together with Lorentzian weighting and the position axis with uniform weighting. MATLAB code for the Bloch solver and signal model are available at https://github.com/fuslab-uofu/mri-signal-model.

2.2. Neural Network Training

Configuration state signals were simulated for a range of MR parameters observed in breast cancer patients in the literature [3, 16] ($T_1=200-1800\mathrm{m}\mathrm{s},T_2=25-250\mathrm{m}\mathrm{s}$). Other parameters were randomly initialized from, $T_2^{\prime }=0.1-\mathrm{10,000}\mathrm{m}\mathrm{s},\mathrm{f}\mathrm{l}\mathrm{i}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}=5-{15}^{\circ }$ with $B_1$ efficiency varying from 5–150%, and $\Delta B_0$ in ±3 μT. The sequence had fixed TR=20 ms and a main magnetic field strength $B_0=3\mathrm{T}$, with 250 repetitions to reach steady-state. Random configurations were used to generate 262,144 samples. When included, gaussian noise was added to the real and imaginary channels separately. Target values were normalized by dividing by the maximum value. At training time, samples were divided into a random 80/20 training/evaluation split.

Neural networks were trained to estimate $T_1,T_2,T_2^{\mathrm{*}}$, and achieved flip angle (FA) using three different normalization schemes: 1) normalization on a sample basis, dividing by the magnitude of the 0th pathway; 2) normalization on a pathway basis, dividing by the maximum achieved signal intensity for a particular pathway over the full dataset; and 3) batch normalization (to standard normal distribution) of each individual feature (4 pathways × 3 echoes = 12 features). Networks had a fully connected architecture with 12 inputs features and a single output with GELU activation at the input to each hidden node, supervised on the simulated data for 200 epochs using Adam optimizer (initial learning rate 1e–4) and plateau learning rate scheduling. Networks were trained without and with added noise (1% of mean, when added), and three variations of network depth and breadth were used for training (number of hidden layers/nodes: [16, 32, 64, 32, 16]; [256, 512, 512, 256]; or [512, 1024, 512]).

Additional experiments were conducted evaluating the performance of networks predicting all relaxation parameters $(T_1,T_2,T_2^{\mathrm{*}})$ with field maps as additional inputs. Network inputs consisted of sample-normalized signal magnitude values and the $\Delta B_0$ offset and achieved FA for each sample (4 pathways × 3 echoes + 2 = 14 inputs). A fully connected network with [512, 1024, 512] hidden nodes and GELU activation at the input to each hidden node were trained for 200 epochs with $T_1,T_2$, and $T_2^{\mathrm{*}}$ as targets, both with and without added noise (noise also added to field map values as 1% of max). To evaluate the need for field maps as inputs, equivalent networks were trained using the same scheme, except without FA and/or $\Delta B_0$ values as inputs. An additional network was trained with the same relaxometry prediction architecture with achieved flip angle as input, but using the output of the batch-normalized FA estimation network as the input FA value.

As a demonstration of the intended final use case, fully connected neural networks were also trained on real data acquired in a salt pork phantom (TR=20 ms; TE=2.9/8.5/14 ms; FA=10°; FOV/sample spacing =256/2 mm cube; total time=2 min 11s), supervised on T1 and T2 maps of the same sample obtained ($T_2^{\mathrm{*}}$ and $B_1$ maps were not acquired in this dataset). Inputs were 3 × 3 × 3 patches of 4 pathways × 3 echoes, normalized using pathway-based normalization. Hidden layers had [512, 1024, 512, 256] nodes, with GELU activation on inputs to hidden layers. All neural network training was conducted using Python 3.9.17 with PyTorch 2.0.1.

3. Results

Results for networks with [512, 1024, 512] hidden nodes trained to estimate $T_1,T_2,T_2^{\mathrm{*}}$, and achieved FA on noisy simulated data with various normalization strategies are summarized in Table 1. Sample normalized inputs gave the most accurate predictions for $T_2$ and $T_2^{\mathrm{*}}$ (Fig. 2b–c). This normalization scheme resulted in poor fits for estimating $T_1$ and FA (Fig. 2a, d), with noiseless training giving nearly equivalent results to the noisy condition (noiseless RMSE/R: 398/0.51 for $T_1$, 2.3/0.85 for FA). Pathway-based normalization resulted in the best performance for $B_1$ and $T_1$ estimation, with slightly degraded performance in estimating $T_2$ and $T_2^{\mathrm{*}}$ (Fig. 2e–h).

Table 1.

Parameter estimation performance for a variety of training conditions and network architectures.

		Normalization			Sample norm + additional inputs
Target	Metric	Sample	Pathway	Batch	None	{FA, B0}	FA	B 0	est. FA
T1 (ms)	RMSE	399	25	69	398	36	36	398	59
	Slope	0.26	0.99	0.97	0.26	0.99	0.99	0.26	0.98
	Intercept	734	5.5	26	743	6.5	8.8	743	17.6
	R	0.51	1.00	0.99	0.51	1.00	1.00	0.51	0.99
T2 (ms)	RMSE	1.6	2.1	6.1	2.1	1.7	1.6	2.0	2.0
	Slope	1.00	1.01	0.99	1.00	1.00	1.00	1.00	1.00
	Intercept	0.12	0.28	0.98	0.15	0.079	0.21	0.15	0.14
	R	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
$T_2^{\mathrm{*}}$ (ms)	RMSE	5.7	6.8	7.9	6.0	5.8	5.7	6.0	7.1
	Slope	0.99	0.99	0.98	0.99	0.99	0.99	0.99	0.98
	Intercept	0.61	0.63	0.92	1.00	1.00	1.00	1.00	1.00
	R	1.00	1.00	0.99	1.00	1.00	1.00	1.00	1.00
FA (°)	RMSE	2.3	0.054	0.23
	Slope	0.72	1.00	1.00
	Intercept	2.8	0.00057	0.038
	R	0.85	1.00	1.00

Fig.2.

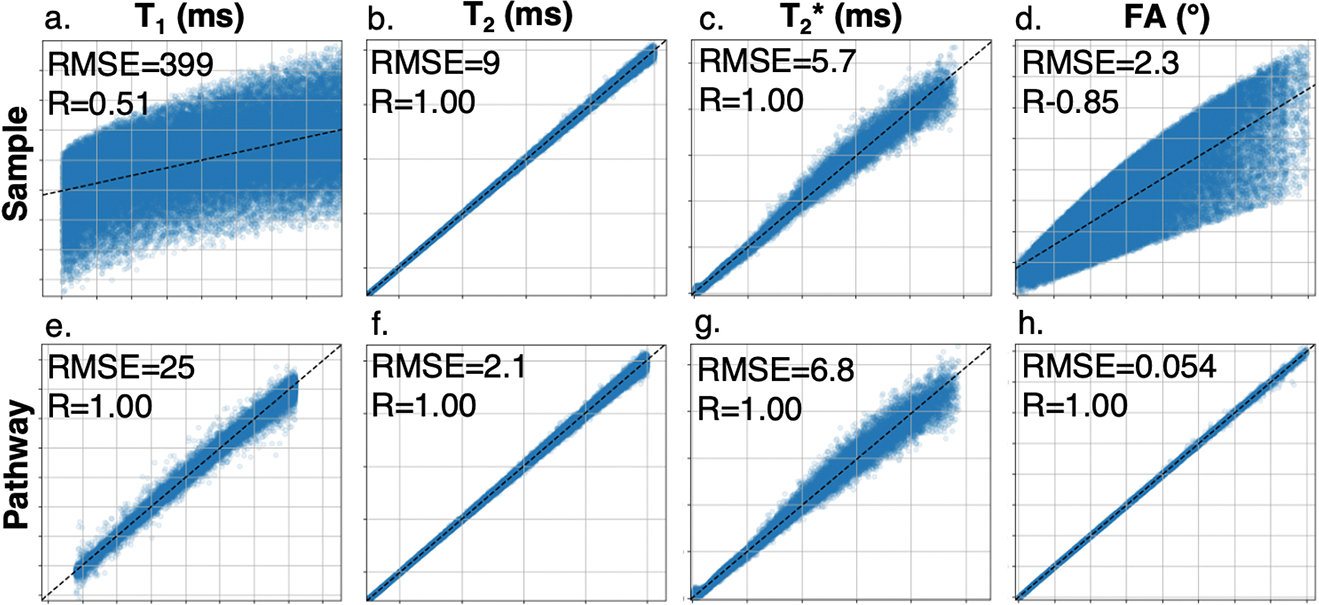
Regression plots of neural network parameter estimates (vertical axis) vs simulated parameter (horizontal axis) for networks trained with sample- (a–d) and pathway-based (e–h) normalization for $T_1$ (range 200–1800), $T_2$ (range 20–250), $T_2^{\mathrm{*}}$ (range 0–250), and achieved FA (range 2.5–22.5).

Providing achieved FA as additional information at the network inputs resulted in improved ability to estimate $T_1$, with negligible improvement in $T_2$ and $T_2^{\mathrm{*}}$ estimation (Table 1). Figure 3 shows the prediction performance in real data acquired in salt pork, comparing the acquired $T_1$ and $T_2$ maps with network training results.

Fig.3.

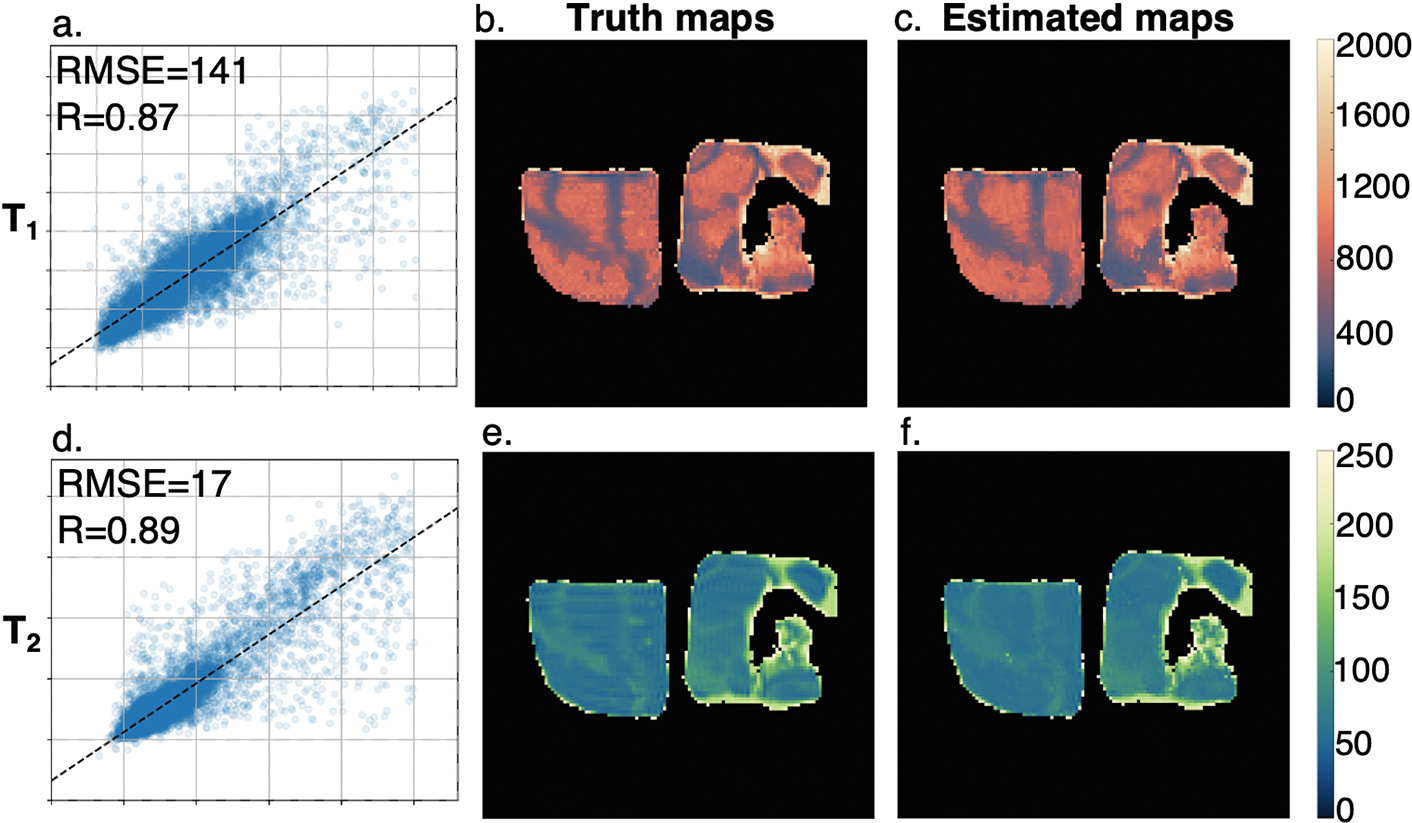
Sample of real data acquired in salt pork and network evaluation results for $T_1$ (a–c) and $T_2$ (d–f). (a, d) Regression plots of performance estimating $T_1$ and $T_2$; (b, e) ground truth parameter maps; (c, f) parameter maps estimated using trained neural network.

4. Discussion

These results provide a preliminary demonstration of the theoretical capacity for configuration state imaging to serve as the basis for rapid quantitative MRI. Trained neural networks were successful in predicting achieved flip angle, $T_1,T_2,T_2^{\mathrm{*}}$, even with noisy data. Unlike the highly undersampled acquisitions used for MR fingerprinting, this technique provides meaningful anatomical images and a readily interpretable basis for neural network-based contrast translation.

The results presented here demonstrate the potential impact of architectural and training decisions on the ability of fully connected neural networks to solve these inverse problems. Even for closely related problems, the optimal configuration may depend on the specific parameter of interest. Sample-based normalization provided the best evaluation performance in estimating $T_2$ and $T_2^{\mathrm{*}}$, but the worst performance for estimating $T_1$ and achieved FA. Including estimated FA as an input to relaxation parameter estimation dramatically improved the ability to estimate $T_1$. Physically meaningful intermediate stages and architectural biases may therefore be important in training networks for this application.

The developed signal modeling technique provides a simulation environment that can test network designs on controlled datasets that include challenges expected in the MRI environment of interest, facilitating the investigation of the limits and guarantees of the resulting machine learning system. Although not evaluated in this work, the technique is extensible to model additional challenges including motion and flow, field drift, and partial voluming. This will enable evaluation of deep operator learning architectures to incorporate sequence parameters (TR, TE) and scanner characteristics (slew rate, field strength) as extra information, providing better tolerance of the variation expected in clinical workflows. The required complexity of forward models for self-supervised physics-informed training can also be evaluated in this environment. It is expected that increasing the incorporation of physics information into the network architecture and training will further improve network performance on real data.

Future work will evaluate the transfer of learned mappings from simulated data to real data and the application of neural interpolators to estimate parameter values for real data. It may also be feasible to leverage redundant spatial information across the pathways to improve SNR of real data. The impact of magnetization transfer, which is not accounted for in the current model, will also be evaluated. Further development of this technique will enable the acquisition of quantitative maps that facilitate clinical decision making during MR-guided treatments.