Comparing the Thin Plate Spline and Gaussian Interpolation Methods in Generating Hill of Visions for X-Linked Retinitis Pigmentosa Patients

Abstract

Purpose

To compare the efficacy of thin plate spline (TPS) and Gaussian interpolation methods in generating hill of visions (HOVs) for patients with X-linked retinitis pigmentosa (XLRP).

Methods

Visual field data from 78 eyes of 39 patients with XLRP were acquired using the Octopus 900 Pro. TPS, Gaussian, and Universal Kriging interpolation methods were implemented to generate HOVs. The volume of the entire grid (V_Tot), a 30-degree region (V₃₀), and the volume ratio (V_Ratio) were calculated. Pearson correlation and Bland–Altman limit of agreement (LOA) analysis were performed to assess the concordance. An undersampled grid was used to assess the accuracy of the interpolation by comparing the interpolated value to the actual measured value.

Results

There were strong positive correlations (R > 0.99, P < 0.001), and LOA analysis revealed minimal differences between the three methods. Gaussian interpolation performed the fastest (P < 0.0001).

Conclusions

TPS and Gaussian interpolation methods demonstrated a high degree of concordance in generating HOVs for patients with XLRP. The choice of methods depends on the specific needs and priorities of researchers and clinicians, factoring in speed, accessibility, ease of implementation, and the ability to fine-tune the interpolation.

Translational Relevance

Accurate HOV analysis is crucial for monitoring and assessing visual field loss progression. TPS and Gaussian interpolation methods are equally effective in generating HOV representations for patients with XLRP. The choice of method can be based on specific needs of researchers or clinicians, enabling more personalized treatment strategies and better disease management.

Introduction

Perimetry is a well-established test that has been widely used in the diagnosis, screening, and monitoring of various ocular disorders, including glaucoma, neurologic diseases, and diseases of retinal degeneration such as retinitis pigmentosa (RP).^1–4 This test is crucial for the evaluation and monitoring of these patients as it allows for early detection, spatial mapping, and monitoring of visual field function.

Static and kinetic visual field tests offer a quantitative measurement of the retinal response to light stimuli of varying sizes and intensities across various locations within the visual field.^3,5 The standard output of these tests consists of heatmaps and various metrics that describe the performance of the test, including mean sensitivity (MS), mean defect (MD), and pattern standard deviation (PSD).⁶ MS represents the average sensitivity, in decibels (dB), across all tested locations. MD, also measured in dB, is the difference between the MS and the anticipated standard sensitivity for a comparable age group.⁵ A negative MD indicates a loss of sensitivity compared to normal. PSD is a measure of the variability of the sensitivity across the tested locations in dB.⁵ A high PSD indicates an irregular pattern of sensitivity loss that may suggest a localized defect or disease. These averages provide a single value that represents the overall or regional performance of the test.⁵ Heatmaps use different colors or shades of gray to indicate the level of sensitivity or deviation from normal at each location.⁵ Put together, these outputs aim to summarize and display the test results concisely, showing the distribution and severity of any visual field loss across the tested areas.⁵

However, these standard outputs have several limitations. The flat, two-dimensional heatmaps are limited by their spatial resolution. Metrics such as MS and MD are global averages and are relatively insensitive to local defects or variations as they favor regions where there is a greater concentration of stimuli relative to more sparsely tested regions.⁷ This ends up limiting the interpretability of these metrics between different grid patterns. Finally, these metrics are global averages and are relatively insensitive to local defects or variations.⁷

To improve visualization, interpretation, and comparability of visual field data, several groups have developed mathematical models to plot, display, and quantify the visual field as a three-dimensional surface, known as a hill of vision (HOV). HOVs are generated using sensitivity values from all tested locations on the grid, enabling visualization of the entire visual field and any associated local defects.⁸ Volumetric calculations of the area beneath the sensitivity surface allow quantifying the visual field, avoiding any weighting biases from unequally spaced grids. HOV volumes can be generated for the entire field or specific regions. Additionally, volumetric indices allow for comparing visual field data acquired from different grid types.⁸

The most commonly used interpolation method for generating the HOV surface is the thin plate spline (TPS) interpolation method.^8–11 Although the TPS interpolation method has several advantages, such as not requiring any a priori knowledge of the functional form of the data or the relationship of interest and automated node number and placement determination, it has its disadvantages. One drawback of the TPS method is that its solution requires the inversion of a dense matrix. This can make the method computationally expensive.^12,13 Another issue with the TPS method is that far-away points can have a large influence on the outcome, making it sensitive to outliers in the data and can lead to overfitting.¹⁴ Furthermore, the smoothing parameter for TPS is usually computed directly from the matrix of constraints; hence, it is not tunable and may create overly smooth surfaces, masking local extrema and incurring overshooting regions.^13,15 Even when it is tunable, the choice for the smoothing parameter is not obvious and may hinder the surface interpolation.

To address these challenges, we have devised a novel approach utilizing Gaussian interpolation methods to create the HOVs. The Gaussian interpolation method estimates unknown values using nearby points, and the width of the surrounding points used for interpolation can be easily adjusted with a single parameter.¹⁶ This allows researchers to easily tune the smoothness parameter and reveal local extrema. Furthermore, in the Gaussian method, the weights of distant points decrease exponentially, resulting in a relatively sparse matrix and faster computational time.¹⁶ This method serves as a promising alternative to the traditional TPS interpolation method.

Methods

Patients

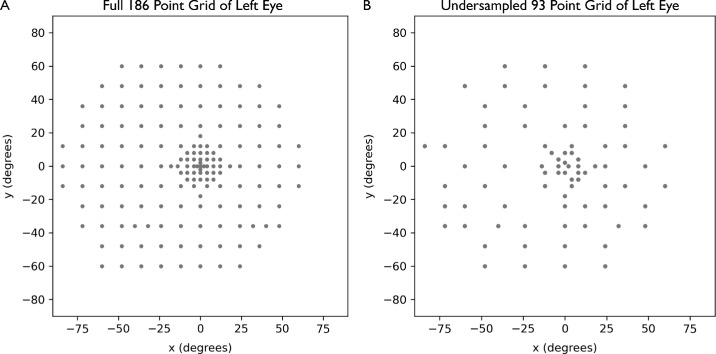
For this study, static, light-adapted, white-on-white perimetry data, acquired using the Octopus 900 Pro (Haag Streit AG, Köniz, Switzerland), were used. Patients with X-linked retinitis pigmentosa (XLRP) enrolled in the Horizon study, a nonrandomized, open-label, phase 1/2 dose escalation study with the objective of determining the safety and efficacy of AGTC-501 (rAAV2tYF-GRK1-RPGR) in adults and children with XLRP caused by RPGR mutations, were included (ClinicalTrials.gov ID NCT03316560). All testing was performed using a custom 186-point grid (Fig. 1A), a Goldman size V stimulus, and the GATE thresholding strategy. Patients with XLRP were excluded if they had any concurrent retinal disease that affects retinal function or any other ocular condition that could affect visual field testing.

Figure 1.

(A) A 186-point custom grid used for patients in the study. (B) Undersampled 93-point grid generated by removing every other point in a circumferential direction. Undersampled grid is used to assess the accuracy of the interpolation by comparing interpolated values at the removed points to the corresponding actual values.

Interpolation Methods

In this study, we implemented and compared two distinct radial basis function (RBF) interpolation approaches. Both methods utilize a specific kernel function applied to the matrix of distances between data points with known values¹⁷ and employ a penalty function (or constraint) to ensure the interpolations pass through the original values. The first approach, TPS interpolation, has been previously reported in the literature for HOV analysis.⁸ The second proposed approach is an interpolation based on a Gaussian function.

The TPS interpolation relies on a kernel function derived from the log of the distances (r) between data points, expressed as follows:

$$\begin{array}{c}\hfill \left(kernel\right)\_\mathit{\text{TPS}}=\left|\right|r\left|\right|{}^{\wedge }2log\left(\left|\right|r\left|\right|\right)\end{array}$$

where || || denotes the norm distance. This kernel describes a steep curve, with surface smoothing achieved through a roughness penalty applied to the constraint during error minimization.

In contrast, the Gaussian-based interpolation approach employs a kernel function defined as follows:

$$\begin{array}{c}\hfill \left(kernel\right)\_Gauss=e{}^{\wedge }\left(\left(-\left(\left|\right|r\left|\right|/\varepsilon \right){}^{\wedge }2-\varepsilon \right)\right)\end{array}$$

where ε is a parameter that adjusts the width of the Gaussian. This kernel allows for more precise control of the smoothness of the interpolation, as not only does the distance between points dictate the radius of influence, but adjusting ε also influences the weight each datapoint has on farther distances. Furthermore, since ε is directly related to the distance between points and the distances being probed by the HOV analysis, it can be fine-tuned to clinically relevant values—that is, the extent of the influence of the point being probed at a specific location. In this study, ε is defined as the average separation between data points, serving as a foundational approximation for the region of influence.

Finally, we also compared the Gaussian approaches with another previously used interpolation method for visual field analysis, universal Kriging.^18,19 We used an exponential variogram model with a sill of 50 decibels squared (dB²), a range of 50 radians, and a nugget of 0.1 dB². An exponential model was chosen for the variogram, and a nugget value was chosen based on the study by Denniss and Astle.¹⁸ A sill of 50 dB was chosen given that the measured sensitivities range from approximately 0 to 30 dB and the assumption that a reasonably well-fit model will have half variance of 50 dB². A range of 50 radians was chosen with the assumption that a correlation would plateau with all the data within 50 radians from the interpolated point. Universal kriging using the above parameters provided well-defined interpolated surfaces, and those parameters were used for all the data.

All interpolation methods were implemented in Python using the SciPy and PyKrige library.^20,21 To constrain the interpolation, a border of 150 points with zero sensitivity value was created in a circular region with a radius of 120 degrees. A grid of 500 × 500 points across the field of view of 120 degrees was then interpolated. The grid’s volume was computed by multiplying the value of each interpolation point by the size of its cell (defined as the distance between each point in the interpolated grid), an approach sometimes referred to as a zero-order hold calculation.

Statistical Analysis

The volume calculations were performed for the entire grid (V_Tot) and for a specific region encompassing 30 degrees (V₃₀). Subsequently, the ratio between the volume of the entire grid and the volume of the 30-degree region (V_Ratio) was computed. The means for V_Tot, V₃₀, and V_Ratio were calculated and presented in the unit of dB multiplied by square radian (dB-sr). The Pearson correlation test was used to assess the correlation. The strength of the correlation was interpreted according to Cohen's guidelines, with values of 0.1, 0.3, and 0.5 indicating small, medium, and large effect sizes, respectively.²² In addition, to evaluate the consistency of the methods, we conducted a Bland–Altman limit of agreement (LOA) analysis and plotted the results using the Bland–Altman plots.²³ Bland–Altman plots are a graphical representation of the difference between two measurements (in this case, the TPS and Gaussian interpolations) plotted against the average of the two measurements. The plots allow for visual inspection of the level of agreement between the two methods where the horizontal lines on the plot represent the LOA limits, and any points outside these limits are considered outliers.

To estimate the accuracy of the interpolation methods, we created an undersampled grid from our existing data by removing every other point from the static perimetry grid, as shown in Figure 1B. From the undersampled grid, we used TPS, Gaussian, and universal Kriging to interpolate the removed points. Mean absolute error (MAE) and root mean squared error (RMSE) for each interpolation were calculated by comparing the interpolated value of the removed points to the actual measured data.

To estimate the computational complexity of each interpolation method, we measured the time it takes for our Python program to run the data set using each interpolation method. For statistical comparison, a two-tailed paired t-test was used to compare the values obtained from TPS and universal Kriging interpolation methods against values obtained from Gaussian.

Results

HOVs were generated for 78 eyes of 39 patients with XLRP using both the TPS and Gaussian interpolation methods.

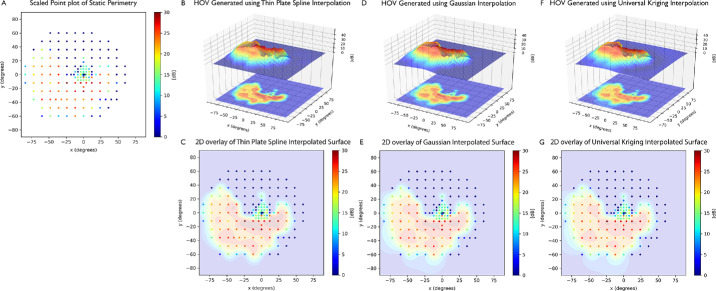
Figure 2 presents exemplary HOVs for an XLRP eye using the TPS, Gaussian, or universal Kriging interpolation method and corresponding two-dimensional projection overlay into a scaled point plot. For most HOVs, there is no significant qualitative difference between the three interpolation methods.

Figure 2.

HOVs of an example eye with a patient with XLRP. (A) Color-coded scaled point plot of static perimetry. HOV was generated using the TPS interpolation method. (B) HOV calculated using TPS interpolation and (C) corresponding two-dimensional projection overlay of the TPS HOV into a scaled point plot. (D, E) HOV calculated using Gaussian interpolation and corresponding two-dimensional projection overlay of the Gaussian HOV into a scaled point plot. (F, G) HOV calculated using universal Kriging interpolation and corresponding two-dimensional projection overlay of the universal Kriging HOV into a scaled point plot. There is no gross qualitative difference in the HOV interpolation across all three plots. In all the plots, color scale ranges from red to blue, where red indicates higher sensitivity and blue indicates lower sensitivity.

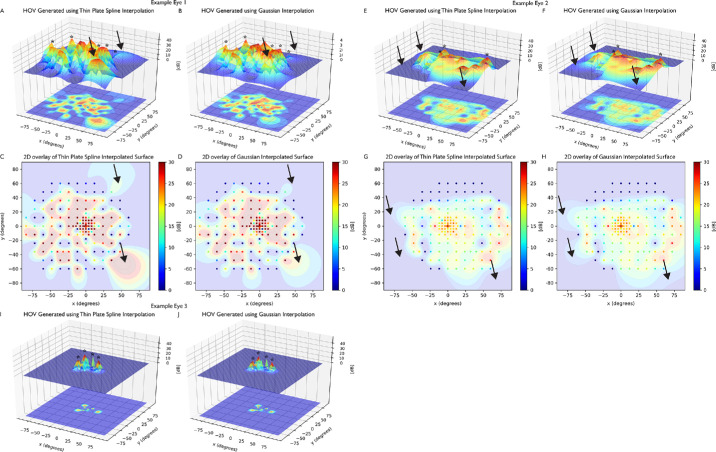
Figure 3 shows an in-depth comparison of TPS and Gaussian interpolation across three static perimetries performed in three different eyes. Figures 3A–D show exemplary HOVs and corresponding two-dimensional HOV overlays with the scaled point plot for example eye 1, whose TPS interpolation estimated a greater V_tot than Gaussian interpolation. Figures 3E–H show exemplary HOVs and corresponding two-dimensional overlays for example eye 2, whose TPS interpolation estimated a lesser V_tot than Gaussian interpolation. Finally, Figures 3I, 3J show exemplary HOVs for example eye 3, whose TPS interpolation estimated a greater V₃₀ than Gaussian interpolation.

Figure 3.

HOVs and two-dimensional HOV overlay into a scaled point plot for three example eyes. (A–D) Example eye 1, where the TPS interpolation estimated a greater volume under the entire surface (V_tot) than Gaussian interpolation. TPS interpolation resulted in large hills at boundary points (black arrows). (E–H) Example eye 2, where the Gaussian interpolation estimated a greater V_tot than TPS interpolation. Gaussian interpolation resulted in more gradual descent at the low-decibel boundary points, resulting in a hill with a wider area (black arrows). (I, J) Example eye 3, where the TPS interpolation estimated a greater volume of the 30-degree region (V₃₀) than Gaussian interpolation. In all three example eyes, Gaussian interpolation generated sharper and more pronounced extrema (asterisks). Color scale ranges from red to blue, where red indicates higher sensitivity and blue indicates lower sensitivity.

In all three example eyes, Gaussian interpolation exhibited sharper and more pronounced local extrema than the TPS interpolation counterparts (asterisks). However, both TPS and Gaussian interpolation occasionally exhibited overestimation errors when interpolating surfaces near the boundary of the static perimetry test (black arrows), as shown in example eyes 1 and 2.

Table 1 presents the mean values of the V_Tot, V₃₀, and V_Ratio for both healthy subjects and patients with RP, derived from HOVs generated using the Gaussian, TPS, and universal Kriging interpolation methods.

Table 1.

Comparison of Mean V_Tot, V₃₀, and V_Ratio for Patients with XLRP Derived from HOVs Generated Using the Gaussian, TPS, Gaussian, and Universal Kriging Interpolation Methods

Characteristic	Gaussian Interpolation	TPS Interpolation	P Value	Universal Kriging	P Value
Mean VTot (dB-sr)	44.9	45.4	0.1998	45.0	0.9241
Mean V30 (dB-sr)	7.15	7.22	0.0002	7.11	<0.0001
Mean VRatio	0.212	0.207	0.0051	0.207	0.0074

There was no statistically significant difference in V_tot between any of the three TPS, Gaussian, and universal Kriging interpolations. Gaussian interpolation produced V₃₀ values significantly lower than those obtained by TPS and significantly greater than those from universal Kriging. This observed variation, however, is smaller than 1% of the mean V₃₀. Gaussian HOVs had significantly greater V_ratio than both TPS HOVs and universal Kriging HOVs.

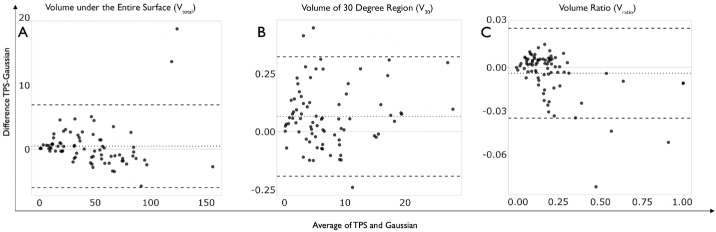
In addition, the correlation results revealed a strong, positive relationship between all three methods, with a Pearson's correlation coefficient (r) greater than 0.99 (P < 0.001) calculated for V_Tot, V₃₀, and V_Ratio. A Bland–Altman LOA analysis was performed to evaluate the consistency between the TPS and Gaussian interpolation methods for generating HOVs (Fig. 4). The mean V_Tot difference between the two methods was 0.44 dB-sr, with 95% limits of agreement ranging from –6.01 dB-sr to 6.90 dB-sr (Fig. 4A). The mean V₃₀ difference between the two methods was 0.07 dB-sr, with 95% limits of agreement ranging from –0.19 dB-sr to 0.32 dB-sr (Fig. 4B). The mean V_Ratio difference between the two methods was 0.005 dB-sr, with 95% limits of agreement ranging from –0.04 dB-sr to 0.03 dB-sr (Fig. 4C).

Figure 4.

Bland–Altman LOA analysis comparing (A) volume under the entire surface (Vtotal), (B) volume of 30-degree region (V30), and (C) volume ratio (Vratio) using TPS and Gaussian interpolation methods for generating HOVs. The dotted line indicates the average difference between TPS and Gaussian, and the dashed lines indicate the 95% upper and lower limits of agreement.

Similarly, a Bland–Altman LOA analysis was performed to evaluate the consistency between the universal Kriging and Gaussian interpolation methods for generating HOVs. The mean V_Tot difference between the two methods was 0.022 dB-sr, with 95% limits of agreement ranging from –3.88 dB-sr to 3.83 dB-sr. The mean V₃₀ difference between the two methods was 0.04 dB-sr, with 95% limits of agreement ranging from –0.07 dB-sr to 0.15 dB-sr. The mean V_Ratio difference between the two methods was 0.006 dB-sr, with 95% limits of agreement ranging from –0.03 dB-sr to 0.04 dB-sr.

Finally, Table 2 shows the mean computation time using each of the three interpolation methods and mean MAE and RMSE calculated from undersampling of the data. Gaussian interpolation was significantly faster than TPS interpolation by approximately 30% and universal Kriging interpolation by approximately 57%. In addition, Gaussian interpolation from undersampled surfaces had significantly lower MAE and RMSE than TPS interpolation from undersampled surfaces, although it had significantly greater MAE and RMSE than universal Kriging interpolation.

Table 2.

Comparison of Mean Time Elapsed, Mean MAE, and Mean RMSE for Patients with XLRP Derived From HOVs Generated Using the Gaussian, TPS, and Universal Kriging Interpolation Methods

Characteristic	Gaussian Interpolation	TPS Interpolation	P Value	Universal Kriging	P Value
Mean time elapsed (s)	1.54	2.25	<0.0001	3.58	<0.0001
Mean MAE (dB-sr)	5.64	5.75	<0.0001	5.59	<0.0001
Mean RMSE (dB-sr)	8.12	8.30	<0.0001	7.99	<0.0001

Discussion

In this study, we sought to compare the efficacy of three interpolation methods, TPS, Gaussian, and universal Kriging, in generating HOVs for patients with XLRP. We additionally provide an in-depth analysis between the two RBF interpolation approaches, TPS and Gaussian, because TPS is the most widely used interpolation method for HOV interpolation.^8–11 Our findings provide valuable insights into how the Gaussian interpolation method differs from the previously described TPS interpolation method.

The strong, positive Pearson correlation coefficient (r) of ≥0.99 (P < 0.001) for TPS and Gaussian methods indicates a high degree of concordance between the two RBF methods in generating HOVs. To further evaluate the consistency between the methods, a Bland–Altman LOA analysis was performed. The mean differences in V_Tot, V₃₀, and V_Ratio were minimal, suggesting a high level of agreement between the two methods.

In their study, Weleber et al.⁸ analyzed a total of 61 examinations from healthy individuals and 344 examinations from patients with RP. They discovered a significant difference in the mean V_Tot, with healthy subjects showing a mean V_Tot of 103 dB-sr, while patients with RP demonstrated a mean V_Tot of 30.1 dB-sr. When considering the sum of the LOA, the worst expected error (15.37) accounted for 25% of the difference between the mean V_Tot of healthy subjects and that of patients with RP (61.2).⁸ This calculation takes into account two standard deviations from the mean for each population. This finding suggests that using either of the RBF methods for generating HOV data is a viable approach in clinical settings in that they effectively distinguish between healthy individuals and patients with RP.

This similarity between TPS and Gaussian is not surprising as both are robust RBF interpolation approaches (Fig. 3). Qualitatively, surfaces from both TPS and Gaussian interpolation look remarkably similar, but there are key differences. Gaussian interpolation exhibits sharper and more pronounced local extrema than TPS.

In addition, TPS interpolation puts greater weight to high-amplitude measurements at or near the boundary of the grid, creating a large hill at the periphery (Figs. 3A–D), while Gaussian interpolation allows more gradual descent at the grid boundary (Figs. 3E–H). These differences in the interpolation surface at the boundary of the grid likely account for some discrepancies in V_tot between the TPS and Gaussian interpolation (Fig. 4A).

On the other hand, the small but statistically significant difference in V₃₀ values between the TPS and Gaussian interpolation methods can be attributed to the higher density of data points within the central 30 degrees of the visual field. This region is crucial for essential visual functions such as reading, facial recognition, and focusing on objects.²⁴ Consequently, measurements in this area are often prioritized during data acquisition, resulting in a higher density of data points compared to the peripheral visual field, including the 186-point grid used in our study. This increased sampling likely enhances the performance of both interpolation methods but at the same time increases the number of local extrema present in the central 30 degrees of the visual field. Since TPS interpolates a rounder, more positively curved surface at the local maxima, the volume calculated under a TPS interpolated surface is likely greater than the volume under the sharper surface interpolated by the Gaussian interpolation, explaining the statistically significant difference observed in V₃₀ among the two interpolations (Figs. 3I, 3J). This subtle difference in interpolation of the local extrema may have profound clinical significance when examining and monitoring the progression of small, localized defects in various retinal pathologies. Regardless, the minimal absolute variation and strong correlation in V₃₀ between TPS and Gaussian (Fig. 4B) further support the robustness of both methods in characterizing the central visual field, which is of particular importance for understanding the pathophysiology of RP and other retinal disorders.

Next, we have shown that Gaussian interpolation of our 186-point grid is significantly faster than TPS. Not only is Gaussian more than 30% faster at this grid size, but we also expect the difference in computational load to increase as the number of points in the grid increases. This may be valuable for researchers who opt for high-density perimetry using modified threshold algorithms.²⁵ In addition, shorter time required to compute Gaussian interpolation can potentially allow researchers to change the smoothness parameter ε in real time to have a closer look at specific features in the HOV surface and identify whether certain hills are real or artifacts of interpolation. However, this additional speed may not be significant in a clinical setting, where the clinicians may not be familiar with the smoothness parameters or have the time to adjust them in a busy clinic.

Finally, we have shown that Gaussian interpolation performs significantly more accurately than TPS interpolation when we interpolate artificially undersampled grids. This method has limitations in that our undersampled grid does not resemble common grids used in static perimetry, but the improved accuracy in Gaussian interpolation may suggest that surface from the Gaussian interpolation adheres more closely to real data than the smoother surface from the TPS interpolation. We suggest future studies using very dense grids over specified regions to further investigate the oversmoothing quality of TPS interpolation.

In this study, we also compared the performance of Gaussian interpolation to universal Kriging interpolation, another method previously explored in the setting of visual field analysis.¹⁸ Correlation and Bland–Altman LOA analyses were performed between Gaussian and universal Kriging interpolations. The analyses resulted in a strong correlation (r ≥ 0.99) and narrower limits of agreements, showing a high degree of concordance and agreement and Gaussian and universal Kriging interpolations. Universal Kriging is an interpolation method based on the interpolation of the regression residuals.¹⁹ Unlike RBF-based interpolation, which is a deterministic method and directly based on surrounding measured values, Kriging uses autocorrelation to predict the surface.²⁶ This method often provides more accurate geostatistical prediction of the surface from the limited points, and our study has shown that universal Kriging performed most accurately when interpolating artificially undersampled grids. However, this approach is much more expensive computationally and needs intricate fine-tuning of the Kriging parameters, such as sill, range, and nugget, which are nontrivial to approximate and must be adjusted for each type of measurement protocol and pathologies to achieve an optimal result. Even in this study, we estimated a variogram of our static perimetry data performed a grid search with multiple combinations of the Kriging parameters to obtain a parameter that can generate a reasonable surface for all of our data set appropriately. Universal Kriging may provide more accurate interpolation with correct optimization in research settings but may not be as robust as TPS or Gaussian when used clinically where different grid layouts are used to investigate a wide range of pathologies.

The TPS interpolation method used to generate HOVs offers several advantages over conventional indices in assessing visual function, particularly in nonlinear testing grids.⁸ As a higher-order method utilizing smooth kernels, TPS interpolation is more accurate than piecewise constant methods when interpolating static visual field data.⁸ The volumetric visual function indices, while comparable in performance to conventional indices such as mean sensitivity and mean deviation, overcome the limitations associated with testing grids featuring central condensation, radial patterns, or unequal spacing.⁸ Conventional indices tend to bias toward regions of higher testing density, leading to weighted averages that restrict comparisons between grids with different sampling patterns and limit sensitivity to focal and small changes.⁸

The Gaussian interpolation method offers not only increased speed and accuracy but also increased accessibility, primarily due to its integration within various statistical software packages, as opposed to the TPS approach. This accessibility is further augmented by the comparative ease of understanding and implementation associated with the Gaussian method. A key advantage of Gaussian over TPS lies in its capacity for visually representing the smoothness factor applied in the interpolation process—the Gaussian width. This enables clinicians and researchers to meticulously fine-tune the degree of smoothness based on the specific disease under investigation, acknowledging that the extent to which data points influence their neighbors may vary according to the disease in question. Consequently, implementing a steeper smoothness factor within the Gaussian framework effectively diminishes the impact that each data point exerts on its neighboring points, thereby offering a flexible and tailored interpolation strategy for diverse scientific applications.

Conclusions

In conclusion, this study demonstrates a high degree of concordance between the TPS and Gaussian interpolation methods in generating HOV representations for patients with XLRP. The strong Pearson correlation coefficient and minimal differences observed in the Bland–Altman LOA analysis indicate that both interpolation methods are robust in characterizing the central visual field, which is essential for understanding the pathophysiology of RP and other retinal disorders. In addition, the Gaussian-based approach showed significantly faster computational time and greater accuracy than the TPS interpolation method. The Gaussian interpolation method provides a more accessible and flexible approach, enabling researchers to tailor the degree of smoothness based on the specific disease under investigation. The choice between the two methods can be based on accessibility, ease of implementation, and the need for fine-tuning, as both perform similarly. Accurate HOV analysis is crucial for monitoring and assessing visual field loss progression in these patients, ultimately leading to more personalized treatment strategies and better disease management. In light of these findings, further studies may explore the application of these methods in assessing other retinal disorders or refining their performance to optimize the characterization of visual function in diverse patient populations.