Fine-grained Patient Similarity Measuring using Contrastive Graph Similarity Networks

Abstract

Predictive analytics using Electronic Health Records (EHRs) have become an active research area in recent years, especially with the development of deep learning techniques. A popular EHR data analysis paradigm in deep learning is patient representation learning, which aims to learn a condensed mathematical representation of individual patients. However, EHR data are often inherently irregular, i.e., data entries were captured at different times as well as with different contents due to the individualized needs of each patient. Most of the work focused on the provision of deep neural networks with attention mechanisms that generate complete patient representations that can be readily used for downstream prediction tasks. However, such approaches fail to take patient similarity into account, which is generally used in clinical reasoning scenarios. This study presents a new Contrastive Graph Similarity Network for similarity calculation among patients in large EHR datasets. Particularly, we apply graph-based similarity analysis that explicitly extracts the clinical characteristics of each patient and aggregates the information of similar patients to generate rich patient representations. Experimental results on real-world EHR databases demonstrate the effectiveness and superiority of our method for the task of vital signs imputation and ICU patient deterioration prediction.

I. Introduction

With the adoption of digital health systems, large amounts of EHRs are available, but the major problem is how to translate the existing information into useful knowledge and decision-support tools to guide clinical practice. Data mining is the process of analyzing large datasets to discover patterns and meaningful insights. Specifically, it involves a process of analysis in which data scientists employ machine learning and statistical methods to build predictive models for decision support.

Various machine learning methods have been developed for clinical and research applications using EHR data, such as clinical risk prediction [1]–[5], phenotype analysis [6]–[8], disease prediction and progression [9]–[11].

However, EHR data are often inherently irregular, i.e., data entries were captured at different times as well as with different contents due to the individualized needs of each patient. For example, vital sign measurements are gathered from multiple sources at various time points during an ICU stay [12], [13]. A patient’s vital signs are measured as indicators of their health status. When a patient’s condition deteriorates or new symptoms appear, the corresponding vital signs are more frequently measured and recorded [14]. Accordingly, this results in the creation of multiple incomplete patient data, where missing values need to be filled with plausible values through imputation. A general practice is to provide missing data recovery in EHR data using deep representation learning. Existing studies focused on the provision of recurrent neural networks or generative adversarial networks with attention mechanisms that generate complete representations that can be readily used for downstream prediction tasks [15]–[20].

Although existing studies have confirmed the effectiveness of deep neural networks with attention mechanisms, the similarity between samples/patients has not been fully taken into consideration in deep representation learning. Patient similarity analysis aims to classify patients into medically relevant groups likely to have similar health outcomes or temporal experiences [21]. In real clinical reasoning scenarios, it is a general practice to utilize data from similar patients to generate hypotheses and make decisions (i.e., precision medicine [22]). Accordingly, we argue that desirable patient representations could be generated by aggregating the information from similar patients. Since no set criteria are available, a new challenge we face is how to calculate the similarity between patients in a large EHR dataset.

In this paper, we present a new Contrastive Graph Similarity Network for similarity calculation among patients in large EHR datasets. The core idea of our method is borrowed from Graph Contrastive Learning (GCL). The GCL is a self-supervised graph learning technique that exploits the structure of graphs with data augmentation techniques for contrastive learning to create different views [23]. To this end, we construct multiple patient-patient similarity graphs using vital signs and demographics as well as diagnosis and procedure codes as relational information and then aggregate the information from similar patients to generate rich patient representations (Figure 1a). To further put similar patients closer and push dissimilar patients apart, we construct positive and negative sample pairs in contrastive learning using the generated patient representations. We arbitrarily select a node as an anchor (Figure 1b). Positive samples for an anchor are defined as (i) the same nodes as the anchor in different views, (ii) the nodes connected to the anchor within the same view, and (iii) the nodes connected to the anchor from different views. The remaining samples are negative. For the imputation task, we construct sample pairs by pairing a positive (or negative) sample with the anchor. For the prediction task, we repeat the above sample pairing process with the constraint that the pairs must be formed between samples with the same binary label. We design a composite loss for imputation and prediction, where two hyper-parameters are used to control the ratio between imputation loss and prediction loss to minimize the overall loss.

Fig. 1.

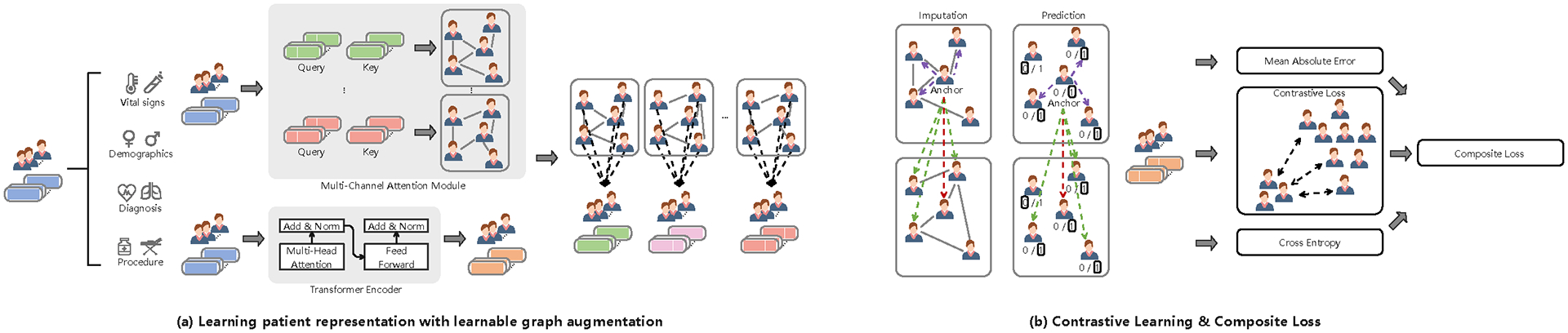
The proposed Contrastive Graph Similarity Network.

The main contributions are listed as follows:

• We present a new Contrastive Graph Similarity Network for similarity calculation among patients in large EHR datasets.

• We apply graph-based similarity analysis that explicitly extracts the clinical characteristics of each patient and aggregates the information of similar patients to generate rich patient representations.

• We evaluate our method against competing baselines on real-world EHR databases, and the results indicate the superiority of our method in vital signs imputation and ICU patient deterioration prediction.

II. Related Work

A. Graph Contrastive Learning

Recent advances in graph contrastive learning have achieved promising performance in node classification [24], social and medication recommendation [25], anomaly detection [26], molecular property prediction [27]. More recent attention has focused on the provision of learnable data augmentation techniques [23], [28]–[31]. These studies aim to create high-quality contrastive views via learnable data augmentation techniques. Different from those found in the literature in the following aspects: (i) we design a learnable graph augmentation technique that uses vital signs and demographics as well as diagnosis and procedure codes as relational information to construct multiple patient-patient similarity graphs and (ii) we propose a novel approach to construct multiple positive sample pairs in contrastive learning. The idea is borrowed from homophily in graphs [32]–[34]. Homophily in our patient-patient similarity graphs is the similarity between connected patient pairs, where connected patients are similar rather than far apart. Moreover, connected patients are considered similar if they share the same binary label.

B. Missing Data Recovery via Deep Representation Learning

A large and growing body of literature has focused on the provision of deep imputation methods. Representative methods include Recurrent Neural Networks (RNN) [15], [35] and Generative Adversarial Networks (GAN) [16]–[18], [20]. GRU-D [35] imputes missing values by combining the empirical mean value and the previous observed value. Brits [15] employs a bidirectional RNN to generate prefilled values for missing values, which are then used to generate imputed values. Given the actual samples with many missing values, GAN-based methods [16]–[18], [20] include making a generator for generating imputed values for missing values and then a discriminator for distinguishing these imputed values from actual values. Through the imputation process, the generated representations are used for downstream prediction tasks. Different from the aforementioned methods, we apply graph-based similarity analysis that explicitly extracts the clinical characteristics of each patient and aggregates the information of similar patients to generate rich patient representations. It is also worth noting that a recent study by [36] integrated graph representation learning and contrastive learning into a stacked neural network architecture. However, there may be conflicts between graph representation learning and contrastive learning, as contrastive learning may push away the connected nodes in the graph. Note that our approach is based on the graph contrastive learning paradigm, which is significantly different from using contrastive learning as a module in the neural network architecture.

III. Method

A. Basic Notations

Let $D={\left\{\left(X_i,Y_i\right)\right\}}_{i=1}^{\left|𝒫\right|}$ represent the EHR dataset with up to $\left|𝒫\right|$ samples/patients. $X$ contains multivariate time series data $X^{\left(t\right)}$ and static data $X^{\left(s\right)}$. Particularly, $X^{\left(t\right)}$ contains vital sign measurements (oxygen saturation, fraction inspired oxygen, and temperature, etc), and $X^{\left(s\right)}$ contains demographics (age, sex, and ethnicity) as well as diagnosis and procedure codes (unique medical codes). $Y$ represents target labels for the benchmarks/tasks. We represent the elements in $X^{\left(t\right)}$ using $\left(x_1^{\left(t\right)},\cdots ,x_T^{\left(t\right)}\right)\in {\mathbb{R}}^{d\times T}$, where $T$ is the number of time steps and $d$ is the number of vital signs. We represent missing values in $X^{\left(t\right)}$ using a mask matrix $M\in {\mathbb{R}}^{d\times T}$.

B. Architecture Overview

Figure 1 displays the overview of the proposed Contrastive Graph Similarity Network.

1). Learning patient representation with learnable graph augmentation:

Let $𝒢=\{𝒫,ℰ\}$ represent a patient-patient similarity graph. $𝒫$ is a set of nodes, where each node represents a patient. $ℰ$ is a set of edges that connects patients. The adjacency matrix $A$ represents the causal connections between patients. For example, $A_{i,j}$ is 1 if patients $i$ and $j$ are connected, and 0 otherwise.

Now, we feed $X$ into a multi-channel attention module to generate up to $N$ adjacency matrices. The multi-channel attention module has up to $N$ channels, where each channel has an attention layer. Specifically, the following steps were taken: (i) we apply adaptive average pooling to $X$ (i.e., at the horizontal dimension) to generate a new feature representation $\bar{X}$. (ii) we apply a linear transformation to $\bar{X}$ to generate query and key vectors. (iii) we take the dot product between query and key vectors and then apply the Softmax function to obtain a set of attention weight matrices. We formulate the above process as:

$$\begin{gathered} Q_i=W_i^Q\cdot \bar{X},K_i=W_i^K\cdot \bar{X}, \\ {A}_i=\mathit{\text{Softmax}}\left(Q_i\cdot K_i^{\top }\right),i\in \left\{1,2,\cdots ,N\right\}, \end{gathered}$$ (1)

where all $W$ are learnable weight matrices. $Q$ and $K$ are query and key vectors. ${\left\{A_i\right\}}_{i=1}^N$ is a set of attention weight matrices, where each attention weight matrix corresponds to a patient-patient similarity graph. We introduce a learnable threshold $\phi$ to those matrices to generate binary matrices as adjacency matrices to consider the information from similar patients.

Next, we feed $X$ into the Transformer encoder [37] to generate a rich feature representation. To be specific, we apply a linear transformation to $X$ to generate $Q^{\prime },K^{\prime }$, and $V^{\prime }$ and then take the dot product between $Q^{\prime }$ and $K^{\prime }$ and apply the Softmax function to obtain attention scores on $V^{\prime }$. We formulate the above process as:

$$\begin{gathered} Q^{\prime }=W_{Q^{\prime }}\cdot X,K^{\prime }=W_{K^{\prime }}\cdot X,V^{\prime }=W_{V^{\prime }}\cdot X, \\ {\alpha }_j=\mathit{\text{Softmax}}\left(Q_j^{\prime }\cdot K_j^{\prime \top }\right), \\ {\mathit{\text{head}}}_j={\alpha }_j\cdot V_j^{\prime },j\in \{1,2,\cdots ,L\}, \\ Z=\left({\mathit{\text{head}}}_1\Vert \cdots \Vert {\mathit{\text{head}}}_L\right)\cdot W_O, \end{gathered}$$ (2)

where all $W$ are learnable weight matrices. || is the concatenation operator. $L$ is the number of heads. Subsequently, we feed $Z$ into a normalized layer with the residual connection [38], followed by a feed-forward network (FFN). In the same vein, we feed the output of FFN into a normalization layer with the residual connection again to obtain $\tilde{Z}$ as:

$$\begin{gathered} Z^{\prime }=\mathit{\text{norm}}(X+Z), \\ {Z}_{FFN}=\mathit{\text{ReLU}}\left(Z^{\prime }\cdot W_1\right)\cdot W_2, \\ \tilde{Z}=\mathit{\text{norm}}\left(Z^{\prime }+Z_{FFN}\right), \end{gathered}$$ (3)

where all $W$ are learnable parameters.

Last, we combine $\tilde{Z}$ with ${\left\{A_i\right\}}_{i=1}^N$ to aggregate the information from similar patients as:

$${\hat{Z}}^{\left(i\right)}=A_i\cdot \tilde{Z},i\in \{1,2,\cdots ,N\}.$$ (4)

Subsequently, we apply adaptive average pooling to $\hat{Z}$ to generate the patient representation $\bar{Z}$.

2). Contrastive Learning:

To further put similar patients closer and push dissimilar patients apart, we construct positive and negative sample pairs in contrastive learning using the generated patient representations ${\left\{{\bar{Z}}^{\left(i\right)}\right\}}_{i=1}^N$. We arbitrarily select a node as an anchor (as shown in Figure 1b). Positive samples for an anchor are defined as (i) the same nodes as the anchor in different views, (ii) the nodes connected to the anchor within the same view, and (iii) the nodes connected to the anchor from different views. The remaining samples are negative. For the imputation task, we construct sample pairs by pairing a positive (or negative) sample with the anchor. For the prediction task, we repeat the above sample pairing process with the constraint that the pairs must be formed between samples with the same binary label. This process is repeated for all nodes.

Contrastive Imputation Loss

We select ${\bar{Z}}_p^{\left(1\right)}$ as an anchor. The contrastive loss between ${\bar{Z}}^{\left(1\right)}$ and ${\bar{Z}}^{\left(2\right)}$ as:

$$\begin{gathered} {ℒ}_{CL}^{\left(\mathit{\text{Imp}}\right)}\left({\bar{Z}}_p^{\left(1\right)}\right)= \\ -\frac{1}{2\left|𝒩\right(p\left)\right|+1}\mathit{\text{log}}\frac{\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_p^{\left(2\right)}\right)/\tau \right)}{\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_j^{\left(1\right)},{\bar{Z}}_p^{\left(2\right)}\right)/\tau \right)} \\ \frac{+\sum _{k\in 𝒩\left(p\right)}\left(\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_k^{\left(1\right)}\right)/\tau \right)\right.}{+\sum _{k\ne p}\left(\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_k^{\left(1\right)}\right)/\tau \right)\right.} \\ \frac{\left.+\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_p^{\left(2\right)}/\tau \right)\right)\right)}{\left.+\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_p^{\left(2\right)}/\tau \right)\right)\right)}, \end{gathered}$$ (5)

where $𝒩\left(p\right)$ is a set of neighbors in ${\bar{Z}}_p^{\left(1\right)}\cdot \mathit{\text{sim}}(\cdot )$ is the dot product operation. $\tau$ is a temperature parameter used to handle the strength of penalties on negative pairs. Since the two views are symmetric, we select ${\bar{Z}}_p^{\left(2\right)}$ as an anchor again. The contrastive loss ${ℒ}_{CL}^{Imp}\left({\bar{Z}}_p^{\left(2\right)}\right)$ can be done in the way as Eq. (5). Accordingly, the contrastive loss between ${\bar{Z}}^{\left(1\right)}$ and ${\bar{Z}}^{\left(2\right)}$ as:

$${ℒ}_{CL}^{\left(Imp\right)}\left({\bar{Z}}^{\left(1\right)},{\bar{Z}}^{\left(2\right)}\right)=\frac{1}{2\left|𝒫\right|}\sum _{p=1}^{\left|𝒫\right|}\left({ℒ}_{CL}^{\left(Imp\right)}\left({\bar{Z}}_p^{\left(1\right)}\right)+{ℒ}_{CL}^{\left(Imp\right)}\left({\bar{Z}}_p^{\left(2\right)}\right)\right).$$ (6)

Through the processes above, we have been able to calculate the contrastive loss between ${\bar{Z}}^{\left(1\right)}$ and ${\bar{Z}}^{\left(2\right)}$. Since ${\left\{{\bar{Z}}^{\left(i\right)}\right\}}_{i=1}^N$ is set of patient representations, we arbitrarily select one and then calculate the contrastive loss between it and the others. Accordingly, we utilize the total contrastive loss as the contrastive imputation loss:

$${ℒ}_{CL}^{\left(Imp\right)}=\frac{1}{N}\sum _{n=1,n\ne l}^N{ℒ}_{CL}^{\left(Imp\right)}\left({\bar{Z}}^{\left(l\right)},{\bar{Z}}^{\left(n\right)}\right).$$ (7)

Contrastive Prediction Loss

We select ${\bar{Z}}_p^{\left(1\right)}$ as an anchor. The contrastive loss between ${\bar{Z}}^{\left(1\right)}$ and ${\bar{Z}}^{\left(2\right)}$ as:

$${ℒ}_{CL}^{\left(\mathit{\text{pre}}\right)}\left({\bar{Z}}_p^{\left(1\right)}\right)=-\frac{1}{2N_{Y_p}+1}log\frac{\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_p^{\left(2\right)}\right)/\tau \right)}{\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_p^{\left(2\right)}\right)/\tau \right)},\frac{+\sum _{k=1}^{\left|P\right|}{1}_{\left[Y_p=Y_k\right]}\left(\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_k^{\left(1\right)}\right)/\tau \right)\right.}{+\sum _{k=1}^{\left|P\right|}{1}_{[k\ne p]}\left(\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_k^{\left(1\right)}\right)/\tau \right)\right.},\frac{\left.+\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_k^{\left(2\right)}/\tau \right)\right)\right)}{\left.+\mathit{\text{exp}}\left(\mathit{\text{sim}}\left({\bar{Z}}_p^{\left(1\right)},{\bar{Z}}_k^{\left(2\right)}/\tau \right)\right)\right)},$$ (8)

where $Y_p$ is the label of node $p$ (i.e., patient $p$). $N_{Y_p}$ is the number of nodes with the same label as node $p.\mathit{\text{sim}}(\cdot )$ is the cosine similarity. $1_{[\cdot ]}$ is an indicator function. Similar to the imputation task, we utilize the total contrastive loss as the contrastive prediction loss:

$$\begin{gathered} {ℒ}_{CL}^{\left(\mathit{\text{pre}}\right)}\left({\bar{Z}}^{\left(1\right)},{\bar{Z}}^{\left(2\right)}\right)=\frac{1}{2\left|𝒫\right|}\sum _{p=1}^{\left|𝒫\right|}\left({ℒ}_{CL}^{\left(\mathit{\text{pre}}\right)}\left({\bar{Z}}_p^{\left(1\right)}\right)+{ℒ}_{CL}^{\left(\mathit{\text{pre}}\right)}\left({\bar{Z}}_p^{\left(2\right)}\right)\right), \\ {ℒ}_{CL}^{\left(\mathit{\text{pre}}\right)}=\frac{1}{N}\sum _{n=1,n\ne l}^N{ℒ}_{CL}^{\left(\mathit{\text{pre}}\right)}\left({\bar{Z}}^{\left(l\right)},{\bar{Z}}^{\left(n\right)}\right). \end{gathered}$$ (9)

3). Composite Loss:

Since the imputation task can be viewed as a regression task, we employ the mean absolute error (MAE) as the objective function between the original $X$ and predicted $\hat{X}$ of each patient as:

$$\begin{gathered} \hat{X}=W_r\cdot \tilde{Z}+b_r, \\ {ℒ}_{MAE}^{\left(Imp\right)}=\frac{1}{\left|𝒫\right|}\sum _{p=1}^{\left|𝒫\right|}\left|X_p\odot M_p-{\hat{X}}_p\odot M_p\right|. \end{gathered}$$ (10)

Accordingly, the imputation loss ${ℒ}^{\left(Imp\right)}$ is the summation of the MAE and the contrastive imputation loss as:

$${ℒ}^{\left(Imp\right)}={\lambda }_{MAE}\cdot {ℒ}_{MAE}^{\left(Imp\right)}+\left(1-{\lambda }_{MAE}\right)\cdot {ℒ}_{CL}^{\left(Imp\right)},$$ (11)

where ${\lambda }_{MAE}$ is a scaling parameter used to make the trade-off between the MAE and the contrastive imputation loss.

In order to perform prediction tasks, we employ the cross entropy (CE) as the objective function between the target label $Y$ and predicted label $\hat{Y}$ of each patient as:

$$\begin{gathered} \hat{Y}=\mathit{\text{Softmax}}\left(Z^{*}\cdot W_c+b_c\right) \\ {ℒ}_{CE}^{\left(\text{Pre}\right)}=-\frac{1}{\left|𝒫\right|}\sum _{p=1}^{\left|𝒫\right|}\left(Y_p^{\top }\cdot log\left({\hat{Y}}_p\right)\right.\left.+{\left(1-Y_p\right)}^{\top }\cdot log\left(1-{\hat{Y}}_p\right)\right), \end{gathered}$$ (12)

where $Z^{*}$ is the pooled representation obtained by applying adaptive average pooling to $\tilde{Z}$ before feeding into the Softmax output layer. Accordingly, the prediction loss ${ℒ}^{\left(\mathit{\text{Pre}}\right)}$ is the summation of the CE and the contrastive prediction loss as:

$${ℒ}^{\left(\mathit{\text{pre}}\right)}={\lambda }_{CE}\cdot {ℒ}_{CE}^{\left(\mathit{\text{pre}}\right)}+\left(1-{\lambda }_{CE}\right)\cdot {ℒ}_{CL}^{\left(\mathit{\text{pre}}\right)},$$ (13)

where ${\lambda }_{CE}$ is a scaling parameter used to make the trade-off between the CE and the contrastive prediction loss.

We design a composite loss for imputation and prediction, where two scaling parameters ${\lambda }^{\left(\mathit{\text{pre}}\right)}$ and ${\lambda }^{\left(Imp\right)}$ are used to make the trade-off between imputation loss and prediction loss as:

$$ℒ={\lambda }^{\left(\mathit{\text{pre}}\right)}\cdot {ℒ}^{\left(\mathit{\text{pre}}\right)}+{\lambda }^{\left(Imp\right)}\cdot {ℒ}^{\left(Imp\right)}.$$ (14)

IV. Experiments

A. Datasets

We conduct extensive experiments on the MIMIC-III¹ and eICU² databases with ICU patient deterioration prediction and vital signs imputation [12], [13]. The details of the two databases are described in the literature [39], [40]. We extract vital sign measurements (e.g., oxygen saturation, fraction inspired oxygen, and temperature), demographics (i.e., age, sex, and ethnicity), as well as diagnosis and procedure codes (i.e., unique medical codes) from the two databases. For the former dataset, the sample size is 17,886, where the Positive (likely to die)/Negative (unlikely to die) ratio is 1:6.59. For the latter dataset, the sample size is 36,670, where the Positive/Negative ratio is 1:7.49.

B. Baseline Methods

We evaluate the performance of our method against representative deep imputation methods, including Recurrent Neural Networks (RNN) based methods [15], [35] and Generative Adversarial Networks (GAN) based methods [16]–[18], [20]. Detailed description of [15]–[18], [20], [35] can be found in the related work. We also compare our method with MTSIT [41]. MTSIT is an attention-based method that combines a Transformer encoder with a linear decoder as the network backbone. The source code and data extraction, statistics of features, as well as implementation details of baselines, are released at the Github repository³.

C. Implementation Details & Evaluation Metrics

The two EHR datasets are derived from the MIMIC-III and eICU databases. Each EHR dataset is randomly split into the training, validation, and testing set in a 0.7:0.15:0.15 ratio. For the former dataset, the number of channels in the multi-channel attention module is 2, and the dimension size of $W_i^Q$ and $W_i^K$ are 17; the number of heads in the Transformer encoder is 4, the number of layers is 1, and the dimension size of $W_Q,W_K$ and $W_V$ is 24; the temperature parameter $\tau$ is 0.6; the scaling parameters ${\lambda }_{MAE}$ and ${\lambda }_{CE}$ are 0.8; the scaling parameters ${\lambda }^{\left(Imp\right)}$ and ${\lambda }^{\left(\mathit{\text{pre}}\right)}$ are 0.5 and 0.7, respectively. For the latter dataset, the number of channels in the multi-channel attention module is 4, and the dimension size of $W_i^Q$ and $W_i^K$ are 16; the number of heads in the Transformer encoder is 2, the number of layers is 1, and the dimension size of $W_Q,$ $W_K$ and $W_V$ is 26; the temperature parameter $\tau$ is 0.5; the scaling parameters ${\lambda }_{MAE}$ and ${\lambda }_{CE}$ are 0.95; the scaling parameters ${\lambda }^{\left(Imp\right)}$ and ${\lambda }^{\left(\text{Pre}\right)}$ are 0.9 and 0.7, respectively. For the ICU patient deterioration prediction, the dropout method is also employed for the Softmax output layer, and the dropout rates of MIMIC-III and EICU are 0.1 and 0.2, respectively. We adopt MAE, MRE (mean relative error), AUROC, AUPRC, F1 Score, and Min(Se, P+) to evaluate imputation and prediction performance. Each experiment is run ten times, and the average performance is reported.

D. Performance Comparison

We report the result of ICU patient deterioration prediction in Table I. As Table I shows, our method reaches the highest AUROC, AUPRC, F1 Score, and Min(Se, P+) with 0.8967, 0.5863, 0.5517, and 0.5668. Besides, there was no significant prediction performance difference between RNN-based methods (GRU-D, Brits) and GAN-based methods (Conditional GAN, STING, MBGAN, SA-EDGAN). It is difficult to explain this result, but it might be related to the quality of the input data. We report the result of vital signs imputation in Figures 2 and 3. Our method reports the lowest MAE and MRE scores. The most striking result from the data comparison is that MTSIT (i.e., an attention-based network architecture) resulted in the lowest MAE and MRE scores among the baselines (except for 48 hours after eICU admission). Therefore, the network architecture could be a major factor, if not the only one, causing the differences in imputation performance.

TABLE I.

Overall performance of ICU patient deterioration prediction on the MIMIC-III and eICU dataset.

MIMIC-III	24 hours after admission
Metrics	AUROC	AUPRC	F1 Score	Min(Se, P+)
GRU-D [35]	0.8821(0.0087)	0.5526(0.0282)	0.5064(0.0633)	0.5669(0.0105)
Brits [15]	0.8816(0.0015)	0.5543(0.0097)	0.5188(0.0531)	0.5627(0.0058)
Conditional GAN [16]	0.8757(0.0061)	0.5374(0.0198)	0.5112(0.0299)	0.5535(0.0313)
STING [17]	0.8784(0.0069)	0.5177(0.0220)	0.5316(0.0256)	0.5369(0.0282)
MBGAN [18]	0.8778(0.0073)	0.5539(0.0287)	0.5257(0.0276)	0.5473(0.0299)
SA-EDGAN [20]	0.8819(0.0098)	0.5448(0.0514)	0.5292(0.0430)	0.5544(0.0424)
MTSIT [41]	0.8775(0.0035)	0.5425(0.0143)	0.5221(0.0425)	0.5558(0.0129)
Our	0.8889(0.0036)	0.5637(0.0073)	0.5414(0.0565)	0.5695(0.0112)
MIMIC-III	48 hours after admission
Metrics	AUROC	AUPRC	F1 Score	Min(Se, P+)
GRU-D [35]	0.8820(0.0097)	0.5568(0.0189)	0.5386(0.0632)	0.5570(0.0189)
Brits [15]	0.8805(0.0017)	0.5524(0.0133)	0.5184(0.0735)	0.5641(0.0051)
Conditional GAN [16]	0.8762(0.0074)	0.5458(0.0214)	0.5293(0.0221)	0.5417(0.0196)
STING [17]	0.8824(0.0043)	0.5349(0.0285)	0.5369(0.0226)	0.5508(0.0183)
MBGAN [18]	0.8705(0.0045)	0.5611(0.0199)	0.5315(0.0239)	0.5561(0.0217)
SA-EDGAN [20]	0.8785(0.0063)	0.5585(0.0178)	0.5361(0.0254)	0.5534(0.0151)
MTSIT [41]	0.8735(0.0032)	0.5352(0.0171)	0.5126(0.0459)	0.5466(0.0190)
Our	0.8967(0.0038)	0.5863(0.0098)	0.5517(0.0104)	0.5668(0.0074)
eICU	24 hours after admission
Metrics	AUROC	AUPRC	F1 Score	Min(Se, P+)
GRU-D [35]	0.8166(0.0198)	0.4618(0.0266)	0.4122(0.0936)	0.4773(0.0221)
Brits [15]	0.8194(0.0077)	0.4601(0.0179)	0.4034(0.0535)	0.4815(0.0161)
Conditional GAN [16]	0.8168(0.0083)	0.4371(0.0175)	0.4533(0.0181)	0.4819(0.0219)
STING [17]	0.8226(0.0061)	0.4355(0.0121)	0.4659(0.0144)	0.4770(0.0105)
MBGAN [18]	0.8193(0.0053)	0.4554(0.0198)	0.4634(0.0192)	0.4741(0.0185)
SA-EDGAN [20]	0.8214(0.0049)	0.4466(0.0256)	0.4723(0.0271)	0.4796(0.0227)
MTSIT [41]	0.8138(0.0031)	0.4322(0.0529)	0.4195(0.0290)	0.4365(0.0110)
Our	0.8385(0.0035)	0.4746(0.0137)	0.4793(0.0253)	0.4941(0.0068)
eICU	48 hours after admission
Metrics	AUROC	AUPRC	F1 Score	Min(Se, P+)
GRU-D [35]	0.8276(0.0054)	0.4275(0.0144)	0.4224(0.0358)	0.4457(0.0061)
Brits [15]	0.8163(0.0122)	0.4248(0.0127)	0.4377(0.0113)	0.4438(0.0135)
Conditional GAN [16]	0.8219(0.0093)	0.4033(0.0217)	0.4275(0.0193)	0.4353(0.0179)
STING [17]	0.8270(0.0070)	0.4084(0.0185)	0.4414(0.0216)	0.4411(0.0173)
MBGAN [18]	0.8235(0.0095)	0.4025(0.0169)	0.4392(0.0201)	0.4521(0.0198)
SA-EDGAN [20]	0.8267(0.0072)	0.4190(0.0165)	0.4440(0.0165)	0.4445(0.0184)
MTSIT [41]	0.8044(0.0025)	0.3921(0.0446)	0.4456(0.0112)	0.3977(0.0190)
Our	0.8420(0.0036)	0.4457(0.0231)	0.4539(0.0217)	0.4611(0.0111)

Fig. 2.

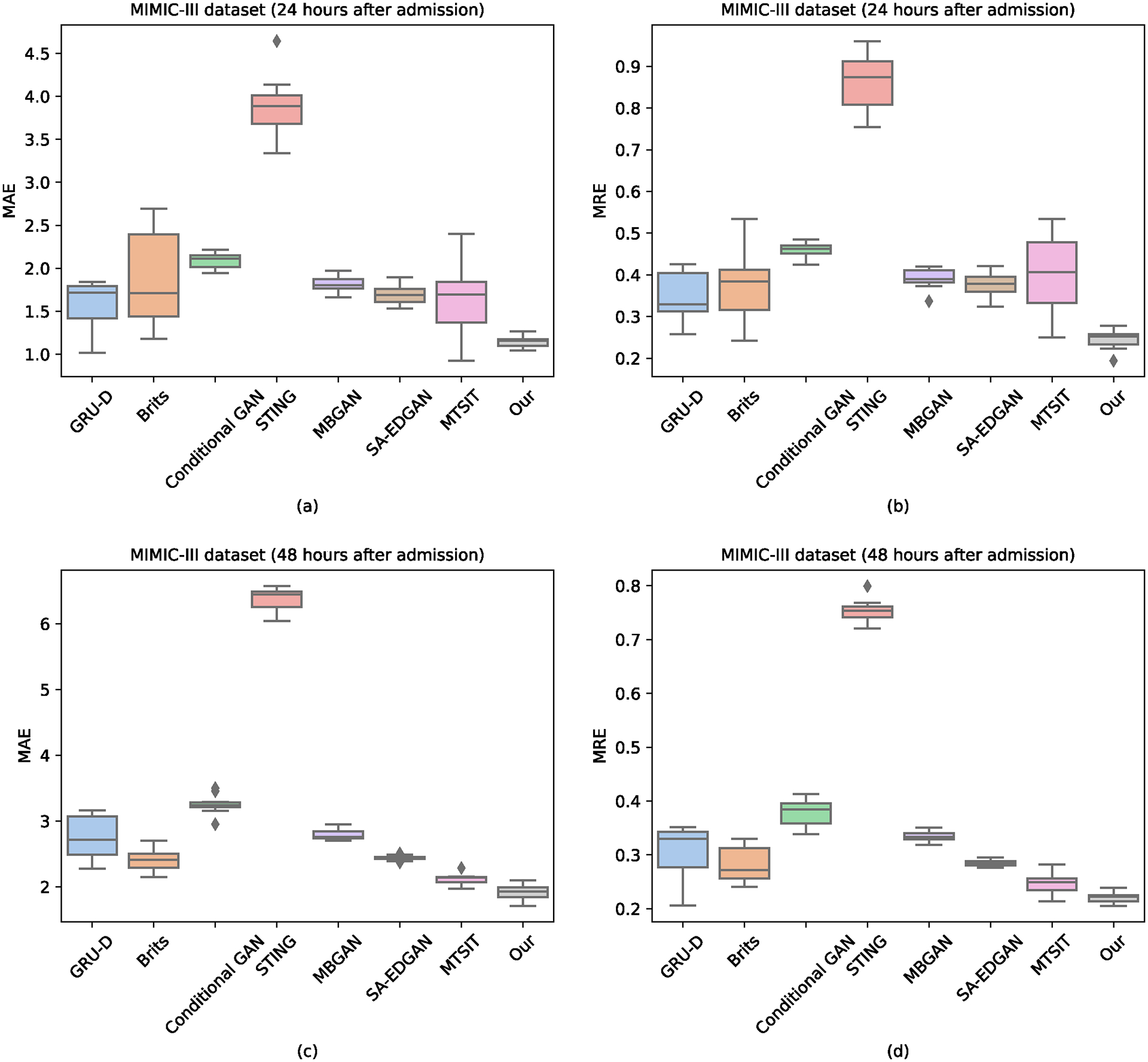
Overall performance of vital signs imputation on the MIMIC-III dataset.

Fig. 3.

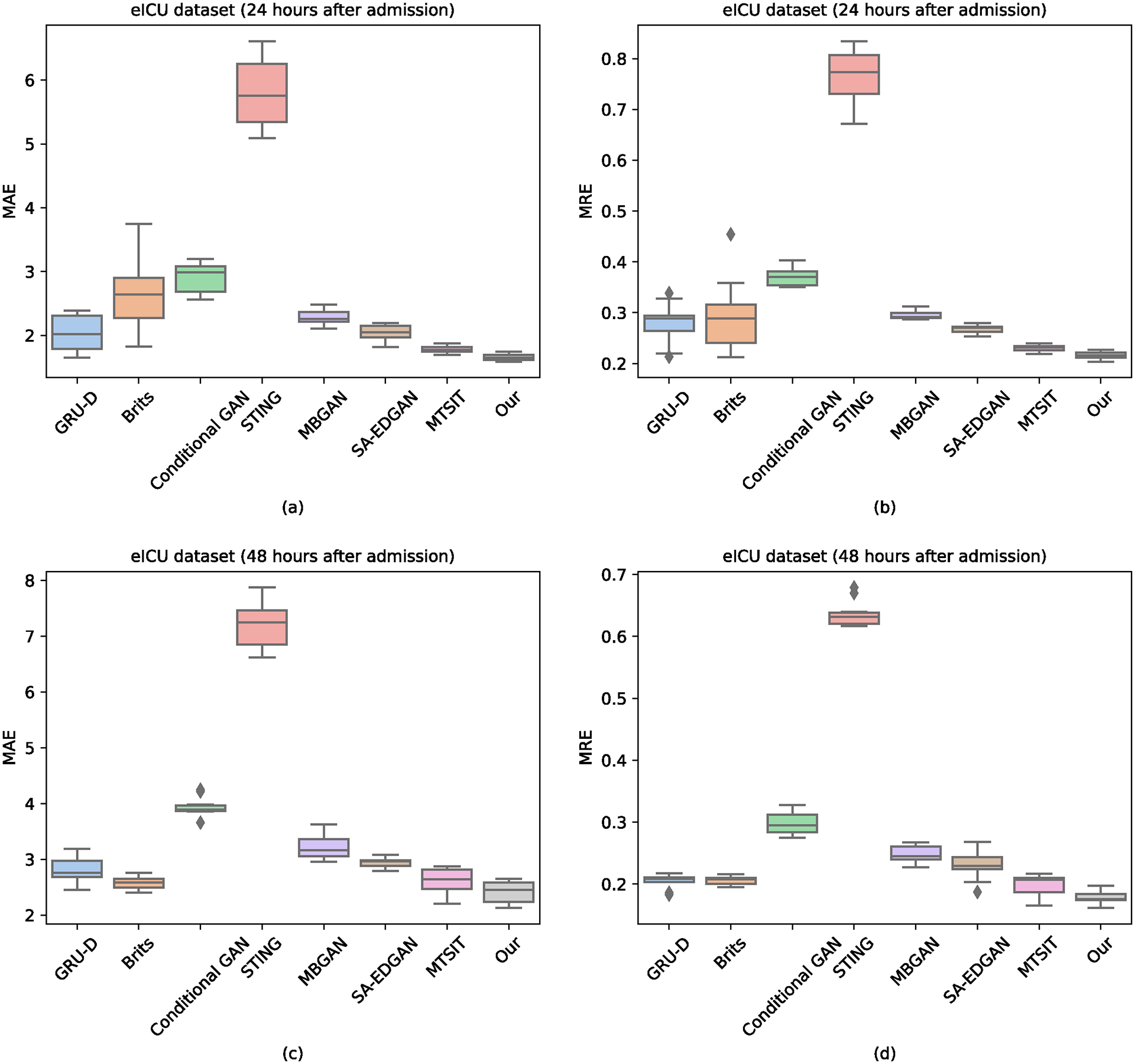
Overall performance of vital signs imputation on the eICU dataset.

E. Analysis of Hyper-parameters

Now, we make a comparison between the proposed method and its variants that change parts of the contrastive learning module. Doing such a comparison can allow us to understand how the contrastive learning module makes decisions. Since our method runs on the network as a unit, this is the way to implement the hyper-parameter (i.e., ${\lambda }^{\left(\text{Pre}\right)}$ and ${\lambda }^{\left(Imp\right)}$) studies. The results obtained from the visualization analysis of the contrastive learning module can be compared in Figure 4. The experimental data were gathered 48 hours after admission (MIMIC-III). As shown in Figure 4, positive represents the patient who died, and negative represents the patient who did not die. From Figure 4a to Figure 4d, we omit the contrastive learning component; ${\lambda }^{\left(Imp\right)}$ is greater than ${\lambda }^{\left(\mathit{\text{Pre}}\right)};{\lambda }^{\left(\mathit{\text{Pre}}\right)}$ is greater than ${\lambda }^{\left(Imp\right)};{\lambda }^{\left(Imp\right)}$ is equal to ${\lambda }^{\left(\mathit{\text{pre}}\right)}$. The two scaling parameters ${\lambda }^{\left(Imp\right)}$ and ${\lambda }^{\left(\mathit{\text{pre}}\right)}$ are used to make the trade-off between imputation loss and prediction loss. Looking at Figure 4a, the instances from the positive and negative classes are scattered. Compared with the instances in Figure 4a, the instances in Figure 4b are clustered together, and each cluster has instances from both positive and negative classes. From the data in Figure 4c, we can see that the instances from the positive and negative classes are clustered together towards two distinguishable clusters. From the data in Figure 4d, we can see the instances from the positive and negative classes in each cluster towards two distinguishable sub-clusters. These results are in agreement with our expectations. We also analyze the prediction performance of our method with different dropout rates, temperature parameters, and number of channels, as shown in Figures 5 and 6.

Fig. 4.

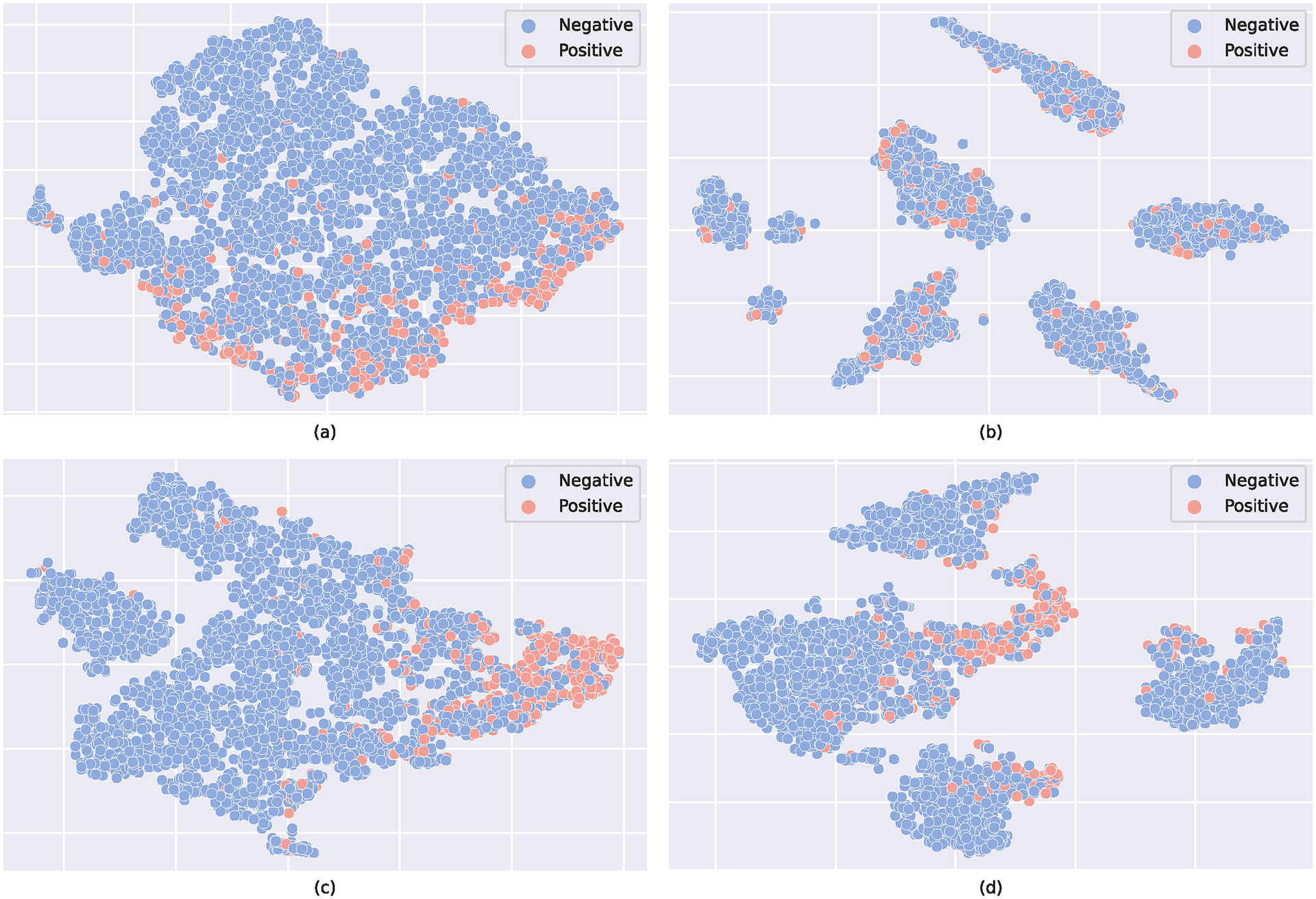
The t-SNE plot of the feature representation $\tilde{Z}$. (a) w/o contrastive learning module; (b) ${\lambda }^{\left(Imp\right)}$ is greater than ${\lambda }^{\left(\mathit{\text{pre}}\right)}$; (c) ${\lambda }^{\left(\mathit{\text{pre}}\right)}$ is greater than ${\lambda }^{\left(Imp\right)};$ (d) ${\lambda }^{\left(Imp\right)}$ is equal to ${\lambda }^{\left(\mathit{\text{pre}}\right)}$.

Fig. 5.

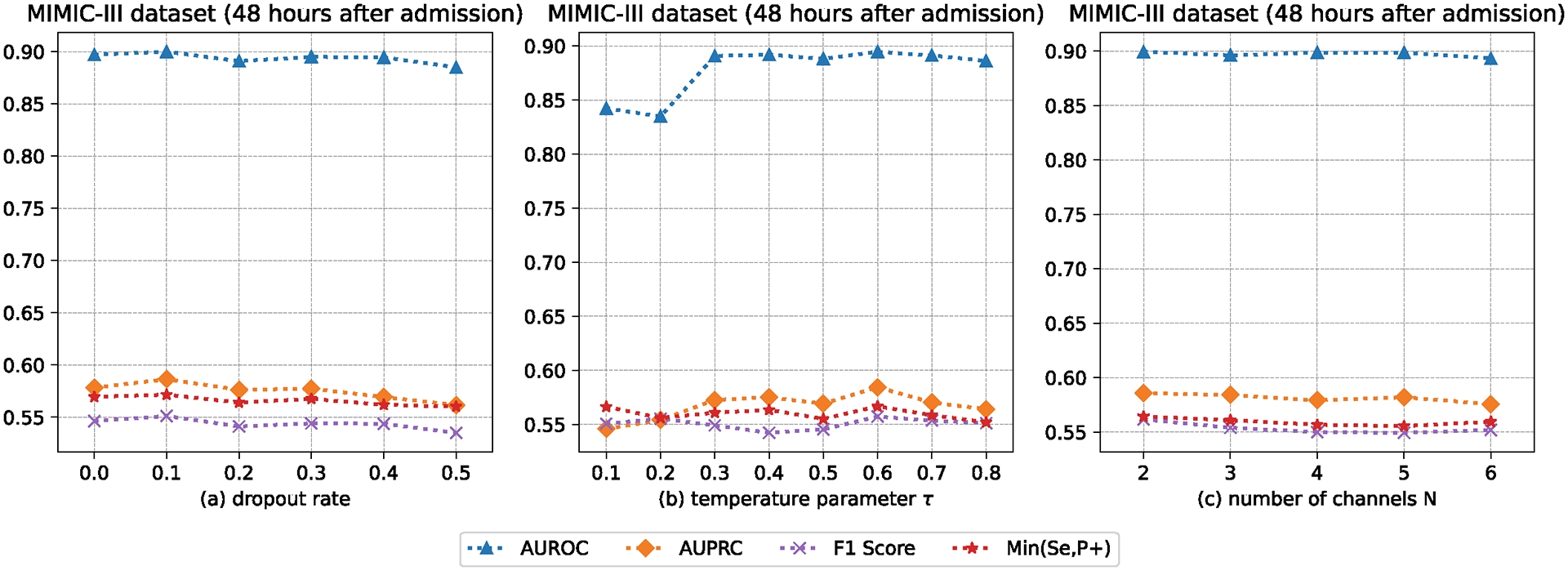
The AUROC, AUPRC, F1 Score, and Min(Se, P+) of our method with different dropout rates, temperature parameters, and number of channels.

Fig. 6.

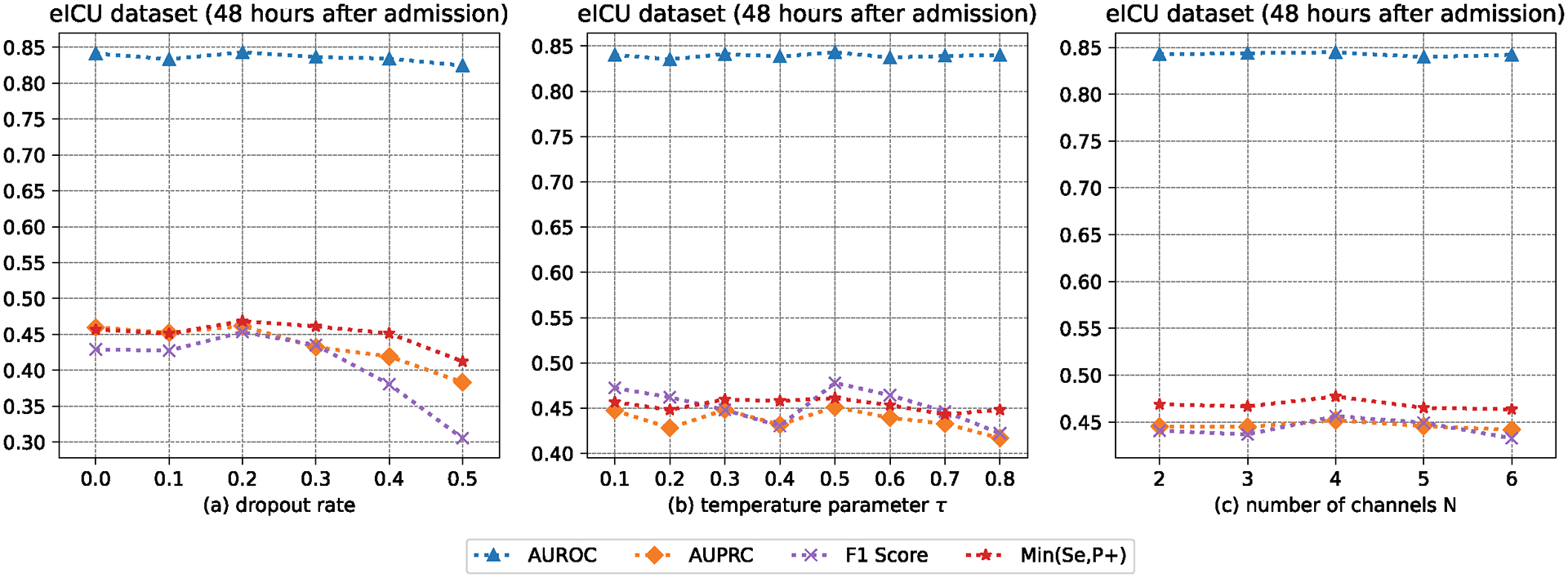
The AUROC, AUPRC, F1 Score, and Min(Se, P+) of our method with different dropout rates, temperature parameters, and number of channels.

V. Conclusions

In this paper, a new Contrastive Graph Similarity Network was presented, which focused on the provision of similarity calculation among patients in large EHR datasets. The core idea of our method is to incorporate graph contrastive learning in representation learning for EHR data. Particularly, we apply graph-based similarity analysis that explicitly extracts the clinical characteristics of each patient and aggregates the information of similar patients to generate rich patient representations. Experimental results indicate the superiority of the proposed method across real-world EHR databases on ICU patient deterioration prediction and vital signs imputation.

VI. Limitations and Future Works

A major problem with the proposed method is that it fails to take the temporal nature of EHR data into account, such as the time interval between vital signs. Since our method runs on the network as a unit, this makes an ablation study on the network architecture extremely difficult. Some of the distribution of patient-specific characteristics, such as age, sex, and ethnicity, are imbalanced, which, although considered, is not thoroughly analyzed when computing patient similarity in the proposed Contrastive Graph Similarity Network. These characteristics are sensitive attributes that may lead to bias in imputation and prediction results. In addition, there might still be many “unseen” attributes that could significantly affect the model training process. For example, the missing rates among vital signs vary significantly, ranging from less than 40% (e.g., diastolic blood pressure, oxygen saturation, and respiratory rate) to exceeding 90% (e.g., capillary refill rate, fraction inspired oxygen, and pH), causing concerns about the fairness of the patient similarity model. Therefore, continued effort should be made to develop patient models that minimize unfairness in the future.