Abstract
The spinning disc atomizer is extensively utilized in agricultural spraying, with optimized operating conditions significantly enhancing atomization performance. In this paper, the atomization characteristics of a spinning disc were studied using photographs taken by a high-speed camera. Ethanol-water solutions were used at various flow rates and the disc speed was varied in a wide range. The influence of disc speed, flow rate, and surface tension on modes of spray formation, droplet size, and size distribution were investigated. The correlations for Reynolds number (Re), Stability number (St), and dimensionless droplet size (d* ) were proposed in a wide range of operational conditions. The Rosin-Rammler (RR) and modified Rosin-Rammler (MRR) distributions appropriately represented the droplet size distribution. It was found that the increase in flow rate resulted in modes of spray formation translation under the same disc speed and ethanol-water solution. The predicted droplet sizes showed good agreement with the experiment values. Most of the predicted droplet sizes were within the band of ±15% of the experiment values. The droplet size decreased with increasing Re or St, but was hardly affected by q. Besides, the droplet size decreased with increasing disc speed and decreasing surface tension. The RR and MRR distribution matched with the calculated cumulative volume fraction from the experimental data reasonably well for the entire range. It was recommended to appropriately elevate Re during the spinning disc atomization process to narrow the range of droplet sizes and enhance uniformity.
Keywords: spinning disc atomizer, spray formation mode, droplet size, droplet size distribution, Rosin-Rammler distribution
1. Introduction
Rotary atomizers, characterized by a narrow droplet size distribution and an open structure that is resistant to clogging, have significant advantages over hydraulic nozzles. Hence, they are extensively used in many applications, such as spray pesticides (Ru et al., 2024; Liu et al., 2024), spray coating (Gödeke et al., 2021; Sidawi et al., 2021), and slag granulation (Mantripragada et al., 2021; Li et al., 2023).
In these rotary atomizers, the liquid is directly fed into the center of a spinning disc, cup, or cage. The liquid is forced to the edge by centrifugal forces, then ejected from the edge, and broken into small droplets (Peng et al., 2017; Sahoo and Kumar, 2024). Hinze and Milborn (1950) identified three different modes of spray formation. As the flow rate increases, the modes of spray formation will transition from direct drop to ligament formation, and then further to sheet formation. Frost (1981) confirmed this phenomenon and highlighted the presence of mixed modes of spray formation. He established dimensionless correlations for the transition of spray formation modes. Glahn et al. (2002); Peng et al. (2016), and Wu et al. (2018) also developed correlations for the transition of spray formation modes on a spinning disc. The correlations from these studies show significant variances, likely due to differences in operational conditions and atomizer configurations (Feng et al., 2021).
To better understand the factors affecting droplet size in spinning disc atomization, various research teams have conducted numerous experiments. Walton and Prewett (1949) estimated the droplet size by impaction of the droplets on magnesium oxide coated slides and measurement of the crater diameters. They found that spinning disc atomization can produce uniform droplet sprays and revealed the relationship between average droplet size, disc speed, surface tension, and density. Boize and Dombrowski (1976) used sub-microsecond spark photography to study the atomization characteristics of oils with different viscosities under various operating conditions. They found that droplet size is mainly influenced by disc speed. Frost (1981) measured droplet size using short-duration spark photography and developed a droplet size correlation. This further revealed the relationship between droplet size and various influencing factors. Ahmed and Youssef (2012) measured droplet sizes under different operating conditions using a phase-doppler particle analyzer. The results indicated that droplet size is related to various dimensionless numbers. Wang et al. (2016) used a high-speed camera to experimentally study the ligament formation and break-up process at the edge of the spinning disc. They established the relationship between average droplet size, disc speed, and liquid physical properties. Kumar and Sarkar (2019) investigated the impact of slotted discs on droplet size, while Prather et al. (2023) analyzed the atomization dynamics and their effect on droplet size in the spinning disc atomization process. Table 1 summarizes the correlations of droplet size with spinning disc atomizers from previous studies, listing the test liquids, range of operating variables, and modes of spray formation. However, the correlations established by these studies are not consistent. The differences are mainly due to variations in droplet size measurement techniques, atomizer structures, and modes of spray formation (Prather et al., 2023; Ahmed and Youssef, 2012). Additionally, different definitions of droplet size may also lead to varying results. The correlation of droplet size is based on droplet distribution corresponding to droplet diameters, including arithmetic mean diameter (D 10), Sauter mean diameter (D 32), and volume median diameter (D V0.5 or VMD) (ASTM E799-03(2020)e1, 2020; Wang et al., 2022). Although these parameters provide measurements of droplet size, D V0.5 is usually used in agricultural spray applications to better evaluate the overall size distribution (Sijs et al., 2021).
Table 1.
Correlations of droplet size by spinning disc atomizers.
| Authors | Liquids | Correlations | Modes of formation | Range of variables |
|---|---|---|---|---|
| (Walton and Prewett, 1949) | Water, mercury, methyl salicylate | Direct drop, ligament, and sheet |
|
|
| (Boize and Dombrowski, 1976) | Oils | Direct drop and ligament |
|
|
| (Frost, 1981) | Aqueous solutions of glycerol and proprietary wetting agent | Ligament |
|
|
| (Ahmed and Youssef, 2012) | Water | Ligament |
|
|
| (Wang et al., 2016) | glycerol/water mixture | Ligament |
|
|
| (Kumar and Sarkar, 2019) | Water | Direct drop and ligament |
|
|
| (Prather et al., 2023) | Compritol 888 | Direct drop and ligament |
In agricultural spray applications, droplet size distribution is a critical factor in determining spraying efficacy, directly impacting coverage, drift risk, and deposition and absorption on target plants (Gong et al., 2022b, 2022a). Droplet size distribution is typically presented as histograms and cumulative distribution curves. Boize and Dombrowski (1976) analyzed droplet size distribution across various liquid viscosities, disc speeds, and flow rates using histograms. Frost (1981) illustrated the uniformity of droplet size distribution using cumulative distribution curves. To more accurately evaluate droplet size distribution, researchers have employed the VMD-NMD (Number median diameter, NMD) ratio, coeficient of variation, and relative span factor (RSF) as assessment metrics. Panneton (2002) assessed the uniformity of droplet size distribution generated by spinning cups under various geometric parameters and operating conditions using the VMD-NMD ratio, and explored key influencing factors. Sahoo and Kumar (2021a) systematically studied the size distribution of primary and secondary droplets in the direct droplet mode of a spinning disc and quantified their coefficient of variation. Ru et al. (2024) employed the RSF to investigate the factors influencing droplet size distribution in rotary nozzles. Additionally, the practical and mathematically simple Rosin-Rammler (RR) distribution has been applied to droplet size distribution in rotating packed beds (Xie et al., 2022; Gao et al., 2015) and rotary-bell atomizers (Corbeels et al., 1992). However, compared to these applications, the droplet size distribution of spinning disc atomizers in agricultural sprays is broader and contains more large droplets, warranting further investigation.
This study used ethanol-water solutions as the test liquids and utilized a high-speed camera to analyze the atomization characteristics of a spinning disc atomizer. The research investigated the effects of disc speed, flow rate, and surface tension on the modes of spray formation, droplet size, and size distribution. Based on the experimental results, a dimensionless correlation for droplet size was established, and the statistical distribution of droplet sizes around DV0.5 was analyzed.
2. Materials and methods
2.1. Experimental setup
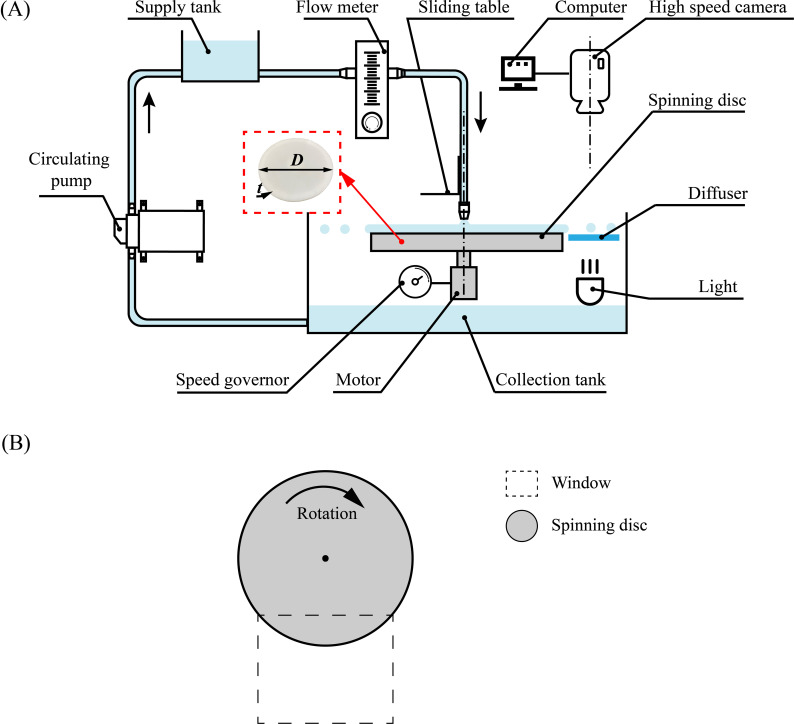
The experimental setup consisted of a spinning disc atomizer, a feed system, and a visualization system ( Figure 1A ). The disc was made of photopolymer resin and polished with fine sandpaper to remove burrs before spraying. The disc had a diameter of 0.06 m and an edge thickness of 0.003 m, and was driven by a stepper motor. The rotational speed was adjusted by a speed governor and varied between 1000 and 4000 r·min-1 in increments of 500 r·min-1. The liquid was delivered to the disc by gravity through a 6 mm diameter circular nozzle from the supply tank. The nozzle was positioned vertically above the disc at a distance of 5 mm from the surface. The liquid volumetric flow rate was adjusted by a flow meter on the supply tube. The droplets were collected in a collection tank and returned to the supply tank by a circulating pump. A high-speed camera (SH6-109, Shenzhen Sincevision Technology Co., Ltd, China) was installed above the disc, with a panel light source positioned below it. Figure 1B presents a top view illustrating the relative positions of the camera window and the disc.
Figure 1.
Schematic diagram of (A) experimental setup for spinning disc atomization and (B) image acquisition windows (top view). The diameter of the disc is D = 0.06 m and the thickness is t = 0.003 m.
2.2. Test liquids
To vary the surface tension of the spray liquid without significantly altering the viscosity, various volume percentages of ethanol-water solutions were used, following Kooij et al. (2018) ( Table 2 ). The surface tension varied with different volume percentages and was measured using the Wilhelmy plate method with a Krüss Force Tensiometer K100. The density was measured using a pycnometer, with each measurement repeated three times. In the experiments, changes in ethanol concentration had minimal effect on viscosity (Yao and Fang, 2013; Kooij et al., 2018). Therefore, the viscosity was approximated to be equal to that of water, which is 0.001 Pa·s.
Table 2.
Surface tension and density of ethanol-water solutions.
| Vol %ethanol | Surface tension (mN·m-1) | Density (kg·m-3) |
|---|---|---|
| 0 | 72.535 ± 0.072 | 997.9 ± 0.4 |
| 9 | 51.764 ± 0.083 | 985.6 ± 1.5 |
| 50 | 29.681 ± 0.025 | 930.1 ± 0.1 |
2.3. Experimental operating conditions
During measurements, the ambient temperature was maintained at approximately 20°C. Five flow rates, three concentrations of ethanol-water solutions, and seven disc speeds were used, resulting in 105 operating points. For capturing images of droplet size measurements, the flow rate varied between 100 and 500 ml·min-1 in increments of 100 ml·min-1. To further capture the space of spray formation modes, additional flow rates (50, 600, and 880 ml·min-1) were tested with a 50% ethanol-water solution. At the operating point, 9500 frames per second were captured at a resolution of 1280 × 1024. To prevent image blurring caused by high-speed rotation, the camera exposure time was set to a low value of 5 μs. Prior to experimentation, images of a 1.5 mm × 1.5 mm checkerboard were captured to determine spatial resolution. Image acquisition commenced approximately 15 seconds after spray initiation, once a stable spray state was achieved. To avoid capturing the same droplet multiple times, images were acquired in intervals: after each pair of images, a 60-frame interval was imposed before capturing the subsequent pair. A minimum of 1088 image pairs were recorded for each operating point. Matlab software (R2019b, MathWorks, Natick, MA, USA) was employed to determine the size and size distribution of droplets in the image. To ensure data reliability, over 2000 droplets were analyzed for each operating point. Each operation was repeated three times, maintaining a coefficient of variation below 7.5%.
2.4. Dimensional analysis
In the study of spinning disc atomization, the relationships among various variables were complex. To simplify the relationships among variables and better understand their effects on D V0.5, dimensional analysis was employed. The density of the surrounding air is negligible compared to the liquid density, thus it is not considered a major variable. Consequently, the D V0.5 of spinning disc atomization depends solely on the liquid’s physical properties (density ρ, viscosity μ, surface tension σ), disc diameter (D), and operating conditions (disc speed ω, flow rate Q). Thus, the studied physical phenomena are summarized in the following relationship:
| (1) |
According to Buckingham’s π theorem, four dimensionless quantities were derived (Buckingham, 1914):
| (2) |
Where: [D V0.5 /D] is defined as dimensionless droplet size, d* ; [D 2 ωρ/μ] is defined as the Reynolds number, Re, representing the ratio of inertial forces to viscous forces; [2μ 2/ρσD] is defined as the Stability number, St, which is proportional to the ratio of viscous to inertial and surface tension forces (Bizjan et al., 2014; Li et al., 2022); [ρQ/Dμ] is defined as the dimensionless flow rate, q.
A widely accepted monomial form was employed for correlating d* as a function of Re, St, and q. The application of the monomial form to Equation 2 gives Equation 3:
| (3) |
2.5. Droplet size distribution functions
To make useful predictions, it is essential to consider the statistical distribution of droplet sizes around the characteristic diameter. Among the various options, the RR distribution function is the most commonly used in droplet breakup studies (Lefebvre and McDonell, 2017; Johansen et al., 2013). The RR distribution is a two-parameter function defined by the characteristic diameter di , corresponding to a specific cumulative volume fraction, and the spread parameter n. The cumulative volume distribution function is:
| (4) |
where ki = -ln(1-Vi ), for Vi = 50%, di represents the median diameter, and ki = -ln(0.5) =0.693. The exponent n indicates a measure of the spread of drop sizes, with higher values of n signifying a more uniform spray distribution.
| (5) |
Rizk and Lefebvre (1985) proposed a Modified Rosin-Rammler (MRR) distribution function to better fit over most of the drop size range, as shown in the following equation:
| (6) |
3. Results and discussion
3.1. Modes of spray formation
3.1.1. Evolution of modes of spray formation
Figure 2 illustrates the transition in modes of spray formation as the flow rate increases, with the spinning disc operating at 1000 r·min-1 and using a constant ethanol-water solution. At a low flow rate of 50 ml·min-1, direct droplet formation is initially observed at the edge of the disc ( Figure 2A ). Driven by centrifugal force, the liquid spreads outward, forming a radial liquid film on the disc surface. Once the liquid film reaches the disc’s edge, it extends a finite distance radially, forming a liquid torus around the edge (Wang et al., 2015; Tan et al., 2019). Rayleigh-Taylor instability, induced by centripetal acceleration, destabilizes the torus, forming one or more bulges (Keshavarz et al., 2020; Eisenklam, 1964). Primary droplets form by elongating the bulge, followed by the creation of smaller satellite droplets from the liquid thread connecting the primary droplet with the bulge (Sahoo and Kumar, 2021a, 2021b). This mode is commonly employed in handheld and aerial rotary atomizers.
Figure 2.
Modes of spray formation of 50% ethanol-water solutions in spinning disc atomization process. (A) Direct droplet formation (50 ml·min-1 and 1000 r·min-1); (B) Droplet-Ligament formation (200 ml·min-1 and 1000 r·min-1); (C) Ligament formation (500 ml·min-1 and 1000 r·min-1); (D) Ligament-Sheet formation (600 ml·min-1 and 1000 r·min-1); (E) Sheet formation (880 ml·min-1 and 1000 r·min-1).
If the disc is oversupplied with liquid, this direct droplet formation mode is disrupted. When the flow rate increases to 200 ml·min-1, a mixture of direct droplet formation and ligament formation is observed ( Figure 2B ). At this stage, ligaments are drawn out from the disc edge, but their distribution is chaotic and disordered. Some droplets still form directly from the disc edge, while others are formed from the breakup of ligaments (Peng et al., 2017). As the flow rate increases to 500 ml·min-1, the mode transitions to ligament formation, with droplets formed directly being completely replaced by those formed from ligaments. Distinct, regular ligaments form with stable, orderly flight trajectories ( Figure 2C ). The ligaments break into droplets due to Plateau–Rayleigh instability, with disturbances of wavelength larger than the ligament diameter causing instability, eventually breaking up the ligaments and forming droplets (Rayleigh, 1879). This mode typically results in the formation of uniform droplets proportional to the disturbance wavelength (Li et al., 2018).
When the flow rate reaches 600 ml·min-1, adjacent ligaments begin to merge, forming a liquid sheet ( Figure 2D ). At a flow rate of 880 ml·min-1, the liquid film on the disc thickens, resulting in fully developed sheet formation ( Figure 2E ). In this mode, the liquid film leaves the disc as a free sheet and then breaks up irregularly (Prather et al., 2023; Li et al., 2018). Although the droplets formed in this mode are less uniform than those from ligament formation, overall, droplets from these three modes are more uniform than those produced by hydraulic nozzles (Salah et al., 2014; Yang et al., 2023).
3.1.2. Space of modes of spray formation
Frost (1981) studied spinning disc atomization using aqueous solutions of glycerol and Agral surfactant. He established transition correlations for spray formation modes through dimensional analysis, see Appendix A .
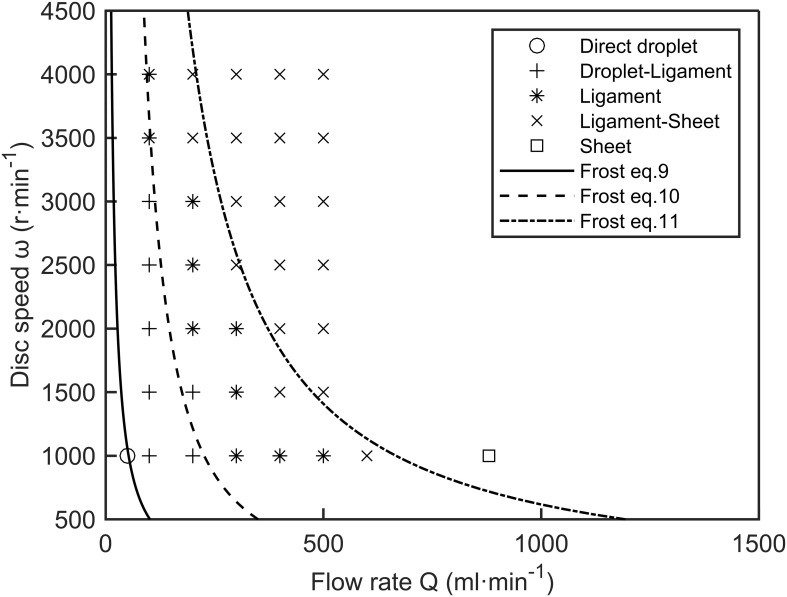
Figure 3 presents the spray formation modes predicted by Frost’s transition correlations (9)-(11), with different symbols indicating various operating points. These modes were identified through visual inspection of recorded images and are depicted by the features shown in Figure 2 . Overall, the predicted spray formation modes closely matched the experimental results, except for ligament formation and ligament-sheet formation. The transition from ligament to sheet formation occurred earlier than predicted, indicating a more abrupt change. This discrepancy may result from subjectivity in defining the mode boundaries or because the equilibrium surface tension used in Frost’s calculations was lower than the actual surface tension. Frost (1981) used aqueous solutions of glycerol and Agral surfactant as test liquids, where the surface tension of the liquid after forming a new surface was equivalent to that of the glycerol solution. Due to the slow molecular dynamics of Agral surfactant, its delivery rate to the droplet surface is insufficient to reach equilibrium, causing the actual surface tension to be higher than the equilibrium surface tension (Kooij et al., 2018; Varghese et al., 2024).
Figure 3.
Space of spray formation modes, as predicted by Frost, overlaid with experimental results of 50% ethanol-water solution. Circles represent direct droplet formation, plus signs represent droplet-ligament formation, asterisks represent ligament formation, crosses represent ligament-sheet formation, and squares represent sheet formation.
3.2. Droplet size analysis and correlations
3.2.1. Correlation for droplet size
D V0.5 represents the droplet diameter at which half of the spray volume consists of droplets smaller than this size, and the other half consists of droplets larger than this size (Xiang et al., 2021). Frost (1981) proposed a correlation to predict the droplet size produced by a spinning disc atomizer, expressed as:
| (7) |
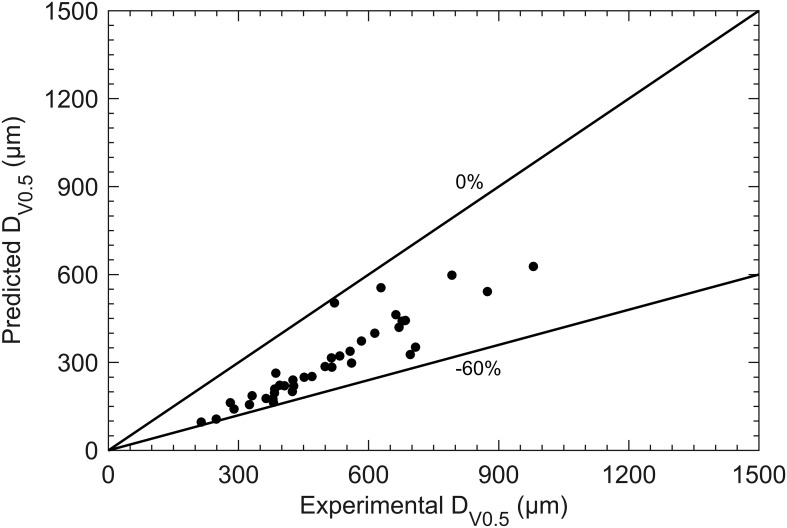
Under the ligament formation mode, Figure 4 shows that the D V0.5 predicted by Frost’s correlation is significantly lower than the experimental results, with an error range from 0% to -60%. This underestimation may be due to the equilibrium surface tension used in Frost’s correlation being lower than the actual surface tension, as previously discussed. Therefore, to improve prediction accuracy, it is preferable to use test liquids with faster molecular dynamics when establishing the correlation.
Figure 4.
Comparison between measurement data (ligament formation mode) and Frost’s correlation (7) predicted data.
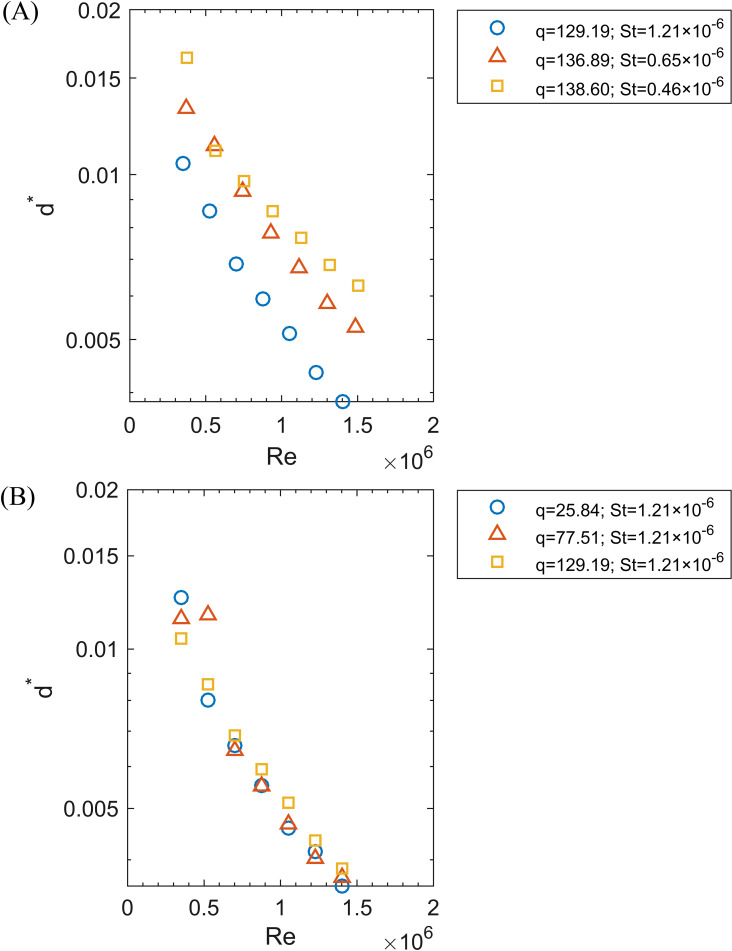
Figure 5 illustrates that as the Re increased from 0.35×106 to 1.50×106, reflecting a rise in disc speed, the d* decreased across all conditions. In Figure 5A , with a nearly constant q ranging from 129.19 to 138.60, an increase in St from 0.46×10-6 to 1.21×10-6, reflecting a decrease in surface tension, led to a reduction in d*. Additionally, at St = 1.21×10-6, Figure 5B demonstrates that the q (from 25.84 to 129.19) associated with flow rate had a negligible effect on d*.
Figure 5.
The relationship between Re (0.35×106 to 1.50×106) and dimensionless droplet size (d*). (A) At a nearly constant q (129.19 to 138.60), St varies from 0.46×10-6 to 1.21×10-6; (B) At St = 1.21×10-6, q varies from 25.84 to 129.19.
The Re values range from 0.35×106 to 1.50×106, St values range from 0.46×10-6 to 1.21×10-6, and q values range from 25.84 to 138.60. The correlation was first fitted according to the Equation 3. However, the p-value for the coefficient γ associated with q is 0.108, being higher than 0.05, indicating this variable is statistically insignificant. This finding aligned with the results shown in Figure 5B . Therefore, q was removed from the dimensionless parameters of interest. By analyzing the coefficients in the Equation 3, a dimensionless droplet size correlation was obtained:
| (8) |
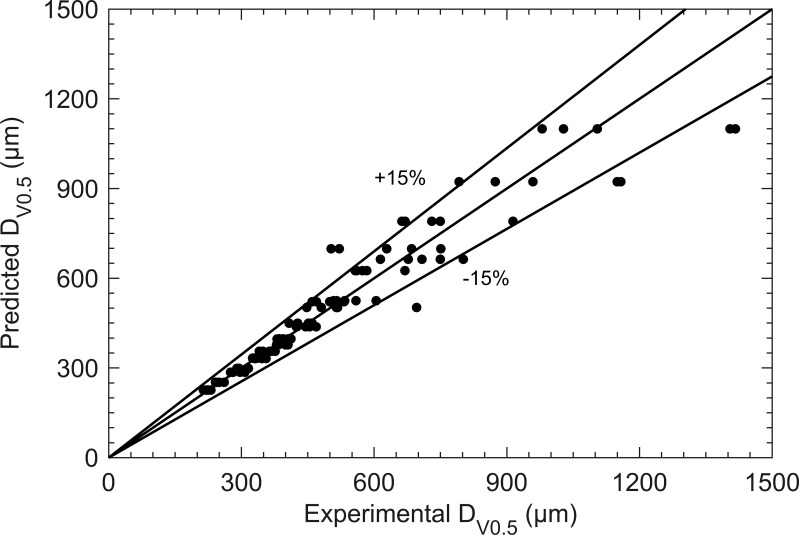
The magnitude of the coefficient associated with each dimensionless number gives some essential guidance on the phenomena’s prevalence in the spinning disc atomization process. The coefficient associated with Re and St in the Equation 8 corroborated the conclusions presented in Figure 5 . Figure 6 presents a comparison of experimental and predicted droplet sizes. The results indicate that the relative error between most experimental and predicted data is within ±15%, demonstrating the high accuracy and reliability of the Equation 8. This consistency also indicates the high regularity of the spinning disc atomization process. However, some larger droplet sizes exceeded the ±15% error range. This discrepancy may result from poor droplet uniformity at these operating points, affecting the measured D V0.5 values.
Figure 6.
Comparison between measurement data and correlation (8) predicted data.
Although this study was conducted in a simplified laboratory environment without considering field complexities such as wind speed, temperature, and humidity, which can indeed influence atomization efficiency and pesticide deposition in practical applications (Lin et al., 2021), the droplet size correlation proposed here holds substantial value for droplet size control. According to the theory of biological optimum droplet size, droplets of specific sizes are more likely to adhere to target organisms, thus enhancing pesticide adhesion and efficacy (Uk, 1977; Chen et al., 2022). Consequently, by adjusting disc speed or liquid surface tension under the guidance of the droplet size correlation, droplets can be generated that align with the biological optimum droplet size, thereby improving pest control effectiveness.
3.2.2. Effect of disc speed on droplet size
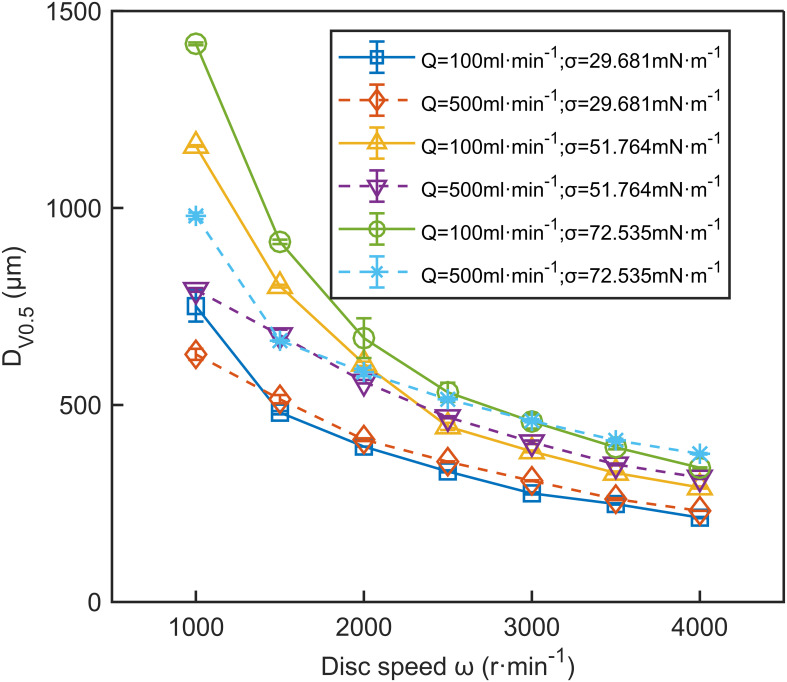
Under all operating conditions, D V0.5 decreased as disc speed increased. Figure 7 illustrates the relationship between disc speed and D V0.5. The blue solid line in Figure 7 indicates that at a flow rate of 100 ml·min-1 and surface tension of 29.681 mN·m-1, D V0.5 decreases from 751 μm to 214 μm as disc speed increases from 1000 r·min-1 to 4000 r·min-1, a total reduction of 537 μm. Between 1000 r·min-1 and 2500 r·min-1, D V0.5 decreased by 420 μm, accounting for 78.2% of the total reduction. This reduction may be due to the increased centrifugal force at higher speeds, which pushes the liquid to the disc edge, thins the liquid film, and forms smaller droplets (Mantripragada and Sarkar, 2017; Ahmed and Youssef, 2012). Moreover, Wu et al. (2018) noted that stronger shear effects within the liquid film and at the liquid-solid and gas-liquid interfaces contribute to smaller droplet sizes. However, as disc speed further increases, the slip velocity between the liquid film and the disc surface increases, slowing the reduction of liquid film thickness, which leads to a plateau in the decrease of D V0.5 at higher disc speeds (Peng et al., 2018a).
Figure 7.
The effect of disc speed on D V0.5. The data in the figure are the average values from three replications. Error bars represent the standard errors of the means.
3.2.3. Effect of flow rate on droplet size
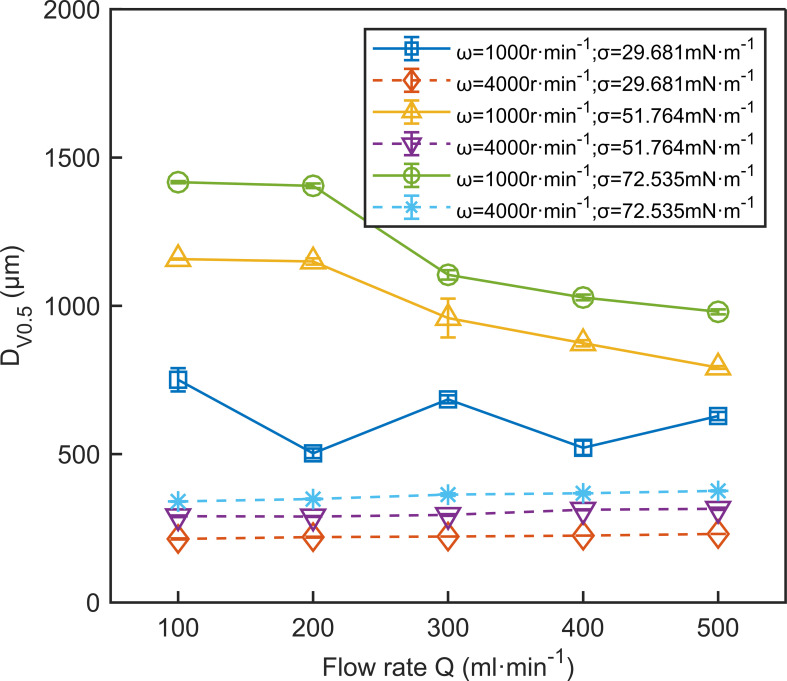
The flow rate influences droplet size, but its effect is less significant than that of disc speed. Figure 8 depicts the effect of flow rate on D V0.5. The solid line in Figure 8 shows that at low disc speeds, D V0.5 heavily depends on the flow rate. At high disc speeds, as indicated by the dashed line, this dependence decreases significantly. At high disc speeds, D V0.5 slightly increases with the rising flow rate. For instance, at a disc speed of 4000 r·min-1, the orange dashed line in Figure 8 shows that as the flow rate increases from 100 ml·min-1 to 500 ml·min-1, D V0.5 increases from 214 μm to 231 μm. This could be due to the spray formation mode showing more liquid ligament characteristics, where long ligaments extend from the disc edge. An increase in flow rate may lead to more liquid ligaments or their elongation, thus accommodating the increased liquid volume (Wang et al., 2016; Peng et al., 2018b). As shown in Figure 7 , when the disc speed exceeds 2500 r·min-1, D V0.5 is primarily controlled by disc speed, and the effect of flow rate becomes negligible. This phenomenon is supported by the study of the Micron ULVA rotary atomizer by Boize and Dombrowski (1976). At low disc speeds, D V0.5 changes significantly with an increasing flow rate. For instance, the goldenrod solid line in Figure 8 shows that at a disc speed of 1000 r·min-1 and a surface tension of 51.764 mN·m-1, increasing the flow rate decreases droplet size. As the flow rate increases from 100 ml·min-1 to 500 ml·min-1, D V0.5 decreases from 1158 μm to 792 μm. This might be due to a change in spray formation mode caused by the increase in flow rate. In the ligament formation mode, the droplet sizes produced are much smaller than those in the direct droplet mode at the same disc speed (Prather et al., 2023).
Figure 8.
The effect of flow rate on D V0.5. The data in the figure are the average values from three replications. Error bars represent the standard errors of the means.
3.2.4. Effect of surface tension on droplet size
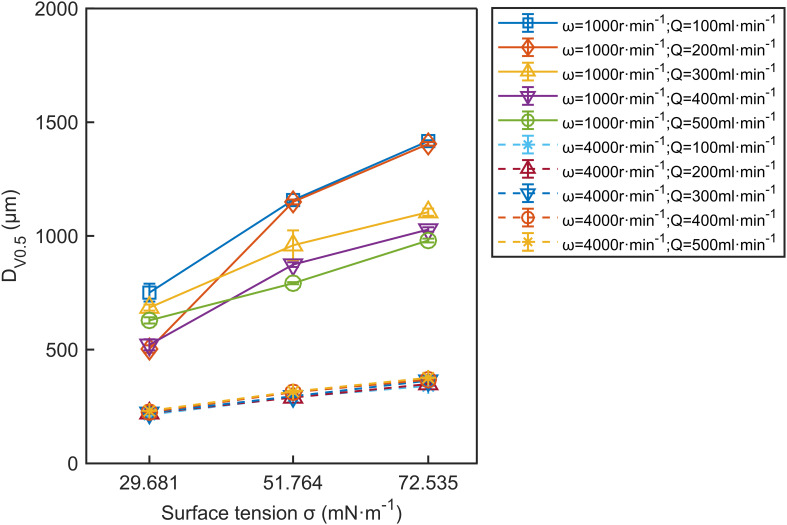
Figure 9 demonstrates the significant impact of surface tension on D V0.5. Lower surface tension results in smaller droplets. The solid lines in Figure 9 indicate that at low disc speeds, D V0.5 is strongly dependent on surface tension. In contrast, the dashed lines show that this dependence decreases significantly at high disc speeds. At high disc speeds, D V0.5 decreases as surface tension decreases. The goldenrod dashed line in Figure 9 shows that at 4000 r·min-1 and a flow rate of 500 ml·min-1, D V0.5 decreases from 376 μm to 231 μm as surface tension drops from 72.535 mN·m-1 to 29.681 mN·m-1. This is likely because surface tension represents the force resisting the formation of new surface areas (Lefebvre and McDonell, 2017). Lower surface tension allows droplets to form more quickly, resulting in smaller droplets (Kooij et al., 2018). At low disc speeds, D V0.5 decreases significantly as surface tension decreases. The blue solid line in Figure 9 shows that at 1000 r·min-1 and a flow rate of 100 ml·min-1, D V0.5 decreases from 1417 μm to 751 μm as surface tension drops from 72.535 mN·m-1 to 29.681 mN·m-1.
Figure 9.
The effect of surface tension on D V0.5. The data in the figure are the average values from three replications. Error bars represent the standard errors of the means.
3.3. Droplet size distribution
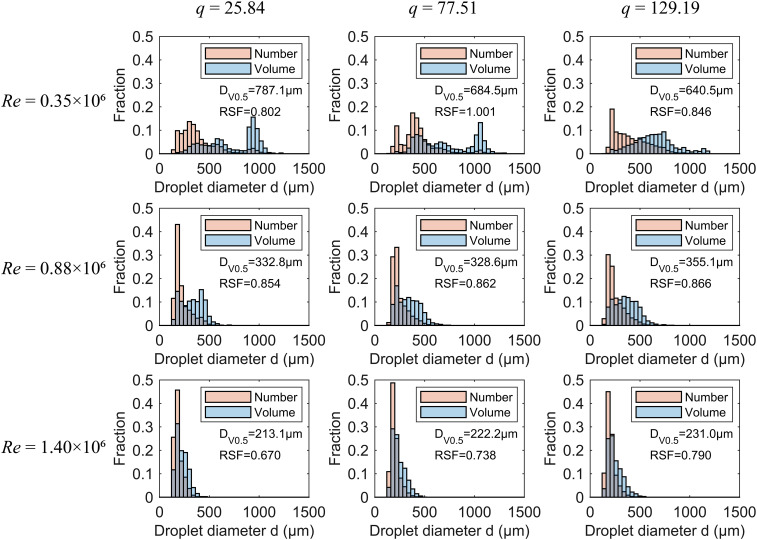
Figure 10 shows the distribution of droplet size in terms of both number and volume as the Re increases from 0.35×106 to 1.40×106, with St of 1.21×10-6, and q varying from 25.84 to 129.19. The results indicate that the droplet size distribution is positively skewed. At low Re and low q, such as Re = 0.35×106 and q of 25.84 and 77.51, small droplets dominate in number but occupy only a small portion of the total volume, with most of the liquid volume concentrated in the few largest droplets. At high Re and high q, the liquid is mainly concentrated in the size range containing the most droplets. This is likely because, at higher Re, the liquid flow is more dominated by inertial forces, leading to flow instabilities (White and Xue, 2021) and, consequently, smaller droplet sizes. Additionally, as Re increases, the droplet size range narrows. For example, at q = 25.84 and Re = 0.35×106, the droplet size range is within 1240 μm. When Re increases to 1.40×106, the size range narrows further, with the maximum droplet size below 480 μm. For a given Re, increasing q from 25.84 to 129.19 slightly expands the droplet size range. Thus, the effect of q on droplet size distribution is less significant than that of Re. The RSF ranging from 0.670 to 1.001 indicates good uniformity in the droplet size distribution from the rotary atomization, as also noted by Zhou et al. (2017). Overall, Re has a greater impact on RSF compared to q. As Re increases, the droplet size distribution becomes more uniform. For example, at q = 77.51, as Re increases from 0.35×106 to 1.40×106, RSF decreases from 1.001 to 0.738. Therefore, to narrow the droplet size range and enhance uniformity, Re should be appropriately increased. Increasing Re can be achieved by enlarging the disc diameter, increasing the disc speed, raising the density, or reducing the viscosity.
Figure 10.
The number and volume fraction distributions for Re of 0.35×106, 0.88×106, and 1.40×106, with St of 1.21×10-6 and q values of 25.84, 77.51, and 129.19. The orange bars represent the number fraction distribution, while the blue bars represent the volume fraction distribution.
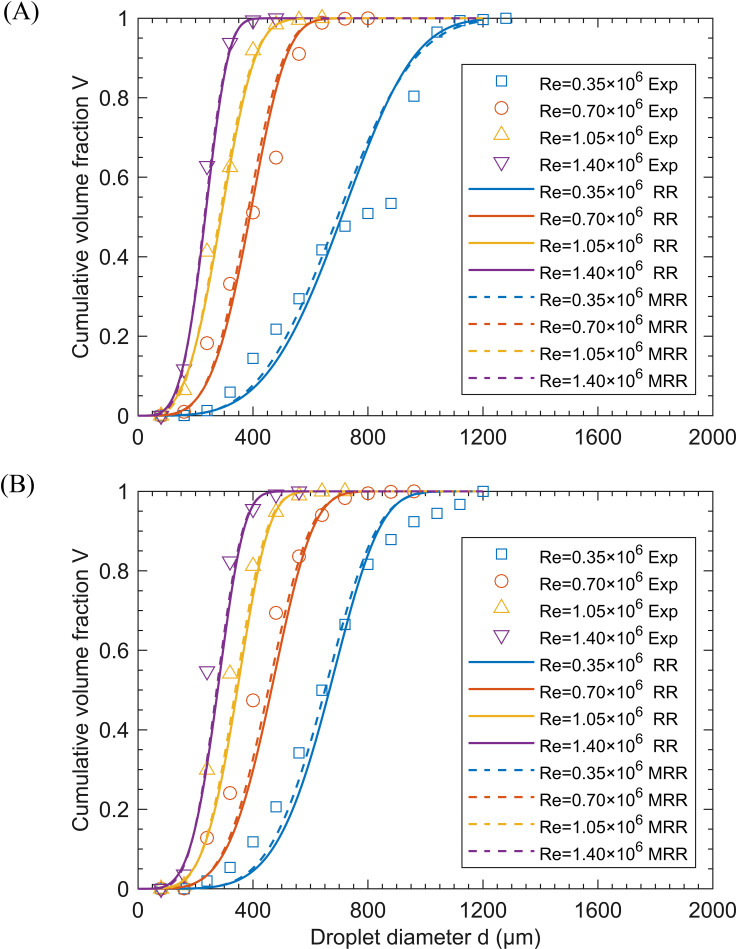
Figure 11 presents the experimental measurements and predicted cumulative volume distributions by Equations 5 and 6 at St = 1.21×10-6, with q values of 25.84 and 129.19, for different Re. As shown in the figure, as Re increases from 0.35×106 to 1.40×106, the curve becomes steeper, indicating a narrower range of droplet size distribution. This observation is consistent with the phenomenon observed in Figure 10 . The curves in Figure 11 , combined with the R² values in Table 3 , indicate that the RR and MRR distributions can accurately describe the droplet size distribution of the spinning disc atomizer, especially at high Re. Additionally, the R² values of the MRR distribution fit are higher compared to the RR distribution. This suggests that the MRR distribution is superior to the RR distribution for spinning disc atomization with larger droplet sizes, consistent with the findings of Rizk and Lefebvre (1985). For most sprays, the RR distribution can be well described with n values between 1.5 and 4 (Lefebvre and McDonell, 2017). In Table 3 , the n values range from 3.5 to 5.3, indicating that the spinning disc atomizer disperses droplets uniformly.
Figure 11.
Cumulative volume fraction of droplets under different Re with St = 1.21×10-6. (A) q = 25.84 and (B) q = 129.19. Experimental data are compared with the fitting curves of the RR distribution (solid line) and the MRR distribution (dashed line).
Table 3.
Parameters of RR and MRR distribution at different Re, with St = 1.21×10-6 and q values of 25.84 and 129.19.
| Distribution | q | Parameter | Re × 106 | |||
|---|---|---|---|---|---|---|
| 0.35 | 0.70 | 1.05 | 1.40 | |||
| n | 4.0 | 4.3 | 3.5 | 4.1 | ||
| RR | 25.84 | D V0.5 | 708.0 | 388.4 | 288.6 | 233.7 |
| R² | 0.948 | 0.948 | 0.977 | 0.984 | ||
| n | 24.5 | 25.1 | 19.9 | 22.7 | ||
| MRR | 25.84 | D V0.5 | 694.3 | 379.2 | 283.9 | 231.3 |
| R² | 0.960 | 0.947 | 0.984 | 0.990 | ||
| n | 5.3 | 4.5 | 4.4 | 4.3 | ||
| RR | 129.19 | D V0.5 | 666.1 | 463.8 | 345.3 | 277.2 |
| R² | 0.868 | 0.889 | 0.926 | 0.923 | ||
| n | 32.9 | 27.2 | 25.8 | 24.2 | ||
| MRR | 129.19 | D V0.5 | 650.4 | 453.0 | 338.9 | 273.5 |
| R² | 0.888 | 0.910 | 0.941 | 0.937 | ||
4. Conclusions
This study used ethanol-water solutions as test liquids to experimentally investigate the atomization characteristics of the spinning disc atomizer using a high-speed camera. The effects of disc speed, flow rate, and surface tension on modes of spray formation, droplet size, and size distribution were analyzed. The main findings are as follows: (1) Under the same disc speed and ethanol-water solution, an increase in flow rate caused the modes of spray formation to transition from direct droplet formation to ligament formation, and finally to sheet formation. Frost’s transition correlations accurately predicted the spray formation modes, with the exception of ligament formation and ligament-sheet formation.
(2) It was found that the droplet sizes predicted by Frost’s correlation were significantly lower than the experimental results, with an error range of 0% to -60%. A correlation between the dimensionless droplet size d* and the dimensionless quantities Re and St was established. The coefficient of determination was R²=0.951, and most predicted droplet sizes deviated from the experimental values by within ±15%. Under experimental conditions, Re and St were important quantities affecting droplet size. Droplet size decreased with increasing Re or St, but was hardly affected by q. Besides, the droplet size decreased with increasing disc speed and decreasing surface tension. At high disc speeds, the dependence of droplet size on flow rate weakened. At low disc speeds, the mode of spray formation affected droplet size, and an increase in flow rate led to a decrease in droplet size.(3) Appropriately increasing Re during the spinning disc atomization process can narrow the droplet size range and improve uniformity. At low Re and low q, small droplets dominate in number but occupy only a small portion of the total volume, with most of the liquid volume concentrated in the few largest droplets. At high Re and high q, the liquid is mainly concentrated in the size range containing the most droplets. The RR and MRR distributions can accurately describe the droplet size distribution, especially at high Re. For larger droplet sizes, the MRR distribution is superior to the RR distribution.
Acknowledgments
The authors express their sincere gratitude to the Qwen 2.5 language model (Alibaba Cloud, Hangzhou, China) for its support in translation and polishing. Subsequently, the authors conducted a comprehensive review and made necessary revisions to ensure the accuracy and clarity of the manuscript. The final content of this publication remains the sole responsibility of the authors.
Appendix A
Table A1.
Frost’s transition correlations and parameter ranges.
| Modes of formation | Transition correlations | Parameter ranges | ||
|---|---|---|---|---|
| Droplet-Ligament |
|
|||
| Ligament |
|
|||
| Ligament-Sheet |
|
Funding Statement
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was made possible by the National Natural Science Foundation of China (No.31971790), a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions(No.PAPD2023-87).
Nomenclature
d, Droplet size, (m); d*, Dimensionless droplet size, (-); D, Disc diameter, (m); D10 , Arithmetic mean diameter, (m); D32 , Sauter mean diameter, (m); DV0.5 (VMD) , Volume median diameter, (m); n, Spread parameter, (-); q, Dimensionless flow rate, (-); Q, Flow rate, (ml·min-1); Re, Reynolds number, (-); St, Stability number, (-); t, Disc thickness, (m); V, Cumulative volume fraction, (-); ω, Disc speed, (r·min-1); μ, Viscosity, (Pa·s); ρ, Density, (kg·m-3); σ, Surface tension, (mN·m-1); MRR, Modified Rosin-Rammler; NMD, Number mean diameter, (m); RR, Rosin-Rammler
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.
Author contributions
JC: Formal analysis, Methodology, Visualization, Writing – original draft, Writing – review & editing. WH: Conceptualization, Formal analysis, Writing – original draft. XD: Writing – review & editing. JL: Conceptualization, Writing – original draft. ZG: Formal analysis, Writing – original draft. BQ: Conceptualization, Funding acquisition, Project administration, Writing – review & editing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
- Ahmed M., Youssef M. S. (2012). Characteristics of mean droplet size produced by spinning disk atomizers. J. Fluids Eng. 134, 071103. doi: 10.1115/1.4006819 [DOI] [Google Scholar]
- ASTM E799-03(2020)e1 . (2020). Standard practice for determining data criteria and processing of liquid drop size analysis. West Conshohocken, PA: ASTM International. doi: 10.1520/E0799-03R20E01 [DOI] [Google Scholar]
- Bizjan B., Širok B., Hočevar M., Orbanić A. (2014). Ligament-type liquid disintegration by a spinning wheel. Chem. Eng. Sci. 116, 172–182. doi: 10.1016/j.ces.2014.04.043 [DOI] [Google Scholar]
- Boize L. M., Dombrowski N. (1976). The atomization characteristics of a spinning disc ultra-low volume applicator. J. Agric. Eng. Res. 21, 87–99. doi: 10.1016/0021-8634(76)90101-3 [DOI] [Google Scholar]
- Buckingham E. (1914). On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 4, 345–376. doi: 10.1103/PhysRev.4.345 [DOI] [Google Scholar]
- Chen C., Li S., Wu X., Wang Y., Kang F. (2022). Analysis of droplet size uniformity and selection of spray parameters based on the biological optimum particle size theory. Environ. Res. 204, 112076. doi: 10.1016/j.envres.2021.112076 [DOI] [PubMed] [Google Scholar]
- Corbeels P. L., Senser D. W., Lefebvre A. H. (1992). Atomization characteristics of a highspeed rotary-bell paint applicator. Atomiz Spr 2, 87–99. doi: 10.1615/AtomizSpr.v2.i2.20 [DOI] [Google Scholar]
- Eisenklam P. (1964). On ligament formation from spinning discs and cups. Chem. Eng. Sci. 19, 693–694. doi: 10.1016/0009-2509(64)85056-9 [DOI] [Google Scholar]
- Feng Y.-H., Zhang Z., Gao J., Feng G.-P., Qiu L., Feng D.-L., et al. (2021). Research status of centrifugal granulation, physical heat recovery and resource utilization of blast furnace slags. J. Analytical Appl. Pyrolysis 157, 105220. doi: 10.1016/J.JAAP.2021.105220 [DOI] [Google Scholar]
- Frost A. R. (1981). Rotary atomization in the ligament formation mode. J. Agric. Eng. Res. 26, 63–78. doi: 10.1016/0021-8634(81)90127-X [DOI] [Google Scholar]
- Gao Z., Ma S., Shi D., Wang J., Bao Y., Cai Z. (2015). Droplet characteristics and behaviors in a high-speed disperser. Chem. Eng. Sci. 126, 329–340. doi: 10.1016/j.ces.2014.12.049 [DOI] [Google Scholar]
- Glahn A., Busam S., Blair M. F., Allard K. L., Wittig S. (2002). Droplet generation by disintegration of oil films at the rim of a rotating disk. J. Eng. Gas Turbines Power 124, 117–124. doi: 10.1115/1.1400753 [DOI] [Google Scholar]
- Gödeke L., Oswald W., Willenbacher N., Ehrhard P. (2021). Dimensional analysis of droplet size and ligament length during high-speed rotary bell atomization. J. Coat Technol. Res. 18, 75–81. doi: 10.1007/s11998-020-00389-2 [DOI] [Google Scholar]
- Gong C., Li D., Kang C. (2022. a). Effect of oil-based emulsion on air bubbles in the spray sheet produced through the air-induction nozzle. Pest Manage. Sci. 78, 5347–5357. doi: 10.1002/ps.7157 [DOI] [PubMed] [Google Scholar]
- Gong C., Li D., Kang C. (2022. b). Visualization of the evolution of bubbles in the spray sheet discharged from the air-induction nozzle. Pest Manage. Sci. 78, 1850–1860. doi: 10.1002/ps.6803 [DOI] [PubMed] [Google Scholar]
- Hinze J. O., Milborn H. (1950). Atomization of liquids by means of a rotating cup. J. Appl. Mechanics 17, 145–153. doi: 10.1115/1.4010093 [DOI] [Google Scholar]
- Johansen Ø., Brandvik P. J., Farooq U. (2013). Droplet breakup in subsea oil releases – Part 2: Predictions of droplet size distributions with and without injection of chemical dispersants. Mar. pollut. Bull. 73, 327–335. doi: 10.1016/j.marpolbul.2013.04.012 [DOI] [PubMed] [Google Scholar]
- Keshavarz B., Houze E. C., Moore J. R., Koerner M. R., McKinley G. H. (2020). Rotary atomization of Newtonian and viscoelastic liquids. Phys. Rev. Fluids 5, 33601. doi: 10.1103/PhysRevFluids.5.033601 [DOI] [Google Scholar]
- Kooij S., Sijs R., Denn M. M., Villermaux E., Bonn D. (2018). What determines the drop size in sprays? Phys. Rev. X 8, 31019. doi: 10.1103/PhysRevX.8.031019 [DOI] [Google Scholar]
- Kumar P., Sarkar S. (2019). Experimental investigation of liquid disintegration on slotted disc in centrifugal atomization process. Chem. Eng. Res. Design 145, 76–84. doi: 10.1016/J.CHERD.2019.02.039 [DOI] [Google Scholar]
- Lefebvre A. H., McDonell V. G. (2017). Atomization and sprays. 2nd (Boca Raton: CRC Press; ). [Google Scholar]
- Li L., Peng L., Zhao W. (2023). Effects of process parameters on the spreading morphology of disc surface and aluminium powder produced by centrifugal atomisation. Powder Metallurgy 66, 1–10. doi: 10.1080/00325899.2023.2223015 [DOI] [Google Scholar]
- Li Y., Sisoev G. M., Shikhmurzaev Y. D. (2018). Spinning disk atomization: Theory of the ligament regime. Phys. Fluids 30, 092101. doi: 10.1063/1.5044429 [DOI] [Google Scholar]
- Li Y.-B., Wen Z.-N., Xu H.-Z., Chu G.-W., Zhang L.-L., Chen J.-F. (2022). Flow pattern transition and liquid element characteristics in a disk-distributor rotating packed bed: A visual study for viscous fluid. Chem. Eng. Sci. 260, 117854. doi: 10.1016/j.ces.2022.117854 [DOI] [Google Scholar]
- Lin J., Ma J., Liu K., Huang X., Xiao L., Ahmed S., et al. (2021). Development and test of an autonomous air-assisted sprayer based on single hanging track for solar greenhouse. Crop Prot. 142, 105502. doi: 10.1016/j.cropro.2020.105502 [DOI] [Google Scholar]
- Liu H., Du Z., Shen Y., Du W., Zhang X. (2024). Development and evaluation of an intelligent multivariable spraying robot for orchards and nurseries. Comput. Electron. Agric. 222, 109056. doi: 10.1016/j.compag.2024.109056 [DOI] [Google Scholar]
- Mantripragada V. T., Kumar K., Kumar P., Sarkar S. (2021). Modeling of powder production during centrifugal atomization. J. Sustain. Metall. 7, 620–629. doi: 10.1007/s40831-021-00370-2 [DOI] [Google Scholar]
- Mantripragada V. T., Sarkar S. (2017). Prediction of drop size from liquid film thickness during rotary disc atomization process. Chem. Eng. Sci. 158, 227–233. doi: 10.1016/j.ces.2016.10.027 [DOI] [Google Scholar]
- Panneton B. (2002). Geometry and performance of a rotary cup atomizer. Appl. Eng. Agric. 18, 435–441. doi: 10.13031/2013.8745 [DOI] [Google Scholar]
- Peng H., Ling X., Wang D., Wang N. (2017). Experimental investigation on transition characteristics of different rotary disk configurations. Ind. Eng. Chem. Res. 56, 11281–11291. doi: 10.1021/acs.iecr.7b02675 [DOI] [Google Scholar]
- Peng H., Shan X., Ling X., Wang D., Li J. (2018. a). Analogue experimental investigation on ligament granulation of molten slag in various rotary disk configurations for waste energy recovery. Results Phys. 11, 385–393. doi: 10.1016/J.RINP.2018.09.037 [DOI] [Google Scholar]
- Peng H., Shan X., Ling X., Wang D., Li J. (2018. b). Ligament-type granulation of molten slag in different rotary disk configurations. Appl. Thermal Eng. 128, 1565–1578. doi: 10.1016/J.APPLTHERMALENG.2017.09.132 [DOI] [Google Scholar]
- Peng H., Wang N., Wang D., Ling X. (2016). Experimental study on the critical characteristics of liquid atomization by a spinning disk. Ind. Eng. Chem. Res. 55, 6175–6185. doi: 10.1021/acs.iecr.6b00401 [DOI] [Google Scholar]
- Prather C. A., Craig C. D., Baumann J. M., Morgen M. M. (2023). Experimental and theoretical investigation of rotary atomization dynamics for control of microparticle size during spray congealing process. Powder Technol. 418, 118278. doi: 10.1016/j.powtec.2023.118278 [DOI] [Google Scholar]
- Rayleigh L. (1879). On the capillary phenomena of jets. Proc. R. Soc Lond. 29, 71–97. doi: 10.1098/rspl.1879.0015 [DOI] [Google Scholar]
- Rizk N. K., Lefebvre A. H. (1985). Drop-size distribution characteristics of spill-return atomizers. J. Propulsion Power 1, 16–22. doi: 10.2514/3.22753 [DOI] [Google Scholar]
- Ru Y., Fang S., Xue J., Hu C., Zhou J. (2024). Experimental study of the influence factors of the droplet size of rotary nozzles during manned helicopter spraying operations. Crop Prot. 177, 106550. doi: 10.1016/j.cropro.2023.106550 [DOI] [Google Scholar]
- Sahoo K., Kumar S. (2021. a). Atomization characteristics of a spinning disc in direct droplet mode. Ind. Eng. Chem. Res. 60, 5665–5673. doi: 10.1021/ACS.IECR.1C00407 [DOI] [Google Scholar]
- Sahoo K., Kumar S. (2021. b). Dynamics of drop release from the edge of a spinning disc. Ind. Eng. Chem. Res. 60, 17174–17182. doi: 10.1021/acs.iecr.1c02172 [DOI] [Google Scholar]
- Sahoo K., Kumar S. (2024). Influence of surface and edge profile of a spinning disc on its atomization characteristics in direct drop mode. Chem. Eng. Sci. 287, 119743. doi: 10.1016/j.ces.2024.119743 [DOI] [Google Scholar]
- Salah S. O. T., Massinon M., Boukhalfa H., Schiffers B., Lebeau F. (2014).Use of rotary atomiser to optimize retention on barley leaves while reducing driftable droplets. In: International advances in pesticide application. Available online at: https://orbi.uliege.be/handle/2268/161491 (Accessed October 21, 2024).
- Sidawi K., Moroz P., Chandra S. (2021). Bell-cup serrations and their effect on atomization in electrostatic rotating bell atomizers. Exp. Fluids 62, 180. doi: 10.1007/s00348-021-03266-9 [DOI] [Google Scholar]
- Sijs R., Kooij S., Bonn D. (2021). How surfactants influence the drop size in sprays from flat fan and hollow cone nozzles. Phys. Fluids 33, 113608. doi: 10.1063/5.0066775 [DOI] [Google Scholar]
- Tan Y., Wang H., Zhu X., Lv Y., He X., Liao Q. (2019). On the centrifugal granulation characteristics by rotary disk: Effect of outer edge structure. Appl. Thermal Eng. 159, 113977. doi: 10.1016/J.APPLTHERMALENG.2019.113977 [DOI] [Google Scholar]
- Uk S. (1977). Tracing insecticide spray droplets by sizes on natural surfaces. The state of the art and its value. Pesticide Sci. 8, 501–509. doi: 10.1002/ps.2780080512 [DOI] [Google Scholar]
- Varghese N., Sykes T. C., Quetzeri-Santiago M. A., Castrejon-Pita A. A., Castrejon-Pita J. R. (2024). Effect of surfactants on the splashing dynamics of drops impacting smooth substrates. Langmuir 40, 8781–8790. doi: 10.1021/acs.langmuir.3c03248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walton W. H., Prewett W. C. (1949). The production of sprays and mists of uniform drop size by means of spinning disc type sprayers. Proc. Phys. Soc B 62, 341–350. doi: 10.1088/0370-1301/62/6/301 [DOI] [Google Scholar]
- Wang D., Ling X., Peng H. (2015). Simulation of ligament mode breakup of molten slag by spinning disk in the dry granulation process. Appl. Thermal Eng. 84, 437–447. doi: 10.1016/j.applthermaleng.2015.03.003 [DOI] [Google Scholar]
- Wang D., Ling X., Peng H., Cui Z., Yang X. (2016). Experimental investigation of ligament formation dynamics of thin viscous liquid film at spinning disk edge. Ind. Eng. Chem. Res. 55, 9267–9275. doi: 10.1021/acs.iecr.6b01428 [DOI] [Google Scholar]
- Wang J., Song Z., Chen R., Yang T., Tian Z. (2022). Experimental study on droplet characteristics of rotating sprinklers with circular nozzles and diffuser. Agriculture-Basel 12, 987. doi: 10.3390/agriculture12070987 [DOI] [Google Scholar]
- White F. M., Xue H. (2021). Fluid mechanics. Ninth (New York, NY: McGraw-Hill; ). [Google Scholar]
- Wu X., Luo Y., Chu G., Xu Y., Sang L., Sun B., et al. (2018). Visual study of liquid flow in a spinning disk reactor with a hydrophobic surface. Ind. Eng. Chem. Res. 57, 7692–7699. doi: 10.1021/acs.iecr.8b00673 [DOI] [Google Scholar]
- Xiang Q., Qureshi W. A., Tunio M. H., Solangi K. A., Xu Z., Lakhiar I. A. (2021). low-pressure drop size distribution characterization of impact sprinkler jet nozzles with and without aeration. Agric. Water Manage. 243, 106458. doi: 10.1016/j.agwat.2020.106458 [DOI] [Google Scholar]
- Xie J., Jia X., Wang D., Li Y., Sun B., Luo Y., et al. (2022). Controllable and high-throughput preparation of microdroplet using an ultra-high speed rotating packed bed. Chin. J. Chem. Eng. 48, 116–124. doi: 10.1016/j.cjche.2021.04.011 [DOI] [Google Scholar]
- Yang Z., Yu J., Duan J., Xu X., Huang G. (2023). Optimization-design and atomization-performance study of aerial dual-atomization centrifugal atomizer. Agriculture 13, 430. doi: 10.3390/agriculture13020430 [DOI] [Google Scholar]
- Yao S., Fang T. (2013). Spray characteristics of a swirl atomiser in trigger sprayers using water–ethanol mixtures. Can. J. Chem. Eng. 91, 1312–1324. doi: 10.1002/cjce.21821 [DOI] [Google Scholar]
- Zhou Q., Xue X., Qin W., Cai C., Zhou L. (2017). Optimization and test for structural parameters of UAV spraying rotary cup atomizer. Int. J. Agric. Biol. Eng. 10, 78–86. doi: 10.25165/ijabe.v10i3.3119 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.