Approximate nearest neighbor graph provides fast and efficient embedding with applications for large-scale biological data

Abstract

Dimension reduction (DR or embedding) algorithms such as t-SNE and UMAP have many applications in big data visualization but remain slow for large datasets. Here, we further improve the UMAP-like algorithms by (i) combining several aspects of t-SNE and UMAP to create a new DR algorithm; (ii) replacing its rate-limiting step, the K-nearest neighbor graph (K-NNG), with a Hierarchical Navigable Small World (HNSW) graph; and (iii) extending the functionality to DNA/RNA sequence data by combining HNSW with locality sensitive hashing algorithms (e.g. MinHash) for distance estimations among sequences. We also provide additional features including computation of local intrinsic dimension and hubness, which can reflect structures and properties of the underlying data that strongly affect the K-NNG accuracy, and thus the quality of the resulting embeddings. Our library, called annembed, is implemented, and fully parallelized in Rust and shows competitive accuracy compared to the popular UMAP-like algorithms. Additionally, we showcase the usefulness and scalability of our library with three real-world examples: visualizing a large-scale microbial genomic database, visualizing single-cell RNA sequencing data and metagenomic contig (or population) binning. Therefore, annembed can facilitate DR for several tasks for biological data analysis where distance computation is expensive or when there are millions to billions of data points to process.

Introduction

Dimension reduction (DR or embedding) is an important statistical technique for big data visualization and pre-processing. There are two categories of algorithms for dimension reduction: those that seek to preserve pairwise distance for all data points such as principal component analysis (PCA) and multi-dimensional scaling (MDS), and those that seek to only preserve local distance over global distance such as t-distributed Stochastic Neighbor Embedding (t-SNE) (1) and Uniform Manifold Approximation and Projection (UMAP) (2). The latter approach is also called non-linear dimension reduction. Recently, non-linear dimension reduction has also been applied to computational biology such as in single-cell RNA sequencing analysis (3,4) and genome binning from metagenomes (5). UMAP was designed to preserve more the global structure with superior run time performance compared to t-SNE and has no computational restrictions on the number of embedding dimensions, despite recent work showing that the type of initial embedding (a less accurate embedding like diffusion map) determines whether or not UMAP can preserve better global structure (6).

For both UMAP and t-SNE, the very first step is to find the closest neighbors for each point in the dataset. The approximate nearest neighbor algorithm used in UMAP and LargeVis, i.e. the NN-Descent and random projection tree, is typically the rate-limiting step especially for high complexity data (2,7). NN-Descent (8) and similar algorithms (9) are popular K-nearest neighbor graph (K-NNG) algorithms based on the neighborhood propagation concept for improving accuracy when finding close neighbors. NN-Descent has been used as the default in UMAP to construct K-NNG with an empirical time complexity O (N^1.14) (no asymptotic complexity analysis available). This empirical time complexity relies heavily on the properties and distributions of the input data (8). Recently, a new concept, called local intrinsic dimension (LID) has been proposed to describe the properties and distributions of the data, which is a measure of the minimum number of variables needed to represent the data without significant loss of information (10). It has been shown that NN-Descent recall is very low for datasets with LID > 20 because the algorithm produces a large amount of incorrect K-nearest neighbors in such cases (8,11). Several fast algorithms for building K-NNG have been proposed with time complexity O(d*n^t) (1 < t < 2, normally 1.2–1.4) or O(d*N*log(N)) (where d is the number of dimensions) that try to circumvent this and related limitations (9,12). Another key aspect of LID or, more generally, the curse of dimensionality, is the hubness concept. A large LID dataset is easier to contain hubs and LID is correlated with hubness. Hubness is defined as the tendency of intrinsically high-dimensional data to contain hubs—points with high in-degrees in the K-NNG or skewness of the distribution of neighbors of points (or clusters, for simplicity). Application of NN-Descent algorithm on datasets with large LID or hubness is problematic (e.g., offers less accurate representations of the true neighbors) (11), despite some recent efforts to alleviate this problem by using -for example- a much larger K (13). Many real-world datasets such as microbial genome collections and single-cell RNA sequencing datasets are distributed highly unevenly, and thus have high LID or contain many hubs.

Finding nearest neighbors based on the graph structure, for example, K-NNG or small world graph, has been extensively studied in the past several years (12,14), and it has been shown that Hierarchical Navigable Small World (HNSW) graphs show high performance and recall in various benchmark studies compared to K-NNG or tree-based nearest neighbor search (NNS) search algorithms due to their hierarchy and small world property (15,16). Some modified K-NNG algorithms, such as K-NNG + graph diversification and diversified proximity graph (DPG), were shown to have similar performance compare to HNSW, even for high LID datasets (17). However, as the LID of the dataset increases further, the accuracy of HNSW and other graph-based methods is compromised if maintaining the same search speed, or the speed will decrease if maintaining the same accuracy/recall, at least for Euclidean distance (18). Therefore, dimension reduction tools should also consider the LID and hubness of the dataset to be embedded for further evaluation of how reliable the NNS step can be. For large datasets, for example, N > 10⁵, N^1.14 (empirical time complexity of K-graph) will be much more expensive than N*log(N) (HNSW complexity), especially when the distance computation is expensive since the total time will represent the number of computations (time complexity) multiplied by the time for each computation. It has been shown that HNSW, compared to other graph-based NNS approaches such as NSG (navigating spread-out graph), can alleviate the hubness issue by limiting the maximum degree for each point (19). t-SNE combines an attractive force between neighboring pairs of points with a repulsive force between all points (1), and mathematical analysis has shown that changing the balance between the attractive and the repulsive forces in t-SNE using the exaggeration parameter yields a spectrum of embeddings characterized by a simple trade-off: stronger attraction can better represent continuous manifold structures, while stronger repulsion can better represent discrete cluster structures (20). UMAP, on the other hand, employs a negative sampling optimization, which strongly lowers the effective repulsion, leading to more clustered embeddings/structures (2). However, if we initiate the nearest neighbors from HNSW graphs (instead of initializing from a list of neighbors for each node), it is possible to adopt a different edge and/or node sampling strategy to have similar effects to the attractive and the repulsive forces using the same loss function as in t-SNE or UMAP. That is, to take into account edge weight distribution and node neighbor density in a HNSW-like graph, which can provide less skewed representation of the data.

Both UMAP and t-SNE have been widely applied to single-cell RNA sequencing studies since they are much faster than PCA for larger number of single cells profiles. For datasets of genomic sequences, alignment-based distance is more appropriate. However, visualizing genomic information or metagenomic binning/clustering (e.g., DNA or RNA sequences clustered by species/genome) using UMAP has several challenges: (i) Genomic/sequence distance estimation is expensive via traditional methods such as Average Nucleotide Identity (ANI) and Average Amino Acid Identity (AAI) (for genomes) or alignment (alignment is possible for short sequences but not whole genomes) (21). (ii) The large number of genomes in public database (e.g., 10 million for the viral genome database) exacerbate the problem. K-mer hashing based on probabilistic data structures (e.g., MinHash) are much faster than traditional ANI/AAI to calculate genomic distance while maintaining ANI/AAI accuracy (22), and thus could help with challenge (ii) above. Specifically, Jaccard index estimated by MinHash algorithms can be transformed into ANI/AAI/identity via the Mash equation: 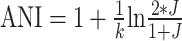(22). However, these algorithms have not been combined with UMAP-like fast dimension reduction technique to further accelerate dimension reduction and visualize genomic datasets.

Visualizing microbial genomic databases such as the GTDB (Genome Taxonomy DataBase) (23), IMG/VR (Integrated Microbial Genomes/Virus) (24) and MyCOcosm (fungal genome database) (25) in an efficient and quick manner can help microbiologists and taxonomists examining, for example, genome affiliation information relative to other genomes, and provide easy-to-catch mislabeled information about overall database composition, hierarchy and evolutionary space of the grouped organisms. In this study, by combining MinHash-like algorithms and HNSW, we created a new data structure to build genomic HNSW graph database (26). Subsequently, we applied UMAP-like algorithms to the HNSW graph to produce a non-linear dimension reduction algorithm to visualize microbial genome databases. Our benchmarking results show that the non-linear dimension reduction achieved by annembed can be very fast while maintaining high accuracy, especially for datasets with billions or more data points, for which current tools were either too slow or failed. We also added the estimation of hubness and calculation of LID of the data to be embedded. Application of annembed to microbial genome database showed that it can visualize millions of genomes in several hours, much faster than UMAP. The idea of visualization genomic database based on MinHash and annembed can be applied to any other sequence database (e.g., nucleotide or amino acid sequences, 18S/ITS gene databases) provided that an appropriate distance metric is available. Accordingly, the annembed library is also applied in GSearch (26), a computer program that uses annembed as a dependency to perform HNSW graph building for millions of microbial genomes, in addition to standalone implementations. Annembed is written in Rust and it is fully parallelized for almost all steps.

Materials and methods

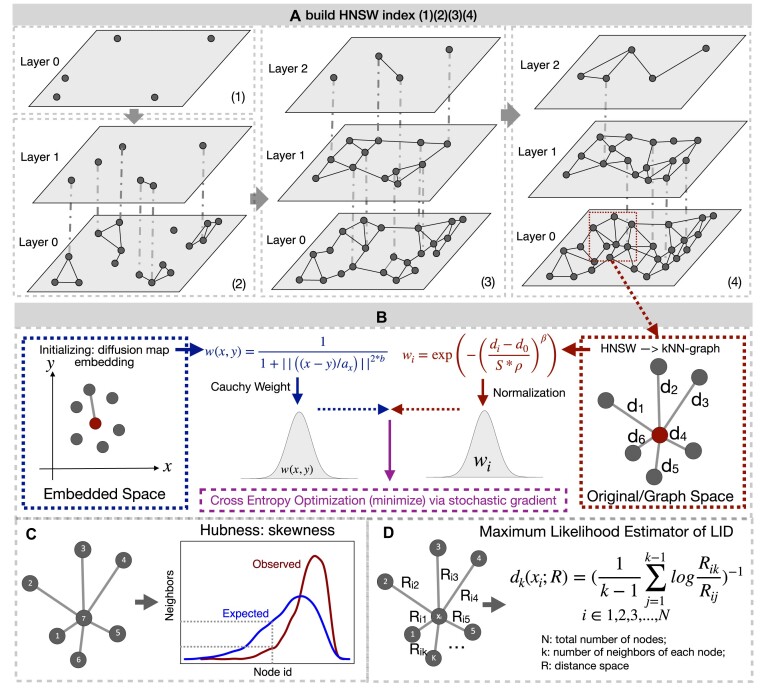
Overall, our implementation is a mixture of HNSW with previously described embedding algorithms such as UMAP and t-SNE. First, the graph is initialized by the HNSW algorithm (Figure 1A), which provides sub-sampling of the data to be embedded by considering only less densely occupied layers (i.e., the upper layers). This corresponds generally to a subsampling of 2–4% of the total data but the small fraction of data used is not problematic as the distance between the points left out by the subsampling and their nearest sampled neighbor are known in the complete HWSW graph. The HNSW structure thus enables an iterative, hierarchical initialization of the embedding by considering an increasing number of layers (until layer 0). The preliminary graph built for the embedding uses an exponential function of distances to neighbor nodes (as in UMAP) but keeps a probability normalization constraint with respect to neighbors (as in t-SNE) (Figure 1B). It is then possible to modulate the initial edge weight by considering a power of the distance function to neighbors or increase/decrease the impact of the local density of points around each node (similar to the repulsive force). We initialized embedded space by a diffusion map (27), instead of Laplacian Eigenmap as in UMAP, the former can be considered as a generalization of the latter, but the order of the top eigenvector is reversed. To minimize divergence between embedded pace and initial distribution probability, we also used a cross-entropy optimization of this initial layout but considered the initial local density estimates of each point in the embedded space when computing the Cauchy weight of an embedded edge as in UMAP (Figure 1B). The corresponding ‘perplexity’ distribution (the same as in t-SNE, a parameter to balance attention between local and global aspects of the data as in t-SNE) is estimated on the fly. We provide a tentative assessment of the continuity/quality of the embedding by varying the perplexity to help selecting among varying results between runs for a given dataset. Quality of embedding is defined as the correct neighbors of node in the embedded space found when comparing with the original data. During this process, LID and hubness were also estimated based on the HNSW graph (Figure 1C and D).

Figure 1.

Overall description of annembed algorithm’s key steps and functionalities. (A) Build a HNSW graph from scratch by gradually adding points in the database in a recursive way with random initialization. When maximum number of allowed neighbors in the graph is reached (M) for each existing point, a representative will be chosen as new point in new layers (above) by collapsing the neighbors. Finding neighbors for a newly added point involves inserting the point into the graph by searching for its neighbors and updating the graph when the M is reached (i.e., newly added point could also be neighbors of other existing points). (B) UMAP-like embedding algorithm by combining t-SNE (edge sampling in left panel) and UMAP (cross entropy optimization). For edge sampling, 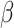is set to 1 to result in exponential weights similar to Umap. 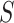is to modulate 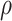and is set to 0.5, while 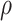is the spacial scale factor and is also set to 1. After normalization the weight will represent a probability distribution. For initial embedding, to define the weight of the edge, we initialize 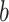as 1 and 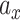is a coefficient related to the scale coefficient in the original space around x computed as follows: for each point x we have its k neighbors y_i [i = 1,2,3…k], for each of its neighbors y_i we get its first neighbor distance d_i. We then average all these distances, that give an idea of distance around a point, a scale_x, 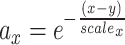. (C) Hubness estimation by evaluating the skewness of neighbor distributions of observed neighbors of each node and the expected ones. (D) LID estimation via the maximum likelihood method. We use Euclidean distance (metric) for R by default, and this can be changed according to user specific case (e.g., Jaccard distance, a metric, can be used for genomes).

Hierarchical navigable small world graph (HNSW)

We use HNSW instead of K-graph to find nearest neighbors for each data point in the dataset to be embedded. Specifically, HNSW incrementally builds a multi-layer structure consisting of a hierarchical set of proximity graphs (layers) for nested subsets of the stored elements, which maintains the small world property (Figure 1A). Then, through smart neighbor selection heuristics, inserting and searching the query elements in the multi-layer proximity graphs can be very fast (due to small world property for each layer and hierarchical structure) while preserving high accuracy/recall. Inserting new data into existing graph is essentially a search process but all neighbor list in the graph will need to be updated once the insertion is completed. We reimplemented the hnswlib library in Rust and benchmark it against standard datasets. Note that HNSW requires metric distance as input for maintaining neighborhood diversity. Build the graph takes O(N*log(N)) time. We then extract K-neighbors of each point/node in the graph database for embedding as mentioned above. Note that building HNSW is the same to search a new element against graph database except that for building, all elements in database need to be searched in a recursively way, during which database graph needs to be updated after search is done.

Embedding and quality of the embedding

Embedding is done by the following steps: (i) Initialized from the HNSW graph, an exponential function of distances to neighbor nodes for all nodes is calculated while keeping a probability normalization constraint with respect to node’s neighbors (Figure 1B, left panel). (ii) Adjust the initial edge weight by considering a power of the distance function to neighbors (increase or decrease local density of points around each node) for the embedded space (Figure 1B, right panel). (iii) Minimize divergence between embedded and initial distribution probability, then perform cross entropy optimization of this initial layout but consider the initial local density estimates of each point when computing the Cauchy weight of an embedded edge (Figure 1B). (iv) Estimate the corresponding ‘perplexity’ distribution. (v) Varying perplexity and evaluate the quality of embeddings as described in the next paragraph. Annembed uses the same loss function for divergence minimization or cross entropy optimization as in UMAP but not the actual implementation in UMAP-python package (28) (see Supplementary Methods).

To quantify the quality of the embedding, annembed tries to assess how well the neighborhood of points in original and in embedded space may match, also called KNN accuracy. Specifically, in each neighborhood of a point taken as center in the initial space, annembed searches the point that has minimal distance to the center of the corresponding neighborhood in the embedded space. The quantiles on this distance are then calculated, which provides a continuity/quality of the embedding, for example, if it is close to 1 then the embedding quality is better.

Hubness

NN-Descent (implemented in UMAP), as the key algorithm to build the K-graph, performs poorly for datasets with large hubness; that is, a skewed distribution of point neighbors is obtained by this algorithm when compared to an expectation (some points might have many more neighbors than others) (8). Annembed estimates the skewness of point neighbors of the dataset by comparing the neighbors actually observed with the expected neighbors (e.g., average number of neighbors) as suggested previously (11) (Figure 1C). At the very beginning, annembed initializes the hubness values of each dataset point to zero. Then, during algorithm execution (K-NN is extracted from HNSW), annembed increases the hubness value of a given point by one if that point is added to the nearest neighbor list of some other point, and analogously, decreases the hubness value by one if the point is removed from some nearest neighbor list.

Local intrinsic dimension

To estimate the LID of a dataset to be embedded, we implemented the maximum likelihood estimation (MLE) (18) because MLE has a significantly smaller standard deviation compared to other methods and converges faster to the mean as the number of samples increases (10). Note that, by default, MLE needs >20 neighbors around each point to have reliable estimation. Specifically, the MLE method to estimate the LID is based on the constant density assumption in a small neighborhood and the Poisson process to model the random sampling in this neighborhood (29). The MLE method provides a way to estimate LID for point x_i in its k-neighborhood (k ≥ 20). That is, let R be the distance metric (e.g., Euclidean) and R_ij ∈ R be the distance between point x_i and x_j under this metric, the MLE of the LID around point x_i, with the distance metric of R, is computed as: 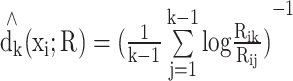, where the summation is over the k-nearest neighbors of point x. Note that 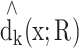is point-specific, dependent on k and the distance metric R (Figure 1D). LID therefore uniquely characterizes the sub-manifolds around x. We then average LID across all points in the database.

MinHash-like algorithms to approximate ANI/AAI estimates of genomic similarity (or distance)

Mash is fast and efficient in computing genomic distance via the MinHash algorithm and correlates well with the golden standard of genomic distance measurement, the ANI, after transformation based on the evolution model (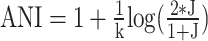) (22). However, MinHash does not consider the kmer abundance (or multiplicity) or the total kmer count of a given genome, which affect the estimation of real genomic distance of genomes (30,31). To consider multiplicity of k-mers, traditional hashing algorithms are not a good choice since they all assume unique set element (k-mer). New MinHash algorithms have been recently designed to solve the above-mentioned problem by utilizing weighted kmers (32–35). Still, those weighted MinHash algorithms do not solve the problem of different set size for genomes of different length, resulting often in biased estimations of weighted Jaccard index (30,31). Accordingly, new locality sensitive hashing algorithms (P-MinHash) for weighted set and different set size were proposed to estimate weighted and normalized (to account for set size difference) Jaccard like index J_p (33,36,37). Among these algorithms, ProbMinHash takes into account both weighted set (k-mer multiplicity) and total set size (total k-mer count), with further computational optimizations (33). More importantly, ProbMinHash provides a proper metric distance and can be used as input to HNSW. We also implemented a more accurate, but slightly slower, MinHash-like algorithm called SuperMinHash (also a locality sensitive hashing) for simple Jaccard index estimation (38). SetSketch, a MinHash-like algorithm but representing a combination of MinHash and HyperLogLog, is also implemented for its space efficiency (e.g., requires less memory and disk space to store the sketched genomic information) (39). Another faster and also as accurate as traditional MinHash (as in Mash) algorithm called One Permutation MinHash with Optimal Densification (Densified Minhash) is also implemented (40). We have recently shown that ProbMinHash/SuperMinHash/SetSketch/Densified MinHash distances correlate well with ANI and AAI, for ANI values in the range of 80–100% and AAI values in the range of 55–95%, after transformation (26). To approximate sequence alignment identity (contiguous sequence like 16S rRNA gene sequence) via MinHash-like algorithms, the Order MinHash (41) was implemented, which allows fast and accurate approximate computation of edit distance for gene sequences (not whole genomes) based on k-mers set distance but not alignment. Order MinHash is similar to that of ProbMinHash except that the weight is the position of the k-mer and that normalization by total k-mer count is not necessary.

Annembed for metagenomic contig binning

We replace t-SNE or PCA in manual binners (e.g., mmgenome2) with annembed for visualizing contig kmer composition versus coverage of the contig. Order MinHash was used to approximate the Edits distance among contigs but not Euclidean distance of k-mer composition as in the original mmgenome2 since the Edit distance is closer to alignment-based distance of contigs than Euclidean distance of k-mer composition (41).

Benchmark and analysis platforms

All analysis and tests were performed on a 24-thread Linux running RHEL v7.9, with an Intel(R) Xeon(R) Gold 6226 CPU, except for testing scalability, where a 128-thread Linux running RHEL v7.9, with an AMD EPYC 7713 processor CPU (2 64-thread NUMA node) was used instead.

Results

Speed and visualization accuracy for standard benchmark datasets

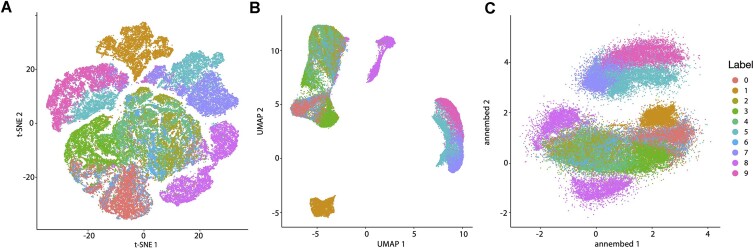
We benchmarked annembed with the standard datasets, MNIST-fashion and MNIST-digits (1). Annembed performed as good as UMAP (Figure 2 and Supplementary Figure S1) with similar running time using 24 threads (Table 1). We then tested the NNS performance (i.e., NNS) with a large dataset called HIGGS (∼11 million data points, 20 dimensions, generated by the Large Hadron Collider) for UMAP (NN-Descent for NNS or Annoy for NNS in another package, called UWOT) and annembed. NNS step took ∼18 min for annembed for this dataset while it cannot finish for UMAP (NN-Descent) within 1 h (Table 1). For the steps after NNS (e.g., minimize the loss function and produce embeddings), our implementation took ∼43 min using 24 threads while UMAP and UWOT took >8 h (not parallelized) (Table 1). UWOT (ANNOY) NNS step is much faster than UMAP (NN-Descent) because of the ANNOY library: NNS step in ANNOY took ∼22 min, similar to that of annembed. However, it has been shown that as K increases (default K is 15 for both UMAP and UWOT), for example, K = 200 or above, to maintain the same accuracy, for example, 95% or higher recall, ANNOY is much slower than HNSW according to Aumüller et al. (15). Both UMAP and annembed use cross-entropy optimization, which is the speed limiting step for UMAP-python and UWOT implementations. However, annembed fully parallelizes this step and allows multi-threaded cross entropy optimization, which is ∼10× times faster than UMAP for the same step when embedding (Table 1). Despite being fast due to parallelization, memory consumption also increases. Therefore, we next compared annembed with Trimap, a highly memory efficient algorithm for non-linear DR, for embedding the HIGGS dataset. Annembed consumed a maximum memory of 58 GB with 24 threads while Trimap only consumed a maximum memory of 15 GB (Supplementary Table S1) but had similar running time with UMAP, and thus was much slower than annembed. We also showed that annembed scaled well with the number of threads for datasets with millions of data points (Supplementary Figure S3). The visualization of embeddings for the HIGGS dataset followed a similar pattern to that observed with smaller datasets (Supplementary Figure S8A and B), with UMAP’s visualization being more compact.

Figure 2.

Dimension reduction for t-SNE (A), UMAP (B) and annembed (C) for the MNIST-fashion dataset. Color indicates different labels (see key to the right, and text for further details). For t-SNE, UMAP and annembed, k = 15 (number of neighbors) was used.

Table 1.

Running time of UMAP and annembed for three benchmark datasets using 24 threads on Linux running RHEL v7.9, with an Intel(R) Xeon(R) Gold 6226 CPU. Running time is average values of three independent runs

Dataset	Number of data points	Dimension	K	UMAP (NN-Descent) NNSa	UMAP (annoy) NNS	UMAP embeddingb	Annembed (HNSW) NNS	Annembed (embedding)
MNIST FASHION	70 000	748	15	2 min and 25 s	44 s	1 min and 1s	27.4s	14.2 s
SIFT_1M	1 M	128	15	53 min and 20 s	14 min and 35s	53 min and 22s	9 min and 21s	16 min and 13s
HIGGS	11 M	20	15	>8 h	1 h and 45 min	>24 h	43 min	1 h and 56 min

^aNN-descent algorithm is not parallelized, and it can only use 1 thread.

^bembedding step in both python version UMAP and R version UWOT are not parallelized.

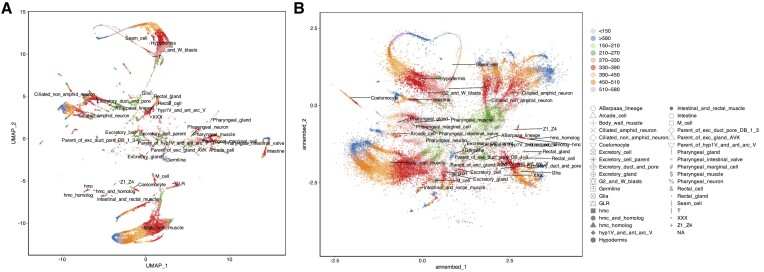
We also compare annembed with UMAP using a standard single-cell RNA sequencing dataset called PBMCs (peripheral blood mononuclear cells) (3) and another single-cell RNA dataset from Caenorhabditis elegans (42). Annembed was able to clearly separate each cell type of the blood cells from each other and showed consistent visualization with UMAP, despite its less compacted visualization (Supplementary Figure S2a and b). The C. elegans dataset also showed consistent results, for example, each cell type and sampling time point were identified consistently between annembed and UMAP (Figure 3A and B). Additionally, the user is able to adjust the spatial scale parameter (via the –scale option) in annembed to allow more or less clustered visualization of the embeddings. The default value was used for the above comparison.

Figure 3.

UMAP (A) and annembed (B) visualization for C. elegans single-cell RNA sequencing dataset. Color indicates time (h) since experiment started while shape indicates cell type used. Major cell types are also labeled in the plot, anchored by the centroid of each cell type. High-resolution figures can be found in the Supplementary Materials. Note the high overall similarity in separating the single cell based on their type between the two methods.

Quality and other metrics of the embeddings

We evaluated the quality of the embeddings by increasing perplexity (a parameter to balance attention between local and global aspects of the data). As perplexity quantile increased from 0.05 to 0.99, the quality of embeddings (matched neighbors in embedded space out of 15 true neighbors in the original space) increased from ∼4 to ∼6 for the FASHION dataset until quantile equaled 0.5, but did not increase any further after this point (Supplementary Table S3). The quality of the embeddings (matched neighbors in embedded space out of 25 true neighbors in the original space) for the GTDB genome database (see section below) increased from 12 to 15 as quantile increases from 0.05 to 0.5, but did not further after this point (Supplementary Table S3). Therefore, annembed can automatically determine the best perplexity to use for different datasets to maximum the quality of embeddings based on this strategy.

LID estimated for the MNIST-digits (22.97) and MNIST-fashion (17.5) datasets by annembed were very similar to those reported previously (i.e., 19.6 and 15.3, respectively). Hubness estimations by annembed of the two standard datasets (i.e., 2.46 and 1.01, respectively) were also close to the original study that proposed the hubness concept (Supplementary Table S2). The hubness of HIGGS dataset is ∼1000 since the number of data points is much larger than the MNIST-fashion dataset.

Visualization of large-scale microbial genome database and identification of inconsistent taxonomic assignments

We combined MinHash-like algorithms for genomic distance estimation (i.e., ANI) with HNSW to produce nearest neighbor information for a database of genomes, that is to build the HNSW graph using MinHash estimated Jaccard index as a proxy of ANI. For GTDB database (prokaryotic genome database clustered at 95% ANI species threshold), tohnsw (subcommand in GSearch to build HNSW graph) took ∼43 min to build the graph and subsequently, the embedding step took 4 min. For NCBI/RefSeq prokaryotic genome database (∼318 K genomes), tohnsw step took ∼2.3 h while the embedding step took 13.2 min. Tohnsw step to build HNSW graph database for ∼3 million virus species took ∼16.4 h while the embedding step took ∼33 min on a 24-thread node. Notably, for traditional dimension reduction methods such as PCA, MDS requires calculation of all versus all pairwise genomic distances among all database genomes, which is impractical for several real-world genome databases such as those mentioned above (N² comparisons; N = number of database genomes) even with fast algorithms such as MinHash (22). Hubness estimation was 153.2 at the amino acid level embedding of the GTDB database and 181.2 for NCBI/RefSeq, consistent with the prediction that biological databases are highly clustered (MNIST-Fashion has a much smaller hubness estimation, see Supplementary Tables S2, with a similar total number of data points), for which the performance of the NN-Descent algorithm degrades significantly.

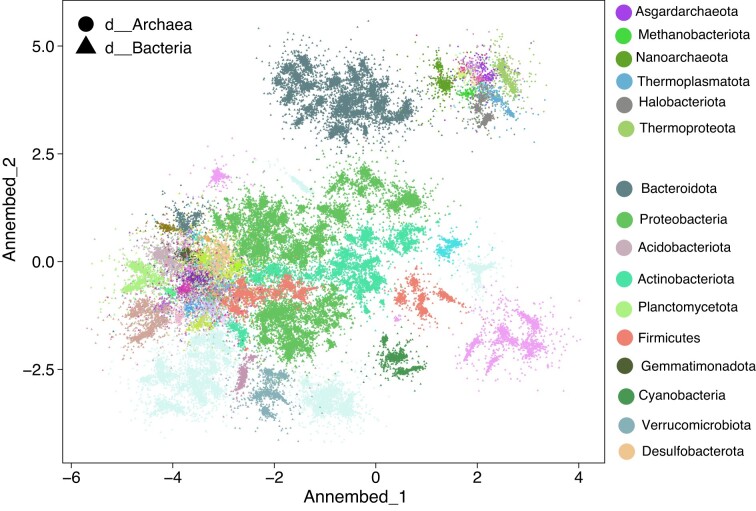
We also visualized the embedding result for GTDB, which is a taxonomically well described (labeled) genome database based on the Relative Evolutionary Distance (RED) values and the ANI concept. The majority of the genome hubs visualized by annembed grouped according to their taxonomy affiliations, for example, genomes within the same phylum affiliation grouped in the same cluster in the two dimension annembed plot (Figure 4). However, we also observed that several genomes such as members of the Firmicutes (red) and Desulfobacterota (orange) phyla clustered within the Proteobacteria (green) cluster, which indicates that the former genomes might have been mislabeled taxonomically. To further confirm this, we extracted the corresponding Firmicutes and Desulfobacterota genomes (three genomes as an example) and calculate universal gene AAI (accurate for phylum level genomic distance/identity) between them and their most similar proteobacterial genome. We found that those genomes had better universal gene AAI values to the most similar genome in Proteobacteria than to the most similar genome in their originally assigned phylum (57.3%, 49.5% and 54.9% versus 50.4%, 42.0% and 47.2%, respectively), consistent with mislabeling of these genomes.

Figure 4.

Annembed plot of the 65 703 genomes available in GTDB (v207) using ProbMinHash as the genomic distance metric. Different shapes indicate bacterial or archaeal genomes (key on top). Major phyla of bacteria and archaea are colored differently (key to the right). ProbMinHash distance was based on predicted gene amino acid sequences of the genomes. Performing this analysis at the nucleotide level is not possible because a pre-clustered database at 95% ANI level is too sparse, and thus many genomes do not have reliable genomic distance estimation to meet the minimum requirement of 15 nearest neighbor genomes in UMAP and annembed.

We then also visualized detailed embedding results at a lower taxonomic rank (e.g. class and order levels) and found that annembed can also clearly differentiate between different classes and orders within the Proteobacteria phylum (Supplementary Figure S4). Therefore, the annembed results can be used to quickly assess the level of consistency in the taxonomy information available in the public databases. Similar results in terms of separating major clades or clusters to those reported above for the NCBI/RefSeq prokaryotic genome database (Supplementary Figure S5) were obtained for the viral and the fungal genome databases (Supplementary Figures S6 and S7).

Visualizing large-scale 16S marker gene databases for prokaryotes

We combined Order MinHash with annembed, a LSH algorithm to approximate edit distance or alignment identity, to visualize the 16S ribosomal RNA (16S) gene database, i.e., SILVA and RDP (average sequence length of an individual 16S gene is ∼1500 bp). Order MinHash is a special case of the weighted MinHash, where weight is the position of the k-mer in a sequence. Running annembed with Order Minhash as the underlying sequence distance estimation for 1.6 million 16S sequences available in the SILVA database took <5 min with 24 threads (NNS step took 33 min). No clear separation of the 16S sequences was observed at the phylum or class levels (Supplementary Figures S9 and S10). These results might indicate that several sequences are taxonomically mislabeled in SILVA, which is consistent with the previous analysis that reported that 20% of the taxonomy annotations in SILVA are incorrect based on examination of the guiding tree (43). We also ran the same analysis for the RDP v18 16S sequences for comparison. We observed a clear separation by taxonomic annotation at phylum, class and even genus level (Supplementary Figures S11 and S12). The RDP sequences are taxonomically identified based on curated isolate and type strain sequences or environmental sequences predicted by the RDP Naive Bayesian Classifier (44), which is thought to be a highly accurate classification system (45), consistent with the results presented here.

Metagenomic binning via embedding contig kmer composition to assist in curating metagenome assembled genomes

t-SNE and UMAP have been applied to manually bin metagenomic contigs for obtaining metagenome assembled genomes (MAGs) (e.g., graphs of contig k-mer coverage plotted versus k-mer composition) because the dimension reduction based on PCA requires all versus all distance computation, which is computationally expensive for thousands of contigs. Here, we replace the t-SNE and UMAP modules in the metagenomic binning software mmgenome (46) with annembed (LSH for Euclidean distance as contig distance estimation method). Annembed with LSH reduced the computation time to calculate contig profile differences and dimension reduction by 3–5 times for a medium size metagenomic assembly (10 000 contigs, average contig length ∼8000 bp) (Supplementary Table S4). For even larger metagenomic assemblies (e.g., millions of contigs), annembed will be even faster than t-SNE or UMAP. Annembed provided similar results to UMAP when manually checking the resulting MAGs from these two approaches (Supplementary Figure S13). However, we noticed that there were several MAGs that annembed was not able to resolve whether their corresponding contigs were from the same or separated clusters (or MAGs), but UMAP was able to distinguish these contigs. We suspect that this is due to the loss function in UMAP that puts more weight on the repulsive force, leading to more compact visualization despite the fact that the actual distance or similarity of these contigs was not preserved in UMAP (see also below for more discussion on the loss function). Therefore, the additional clusters observed by UMAP may not necessarily represent reliable information for curating MAGs.

Discussion

In this study, we improved the speed and capabilities of UMAP and UMAP-like algorithms by applying a fast and efficient graph-based neighbor search algorithm and providing additional parameter estimations for large scale non-linear dimension reduction tasks. We showed that in real world datasets with millions of data points, our annembed library is at least 8–10 times faster while maintaining similar visualization accuracy due to the application of both HNSW and the parallelized embedding step. Annembed will be even faster as the data set size grows because of the O(N*log(N)) complexity of the HNSW graph database build step. The LID and hubness estimation annembed provide offer more information about the structure and distribution of the data than common UMAP implementations, especially for high dimensional data, and thus should help to perform better NNS. For example, when LID is very high, for example, several thousands, users should avoid using the NN-Descent algorithm and use annembed instead. These two features were not included in neither the original NN-Descent nor the UMAP implementation (2), but several recent studies have shown that they affect the accuracy in finding the true neighbor for each data point (11,13) and the performance of NNS finding step (18), a limiting step for UMAP-like or t-SNE-like algorithms. The MLE estimation of LID we implemented is widely applied (47,48) but also requires at least 20 neighbors to be accurate. This is not a problem for testing datasets, but it could be a substantial challenge for microbial genome datasets because there are not often enough closely enough related genomes to use in distance estimations, especially when embedding genomes at the nucleotide level. The amino acid level could be used instead (e.g., AAI) in such cases to partially alleviate this problem, although there might still be several deep-branching genomes with <20 relatives at this level. Alternatively, the newly proposed LID estimation algorithm that does not require at least 20 neighbors (49) could be employed.

The speed of NNS finding is especially important for real world applications like genome analysis because total running time is related to the number of comparisons for the entire database and the time required for a single pair comparison. With a O(N*log(N)) complexity, HNSW is orders of magnitude faster than NN-Descent for large datasets, and it is fully parallelizable in Rust, a difficult task for other languages like C/C++ due to clear data race when multiple threads work on the same graph data structure. Also, for large datasets, memory requirement for NNS finding is a key limiting step for both NN-Descent and Annoy. Here, we implemented a memory map in the hnswlib-rs library for running datasets with billions of data points without large memory requirements. More importantly, we provide an option in the hnswlib-rs library to allow users to implement their own distance estimation. This provided an opportunity to combined MinHash-like probabilistic data structures with HNSW since set similarity, for example, Jaccard index, can be estimated in a sub-linear running time using the mentioned probabilistic data structures. We provide several MinHash-like implementations as part of the distance estimation step, aiming at accuracy or space- (disk-) efficiency purposes, depending on the computing resources available to the users.

The application of annembed to visualization of genome database based on the idea mentioned above can be useful in checking, for example, the label accuracy of taxonomically annotated databases. For instance, we found that many genomes labeled as phylum Desulfobacterota are actually Alphaproteobacteria (a class of the Proteobacteria phylum) (Figure 4). Further, very high hubness for genome datasets (GTDB or RefSeq) indicates either discontinuous evolutionary space (51) or biased sequencing/sampling efforts towards existing genome sequences (52). Thus, application of annembed to these datasets can identify under-sampled lineages for further genomic characterization in the future. More broadly, the abovementioned MinHash-like algorithms combined with HNSW for annembed can also work for text/document files or websites, not only genomes, providing an opportunity to run dimension reduction and visualization for various types of datasets.

It is also worth mentioning that in addition to the Jaccard index and Edit distance (string matching), Euclidean distance, Hamming distance and Angular distance can be all computed via hashing-like algorithms (53–56), making the idea of combining them with HNSW even more attractive for various applications that required these other distance metrics (e.g., strings, vectors and text/document). We provide an example in which we used order MinHash to approximate Edit distance for DNA sequences of single genes and visualize them via annembed. This application helps to identify mislabeled taxonomic information in widely used reference sequence databases such as the 16S rRNA gene databases. However, when distance of interest is not a metric distance, HNSW is limited in terms of accuracy, and UMAP based on NN-Descent will be a better option (NN-Descent works for non-metric distance) until recent efforts to generalize HNSW to non-metric distances become more robust (57). Nonetheless, it should be mentioned that the problems of NN-Descent discussed above for non-metric distance is not clear because LID and hubness are studied under the metric distance assumption (47).

New metagenomic binning algorithms such as Rosella (58), BinArena (59) and mmgenomes (46) rely on UMAP or t-SNE for visualization of contigs after obtaining the composition of contigs (e.g., Euclidean distance based on k-mer composition of contigs) to avoid all versus all distance computation. Subsequently, contigs are typically manually binned via human intuition or clustering algorithms. As the metagenomic sequencing capabilities are growing, it is possible to have millions of contigs assembled and subsequently binned. Annembed can be 10 times faster or more in these cases than UMAP or t-SNE. Further, the distance among contigs in the embedded space of UMAP or t-SNE is not the actual genomic distance in the original Euclidean space consisting of k-mers, unlike annembed, because the global distance is not well preserved in non-linear dimension reduction algorithms, which represents another advantage of annembed.

It has to be noted, however, that the HNSW graph building is still not so fast for large datasets due to O(N*(log(n))) despite being one of the fastest nearest neighbor graph building algorithms. Recently, a new algorithm combining LSH with HNSW or approximate proximity graph (APG) structure has been proposed to further accelerate graph database building step from O(N*log(N)) to O(N*c), where c is a constant independent of N. LSH-APG builds an APG via consecutively inserting points based on their nearest neighbor relationship with an efficient and accurate LSH-based search strategy (60). A high-quality entry point selection technique and an LSH-based pruning condition are developed to accelerate index construction and query processing by reducing the number of points to be accessed during the search for each query. Annembed could be further accelerated by adopting this idea when building HNSW graph to improve on the O(N*log(N)) run time limit.

Finally, the new UMAP-like algorithm SpaceMAP, which considers a restricted k-nearest neighborhood (part of the manifold, thus ignoring the hierarchical structure) by matching the ‘capacity’ of high- and low-dimensional/embedded space via analytical transformation of distances adjusted by LID (48), has solved the widely accepted problem that there are geometrical distortions between two spaces (original space and embedded space). It might be useful to change the optimization procedure of UMAP to decrease the repulsion per edge by considering non-KNN graph edges in loss function (28) as implemented in SpaceMAP, and we will explore it in future work. There isn’t an explicit index available to evaluate how well overall annembed, or another library, preserves the global structure compare to the original space. TriMap and SpaceMAP attempt to implement such an index to calculate how well the global structure is preserved by using PCA as the standard (50). We will explore these ideas in the future to provide a similar index of how well the global structure is preserved.

We believe that annembed library will accelerate large scale (e.g., millions or even billions) non-linear dimension reduction tasks, where alternative methods are limited by the NNS step and downstream single-threaded computations. Annembed can also help visualizing large-scale genomic databases or single-cell RNA sequencing studies and advance scientific discoveries related to cancer and other diseases.

Data availability

Annembed library can be found via Zenodo (https://doi.org/10.5281/zenodo.13761466) or Github (https://github.com/jean-pierreBoth/annembed). GSearch (visualizing genomes) can be found via Zenodo (https://doi.org/10.5281/zenodo.10543594) or Github (https://github.com/jean-pierreBoth/gsearch). R and python scripts for reproducing all the analysis can be found via Zenodo (https://doi.org/10.5281/zenodo.13763717) or Github (https://github.com/jianshu93/annembed_analysis).

Supplementary data

Supplementary Data are available at NARGAB Online.

Funding

This work was supported, in part, by the US National Science Foundation [1759831, 2129823 to K.T.K.].

Conflict of interest statement. None declared.