Spall: accurate and robust unveiling cellular landscapes from spatially resolved transcriptomics data using a decomposition network

Abstract

Recent developments in spatially resolved transcriptomics (SRT) enable the characterization of spatial structures for different tissues. Many decomposition methods have been proposed to depict the cellular distribution within tissues. However, existing computational methods struggle to balance spatial continuity in cell distribution with the preservation of cell-specific characteristics. To address this, we propose Spall, a novel decomposition network that integrates scRNA-seq data with SRT data to accurately infer cell type proportions. Spall introduced the GATv2 module, featuring a flexible dynamic attention mechanism to capture relationships between spots. This improves the identification of cellular distribution patterns in spatial analysis. Additionally, Spall incorporates skip connections to address the loss of cell-specific information, thereby enhancing the prediction capability for rare cell types. Experimental results show that Spall outperforms the state-of-the-art methods in reconstructing cell distribution patterns on multiple datasets. Notably, Spall reveals tumor heterogeneity in human pancreatic ductal adenocarcinoma samples and delineates complex tissue structures, such as the laminar organization of the mouse cerebral cortex and the mouse cerebellum. These findings highlight the ability of Spall to provide reliable low-dimensional embeddings for downstream analyses, offering new opportunities for deciphering tissue structures.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12859-024-06003-1.

Introduction

Complex tissues are composed of various types of cells, each playing its particular roles [1]. Understanding the relationship between spatial location and gene expression patterns of cells is crucial for exploring biological processes such as tissue growth, development, and disease [2, 3]. The emergence of spatially resolved transcriptomics (SRT) enables the simultaneous measurement of gene expression and spatial location of cells, overcoming the limitations of scRNA-seq in capturing spatial context. Currently, SRT technologies are mainly classified into two categories, which are imaging-based and sequencing-based. Imaging-based techniques, such as MERFISH [4] and seqFISH [5], enable high-resolution measurements at the cellular or subcellular level. However, these methods detect only hundreds to thousands of transcripts in a slice. In contrast, sequencing-based methods, like Slide-seq [6] and 10 × Visium, allow for whole-transcriptome measurements. Nevertheless, they capture gene expression in small areas (i.e., spots) that typically contain multiple cells, resulting in lower resolution compared to imaging-based techniques.

In SRT data analysis, a key challenge is to decipher the functions of cells or tissues through the expression patterns of genes. Although imaging-based techniques can achieve high resolution at the cellular or subcellular level, they are limited by the number of detectable genes [7]. This limitation hinders a deep exploration of the molecular mechanisms underlying biological functions. On the other hand, sequencing-based methods can provide comprehensive transcriptome information but often fall short in achieving cellular-level resolution. Therefore, there is an urgent need for a computational approach that can accurately identify the spatial distribution patterns of different cells from sequencing-based SRT data.

Fortunately, single-cell sequencing technologies provide a solid data foundation for understanding cell-type-specific gene expression patterns [8]. It also serves as a reliable reference for inferring the spatial localization of different cell types. The method of combining scRNA-seq with sequencing-based SRT data to infer spatial distribution patterns of cells is known as expression profile decomposition. Currently, several decomposition methods tailored to SRT data have been proposed. For example, methods such as Stride [9], SPOTlight [10], and CARD [11] are based on non-negative least squares (NNLS) or non-negative matrix factorization (NMF) algorithms. These algorithms have been widely applied in the decomposition of bulk gene expression data [12]. However, although the spots in sequencing-based SRT data contain multiple cells, their data are more similar to single-cell data. To address this, methods like RCTD [2], Cell2location [13], and Stereoscope [14] utilizing probabilistic models based on Poisson or negative binomial distributions are proposed. With the advancement of deep learning technologies, approaches that considers spatial relationships have also been developed, like DSTG [15] and GTAD [16]. These methods are based on graph neural networks (GNNs) and generate pseudo-spots using single-cell data for model training.

Current methods have partially addressed the estimation of spatial distribution patterns of different cells in SRT data. However, they still fall short in balancing the changes in cellular proportion distribution patterns across space with cell-specific characteristics, leading to unstable decomposition results. For instance, while methods such as NMF and NNLS provide stable results when processing bulk gene expression data, their performance on the SRT data with sparsity is less effective. Additionally, many probability-based methods, despite addressing data sparsity, often overlook the spatial relationships between spots. This oversight results in a lack of spatial continuity in the distribution patterns of predicted cellular proportions. Furthermore, deep learning approaches using GNNs can cause over-smoothing during the message passing and aggregation process, which diminishes the specificity of cellular expression within a spot, especially for rare cell types that are dispersed across the space.

To fill this gap, we propose a decomposition network for sequencing-based SRT data, named Spall. Spall works in a transductive learning manner, employing geometric deep learning to integrate gene expression and location information of spots. To precisely capture subtle changes in the spatial distribution patterns of cellular proportions, we introduced the graph attention network version 2 (GATv2) module [17]. Compared to the static attention in the GAT module, GATv2 has more flexible attention mechanism, thereby enhancing the robustness and continuity of the predicted proportions. Moreover, to overcome the loss of cell-specific information during message passing in GNNs, we incorporated a skip-connection into Spall. This allows the network to retain the original expression information of spots, enhancing its capability to capture cell-specific information. By conducting analyses of Spall using samples from multiple platforms, we found that Spall surpasses existing state-of-the-art (SOTA) methods in terms of robustness and accuracy. In human pancreatic ductal adenocarcinoma sample, Spall accurately captured tumor heterogeneity and identified rare cell populations, underscoring its capability to discover important cellular subtypes. Further, we successfully delineated the laminar structures of the mouse cerebral cortex and the consistency between cell distribution and layer structure in mouse cerebellum, highlighting that the cell proportions inferred by Spall can serve as interpretable low-dimensional embeddings for downstream analyses. Lastly, applying Spall to the mouse olfactory bulb slice obtained via Stereo-seq revealed consistent relationships between tissue spatial domains, cell distribution patterns, and gene expression.

Results

Overview of spall

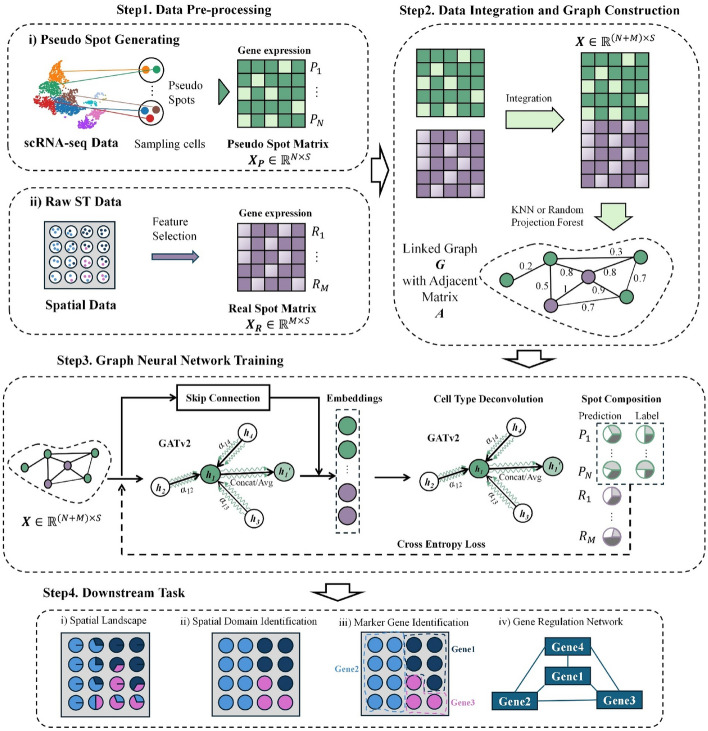
The workflow of Spall can be divided into four steps (Fig. 1). Assuming there are $M$ real spots in SRT dataset and Spall will estimate the proportions of $K$ different cell types. First, Spall takes scRNA-seq data to generate $N$ pseudo spots ($P_N$). Specifically, Spall randomly samples 2–10 cells from scRNA-seq data and the aggregation of expression levels from these cells are regarded as expression profile of the pseudo spot. For these pseudo spots, the cellular component proportions ${\mathit{F}}_{\mathit{P}}\in {\mathbb{R}}^{N\times K}$ are known and used as the ground truth during the training stage. Next, Spall adopts K-Nearest Neighbors (KNN) or Random Projection Forest to construct the linked graph (denote as $\mathit{G}$) using expression profiles ${\mathit{X}}_{\mathit{R}}\in {\mathbb{R}}^{M\times S}$ and ${\mathit{X}}_{\mathit{P}}\in {\mathbb{R}}^{N\times S}$ from real spots ($R_M$) and pseudo spots respectively, where $S$ is the number of feature genes selected during the pre-processing stage. Then, the adjacency matrix $\mathit{A}\in {\mathbb{R}}^{(N+M)\times (N+M)}$ and node attribute matrix $\mathit{X}\in {\mathbb{R}}^{(N+M)\times S}$ of graph $\mathit{G}$ is passed to the decomposition module. This module consists of two GATv2 layers. The first GATv2 layer integrates information from neighboring spots, while the second layer performs cellular component decomposition. To prevent the loss of cell-specific information due to over-smoothing, we introduced skip connections. We trained the model using $\mathit{X}$ and ${\mathit{F}}_{\mathit{P}}$ in a transductive learning manner. Finally, the cellular proportions of real spots ${\mathit{F}}_{\mathit{R}}\in {\mathbb{R}}^{M\times K}$ are predicted and used for downstream analysis such as spatial domain identification. A more detailed introduction can be found in Methods.

Fig. 1.

The workflow of Spall. (1) Data preprocessing: generation of pseudo spots from reference scRNA-seq data and feature selection both on original SRT and scRNA-seq data. (2) Integration and graph construction: data integration followed by graph construction using either KNN or Random Projection Forest, depending on dataset scale. (3) Graph neural network training: implementation of two GATv2 modules and one skip connection module. (4) Downstream analysis: application of decomposition results estimated by Spall to various analytical tasks

Dataset

We employed five synthetic datasets and four real datasets to validate the effectiveness of Spall. For the simulation data, we followed the previous research to generate four SRT datasets with different cell distribution patterns [18]. Additionally, we incorporated a synthetic dataset generated using STARmap data [19]. Furthermore, we tested Spall on real SRT data from four different platforms shown in Table 1.

Table 1.

Datasets used in this study

Platform	Tissue	Section	#Spots	#Genes
10 × Visium	Mouse brain (Sagittal-Anterior)	N/A	2696	31,053
Slide-seq V2	Mouse cerebellum	N/A	18,460	23,096
ST	Human pancreatic ductal adenocarcinomas	GSM3036911	428	19,738
Stereo-seq	Mouse olfactory bulb	S1	107,416	26,145

Benchmark

To systematically evaluate the performance of Spall, we generated synthetic SRT data and compared the decomposition results from 10 SOTA algorithms. Inspired by the previous work [18], we selected scRNA-seq data from the mouse primary visual cortex (EL4, EL5, EL6, and endothelial cells) provided by the Allen Institute to construct synthetic SRT data with different spatial patterns. We generated two spatial patterns, layered and block patterns (the details of the generation process can be found in the Data Availability section). In the layered pattern, the entire region is divided into four layered subregions, each mainly composed of one cell type. The block pattern, on the other hand, divides the region into block-like subregions. For these two spatial patterns, we also created different modes of cell type transitions. The first transition mode is jump transition, where there is no intermediate transition zone between subregions, resulting in a clear boundary. The other transition mode introduces a buffer zone between subregions, where cell types gradually shift from one side of the subregion to the other. This transition is referred to as a gradient transition. Additionally, to more accurately simulate sequencing-based SRT data, we generated synthetic data based on the data with single-cell resolution using STARmap [19, 20]. Specifically, we defined an artificial square region on the STARmap data. As the former study, we set the side length of approximately 51.5 $\mu m$[20]. All cells within this square region were considered as a pseudo-spot. In total, we obtained 581 pseudo-spots, with each pseudo-spot containing between 1 and 12 cells, including up to 6 different cell types. We used scRNA-seq data from the mouse primary visual cortex provided by the Allen Institute as a reference. For comparison, we adopted 10 SOTA algorithms (Table 2), including Cell2location [13], RCTD [2], SpatialDecon [21], CARD [11], Tangram [22], DestVI [23], NMFreg [24], SPOTLight [10], STRIDE [9], and GTAD [16].

Table 2.

Benchmarking methods

Method	Characteristics	Refs
Cell2location	Bayesian model	[13]
RCTD	Maximum-likelihood estimation (MLE)	[2]
SpatialDecon	Log-normal regression	[21]
CARD	NMF	[11]
Tangram	Correlation	[22]
DestVI	Conditional deep generative model	[23]
NMFreg	NMF	[24]
SPOTLight	Seeded NMF regression & topic model	[10]
STRIDE	NNLS	[9]
GTAD	Graph Neural Network	[16]

We adopted Jensen–Shannon divergence (JSD), root mean square error (RMSE) as well as Pearson’s correlation coefficient (PCC) to quantify the performance of each method (see Benchmarking Metrics). JSD is utilized to assess the overall similarity between the predicted and actual cell type distributions. RMSE is used for quantifying the magnitude of prediction errors, offering an absolute measure of the discrepancy between predicted and actual cell type proportions. PCC is employed to capture the linear relationship between predicted and true distributions, reflecting the method’s ability to accurately rank the relative abundances of different cell types. For one spot, a higher PCC or lower RMSE/JSD value indicates better prediction accuracy.

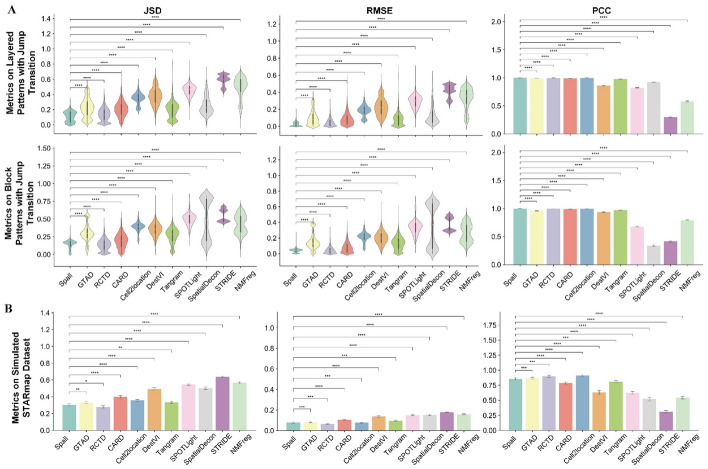
We compared the performance of different methods on these datasets. Figure 2A illustrates the decomposition results on datasets generated using scRNA-seq data. As shown in Fig. 2A, Spall and RCTD significantly outperform other decomposition methods. On simulated data with jump transition patterns (the first two rows of Fig. 2A), Spall slightly outperforms RCTD. In these datasets, Spall ranks first in JSD, RMSE, and PCC, followed closely by GATD, Tangram, CARD, and Cell2location. For simulated data with gradient transition patterns (Supplementary Figure S1), Spall and RCTD perform comparably, while GATD, CARD, Cell2location, and Tangram show lower performance in terms of JSD and RMSE. For the simulated samples generated using STARmap data (Fig. 2B), both Spall and RCTD exhibit the best performance. These two methods show a significant lead especially both in terms of JSD and RMSE, indicating that the predicted results from these methods not only closely match the distribution of true data but also achieve the lowest prediction error. Furthermore, Spall shows more stable performance on the data with noise interference compared to RCTD (Supplementary Figure S2).

Fig. 2.

Results of different methods using synthetic datasets. A The performance across two spatial patterns with jump transition generated using scRNA-seq. In the violin plots: the center line represents the median; box limits denote the upper and lower quartiles; whiskers extend to 1.5 × the interquartile range. In the bar plot: bar height represents the mean value, with whiskers indicating the mean ± 95% confidence intervals; The experiments were repeated for 10 times. B Results on STARmap-based in silico dataset. Bar plots display the mean values, with whiskers indicating the mean ± 95% confidence intervals. (p-values indicate the significance level under one-sided t-test for positive correlation. ****p ≤ 0.0001, ***p ≤ 0.001, **p ≤ 0.01, *p ≤ 0.05, ⋅p ≤ 0.1, ns: p > 0.1)

Notably, though both Spall and GTAD being based on GNN, Spall consistently outperforms GTAD. We attribute this superiority to the introduction of skip connection (Supplementary Figure S3). Since the spatial distribution of cells is not uniform, the number of cells within each spot in sequencing-based SRT data varies. During the training procedure of GNN, the message passing and aggregation processes may diminish this inherent characteristic of each spot, leading to inaccurate decomposition. However, the introduction of skip connection effectively reduces the loss of such inherent characteristics, allowing Spall to better preserve spot identity information during decomposition.

Spall characterized the distribution of tumor cells in human pancreatic ductal adenocarcinoma

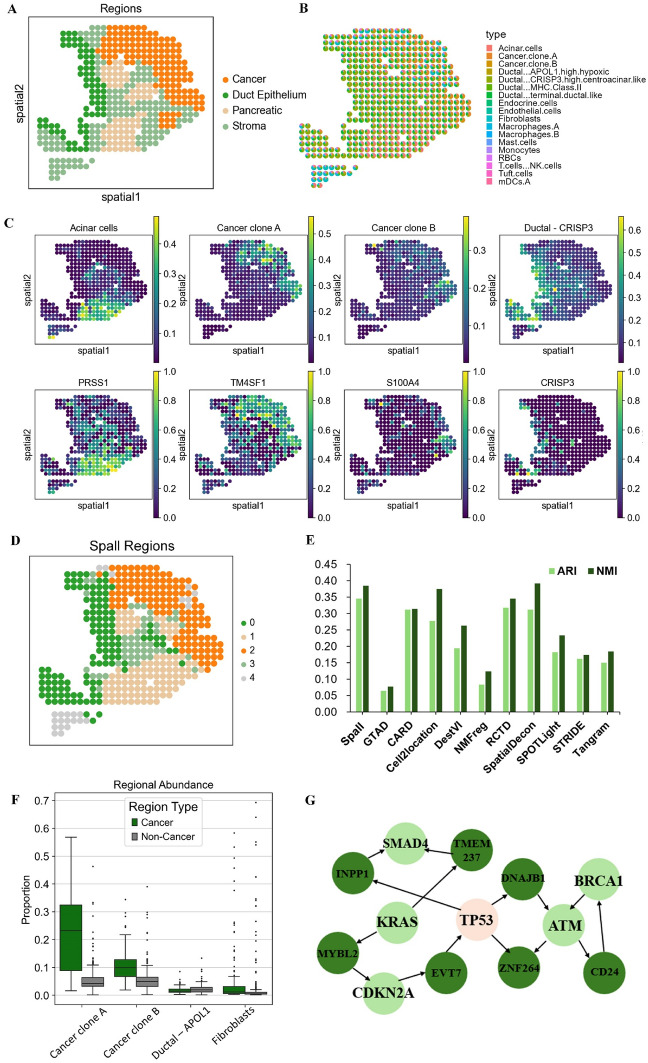
To evaluate the performance of Spall on real datasets, we first applied it to a human pancreatic ductal adenocarcinoma (PDAC) dataset, which was generated using Spatial Transcriptomics (ST) technology [25]. This PDAC tissue is composed of four main areas (cancer, ductal epithelium, stroma, and pancreatic), as shown in Fig. 3A.

Fig. 3.

Analysis results of Spall on PDAC dataset. A Manual annotation of the PDAC dataset. B Pie plots showing the cell type composition for each spot using Spall. C Top: Proportions of specific cell types as predicted by Spall. Bottom: Spatial distribution of the corresponding marker genes for these cell types. D Spatial region clustering results based on cell type proportions inferred by Spall. E ARI and NMI scores comparing the region annotations with clustering results obtained by Spall and 10 other algorithms. F Comparative analysis of the abundance of four cell types in cancerous regions (n = 137 spots) versus non-cancerous regions (n = 289 spots); the center line represents the median, box limits show the upper and lower quartiles, and whiskers indicate 1.5 × the interquartile range. G TP53 related gene regulatory network analysis in cancerous regions

Utilizing scRNA-seq data as a reference [25], we successfully mapped the spatial distribution patterns of cells using the Spall. As illustrated in Fig. 3B, each spot represents a distinct location, and the pie plots display the proportional composition of different cell types at each spot. This visualization clearly reveals the spatial distribution patterns of different cell types. Specifically, Spall predicts that Ductal cells are predominantly located in the left of the section, while cancer cells are mainly found in the upper right corner, consistent with the ground truth. Particularly noteworthy is the discovery that macrophages exhibit a distinct spatial preference, with a rare amount distributed near cancer cells. This distribution aligns with previous observations of macrophages forming spatial barriers around tumors [26, 27]. The aggregation of macrophages may form a barrier surrounding the tumor, which not only induces the epithelial-mesenchymal transition program to promote cell invasion but also enhances the response of regulatory T cells, thereby protecting tumor cells from attack by CD8 + T cells [26, 27]. This spatial heterogeneity of tumor-associated macrophages impacts tumor immune surveillance and immune escape strategies, potentially informing future therapeutic strategies for PDAC.

Additionally, we observed that the spatial distribution of cell types identified by Spall closely matches the spatial expression patterns of their marker genes. For example, in Fig. 3C, the regions enriched with the cancer cell marker genes (TM4SF1 and S100A4) are highly consistent with the distribution of cancer clone A and B. Central ductal cells are primarily concentrated in the ductal epithelium, which aligns with the expression pattern of their marker gene CRISP3, a cysteine-rich secretory protein. Similarly, acinar cells are predominantly located in the pancreatic region, corresponding to the spatial expression of their marker gene PRSS1. Furthermore, Spall can accurately identify the abundance of cancer cells in different regions. In Fig. 3F, the enrichment of cancer clones A and B in the cancerous region is significantly higher than in other regions. In contrast, the enrichment of other cell types, such as APOL1-expressing ductal epithelial cells and fibroblasts, in the cancerous region does not differ significantly from that in other regions.

To further evaluate the accuracy of the cell spatial distribution identified by Spall and demonstrate its applicability in downstream tasks, we performed spatial region clustering using the cell proportion inferenced by Spall. As shown in Fig. 3D, the boundary between the cancerous region and other regions is clearly defined. We applied the same analysis to the results of other methods and compared their clustering outcomes with the region annotations. The comparison was performed by the assessment of Adjusted Rand Index (ARI) and Normalized Mutual Information (NMI) between the annotations and the clustering outcomes. From Fig. 3E, it is evident that Spall achieved the highest ARI and NMI scores. In addition, we conducted a gene regulatory network analysis on the cancer region identified by Spall. A TP53-related subnetwork was extracted and is shown in Fig. 3G. In this subnetwork, several well-known PDAC-related cancer driver genes, such as SMAD4, KARS, CDKN2A, BRCA1, and ATM, were identified [28]. This further validates that Spall can accurately decipher the spatial distribution of tissues.

Accurate decomposition of 10X Visium data reveals laminar structure of the mouse cerebral cortex

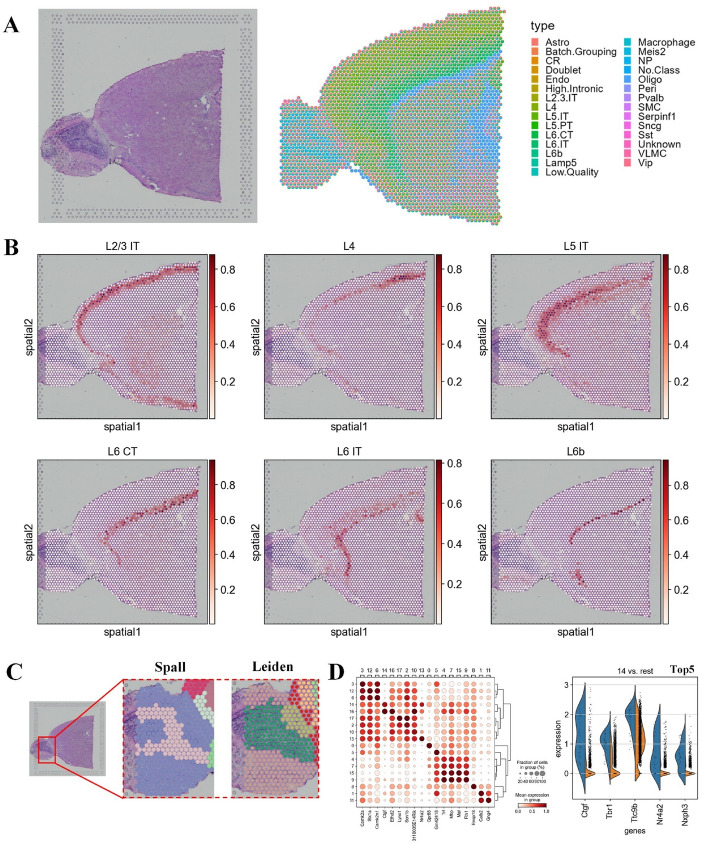
To further validate the effectiveness of Spall across different sequencing platforms, we applied it to a dataset generated by 10X Visium technology. Considering the well-defined laminar structure of the cerebral cortex, we adopted a slice from the mouse cerebral cortex. This slice contains 2,696 spots, with each spot covering 31,053 genes. Additionally, we used a high-quality scRNA-seq dataset comprising 29 distinct cell types as a reference [29].

First, we estimated the spatial distribution of different cell types in the dataset. As shown in Fig. 4A, Spall successfully reconstructs the laminar structure of the mouse cerebral cortex. Notably, the prediction of the laminar organization for six excitatory neuron is particularly clear (Fig. 4B). For example, cell types such as L2/3, L4, and L5 are primarily located in the outer and middle regions of the cortex, while L6 cells are mainly concentrated in the inner regions. This laminar organization is highly consistent with previous studies [29]. Additionally, we compared Spall with other decomposition algorithms, and the results demonstrated that Spall provided more accurate predictions of the spatial distribution patterns of different cell types (Supplementary Figure S4). Therefore, the results predicted by Spall maintain the characteristic of a continuous distribution of cellular proportions, exhibiting remarkable robustness.

Fig. 4.

Analysis of mouse cerebral cortex tissue using Spall. A Left: Image of the mouse brain tissue slice. Right: Pie plots representing the cell type composition at each spot, decomposed by Spall. B Spatial distribution of six layer-specific neuron populations predicted by Spall. C Comparison of spatial domain identification based on cell type proportions inferred by Spall versus direct use of gene expression profiles. D Left: Differential gene expression analysis of domains identified by Spall. Right: Top 5 differentially expressed genes in domain 14

Next, we used the results from Spall to analyze the molecular features of the mouse cerebral cortex. We identified spatial domains using the cell proportion estimated from Spall. As shown in Fig. 4C and Supplementary Figure S5, Spall can identify complex spatial structures, which could not be detected using clustering methods based on the gene expression profiles directly. Furthermore, using these results, we identified domain-specific genes (Fig. 4D and Supplementary Figure S6). We found that these differentially expressed genes are highly consistent with known marker genes. For example, in cluster 14, its distribution closely matches that of L6b neurons. The top five differentially expressed genes identified in this cluster (Fig. 4D, right) are consistent with previously reported L6b marker genes [30]. Additionally, we observed that these differentially expressed genes in spatial domains were not exclusively expressed by a single cell type (Fig. 4D). This explains why clustering based on the cell proportions obtained from Spall outperformed clustering directly using gene expression profiles. Therefore, cell proportion distributions can be considered a more interpretable low-dimensional embedding of the SRT data. These findings also demonstrate the superiority of the Spall in analyzing SRT data, as it not only accurately reconstructs the spatial distribution of cells but also provides a solid foundation for subsequent functional analyses.

Spall accurately identified consistency between cell distribution and layer structure in mouse cerebellum

To validate the multi-platform adaptability of Spall, we applied it to mouse cerebellum data obtained from the Slide-seqV2 [31]. Similar to the mouse cortex, the cerebellum exhibits more complex and well-characterized laminar organization. We adopted scRNA-seq data from previous research as a reference and employed Spall to infer the proportions of cells within each spot [16].

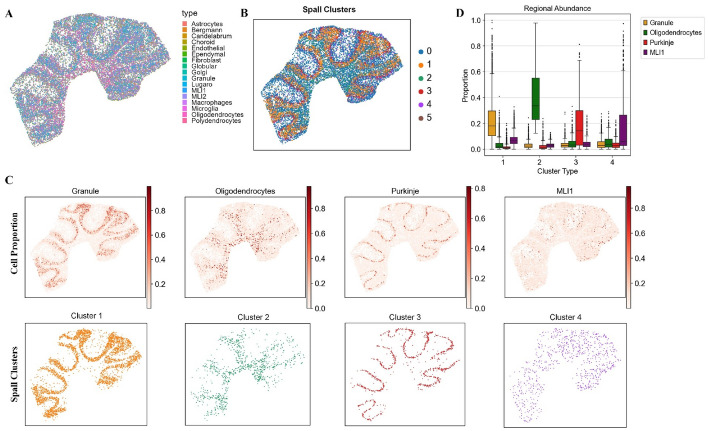
According to the previous study, the cerebellar slice can be divided into four regions [16], ordered from outer to inner layers: the molecular layer, Purkinje layer, granular layer, and white matter region. Based on the cell proportions inferred by Spall, we mapped the spatial distribution of these cells (Fig. 5A) and performed clustering based on the cell proportions (Fig. 5B). As shown in Fig. 5C, we can cluster mouse cerebellum into distinct regions with evident layer structures based on the inferred cell proportions. Furthermore, by comparing the cell spatial distribution and clustering results layer by layer, we found that the spatial distribution of cells predicted by Spall aligns closely with the four anatomical regions of the cerebellum (Fig. 5C). For example, granule cells, which are known as the primary component of the Granular layer, were predominantly located in the Granular layer. It has also been reported that oligodendrocytes are the main cell type in the white matter [32]. Our analysis clearly demonstrates that oligodendrocytes are primarily distributed in the innermost region which corresponds to the white matter. We also focused on the distribution of Purkinje cells. Purkinje cells are neurons unique to the cerebellum, residing in the Purkinje layer between the Molecular and Granular layers. They serve as the vital neurons of the cerebellum, playing pivotal roles in coordination, control, and learning of movements [33]. In Fig. 5C, Purkinje cells are concentrated in the middle layer, forming a band-like distribution that is consistent with their anatomical location in the Purkinje layer. Further analysis of the cellular composition within the clustered layers (Fig. 5D) was conducted. We specifically examined clusters 1–4 and plotted the proportional distribution of four cell types across these clusters. The results reveal that each cell type exhibits peak abundance in its corresponding cluster, aligning with our earlier observations. This finding supports the assertion that the decomposition results provide a highly reliable and interpretable low-dimensional embedding for downstream analyses.

Fig. 5.

The results of Spall for mouse cerebellum. A Pie plots showing the cell type composition at each spot, deconvolved by Spall from cerebellar tissue data. B Spatial domain identification based on cell type proportions estimated by Spall. C Top: spatial proportions of four layer-specific cell types predicted by Spall. Bottom: Corresponding spatial domains identified using proportions predicted by Spall. D Cell type abundance analysis across the four spatial domains. The center line represents the median, box limits indicate the upper and lower quartiles, and whiskers correspond to 1.5 × the interquartile range

In addition, we observed a notable association between the distribution of molecular layer interneurons (MLI1) cells and Purkinje cells. As shown in Fig. 5C, MLI1 cells are mainly distributed in the outer layer of the cerebellar slice, which corresponds to their position in the Molecular layer [34]. Moreover, we found that MLI1 cells are situated close to Purkinje cells, distributed above them in the outer layer. Research reported that MLI1 cells play a role in finely regulating the rhythm and precision of movement by locally inhibiting Purkinje cells [35]. If MLI1 cell function is impaired, it could lead to either over-excitation or inhibition of Purkinje cells, potentially causing cerebellum-related neurological disorders [36–38]. We think that the spatial proximity of MLI1 cells to Purkinje cells facilitates precise control over motor regulation. This discovery may be valuable in understanding and treating cerebellum-related neurological disorders.

Spall localized the spatial distribution of cell subtypes on mouse olfactory bulb data acquired by Stereo-seq

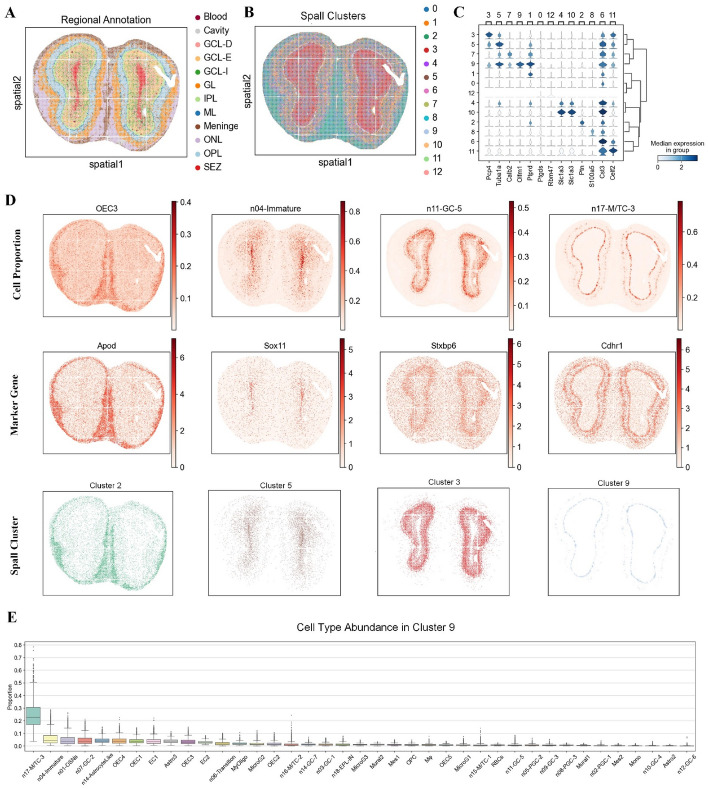
To validate the performance of Spall on SRT data with high-resolution, we applied it to a mouse olfactory bulb (MOB) slice generated by the Stereo-seq sequencing [39]. This dataset consists of 107,416 spots (slice S1, 14 × 14 DNA nanoballs). According to the annotation by Chen et al. [40], the MOB tissue is divided into 12 layers (Fig. 6A), including the olfactory nerve layer (ONL), outer plexiform layer (OPL), glomerular layer (GL), granular cell zone deep (GCL-D), granular cell layer externa (GCL-E), granular cell layer internal (GCL-I), internal plexiform layer (IPL), mitral layer (ML), and subependymal zone (SEZ).

Fig. 6.

Analysis of the large-scale MOB dataset generated from Stereo-seq using Spall. A Regional annotation of the MOB dataset. B Spatial domains identified based on cell type proportions estimated by Spall. C. Stacked violin plot showing differential gene expression across the spatial domains identified by Spall. D Top: Spatial proportions of four layer-specific cell types predicted by Spall. Middle: Spatial expression of corresponding cell-type-specific marker genes. Bottom: The four corresponding spatial domains identified from decomposition results inferred by Spall. E Cell type abundance analysis in domain 9. The center line represents the median, box limits show the upper and lower quartiles, and whiskers indicate 1.5 × the interquartile range

We adopted a publicly available MOB scRNA-seq dataset as a reference [40] and used Spall to decompose the cell proportions. The proportions were then utilized to identify spatial domains based on their spatial distribution. As shown in Fig. 6B, the spatial domains obtained using proportions clearly reveals the hierarchical structure of the slice, from the innermost to the outermost layers. Next, we investigated the key functional genes within specific domains. We performed domain-specific gene analysis based on the identified spatial domains and searched for genes with high specificity of expression, resulting in the stacked violin plot shown in Fig. 6C. We found that the spatial regions identified using cell proportion effectively capture previously reported key functional genes. For example, the Pcp4 gene was specifically expressed in cluster 3, which corresponds to the GCL-E region in Fig. 6A, consistent with earlier reports [41]. The S100a5 gene showed strong expression in cluster 8, which corresponds to the olfactory nerve layer. In the olfactory nerve layer, S100A5 is a calcium-binding protein, and its mRNA and protein abundance are closely associated with the activity of olfactory sensory neurons [42].

Next, we visualized the consistency between cell proportion distributions, marker gene expressions and spatial domains. We examined four cell subtypes (olfactory ensheathing cells (OEC3), developing immature neurons (n04-Immature), granule cells (n11-GC-5), and mitral and tufted (M/T) cells (n17-M/TC-3)) with distinct regional distribution patterns as previous work [43]. The spatial distribution of their marker genes aligned with the cell spatial distributions predicted by Spall (Fig. 6D). For example, n04-Immature cells were primarily enriched in the subependymal zone, and their marker gene Sox11 also showed high expression in this region [44]. Additionally, Spall identified n11-GC-5 cells, which were mainly enriched in the granular cell zone, and the high expression of their marker gene Stxbp6 in this area further validated the accuracy of the results [45]. On the other hand, the clustered domains identified by Spall closely aligned with the cell subtype distribution patterns (Fig. 6D). Finally, we conducted analysis of the cellular composition within the clustered regions, as illustrated in Fig. 6E. Specifically, we extracted Cluster 9 to examine its cell type abundance profile. The analysis reveals that n17-M/TC-3 cells exhibit the highest relative abundance in this spatial domain. This finding is consistent with above observations and reinforces the spatial patterns identified in the preceding analyses.

Discussion and conclusion

Spatial transcriptomics has provided us a more comprehensive perspective for understanding the complex structures and functions of tissues, offering unprecedented opportunities for clinical medicine and biological research. Predicting the spatial distribution patterns of cellular proportions through decomposition is particularly crucial for revealing the biological mechanisms of development and disease. However, despite the development of various decomposition methods, balancing the changes in cellular proportion distribution patterns across space with cell-specific characteristics remains a challenge. To this end, we have developed a new decomposition network called Spall, which integrates spatial location and expression information. Spall utilizes the flexible GATv2 architecture to learn the spatial patterns of gene expression and incorporates skip connections to address the issue of cell-specific information loss. We have validated the performance of Spall on various simulated and real datasets, and the results demonstrate its ability to precisely predict the spatial distribution patterns of cellular proportions.

To thoroughly assess the effectiveness of Spall, we conducted a series of biological analyses using SRT data from different platforms. Analysis of human pancreatic ductal adenocarcinoma data revealed the heterogeneity of tumor tissues and observed the formation of spatial barriers by macrophages around the tumors. These findings demonstrate that Spall is capable of not only predicting the continuous spatial distribution of cellular proportions but also effectively capturing information about rare cell types. In addition, the cellular proportions predicted by Spall serve as a reliable, low-dimensional, interpretable embedding, offering robust support for downstream analyses. For example, the decomposition results for the mouse cerebral cortex and cerebellum can be directly used for the clustering of tissue regions and align well with known laminar structures. Additionally, the analysis of high-resolution Stereo-seq data demonstrates that decomposition results from Spall closely match the spatial organization and marker genes of the mouse olfactory bulb.

In summary, Spall integrates scRNA-seq data as a reference to reconstruct the distribution of cell types within complex tissues with high robustness and accuracy. Spall does not require complex parameter adjustments, which enhances its usability. We believe that the development of Spall not only advances the analytical methodologies for SRT data but also promotes the progress of life sciences and precision medicine.

Methods

Data preprocessing

We utilized reference scRNA-seq data for feature selection. Using the Wilcoxon Rank-Sum test, we performed differential expression analysis for each cell subtype. We identified the top $n$ ($n=30$) most significantly differentially expressed genes for each subtype as distinctive genetic markers. These selected genes served as features for screening both the original scRNA-seq and SRT datasets.

Pseudo spots simulation

In this work, reference scRNA-seq data are employed to construct pseudo spots, aiming to mimic the sparse gene expression patterns within each real spot. Specifically, to simulate the cellular mixture of a particular spot, we randomly select between 2 to 10 cells from the scRNA-seq dataset and combine their transcriptomic profiles to form pseudo spots. The number of generated pseudo spots is denoted as $N$, which is close to the number of real spots $M$. Here, since the number of the selected cells is known, the exact proportions of cell types within each pseudo spot, ${\mathit{F}}_{\mathit{P}}\in {\mathbb{R}}^{N\times K}$, can serve as supervision for network training, where $K$ represents the total number of cell subtypes.

To better mimic the real spots, we ensure that the total count of unique molecular identifiers (UMIs) in each generated pseudo spot does not exceed that of the real spots. If it does, we down-sample the pseudo spot accordingly. As a result, the feature matrix of the pseudo spots, ${\mathit{X}}_{\mathit{P}}\in {\mathbb{R}}^{N\times S}$, exhibits a high degree of similarity to the feature matrix of real spots, ${\mathit{X}}_{\mathit{R}}\in {\mathbb{R}}^{M\times S}$.

During the generation of pseudo spots, we considered three types of link relationships: between real spots, between real spots and pseudo spots, and between pseudo spots. The link relationship between real spots is defined by their coordinates. Given the challenges of directly generating spatial coordinate information for pseudo spots, the link relationships involving pseudo spots are established by calculating the similarity of their projected gene profiles.

Graph construction

To establish connections between the real spots feature ${\mathit{X}}_{\mathit{R}}$ and the pseudo spots feature${\mathit{X}}_{\mathit{P}}$, we treat the gene expression of each spot as a node in a graph. We then use graph construction techniques to create edges that connect spots with similar expression profiles, thereby achieving the integration of simulated and real ST data. We integrate the two matrices using cross-dataset anchor point method provided by Seurat [46]. The resulting integrated feature matrix $\mathit{X}\in {\mathbb{R}}^{(N+M)\times S}$ serves as node features for graph$\mathit{G}$. We then apply graph construction algorithms (KNN or Random Projection Forest) to generate an adjacency matrix$\mathit{A}$. Elements in this matrix $A_{\mathit{ij}}$ indicate connectivity between nodes (spots) $i$ and $j$.

Model construction of spall

Compared to traditional GNNs [47], GAT [48], especially its second version GATv2 [17], incorporates an attention mechanism that introduces weighted edges into the graph. The weights of these edges are determined by the attention module within the network, which computes the attention coefficients for each edge.

Assume a set of $N$ interconnected graph nodes with a feature matrix $\mathit{h}=⟨{\mathit{h}}_1,{\mathit{h}}_2,\cdots ,{\mathit{h}}_N⟩$, where ${\mathit{h}}_i\in {\mathbb{R}}^S$, and $S$ is the dimension of each feature for the graph node. The attention coefficient can be calculated as:

$$e_{\mathit{ij}}={\mathit{\alpha }}^T·LeakyReLU\left(\mathit{W},\bullet ,\left[h_i,||,h_j\right]\right)$$

where $e_{\mathit{ij}}$ is the attention coefficient between node $i$ and $j$, and $\mathit{W}$ and ${\mathit{\alpha }}^T$ are the learnable parameters of the network. For GAT, $e_{\mathit{ij}}=LeakyReLU\left({\mathit{\alpha }}^T,·,\left[{\mathit{W}h}_i,||,\mathit{W},h_j\right]\right)$. The weight parameters of GAT are fixed on nodes $h_i$ and $h_j$, which leads to the attention order between the central node and its neighboring nodes remaining unchanged. In contrast, in GATv2, by concatenating $h_i$ and $h_j$ before calculating the weights, dynamic attention can be formed.

After obtaining the attention coefficients between each neighbor, the adjacency matrix can be updated as:

$$\mathit{V}=\mathit{E}\bullet \mathit{A}$$

where $\mathit{V}$ is the updated adjacency matrix, $\mathit{E}$ is the attention coefficient matrix, and $\mathit{A}$ is the original adjacency matrix. To ensure consistency in the weight scale, normalization is required:

$${\alpha }_{\mathit{ij}}=softmax\left(v,\left({\mathit{h}}_i,,,{\mathit{h}}_j\right)\right)=\frac{exp\left(v,\left({\mathit{h}}_i,,,{\mathit{h}}_j\right)\right)}{{\sum }_{j\in N}exp\left(v,\left({\mathit{h}}_i,,,{\mathit{h}}_j\right)\right)}$$

where ${\alpha }_{\mathit{ij}}$ is the normalized attention coefficient of the node $i$ respect to node $j$.

Multiple attention heads can capture diverse weighting patterns. To model these, we employ a multi-head attention mechanism. By combining these heads, we obtain comprehensive new features. The calculation is as follows:

$${\mathbf{h}}_i^{\text{'}}=Concat/Avg{||}_{l=1}^L\sigma \left(\sum _{j\in N}{\alpha }_{\mathit{ij}}^{\left(l\right)}{\mathbf{W}}^{\left(l\right)}{\mathbf{h}}_j\right)$$

where ${\mathit{h}}_i\prime$ is the new feature of the node $i$, $L$ denotes the number of the heads, and the $\sigma$ is the activation function. In this way, a feature matrix integrating dynamic weights of adjacent node information can be obtained.

Skip connection

When using GNNs for spatial decomposition, there is an issue of over-smoothing. Therefore, we propose to integrate the original gene expression information through skip connections in the first layer of the network. Skip connections were originally introduced to mitigate gradient vanishing and exploding problems in deep networks [49]. They add shallow information to deeper layers, allowing primitive information to propagate through the network and effectively increase its depth. In our implementation, the calculation process is as follows:

$$\mathit{H}\left(\mathit{x}\right)=\mathit{F}\left(\mathit{x}\right)+\mathit{x},$$

where $\mathit{H}\left(\mathit{x}\right)$ is the added feature, $\mathit{F}\left(\mathit{x}\right)$ is the updated feature, and x is the original feature.

Benchmarking metrics

To measure the performance of different methods, this work adopts three metrics respectively: RMSE, JSD, and PCC. Their definitions are:

1. RMSE:

$$RMSE=\sqrt{\frac{1}{M}\sum _{j=1}^M{\left({\tilde{x}}_{\mathit{ij}},-,x_{\mathit{ij}}\right)}^2},$$

where $M$ is the total number of the spots, $x_{\mathit{ij}}$ is the cell type composition of cell type $i$ in the ground truth of spot $j$, ${\tilde{x}}_{\mathit{ij}}$ is the corresponding values of the predicted results. For a cell type, a lower RMSE value represents better decomposition quality.

2. JSD:

$$JS=\frac{1}{2}KL\left({\tilde{\mathit{P}}}_i,|,\frac{{\tilde{\mathit{P}}}_i+{\mathit{P}}_i}{2}\right)+\frac{1}{2}KL\left({\mathit{P}}_i,|,\frac{{\tilde{\mathit{P}}}_i+{\mathit{P}}_i}{2}\right)$$

$$KL\left({\mathit{a}}_i,||,{\mathit{b}}_i\right)={\sum }_{j=0}^M\left(a_{\mathit{ij}},,\ast ,l,o,g,\frac{a_{\mathit{ij}}}{b_{\mathit{ij}}}\right)$$

where ${\tilde{\mathit{P}}}_i$ and ${\mathit{P}}_i$ are the spatial distribution of the cell type $i$ in the predicted results and ground truth. A lower JSD score represents higher decomposition accuracy.

3. PCC:

$$PCC=\frac{E\left[\left({\tilde{x}}_i,-,{\tilde{u}}_i\right),\left(x_i,-,u_i\right)\right]}{{\tilde{s}}_i{s}_i}$$

where $x_i$ is the cell type composition of cell type $i$ in the ground truth, $u_i$ is the average cell type composition of cell type $i$ in the ground truth, $s_i$ is the standard deviation of the ground truth. ${\tilde{x}}_i$,${\tilde{u}}_i$ and ${\tilde{s}}_i$ are the corresponding values of the predicted results. A higher PCC value is better.

Author contributions

ZJ, RHWL and WZ designed the algorithm and programs, ZJ conducted the experiments and wrote the manuscript. RHWL, WZ and WH revised the manuscript. All authors read and approved the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China [62303271], the Natural Science Foundation of Shandong Province [ZR2023QF081], the Hong Kong Research Grant Council [GRF 11217323]. Funding for open access charge: National Natural Science Foundation of China [Nos. 62303271].

Availability of data and material

The simulation method can be accessed at: https://github.com/Honchkrow/SSTD. For the mouse brain data, the SRT data can be accessed from 10X Genomic Datasets (https://www.10xgenomics.com/cn/resources/datasets) by the name “Mouse Brain Serial Sect. 1 (Sagittal-Anterior)”. The scRNA-seq data for mouse brain was available at GSE115746. For the mouse cerebellum, the ST data and scRNA-seq data were both sourced from a previously research, RCTD (https://singlecell.broadinstitute.org/single_cell/study/SCP948). For the PDAC data, the SRT dataset can be obtained from SODB [50], a publicly available dataset website (https://gene.ai.tencent.com/SpatialOmics/dataset?datasetID=15), with the slice ID GSM3036911. It can also be accessed using cancerSRT [51]. The scRNA-seq data was sourced at GSE111672. For the Mouse Olfactory bulb, the SRT data can be accessed at SODB with the slice ID “Mouse_olfa_S2”, while the scRNA-seq data was sourced at GSE121891. The source code and tutorial can be accessed at: https://github.com/znjiang1/Spall.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.