Prediction and mapping of leaf water content in Populus alba var. pyramidalis using hyperspectral imagery

Abstract

Leaf water content (LWC) encapsulates critical aspects of tree physiology and is considered a proxy for assessing tree drought stress and the risk of forest decline; however, its measurement relies on destructive sampling and is thus less efficient. Advancements in hyperspectral imaging technology present new prospects for noninvasively evaluating LWC and mapping drought severity across forested regions. In this study, leaf samples were obtained from Populus alba var. pyramidalis, a species widely employed for constructing farmland shelterbelts in water-limited regions of northern China but notably susceptible to drought. These samples were dehydrated to varying degrees to generate concurrent LWC measurements and hyperspectral images, enabling the development of narrow-band and multivariate spectral prediction models for LWC estimation. Two visible-spectrum narrow-band indices identified, the single-band index (R₆₂₇) and the band subtraction index (R₄₃₇ − R₄₄₄), demonstrated a strong correlation with LWC. Despite certain influences of variable preprocessing and selection on multivariate model performance, most models exhibited robust predictive accuracy for LWC. The FDRL-UVE-PLSR combination emerged as the optimal multivariate model, with R² values reaching 0.9925 and 0.9853 and RMSE values below 0.0124 and 0.0264 for the calibration and validation datasets, respectively. Using this optimal model, along with localized spectral smoothing, moisture distribution across leaf surfaces was visualized, revealing lower water retention at the leaf margins compared to central regions. These methodologies provide critical insights into subtle water-associated physiological processes at the leaf scale and facilitate high-frequency, large-scale assessments and monitoring of drought stress levels and the risk of drought-induced tree mortality and forest degradation in drylands.

Introduction

Climate change, driven by anthropogenic greenhouse gas emissions, has altered global climate patterns, resulting in a noticeable warming and drying trend in vast regions across the globe [17, 49, 64]. The altered weather patterns, characterized by longer and more intense periods of drought, exert immense pressure on forest ecosystems, leading to widespread tree mortality and forest decline, especially in water-limited areas [4, 29]. Drought-induced tree mortality has a noteworthy influence on forest structure and functionality, thereby impacting crucial ecosystem services such as carbon sequestration and timber production [8, 70]. In the scenarios of more frequent and severe drought events, monitoring forest degradation risks by assessing the physiological status of trees is crucial for understanding forest resilience under the backdrop of climate change, and for implementing timely management strategies to mitigate the impacts of climate change on forest ecosystems. It also enables the assessment of carbon sequestration potential and the identification of areas requiring reforestation or conservation efforts to maintain forest ecosystem services.

Hydraulic failure has been proposed as the pivotal physiological mechanism causing tree mortality under drought conditions intensified by warming and drying climates [2, 5, 16, 42, 44]. This mechanism is primarily driven by the inability of trees to transport water from the roots to the leaves under drought, leading to tissue dehydration and eventual death [2, 5, 41]. A relevant parameter that mirrors the degree of water stress in trees is supposed to facilitate predicting the risk of drought-associated tree mortality. One of the most commonly used approaches to investigate the effects of drought on plants involves measuring leaf water content. Emerging evidence suggests that leaf water content holds considerable promise in projecting tree drought stress as it is a direct measure of plant water status, closely related to cell volume, turgidity, and thus xylem hydraulic functioning [43, 65]. Physiologically, leaf water content effectively integrates the water relations of plants, reflecting their water supply, demand, and retention [56, 57]. Apart from its association with xylem hydraulic functioning, several investigations have documented the close connection between leaf water content and essential physiological characteristics such as stomatal conductance, photosynthetic capacity, respiration rate, and non-structural carbohydrate reserves [30, 71]. These findings imply that leaf water content may potentially perform crucial roles in drought-induced tree mortality by influencing plant carbon economics. Although leaf moisture content serves as a reliable metric for quantifying drought status in trees, its measurement necessitates on-site leaf collection through destructive sampling. This requirement imposes significant limitations on large-scale and high-frequency monitoring efforts.

Hyperspectral remote sensing technology has shown great potential in retrieving plant physiological properties and functional traits due to its ability to capture detailed spectral information across hundreds of narrow contiguous spectral bands. Consequently, the utilization of hyperspectral remote sensing technology, coupled with unmanned aerial vehicles, aerocrafts, and satellite platforms, has emerged as a burgeoning methodology for the non-destructive assessment of plant physiological status at a larger scale or in a high-frequency manner [19, 39, 72]. The variances in reflectance spectroscopy among leaves in distinct bands are intimately associated with their chemical composition, cellular structure, and physiological characteristics [18, 23, 53, 59]. Indeed, numerous studies have successfully utilized rich spectral information from hyperspectral sensors to estimate leaf element concentrations [68], chlorophyll content [74], photosynthetic capacity [45], and water content [62] in crops. Advanced hyperspectral sensors have demonstrated significant utility as non-destructive tools for the assessment and monitoring of the physiological status of crops [69]. Nevertheless, due to limited data accessibility, high structure complexity, and strong community heterogeneity, there remains a paucity of research regarding the accurate inversion of leaf water content for trees in forested environments using leaf spectroscopy [75].

Based on the spectral data of a spectrometer, narrow- and full-band models can be developed. Narrow-band models predict plant physiological characteristics utilizing reflectance within specific, narrow spectral ranges. Vegetation indices derived from narrow-band models offer advantages in terms of fast computation and are well-suited for large-scale data evaluations. Numerous spectral indices have been developed to estimate plant physiological indicators, such as the water index (WI), normalized difference water index (NDWI), simple ratio water index (SRWI), normalized difference infrared index (NDII), etc., and they are powerful tools for quickly assessing and monitoring changes in the physiological status of plants [27, 52, 66]. In contrast, full-band modeling leverages the entire spectral dataset, performing derivative preprocessing and feature band selection, often combined with machine learning algorithms, to build more accurate predictive models. Derivative preprocessing techniques such as the reciprocal logarithm of reflectance (RLR), second-order derivative (2D), and Savitzky-Golay (S-G) filtering effectively mitigate baseline drift and multiple scattering effects [1, 15, 55, 61]. Feature band selection, which aims to reduce the dimensionality of spectral data, is another key aspect of full-band modeling. Popular band selection algorithms include competitive adaptive reweighted sampling (CARS), least absolute shrinkage and selection operator (LASSO), and uninformative variable elimination (UVE), which excel in identifying the most valuable features from numerous spectral bands [15, 32, 46]. Additionally, researchers have applied machine learning based regression algorithms including multiple linear regression (MLR), partial least squares regression (PLSR), and support vector machine regression (SVR) to develop predictive models, demonstrating these methods’ adaptability across diverse datasets for spectral modeling and analysis [40, 75]. These models have proven to be valuable resources for non-destructive assessment and monitoring of the physiological status of plants. Moreover, the recent advancements in hyperspectral camera technology have facilitated the visualization of spatial patterns and temporal changes in the physiological status of plants. Precise spectral models based on hyperspectral imagery for leaf water content prediction and visualization are an important prerequisite for monitoring tree drought severity and mapping the risk of drought-induced tree mortality over a large spatial range and at a higher time frequency.

In this study, leaves of Populus alba var. pyramidalis (Xinjiang poplar) seedlings were sampled and exposed to dehydration, during which leaf water content and hyperspectral images were periodically determined. Our specific objectives are: (1) to investigate narrow-band models and identify spectral indices that are indicative of leaf water content; (2) to evaluate the robustness of prediction models for leaf water content developed through various combinations of spectral preprocessing, feature band screening, and multivariate regression methods; and (3) to visualize the distribution of moisture content across the leaf surface using the optimal multivariate model based on full-band reflectance spectrum. This study may offer reliable methods and technical support for non-destructive monitoring of drought stress levels and decline risks in Xinjiang poplar shelterbelts established in drought-prone areas.

Materials and methods

Plant materials

Populus alba var. pyramidalis, commonly known as Xinjiang poplar, is a commonly used tree species for afforestation in the Three-North (North, Northeast, and Northwest) region of China. This species is particularly valued for its role in establishing shelterbelts around farmland, where it effectively reduces wind speed, minimizes soil erosion, and modifies microclimates. In the context of ongoing climatic shifts, northern China is undergoing pronounced patterns of warming and aridification, which are paralleled by the escalating severity of drought. The intensified drought conditions have imparted severe challenges to the P. alba var. pyramidalis shelterbelts in water-limited regions, manifesting in pronounced decline and mortality [39], thereby exerting substantial detrimental effects on the local ecological environment. This underscores the necessity of utilizing remote sensing technology to develop hyperspectral models for this species, facilitating the inversion of leaf water content and thereby enabling the monitoring of drought stress levels and associated mortality risks in Xinjiang poplar shelterbelts.

Experimental design and study framework

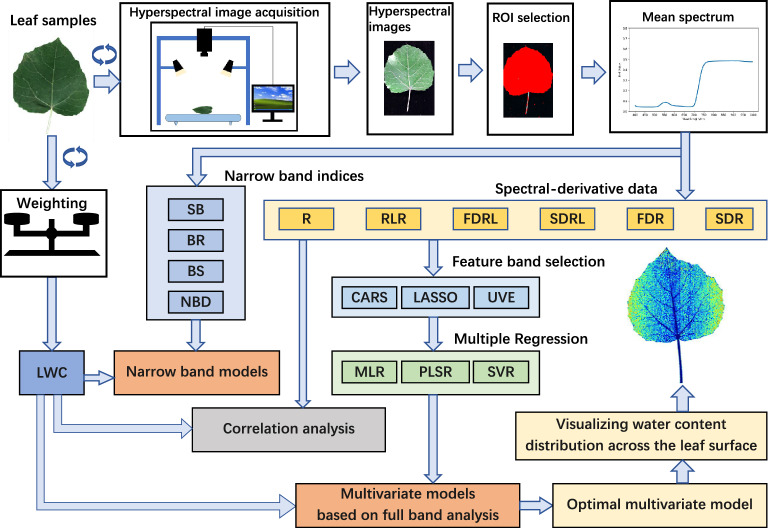
The research concept and framework of this study are illustrated in Fig. 1. Initially, a hyperspectral image acquisition system was designed, assembled, and employed to capture spectral images of P. alba var. pyramidalis leaves with varying water statuses, while concurrently measuring leaf water content (LWC). The spectral images were then subjected to correction, segmentation, and averaging to derive the spectral curve for each sample. Based on these curves, the four selected narrow-band models were developed, and the performance of each model with different band or band combinations for LWC prediction was evaluated to identify the relevant indices. Subsequently, the correlation between the spectral-derivative data and LWC was examined, integrating band selection and regression methodologies to determine the optimal multivariate model. Finally, this optimal model was applied to visualize the distribution of water content across the leaf surface.

Fig. 1.

Framework for predicting leaf water content (LWC) in Populus alba var. pyramidalis. See Tables 1–4 for abbreviations

Leaf water content measurement

Leaf samples were collected from six three-year-old P. alba var. pyramidalis seedlings naturally growing in the Daqinggou Ecological Research Station, Institute of Applied Ecology, Chinese Academy of Sciences (119°25′E, 42°54′N). Specifically, five to six sun-exposed and mature leaves located in the middle section of the canopy were excised from different individual seedlings. Immediately after collection, each leaf sample was promptly sealed in a plastic bag along with a moist paper towel slice to maintain its moisture content and then transported to the laboratory for LWC measurements and spectral analyses. Upon arrival at the laboratory, the leaves were allowed to dehydrate on the laboratory bench in a darkroom, and the mass of each leaf sample was repeatedly measured at intervals of 20–30 min using an electronic analytical balance (CPA 225D, Sartorius Inc., Göttingen, Germany) throughout the dehydration process. Following each mass determination, the spectral information for each leaf was immediately captured using a hyperspectral image acquisition system (see below for details). This measurement process continued continually until the leaf mass exhibited minimal fluctuations after approximately 20 rounds of measurements. Following this phase, the sampled leaves were subjected to oven-drying at 65 °C for 48 h to obtain their dry mass. LWC was calculated as:

$$\text{LWC}=\frac{\left(\text{FW},-,\text{DW}\right)}{\text{FW}}$$

where FW represents the fresh leaf mass measured at a specific time during the dehydration process, and DW denotes the dry mass of the corresponding leaf sample.

In the present study, a total of 29 leaf samples were collected, obtained from five batches of leaves. Each batch consisted of five leaves in the first batch and six leaves in the subsequent batches. Totally, a comprehensive collection of 574 paired foliar spectral and LWC data was produced. All the 574 sets of records were included in the subsequent analysis. For the purpose of model training and evaluation, 454 sets of data originating from the first four batches were utilized as the training and calibration dataset, while the remaining 120 sets of data from the last batch were reserved for testing and evaluation.

Spectral reflectance data acquisition

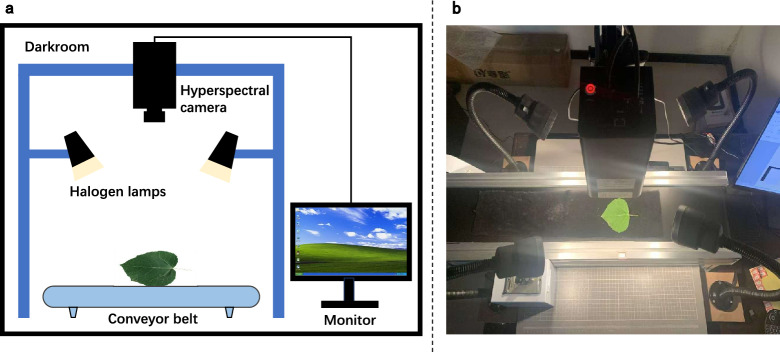
A push-broom hyperspectral camera (GaiaSky-mini2, Dualix Spectral Imaging, China) was used to capture hyperspectral images. The camera covers a spectral range of 393.7–1001.4 nm, comprising 176 bands with a spectral resolution of 3.5 ± 0.5 nm. To minimize light interference, spectral data collection was conducted in a darkroom equipped with a custom hyperspectral image acquisition system (Fig. 2). The system consisted of four 50 W halogen lamps, a conveyor belt, and a monitor. The halogen lamps were preheated for 20 min before image acquisition to ensure stable and uniform illumination. The conveyor speed was set to 2.5 cm/s, and the camera was positioned at a height of 35 cm.

Fig. 2.

Schematic diagram (a) and physical picture (b) of the hyperspectral image acquisition system used in this study

Before capturing the images, a white Teflon plate was used to obtain a white reference image, and an opaque lens cap was placed over the camera lens to acquire a dark reference image. These two reference images were subsequently used for reflectance correction, following the formula below:

$$R_c=\frac{I_{\mathit{original}}-I_{\mathit{dark}}}{I_{\mathit{white}}-I_{\mathit{dark}}}\times R_{\mathit{white}}$$

where $R_c$ is the corrected reflectance of a hyperspectral image, $I_{\mathit{original}}$ is the original hyperspectral image, $I_{\mathit{white}}$ is the white reference image, $I_{\mathit{dark}}$ is the dark reference image, and $R_{\mathit{white}}$ is the reflectance of the white Teflon plate (approximately 100%).

The hyperspectral images were corrected for lens distortion and reflectance using SpecView software (Dualix Spectral Imaging, China) to obtain standardized images. In Envi 5.3 software (RSI, USA), threshold segmentation was applied to eliminate background pixels and delineate regions of interest (ROI), and the average spectral values of the leaves were extracted using binarization and mask processing.

Narrow-band models

Common narrow-band models can be categorized into four types: single band (SB), band ratio (BR), band subtraction (BS), and normalized band difference (NBD) models (Table 1). The single band (SB) model represents the most straightforward computational method, using only the reflectance value of a single band to derive the target index. The formula for the SB model is:

$$SB=b1$$

where b1 denotes the spectral reflectance value of a specific band.

Table 1.

The optimal band or band combinations for the four studied narrow-band models

Models	Calculation equations	Band or band combinations	Calibration (n = 454)		Validation (n = 120)
			R2	RMSE	R2	RMSE
SB	Band1	627	0.7055	0.0959	0.6875	0.0926
BR	Band1/Band2	755, 759	0.0526	0.172	0.0981	0.1574
BS	Band1 − Band2	437, 444	0.8121	0.0766	0.7911	0.0757
NBD	(Band1 − Band2)/(Band1 + Band2)	755, 759	0.0507	0.1721	0.0962	0.1575

For SB, only one optimal band was selected; for the other three, “Band1” and “Band2” represent the best band combinations. The model with the highest R² value for the calibration dataset was shown in bold

SB single band, BR band ratio, BS band subtraction, NBD normalized band difference

The band ratio (BR) model computes the ratio of the reflectance values of two bands, which enhances the vegetation signal while minimizing the effects of atmospheric conditions and soil background. The formula for the BR model is:

$$BR(b1,b2)=\frac{b1}{b2}$$

where b1 and b2 are the spectral reflectance values of designated bands.

The band subtraction (BS) model computes the difference between the reflectance values of two bands, proving particularly effective for identifying absorption features at specific wavelengths. The formula for the BS model is:

$$BS(b1,b2)=b1-b2$$

where b1 and b2 are the spectral reflectance values of chosen bands.

The normalized band difference (NBD) model is an improved version of the BS model. It calculates the ratio of the difference and the sum of the reflectance values of two bands, contributing to minimizing the effects of external factors such as lighting conditions. The formula for the NBD model is:

$$NBD(b1,b2)=\frac{b1-b2}{b1+b2}$$

where b1 and b2 are the spectral reflectance values of specific bands.

Multivariate models

Spectral reflectance preprocessing

Initially, the raw reflectance data underwent preprocessing through the calculation of spectral derivatives. This derivative analysis elucidates trends and features, reduces noise, and enhances the correlation between spectral signals and the properties of the target substance, thereby improving the accuracy and interpretability of the analysis. In this study, several prevalent methods for calculating spectral derivatives were employed, including reciprocal logarithm of reflectance (RLR), first-order differential of reflectance (FDR), second-order differential of reflectance (SDR), first-order differential of reciprocal logarithm (FDRL), and second-order differential of reciprocal logarithm (SDRL).

RLR applies a reciprocal and logarithmic transformation to the spectral curve, effectively reducing background interference, particularly in the presence of significant baseline drift. The formula for the RLR transformation is:

$$RLR=\text{log}\left(\frac{1}{R}\right)$$

FDR accentuates the slope characteristics of the spectral curve by calculating the rate of change, rendering the peaks and valleys of the spectral curve more pronounced. The formula for the FDR transformation is:

$$FDR=\frac{R(\lambda +\mathrm{\Delta }\lambda )-R(\lambda -\mathrm{\Delta }\lambda )}{2\mathrm{\Delta }\lambda }$$

SDR further emphasizes the acceleration of changes in the spectral curve, enhancing the details of inflection points and curve variations, and is particularly adept at capturing local features in the spectral signal. The formula for the SDR transformation is:

$$SDR=\frac{FDR(\lambda +\mathrm{\Delta }\lambda )-FDR(\lambda -\mathrm{\Delta }\lambda )}{2\mathrm{\Delta }\lambda }$$

FDRL combines the advantages of logarithmic transformation and first-order differentiation, eliminating baseline drift while emphasizing changes in the spectral signal. The formula for the FDRL transformation is:

$$FDRL=\frac{RLR(\lambda +\mathrm{\Delta }\lambda )-RLR(\lambda -\mathrm{\Delta }\lambda )}{2\mathrm{\Delta }\lambda }$$

SDRL further enhances the detail of spectral signals through second-order differentiation of the logarithmic form of the spectrum. The formula for the SDRL transformation is:

$$SDRL=\frac{FDRL(\lambda +\mathrm{\Delta }\lambda )-FDRL(\lambda -\mathrm{\Delta }\lambda )}{2\mathrm{\Delta }\lambda }$$

Feature band screening

Feature band screening refers to the process of identifying the most representative and relevant bands from spectral data for model building, data analysis, or addressing specific research questions. The significance of band selection lies in optimizing model performance, simplifying model complexity, improving interpretability and predictive ability, and reducing interference from irrelevant information. The outcomes of band selection can significantly affect both the fit of the model and its ability to generalize across diverse datasets. In the present study, three band selection methods were employed: competitive adaptive reweighted sampling (CARS), least absolute shrinkage and selection operator (LASSO), and uninformative variable elimination (UVE).

CARS is a band selection algorithm based on partial least squares regression (PLSR). Through Monte Carlo sampling, CARS randomly selects subsets from the hyperspectral data during each iteration and builds a PLSR model. The importance of each band is assessed based on its regression coefficients within the PLS model. An adaptive weighting mechanism progressively eliminates less important bands, retaining those that most contribute to the model’s predictive performance. Through iterative sampling and competitive selection, CARS effectively eliminates redundant information and noise, resulting in an optimal set of bands that enhance the accuracy and stability of the model [36].

LASSO is a regression method based on L1 regularization to achieve feature selection by imposing constraints on regression coefficients. In hyperspectral image analysis, LASSO automatically selects important bands by shrinking the coefficients of less important bands to zero, thus reducing model complexity and redundant information. The regularization parameter, λ, governs the degree of band selection, enabling the model to maintain predictive accuracy while avoiding overfitting and improving generalization ability [63].

UVE is a band selection technique predicated on the evaluation of variable importance. It ranks and filters bands by assessing their contribution to the prediction of the target variable. In hyperspectral data processing, the UVE method aids in identifying and eliminating bands that have minimal or no influence on the target variable, thus simplifying the model and improving predictive accuracy [14].

Regression algorithms

Three machine learning regression algorithms were used in this study: multiple linear regression (MLR), partial least squares regression (PLSR), and support vector regression (SVR). These algorithms, when combined with various reflectance processing and feature band selection techniques, exhibit varying performance across both training and testing datasets.

MLR is a foundational regression algorithm designed to model the linear relationships between one or more independent variables and a dependent variable. The primary objective of MLR is to derive a linear equation that minimizes the discrepancy between the predicted and observed values. This is achieved by estimating regression coefficients that minimize the sum of squared residuals, thereby constructing an optimal model. While MLR is effective for analyzing linear relationships, it may necessitate the application of more sophisticated regression algorithms to adequately address nonlinear relationships or issues related to multicollinearity.

PLSR is a statistical algorithm utilized to develop predictive models, particularly advantageous for high-dimensional data and scenarios involving multicollinearity. PLSR projects both independent and dependent variables into a new dimensional space, identifying the optimal combination of latent variables to maximize the correlation between the two. This approach is particularly effective in addressing challenges arising from highly correlated independent variables, thus circumventing issues associated with multicollinearity.

SVR is a machine learning algorithm derived from support vector machines, specifically tailored for regression tasks. SVR seeks to identify a hyperplane that effectively partitions the input data while maximizing the margin between the hyperplane and the nearest data points. Support vector machines are capable of employing various kernel functions to accommodate nonlinear relationships, demonstrating exceptional performance in the analysis of high-dimensional data. In this study, radial basis function (RBF) kernel, also known as the Gaussian kernel, was used.

Model evaluation

The coefficient of determination (R²) and root mean square error (RMSE) were used as metrics to evaluate model performance. The R² value indicates the model's capacity to explain the variability in the actual data, with a range from 0 to 1, where values closer to 1 signify a superior fit. The formula for R² is expressed as:

$$R^2=1-\frac{{\sum }_1^n{\left(y-\widehat{y}\right)}^2}{{\sum }_1^n{\left(y-\overline{y}\right)}^2}$$

where n represents the number of samples, y denotes the actual LWC value for each sample, $\overline{y}$ signifies the mean of the actual LWC, and ŷ indicates the predicted LWC value.

RMSE quantifies the average deviation between predicted and observed values, with lower RMSE values indicating more accurate predictions. The formula for RMSE is expressed as:

$$RMSE=\sqrt{\frac{{\sum }_1^n{\left(y-\widehat{y}\right)}^2}{n}}$$

where n denotes the number of samples, y represents the actual LWC value, and ŷ signifies the predicted LWC value.

By comparing the R² and RMSE values, the model’s fitting performance can be systematically assessed, with higher R² values and lower RMSE values indicating a stronger ability of the model to elucidate the data.

Visualization of water content across the leaf surface

For developing spectral prediction models, the average spectral curve derived from hyperspectral images was used for training and testing purposes. This method effectively reduces spectral noise through global averaging, yielding smoother spectral signals. However, this global averaging process results in a loss of spatial information inherent in the images. To further reveal the spatial distribution of water moisture within leaves, it is imperative to preserve the spatial characteristics of the spectral images. In this study, a local spectral smoothing method was implemented. Specifically, a 5 × 5 pixel window was used, sliding across the image with a step size of 1 pixel. The spectral curve of each window was averaged and subsequently assigned to the center pixel of that window. This local smoothing approach facilitates the generation of more representative and refined spectral data while retaining the spatial distribution features of the image. Following this, the established optimal multivariate model was applied to predict the LWC for each pixel, thereby generating a leaf water content distribution map.

Results

Reflectance changes induced by dehydration

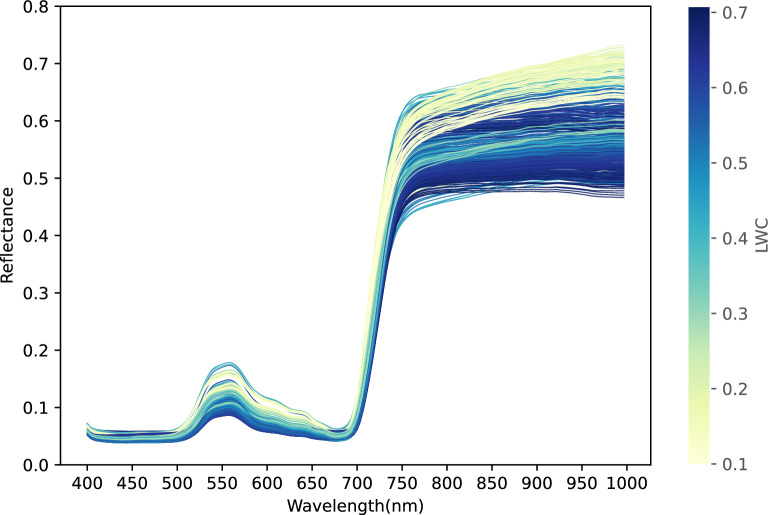
The foliar reflectance spectra exhibited significant alterations in response to changes in LWC induced by dehydration (Fig. 3). Our bench-dehydration experiment conducted on detached P. alba var. pyramidalis leaves generated a dataset consisting of various LWC values spanning 0.0987 to 0.7065, with mean and median values of 0.5015 and 0.5750, respectively. Overall, irrespective of leaf desiccation status, the reflectance of P. alba var. pyramidalis leaves exhibited lower values across the majority of the visible (VIS) spectrum (380–700 nm), characterized by a conspicuous peak around 550 nm (Fig. 3). This was followed by a marked increase in leaf reflectance within the 700–750 nm range, referred to as the red-edge effect. Subsequently, reflectance values consistently maintained higher within the near-infrared (NIR) spectrum (780–1000 nm). Generally, the reflectance of leaves from the studied P. alba var. pyramidalis seedlings increased with decreasing LWC, with this trend being more pronounced in the NIR spectral range (Fig. 3).

Fig. 3.

Spectral reflectance of Populus alba var. pyramidalis leaves with contrasting leaf water content (LWC)

Performance of narrow-band models

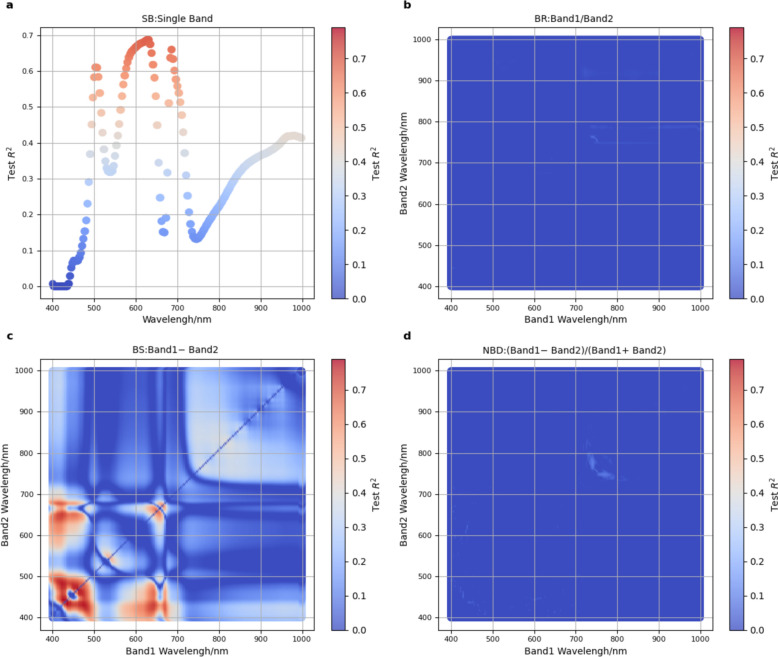
Among the four narrow-band models assessed, the BS model showed the most accurate predictive capability (Table 1). The optimal spectral range for the BS model in predicting LWC was observed within the wavelength interval of 400–500 nm, as well as in the combined spectrum of 400–500 and 600–700 nm (Fig. 4c). The calculated R² and RMSE values for the identified BS index (R₄₃₇ − R₄₄₄) were 0.8121 and 0.0766 for the calibration dataset, and 0.7911 and 0.0757 for the validation dataset (Table 1). Furthermore, the SB model also demonstrated favorable predictive performance, with the spectral bands around 500 and 680 nm, and between 580 and 630 nm, showing superior prediction accuracy (Fig. 4a). The identified SB index at 627 nm (R₆₂₇) yielded R² values of 0.7055 and 0.6875, along with RMSE values of 0.0959 and 0.0926, for the calibration and validation datasets, respectively (Table 1). In contrast, the BR and NBD models exhibited inadequate predictive capacities (Table 1). The prediction band showing relatively better performance for both models was concentrated at 750 nm (Fig. 4b, d), with the identified band combination remaining consistent (i.e., 755 and 759 nm, Table 1). The identified BR index R₇₅₅/R₇₅₉ and NBD index (R₇₅₅ − R₇₅₉)/(R₇₅₅ + R₇₅₉) consistently yielded lower R² values and higher RMSE values for both the calibration and validation datasets.

Fig. 4.

Visualization of the coefficient of determination (R²) for the optimal band or band combinations of the four narrow-band models against leaf water content (LWC) of Populus alba var. pyramidalis. SB single band (a), BR band ratio (b), BS band subtraction (c), NBD normalized band difference (d)

Performance of multivariate models

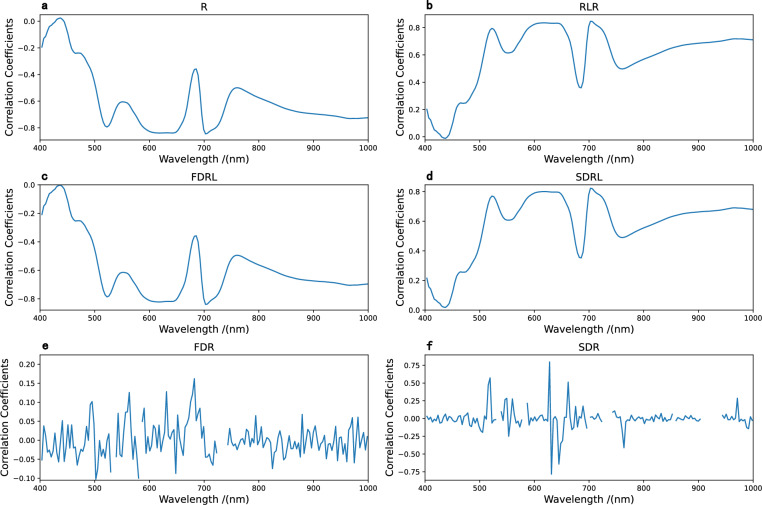
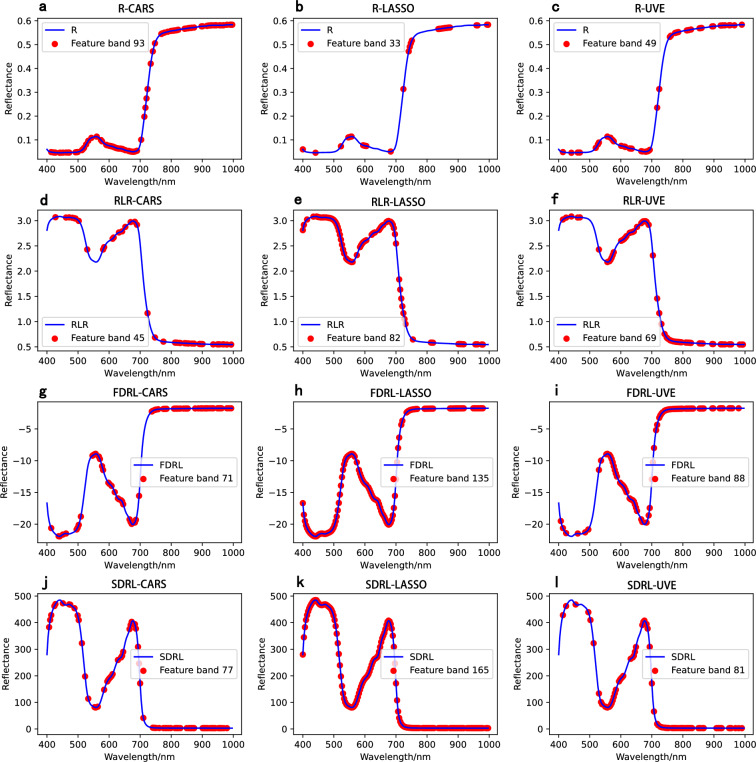
While most of the multivariate models developed in this study demonstrated a high degree of robustness in predicting LWC, spectral preprocessing, feature band screening, and the choice of regression algorithm significantly influenced model accuracy (Tables 2–4). Notably, when comparing different leaf reflectance preprocessing methods, R, RLR-, FDRL- and SDRL-transformed reflectance exhibited stronger correlations with LWC, achieving correlation coefficients of 0.8 or higher across multiple wavelengths (Fig. 5a–d). In contrast, the correlations between FDR- and SDR-preprocessed leaf reflectance and LWC were notably weaker, with correlation coefficients nearing zero across almost all wavelengths (Fig. 5e, f). Therefore, in subsequent multivariate modeling, R, RLR-, FDRL-, and SDRL-transformed leaf reflectance were utilized as input. Regarding feature band screening, raw leaf spectral reflectance (R) yielded the highest number of selected feature bands for CARS (Fig. 6a), whereas it yielded the fewest number for both LASSO and UVE (Fig. 6b, c). Overall, CARS resulted in the lowest number of selected feature bands for the preprocessed reflectance data (Fig. 6d, g, j), whereas LASSO identified the highest number (Fig. 6e, h, k). Regardless of the employed method, there was no fundamental difference in the number of selected feature bands between the VIS and NIR spectra.

Table 2.

Evaluation of LWC prediction models fitted by MLR

Spectrally-derived data	Feature band screening methods	Calibration (n = 454)		Validation (n = 120)
		R2	RMSE	R2	RMSE
R	None	0.9961	0.009	0.8539	0.0831
	CARS	0.9932	0.0118	0.9779	0.0323
	LASSO	0.9802	0.0202	0.9245	0.0598
	UVE	0.9945	0.0106	0.8911	0.0718
RLR	None	0.996	0.009	0.8719	0.0779
	CARS	0.9941	0.011	0.9754	0.0341
	LASSO	0.9927	0.0123	0.9349	0.0555
	UVE	0.9948	0.0104	0.9139	0.0638
FDRL	None	0.9954	0.0097	0.9423	0.0523
	CARS	0.9936	0.0115	0.98	0.0307
	LASSO	0.9944	0.0107	0.9448	0.0511
	UVE	0.994	0.0111	0.9743	0.0349
SDRL	None	0.9943	0.0108	0.936	0.055
	CARS	0.9929	0.0121	0.9531	0.0471
	LASSO	0.994	0.0111	0.9301	0.0575
	UVE	0.9901	0.0142	0.9479	0.0497

The model with the highest R² value for the calibration dataset was shown in bold

R raw reflectance, RLR the reciprocal logarithm of reflectance, FDRL first-order differential of the reciprocal logarithm of reflectance, SDRL second-order differential of the reciprocal logarithm of reflectance, CARS competitive adaptive reweighted sampling, LASSO least absolute shrinkage and selection operator, UVE uninformative variable elimination

Table 4.

Evaluation of LWC prediction models fitted by SVR

Spectrally-derived data	Feature band screening methods	Calibration (n = 454)		Validation (n = 120)
		R2	RMSE	R2	RMSE
R	None	0.9705	0.0246	0.9352	0.0554
	CARS	0.9616	0.028	0.9078	0.0661
	LASSO	0.9529	0.0311	0.8841	0.0741
	UVE	0.9679	0.0256	0.9248	0.0597
RLR	None	0.9793	0.0206	0.964	0.0413
	CARS	0.9845	0.0178	0.9606	0.0432
	LASSO	0.9757	0.0223	0.9387	0.0539
	UVE	0.9851	0.0175	0.9468	0.0502
FDRL	None	−20.0427	0.6568	−15.684	0.8887
	CARS	−2.0746	0.251	−0.3743	0.2551
	LASSO	−19.246	0.6442	−38.9445	1.3751
	UVE	−8.8804	0.45	−10.3724	0.7337
SDRL	None	−3,401,226.87	264.0478	−3,400,301	401.2004
	CARS	−875,789.720	133.9877	−849,911.9	200.581
	LASSO	−4,670,267.21	309.4109	−2,675,497	355.8812
	UVE	−603,805.878	111.2535	−933,232.4	210.1831

The model with the highest R² value for the calibration dataset was shown in bold

R raw reflectance, RLR the reciprocal logarithm of reflectance, FDRL first-order differential of the reciprocal logarithm of reflectance, SDRL second-order differential of the reciprocal logarithm of reflectance, CARS competitive adaptive reweighted sampling, LASSO least absolute shrinkage and selection operator, UVE uninformative variable elimination

Fig. 5.

Correlation coefficients between leaf water content (LWC) and raw and preprocessed spectral reflectance. R raw reflectance (a), RLR the reciprocal logarithm of reflectance (b), FDRL first-order differential of the reciprocal logarithm of reflectance (c), SDRL second-order differential of the reciprocal logarithm of reflectance (d), FDR first-order differential of reflectance (e), SDR second-order differential of reflectance (f)

Fig. 6.

Distribution of feature bands of different pre-processed spectral reflectance with the three featured band screening methods. R raw reflectance, RLR the reciprocal logarithm of reflectance, FDRL first-order differential of the reciprocal logarithm of reflectance, SDRL second-order differential of the reciprocal logarithm of reflectance, CARS competitive adaptive reweighted sampling, LASSO least absolute shrinkage and selection operator, UVE uninformative variable elimination. For each panel, the number of selected feature bands was shown

Based on the selected feature bands derived from R, RLR-, FDRL-, and SDRL-preprocessed reflectance spectra, multivariate models using MLR, PLSR, and SVR were established for LWC prediction. Overall, MLR showed strong prediction performance, with all models achieving R² values exceeding 98% for the calibration dataset (Table 2). Among these models, the FDRL-CARS-MLR combination demonstrated the highest robustness, displaying excellent statistical metrics for the calibration dataset (R² of 0.9936 and RMSE of 0.0115) and excellent performance for the validation dataset (R² of 0.98 and RMSE of 0.0307). For the PLSR algorithm, all models demonstrated outstanding prediction effectiveness, characterized by higher R² and lower RMSE values for both the calibration and validation datasets (Table 3). Among them, the FDRL-UVE-PLSR combination exhibited superior model performance, yielding notably high R² values of 0.9925 and 0.9853 for the calibration and validation datasets, respectively, along with correspondingly low RMSE values of 0.0124 and 0.0264. Notably, this multivariate model achieved optimal statistical performance for the validation dataset in the present study (Tables 2–4 and Fig. 7). For the SVR method, models utilizing R and RLR-preprocessed reflectance exhibited reliable predictive capabilities, with the RLR-transformed reflectance model without feature band selection demonstrating the best model performance, i.e., R² values of 0.9793 and 0.964 and RMSE values of 0.0206 and 0.0413 for the calibration and validation datasets, respectively (Table 4). However, models based on FDRL- and SDRL-preprocessed reflectance data exhibited poor performance, as evidenced by negative R² values and/or exceptionally high RMSE values (Table 4).

Table 3.

Evaluation of LWC prediction models fitted by PLSR

Spectrally-derived data	Feature band screening methods	Calibration (n = 454)		Validation (n = 120)
		R2	RMSE	R2	RMSE
R	None	0.9934	0.0116	0.9656	0.0404
	CARS	0.9925	0.0124	0.9763	0.0335
	LASSO	0.9802	0.0202	0.9245	0.0598
	UVE	0.9932	0.0118	0.9688	0.0384
RLR	None	0.9938	0.0113	0.9497	0.0488
	CARS	0.9933	0.0117	0.9806	0.0303
	LASSO	0.9913	0.0133	0.9356	0.0552
	UVE	0.9936	0.0114	0.9742	0.0349
FDRL	None	0.9931	0.0119	0.9543	0.0465
	CARS	0.9925	0.0124	0.9839	0.0276
	LASSO	0.9923	0.0126	0.9431	0.0519
	UVE	0.9925	0.0124	0.9853	0.0264
SDRL	None	0.9896	0.0146	0.9182	0.0622
	CARS	0.9897	0.0145	0.9508	0.0482
	LASSO	0.9895	0.0147	0.9115	0.0647
	UVE	0.9882	0.0155	0.9722	0.0363

The model with the highest R² value for the calibration dataset was shown in bold

R raw reflectance, RLR the reciprocal logarithm of reflectance, FDRL first-order differential of the reciprocal logarithm of reflectance, SDRL second-order differential of the reciprocal logarithm of reflectance, CARS competitive adaptive reweighted sampling, LASSO least absolute shrinkage and selection operator, UVE uninformative variable elimination

Fig. 7.

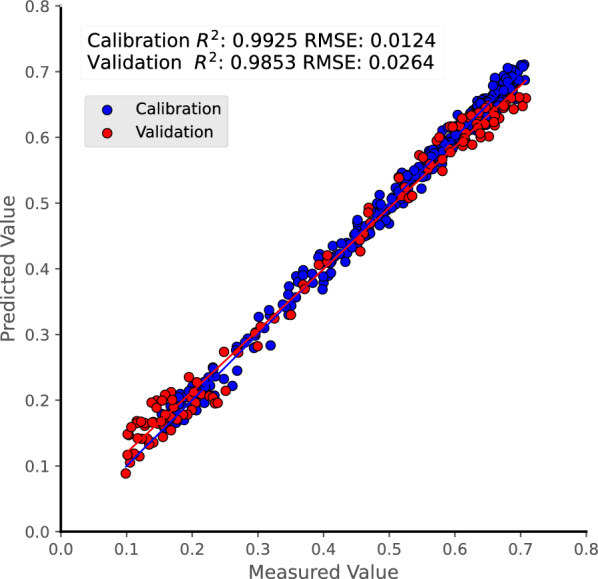
Measured vs. model-predicted scatter plots for leaf water content (LWC) of P. alba var. pyramidalis. The predicted values were produced using the best multivariate models. Data points and the corresponding fitted regression for the calibration dataset are shown in blue, and the validation dataset in red

Leaf water content mapping

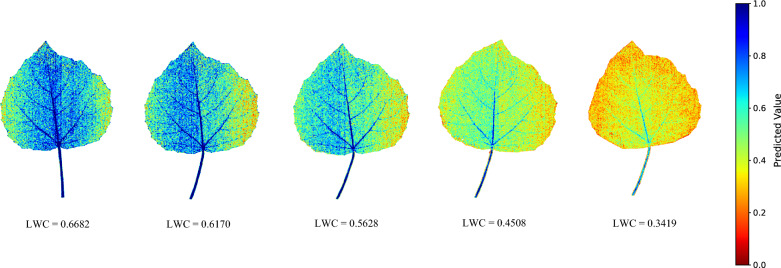
Utilizing the optimal multivariate LWC prediction model, detailed, pixel-level mapping of water content distribution within the leaves was conducted throughout the dehydration sequence. During this sequence, the margins of the leaf lamina exhibited a more accelerated rate of water loss compared to the central region, while the leaf veins retained relatively higher moisture content until the surface-averaged LWC reached significantly diminished levels (Fig. 8). Notably, the predicted water content exhibited spatial heterogeneity across the leaf surface for each measurement, manifesting lower moisture content at the margins in contrast to the middle region wherein the veins converged (Fig. 8). Furthermore, similar to the leaf veins, the petiole also displayed higher water content and demonstrated a stronger water-holding capacity against dehydration.

Fig. 8.

Contours of moisture content distribution across detached Populus alba var. pyramidalis leaves with contrasting surface-averaged water content. The value below each leaf contour indicates its surface-averaged water content (LWC)

Discussion

Based on spectral reflectance and water content data from detached P. alba var. pyramidalis leaves subjected to varying degrees of dehydration, we developed narrow-band and full-band (VIS–NIR) models for LWC prediction. We identified two narrow-band indices along with the optimal algorithmic combination of multivariate models. The two narrow-band indices derived from the visible spectrum effectively encapsulated the comprehensive physiological response of leaves to dehydration. While the predictive accuracy of the multivariate models developed through three machine learning regression algorithms exceeded that of the narrow-band models, the performance of these multivariate models was affected by spectral preprocessing and the selection of characteristic variables. Furthermore, the visualization of water content across the leaf surface, using the optimal multivariate model, elucidated the foliar water profile under various desiccation levels. This advancement broadens our comprehension of leaf-scale water-related physiology and contributes to monitoring forest health and assessing risks associated with drought-induced tree mortality and forest decline.

Performance of narrow-band spectral indices

The identified narrow-band indices from the visible spectrum exhibited promising potential for predicting LWC in P. alba var. pyramidalis. Narrow-band spectral models are widely utilized in vegetation remote sensing due to their high effectiveness in characterizing plant attributes. Commonly employed indices for assessing canopy and leaf water content include R₉₀₀/R₉₇₀ for the WI [52], R₉₇₀/R₉₀₀ for the water band index (WBI) [50], [(R₈₆₀ − R₁₂₄₀)/(R₈₆₀ + R₁₂₄₀)] for the NDWI [27], R₈₆₀/R₁₂₄₀ for the SRWI [73], R₁₃₀₀/R₁₄₅₀ for the leaf water index (LWI) [58], and R₁₆₀₀/R₈₂₀ for the moisture stress index (MSI) [31]. These indices have been extensively used for the rapid evaluation of plant water status across various species, biomes, and geographical regions [28, 39, 72]. The derivation of these narrow-band indices relies on the ratio and/or normalized difference calculation of distinct near-infrared bands, reflecting the fact that moisture absorption predominantly occurs within the infrared range of the plant spectrum [12]. However, investigations exploring the efficacy of remote sensing in predicting plant water status using spectral information from the visible spectrum remain limited. In the present study, we identified two narrow-band spectral indices from the visible spectrum that demonstrate high accuracy in forecasting LWC in the studied tree species, i.e., the single band index (R₆₂₇) and the band subtract index (R₄₃₇ − R₄₄₄). These visible spectral bands, which are primarily influenced by leaf pigment concentration, generally do not directly reflect the absorption of radiation by water. However, dehydration can reduce the absorption of radiation by pigment, enabling secondary effects of water content to influence visible reflectance [13]. As a result, these pigment-sensitive bands may also serve as proxies for predicting LWC to some extent [12, 51, 67]. Leaf pigment concentration has been suggested to be closely associated with water content, and severe dehydration may damage leaf cellular structure, leading to pigment degradation. Under water-stressed conditions, pigment instability may reduce absolute pigment content, resulting in detectable changes in corresponding sensitive spectra [37, 60]. Even if the absolute pigment content remains stable or undergoes slight variations, dehydration-induced reductions in leaf cell volume, area, and weight may alter relative pigment content, affecting pigment-sensitive spectra [33]. Consequently, the narrow-band indices identified in this study may encapsulate bands that collectively capture the comprehensive sensitivity of various leaf components to water stress, though further investigations into the coupled changes in leaf pigment concentration, element composition, and cellular structure during dehydration are needed. These indices offer a theoretical foundation for the design and development of cost-effective spectrometers equipped with a limited number of specific bands in the visible spectrum, enabling rapid and efficient field assessment of water status in drought-prone species such as P. alba var. pyramidalis.

Influence of spectral preprocessing, band selection, and regression algorithms on the robustness of multivariate models

Overall, the majority of the multivariate models we developed demonstrated robust predictive capabilities for LWC; however, the selection and combination of methodologies for spectral preprocessing, feature variable screening, and regression significantly influenced their predictive performance. High-quality spectral data forms the foundation for ensuring model accuracy. To acquire spectra from leaves with varying moisture contents, we utilized a darkroom illuminated by halogen lamps, effectively minimizing stray light interference and enhancing data quality [21]. Furthermore, in conjunction with high-quality spectral data and corresponding physiological measurements, reducing data noise, extracting relevant variables, and selecting suitable regression algorithms are critical factors contributing to model accuracy [15]. We found that the integration of differential and reciprocal transformations enhanced the correlation between spectra data and LWC, whereas the application of differential transformation alone proved inadequate for establishing this correlation. This emphasizes the critical role of reciprocal transformation in attenuating background interference in spectral data [25]. Concerning feature band selection methods, CARS identified the fewest characteristic bands, while LASSO yielded the most. This discrepancy can be ascribed to their differing methodologies and selection criteria. CARS utilizes an adaptive, iterative selection process that emphasizes the identification of the most relevant wavelengths across multiple stages, while LASSO adopts a regularization strategy that inherently reduces the number of features by promoting sparsity within the model. Consequently, CARS permits more confined feature selection, identifying and retaining fewer bands than LASSO in spectral analysis contexts [36, 63].

Among the machine learning regression methods used in this study, PLSR exhibited the most favorable performance, particularly when integrated with feature band subsets selected via UVE. This finding aligns with prior research indicating that PLSR is well-suited for developing multivariate spectral prediction models for plant attributes [11, 75]. Although MLR demonstrated overall stability and strong generalization capabilities with the derived data, its validation performance was inferior to that of PLSR, suggesting that relatively complex model could achieve enhanced predictive robustness [7]. SVR performed adequately in certain instances; however, it proved entirely ineffective with the FDRL and SDRL-transformed data. This limitation likely arises from the fact that, while both FDRL and SDRL transformations enhance the fine details of spectral signals, they can also lead to uneven feature distributions or the inappropriate amplification or compression of feature magnitudes. These effects can undermine the performance of regression algorithms, such as SVR equipped with the RBF kernel, which is particularly sensitive to the scale and distribution of input features. As a result, this misalignment can cause issues such as underfitting or misfitting. The poor performance of the SVR models combined with FDRL and SDRL transformation underscores the substantial impact of spectral reflectance preprocessing on the predictive performance of multivariate models [22, 47]. These results highlight the necessity of considering various combinations of methods for reflectance preprocessing, feature variable selection, and regression algorithms in the development of optimal predictive models.

Significance of visualizing water distribution across the leaf surface

The visualization of water distribution across the leaf surface provides insights into leaf-scale water-related physiology. Compared to fiber-optic spectrometers, hyperspectral cameras offer advantages in capturing both detailed spectral information and spatial variations, thereby providing additional insights for retrieving and visualizing plant physiological status [6]. In the study of plant water physiology, mapping the spatial distribution of water content within leaves contributes to the exploration of intricate mechanisms related to foliar water transport, allocation, storage, and utilization, thus providing intuitive evidence for investigating plant water relations under desiccation risks [54]. By observing variations in the spatial distribution of leaf water content under different levels of dehydration, the responsive patterns and resilience mechanisms of plants to drought stress can be investigated [9, 35]. Our findings indicate that moisture content decreased more rapidly at the leaf margin, while regions around the midrib exhibited relatively strong water-holding capacity. This aligns with previous research quantifying leaf water profiles using neutron imaging, terahertz radiation, and hyperspectral reflectance [10, 20, 48, 62]. The accelerated rate of water loss at the leaf margin can be attributed to heterogeneous lamina thickness and uneven distribution of veins, characterized by thinner mesophyll and a less extensive venation network at the leaf edge, rendering the margin more susceptible to dehydration [76].

Mapping moisture distribution within leaves based on spectral prediction models and hyperspectral imagery opens up opportunities for monitoring drought stress in forest canopies and assessing forest health with increased temporal resolution and over extensive spatial areas. A notable advantage of visualizing leaf water profiles using hyperspectral imagery lies in its non-contact nature, distinguishing it from conventional physiological measurements that rely on the physical contact between sensors and measurement point or chemical analysis of detached samples in laboratory settings [34]. This noninvasive characteristic eliminates the need for contact-type analysis or destructive sampling, allowing for repeated measurements over time and thus facilitating the long-term in situ assessment and monitoring of drought stress dynamics, even at high temporal resolution [3, 62]. Importantly, the ability to detect early signs of water stress in leaves and through imaging technology provides valuable information for forest managers, enabling them to identify areas at increased drought stress and associated mortality risk within forest ecosystems and implement timely, targeted interventions to mitigate drought impacts on forest health [26, 39]. Furthermore, the development of these methodologies has the potential to enhance remote sensing applications, as hyperspectral cameras can be mounted on handheld, airborne, or satellite platforms to perform ground-, flight-, and space-based sensing of the water status of individual leaves, whole trees, and forest stands following the model transfer learning. This enables high-frequency monitoring of forest drought stress over extensive areas, providing valuable information for regional and global assessments of forest drought resilience [24, 38].

Concluding remarks

The spectral prediction models developed in this study present an innovative, reliable method for determining LWC in plants, contributing to non-destructive monitoring of drought stress levels and decline risks of vegetation in drought-prone areas. We identified two narrow-band indices that showed satisfactory LWC prediction accuracy, providing a straightforward and efficient solution for expeditiously estimating LWC in field conditions. While the predictive performance varied slightly with the combinations of methods for reflectance preprocessing, band selection, and regression, the developed multivariate models based on full-band spectrum were mostly highly robust in predicting LWC. The optimal multivariate model effectively depicted the leaf water profile, enhancing our understanding of leaf-scale water-related physiology and contributing to the mapping of forest health conditions and associated risks of drought-induced mortality. The prediction models developed based on hyperspectral imagery, along with the method for visualizing moisture content distribution across the leaf surface, serve as valuable tools for evaluating the impacts of heightened drought stress and implementing timely interventions to mitigate its effects on forest ecosystems in drought-prone areas.

Author contributions

Z.-K.: Data Curation, Investigation, Methodology, Validation, Writing—Review & Editing. H.-L. Data Curation, Investigation, Visualization, Formal analysis, Software. X.-W. Conceptualization, Investigation, Formal analysis, Methodology, Project administration, Writing—Original Draft. H.-F. Formal analysis. G.-Y. Funding acquisition, Resources, Supervision, Validation, Writing—Review & Editing.

Funding

This work was supported by the National Key R & D Program of China (2020YFA0608100, 2023YFF1304201), the National Natural Science Foundation of China (32220103010, 32192431, 32360282), the Major Program of Institute of Applied Ecology, Chinese Academy of Sciences (IAEMP202201), the Liaoning Provincial Science and Technology Major Project (2023JH1/10400001), the CAS Project for Young Scientists in Basic Research (YSBR-108), the China Postdoctoral Science Foundation (2023M733674), the Project of Doctoral Research Startup Fund of Liaoning Province (2023‐BS‐021), and the Fund of CAS Key Laboratory of Forest Ecology and Silviculture, Institute of Applied Ecology, Chinese Academy of Sciences (KLFES-2035, KLFES-2025).

Data availability

The data that support the findings of this study are not openly available due to reasons of sensitivity and are available from the corresponding author upon reasonable request.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.