A Generalized Multi-Detector Combination Approach for Differential Item Functioning Detection

Abstract

Many studies on differential item functioning (DIF) detection rely on single detection methods (SDMs), each of which necessitates specific assumptions that may not always be validated. Using an inappropriate SDM can lead to diminished accuracy in DIF detection. To address this limitation, a novel multi-detector combination (MDC) approach is proposed. Unlike SDMs, MDC effectively evaluates the relevance of different SDMs under various test conditions and integrates them using supervised learning, thereby mitigating the risk associated with selecting a suboptimal SDM for DIF detection. This study aimed to validate the accuracy of the MDC approach by applying five types of SDMs and four distinct supervised learning methods in MDC modeling. Model performance was assessed using the area under the curve (AUC), which provided a comprehensive measure of the ability of the model to distinguish between classes across all threshold levels, with higher AUC values indicating higher accuracy. The MDC methods consistently achieved higher average AUC values compared to SDMs in both matched test sets (where test conditions align with the training set) and unmatched test sets. Furthermore, MDC outperformed all SDMs under each test condition. These findings indicated that MDC is highly accurate and robust across diverse test conditions, establishing it as a viable method for practical DIF detection.

Introduction

Differential item functioning (DIF) refers to functional differences across groups that are unrelated to the purpose of the test. Specifically, it describes the tendency of a test item to be easier or more difficult for one group of test takers compared to another group of equally competent individuals. DIF detection is a valuable statistical tool for identifying potential test bias (Ackerman, 1992). Therefore, developing accurate DIF detection methods remains a key focus in both applied and methodological research.

Given the various interpretations and definitions of DIF, numerous DIF detection methods have been developed (Hutchinson & Mitchell, 2019). Recent advancements have further refined these methods (Bauer, 2023; Hladká et al., 2023). Many DIF detection studies employ a single detection method (SDM). However, each SDM relies on specific assumptions and may be influenced by varying test conditions. These conditions can be categorized into observable and unobservable types. Observable conditions, such as sample size, can impact DIF detection; for example, when sample sizes per group are fewer than 500, applying Item Response Theory (IRT) methods to estimate DIF becomes challenging (Martinková et al., 2017). Unobservable conditions, such as proportions of DIF items (Gierl et al., 2004) and DIF types (uniform and nonuniform) (Berger & Tutz, 2016), add further complexity. The interaction of these factors can complicate the identification of appropriate DIF detection methods, posing challenges even for experienced researchers.

Additionally, DIF detection results from different methods often exhibit inconsistencies (Karami & Salmani Nodoushan, 2011). Relying solely on one method can introduce significant risks, underscoring the need for multiple methods to achieve more robust results. While several software packages offer a range of DIF detection methods (Magis et al., 2010; Martinkova & Hladka, 2018), current practice typically involves either listing results from different methods or using a simple average or voting method without a comprehensive synthesis of the outcomes. Methods that integrate multiple DIF detection results in a simplistic manner (e.g., voting) are termed simple integration methods (SIMs), which often oversimplify the process. These methods do not account for the varying weights of results derived from different methods under specific testing conditions. For example, in small sample sizes, non-IRT DIF detection methods should be prioritized over IRT methods. Furthermore, integrated results may be unstable; for instance, employing more IRT methods in small sample sizes can yield less reliable results compared to using only non-IRT methods.

In contrast to the aforementioned approaches, the proposed Multi-Detectors Combination (MDC) framework facilitates the simultaneous application of multiple SDMs under specific test conditions and integrates the results into a final prediction using supervised learning methods. This study aimed to evaluate the effectiveness of the MDC approach in DIF detection by addressing the following questions: (1) Overall Accuracy: Does the MDC framework offer superior overall accuracy compared to individual SDMs? (2) Robustness: Can the MDC framework maintain high accuracy across various test conditions?

The remainder of this study is structured as follows: Section 2 reviews related work supporting the MDC framework. Section 3 details the MDC procedures. Sections 4 (Method) and 5 (Results) validate the MDC through simulation experiments. Section 6 applies the MDC to a real data example. Finally, Section 7 discusses the findings.

Related Works

DIF Detection Methods

Mantel-Haenszel (MH)

The MH method is similar to a chi-square test and is expressed by the formula (Holland & Thayer, 1986; Martinková et al., 2017): ${\chi }_{MH}^2={\frac{\left\{\left|{\sum }_k\left[A_k-\frac{\left(A_k+B_k\right)\left(A_k+C_k\right)}{N_k}\right]\right|-0.5\right\}}{{\displaystyle \sum }_k\frac{\left(A_k+B_k\right)\left(A_k+C_k\right)\left(B_k+D_k\right)\left(C_k+D_k\right)}{N_k^2\left(N_k=1\right)}}}^2$ . In this formula, $A_k$ and $B_k$ represent the counts of examinees in the reference group that scored “k” and answered correctly or incorrectly, respectively, while $C_k$ and $D_k$ denote the counts for the focal group. Here, $N_k=A_k+B_k+C_k+D_k$ .

Standardization Approach

The Standardization approach (Dorans et al., 1992) is another commonly used method defined as follows: $STD\hspace{0.17em}P-DIF=\frac{\sum \left\{W_S\left[P_{fs}-P_{rs}\right]\right\}}{\sum \left\{W_S\right\}}$ , where $\frac{W_s}{\sum \left\{W_S\right\}}$ denotes the weighting factor based on the focal group distribution, implemented at the score level designated as “S,” $\left[P_{fs}-P_{rs}\right]$ represents the difference in the proportions of correct responses between the focal group ( $P_{fs}$ ) and the reference group ( $P_{rs}$ ).

Logistic Regression (LR)

The LR formula is expressed as follows (Rogers & Swaminathan, 1993): $Z={\tau }_0+{\tau }_1\theta$ $+{\tau }_{2}g+{\tau }_3\left(\theta g\right)$ , where Z denotes the probability of a correct response, $\theta$ is the observed trait level of the examinee (usually total test score), and g represents group membership. ${\tau }_1$ is a main effect of score, ${\tau }_2$ is a main effect of group, and ${\tau }_3$ is an interaction of score with group.

Lord’s Chi-Squared Test

Lord’s Chi-squared method is based on the IRT framework. For example, using the two-parameter IRT model, the formula is represented as

$$P\left(U_{i,j}=1|{\theta }_i,{\alpha }_j,{\beta }_j\right)=\frac{\mathit{exp}\left({\alpha }_j\left({\theta }_i-{\beta }_j\right)\right)}{1+\mathit{exp}\left({\alpha }_j\left({\theta }_i-{\beta }_j\right)\right)}$$ (1)

where (P) represents the probability of respondent (i) answering item (j) correctly, ${\theta }_i$ denotes the ability of respondent (i), ${\alpha }_j$ denotes the discrimination of item item (j), and ${\beta }_j$ denotes the item difficulty. This method first estimates the item parameters for both the focal and reference groups separately. Lord’s chi-squared test then evaluates whether the item parameters are equal across the subpopulations; if not, the item is flagged as exhibiting DIF (McLaughlin & Drasgow, 1987).

Raju Area

The Raju area method estimates the significance of the area between two Item Response Functions (IRFs; Raju, 1990). It provides the asymptotic sampling distribution for the area between the IRFs of the focal and reference groups, which helps determine if the differences in IRFs are significant for detecting DIF.

Supervised Learning

Commonly used supervised learning methods include LR, Naive Bayes (NB), Support Vector Machine (SVM), and Tree Augmented Naive Bayes (TAN).

The formula for LR is

$$P\left(TrueDIF\mid \text{SDM}\right)=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_1{\text{SDM}}_1...{\beta }_n{\text{SDM}}_n\right)}}$$ (2)

Based on the training dataset, the coefficients { ${\mathrm{\beta }}_0,\dots {\mathrm{\beta }}_{\mathrm{n}}$ } are estimated, with each ${\mathrm{\beta }}_{\mathrm{i}}$ representing the weight of ${\text{SDM}}_i$ in predicting TrueDIF.

The NB method operates probabilistically, assuming independence among different SDMs, resulting in the following formula:

$$P\left(TrueDIF|\text{SDM}\right)=\frac{1}{z}P\left(TrueDIF\right){\displaystyle \prod }_{i=1}^{n}P\left({\text{SDM}}_i|TrueDIF\right)$$ (3)

Here, Z is a scaling factor ensuring that probabilities remain between 0 and 1. The conditional distributions $P\left({\text{SDM}}_i\mid TrueDIF\right)$ represent the influence of each SDM on TrueDIF.

The TAN method addresses the independence assumption of NB by incorporating a tree structure (Friedman et al., 1997). This is represented graphically in Figure S1, where circles denote variable nodes such as TrueDIF and SDMs, and directed edges (arrows) indicate relationships between nodes. Specifically, an arrow from TrueDIF to SDMs suggests that TrueDIF influences SDMs, indicating $P\left({\text{SDM}}_i\right)\ne P\left({\text{SDM}}_i\mid TrueDIF\right)$ . The directed edges can be denoted as Parent ( ${\text{SDM}}_i$ ) = { $TrueDIF$ }. Unlike NB, where no edges exist between SDMs, TAN facilitates interdependence between SDMs. For example, SDM₁ influences SDM₂ in TAN, indicating that Parent ( ${\text{SDM}}_2$ ) = { $TrueDIF$ , ${\text{SDM}}_1$ }.

The formulation for TAN extends Formula (3) as follows:

$$P\left(TrueDIF|\text{SDM}\right)=\frac{1}{z}P\left(TrueDIF\right){\displaystyle \prod }_{i=1}^{n}P\left({\text{SDM}}_i|Parent\left({\text{SDM}}_i\right)\right)$$ (4)

Structural learning is employed to determine the relationships between nodes. This process involves computing the mutual information between pairs of SDMs, selecting the pair with the maximum mutual information to establish the initial edge, and constructing a tree structure based on pairwise mutual information (Chow & Liu, 1968). The formula for mutual information is as follows: $I\left(X_i,X_{\mathrm{j}}\right)={\displaystyle \sum }_{X_i,X_{\mathrm{j}}}P\left(X_i,X_{\mathrm{j}}\right)\mathit{log}\frac{P\left({X_i,X}_j\right)}{P\left(X_i\right)P\left(X_j\right)}$ . Here, $X_i$ represents the nodes.

SVM is a robust supervised learning algorithm commonly used for classification and regression tasks (Cervantes et al., 2020). The core concept of SVM is to identify an optimal hyperplane that maximally separates different classes of data points. In a two-dimensional space with features (SDM₁ and SDM₂) and a binary target variable (TrueDIF), SVM aims to find the hyperplane that best distinguishes data points where TrueDIF equals 1 from those where TrueDIF equals 0. This concept can be extended to higher-dimensional spaces (SDM₁ …SDM_i), where the hyperplane becomes a higher-dimensional decision boundary. SVM is particularly effective in high-dimensional spaces and is robust to overfitting, especially when the number of dimensions exceeds the number of samples. However, SVM may become less efficient with very large datasets and requires careful tuning of parameters such as the kernel type and regularization term.

Model Evaluation Metrics and Thresholds

In supervised learning, prediction results are expressed as probability values. By applying a threshold, these probabilities can be converted into binary outcomes: DIF or noDIF. Specificity and Sensitivity are commonly used metrics for evaluating models with binary outcomes. Specificity is defined as P (True Value = DIF | Prediction = DIF), which is equivalent to 1 minus the Type I error rate. Sensitivity, akin to power, is defined as P (True Value = noDIF | Prediction = noDIF). As the threshold increases, classifying a case as DIF becomes more challenging. Consequently, specificity increases while sensitivity decreases. The variability in specificity and sensitivity complicates direct comparisons between models.

To address this issue, the Area Under the Curve (AUC) provides a more stable and comprehensive assessment (Jin & Ling, 2005). The AUC is introduced as a robust evaluation criterion, as supported by previous research (Magis & Tuerlinckx, 2016). As illustrated in Figure S2, the receiver operating characteristic (ROC) curve is plotted by graphing sensitivity against (1 - specificity) at various thresholds. The area under this curve quantifies the model’s predictive performance. For example, Model B exhibits a higher AUC than Model A, indicating that for the same sensitivity level (e.g., 81.4%), Model B achieves a higher specificity (75%) compared to Model A (30%).

When converting final results into binary outcomes, researchers can select a threshold based on given preferences for sensitivity or specificity. In the absence of a clear preference, a classic approach involves maximizing the sum of sensitivity and specificity, which corresponds to finding the threshold that maximizes the distance from the identity (diagonal) line (Youden, 1950). As depicted in Figure S2, by exhaustively evaluating all possible thresholds, the optimal threshold (Best_T) is identified as the point that maximizes the combined sum of sensitivity and specificity.

Procedures of Multi-Detectors Combination (MDC) Framework

The MDC framework involves three primary stages: establishing a training dataset, MDC modeling, and applying the MDC. DIF analysis on a target dataset involves the following steps:

Establishing the Training Dataset

The objective of this stage is to establish a training dataset that accurately represents the target data. The training data is generated through simulation.

• Step 1: Generating Response Data. This involves selecting a measurement model and setting the test conditions. For each combination of test conditions, several replications are simulated to serve as representatives of the target dataset.

• Step 2: Calculating SDM. For each data unit, different DIF detection methods are applied to obtain the i $\text{SDM}$ .

• Step 3: Constructing the Training Set. The SDM results of each item are combined with its TrueDIF label, and the results of all replications are merged to form the overall training set.

MDC Modeling

• Step 4: Model Training. Supervised learning methods are applied on the training dataset. In this process, TrueDIF serves as the dependent variable, while SDM values are the independent variables. This results in the construction of S ${\text{Model}}_s$ , where S represents the number of supervised learning approaches employed.

• Step 5: Setting Thresholds. The models developed in Step 4 generate probability values. A threshold is applied to classify items as DIF or non-DIF. The threshold is determined based on specific criteria, such as the Youden Index.

Applying MDC

The MDC framework is applied to the target dataset. The SDM values (as described in Step 2) are calculated and used as predictor variables. The trained models and thresholds (from Steps 4 and 5) are utilized to determine whether an item is flagged as DIF (binary classification).

Methodology

Simulated Data

This study employed the two-parameter IRT model (Formula (1)) to investigate uniform and nonuniform DIF. Item parameters for the focal and reference groups were used to calculate the probability (P) of correctly answering each item under various test conditions, and response data matrices were subsequently generated based on (P).

The test conditions for data simulation were designed to generate three primary categories: the Training Set (TS), the Matching Test Set (MTS), which aligns with the conditions of the training set, and the Unmatching Test Set (UMTS), which does not match the conditions of the training set and was used to assess the generalizability of the model (Goretzko & Bühner, 2020). The detailed specifications are provided in Table S1.

Observable Test Conditions: The MDC framework relies on specific observable test conditions. Thus, TS, MTS, and UMTS were set with consistent observable parameters, including: sample size at three levels—Small (n = 500), Medium (n = 1000), and Large (n = 2000) (Ma et al., 2021); sample size ratio at two levels—Balanced (0.5, indicating that the reference group constitutes 50% of the total sample) and Unbalanced (0.8, indicating that the reference group constitutes 80%) (Jin et al., 2018); test length at three levels: Short (20 items), Medium (40 items), and Long (60 items) tests.

DIF-Related Test Conditions: DIF types were defined based on differences in item parameters between the focal and reference groups. The discrimination differences (two levels) were of two types: uniform (Δ alpha = 0) and nonuniform DIF (Δ alpha = −1). The difficulty differences (two levels) were of two types: small (Δ beta = 0.4) and large effects (Δ beta = 0.8) (Jiang, 2019). The extent of parameter differences considered as DIF was determined based on specific research objectives or preferences. Consequently, TS, MTS, and UMTS were established with consistent DIF definitions. Proportions of DIF (two levels), which indicate the proportion of items displaying DIF: mild (0.2) and severe (0.3) in TS and MTS (Lim et al., 2022; Liu & Jane Rogers, 2022), and mild (0.1) and severe (0.4) in UMTS (Ma et al., 2021), with no overlap between conditions.

Other unobservable test conditions: Impact represents the differences in ability distributions between the focal and reference groups. TS and MTS had two levels: No Impact (R: N (0,1), indicating the ability distribution of the reference group R follows a normal distribution with mean = 0 and SD = 1; F: N (0,1)); Impact (R: N (0,1); F: N (−0.5,1)) (Lim et al., 2022). In UMTS (two levels): Significant impact (R: N (0,1); F: N (−1,1)); Reverse impact (R: N (−0.5,1); F: N (0,1)) (Lee, 2017). Item parameters for the reference group were initially determined. For TS and MTS, the discrimination parameter (aR) was drawn from N (1, 0.2), and the difficulty parameter (bR) was drawn from N (0,1) (Liu & Jane Rogers, 2022). In UMTS, aR was drawn from U (0.9, 2.5), while bR was drawn from U (−1.5, 1.5) (Frick et al., 2015). Based on the DIF proportions, the number of DIF items was determined. For DIF items, parameters were adjusted as follows: aR = aR + Δ alpha and bR = bR + Δ beta. For no-DIF items, the item parameters for the focal group were identical to those for the reference group.

A total of 288 test condition combinations were established, including 18 observable test condition combinations. For TS, 20 replications were generated for each combination of test conditions, while 100 replications were generated for MTS and UMTS. Data generation was performed using the “irtoys” package (Partchev et al., 2022).

Conducting MDC Procedures

After the generation of simulated data, the MDC process was applied to each dataset. In Step 2, the calculation of SDM involved assessing DIF using five detection methods: MH, Standardization Approach, LR, Lord’s Chi-squared Test, and Raju’s Area. A “purification” process was employed, involving iterative removal of items identified as DIF from the set used for equal means anchoring (Candell & Drasgow, 1988). This procedure was repeated until either the same items were identified twice as functioning differently or the maximum number of iterations (set to 10) was reached.

For Lord’s Chi-squared Test and Raju’s Area, Marginal Maximum Likelihood Estimation (MMLE) was used. MMLE assumes that respondents are a random sample from a population, and their abilities follow a standard normal distribution (Rizopoulos, 2007). Parameters were estimated separately for the focal and reference groups, and linked parameter estimates were performed on a common scale using a linear transformation (Cook & Eignor, 1991). Specifically, if the means of the difficulty parameters for the two groups are $\overline{b_R}$ and $\overline{b_F}$ , and the standard deviations are $S_{b_R}$ and $S_{b_F}$ , A and the intercept $B$ can be determined as $\raisebox{1ex}{$S_{b_R}$}\!\left/ \!\raisebox{-1ex}{$S_{b_F}$}\right.$ and $\overline{b_R}-A·\overline{b_F}$ , respectively. The transformation formulas $b_F^T=A·b_F+B$ and $a_F^T=\raisebox{1ex}{$a_F$}\!\left/ \!\raisebox{-1ex}{$A$}\right.$ were applied, where $b_F^T$ and $a_F^T$ represent the transformed item difficulties and discrimination parameters, respectively.

DIF was flagged based on a significance level (p-value) of 0.05. DIF detection was conducted using the “difR” package (Magis et al., 2010).

Under each observable condition (a total of 18 types), a unique training set was used, comprising multiple replications generated through simulation. For each training set, four supervised learning methods were employed: LR, NB, SVM, and TAN. The “glm” function was used for LR, the “e1071” package (Dimitriadou et al., 2008) for SVM, and the “bnlearn” package (Scutari & Denis, 2021) for NB and TAN. The “pROC” package (Robin et al., 2014) was used to determine the threshold for each model.

Additionally, two Simple Integration Methods (SIM) were calculated for comparison. The first method, Voting, considers an item as DIF if three or more out of five SDM results indicate DIF. The second method, Anyflagged, classifies an item as DIF if any one of the SDM results indicates DIF.

Outcome Measures Analysis

The subsequent analyses were conducted separately for the two validation sets, MTS and UMTS. Initially, MDC was applied to each replicate to predict DIF, and these predictions were compared with the True DIF. Metrics including the AUC, specificity, and sensitivity were calculated.

Subsequently, the overall means for AUC, specificity, and sensitivity were computed and compared using Cohen’s d. Marginal means for AUC under varying test conditions were also calculated, and a repeated measures ANOVA was performed on AUC. This analysis assessed both the main effects and the interaction effects of the DIF detection method and different test conditions. The ANOVA analyses were conducted using the “rstatix” package (Blanca et al., 2023). Finally, the correlations were compared to explore the relationship between SDM and MDC.

Results

Overall Comparison of Different Methods’ Performance

Table 1 presents the AUC values for the MTS, where all MDC methods demonstrated superior performance, with AUCs ranging from 79.8% to 81.4%. Among these, MDC (LR) achieved the highest AUC. Using MDC (LR) as the baseline, Cohen’s d were computed to compare the AUC values of other methods, revealing only minor differences among the four MDC methods, with effect sizes ranging from 0.014 to 0.109. In contrast, the AUC values for SDMs were generally lower, with Logistic yielding the highest AUC of 79.0%. Compared to MDC (LR), all SDM methods, except Logistic, exhibited significant effect sizes ranging from 0.377 to 1.136, while Logistic had a nearly small effect size of 0.180. A similar pattern was observed with the SIM, where the AUC of MDC (LR) compared to SIM exhibited Cohen’s d values ranging from 0.583 to 1.228.

Table 1.

Summary of Model Performance on MTS and UMTS.

Method		Matching test set (MTS)						Unmatching test set (UMTS)
		AUC		Specificity		Sensitivity		AUC		Specificity		Sensitivity
		M(%)	D	M(%)	d	M(%)	d	M(%)	d	M(%)	d	M(%)	d
Multi-Detectors combination (MDC)	LR	81.4	0.000	86.4	0.000	76.4	0.000	79.8	0.000	83.4	0.000	76.1	0.000
	NB	80.6	0.058	86.0	0.032	75.2	0.043	79.5	0.021	83.2	0.010	75.7	0.016
	SVM	79.8	0.109	94.5	−0.836	65.0	0.383	77.6	0.145	93.0	−0.685	62.2	0.491
	TAN	81.2	0.014	87.5	−0.100	74.8	0.056	79.8	−0.004	84.5	−0.065	75.1	0.038
Single detection methods (SDM)	M.H	76.6	0.377	85.8	0.046	67.4	0.337	75.8	0.282	83.3	0.004	68.3	0.301
	Stand	72.3	0.659	97.1	−1.185	47.5	1.037	71.0	0.614	96.7	−1.044	45.3	1.137
	Logistic	79.0	0.180	80.0	0.449	78.0	−0.057	78.2	0.106	77.2	0.333	79.3	−0.120
	Lord	63.2	1.136	55.4	1.025	69.1	0.242	67.8	0.703	62.7	0.702	71.8	0.151
	Raju	67.3	0.906	50.4	1.243	41.6	1.289	66.6	0.816	56.0	0.961	51.0	0.911
Simple integration methods (SIM)	Voting	73.8	0.583	81.9	0.313	65.6	0.386	74.5	0.363	81.0	0.131	67.9	0.301
	AnyFlagged	64.3	1.228	44.5	1.568	83.9	−0.290	67.1	0.834	49.1	1.273	85.1	−0.367

Note. M (%) represents the mean value in percentage (%). The effect size (d) represents Cohen’s d, using MDC (LR) as the baseline for comparison with each method.

In the UMTS, all MDC methods also demonstrated strong AUC values, ranging from 77.6% to 79.8%, with both MDC (LR) and MDC (TAN) achieving the highest AUC. Comparing the four MDC methods, effect sizes ranged from −0.004 to 0.145, with MDC (SVM) exhibiting the lowest AUC. Compared to MDC (LR), all SDM and SIM methods demonstrated notable differences, with effect sizes ranging from 0.106 to 0.834. Although the advantage of MDC methods over SDM and SIM methods diminished in the UMTS, MDC methods still outperformed SDM and SIM methods in terms of AUC.

Regarding sensitivity and specificity in MTS, AnyFlagged emerged as the most aggressive method, achieving the highest sensitivity (83.9%) but the lowest specificity (44.5%), which resulted in a comparatively lower overall AUC (64.3%). Conversely, Std exhibited the highest specificity (97.1%) but the lowest sensitivity (47.5%). In comparison, SVM demonstrated similar specificity (94.5%) but higher sensitivity (65.0%), resulting in a higher AUC than Std (79.8%).

Moreover, all results indicated specificity greater than 86.0% and sensitivity higher than 65.0%, avoiding particularly low values and extreme risks. This suggests a more favorable balance between sensitivity and specificity. A similar trend was observed in the UMTS.

The primary focus of this study was to evaluate the effectiveness of different methods in detecting DIF. Therefore, subsequent analyses focused on the AUC, considering its applicability in comprehensively assessing sensitivity and specificity.

Comparisons of AUC Under Various Test Conditions on MTS

Table S2 displays the AUC (%) for different methods under various test conditions in the MTS. The MDC methods (LR, NB, SVM, TAN) consistently outperform the best methods from SDM and SIM, demonstrating their robustness across test conditions.

Table S3 presents the results of the repeated measures ANOVA analysis for AUC on MTS. The analysis indicates that the method has a significant and large effect on AUC (η² = 0.327). Among the test condition factors, DIFmagnitudes_a (η² = 0.178), DIFmagnitudes_b (η² = 0.097), ProportionsofDIF (η² = 0.055), and Samplesize (η² = 0.030) exhibited effect sizes ranging from small to large.

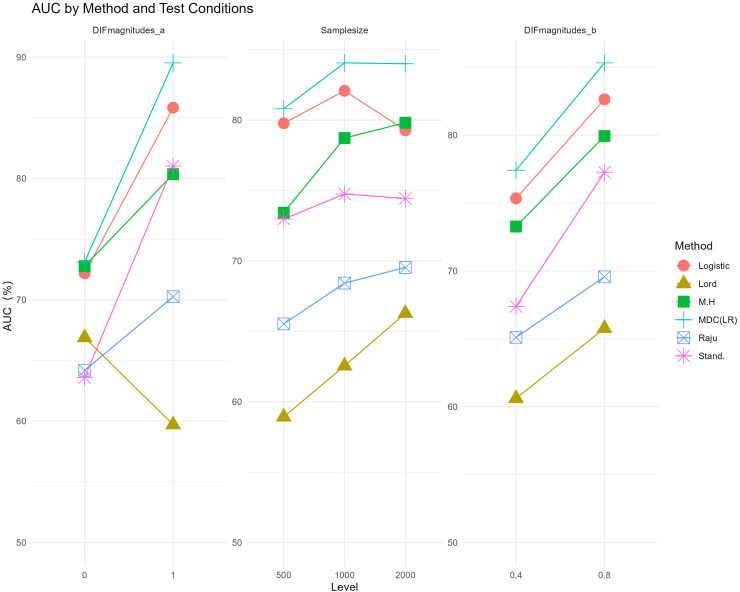
Regarding interaction effects, the interaction between Method and DIFmagnitudes_a was significant with a large effect size (η² = 0.196), while the interactions between Method and SampleSize (η² = 0.007) and Method and DIFmagnitudes_b (η² = 0.007) were close to small effects. As shown in Table S3, when DIFmagnitudes_a was 0, the best SDM was MH (AUC = 72.8%), while the corresponding MDC (LR) was 73.1%. When DIFmagnitudes_a was 1, the best SDM is Logistic (AUC = 85.8%), whereas the corresponding MDC (LR) was 89.6%. Similarly, as SampleSize increased from 500 to 2000, most methods demonstrated an increase in AUC owing to improved estimation accuracy, except for Logistic and Standardization, which experienced a decrease due to Type 1 error inflation. Additionally, as DIFmagnitudes_b increased from 0.4 to 0.8, all AUCs increased, but the rate of increase varied. The Standardization method exhibited a faster increase. In summary, the performances of different SDM methods and the best SDM vary with changes in test conditions. However, MDC (LR) consistently performs slightly better than the best SDM under the current test conditions. (Figure 1)

Figure 1.

AUC Under Various Test Conditions on MTS. Note: For simplicity, only MDC (LR) is presented as a representative of MDC, alongside five SDMs. An AUC of 50% indicates random guessing (equivalent to a correlation of 0); therefore, the Y-axis starts at 50%.

Comparisons of AUC Under Various Test Conditions on UMTS

To assess generalizability, the model performance was examined on UMTS (Unmatching Test Set). As shown in Table S4, although SVM underperformed compared to the best SDM under certain test conditions, MDC (LR) consistently outperformed the best SDM across all conditions.

Table S5 provides the results of the repeated measures ANOVA analysis for AUC on UMTS. ProportionsofDIF demonstrated a significant and large effect on AUC (η² = 0.201). Notably, the ProportionsofDIF for UMTS ranged from 0.1 to 0.4, whereas, for the MTS, it ranged from 0.2 to 0.3. Thus, the proportion of DIF items substantially influences model performance. Consequently, the η² values for other effects were relatively smaller. However, the main effects and interaction patterns were similar to those observed in the MTS.

Impact of SDMs on MDC

The correlation between the results of five SDMs and two SIMs with those of MDC (LR) was calculated for both MTS and UMTS, resulting in seven correlation values under each test condition. Detailed results for each test condition are presented in Tables S6 and S7. Additionally, AUC and correlation values for each method were ranked separately under different test conditions, and a Spearman correlation analysis of two ranking was performed.

A high Spearman correlation of 0.868 indicates that a higher AUC for an SDM is more likely to influence the MDC results, as reflected by a higher correlation with MDC (LR). As shown in Table S6, when the sample size increased from 1000 to 2000, the correlation for MH with MDC (LR) increased from 0.849 to 0.870, while the AUC for MH improved from 77.9% to 79.8% (see Table S2). Similarly, the correlation for LR with MDC (LR) decreased slightly from 0.817 to 0.781, with its AUC decreasing from 80.5% to 79.1%. While MDC was most influenced by the best SDM under the current test conditions, it was also affected by the performance of other methods.

Real Data Analysis

This study utilized partial data from the Chinese Proficiency Test. The process of simulating training data involves first estimating Observable Test Conditions based on the empirical data, including a sample size of 1212 participants and 26 items (Test Length). The sample size ratio was calculated as follows: the male group (n = 653) was designated as the reference group, while the female group (n = 559) served as the focal group, resulting in a sample size ratio of 1.19 (653/559). Secondly, for DIF-Related Test Conditions and Other Unobservable Test Conditions, we referred to the settings in the simulation study section of this study (see Table S1).MDC modeling was then performed using four different supervised learning methods individually. Thresholds were determined by maximizing the sum of sensitivity and specificity. Figure S3 illustrates the AUCs for the four MDC models and their corresponding threshold settings.

In the test dataset, the established MDC models were used to predict the final DIF-flagged results based on the determined thresholds, and model performance was validated. As shown in Table S8, the AUCs for NB (85.5%), LR (85.1%), and TAN (84.2%) in MDC were all higher than those for the SDM methods, with the exception of SVM (83.7%). For reference, an AUC of 85% approximately corresponded to Cohen’s d = 1.50 and Point-Biserial Correlation = 0.600 (Rice & Harris, 2005). Given the similarity in AUCs among NB, LR, and TAN, subsequent analyses primarily employed the MDC (LR) model for interpreting MDC mechanisms.

In MDC (LR) modeling, the parameters were specified as follows: $P\left(TrueDIF\mid \text{SDM}\right)=\frac{1}{1+e^{-\left({\mathrm{\beta }}_0+{\mathrm{\beta }}_1{\text{SDM}}_1\dots {\mathrm{\beta }}_n{\text{SDM}}_n\right)}\hspace{0.17em}}$ As shown in Table 2, the results of the SDM methods influenced the MDC predictions. For example, when MH changed from 0 (no DIF) to 1 (DIF), the odds ratio (OR) for DIF relative to no DIF increased by a factor of 4.067 (exp (1.403)). The coefficient for Std was notably large (18.610), which may be attributed to Std’s high specificity of 99.4% (Table S8), resulting in a lower likelihood of flagging items as DIF. Additionally, the negative coefficient for Raju may be attributed to its lower accuracy in this context or potential collinearity with Lord.

Table 2.

Coefficients of the MDC (Logistic Regression) Model.

Intercept	MH	Std	Logistic	Lord	Raju
−3.005	1.403	18.610	1.335	2.366	−2.866

Discussion and Conclusions

Advantages of MDC Compared to SDM and SIM

The MDC approach offers a notable advantage by reducing the risk associated with selecting an inappropriate single DIF detection method. As demonstrated in Table S2, when the sample size was 500, the performance of Lord’s test and Raju’s area method was suboptimal (AUC = 58.9% and 64.1%, respectively). However, combined with other SDM methods, particularly LR (AUC = 77.3%), the MDC (LR) method achieved an AUC of 78.5%, highlighting the robustness of MDC.

Although MDC is influenced by the performance of the best SDM, it generally outperforms the best SDM in overall performance. Pre-specifying the optimal SDM involves considerable uncertainty and requires specialized knowledge, which is not always feasible. As shown in Table S2, when the sample size increased to 2000, MH performed better (AUC = 79.8%), and when DIF magnitudes_a = 0, MH also outperformed other methods (AUC = 72.8%). Given that test conditions are not always observable, pre-specifying a particular SDM poses significant risks. Furthermore, while identifying the best SDM in the training set is possible through simulation, that the consistency of the best SDM in new datasets cannot be ensured. This study demonstrated that MDC exhibits strong generalizability in the UMTS, enhancing its practical applicability.

Comparisons of Supervised Learning Methods in MDC

This study evaluated four supervised learning methods: TAN, LR, NB, and SVM. As indicated in Table 1, SVM performed relatively poorly in both MTS and UMTS, while TAN, LR, and NB exhibited similar performance. In this context, MDC (LR) is recommended for its enhanced interpretability.

Only five conventional DIF detection methods were utilized in this study. “Single detector” encompasses any method providing useful information for DIF prediction. Beyond binary outcomes, additional information, such as effect sizes, should be considered. With an increased number of predictor variables, exploring more complex supervised learning methods may be warranted.

Practical Applicability of MDC

The MDC method involves several complex steps. Therefore, an R language function will be developed to enhance user accessibility. Users will only need to input their data, and with default parameters, they can obtain DIF detection results efficiently.

Although MDC (LR) consistently outperformed all SDMs in the UMTS, demonstrating its generalizability, its performance was slightly better in the MTS. Hence, MDC is more effective when the test conditions of the target dataset are well-represented in the training set, highlighting the importance of a broad and diverse training set. Training from scratch can be time-consuming; thus, utilizing larger datasets and more complex supervised learning methods as pre-trained models could be a promising direction for future development.

Conclusions

In this study, the MDC method demonstrated superior performance in DIF detection, consistently achieving higher accuracy and robustness across various test conditions compared to the best SDM in terms of AUC. The advantages of MDC were validated even under test conditions that differ from the training set, confirming its generalizability. Therefore, MDC can be effectively utilized to enhance DIF detection accuracy and robustness, contributing to greater test fairness.

MDC is not a static technology but a flexible framework with significant potential for future development. This study is expected to inspire researchers to integrate more effective DIF detection techniques and advanced machine learning approaches within the MDC framework, thereby continuously improving DIF analysis accuracy.

ORCID iD

Shan Huang https://orcid.org/0009-0008-8779-155X