Mixed-effects neural network modelling to predict longitudinal trends in fasting plasma glucose

Abstract

Background

Accurate fasting plasma glucose (FPG) trend prediction is important for management and treatment of patients with type 2 diabetes mellitus (T2DM), a globally prevalent chronic disease. (Generalised) linear mixed-effects (LME) models and machine learning (ML) are commonly used to analyse longitudinal data; however, the former is insufficient for dealing with complex, nonlinear data, whereas with the latter, random effects are ignored. The aim of this study was to develop LME, back propagation neural network (BPNN), and mixed-effects NN models that combine the 2 to predict FPG levels.

Methods

Monitoring data from 779 patients with T2DM from a multicentre, prospective study from the shared platform Figshare repository were divided 80/20 into training/test sets. The first 10 important features were modelled via random forest (RF) screening. First, an LME model was built to model interindividual differences, analyse the factors affecting FPG levels, compare the AIC and BIC values to screen the optimal model, and predict FPG levels. Second, multiple BPNN models were constructed via different variable sets to screen the optimal BPNN. Finally, an LME/BPNN combined model, named LMENN, was constructed via stacking integration. A 10-fold cross-validation cycle was performed using the training set to build the model and evaluate its performance, and then the final model was evaluated on the test set.

Results

The top 10 variables screened by RF were HOMA-β, HbA1c, HOMA–IR, urinary sugar, insulin, BMI, waist circumference, weight, age, and group. The best-fitting random-intercept mixed-effects (lm22) model showed that each patient’s baseline glucose levels influenced subsequent glucose measurements, but the trend over time was consistent. The LMENN model combines the strengths of LME and BPNN and accounts for random effects. The RMSE of the LMENN model ranges were 0.447–0.471 (training set), 0.525–0.552 (validation set), and 0.511–0.565 (test set). It improves the prediction performance of the single LME and BPNN models and shows some advantages in predicting FPG levels.

Conclusions

The LMENN model built by integrating LME and BPNN has several potential applications in analysing longitudinal FPG monitoring data. This study provides new ideas and methods for further research in the field of blood glucose prediction.

Background

Diabetes mellitus (DM) is a metabolic disorder characterised by hyperglycaemia due to insufficient insulin secretion (type 2, T2) or inability to secrete insulin (type 1, T1) and/or resistance of peripheral tissues to the action of insulin [1]. DM can cause complications and even death if not properly controlled. The increase in the prevalence of DM is caused mainly by the increase in T2DM, which accounts for approximately 90% of the total population of individuals with DM [2].

Currently, the treatment of DM is centred on self-management of the disease, particularly keeping blood glucose levels within recommended ranges, which involves active monitoring of blood glucose levels and appropriate physical activity, diet and insulin use. During this period, the prediction of blood glucose levels is key. Technologies such as the prediction of blood glucose and the modelling of blood glucose dynamics are at the heart of technological developments in DM management. How to predict patients’ blood glucose levels in a timely manner, control fluctuations in blood glucose and prevent complications through a convenient, practical mechanism with good predictive performance is a very meaningful task. The blood glucose prediction model can be used to detect impending symptoms of hyperglycaemia or hypoglycaemia so that patients can take measures regarding diet, medication or exercise therapy in advance to stabilise blood glucose levels before adverse events occur and ultimately control fluctuations in blood glucose within the normal range.

Currently, the adoption and implementation of advanced analytics in healthcare are lagging relatively behind, in part owing to the complexity, heterogeneity, and longitudinal nature of most health-related data, as well as the often insufficient quality and availability of clinical data [3]. ML, which represents the intersection of computer science and statistics [4, 5], enables computers to learn from data through the training of algorithms and models and to make predictions or decisions on the basis of the learned experience [6]. With the increasing popularity of machine learning (ML) and data mining in recent years, their application in DM research, especially in glycaemic prediction studies, continues to grow.

(Generalised) linear mixed-effects (LME) models is a traditional and most commonly used method by practitioners for analysing longitudinal data. In a broad sense, a (generalised) linear mixed-effects model is a model in the field of machine learning that falls under the umbrella of statistical modelling and is equally applicable to machine learning application scenarios. Khatirnamani et al. [5] studied the longitudinal trend of fasting plasma glucose (FPG) and related factors in patients with T2DM via linear mixed models and reported a decreasing trend in FPG during follow-up. Silvestre et al. [7] used a multivariable LME regression model (multivariable LME regression models and generalised additive mixed effect logistic models) to investigate the role of HbA1c and glucose-related variables in the prediction of weight loss and overweight and hyperglycaemic patients in predicting weight loss and glycaemic changes. Bozzetto et al. [8]used mixed-effects linear regression modelling to study T1DM intraindividual (between meals) and interindividual (between subjects) variability in the postprandial glucose response (PGR) in patients. Ritz et al. [9] used linear mixed-effects (LME) models to investigate how 2 diets affect body weight according to pretreatment FPG and fasting insulin (FI) levels to gain insight into the heterogeneity of treatment effects, and the resulting models achieved individually tailored predictions. Through simulation and empirical studies, Hu et al. [10] explored statistical mixed-effects models for longitudinal data analysis, piecewise LME models, and six ML methods (decision trees, bagging, random forest (RF), boosting, support-vector machine and neural network (NN), and they reported that piecewise LME models can adequately fit the original data and are even more effective than ML methods. The shortcoming is that they are limited to building traditional models (generalised LME model (GLMM) or LME model) to analyse longitudinal data [10]. Although Hu et al. [10] built both mixed-effects and ML models and compared their fitting ability, they did not further explore and compare the performance difference with that of the mixed-effects ML model.

LME is an approach based on statistical theory and certain assumptions, as opposed to some machine learning algorithms that do not rely on strict statistical assumptions, but instead rely on training algorithms and models to learn from data and make predictions or decisions based on the lessons learnt [6] (e.g., RF and support vector machine (SVM), etc.). For example, Manzini et al. [11] used a kernel-autoencoder algorithm for longitudinal clustering of T2DM trajectories and obtained seven longitudinal phenotypic clusters of T2DM patients with different clinical evolutions. Faruqui et al. [12] developed a deep learning model based on a recurrent NN with long- and short-term memory for predicting the next day’s blood glucose level in individual patients. Nagaraj et al. [13] constructed generalised linear models on the basis of elastic network regularisation, SVM and RF to assess short- and long-term glycated haemoglobin (HbA1c) response after insulin treatment initiation in patients with T2DM. Alhassan et al. [14] used multivariate logistic regression, RF, support vector machines, logistic regression, and multilayer perceptron models based on longitudinal and nonlongitudinal data to investigate their performance in predicting the risk of current HbA1c elevation. However, the application of such ML methods to longitudinal data is still challenging compared to the application of such ML methods to cross-sectional studies [15]. The downside, however, is that the underlying theory behind most such ML algorithms assumes that the data are independent and identically distributed, that longitudinal data trajectories can be very complex and nonlinear (e.g., with large interindividual variance), and that repeated measures of individuals tend to correlate with each other; not all ML algorithms are suitable for modelling these correlations, which breaks the so-called “independent and identically distributed” (“i.i.d.“) assumption, which also renders them ineffective in longitudinal supervised learning [3, 15].

Recently, the integration of mixed-effects models into nonlinear ML models has resulted in a novel ML framework for analysing complex longitudinal data: the mixed-effects ML (MEML) framework [3, 16, 17]. For example, Ngufor et al. [3] built MEML (MErf, MEgbm, MEmob and MEctree), GLMM, logistic regression, GBM and RF models for predicting longitudinal changes in haemoglobin A1c (HbA1c), resulting in MEML being comparable to traditional GLMM but performing much better than standard ML models that do not consider random effects. Mosquera-Lopez et al. [16] modelled the risk of hypoglycaemia during and up to 24 h after physical activity to help prevent postexercise hypoglycaemia in patients with T1D via mixed-effects logistic regression (MELR) and mixed-effects RF (MERF) models, and the results revealed that random effects play a crucial role in the accuracy of the two models. The MERF model had a higher predictive accuracy than the MELR model. McCoy et al. [18] constructed mixed-effects ML models to identify different longitudinal trajectories of HbA1c levels among U.S. adults with newly diagnosed DM (T1DM and T2DM) over a 3-year follow-up period and used polynomial regression to describe the factors associated with each trajectory.

Although the mixed-effects ML framework provides a novel research basis for longitudinal glucose prediction studies, most of the current longitudinal glucose prediction studies have focused on HbA1c trends in patients with T1DM [8, 16, 19–21]. Previous studies also did not consider NN models incorporating random effects to establish a linear mixed-effects NN model to predict the longitudinal trend of FPG levels in patients with T2DM. Owing to the differences between T1DM and T2DM in terms of pathogenesis, disease progression, and risk of complications, T2DM may pose a more serious long-term hazard to patients than T1DM does [22]. Therefore, our main contribution in this study is to construct a linear mixed-effects NN model by using the BPNN model to account for random effects. In addition, inspired by the MEML framework proposed by Ngufor et al. [3], we conducted a further study to model the FPG of type 2 diabetes patients using linear mixed-effects, BPNN, and mixed-effects neural network model (linear mixed effects and BPNN models for integration), and also compared and analysed the predictive performances of the three models separately, aiming to more accurately predict and understand the changing patterns of FPG in type 2 diabetes patients.

Materials and methods

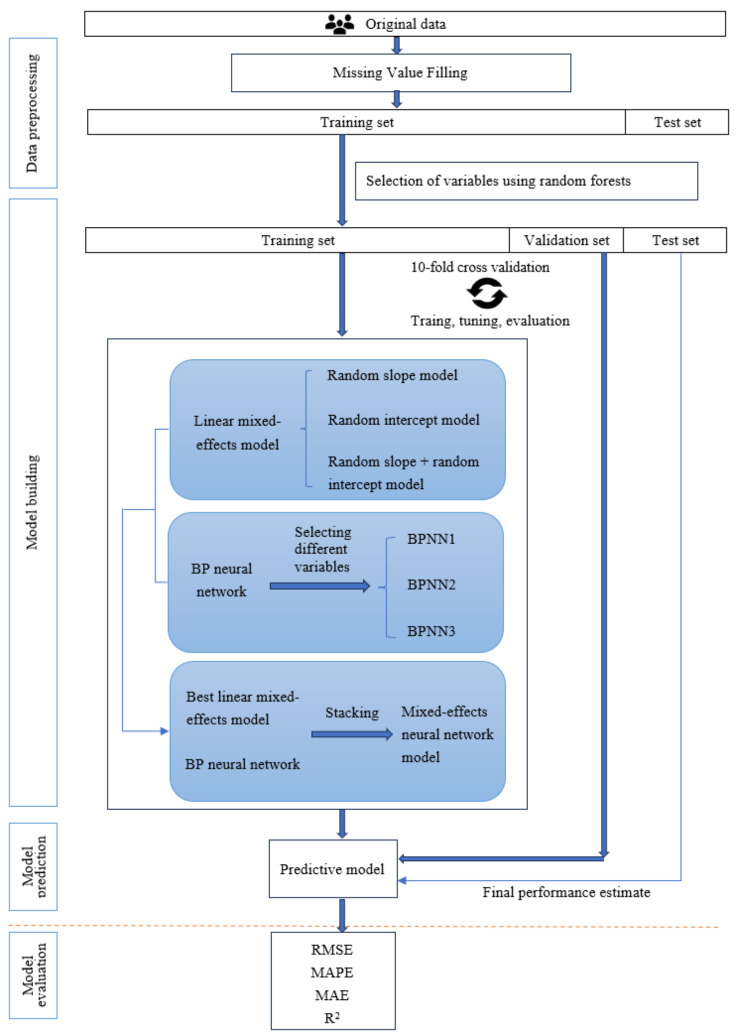
Figure  1 shows the overall systematic research framework of this study.

Fig. 1.

System framework

Data sources

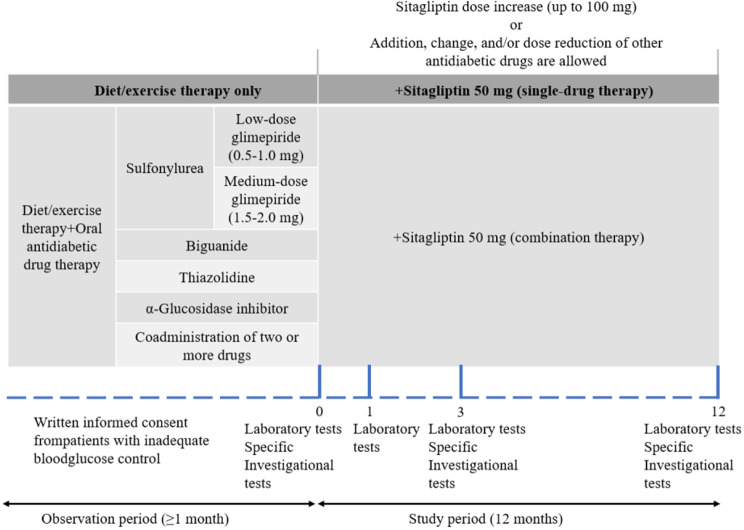
Data were obtained from the DM dataset in the studies by Sakura et al. [23] and Tomonaga et al. [24, 25], which were downloaded from the Figshare repository, a free dataset-sharing platform (download URL: https://figshare.com/articles/dataset/JAMP_DATA0722figshaer_xlsx/4924037/1). This dataset [25] was derived from an open-label, centre-registered, multicentre, prospective observational study conducted by Tokyo Women’s Medical University Hospital and 69 collaborating institutions in Japan with a study design [23], as shown in Fig. 2.

Fig. 2.

Study design [23]

Data preprocessing

Data on C-peptide, CPI, 1,5-anhydroglucitol, 1,4-anhydro(-D)-glucitol, glycoalbumin, proinsulin, proinsulin/insulin, and glycoinsulin levels and the urinary albumin/creatinine ratio were only included in 3 follow-up records for each patient; thus, the urinary albumin/creatinine ratio variable was not included in this study, and data on 30 clinical detection variables that were provided in 4 follow-up records for each patient were included in the analysis. In addition, any history of complications, including hypertension, dyslipidaemia, hyperuricaemia, retinopathy, arteriosclerosis obliterans, atrial fibrillation, kidney disease, liver disease, myocardial infarction, cerebral infarction, angina pectoris, and heart failure, was considered to indicate a history of complications, whereas zero complications was considered to indicate a history of no complications. The “history of complications” variable in the raw data was not included in our analyses because there was already a history of whether the patient had suffered from a specific type of complication in the past (e.g., dyslipidaemia). The final data used in this study were a dataset of 141 variable columns for 779 patients, including 21 unique variables (including patient number) and 30 clinical test variables (with 4 follow-up records).

The missing data rate of a few clinical test index variables was greater than 50%, the overall missing data rate of 779 instances was 17.94%, and we used the “mice()” function for multiple imputation of missing data. In the process of constructing the prediction model, feature extraction is a crucial step. We used RF to filter out the 10 important variables that have a large impact on the dependent variable FPG for modelling. Sex was recoded from ‘1 = male, 2 = female’ to ‘0 = female, 1 = male’.

Statistical analysis and methodology

All analyses were performed with R 4.2.2 software. Qualitative information was described via the number of cases and the constitutive ratio (%), and comparisons between the training and test set groups were made using the chi-square test or Fisher’s exact test. Measurement information was expressed as the median (interquartile spacing), and comparisons between the two groups were made using non-parametric tests. P < 0.05 was considered to indicate statistical significance. We attempted to analyse the repeated-measures diabetic blood glucose monitoring index results via the LME model, which is the conventional method used by most practitioners, the NN model, which has the advantages of not being restricted to the type of a priori distribution of the data and can be used to address linear and complex nonlinear relationships, and the linear mixed-effects NN model (random effects are added to the NN model), which is the integration of the two stacks. The root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE) and R² metrics were used to evaluate the model prediction results. Initially, the data were divided into an 80% training set and a 20% test set. Then, the 80% training data set were further divided into a 90% training set and 10% validation set via 10-fold cross-validation. The model was built and evaluated for its performance via the cycle of 10-fold cross-validation. The test set was used for the final model evaluation. In the end, we obtained the mean of the 10 results of the model tested on the training and validation sets and the final evaluation results tested on the test set. A random slope model, a random intercept model, a random slope plus random intercept model, etc., were constructed, and the Akaike information criterion (AIC) and Bayesian information criterion (BIC) were compared to arrive at a mixed-effects model that best fit the present data. Second, multiple BPNN models were constructed based on different combinations of independent variables to compare their AIC and BIC values. The goal is for the AIC and BIC to be as small as possible. Finally, the best LME and BPNN were used to build a linear mixed-effects NN model on the basis of the stacking integration principle, and the prediction performances of the three types of models constructed were compared.

Model construction

Mixed-effects model construction

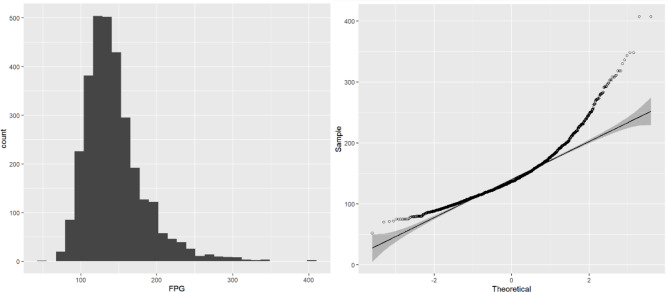
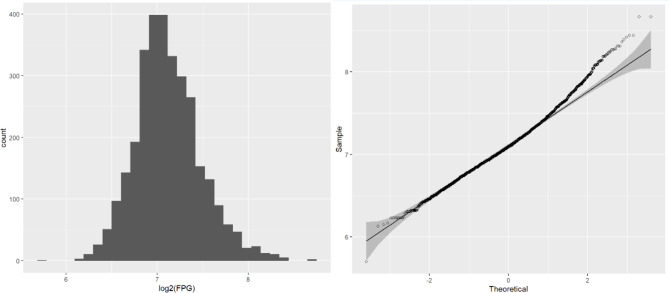
The longitudinal FPG data showing the individual distribution in the diabetic patients are presented in Fig. 3. To carry out further modelling, we used the “pivot_longer()” function to transform the wide data to long data. We then plotted histograms and Q-Q plots of the repeated measurements of the FPG values to see their normality, as shown in Fig. 4, the results were obviously deviated from the normal distribution, and logarithmic transformation [26, 27] significantly improved the degree of deviation, as shown in Fig. 5. Although log(FPG) still deviated from the normal distribution, given the sample size (n = 779), the LME model can still be used to analyse it as the model shows strong robustness to deviations from the normality assumption for large samples of data [28, 29]. This resulted in a nonnormal distribution, whereas the logarithmic transformation of the FPG was improved and more closely approximated a normal distribution (as shown in Fig. 5).

Fig. 3.

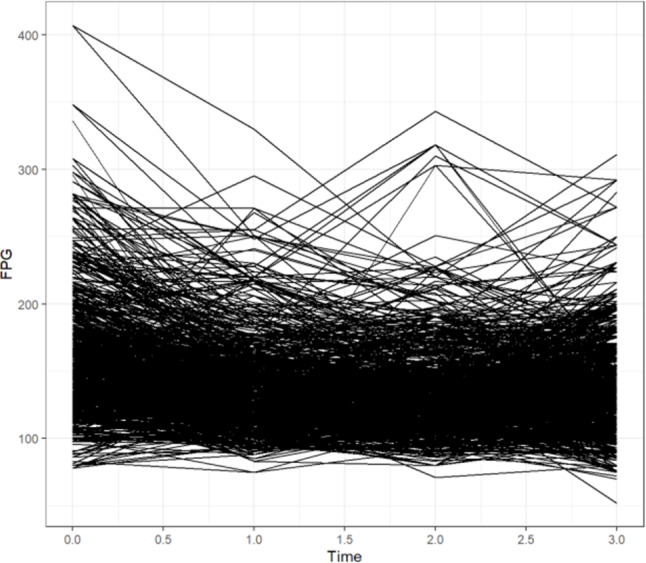
Individual profile

Fig. 4.

Histogram (A) and Q-Q plot (B) of FPG

Fig. 5.

FPG log-transformed histogram (A) and Q-Q plot (B)

We then plotted histograms and Q-Q plots of the repeated measurements of FPG values to assess the normality of the data. As shown in Fig. 4, the results were obviously deviated from the normal distribution, and the logarithmic transformation processing significantly improved the degree of deviation, as shown in Fig. 5.

The logarithmic value of FPG measured at each follow-up point was used as the dependent variable, and the variables of follow-up time, group, age, sex, smoking status, DM duration, alcohol consumption status, and history of complications were used as the independent variables. The continuous variables were log-transformed accordingly for ease of interpretation of the results. ID and time were used as random variables to construct a random slope model (named lm1), a random intercept model (named lm2) and a random intercept plus random slope linear mixed model (named lm3), leaving the independent variables with P < 0.05 in the previously established LME model, named lm11, lm22 and lm33, respectively, to construct the model again in turn and finally screening out the mixed-effects model that fits the present data relatively best according to the AIC and BIC values. The LME model was constructed via the “lme()” function in the nlme package of R software. For the parameter estimation methods of LME models, the restricted maximum likelihood (REML) or maximum likelihood (MLE) methods are usually considered [30]. Both methods have advantages and disadvantages [30]. The REML method is more unbiased in estimating the random-effects variance. Excluding the fixed effects from the calculation of the log-likelihood function provides more reliable estimates of the variance components. REML can provide more stable estimates when the sample size is small [30]. However, one of the main limitations of REML is that it cannot be used to compare different fixed-effects models because the log-likelihood values in different models are not directly comparable [30]. The MLE method includes the estimation of fixed and random effects so that the log-likelihood values can be used for model comparison, e.g., by AIC, BIC, or likelihood ratio tests. The method is useful when comparing fixed-effects models, as it enables comparison of log-likelihood values across models. However, the disadvantage is that the MLE method can be biased in estimating variance components, especially with small sample sizes [30]. We used the MLE method for model fitting because model comparisons were needed.

NN model construction

On the basis of the above multiple mixed models used to explore the optimal model, the statistically significant variables in LME were retained to build multiple BPNN models separately for exploration. A BPNN all-variable model (named BPNN1) was established with FPG levels as the dependent variable and 11 independent variables: time, HOMA-β, HbA1c, HOMA–IR, urinary glucose, insulin, BMI, waist circumference, weight, age, and group. Eight independent variables, namely time, HOMA-β, HbA1c, HOMA-IR, urinary glucose, insulin, BMI, and group, were used to build the BPNN model (named BPNN2), and six independent variables, namely, time, HOMA-β, HbA1c, HOMA-IR, urinary glucose, and insulin, were used to build the BPNN model (named BPNN3). The “train()” function in the R software nnet package was used to establish the BPNN model, and the model parameters (including optimal hidden layer nodes and weight decay parameters) were adjusted by setting a 10-fold cross-validation using “trainControl()”. We used the commonly used empirical formula [31] [h = 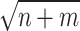+ 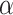, 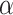∈ (1,10)] to determine the range of the hidden layer nodes, where 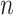is the number of nodes in the input layer, 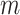is the number of nodes in the output layer, and 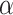has a minimum of 1 and a maximum of 10. The input layer nodes of the BPNN1, BPNN2, and BPNN3 models were 20, 17, and 10, respectively, while the output layer nodes were all to 1. Therefore, the ranges of the hidden layer nodes for the BPNN-1, BPNN-1, and BPNN-3 models were set to [5, 15], and [4, 14], respectively. The weight decay parameter range was set to [0, 0.001, 0.01, 0.1]. The model was built and evaluated through a 10-fold cross-validation process while outputting the optimal parameters. The optimal number of hidden nodes and decay for the BPNN1 model were 11 and 0.1, respectively, the optimal number of hidden nodes and decay for the BPNN2 model were 14 and 0.1, and the optimal number of hidden layer nodes and decay for the BPNN3 model were 13 and 0.1, respectively. The optimal parameters were used to build the final model, which was fed into the test set for further evaluation. Finally, the “plotnet()” and “garson()” functions in the NeuralNetTools package of R language were used to draw the network structure diagram and feature importance diagram of the NN model, which facilitates a better understanding of the model.

Linear mixed-effects NN model construction

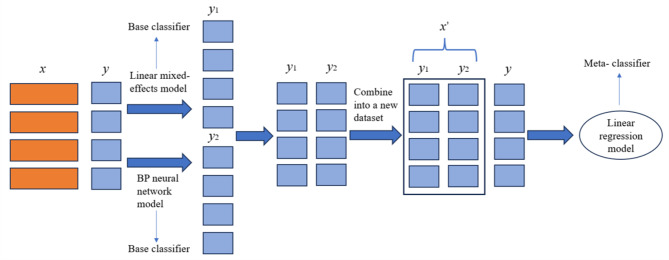
The LME model and BPNN were stacking integrated to establish the linear mixed-effects NN model, named LMENN, and a schematic diagram of the two stacking integrations is shown in Fig. 6. The LME model and BPNN were used as the base learner, and then simple linear regression was chosen as the meta-learner. First, the data were input into the mixed-effects model and BPNN model, and the 2 models were trained separately. Then, the output values of the 2 models and the original dependent variable columns were stacked to form new sample data and finally input into the meta-learner for fitting. On the basis of the principle of stacking integration, from the point of view of the goodness of fit of the models to the present data, lm22 had a relatively better fit among the 6 LMEs (Table  1; Fig. 8). After integrating lm22 with the BPNN1, BPNN2 and BPNN3 models, the models were named lm22-BPNN1, lm22-BPNN2 and lm22-BPNN3 respectively. On the other hand, from the point of view of the model’s prediction performance on the data, lm11 had the best performance (Table 2). After integrating lm11 with the BPNN1, BPNN2 and BPNN3 models, the models were named lm11-BPNN1, lm11-BPNN2 and lm11-BPNN3, respectively. Additionally, on the basis of the empirical formula [31], the hidden layer nodes of the BPNN in the LMENN model ranged from [4, 5, 14, 15], and the range of the decay parameter was set to [0, 0.001, 0.01, 0.1]. Ten-fold cross-validation was used to adjust the model parameters, which resulted in the lm22-BPNN1, lm22-BPNN2, and lm22-BPNN3 models having optimal numbers of hidden nodes of 6, 5, and 4, respectively, and the decays were all set at 0.1. The lm11-BPNN1, lm11-BPNN2 and lm11-BPNN3 models have optimal numbers of hidden layer nodes of 6, 5, and 4, respectively, and all decays were 0.1. Finally, the optimal parameters were used to build the final model, which was input into the test set for final evaluation.

Fig. 6.

Mixed effects neural network model

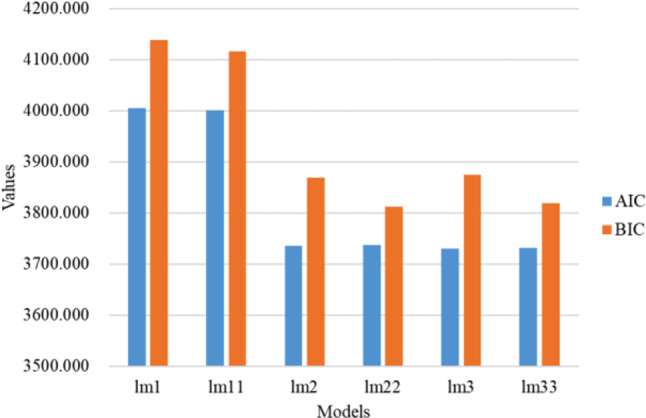
Table 1.

AIC and BIC values for linear mixed effects models

Formulae when modelling the lme ( ) function		AIC	BIC
lm1 = lme(FPG_log2 ~ time + HOMA-β + HbA1c + HOMA-IR + Urinary sugar + Insulin + BMI + Waist + weight + Age + Group, random = ~ 0 + time|new_id, data = data, method = “ML”)	Random slope model	4004.980	4138.897
lm11 = lme(FPG_log2 ~ time + HOMA-β + HbA1c + HOMA-IR + Urinary sugar + Insulin + BMI + Group, random = ~ 0 + time|new_id, data = data, method = “ML”)	Random slope model	4000.553	4117.002
lm2 = lme(FPG_log2 ~ time + HOMA-β + HbA1c + HOMA-IR + Urinary sugar + Insulin + BMI + Waist + weight + Age + Group, random = ~ 1|new_id, data = data, method = “ML”)	Random intercept model	3735.778	3869.695
lm22 = lme(FPG_log2 ~ time + HOMA-β + HbA1c + HOMA-IR + Urinary sugar + Insulin, random = ~ 1|new_id, data = data, method = “ML”)	Random intercept model	3736.811	3812.503
lm3 = lme(FPG_log2 ~ time + HOMA-β + HbA1c + HOMA-IR + Urinary sugar + Insulin + BMI + Waist + weight + Age + Group, random = ~ 1 + time|new_id, data = data, method = “ML”)	Random intercept + random slope model	3729.655	3875.217
lm33 = lme(FPG_log2 ~ time + HOMA-β + HbA1c + HOMA-IR + Urinary sugar + Insulin, random = ~ 1 + time|new_id, data = data, method = “ML”)	Random intercept + random slope model	3731.114	3818.451

Fig. 8.

Comparison of AIC and BIC for linear mixed effects models

Table 2.

Comparison of predictive performance of linear mixed effects model, BPNN model and linear mixed effects neural network model

Models			RMSE	MAPE	MAE	R 2
Linear mixed-effects model	lm1	Training set	0.547	1.364	0.400	0.700
		Validation set	0.557	1.389	0.408	0.680
		Test set	0.558	1.645	0.412	0.688
	lm11	Training set	0.547	1.368	0.400	0.700
		Validation set	0.555	1.386	0.407	0.681
		Test set	0.557	1.647	0.411	0.689
	lm2	Training set	0.548	1.374	0.403	0.699
		Validation set	0.584	1.370	0.430	0.647
		Test set	0.562	1.678	0.416	0.684
	lm22	Training set	0.554	1.388	0.407	0.693
		Validation set	0.557	1.397	0.410	0.679
		Test set	0.559	1.624	0.411	0.687
	lm3	Training set	0.548	1.374	0.403	0.699
		Validation set	0.557	1.393	0.409	0.679
		Test set	0.562	1.676	0.417	0.684
	lm33	Training set	0.554	1.388	0.408	0.693
		Validation set	0.557	1.398	0.411	0.679
		Test set	0.559	1.622	0.411	0.687
BPNN model	BPNN1	Training set	0.505	1.215	0.376	0.745
		Validation set	0.588	1.338	0.429	0.644
		Test set	0.626	1.658	0.446	0.608
	BPNN2	Training set	0.515	1.218	0.381	0.734
		Validation set	0.573	1.313	0.421	0.660
		Test set	0.600	1.649	0.433	0.639
	BPNN3	Training set	0.527	1.240	0.388	0.722
		Validation set	0.573	1.291	0.417	0.661
		Test set	0.593	1.651	0.422	0.648
Mixed-effects neural network model	lm22-BPNN1	Training set	0.447	1.322	0.322	0.800
		Validation set	0.552	1.444	0.380	0.682
		Test set	0.542	1.565	0.393	0.706
	lm22-BPNN2	Training set	0.456	1.306	0.325	0.792
		Validation set	0.527	1.390	0.369	0.708
		Test set	0.551	1.574	0.401	0.696
	lm22-BPNN3	Training set	0.471	1.287	0.331	0.778
		Validation set	0.527	1.347	0.361	0.709
		Test set	0.565	1.628	0.411	0.680
	lm11-BPNN1	Training set	0.447	1.323	0.322	0.800
		Validation set	0.552	1.444	0.380	0.682
		Test set	0.511	1.412	0.359	0.738
	lm11-BPNN2	Training set	0.456	1.306	0.325	0.792
		Validation set	0.527	1.389	0.369	0.708
		Test set	0.518	1.411	0.361	0.731
	lm11-BPNN3	Training set	0.471	1.291	0.330	0.778
		Validation set	0.525	1.351	0.359	0.711
		Test set	0.526	1.455	0.365	0.723

Results

Basic information

As shown in Table 3, there were 779 patients with T2DM, with a total of 3,116 records after the wide data were converted to long data, and the dataset was divided to ensure that the records of the four follow-up visits for each patient were either all in the training set or all in the test set. The training set had 2496 records (80%), and the test set had 620 records (20%). As shown in Fig. 7, the distribution of FPG levels in T2DM patients at months 1, 3 and 12 decreased compared with that at month 0.

Table 3.

The demographic and clinical characteristics of participants (n = 779)

Number	Variables	Total (n = 3116)	Training set (n = 2496)	Test set (n = 620)	P value
1	Group				< 0.001*
	0 = Medium-dose glimepiride	244 (7.8)	208 (8.3)	36 (5.8)
	1 = Diet/exercise therapy	876 (28.1)	672 (26.9)	204 (32.9)
	2 = Low-dose glimepiride	340 (10.9)	272 (10.9)	68 (11.0)
	3 = Biguanide	452 (14.5)	364 (14.6)	88 (14.2)
	4 = Thiazolidine	176 (5.6)	140 (5.6)	36 (5.8)
	5 = α-Glucosidase inhibitor	92 (3.0)	60 (2.4)	32 (5.2)
	6 = Combination of two or more of the above drugs	936 (30.0)	780 (31.2)	156 (25.2)
2	Age (years)	64.00 (56.00–73.00)	64.00 (56.00–73.00)	63.00 (55.00–73.00)	0.495
3	Sex				0.800
	0 = Female	1032 (33.1)	824 (33.0)	208 (33.5)
	1 = Male	2084 (66.9)	1672 (67.0)	412 (66.5)
4	Height (cm)	164.00 (155.00-170.00)	163.90 (155.00-170.00)	164.00 (155.00-169.00)	0.461
5	Waist (cm)	87.50 (81.50–94.00)	87.50 (81.50–94.00)	87.00 (82.00–95.00)	0.224
6	Smoking				0.583
	0 = No	1596 (51.2)	1280 (51.3)	316 (51.0)
	1 = Yes	720 (23.1)	584 (23.4)	136 (21.9)
	2 = Past	800 (25.7)	632 (25.3)	168 (27.1)
7	Drinking				0.832
	0 = No	1600 (51.3)	1284 (51.4)	316 (51.0)
	1 = Yes	1516 (48.7)	1212 (48.6)	304 (49.0)
8	Duration of T2DM (months)	90.00 (48.00-139.00)	96.00 (47.50–144.00)	72.00 (48.00-120.00)	< 0.001*
9	History of hypertension				0.437
	0 = No	1244 (39.9)	988 (39.6)	256 (41.3)
	1 = Yes	1872 (60.1)	1508 (60.4)	364 (58.7)
10	History of dyslipidemia				0.049*
	0 = No	1140 (36.6)	892 (35.7)	248(40.0)
	1 = Yes	1976 (63.4)	1604 (64.3)	372 (60.0)
11	History of hyperuricemia				0.138
	0 = No	2804 (90.0)	2256 (90.4)	548 (88.4)
	1 = Yes	312 (10.0)	240 (9.6)	72 (11.6)
12	History of retinopathy				0.107
	0 = No	2888 (92.7)	2304 (92.3)	584 (94.2)
	1 = Yes	228 (7.3)	192 (7.7)	36 (5.8)
13	History of arteriosclerosis obliterans				0.153
	0 = No	2872 (92.2)	2292 (91.8)	580 (93.5)
	1 = Yes	244 (7.8)	204 (8.2)	40 (6.5)
14	History of atrial fibrillation				0.004*
	0 = No	3044 (97.7)	2448 (98.1)	596 (96.1)
	1 = Yes	72 (2.3)	48 (1.9)	24 (3.9)
15	History of kidney disease				0.238
	0 = No	2880 (92.4)	2300 (92.1)	580 (93.5)
	1 = Yes	236 (7.6)	196 (7.9)	40 (6.5)
16	History of liver disease				0.832
	0 = No	2848 (91.4)	2280 (91.3)	568 (91.6)
	1 = Yes	268 (8.6)	216 (8.7)	52 (8.4)
17	History of myocardial infarction				0.843
	0 = No	3032 (97.3)	2428 (97.3)	604 (97.4)
	1 = Yes	84 (2.7)	68 (2.7)	16 (2.6)
18	History of cerebral infarction				0.584
	0 = No	2912 (93.5)	2328 (93.3)	584 (94.2)
	1 = Hemorrhagic	4 (0.1)	4 (0.2)	0 (0.0)
	2 = Infarction	200 (6.4)	164 (6.6)	36 (5.8)
19	History of angina pectoris				0.614
	0 = No	2984 (95.8)	2388 (95.7)	596 (96.1)
	1 = Yes	132 (4.2)	108 (4.3)	24 (3.9)
20	History of heart failure				0.003*
	0 = No
	1 = Yes	56 (1.8)	36 (1.4)	20 (3.2)
21	SBP (mmHg)	130.00 (120.00-140.00)	130.00 (120.00-140.00)	130.00 (121.00-140.00)	0.711
22	DBP (mmHg)	76.00 (70.00–82.00)	76.00 (70.00–82.00)	77.00 (70.00–82.00)	0.214
23	Pulse rate (bpm)	76.00 (69.75-85.00)	76.00 (70.00–85.00)	74.50 (69.00–84.00)	0.018*
24	Weight (kg)	65.50 (57.18-75.00)	65.20 (57.50-75.12)	66.00 (56.00–74.00)	0.302
25	BMI (kg/m2)	24.57 (22.46–27.51)	24.56 (22.50-27.62)	24.70 (22.34–27.13)	0.234
26	HbA1c (%)	7.20 (6.70–7.90)	7.20 (6.70–7.90)	7.20 (6.70–7.90)	0.588
27	FPG (mg/dL)	137.00 (119.00-161.00)	137.00 (119.00-161.00)	137.00 (116.00-163.00)	0.714
28	Insulin (µU/mL)	6.30 (4.20–9.40)	6.40 (4.21–9.40)	5.96 (3.98–9.30)	0.079
29	HOMA-IR	2.13 (1.34–3.34)	2.15 (1.34–3.36)	2.10 (1.29–3.29)	0.204
30	HOMA-β (%)	32.10 (19.20–53.30)	32.40 (19.40–52.80)	30.85 (18.30-56.05)	0.753
31	RBC (×104/µL)	455.00 (424.00-488.00)	454.00 (424.75–487.00)	461.00 (423.00-494.00)	0.195
32	WBC (/µL)	6100.00 (5087.50-7322.50)	6165.00 (5100.00-7380.00)	5965.00 (5000.00-7200.00)	0.043*
33	Hemoglobin (g/dL)	14.00 (12.90–15.00)	13.90 (12.90–15.00)	14.10 (13.00-14.90)	0.649
34	Hematocrit (%)	42.60 (39.80–45.30)	42.60 (39.80–45.20)	42.85 (39.90–45.50)	0.495
35	Platele (×104/µL)	21.70 (18.50–25.60)	21.70 (18.40–25.40)	21.95 (18.80–26.60)	0.013*
36	TG (mg/dL)	121.00 (85.00-177.00)	123.00 (86.00-179.00)	111.50 (80.00-170.25)	0.002*
37	HDL-C (mg/dL)	52.00 (44.00–62.00)	52.00 (44.00–61.00)	53.00 (46.00–64.00)	0.006*
38	LDL-C (mg/dL)	109.00 (91.00-130.00)	109.00 (92.00-130.00)	110.00 (89.75–131.00)	0.593
39	AST (U/L)	21.00 (18.00–27.00)	21.00 (18.00–27.00)	21.00 (18.00–28.00)	0.495
40	ALT (U/L)	21.00 (15.00–31.00)	21.00 (15.00–31.00)	20.00 (15.00–30.00)	0.749
41	-GTP (U/L)	30.00 (19.00–49.00)	30.00 (19.00–49.00)	29.50 (19.00–51.00)	0.727
42	BUN (mg/dL)	14.90 (12.20–17.90)	14.95 (12.20–18.00)	14.40 (12.10-17.83)	0.337
43	UA (Uric acid-mg/dL)	5.30 (4.40–6.20)	5.40 (4.50–6.30)	5.10 (4.30–6.10)	0.008*
44	Creatinine (mg/dL)	0.74 (0.62–0.88)	0.75 (0.62–0.88)	0.72 (0.61–0.86)	0.015*
45	Na (mEq/L)	140.00 (139.00-142.00)	140.00 (139.00-142.00)	140.00 (138.00-142.00)	0.003*
46	Cl (mEq/L)	103.00 (101.00-105.00)	103.00 (101.00-105.00)	103.00 (101.00-104.00)	0.244
47	K (mEq/L)	4.30 (4.00-4.60)	4.30 (4.00-4.60)	4.40 (4.00-4.70)	0.009*
48	Urinary protein				0.022*
	0=”-”	2196 (70.5)	1766 (70.8)	430 (69.4)
	1="±”	476 (15.3)	392 (15.7)	84 (13.5)
	2="+”	257 (8.2)	188 (7.5)	69 (11.1)
	3="++”	110 (3.5)	92 (3.7)	18 (2.9)
	4="+++”	77 (2.5)	58 (2.3)	19 (3.1)
	5="++++”	2196 (70.5)	1766 (70.8)	430 (69.4)
49	Urinary sugar				0.120
	0=”-”	2098 (67.3)	1704 (68.3)	394 (63.5)
	1="±”	184 (5.9)	151 (6.0)	33 (5.3)
	2="+”	273 (8.8)	207 (8.3)	66 (10.6)
	3="++”	206 (6.6)	162 (6.5)	44 (7.1)
	4="+++”	331 (10.6)	255 (10.2)	76 (12.3)
	5="++++”	24 (0.8)	17 (0.7)	7 (1.1)
50	eGFR (mL/min/1.73 m²)	75.41 (63.80–89.10)	74.77 (63.35–88.10)	77.85 (65.67–92.39)	< 0.001*

Note: ^*P < 0.05. Categorical variables are expressed as frequencies (%), and quantitative variables are expressed as medians (IQR). (height: body height at month 0; waist: waist circumstances at month 0; smoking: smoking habit; drinking: drinking habit; SBP: systolic blood pressure; DBP: diastolic blood pressure; weight: body weight; BMI: body mass index; HbA1c: haemoglobin A1c; FPG: fasting plasma glucose; HOMA-IR: homeostatic model assessment for insulin resistance; HOMA-β: homeostasis model assessment-beta; RBC: red blood cell; WBC: white blood cell; TG: triglyceride; HDL-C: high-density lipoprotein cholesterol; LDL-C: low-density lipoprotein cholesterol; AST: aspartate transaminase; ALT: alanine aminotransferase; γ-GTP: γ-glutamyl transpeptidase; BUN: blood urea nitrogen; UA: uric acid; eGFR: estimated glomerular filtration rate)

Fig. 7.

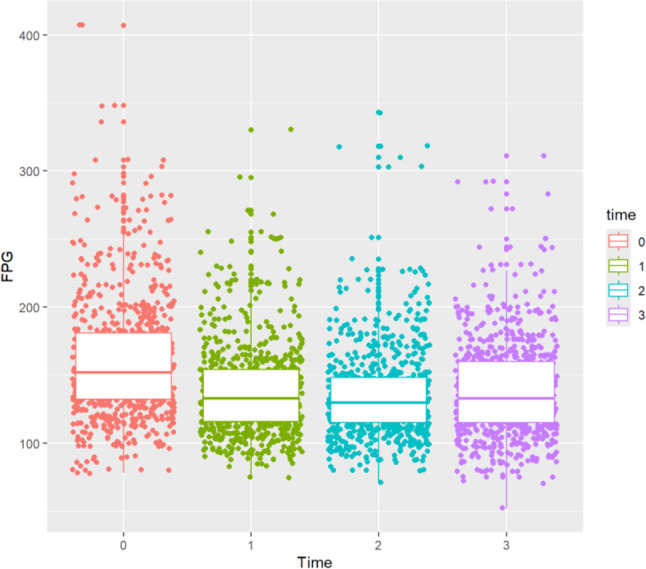
Distribution of FPG at different measurement time points in T2DM patients

LME model results

As shown in Table 1 and visualised in Fig. 8, it was found that the lowest AIC value (3729.655) was observed with the lm3 model, and the lowest BIC (3812.503) was observed with the lm22 model. The combined AIC and BIC metrics revealed that the lm22 model had the relatively best fit (Table 1; Fig. 8), with an intragroup correlation coefficient of 0.382. The random intercept model (lm22) indicated a correlation between baseline blood glucose levels and subsequent blood glucose monitoring values for each patient, and the trend over time was consistent (no significant random effect for slope).

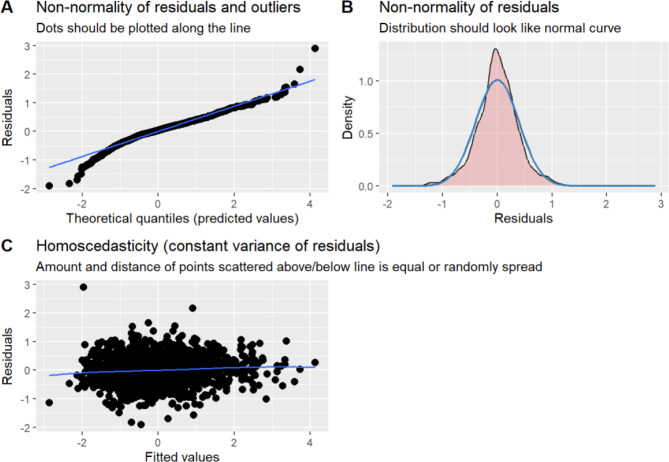
Table 4 shows the results of the lm22 model, and the variables time, HOMA-β, HbA1c, HOMA-IR, urinary glucose, and insulin were statistically significant (P < 0.05). Time, HOMA-β, and insulin were negatively correlated with FPG levels, and HbA1c, HOMA-IR, HbA1c, HOMA-IR, and urinary glucose were positively correlated with FPG levels. This finding indicated that there was a tendency for FPG to decrease with prolonged treatment time (β=-0.040, P = 0.005); the higher the HOMA-β was, the lower the value of FPG (β=-0.204, P < 0.001); the higher the insulin level was, the lower the value of FPG (β=-0.663, P < 0.001); and the higher the HbA1c level was, the higher the value of FPG (β = 0.279, P < 0.001). Those with higher HOMA-IR values had higher FPG values (β = 1.024, P < 0.001). Those with a urinary glucose result of “±” had higher FPG values than those with a urinary glucose result of “-” (β = 0.074, P < 0.001); those with a urinary glucose result of “+” had higher FPG values than those with a urinary glucose result of “-” (β = 0.187, P < 0.001); those with a urinary glucose result of “++” had higher FPG values than those with a urinary glucose result of “-” (β = 0.254, P < 0.001); those with a urinary glucose result of “+++” had higher FPG values than those with a urinary glucose result of “-” (β = 0.342, P < 0.001); and those with a urinary glucose result of “++++” had higher FPG values than those with a urinary glucose result of “-” (β = 0.698, P < 0.001). After fitting the model, it was also necessary to verify that the model satisfied the assumptions of a linear mixed-effects model. The visualisation of the hypothesis testing of the better fitted lm22 model is shown in Fig. 9. The distribution of the residuals roughly conformed to a normal distribution, as shown in Fig. 9 (A) and Fig. 9 (C), and the blue lines in Fig. 9 (B) are flat and parallel to each other, indicating that the variances of the residuals were homogeneous. The lm22 model was consistent with the assumptions of a linear mixed-effects model.

Table 4.

Results for the random intercept model lm22

Effects	Estimate	S.E	df	t value	P value
Fixed effects
Intercept	-0.040	0.022	1862	-1.795	0.073
time	-0.024	0.008	1862	-2.822	0.005*
HOMA-β	-0.204	0.020	1862	-9.988	< 0.001*
HbA1c	0.279	0.015	1862	18.178	< 0.001*
HOMA-IR	1.024	0.037	1862	27.671	< 0.001*
Urinary sugar			1862
1=“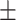”	0.074	0.043	1862	1.704	0.089
2="+”	0.187	0.038	1862	4.861	< 0.001*
3="++”	0.254	0.043	1862	5.844	< 0.001*
4="+++”	0.342	0.041	1862	8.265	< 0.001*
5="++++”	0.698	0.137	1862	5.100	< 0.001*
0=”-”	0.000	-	-	-	-
Insulin	-0.663	0.044	1862	-14.940	< 0.001*
Random effects
SDintercept	0.343
SDresidual	0.435

Note: ^*P < 0.05, S.E: standard error, SD_intercept: standard deviation of random intercepts, SD_{residual error}: standard deviation of residuals

Fig. 9.

Results of hypothesis testing for the lm22 model. Note: (A): Residual normal distribution and outliers test plot, (B): Residual normal distribution test plot, (C): Residual variance homogeneity test plot

Model prediction results

As shown in Table 2, among the six LME models, the lm1 model training set had an average RMSE of 0.547, an average MAPE of 1.364, an average MAE of 0.400, and an average R² of 0.700, which was better than the results of the other models; however, the lm11 model had the same RMSE, MAE, and R² as the lm1 model (all of 0.547, 0.400, and 0.700), and the average MAPE values were different but not significant. For the validation set, the lm11 model had the lowest average RMSE and average MAE (0.555, 0.407) and the highest average R² value (0.681) of all the LME models, whereas the lm2 model had the lowest average MAPE value (1.370) of all the LME models. In the final test, the lm11 model had the lowest RMSE of all LME models (0.557), the lm33 model had the lowest MAPE (1.622), the lm11, lm22, and lm33 models had the lowest MAE (0.411), and the lm11 model had the highest R² (0.689). The HOMA–IR, urinary glucose, insulin, BMI and Group independent variables explained 68.9% of the variation in the dependent variable (FPG levels). Taken together, the lm11 model seemed to have the best predictive performance.

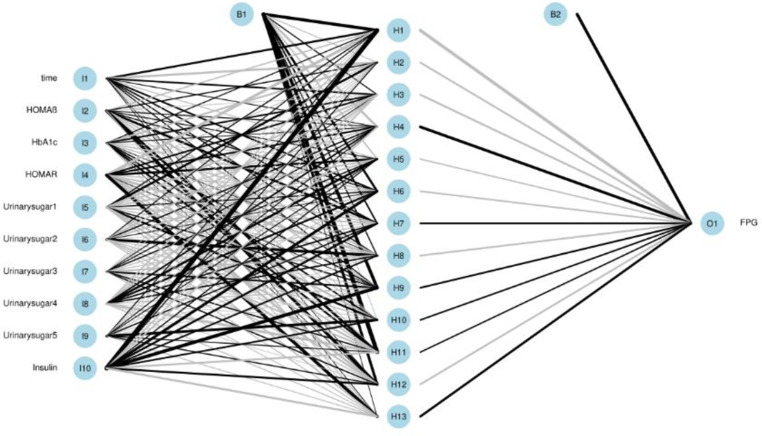
Among the three NN models, the BPNN1 model had the lowest average RMSE, average MAPE, and average MAE on the training set (0.505, 121.488, and 0.376) and the highest average R² (0.745) among the three BPNN models. The average RMSE on the validation set for the 10-fold cross-validation of the BPNN2 and BPNN3 models was the lowest among the three BPNNs (0.573 for both), with the lowest value of 0.573. The BPNN3 model validation set had the lowest average MAPE and MAE (1.291, 0.417) and the highest average R² (0.661). When evaluated in the final test, BPNN2 had the lowest MAPE (1.649), and BPNN3 had the lowest RMSE and MAE (0.593, 0.422) and the highest R² (0.648) among the three BPNNs. In summary, the BPNN3 model had the relatively best predictive performance among the 3 BPNN models. The network structure diagram and feature importance diagram of the BPNN3 model are shown in Figs. 11 and 12. HOMA-IR, urinary glucose (3), urinary glucose (5), HbA1c, urinary glucose (4), and HOMA-β played positive roles in the prediction of FPG and urinary glucose (2). urinary glucose (1), time, and insulin played negative roles in the prediction of FPG levels.

Fig. 11.

Network structure of BPNN3

Fig. 12.

Characteristic importance of the BPNN3 model

Among the six LMENN models built, on the training set, lm22-BPNN1 and lm11-BPNN1 had the lowest average RMSE and average MAE (0.447 and 0.322, respectively), while their average R² was the highest (0.800), and the average MAPE was the lowest (1.287) for lm22-BPNN3. For the validation set, the lm11-BPNN3 model had the lowest average RMSE (0.525) and average MAE (0.359) and the highest average R² (0.711). The lm22-BPNN3 model had the lowest mean MAPE (1.347) on the validation set. For the test set, lm11-BPNN2 had the lowest MAPE (1.411), while lm11-BPNN1 had the lowest RMSE (0.511) and MAE (0.359) and the highest R² (0.738). Thus, the lm11-BPNN1 model had relatively the best predictive performance among the six LMENN models.

The RMSE for the training set of the LME models (including the six LME models built) ranged from 0.547 to 0.554, the MAPE ranged from 1.364 to 1.388, the MAE ranged from 0.400 to 0.408, and the R² ranged from 0.693 to 0.700. The RMSE on the validation set ranged from 0.555 to 0.584, the MAPE ranged from 1.370 to 1.398, the MAE ranged from 0.407 to 0.430, and the R² ranged from 0.647 to 0.681. The RMSE on the test set ranged from 0.557 to 0.562, the MAPE ranged from 1.622 to 1.678, the MAE ranged from 0.411 to 0.417, and the R² ranged from 0.684 to 0.689.

The RMSE for the training set of the BPNN model (including the three BPNN models built) ranged from 0.505 to 0.527, the MAPE ranged from 1.215 to 1.240, the MAE ranged from 0.376 to 0.388, and the R² ranged from 0.722 to 0.745. The RMSE for the validation set of the BPNN model ranged from 0.573 to 0.588, the MAPE ranged from 1.291 to 1.338, the MAE ranged from 0.417 to 0.429, and the R² ranged from 0.644 to 0.661. The RMSE on the test set ranged from 0.593 to 0.626, the MAPE ranged from 1.649 to 1.658, the MAE ranged from 0.422 to 0.446, and the R² ranged from 0.608 to 0.648.

The RMSE for the training set of the LMENN model (including the six LMENN models built) ranged from 0.447 to 0.471, the MAPE ranged from 1.287 to 1.323, the MAE ranged from 0.322 to 0.331, and the R² ranged from 0.778 to 0.800. The RMSE on the validation set ranged from 0.525 to 0.552, the MAPE ranged from 1.347 to 1.444, the MAE ranged from 0.359 to 0.380, and the R² ranged from 0.682 to 0.711. The RMSE on the test set ranged from 0.511 to 0.565, the MAPE ranged from 1.411 to 1.628, the MAE ranged from 0.359 to 0.411, and the R² ranged from 0.680 to 0.738.

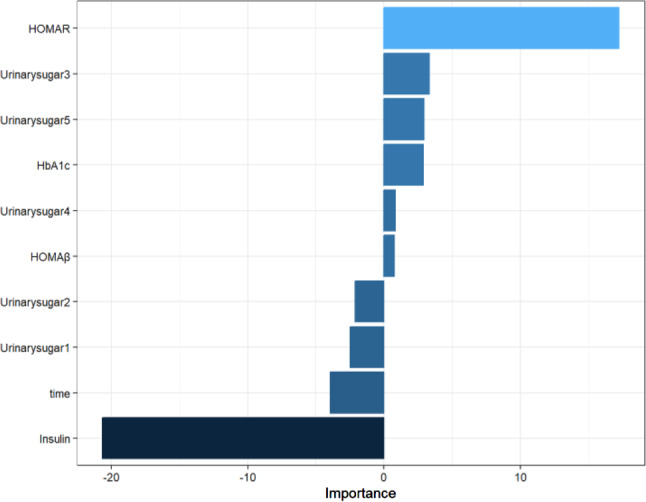
In summary, for the training set, the RMSE and MAE range values of the LMENN model were LME > BPNN > LMENN, the MAPE range was LME > LMENN > BPNN, and the R² range value was LMENN > BPNN > LME. For the validation set, the RMSE and MAE ranges of the LMENN model were the lowest, and the MAPE range was the lowest for the BPNN model. The R² range was highest for the LMENN model. For the test set, the LMENN model had an upper RMSE range value that was about the same as that for the LME, but had a much lower range; the MAPE range was relatively the lowest, and the MAE range values were BPNN > LME > LMENN, the BPNN model has the lowest R² range. The LMENN model had an R² range value with a lower limit that was about the same as that of the LME model, but had an upper limit that was higher than that of the LME model. These results indicate that the LMENN model indeed performs better than the single LME and BPNN models do, probably because the LMENN combines the advantages of the two models. The LME model performed better than the BPNN model on the test set, but did not perform as well as the BPNN on the training and validation sets, which may be due to the fact that with fewer feature variables, the BPNN model learns less information about the data, resulting in poorer performance of the model on the test set. Moreover, on the one hand, this may be because the BPNN model was affected by overfitting, although the risk of overfitting had been reduced slightly by 10-fold cross-validation. On the other hand, it may be because random effects are considered in LME models, whereas they are not considered in BPNN models. The magnitude of the variation in the range of values of each metric in the LMENN model was larger than that of the LME, probably because we chose the optimal LME from two perspectives to build the LMENN model: the optimal LME was chosen from the perspective of the model’s goodness-of-fit and complexity (AIC), and the optimal LME model was chosen from the perspective of the model’s goodness of fit and complexity (AIC and BIC) (lm22) and from the perspective of the model’s better predictive performance for FPG (lm11).

For the models integrated by lm22 and the three BPNNs alone (lm22-BPNN1, lm22-BPNN2 and lm22-BPNN3, collectively referred to as lm22-BPNN), the RMSE for the training set ranged from 0.447 to 0.471, the MAPE ranged from 1.287 to 1.322, the MAE ranged from 0.322 to 0.331, and the R² ranged from 0.778 to 0.800. The validation set had an RMSE range of 0.527–0.552, a MAPE range of 1.347–1.444, a MAE range of 0.361–0.380, and an R² range of 0.682–0.709. The test set had an RMSE range of 0.542–0.565, a MAPE range of 1.565–1.628, a MAE range of 0.393–0.411 and an R² range of 0.680–0.706.

For the training set, the range values of the RMSE and MAE were LME > BPNN > lm22-BPNN, the range value of the MAPE was LME > lm22-BPNN > BPNN, and the range value of R² was lm22-BPNN > BPNN > LME. On the validation set, the range values of the RMSE and MAE were the lowest for lm22-BPNN, BPNN had the lowest MAPE range value, and the range value of lm22-BPNN had the highest R². For the test set, BPNN had the highest RMSE range value, LME and LMENN had about the same RMSE range value, and the MAPE range value was BPNN > LME > lm22-BPNN, the MAE range value was BPNN > LME > lm22-BPNN, and the R² range value was lm22-BPNN > LME > BPNN.

For the model built by integrating lm11 with BPNN alone (lm11-BPNN1, lm11-BPNN2 and lm11-BPNN3 are collectively referred to as lm11-BPNN), the RMSE of the training set ranged from 0.447 to 0.471, the MAPE ranged from 1.291 to 1.323, the MAE ranged from 0.322 to 0.330, and R² ranged from 0.778 to 0.800. The RMSE for the validation set ranged from 0.525 to 0.552, the MAPE ranged from 1.351 to 1.444, the MAE ranged from 0.358 to 0.380, and the R² ranged from 0.682 to 0.711. The RMSE for the test set ranged from 0.511 to 0.526, the MAPE ranged from 1.411 to 1.455, the MAE ranged from 0.359 to 0.365, and R² ranged from 0.723 to 0.738.

The training set had the lowest RMSE range value; both the MAPE and MAE range values were LME > BPNN > lm11-BPNN; the MAPE range was LME > lm11-BPNN > BPNN; and the R² range value was lm11-BPNN > BPNN > LME. On the validation set, the lm11-BPNN had the lowest RMSE range value, the BPNN had the lowest MAPE range value, the lm11-BPNN had the lowest MAE range value, and the lm11-BPNN had the highest R² range value. For the test set, the range value of the RMSE was BPNN > LME > lm11-BPNN, the lm11-BPNN had the lowest range value of the MAPE, the range value of the MAE was BPNN > LME > lm11-BPNN, and the range value of R² was lm11-BPNN > LME > BPNN.

According to the results of the visualisation of the predictive metric values of each model on the test set (shown in Fig. 10), the RMSE, MAPE, and MAE values of the LMENN model were overall lower than those of the BPNN model and the LME model, whereas the R² was higher than those of all of them, and the LMENN model truly enhanced the predictive performance of the single LME and the BPNN model. lm11-BPNN1 had the best relative performance, with an RMSE of 0.511, MAPE of 1.412, MAE of 0.359, and R² of 0.738 on the test set. The predictive performance of lm11-BPNN was better overall than that of lm33-BPNN, probably because lm11 itself had the best predictive performance for FPG among the LME models, whereas lm33 was selected only by comparing the AIC and BIC values to fit the data of this study better, so naturally, from the aspect of predictive performance, the model obtained from its integration was not as good as the one integrated with lm11 and BPNN.

Fig. 10.

Comparison of prediction performance on the model test set

Discussion

We used an LME model to analyse FPG levels in patients with T2DM, and we were able to effectively fit these monitoring data and analyse the influencing factors of FPG changes. To predict the longitudinal trend of FPG levels in patients with T2DM, we developed multiple LME models, a BPNN model, and an LMENN model combining the 2. We improved the reliability of the assessment and reduced the risk of overfitting via 10-fold cross-validation. The results show that the LMENN model was competitive with the traditional LME model and the BPNN model, which do not take random effects into account, and these results are in line with the findings of Ngufor et al. [3]. The LMENN model developed in this study predicted FPG in patients with T2DM, with RMSE values ranging from 0.511 to 0.552, MAPE values ranging from 1.411 to 1.601, MAE values ranging from 0.359 to 0.403, and R² values ranging from 0.694 to 0.738 on the test set, in which the random slope NN model (lm11-BPNN1) achieved relatively good predictive performance. Although a few scholars have previously conducted studies on mixed-effects ML [3, 16, 18], to our knowledge, this is the first study that accounts for random effects in an NN model and builds and compares the performance of LME, BPNN, and LMENN models in predicting the longitudinal trend of FPG levels in patients with T2DM.

The factors affecting the effectiveness of DM treatment are very complex and include age, sex, weight, disease duration, family history of DM, type of DM, dietary habits, lifestyle, and organ function. Therefore, in the treatment of T2DM, practitioners need to consider multiple risk factors according to the actual diagnosis and treatment of the patient and provide appropriate treatment plans for different patients. Effective assessment and prediction of glycaemic improvement after treatment can help clinicians better provide personalised treatment services to patients. The LMENN prediction model in this study can help physicians more accurately predict patients’ future blood glucose levels, which can lead to more personalised treatment plans and improve the efficiency and quality of diabetes management. At the same time, the model can help provide doctors with real-time feedback on patients’ blood glucose changes, which can help them make timely adjustments to their treatment plans and reduce the occurrence of hypoglycaemic or hyperglycaemic events. As for patients, they can understand their own blood glucose trends through the model and improve their self-management ability.

FPG and HbA1c are the most commonly accepted key indicators of glycaemic improvement for the management of diabetic patients. An LME model was used to analyse the factors influencing FPG levels in patients with T2DM, and the relatively best fit to the data in this study was the random intercept (lm22) model, which demonstrated that a correlation between baseline blood glucose levels and subsequent blood glucose monitoring values for each patient, and the trend over time was consistent (no significant random effect for slope). The lm22 results revealed low urinary glucose, low HOMA-IR, low HbA1c, high time, high HOMA-β, high insulin, and low FPG were associated with each other, which is consistent with the findings of clinical practice. The negative correlation of time with FPG levels in this study may be because as the follow-up time increased, the patients received therapeutic or lifestyle interventions, which may have led to a decrease in FPG levels. Patients with DM are advised to monitor FPG and postprandial glucose levels, as well as HbA1c, on a regular basis to detect and manage fluctuations in blood glucose in a timely manner. To obtain a complete picture of glycaemic control, the American Diabetes Association (ADA) recommends assessing glycaemic status at least twice a year in patients with stable glycaemic control [32]. It is also recommended that glycaemic status be assessed at least quarterly and as needed for patients who have recently changed treatment and/or are not meeting their glycaemic targets [32]. Existing evidence from randomised controlled trials suggests that lifestyle interventions are more effective than standard treatment for glycaemic control in people with T2DM [33].

Takai et al. [34] studied blood glucose fluctuations and glycaemic control in Japanese patients with T2DM in relation to pancreatic β-cell function. When studying the relationship between blood glucose fluctuations and average blood glucose levels in Japanese patients with T2DM, the results revealed that fluctuations in blood glucose levels and average blood glucose levels were correlated with HOMA-β. HOMA-β is an indicator for assessing β-cell function, and in the present study, HOMA-β was negatively correlated with FPG levels, suggesting that patients with higher HOMA-β values had lower levels of FPG. Higher HOMA-β values indicate that pancreatic β-cells function better and are able to secrete enough insulin to regulate blood glucose, which leads to lower FPG levels; this finding is clinically consistent with the findings of Takai et al. [34] Higher HOMA-β is protective against the development of DM [35], so improving β-cell function is necessary for DM management. To improve β-cell function, it is recommended that patients adopt a proper diet (e.g., following a balanced diet, avoiding foods high in sugar and fat, increasing dietary fibre intake), moderate exercise, and medication.

Insulin is negatively correlated with FPG levels, which is in line with the findings of clinical practice. Silvestre et al. [7] also predicted the normalisation of FPG levels via fasting insulin levels; during fasting, when insulin levels in the body are high, the body tries to lower blood glucose in an effort to regulate high blood glucose levels. If insulin secretion is normal and efficient, this results in lower FPG levels. Closed-loop control of insulin can further improve the quality of glycaemic control [36].

HbA1c is a product of the irreversible binding of glucose in the blood to haemoglobin in red blood cells and reflects the average blood glucose level over the past 2–3 months [32]; therefore, higher HbA1c values are usually associated with higher long-term glucose levels. HbA1c has become the gold standard for measuring the effectiveness of glycaemic control and is widely used to guide DM clinical management decisions [37]. Regular HbA1c testing (every 3 months) is recommended to assess long-term glycaemic control. Klein et al. [38] advocated setting HbA1c targets of less than 7% for the majority of the population, while emphasising that glycaemic targets will continue to evolve as new technologies and glucose-lowering medications are developed. Therefore, it is more effective to develop flexible, iterative and personalised management plans for patients than to follow strict guidelines.

HOMA-IR values are positively correlated with FPG levels. The HOMA-IR is an indicator used to assess the degree of insulin resistance. Higher HOMA-IR values indicate greater insulin resistance, and the body needs to secrete more insulin to maintain normal blood glucose levels. In the case of insulin resistance, blood glucose levels are relatively high. It is recommended that insulin resistance be reduced by losing weight, increasing physical activity and using insulin. Studies suggest that a high-protein diet does not significantly improve glycaemic control or blood pressure but reduces HOMA-IR levels in patients with T2DM; thus, an appropriately increased intake of high-protein foods may be advisable when HOMA-IR values are high [39].

Urinary glucose levels are positively correlated with FPG levels. Urinary glucose is detected when individuals are in a state of hyperglycaemia, and when the blood glucose level rises above the threshold of renal reabsorption capacity (usually approximately 180 mg/dL), the kidneys are no longer able to efficiently reabsorb all the glucose back into the bloodstream, resulting in a marked excess of glucose entering the urine and producing urinary glucose. As a result, higher FPG levels are usually accompanied by higher levels of urinary glucose, and the two are positively correlated. Urinary glucose monitoring can be used as a supplementary indicator of blood glucose control. More attention should be given to changes in the colour and smell of urine in general, and medical attention should be sought if there are any abnormalities.

The present longitudinal study of FPG levels revealed that HOMA-β, HbA1c, HOMA-IR, urinary glucose, and insulin had greater effects on changes in blood glucose values during the follow-up period. There was a trend towards decreasing FPG levels in the patients followed in this study, which may be due to better adherence to medication or diet/exercise interventions as a result of follow-up, reflecting the importance of follow-up. High FPG levels due to poor control is strongly associated with the development of diabetic complications such as retinopathy, neuropathy and cardiovascular disease [40]. The aim of hyperglycaemic management of DM is to alleviate the symptoms of hyperglycaemia, reduce complications, especially microvascular complications, and minimise side effects, including hypoglycaemia [41]. In addition, owing to the progressive nature of T2DM, medication alone is not sufficient to maintain normal blood glucose over the long term. Therefore, it is recommended that patients with DM undergo concurrent dietary and lifestyle management after starting medication.

Research strengths and limitations

There are several limitations to this study, including the following: the data were obtained from a specific population of patients (Japan), and it is not known how these models would perform in different demographic or geographic contexts; thus, the results are not generalizable, and further studies are needed to determine whether they can be replicated further, but the results are valuable. The data are publicly available from other articles rather than from our own collection, and the variable “group” is important, but in this study, “group” is limited to different treatments, among which the “combination of two or more of the above drugs” was representative of the majority of the study population. It was therefore not possible to analyse the specific drug combinations separately or to explore each treatment indicator in depth as an independent feature. Studies have recommended the use of a minimum sample size of 50 times the weight in NNs [42]. The sample size (n = 779) in this study may be an underrepresentation of the data, the generalisability of the model may be limited, and the risk of overfitting may be increased. Although we have used 10-fold cross-validation to ameliorate this limitation, slight overfitting remains. We have successfully and simultaneously compared and analysed the performance of three models, the LME, BPNN, and Linear Mixed-Effects (LMENN) models, for predicting FPG levels in patients with type 2 diabetes. However, we have not yet considered the application of Bayesian Neural Network (BNN) for this prediction task. Compared to the LMEs and MLs used in this paper, BNN have significant advantages: first, BNN exhibited strong robustness, as it does not depend on specific distributional assumptions and can easily cope with skewness in, for example, log(FPG) distributions (as shown in Fig. 5). Second, BNN is not prone to overfitting, which is very different from some ML methods that are notorious for overfitting.

Conclusion

Using longitudinal FBG monitoring data, we successfully established a novel LMENN model by taking random effects into account in the BPNN, and 10-fold cross-validation mitigated the risk of overfitting and enhanced the robustness of the model, achieving effective prediction of FPG levels in T2DM patients with the present data, which is highly important for the accurate management of diabetic patients, therapeutic decision-making, and improvement of patients’ quality of life. In the future, we will continue to optimise the model algorithm and aim to incorporate a wider range of large sample datasets with demographic and geographic distribution characteristics to increase the generalizability of the model. Moreover, we actively explore ways to improve the interpretability of the model and rigorously review its fairness to ensure that it is widely used and trusted by different patient groups. Finally, in response to the fact that the application of the BNN method for the prediction task has not yet been considered, and in view of the significant advantages demonstrated by BNN over LME and ML, as a future research direction, we will explore in depth the potential of BNN for the prediction of FPG levels in patients with type 2 diabetes mellitus.

Author contributions

Qiong Zou and Borui Chen contributed equally to this work. All authors contributed to the study origin and design. Data download and all analyzes were performed by Qiong Zou, Borui Chen, and Yang Zhang. The initial manuscript and its subsequent revisions were done by Qiong Zou and Borui Chen, while Xi Wu and Yi Wan analysed the feasibility of the study. Changsheng Chen critically checked the final version of the paper. all authors (Qiong Zou, Borui Chen, Yang Zhang, Xi Wu, Yi Wan, and Changsheng Chen) read and revised the manuscript and accepted the final version of the manuscript and were accountable for all aspects of the work.

Funding

This work was supported by the National Natural Science Foundation of China (grant number: 82073663).

Data availability

No datasets were generated or analysed during the current study.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.