Correlation-weighted ²³Na magnetic resonance fingerprinting in the brain

Abstract

We developed a new sodium magnetic resonance fingerprinting (²³Na MRF) method for the simultaneous mapping of ${\mathrm{T}}_1,{\mathrm{T}}_{2,\text{long}}^{\mathrm{*}},{\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ and sodium density with built-in $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ (radiofrequency transmission inhomogeneities) and $\mathrm{\Delta }{\mathrm{f}}_0$ corrections (frequency offsets). We based our ²³Na MRF implementation on a 3D FLORET sequence with 23 radiofrequency pulses. To capture the complex spin $\frac{3}{2}$ dynamics of the ²³Na nucleus, the fingerprint dictionary was simulated using the irreducible spherical tensor operators formalism. The dictionary contained 831,512 entries covering a wide range of ${\mathrm{T}}_1,{\mathrm{T}}_{2,\text{long}}^{\mathrm{*}},{\mathrm{T}}_{2,\text{short}}^{\mathrm{*}},\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor and $\mathrm{\Delta }{\mathrm{f}}_0$ parameters. Fingerprint matching was performed using the Pearson correlation and the resulting relaxation maps were weighted with a subset of the highest correlation coefficients corresponding to signal matches for each voxel. Our ²³Na MRF method was compared against reference methods in a 7-compartment phantom, and applied in brain in five healthy volunteers at 7 T. In phantoms, ²³Na MRF produced values comparable to those obtained with reference methods. Average sodium relaxation time values in cerebrospinal fluid, gray matter and white matter across five healthy volunteers were in good agreement with values previously reported in the literature.

1. Introduction

Sodium ions (Na⁺) plays a critical role in the human body and are invariably linked to the maintenance of ionic homeostasis as well as many physiological and electrochemical processes of metabolism (1, 2). For this reason, the non-invasive detection of these ions from the nuclear magnetic resonance (NMR) signal of the sodium isotope ²³Na (spin $\frac{3}{2}$) has become an important modality for the study of metabolic regulation and biochemical status throughout the body (1, 2). In brain, ²³Na MRI has been used to study neurodegenerative disease (1–7), tumor pathology (1, 2, 8, 9) and neurological events, such as stroke (2, 10) and traumatic brain injury (11). The intracellular and extracellular spaces in brain tissues both represent motion-restricted environments that give rise to signal contributions coming from the central and satellite transitions, which are strongly influenced by the quadrupolar interactions of the ²³Na nuclear spin system with its surroundings (2). These dynamics result in a biexponential transverse relaxation decay, i.e. a long component (${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$) and a short component (${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$), in both the intracellular and extracellular spaces. As a consequence, both gray matter (GM) and white matter (WM) in brain will also exhibit an overall ²³Na biexponential transverse relaxation, as a weighted average of the relaxation processes from the intracellular and extracellular spaces. Similarly, ²³Na longitudinal relaxation follows the same biexponential pattern from the intracellular and extracellular spaces. However, in soft biological tissues, both the short and long components are often very close to each other and longitudinal relaxation is usually measured as a monoexponential process (${\mathrm{T}}_{1,\text{short}}\sim {\mathrm{T}}_{1,\text{long}}\sim {\mathrm{T}}_1$) in GM and WM. In fluids such as cerebrospinal fluid (CSF), the quadrupolar interaction averages to zero as a result of rapid motion allowing the signal dynamics to be often modeled as a monoexponential relaxation for both transverse and longitudinal magnetization components. Collectively, the spin $\frac{3}{2}$ nature of the ²³Na nucleus and the low concentration of Na⁺ ions in brain tissue (on the order of 40–50 mM on average) combined with the inhomogeneous structure of the brain, makes it difficult to simultaneously quantify ²³Na relaxation times and density (1, 2, 12).

Proton magnetic resonance fingerprinting (¹H MRF) has become a popular technique for the simultaneous quantification of physical properties within a system (13–17). Recently, sodium MRF (²³Na MRF) studies in the brain have demonstrated promising initial results. Kratzer et al. (18, 19) implemented a version of ²³Na MRF capable of quantifying relaxation parameters in CSF and brain tissue (combined GM and WM) that utilized a 3D radial sequence with variable repetition times (TR), echo times (TE) and flip angles (FA). Our group previously introduced a multi-pulse approach to multicompartmental Na⁺ concentration quantification (20), which we now expanded for quantifying ²³Na relaxation in the brain.

In this work, we present a ²³Na MRF technique that is sensitive enough to quantify differences in average relaxation times over whole GM, WM, and CSF. Our method simultaneously maps ²³Na ${\mathrm{T}}_1,{\mathrm{T}}_{2,\text{long}}^{\mathrm{*}},{\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, sodium density (SD), and experimental imperfections arising from radiofrequency (RF) transmission inhomogeneities ($\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor) and frequency offsets from B₀ inhomogeneities $\left(\mathrm{\Delta }{\mathrm{f}}_0\right)$. The ²³Na MRF pulse train with variable FAs and phase angles (PA) was designed by incorporating the irreducible spherical tensor operator (ISTO) formalism into a genetic algorithm (GA) that minimizes signal correlation between GM and WM, assuming average relaxation times from the literature for these two tissues (21–23) during this optimization phase. A 3D Fermat looped orthogonally encoded trajectory (FLORET) (24) was used to fully sample k-space with constant TE. The proposed ²³Na MRF sequence can acquire data over the full brain with 5-mm isotropic resolution in about 30 min at 7 T. We tested our ²³Na MRF approach in a 7-compartment phantom and in five healthy volunteers.

2. Material and Methods

²³Na spin dynamics simulation

The dynamics of the ²³Na spin $I=\frac{3}{2}$ were modeled using the ISTO framework under the conventions described in Madelin et al. (2), Lee et al. (12), and Gilles et al. (20). Within this formalism, the evolution of the ²³Na spin system is described by the Liouville-von Neumann (master) equation (with convention $\hslash \equiv 1$):

$$\frac{d}{dt}\rho \left(t\right)=-i\left[H,\rho \left(t\right)\right]-\stackrel{\mathrm{ˆ}}{\mathrm{\Gamma }}\left\{\rho \left(t\right)-{\rho }^{th}\right\},$$ (1)

where ${\rho }^{th}$ is the density operator of the spin system at thermal equilibrium, $H$ is the total spin Hamiltonian and $\stackrel{\mathrm{ˆ}}{\mathrm{\Gamma }}$ is the Redfield relaxation superoperator. The total Hamiltonian $H$ is the sum of the main Hamiltonians acting on the density operator, such as the Zeeman Hamiltonian $H_Z$ (interaction of the spins with the constant $B_0$ field), the residual quadrupolar coupling Hamiltonian $H_Q$ (interaction of the quadrupole moment of the nuclei with the residual average electric field gradient in anisotropic environments), and the RF field Hamiltonian $H_1\left(t\right)$ (interaction of the spins with time-varying transmit RF field $B_1^{+}\left(t\right)$). In soft quasi-isotropic brain tissues, $H_Q$ can be considered negligible. Since we are also operating in the rotating frame for the spin dynamics simulation, the main Hamiltonians acting on the spin system are $H_Z$ related to $B_0$ inhomogeneities only, and $H_1\left(t\right)$.

The Redfield relaxation superoperator acting on the density operator of the spin system is described by:

$$\begin{array}{r}\stackrel{\mathrm{ˆ}}{\mathrm{\Gamma }}\left\{\rho -{\rho }^{th}\right\}=A\sum _{m=-2}^2(-1{)}^m\left[T_{2,m},\left[T_{2,-m},\rho -{\rho }^{th}\right]\right]\\ \times (J(m\omega )-iK(m\omega )),\end{array}$$ (2)

where $A$ is a constant that depends on the convention used to describe spectral densities, $T_{2,m}$ is the ISTO of rank 2 and order $m,J(m\omega )$ is the spectral density function, and $K(m\omega )$ is the imaginary term associated with dynamic frequency shift, which in our case can be omitted due to its negligible observable effect in soft tissues (2). The matrix formulation of $\stackrel{\mathrm{ˆ}}{\mathrm{\Gamma }}$ and relaxation rates $R_i=\frac{1}{T_i}$ with $i=(1,short),(1,long),(2,short),(2,long)$, are given by (12):

$$R_{1,\mathit{short}}=6J(0)$$ (3)

$$R_{1,\mathit{long}}=6J(\omega )$$ (4)

$$R_{2,\mathit{short}}=3J(0)+3J(\omega )$$ (5)

$$R_{2,\mathit{long}}=3J(\omega )+3J(2\omega ).$$ (6)

When simulating the spin dynamics for ²³Na MRF pulse train optimization or for generating the final fingerprint dictionary, the algorithm takes the relaxation times as input, then calculates the spectral density functions according to Equations 3–6 and uses the results to construct the Redfield relaxation superoperator in Equation 2, which is then added to the Liouville equation. After each time step of the simulation (100 μs), the simulated ²³Na MR signal, which corresponds to the MR-observable transverse magnetization, is calculated as the average rank-1 single quantum coherence $T_{1,-1}=\frac{1}{\sqrt{2}}{I}_{-}=\frac{1}{\sqrt{2}}\left(I_x-i{I}_y\right)$ using the standard formula $⟨T_{1,-1}⟩=\mathrm{T}\mathrm{r}\left(\rho T_{1,-1}\right)$, where $\mathrm{T}\mathrm{r}(A)$ is the trace of matrix $A$.

Pulse sequence design for 3D ²³Na MRF

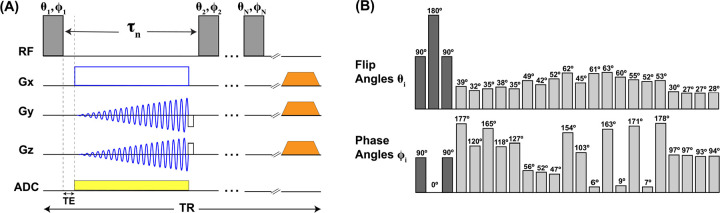
Figure 1(A) presents the ²³Na MRF sequence. System excitation was driven by a series of $N$ non-selective rectangular RF pulses with $\mathrm{F}\mathrm{A}{\theta }_i$ and $\mathrm{P}\mathrm{A}{\varphi }_i$ followed by a delay ${\tau }_i$ $(i=1,2,\dots ,N)$, forming the MRF pulse train shown in Figure 1(B). An initial magnetization inversion using a 90°–180°–90° (dark gray) composite 3-pulse block (25) was used to increase ${\mathrm{T}}_1$ sensitivity and improve RF homogeneity for the inversion before initiating the 20-pulse variable FA/PA train (light gray).

Figure 1. Pulse sequence diagram for 3D ²³Na MRF.

The overall pulse scheme is shown in (A). The diagram in (B) represents the variable flip angle (FA) and phase angle (PA) MRF train. There were a total of $N=23$ non-selective rectangular RF pulses of duration ${\tau }_{RF}=0.8\mathrm{m}\mathrm{s}$. Each pulse was followed by a time period ${\tau }_i$. On the RF channel in (A), the gray rectangles correspond to a single $\mathrm{F}\mathrm{A}={\theta }_i$ and $\mathrm{P}\mathrm{A}={\varphi }_i$ combination in train (B). In (B), the dark gray rectangles represent a 3-pulse inversion composite block (25) used to increase ${\mathrm{T}}_1$ sensitivity of the sequence and improve RF homogeneity for the magnetization inversion. Within the composite block, ${\tau }_1={\tau }_2=7.5\mathrm{m}\mathrm{s}$. The light gray rectangles indicate the 20-pulse variable FA and PA train. All $\mathrm{F}\mathrm{A}={\theta }_i$ and $\mathrm{P}\mathrm{A}={\varphi }_i$ are listed at the top of each rectangle and ${\tau }_i=15\mathrm{m}\mathrm{s}$ for $i\ge 3$. During each delay ${\tau }_i$, a time period TE = 0.2 ms was followed by the ADC event, indicated by a yellow block on the ADC channel. A 3D spiral encoding scheme using the FLORET trajectory (20, 24, 26) (3 hubs at 45°, 100 interleaves/hub), indicated in blue, was played over the gradient channels. Immediately after the ADC, a rewind gradient was also played out and then the next RF pulse in the MRF train was initiated. After $N$ pulses and $N{\tau }_i$ delays have played out, a 5-ms spoiling gradient at 70% maximum gradient strength, indicated by an orange trapezoid, was applied in all directions. The entirety of this scheme represented one TR of the sequence.

The RF pulse durations were fixed at ${\tau }_{RF}=0.8\mathrm{m}\mathrm{s}$, and interpulse delay periods were fixed at ${\tau }_i=7.5\mathrm{m}\mathrm{s}$ within the composite block $(i=1,2)$ and ${\tau }_i=15\mathrm{m}\mathrm{s}$ for the next pulses $(i\ge 3)$. The interpulse delays were set according to our prior work on simultaneous ¹H/²³Na MRI (27, 28) and in anticipation of integrating this method into simultaneous ¹H/²³Na MRF.

The FLORET trajectory (20, 24, 26) was used to readout the signal followed by a rewinder to balance the gradient moment. After $N$ pulses and $N{\tau }_i$ delays, a spoiling gradient (duration = 5 ms, 70% of maximum gradient strength) was applied simultaneously in all directions to ensure complete dephasing of residual transverse magnetization prior to beginning the next TR. A delay of ~300 ms was inserted between RF pulse trains to allow recovery of the longitudinal magnetization and reduce specific absorption rate (SAR). A constant TE = 0.2 ms was used throughout the sequence.

The variable 20-pulse FA/PA train was optimized using a genetic algorithm (GA) implemented in MATLAB R2020b (The MathWorks Inc., Natick, Massachusetts, USA) on an Apple MacBook Pro (16-inch, 2019) laptop with a 2.4 GHz 8-Core Intel Core i9 processor. The 3-pulse block used in the initial inversion was included in the optimization with FA and PA kept constant, resulting in a final 23-pulse train. The GA minimized an objective function estimating the Pearson correlation (PC) coefficient (29) between ²³Na MR signals arising from GM and WM. Input tissue relaxation times for the simulation were based on average values reported in the literature (1, 2, 30): for GM, ${\mathrm{T}}_1=30.2\mathrm{m}\mathrm{s}$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}=26.4\mathrm{m}\mathrm{s}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}=4.0\mathrm{m}\mathrm{s}$; for WM, ${\mathrm{T}}_1=29.2\mathrm{m}\mathrm{s}$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}=22.1\mathrm{m}\mathrm{s}$ and ${\mathrm{T}}_{2,\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}^{\mathrm{*}}=3.9\mathrm{m}\mathrm{s}$. Initial values for the $N$-pulse train (where $N_{\mathit{pulse}}=4,\dots ,23$ and $i=1,\dots ,N_{\mathit{pulse}}$ ) were ${\theta }_i={35}^{\circ }$ and ${\varphi }_i=0^{\circ }$ with period ${\tau }_i=15\mathrm{m}\mathrm{s}$. The composite block, corresponding to $i=1,2,3$ with ${\tau }_1={\tau }_2=7.5\mathrm{m}\mathrm{s}$, was also included in the simulation as a non-variable parameter. Limitations were imposed on FA ($0^{\circ }\le {\theta }_i\le {70}^{\circ }$) and PA ($0^{\circ }\le {\varphi }_i\le {180}^{\circ }$) in consideration of SAR limits. The GA optimized the system for 100 generations in 8 h. The algorithm was applied a total of three times, first using the initial input values for the variable 20-pulse part of the pulse train, followed by two iterations in which the solution of the previous computation was taken as input for the next one. This way, the optimized pulse train could be inspected after every 100^th generation cycle.

Fingerprint dictionary simulation

Simulation of the fingerprint dictionary was performed in MATLAB R2020b on a Cray CS500–1211 cluster with Intel Xeon Gold 6148 high memory CPUs at the NYU Langone High Performance Computing Core facility (New York City, NY, USA). The simulation code is freely available in Matlab File Exchange (see Data Availability section for the link). Signals were simulated starting from thermal equilibrium and propagated under the optimized 23-pulse ²³Na MRF train (Figure 1(B)). Parameter ranges ([begin:step:end]) to build the dictionary were ${\mathrm{T}}_{1,\text{long}}=[20:2:74]\mathrm{m}\mathrm{s}$, ${\mathrm{T}}_{1,\text{short}}=[20:2:74]\mathrm{m}\mathrm{s}$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}=[10:2:66]\mathrm{m}\mathrm{s}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}=[0.5:0.5:2.0,2:2:66]\mathrm{m}\mathrm{s},\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor = [0.7:0.1:1.3] (applied as a multiplying factor to the RF amplitude FA) and $\mathrm{\Delta }{\mathrm{f}}_0=[-60:10:60]\mathrm{H}\mathrm{z}$. For ${\mathrm{T}}_1$ quantification, we originally assumed that ${\mathrm{T}}_{1,\text{long}}={\mathrm{T}}_{1,\text{short}}$. To insure that spectral densities where $J(0)\ne J(\omega )$ were included in the dictionary, a constant (±ΔT₁) that added 1 ms to every entry for ${\mathrm{T}}_{1,\text{long}}$ and subtracted 1 ms to every entry for ${\mathrm{T}}_{1,\text{short}}$ was included in the simulations.

Parameter combinations where ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}>{\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}>{\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ were omitted from the computation. Due to the memory expense incurred by the simulation, the dictionary was generated in two parts and concatenated. In total, 831,512 entries were generated. The total simulation time was 6.4 days.

Experiments

All experiments were performed at 7 T (MAGNETOM, Siemens, Erlangen, Germany) using a 16-channel transmit/receive ¹H/²³Na RF brain coil constructed in-house (8 ¹H channels, 8 ²³Na channels) (31).

Phantom

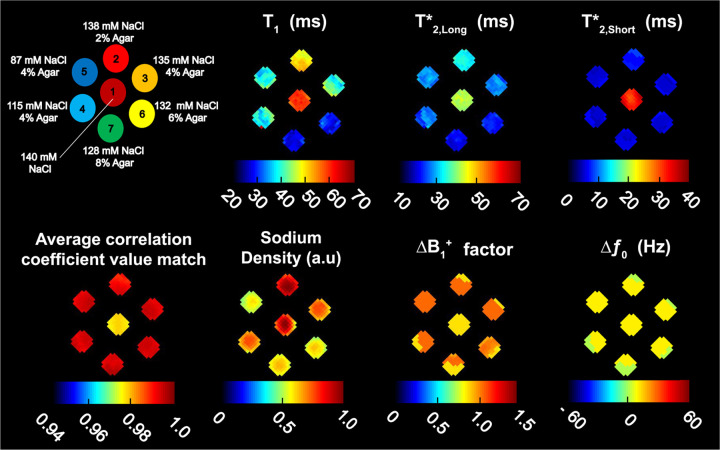
Our test phantom was constructed using a 2.3-L cylinder (outer diameter OD = 20 cm, length = 35 cm) filled with a solution of 70 mM NaCl and which contained seven 50-mL polypropylene cylinders (OD = 30 mm, length = 115 mm) arranged as 6 outer samples each containing a different concentration of NaCl and agar circling the 7^th sample placed in the middle and containing a solution of 140 mM NaCl. A diagram of the phantom with sodium/agar concentrations in the axial orientation is shown in Figure 2. The regions-of-interest (ROI) in the 7 samples were generated from a 3D mask of equal diameter to each sample such that all ROI volumes would be the same.

Figure 2. ²³Na MRF maps of the 7-compartment phantom.

Fingerprint matching was performed over an average of 2 center axial slices with 20 correlation coefficients included in the weighted average. A diagram of the 7-compartment phantom is shown in the top left corner. Maps for ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ are shown on the top row. A map showing the average correlation coefficient values matched for 20 correlations is shown at bottom left, followed by maps for normalized SD in arbitrary units (a.u), $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor (unitless) and $\mathrm{\Delta }{\mathrm{f}}_0$ in Hz.

For ²³Na MRF, one scan consisting of 16 averages with TR = 511 ms, isotropic resolution = 5 mm and isotropic FOV = 320 mm, was acquired with the FLORET parameters: 3 hubs/45° with 100 interleaves/hub, TE = 0.2 ms, total scan time = 40:52 min.

We measured the reference ${\mathrm{T}}_1$ using a saturation recovery (SR) reference experiment that consisted of a series of eight scans. Each scan consisted of a FLORET sequence (3 hubs/45° with 100 interleaves per hub) with different TRs = [60, 100, 140, 180, 260, 300, 360, 420] ms and fixed TE = 0.1 ms, 4 averages, isotropic resolution = 5 mm, isotropic FOV = 320 mm, rectangular RF excitation pulses with FA = 90° and ${\tau }_{RF}=0.8\mathrm{m}\mathrm{s}$. The total scan time for the SR experiments running sequentially was 1:49 h.

Similarly, we measured the reference mono- and biexponential ${\mathrm{T}}_2^{\mathrm{*}}$ using a multi-TE experiment that consisted of a series of 13 scans. Each scan consisted of a FLORET sequence (3 hubs/45° with 100 interleaves per hub) with TEs = [0.1, 0.5, 1.0, 1.5, 2, 5, 7.5, 10, 15, 25, 35, 50, 65] ms and fixed TR = 150 ms, 4 averages, isotropic resolution = 5 mm, isotropic FOV = 320 mm, rectangular RF excitation pulses with FA = 90° and ${\tau }_{RF}=0.8\mathrm{m}\mathrm{s}$. The total scan time for the multi-TE experiments running sequentially was 1:57 h.

Brain

Five healthy volunteers (1 female, 4 males, mean age 36 ± 8.5 years) were recruited under a protocol approved by the New York University Grossman School of Medicine institutional review board. All parts of the study were performed in accordance with the relevant guidelines and regulations set forth by the Human Research Protections Program. Informed consent was obtained before each scanning session. For ²³Na MRF, we acquired 4 separate scans consisting of 2 averages per scan. These 4 scans were acquired consecutively within 29.8 ± 1.3 min. We chose to divide the ²³Na MRF scanning portion of the session into separate 2-average scans in order to communicate with the volunteers during the acquisition. The average TR over all volunteer scans was TR = 704 ± 4 ms, which varied between subjects due to head size and coil loading. The minimum TR was calculated by the scanner to keep SAR within the maximum limit of 100%. Setting TR >700 ms allowed for full ${\mathrm{T}}_1$ recovery for about 380 ms after the last RF pulse, which was more than 5 times the longest expected ²³Na ${\mathrm{T}}_1$ in brain from CSF (T₁ ~ 50–60 ms (2, 19)). All brain scans were acquired with isotropic resolution = 5 mm and FOV = 320 mm.

For reference, a ¹H MPRAGE was acquired with 1 average, TR = 2300 ms, TE = 2.84 ms, FOV = 256×216 mm², slice thickness = 1 mm, 176 slices/slab and GRAPPA acceleration factor 2, for a total acquisition time of 4:32 min. The average total session time for calibration, shimming and scanning across all volunteers was 55 ± 3 min.

Data processing

All images were reconstructed offline in MATLAB. For each channel, raw k-space data acquired during the ²³Na MRF sequence was filtered with a Hamming kernel then reconstructed using gridding (32, 33) to produce a set of 23 complex images with a final nominal resolution 2.5×2.5×2.5 mm³ (128×128×128 matrix). The images from the 8 channels were combined using coil sensitivity profiles as described by Bydder et al. (34). The average time for image reconstruction in the brain across all five volunteers was 42 s, and 38 s in the phantom. For the brain images, an additional denoising step was performed on the complex images using the Marchenko-Pastur method (35–37). This added another 15 s to the brain image reconstruction time. Supplementary Figure S1 shows 23 axial images for a center slice in the phantom. Supplementary Figures S2 and S3 show 23 reconstructed axial images for a center slice in the brain of volunteer 5.

Phantom images from FLORET for ${\mathrm{T}}_1$ and ${\mathrm{T}}_2^{\mathrm{*}}$ reference experiments were reconstructed in the same way as the ²³Na MRF data. Curve fitting was applied voxelwise over the axial plane in the central slice of the phantom using the Levenberg-Marquardt algorithm applied using lsqcurvefit in MATLAB. A monoexponential kernel was assumed for ${\mathrm{T}}_1$ (38) according to Equation 7:

$$S\left(\mathrm{T}\mathrm{R},{\mathrm{T}}_1\right)=B\sqrt{{\left(1-e^{-\frac{\mathrm{T}\mathrm{R}}{{\mathrm{T}}_1}}\right)}^2+{𝒩}^2},$$ (7)

where coefficient $B$ and noise floor $𝒩$ were variable over the fit optimization. ${\mathrm{T}}_1$ values were restricted to a lower bound of 20 ms and upper bound of 80 ms, and TR was the repetition time from the FLORET acquisitions. Time required for this process was 33 s.

For ${\mathrm{T}}_2^{\mathrm{*}}$, we applied the biexponential kernel shown in Equation 8 as descibed by Ridley et. al (38, 39).

$$\begin{array}{r}S(\mathrm{T}\mathrm{E},{\mathrm{T}}_2^{\mathrm{*}})=\\ \sqrt{A^2\left(f\cdot e^{-\frac{\mathrm{T}\mathrm{E}}{{\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}}}+(1-f)e^{-\frac{\mathrm{T}\mathrm{E}}{{\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}}}\right)+n^2},\end{array}$$ (8)

The amplitude scaling factor $A$ was initialized as 1 and allowed to vary during the optimization with the lower bound set at 0 and the upper bound set at infinity. The Rician noise parameter $n$ was initialized as 0.1 based on the average noise measured in a background region outside of the phantom on the magnitude image, as described in Qian et al. (40). In this case, the upper bound was set at 1 with a lower bound of 0.01. The sodium signal fraction $f$ was initialized at 0.6 and allowed to vary between a lower bound of 0.4 and an upper bound of 0.8. The TE variable corresponded to TEs from the FLORET acquisitions. ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ was bound between 0.5 ms and 60 ms and ${\mathrm{T}}_{2,\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}^{\mathrm{*}}$ was bound between 10 ms and 80 ms.

In both fits, the upper and lower bounds for relaxation times were chosen to coincide with those parameter ranges simulated in the ²³Na MRF dictionary. Finally, the average relaxation values from the 7 individual phantom samples were calculated from the resultant 2D relaxation maps after masking. The time required for fitting was 27 s. Collectively, this process was referred to as the reference method (RM).

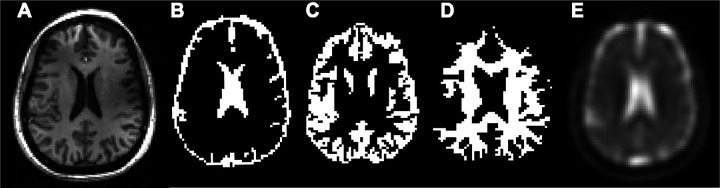
For each volunteer, images from the ¹H MPRAGE DICOM datasets were co-registered to the ²³Na MRF data using SPM12 (UCL, London, UK) (28, 41). The ²³Na MRF image used for co-registration was the one acquired just after the first pulse in the ²³Na MRF train. Tissue probability maps were generated from the normalized and co-registered MPRAGE images and segmented into CSF, GM and WM tissue classes using SPM12 (28, 41). The segmentated regions for CSF, GM and WM were then binarized with a 90% threshold to generate tissue ROI masks in MATLAB. These images are presented in Figure 3. The high threshold was chosen to reduce the likelihood of contamination between different tissues.

Figure 3. Images of a center slice of the brain in the axial position from volunteer 5.

(A) ¹H MPRAGE. (B) Binary mask for CSF. (C) Binary mask for GM. (D) Binary mask for WM. (E) ²³Na image acquired after first RF pulse of the MRF pulse train.

Fingerprint dictionary matching

The fingerprint dictionary (size = 831,512 entries) was matched voxelwise to the complex ²³Na image data using Pearson correlation. In the phantom, matching was performed on the average of two center slices in the axial plane. Matching required 10:34 min per slice followed by reconstruction of the correlation-weighted maps which added another 10 s. In brain, matching was performed over one center slice in each of the axial, coronal and sagittal positions for all five volunteers. Additionally, a slab of 20 axial slices were matched for volunteer 5. Matching required an average of 9:42 min per slice plus 10 s for reconstruction of the correlation-weighted maps. All these processes were also performed on an Apple MacBook Pro (2019, 2.4 GHz 8-Core Intel Core i9).

Because of the dictionary size, and due to the low SNR of the sodium images, it was therefore possible that more than one match could generate a high correlation for a single voxel. To account for this, we included matches for a subset of the top correlations for each voxel $v$, and generated the final maps by calculating the correlation-weighted parameter $X_v$ from the dictionary of values $X_{v,i}$ corresponding to the matching correlation coefficient $w_{v,i}$ according to:

$$X_v=\frac{\sum _{i=1}^k{w}_{v,i}{X}_{v,i}}{\sum _{i=1}^k{w}_{v,i}},$$ (9)

where $k$ was the maximum number of correlation coefficients used for weighting and $X_{v,i}$ and $X_v$ were the unweighted and weighted parameters ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{\Delta }\mathrm{B}}_1^{+}$ factor or $\mathrm{\Delta }{\mathrm{f}}_0$, respectively.

SD was calculated as the mean absolute value of signal per correlation for each voxel $v$, normalized by the highest voxel intensity in the image. Weighting was then done according to Equation 9, where $X_{v,i}$ was the unweighted SD and $X_v$ was the weighted SD.

Correlation coefficient weighting

We investigated the effect of the correlation weighting on the maps by directly evaluating both phantom and brain ²³Na MRF maps weighted with the maximum correlation coefficient only (k = 1) though the k = 1000 highest correlation coefficients.

To better choose the number of correlation coefficients to apply as a weighting factor in the final maps, we devised a method of selection using limits based on our RM and a priori information. First, for each relaxation parameter, a 2D map was generated using ²³Na MRF for every level of unweighted correlation ($\mathrm{k}=1,2,...,1000$). For the phantom experiments, a range of ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ determined by the RM were used as limits. For the brain data range, values from the literature for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in CSF, GM and WM, and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ for GM and WM were used (19, 21–23, 39, 42, 43). We chose to omit ${\mathrm{T}}_1$ in brain from this analysis due to the lack of ²³Na ${\mathrm{T}}_1$ values reported at 7 T in the literature.

These limits were then applied to the maps to generate a set of indices providing the location of pixels where the value of the masked ²³Na MRF mapped parameter fell within the range of the reference. This index set was then used to create a binary mask which was applied back to the original ²³Na MRF 2D maps. These results were plotted as the maximum number of matches made to the subset of pixels within the reference range versus the number k included in matching.

Statistical Analysis

We used the two-sided Wilcoxon rank-sum test (WRST) (44) in MATLAB to compare the values in the ROIs of the 7-compartment phantom, mapped using the RM against ²³Na MRF. Similarly, we used the same test to examine the sensitivity of ²³Na MRF for distinguishing between CSF, GM and WM in brain.

3. Results

Phantom

Figure 2 shows a diagram of the 7-compartment phantom and the maps from ²³Na MRF: ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, SD, $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor, $\mathrm{\Delta }{\mathrm{f}}_0$, as well as a map of the average correlation coefficient associated with the signals matched in each ROI (average from 20 correlation coefficients). The ROIs are numbered in correspondence with the data given in Table 1, which lists the mean relaxation times calculated for each individual ROI, with their respective standard deviations (STDV), measured using ²³Na MRF and with RM.

Table 1. ²³Na relaxation times measured in the 7-compartment phantom.

Measurements are shown as mean value ± standard deviation, from our ²³Na MRF method and from the average of two repetitions of the reference method.

	Concentration		23NaMRF			Reference Method
ROI	Agar (%)	NaCl (mM)	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)
1	0	140	58.9 ± 1.2	40.6 ± 0.9	32.9 ± 1.9	57.4 ± 2.0	52.1 ± 3.5	37.2 ± 2.7
2	2	138	49.8 ± 2.0	32.3 ± 1.3	7.6 ± 0.8	49.4 ± 1.9	30.5 ± 2.6	10.4 ± 0.8
3	4	135	41.2 ± 2.9	26.5 ± 1.5	6.2 ± 0.6	42.8 ± 2.3	26.6 ± 1.4	6.1 ± 0.4
4	4	115	40.0 ± 4.7	25.5 ± 2.2	6.2 ± 0.6	43.0 ± 1.1	26.3 ± 1.1	6.5 ± 0.7
5	4	87	39.4 ± 2.5	27.2 ± 1.2	6.1 ± 0.4	44.7 ± 0.6	25.9 ± 0.8	6.4 ± 0.2
6	6	132	29.7 ± 1.9	21.9 ± 1.1	6.2 ± 0.5	38.3 ± 1.6	23.6 ± 0.8	4.5 ± 0.3
7	8	128	28.5 ± 1.3	20.2 ± 1.2	6.3 ± 0.4	36.8 ± 0.7	23.0 ± 0.7	5.7 ± 0.3

The average relaxation times listed in Table 1 for ²³Na MRF measurements can be easily estimated by visual inspection of the relaxation maps in Figure 2.

The center ROI 1 contained a solution of 140 mM NaCl and showed slight variations in uniformity for ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ and SD maps, but appeared uniform in maps of $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor and $\mathrm{\Delta }{\mathrm{f}}_0$. The mean ${\mathrm{T}}_1$ for ²³Na MRF was 58.9 ± 1.2 ms versus 57.4 ± 2.0 ms for RM. The mean ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ for ²³Na MRF was shorter than ${\mathrm{T}}_1$ for ²³Na MRF by 18.2 ± 2.4 ms. For RM, the mean ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (53.1 ± 3.5) was similar to the mean ${\mathrm{T}}_1$ (57.4 ± 2.0 ms). The difference between mean ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ for ²³Na MRF and RM was 11.5 ± 3.6 ms, where RM was higher. Mean ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ values for both ²³Na MRF and RM were lower than ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$. The difference between ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in ²³Na MRF was 26 ± 2.2 ms while the difference between ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ was 7.7 ± 2.1 ms. For RM, the difference between ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ was 20.2 ± 3.4 ms and the difference between ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ was 14.9 ± 4.4 ms.

Loss of uniformity in the phantom compartments was seen in the ${\mathrm{T}}_1$ maps of ROI 3 (41.2 ± 2.9 ms), ROI 4 (40.0 ± 4.7 ms) and ROI 5 (39.4 ± 2.5 ms). Out of these ROIs, the most notable artifact appeared in the ${\mathrm{T}}_1$ map for ROI 4. In this case, we can align the artifact in the ${\mathrm{T}}_1$ map with perturbations in the maps of $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor and $\mathrm{\Delta }{\mathrm{f}}_0$. The variation noted for the ${\mathrm{T}}_1$ map in ROI 4 could also be outlined in the maps for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$. Mean ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in ROI 4 was 25.5 ± 2.2 ms, which represented the highest STDV for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ out of all ROIs. Mean ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in ROI 4 was 6.2 ± 0.6 ms.

Relaxation time data is also presented as boxplots in Figure 4 for comparing ²³Na MRF with RM. SD data is shown in the same figure as a comparison between ²³Na MRF measurements and ground truth (GT), presented as mean value ±5% STDV.

Figure 4. Boxplots of ${\mathbf{T}}_{\mathbf{1}}$, ${\mathbf{T}}_{\mathbf{2},\mathbf{long}}^{\mathbf{*}}$, ${\mathbf{T}}_{\mathbf{2},\mathbf{short}}^{\mathbf{*}}$ and SD in the phantom compartments: ²³Na MRF vs. reference method (RM).

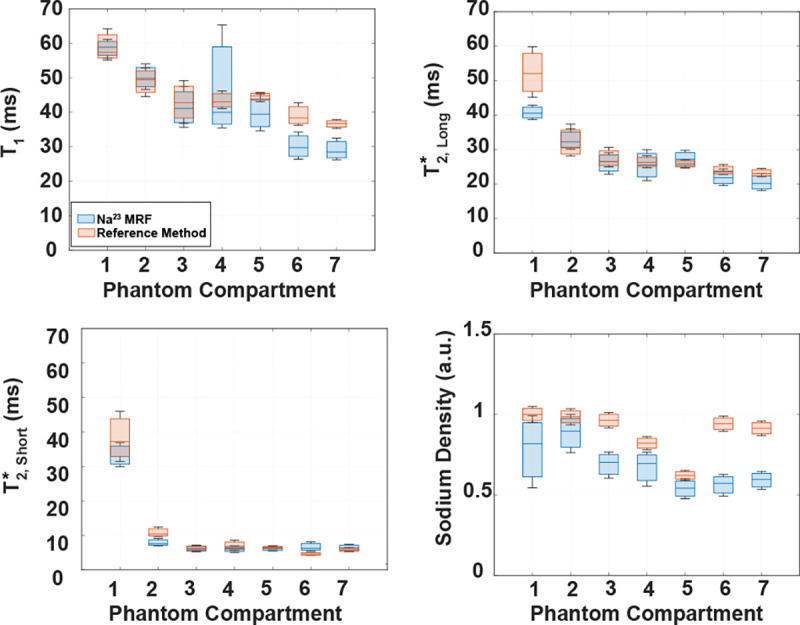
Relaxation time data corresponds to data listed in Table 1. SD calculated using ²³Na MRF was compared to the ground truth (mean value ±5%) (see Figure 2). Blue boxes represent data from our ²³Na MRF method. Red boxes represent data from RM for relaxation times, and from ground truth for SD.

The boxplots for ${\mathrm{T}}_1$ overlap within the interquartile range for ROIs 1 through 5 of the 7-compartment phantom. For ROI 6, the maximum ${\mathrm{T}}_1$ for ²³Na MRF falls 1.93 ms below the minimum for the RM ${\mathrm{T}}_1$. In ROI 7 the ${\mathrm{T}}_1$ for ²³Na MRF was 2.82 ms below the minimum for RM ${\mathrm{T}}_1$. A non-statistically significant difference between RM and ²³Na MRF was found only in ROI 2 with WRST (p = 0.0526).

The boxplot for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ for ROI 1 shows that the maximum ²³Na MRF ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ is 2.31 ms below the minimum RM ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$. For ROIs 2 through 7, there is overlap within the interquartile ranges between RM and ²³Na MRF. However, a non-statistically significant difference between RM and ²³Na MRF was only found for ROI 4 with WRST (p = 0.0930).

Interquartile overlap was noted between ²³Na MRF and RM for ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in ROIs 1, 3, 4, 5 and 7. The WRST analysis for these ROIs supported non-statistically significant difference between ²³Na MRF and RM in ROIs 4, 5 and 7 with p = 0.7919, 0.0802 and 0.9054, respectively. In ROI 2, the RM minimum was ~0.6 ms greater than the maximum ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ from ²³Na MRF. Finally, for ROI 6, the minimum ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ for ²³Na MRF was ~0.6 ms greater than the maximum for RM.

SD of the GT was consistently higher than SD from ²³Na MRF. Overlap in the distributions occured only between the 2^nd quartile of the GT and 4^th quartile of ²³Na MRF in ROI 1, between the 2^nd quartile of GT and 3^rd quartile of ²³Na MRF in ROI 2, and between the 1^st quartile of GT and 4^th quartile of ²³Na MRF in ROI 5.

Supplementary Figure S4 shows scatter plots with linear fits between ²³Na MRF and RM for ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, and between ²³Na MRF and GT (mean value ±5% STDV) for SD, using data from Table 1.

Brain

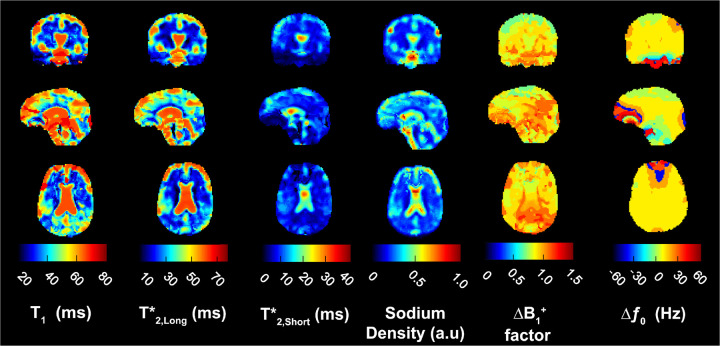
Figure 5 shows the maps for ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, $\mathrm{S}\mathrm{D}$, $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ and $\mathrm{\Delta }{\mathrm{f}}_0$ from volunteer 5 in coronal, sagittal and axial slices. We used a weighting factor of k = 20 correlation coefficients during the PC matching process for all volunteers. The most apparent feature in the relaxation times and SD maps was the CSF-filled central ventricles. Contrast from the long ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ values in CSF dominate the central ventricular structure in all three planes. Contrast from CSF can also be seen within subarachnoid spaces and the cavity along the gyri of the cerebral cortex overall cross sections. In the sagittal slice, we identified the third and fourth ventricles and the occipital horn of the lateral ventricle in maps for ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ and SD. The overall contrast for ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in CSF was reduced compared to ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$. Here the highest values for ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ were concentrated in the center of the central ventricle in each cross-section. Mean ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ values reported in Table 2 were the result of this unequal distribution of ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ over the collective CSF ROI. Mean ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in the voxels at the center of the central ventricle across all 5 volunteers was 40.1 ± 0.1 ms.

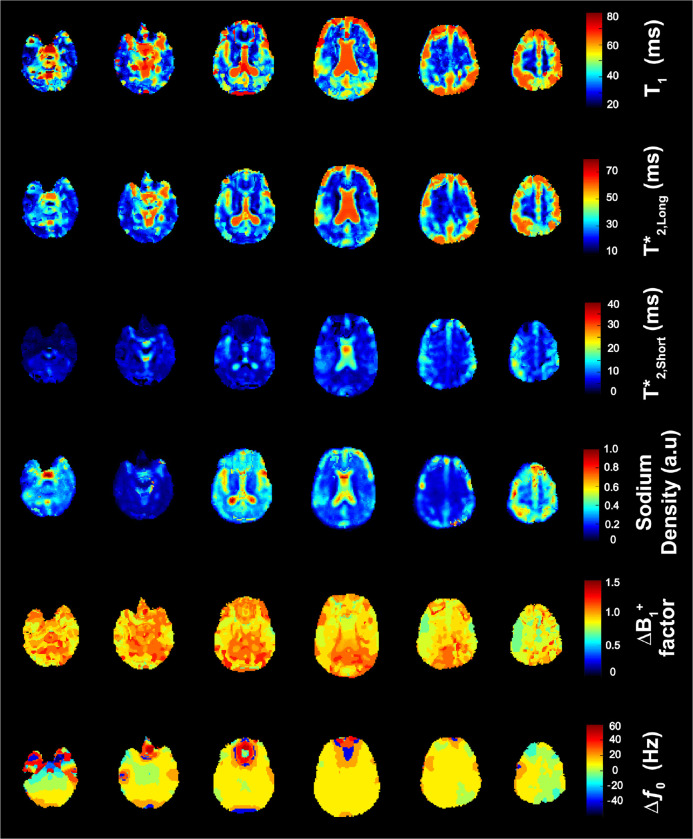
Figure 5. Brain maps from ²³Na MRF.

Examples of coronal, sagittal and axial slices for ²³Na relaxation times, SD, $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor and $\mathrm{\Delta }{\mathrm{f}}_0$ from volunteer 5. All maps were calculated with a correlation coefficient weighting of k = 20.

Table 2. Mean ²³Na MRF values in brain in 5 volunteers.

Data shown represents mean relaxation times and normalized sodium density (SD) ± standard deviations (STDV) measured in three brain tissue ROIs (cerebrospinal fluid [CSF], grey matter [GM], white matter [WM]) for each volunteer (VOL). Mean values were calculated over the center slices of the axial, coronal and sagittal planes of the brain. The bottom row of each column corresponds to the mean value ± STDV of the mean values measured in each ROI across all volunteers

	CSF				GM				WM
VOL	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)	SD	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)	SD	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)	SD
1	50.7 ± 15.1	41.7 ± 16.3	10.0 ± 8.8	0.246 ± 0.134	44.1 ± 12.5	33.0 ± 11.2	6.6 ± 3.6	0.212 ± 0.072	43.0 ± 13.6	27.9 ± 12.1	6.6 ± 3.9	0.177 ± 0.054
2	62.1 ± 7.0	55.0 ± 9.6	17.2 ± 9.4	0.467 ± 0.172	44.1 ± 12.0	31.2 ± 9.2	7.4 ± 3.8	0.234 ± 0.067	36.5 ± 10.5	23.1 ± 8.5	5.4 ± 2.9	0.191 ± 0.063
3	61.8 ± 10.2	47.3 ± 13.9	12.4 ±7.8	0.42 ± 0.169	42.9 ± 12.5	30.9 ± 9.2	5.3 ± 2.7	0.262 ± 0.711	39.5 ± 13.3	26.3 ± 9.8	4.6 ± 3.0	0.213 ± 0.061
4	59.1 ± 10.3	47.4 ± 12.9	9.9 ± 7.2	0.41 ± 0.165	40.4 ± 12.8	27.3 ± 8.3	6.3 ± 3.1	0.234 ± 0.060	34.2 ±11.8	20.2 ± 9.7	4.9 ± 2.6	0.176 ± 0.062
5	63.1 ± 5.7	57.3 ± 7.6	13.1 ± 7.1	0.43 ± 0.128	46.3 ± 12.9	35.1 ± 11.1	7.7 ± 3.4	0.242 ± 0.071	42.2 ± 11.0	28.5 ± 12.2	5.9 ± 2.7	0.185 ± 0.061
Mean	59.4 ± 5.1	49.7 ± 6.3	12.5 ± 3.0	0.395 ± 0.086	43.6 ± 2.1	31.5 ± 2.9	6.7 ± 1.0	0.237 ± 0.018	39.1 ± 3.7	25.2 ± 3.5	5.5 ± 0.8	0.188 ± 0.151

The normalized SD maps demonstrated high sodium concentration within CSF and lower sodium concentration in GM and WM. For $\mathrm{\Delta }{\mathrm{f}}_0$, extremely negative and positive shifts were mapped around the medial frontal gyrus, shown in the axial position, over the frontal lobe above the nasal sinus cavity, shown in the sagittal plane, and at the base of the medulla near the posterior cerebellum, shown in the coronal plane.

Figure 6 presents the ²³Na MRF maps in six equidistant axial slices for volunteer 5 with a weighting factor of k = 20 correlation coefficients.

Figure 6. Examples of six equally-spaced axial slices of brain maps from ²³Na MRF.

Maps shown are ²³Na relaxation times, SD, $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor and $\mathrm{\Delta }{\mathrm{f}}_0$ from volunteer 5. All maps were calculated with a correlation coefficient weighting of k = 20.

Table 2 lists the mean ²³Na relaxation times and SD with their respective STDVs in CSF, WM and GM for all 5 subjects. The bottom row lists the mean values with corresponding STDV for each tissue across all five volunteers. The greatest deviation from mean relaxation time across volunteers was recorded in CSF. The shortest ${\mathrm{T}}_1$ was measured in volunteer 1 along with the highest STDV (50.7 ± 15.1 ms) while the longest ${\mathrm{T}}_1$ and lowest STDV were recorded in volunteer 5 (63.1 ± 5.7 ms). The wide range of these values contributed to an overall 8.6% STDV amongst volunteers. This trend was also observed for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in CSF, where volunteer 1 contributed 41.7 ± 16.3 ms and volunteer 5 contributed 57.3 ± 7.6 ms, toward a mean ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ 49.7 ± 6.3 ms across all five volunteers. For ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in CSF, a mean value of 12.5 ± 3.0 ms was measured over the five volunteers with 23Na MRF. Finally, a good agreement between relaxation times in GM and WM was noted across volunteers, as indicated by the low corresponding STDVs.

Figure 7 summarizes the results from Table 2 into boxplots. We found that the median ${\mathrm{T}}_1$ in CSF was 61.8 ms and that there was no overlap in ${\mathrm{T}}_1$ ranges between either the GM or WM groups. Strong differentiation between CSF and GM/WM was corroborated statistically by WRST (p = 0.0079). The median ${\mathrm{T}}_1$ for GM was 44.1 ms and the median ${\mathrm{T}}_1$ for WM was 39.5 ms. The lower adjacent value in GM (40.4 ms) was positioned below the third quartile of WM with the upper adjacent value in WM (43 ms) positioned above the first quartile of GM. Despite the overlap in these regions, a statistically significant difference between ${\mathrm{T}}_1$ in GM and WM was observed (p = 0.0476).

Figure 7. Boxplots of the mean ${\mathbf{T}}_{\mathbf{1}}$, ${\mathbf{T}}_{\mathbf{2},\mathbf{long}}^{\mathbf{*}}$, ${\mathbf{T}}_{\mathbf{2},\mathbf{short}}^{\mathbf{*}}$ and SD in CSF, GM and WM measured in the brain of 5 volunteers.

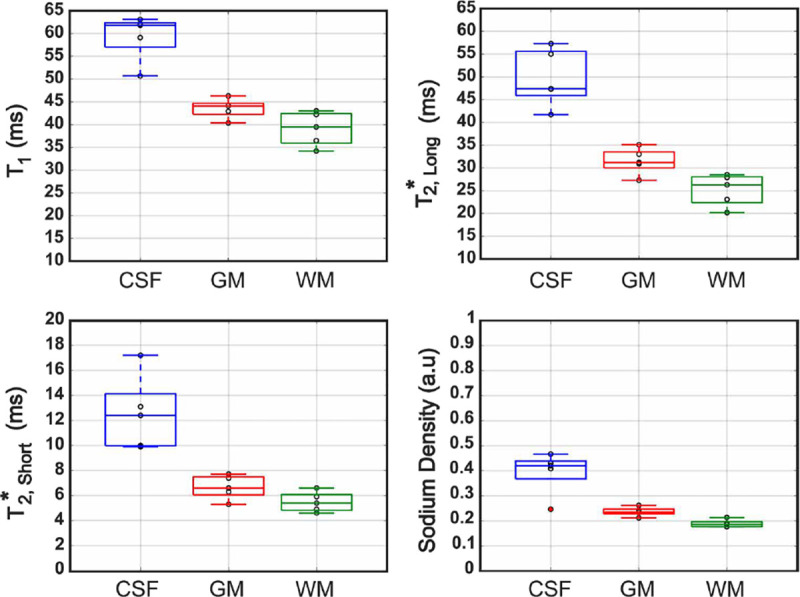
Mean values were measured on the center slice of each of the three planes (see Table 2). Data points for individual volunteers are indicated with black circles, and outliers are marked in red. The lines inside each box represent the median values. Abbreviations: GM, grey matter; WM, white matter; CSF, cerebrospinal fluid.

For ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in CSF, the median value was 47.4 ms. Again, there was no overlap of ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ for CSF with ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in either GM or WM. The differences were statistically significant (p = 0.0079) between GM and CSF, and between WM and CSF. The median ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in GM was 31.2 ms with a lower adjacent value of 27.3 ms, which fell below the third quartile of WM. The median ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in WM was 26.3 ms. WRST comparison between ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in GM and WM indicated a statistically significant difference (p = 0.0317).

Median ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in CSF, GM and WM were 12.4 ms, 6.6 ms and 5.4 ms, respectively. As was the case in ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, the range of ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ shown for the boxplot of CSF in Figure 7 did not align within the ranges of ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in GM or WM. Similarly to statistical results results for ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in CSF was statistically significantly different from ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in both GM and WM (p = 0.0079). There was no statistically significant difference in ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ between GM and WM (p = 0.1111). This was corroborated by the respective boxplots in Figure 7 where we noted that the upper adjacent of WM was equal to the median of GM (6.6 ms).

For normalized SD in CSF, we found a maximum of 0.467, a median of 0.420 and a minimum of 0.0246, which was considered an outlier. The lower adjacent of CSF was 0.368 and did not overlap with any data grouped for either GM or WM. The minimum value recorded for GM was 0.212, which was nearly equivalent to the maximum of WM (0.213). A statistically significant difference was observed for SD between GM and WM (p = 0.0159).

Table 3 provides a comparison between the relaxation times obtained using our ²³Na MRF method and those reported in the literature at 7 T. For ${\mathrm{T}}_1$ in CSF measured using our proposed ²³Na MRF, the mean value (59.4 ± 5.1 ms) was comparable to the mean ${\mathrm{T}}_1$ reported by Kratzer et al. (19) (61.9 ± 2.8 ms) using their ²³Na MRF method. ${\mathrm{T}}_2^{\mathrm{*}}$ values for CSF were reported throughout the literature as monoexponential fits with values ranging from 46.3 ± 6.3 ms (19) to 57.2 ± 6.6 ms (23). This range indicated that our measured value of 49.7 ± 6.3 ms for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ was in good agreement with the literature. Our mean measurement of 12.5 ± 3.0 ms for ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, however, was out of range compared to these same values.

Table 3. Comparison of the relaxation times measured in brain at 7 T between the correlation-weighted (CW)²³Na MRF method and values from the literature.

Relaxation times values were compared in cerebrospinal fluid (CSF), grey matter (GM) and white matter (WM). “Brain Tissue” was included where a distinction was not made between GM and WM.

		CSF			GM			WM			Brain Tissue
Reference	Method	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_1$ (ms)	${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ (ms)	${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ (ms)
Kratzer et al. (19)	23Na MRF	61.9 ± 2.8	46.3 ± 4.5								35.0 ± 3.2	29.3 ± 3.8	5.5 ± 1.3
Lommen et al. (42)	DA-3DPR		53.6 ± 6.9						35.7 ± 2.4	5.1 ± 0.8
	DA-3DPR		54.4 ± 5.7						34.4 ± 1.5	4.2 ± 0.4
Ridley (39)	DA-3DPR					33.9 ± 5.9	5.0 ± 0.9		34.0 ± 5.2	4.5 ± 0.6
Blunck et al. (23)	3D-MERINA		57.2 ± 6.6			25.9 ± 8.3	2.0 ± 2.1		22.4 ± 7.8	2.0 ± 2.1
Niesporek (22)	DA-3DPR		46.9 ± 2.1			36.4 ± 3.1	5.4 ± 0.2		23.3 ± 2.6	3.5 ± 0.1
Nagel et al. (21)	DA-3DPR		56.0 ± 4.0
Fleysher et al. (43)	GRE		54.0 ± 4.0			28.0 ± 2.0			29.0 ± 2.0
Our work	CW 23Na MRF	59.4 ± 5.1	49.7 ± 6.3	12.5 ± 3.0	43.6 ± 2.1	31.5 ± 2.9	6.7 ± 1.0	39.1 ± 3.7	25.2 ± 3.5	5.5 ± 0.8

We did not find values for ${\mathrm{T}}_1$ specific to GM and WM during our literature search (which we limited to data recorded at 7 T), so we compared our results to the ${\mathrm{T}}_1$ for unspecified brain tissue determined by Kratzer et al. (19). In this case, our ${\mathrm{T}}_1$ measurement for WM was in good agreement with their value for brain tissue, but our value for GM was ~11 ms longer.

For ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in GM, our measured value of 31.5 ± 2.9 ms was in agreement with previous reports (22, 23, 39, 43), while our measured value of 6.7 ± 1.0 ms for ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ was similar to that found by Ridley et al. (39), but slightly longer than other reports (22, 23).

For ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in WM, we calculated a mean of 25.2 ± 3.5 ms, which was within the range of 40.0 ± 5.2 ms (39) to 22.4 ± 7.8 ms (23) reported for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in the literature. Our WM ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ value of 5.5 ± 0.8 ms was within range of two sources (39, 42) and slightly longer than the other three references (22, 23, 42). Finally, both the ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ values that we measured in GM and WM were in good agreement with values reported for brain tissue (19).

Correlation coefficient weighting

Supplementary Figure S5 shows the maps of the 7-compartment phantom produced after matching was performed using different numbers of correlation coefficients as weighting factors, from the maximum correlation only (k = 1) through k = 1000.

Supplementary Figure S6 shows the maps for volunteer 5 representing brain results produced after matching was performed using different numbers of correlation coefficients as weighting factors, from the maximum correlation only (k = 1) through k = 1000.

Supplementary Figure S7 summarizes the results of matching in the 7-compartment phantom with different k values against the RM in a series of boxplots. When k = 20, there was more overlap between the interquartile regions of RM and ${\mathrm{T}}_1$ as compared to the single maximum valued correlation, and the most overlap in interquartile regions for all ROIs in ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$. Although STDV was reduced for ${\mathrm{T}}_1$ as the number of correlation coefficients increases, there was loss of overlap between RM and ²³Na MRF for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in ROIs 6 and 7, respectively. Overall, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ did not change significantly between k = 1 and k = 200.

Supplementary Figure S8 shows a series of graphs for the relaxation times measured in each ROI of the 7-compartment phantom plotting the maximum number of matches made to a subset of pixels within a reference range limited by values from the RM. Examining the trends in the graphs for the phantom, we noted that the plot most often changed direction in ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ from a high number of maximum correlations per pixel match to a global decrease followed by leveling off in the region between k = 10 to k = 50. Direction changes were also noted in ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ graphs in the neighborhood of k = 100.

Supplementary Figure S9 shows similar graphs for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in CSF, GM and WM and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in GM and WM for each of the 5 volunteers. The maximum number of matches made to a subset of pixels within each ROI were limited by ranges defined by literature values taken from Table 3. While graphs of ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ do not show any notable trend, there are direction changes in the graphs of ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in the neighborhood of k = 20 for CSF, GM and WM.

4. Discussion

In this work we demonstrated a refined approach to quantitative mapping of ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ and SD using ²³Na MRF with correlation coefficient weighting. We constructed a comprehensive dictionary that included combinations of ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor and $\mathrm{\Delta }{\mathrm{f}}_0$. We implemented a 3D FLORET sequence with an optimized 23-pulse variable FA/PA MRF train capable of full brain coverage in about 30 min without varying TE or delays between the pulses in the ²³Na MRF pulse train. While the ISTO spin system simulation and PC matching procedure were based on our previous work (20), this study integrated a new ²³Na MRF pulse train optimization protocol and refined matching criteria. Our method was tested in a 7-compartment phantom, and successfully applied for brain mapping in five healthy volunteers at 7 T.

Because $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ and $\mathrm{\Delta }{\mathrm{f}}_0$ were included as dictionary parameters, the spatial influences of transmit inhomogeneity and frequency shift on relaxation times were partially accounted for in the matching process. RF field variations were most pronounced in the phantom data (Figure 2), due to its high average relative permittivity. On the other hand, $\mathrm{\Delta }{\mathrm{f}}_0$ variations were more pronounced in vivo, due to air-filled structures such as the ear canal and maxillary sinus cavities (Figure 6). Some of the artifacts noted in the relaxation maps could be lined up with similar artifacts in maps of $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ and $\mathrm{\Delta }{\mathrm{f}}_0$. This indicated that broadening the ranges for $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ and $\mathrm{\Delta }{\mathrm{f}}_0$ in the dictionary, or reducing the step size for these entries, might improve the appearance of these artifacts in the parameter maps.

The low resolution used to offset the sodium SNR deficits makes precise measurements in isolated tissues difficult. Even at the current resolution, low SNR remains a hurdle. Speckle noise can be seen in some of the maps in Figures 5 and 6, that overlap in regions where changes in $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor or $\mathrm{\Delta }{\mathrm{f}}_0$ were apparent, corresponding to areas of low SNR. We first tried to overcome some of these caveats by denoising the images prior to matching. While denoising did offer subtle improvement in image quality by removing some pixels with outlying intensity, the image quality was not enhanced enough to make a difference in the matching process.

Matching with PC was performed voxelwise between the data and the dictionary. We ordered the signal matches for each individual voxel according to their respective correlation coefficients and then produced maps reflecting data that included a subset of matches for each voxel. We later refined this technique by using the correlation coefficient value per voxel signal match as a weighting factor. While the time required for matching and map reconstruction was longer than the fitting times of the RM for ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, the ²³Na MRF method has the benefit of mapping not only ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ but also $\mathrm{\Delta }{\mathrm{B}}_1^{+},\mathrm{\Delta }{\mathrm{f}}_0$ and SD in a single acquisition. Furthermore, the combined scan time for RM based on the scan time in the phantom, would be more than 2 h versus a scan time of about 30 min for brain ²³Na MRF.

Changes in the maps of correlation coefficient value averaged over increasing numbers of coefficients were minor. This was because the differences between the maximum value and an average of some subset of coefficients for any single voxel were in the thousandths. Despite such minor changes in value, each correlation represents a potential match between the dictionary and data. We acknowledge that examining correlation in non-convex space and within a noisy environment opens the possibility that some higher valued correlations were calculated for signals representing local minima as opposed to a “true” match. Our choice to include multiple matches based on correlation coeffcient weighting increased the probability that some match resulted from a “true” match as opposed to a local minimum. It may be possible to further improve matching by accounting for non-convexity in the reconstruction process (45–47).

In the phantom, we weighted the data with 20 coefficients. This reduced the slight inhomogeneity in ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and provided the best agreement between ²³Na MRF and the RM data. While weighting beyond 20 coefficients continued to slightly smooth artifacts and improve the agreement between ²³Na MRF and RM in ${\mathrm{T}}_1$, the agreement to RM in ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ began to diverge in ROIs 6 and 7 at k = 50. There was no significant change in values beyond the maximum correlation for ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$. Similarly, for SD, an improved overlap in the boxplots between ²³Na MRF and RM is seen at k = 20 with no change beyond this value.

Matching in vivo was also completed using weighting with k = 20 correlation coefficients. In this case, increasing the number of coefficients introduced signals with lower value correlation coefficients for CSF. Interestingly, this had the effect of increasing the values of ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ within CSF while slightly decreasing ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$. This was combined with an overall increase in the ${\mathrm{T}}_1$ of brain tissue and decrease in SD. Essentially, weighting signals by their correlation coefficients operated as a smoothing kernel by including a range of highly similar fingerprints. We compared the smoothing effect to that of applying a Gaussian filter prior to matching which is shown in Supplementary Figure S10. Comparison of parameter maps at the maximum correlation with and without the addition of the Gaussian filter demonstrated no effective improvement in the visual appearance for the brain data. Furthermore, this outcome did not change when additional correlations were included.

Visually, we could not differentiate between GM and WM in the brain maps of the five volunteers. However, our statistical analysis indicated that the mean ${\mathrm{T}}_1$ and ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ were different enough to distinguish between GM and WM. As listed in Table 3, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ were reported in several studies where a wide range between the shortest and longest ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ was noted amongst different sources. While different fitting techniques or data acquisition schemes could be the culprit, there may also be variations in relaxation time within GM and WM. Some recent works suggest that regional differences in structural composition within GM and WM (39, 48) are contributing factors, or that local changes are induced within the cellular environment of the respective tissues (3). These considerations, combined with the inherently low SNR of sodium, make distinguishing GM and WM through relaxation mapping difficult.

The ISTO simulation that we used to model ${\mathrm{T}}_2^{\mathrm{*}}$ relaxation included dictionary ranges from 10 to 66 ms for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and from 0.5 to 66 ms for ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$. We hypothesized that average values for ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ and ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ CSF would be equal or very close to each other. However, the mean ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ was significantly shorter than ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ in our measurements in CSF. Similar issues with ${\mathrm{T}}_2^{\mathrm{*}}$ fitting in CSF have been mentioned in the literature (23, 49) where the difficulty arose from using discrete biexponential or monoexponential models. Fingerprint matching, however, operates across a pseudo-continuum and is based on the dynamics of the spin system. Theoretically, this would circumvent some of the shortcomings associated with fitting discrete models. The concentration of higher value ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in CSF in the center in the central ventricle indicated that partial volume effects from surrounding tissue may have contributed to the low ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$. Eroding the tissue masks did not significantly change the distribution of ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$ in CSF, however, any contamination of the ROI could have resulted in a reduced apparent ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$.

It is also worth noting that our ²³Na MRF method, and the ISTO simulation that we used to generate the fingerprint dictionary, do not make any assumption about either the compartmental homogeneity within the voxel, nor the ratios between relaxation processes for the central and satellite transitions of the ²³Na spins $\frac{3}{2}$ (i.e. the long and short relaxation components). Both ²³Na MRF and the ISTO simulation simply estimate average relaxation times in each voxel, which is very likely a volume weighted average of multiple intra-voxel compartments (extracellular and intracellular spaces from multiple cell types) and local magnetic field inhomogeneities. Consequently, there is very little chance to measure the ideal ratio of 0.6:0.4 for ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}:{\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ due to quadrupolar relaxation processes. Indeed, if we were to specifically measure the ratio of ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}:{\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$ with a fitting method (which MRF is not), the ratio of 0.6:0.4 would occur only in a perfectly ideal model where relaxation is purely quadrupolar. This is usually not the case in real samples, including gels, fluids and biological tissues. In reality, dipolar coupling, residual quadrupolar interaction (due to local structural anisotropies), local field inhomogeneities (chemical shift interaction) of various nature, and even spin-orbit interaction where the spin interacts with the magnetic fields generated by the rotational motion of the ion itself, can occur and influence the relaxation process of the ²³Na spins. Such influences effectively act as pertubations to the main quadrupolar relaxation process, and thus generate ²³Na relaxation times that deviate from the ideal case of pure quadrupolar relaxation (50–52).

5. Conclusion

In conclusion, we demonstrated an implementation of ²³Na MRF from a 3D 23-pulse FLORET acquisition that enabled quantitative mapping of ${\mathrm{T}}_1$, ${\mathrm{T}}_{2,\text{long}}^{\mathrm{*}}$, ${\mathrm{T}}_{2,\text{short}}^{\mathrm{*}}$, $\mathrm{S}\mathrm{D}$, $\mathrm{\Delta }{\mathrm{B}}_1^{+}$ factor and $\mathrm{\Delta }{\mathrm{f}}_0$ in about 30 min over the whole brain with 5-mm isotropic resolution at 7 T. Furthermore, we introduced correlation coefficient weighting in the data reconstruction to enhance the robustness of the method and smooth the final maps.

The proposed ²³Na MRF method could finally be combined with ¹H MRF based on our previous work on simultaneous acquisition of ¹H MRF and ²³Na MRI (27, 28, 53) to generate a fully simultaneous ¹H/²³Na MRF technique (54).

Data availability

Data analyzed in this study is available on GitHub: https://github.com/LaurenFODonnell/Sodium_MRF_Datasets.git. The Matlab code for sodium NMR dynamics simulation used for generating the fingerprint dictionary is available on Matlab File Exchange: https://www.mathworks.com/matlabcentral/fileexchange/67472-simulation-of-sodium-nmr.