Abstract
The landmark discovery of gold catalysts has aroused substantial interest in heterogeneous catalysis, yet the catalytic mechanism remains elusive. For carbon monoxide oxidation on gold nanoparticles (NPs) supported on ceria surfaces, it is widely believed that carbon monoxide adsorbs on the gold particles, while the reaction occurs at the gold/ceria interface. Here, we have investigated the dynamic changes of supported gold NPs with various sizes in a carbon monoxide oxidation atmosphere using deep potential molecular dynamics simulations. Our results reveal that the structure of tiny gold particles in carbon monoxide atmospheres becomes highly disordered and undergoes phase transition. Such a liquid-like structure provides massive reactive sites, enabling facile carbon monoxide oxidation on the solid-state gold NP rather than just at the gold/ceria interface. This result is further corroborated by catalytic experiments. This work sheds light on both the size effects and activity in noble metal catalysis and provides insights for the design of more effective nanocatalysts.
Gold nanoparticles in a CO atmosphere undergo dynamic phase transition, enhancing CO oxidation beyond the Au/ceria interface.
INTRODUCTION
Heterogeneous gold catalysts are composed of support and supported Au nanoparticles (NPs) (1, 2). One of the most investigated heterogeneous gold catalytic reactions is CO oxidation on Au NPs supported on ceria (CeO2) surfaces. This reaction attracts substantial attention due to its potential applications in CO removal from industrial gas streams, such as in automotive exhaust systems and fuel cells (3). Moreover, owing to the recognizable adsorption behaviors, CO oxidation has been extensively studied as an ideal model reaction to obtain mechanism insight toward the catalytic process. Since the 1980s, very small Au NPs, approximately 2 to 5 nm in size, have been demonstrated to catalyze the oxidation of both CO and H2 at low temperatures (4–6). An atomic-level understanding of the catalytic process is yet to be developed, especially regarding the significant size effect of gold catalysts.
With numerous experimental and theoretical efforts, the metal/ceria interface is believed to be the reactive site for CO oxidation on gold NPs (7). The conventional mechanism for this CO oxidation reaction involves the adsorption of CO molecules on the surface of Au NPs, followed by the reaction with adsorbed O2 molecules at the ceria surface and Au/ceria interface (7–10). Smaller Au NPs are more effective for catalyzing CO oxidation reaction, as they have a higher interface-to-volume ratio. This higher ratio presumably would result in more interface sites available for CO molecules to adsorb (7), thereby increasing the number of CO molecules available to react at the Au/ceria interface and leading to a higher overall reaction rate. However, this static mechanism does not account for the variations in reaction temperature observed with Au NPs of different sizes (11, 12). Moreover, the direct reaction pathways on pure Au NPs have yet to be elucidated, especially for those whose diameters are smaller than 3 nm, which has a severe dynamic effect (7, 13, 14).
To understand the size-activity or structure-activity relationships for supported gold catalysts on oxides, we and others have developed various theoretical models (8, 15, 16). These models aim at describing the chemical potential of supported gold NPs and their transformation between single-atom catalysts under different conditions. The effectiveness of these models is demonstrated in explaining and predicting the stability and sintering of supported metal catalysts (17–19). The underlying assumption of these models is that supported gold NPs are solid and their chemical potential and morphology remain largely unaffected by phase changes at the melting point, even in the presence of reactants. However, phase transitions often occur during reactions, as the melting point of Au NPs can decrease markedly with the size reduction of catalysts, potentially falling below the reaction temperature and markedly affecting the reaction’s activity.
Time- and space-resolved experimental characterization of the dynamic evolution of small catalysts, such as supported Au NPs, under realistic catalytic conditions is challenging because of the complexity of the reaction environment (14, 20–22). In heterogeneous catalytic reactions, the solid catalysts are in contact with gas molecules or a liquid phase containing the reactants, complicating the direct observation of the catalysts’ structures and movements using traditional ex situ techniques. One approach to characterizing catalysts under actual catalytic conditions involves the use of in situ techniques, which allow for the direct observation of the evolution of catalysts during the reaction (10). For instance, we have used in situ aberration-corrected environmental transmission electron microscopy to observe the structures and movements of Au NPs on ceria support during a CO oxidation reaction (10), allowing for real-time observation of the catalysts in real space. Recent scanning tunneling microscopy studies have observed in situ adsorbate-induced active-site formation by CO exposure on defective Ni, Cu, or Au surfaces (23–25). Molecular dynamics simulations, particularly with density functional theory (DFT)–based ab initio molecular dynamics (AIMD), are also extensively used to simulate dynamic changes during the catalytic process. However, AIMD is computationally intensive and time consuming, limiting its application to large systems of more than 1000 atoms or long-time durations exceeding 100 ps (8, 9, 15, 26). Recently, machine learning–based deep potential molecular dynamics (DPMD) has emerged as a powerful technique (16, 27, 28), as it applies machine learning techniques to construct the potential energies and forces, offering a much faster approach to accurately describing large catalytic systems (16).
In this work, we use a state-of-the-art, machine learning–based DPMD method, combined with thermodynamic analysis and microkinetic modeling, to explore the intrinsic activity of small Au NPs supported on ceria under a CO oxidation atmosphere. Our results reveal that very small Au particles, when exposed to CO atmospheres, undergo a transformation where their crystal structure falls down and becomes liquid-like, which produces more low-coordinated apex Au atoms. This transformation provides ideal active sites for CO oxidation by associative Langmuir-Hinshelwood (L-H) mechanism, leading to CO oxidation occurring across the entire Au particle, rather than just at the Au/ceria interface. By incorporating dynamic catalytic theory into our investigation, this finding underscores the pivotal role of structural dynamics in enhancing the catalytic activity of heterogeneous catalysts.
RESULTS
Deep potential molecular dynamics
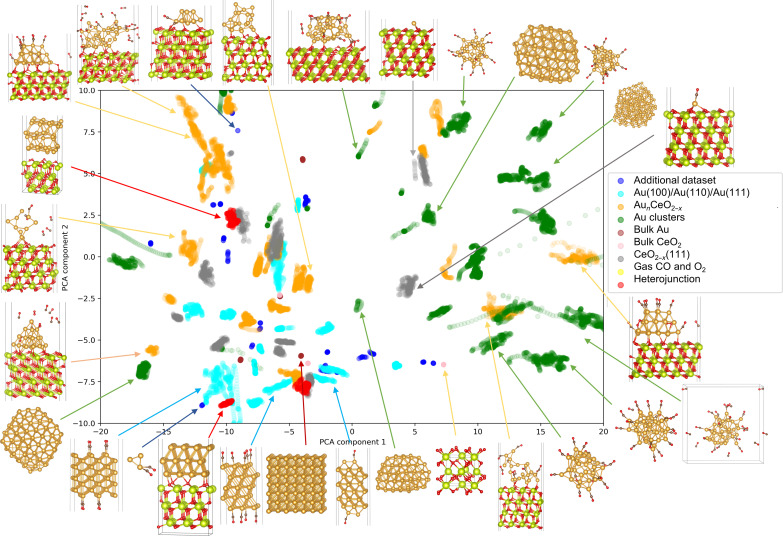
From computational modeling of the dynamic behavior of Au NPs on the ceria surface in a vacuum environment (16), it becomes clear that in the absence of adsorbates, Au NPs on the ceria surface retain their face-centered cubic (fcc) lattice pattern, particularly at step sites. To gain a better understanding of how Au NPs behave in the presence of CO gas, we develop here a machine learning force field (MLFF) that includes CO, CO2, and O2 adsorbates. Creating an accurate MLFF requires collecting data from DFT calculations to cover as many configurations in the phase space as possible. We initiated with over 120 AIMD trajectories, each beginning with different initial compositions and configurations as discussed in the Supplementary Materials (figs. S1 to S3). We extracted local structural and elemental feature matrices from the local environment embedding networks of the training set. The distribution and clustering of different local environments in the high-dimensional space were reduced to two dimensions using principal components analysis (PCA). As illustrated by the atomic configurations, different regions of the PCA map correspond to distinct structures, with clear groupings of similar structures and separations of dissimilar ones. This highlights the diversity of the dataset and the quality of the learned descriptors (Fig. 1 and fig. S4). The MLFF we developed proved to be highly accurate with force and energy errors lower than 89.2 meV/Å and 1.85 meV per atom, respectively (figs. S5 and S6), which allows one to directly simulate the dynamic behavior of supported Au NPs on ceria surfaces with vacancies.
Fig. 1. PCA-based similarity map of the training set for the local environment embedding networks consisting of 34,158 structures.
The structures are colored according to their types from the initial dataset. The plot visualizes the distribution and clustering of different local environments in the high-dimensional space, reduced to two dimensions using PCA. Examples of atomic configurations from various regions of the map are provided to illustrate the dataset’s diversity. The color code for elements is as follows: Au, yellow; Ce, green; O, red; C, gray.
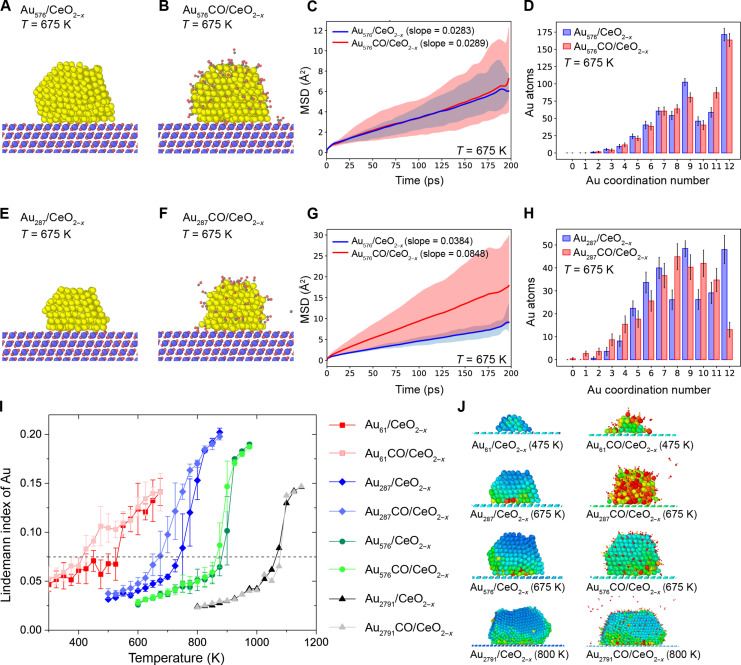
A series of supported Au NPs including Au61 (1.5 nm double-layer), Au287 (2.4 nm), Au576 (3.0 nm), and Au2791 (5.6 nm) on defected CeO2(111) was investigated using DPMD simulations at temperatures ranging from 300 to 1150 K (figs. S7 to S20). A relatively large Au576 NP with a diameter of ~3.0 nm exhibits clearly defined fcc structures at 675 K (Fig. 2, A and B). During the DPMD simulations, the Au(111) and Au(100) surfaces of Au576 are kept intact, and only slight disorder is observed at the Au/ceria interface. Upon injecting CO molecules into the system, the edges of the Au576 NPs are quickly occupied by adsorbed CO molecules, while the overall crystal structure of Au576 remains nearly unchanged. The mean square displacement (MSD) slopes of Au576 without and with CO are 0.0283 and 0.0289 Å2/ps, respectively, at 675 K. In addition, all MSDs performed between 600 and 975 K also show no significant difference with or without CO as shown in Fig. 2C and fig. S10. A sudden increase in MSD occurs at 875 K, corresponding to the melting point of Au576 NP. Most coordination numbers of the Au atom are found to be 12 and 9, corresponding to the inner bulk atoms and Au(111) surface atoms, respectively. The distribution of coordination numbers of Au atoms remains nearly unchanged with and without CO adsorption at 675 K, indicating that the fcc structure of Au NPs is stable during the simulations (Fig. 2D).
Fig. 2. DPMD simulations of supported Au61, Au287, Au576, and Au2791 NPs on defected CeO2(111).
Snapshot pictures at 200 ps for (A and B) Au576/CeO2−x(111) without and with a CO atmosphere and (E and F) Au287/CeO2−x without and with a CO atmosphere at a temperature of 675 K during DPMD simulations. The color code for elements is as follows: Au, yellow; Ce, blue; O, red; C, gray. (C and G) Corresponding MSDs averaged over five DPMD simulation trajectories. (D and H) Coordination number distribution of Au atoms without and with CO adsorption with a Au─Au bond cutoff criterion of 3.4 Å. (I) Lindemann index versus temperature during DPMD simulations for Au61/CeO2−x(111), Au287/CeO2−x(111), Au576/CeO2−x(111), and Au2791/CeO2−x(111) without and with a CO atmosphere. (J) Colored local Lindemann index snapshots at 200 ps, where the big balls are Au and Ce atoms, and the small balls represent C and O atoms. Blue balls denote that the Au atoms keep their fcc crystal structure, and red balls denote that Au atoms are disordered.
By comparison, a smaller Au287 NP with a diameter of approximately 2.3 nm and 287 atoms is also constructed on a defected CeO2(111) surface. This Au287 NP also has an fcc structure, albeit slightly disordered (Fig. 2, E and F). In contrast to the larger NPs, when CO molecules are introduced into the system, the solid structures quickly break down, and the adsorbed CO molecules pull some Au atoms out of the NPs’ surface, resulting in a low-coordinated apex gold site for forming Au-CO species. The MSD curve indicates that the slopes increase markedly from 0.0384 to 0.0848 Å2/ps at 675 K (Fig. 2G), which suggests an obvious disorder of Au NPs. Unlike the larger NP, the coordination number of Au in Au287/CeO2−x also changes significantly, as shown in Fig. 2H. Specifically, the numbers of 12-coordinated and 9-coordinated Au atoms decrease, indicating the breakdown of the fcc crystal structure. Meanwhile, the numbers of two-coordinated and one-coordinated Au atoms increase, which are leached Au atoms resulting from CO adsorption.
To figure out the triggering temperature of the disordering for supported Au NPs, we used diffusivity (D) and the Lindemann index (L), which is a measure of the root mean square fluctuation of interatomic distances, as criteria to determine the melting point. As shown in Fig. 2 (I and J), the Lindemann indexes of Au576 and Au2791 are almost unaffected by CO adsorption, with L = 0.075 serving as the threshold for melting. The melting point of supported Au576 is only reduced by about 25 K from ~900 to ~875 K. Most of Au576 remains stable (blue or green colored) in the colored local Lindemann index snapshots, with only a few Au atoms at the Au/ceria interface exhibiting disorder at 675 K (Fig. 2J). In contrast, the melting point of supported Au287 is significantly lowered from ~750 to ~675 K, with disordered Au atoms spreading from the interface to the entire NPs at 675 K due to CO adsorption. The smaller Au61 double-layer cluster already shows disorder at approximately 425 K with CO adsorption, making a decrease of about 125 K. In addition, we observed some Au atoms without any Au─Au bond during the simulations, dynamically forming isolated Au-CO species that leach out of the NPs and are supported on the ceria surface, which is consistent with previous AIMD results (9).
Thermodynamic analysis
The Gibbs-Thomson effect, with small NPs having a lower melting point, arises from the high curvature and increased vapor pressure of small NPs. The Gibbs-Thomson equation can be used to calculate the structural melting point (Tm) depression for an isolated spherical metal particle of radius r. The equation can be expressed as follows
| (1) |
where is the bulk phase change temperature, σsl is the surface tension of the solid/liquid interface, Lm is the bulk enthalpy of fusion, and ρs is the density of solid. This equation demonstrates how the melting point decreases as the curvature at the interface increases.
As discussed previously by Buffat and Borel (29) and Font and Myers (30), the generalized Gibbs-Thomson relation takes into account the pressure and specific heat factors, in which the surface tension (σsl) can be further detailed, and the Tm can be refined as follows
| (2) |
where γs and γl represent the surface tension of solid and liquid gold, respectively. ρs and ρl are the densities of solid and liquid gold, respectively. It is evident that changes in surface tension play a crucial role in determining the melting point of NPs under real reaction conditions. In particular, the surface tension changes remarkably when CO molecules adsorb on the solid and liquid gold surfaces, thereby substantially affecting the melting point of metal NPs. The changes of γs and γl denoted as Δγs(T, P) and Δγl(T, P), respectively, are functions of temperature (T) and CO pressure (P).
The surface tension of solid gold NPs can be obtained by averaging the surface energies based on the Curie-Wulff relationship (tables S1 to S4), as expressed by Eq. 3.
| (3) |
Here, γi represents the surface tension of a specific facet, while fi is the percentage of that facet. From our reported method (8), Eq. 4 expresses the change in γ with CO adsorption, where Δγi(T, P) is the change in surface tension of facet i due to CO adsorption, which is discussed in the Supplementary Materials (figs. S21 and S22 and tables S5 to S7)
| (4) |
where θi is the coverage of CO on the Au surface and is the average adsorption energy. Ai is the unit surface area, and μCO(T, P) is the chemical potential of CO molecules. On the basis of the above equations, the melting point of Au NPs is influenced by their size, as well as the temperature and pressure of the CO molecule. Particularly noteworthy is the fact that the CO adsorption on the liquid Au surface is stronger than that on the solid Au, leading to a larger difference between γl and γs with CO adsorption. Consequently, this results in a decrease in melting points, particularly under high μCO(T, P) conditions, where the CO pressure is high and the temperature is low.
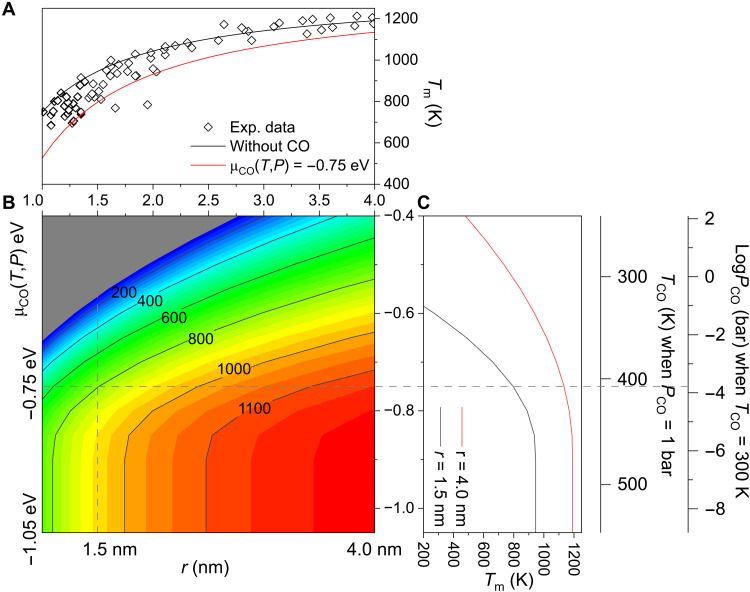
According to the Gibbs-Thomson equation, the simulated melting points of supported bare Au NPs fit well with this trend, as depicted by the black line in Fig. 3A. Following this relationship, the estimated trend of melting point change with the radius of supported Au NPs agrees well with the experimental data (29). Inasmuch as the electronic interaction of Au NPs on ceria is stronger than that on inert supports such as carbon materials and silica surfaces (16), the simulated melting points of Au NPs on ceria are a little higher than those measured experimentally on inert substrates. Besides, the melting points of Au NPs decrease rapidly with decreasing radius, regardless of the presence of CO. Smaller Au NPs are more susceptible to the presence of CO in their environment. At a chemical potential of μCO(T, P) = −0.75 eV, the decrease in melting point is around 220 K for NPs with a radius of 1 nm, but for NPs with a radius larger than 4 nm, the decrease in melting point is only about 60 K (Fig. 3B), which is in good agreement with the DPMD simulations. Larger NPs require a higher temperature to melt, but at high temperatures, most CO molecules will desorb from both the solid and liquid surfaces, leading to little influence on their surface tension. The effects of temperature and CO pressure on the chemical potential and melting point are illustrated in Fig. 3C. At low temperatures and high CO pressures, the μCO(T, P) will increase, leading to a decrease in Tm. Such a size-dependent reduction in melting point may provide an intrinsic explanation for the size effect observed in CO oxidation and water-gas shift reactions.
Fig. 3. Melting point (Tm) of Au NPs with different sizes.
(A) Size dependence of the melting point. The black line represents Tm from Gibbs-Thomson equations without CO adsorption, and the red line is plotted with CO adsorption at μCO(T, P) = −0.75 eV. Diamonds are experimental data from Buffat and Borel (29) of Au NPs on carbon films. (B) Contour plot of Tm versus chemical potential [μCO(T, P)] and radius of NPs (r). (C) Tm of Au NPs versus μCO(T, P) with radii of 4.0 nm (red line) and 1.5 nm (black line). The relations between μCO(T, P) and T at PCO = 1 bar and PCO at T = 300 K are indicated on the ordinate.
Reaction mechanism
Under CO oxidation conditions, the dynamic changes of Au NPs can significantly influence the reaction mechanism and the turnover frequencies (TOFs). In the case of CO oxidation on supported Au/CeO2 systems, three possible reaction pathways have been proposed, including Mars–van Krevelen (M-vK) (31), Eley-Rideal, and L-H mechanisms (32–34). The M-vK mechanism involves CO oxidation facilitated by surface O on ceria at the Au/CeO2 interface and is considered the most probable reaction mechanism for CO oxidation reactions (Fig. 4B) (35). However, it cannot explain the differences in the onset reaction temperature observed for supported Au catalysts with various sizes (11, 12). Au NPs with small size undergo a phase transition and become liquid-like at relatively low temperatures. This enhances the adsorption of CO molecules, thus leading to the L-H mechanism where CO interacts with adsorbed O2 to produce CO2 molecules (Fig. 4B, figs. S23 to S32, and tables S8 to S10).
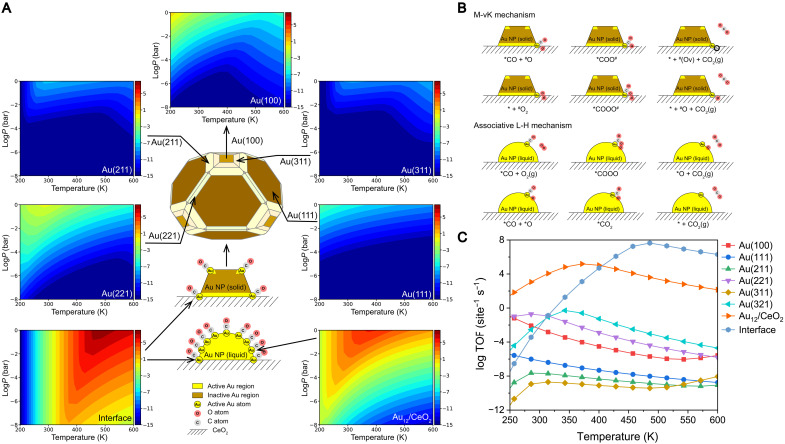
Fig. 4. Reaction TOF and reaction mechanisms for CO oxidation.
(A) Schematic representation of the Wulff construction of solid Au NPs in vacuum and liquid-like Au NPs on ceria. Corresponding TOF of Au(100), Au(211), Au(311), Au(221), Au (111), Au12/CeO2 interface, and Au site on Au12/CeO2 at a range of total pressure from 10−8 to 1 bar and a range of temperature from 200 to 600 K. The ratio of CO is set to 0.01, and the ratio of O2 is set to 0.2. (B) Schematic illustration of M-vK and associative L-H mechanisms of CO oxidation reaction on Au/CeO2. (C) TOF of CO2 versus given temperature on Au(100), Au(111), Au(211), Au(221), Au(311), and Au(321) surface, Au site on Au12/CeO2, and Au/CeO2 interface at PCO = 0.01 bar and = 0.2 bar.
To determine the catalytic activity, we carry out further microkinetic modeling. The supported solid Au NPs on the CeO2(111) surface are constructed on the basis of Wulff construction (Fig. 4A). For solid Au surfaces, although Au(100), Au(321), and Au(221) surfaces are more active than the most exposed Au(111) surface, their TOFs under real reaction conditions are still lower than 1 site−1 s−1 (Fig. 4C). Thus, the activity of CO oxidation on pure solid Au NPs is relatively low. Meanwhile, the M-vK mechanism contributes substantially at relatively higher temperatures, T > 400 K, occurring at the Au/CeO2 interface (Fig. 4C). Therefore, the activity of large solid NPs from the M-vK mechanism at relatively higher temperatures cannot solely explain the phenomena of low-temperature CO oxidation in gold catalysis.
Considering the melting of small Au NPs under reaction conditions, we investigated the supported disordered multilayer cluster on the CeO2(111) surface (Au12/CeO2), representing the supported liquid-like Au NPs. In the temperature range from 250 to 400 K, the low-coordinated Au atoms on Au12/CeO2 are the most active sites rather than the interface sites. This low-temperature activity stems from the L-H mechanism on liquid-like Au with small size, rather than from the M-vK mechanism. The L-H mechanism can be divided into dissociative and associative pathways. The dissociative L-H mechanism requires the direct dissociation of O2 into two *O adsorbates, followed by the coupling of adsorbed *CO and *O to form CO2 molecules. However, the dissociation barrier of O2 on the Au metal surface is too high, hindering the subsequent reaction and, thus, resulting in low CO2 productivity. The associative L-H mechanism involves the reaction between *CO and adsorbed *O2 to form *OCOO species, which is the precursor of CO2. The reaction barrier for the combination of *CO and *O2 species in the associative pathway is much lower than that for direct O2 dissociation (32). Therefore, the associative pathway would dominate when the L-H mechanism occurs on Au surfaces and liquid-like Au sites.
To further quantify the reactivity of Au/CeO2 catalysts of various sizes, we modeled a statistical TOF on the basis of the various active sites on Au NPs and microkinetic analysis (figs. S33 to S41). For a supported Au NP of a specific size, the catalytic activity in the solid phase is determined by the weighted average L-H TOF of exposed surfaces based on Wulff construction and the M-vK TOF of the interface active site. Meanwhile, the activity of liquid Au NP depends on the average L-H TOF of exposed liquid Au atoms and the M-vK TOF of interface atoms. The statistical TOF of supported Au NPs in solid and liquid states can be expressed as Eqs. 5 and 6
| (5) |
| (6) |
where , , and represent the ratio of the number of exposed surface atoms, interface atoms on Au/CeO2, and exposed liquid atoms to the total number of atoms on supported Au NP, respectively. In addition, , , and correspond to calculated TOFs for exposed solid Au surfaces, the Au12/CeO2 interface, and the liquid Au sites on Au12/CeO2, respectively, with calculation details discussed in Materials and Methods.
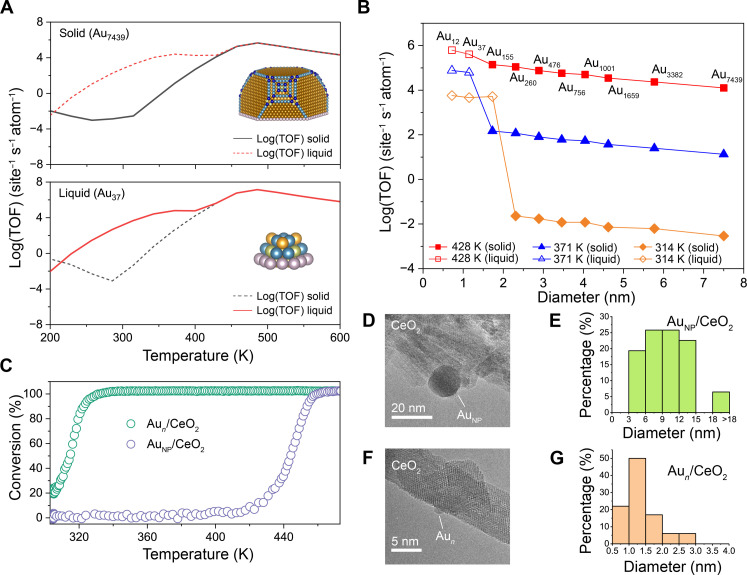
It is evident from the analysis that the morphology of Au NPs significantly influences their activity at low temperatures for CO oxidation. The calculated log(TOF) values for supported Au7439, Au3382, Au1659, Au1001, Au756, Au476, Au260, Au155, and Au37 NPs on CeO2(111) are compared (tables S11 and S12). The TOF at temperatures above ~430 K is similar for both solid and liquid states, while the TOF at temperatures below ~400 K for the liquid state is two to four orders of magnitude higher than that for the solid state because of a differing L-H mechanism as discussed above. Larger NPs, such as Au7439, remain in a solid state under reaction conditions, whereas smaller NPs, such as Au37, are liquid across all reaction temperature ranges. This finding indicates a critical size for the phase transition that triggers the activity of Au/CeO2 catalysts of various sizes (Fig. 5A). The critical size is found to increase with decreasing temperature due to the higher CO chemical potential, which can accelerate the phase transition (Fig. 5B and figs. S33 to S41). This implies that lower temperatures are more conducive to CO adsorption on small Au NPs, thereby accelerating the phase transition. Conversely, at temperatures above ~430 K, the phase transition does not significantly affect activity. At these higher temperatures, the M-vK mechanism at the interface predominates in the CO oxidation reaction, irrespective of the Au NP size.
Fig. 5. Statistical TOF and catalytic experiments of Au NPs with various diameters for CO oxidation.
(A) Statistical TOF per Au atom of Au7439 and Au37 at solid and liquid status. The inset picture shows corresponding NP configurations of its solid state, where different colors represent specific active sites used to calculate weighted TOF. (B) Statistical TOF per Au atom versus Au NP’s diameter based on the phase transition temperature of Au NPs and microkinetic analysis. (C) Experimentally measured CO oxidation conversion of Au/CeO2 for large (~10 nm; AuNP/CeO2) and small (~1 nm; Aun/CeO2) NPs at various temperatures. Reaction conditions: 1% CO/20% O2/N2 and GHSV = 80,400 ml/gcat per hour. (D and F) Corresponding high-resolution transmission electron microscopy image of AuNP(10 nm)/CeO2 and Aun(1 nm)/CeO2 and (E and G) their size distribution statistics.
To experimentally verify the aforementioned relationship between size and reactivity, we synthesized a series of Au NP catalysts with the same weight of Au loading (1%) on ceria nanorod supports (Fig. 5, D to G, and fig. S42). The temperature required to achieve 50% conversion of CO for Au NPs larger than 10 nm is approximately 445 K, whereas for Au NPs around 1 nm, the temperature drops to about 310 K. These differing activation temperatures suggest distinct reaction mechanisms for large and small NPs on the ceria support. For large NPs, the reaction temperature corresponding to high CO conversion is consistent with the temperature range most favorable for the M-vK mechanism at interface sites. Conversely, the optimal temperature for CO2 production from small NPs matches well with the conditions favorable for the L-H mechanism in liquid Au NPs (Figs. 4C and 5C).
DISCUSSION
In summary, by combining DPMD simulations, thermodynamic analysis, microkinetic modeling, and catalytic experiments, we have elucidated the relationship between the dynamic phase transition of Au NPs of varying sizes and the CO oxidation mechanisms on ceria surfaces under actual reaction conditions. The developed MLFF proves to be rather accurate, facilitating the simulations of the dynamic evolution of supported Au NPs in the presence of reactants. The finding underscores that the stability and activity of Au NPs are significantly size dependent, with smaller NPs being more susceptible to disordering under a CO atmosphere. Moreover, integrating microkinetic modeling with experimental investigation reveals that low-temperature activities are primarily governed by the associative L-H mechanism, which is feasible on low-coordinated apex Au atoms, such as those in liquid-like small Au NPs. In contrast, the high-temperature activities are predominantly driven by the M-vK mechanism at the Au/CeO2 interface, independent of Au NP size. We find that the phase transition facilitating Au/CeO2 activity occurs at temperatures below ~460 K for small sizes, as lower temperatures favor CO adsorption and thus accelerate the phase transition in small Au NPs.
The finding here provides insights to advance our understanding of catalyst dynamics under a catalytic atmosphere and underscores the significance of accounting for metal NP size in evaluating catalyst morphology and performance. Our work paves the way for the design and optimization of more effective catalysts for practical applications, highlighting the necessity of incorporating realistic conditions into computational catalytic studies.
MATERIALS AND METHODS
DFT calculations
All spin-polarized DFT calculations were carried out using the Perdew-Burke-Ernzerhof (36) functional as implemented in Vienna Ab initio Simulation Program (VASP) 6.3.0 (37). The kinetic energy cutoff for the plane-wave basis set was set to 400 eV to approximate the valence electron densities, and the projector augmented wave (38) method was used to account for the core-valence interaction. The DFT + U method with U − J = 5.0 eV was used to describe the strong correlation of the localized Ce 4f states (39, 40). Reciprocal space sampling was spaced 0.2 Å−1. The geometry optimization and self-consistent field convergence criterion were set to 0.02 eV/Å and 10−6 eV, respectively.
Molecular dynamics simulations and deep potential training dataset
The AIMD simulations were performed to construct the deep potential training dataset using the VASP 6.3.0 package for 3 ps with a time step of 1 fs. The canonical (NVT) ensemble and Nosé-Hoover thermostats (41, 42) were used with annealing temperatures from 300 to 1200 K to cover the temperature range simulated by DPMD in this work. The initial training dataset comprised over 130 trajectories from AIMD or optimization processes. Given the extensive existence of oxygen vacancies on ceria, several surface oxygen atoms were removed to model a partially reduced ceria support (43–45). To minimize redundancy, an image was captured every 10 frames throughout the AIMD trajectories. Part of structures and frame numbers are listed in figs. S1 to S3, including the following:
1) Bulk Au and bulk CeO2 crystal (fig. S1)
2) Gas CO and O2 molecules (fig. S1)
3) Bare Au(111), Au(110), and Au(100) surfaces (fig. S1)
4) CO adsorption on Au(111), Au(110), and Au(100) surfaces (fig. S1)
5) CO adsorption on Au23, Au25, Au31, and Au35 clusters (fig. S1)
6) Bare and CO-adsorbed Au201, Au182, and Au38 NPs (fig. S1)
7) Supported Au10, Au20, and Au34 clusters on the CeO2(111) surface with oxygen vacancies (fig. S2)
8) CO and/or O2 adsorption on Au10/CeO2, Au20/CeO2, and Au34/CeO2 (fig. S2)
9) Au(111)/CeO2(111) heterojunction with one, four, and five oxygen vacancies (fig. S3)
10) Au1 single atom on the CeO2 surface with and without oxygen vacancies (fig. S3)
11) CO and/or O2 adsorption on Au1/CeO2 (fig. S3)
The dataset covers a wide range of systems and configurations to ensure the accuracy and applicability of the trained deep potential.
Deep potential training
DPMD simulations were conducted using the DeePMD-kit package interfaced with LAMMPS (27, 46, 47). The machine learning descriptor used in the simulations was constructed from both angular and radial atomic configurations. The embedding network comprised three layers with 25, 50, and 100 neurons in each layer, and the model was trained over 2,000,000 iterations. The energy and force start and limit factors were set to 0.02, 0.5, 1000, and 2, respectively. The neighbor searching cutoff radius was set to 7.0 Å. The accuracy of the DPMD simulations was validated using the root mean square error (RMSE) for energies and forces and radial distribution function. The RMSE for energies was found to be only ~1.85 meV per atom for the Au20CO/CeO2-Ov system, while the RMSE for forces was ~89 meV/Å (fig. S5). Furthermore, the calculated radial distribution functions of AIMD and DPMD coincided well for Au─Au, Au─O, Au─C, Ce─O, and C─O pairs, indicating that DPMD was capable of accurately predicting the local atomic bonding and coordination with DFT-level accuracy (fig. S5).
DPMD is a powerful technique offering several advantages for simulating catalytic reactions and understanding their underlying mechanisms. One of its key advantages is computational efficiency, which allows for the simulation of large systems containing millions of atoms at a cost similar to classical force field–based molecular dynamics simulations. Another key advantage of DPMD is its ability to accurately describe the structures and properties of materials with complex bonding environments, such as Au─Au, Au─C, C─O, Ce─O, and Au─O bonds. It can accurately predict the properties of materials under a wide range of conditions, including high temperatures and pressures, essential for studying catalytic reactions under industrially relevant conditions. The ability of DPMD to accurately describe local atomic bonding and coordination with DFT accuracy makes it a valuable tool for exploring the mechanisms of catalytic processes.
Microkinetic modeling
The present study used DFT-based mean-field microkinetic simulations to predict the reaction rates and coverages of intermediates. These simulations were conducted using the CatMAP package (48). The model was constructed by numerically solving differential equations describing the coverage of each surface intermediate under the steady-state approximation. The rate constant of each elementary step was calculated using the widely adopted harmonic transition state theory, where the activation energy for each reaction step is obtained from the vibrational frequencies of the transition state. The free energies of the gas-phase molecules were estimated using the ideal gas approximation, accounting for the contributions of vibrational, rotational, and translational degrees of freedom to both entropy and enthalpy. Specifically, we adopted a mixture of CO and O2 at a 1:20 ratio and varied the temperature from 200 to 600 K and the pressure from 10−8 to 1 bar. These conditions are commonly used in studies of surface chemistry.
Statistical TOF
As described above, the statistical TOF of supported Au NPs in solid and liquid states is expressed by Eqs. 5 and 6, and the involved ratios , , and are calculated as follows
| (7) |
| (8) |
| (9) |
where , , , and represent the number of exposed solid Au surface atoms, interface atoms on Au/CeO2, and exposed liquid-like atoms on supported Au NP and the total number of atoms in the Au NP, respectively.
For supported Au7439, Au3382, Au1659, Au1001, Au756, Au476, Au260, Au155, and Au37 NPs on CeO2(111), the numbers of atoms on the exposed solid Au surfaces and the Au/CeO2 interface are listed in table S11, along with the values of and . For exposed liquid-like atoms, coordination numbers ranging from 0 to 9 for Au atoms were considered, where the six-, eight-, and nine-coordinated atoms represent atoms on the surfaces of Au(321), Au(100), and Au(111), respectively, and the seven-coordinated ones represent atoms on the surfaces of Au(211), Au(221), and Au(311) (table S12). Therefore, the numbers of atoms at different sites and the values of , , and are calculated.
Preparation of Aun/CeO2 and AuNP/CeO2 catalysts
First, the ceria support was prepared using a hydrothermal method (49), during which Ce(NO3)3⋅6H2O (4.5 mmol) was mixed with an aqueous NaOH (6 M, 60 ml) solution in a Teflon bottle under vigorous stirring. Subsequently, the hydrothermal procedure was carried out in an oven at 100°C for 24 hours, and the as-formed precipitates were separated several times by centrifugation. The Aun/CeO2 samples were synthesized via a deposition-precipitation method, following previous work (50). The dried ceria support (0.5 g) was suspended in 50 ml of Millipore water and stirred for 15 min, followed by addition of an ammonium carbonate solution (25 ml, 1 M) as a precipitant agent. After that, a certain amount of HAuCl4⋅3H2O (0.058 mmol) dissolved in 25 ml of Millipore water was added dropwise into the mixture. The as-formed precipitates were separated by filtration and washed with hot Millipore water (~80°C). The Aun/CeO2 sample was lastly obtained after drying at 70°C for 4 hours and calcination at 400°C under an air atmosphere for 4 hours. The AuNP/CeO2 sample was prepared according to a modified colloidal deposition method (51). A 0.5 wt % polyvinyl alcohol (0.202 ml; Mw = 10,000, 80% hydrolyzed; Sigma-Aldrich) solution and 2 ml of HAuCl4 solution (0.0125 M) were mixed into 48 ml of Millipore water at room temperature under vigorous stirring. After rapidly injecting 6.50 ml of 0.1 M NaBH4 aqueous solution, 0.5 g of ceria support powder was introduced into the colloidal gold solution with continuous stirring. After another 1 hour, the solid products were separated by filtration and washed several times with Millipore water. Last, the AuNP/CeO2 sample was collected after drying at 70°C overnight and calcined at 300°C under an air atmosphere for 4 hours.
Catalyst test for CO oxidation
The catalytic tests were conducted in a flow reactor, where a mixture of 1% CO/20% O2/N2 was used as the feed gas. The components of the exhaust gas were quantified by nondispersive infrared spectroscopy (Gasboard-3500, Wuhan Sifang Company, Wuhan, China). Before the catalytic test, both the Aun/CeO2 and AuNP/CeO2 catalysts were pretreated in 5% H2/Ar at 300°C for 30 min. Subsequently, the CO oxidation tests were carried out with the temperature elevating from room temperature to 300°C at a ramp rate of 3°C/min.
Acknowledgments
Funding: This work was supported by the National Natural Science Foundation of China (NSFC nos. 22402087, 22033005, 22075166, and 52271049), the Fundamental Research Funds for the Central Universities (63241409), the NSFC Center for Single-Atom Catalysis (22388102), the National Key R&D Program of China and National Key Research and Development Project (nos. 2021YFA1601004, 2021YFA1501103, 2022YFA1503900, and 2022YFA1503000), and the National Science Fund for Distinguished Young Scholars of China (22225110). The calculations were performed using the Jinan Gengzi Supercomputing Center.
Author contributions: Conceptualization: Y.H., C.-J.J., J.L., and J.-C.L. Methodology: L.Z., X.-P.F., R.W., and J.-C.L. Investigation: L.Z., X.-P.F., R.W., C.-X.W., F.L., H.Y., and J.-C.L. Visualization: L.Z., X.-P.F., and J.-C.L. Funding acquisition: Y.H., C.-J.J., J.L., and J.-C.L. Project administration: J.-C.L. Supervision: Y.H., C.-J.J., J.L., and J.-C.L. Writing—original draft: L.Z. and J.-C.L. Writing—review and editing: Y.H., C.-J.J., J.L., and J.-C.L. All the authors confirmed and discussed the results.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. The frozen and compressed Au─Ce─C─O model, Au─Ce─C─O dataset, DeePMD-kit and LAMMPS input files, and DPMD trajectories have been deposited in a Zenodo repository under https://zenodo.org/records/11532142.
Supplementary Materials
The PDF file includes:
Supplementary Text
Figs. S1 to S42
Tables S1 to S12
Legends for movies S1 to S8
Legends for data S1 to S5
Other Supplementary Material for this manuscript includes the following:
Movies S1 to S8
Data S1 to S5
REFERENCES AND NOTES
- 1.Boronat M., Leyva-Pérez A., Corma A., Theoretical and experimental insights into the origin of the catalytic activity of subnanometric gold clusters: Attempts to predict reactivity with clusters and nanoparticles of gold. Acc. Chem. Res. 47, 834–844 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Hashmi A. S. K., Hutchings G. J., Gold catalysis. Angew. Chem. Int. Ed. 45, 7896–7936 (2006). [DOI] [PubMed] [Google Scholar]
- 3.Ding K., Gulec A., Johnson A. M., Schweitzer N. M., Stucky G. D., Marks L. D., Stair P. C., Identification of active sites in CO oxidation and water-gas shift over supported Pt catalysts. Science 350, 189–192 (2015). [DOI] [PubMed] [Google Scholar]
- 4.Haruta M., Kobayashi T., Sano H., Yamada N., Novel gold catalysts for the oxidation of carbon monoxide at a temperature far below 0 °C. Chem. Lett. 16, 405–408 (1987). [Google Scholar]
- 5.Hutchings G. J., Vapor phase hydrochlorination of acetylene: Correlation of catalytic activity of supported metal chloride catalysts. J. Catal. 96, 292–295 (1985). [Google Scholar]
- 6.Haruta M., Size- and support-dependency in the catalysis of gold. Catal. Today 36, 153–166 (1997). [Google Scholar]
- 7.Cargnello M., Doan-Nguyen V. V. T., Gordon T. R., Diaz R. E., Stach E. A., Gorte R. J., Fornasiero P., Murray C. B., Control of metal nanocrystal size reveals metal-support interface role for ceria catalysts. Science 341, 771–773 (2013). [DOI] [PubMed] [Google Scholar]
- 8.Liu J.-C., Wang Y.-G., Li J., Toward rational design of oxide-supported single-atom catalysts: Atomic dispersion of gold on ceria. J. Am. Chem. Soc. 139, 6190–6199 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Wang Y.-G., Mei D., Glezakou V.-A., Li J., Rousseau R., Dynamic formation of single-atom catalytic active sites on ceria-supported gold nanoparticles. Nat. Commun. 6, 6511 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.He Y., Liu J.-C., Luo L., Wang Y.-G., Zhu J., Du Y., Li J., Mao S. X., Wang C., Size-dependent dynamic structures of supported gold nanoparticles in CO oxidation reaction condition. Proc. Natl. Acad. Sci. U.S.A. 115, 7700–7705 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Overbury S., Schwartz V., Mullins D., Yan W., Dai S., Evaluation of the Au size effect: CO oxidation catalyzed by Au/TiO2. J. Catal. 241, 56–65 (2006). [Google Scholar]
- 12.Chen S., Luo L., Jiang Z., Huang W., Size-dependent reaction pathways of low-temperature CO oxidation on Au/CeO2 catalysts. ACS Catal. 5, 1653–1662 (2015). [Google Scholar]
- 13.Herzing A. A., Kiely C. J., Carley A. F., Landon P., Hutchings G. J., Identification of active gold nanoclusters on iron oxide supports for CO oxidation. Science 321, 1331–1335 (2008). [DOI] [PubMed] [Google Scholar]
- 14.Hansen P. L., Wagner J. B., Helveg S., Rostrup-Nielsen J. R., Clausen B. S., Topsøe H., Atom-resolved imaging of dynamic shape changes in supported copper nanocrystals. Science 295, 2053–2055 (2002). [DOI] [PubMed] [Google Scholar]
- 15.Wang Y.-G., Cantu D. C., Lee M.-S., Li J., Glezakou V.-A., Rousseau R., CO oxidation on Au/TiO2: Condition-dependent active sites and mechanistic pathways. J. Am. Chem. Soc. 138, 10467–10476 (2016). [DOI] [PubMed] [Google Scholar]
- 16.Liu J.-C., Luo L. L., Xiao H., Zhu J. F., He Y., Li J., Metal affinity of support dictates sintering of gold catalysts. J. Am. Chem. Soc. 144, 20601–20609 (2022). [DOI] [PubMed] [Google Scholar]
- 17.Campbell C. T., Sellers J. R. V., Anchored metal nanoparticles: Effects of support and size on their energy, sintering resistance and reactivity. Faraday Discuss. 162, 9–30 (2013). [DOI] [PubMed] [Google Scholar]
- 18.Campbell C. T., The energetics of supported metal nanoparticles: Relationships to sintering rates and catalytic activity. Acc. Chem. Res. 46, 1712–1719 (2013). [DOI] [PubMed] [Google Scholar]
- 19.Campbell C. T., Parker S. C., Starr D. E., The effect of size-dependent nanoparticle energetics on catalyst sintering. Science 298, 811–814 (2002). [DOI] [PubMed] [Google Scholar]
- 20.Yoshida H., Kuwauchi Y., Jinschek J. R., Sun K., Tanaka S., Kohyama M., Shimada S., Haruta M., Takeda S., Visualizing gas molecules interacting with supported nanoparticulate catalysts at reaction conditions. Science 335, 317–319 (2012). [DOI] [PubMed] [Google Scholar]
- 21.Yuan W., Zhu B., Fang K., Li X.-Y., Hansen T. W., Ou Y., Yang H., Wagner J. B., Gao Y., Wang Y., Zhang Z., In situ manipulation of the active Au-TiO2 interface with atomic precision during CO oxidation. Science 371, 517–521 (2021). [DOI] [PubMed] [Google Scholar]
- 22.Zhang Z., Zandkarimi B., Alexandrova A. N., Ensembles of metastable states govern heterogeneous catalysis on dynamic interfaces. Acc. Chem. Res. 53, 447–458 (2020). [DOI] [PubMed] [Google Scholar]
- 23.Xu L., Papanikolaou K. G., Lechner B. A. J., Je L., Somorjai G. A., Salmeron M., Mavrikakis M., Formation of active sites on transition metals through reaction-driven migration of surface atoms. Science 380, 70–76 (2023). [DOI] [PubMed] [Google Scholar]
- 24.Wang J., McEntee M., Tang W., Neurock M., Baddorf A. P., Maksymovych P., Yates J. T. Jr., Formation, migration, and reactivity of Au–CO complexes on gold surfaces. J. Am. Chem. Soc. 138, 1518–1526 (2016). [DOI] [PubMed] [Google Scholar]
- 25.Eren B., Zherebetskyy D., Patera L. L., Wu C. H., Bluhm H., Africh C., Wang L.-W., Somorjai G. A., Salmeron M., Activation of Cu(111) surface by decomposition into nanoclusters driven by CO adsorption. Science 351, 475–478 (2016). [DOI] [PubMed] [Google Scholar]
- 26.Wang Y.-G., Yoon Y., Glezakou V.-A., Li J., Rousseau R., The role of reducible oxide–metal cluster charge transfer in catalytic processes: New insights on the catalytic mechanism of CO oxidation on Au/TiO2 from ab initio molecular dynamics. J. Am. Chem. Soc. 135, 10673–10683 (2013). [DOI] [PubMed] [Google Scholar]
- 27.Wang H., Zhang L., Han J., E W., DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 228, 178–184 (2018). [Google Scholar]
- 28.Hu S., Li W.-X., Sabatier principle of metal-support interaction for design of ultrastable metal nanocatalysts. Science 374, 1360–1365 (2021). [DOI] [PubMed] [Google Scholar]
- 29.Buffat P., Borel J.-P., Size effect on the melting temperature of gold particles. Phys. Rev. A 13, 2287–2298 (1976). [Google Scholar]
- 30.Font F., Myers T. G., Spherically symmetric nanoparticle melting with a variable phase change temperature. J. Nanopart. Res. 15, 2086 (2013). [Google Scholar]
- 31.Song W., Hensen E. J. M., A computational DFT study of CO oxidation on a Au nanorod supported on CeO2(110): On the role of the support termination. Cat. Sci. Technol. 3, 3020–3029 (2013). [Google Scholar]
- 32.Fajín J. L. C., Cordeiro M. N. D. S., Gomes J. R. B., DFT study of the CO oxidation on the Au(321) surface. J. Phys. Chem. C 112, 17291–17302 (2008). [Google Scholar]
- 33.Liu Z.-P., Hu P., Alavi A., Catalytic role of gold in gold-based catalysts: A density functional theory study on the CO oxidation on gold. J. Am. Chem. Soc. 124, 14770–14779 (2002). [DOI] [PubMed] [Google Scholar]
- 34.Falsig H., Hvolbæk B., Kristensen I. S., Jiang T., Bligaard T., Christensen C. H., Nørskov J. K., Trends in the catalytic CO oxidation activity of nanoparticles. Angew. Chem. Int. Ed. 47, 4835–4839 (2008). [DOI] [PubMed] [Google Scholar]
- 35.Mars P., van Krevelen D. W., Oxidations carried out by means of vanadium oxide catalysts. Chem. Eng. Sci. 3, 41–59 (1954). [Google Scholar]
- 36.Perdew J. P., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- 37.Kresse G., Furthmüller J., Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996). [Google Scholar]
- 38.Kresse G., Joubert D., From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 59, 1758–1775 (1999). [Google Scholar]
- 39.Anisimov V. I., Aryasetiawan F., Lichtenstein A. I., First-principles calculations of the electronic structure and spectra of strongly correlated systems: The LDA+U method. J. Phys. Condens. Matter 9, 767–808 (1997). [Google Scholar]
- 40.Tang Y., Zhao S., Long B., Liu J.-C., Li J., On the nature of support effects of metal dioxides MO2 (M = Ti, Zr, Hf, Ce, Th) in single-atom gold catalysts: Importance of quantum primogenic effect. J. Phys. Chem. C 120, 17514–17526 (2016). [Google Scholar]
- 41.Hoover W. G., Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697 (1985). [DOI] [PubMed] [Google Scholar]
- 42.Nosé S., A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984). [Google Scholar]
- 43.Campbell C. T., Peden C. H. F., Oxygen vacancies and catalysis on ceria surfaces. Science 309, 713–714 (2005). [DOI] [PubMed] [Google Scholar]
- 44.Esch F., Fabris S., Zhou L., Montini T., Africh C., Fornasiero P., Comelli G., Rosei R., Electron localization determines defect formation on ceria substrates. Science 309, 752–755 (2005). [DOI] [PubMed] [Google Scholar]
- 45.Farmer J. A., Campbell C. T., Ceria maintains smaller metal catalyst particles by strong metal-support bonding. Science 329, 933–936 (2010). [DOI] [PubMed] [Google Scholar]
- 46.Zhang Y., Wang H., Chen W., Zeng J., Zhang L., Wang H., E W., DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun. 253, 107206 (2020). [Google Scholar]
- 47.Thompson A. P., Aktulga H. M., Berger R., Bolintineanu D. S., Brown W. M., Crozier P. S., Veld P. J., Kohlmeyer A., Moore S. G., Nguyen T. D., Shan R., Stevens M. J., Tranchida J., Trott C., Plimpton S. J., LAMMPS - A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022). [Google Scholar]
- 48.Medford A. J., Shi C., Hoffmann M. J., Lausche A. C., Fitzgibbon S. R., Bligaard T., Nørskov J. K., CatMAP: A software package for descriptor-based microkinetic mapping of catalytic trends. Catal. Lett. 145, 794–807 (2015). [Google Scholar]
- 49.Mai H.-X., Sun L.-D., Zhang Y.-W., Si R., Feng W., Zhang H.-P., Liu H.-C., Yan C.-H., Shape-selective synthesis and oxygen storage behavior of ceria nanopolyhedra, nanorods, and nanocubes. J. Phys. Chem. B 109, 24380–24385 (2005). [DOI] [PubMed] [Google Scholar]
- 50.Si R., Flytzani-Stephanopoulos M., Shape and crystal-plane effects of nanoscale ceria on the activity of Au-CeO2 catalysts for the water–gas shift reaction. Angew. Chem. Int. Ed. 47, 2884–2887 (2008). [DOI] [PubMed] [Google Scholar]
- 51.Comotti M., Li W.-C., Spliethoff B., Schüth F., Support effect in high activity gold catalysts for CO oxidation. J. Am. Chem. Soc. 128, 917–924 (2006). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S42
Tables S1 to S12
Legends for movies S1 to S8
Legends for data S1 to S5
Movies S1 to S8
Data S1 to S5