A Computational Strategy for the Rapid Identification and Ranking of Patient‐Specific T Cell Receptors Bound to Neoantigens

Zachary A Rollins; Matthew B Curtis; Steven C George; Roland Faller

doi:10.1002/marc.202400225

. 2024 Jun 12;45(24):2400225. doi: 10.1002/marc.202400225

A Computational Strategy for the Rapid Identification and Ranking of Patient‐Specific T Cell Receptors Bound to Neoantigens

Zachary A Rollins ¹, Matthew B Curtis ², Steven C George ², Roland Faller ^1,^3,^✉

PMCID: PMC11661661 PMID: 38839076

Abstract

T cell receptor (TCR) recognition of a peptide–major histocompatibility complex (pMHC) is crucial for adaptive immune response. The identification of therapeutically relevant TCR‐pMHC protein pairs is a bottleneck in the implementation of TCR‐based immunotherapies. The ability to computationally design TCRs to target a specific pMHC requires automated integration of next‐generation sequencing, protein–protein structure prediction, molecular dynamics, and TCR ranking. A pipeline to evaluate patient‐specific, sequence‐based TCRs to a target pMHC is presented. Using the three most frequently expressed TCRs from 16 colorectal cancer patients, the protein–protein structure of the TCRs to the target CEA peptide–MHC is predicted using Modeller and ColabFold. TCR‐pMHC structures are compared using automated equilibration and successive analysis. ColabFold generated configurations require an ≈2.5× reduction in equilibration time of TCR‐pMHC structures compared to Modeller. The structural differences between Modeller and ColabFold are demonstrated by root mean square deviation (≈0.20 nm) between clusters of equilibrated configurations, which impact the number of hydrogen bonds and Lennard‐Jones contacts between the TCR and pMHC. TCR ranking criteria that may prioritize TCRs for evaluation of in vitro immunogenicity are identified, and this ranking is validated by comparing to state‐of‐the‐art machine learning‐based methods trained to predict the probability of TCR‐pMHC binding.

Keywords: molecular dynamics, protein structure, T cells

Process flow diagram for the protein–protein structure prediction of proteins (here TCRs) to a target protein (here pMHC) is presented. The process begins with single‐cell sequencing from patients. Then, protein–protein structure prediction of proteins sequenced is performed. Finally, molecular dynamics simulations equilibrate the structure and rank proteins based on the number of interactions at equilibrium.

1. Introduction

Cytotoxic (CD8+) T cells are part of the adaptive immune system and eradicate potentially harmful cells—including cancer cells—by recognition of the peptide‐major histocompatibility complex (pMHC) on target cells. Tumor‐specific pMHCs are comprised of a peptide derived from a mutated and/or aberrantly expressed intracellular protein^[ ¹ ^] presented to the cell membrane in a pocket formed by the MHC α and β chains.^[ ² ^] The wide diversity of peptide‐MHCs (≈10^6–12)^[ ³ ^] is matched by the even wider diversity of TCRs (>10^20–61)^[ ⁴ , ⁵ ^] through random V(D)J recombination of the hypervariable complementarity determining regions (CDRs). The function of the adaptive immune response ultimately depends on the ability to produce appropriate immunogenic TCRs (on‐target) while minimizing response to self pMHCs (off‐target effects).

Despite breakthrough clinical potential for TCR‐T cell therapies in solid tumors,^[ ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ ^] the implementation is hindered by three central challenges: 1) identifying tumor‐specific pMHC ligands; 2) matching immunogenic TCRs with identified pMHCs, and 3) minimizing off‐target (side) effects.^[ ¹¹ ^] Combining next generation sequencing and machine learning, significant advancements have been made to identify and rank tumor‐specific pMHC ligands,^[ ¹² , ¹³ , ¹⁴ ^] thus addressing the first challenge.

Addressing the second challenge has been difficult as the identification of patient‐specific TCR repertoires has involved methods that are low‐throughput or limited to a single chain.^[ ¹⁵ , ¹⁶ , ¹⁷ ^] However, recent breakthroughs in single‐cell sequencing allow determination of the CDR3 regions of the α and β chain of the TCR in a high‐throughput manner.^[ ¹⁸ , ¹⁹ , ²⁰ , ²¹ ^] This technological breakthrough facilitates an unprecedented exploration of the vast TCR information space and allows the scientific community to refocus attention on fundamental questions related to recombination, maturation, and intersecting diversity of patient‐specific TCR repertoires. This advance also provides an opportunity to leverage machine learning to predict TCR antigen binding specificity from primary amino acid sequence^[ ²² , ²³ , ²⁴ , ²⁵ ^] or from structural features of TCR‐pMHC homology models.^[ ²⁶ ^] However, the training sets to characterize and rank TCRs by their immunogenicity are restricted by either insufficient data on the relevant TCR‐pMHC binding parameters^[ ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³² ^] or a limited number of known TCR‐pMHC structures (≥645 on STCRDab).^[ ³³ ^] Moreover, machine learning (ML) based methods to predict TCR‐pMHC binding probability are strongly biased to the sequence training distributions and fail to generalize to unseen pMHC and TCR sequences.^[ ³⁴ , ³⁵ ^]

Despite significant advances in protein–protein structure prediction,^[ ³⁶ , ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ , ⁴² , ⁴³ ^] the prediction of TCRs bound to a target pMHC from patient‐specific sequences is fundamentally biased to the features of known protein structures. Moreover, ranking TCRs is not possible without detailed information on the relationship between bond strength and immunogenic response.^[ ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³² ^] Previously, we have identified several physiochemical parameters of the TCR‐pMHC interaction that correspond with immunogenicity.^[ ³⁰ , ⁴⁴ ^] Herein, we present an automated pipeline to assess TCRs to a target pMHC (Figure 1 ). This pipeline begins with single‐cell sequencing to identify the amino acids in the CDR3αβ loops from T cells resected from the tumors of 16 colorectal cancer (CRC) patients.^[ ²⁰ , ²¹ ^] Next, we restrict the carcinoembryonic (CEA) peptide (CEA_571–579:YLSGANLNL) to the MHC (HLA‐0201), known to be expressed in CRC patients^[ ¹¹ , ⁴⁵ , ⁴⁶ , ⁴⁷ ^] and predict several TCR‐pMHC complexes using TCRs sequenced from patients.^[ ²⁰ , ²¹ ^] The predicted protein structures are equilibrated at physiological conditions by molecular dynamics simulations and an automated equilibration^[ ⁴⁸ ^] is implemented to assess the starting structures from either Modeller^[ ³⁹ , ⁴⁰ ^] or the recently developed ColabFold^[ ³⁶ , ³⁷ , ³⁸ ^] (Figure 1). Our results demonstrate that ColabFold creates structures that are ≈2.5X faster to equilibrate, and thus reduce overall computational cost compared to Modeller. However, the clusters of structures generated by Modeller and ColabFold are consistently divergent despite structural equilibration. Moreover, we provide potential criteria for ranking the TCRs after structural equilibration including the number of hydrogen bonds and Lennard‐Jones contacts. This methodology is generally applicable to identify TCRs with relevant and quantifiable binding parameters to a target pMHC.

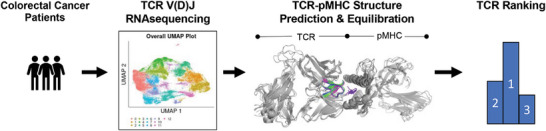
Process flow diagram for the protein–protein structure prediction of TCRs to a target pMHC. The process begins with single cell V(D)J RNA sequencing of the T cells from resected tumors of 16 colorectal cancer patients (left). Then, protein–protein structure prediction of TCRs sequenced from patients bound to a pMHC (HLA‐A2) with a restricted target peptide CEA_571–579 (middle right) is performed. Finally, we run molecular dynamics simulations to equilibrate the structure and rank TCRs based on the number of interactions at equilibrium (right).

2. Experimental Section

2.1. Single‐Cell RNA V(D)J Sequencing of CRC Patient T Cells

T lymphocyte single cell RNA‐Seq data were made available to us from the Han group and has been previously published.^[ ²⁰ , ²¹ ^] Raw data were first put through a quality control process to exclude cells with less than 200 unique genes, more than 7500 unique genes, and/or more than 10% mitochondrial gene expression. In addition, any genes that were present in fewer than three total cells were excluded from downstream analysis. All single‐cell analysis was performed using the Seurat pipeline.^[ ⁴⁴ ^] T lymphocytes were clustered using 0.3 as the value for the “resolution” parameter. Cytotoxic T lymphocyte clusters were identified by expression of Cd3d and Cd8a, and the absence of Cd4 expression. TCR CDR3α and CDR3β sequences from the 10X Genomics 5′ VDJ analysis pipeline were matched to their corresponding cells for downstream analysis. After the segregation of CD3D+CD4‐CD8A+ T cells, the top 3 most frequent TCR clonotypes were identified (Figure S8, Supporting Information).

2.2. TCR‐pMHC Protein–Protein Structure Prediction

To demonstrate the feasibility of the proposed pipeline, the starting structures for the three most common TCRs were generated independently using Modeller V10.1^[ ³⁹ , ⁴⁰ ^] and ColabFold V 1.2.0^[ ³⁶ , ³⁷ , ³⁸ ^] denoted TCR1, TCR2, and TCR3, respectively. Importantly, this methodology might benefit from recent and future models that fine‐tune structure prediction methods on TCR‐pMHC structure databases.^[ ⁴² , ⁴³ ^] This benefit would likely reduce the required molecular dynamics simulation time to equilibrate approximated structures. The primary amino sequence used for multiple sequence alignment was derived from the DMF5 TCR bound to the HLA‐A2 (MHC) restricted MART1 (PDB:3QDJ).^[ ⁴⁹ ^] For sequence alignment, the CDR3α (CAVNFGGGKLIF), CDR3β (CASSLSFGTEAFF), and MART1 peptide (AAGIGILTV) were substituted with the respective CDR3 loops found from patient TCR clonotypes (Table 1 ) and the CEA_571–579 peptide (YLSGANLNL) known to be restricted to the HLA‐A2 (MHC). The TCR CDR3s were substituted as follows: TCR1 (CDR3α: CAVNGDDYKLSF, CDR3β: CASRKRDDSEQYF), TCR2 (CDR3α: CAVSDNARLMF, CDR3β: CASSPFGGGNEQFF), and TCR3 (CDR3α: CAYRISAYDKVIF, CDR3β: CASSQTGGADTDTQYF). For Modeller, the MART1 (PDB:3QDJ) crystal structure was used as the template, ten model structures were generated from the alignment of the respective TCR, and the structure with lowest DOPE score^[ ⁵⁰ ^] was selected for MD equilibration. ColabFold^[ ³⁸ ^] is, in part, a server that performs rapid MSA/homology search combined with the trained network architecture of AlphaFold2^[ ³⁶ , ³⁷ ^] for prediction of the 3D atomic coordinates of folded protein structures. For ColabFold, five model structures were generated from the alignment of the respective TCR, and the structure with the highest pTMscore^[ ³⁶ , ³⁷ ^] was selected for MD equilibration. Multiple structures were generated from both Modeller and ColabFold to maintain best practice at producing the most accurate starting structure as described in their methods.^[ ³⁸ , ⁵⁰ ^]

Table 1.

Rank of TCRs binding to CEA_571–579 pMHC.

TCR rank method	TCR1	TCR2	TCR3
ERGO‐II‐AE‐VDJdb^[ ²² ^]	2	1	3
ERGO‐II‐LSTM‐McPAS^[ ²² ^]	3	1	2
NetTCR‐2.2^[ ²³ ^]	2	3	1
pMTNet^[ ²⁴ ^]	3	1	2
pMTnet‐Omni^[ ²⁵ ^]	3	1	2
*ML – average rank*	*2.6*	*1.4*	*2.0*
MD‐H‐bonds (Modeller)	2	1	3
MD‐LJ‐contacts (Modeller)	3	1	2
MD‐H‐bonds (ColabFold)	2	3	1
MD‐LJ‐contacts (ColabFold	2	1	3
*MD – average rank*	*2.25*	*1.5*	*2.25*

Open in a new tab

Note: This includes the rank determined by the probability of binding from numerous machine learning (ML) based methods (top). The rank based on molecular dynamics (MD) interactions is also provided (bottom). The average rank is italicized under the respective ranking methodology.

2.3. Molecular Dynamics: Setup, Energy Minimization, and Equilibration

The predicted Modeller or ColabFold structures were used as starting configurations for a seven‐step molecular dynamics pipeline to determine their equilibrated structures at physiological conditions. All MD Simulations were performed in full atomistic detail with Gromacs 2019.1^[ ⁵¹ , ⁵² ^] using the CHARMM22 with CMAP force field^[ ⁵³ ^] in orthorhombic periodic boundary conditions. The force field was chosen to be consistent with earlier studies.^[ ³⁰ , ⁴⁴ ^] For the particular question under study here the exact choice of force field is not very relevant. 1) The residue protonation states were determined by calculating pKa values using propka3.1^[ ⁵⁴ , ⁵⁵ ^] and deprotonated if pKa values are below pH 7.4. 2) The properly protonated or deprotonated protein structures were solvated in orthorhombic water boxes large enough to satisfy minimum image convention using the TIP3P water model.^[ ⁵⁶ ^] 3) Na⁺ and Cl⁻ ions were added to reach salt concentration ≈150 × 10⁻³ m and neutral charge. Box sizes were 10.627 × 7.973 × 10.685 nm with ≈48 000 water molecules, ≈300 ions, and ≈157 000 total atoms. Full specifications can be found in the Dryad repository:^[ ⁵⁷ ^] 4) To avoid steric clashes, steepest descent energy minimization (emtol = 1000 kJ mol⁻¹ nm⁻¹) was performed. 5) To relax solute–solvent contacts, a 100 ps simulation was run in the constant volume ensemble (NVT) with 0.2 fs timestep (T = 310 K). Temperature was maintained by coupling protein and nonprotein atoms to separate baths using a velocity rescale thermostat^[ ⁵⁸ ^] with a 0.1 ps time constant. 6) To maintain pressure at 1.0 bar, a 100 ps simulation was run in the constant pressure (NPT) ensemble using isotropic Berendsen pressure coupling,^[ ⁵⁹ ^] a 2.0 ps time constant, and 2 fs timestep. Steps (5) and (6) used position restraints (harmonic force constant = 1000 kJ mol⁻¹ nm⁻²) on all protein atoms. 7) Equilibration MD simulations were conducted for 100–300 ns with no restraints. Equilibration runs were extended in 50 ns increments until the root mean square deviation (RMSD) of the TCR‐pMHC complex was in equilibrium for a minimum of 50 ns determined by the variance‐bias trade‐off algorithm.^[ ⁴⁸ ^] Such equilibration lengths were sufficient for this problem, but additional longer term conformational changes in atomistic simulations were cannot be excluded. To maintain temperature and pressure during the production runs, the Nosé–Hoover thermostat^[ ⁶⁰ ^] and Parrinello–Rahman barostat^[ ⁶¹ ^] were used with time constants 2.0 and 1.0 ps, respectively. The isothermal compressibility of water was used as 4.5 × 10⁻⁵ bar⁻¹. Simulations used the particle Ewald mesh algorithm^[ ⁶² , ⁶³ ^] for long‐range electrostatic calculations with cubic interpolation and 0.12 nm grid spacing. Short‐range nonbonded interactions were cut off at 1.2 nm. All water bond lengths were constrained with SETTLE,^[ ⁶⁴ ^] and all other bond lengths were constrained using the LINCS algorithm.^[ ⁶⁵ ^] The leap‐frog algorithm was used for integrating equations of motion with a 2 fs time step.

2.4. Data and Statistical Analysis

Selected TCR‐pMHC structures from MD trajectories were visualized using the Pymol v2.4.0 Molecular Graphics System (Schrodinger, LLC; New York, NY). The selected frames for visualization were chosen to be from the top three clusters (two from each cluster) after TCR‐pMHC structure equilibration (Figures S1 and S2, Supporting Information). This resulted in a total of 12 structures for each TCR: 6 from Modeller (TCR1: Cluster 1, 2, & 7, TCR2: Cluster 1, 9, & 12, and TCR3: Cluster 1, 6, & 9) and 6 from ColabFold (TCR1: Cluster 1, 2, & 4, TCR2: Cluster 1, 3, & 4 and TCR3: Cluster 1, 3, & 6) (Figures S3–S5, Supporting Information). The clusters were selected because they were after the simulation time required for equilibration (e.g., for Modeller TCR1, Clusters 1, 2, & 7 were chosen because Clusters 3–6 were only dominant during the 249 ns equilibration time). The all‐to‐all alignment of TCR‐pMHC structures was performed in Pymol using the align command on the C^α atoms to compute RMSD between pairs of structures. Data analysis from MD simulations was performed with tools from the Gromacs suite:^[ ⁵¹ , ⁵² ^] gmx make_ndx, gmx hbond, gmx rms, gmx rmsf, and gmx cluster. These results were complemented with a secondary analysis utilizing python packages for data handling and visualization including: numpy,^[ ⁶⁶ ^] pandas,^[ ⁶⁷ ^] matplotlib,^[ ⁶⁸ ^] GromacsWrapper,^[ ⁶⁹ ^] scipy,^[ ⁷⁰ ^] and pingouin,^[ ⁷¹ ^] and pymbar.^[ ⁴⁸ ^] Custom bash shell python scripts relevant to the production of figures were deposited in a GitHub repository.^[ ⁷² ^] The geometry of a Lennard‐Jones contact is defined as a distance of less than 0.35 nm between atoms. Results were presented as mean ± SEM. As indicated in figures, statistics were performed in python using scipy for one‐way analysis of variance (ANOVA), and pingouin for pairwise Tukey‐HSD post hoc tests. Detailed outputs of statistical analysis were written to excel and are provided in a Dryad repository.^[ ⁵⁷ ^]

2.5. Machine Learning Based TCR‐pMHC Binding Predictions

The TCR ranking method based on physical interactions was compared with the pMHC to numerous state‐of‐the‐art machine learning methods. Recent machine learning methods were typically trained on sequence representations of the TCR‐pMHC and their binary binding label. The positive binding label data were derived from 10X Genomics sequencing datasets after redundancy reductions.^[ ⁷³ ^] The dataset sizes vary depending on the methodology used for redundancy reductions as well as the resolution capability of the sequencing dataset: CDR3β‐peptide, CDR3α‐CDR3β‐peptide, or CDR1α‐CDR2α‐CDR3α‐CDR1β‐CDR2β‐CDR3β‐peptide. The negative binding label data were usually generated assuming that known TCR‐peptide binders do not cross react with additional peptides. For more details, the authors referred to the methods of the machine learning based method used to predict the TCR‐pMHC binding probability of TCR1, TCR2, and TCR3 to the CEA_571–579 peptide: ERGO‐II‐AE‐VDJdb,^[ ²² ^] ERGO‐II‐LSTM‐McPAS,^[ ²² ^] NetTCR‐2.2,^[ ²³ ^] pMTNet,^[ ²⁴ ^] and pMTNet‐Omni.^[ ²⁵ ^] For each method, the instructions on the respective GitHub repository were followed, and only the sequence information used to train the model was provided. The TCR‐pMHC pairs were then ranked by the predicted binding probability (Table 1). Results from the machine learning based model predictions are made available on the GitHub repository:^[ ⁷² ^] https://github.com/zrollins/TCR_homology.git.

3. Results

To design TCRs to target the CEA_571–579 peptide restricted to the HLA‐A2 (MHC), TCR clonotypes were identified utilizing the single cell RNA V(D)J sequenced T cells resected from colorectal tumors of 16 CRC patients.^[ ²⁰ , ²¹ ^] This technique identifies TCR clonotypes by matching the amino acids from the CDR3 regions of the α and β chain of the TCR.^[ ¹⁸ , ¹⁹ , ²⁰ , ²¹ ^] First, T cells were identified by the expression of Cd3d and Cd8a (and the absence of Cd4 expression), as only CD8+ T cells can bind to the HLA‐A2 (MHC). Of the 37931 T cells analyzed (Figure 2Ai), there were 9709 Cd3d+/Cd4−/Cd8a+ T cells (corresponding to clusters 2, 6, 7, 9, and 11; Figure 2Aii–iv), and 3931 identified Cd3d+/Cd4−/Cd8a+ TCRαβ clonotypes (Figure 2B and Table 1). The three most frequently identified TCRs (Table 1) from patient tumors (denoted clonotype TCR1, TCR2, and TCR3) were then used to predict TCR‐pMHC structures.

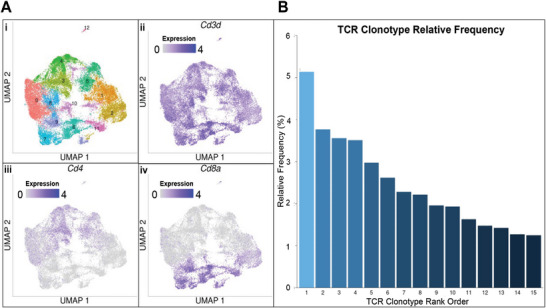
Identified TCRαβ clonotypes from CRC patient tumors. UMAP projection of T cell gene expression data from Han et al. include the A) i) total number of unsupervised clusters, ii) distribution of *Cd3d* expression, iii) distribution of *Cd4* expression, and iv) distribution of *Cd8a* expression across the dataset. TCRαβ clonotypes were identified from the subset of T cells with high *Cd8a* expression and the relative frequency B) of those *Cd8a* ⁺ clonotypes. Single cell data from refs. [20, 21].

To determine the best method for generating TCR‐pMHC starting configurations, we generated the configurations by either Modeller^[ ³⁹ , ⁴⁰ ^] or ColabFold.^[ ³⁶ , ³⁷ , ³⁸ ^] The structures generated in Modeller utilized the DMF5 TCR bound to the HLA‐A2 (MHC) restricted MART1 (PDB:3QDJ)^[ ⁴⁹ ^] as template structure, and the ColabFold structures were predicted from trained neural networks.^[ ³⁶ , ³⁷ , ³⁸ ^] The resulting starting configurations were then solvated in all‐atom molecular dynamics simulations at physiological conditions (see the Experimental Section) for 150–300 ns to equilibrate the protein structures. Equilibration is indicated by the flattening of the RMSD from the initial configuration with fluctuations less than 0.2 nm for the entire TCR‐pMHC structure (Figure S1, Supporting Information). A bias‐variance trade‐off algorithm^[ ⁴⁸ ^] was used to automate the detection of the equilibrated TCR‐pMHC structure (Figure S1, Supporting Information). The equilibration time required for TCR1 (249 & 9 ns), TCR2 (127 & 61 ns), and TCR3 (149 & 136 ns) from Modeller and ColabFold, respectively, demonstrates ≈61% reduction in computational cost—on average—using ColabFold.

We next evaluated the structural similarity of the TCR‐pMHC structures throughout the equilibration using the GROMOS clustering algorithm (Figure S2, Supporting Information).^[ ⁷⁴ ^] Using a C^α RMSD cutoff of 0.2 nm, the top ten equilibrated clusters contain most of the configurations for TCR1 (86.8% and 98.3%), TCR2 (92.7% and 97.0%), and TCR3 (71.0% and 97.7%) from Modeller and ColabFold, respectively. Interestingly, the top cluster contains a plurality of structures and occurs after the estimated equilibration time indicating not a single, but a set of converged TCR‐pMHC structures (Figure S2, Supporting Information).

To evaluate the structural similarity at the TCR‐pMHC interface of TCR1, TCR2, and TCR3, we selected and aligned a subset of the equilibrated structures (12 structures—6 Modeller + 6 ColabFold—see the Experimental Section) (Figure 3A–C). An all‐to‐all structural alignment (72 unique comparisons) was performed to calculate the pairwise RMSD (after equilibration) within and between TCR‐pMHC structures generated by Modeller and ColabFold. The average RMSD for TCRs generated within either Modeller or ColabFold is consistent for TCR1‐pMHC (0.19 ± 0.04 nm), TCR2‐pMHC (0.20 ± 0.07 nm), and TCR3‐pMHC (0.19 ± 0.05 nm). However, there is a consistent increase in average RMSD when comparing equilibrated structures between Modeller and ColabFold for TCR1‐pMHC (0.41 ± 0.05 nm), TCR2‐pMHC (0.40 ± 0.05 nm), and TCR3‐pMHC (0.33 ± 0.04 nm) (Figures S3–S5, Supporting Information). The increase in RMSD occurs despite selecting TCR‐pMHCs from distinct equilibration clusters (Figure S2, Supporting Information). The increase in configuration dissimilarity between Modeller and ColabFold at the TCR‐pMHC interface can be visualized by the aligned and overlaid structures (Figure 3A–C). To investigate the relative fluctuations of the substructures at the TCR‐pMHC interface, the root mean square fluctuations were calculated after equilibration for CDR3α, CDR3β, and the CEA peptide (Figure 3A–C). Fluctuations for all TCRs and TCR substructures are approximately 0.10 nm.

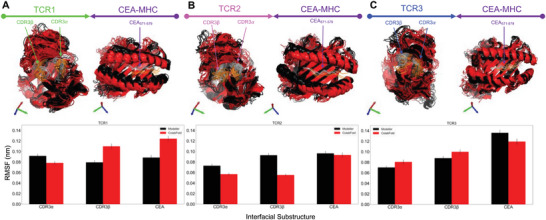
Equilibrated patient‐specific TCRs bound to CEA_571–579 pMHC. The structures of the three most frequently found TCRs from 16 CRC patients were predicted (using Modeller or ColabFold) and equilibrated at physiological conditions using molecular dynamics simulations. A–C) The most frequent TCRs: TCR1, TCR2, and TCR3 are displayed with colors green, magenta, and blue, respectively. The starting structures were created from Modeller (black) and ColabFold (red) and 12 TCR‐pMHC structures (6 from Modeller + 6 from ColabFold) are aligned after equilibration with the TCR (on the left, in respective color) and pMHC (on the right, in purple). In addition, the mutated substructures of the TCR and pMHC are indicated by arrows and highlighted in the following colors: CDR3α, CDR3β, and CEA_571–579 (Modeller: gray and ColabFold: orange). After structural equilibration, the root mean square fluctuation (RMSF) for each TCR is calculated for the regions that were mutated: CDR3α, CDR3β, and CEA_571–579 (bottom). The RMSF is calculated for both the Modeller (black) and ColabFold (red) generated starting structures.

After structural equilibration, the number of molecular‐level interactions between the TCRs and pMHC were evaluated to assess potential differences between the TCR‐pMHCs complexes, and thus provide insight into potential methods to rank the TCRs (Figure 4 ). We selected hydrogen bonds (H‐bonds) and Lennard‐Jones contacts (LJ‐contacts) between the TCRs and pMHC to understand the relative importance of coulombic and hydrophobic interactions. The number of hydrogen bonds (Figure S6, Supporting Information) and the number of Lennard‐Jones contacts (Figure S7, Supporting Information) were calculated as a function of simulation time, and these plots were used to calculate the probability densities. The probability density of interactions is an index to describe the relative likelihood of interactions that occur at any timepoint during the equilibration. Our results demonstrate that TCR2 (expected value: 14.2) is significantly more likely to have more hydrogen bonds than TCR1 (expected value: 12.5) and TCR3 (expected value: 11.7) for structures generated by Modeller (Figure 4). In contrast, for structures generated by ColabFold, TCR1 (expected value: 10.5) and TCR3 (expected value: 10.9) are significantly more likely to have more hydrogen bonds than TCR2 (expected value: 6.8) (Figure 4A). In addition, TCR2 (expected value: 404) is more likely to have more Lennard‐Jones contacts than TCR1 (expected value: 279) and TCR3 (expected value: 294) for structures generated by Modeller. Consistently, for structures generated by ColabFold, TCR2 (expected value: 328) is more likely to have more Lennard‐Jones contacts than TCR3 (expected value: 294) and TCR1 (expected value: 306) (Figure 4B). Despite TCR1 being detected more frequently in patient tumors (Figure 2B), TCR2 may have more binding interactions to CEA_571–579 pMHC at equilibrium (Figure 4C).

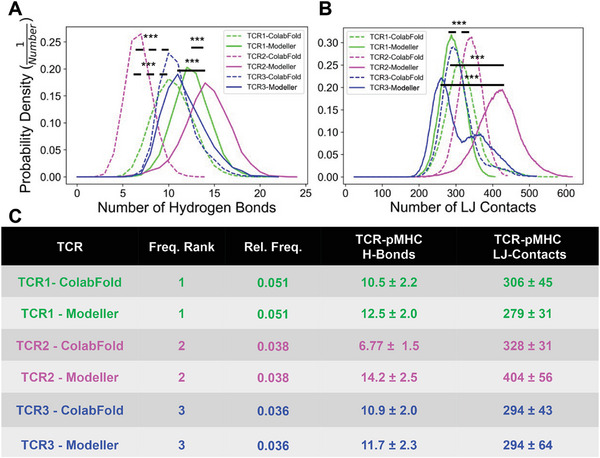
Interactions of patient specific TCRs with pMHC in equilibrium. A) The probability density for the number of hydrogen bonds between the pMHC and TCR1 (green), TCR2 (magenta), and TCR3 (blue), respectively. B) The probability density for the number of Lennard‐Jones Contacts between the pMHC and TCR1 (green), TCR2 (magenta), and TCR3 (blue), respectively. The interaction distributions after equilibration are separated for Modeller (solid line) and ColabFold (dashed line). C) The expected value and standard deviation of H‐bonds and LJ‐contacts with the TCRs ranked by relative frequency found in CRC patients. The number of interactions throughout the simulations was statistically compared: *p < 0.05, **p < 0.01, ***p < 0.001 by one‐way ANOVA followed by Tukey‐HSD post hoc test. Statistical significance was only displayed for comparisons with Cohen effect size d > 0.5. Significance was displayed by solid and dashed lines for Modeller and ColabFold comparisons, respectively.

To get a composite score for the MD based TCR rank, we categorized TCR‐pMHC pairs as higher probability of binding the CEA_571–579 pMHC if they had more interactions at equilibrium: more H‐bonds or LJ‐contacts for both the Modeller and ColabFold based starting structures (Table 1). We found that, on average, TCR2 has more physical interactions with the based CEA_571–579 pMHC with a MD rank of 1.5. In addition, TCR1 and TCR3 had the same MD rank of 2.25. Interestingly, TCR2 was also predicted to have the highest probability of binding the CEA_571–579 pMHC in 4/5 machine learning based methods (Table 1) and achieved an average ML rank of 1.4. In addition, TCR2 and TCR3 resulted in a ML rank of 2.6 and 2.0, respectively.

4. Discussion

Using a combination of single cell sequencing of T cells derived from patient tumors, protein structure prediction algorithms, and MD simulations, we present a pipeline to rank TCRs based on their molecular level interactions with a target pMHC at equilibrium. To commence a pipeline to assess TCRs in silico, we chose only the three most frequently expressed clonotypes in 16 patients with colorectal cancer as a case study. Although the selection of the most frequent TCRs from the clonal pool present in the tumor microenvironment is somewhat arbitrary, the relatively expanded clonal pool in the tumor microenvironment is more likely to be immunogenic to the tumor than a random selection of low‐frequency clones. Nonetheless, our pipeline is easily adapted to selecting clonotypes from alternate sources (e.g., peripheral blood), or alternate strategies (e.g., selecting from the entire clonal pool in the tumor microenvironment.

Our study also presented an opportunity to assess two fundamentally different protein predictions tools: ColabFold—a recently released trained deep learning network; and Modeller—a traditional template‐based protein‐prediction model. We found that the MD equilibration of 3D atomic coordinates of TCR‐pMHC structures was ≈2.5× faster using ColabFold generated structures (Figure S1, Supporting Information). This finding is based on a small number of protein–protein structures, and there was significant variation. Nonetheless, our results demonstrate that ColabFold may be a superior computational tool for protein structure prediction, and thus may have implications on the scale‐up of assessing a larger set (i.e., thousands) of TCRs generated from sequencing data. Moreover, the compute cost may be further reduced by utilizing recently fine‐tuned structure prediction methods on TCR‐pMHC databases^[ ⁴³ ^] which may reduce the required simulation time to equilibrate approximated protein‐protein structures. A reason why ColabFold is faster in equilibration might be that it uses a multitude of templates and not only one.

To automate and remove human bias from determining the required simulation time to reach an equilibrated TCR‐pMHC structure, we used a variance‐bias trade‐off algorithm^[ ⁴⁸ ^] and required a minimum equilibration time of 50 ns (Figure S1, Supporting Information). In addition, we performed a cluster analysis to identify the set of converged clusters after equilibration (Figure S2, Supporting Information). Moreover, we found that the root‐mean‐square fluctuations after equilibration for CDR3α, CDR3β, and the CEA peptide (Figure 3A–C) were ≈0.10 nm. The fluctuations for CDR3α, CDR3β, and peptide are consistent with equilibrated TCRs with a known crystal structure,^[ ³⁰ ^] and thus consistent with equilibration.

After equilibration, we assessed several clusters of configurations and found that within a protein‐protein structure predictor (i.e., Modeller or ColabFold) there is a pairwise RMSD of ≈0.20 nm. Interestingly, across structure predictors there is an increase in pairwise RMSD ≈0.40 nm (Figures S3–S5, Supporting Information). This trend is consistent for TCR1, TCR2, and TCR3 indicating that the structure prediction method can influence the set of equilibrated TCR‐pMHC configurations, and molecular level interactions. We found that TCR2 had more hydrogen bonds compared to TCR1 and TCR3 when generated by Modeller, but less hydrogen bonds when generated by ColabFold (Figure 4A). These results indicate that the differences in configurations generated by Modeller and ColabFold can also influence the number of molecular level interactions between the TCR and pMHC. We observed consistent results between Modeller and ColabFold for the number Lennard‐Jones contacts across the three TCRs (Figure 4B). The probability density of hydrogen bonds and Lennard‐Jones contacts may provide a rudimentary criterion to rank TCRs based on their relative strength of interaction^[ ³⁰ ^] at equilibrium. For example, TCR2 may be a more ideal target to the CEA_571–579 pMHC because of the consistent increase in Lennard‐Jones contacts.

To develop a composite TCR ranking index, we summarized the results found from the MD simulations (Table 1). After ranking the TCRs based on the number of interactions with the CEA_571–579 pMHC, we found that TCR2 had the highest average rank of 1.5. This was consistent with machine learning based methods that predict the probability of TCR‐pMHC binding (Table 1). In fact, TCR2 had the highest probability of binding in 4/5 methods and achieved a similar average rank of 1.4 across the methodologies. Although these results are based on a small set of TCRs, this demonstrates that the MD rank of TCRs derived from molecular interactions at equilibrium is consistent with state‐of‐the‐art ML methods.^[ ²² , ²³ , ²⁴ , ²⁵ ^] Moreover, a major limitation in ML methods is difficulty at predicting TCR‐pMHC binding pairs that are not included in the training distribution.^[ ³⁴ , ³⁵ ^] This methodology may be better suited for generalization to disparate TCR‐pMHC pairs because the ranking is derived from physical interactions. Future work will require a comprehensive dataset that will assess the physiochemical properties of TCR‐pMHC interactions that determine immunogenicity. Also, extensive experimental validation would be very useful.

5. Conclusions

The identification of tumor‐specific TCRs will be augmented by computational methodologies that accurately rank TCRs based on the immunogenic response to a target pMHC. We have integrated next‐generation sequencing with protein‐protein structure prediction and MD to introduce a potential pipeline to evaluate TCRs. We found that ColabFold outperforms Modeller (≈2.5×) in the required simulation time to generate equilibrated TCR‐pMHC structures, and thus may be a superior computational tool to utilize in a computational algorithm built to predict TCR immunogencity. In addition, the protein structure prediction method influences the set of equilibrated configurations and the number of interactions between the TCR and pMHC, and thus may impact the accuracy of predicting TCR‐pMHC bond strength or immunogenic response. On average, the MD‐based ranking of TCR‐pMHC pairs was consistent with state‐of‐the‐art ML based ranking methods and may provide an additional benefit of generalizability to unseen TCR‐pMHC pairs.

Conflict of Interest

The authors declare no conflict of interest.

Author Contributions

S.C.G. and R.F. contributed equally to this work. Z.A.R. performed the simulations, analyzed, and interpreted the data, and wrote the manuscript. M.B.C. analyzed and interpreted the scRNA‐Seq data and wrote the manuscript. R.F. designed the experiments, analyzed and interpreted the data, wrote the manuscript, and secured computer time. S.C.G. designed the experiments, analyzed, and interpreted the data, wrote the manuscript, and secured the funding.

Supporting information

Supporting Information

MARC-45-2400225-s001.pdf^{(1.6MB, pdf)}

Acknowledgements

Single cell V(D)J and single cell gene expression RNA sequencing data was a generous gift from Prof. Arnold Han at Columbia University. Simulations were performed on the hpc1/hpc2 clusters at UC Davis. This work was supported in part by startup funding to SCG from the Department of Biomedical Engineering.

Rollins Z. A., Curtis M. B., George S. C., Faller R., A Computational Strategy for the Rapid Identification and Ranking of Patient‐Specific T Cell Receptors Bound to Neoantigens. Macromol. Rapid Commun. 2024, 45, 2400225. 10.1002/marc.202400225

Data Availability Statement

TCR‐pMHC structures generated from protein–protein structure predictors have been made available ArrayExpress #E‐MTAB‐9455. In addition, the structures, box sizes, and atom counts are all deposited in a Dryad repository:^[ ⁵⁷ ^] https://doi.org/10.25338/B83S70. All scripts relevant to the production of figures have been made available on GitHub:^[ ⁷² ^] https://github.com/zrollins/TCR_homology.git.

References

1. Weekes M. P., Antrobus R., Lill J. R., Duncan L. M., Hör S., Lehner P. J., J. Biomol. Tech. 2010, 21, 108. [PMC free article] [PubMed] [Google Scholar]
2. Murphy K., Weaver C., Janeway's Immunbiology, Garland Science, New York: 2017. [Google Scholar]
3. Rock K. L., Reits E., Neefjes J., Trends Immunol. 2016, 37, 724. [DOI] [PMC free article] [PubMed] [Google Scholar]
4. de Greef P. C., Oakes T., Gerritsen B., Ismail M., Heather J. M., Hermsen R., Chain B., de Boer R. J., Elife 2020, 9, 49900. [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Zarnitsyna V. I., Evavold B. D., Schoettle L. N., Blattman J. N., Antia R., Front. Immunol. 2013, 4, 485. [DOI] [PMC free article] [PubMed] [Google Scholar]
6. Johnson L. A., Morgan R. A., Dudley M. E., Cassard L., Yang J. C., Hughes M. S., Kammula U. S., Royal R. E., Sherry R. M., Wunderlich J. R., Lee C.‐C. R., Restifo N. P., Schwarz S. L., Cogdill A. P., Bishop R. J., Kim H., Brewer C. C., Rudy S. F., Van Waes C., Davis J. L., Mathur A., Ripley R. T., Nathan D. A., Laurencot C. M., Rosenberg S. A., Blood 2009, 114, 535. [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Linette G. P., Stadtmauer E. A., Maus M. V., Rapoport A. P., Levine B. L., Emery L., Litzky L., Bagg A., Carreno B. M., Cimino P. J., Binder‐Scholl G. K., Smethurst D. P., Gerry A. B., Pumphrey N. J., Bennett A. D., Brewer J. E., Dukes J., Harper J., Tayton‐Martin H. K., Jakobsen B. K., Hassan N. J., Kalos M., June C. H., Blood 2013, 122, 863. [DOI] [PMC free article] [PubMed] [Google Scholar]
8. Moore T., Wagner C. R., Scurti G. M., Hutchens K. A., Godellas C., Clark A. L., Kolawole E. M., Hellman L. M., Singh N. K., Huyke F. A., Wang S.‐Y., Calabrese K. M., Embree H. D., Orentas R., Shirai K., Dellacecca E., Garrett‐Mayer E., Li M., Eby J. M., Stiff P. J., Evavold B. D., Baker B. M., Le Poole I. C., Dropulic B., Clark J. I., Nishimura M. I., Cancer Immunol. Immunother. 2018, 67, 311. [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Morgan R. A., Dudley M. E., Wunderlich J. R., Hughes M. S., Yang J. C., Sherry R. M., Royal R. E., Topalian S. L., Kammula U. S., Restifo N. P., Zheng Z., Nahvi A., de Vries C. R., Rogers‐Freezer L. J., Mavroukakis S. A., Rosenberg S. A., Science 2006, 314, 126. [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Robbins P. F., Morgan R. A., Feldman S. A., Yang J. C., Sherry R. M., Dudley M. E., Wunderlich J. R., Nahvi A. V., Helman L. J., Mackall C. L., Kammula U. S., Hughes M. S., Restifo N. P., Raffeld M., Lee C.‐C. R., Levy C. L., Li Y. F., El‐Gamil M., Schwarz S. L., Laurencot C., Rosenberg S. A., J. Clin. Oncol. 2011, 29, 917. [DOI] [PMC free article] [PubMed] [Google Scholar]
11. He Q., Jiang X., Zhou X., Weng J., J. Hematol. Oncol. 2019, 12, 139. [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Nielsen M., Lundegaard C., Blicher T., Lamberth K., Harndahl M., Justesen S., Røder G., Peters B., Sette A., Lund O., Buus S., PLoS One 2007, 2, e796. [DOI] [PMC free article] [PubMed] [Google Scholar]
13. Koşaloğlu‐Yalçın Z., Lanka M., Frentzen A., Premlal A. L. R., Sidney J., Vaughan K., Greenbaum J., Robbins P., Gartner J., Sette A., Peters B., Oncoimmunology 2018, 7, e1492508. [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Gartner J. J., Parkhurst M. R., Gros A., Tran E., Jafferji M. S., Copeland A., Hanada K.‐I., Zacharakis N., Lalani A., Krishna S., Sachs A., Prickett T. D., Li Y. F., Florentin M., Kivitz S., Chatmon S. C., Rosenberg S. A., Robbins P. F., Nat. Cancer 2021, 2, 563. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Kim S.‐M., Bhonsle L., Besgen P., Nickel J., Backes A., Held K., Vollmer S., Dornmair K., Prinz J. C., PLoS One 2012, 7, e37338. [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Turchaninova M. A., Britanova O. V., Bolotin D. A., Shugay M., Putintseva E. V., Staroverov D. B., Sharonov G., Shcherbo D., Zvyagin I. V., Mamedov I. Z., Linnemann C., Schumacher T. N., Chudakov D. M., Eur. J. Immunol. 2013, 43, 2507. [DOI] [PubMed] [Google Scholar]
17. Han A., Glanville J., Hansmann L., Davis M. M., Nat. Biotechnol. 2014, 32, 684. [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Howie B., Sherwood A. M., Berkebile A. D., Berka J., Emerson R. O., Williamson D. W., Kirsch I., Vignali M., Rieder M. J., Carlson C. S., Robins H. S., Sci. Transl. Med. 2015, 7, 301ra131. [DOI] [PubMed] [Google Scholar]
19. Dupic T., Marcou Q., Walczak A. M., Mora T., PLoS Comput. Biol. 2019, 15, e1006874. [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Masuda K., Kornberg A., Miller J., Lin S., Suek N., Botella T., Secener K. A., Bacarella A. M., Cheng L., Ingham M., Rosario V., Al‐Mazrou A. M., Lee‐Kong S. A., Kiran R. P., Stoeckius M., Smibert P., Del Portillo A., Oberstein P. E., Sims P. A., Yan K. S., Han A., JCI Insight 2022, 7, e154646. [DOI] [PMC free article] [PubMed] [Google Scholar]
21. Masuda K., Kornberg A., Lin S., Ho P., Secener K., Suek N., Bacarella A. M., Ingham M., Rosario V., Al‐Masrou A. M., Lee‐Kong S. A., Kiran P. R., Yan K. S., Stoeckius M., Smibert P., Oberstein P. E., Sims P. A., Han A., bioRxiv 2020, https://www.biorxiv.org/content/10.1101/2020.09.27.313445v2 (accessed: June 2023).
22. Springer I., Tickotsky N., Louzoun Y., Front. Immunol. 2021, 12, 664514. [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Jensen M. F., Nielsen M., Elife 2024, 12, RP93934. [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Lu T., Zhang Z., Zhu J., Wang Y., Jiang P., Xiao X., Bernatchez C., Heymach J. V., Gibbons D. L., Wang J., Xu L., Reuben A., Wang T., Nat. Mach. Intell. 2021, 3, 864. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Han Y., Yang Y., Tian Y., Fattah F. J., von Itzstein M. S., Zhang M., Kang X., Yang D. M., Liu J., Xue Y., Liang C., Raman I., Zhu C., Xiao O., Hu Y., Dowell J. E., Homsi J., Rashdan S., Yang S., Gwin M. E., Hsiehchen D., Gloria‐McCutchen Y., Pan K., Wu F., Gibbons D., Wang X., Yee C., Huang J., Reuben A., Cheng C., et al., bioRxiv 2023, 10.1101/2023.12.01.569599. [DOI] [Google Scholar]
26. Milighetti M., Shawe‐Taylor J., Chain B., Front. Physiol. 2021, 12, 1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Zhu C., Jiang N., Huang J., Zarnitsyna V. I., Evavold B. D., Immunol. Rev. 2013, 251, 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
28. Liu B., Chen W., Evavold B. D., Zhu C., Cell 2014, 157, 357. [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Limozin L., Bridge M., Bongrand P., Dushek O., van der Merwe P. A., Proc. Natl. Acad. Sci. USA 2019, 116, 201902141. [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Rollins Z. A., Faller R., George S. C., Comput. Struct. Biotechnol. J. 2022, 20, 2124. [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Feng Y., Zhao X., White A. K., Garcia K. C., Fordyce P. M., Biohub C. Z., bioRxiv 2021, https://www.biorxiv.org/content/10.1101/2021.04.24.441194v1. (accessed: June 2023).
32. Kitano S., Ito A., Kim Y., Inoue M., Fuse M., Tada K., Yoshimura K., Cell. Immunol. 2015, 6, 2. [Google Scholar]
33. Leem J., De Oliveira S. H. P., Krawczyk K., Deane C. M., Nucleic Acids Res. 2018, 46, D406. [DOI] [PMC free article] [PubMed] [Google Scholar]
34. Grazioli F., Mösch A., Machart P., Li K., Alqassem I., O'Donnell T. J., Min M. R., Front. Immunol. 2022, 13, 1014256. [DOI] [PMC free article] [PubMed] [Google Scholar]
35. Deng L., Ly C., Abdollahi S., Zhao Y., Prinz I., Bonn S., Front. Immunol. 2023, 14, 1128326. [DOI] [PMC free article] [PubMed] [Google Scholar]
36. Jumper J., Evans R., Pritzel A., Green T., Figurnov M., Ronneberger O., Tunyasuvunakool K., Bates R., dek A. Z., Potapenko A., Bridgland A., Meyer C., Kohl S. A. A., Ballard A. J., Cowie A., Romera‐Paredes B., Nikolov S., Jain R., Adler J., Back T., Petersen S., Reiman D., Clancy E., Zielinski M., Steinegger M., Pacholska M., Berghammer T., Bodenstein S., Silver D., Vinyals O., et al., Nature 2021, 596, 583. [DOI] [PMC free article] [PubMed] [Google Scholar]
37. Evans R., O'Neill M., Pritzel A., Antropova N., Senior A., Green T., Žídek A., Bates R., Blackwell S., Yim J., Ronneberger O., Bodenstein S., Zielinski M., Bridgland A., Potapenko A., Cowie A., Tunyasuvunakool K., Jain R., Clancy E., Kohli P., Jumper J., Hassabis D., bioRxiv 2021, https://www.biorxiv.org/content/10.1101/2021.10.04.463034v1 (accessed: June 2023).
38. Mirdita M., Schütze K., Moriwaki Y., Heo L., Ovchinnikov S., Steinegger M., bioRxiv 2022, https://www.biorxiv.org/content/10.1101/2021.08.15.456425v3 (accessed: June 2023). [DOI] [PMC free article] [PubMed]
39. Fiser A. S., Šali A., Methods Enzymol. 2003, 374, 461. [DOI] [PubMed] [Google Scholar]
40. Webb B., Sali A., Curr. Protoc. Bioinf. 2016, 54, 5.6.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
41. Klausen M. S., Anderson M. V., Jespersen M. C., Nielsen M., Marcatili P., Nucleic Acids Res. 2015, 43, W349. [DOI] [PMC free article] [PubMed] [Google Scholar]
42. Jensen K. K., Rantos V., Jappe E. C., Olsen T. H., Jespersen M. C., Jurtz V., Jessen L. E., Lanzarotti E., Mahajan S., Peters B., Nielsen M., Marcatili P., Sci. Rep. 2019, 9, 14530. [DOI] [PMC free article] [PubMed] [Google Scholar]
43. Yin R., Ribeiro‐Filho H. V., Lin V., Gowthaman R., Cheung M., Pierce B. G., Nucleic Acids Res. 2023, 51, W569. [DOI] [PMC free article] [PubMed] [Google Scholar]
44. Rollins Z. A., Huang J., Tagkopoulos I., Faller R., George S. C., Comput. Struct. Biotechnol. J. 2022, 20, 3473. [DOI] [PMC free article] [PubMed] [Google Scholar]
45. Gold P., Goldberg N. A., McGill J. Med. 2020, 3, 46. [Google Scholar]
46. Tsang K. Y., Zaremba S., Nieroda C. A., Zhu M. Z., Hamilton J. M., Schlom J., JNCI, J. Natl. Cancer Inst. 1995, 87, 982. [DOI] [PubMed] [Google Scholar]
47. Parkhurst M. R., Yang J. C., Langan R. C., Dudley M. E., Nathan D. A. N., Feldman S. A., Davis J. L., Morgan R. A., Merino M. J., Sherry R. M., Hughes M. S., Kammula U. S., Phan G. Q., Lim R. M., Wank S. A., Restifo N. P., Robbins P. F., Laurencot C. M., Rosenberg S. A., Mol. Ther. 2011, 19, 620. [DOI] [PMC free article] [PubMed] [Google Scholar]
48. Chodera J. D., J. Chem. Theory Comput. 2016, 12, 1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
49. Borbulevych O. Y., Piepenbrink K. H., Baker B. M., J. Immunol. 2011, 186, 2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
50. Shen M. Y., Sali A., Protein Sci. 2006, 15, 2507. [DOI] [PMC free article] [PubMed] [Google Scholar]
51. Van Der Spoel D., Lindahl E., Hess B., Groenhof G., Mark A. E., Berendsen H. J. C., J. Comput. Chem. 2005, 26, 1701. [DOI] [PubMed] [Google Scholar]
52. Abraham M. J., Murtola T., Schulz R., Páll S., Smith J. C., Hess B., Lindahl E., SoftwareX 2015, 1, 19. [Google Scholar]
53. MacKerell A. D., Bashford D., Bellott M., Dunbrack R. L., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph‐McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., Reiher W. E., Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiórkiewicz‐Kuczera J., Yin D., Karplus M., J. Phys. Chem. B 1998, 102, 3586. [DOI] [PubMed] [Google Scholar]
54. Olsson M. H. M., SØndergaard C. R., Rostkowski M., Jensen J. H., J. Chem. Theory Comput. 2011, 7, 525. [DOI] [PubMed] [Google Scholar]
55. Søndergaard C. R., Olsson M. H. M., Rostkowski M., Jensen J. H., J. Chem. Theory Comput. 2011, 7, 2284. [DOI] [PubMed] [Google Scholar]
56. Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., Klein M. L., J. Chem. Phys. 1983, 79, 926. [Google Scholar]
57. Rollins Z., Faller R., George S. C., TCR‐pMHC Starting Configurations & Atomic Motion Supplementary Videos UC Davis, Dryad Dataset 2021, 10.25338/B8FK8D. [DOI]
58. Bussi G., Donadio D., Parrinello M., J. Chem. Phys. 2007, 126, 014101. [DOI] [PubMed] [Google Scholar]
59. Berendsen H. J. C., Postma J. P. M., Van Gunsteren W. F., Dinola A., Haak J. R., J. Chem. Phys. 1984, 81, 3684. [Google Scholar]
60. Evans D. J., Holian B. L., J. Chem. Phys. 1985, 4069, 83. [Google Scholar]
61. Parrinello M., Rahman A., J. Appl. Phys. 1981, 52, 7182. [Google Scholar]
62. Ewald P. P., Ann. Phys. 1921, 369, 253. [Google Scholar]
63. Di Pierro M., Elber R., Leimkuhler B., J. Chem. Theory Comput. 2015, 11, 5624. [DOI] [PMC free article] [PubMed] [Google Scholar]
64. Miyamoto S., Settle K. P. A., J. Comput. Chem. 1992, 13, 952. [Google Scholar]
65. Hess B., Bekker H., Berendsen H. J. C., Fraaije J. G. E. M., J. Comput. Chem. 1997, 18, 1463. [Google Scholar]
66. Harris C. R., Millman K. J., van der Walt S. J., Gommers R., Virtanen P., Cournapeau D., Wieser E., Taylor J., Berg S., Smith N. J., Kern R., Picus M., Hoyer S., van Kerkwijk M. H., Brett M., Haldane A., del Río J. F., Wiebe M., Peterson P., Gérard‐Marchant P., Sheppard K., Reddy T., Weckesser W., Abbasi H., Gohlke C., Oliphant T. E., Nature 2020, 585, 357. [DOI] [PMC free article] [PubMed] [Google Scholar]
67. Mckinney W., Data Structures for Statistical Computing in Python. 2010.
68. Hunter J. D., Comput. Sci. Eng. 2007, 9, 90. [Google Scholar]
69. Beckstein O., GromacsWrapper [Internet], https://github.com/Becksteinlab/GromacsWrapper (accessed: June 2023).
70. Virtanen P., Gommers R., Oliphant T. E., Haberland M., Reddy T., Cournapeau D., Burovski E., Peterson P., Weckesser W., Bright J., van der Walt S. J., Brett M., Wilson J., Millman K. J., Mayorov N., Nelson A. R. J., Jones E., Kern R., Larson E., Carey C. J., Polat I., Feng Y., Moore E. W., VanderPlas J., Laxalde D., Perktold J., Cimrman R., Henriksen I., Quintero E. A., Harris C. R., et al., Nat. Methods 2020, 17, 261. [DOI] [PMC free article] [PubMed] [Google Scholar]
71. Vallat R., J. Open Source Software 2018, 3, 1026. [Google Scholar]
72. Rollins Z. A., https://github.com/zrollins/TCR_homology.git 2022.
73. Genomics 10 X, A New Way of Exploring Immunity – Linking Highly Multiplexed Antigen Recognition to Immune Repertoire and Phenotype | Technology Networks [Internet], https://www.technologynetworks.com/immunology/application‐notes/a‐new‐way‐of‐exploring‐immunity‐linking‐highly‐multiplexed‐antigen‐recognition‐to‐immune‐repertoire‐332554 (accessed: June 2023).
74. Daura X., Gademann K., Jaun B., Seebach D., van Gunsteren W. F., Mark A. E., Angew. Chem., Int. Ed. Engl. 1998, 31, 1387. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information

MARC-45-2400225-s001.pdf^{(1.6MB, pdf)}

Data Availability Statement

[marc202400225-bib-0001] 1. Weekes M. P., Antrobus R., Lill J. R., Duncan L. M., Hör S., Lehner P. J., J. Biomol. Tech. 2010, 21, 108. [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0002] 2. Murphy K., Weaver C., Janeway's Immunbiology, Garland Science, New York: 2017. [Google Scholar]

[marc202400225-bib-0003] 3. Rock K. L., Reits E., Neefjes J., Trends Immunol. 2016, 37, 724. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0004] 4. de Greef P. C., Oakes T., Gerritsen B., Ismail M., Heather J. M., Hermsen R., Chain B., de Boer R. J., Elife 2020, 9, 49900. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0005] 5. Zarnitsyna V. I., Evavold B. D., Schoettle L. N., Blattman J. N., Antia R., Front. Immunol. 2013, 4, 485. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0006] 6. Johnson L. A., Morgan R. A., Dudley M. E., Cassard L., Yang J. C., Hughes M. S., Kammula U. S., Royal R. E., Sherry R. M., Wunderlich J. R., Lee C.‐C. R., Restifo N. P., Schwarz S. L., Cogdill A. P., Bishop R. J., Kim H., Brewer C. C., Rudy S. F., Van Waes C., Davis J. L., Mathur A., Ripley R. T., Nathan D. A., Laurencot C. M., Rosenberg S. A., Blood 2009, 114, 535. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0007] 7. Linette G. P., Stadtmauer E. A., Maus M. V., Rapoport A. P., Levine B. L., Emery L., Litzky L., Bagg A., Carreno B. M., Cimino P. J., Binder‐Scholl G. K., Smethurst D. P., Gerry A. B., Pumphrey N. J., Bennett A. D., Brewer J. E., Dukes J., Harper J., Tayton‐Martin H. K., Jakobsen B. K., Hassan N. J., Kalos M., June C. H., Blood 2013, 122, 863. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0008] 8. Moore T., Wagner C. R., Scurti G. M., Hutchens K. A., Godellas C., Clark A. L., Kolawole E. M., Hellman L. M., Singh N. K., Huyke F. A., Wang S.‐Y., Calabrese K. M., Embree H. D., Orentas R., Shirai K., Dellacecca E., Garrett‐Mayer E., Li M., Eby J. M., Stiff P. J., Evavold B. D., Baker B. M., Le Poole I. C., Dropulic B., Clark J. I., Nishimura M. I., Cancer Immunol. Immunother. 2018, 67, 311. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0009] 9. Morgan R. A., Dudley M. E., Wunderlich J. R., Hughes M. S., Yang J. C., Sherry R. M., Royal R. E., Topalian S. L., Kammula U. S., Restifo N. P., Zheng Z., Nahvi A., de Vries C. R., Rogers‐Freezer L. J., Mavroukakis S. A., Rosenberg S. A., Science 2006, 314, 126. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0010] 10. Robbins P. F., Morgan R. A., Feldman S. A., Yang J. C., Sherry R. M., Dudley M. E., Wunderlich J. R., Nahvi A. V., Helman L. J., Mackall C. L., Kammula U. S., Hughes M. S., Restifo N. P., Raffeld M., Lee C.‐C. R., Levy C. L., Li Y. F., El‐Gamil M., Schwarz S. L., Laurencot C., Rosenberg S. A., J. Clin. Oncol. 2011, 29, 917. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0011] 11. He Q., Jiang X., Zhou X., Weng J., J. Hematol. Oncol. 2019, 12, 139. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0012] 12. Nielsen M., Lundegaard C., Blicher T., Lamberth K., Harndahl M., Justesen S., Røder G., Peters B., Sette A., Lund O., Buus S., PLoS One 2007, 2, e796. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0013] 13. Koşaloğlu‐Yalçın Z., Lanka M., Frentzen A., Premlal A. L. R., Sidney J., Vaughan K., Greenbaum J., Robbins P., Gartner J., Sette A., Peters B., Oncoimmunology 2018, 7, e1492508. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0014] 14. Gartner J. J., Parkhurst M. R., Gros A., Tran E., Jafferji M. S., Copeland A., Hanada K.‐I., Zacharakis N., Lalani A., Krishna S., Sachs A., Prickett T. D., Li Y. F., Florentin M., Kivitz S., Chatmon S. C., Rosenberg S. A., Robbins P. F., Nat. Cancer 2021, 2, 563. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0015] 15. Kim S.‐M., Bhonsle L., Besgen P., Nickel J., Backes A., Held K., Vollmer S., Dornmair K., Prinz J. C., PLoS One 2012, 7, e37338. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0016] 16. Turchaninova M. A., Britanova O. V., Bolotin D. A., Shugay M., Putintseva E. V., Staroverov D. B., Sharonov G., Shcherbo D., Zvyagin I. V., Mamedov I. Z., Linnemann C., Schumacher T. N., Chudakov D. M., Eur. J. Immunol. 2013, 43, 2507. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0017] 17. Han A., Glanville J., Hansmann L., Davis M. M., Nat. Biotechnol. 2014, 32, 684. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0018] 18. Howie B., Sherwood A. M., Berkebile A. D., Berka J., Emerson R. O., Williamson D. W., Kirsch I., Vignali M., Rieder M. J., Carlson C. S., Robins H. S., Sci. Transl. Med. 2015, 7, 301ra131. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0019] 19. Dupic T., Marcou Q., Walczak A. M., Mora T., PLoS Comput. Biol. 2019, 15, e1006874. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0020] 20. Masuda K., Kornberg A., Miller J., Lin S., Suek N., Botella T., Secener K. A., Bacarella A. M., Cheng L., Ingham M., Rosario V., Al‐Mazrou A. M., Lee‐Kong S. A., Kiran R. P., Stoeckius M., Smibert P., Del Portillo A., Oberstein P. E., Sims P. A., Yan K. S., Han A., JCI Insight 2022, 7, e154646. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0021] 21. Masuda K., Kornberg A., Lin S., Ho P., Secener K., Suek N., Bacarella A. M., Ingham M., Rosario V., Al‐Masrou A. M., Lee‐Kong S. A., Kiran P. R., Yan K. S., Stoeckius M., Smibert P., Oberstein P. E., Sims P. A., Han A., bioRxiv 2020, https://www.biorxiv.org/content/10.1101/2020.09.27.313445v2 (accessed: June 2023).

[marc202400225-bib-0022] 22. Springer I., Tickotsky N., Louzoun Y., Front. Immunol. 2021, 12, 664514. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0023] 23. Jensen M. F., Nielsen M., Elife 2024, 12, RP93934. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0024] 24. Lu T., Zhang Z., Zhu J., Wang Y., Jiang P., Xiao X., Bernatchez C., Heymach J. V., Gibbons D. L., Wang J., Xu L., Reuben A., Wang T., Nat. Mach. Intell. 2021, 3, 864. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0025] 25. Han Y., Yang Y., Tian Y., Fattah F. J., von Itzstein M. S., Zhang M., Kang X., Yang D. M., Liu J., Xue Y., Liang C., Raman I., Zhu C., Xiao O., Hu Y., Dowell J. E., Homsi J., Rashdan S., Yang S., Gwin M. E., Hsiehchen D., Gloria‐McCutchen Y., Pan K., Wu F., Gibbons D., Wang X., Yee C., Huang J., Reuben A., Cheng C., et al., bioRxiv 2023, 10.1101/2023.12.01.569599. [DOI] [Google Scholar]

[marc202400225-bib-0026] 26. Milighetti M., Shawe‐Taylor J., Chain B., Front. Physiol. 2021, 12, 1358. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0027] 27. Zhu C., Jiang N., Huang J., Zarnitsyna V. I., Evavold B. D., Immunol. Rev. 2013, 251, 49. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0028] 28. Liu B., Chen W., Evavold B. D., Zhu C., Cell 2014, 157, 357. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0029] 29. Limozin L., Bridge M., Bongrand P., Dushek O., van der Merwe P. A., Proc. Natl. Acad. Sci. USA 2019, 116, 201902141. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0030] 30. Rollins Z. A., Faller R., George S. C., Comput. Struct. Biotechnol. J. 2022, 20, 2124. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0031] 31. Feng Y., Zhao X., White A. K., Garcia K. C., Fordyce P. M., Biohub C. Z., bioRxiv 2021, https://www.biorxiv.org/content/10.1101/2021.04.24.441194v1. (accessed: June 2023).

[marc202400225-bib-0032] 32. Kitano S., Ito A., Kim Y., Inoue M., Fuse M., Tada K., Yoshimura K., Cell. Immunol. 2015, 6, 2. [Google Scholar]

[marc202400225-bib-0033] 33. Leem J., De Oliveira S. H. P., Krawczyk K., Deane C. M., Nucleic Acids Res. 2018, 46, D406. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0034] 34. Grazioli F., Mösch A., Machart P., Li K., Alqassem I., O'Donnell T. J., Min M. R., Front. Immunol. 2022, 13, 1014256. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0035] 35. Deng L., Ly C., Abdollahi S., Zhao Y., Prinz I., Bonn S., Front. Immunol. 2023, 14, 1128326. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0036] 36. Jumper J., Evans R., Pritzel A., Green T., Figurnov M., Ronneberger O., Tunyasuvunakool K., Bates R., dek A. Z., Potapenko A., Bridgland A., Meyer C., Kohl S. A. A., Ballard A. J., Cowie A., Romera‐Paredes B., Nikolov S., Jain R., Adler J., Back T., Petersen S., Reiman D., Clancy E., Zielinski M., Steinegger M., Pacholska M., Berghammer T., Bodenstein S., Silver D., Vinyals O., et al., Nature 2021, 596, 583. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0037] 37. Evans R., O'Neill M., Pritzel A., Antropova N., Senior A., Green T., Žídek A., Bates R., Blackwell S., Yim J., Ronneberger O., Bodenstein S., Zielinski M., Bridgland A., Potapenko A., Cowie A., Tunyasuvunakool K., Jain R., Clancy E., Kohli P., Jumper J., Hassabis D., bioRxiv 2021, https://www.biorxiv.org/content/10.1101/2021.10.04.463034v1 (accessed: June 2023).

[marc202400225-bib-0038] 38. Mirdita M., Schütze K., Moriwaki Y., Heo L., Ovchinnikov S., Steinegger M., bioRxiv 2022, https://www.biorxiv.org/content/10.1101/2021.08.15.456425v3 (accessed: June 2023). [DOI] [PMC free article] [PubMed]

[marc202400225-bib-0039] 39. Fiser A. S., Šali A., Methods Enzymol. 2003, 374, 461. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0040] 40. Webb B., Sali A., Curr. Protoc. Bioinf. 2016, 54, 5.6.1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0041] 41. Klausen M. S., Anderson M. V., Jespersen M. C., Nielsen M., Marcatili P., Nucleic Acids Res. 2015, 43, W349. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0042] 42. Jensen K. K., Rantos V., Jappe E. C., Olsen T. H., Jespersen M. C., Jurtz V., Jessen L. E., Lanzarotti E., Mahajan S., Peters B., Nielsen M., Marcatili P., Sci. Rep. 2019, 9, 14530. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0043] 43. Yin R., Ribeiro‐Filho H. V., Lin V., Gowthaman R., Cheung M., Pierce B. G., Nucleic Acids Res. 2023, 51, W569. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0044] 44. Rollins Z. A., Huang J., Tagkopoulos I., Faller R., George S. C., Comput. Struct. Biotechnol. J. 2022, 20, 3473. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0045] 45. Gold P., Goldberg N. A., McGill J. Med. 2020, 3, 46. [Google Scholar]

[marc202400225-bib-0046] 46. Tsang K. Y., Zaremba S., Nieroda C. A., Zhu M. Z., Hamilton J. M., Schlom J., JNCI, J. Natl. Cancer Inst. 1995, 87, 982. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0047] 47. Parkhurst M. R., Yang J. C., Langan R. C., Dudley M. E., Nathan D. A. N., Feldman S. A., Davis J. L., Morgan R. A., Merino M. J., Sherry R. M., Hughes M. S., Kammula U. S., Phan G. Q., Lim R. M., Wank S. A., Restifo N. P., Robbins P. F., Laurencot C. M., Rosenberg S. A., Mol. Ther. 2011, 19, 620. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0048] 48. Chodera J. D., J. Chem. Theory Comput. 2016, 12, 1799. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0049] 49. Borbulevych O. Y., Piepenbrink K. H., Baker B. M., J. Immunol. 2011, 186, 2950. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0050] 50. Shen M. Y., Sali A., Protein Sci. 2006, 15, 2507. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0051] 51. Van Der Spoel D., Lindahl E., Hess B., Groenhof G., Mark A. E., Berendsen H. J. C., J. Comput. Chem. 2005, 26, 1701. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0052] 52. Abraham M. J., Murtola T., Schulz R., Páll S., Smith J. C., Hess B., Lindahl E., SoftwareX 2015, 1, 19. [Google Scholar]

[marc202400225-bib-0053] 53. MacKerell A. D., Bashford D., Bellott M., Dunbrack R. L., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph‐McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., Reiher W. E., Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiórkiewicz‐Kuczera J., Yin D., Karplus M., J. Phys. Chem. B 1998, 102, 3586. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0054] 54. Olsson M. H. M., SØndergaard C. R., Rostkowski M., Jensen J. H., J. Chem. Theory Comput. 2011, 7, 525. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0055] 55. Søndergaard C. R., Olsson M. H. M., Rostkowski M., Jensen J. H., J. Chem. Theory Comput. 2011, 7, 2284. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0056] 56. Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., Klein M. L., J. Chem. Phys. 1983, 79, 926. [Google Scholar]

[marc202400225-bib-0057] 57. Rollins Z., Faller R., George S. C., TCR‐pMHC Starting Configurations & Atomic Motion Supplementary Videos UC Davis, Dryad Dataset 2021, 10.25338/B8FK8D. [DOI]

[marc202400225-bib-0058] 58. Bussi G., Donadio D., Parrinello M., J. Chem. Phys. 2007, 126, 014101. [DOI] [PubMed] [Google Scholar]

[marc202400225-bib-0059] 59. Berendsen H. J. C., Postma J. P. M., Van Gunsteren W. F., Dinola A., Haak J. R., J. Chem. Phys. 1984, 81, 3684. [Google Scholar]

[marc202400225-bib-0060] 60. Evans D. J., Holian B. L., J. Chem. Phys. 1985, 4069, 83. [Google Scholar]

[marc202400225-bib-0061] 61. Parrinello M., Rahman A., J. Appl. Phys. 1981, 52, 7182. [Google Scholar]

[marc202400225-bib-0062] 62. Ewald P. P., Ann. Phys. 1921, 369, 253. [Google Scholar]

[marc202400225-bib-0063] 63. Di Pierro M., Elber R., Leimkuhler B., J. Chem. Theory Comput. 2015, 11, 5624. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0064] 64. Miyamoto S., Settle K. P. A., J. Comput. Chem. 1992, 13, 952. [Google Scholar]

[marc202400225-bib-0065] 65. Hess B., Bekker H., Berendsen H. J. C., Fraaije J. G. E. M., J. Comput. Chem. 1997, 18, 1463. [Google Scholar]

[marc202400225-bib-0066] 66. Harris C. R., Millman K. J., van der Walt S. J., Gommers R., Virtanen P., Cournapeau D., Wieser E., Taylor J., Berg S., Smith N. J., Kern R., Picus M., Hoyer S., van Kerkwijk M. H., Brett M., Haldane A., del Río J. F., Wiebe M., Peterson P., Gérard‐Marchant P., Sheppard K., Reddy T., Weckesser W., Abbasi H., Gohlke C., Oliphant T. E., Nature 2020, 585, 357. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0067] 67. Mckinney W., Data Structures for Statistical Computing in Python. 2010.

[marc202400225-bib-0068] 68. Hunter J. D., Comput. Sci. Eng. 2007, 9, 90. [Google Scholar]

[marc202400225-bib-0069] 69. Beckstein O., GromacsWrapper [Internet], https://github.com/Becksteinlab/GromacsWrapper (accessed: June 2023).

[marc202400225-bib-0070] 70. Virtanen P., Gommers R., Oliphant T. E., Haberland M., Reddy T., Cournapeau D., Burovski E., Peterson P., Weckesser W., Bright J., van der Walt S. J., Brett M., Wilson J., Millman K. J., Mayorov N., Nelson A. R. J., Jones E., Kern R., Larson E., Carey C. J., Polat I., Feng Y., Moore E. W., VanderPlas J., Laxalde D., Perktold J., Cimrman R., Henriksen I., Quintero E. A., Harris C. R., et al., Nat. Methods 2020, 17, 261. [DOI] [PMC free article] [PubMed] [Google Scholar]

[marc202400225-bib-0071] 71. Vallat R., J. Open Source Software 2018, 3, 1026. [Google Scholar]

[marc202400225-bib-0072] 72. Rollins Z. A., https://github.com/zrollins/TCR_homology.git 2022.

[marc202400225-bib-0073] 73. Genomics 10 X, A New Way of Exploring Immunity – Linking Highly Multiplexed Antigen Recognition to Immune Repertoire and Phenotype | Technology Networks [Internet], https://www.technologynetworks.com/immunology/application‐notes/a‐new‐way‐of‐exploring‐immunity‐linking‐highly‐multiplexed‐antigen‐recognition‐to‐immune‐repertoire‐332554 (accessed: June 2023).

[marc202400225-bib-0074] 74. Daura X., Gademann K., Jaun B., Seebach D., van Gunsteren W. F., Mark A. E., Angew. Chem., Int. Ed. Engl. 1998, 31, 1387. [Google Scholar]

PERMALINK

A Computational Strategy for the Rapid Identification and Ranking of Patient‐Specific T Cell Receptors Bound to Neoantigens

Zachary A Rollins

Matthew B Curtis

Steven C George

Roland Faller

Abstract

1. Introduction

Figure 1.

2. Experimental Section

2.1. Single‐Cell RNA V(D)J Sequencing of CRC Patient T Cells