Mechanism-based Modelling for Fitting the Double-exponential Progress Curves of Cellulase Reaction

Abstract

Enzymatic hydrolysis of cellulosic biomass is a complex process involving many factors, including multiple enzymes, heterogeneous substrates, and multi-step enzyme reactions. Cellulase researchers have conventionally used a double-exponential equation to fit the experimental time course of product formation, but no theoretical basis for this has been established. Here we present a mechanism-based equation that fits well the progress curves of cellulase reaction, incorporating the concepts of non-productive and productive binding on the cellulose surface and processivity. The derived equation is double exponential. Our findings indicate that the reaction mechanism of cellulase itself can account for the double-exponential nature of the progress curve independently of other factors that may contribute, such as substrate heterogeneity and involvement of other enzymes.

Abbreviations

CBD, cellulose-binding domain; CBH, cellobiohydrolase; CD, catalytic domain; EG, endo-glucanase; GH, glycoside hydrolase; HS-AFM, high-speed atomic force microscopy.

INTRODUCTION

In progressing towards a carbon-neutral society, enzymatic hydrolysis of cellulose is a bottleneck in the production of soluble saccharides such as glucose and cellobiose from non-edible biomass [1]. Cellulase is an attractive option for converting cellulosic biomass because it can hydrolyze cellulose under mild conditions, and it is becoming more widely utilized as recent developments in biotechnology have reduced its cost [2]. Therefore, it is important to understand its mechanism of action in detail to maximize its utility.

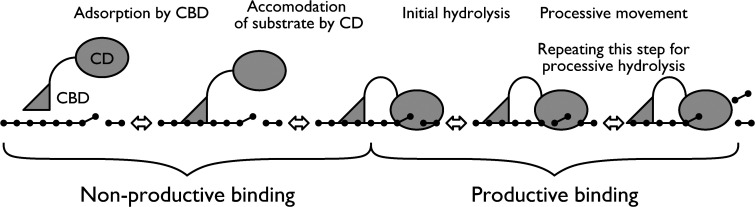
Cellulases that act on insoluble cellulose typically consist of two domains, the cellulose-binding (CBD) and catalytic (CD) domains [3, 4]. As shown in Fig. 1, cellulose hydrolysis is typically initiated by the adsorption of the enzyme on the cellulose surface, mediated by the CBD, though the resulting enzyme-substrate complex is “non-productive” because adsorption on cellulose itself does not produce any products [5, 6]. The following reaction is highly dependent on the characteristics of the CD for saccharide production [7, 8], i.e., the cellulose chain is retained after the initial hydrolysis and a further hydrolytic reaction occurs to produce soluble saccharide (typically cellobiose); this is called the “processive reaction” [9]. However, if the CD leaves the chain soon after the initial hydrolysis reaction, the reaction is called “non-processive”. Processivity is the key to the degradability of crystalline cellulose by the enzyme [10, 11]. We previously used high-speed atomic force microscopy (HS-AFM) to visualize the processive movement of microbial cellobiohydrolases (CBHs) [12, 13, 14] and we discussed the structure-function relationships of CBHs based on the idea of convergent evolution of cellulolytic bacteria and fungi [15]. These recent studies indicate that a combination of cutting-edge biophysical approaches with quantitative biochemical analysis is required to understand the reaction mechanism of the enzyme.

Fig. 1. Mechanism of action of cellulase with a dual domain structure, used to construct the theoretical equation.

　CBD, cellulose-binding domain; CD, catalytic domain.

Many biochemical approaches have been used to examine the time course of product formation (the progress curve) by cellulases, but no consistent understanding has emerged, probably because of the complexity of enzymatic cellulose hydrolysis [11, 16]. In early investigations, it was suggested that the heterogeneity of cellulose, i.e., the presence of a mixture of crystalline and amorphous regions, might be important because of the endo-exo theory, i.e., that endo-glucanases (EGs) degrade amorphous regions of cellulose while crystalline cellulose is hydrolyzed by exo-type enzymes later called CBHs [17, 18, 19, 20, 21]. Since amorphous regions are quickly degraded by EGs while the degradation of crystalline part is slow, it seems reasonable to apply a two-term equation, such as a double exponential, to fit the progress curves. However, it was found that degradation was biphasic even when a single, highly purified enzyme was applied to highly crystalline cellulose [6, 11]. Thus, it appeared that the fitting of the observations to a double-exponential equation is not simply due to substrate heterogeneity or involvement of multiple enzymes.

In the present manuscript, we have developed a mechanism-based double-exponential equation that fits well the progress curve of the cellulase reaction, thereby providing a theoretical basis for the observation that the progress curve of cellulase shows a double-exponential character. This approach should be applicable not only to cellulases, but also to other enzymes that act on insoluble substrates with or without processivity.

MATERIALS AND METHODS

The theoretical development is presented step-by-step in the following Results and Discussion section. The kinetic data of glycoside hydrolase (GH) family 6 CBH from Phanerochaete chrysosporium (PcCel6A) [22] and GH7 CBH from Trichoderma reesei (TrCel7A) [6] towards highly crystalline cellulose from green algae Cladphora spp. used in this study are taken from the cited references. Global fitting of the data was done using Igor Pro (ver. 8.04, Wavemetric, Inc.)

RESULTS AND DISCUSSION

Recent biophysical experiments using HS-AFM indicate that cellulases, especially processive enzymes, move along the substrate chains of crystalline cellulose [12, 13, 14], and biochemical results need to be reanalyzed to take account of the dynamics of the enzyme. However, as regards the parameters, Väljamäe and coworkers' stated “It must be pointed out that we do not attach any physical interpretation to these constants since they are empirical” [11], and this situation has not changed in the past quarter of a century. In the present manuscript, we take a bottom-up approach based on the molecular mechanism of the enzyme.

As shown in Fig. 1, cellulase molecules may exist in three states: in solution, and on cellulose in a non-productive or productive manner. Chemical equations for the process are written as

$$E_s{}_{\underset{k_{-1}}{\leftarrow }}^{\stackrel{k_1}{\to }}{E}_{\mathit{np}}{}_{\underset{k_{-2}}{\leftarrow }}^{\stackrel{k_2}{\to }}{E}_p+P$$

$$E_p\stackrel{k_3}{\to }{E}_s+\mathit{\nu P}$$

where E_s, E_np, E_p, and P are the concentrations of the enzyme molecule in solution, non-productively bound enzyme, productively bound enzyme, and the products, respectively. ν is the number of processive movements before the enzyme leaves from the cellulose surface. Note that we define the completion of productive binding when a cellulose chain is fully accommodated into the end of the tunnel in CD of the cellulase, simultaneously hydrolyzed and yielding a single cellobiose molecule [7]. Also, we assumed that the transition from non-productive binding to productive binding is reversible, given that this process is driven by the gradient of the potential energy, which could be perturbated by thermal fluctuations [23]. The following relationships hold, where E₀ is the total amount of enzyme in the reaction mixture:

$$E_s+E_{\mathit{np}}+E_p=E_0$$ (1)

$${\dot{E}}_{\mathit{np}}=k_1{E}_s+k_{-2}{E}_p-k_{-1}{E}_{\mathit{np}}-k_2{E}_{\mathit{np}}$$ (2)

$${\dot{E}}_p=k_2{E}_{\mathit{np}}-(k_{-2}+k_3)E_p$$ (3)

$$\dot{P}=k_2{E}_{\mathit{np}}+\nu k_3{E}_p$$ (4)

Note that in Eq. (2), the term for the transition from productive to non-productive binding was denoted as k₋₂E_p instead of k₋₂E_pP because this process only involves mechanical detachment and does not require the hydrolyzed cellobiose molecule. From Eqs. (1) and (2), and (1) and (3), we obtain the following relationships:

$$\begin{array}{c}{\dot{E}}_{\mathit{np}}=k_1(E_0{-E}_p-E_{\mathit{np}})+k_{-2}{E}_p-(k_{-1}+k_2)E_{\mathit{np}}\\ \phantom{E_{np}}=k_1{E}_0-\left(k_1-k_{-2}\right)E_p-(k_1+k_{-1}+k_2)E_{\mathit{np}}\hfill \end{array}$$ (5)

$${\dot{E}}_p=k_2{E}_{\mathit{np}}-(k_{-2}+k_3)E_p$$ (6)

The following relationships are defined:

$$k_1{E}_0\equiv C_1$$

$$\left(k_1-k_{-2}\right)\equiv C_2$$

$$k_1+k_{-1}+k_2\equiv C_3$$

$$k_2\equiv C_4$$

$$k_{-2}+k_3\equiv C_5$$

$$E_{\mathit{np}}\equiv x$$

$$E_p\equiv y$$

$$\dot{x}=C_1-C_{2}y-C_{3}x$$ (7)

$$\dot{y}=C_{4}x-C_{5}y$$ (8)

From Eqs. (7) and (8),

$$\begin{array}{c}\ddot{x}={-C}_2\dot{y}-C_3\dot{x}\hfill \\ \phantom{x}={-C}_2(C_{4}x-C_{5}y)-C_3\dot{x}\hfill \\ \phantom{x}={{-C}_{2}C}_{4}x+C_5(-\dot{x}{-C}_{3}x+C_1)-C_3\dot{x}\hfill \end{array}$$

$$\ddot{x}+\left(C_3+C_5\right)\dot{x}+\left(C_2{C}_4+C_3{C}_5\right)x-C_1{C}_5=0$$

$$\ddot{x}+\left(C_3+C_5\right)\dot{x}+\left(C_2{C}_4+C_3{C}_5\right)\left(x-\frac{C_1{C}_5}{C_2{C}_4+C_3{C}_5}\right)=0$$

Simplifying, we have

$$x-\frac{C_1{C}_5}{C_2{C}_4+C_3{C}_5}\equiv X$$

$$\ddot{X}+\left(C_3+C_5\right)\dot{X}+\left(C_2{C}_4+C_3{C}_5\right)X=0$$ (9)

The eigenvalues of this second-order linear differential equation λ₁ and λ₂ are obtained as follows:

$${\lambda }_1+{\lambda }_2=-\left(C_3+C_5\right)$$

$${\lambda }_1{\lambda }_2=\left(C_2{C}_4+C_3{C}_5\right)$$

$$\begin{array}{c}{\lambda }_1,{\lambda }_2=\frac{-\left(C_3+C_5\right)\pm \sqrt{{\left(C_3+C_5\right)}^2-4\left({C_{2}C}_4+C_3{C}_5\right)}}{2}\hfill \\ \phantom{{\lambda }_1,{\lambda }_2}=\frac{-\left(k_1+k_{-1}+k_2+k_{-2}+k_3\right)\pm \sqrt{{\left(k_1+k_{-1}+k_2+k_{-2}+k_3\right)}^2-4\left(k_1{k}_2+{k_{1}k}_{-2}+k_1{k}_3+k_{-1}{k}_{-2}+k_{-1}{k}_3+k_2{k}_3\right)}}{2}\hfill \end{array}$$

Given that E_s is generally much larger than E_np and E_p (since only cellulases near the surface of cellulose contribute to the reaction), in the situation where k₁ < k₋₂ (i.e., C₂ < 0), both λ₁ and λ₂ become negative real numbers. This was confirmed by fitting to actual data as described later.

Thus, the solution of the differential Eq. (9) can be expressed as

$$X={\omega }_1{e}^{{\lambda }_{1}t}+{\omega }_2{e}^{{\lambda }_{2}t},$$

and thus, we obtain

$$x={\omega }_1{e}^{{\lambda }_{1}t}+{\omega }_2{e}^{{\lambda }_{2}t}+\frac{\left(k_1{k}_{-2}+{k_{1}k}_3\right)E_0}{k_1{k}_2+{k_{1}k}_{-2}+k_1{k}_3+k_{-1}{k}_{-2}+k_{-1}{k}_3+k_2{k}_3}$$ (10)

where ω₁ and ω₂ are constants satisfying the following relationships derived from x(0)=0

and $\dot{x}$(0)=k₁E₀ , respectively:

$${\omega }_1+{\omega }_2=-\frac{\left(k_1{k}_{-2}+{k_{1}k}_3\right)E_0}{k_1{k}_2+{k_{1}k}_{-2}+k_1{k}_3+k_{-1}{k}_{-2}+k_{-1}{k}_3+k_2{k}_3}$$

$${\lambda }_1{\omega }_1+{\lambda }_2{\omega }_2=k_1{E}_0$$

Similar equations for y can also be derived from Eqs. (7) and (8):

$$\begin{array}{c}\ddot{y}=C_4\dot{x}-C_5\dot{y}\hfill \\ \phantom{\ddot{y}}=C_4(C_1-C_{2}y-C_{3}x)-C_5\dot{y}\hfill \\ \phantom{\ddot{y}}={C_{1}C}_4-C_2{C}_{4}y-C_3(\dot{y}+C_{5}y)-C_5\dot{y}\hfill \end{array}$$

$$\ddot{y}+\left(C_3+C_5\right)\dot{y}+\left(C_2{C}_4+C_3{C}_5\right)y-C_1{C}_4=0$$

$$\ddot{y}+\left(C_3+C_5\right)\dot{y}+\left(C_2{C}_4+C_3{C}_5\right)\left(y-\frac{C_1{C}_4}{C_2{C}_4+C_3{C}_5}\right)=0$$

Simplifying, we have

$$y-\frac{C_1{C}_4}{C_2{C}_4+C_3{C}_5}\equiv Y$$

$$\ddot{Y}+\left(C_3+C_5\right)\dot{Y}+\left(C_2{C}_4+C_3{C}_5\right)Y=0$$ (11)

Since Eq. (11) is similar to (9),

$$Y={\omega }_3{e}^{{\lambda }_{1}t}+{\omega }_4{e}^{{\lambda }_{2}t}$$

$$y={\omega }_3{e}^{{\lambda }_{1}t}+{\omega }_4{e}^{{\lambda }_{2}t}+\frac{k_1{k}_2{E}_0}{k_1{k}_2+{k_{1}k}_{-2}+k_1{k}_3+k_{-1}{k}_{-2}+k_{-1}{k}_3+k_2{k}_3}$$ (12)

where ω₃ and ω₄ are constants satisfying the following relationships derived from $\dot{y}$(0) = 0 and y(0) = 0, respectively:

$${\omega }_3+{\omega }_4=-\frac{k_1{k}_2{E}_0}{k_1{k}_2+{k_{1}k}_{-2}+k_1{k}_3+k_{-1}{k}_{-2}+k_{-1}{k}_3+k_2{k}_3}$$

$${\lambda }_1{\omega }_3+{\lambda }_2{\omega }_4=0$$

Finally, a differential equation for P is derived from Eqs. (4), (10) and (12);

$$\begin{array}{c}\frac{\mathit{dP}}{\mathit{dt}}=k_{2}x+{\mathit{\nu k}}_{3}y\hfill \\ \phantom{\frac{\mathit{dP}}{\mathit{dt}}}=k_2\left({\omega }_1{e}^{{\lambda }_{1}t}+{\omega }_2{e}^{{\lambda }_{2}t}+{\xi }_x\right)+{\mathit{\nu k}}_3\left({\omega }_3{e}^{{\lambda }_{1}t}+{\omega }_4{e}^{{\lambda }_{2}t}+{\xi }_y\right)\hfill \\ \phantom{\frac{\mathit{dP}}{\mathit{dt}}}=\left({k_2\omega }_1+{{\mathit{\nu k}}_3\omega }_3\right)e^{{\lambda }_{1}t}+\left({k_2\omega }_2+{{\mathit{\nu k}}_3\omega }_4\right)e^{{\lambda }_{2}t}+{k_2\xi }_x+{{\mathit{\nu k}}_3\xi }_y\hfill \end{array}$$

where

$${\xi }_x=\frac{\left(k_1{k}_{-2}+{k_{1}k}_3\right)E_0}{k_1{k}_2+{k_{1}k}_{-2}+k_1{k}_3+k_{-1}{k}_{-2}+k_{-1}{k}_3+k_2{k}_3}$$

$${\xi }_y=\frac{k_1{k}_2{E}_0}{k_1{k}_2+{k_{1}k}_{-2}+k_1{k}_3+k_{-1}{k}_{-2}+k_{-1}{k}_3+k_2{k}_3}$$

The equation is then integrated as

$$\int \frac{\mathit{dP}}{\mathit{dt}}\cdot \mathit{dt}=\frac{{\mu }_1}{{\lambda }_1}{e}^{{\lambda }_{1}t}+\frac{{\mu }_2}{{\lambda }_2}{e}^{{\lambda }_{2}t}+{\mu }_{3}t+C_p$$

where

$${\mu }_1={k_2\omega }_1+{{\mathit{\nu k}}_3\omega }_3$$

$${\mu }_2={k_2\omega }_2+{{\mathit{\nu k}}_3\omega }_4$$

$${\mu }_3={k_2\xi }_x+{{\mathit{\nu k}}_3\xi }_y$$

and C_p is a constant,

Using the initial condition, P(t=0)=0,

$$\begin{array}{c}P=-\frac{{\mu }_1}{{\lambda }_1}\left(1-e^{{\lambda }_{1}t}\right)-\frac{{\mu }_2}{{\lambda }_2}\left({1-e}^{{\lambda }_{2}t}\right)+{\mu }_{3}t\hfill \\ \phantom{P}=-\frac{{k_2\omega }_1+{{\mathit{\nu k}}_3\omega }_3}{{\lambda }_1}\left(1-e^{{\lambda }_{1}t}\right)-\frac{{k_2\omega }_2+{{\mathit{\nu k}}_3\omega }_4}{{\lambda }_2}\left({1-e}^{{\lambda }_{2}t}\right)+\frac{k_1{k}_2{k}_{-2}+{k_1{k}_{2}k}_3\left(1+\nu \right)}{k_1{k}_2+{k_{1}k}_{-2}+k_1{k}_3+k_{-1}{k}_{-2}+k_{-1}{k}_3+k_2{k}_3}{E}_{0}t\hfill \end{array}$$ (13)

Therefore, Eq. (13) can be simplified into the following double-exponential form with a linear term as follows:

$$P\left(t\right)=\frac{a}{b}\left(1-e^{\mathit{bt}}\right)+\frac{c}{d}\left({1-e}^{\mathit{dt}}\right)+f{E}_{0}t$$ (14)

where b < 0, d < 0 and f > 0.

In the derivation of Eq. (14), there is no assumption that heterogeneity, i.e. amorphous or crystalline form of cellulose, or involvement of other enzymes such as EGs and CBHs plays a role. Instead, the double exponential equation simply arises from the reaction mechanism of single enzyme. However, we should point out that this does not exclude contributions of other factors such as those mentioned above. Nevertheless, a double exponential equation can be expected simply on the basis of the substrate/enzyme combination alone.

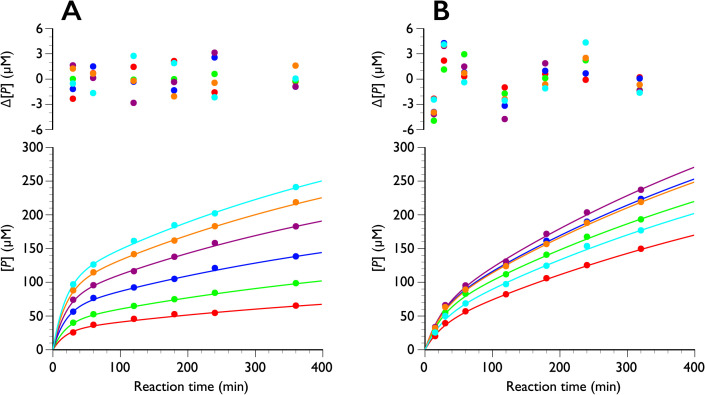
The progress curves of PcCel6A and TrCel7A were then re-analyzed using global fitting together with Eq. (14). Global fitting has recently been utilized to analyze enzyme kinetics because multiple parameters are optimized at once by non-linear regression. When the famous Michaelis-Menten study of sucrose hydrolysis by sucrase (invertase) was re-analyzed using this technique [24], it became apparent that substrate inhibition had not been considered in the initial kinetic study by Michaelis and Menten [25]. Moreover, we have applied global fitting to the complicated substrate loading system in processive cellulases [26]. Thus, global fitting is a powerful tool when multiple parameters must be considered. Since λ₁ and λ₂ (b and d in Eq. (14), respectively) are usually treated as rate constants and they do not include enzyme concentration (E₀), these parameters were fixed at all enzyme concentrations tested, and other parameters were simulated from the data of PcCel6A [22] and TrCel7A [6] using Eq. (14) as shown in Fig. 2. The obtained parameters are listed in Tables 1, 2, 3.

Fig. 2. Time course of product formation from crystalline cellulose I_α at 30 ˚C.

　The progress curves of PcCel6A (A) and TrCel7A (B) were globally fitted to Eq. (14). The residue values between the experimental data and the curve fitting are shown above the plots. Red, green, blue, purple, orange and cyan are 0.25, 0.51, 1.0, 2.2, 5.4, and 8.9 μM for PcCel6A in (A), and 0.40, 0.84, 1.3, 2.2, 4.3, and 8.6 μM for TrCel7A in (B), respectively.

Table 1. Parameters of crystalline cellulose hydrolysis by PcCel6A estimated using global fitting.

E 0	a	b	c	d	a/b	c/d
(μM)		(=λ1)		(=λ2)
0.25	−1.55±0.12	−0.0541	−0.136±0.015	−0.00180	28.6±2.0	75.5±11.0
0.51	−2.21±0.14	±0.0040	−0.215±0.021	±0.00037	40.8±2.3	120±16
1.0	−3.23±0.18		−0.297±0.027		59.6±2.8	165±21
2.2	−4.01±0.20		−0.410±0.035		74.0±3.4	228±29
5.4	−4.84±0.24		−0.478±0.041		89.4±3.8	265±34
8.9	−5.47±0.27		−0.525±0.045		101±4	291±37

Table 2. Parameters of crystalline cellulose hydrolysis by TrCel7A estimated using global fitting without f in Eq. (14).

E 0	a	b	c	d	a/b	c/d
(μM)		(=λ1)		(=λ2)
0.40	−1.33±0.14	−0.0412	−0.455±0.053	−0.00146	32.2±5.1	311±81
0.84	−2.13±0.16	±0.0062	−0.556±0.066	±0.00053	51.6±6.5	381±97
1.3	−2.33±0.17		−0.650±0.076		56.5±7.2	445±114
2.2	−2.35±0.17		−0.705±0.081		57.1±7.5	484±124
4.3	−2.28±0.17		−0.638±0.075		55.5±7.1	437±112
8.6	−1.68±0.15		−0.533±0.062		40.7±5.8	365±95

Table 3. Parameters of crystalline cellulose hydrolysis by TrCel7A estimated using global fitting including f in Eq. (14).

E 0	a	b	c	d	f	a/b	c/d
(μM)		(=λ1)		(=λ2)
0.40	−1.31±0.15	−0.0413	−0.459±0.057	−0.00158	0.0108	31.7±5.4	291±87
0.84	−2.11±0.17	±0.0063	−0.555±0.071	±0.00064	±0.0291	51.1±6.8	353±109
1.3	−2.31±0.18		−0.644±0.084			56.0±7.5	409±131
2.2	−2.34±0.18		−0.689±0.101			56.7±7.7	437±153
4.3	−2.23±0.17		−0.590±0.158			55.5±7.2	375±177
8.6	−1.73±0.21		−0.422±0.316			41.8±6.8	268±251

As shown in Fig. 2, the progress curves of both enzymes are well fitted by the equation. In the case of PcCel6A, all progress curves at various enzyme concentrations (0.25 to 8.9 μM) were well fitted by Eq. (14) and the f-value converged to almost 0 (<10⁻¹⁸). Therefore, the parameters were obtained using f = 0. From Eq. (13), this assumption implies that k₂, the rate of forming a productive binding, is significantly smaller than k₁ and k₃, which is reasonable considering the limited access to the reaction. On the other hand, progress curves of TrCel7A seem to include an f-value, though the errors of each parameter were large, especially for the second exponential term, c and c/d, possibly because the second exponential term and linear term are quite similar to each other. Therefore, we also analyzed the data using Eq. (14) without f (i.e., f=0) for TrCel7A. The rate constants of the two enzymes are rather similar, though that of PcCel6A is slightly faster, in agreement with reported data.

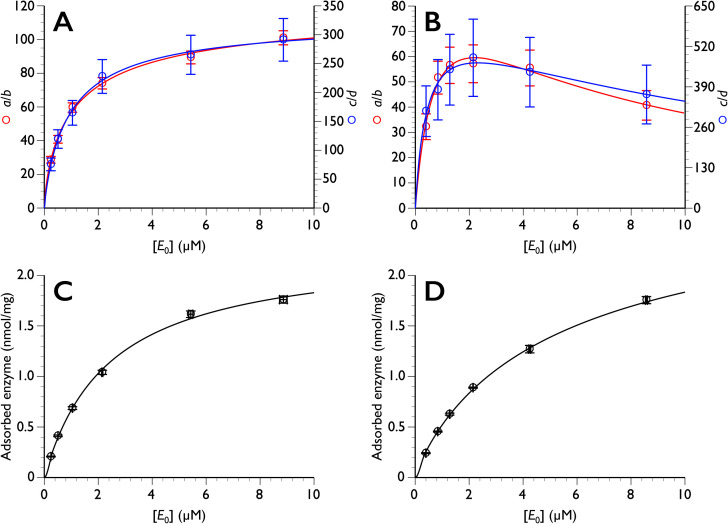
However, the enzyme concentration dependence of the amplitudes of the exponential terms, a/b and c/d values, are very different from each other. As shown in Fig. 3, the enzyme concentration dependence of both a/b and c/d was hyperbolic in the case of PcCel6A, while that of TrCel7A decreased with increasing enzyme concentration, which is similar to a typical substrate inhibition curve [27, 28, 29]. In a previous kinetic study of TrCel7A, we proposed possible crowding effects, and our hypothesis has been confirmed by biophysical HS-AFM and simulation studies [30]. Indeed, HS-AFM examination of processivity [15] indicated that the velocity of processive cellulase tends to decrease with increasing concentration of the enzyme, due to a “traffic jam” effect [13]. When we look at the construction of Eq. (14), most of the parameters except for λ₁ and λ₂ are dependent on E₀, and it is difficult to clarify the relationship between each parameter and E₀. However, it is clear that a/b and c/d are highly dependent on the amount of adsorbed enzyme, indicating that it is important to distinguish productive and non-productive adsorption.

Fig. 3. The enzyme concentration dependence of both a/b and c/d.

　Top: enzyme concentration (E₀) dependence of a/b and c/d for PcCel6A (A) and TrCel7A (B). Bottom: amount of adsorbed enzyme plotted versus E₀ for PcCel6A (C) and TrCel7A (D). The data in A, C, and D were fitted to typical hyperbolic curve (y = (a×x) / (b+x) where a and b are constants) while inhibition is considered (y = (a×x) /{b+x+(x²/c)｝ where a, b and c are constants) in B. Note that the E₀ dependence of adsorption (C and D) does not correspond to a typical Langmuir plot of E_S versus adsorbed enzyme.

In this paper, we modeled the formation of a productive binding event with the assumption that one product is generated. Even if we adopted the formulation including this term in the processive reaction, the conclusion that the time course of the product follows a double exponential form remains valid. This is because, in this case, the first term on the right side of Eq. (4) would be eliminated, making P dependent solely on E_p, which itself has a double exponential form.

So far, progress curves of cellulase have been fitted conventionally by a single or double exponential equation, or a single exponential equation with a linear function [6, 11]. Equation (14) includes all terms in those equations, and therefore curve-fitting with this equation is reasonable. Looking at the Eq. (13), however, several values, such as λ and ω, remain undetermined because the experimental data is not accurate enough. Nevertheless, it should be possible to estimate them individually, for example, by adsorption experiments for k₁/k₋₁ ratio, pre-steady-state kinetics for k₂/k₋₂, processivity measurement by HS-AFM for ν, and so on. Recently we succeeded in simulating approximately 100 million cellulase molecules using a customized traffic simulator and demonstrated that consideration of the dual domain structure of cellulase is indispensable to explain the gap between single-molecule behavior and bulk biochemical results [30]. In the simulation study, we defined the parameters for adsorption, non-productive and productive enzymes, and processivity, and the obtained progress curve fitted well to the actual biochemical plots, supporting the idea that theoretical and simulated approaches can give insight into real biophysical and biochemical observations.

In conclusion, we have constructed a mechanism-based equation that for the first time provides a theoretical basis for the double-exponential character of the progress curve of cellulase reaction. Thus, it is not necessary to consider the heterogeneity of the substrate or the involvement of multiple enzymes in order to explain the double-exponential nature of the progress curve, although we cannot rule out a contribution of such effects. We believe this work represents an important step towards understanding the actual saccharification of cellulosic biomasses. Furthermore, since the developed equation describes a model consisting of a simple enzymatic reaction at a solid/liquid interface, a similar approach may be appliable to many other enzymatic reactions involving insoluble substrates. The origin of the double exponential time course lies in a two-step reaction process involving long timescale equilibration. While such a form can arise in general two-step enzyme reactions, if the relaxation rates of each process are sufficiently fast, the behavior would effectively follow a single exponential.

CONFLICTS OF INTEREST

The authors declare no conflict of interests.