Abstract

We discuss the prospects for accurate 11B magic-angle-spinning (MAS) nuclear magnetic resonance (NMR) spectral deconvolutions for reaching beyond the readily extracted borate speciations offered by the integrated resonances of the coexisting B[3] and B[4] species of the respective BO3 and BO4 network groups in borosilicate (BS) glasses. We critically review hitherto proposed 11B[3] and 11B[4] NMR-peak assignments relating to their neighboring Si, B[3] and B[4] species, as quantified by MAS NMR spectral deconvolution. Guidance to these resonance assignments was offered from double-quantum–single-quantum (2Q–1Q) 11B MAS NMR experiments that inform about the B[p]–O–B[q] network linkages. The NMR spectral deconvolutions from two BS glass series with low nonbridging oxygen (NBO) contents and fixed molar ratios nSi/nB = {1.0, 2.0} but variable network-modifying cations of alkali metals and Mg2+ revealed a dominance of B[4]–O–Si linkages, yet with a significant dependence on the BO3 population of the glass, which was rationalized by the different propensities for B[4]–O–{Si, B[3], B[4]} linkage formation. For BS glasses with comparable B and Si contents, we recommend three-peak deconvolutions of the 11B[4] spectral region, whose 11B[4](mSi) sites differ in their (average) numbers of m B[4]–O–Si and 4 – m B[4]–O–B[p] bonds, where B[p] may assume B[3]or B[4]. We also discuss the structural origin of the two rather arbitrarily classified “ring” and “non-ring” B[3] entities, where 2Q–1Q 11B NMR suggests the former to primarily constitute BO3 groups that coexist with BO4 moieties in (superstructural) ring units largely devoid of bonds to Si, whereas the “non-ring” B[3] sites involve linkages to all of B[3], B[4], and Si, with B[3]–O–Si linkages prevailing. The limitations of 11B NMR spectral deconvolutions are discussed, including the remaining challenges in analyzing NBO-rich BS glasses.
1. Introduction
Borosilicate (BS) glasses constitute networks of SiO4, BO3, and BO4 polyhedra that are interlinked by bridging oxygen (BO) atoms between the network-forming (F) species F = {B[3], B[4], Si ≡ Si[4]}, where the superscript denotes the coordination number with respect to O. The B[3] and B[4] populations of a B-bearing glass depend strongly on the precise glass composition,1−4 in particular on the amounts of electropositive Mz+ cations, whose incorporation into a silicate/phosphate glass breaks up its network by converting BO atoms into nonbridging O (NBO; O–) anions, but for a BS glass also altering its borate speciation,1−4 and thereby the physical glass properties.5−11 Hence, there is a long-standing interest in characterizing not only the B[3]/B[4] populations but also their B[p]–O–F bonding partners. For a clear-cut discrimination between the structural Mz+ and F entities, we employ the old “network modifier” term when referring to the M+/M2+ cations.
The two most widely applied routine techniques for probing the local B environments in BS-based glasses, encompassing those with additional network formers (such as Al and P), are Raman11−17 and 11B nuclear magnetic resonance (NMR) spectroscopy,6,10,17−43 the latter nowadays normally performed under magic-angle-spinning (MAS) conditions.2−4 Both methods are complementary and have inherent (dis)advantages. The Raman vibrations are sensitive to network-group aggregates, referred to as “superstructural units”1,44,45 (Section 3.2), whereas the 11B central-transition (CT) MAS NMR spectral region readily permits discrimination and accurate quantification of the two B[3]/B[4] coordinations.2−4 However, both Raman and 11B NMR spectra manifest insufficient spectral resolution and assignment ambiguities. Raman spectral resolution is compromised for all but the simplest M2O–B2O3 glasses,13,16,45 which complicates unambiguous spectral interpretations, which is also reflected in Raman band reassignments over time.13−16,45
Likewise, reaching beyond {B[3], B[4]} speciation quantifications of BS glasses is nontrivial by routine 11B MAS NMR experiments, owing to the structural disorder that disperses the 11B[3] and 11B[4] chemical shifts and smears out the spectral responses, which, besides distributions of interpolyhedral bond angles and B[p]–O distances, stem both from variable numbers of B[p]–O–{B[3], B[4], Si} linkages and the BO/NBO distribution at the BO3 groups.2−4 Following pioneering multinuclear MAS NMR studies on the network-group intermixing,17,21−23,25−27,46−48 it is nowadays standard practice to attempt extracting more detailed information about the local 11B[3] and 11B[4] environments from a BS glass by deconvoluting its 11B CT NMR spectral region.25−34,37−39,49 For the B[4] ensemble, such analyses aim at quantifying the relative populations of B[4](mSi) ≡ 11B[4](OSi)m(OB)4–m motifs with m Si and 4 – m B neighbors, whose resonances overlap heavily across the narrow 11B[4] CT MAS NMR region. Precise 11B[3] resonance assignments are even more challenging, where two resonances are traditionally attributed to “ring” (R) and “non-ring” (NR) 11B[3] sites in BS-based glasses,25−34,37−39,49,50 yet without any widespread consensus of their precise structural meaning because the R/NR concept originates from the much simpler case of vitreous B2O3,51−54 whose BO3-built structure presents no complexities from Si, B[4], and NBO species.
Given the ambiguities of 11B MAS NMR spectral deconvolutions for gaining more detailed structural information about B[p]–O–F motifs, an attractive alternative is to exploit the magnetic 11B–29Si dipolar interaction, which is mediated directly through space and scales as the inverse cube of the 11B–29Si distance.3,55 Advanced NMR experimentation relying on such heteronuclear dipolar interactions offers interconnectivity information on BS-based glass networks,30,33,40,56−60 and may also assist 11B[4](mSi) NMR-peak assignments.30,33 However, probing of the B/Si intermixing in BS glasses via 11B–29Si dipolar interactions remains sparse, mainly because high-quality NMR data enabling quantitative analyses are normally precluded by the low natural abundance of the NMR-active 29Si isotope (4.7%), necessitating glass preparation from very expensive 29SiO2.33,40,58 Another option for gaining B/Si interconnectivity information is 17O triple-quantum MAS61 (3QMAS),24−27,35,36,62−66 which, besides requiring costly isotopic 17O enrichment, may not unambiguously discriminate between the two p = {3, 4} coordinations of B[p]–O–Si and B[p]–O–B[q] linkages (although such B[p] assignments have been claimed from multipeak fitting25−27,63).
Following our recent work on the identification and quantification of borate-group linkages in BS-based glasses,41,67,68 by utilizing the homonuclear 11B–11B interactions in double-quantum–single-quantum (2Q–1Q) correlation 11B NMR experiments,69−72 we here investigate to what extent they may assist resonance assignments of routinely acquired “single-pulse” (Bloch-decay) 11B MAS NMR spectra. The 1D analog of a 2Q–1Q 2D NMR acquisition resulting from solely employing the t1 = 0 data point is termed a double-quantum filtration (2QF) NMR experiment,71,72 yielding the projection along the horizontal 2D NMR spectral dimension. Although not revealing the detailed B[3]–O–B[3], B[3]–O–B[4], and B[4]–O–B[4] linkages from a B-bearing glass, its recording is at least 101 times shorter than arranging the 2D NMR spectrum.71,72 The 2QF NMR spectrum only comprises resonances from 11B[p] sites featuring at least one B[p]–O–B[q] linkage, whose intensities emphasize concurrently with the number of B[p](OB) bonds. In contrast, all 11B NMR signals from (for instance) B[4](OSi)4, B[3](OSi)3, and B[3](OSi)2 NBO sites are absent, despite that they appear in the standard Bloch-decay MAS NMR spectrum. Notwithstanding that 11B/29Si-based NMR has a decisive advantage of directly informing about B[p]–O–Si interconnectivities, 2QF 11B NMR experimentation is readily applied to any glass prepared from inexpensive oxide precursors (thanks to the high 11B natural abundance of 80%), while the receptivity of the 11B nuclide is superior relative to both 29Si and 17O.2−4
Herein, 11B MAS NMR spectra recorded from nine BS glass specimens (Section 2) in the presence and absence of 2QF were deconvoluted. They constitute a subset of a large ensemble of ternary M2O–B2O3–SiO2 and quaternary M(2)O–Na2O–B2O3–SiO2 glasses with variable B, Si, and NBO contents,10 for which several physical properties were reported and their composition–property relationships discussed,10 along with their borate-group interconnectivities.68 Besides two Mg-bearing specimens, all glasses herein are alkali-metal based, furnishing two series with fixed molar ratios of nSi/nB = 1.0 and nSi/nB = 2.0, while exhibiting (very) low NBO contents, which, besides simplifying 11B NMR spectral deconvolutions, conform to the mainstream BS-glass composition range targeted in previous 11B NMR spectral deconvolutions.25−33
2. Materials and Methods
2.1. Present Borosilicate Glasses
Table 1 presents the nominal compositions of the 9 BS glasses targeted herein, which are expressed both as their oxide equivalents and the sets of atomic fractions of each element E in the M–(Na)–B–Si–O glass,
| 1 |
where nE is the corresponding stoichiometric amount. We employ the {K, R} parameters
| 2 |
| 3 |
generalized from the definitions introduced by Bray and co-workers for RNa2O–B2O3–KSiO2 glasses.19,20 The glass specimens exhibit a fixed R = 0.75 value along with either K = 2.0 or K = 4.0. Each ternary 0.75Na2O–B2O3–KSiO2 and 0.75K2O–B2O3–KSiO2 glass is denoted by NaK and KK, respectively, whereas each quaternary 0.75[0.5M(2)O–0.5Na2O]–B2O3–KSiO2 member is labeled MNaK with Mz+ = {Rb+, Li, Mg2+}.
Table 1. Borosilicate Glass Compositions and Borate Speciationsa.
| Oxide Equivalents (mol %) |
Atomic Fractions |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Glass | M(2)O | Na2O | B2O3 | SiO2 | xM | xNa | xB | xSi | xO |  |
xNBO |
| K2.0 | 20.0 | 26.7 | 53.3 | 0.114 | 0.151 | 0.151 | 0.584 | 0.628 | 0.031 | ||
| RbNa2.0 | 10.0 | 10.0 | 26.7 | 53.3 | 0.057 | 0.057 | 0.151 | 0.151 | 0.584 | 0.603 | 0.038 |
| Na2.0 | 20.0 | 26.7 | 53.3 | 0.114 | 0.151 | 0.151 | 0.584 | 0.604 | 0.038 | ||
| LiNa2.0 | 10.0 | 10.0 | 26.7 | 53.3 | 0.057 | 0.057 | 0.151 | 0.151 | 0.584 | 0.563 | 0.048 |
| MgNa2.0 | 10.0 | 10.0 | 26.7 | 53.3 | 0.029 | 0.058 | 0.155 | 0.155 | 0.603 | 0.361 | 0.100 |
| K4.0 | 13.0 | 17.4 | 69.6 | 0.078 | 0.104 | 0.208 | 0.610 | 0.681 | 0.012 | ||
| RbNa4.0 | 6.5 | 6.5 | 17.4 | 69.6 | 0.039 | 0.039 | 0.104 | 0.208 | 0.610 | 0.651 | 0.017 |
| Na4.0 | 13.0 | 17.4 | 69.6 | 0.078 | 0.104 | 0.208 | 0.610 | 0.618 | 0.022 | ||
| MgNa4.0 | 6.5 | 6.5 | 17.4 | 69.6 | 0.020 | 0.040 | 0.106 | 0.212 | 0.622 | 0.313 | 0.074 |
Nominal compositions of ternary
0.75M2O–B2O3–KSiO2 glasses—denoted
by MK—and quaternary 0.75[0.5M(2)O–0.5Na2O]–B2O3–KSiO2 glasses—denoted
by MNaK, along with the corresponding
atomic fractions {xM, xNa, xB, xSi, xO} given by Equation 1. 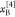 (uncertainty ±0.01) and xNBO (uncertainty ±0.01) represent the 11B NMR-derived fractional population of B[4] coordinations
and NBO species, respectively. The
(uncertainty ±0.01) and xNBO (uncertainty ±0.01) represent the 11B NMR-derived fractional population of B[4] coordinations
and NBO species, respectively. The 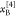 values were obtained from the integrated 11B[p] NMR intensities of the Bloch-decay
NMR spectra and were corrected for the signal intensity of the satellite-transition
centerband (Section 2.3), whereas the NBO fraction was calculated from the expression
values were obtained from the integrated 11B[p] NMR intensities of the Bloch-decay
NMR spectra and were corrected for the signal intensity of the satellite-transition
centerband (Section 2.3), whereas the NBO fraction was calculated from the expression 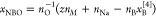 .
.
The borate speciation of a BS glass depends strongly on the Mz+cation field strength (CFS),73
| 4 |
where rO = 1.36
Å73 and rM is the cation radius for the (as-assumed) 6-fold
coordination (M[6]) with charge z.74 All figures/tables herein
list the specimens within each K = {2.0, 4.0} series
from top to bottom according to increasing averageMz+/Na+ CFS: 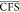 = (CFSM + CFSNa)/2, whose values are listed in Table S1.
= (CFSM + CFSNa)/2, whose values are listed in Table S1.
Table 1 also presents
the 11B MAS NMR-derived fractional population of B[4] coordinations (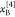 ) out of the entire borate speciation of
the glass; the remaining constitutes B[3] species, whose
respective population (
) out of the entire borate speciation of
the glass; the remaining constitutes B[3] species, whose
respective population (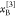 ) is obtained from the normalization condition
) is obtained from the normalization condition
| 5 |
All glass networks but those of the two Mg-bearing
glasses are dominated by BO4 groups. From each 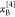 value, the fractional population of NBO
anions (O[1] coordinations) out of all NBO and BO (O[2]) species was extracted via
value, the fractional population of NBO
anions (O[1] coordinations) out of all NBO and BO (O[2]) species was extracted via  ,10,68 where xBO + xNBO = 1. The NBO fractions
are listed in Table 1.
,10,68 where xBO + xNBO = 1. The NBO fractions
are listed in Table 1.
2.2. Glass Preparation
All BS glass preparation and characterization procedures were identical to those reported previously by Lv et al.,10,38,68 to which we refer for details. The samples were prepared in batches of 5–8 g by melt-quenching from analytical grade (purity 99.9%+) precursors of SiO2, H3BO3, and anhydrous carbonates of the metal cations, except for Mg2+ which was introduced from MgO. After preheating at 950 °C for 24 h to remove potential OH/H2O contaminations of the SiO2 powder, the precursors were mixed thoroughly and subsequently decarbonated in a Pt crucible at 950 °C for 2 h, before heating up to the final temperature in the 1125–1275 °C range, where precise temperatures are given in ref (10). The melt was kept for 20–30 min and then quenched by immersing the crucible bottom in cold water. All glass specimens were free of crystalline impurities. From the NMR-analyzed B contents and negligible mass losses during heating, we concluded that all nominal stoichiometries listed in Table 1 are very close to the “physical” glass compositions,10,68 as confirmed by elemental analyses of all K = 4.0 glasses.38
2.3. Solid-State NMR Experiments
All 11B (spin-3/2) NMR experiments were performed with a Bruker Avance-III spectrometer at a magnetic field (B0) of 14.1 T (−192.5 MHz 11B Larmor frequency) using 3.2 mm zirconia rotors undergoing MAS at 24.00 kHz. Neat BF3·OEt2 was used for 11B shift referencing and for determining 11B nutation frequencies (νB).
The {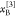 ,
,  } values of each glass were estimated from
the integrated signal intensities of 11B MAS NMR spectra
recorded by strong/short radio frequency (rf) pulses (0.33 μs;
13° flip angle; νB = 105 kHz), as reported and
discussed previously by Lv et al.10,68 The only difference
herein was the use of a larger zero filling of the time-domain data
to improve the as-acquired data of ref (68), yielding a spectral resolution of 0.038 ppm. 11B NMR probehead “background” signals were eliminated
by subtracting the NMR spectrum observed from the empty rotor under
otherwise identical experimental conditions (such artifacts are removed
identically by the 2QF process; vide infra). The
as-integrated 11B CT NMR signal intensities were corrected
for the satellite-transition (ST) centerband peak that overlaps with
the main CT 11B[4] signal by using standard
procedures.75
} values of each glass were estimated from
the integrated signal intensities of 11B MAS NMR spectra
recorded by strong/short radio frequency (rf) pulses (0.33 μs;
13° flip angle; νB = 105 kHz), as reported and
discussed previously by Lv et al.10,68 The only difference
herein was the use of a larger zero filling of the time-domain data
to improve the as-acquired data of ref (68), yielding a spectral resolution of 0.038 ppm. 11B NMR probehead “background” signals were eliminated
by subtracting the NMR spectrum observed from the empty rotor under
otherwise identical experimental conditions (such artifacts are removed
identically by the 2QF process; vide infra). The
as-integrated 11B CT NMR signal intensities were corrected
for the satellite-transition (ST) centerband peak that overlaps with
the main CT 11B[4] signal by using standard
procedures.75
The 2Q–1Q 11B NMR experiments utilized the rf-pulse
protocol of Figure 2d of Edén71 with one completed
90°-pulse-sandwiched SR212 dipolar recoupling sequence,70,76,77 for excitation of two-spin CT
2Q coherences (2QC), along with equal 2QC excitation/reconversion
intervals of τexc = 4τr = 167 μs, where 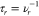 is the rotor period and νr is the spinning speed. The 11B–11B dipolar recoupling pulses operated at
is the rotor period and νr is the spinning speed. The 11B–11B dipolar recoupling pulses operated at  kHz, while the CT-selective 90° (16
μs) and 180° (32 μs) pulses employed
kHz, while the CT-selective 90° (16
μs) and 180° (32 μs) pulses employed 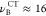 kHz. The t1-evolution stage of each 2Q–1Q 2D NMR spectrum was preceded
by a Hahn-echo of duration 2τr for
ensuring rotor-synchronized 2QC excitation and reconversion stages,70 with the CT-selective 180° pulse of the
echo segment cycled in 8 steps to eliminate all undesirable single-spin ST 2QC69 (ref (78) provides the shortest
rf-phase cycle enabling that task by a standard nested phase cycling79). 1536–3456 NMR-signal transients were
accumulated with relaxation delays of 1.5 s. All 2Q–1Q correlation 11B NMR spectra presented herein are reproduced from raw data
published by Lv et al.68
kHz. The t1-evolution stage of each 2Q–1Q 2D NMR spectrum was preceded
by a Hahn-echo of duration 2τr for
ensuring rotor-synchronized 2QC excitation and reconversion stages,70 with the CT-selective 180° pulse of the
echo segment cycled in 8 steps to eliminate all undesirable single-spin ST 2QC69 (ref (78) provides the shortest
rf-phase cycle enabling that task by a standard nested phase cycling79). 1536–3456 NMR-signal transients were
accumulated with relaxation delays of 1.5 s. All 2Q–1Q correlation 11B NMR spectra presented herein are reproduced from raw data
published by Lv et al.68
Figure 2.
A selection of 2Q–1Q correlation 11B NMR spectra recorded at 14.1 T and 24.00 kHz MAS from BS glasses featuring K = 2.0 (left panel) and K = 4.0 (right panel) with (a, b) K+, (c, d) Na+, and (e, f) Mg2+/Na+ as glass-network modifiers. Projections along the 2Q and 1Q dimensions of the 2D NMR spectra are displayed at the right and at the top, respectively, where each 1Q projection is shown together with its B[3](R) [green traces], B[3](NR) [cyan traces], and B[4](mSi) (red traces) peak components. The 2D NMR signals associated with each 11B[3]–O–11B[3], 11B[3]–O–11B[4], and 11B[4]–O–11B[4] linkage are indicated in (a). The vertical red and cyan dotted lines mark the 11B shift extension of the 11B[3]–O–11B[3] and 11B[4]–O–11B[4] autocorrelation signals extending along the diagonal of slope 2 (dotted line). The spectra are presented with the lowest contour level of ≈5 % of the maximum 2D NMR peak amplitude.
2.4. 11B MAS NMR Spectral Fitting
The 11B CT MAS NMR region observed in directly excited spectra and upon 2QF (i.e., the horizontal projection of the 2Q–1Q NMR spectrum) was deconvoluted into five 11B[p] NMR peaks for each glass: three components reflecting 11B[4](mSi) ≡ 11B[4](OSi)m(OB)4–m environments with m = {2, 3, 4}, along with two “B[3](R)” and “B[3](NR)” contributions from trigonal 11B sites in “ring” or “non-ring” constellations, respectively. The spectral deconvolutions utilized software developed in our laboratory to represent the 11B[3] and 11B[4] NMR peak shapes by numerically exact simulations80 and efficient powder averaging.81 All 11B[p] resonances were fitted with unconstrained populations, i.e., integrated intensities. The deconvolution of each unique NMR spectrum started from an initial fitting with unconstrained chemical shifts and quadrupolar parameters to locate reasonable ranges for subsequent parameter constraints.
The resulting best-fit parameters are collected in Table S2. Besides the two { (NR)} populations, the iterative fitting
of each 11B[3](R) and 11B[3](NR) resonance involved four parameters: {
(NR)} populations, the iterative fitting
of each 11B[3](R) and 11B[3](NR) resonance involved four parameters: { }. They encompass the quadrupolar
coupling constant,
}. They encompass the quadrupolar
coupling constant,  , the asymmetry parameter of the electric
field gradient (efg) tensor,
, the asymmetry parameter of the electric
field gradient (efg) tensor,  , and a Gaussian chemical-shift distribution with full width at half-maximum (fwhm) width
of
, and a Gaussian chemical-shift distribution with full width at half-maximum (fwhm) width
of 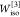 and centered at the isotropic chemical
shift
and centered at the isotropic chemical
shift .4 The chemical-shift
distribution of all 11B[3] and 11B[4] sites was confined to 2.4 ± 0.6 ppm.
.4 The chemical-shift
distribution of all 11B[3] and 11B[4] sites was confined to 2.4 ± 0.6 ppm. 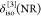 was restricted within 13.5–15.0
ppm, whereas
was restricted within 13.5–15.0
ppm, whereas 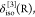
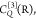
 and the accompanying asymmetry parameters
were unconstrained. Although the resulting best-fit
and the accompanying asymmetry parameters
were unconstrained. Although the resulting best-fit 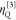 values conformed to 0.35 ± 0.1, reliable
and physically meaningful asymmetry parameters (distributions) are
not expected from these spectral deconvolutions.4 Consequently, we only give relevance to the quadrupolar
products (
values conformed to 0.35 ± 0.1, reliable
and physically meaningful asymmetry parameters (distributions) are
not expected from these spectral deconvolutions.4 Consequently, we only give relevance to the quadrupolar
products ( ) of each {11B[3](R), 11B[3](NR), 11B[4](mSi)} environment, defined as the root-mean-square (rms)
value over the quadrupolar products of all such N11B[p]j sites in the glass:4
) of each {11B[3](R), 11B[3](NR), 11B[4](mSi)} environment, defined as the root-mean-square (rms)
value over the quadrupolar products of all such N11B[p]j sites in the glass:4
| 6 |
Each of the three 11B[4](mSi) NMR-peak components with m = {2, 3, 4} was modeled
by the four parameters {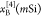 ,
, 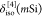 ,
,  ,
,  }, where the efg tensor-parameters assumed
a Czjzek distribution.82,83 The chemical shifts were constrained
to ±0.25 ppm. Initial numerical fitting of the 11B[4] NMR signal region without shift distributions
}, where the efg tensor-parameters assumed
a Czjzek distribution.82,83 The chemical shifts were constrained
to ±0.25 ppm. Initial numerical fitting of the 11B[4] NMR signal region without shift distributions  resulted in unreasonably large values
resulted in unreasonably large values  . Besides implying that the set
. Besides implying that the set 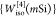 governs all peak widths, the very small
quadrupolar products could not be extracted by numerical fitting of
the present 11B NMR spectra recorded at 14.1 T. Hence,
based on previous rough assessments of
governs all peak widths, the very small
quadrupolar products could not be extracted by numerical fitting of
the present 11B NMR spectra recorded at 14.1 T. Hence,
based on previous rough assessments of  MHz,67 the values
were (rather arbitrarily) fixed according to
MHz,67 the values
were (rather arbitrarily) fixed according to 
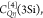
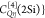 = {0.24, 0.31, 037} MHz, along with expectations
of a minor increase in quadrupolar products for decreasing symmetry
in the second coordination sphere of B[4].31 These findings also consolidate the most common approach
of representing each 11B[4](mSi) NMR peak by more readily implemented Gaussian (or Gaussian/Lorentzian)
curves,25,26,29,30,37,49,50,84 which we recommend also for future deconvolutions.
= {0.24, 0.31, 037} MHz, along with expectations
of a minor increase in quadrupolar products for decreasing symmetry
in the second coordination sphere of B[4].31 These findings also consolidate the most common approach
of representing each 11B[4](mSi) NMR peak by more readily implemented Gaussian (or Gaussian/Lorentzian)
curves,25,26,29,30,37,49,50,84 which we recommend also for future deconvolutions.
High-quality spectral deconvolutions resulted for all single-pulse 11B MAS NMR spectra by representing the net 11B[4] resonance by three peak components, which gave consistently better fits than the more common use of only two signals from the 11B[4](3Si) and 11B[4](4Si) sites (Sections 3.1 and 5.2). Although the resonance intensities of these NMR spectra quantitatively reflect the underlying site populations, these numerical multiparameter fits should not be taken too literally because the parameter uncertainties—estimated as the standard error of the rms deviation between the best fit and experiment—only reflect their as-assumed/selected number of peak components.
The numerical fitting of the 2Q–1Q NMR spectral projections
(2QF NMR spectra), however, left some unaccounted signal regions at
the outermost high/low ppm ranges of the respective 11B[3]/11B[4] resonance flanks, which are
essentially artifacts of the 2D NMR spectra. There are also more fundamental
obstacles compromising the determination of nuclear-site populations
by 2QF NMR experiments in the networks of amorphous inorganic materials,
notably so for quadrupolar nuclides,71,72 such as 11B. The fractional-population set of {B[3]–O–B[3], B[3]–O–B[4], B[4]–O–B[4]} linkages in a BS glass
may be estimated reasonably accurately via their corresponding integrated
2Q–1Q 11B NMR spectral intensities by applying a
correction procedure67,68 that accounts for an overrepresented 11B[3] spectral intensity upon 2QF application and
mainly stemming from the higher 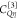 values relative to
values relative to 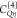 .76,85 Such corrections, however,
are not possible for the 2QF NMR spectra. We may consequently only
make qualitative comparisons among the relative integrated
2QF NMR intensities (“apparent site populations”) within each group of trigonal {B[3](R), B[3](NR)} and tetrahedral {B[4](2Si), B[4](3Si), B[4](4Si)} sites, whose members manifest very similar
quadrupolar products around ∼2.7 MHz and <0.5 MHz, respectively
(Table S2).
.76,85 Such corrections, however,
are not possible for the 2QF NMR spectra. We may consequently only
make qualitative comparisons among the relative integrated
2QF NMR intensities (“apparent site populations”) within each group of trigonal {B[3](R), B[3](NR)} and tetrahedral {B[4](2Si), B[4](3Si), B[4](4Si)} sites, whose members manifest very similar
quadrupolar products around ∼2.7 MHz and <0.5 MHz, respectively
(Table S2).
3. Previously Proposed 11B MAS NMR Assignment Options
3.1. B[4] Environments
A hitherto
incompletely settled issue concerns the unambiguous identification
of the populations of the set of coexisting 11B[4](mSi) environments with m Si and
4 – m B[p] neighbors
and their accompanying isotropic chemical shifts, {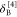 (mSi)}, along with accurate
experimental determination of their populations. The very narrow 11B[4]-resonance span (Section 4.1) complicates even the decision of how many distinct B[4](mSi)
moieties coexist, while the relative numbers of bonds to B/Si atoms
in the second coordination sphere of 11B[4] affect
its chemical shift.2−4 However, except for a few reports explicitly stating
the assumed sole presence of B[4]–O–{B[3], Si} linkages (i.e., absence of B[4]–O–B[4]),25−27,49,50,86 the literature is very vague
concerning the precise meaning and coordination of “B”
of the typically employed “B[4](mSi, [4 – m]B)” notation,28,32,36,37 which we herein abbreviate by B[4](mSi) and discuss in relation to hitherto largely unaccounted B[4]–O–B[4] bonds.67,68 Likewise, for NBO-rich BS glasses, potential 11B[4] shift effects from NBO bonds are currently implicitly/explicitly
ignored, although such bonds are predicted from atomistic MD simulations41,67,68,87−89 (Section 5.3). Fortunately, B[4]–NBO bonding is irrelevant
for our present NBO-poor BS glasses, as well as for most of those
in the literature invoking 11B MAS NMR spectral deconvolutions.25−33
(mSi)}, along with accurate
experimental determination of their populations. The very narrow 11B[4]-resonance span (Section 4.1) complicates even the decision of how many distinct B[4](mSi)
moieties coexist, while the relative numbers of bonds to B/Si atoms
in the second coordination sphere of 11B[4] affect
its chemical shift.2−4 However, except for a few reports explicitly stating
the assumed sole presence of B[4]–O–{B[3], Si} linkages (i.e., absence of B[4]–O–B[4]),25−27,49,50,86 the literature is very vague
concerning the precise meaning and coordination of “B”
of the typically employed “B[4](mSi, [4 – m]B)” notation,28,32,36,37 which we herein abbreviate by B[4](mSi) and discuss in relation to hitherto largely unaccounted B[4]–O–B[4] bonds.67,68 Likewise, for NBO-rich BS glasses, potential 11B[4] shift effects from NBO bonds are currently implicitly/explicitly
ignored, although such bonds are predicted from atomistic MD simulations41,67,68,87−89 (Section 5.3). Fortunately, B[4]–NBO bonding is irrelevant
for our present NBO-poor BS glasses, as well as for most of those
in the literature invoking 11B MAS NMR spectral deconvolutions.25−33
Two or three distinct-m B[4](mSi) environments are normally introduced for deconvoluting the 11B[4] NMR spectral region, but the degree of 11B[4]deshielding (increased chemical shift) per 11B[4]–O–Si → 11B[4]–O–B[3] substitution remains ill-defined, where 0.5–1.0 ppm,22,33 ≈1.5 ppm,37,38 and 1.7–2.0 ppm25−27,31,32 have been used. The consensus is that 11B[4](4Si) environments exhibit shifts within −1.8 ± 0.3 ppm for BS glasses with low NBO contents (xNBO ≲ 0.1),25−27,30−33,37,38 whereas the precise number and chemical shifts of the other 11B[4](mSi) environments are less defined. 11B NMR analyses of nearly NBO-free and Si-rich BS glasses (such as all K = 4.0 members herein) often assumed two peak components from B[4](4Si) and B[4](3Si) motifs.25,28−33 Moreover, within that assumption of solely m = {3, 4} groups being present, Angeli et al.31 demonstrated a simple and efficient approach for their discrimination by utilizing a Hahn spin–echo, where the 11B[4](4Si) signal manifests a slower T2 relaxation-stemming NMR-signal decay than 11B[4](3Si).31
To support the 11B[4](mSi) NMR-peak assignments in spectra from Si-rich BS glasses, additional information about the degree of B[4]–O–Si bonding, gauged from dipolar-based double-resonance 11B/29Si NMR experimentation suggested that either B[4](3Si) groups,30 or B[4](2Si) along with B[4](1Si) environments,33 coexisted with the B[4](4Si) moieties. For the very silica-rich (83 mol %; K = 7.2) Pyrex glass, Tricot30 deduced from such experiments in conjunction with 11B MAS NMR spectral fitting, that {δ[4]B(3Si), δ[4]B(4Si)} ≈ {−0.25, −2.0} ppm. In contrast, from double rotation90,9111B–11B correlation NMR applied to Pyrex glass, Howes et al.34 assigned a resonance at δ[4]B ≈ −1.4 ppm as merely stemming from both B[4](3Si) and B[4](4Si) moieties, along with another δ[4]B ≈ 0.5 ppm signal that was attributed to 11BO4 groups in superstructural units without B[p]–O–Si linkages.34 Hence, 11B[4] NMR-peak assignments are far from settled, even for the most widely examined Si-rich/NBO-poor BS-based glass composition domain.
Du and Stebbins26,27 introduced three-peak deconvolutions of the 11B[p]-resonance region with {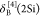 ,
, 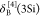 ,
,  } ≈ {1.5, −0.2, −2.2}
ppm, i.e., with a 1.7–2.0 ppm shift separation between neighboring m ± 1 values. Krishnamurthy and Kroeker37 employed a slightly different shift triplet,
fixed at {1.3, −0.1, −1.7} (±0.2) ppm, for analyzing
aluminoborosilicate glasses, which is very close to that recently
employed by some of us38 and amounts to
a
} ≈ {1.5, −0.2, −2.2}
ppm, i.e., with a 1.7–2.0 ppm shift separation between neighboring m ± 1 values. Krishnamurthy and Kroeker37 employed a slightly different shift triplet,
fixed at {1.3, −0.1, −1.7} (±0.2) ppm, for analyzing
aluminoborosilicate glasses, which is very close to that recently
employed by some of us38 and amounts to
a  ppm deshielding for each 11B[4]–O–Si → 11B[4]–O–B replacement. That is also
well aligned with earlier studies concluding that
ppm deshielding for each 11B[4]–O–Si → 11B[4]–O–B replacement. That is also
well aligned with earlier studies concluding that 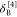 (3Si) ≈ 0.0 ± 0.5 ppm.25,28,30−32
(3Si) ≈ 0.0 ± 0.5 ppm.25,28,30−32
3.2. B[3] Environments
Vitreous B2O3 is well-known to comprise three BO3 groups in a boroxol ring, B3O6 (Figure 1a), along with a minor “non-ring” population of boroxol-ring-interlinking B[3](NR) sites.51−54 For BS as well as NBO-bearing binary borate glasses, however, it remains unclear what precisely those “R” and “NR” structural motifs represent and, more importantly, whether ad-hoc assumed two-peak deconvolutions of the CT 11B[3] NMR spectral region are adequate or too oversimplified. Most authors classified “ring” sites in borate/BS glasses strictly as boroxol moieties,25−28,31,33,34,49,50,92 while others attributed them to B[3] sites present in any B[3]/B[4] ring constellation,29,30,32,93,94 such as those depicted in Figure 1b–d. The B[3](NR) environments in BS glass networks are typically identified by BO3 groups present in chain-like (i.e., non-ring) structural moieties featuring a significant interlinking with Si,25−28,31,33,94 but they have also been attributed to B[3] sites in the BO4-bearing superstructural (ring) units shown in Figure 1b–d.34 Hence, analyses of the 11B[3] NMR spectral region from BS glasses remain ambiguous. Our results do not offer any definite solution to this long-standing open question but will provide some qualitative constraints and guide future research directions that may possibly resolve the ambiguities.
Figure 1.

Depiction of (a–d) borate and (e, f) borosilicate superstructural units well-known to build the structures of crystalline borates and/or borosilicates, and proposed to also exist in the corresponding glassy structures.1,20,44 All O atoms are bridging (BO): Ointra refers to BO sites within each superstructural unit, whereas Ointer specifies atoms shared between adjacent units (not shown). Adapted from Edén3 with permission from Elsevier.
The two 11B[3](R) and 11B[3](NR) environments of BS glasses manifest different
isotropic
chemical shift ranges of 16–18 ppm and 12–15 ppm, respectively
(refs (25−28, 30−32, 34−36, 38, 49, 50, and 86)), which is observed in essentially
any B-bearing phase, encompassing crystalline borates,95 vitreous B2O3,51−54 as well as binary M2O–B2O392,93 and B2O3–SiO256,96 glasses. For amorphous
B2O3 and binary B2O3–SiO2 glasses, the deshielding has been traced to wider average
interpolyhedral bond angles of θ̅(B[3]–O–B[3]) ≈ 135° 52−54 and θ̅(B[3]–O–B[3]/Si) ≈ 141°,96 respectively, around the B[3](NR)
sites relative to their B[3](R) counterparts with average
bond angles ∼ 120°. Hence, larger B[3]–O–Si
bond angles may contribute to the progressively decreased 11B[3] chemical shifts observed for increasing Si content
in BS glasses and attributed to shielding effects from Si,18,21,23,26,97 as recently corroborated by density functional
theory (DFT) calculations that verified a decrease in 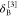 for increasing number of 11B[3]–O–Si bonds.89 Moreover, in NBO-rich borate/BS glasses, 11B
deshielding from NBO species at the BO3 groups may also
account for the higher
for increasing number of 11B[3]–O–Si bonds.89 Moreover, in NBO-rich borate/BS glasses, 11B
deshielding from NBO species at the BO3 groups may also
account for the higher  values,95,98,99 regardless of the B[3] participation in
R or NR motifs (Section 5.3).
values,95,98,99 regardless of the B[3] participation in
R or NR motifs (Section 5.3).
The hitherto perhaps most clear-cut assignments of the 11B[3](R) and 11B[3](NR) motifs—moreover deduced from complementary advanced MAS NMR experiments—may be those by Tricot30 for Pyrex glass (see Figure 8 of ref (30)). Both B[3](R) and B[3](NR) groups were concluded to interlink with “reedmergnerite” (Figure 1e) BS networks but differ in their contact modes: B[3](NR) bonds directly via B[3]–O–Si linkages,30 whereas B[3](R) participates in boroxol rings but also interlinks via B[3]–O–B[4] bridges to B[4](3Si) moieties, along previous inferences of Murakami et al.29 Howes et al.34 had earlier proposed a Pyrex-structure model related to that of Tricot,30 but involving both reedmergnerite19,20 and “danburite”14,17,31 (Figure 1f) motifs present in the B[4]/Si network, interleaved by boroxol rings (of B[3](R) sites), via primarily triborate (Figure 1b) and pentaborate (Figure 1d) superstructural units.1 Hence, the “B[3](NR)” sites resonating at ≈14 ppm also constitute “ring” sites in superstructural units comprising both B[3]/B[4] coordinations.34
Although consistent with the experimental NMR results from the Si-rich and NBO-free Pyrex glass, however, it remains unclear how well the structural models of refs (29, 30, and 34) account for B-richer BS glasses. The 2Q–1Q 11B NMR spectrum from Pyrex revealed no B[4]–O–B[4] linkages,30 whose nonetheless expected very low population would remain within the spectral noise in Figure 4 of ref (30), whereas B[4]–O–B[4] bridges are readily identified from B-richer glasses.41,49,50,67,68 Notably, out of all superstructural units shown in Figure 1 and proposed by Howes et al.34 to build the Pyrex structure, only diborate groups involve a B[4]–O–B[4] linkage (Figure 1c). Incidentally, eq 10 of ref (68) predicts a fraction of ≈3% B[4]–O–B[4] linkages out of all B–O–B bridges in Pyrex glass, which agrees very well with the fraction of diborate groups deduced by Howes et al.34
4. Results
4.1. 2Q–1Q and 2QF 11B NMR Results
Figure 2 shows a selection of 2Q–1Q correlation 11B NMR spectra acquired from the sets of K = {2.0, 4.0} BS glasses. As for a standard Bloch-decay 11B MAS NMR spectrum, the horizontal “1Q dimension” of
the 2Q–1Q NMR counterpart comprises a broad high-shift (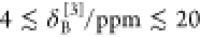 ) resonance from the lower-symmetry 11BO3 sites, along with a much narrower
peak from the more symmetric 11BO4 tetrahedra, centered at
) resonance from the lower-symmetry 11BO3 sites, along with a much narrower
peak from the more symmetric 11BO4 tetrahedra, centered at  ppm. However, the 2D NMR spectrum provides
direct insight into the various interlinked 11BOp–11BOqpairs present in the glass network, which are revealed
along the vertical “2Q dimension” (Figure 2). Indeed, regardless of the
precise network-modifier cation(s), all BS glasses comprise all three 11B[3]–O–11B[3], 11B[3]–O–11B[4], and 11B[4]–O–11B[4] linkages, which resonate at the sum of 1Q shifts centered around
ppm. However, the 2D NMR spectrum provides
direct insight into the various interlinked 11BOp–11BOqpairs present in the glass network, which are revealed
along the vertical “2Q dimension” (Figure 2). Indeed, regardless of the
precise network-modifier cation(s), all BS glasses comprise all three 11B[3]–O–11B[3], 11B[3]–O–11B[4], and 11B[4]–O–11B[4] linkages, which resonate at the sum of 1Q shifts centered around 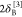 ,
, 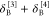 , and 2
, and 2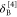 , respectively. Note that the two 11B[3]–11B[3] and 11B[3]–11B[4] correlations
in Figure 2 appear
as elongated “ridges” because the second-order quadrupolar
broadening of the 11B[3] signals extends along
both spectral dimensions.3,72
, respectively. Note that the two 11B[3]–11B[3] and 11B[3]–11B[4] correlations
in Figure 2 appear
as elongated “ridges” because the second-order quadrupolar
broadening of the 11B[3] signals extends along
both spectral dimensions.3,72
We focus onward on the 1Q projection of each 2Q–1Q NMR spectrum, which is equivalent to a 2QF 11B NMR spectrum. A key feature of Figure 2 is that each 11B[4] resonance detected in the 2QF NMR spectrum is a sum over both 11B[4]–11B[4] and 11B[4]–11B[3] 2D NMR peaks, while each 2QF 11B[3] resonance is a superposition of 11B[3]–11B[3] and 11B[3]–11B[4]. The pairs of red and cyan vertical guidelines in each 2Q–1Q NMR spectrum of Figure 2 mark the extent of the respective 11B[3]–11B[3] and 11B[4]–11B[4] “autocorrelation” ridge appearing along the spectral diagonal. The two narrow 11B[4]–11B[3] and 11B[4]–11B[4] correlation peaks overlap completely across the ±3 ppm range along the horizontal 1Q dimension. Likewise, the 11B[3] spectral region with two broader 11B[3]–11B[3] and 11B[3]–11B[4] correlation ridges reveals that the latter spans a wider range of both higher and, in particular, lower, shifts than its 11B[3]–11B[3] counterpart (Figure 2a–d). As may be verified from the more complete set of 2Q–1Q 11B NMR spectra presented in refs (67 and 68), those 2D spectral characteristics are general, except for BO3-dominated BS glasses, such as the Mg-bearing specimens (Figure 2e,f).
These trends offer the following important qualitative conclusions, which have direct implications for NMR peak assignments into {B[4](mSi)} and {B[3](R), B[3](NR)} structural entities, as discussed further in Sections 4.2 and 4.3, respectively: Both B[3](R) and B[3](NR) structural motifs involve significant B[3]–O–B[4] bonding, whereas both B[3] and B[4] species interlink with the B[4](3Si) and B[4](2Si) sites. Consequently, the results of Figure 2 supports previous proposals that even the highest-ppm 11B[3] NMR spectral region attributed to “ring” sites cannot solely constitute B[3]–O–B[3] motifs of boroxol rings but must also involve B[3]–O–B[4] linkages.29,30,32,93,94
Figure 3 contrasts each 2QF 11B MAS NMR spectrum with that of its directly excited Bloch-decay counterpart. Significant alterations are observed throughout the spectral region upon 2QF, manifested by a depletion of the low-ppm intensity of each 11B[3] and 11B[4] resonance region that consequently skews toward higher shifts. This feature stems from a reduced 11B[p] shielding from Si atoms (Section 3), where we remind that the 2QF NMR spectrum (Figure 3) only comprises resonances from BOp groups interlinked with at least one BOq moiety. The emphasized high-ppm 11B[3] resonance-intensities upon 2QF are more transparent in Figure S1, whereas Figure 3 conveys best the NMR peak-shape alterations observed for the 11B[4] NMR spectral region, which reflects changes in the relative contributions from B[4](mSi) structural motifs of each BS glass, whose 11B[4](4Si) NMR-signal contributions are absent after 2QF application. The 11B NMR spectral deconvolutions discussed in sections 4.2 and 4.3 rationalize and quantify the following gross characteristics of Figures 3 and S1:
Figure 3.
Projections of the 2Q–1Q 11B NMR spectra along the 1Q dimension (black traces; “2QF”) and 11B MAS NMR spectra obtained by single rf pulses (red traces; “1pls”) from the as-indicated K = 2.0 (left panel) and K = 4.0 (right panel) glass members. The black and red numbers at the rightmost spectral portions mark the shifts at the 11B[4] NMR-peak maxima. No 2QF NMR result is available for the LiNa2.0 glass in (h).
Regardless of the precise B and Si contents of
the glass (i.e.,
its K-value) and which network-modifier species are
present, the 2QF application emphasizes the 11B[3] resonance intensity significantly at the expense of 11B[4]. Although partially reflecting a higher retention
of the 2Q NMR signals involving 11B[3] sites
relative to those of 11B[4] (Section 2.4), this trend suggests that
the BO3 groups involve a comparatively larger fraction
of bridges to other B[p] sites than their
BO4 counterparts that interlink with SiO4 groups
to a higher extent. The most significant net 11B[4] NMR peak-maximum ( ) displacements upon 2QF result for the
Si-richest K = 4.0 BS glasses (Figure 3), for which the fractional populations of
the lowest-shift 11B[4](4Si)
environments are indeed expected to be largest, whereas much smaller
) displacements upon 2QF result for the
Si-richest K = 4.0 BS glasses (Figure 3), for which the fractional populations of
the lowest-shift 11B[4](4Si)
environments are indeed expected to be largest, whereas much smaller 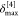 alterations are observed after 2QF for
the B-richer K = 2.0 glasses. These trends apply
regardless of the precise metal cation species in the BS structure,
except for the Mg-bearing ones, which manifest markedly lower BO4 populations than any other glass. Moreover, the 2QF 11B[4] NMR responses of the MgNa2.0 and, in particular,
MgNa4.0 glasses remain much closer to their directly excited NMR counterparts
(Figure 3i,j), which
suggests comparatively fewer B[4]–O–Si linkages
in the Mg-bearing glasses. The results of the MgNaK glasses are discussed separately in Section 4.4.
alterations are observed after 2QF for
the B-richer K = 2.0 glasses. These trends apply
regardless of the precise metal cation species in the BS structure,
except for the Mg-bearing ones, which manifest markedly lower BO4 populations than any other glass. Moreover, the 2QF 11B[4] NMR responses of the MgNa2.0 and, in particular,
MgNa4.0 glasses remain much closer to their directly excited NMR counterparts
(Figure 3i,j), which
suggests comparatively fewer B[4]–O–Si linkages
in the Mg-bearing glasses. The results of the MgNaK glasses are discussed separately in Section 4.4.
4.2. Double-Quantum-Assisted 11BO4 NMR-Peak Assignments
Figure 4 depicts the three-peak deconvolutions of the 11B[4] resonance region in the absence and presence of 2QF, while Table 2 lists the corresponding sets of isotropic 11B[4](mSi) chemical shifts, {δ[4]B(mSi)}, and fractional populations, {x[4]B(mSi)}. An inherent ambiguity of these spectral deconvolutions is to discriminate between the cases of (A) invariant δ[4]B(mSi) values but variable {x[4]B(mSi)} populations from that of (B) altered δ[4]B(mSi) shifts but (essentially) constant fractional populations, or (C) a combination of both. As discussed further in Section 5.2, however, significant population changes do occur among the coexisting B[4](mSi) ensembles for increasing (average) CFS of the network modifiers.27,38
Figure 4.
Experimental 11B NMR spectra (black traces) acquired at 14.1 T and 24.00 kHz MAS by either single pulses (“1pls”; a–d; i–l) or by 2QF (“2QF”; e–h; m–p) from the as-indicated BS glass series with K = {2.0, 4.0}. Red traces correspond to best-fit NMR spectra, whose peak components are identified by the legend in (j) and encompassing the following: “ring” (labeled “R”) and “non-ring” (“NR”) 11B[3] NMR peaks, which are identified in (d), along with those from 11B(4Si), 11B(3Si), and11B(2Si) environments.
Table 2. Best-Fit 11B[p] Chemical Shifts and Fractional Populations before and after 2QFa.
| Fractional Populationb |
Isotropic Chemical Shift (ppm) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
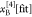 c c
|
11B[3] |
11B[4](mSi) |
11B[3] |
11B[4](mSi) |
|||||||
| Glass | 1pls(2QF) | Ring | Non-ring | 2Si | 3Si | 4Si | Ring | Non-ring | 2Si | 3Si | 4Si |
| K2.0 | 0.660(0.463) | 0.265(0.517) | 0.075(0.020) | 0.157(0.199) | 0.299(0.175) | 0.204(0.089) | 17.95(18.54) | 14.97(17.00) | 1.00(0.97) | –0.37(−0.21) | –1.90(−1.90) |
| 0.779(0.963) | 0.221(0.037) | 0.237(0.430) | 0.453(0.377) | 0.309(0.192) | |||||||
| RbNa2.0 | 0.634(0.435) | 0.300(0.533) | 0.066(0.031) | 0.143(0.223) | 0.315(0.154) | 0.175(0.058) | 17.82(18.26) | 14.56(15.67) | 1.00(1.20) | –0.32(−0.08) | –1.90(−1.70) |
| 0.820(0.944) | 0.180(0.056) | 0.226(0.513) | 0.497(0.355) | 0.277(0.132) | |||||||
| Na2.0 | 0.635(0.472) | 0.276(0.500) | 0.089(0.028) | 0.121(0.154) | 0.284(0.217) | 0.231(0.101) | 17.88(17.90) | 14.59(14.62) | 1.00(1.10) | –0.12(−0.06) | –1.68(−1.70) |
| 0.757(0.947) | 0.243(0.053) | 0.190(0.327) | 0.447(0.459) | 0.364(0.214) | |||||||
| LiNa2.0 | 0.597(0.435) | 0.302(0.529) | 0.101(0.036) | 0.123(0.149) | 0.291(0.222) | 0.183(0.065) | 17.82(18.10) | 14.95(16.10) | 1.05(1.50) | –0.04(0.02) | –1.63(−1.74) |
| 0.749(0.936) | 0.251(0.064) | 0.206(0.342) | 0.488(0.510) | 0.306(0.148) | |||||||
| MgNa2.0 | 0.388(0.277) | 0.409(0.592) | 0.203(0.131) | 0.077(0.089) | 0.193(0.134) | 0.118(0.053) | 17.64(18.09) | 14.44(15.54) | 1.05(1.30) | 0.03(0.10) | –1.62(−1.62) |
| 0.669(0.818) | 0.331(0.182) | 0.198(0.322) | 0.499(0.485) | 0.303(0.193) | |||||||
| K4.0 | 0.713(0.423) | 0.178(0.475) | 0.109(0.102) | 0.057(0.099) | 0.254(0.239) | 0.402(0.086) | 17.50(17.90) | 14.35(14.86) | 1.00(1.30) | –0.58(−0.28) | –2.13(−1.96) |
| 0.621(0.823) | 0.379(0.177) | 0.079(0.233) | 0.356(0.564) | 0.565(0.203) | |||||||
| RbNa4.0 | 0.686(0.402) | 0.206(0.509) | 0.108(0.089) | 0.040(0.073) | 0.289(0.240) | 0.358(0.090) | 17.41(18.44) | 14.06(16.00) | 1.30(1.40) | –0.48(−0.22) | –2.10(−1.90) |
| 0.657(0.852) | 0.343(0.148) | 0.058(0.181) | 0.421(0.596) | 0.522(0.222) | |||||||
| Na4.0 | 0.650(0.414) | 0.214(0.525) | 0.135(0.061) | 0.050(0.090) | 0.283(0.237) | 0.318(0.086) | 17.46(18.15) | 14.13(15.88) | 1.07(1.30) | –0.40(−0.26) | –2.02(−2.02) |
| 0.613(0.895) | 0.387(0.105) | 0.076(0.217) | 0.435(0.574) | 0.489(0.208) | |||||||
| MgNa4.0 | 0.338(0.247) | 0.360(0.629) | 0.303(0.124) | 0.042(0.048) | 0.182(0.138) | 0.113(0.061) | 17.52(18.30) | 13.83(14.54) | 1.13(1.37) | –0.17(−0.03) | –1.96(−1.80) |
| 0.543(0.835) | 0.457(0.165) | 0.125(0.196) | 0.540(0.556) | 0.334(0.248) | |||||||
Fractional populations and isotropic 11B chemical shifts obtained by deconvoluting the 11B MAS NMR spectrum obtained directly by single-pulse excitation (“1pls”) and the projection along the 1Q dimension of the 2Q–1Q correlation 2D NMR spectrum (“2QF”; values within parentheses). Data uncertainties are listed in Table S2.
Fractional populations
normalized
to a unity sum over all B[3] and B[4] species
in the glass (top row for each glass). The row beneath lists the corresponding
data normalized to a unity sum within each set of B[3] and
B[4] populations:  and
and 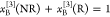 , where “R” and “NR”
represent “ring” and “non-ring” sites,
respectively.
, where “R” and “NR”
represent “ring” and “non-ring” sites,
respectively.
Net fractional
population of the
best-fit {x[4]B(mSi)} set: 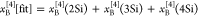 . The minor discrepancy to its
. The minor discrepancy to its 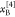 counterpart (“1pls”) listed
in Table 1 stems partially
from uncertainties in the spectral deconvolutions but primarily from
the centerband ST 11B[4] resonance intensity,
which was not accounted for by the spectral deconvolution and leading
to an overestimation of
counterpart (“1pls”) listed
in Table 1 stems partially
from uncertainties in the spectral deconvolutions but primarily from
the centerband ST 11B[4] resonance intensity,
which was not accounted for by the spectral deconvolution and leading
to an overestimation of 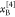 by ≈ 0.03.
by ≈ 0.03.
We first consider the deconvolutions of the Bloch-decay
NMR spectra.
The Si-rich K = 4.0 glass structures involve dominantly
B[4](4Si) and B[4](3Si) environments that out
of all tetrahedral sites account for 49–56% and 36–44%,
respectively (Table 2), whereas the B-richer glasses manifest consistently higher B[4](2Si) but lower B[4](4Si) populations than their K = 4.0 counterparts, thereby rendering B[4](3Si)
motifs most abundant, and amounting to 45–50% of all B[4](mSi) groups. In contrast to the previous
spectral deconvolutions conducted for a larger set of K = 4.0 BS glasses reported by Lv et al.,38 we herein allowed the chemical shifts of the distinct-m11B[4](mSi) moieties to vary
slightly (within ±0.25 ppm). Within the caveats commented above, Table 2 reveals a weak chemical
shift increase of 0.2–0.4 ppm for both δ[4]B(3Si) and δ[4]B(4Si) species
for increasing CFS 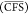 of the glass-network modifier(s). The K = 2.0 glasses featured the most typical isotropic chemical
shifts of {
of the glass-network modifier(s). The K = 2.0 glasses featured the most typical isotropic chemical
shifts of { (2Si),
(2Si), 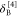 (3Si),
(3Si), 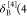 Si)} ≈ {1.0, −0.2, −1.7}
(±0.2) ppm, whereas the respective δ[4]B(3Si) and δ[4]B(4Si) values
of the K = 4.0 glasses are ≈0.20 ppm lower.
Altogether, this amounted in chemical-shift separations of 1.6 ±
0.1 ppm between δ[4]B(3Si) and δ[4]B(4Si) for all Bloch-decay-derived NMR spectra,
and somewhat more variable
Si)} ≈ {1.0, −0.2, −1.7}
(±0.2) ppm, whereas the respective δ[4]B(3Si) and δ[4]B(4Si) values
of the K = 4.0 glasses are ≈0.20 ppm lower.
Altogether, this amounted in chemical-shift separations of 1.6 ±
0.1 ppm between δ[4]B(3Si) and δ[4]B(4Si) for all Bloch-decay-derived NMR spectra,
and somewhat more variable 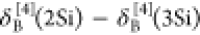 differences of 1.0–1.5 ppm (
differences of 1.0–1.5 ppm (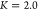 ) and 1.3–1.8 ppm (K = 4.0).
) and 1.3–1.8 ppm (K = 4.0).
Figure 4 evidences
a consistent displacement of the net 11B[4] resonance
upon 2QF. Although that trend is indeed reflected in a minor deshielding
by typically 0.1–0.3 ppm of each 11B[4](mSi) site-ensemble, it derives primarily from a
significant increase in the “apparent” best-fit  population while that of
population while that of  is concurrently reduced. Naturally, the
NMR-peak shape effects are most drastic for the Si-richer K = 4.0 BS glasses, for which B[4]B(4Si) environments are most abundant
(Table 2). Likewise,
the dominance of B[4]B(3Si) motifs in the K = 2.0 glasses with
higher B contents readily account for the modest NMR peak maximum
shift
is concurrently reduced. Naturally, the
NMR-peak shape effects are most drastic for the Si-richer K = 4.0 BS glasses, for which B[4]B(4Si) environments are most abundant
(Table 2). Likewise,
the dominance of B[4]B(3Si) motifs in the K = 2.0 glasses with
higher B contents readily account for the modest NMR peak maximum
shift  alterations upon 2QF application in Figure 3. We underscore that
the entire NMR peak intensity associated with the 11B[4] resonance centered at the most negative shift (≈ –1.90 ± 0.2 ppm) would
vanish upon 2QF application if it solely derived
from 11B[4](4Si) sites. The minor 5–10%
of the integrated NMR intensities (out of all 11B[p] sites) remaining after 2QF (Table 2) may partially stem from experimental artifacts
and uncertainties in the deconvolutions but, most likely, also derive
from an incorrect assumption about the structural
origin of the NMR peak attributed solely to B[4](4Si) sites.
Hence, some of the NMR-signal intensity appearing
alterations upon 2QF application in Figure 3. We underscore that
the entire NMR peak intensity associated with the 11B[4] resonance centered at the most negative shift (≈ –1.90 ± 0.2 ppm) would
vanish upon 2QF application if it solely derived
from 11B[4](4Si) sites. The minor 5–10%
of the integrated NMR intensities (out of all 11B[p] sites) remaining after 2QF (Table 2) may partially stem from experimental artifacts
and uncertainties in the deconvolutions but, most likely, also derive
from an incorrect assumption about the structural
origin of the NMR peak attributed solely to B[4](4Si) sites.
Hence, some of the NMR-signal intensity appearing  ppm may merely associate with 11B[4](3Si) environments.
ppm may merely associate with 11B[4](3Si) environments.
The detected 11B[4] resonances of the horizontal projection of the 2Q–1Q NMR spectra constitute a sum from two correlation signals, 11B[4]–O–11B[3] and 11B[4]–O–11B[4], both of which overlap completely across the 11B[4] resonance region (Figure 2), as is also evident from 2Q–1Q NMR results from other BS-based glasses.41,49,50 Hence, the overall narrow net resonance in MAS NMR spectra reflects shift perturbations of 11B[4] from all of Si, B[3], and B[4] as neighbors, which is also corroborated by recent DFT-derived 11B chemical shifts.89 Although B[4]–O–11B[3] linkages are strongly preferred59,67,68,100 and do dominate over B[4]–O–11B[4] (Section 5.2), assumptions about Si and B[3] species as sole bonding partners of B[4] (refs (25−27, 30, 49, 50, and 86)) should be abandoned.
Yet, further guidance from advanced NMR experiments and computational modeling is required to enable more specific NMR-peak assignments of the various 11B[4](mSi) environments and possibly disentangle the contributions from the variable numbers of B[3]/B[4] neighbors of the B[4](mSi) sites. Until then, we recommend to pragmatically pursue spectral deconvolutions with three {B[4](mSi)} environments in general, where the 4 – m B[4]–O–B[p] linkages (i.e., “B[4]–O–B”) are acknowledged to involve either B[3]or B[4]. At least from Si-rich glasses (nearly) devoid of NBO species, that strategy appears to offer reasonably accurate {x[4]B(mSi)} populations (Section 5.2), which likely reflects a partial error cancellation due to overlapping chemical shifts of the various 11B[4]–O–{B[3], B[4], Si} environments to justify the B[3]/B[4] grouping of each fixed-m11B[4](mSi) resonance.
4.3. Double-Quantum-Assisted 11BO3 NMR-Peak Assignments
We pursued the prevailing ad hoc two-component 11B[3] NMR spectral-region deconvolution and contrast the results both with and without a 2QF stage (Figure 4), which shed further light onto the nature of the “ring” and “non-ring” 11B[3] sites. We first consider the Bloch-decay-stemming NMR spectra and their deconvolutions, whose fractional populations quantitatively reflect the two trigonal 11B[3](R) and 11B[3](NR) types, within the caveats of the categorically simplified two-peak fitting. As expected,25−28,31,33,94,96 both 11B[3](R) and 11B[3](NR) environments manifest very similar quadrupolar products of 2.6–2.7 MHz throughout and mainly differ in their isotropic chemical shifts of 17.5–18 ppm and 14–15 ppm, respectively (Table 2). The most popular B[3](NR) site-identification in the BS glass context involves BO3 groups in chain motifs with a significant degree of B[3]–O–Si bonding.25−28,31,33,94 The results herein support that notion, where the Si-richer K = 4.0 glasses reveal slightly lower δ[3]B(NR) shifts than their K = 2.0 counterparts, while exhibiting markedly higher NR:R ratios that roughly amount to 1:2, in contrast with those around 1:4 for the K = 2.0 glass members (Table 2).
The characteristics of a vast dominance of B[3]–O–B[3]/B[4] bridges at the B[3](R) sites are corroborated by the spectral alterations upon 2QF application (Figure 4): the high-ppm 11B[3] resonance region stemming from B[3](R) sites is significantly emphasized upon 2QF NMR application, but the isotropic chemical shift increases are more modest (typically within 0.6 ppm) than those of the Si-interlinked B[3](NR) sites (1–2 ppm). We remind that the net 11B[3] NMR peak observed in each 2QF MAS spectrum carries contributions from both11B[3]–O–B[3]and11B[3]–O–B[4] linkages (Section 4.1), whose resonance spread across the entire 11B[3] region. Hence, both B[3](R) and B[3](NR) ensembles feature linkages to both B[3] and B[4] sites, which yields two possibilities: Either B[3](R) environments only participate in boroxol rings that are interlinked via “non-ring” BO4 tetrahedra. Given the comparable number of 11B[3]–O–B[4] linkages relative to 11B[3]–O–B[3] (as reflected in their respective 2D NMR signal intensities of Figure 2),68 however, it appears much more likely that most BO3 and BO4 groups share the same ring-structures, as in the superstructural units of Figure 1b–d. Hence, B[3](R) is attributed to trigonal B sites mainly present in so-called “modified rings”.29,30,32,93,94
Because only resonances from 11B[3](NR)–(OSi)3 motifs are removed
identically by the 2QF process in these essentially NBO-free glasses
(or 11B[3](OSi)p(NBO)3–p in NBO-bearing
glasses), the 11B[3](NR) signal fractions out
of the entire 2QF 11B NMR intensity remain low but non-negligible,
accounting for ≈5% and ≈15% for the K = 2.0 and K = 4.0 glasses, respectively (Table 2). Hence, the incomplete 11B[3](NR) resonance-suppression implies that the
“non-ring” BO3 groups cannot solely involve B[3]–O–Si linkages and that a significant
fraction thereof must comprise at least one B[3]–O–B[3]/B[4] linkage. We conclude
that the B[3](NR) sites in these BS glasses with 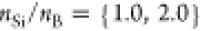 feature a range of linkages
to all of the
feature a range of linkages
to all of the  network formers. Our qualitative findings
from 2Q–1Q 11B NMR are aligned with earlier results
from 11B/29Si double-resonance NMR by Wegner
et al.,33 as well as by Du and Stebbins,
who concluded from 3QMAS 17O NMR that ≈2/3 and ≲1/3
of all B[3](NR) and B[3](R) sites involve B[3]–O–Si linkages, respectively,25,26 along with a near-statistical B[p]/Si
intermixing around the B[3](NR) sites.26 Although there is a range of such B[3](NR) sites
with a variable number of B[p]/Si atoms
in their second coordination spheres, the relative extents of B[3]–O–{B[3], B[4], Si}
bonding cannot be inferred directly from our experimental data. Hence,
spectral deconvolutions with additional 11B[3] NMR peaks from further “non-ring” subsets are currently
not warranted.
network formers. Our qualitative findings
from 2Q–1Q 11B NMR are aligned with earlier results
from 11B/29Si double-resonance NMR by Wegner
et al.,33 as well as by Du and Stebbins,
who concluded from 3QMAS 17O NMR that ≈2/3 and ≲1/3
of all B[3](NR) and B[3](R) sites involve B[3]–O–Si linkages, respectively,25,26 along with a near-statistical B[p]/Si
intermixing around the B[3](NR) sites.26 Although there is a range of such B[3](NR) sites
with a variable number of B[p]/Si atoms
in their second coordination spheres, the relative extents of B[3]–O–{B[3], B[4], Si}
bonding cannot be inferred directly from our experimental data. Hence,
spectral deconvolutions with additional 11B[3] NMR peaks from further “non-ring” subsets are currently
not warranted.
4.4. Mg-Bearing Glass Structures
As discussed
further in Section 5.2, the strikingly different Bloch-decay and 2QF 11B NMR
responses of the two Mg-bearing glasses shown in Figure 4 may be traced to their markedly
higher B[3] populations and accompanying larger number
of B[3]–O–Si linkages at the expense of the
typically prevailing B[4]–O–Si counterparts.40 However, if we disregard the reduction of all 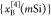 values resulting from the lower net BO4 populations and merely focus on the populations normalized
to a unity sum within each group of B[3] and B[4] coordinations, the B-richer MgNa2.0 glass does not reveal any striking
differences to the other K = 2.0 glass members (Table 2). The Si-richer MgNa4.0
structure, on the other hand, manifests much fewer B[4](4Si) moieties along with a significantly boosted B[3](NR) abundance and x[3]B(NR):x[3]B(R) ratio. The
2Q–1Q 11B NMR spectra from both Mg-bearing glasses
(Figure 2e,f) also
manifest more intense 11B[3]–O–11B[3] correlation ridges than all other glasses,
suggesting that their networks may comprise a larger number of boroxol
rings (Figure 1a).
Altogether, the introduction of Mg in the Na4.0 glass amounts in a
partial conversion of B[3](R) sites with solely B[3]–O–{B[3], B[4]} linkages into
(i) B[3](R) counterparts with emphasized
B[3]–O–B[3] interlinking at the
expense of B[3]–O–B[4] bridges,
along with (ii) B[3](NR) sites featuring
B[3]–O–Si linkages. The latter observation
agree with an increased (decreased) number of B[3]–O–Si
(B[4]–O–Si) linkages inferred by a direct
probing of the B[p]/Si intermixing via
double-resonance 11B/29Si NMR experiments.40
values resulting from the lower net BO4 populations and merely focus on the populations normalized
to a unity sum within each group of B[3] and B[4] coordinations, the B-richer MgNa2.0 glass does not reveal any striking
differences to the other K = 2.0 glass members (Table 2). The Si-richer MgNa4.0
structure, on the other hand, manifests much fewer B[4](4Si) moieties along with a significantly boosted B[3](NR) abundance and x[3]B(NR):x[3]B(R) ratio. The
2Q–1Q 11B NMR spectra from both Mg-bearing glasses
(Figure 2e,f) also
manifest more intense 11B[3]–O–11B[3] correlation ridges than all other glasses,
suggesting that their networks may comprise a larger number of boroxol
rings (Figure 1a).
Altogether, the introduction of Mg in the Na4.0 glass amounts in a
partial conversion of B[3](R) sites with solely B[3]–O–{B[3], B[4]} linkages into
(i) B[3](R) counterparts with emphasized
B[3]–O–B[3] interlinking at the
expense of B[3]–O–B[4] bridges,
along with (ii) B[3](NR) sites featuring
B[3]–O–Si linkages. The latter observation
agree with an increased (decreased) number of B[3]–O–Si
(B[4]–O–Si) linkages inferred by a direct
probing of the B[p]/Si intermixing via
double-resonance 11B/29Si NMR experiments.40
5. Discussion
5.1. Role of Magnetic Field for Identifying 11B[p] Environments
The precise external magnetic field utilized for 11B MAS NMR acquisitions sets some restrictions on how many, and which, 11B[4](mSi) resonances may be detected and justified for subsequent spectral deconvolutions. It is well-known that 11B MAS NMR spectra obtained at B0 < 11.7 T reveal severely overlapping 11B[3] and 11B[4] signal regions; e.g., see refs (17, 28, 30, 42, and 101). While B0 = 11.7 T enables a near-complete 11B[3]/11B[4] resonance separation, a significant overlap remains in the shift range of 1–4 ppm, as may be verified from the NMR spectra of refs (21, 28, 29, 31, 50, and 86). The typically minor 11B[4](2Si) species resonate in that spectral range, which complicates the justification for their introduction into spectral deconvolutions. Although the resonance overlap is not fully suppressed at B0 = 14.1 T in all single-pulse NMR spectra of Figure 4, it appears to be the minimum field for sufficient NMR-signal separation to attempt deconvolutions into three {11B[4](mSi)} signals, besides those from 11B[3](R) and B[3](NR) moieties.
Out of the plethora of existing reports invoking 11B MAS
NMR spectral deconvolutions, encompassing those herein, only those
from the very Si-rich and NBO-free Pyrex glass28−30 are truly unambiguous
because high-field spectra (B0 ⩾
18.8 T) proved that essentially all 11B[4] spectral
intensity is confined to two resonances, which thanks to the high nSi/nB = 3.58 ratio
of Pyrex may safely be attributed to B[4](3Si) and B[4](4Si) environments.28−30 Moreover, both Tricot30 and Prasad et al.28 deduced that  along with near-equal fractional populations
of B[4](4Si) and B[4](3Si), which agreed excellently
between the two studies once considering the data uncertainties. The 11B MAS NMR spectrum recorded at B0 = 21.8 T by Murakami et al.29 and decomposed
into 11B[4](3Si) and 11B[4](4Si) NMR peaks also accords well with those of refs (28 and 30). Interestingly, a close inspection
of Figure 1d of ref (29), however, reveals a very minor deviation between their experimental
and best-fit spectra in the 1–2 ppm spectral region that likely
reflects a minor unaccounted 11B[4](2Si) resonance.
The latter is even more evident from the 11B MAS NMR spectra
shown in Figure 2 of Möncke et al.,60 and acquired from B-richer glasses at 18.8 T.
along with near-equal fractional populations
of B[4](4Si) and B[4](3Si), which agreed excellently
between the two studies once considering the data uncertainties. The 11B MAS NMR spectrum recorded at B0 = 21.8 T by Murakami et al.29 and decomposed
into 11B[4](3Si) and 11B[4](4Si) NMR peaks also accords well with those of refs (28 and 30). Interestingly, a close inspection
of Figure 1d of ref (29), however, reveals a very minor deviation between their experimental
and best-fit spectra in the 1–2 ppm spectral region that likely
reflects a minor unaccounted 11B[4](2Si) resonance.
The latter is even more evident from the 11B MAS NMR spectra
shown in Figure 2 of Möncke et al.,60 and acquired from B-richer glasses at 18.8 T.
Although the 11B MAS NMR spectral resolution improves concurrently for increasing B0 across the narrow 11B[4] resonance region, as well as enhancing the 11B[3]/11B[4] frequency separation, the concomitant 11B[3] resonance-narrowing may compromise the discrimination among B[3](R) and B[3](NR) environments, unless sufficiently high fields (>20 T) are employed to significantly suppress the second-order quadrupolar broadening.29 Hence, if two distinct magnetic fields are available, numerical deconvolutions of NMR spectra recorded at both fields are recommended.28−32
5.2. Glass Composition Constraints on the {B[4](mSi)} Set
Here, we discuss the
strong bearings of the B[4](mSi) populations
of the BS glass network on its (I) nSi/nB molar ratio (i.e., on
the K-value), (II) {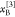 ,
,  } speciation, and (III)
NBO content. The number of coexisting B[4](mSi) groups, however, is a priori unknown because
the underlying preferences of the B[4] sites to interlink
with Si, B[3], and B[4] are not known quantitatively
by experiments, which underlies why the current choices of either
two- or three-peak spectral deconvolutions are rarely justified. Here
we make an attempt with guidance from MD simulations.
} speciation, and (III)
NBO content. The number of coexisting B[4](mSi) groups, however, is a priori unknown because
the underlying preferences of the B[4] sites to interlink
with Si, B[3], and B[4] are not known quantitatively
by experiments, which underlies why the current choices of either
two- or three-peak spectral deconvolutions are rarely justified. Here
we make an attempt with guidance from MD simulations.
Table 3 compares each NMR-derived {x[4]B(mSi)} set of the Na2.0 and Na4.0 glasses and their Mg-bearing counterparts with those obtained from atomistic MD simulations available from the glass models presented by Lv et al.40 Each set of experimental and modeled populations is normalized to a unity sum and is contrasted with those predicted for an unconstrained statistical B[4]–O–{Si, B[3], B[4]} linkage formation, calculated from the {xF} fractions of Table 3 along with equal bonding preferences, and assuming the absence of NBO. That assumption is well justified by the very close statistical populations deduced from the MD-generated glass models when rigorously accounting for their actual average number of BO atoms per F atom (Table 3). For a statistical B[4]–O–F linkage formation, all K = {2.0, 4.0} glass structures would comprise four distinct-m B[4](mSi) moieties with non-negligible populations [i.e., all but B[4](0Si)], revealing average numbers m̅ ≈ 2.1 and m̅ ≈ 2.8 for the K = 2.0 and K = 4.0 glasses, respectively. The three-peak deconvolutions of the NMR spectra, however, yielded significantly higher values of m̅ = 3.2 and m̅ = 3.4 for the Na2.0 and Na4.0 glasses, respectively, whereas the modeled m̅ values are intermediate of the experimental and statistical counterparts. A more disordered modeled m-distribution than that inferred by NMR is reminiscent of the BO/NBO partitioning among the SiO4 groups in silicate glasses.102−104
Table 3. NMR- and MD-Derived Fractional Populations of B[4](mSi) Groupsa.
| Molar
Fractions |
B[4](mSi)
Fractions |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Glass | xSi |  |
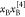 |
m̅b | 0 | 1 | 2 | 3 | 4 | |
| Na2.0 | NMR | 0.500 | 0.182 | 0.318 | 3.18(2.10) | 0.000(0.051) | 0.000(0.226) | 0.190(0.374) | 0.446(0.274) | 0.364(0.075) |
| MD | 0.500 | 0.227 | 0.273 | 2.50(2.12) | 0.019(0.049) | 0.116(0.220) | 0.358(0.372) | 0.365(0.280) | 0.142(0.079) | |
| c(2.14) | c(0.047) | c(0.215) | c(0.371) | c(0.285) | c(0.082) | |||||
| MgNa2.0 | NMR | 0.500 | 0.306 | 0.194 | 3.11(2.17) | 0.000(0.044) | 0.000(0.209) | 0.198(0.370) | 0.499(0.291) | 0.303(0.086) |
| MD | 0.500 | 0.323 | 0.177 | 2.36(2.18) | 0.026(0.043) | 0.156(0.206) | 0.354(0.369) | 0.358(0.294) | 0.106(0.088) | |
| c(2.23) | c(0.038) | c(0.192) | c(0.365) | c(0.308) | c(0.097) | |||||
| Na4.0 | NMR | 0.667 | 0.117 | 0.216 | 3.41(2.75) | 0.000(0.010) | 0.000(0.084) | 0.076(0.278) | 0.435(0.406) | 0.489(0.222) |
| MD | 0.667 | 0.157 | 0.176 | 3.06(2.78) | 0.002(0.009) | 0.040(0.080) | 0.176(0.270) | 0.458(0.409) | 0.324(0.232) | |
| c(2.79) | c(0.008) | c(0.078) | c(0.268) | c(0.410) | c(0.236) | |||||
| MgNa4.0 | NMR | 0.667 | 0.220 | 0.113 | 3.21(2.82) | 0.000(0.008) | 0.000(0.072) | 0.125(0.259) | 0.540(0.414) | 0.335(0.248) |
| MD | 0.667 | 0.233 | 0.100 | 2.89(2.83) | 0.005(0.007) | 0.054(0.071) | 0.242(0.257) | 0.448(0.413) | 0.251(0.251) | |
| c(2.87) | c(0.006) | c(0.064) | c(0.246) | c(0.418) | c(0.266) | |||||
Fractional populations of B[4](mSi) groups,  (mSi), obtained either
by fitting the Bloch-decay 11B MAS NMR spectra (“NMR”)
or calculated by MD simulations (“MD”).40 The values in parentheses represent populations predicted
from an unconstrained statistical distribution of B[4]–O–Si/B[p] linkages, calculated from the binomial
expression
(mSi), obtained either
by fitting the Bloch-decay 11B MAS NMR spectra (“NMR”)
or calculated by MD simulations (“MD”).40 The values in parentheses represent populations predicted
from an unconstrained statistical distribution of B[4]–O–Si/B[p] linkages, calculated from the binomial
expression  , with 0 ⩽ m ⩽
4 and
, with 0 ⩽ m ⩽
4 and  . The {
. The { ,
, 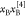 } data of the glass was employed, with borate
speciations extracted either from the glass models or the
} data of the glass was employed, with borate
speciations extracted either from the glass models or the 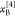 [fit] data listed in Table 2. The minor degree of F–NBO
bonding was ignored.
[fit] data listed in Table 2. The minor degree of F–NBO
bonding was ignored.
Average
number of B[4]–O–Si bonds calculated from  (mSi).
(mSi).
Statistical { (mSi)} results calculated
from a binomial distribution with
(mSi)} results calculated
from a binomial distribution with 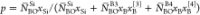 , where {
, where {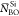 ,
,  ,
, 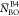 } is the set of MD-derived average number
of F–BO bonds at the respective {Si, B[3], B[4]} ensembles in the glass model.68 The very good agreement with the statistical
populations obtained when ignoring the small number of F–NBO bonds (data on line above) justifies their use for both
the experimental and modeled data.
} is the set of MD-derived average number
of F–BO bonds at the respective {Si, B[3], B[4]} ensembles in the glass model.68 The very good agreement with the statistical
populations obtained when ignoring the small number of F–NBO bonds (data on line above) justifies their use for both
the experimental and modeled data.
Both modeled and experimental {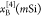 } data sets of Table 3 suggest significant {B[4](2Si),
B[4](3Si), B[4](4Si)} populations throughout
all glass structures. The previously25−27 and herein observed
markedly stronger B[4]–O–Si interlinking
than that of a statistical B[4]/F intermixing,
may be rationalized from the widely differing {xF} abundances and propensities of Si, B[3], and B[4] to interlink with BO4 groups40,68 (Table S3). Although B[4]–O–B[3] linkages are preferred over B[4]–O–Si, P(B[4]–O–B[3]) > P(B[4]–O–Si), the markedly higher
Si abundance coupled with its 4/3 larger number of available BO sites,
promotes B[4]–O–Si bridges over B[4]–O–B[3], and notably so B[4]–O–B[4], which are preferentially avoided due to P(B[4]–O–B[4]) ≈ 0.5.40,68 The deviation from unity of the preference factor P(B[4]–O–F) marks the degree
of preference [P(B[4]–O–F) > 1] or reluctance [P(B[4]–O–F) > 1] for creating B[4]–O–F linkages. The {xF} and {P(B[4]–O–F)} entities together rationalize
the dominance of ≈2.5 and ≈3 Si atoms in the second
coordination sphere of the B[4] sites in the respective K = 2.0 and K = 4.0 MD-derived glass models
(Table 3).
} data sets of Table 3 suggest significant {B[4](2Si),
B[4](3Si), B[4](4Si)} populations throughout
all glass structures. The previously25−27 and herein observed
markedly stronger B[4]–O–Si interlinking
than that of a statistical B[4]/F intermixing,
may be rationalized from the widely differing {xF} abundances and propensities of Si, B[3], and B[4] to interlink with BO4 groups40,68 (Table S3). Although B[4]–O–B[3] linkages are preferred over B[4]–O–Si, P(B[4]–O–B[3]) > P(B[4]–O–Si), the markedly higher
Si abundance coupled with its 4/3 larger number of available BO sites,
promotes B[4]–O–Si bridges over B[4]–O–B[3], and notably so B[4]–O–B[4], which are preferentially avoided due to P(B[4]–O–B[4]) ≈ 0.5.40,68 The deviation from unity of the preference factor P(B[4]–O–F) marks the degree
of preference [P(B[4]–O–F) > 1] or reluctance [P(B[4]–O–F) > 1] for creating B[4]–O–F linkages. The {xF} and {P(B[4]–O–F)} entities together rationalize
the dominance of ≈2.5 and ≈3 Si atoms in the second
coordination sphere of the B[4] sites in the respective K = 2.0 and K = 4.0 MD-derived glass models
(Table 3).
For decreasing (average) CFS of the network modifier(s) across the K = 4.0 glass branch, both the net BO4 population and the B[4]/Si intermixing increase concurrently, where Lv et al.40 demonstrated a linear correlation between the decreasing fraction of B[4]–O–Si linkages for increasing Mz+ CFS. The strong interplay between the three {P(B[4]–O–F)} preferences, the nSi/nB ratio of the BS glass, and its {B[3], B[4]} speciation is reflected in the 11B MAS NMR spectra shown in Figure 5 for a larger number of ternary M2O–B2O3–SiO2 and quaternary M(2)O–Na2O–B2O3–SiO2 glasses with different alkali and alkaline-earth metal cations.10 For increasing (average) CFS of the M+/M2+ cation(s), the fractional BO3 populations are increased at the expense of BO4, as is most evident from the full 11B CT MAS NMR spectral regions displayed in Figure 5a,c.
Figure 5.
Bloch-decay 11B NMR spectra recorded at 14.1 T and 24.00 kHz MAS from glasses with network modifiers specified in the legend and featuring (a, b) K = 2.0 and (c, d) K = 4.0, where (a, c) display the entire CT NMR spectral region and (b, d) are zooms over the 11B[4] resonances.
We onward focus on the 11B[4] NMR peak shapes
shown in Figure 5b,d,
where strikingly different responses are observed between the two
glass branches: the Si-richer glasses manifest a conversion from a
dominance of 11B[4](4Si) NMR-signal intensity
observed from the low-CFS alkali-based glasses to progressively more
intense 11B[4](3Si) resonances for increasing M2+ CFS. Indeed, the NMR spectra of the MgNa4.0
and CaNa4.0 specimens are closer to those of the B-richer glasses
shown in Figure 5b.
Their common spectral signature, peaking around the typical shift
of 11B[4](3Si) groups, is attributed to higher
BO3 populations (Table 3) that boost the number of B[4]–O–B[3] bridges. Likewise, the much larger B[4](4Si)
populations of the MNa4.0 glasses with low-CFS M+ cations stem from their comparably low B[3] abundances, which restrict formation of the most preferred
B[4]–O–B[3] linkages,59,68,100 while there is a reluctance for forming the otherwise statistically favored B[4]–O–B[4] bridges. Hence, B[4]–O–Si linkages
become boosted due to their stronger formation preference than B[4]–O–B[4] along with the high Si
content of the glass (Table S3). Note that
whenever 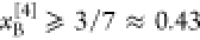 , B[4]–O–B[4] bridges must exist in any NBO-free M(2)O–B2O3 glass,
while B[4]–O–Si linkages are effectively
promoted in the BS glass analog.
, B[4]–O–B[4] bridges must exist in any NBO-free M(2)O–B2O3 glass,
while B[4]–O–Si linkages are effectively
promoted in the BS glass analog.
The results of Table 3 and Figure 5 underscore
the strong bearings from both the  ratio of the glass and its BO3 population on the precise {B[4](mSi)}
speciation. Notably, the B[3] reservoir of the MgNa4.0
glass (
ratio of the glass and its BO3 population on the precise {B[4](mSi)}
speciation. Notably, the B[3] reservoir of the MgNa4.0
glass ( ) is close to that of its B-richer Na2.0
counterpart (
) is close to that of its B-richer Na2.0
counterpart (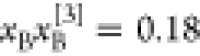 ), as is mirrored in similar average numbers m̅ ≈ 3.2 of B[4]–O–Si
linkages observed by NMR (Table 3). Owing to a previously discussed MD-derived increasing
preference for F–NBO bonding according to
B[4] ≪ Si < B[3],40,41,68,100 the number
of B[4]–O–Si linkages grows for increasing
NBO content of the BS glass, which is verified by the {
), as is mirrored in similar average numbers m̅ ≈ 3.2 of B[4]–O–Si
linkages observed by NMR (Table 3). Owing to a previously discussed MD-derived increasing
preference for F–NBO bonding according to
B[4] ≪ Si < B[3],40,41,68,100 the number
of B[4]–O–Si linkages grows for increasing
NBO content of the BS glass, which is verified by the {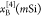 } sets obtained from Na+ and
Na+/Ca2+ glass models (data not shown) but remains
to be shown experimentally.
} sets obtained from Na+ and
Na+/Ca2+ glass models (data not shown) but remains
to be shown experimentally.
We conclude by noting that although
the 11B[4](2Si) resonance remains swamped by
the dominant 11B[4](3Si) NMR peak in Figures 3 and 4, three 11B[4](4Si), 11B[4](3Si), and 11B[4](2Si) signal components
were required in our deconvolutions.
Besides the 3QMAS 11B NMR results of Du and Stebbins,26 minor 11B[4](2Si) NMR
intensities are hinted (but not commented) in other 11B
NMR spectra in the literature.29,60 Non-negligible B[4](1Si) populations are moreover anticipated for BS glasses
with K < 2.0, notably for those featuring high
BO3 populations (vide supra). Attempting
such three-/four-peak deconvolutions from the set {11B[4](3Si), 11B[4](2Si), 11B[4](1Si), 11B[4](0Si)}, however, requires
further knowledge of the chemical-shift dependence on m. That demands additional work on δ[4]B(mSi) predictions
by DFT calculations,43,89 along with 11B MAS
NMR experiments on BS glasses with variable nSi/nB ratios at very high field
(B0 > 20 T), which is likely also needed
for enabling sufficient discrimination among the various coexisting 11B[3], 11B[4](0Si), and 11B[4](1Si) resonances, as well as shedding light
on the current enigma concerning the unknown (in)variance of the 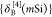 shifts for glasses incorporating different
glass-network modifiers (Section 4.2).
shifts for glasses incorporating different
glass-network modifiers (Section 4.2).
5.3. Remaining Challenges: NBO-Rich Glasses
With a few recent exceptions,49,50,84 previous 11B NMR spectral deconvolutions predominantly concerned BS-based glasses with low NBO contents. Analyses of glasses with non-negligible NBO populations must account for the bearings from B[3]–NBO bonds and possibly also B[4]–NBO. Here, we review the current state of affairs and identify future research directions required for potentially reaching more realistic 11B NMR spectral deconvolutions of NBO-rich BS-based glasses. We note that although 17O NMR may distinguish NBO bonding to Si and B,24,64 it cannot discriminate between the two B[3]–NBO and B[4]–NBO scenarios (Section 1). 11B/17O double-resonance NMR is the most direct experimental approach to probe both B[3]–NBO (Section 5.3.1) and B[4]–NBO bonding, which is currently being explored. Below we focus on the effects of 11B[p] coordination upon NBO coordination.
5.3.1. B[3]–NBO Bonding
NBO-for-BO substitutions in the first coordination sphere of a network-forming F site are well-known to increase its chemical shift, as
is long known to hold for the 29Si and 31P nuclides.2−4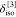 increases concurrently by a few ppm for
each B[3]–BO → B[3]–NBO
bond replacement.98,99,105 For NBO-bearing binary borate glasses, the 11B[3] NMR spectral regions are traditionally analyzed solely in terms
of distinct B[3](qNBO) environments (featuring q B[3]–NBO bonds),95,98,99,105,106 rather than the B[3](R) and B[3](NR) counterparts. The discrimination among distinct-q11B[3](qNBO) resonances is
not primarily based on their isotropic chemical shifts but rather
on the distinct ranges of the quadrupolar asymmetry parameters. Here,
the formally axially symmetric efg tensor (
increases concurrently by a few ppm for
each B[3]–BO → B[3]–NBO
bond replacement.98,99,105 For NBO-bearing binary borate glasses, the 11B[3] NMR spectral regions are traditionally analyzed solely in terms
of distinct B[3](qNBO) environments (featuring q B[3]–NBO bonds),95,98,99,105,106 rather than the B[3](R) and B[3](NR) counterparts. The discrimination among distinct-q11B[3](qNBO) resonances is
not primarily based on their isotropic chemical shifts but rather
on the distinct ranges of the quadrupolar asymmetry parameters. Here,
the formally axially symmetric efg tensor ( ) associated with 11B[3](0NBO) sites typically reveals
) associated with 11B[3](0NBO) sites typically reveals 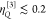 , whereas those with 1–2 B[3]–NBO bonds manifest larger asymmetry parameters
, whereas those with 1–2 B[3]–NBO bonds manifest larger asymmetry parameters 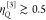 .95,98,99 Early wide-line 11B NMR on static BS glass powders enabled
estimations of the 11B[3](0NBO) population relative
to its NBO-bearing (q ⩾ 1) counterparts,19,20 but convincing MAS NMR spectral deconvolution analyses are still
lacking.
.95,98,99 Early wide-line 11B NMR on static BS glass powders enabled
estimations of the 11B[3](0NBO) population relative
to its NBO-bearing (q ⩾ 1) counterparts,19,20 but convincing MAS NMR spectral deconvolution analyses are still
lacking.
Saini et al.84 analyzed
the 11B[3] NMR signal regions from a large series
of BS glasses with variable B and NBO contents by employing the prevailing
two-peak deconvolution into B[3](R) and B[3](NR) contributions, where the latter was assigned to non-ring B[3] sites interlinking with Si. For the NBO-bearing glasses,
however, the “B[3](NR)” sites were on the
basis on their high best-fit 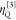 values of 0.6–0.7 attributed to
B[3](1NBO) environments,84 implying
that all B[3]–NBO bonds occur at the non-ring/Si-interlinked
BO3 moieties, which would then coexist with B[3](R) sites without bonds to NBO anions. It is difficult to estimate
both
values of 0.6–0.7 attributed to
B[3](1NBO) environments,84 implying
that all B[3]–NBO bonds occur at the non-ring/Si-interlinked
BO3 moieties, which would then coexist with B[3](R) sites without bonds to NBO anions. It is difficult to estimate
both 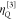 values of the B[3](R) and B[3](NR) species accurately, which already represent simplified
structural entities across a potentially much more complex BO3 ensemble with variable numbers of both BO/NBO bonds and {Si,
B[3], B[4]} neighbors, and thereby also
values of the B[3](R) and B[3](NR) species accurately, which already represent simplified
structural entities across a potentially much more complex BO3 ensemble with variable numbers of both BO/NBO bonds and {Si,
B[3], B[4]} neighbors, and thereby also 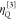 values. It therefore remains unclear how
to merge the two hitherto proposed but distinctly different B[3] classifications of B[3](qNBO)
motifs devoid of B[3]–O–Si bonds with the
prevailing B[3](R)/B[3](NR) moieties introduced
for NBO-free borate/BS glasses.
values. It therefore remains unclear how
to merge the two hitherto proposed but distinctly different B[3] classifications of B[3](qNBO)
motifs devoid of B[3]–O–Si bonds with the
prevailing B[3](R)/B[3](NR) moieties introduced
for NBO-free borate/BS glasses.
5.3.2. B[4]–NBO Bonding
As for the presence of B[4]–O–B[4] linkages of BS-based glasses (Section 4.2), potential chemical-shift effects from 11B[4]–NBO bonds also remain ignored in the literature. Notwithstanding their expected absence in all but (very) NBO-rich glasses,39,41,67,68,88,89 their potential presence would severely complicate 11B MAS NMR spectral deconvolutions from NBO-rich BS glasses, where the NMR parameters of the distinct-m11B[4](mSi) moieties are modified depending on the presence/absence of NBO anions at the tetrahedron. While such ambiguities of the 11B[4](mSi) chemical shifts from B[4]–NBO bonding are irrelevant for the present analysis of low-NBO glasses, the following observations are noteworthy:
(i) DFT calculations predict increased 11B[4] chemical shifts upon NBO coordination.89 (ii) Borophosphosilicate glasses with high Si and
NBO contents reveal consistently slightly higher 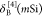 values (by ≈0.5 ppm) than their
NBO-poor counterparts,39,43 which might stem from a minor
degree of B[4]–NBO bonding. (iii) 2Q–1Q correlation 11B NMR experiments of NBO-rich
BS glasses also suggest slightly higher 11B[4] shifts relative to their NBO-poor counterparts. That
feature is most evident from the 2Q projections of 2Q–1Q 11B NMR spectra shown in Figure 6a, which were recorded from a series of RNa2O–B2O3–2.0SiO2 glasses with increasing Na2O content R, where we employ the more general MK–R or MNaK–R glass notation of refs (40 and 68). The NBO contents are negligible in all R ⩽
0.75 glasses but significant for the R = {2.1, 2.5}
counterparts (the 2D NMR spectra are displayed in Figure 2 of Lv et
al.68). Notably, the NBO-free Na BS glasses
reveal near-constant peak-maxima shifts of ≈0.0 ppm for the 11B[4]–O–11B[4] correlation peak, whereas those of the two Na2.0–2.1 and
Na2.0–2.5 glasses are markedly higher by ≈2 ppm. Likewise,
the 2Q peak maxima observed from the 2.0–2.1 glass series with xNBO ≈ 0.36 shown in Figure 6b are consistently ≈1.7
ppm higher than their NBO-free 2.0–0.75 counterparts displayed
in Figure 6c.
values (by ≈0.5 ppm) than their
NBO-poor counterparts,39,43 which might stem from a minor
degree of B[4]–NBO bonding. (iii) 2Q–1Q correlation 11B NMR experiments of NBO-rich
BS glasses also suggest slightly higher 11B[4] shifts relative to their NBO-poor counterparts. That
feature is most evident from the 2Q projections of 2Q–1Q 11B NMR spectra shown in Figure 6a, which were recorded from a series of RNa2O–B2O3–2.0SiO2 glasses with increasing Na2O content R, where we employ the more general MK–R or MNaK–R glass notation of refs (40 and 68). The NBO contents are negligible in all R ⩽
0.75 glasses but significant for the R = {2.1, 2.5}
counterparts (the 2D NMR spectra are displayed in Figure 2 of Lv et
al.68). Notably, the NBO-free Na BS glasses
reveal near-constant peak-maxima shifts of ≈0.0 ppm for the 11B[4]–O–11B[4] correlation peak, whereas those of the two Na2.0–2.1 and
Na2.0–2.5 glasses are markedly higher by ≈2 ppm. Likewise,
the 2Q peak maxima observed from the 2.0–2.1 glass series with xNBO ≈ 0.36 shown in Figure 6b are consistently ≈1.7
ppm higher than their NBO-free 2.0–0.75 counterparts displayed
in Figure 6c.
Figure 6.
Projections along the 2Q dimension of 2Q–1Q 11B NMR spectra from K–R BS glasses, with R given by Equation 3: (a) Na2.0–R with R increasing (see legend), (b) 2.0–2.1, and (c) 2.0–0.75. Each legend specifies the NBO content (xNBO) of the glass, along with its network modifier(s) in (b, c). As indicated in (a), each 2Q spectrum comprises three groups of 2Q signals from 11B[3]–O–11B[3] (left), 11B[3]–O–11B[4] (middle), and 11B[4]–O–11B[4] (right) linkages.
Although both trends (ii) and
(iii) evidence a minor but consistent 11B[4] deshielding
for elevating NBO contents, further studies are needed for confirming
that they indeed stem from B[4]–NBO bonds and not
from other structural changes, such as 11B deshielding
from altered bond-angle distributions around the tetrahedral sites,
where decreased B[4]–O–F bond angles are also expected to increase 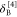 .95
.95
6. Conclusions
The “spectral editing” features of double-quantum filtration as probed via the horizontal projection of a 2Q–1Q 11B 2D NMR spectrum offered qualitative constraints on the 11B[3] and 11B[4] resonance assignments concerning their degrees of intermixing with the SiO4, BO3, and BO4 network groups in two BS glass branches with variable network modifiers but (very) low NBO contents and fixed molar ratios nSi/nB of 1.0 (K = 2.0) and 2.0 (K = 4.0). 2QF suppresses 11B[p] resonances from sites without any direct O linkage to another B neighbor, whereas those from 11B[p] sites with several B neighbors become emphasized.
The 2Q–1Q correlation NMR results show conclusively that
the BO4 groups may interlink with any {Si,
B[3], B[4]} species but the correspondingly
decreasing preference factors P(B[4]–O–B[3]) > P(B[4]–O–Si)
≫ P(B[4]–O–B[4]),40,67,68 along with the nSi/nB molar ratio and { ,
, 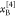 } speciation, strongly affect the B[4]–O–{Si, B[3], B[4]}
intermixing. Hence, for Si-rich glasses with dominantly BO4 groups—such as all K = 4.0 glasses herein
with low-CFS alkali-metal cations—limits the formation of the most preferred B[4]–O–B[3] linkages and effectively boosts the number of B[4]–O–Si
bridges, which are strongly preferred over B[4]–O–B[4]. Hence, as observed previously for similar glass compositions,25−27 our 11B MAS NMR spectral deconvolutions revealed that
B[4]–O–Si linkages dominate and implying
on average ≈3.1 and ≈3.4 Si atoms around the B[4] sites in the K = 2.0 and K = 4.0
glasses, respectively. However, because the borate speciation depends
strongly on the field strength of the network modifiers and the BO3 abundance increases concurrently with the Mz+ CFS,10,38 both the 11B[4] MAS NMR spectrum and the average number of
B[4]–O–Si linkages of the MgNa4.0 glass are
much closer to those of the B-richer MNa2.0 glasses
than its Si-rich sister glasses.
} speciation, strongly affect the B[4]–O–{Si, B[3], B[4]}
intermixing. Hence, for Si-rich glasses with dominantly BO4 groups—such as all K = 4.0 glasses herein
with low-CFS alkali-metal cations—limits the formation of the most preferred B[4]–O–B[3] linkages and effectively boosts the number of B[4]–O–Si
bridges, which are strongly preferred over B[4]–O–B[4]. Hence, as observed previously for similar glass compositions,25−27 our 11B MAS NMR spectral deconvolutions revealed that
B[4]–O–Si linkages dominate and implying
on average ≈3.1 and ≈3.4 Si atoms around the B[4] sites in the K = 2.0 and K = 4.0
glasses, respectively. However, because the borate speciation depends
strongly on the field strength of the network modifiers and the BO3 abundance increases concurrently with the Mz+ CFS,10,38 both the 11B[4] MAS NMR spectrum and the average number of
B[4]–O–Si linkages of the MgNa4.0 glass are
much closer to those of the B-richer MNa2.0 glasses
than its Si-rich sister glasses.
For the hitherto most common range of BS glasses with comparable Si and B contents and low NBO contents, such as those with molar fractions 1 ⩽ nSi/nB ⩽ 2 considered herein, we recommend deconvoluting the 11B[4] resonance region with three peak components, i.e., {B[4](2Si), B[4](3Si), B[4](4Si)}, where B[4](mSi) implies 4 – m bonds to “B”, which may constitute either of B[3] and B[4] but with the former dominating. The hitherto most popular two-peak deconvolution that only accounts for B[4](3Si) and B[4](4Si) sites, however, will significantly overestimate the degree of B[4]–O–Si linkages at the expense of B[4]–O–B[p] for comparatively B-rich BS-based glasses (nSi/nB < 2). It is therefore only justified for NBO-free but very Si-rich glasses, such as Pyrex.28−30
Concerning the 11B[3] NMR spectral region, we employed the prevailing but rather arbitrary two-component deconvolution into resonances from B[3](R) (“ring”) and B[3](NR) (“non-ring”) sites. 2QF application strongly emphasizes the NMR signal intensities from the B[3](R) sites, implying that they involve very few (if any) bonds to Si but comparable amounts of B[3]–O–B[3] and B[3]–O–B[4] linkages, consistent with BO3 and BO4 groups that coexist in superstructural “ring” units. Yet a non-negligible fraction of the B[3] sites may form boroxol groups, notably so in glasses with dominant BO3 populations, such as in Mg-bearing glasses (Figure 2). The B[3](NR) sites, on the other hand, involve a significant B[3]–O–Si bonding, in particular in the Si-rich MgNa4.0 glass, as verified from their markedly lower NMR-signal intensities resulting after 2QF. Combining the NMR results herein and in ref (40) conclusively shows that the B[3](NR) sites feature linkages to all of B[3], B[4], and Si, where the latter are likely dominating, along previous findings.25,26,33
Although these two- and three-NMR-peak representations of the respective B[3] and B[4] environments in BS glasses are obviously oversimplified, they currently appear to be the only option for even attempting to characterize the F = {Si, B[3], B[4]} intermixing around the tri- and tetragonal B sites in BS-based glasses via routine 11B MAS NMR experiments. In general, however, such multiparameter spectral-deconvolution analyses may at best provide semiquantitative site populations. More reliable and accurate data are only expected in limited cases, such as for 11B MAS NMR spectra recorded at high magnetic fields (⩾18.8 T) from very Si-rich glasses.28−30 We also underscore that these caveats concern essentially NBO-free BS glasses, while we discourage even attempting spectral deconvolutions from glasses with significant NBO contents. Circumstantial evidence does suggest that 11B[4] chemical shifts are consistently higher in NBO-rich glasses. Yet additional insight from complementary spectroscopic techniques and advanced 11B/17O MAS NMR experimentation, along with structure/chemical-shift investigations by DFT calculations, is required to gain further insight. This is currently underway in our laboratory.
Acknowledgments
This research was funded by the Swedish Research Council (project VR 2022-03652) and, in part, by the China Postdoctoral Science Foundation (project 2022M711445), as well as a scholarship awarded by the China Scholarship Council to PL as a visiting PhD student at Stockholm University. The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through grant agreement no. 2022-06725.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.4c06721.
Tables with additional data of CFS values, best-fit parameters and data uncertainties of the spectral deconvolutions, and MD-derived preference factors for the Si/B[p] intermixing (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Wright A. C. Borate Structures: Crystalline and Vitreous. Phys. Chem. Glass: Eur. J. Glass Sci. Technol., Part B 2010, 51, 1–39. [Google Scholar]
- MacKenzie K. J. D.; Smith M. E.. Multinuclear Solid-State NMR of Inorganic Materials; Pergamon Press: Amsterdam, 2002. [Google Scholar]
- Edén M.NMR of Glasses, in NMR of Inorganic Nuclei. In Comprehensive Inorganic Chemistry III, Bryce D. L.; Reedijk J.; Poeppelmeier K. R, Eds.; Elsevier: Oxford, 2023; Vol. 9, pp. 583–659. [Google Scholar]
- Edén M. Probing Oxide-Based Glass Structures by Solid-State NMR: Opportunities and Limitations. J. Magn. Reson. Open 2023, 16–17, 100112. 10.1016/j.jmro.2023.100112. [DOI] [Google Scholar]
- Abe T. Borosilicate Glasses. J. Am. Ceram. Soc. 1952, 35, 284–299. 10.1111/j.1151-2916.1952.tb13051.x. [DOI] [Google Scholar]
- Grandjean A.; Malki M.; Montouillout V.; Debruycker F.; Massiot D. Electrical Conductivity and 11B NMR Studies of Sodium Borosilicate Glasses. J. Non-Cryst. Solids 2008, 354, 1664–1670. 10.1016/j.jnoncrysol.2007.10.007. [DOI] [Google Scholar]
- Kato Y.; Yamazaki H.; Kubo Y.; Yoshida S.; Matsuoka J.; Akai T. Effect of B2O3 Content on Crack Initiation under Vickers Indentation Test. J. Ceram. Soc. Jpn. 2010, 118, 792–798. 10.2109/jcersj2.118.792. [DOI] [Google Scholar]
- Neyret M.; Lenoir M.; Grandjean A.; Massoni N.; Penelon B.; Malki M. Ionic Transport of Alkali in Borosilicate Glass. Role of Alkali Nature on Glass Structure and on Ionic Conductivity at the Glassy State. J. Non-Cryst. Solids 2015, 410, 74–81. 10.1016/j.jnoncrysol.2014.12.002. [DOI] [Google Scholar]
- Limbach R.; Winterstein-Beckmann A.; Dellith J.; Möncke D.; Wondraczek L. Plasticity, Crack Initiation and Defect Resistance in Alkali-Borosilicate Glasses: From Normal to Anomalous Behavior. J. Non-Cryst. Solids 2015, 417–418, 15–27. 10.1016/j.jnoncrysol.2015.02.019. [DOI] [Google Scholar]
- Lv P.; Wang C.; Stevensson B.; Yu Y.; Wang T.-S.; Edén M. Impact of the Cation Field Strength on Physical Properties and Structures of Alkali and Alkaline-Earth Borosilicate Glasses. Ceram. Int. 2022, 48, 18094–18107. 10.1016/j.ceramint.2022.03.022. [DOI] [Google Scholar]
- Chryssikos G. D.; Kamitsos E. I.; Karakassides M. A. Structure of Borate Glasses. Part 2. Alkali Induced Network Modifications in terms of Structure and Properties. Phys. Chem. Glasses 1990, 31, 109–116. [Google Scholar]
- Kamitsos E. I.; Chryssikos G. D.; Karakassides M. A. New Insights into the Structure of Alkali Borate Glasses. J. Non-Cryst. Solids 1990, 123, 283–285. 10.1016/0022-3093(90)90796-O. [DOI] [Google Scholar]
- Konijnendijk W. L.; Stevels J. M. The Structure of Borosilicate Glasses Studied by Raman Scattering. J. Non-Cryst. Solids 1976, 20, 193–224. 10.1016/0022-3093(76)90132-0. [DOI] [Google Scholar]
- Manara D.; Grandjean A.; Neuville D. R. Advances in Understanding the Structure of Borosilicate Glasses: A Raman Spectroscopy Study. Am. Mineral 2009, 94, 777–784. 10.2138/am.2009.3027. [DOI] [Google Scholar]
- Liu H.; Smedskjaer M. M.; Tao H.; Jensen L. R.; Zhao X.; Yue Y. A Medium Range Order Structural Connection to the Configurational Heat Capacity of Borate–Silicate Mixed Glasses. Phys. Chem. Chem. Phys. 2016, 18, 10887–10895. 10.1039/C6CP00749J. [DOI] [PubMed] [Google Scholar]
- Meera B. N.; Ramakrishna J. Raman Spectral Studies of Borate Glasses. J. Non-Cryst. Solids 1993, 159, 1–21. 10.1016/0022-3093(93)91277-A. [DOI] [Google Scholar]
- Bunker B. C.; Tallant D. R.; Kirkpatrick R. J.; Turner G. L. Multinuclear Nuclear Magnetic Resonance and Raman Investigation of Sodium Borosilicate Glass Structures. Phys. Chem. Glasses 1990, 31, 30–41. [Google Scholar]
- van Wüllen L.; Müller-Warmuth W. 11B MAS NMR Spectroscopy for Characterizing the Structure of Glasses. Solid State Nucl. Magn. Reson. 1993, 2, 279–284. 10.1016/0926-2040(93)90009-C. [DOI] [PubMed] [Google Scholar]
- Yun Y. H.; Bray P. J. Nuclear Magnetic Resonance Studies of the Glasses in the System Na2O–B2O3–SiO2. J. Non-Cryst. Solids 1978, 27, 363–380. 10.1016/0022-3093(78)90020-0. [DOI] [Google Scholar]
- Dell W. J.; Bray P. J.; Xiao S. Z. 11B NMR Studies and Structural Modeling of Na2O–B2O3–SiO2 Glasses of High Soda Content. J. Non-Cryst. Solids 1983, 58, 1–16. 10.1016/0022-3093(83)90097-2. [DOI] [Google Scholar]
- Turner G. L.; Smith K. A.; Kirkpatrick R. J.; Oldfield E. Boron-11 Nuclear Magnetic Resonance Spectroscopic Study of Borate and Borosilicate Minerals and a Borosilicate Glass. J. Magn. Reson. 1986, 67, 544–550. 10.1016/0022-2364(86)90391-4. [DOI] [Google Scholar]
- van Wüllen L.; Müller-Warmuth W.; Papageorgiou D.; Pentinghaus H. J. Characterization and Structural Developments of Gel-Derived Borosilicate Glasses: A Multinuclear MAS-NMR Study. J. Non-Cryst. Solids 1994, 171, 53–67. 10.1016/0022-3093(94)90032-9. [DOI] [Google Scholar]
- Martens R.; Müller-Warmuth W. Structural Groups and Their Mixing in Borosilicate Glasses of Various Compositions – an NMR Study. J. Non-Cryst. Solids 2000, 265, 167–175. 10.1016/S0022-3093(99)00693-6. [DOI] [Google Scholar]
- Du L.-S.; Stebbins J. F. Network Connectivity in Aluminoborosilicate Glasses: A High-Resolution 11B, 27Al and 17O NMR Study. J. Non-Cryst. Solids 2005, 351, 3508–3520. 10.1016/j.jnoncrysol.2005.08.033. [DOI] [Google Scholar]
- Du L.-S.; Stebbins J. F. Solid-State NMR Study of Metastable Immiscibility in Alkali Borosilicate Glasses. J. Non-Cryst. Solids 2003, 315, 239–255. 10.1016/S0022-3093(02)01604-6. [DOI] [Google Scholar]
- Du L.-S.; Stebbins J. F. Nature of Silicon-Boron Mixing in Sodium Borosilicate Glasses: A High-Resolution 11B and 17O NMR Study. J. Phys. Chem. B 2003, 107, 10063–10076. 10.1021/jp034048l. [DOI] [Google Scholar]
- Du L.-S.; Stebbins J. F. Site Preference and Si/B Mixing in Mixed-Alkali Borosilicate Glasses: A-High Resolution 11B and 17O NMR Study. Chem. Mater. 2003, 15, 3913–3921. 10.1021/cm034427r. [DOI] [Google Scholar]
- Prasad S.; Clark T. M.; Sefzik T. H.; Kwak H.-T.; Gan Z.-H.; Grandinetti P. J. Solid-State Multinuclear Magnetic Resonance Investigations of Pyrex®. J. Non-Cryst. Solids 2006, 352, 2834–2840. 10.1016/j.jnoncrysol.2006.02.085. [DOI] [Google Scholar]
- Murakami M.; Shimizu T.; Tansho M.; Akai T.; Yazawa T. 11B–11B Two-Dimensional Correlation Nuclear Magnetic Resonance on Sodium Borosilicate Glass. Chem. Lett. 2010, 39, 32–33. 10.1246/cl.2010.32. [DOI] [Google Scholar]
- Tricot G. The Structure of Pyrex® Glass Investigated by Correlation NMR Spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 26764–26770. 10.1039/C6CP02996E. [DOI] [PubMed] [Google Scholar]
- Angeli F.; Charpentier T.; de Ligny D.; Cailleteau C. Boron Speciation in Soda-Lime Borosilicate Glasses Containing Zirconium. J. Am. Ceram. Soc. 2010, 93, 2693–2704. 10.1111/j.1551-2916.2010.03771.x. [DOI] [Google Scholar]
- Angeli F.; Villain O.; Schuller S.; Charpentier T.; de Ligny D.; Bressel L.; Wondraczek L. Effect of Temperature and Thermal History on Borosilicate Glass Structure. Phys. Rev. B 2012, 85, 054110. 10.1103/PhysRevB.85.054110. [DOI] [Google Scholar]
- Wegner S.; van Wüllen L.; Tricot G. The Structure of Phosphate and Borosilicate Glasses and Their Structural Evolution at High Temperatures as Studied with Solid State NMR Spectroscopy: Phase Separation, Crystallisation and Dynamic Species Exchange. Solid State Sci. 2010, 12, 428–439. 10.1016/j.solidstatesciences.2009.03.021. [DOI] [Google Scholar]
- Howes A. P.; Vedishcheva N. M.; Samoson A.; Hanna J. V.; Smith M. E.; Holland D.; Dupree R. Boron Environments in Pyrex® Glass—a High Resolution, Double-Rotation NMR and Thermodynamic Modelling Study. Phys. Chem. Chem. Phys. 2011, 13, 11919–11928. 10.1039/c1cp20771g. [DOI] [PubMed] [Google Scholar]
- Angeli F.; Charpentier T.; Molières E.; Soleilhavoup A.; Jollivet P.; Gin S. Influence of Lanthanum on Borosilicate Glass Structure: A Multinuclear MAS and MQMAS NMR Investigation. J. Non-Cryst. Solids 2013, 376, 189–198. 10.1016/j.jnoncrysol.2013.05.042. [DOI] [Google Scholar]
- Angeli F.; Charpentier T.; Gaillard M.; Jollivet P. Influence of Zirconium on the Structure of Pristine and Leached Soda-Lime Borosilicate Glasses: Towards A Quantitative Approach by 17O MQMAS NMR. J. Non-Cryst. Solids 2008, 354, 3713–3722. 10.1016/j.jnoncrysol.2008.03.046. [DOI] [Google Scholar]
- Krishnamurthy A.; Kroeker S. Improving Molybdenum and Sulfur Vitrification in Borosilicate Nuclear Waste Glasses Using Phosphorus: Structural Insights from NMR. Inorg. Chem. 2022, 61, 73–85. 10.1021/acs.inorgchem.1c01913. [DOI] [PubMed] [Google Scholar]
- Lv P.; Sun Z.; Wang F.; Yu Y.; Yang F.; Yue S.; Edén M.; Chen L.; Wang T. Cation Field-Strength Effects on Ion Irradiation-Induced Mechanical Property Changes of Borosilicate Glass Structures. J. Am. Ceram. Soc. 2023, 106, 5766–5780. 10.1111/jace.19213. [DOI] [Google Scholar]
- Yu Y.; Edén M. Structure-Composition Relationships of Bioactive Borophosphosilicate Glasses Probed by Multinuclear 11B, 29Si, and 31P Solid-State NMR. RSC Adv. 2016, 6, 101288–101303. 10.1039/C6RA15275A. [DOI] [Google Scholar]
- Lv P.; Stevensson B.; Mathew R.; Wang T.; Edén M. Sub-Nanometer-Range Structural Effects From Mg2+ Incorporation in Na-Based Borosilicate Glasses Revealed by Heteronuclear NMR and MD Simulations. J. Phys. Chem. B 2024, 128, 6922–6939. 10.1021/acs.jpcb.4c01840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y.; Stevensson B.; Edén M. Medium-Range Structural Organization of Phosphorus-Bearing Borosilicate Glasses Revealed by Advanced Solid-State NMR Experiments and MD Simulations: Consequences of B/Si Substitutions. J. Phys. Chem. B 2017, 121, 9737–9752. 10.1021/acs.jpcb.7b06654. [DOI] [PubMed] [Google Scholar]
- Edén M.; Sundberg P.; Stålhandske C. The Split Network Analysis for Exploring Composition–Structure Correlations in Multi-Component Glasses: II. Multinuclear NMR Studies of Alumino-Borosilicates and Glass-Wool Fibers. J. Non-Cryst. Solids 2011, 357, 1587–1594. 10.1016/j.jnoncrysol.2010.11.101. [DOI] [Google Scholar]
- Stone-Weiss N.; Bradtmüller H.; Fortino M.; Bertani M.; Youngman R. E.; Pedone A.; Eckert H.; Goel A. Combined Experimental and Computational Approach toward the Structural Design of Borosilicate-Based Bioactive Glasses. J. Phys. Chem. C 2020, 124, 17655–17674. 10.1021/acs.jpcc.0c04470. [DOI] [Google Scholar]
- Krogh-Moe J. New Evidence on the Boron Co-ordination in Alkali Borate Glasses. Phys. Chem. Glasses 1962, 3, 1–6. [Google Scholar]
- Konijnendijk W. L.; Stevels J. M. The Structure of Borate Glasses Studied by Raman Scattering. J. Non-Cryst. Solids 1975, 18, 307–331. 10.1016/0022-3093(75)90137-4. [DOI] [Google Scholar]
- El-Damrawi G.; Müller-Warmuth W.; Doweidar H.; Gohar I. A. Structure and Heat Treatment Effects of Sodium Borosilicate Glasses as Studied by 29Si and 11B NMR. J. Non-Cryst. Solids 1992, 146, 137–144. 10.1016/S0022-3093(05)80485-5. [DOI] [Google Scholar]
- Züchner L.; Chan J. C. C.; Müller-Warmuth W.; Eckert H. Short-Range Order and Site Connectivities in Sodium Aluminoborate Glasses: I. Quantification of Local Environments by High-Resolution 11B, 23Na, and 27Al Solid-State NMR. J. Phys. Chem. B 1998, 102, 4495–4506. 10.1021/jp980587s. [DOI] [Google Scholar]
- Bertmer M.; Züchner L.; Chan J. C. C.; Eckert H. Short and Medium Range Order in Sodium Aluminoborate Glasses: 2. Site Connectivities and Cation Distributions Studied by Rotational Echo Double Resonance NMR Spectroscopy. J. Phys. Chem. B 2000, 104, 6541–6553. 10.1021/jp9941918. [DOI] [Google Scholar]
- Soudani S.; Paris M.; Morizet Y. Influence of High-Pressure on the Short-Range Structure of Ca or Na Aluminoborosilicate Glasses from 11B and 27Al Solid-State NMR. J. Non-Cryst. Solids 2024, 638, 123085. 10.1016/j.jnoncrysol.2024.123085. [DOI] [Google Scholar]
- Soudani S.; Paris M.; Morizet Y. The Effect of Iodine on the Local Environment of Network-Forming Elements in Aluminoborosilicate Glasses: An NMR Study. J. Am. Ceram. Soc. 2024, 107, 4557–4571. 10.1111/jace.19764. [DOI] [Google Scholar]
- Youngman R. E.; Haubrich S. T.; Zwanziger J. W.; Janicke M. T.; Chmelka B. F. Short- and Intermediate-Range Structural Ordering in Glassy Boron Oxide. Science 1995, 269, 1416–1420. 10.1126/science.269.5229.1416. [DOI] [PubMed] [Google Scholar]
- Umari O.; Pasquarello A. Fraction of Boroxol Rings in Vitreous Boron Oxide from a First-Principles Analysis of Raman and NMR Spectra. Phys. Rev. Lett. 2005, 95, 137401. 10.1103/PhysRevLett.95.137401. [DOI] [PubMed] [Google Scholar]
- Zwanziger J. W. The NMR Response of Boroxol Rings: A Density Functional Theory Study. J. Non-Cryst. Solids 2005, 27, 5–9. 10.1016/j.ssnmr.2004.08.004. [DOI] [PubMed] [Google Scholar]
- Hung I.; Howes A. P.; Parkinson B. G.; Anupold T.; Samoson A.; Brown S. P.; Harrison P. F.; Holland D.; Dupree R. Determination of the Bond-Angle Distribution in Vitreous B2O3 by 11B Double Rotation (DOR) NMR Spectroscopy. J. Solid State Chem. 2009, 182, 2402–2408. 10.1016/j.jssc.2009.06.025. [DOI] [Google Scholar]
- Eckert H.Advanced Dipolar Solid State NMR Spectroscopy of Glasses, in Modern Glass Characterization. Affatigato M.John Wiley & Sons, Ltd; Vol. 92015. pp. 1–46. [Google Scholar]
- van Wüllen L.; Schwering G. 11B MQMAS and 29Si–11B Double-Resonance NMR Studies on the Structure of Binary B2O3–SiO2 Glasses. Solid State Nucl. Magn. Reson. 2002, 21, 134–144. 10.1006/snmr.2002.0054. [DOI] [Google Scholar]
- Martineau C.; Michaelis V.; Schuller S.; Kroeker S. Liquid-Liquid Phase Separation in Model Nuclear Waste Glasses: A Solid-State Double-Resonance NMR Study. Chem. Mater. 2010, 22, 4896–4903. 10.1021/cm1006058. [DOI] [Google Scholar]
- Venkatachalam S.; Schröder C.; Wegner S.; van Wüllen L. The Structure of Borosilicate and Phosphosilicate Glasses and its Evolution at Temperatures Above the Glass Transition Temperature: Lessons from In Situ MAS NMR. Phys. Chem. Glas.: Eur. J. Glass Sci. Technol., Part B 2014, 55, 280–287. [Google Scholar]
- Möncke D.; Tricot G.; Winterstein-Beckmann A.; Wondraczek L.; Kamitsos E. I. On the Connectivity of Borate Tetrahedra in Borate and Borosilicate Glasses. Phys. Chem. Glas.: Eur. J. Glass Sci. Technol., Part B 2015, 56, 203–211. 10.13036/1753-3562.56.5.203. [DOI] [Google Scholar]
- Möncke D.; Tricot G.; Winterstein A.; Ehrt D.; Kamitsos E. I. Preferential Bonding in Low Alkali Borosilicate Glasses. Phys. Chem. Glas.: Eur. J. Glass Sci. Technol., Part B 2017, 58, 171–179. 10.13036/17533562.58.4.171. [DOI] [Google Scholar]
- Frydman L.; Harwood J. S. Isotropic Spectra of Half-Integer Quadrupolar Spins from Bidimensional Magic-Angle-Spinning NMR. J. Am. Chem. Soc. 1995, 117, 5367–5368. 10.1021/ja00124a023. [DOI] [Google Scholar]
- Wang S.; Stebbins J. F. Multiple-Quantum Magic-Angle Spinning 17O NMR Studies of Borate, Borosilicate, and Boroaluminate Glasses. J. Am. Ceram. Soc. 1999, 82, 1519–1528. 10.1111/j.1151-2916.1999.tb01950.x. [DOI] [Google Scholar]
- Du L.-S.; Stebbins J. F. Site Connectivities in Sodium Aluminoborate Glasses: Multinuclear and Multiple Quantum NMR Results. Solid State Nucl. Magn. Reson. 2005, 27, 37–49. 10.1016/j.ssnmr.2004.08.003. [DOI] [PubMed] [Google Scholar]
- Zhao P.; Kroeker S.; Stebbins J. F. Non-Bridging Oxygen Sites in Barium Borosilicate Glasses: Results from 11B and 17O NMR. J. Non-Cryst. Solids 2000, 276, 122–131. 10.1016/S0022-3093(00)00290-8. [DOI] [Google Scholar]
- Stebbins J. F.; Kroeker S.; Lee S. K.; Kiczenski T. J. Quantification of Five- and Six-Coordinated Aluminum Ions in Aluminosilicate and Fluoride-Containing Glasses by High-Field, High-Resolution 27Al NMR. J. Non-Cryst. Solids 2000, 275, 1–6. 10.1016/S0022-3093(00)00270-2. [DOI] [Google Scholar]
- Michaelis V.; Aguiar P. M.; Kroeker S. Probing Alkali Coordination Environments in Alkali Borate Glasses by Multinuclear Magnetic Resonance. J. Non-Cryst. Solids 2007, 353, 2582–2590. 10.1016/j.jnoncrysol.2007.04.029. [DOI] [Google Scholar]
- Yu Y.; Stevensson B.; Edén M. Direct Experimental Evidence for Abundant BO4–BO4 Motifs in Borosilicate Glasses from Double-Quantum 11B NMR Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 6372–6376. 10.1021/acs.jpclett.8b02907. [DOI] [PubMed] [Google Scholar]
- Lv P.; Stevensson B.; Yu Y.; Wang T.; Edén M. BO3/BO4 Intermixing in Borosilicate Glass Networks Probed by Double-Quantum 11B NMR: What Factors Govern BO4–BO4 Formation?. J. Phys. Chem. C 2023, 127, 20026–20040. 10.1021/acs.jpcc.3c03577. [DOI] [Google Scholar]
- Mali G.; Fink G.; Taulelle F. Double-Quantum Homonuclear Correlation Magic Angle Sample Spinning Nuclear Magnetic Resonance Spectroscopy of Dipolar-Coupled Quadrupolar Nuclei. J. Chem. Phys. 2004, 120, 2835–2845. 10.1063/1.1638741. [DOI] [PubMed] [Google Scholar]
- Edén M.; Zhou D.; Yu J. Improved Double-Quantum NMR Correlation Spectroscopy of Dipolar-Coupled Quadrupolar Spins. Chem. Phys. Lett. 2006, 431, 397–403. 10.1016/j.cplett.2006.09.081. [DOI] [Google Scholar]
- Edén M. Homonuclear Dipolar Recoupling of Half-Integer Spin Quadrupolar Nuclei: Techniques and Applications. Solid State Nucl. Magn. Reson. 2009, 36, 1–10. 10.1016/j.ssnmr.2009.06.005. [DOI] [PubMed] [Google Scholar]
- Edén M.Recent Progress in Homonuclear Correlation Spectroscopy of Quadrupolar Nuclei. In Modern Magnetic Resonance 2nd ed.; Springer: Cham: 2018. pp. 1093–1124. [DOI] [Google Scholar]
- Dietzel A. Die Kationenfeldstärken und ihre Beziehungen zu Entglasungsvorgängen, zur Verbindungsbildung und zu den Schmelzpunkten von Silicaten. Z. Electrochem. 1942, 48, 9–23. 10.1002/bbpc.19420480104. [DOI] [Google Scholar]
- Shannon R. D. Revised Effective Ionic-Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. 1976, A32, 751–767. 10.1107/S0567739476001551. [DOI] [Google Scholar]
- Massiot D.; Bessada C.; Coutures J. P.; Taulelle F. A Quantitative Study of 27Al MAS NMR in Crystalline YAG. J. Magn. Reson. 1990, 90, 231–242. 10.1016/0022-2364(90)90130-2. [DOI] [Google Scholar]
- Lo A. Y. H.; Edén M. Efficient Symmetry-Based Homonuclear Dipolar Recoupling of Quadrupolar Spins: Double-Quantum NMR Correlations in Amorphous Solids. Phys. Chem. Chem. Phys. 2008, 10, 6635–6644. 10.1039/b808295b. [DOI] [PubMed] [Google Scholar]
- Teymoori G.; Pahari B.; Edén M. Low-Power Broadband Homonuclear Dipolar Recoupling in MAS NMR by Two-Fold Symmetry Pulse Schemes for Magnetization Transfers and Double-Quantum Excitation. J. Magn. Reson. 2015, 261, 205–220. 10.1016/j.jmr.2015.09.004. [DOI] [PubMed] [Google Scholar]
- Edén M. Two-Dimensional MAS NMR Correlation Protocols Involving Double-Quantum Filtering of Quadrupolar Spin-Pairs. J. Magn. Reson. 2010, 204, 99–110. 10.1016/j.jmr.2010.02.007. [DOI] [PubMed] [Google Scholar]
- Ernst R. R.; Bodenhausen G.; Wokaun A.. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Clarendon Press: Oxford, 1987 [Google Scholar]
- Edén M.; Lee Y. K.; Levitt M. H. Efficient Simulation of Periodic Problems in NMR. Application to Decoupling and Rotational Resonance. J. Magn. Reson. Ser. A 1996, 120, 56–71. 10.1006/jmra.1996.0099. [DOI] [Google Scholar]
- Stevensson B.; Edén M. Efficient Orientational Averaging by the Extension of Lebedev Grids via Regularized Octahedral Symmetry Expansion. J. Magn. Reson. 2006, 181, 162–176. 10.1016/j.jmr.2006.04.008. [DOI] [PubMed] [Google Scholar]
- Czjzek G.; Fink J.; Götz F.; Schmidt H.; Coey J. M. D.; Rebouillat J.-P.; Liénard A. Atomic Coordination and the Distribution of Electric Field Gradients in Amorphous Solids. Phys. Rev. B 1981, 23, 2513–2530. 10.1103/PhysRevB.23.2513. [DOI] [Google Scholar]
- d’Espinose de Lacaillerie J.-B.; Fretigny C.; Massiot D. MAS NMR Spectra of Quadrupolar Nuclei in Disordered Solids: The Czjzek Model. J. Magn. Reson. 2008, 192, 244–251. 10.1016/j.jmr.2008.03.001. [DOI] [PubMed] [Google Scholar]
- Saini R.; Kapoor S.; Neuville D. R.; Youngman R. E.; Cerrutti B. M.; McCloy J. S.; Eckert H.; Goel A. Correlating Sulfur Solubility with Short-to-Intermediate Range Ordering in the Structure of Borosilicate Glasses. J. Phys. Chem. B 2022, 126, 655–674. 10.1021/acs.jpcc.1c08654. [DOI] [Google Scholar]
- Yu Y.; Keil P.; Stevensson B.; Hansen M. R.; Edén M. Assessment of new symmetry-based dipolar recoupling schemes for homonuclear magnetization exchange between quadrupolar nuclei in two-dimensional correlation MAS NMR. J. Magn. Reson 2020, 316, 106734. 10.1016/j.jmr.2020.106734. [DOI] [PubMed] [Google Scholar]
- Wu X.; Youngman R. E.; Dieckmann R. Sodium Tracer Diffusion and 11B NMR Study of Glasses of the Type (Na2O)0.17(B2O3)x(SiO2)0.83-x. J. Non-Cryst. Solids 2013, 378, 168–176. 10.1016/j.jnoncrysol.2013.06.012. [DOI] [Google Scholar]
- Barlet M.; Kerrache A.; Delaye J.-M.; Rountree C. L. SiO2–Na2O–B2O3 Density: A Comparison of Experiments, Simulations, and Theory. J. Non-Cryst. Solids 2013, 382, 32–44. 10.1016/j.jnoncrysol.2013.09.022. [DOI] [Google Scholar]
- Pacaud F.; Delaye J.-M.; Charpentier T.; Cormier L.; Salanne M. Structural Study of Na2O–B2O3–SiO2 Glasses from Molecular Simulations Using a Polarizable Force Field. J. Chem. Phys. 2017, 147, 161711. 10.1063/1.4992799. [DOI] [PubMed] [Google Scholar]
- Fortino M.; Berselli A.; Stone-Weiss N.; Deng L.; Goel A.; Du J.; Pedone A. Assessment of Interatomic Parameters for the Reproduction of Borosilicate Glass Structures via DFT-GIPAW Calculations. J. Am. Ceram. Soc. 2019, 102, 7225–7243. 10.1111/jace.16655. [DOI] [Google Scholar]
- Llor A.; Virlet J. Towards High-Resolution NMR of More Nuclei in Solids: Sample Spinning with Time-Dependent Spinner Axis Angle. Chem. Phys. Lett. 1988, 152, 248–253. 10.1016/0009-2614(88)87362-7. [DOI] [Google Scholar]
- Samoson A.; Lippmaa E.; Pines A. High Resolution Solid-State N.M.R. Averaging of Second-Order Effects by Means of a Double Rotor. Mol. Phys. 1988, 65, 1013–1018. 10.1080/00268978800101571. [DOI] [Google Scholar]
- Youngman R. E.; Zwanziger J. W. On the Formation of Tetracoordinate Boron in Rubidium Borate Glasses. J. Am. Chem. Soc. 1995, 117, 1397–1402. 10.1021/ja00109a026. [DOI] [Google Scholar]
- Youngman R. E.; Zwanziger J. W. Network Modification in Potassium Borate Glasses: Structural Studies with NMR and Raman Spectroscopies. J. Phys. Chem. 1996, 100, 16720–16728. 10.1021/jp961439+. [DOI] [Google Scholar]
- Wu J.; Stebbins J. F. Quench Rate and Temperature Effects on Boron Coordination in Aluminoborosilicate Melts. J. Non-Cryst. Solids 2010, 356, 2097–2108. 10.1016/j.jnoncrysol.2010.08.015. [DOI] [Google Scholar]
- Alderman O. L. G.; Iuga D.; Howes A. P.; Pike K. J.; Holland D.; Dupree R. Spectral Assignments and NMR Parameter-Structure Relationships in Borates Using High-Resolution 11B NMR and Density Functional Theory. Phys. Chem. Chem. Phys. 2013, 15, 8208–8221. 10.1039/c3cp50772f. [DOI] [PubMed] [Google Scholar]
- Soleilhavoup A.; Delaye J.-M.; Angeli F.; Caurant D.; Charpentier T. Contribution of first-principles calculations to multinuclear NMR analysis of borosilicate glasses. Magn. Reson. Chem. 2010, 48, S159–S170. 10.1002/mrc.2673. [DOI] [PubMed] [Google Scholar]
- Irwin A. D.; Holmgren J. S.; Jonas J. Solid State 29Si and 11B NMR Studies of Sol-Gel Derived Borosilicates. J. Non-Cryst. Solids 1988, 101, 249–254. 10.1016/0022-3093(88)90160-3. [DOI] [Google Scholar]
- Kroeker S.; Stebbins J. F. Three-Coordinated Boron-11 Chemical Shifts in Borates. Inorg. Chem. 2001, 40, 6239–6246. 10.1021/ic010305u. [DOI] [PubMed] [Google Scholar]
- Aguiar P. M.; Kroeker S. Boron Speciation and Non-Bridging Oxygens in High-Alkali Borate Glasses. J. Non-Cryst. Solids 2007, 353, 1834–1839. 10.1016/j.jnoncrysol.2007.02.013. [DOI] [Google Scholar]
- Stevensson B.; Yu Y.; Edén M. Structure–Composition Trends in Multicomponent Borosilicate-Based Glasses Deduced from Molecular Dynamics Simulations with Improved B–O and P–O Force Fields. Phys. Chem. Chem. Phys. 2018, 20, 8192–8209. 10.1039/C7CP08593A. [DOI] [PubMed] [Google Scholar]
- Nanba T.; Nishimura M.; Miura Y. Theoretical Interpretation of the Chemical Shift of 29Si NMR Peaks in Alkali Borosilicate Glasses. Geochim. Cosmochim. Acta 2004, 68, 5103–5111. 10.1016/j.gca.2004.05.042. [DOI] [Google Scholar]
- Tilocca A.; de Leeuw N. H.; Cormack A. N. Shell-Model Molecular Dynamics Calculations of Modified Silicate Glasses. Phys. Rev. B 2006, 73, 104209. 10.1103/PhysRevB.73.104209. [DOI] [Google Scholar]
- Pedone A.; Charpentier T.; Malavasi G.; Menziani M. M. New Insights into the Atomic Structure of 45S5 Bioglass by Means of Solid-State NMR Spectroscopy and Accurate First-Principles Simulations. Chem. Mater. 2010, 22, 5644–5652. 10.1021/cm102089c. [DOI] [Google Scholar]
- Mathew R.; Stevensson B.; Tilocca A.; Edén M. Toward a Rational Design of Bioactive Glasses with Optimal Structural Features: Composition-Structure Correlations Unveiled by Solid-State NMR and MD Simulations. J. Phys. Chem. B 2014, 118, 833–844. 10.1021/jp409652k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stebbins J. F.; Zhao P.; Kroeker S. Non-Bridging Oxygens in Borate Glasses: Characterization by 11B and 17O MAS and 3QMAS NMR. Solid State Nucl. Magn. Reson. 2000, 16, 9–19. 10.1016/S0926-2040(00)00050-3. [DOI] [PubMed] [Google Scholar]
- Wu J.; Stebbins J. F. Cation Field Strength Effects on Boron Coordination in Binary Borate Glasses. J. Am. Ceram. Soc. 2014, 97, 2794–2801. 10.1111/jace.13100. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.







