A Contactless Method for Measuring the Redox Potentials of Metal Nanoparticles

Abstract

The standard redox potentials of metal nanoparticles are important for understanding their chemical properties. Traditionally, these redox potentials are measured by using voltammetry. Although voltammetry is fast and cost-effective, loading or landing the nanoparticles on electrodes alters their electrochemical properties, posing a challenge for accurately determining their intrinsic redox potentials. Here, a contactless method was developed utilizing chemical assays and the Nernst equation to measure the standard reduction potentials of gold nanoparticles in their colloidal state. To showcase the versatility and accuracy of this Nernstian approach, the reduction potentials were measured for a size range of 5.0–73 nm, revealing their scaling law and dependence on the nanoparticle surface energy.

Determining the reduction or oxidation potentials of metal nanoparticles is important for understanding their chemical properties and developing their applications.¹⁻³ Powerful electrochemical techniques like anodic stripping voltammetry have enabled the investigation of metal nanoparticles’ oxidation potentials in relation to their size,⁴ elemental composition,⁵ surface charge,⁶ and dispersity.⁷ While voltammetry methods are fast and cost-effective, they require the loading or landing of the nanoparticles onto the electrodes (Figure 1a). Consequently, the interactions between the particles and electrodes alter the original redox potentials of the nanoparticles because two contacted materials with different work functions can exchange charge.⁶⁻⁸ In this work, the redox potentials of gold nanoparticles are determined when they are in a colloidal form. The particles establish a redox reaction equilibrium with a redox couple in solution, which can probe the particle potentials (Figure 1b). This contactless method utilizes the Nernst equation to provide, for the first time, the standard reduction potentials of colloidal nanoparticles in solution and their size-dependent property.

Figure 1.

Contactless method for determining standard reduction potentials (E⁰) of nanoparticles. (a) Comparison of the voltammetry method with our approach for determining reduction potentials of metallic nanoparticles. (b) Equilibrated reaction between gold nanoparticles and a redox couple for determining their E⁰. (c) Redox equilibrium of AuBr₂^–/Au^NP_n and Fe^3+/2+ couple, and the complexation between CTA micelles and AuBr₂^–. (d and e) Time-lapsed UV–vis spectra (arrow indicates the reaction progress) and kinetic trace at plasmon resonance of a typical reaction between 10.9 nm nanoparticles and Fe³⁺. (f) Kinetic trace at the plasmon resonance of the reaction when the CTA⁺ concentration is increased from 0.1 to 1.9 mM.

Since standard reduction potentials (E⁰) provide an intrinsic redox characteristic of nanoparticles, the method developed in this Letter showcases its accuracy for investigating the particle-size-dependent property of E⁰. This trend was predicted by the Plieth equation, which states that the reduction potentials of smaller nanoparticles are lower than those of larger or bulk metals by a factor proportionally related to their total surface energy.⁹ Early work by Henglein estimated a significant drop in the E⁰ of Ag⁺/Ag⁰ from a bulk value of +0.799 V (vs NHE) down to lower values for silver nanoparticles, reaching −1.8 V for a single silver atom.¹⁰ Later study on the stability of silver nanoparticles in redox buffers confirmed a lower reduction potential for smaller sizes, and the drop in potentials follows a form of the Gibbs–Thomson equation.¹¹ Note that the Plieth equation is similar to the Gibbs–Thomson equation with the former developed specifically for electrochemical potentials and the latter for chemical potentials. Nevertheless, an accurate measurement of E⁰ for nanoparticles is crucial to establish this scaling law. The experimental E⁰ obtained for a wide size range by our Nernstian approach reveals the influence of ligand adsorption on the potentials as well as their particle-size-dependent trend.

Experimentally, E⁰ values were obtained by utilizing a redox reaction equilibrium, chemical assays, and the Nernst equation. To establish conditions for using the Nernst equation, the reaction between gold nanoparticles of each size and FeCl₃ was allowed to reach equilibrium as shown in the elementary reactions below (see also Figure 1c).

1

2

3

The net reaction is written as

4

where n is the number of gold atoms in individual nanoparticles, β = 10¹² is the formation constant of AuBr₂^–,¹² and K_m is the binding constant of AuBr₂^– to cetyltrimethylammonium micelles (CTA⁺_mic). NP and s denote the nanoparticle and solid forms of gold, respectively. Furthermore, the reaction products of gold are in the Au(I) oxidation state as shown by previous work, which confirmed that Au(I) complex, not Au(III), is the only gold ion product at the reaction equilibrium (see the SI).^13,14

Cetyltrimethylammonium bromide (CTAB, 1.1 mM) was used to drive reaction 1 as Br^– creates a stable complex with Au⁺ (≤0.25 mM) through reaction 2. As the gold nanoparticles were stabilized in cetyltrimethylammonium chloride (CTAC) stock solution, both CTAC (0.25–3.85 mM)¹⁵ and CTAB are involved in reaction 3. The counterion CTA⁺, dissociated from CTAC and CTAB, also affects reactions 1 and 2 as it creates a complex with AuBr₂^–. AuCl₂^– is not of concern as its formation constant is 3 orders of magnitude lower than that of AuBr₂^–.^12,14 When CTA⁺ is above the critical micelle concentration (CMC, ∼1 mM for CTAB or CTAC),¹⁶ oxidation of the gold nanoparticles by Fe³⁺ is favored due to the complexation between CTA⁺ micelles and AuBr₂^– (Figure 1f).¹⁷Figure 1c (top) shows the simple form of the redox reaction, but the reaction conditions always have CTA⁺ above the critical micelle concentration, and CTA_micAuBr₂ complexes (Figure 1c, bottom) must be accounted for as the final product. The entire reaction system can be treated as an electrochemical cell having two “half-cell” reactions (Figure 1b,c). At the equilibrium point of eq 4, the Gibbs free energy of the reaction and the imaginary E_cell (Figure 1b, see SI for the half-cell reactions) must be zero, as shown in eq 5.

5

Using the Nernst equation for eq 5, E⁰ of gold nanoparticles with their final sizes at the equilibrium can be determined as in the following (see the details of all terms in the SI):

6

Equation 6 offers E⁰ for the half reaction of Au⁺_(aq) + e^– + Au^NP_n–1(s) ⇌ Au^NP_n(s). E^°_Au⁺/AuNP values will approach the standard electrode potential of gold, E^°_{Au⁺/Au(bulk)} = 1.83 V (vs SHE),¹⁸ when the gold nanoparticle is large enough to behave like bulk gold. One important property of eq 6 is that it does not depend on the number of gold nanoparticles at the reaction equilibrium because they are in the solid phase. In other words, changing the number of particles only influences the number of gold atoms oxidized per particle, resulting in a different particle size at the reaction equilibrium. Therefore, if the number of gold nanoparticles used at the beginning of the reaction is different, the equilibrium (as described by eq 4) will shift to a new point to reflect the new equilibrium size. Thus, E^°_Au⁺/AuNP will also reflect the particle size at this new equilibrium but not the number of particles. This property allows us to determine and compare E^°_Au⁺/AuNP for various sizes, even though there are fewer particles in the reaction solutions for the larger sizes.

Each reaction solution started with one particular size within a range of 4.4–74 nm (Figure S1), and the corresponding size at reaction equilibrium was from 5.0 to 73 nm (Figure S4). Note that UV–vis spectroscopy was used to observe the reactions as they progressed to their equilibrium points (Figure 1d,e, and Figure S2). A control reaction in the absence of gold nanoparticles showed that no Fe²⁺ product was formed (Figure S3). We noticed that the Oswalt ripening became visible for the two smallest sizes due to the long reaction time, resulting in a small increase in the average size as determined by electron microscopy (see SI, Figure S5). This process may seem counterintuitive, but chemical assay and UV–vis spectroscopy proved that reaction 4 did occur, which would typically result in a decrease in the nanoparticle size. The explanation for this observation is the dissolution of some small particles and the growth of other particles during the ripening process, reducing the number of nanoparticles at reaction equilibrium. Additional evidence for this Oswalt ripening is the increased plasmonic absorption of the ripened particles in the reaction solution because the slightly larger particles effectively have a much larger extinction cross section than the smaller particles (Figure S2a,b).¹⁹ As noted above, the number of nanoparticles in a reaction solution does not affect a measured reduction potential, as long as we can determine the particle size at equilibrium and assign the potential to this size.

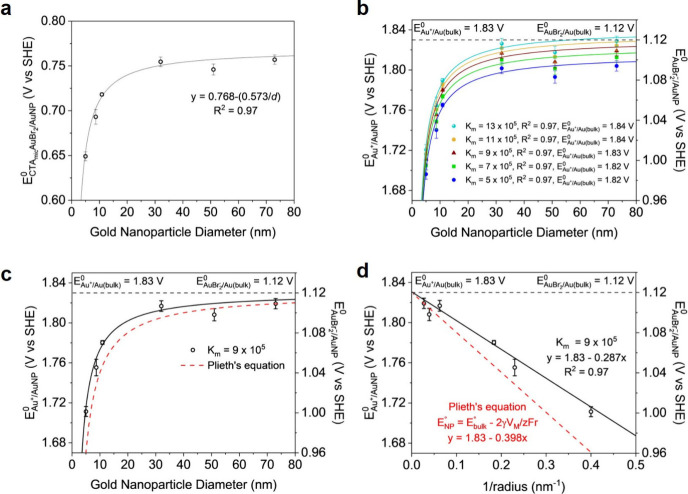
Once the reaction for each size reaches equilibrium, the activities and concentrations of Fe³⁺, Fe²⁺, CTA_micAuBr₂, and Br^– can be experimentally determined (see the SI) to calculate E^°_Au⁺/AuNP. Briefly, the Fe²⁺ concentration can be quantified by a chemical assay using the absorbance of the Fe(II)-phenanthroline complex and a standard curve. The Fe²⁺ concentration was then used to determine the concentrations of Fe³⁺, CTA_micAuBr₂, and Br^– at equilibrium. Furthermore, the extinction at the localized surface plasmon resonance of the gold nanoparticles was monitored to observe the reaction equilibrium but not necessarily to quantify the amount of elemental Au etched (see the SI). K_m is the only unknown parameter in eq 6. To estimate K_m, we randomly set E^°_Au⁺/AuNP in eq 6 for the 31.9 and 73 nm particles to the corresponding values of 1.805 and 1.819 V (vs SHE) predicted by the Plieth equation (see the SI). This step helps to narrow the search range for true K_m. Using experimental activities for rest parameters in eq 6 for these two particle sizes, the K_m was initially estimated as 6 × 10⁵ or 9 × 10⁵. To determine the most accurate K_m, we first tried five K_m values within the range from 5 × 10⁵ to 13 × 10⁵. Using eq 6 with these trial K_m values and corresponding experimental activities for all nanoparticle sizes, five sets of data were plotted in Figure 2b. We then fit these data to a A – B/d function (d is the nanoparticle diameter) and extrapolated E^°_Au⁺/AuNP to the bulk value. The fitting curve with K_m = 9 × 10⁵ gives the closest prediction of 1.83 V (vs SHE) for E^°_{Au⁺/Au(bulk)} of bulk gold (see Figure 2b and Table S4). In order to establish the above mathematical form of our fitting curves in Figure 2b, we initially calculated E^°_{CTAmicAuBr2/AuNP} at various particle sizes (see equation S3) as the calculation is straightforward from experimental activities. The calculated E^°_{CTAmicAuBr2/AuNP} follows an A – B/d function as shown in Figure 2a. Although the initially estimated K_m values relied on the Plieth equation, all the fitting curves did not. In principle, the K_m can be independently determined without referencing the Plieth equation if we scan K_m with a wider range. These results indicate that our method of measuring E⁰ can resolve its size dependence across a wide range without relying on any previous model. We also show that when concentrations, instead of activities, were used in the Nernst equation, the formal reduction potential E^0′ was quite comparable to E⁰ (see the SI). This indicates that E^0′ can be practically used in future studies with less concern about correcting concentrations for activities.

Figure 2.

Measuring standard reduction potential of colloidal gold nanoparticles with various size. (a) Reduction potential of gold nanoparticles when CTA_micAuBr₂ is the product. (b) Five trial K_m values were used to find the most accurate K_m. The curves were fitted into an E⁰ = A – B/d function, where A and B are the fitting parameters. (c) Comparison of our experimental data to Plieth equation. (d) Data in panel c are replotted as E⁰ vs 1/r for better visualization of the two slopes.

When E^°_Au⁺/AuNP is accurately determined for various particle sizes, not only the size but also the nature of the particle surface appears to dictate the reduction potential. Plieth derived an equation to account these two factors, where a nanoparticle and its bulk counterpart are treated as the two electrodes of an electrochemical cell.⁹ The lower reduction potential of the nanoparticles as compared to the bulk counterpart is related to the free energy creating the surface of the nanoparticle from the bulk metal (eq 7, aka the Plieth equation).

7

where E^°_{Au⁺/Au(bulk)} is the standard reduction potential of bulk gold; γ and V_M are the surface energy and molar volume of gold nanoparticles, respectively; z is the number of electrons involved in the reduction reaction; F is the Faraday constant; and r is the nanoparticle radius. The Plieth equation can also be further developed to account for the effect of charge on the reduction potential as nanoparticles can have excess charge.^1,20 However, further investigation confirms that our particles have a very small amount of charge and its effect on E⁰ is neglectable (see the SI).

Previous voltametric measurements also confirmed that the peak potentials for oxidizing silver or gold nanoparticles followed the Plieth equation.^4,21 However, extracting γ may not be ideal due to the previously mentioned limitations of this method. When using γ = 1.88 J m^–2 for bulk gold from Plieth’s work, our experimental data shows a deviation from this equation (Figure 2c,d). Figure 2d gives the experimental γV_M product of 1.38 × 10^–5 J m mol^–1, which is smaller than the original value that Plieth used (γV_M = 1.92 × 10^–5 J m mol^–1, V_{M(bulk gold)} = 1.021 × 10^–5 m³ mol^–1, and γ_(bulk gold)= 1.88 J m^–2). One possibility is the reduction of V_M for the nanoparticles, originating from a lattice contraction compared to the bulk counterpart. However, a lattice contraction of 1.74% was measured for an 8.6 nm gold nanoparticle in our sample. This translates into a 6.3% reduction of V_M, which is too small to explain for our data (see details in SI). Lattice contraction is more pronounced for particles with the size of a few nanometers and can be compensated by the interaction between the metal surface and ligand.²² The metal–ligand interaction weakens the metal–metal bond on the nanoparticle surface, reducing the surface tension and lattice contraction. Using this new V_M, the surface energy of our nanoparticles is 1.45 J m^–2, which is 22.9% lower than the value for clean surface of bulk gold.^9,23,24 The linear regression in Figure 2d indicates that the specific surface energy does not change within the particle sizes covered in this study. The lower surface energy of our colloidal nanoparticles can be attributed to ligand adsorption on the nanoparticle surfaces. Previous work on stability of silver nanoparticles also has a similar conclusion.¹¹ Surface energy modification by adsorbates could have a large effect on their E⁰.

In conclusion, the contactless method introduced here can be used to measure the surface energy and E° of gold nanoparticles. These are the two important thermodynamic quantities for understanding their physical and chemical properties. Furthermore, this method can be adapted to other nanoparticles as long as a redox reaction between the particles and a redox couple in solution is established, and the Nernst equation can be applied at reaction equilibrium to determine the standard reduction potentials of the nanoparticles.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.4c02998.

• Additional experimental details, gold nanoparticle synthesis, redox reaction conditions, chemical assay procedures, TEM images, UV–vis spectra, Nernst equation calculations, molar volume estimation, binding constant (K_m) calculations, and excess particle charge calculations (PDF)

• Transparent Peer Review report available (PDF)

Author Contributions

^# R.E. and D.V.C contributed equally to this work.

The authors declare no competing financial interest.